1 Introduction

It is believed that the expansion of the universe is accelerated with the passage of time. This is due to mysterious form of force called dark energy (DE) which possess enough negative pressure to put matter apart from each other. The confirmation of presence of this type of force is obtained through different observational study on this phenomenon (Perlmutter et al. 1998; Riess et al. 1998; Tegmark et al. 2004; Spergel et al. 2003). In order to analyze this accelerated expansion phenomenon in the presence of DE and its nature, different DE models have been put forward. The pioneer candidate of DE is cosmological constant, but its theoretical and observational values are inconsistent (Peebles 2003). Due to this reason, two alternative ways have been adopted, e.g., dynamical DE models and modified (or extra dimensional) theories of gravity. The detailed review about DE models as well as modified gravity is available in the references (Copeland et al. 2006; Nojiri and Odintsov 2007; Setare et al. 2007; Setare 2007; Setare and Jamil 2010a, 2010b; Amendola and Tsujikawa 2010; Clifton et al. 2012; Bamba et al. 2012).

Nowadays, the holographic dark energy (HDE) has attained much attraction because of its global property of the universe (a direct relationship with spacetime). This model is based on the holographic principle (Susskind 1995) and developed by Hsu (2004) and Li (2004) on the basis of Cohen et al. (1999) relation. This relation is about the vacuum energy of a system with specific size whose maximum amount should not exceed the black hole mass with the same size. The mathematical form of HDE is given by

$$ \rho_{\varLambda}=3\zeta^{2}M^{2}_pL^{-2}, $$
(1)

here ζ is the dimensionless HDE constant parameter and M p is the reduced plank mass. The interesting feature of HDE density is that it provides a relation between ultraviolet (bound of vacuum energy density) and IR (size of the universe) cutoffs. However, a controversy about the selection of IR cutoff of HDE has been raised since its birth. As a result, different people have suggested different expressions.

Moreover, Wei (2012) proposed a new DE model called as PDE on the basis of fact that black hole formation can be avoided through the strong repulsive force of the type of DE. It is also argued that phantom DE can play important role in this regard instead of other types of DE. This argument also coincided with the idea of Babichev et al. (2004), i.e., black hole mass reduces due to phantom accretion phenomenon. In the favor of accretion phenomenon, many analysis has been done (Babichev et al. 2008; Sharif and Abbas 2011; Jamil and Qadir 2011; Bhadra and Debnath 2012; Sharif and Jawad 2013). There is also present an analysis about the avoidance of event horizon in the presence of phantom-like DE (Lobo 2005a, 2005b; Sushkov 2005; Sharif and Jawad 2014). The PDE model has also been analyzed in different modified gravities (Sharif and Rani 2014; Chattopadhyay et al. 2014).

The proposal of Wei is also based on the prediction that phantom DE with strong negative pressure can push the universe towards the big-rip singularity where all the physical objects lose the gravitational bounds and finally dispersed. Moreover, Wei (2012) analyzed the effects of PDE model on the BH formation observational and theoretical ways by taking the Hubble horizon. We have analyzed this proposal in detail by choosing the different IR cutoffs through well-known cosmological parameters in flat and non-flat universes (Sharif and Jawad 2013a, 2013b, 2014).

The scalar field DE models also belong to the family of dynamical DE models which explain the DE phenomenon. A wide variety of these models exists in literature including quintessence, K-essence, tachyon, phantom, ghost condensates and dilaton (Amendola and Tsujikawa 2010). Also, the well-known theories such as the supersymmetric, string and M theories cannot describe potential of the scalar field independently. It would be interesting to reconstruct the potential of DE models so that the scalar fields may describe the cosmological behavior of the quantum gravity.

In the present paper, we provide the correspondence of interacting PDE (Hubble horizon as an IR cutoff) with different scalar field models in the flat FRW universe. Rest of the paper is organized as follows: Sect. 2 contains the basic scenario of interacting PDE and discussion of equation of state (EoS) parameter. In Sect. 3, we give the correspondence of interacting PDE with scalar field models. The last section contains the summary of the results.

2 Basic equations

In this section, we provide basic cosmological equations of interacting PDE with cold dark matter (CDM) and analyze the behavior of EoS parameter. We assume the flat FRW universe whose equation of motion is

$$ H^{2}=\frac{1}{3M_{p}^{2}}(\rho_{m} + \rho_{\varLambda}). $$
(2)

Here, ρ Λ and ρ m represent the energy density of DE and CDM, respectively, and H is the Hubble parameter. In terms of fractional energy densities, Eq. (2) turns out to be

$$\begin{aligned} \varOmega_{m}+\varOmega_{\varLambda}=1,\qquad \varOmega_{m}=\frac{\rho_{m}}{3M_{p}^{2}H^{2}},\qquad \varOmega_{\varLambda}=\frac{\rho_{\varLambda}}{3M_{p}^{2}H^{2}}. \end{aligned}$$
(3)

In this set up, we take the interaction of CDM and DE, so the equations of continuity become

$$\begin{aligned} &{\dot{\rho_{m}}+3H\rho_{m} = Q,} \end{aligned}$$
(4)
$$\begin{aligned} &{\dot{\rho_{\varLambda}}+3H\rho_{\varLambda}(1+ \omega_{\varLambda}) = -Q,} \end{aligned}$$
(5)

where \(\omega_{\varLambda}=\frac{p_{\varLambda}}{\rho_{\varLambda}}\) is EoS and Q represents the interaction parameter. Also, we take the interaction term as Q=3d 2 Hρ m where d 2 is interacting constant. Next, the PDE model is defined as follows

$$ \rho_{\varLambda}=3c^{2} m_p^{4-s}L^{-s}, $$
(6)

where c is constant interacting parameter and we choose the IR cutoff L=H −1 in the present work. By taking the time derivative of Eq. (6) and using Eq. (2), we get

$$ \dot{\rho_{\varLambda}} = -\frac{3}{2}c^{2}m_{p}^{2-s}sH^{s-1} \rho_{D}\bigl[H^{2-s}+\omega_{\varLambda}\bigr]. $$
(7)

In view of above equations, the EoS parameter becomes

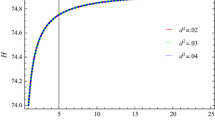
$$ \omega_{\varLambda} = \frac{m_{p}^{2-s}s-2b^{2}-2}{2-s\varOmega_{\varLambda}}. $$
(8)

We have plot ω Λ versus a numerically by taking initial value of H[1]=70 as shown in Fig. 1. Also, we assume three values of interaction parameter d 2=0, 0.4, 0.8 and other constant cosmological parameters are c=0.21, s=1, H 0=70, Ω m0=0.27. For d 2=0, 0.4, it can be observed that the EoS parameter starts from quintessence DE era and goes towards phantom DE era by evolving the vacuum DE era. Also, the trajectory corresponding to d 2=0.8, the EoS parameter corresponds to phantom region forever. Hence, PDE model in this scenario also gives support to PDE phenomenon.

Fig. 1
figure 1

Plot of ω Λ versus a

Full size image

3 Reconstruction of scalar field models

In this section, we provide the correspondence of interacting PDE with Hubble horizon with different scalar field models through correspondence phenomenon. Scalar field models have been developed through particle physics as well as string theory and nowadays these are used as a DE candidate.

3.1 Quintessence model

The quintessence scalar field models provide the scaling and attractor solutions which help to explain the phenomenon of accelerated expansion of the universe (Copeland et al. 2006). The energy density and pressure are defined as

$$\begin{aligned} \rho_{q}=\frac{1}{2}\dot{\phi^{2}}+V( \phi),\qquad p_{q} = \frac{1}{2}\dot{\phi^{2}}-V(\phi). \end{aligned}$$
(9)

This equation gives the EoS parameter as

$$ \omega_{q}=\frac{\dot{\phi}^{2}-2V(\phi)}{\dot{\phi}^{2}+2V(\phi)}. $$
(10)

The potential and the kinetic energy of quintessence scalar field model can be written as

$$\begin{aligned} &{V(\phi)=\frac{(1-\omega_{q})\rho_{q}}{2},} \end{aligned}$$
(11)
$$\begin{aligned} &{\dot{\phi^{2}}=(1+\omega_{q})\rho_{q}.} \end{aligned}$$
(12)

In order to obtain V(ϕ) and \(\dot{\phi^{2}}\) in terms of scale factor, we use correspondence phenomenon i.e., ρ q =ρ Λ and ω q =ω Λ . This gives

$$\begin{aligned} &{\dot{\phi^{2}} = 3m_{p}^{4-s}c^{2} \biggl(1+\frac{m_{p}^{2-s}s-2d^{2}-2}{2-s\varOmega _{\varLambda}} \biggr)H^{s},} \end{aligned}$$
(13)
$$\begin{aligned} &{V(\phi) = \frac{3c^{2}m_{p}^{4-2s}}{2} \biggl(\frac{\varOmega_{\varLambda }}{c^{2}} \biggr)^{\frac{s}{s-2}} \biggl(1-\frac{m_{p}^{2-s}s-2d^{2}-2}{2-s\varOmega_{\varLambda}} \biggr).} \end{aligned}$$
(14)

Using the value of \(\varOmega_{\varLambda}=\frac{\rho_{\varLambda}}{3m_{p}^{2}H^{2}}\), we get

$$\begin{aligned} \dot{\phi} = \sqrt{\biggl(1+\frac{m_{p}^{2-s}s-2d^{2}-2}{2-s\varOmega_{\varLambda }}\biggr) \bigl(3c^{2}m_{p}^{4-s}\bigr) \biggl( \frac{\varOmega_{\varLambda}}{c^{2}m_{p}^{2-s}}\biggr)^{\frac{s}{s-2}}}. \end{aligned}$$
(15)

We solve above differential equation for scalar field ϕ(a) and plot it against scale factor a as shown in Fig. 2. The constants parameters are same as used in previous section. It can be seen that quintessence scalar field shows increasing behavior with the increase of scale factor. This increasing behavior exhibits the decreasing behavior of kinetic energy in this scenario. We have also plotted the potential energy V(ϕ) versus scalar field as shown in Fig. 3. These figures show that V(ϕ) exhibits decreasing behavior in this case predicted the consistency between them. The potential V(ϕ) in terms of ϕ attains greater value initially which corresponds to accelerated expansion of the universe and it is consistent behavior with phase space analysis (Copeland et al. 2006). The behavior of V(ϕ) in terms of ϕ is also consistent with the universe accelerated expansion phenomenon because quintessence potential goes to positive and non-zero minima but kinetic energy goes to zero (Eq. (10)).

Fig. 2
figure 2

Plot of ϕ(a) versus a in quintessence model

Full size image
Fig. 3
figure 3

Plot of V(a) versus ϕ(a) in scalar field model

Full size image

3.2 Tachyon model

It is argued that the rolling tachyon condensates (a class of string theories) give useful cosmological consequences. In this way, Sen (2002a, 2002b) investigated that a pressureless gas contains finite energy density (shows resemblance with classical dust) and it can be obtained from the decay of D-branes. The interpolation of EoS parameter between −1 to 0 of the rolling tachyon is an interesting result of this model (Copeland et al. 2006). This important feature is used in many attempts to build a feasible cosmological model (Mazumdar et al. 2001), which produces some problems about density perturbations and reheating of tachyon inflation in open string models. It is believed that tachyon model can be used as a candidate of DE. The energy density and the pressure of tachyon has the following form

$$\begin{aligned} \rho_{t}=\frac{V(\phi)}{\sqrt{1-\dot{\phi}^{2}}},\qquad p_{t} = -V(\phi)\sqrt{1-\dot{\phi}^{2}}. \end{aligned}$$
(16)

Thus EoS parameter of tachyon model is

$$\begin{aligned} \omega_{t} = \frac{p_t}{\rho_t} = \dot{\phi}^{2}-1. \end{aligned}$$
(17)

Through correspondence phenomenon, we get

$$\begin{aligned} &{\dot{\phi} = \sqrt{1+\frac{m_{p}^{2-s}s-2b^{2}-2}{2-s\varOmega_{\varLambda}}},} \end{aligned}$$
(18)
$$\begin{aligned} &{V(\phi) = 3c^{2}m_{p}^{4-s} \biggl(\frac{\varOmega_{\varLambda}}{c^{2}m_{p}^{2-s}} \biggr)^{\frac{s}{s-2}} \sqrt{ \frac{2-m_{p}^{2-s}s+2d^{2}}{2-s\varOmega_{\varLambda}}}.} \end{aligned}$$
(19)

In this case, the plot of scalar field ϕ(a) versus a is shown in Fig. 4 by keeping the same values of constant parameter. It can be observed from Fig. 4 that ϕ(a) shows increasing behavior with the increase of a. The increasing behavior of ϕ exhibits the decreasing kinetic energy of the tachyon model in the later epoch. The vanishing kinetic energy \((\dot{\phi}\rightarrow0)\) indicates the vacuum energy to drive the accelerated expansion of the universe which is obvious from Eq. (17). Also, we note from Eq. (16) that the strong energy condition (ρ+3p≥0) takes the form \(\rho_{t}+3p_{t}=-\frac{2V(\phi)}{\sqrt{1-\dot{\phi}^{2}}}(1-\frac{3}{2}\dot {\phi}^{2})\) which violates for the small values of \(\dot{\phi}\) and leads to expansion with acceleration (Copeland et al. 2006). The plot of tachyon potential against scalar field is shown in Fig. 5. It can be seen that the tachyon potential shows decreasing behavior and becomes more steeper with the increase of d 2. This behavior obeys inverse square power law condition that corresponds to scaling solutions (Copeland et al. 2006).

Fig. 4
figure 4

Plot of ϕ(a) versus a in tachyon field

Full size image
Fig. 5
figure 5

Plot of V(a) versus ϕ(a) in tachyon field

Full size image

3.3 K-essence model

Quintessence depends upon the potential energy of scalar field which provides information about the late time cosmic acceleration. Armendáriz-Picón et al. (1999) proposed the concept of K-inflation (means kinetic energy driven inflation) in order to discuss early universe inflation at high energies, while Chiba et al. (2000) introduced this model for DE purposes. Armendáriz-Picón et al. (2000) extended it for the generalized form of Lagrangian and named it as “K-essence”. The EoS parameter for K-essence model is

$$ \omega_{k}=\frac{1-\chi}{1-3\chi} $$
(20)

with

$$\begin{aligned} \rho_{k}=V(\phi) \bigl(-\chi+3\chi^{2}\bigr), \qquad p_{k}=V(\phi) \bigl(-\chi+\chi^{2}\bigr), \end{aligned}$$
(21)

where \(\chi=\frac{1}{2}\dot{\phi}^{2}\). Through correspondence phenomenon, one can get

$$\begin{aligned} \chi= \frac{\omega_{\varLambda}-1}{3\omega_{\varLambda}-1}, \end{aligned}$$
(22)

which turns out to be

$$\begin{aligned} \chi=\frac{m_{p}^{2-s}s-2b^{2}-4+s\varOmega_{\varLambda }}{3m_{p}^{2-s}s-6d^{2}-8+s\varOmega_{\varLambda}}. \end{aligned}$$
(23)

By using the relation \(X=\frac{\dot{\phi}^{2}}{2}\) and Eq. (23), we obtain

$$\begin{aligned} {\dot{\phi}^{2}} = \frac{4b^{2}-2m_{p}^{2-s}s+8-2s\varOmega_{\varLambda }}{3m_{p}^{2-s}s-6b^{2}-8+s\varOmega_{\varLambda}} \end{aligned}$$
(24)

and

$$\begin{aligned} V(\phi)=\frac{3c^{2}m_{p}^{4-s}(\frac{\varOmega_{\varLambda }}{c^{2}m_{p}^{2-s}})^{\frac{s}{s-2}}}{ (\frac{m_{p}^{2-s}s-2b^{2}-4+s\varOmega_{\varLambda }}{3m_{p}^{2-s}s-6b^{2}-8+s\varOmega_{\varLambda}} ) (3({\frac{m_{p}^{2-s}s-2b^{2}-4+s\varOmega_{\varLambda }}{3m_{p}^{2-s}s-6b^{2}-8+s\varOmega_{\varLambda}}})-1 )}. \end{aligned}$$
(25)

The plot of K-essence scalar field versus a (numerically) is shown in Fig. 6 which shows increasing behavior and hence exhibits the decreasing behavior of corresponding kinetic energy. It can be observed that the EoS of tachyon DE model is compatible with the accelerated expansion of the universe in the range \(\frac{1}{3}<\chi<\frac{2}{3}\). Also in this framework, Fig. 7 shows that χ lies in this interval for all cases of d 2. For \(\chi<\frac{1}{2}\), it gives phantom DE era which corresponds to late time attractor (Chiba et al. 2000). Also, Fig. 8 indicates that the K-essence potential decreases with the increase of the field ϕ initially, and then shows increasing behavior after short interval.

Fig. 6
figure 6

Plot of ϕ(a) versus a in K-essence model

Full size image
Fig. 7
figure 7

Plot of χ versus a in K-essence model

Full size image
Fig. 8
figure 8

Plot of V(a) versus ϕ(a) in K-essence model

Full size image

3.4 Dilaton field

The dilaton field is used as an alternative candidate to explain the DE puzzle. Its pressure and energy density are (Copeland et al. 2006)

$$\begin{aligned} p_d = -X+\alpha e^{\lambda\phi}\chi^{2}, \qquad\rho_d = -X+3\alpha e^{\lambda\phi}X^{2}. \end{aligned}$$
(26)

Here λ and α are positive constants and \(X=\frac{\dot{\phi}^{2}}{2}\). The EoS parameter in this model becomes

$$\begin{aligned} \omega_{d} = \frac{1-\alpha e^{\lambda\phi}X^{2}}{1-3\alpha e^{\lambda\phi}X^{2}}. \end{aligned}$$
(27)

To establish the correspondence between PDE and dilaton field, we equate their EoS parameters, i.e. ω d =ω Λ , which gives

$$\begin{aligned} \chi e^{\lambda\phi} = \frac{1-\omega_{\varLambda}}{\alpha (1-3\omega_{\varLambda})}. \end{aligned}$$
(28)

We plot this expression against a by assuming α=1.5 as shown in Fig. 9. This represents that the kinetic energy term \(e^{b_{2}\phi}\chi\) of dilaton scalar field lies in the interval \((\frac{2}{9},\frac{4}{9})\) (where EoS parameter ω d predicts the accelerated expansion of the universe). This shows that the PDE version of dilaton field is consistent with present observations of the universe. After some simplification, we get

$$\begin{aligned} &{\phi(a)} \\ &{\quad=\frac{2}{\lambda}\ln \biggl(1} \\ &{\qquad{}+\int\frac{\lambda}{2aH}\sqrt {\frac {8-2sc^{2}H^{s-2}-2m_{p}^{2}s +4d^{2}}{\alpha(2-sc^{2}H^{s-2}-3m_{p}^{2}s+6b^{2}+6)}}da \biggr).} \end{aligned}$$
(29)

Its graphical presentation is shown in Fig. 10 which exhibits direct proportionality with respect to a leading to the scaling solutions for dilaton model (Piazza and Tsujikawa 2004).

Fig. 9
figure 9

Plot of Xe λϕ versus a in dilaton field

Full size image
Fig. 10
figure 10

Plot of ϕ(a) versus a in dilaton field

Full size image

4 Conclusion and discussion

In this work, we have discussed the correspondence of interacting PDE (Hubble horizon as an IR cutoff) with different scalar field models in the framework of flat FRW universe. The scalar field models of DE (like quintessence, tachyon, K-essence and dilaton) are effective theories of an underlying theory of DE. So, we have constructed the scalar field as well as corresponding scalar potentials which describe the dynamics of the scalar fields graphically. The physical interpretations of all the DE models are summarized as follows.

The plot ω Λ versus a numerically by taking initial value of H[1]=70 as shown in Fig. 1. Also, we have assumed three values of interaction parameter d 2=0, 0.4, 0.8 and other constant cosmological parameters are c=0.21, s=1, H 0=70, Ω m0=0.27. For d 2=0, 0.4, it can be observed that the EoS parameter starts from quintessence DE era and goes towards phantom DE era by evolving the vacuum DE era. Also, the trajectory corresponding to d 2=0.8, the EoS parameter corresponds to phantom region forever. Hence, PDE model in this scenario also gives support to PDE phenomenon.

The evolution trajectory of quintessence scalar field shows increasing behavior with the increase of scale factor as shown in Fig. 2. This increasing behavior exhibits the decreasing behavior of kinetic energy in this scenario. We have also plotted the potential energy V(ϕ) versus scalar field as shown in Fig. 3. These figures show that V(ϕ) exhibits decreasing behavior in this case predicted the consistency between them. The potential V(ϕ) in terms of ϕ attains greater value initially which corresponds to accelerated expansion of the universe and it is consistent behavior with phase space analysis (Copeland et al. 2006). The behavior of V(ϕ) in terms of ϕ is also consistent with the universe accelerated expansion phenomenon because quintessence potential goes to positive and non-zero minima but kinetic energy goes to zero (Eq. (10)).

Figure 4 shows increasing behavior of ϕ(a) with the increase of a. The increasing behavior of ϕ exhibits the decreasing kinetic energy of the tachyon model in the later epoch. The vanishing kinetic energy \((\dot{\phi}\rightarrow0)\) indicates the vacuum energy to drive the accelerated expansion of the universe which is obvious from Eq. (16). Also, we note from Eq. (16) that the strong energy condition (ρ+3p≥0) takes the form \(\rho_{t}+3p_{t}=-\frac{2V(\phi)}{\sqrt{1-\dot{\phi}^{2}}}(1-\frac{3}{2}\dot {\phi}^{2})\) which violates for the small values of \(\dot{\phi}\) and leads to expansion with acceleration (Copeland et al. 2006). The plot of tachyon potential against scalar field is shown in Fig. 5. It can be seen that the tachyon potential shows decreasing behavior and becomes more steeper with the increase of d 2. This behavior obeys inverse square power law condition that corresponds to scaling solutions (Copeland et al. 2006).

The trajectory of K-essence scalar field versus a (numerically) is shown in Fig. 6 which shows increasing behavior and hence exhibits the decreasing behavior of corresponding kinetic energy. It can be observed that the EoS of tachyon DE model is compatible with the accelerated expansion of the universe in the range \(\frac{1}{3}<\chi<\frac{2}{3}\). Also in this framework, Fig. 7 shows that χ lies in this interval for all cases of d 2. For \(\chi<\frac{1}{2}\), it gives phantom DE era which corresponds to late time attractor (Chiba et al. 2000). Also, Fig. 8 indicates that the K-essence potential decreases with the increase of the field ϕ initially, and then shows increasing behavior after short interval.

We have also plotted the kinetic energy of dilaton model against a by assuming α=1.5 as shown in Fig. 9. This represents that the kinetic energy term \(e^{b_{2}\phi}\chi\) of dilaton scalar field lies in the interval \((\frac{2}{9},\frac{4}{9})\) (where EoS parameter ω d predicts the accelerated expansion of the universe). This shows that the PDE version of dilaton field is consistent with present observations of the universe. The dilaton scalar field have shown in Fig. 10 which exhibits direct proportionality with respect to a leading to the scaling solutions for dilaton model (Piazza and Tsujikawa 2004).