1 Introduction

Independent and huge number of cosmological observations confirm that the current Universe undergoes acceleration expansion [1,2,3,4]. This epoch of the Universe is the one of the mysterious puzzles in modern cosmology. Nowadays, there is a general consensus among cosmologists about of the existence extra and unknown field so-called dark energy, which onsets trigger of current era. Exploring general relativity reveals that such field carries negative pressure, i.e., \(p < 0\) [5]. There is the wide spectrum of models proposed to handle the dark energy. The cosmological constant is one of pioneer models which satisfies observations [6]. However, this model suffers from coincidence and fine-tuning problems [7]. Former problem traces back to current values of the densities of dark energy and matter in which they are in same order of magnitude, \(\rho_X /\rho_m \sim {{\mathcal{O}}}(1)\). This indicates we are in a special period of the cosmic history that requires very special initial conditions in the early Universe. the corresponding ‘why now’ question constitutes the cosmological ‘coincidence problem’ while the last problem is turning back to duality between magnitude of the cosmological constant according to observations and zero-energy level of spacetime. Quantum mechanical calculations reveals that the sum of the all vacuum modes below an ultraviolet cutoff at the Planck scale given value of the vacuum energy density \(\rho_{\Lambda } \sim 10^{112} \,{\text{erg}}/{\text{cm}}^3\). This exceeds the cosmologically observed value of \(\rho_{\Lambda } \sim 10^{ - 8} \,{\text{erg}}/{\text{cm}}^3\) by about 120 orders of magnitude.

To alleviates these problems, there is a dozen different approaches are suggested. Using modified theories of gravity is one of these approaches in which the standard Einstein-Hilbert action gets more terms built by Riemann tensor and its derivatives [8,9,10,11,12], mixing matter and geometry as linear and or non-linear methods [13, 14] and or introducing non-Einsteinian matter field [15, 16].

In another approach, there is a hypothesis known as the holographic principle [17], which plays key role in quantum gravity and inspired by the investigation of thermodynamics of black hole [18]. According to this principle all of the information contained in a volume of space can be given as a hologram, which corresponds to a theory locating on the boundary of that space. Thus, and in following of this principle the short distance cut-off is related to a long-distance cut-off through \(l^3 \rho_0 \le \ell m_P^2\) when \(\rho_0\) denotes the quantum zero-point energy density [19]. Hence, the largest (infrared cut-off) length allowed one to have:

$$ \rho_0 = 3m_P^2 c^2 \ell^{ - 2} . $$
(1)

where \(c\) presents an arbitrary constant, and \(m_P\) is the reduced Planck mass. This holographic model has been widely used in cosmology, especially for description of dark energy field and it is commonly known as holographic dark energy [20]. This version of dark energy is well-fixed with observations. However, selecting valuable cut-off length \(\ell\) is one challenges in this model of dark energy. For instance, as proposed in [21, 22], one may scale cut-off length with Hubble parameter, i.e., \(\ell \sim H^{ - 1}\). As result, the fine-tuning problem is alleviated by scaling the density of dark energy using the cosmological scale rather than the Planck length. However, such selection for cut-off length shows that dark energy evolves like pressureless matter during expansion of the Universe, \(\omega_X = 0\) and thus it cannot illustrate late time acceleration epoch [23]. In another possible model, the infrared cut-off length may be scaled by future event horizon which describes the thermal history of the Universe, with the sequence of matter and dark energy eras [24]. Furthermore, it is shown that this model predicts the observed current acceleration of the Universe. However, this kind of cut-off length displays the causality problem [25]. In another attempt, Granda and Oliveros have proposed other form of cut-off \(\ell\) in which in addition to the square of the Hubble parameter, it also includes the time derivative of the Hubble parameter, namely [26]

$$ \ell = \left( {\alpha H^2 + \beta \dot{H}} \right)^{ - 1/2} . $$
(2)

in which \(\alpha\) and \(\beta\) are two free parameters of model. This cut-off succeeds to avoid the causality problem and also explain current Universe expansion. Recently, authors through considering the length of particle horizon and its second time derivative derived this cut-off, theoretically [27]. Moreover, such infrared cut-off can unify primary (inflation) and late time acceleration phases as single field [28].

In this paper and in following expanding applications of new modified theory of gravity so-called ‘non-conserved theory’, it is worthwhile to analyze this version of holographic dark energy in cosmology context.

The article is organized as follows: In Sect. 2 we revisited the non-conserved theory of gravity, briefly. Section 3 is allocated to investigate Granda–Oliveros cut-off length (2) and its application in evolution of the late time Universe for non-interaction and interaction scenarios. The remarks given in Sect. 4.

2 Revisite non-conserved theory

The transformation of heat and temperature in relativity theory under the Lorentz group is one of the unsolved issues and opening topics in this theory. For instance, Einstein and Planck proposed [29, 30]

$$ \delta Q = \delta Q_0 \gamma^{ - 1} ,\quad T = T_0 \gamma^{ - 1} , $$
(3)

while Ott and Arzelies proposed other transformation form [31, 32]

$$ \delta Q = \delta Q_0 \gamma ,\quad T = T_0 \gamma . $$
(4)

where \(\delta Q\) and \(T\) denote heat and temperature, respectively, the variables with subscript 0 represent those observed in the comoving frame, and \(\gamma\) is the Lorentz factor. In addition to these options, Landsberg suggested that heat and temperature behave as absolute parameters and thus comoving and independent observers measure same heat and temperature [33, 34]. However, just two first options (3) and (4) can satisfy a relativistic Carnot cycle [35]. The covariant form of relativity theory, in particular, may be essential to formulate relativistic laws of thermodynamics. In this context, one of the pioneer attempts given by Israel and collaborators [36]:

$$ \sum \limits_i S_{ i,\mu }^\mu = - \sum \limits_i \left( { \sum \limits_j \alpha_{ji} J_{ ji,\mu }^\mu + \beta_{\nu i} {{\mathcal{T}}}_{i,\mu }^{\mu \nu } } \right) $$
(5)

where number of 4-vector \(J_{ji}^\mu = n_{ji} u^\mu\), representing the flux densities of conserved charges \(j\) for component \(i\)-th and \(S_i^\mu\) expresses the 4-flux of entropy of fluid \(i\)-th. \(\beta_\nu = u_\nu /T_0\) presents the inverse temperature 4-vector proposed by Van Kampen [37], and \(\alpha_j = \zeta_j /T_0\). The parameter \(\zeta_j\) denotes the relativistic injection energy or chemical potential per particle of type \(j\), related to its classical counterpart by:

$$ \zeta_j = m_j + \zeta_j^{(classic)} . $$
(6)

It is to be noted that the 4-vector \(S^\mu\) for the flux of entropy behaves in similar way to the 4-vector for the flux of particle number. So, like the particle number that is scalar for comoving observer, it is shown that entropy in its comoving frame is a scalar as well [38]. As result, this model is not in conflict with standard expression of thermodynamical expression only when it is considered in comoving frame. Relation (5) shows that not only Rastall’s idea is true in curved spacetime, but is valid even in Minkowskian geometry when flux of energy–momentum tensor given as evolution in entropy and temperature of whole system.

To expand this model to curved geometry, one just need to apply principle of the general relativity [39],

$$ \sum \limits_i S_{ i;\mu }^\mu = - \sum \limits_i \left( { \sum \limits_j \alpha_{ji} J_{ ji;\mu }^\mu + \beta_{\nu i} {{\mathcal{T}}}_{i;\mu }^{\mu \nu } } \right) $$
(7)

in which usual (scalar) derivative replaced by covariant derivative. Hence, after some manipulations, the field equations derived such as

$$ G_{\mu \nu } - \kappa^{\prime} \sum \limits_i u_{\nu_i } \left( {T_0 S_{\mu_i } + \sum \limits_j \zeta_{j_i } J_{j\mu_i } } \right) = \kappa^{\prime} \sum \limits_i {{\mathcal{T}}}_{\mu \nu_i } $$
(8)

where \(\kappa^{\prime}\) is proportional constant. Taking covariant derivative of above field equations and using \(G_{\mu \nu ;\mu } = 0\) recasts Eqs. (8) to (7). Defining non-conserved term for each component participated in our system as

$$ {{\mathcal{E}}}_{\mu \nu } = u_\nu \left( {T_0 S_\mu + \sum \limits_j \zeta_j J_{j\mu } } \right) $$
(9)

let one to have compact form for field Eqs. (8), namely

$$ G_{\mu \nu } - \kappa^{\prime} \sum \limits_i {{\mathcal{E}}}_{\mu \nu_i } = \kappa^{\prime} \sum \limits_i {{\mathcal{T}}}_{\mu \nu_i } $$
(10)

which shows each fluid (component) plays explicit role in field equations. Summation on all different components participated in system (summation on index \(i\)), yields,

$$ G_{\mu \nu } - \kappa^{\prime} {{\mathcal{E}}}_{\mu \nu }^{[e]} = \kappa^{\prime} T_{\mu \nu }^{[e]} . $$
(11)

where we denote the effective terms \({{\mathcal{E}}}_{\mu \nu }^{[e]}\) and \(T_{\mu \nu }^{[e]}\) through

$$ \sum \limits_i X_{\mu \nu_i } = X_{\mu \nu }^{[e]} $$
(12)

when \(X = {{\mathcal{E}}}\) and or \(T\). Since this field equations must shrink to standard Einstein field equations when non-conserved term ignored, without lose generality one can assume \(\kappa^{\prime} = \kappa\) [39].

In the follows we assume that the Universe is homogenous and isotropic medium and describe by Friedmann–Robertson–Walker metric

$$ ds^2 = - dt^2 + a^2 \left( {\frac{dr^2 }{{1 - kr^2 }} + r^2 d\theta^2 + r^2 sin^2 \theta d\phi^2 } \right). $$
(13)

where \(a = a(t)\) is the cosmic scale factor and \(k = 0\), 1 and − 1 correspond to flat, close, and open Universe, respectively. Observations confirm that the Universe is flat and thus we assume \(k = 0\). With aid of this assumption and using field Eqs. (13), the Friedmann equations become

$$ 3H^2 = \kappa \left( {\rho_m + {{\mathcal{E}}}_{tt}^{[e]} + \rho_X } \right), $$
(14)
$$ 2\dot{H} + 3H^2 = - \kappa p_X . $$
(15)

in which we consider matter as dust field and subscripts \(m\) and \(X\) denotes matter and dark energy fields, respectively.

With these Friedmann equations at hand, we will consider late-time Universe for non-interaction and interaction scenarios in next two sections while dark energy density given Eq. (2),

$$ \rho_X = \alpha H^2 + \beta \dot{H}, $$
(16)

At the end of this section, we encourage interested readers to see main paper of non-conserved theory of gravity to review and check the effects of the cosmological constant and also evolution of the Universe in inflation era [39].

3 Late time cosmology

In this section we will consider Friedmann Eqs. (14) and (15) for dark energy density given by Eq. (16) for two non-interaction and interaction scenarios.

Plugging Eq. (16) into first Friedmann Eq. (14) yields

$$ 3H^2 = \kappa \left( {\rho_m + {{\mathcal{E}}}_{tt}^{[e]} + \alpha H^2 + \frac{\beta }{2}\frac{dH^2 }{{dx}}} \right), $$
(17)

where we use e-folding number \(x = {\text{ln}}(a)\).

To solve this differential equation to find explicit form of Hubble parameter one should have exact form of non-conservation term \({{\mathcal{E}}}_{tt}^{[e]}\). Hence, considering Eq. (9) reveals that it includes two parts, \(T_0 S_t\) and all interactions among particles. Keeping the second law of thermodynamics shows that \(T_0 S_t\) must grow up with time, and thus it can be given by \(e^{\gamma x}\) in which \(\gamma > 0\), while due to relation (6), the second part is proportional to density of matter field, namely

$$ \sum \limits_j \zeta_j J_{jt} \propto \rho_m $$
(18)

Consequently, and with these assumptions for expanding Universe, we may suggest that

$$ {{\mathcal{E}}}_{tt}^{\left[ e \right]} = {{\mathcal{E}}}_0 e^{\gamma x} . $$
(19)

where \({{\mathcal{E}}}_0\) is proportional constant. This selection illustrates that non-conserved term is depending on evolution of first part of Eq. (9) rather than its second one in late time expansion; interaction among different particles is not tangible effects in current Universe.

Consequently, using Eqs. (19) into (17), one obtains

$$ H^2 = \frac{{\kappa \rho_{m0} }}{3}e^{ - 3x} + \frac{{\kappa {{\mathcal{E}}}_0 }}{3}e^{\gamma x} - \frac{{\rho_{m0} \left( {3\alpha - 2\beta } \right)\kappa^2 }}{{18 + \kappa \left( {9\alpha - 6\beta } \right)}}e^{ - 3x} + \frac{{{{\mathcal{E}}}_0 \left( {\alpha \gamma + 2\beta } \right)\kappa^2 }}{{18 - \kappa \left( {3\alpha \gamma + 6\beta } \right)}}e^{\gamma x} + c_0 e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\alpha \kappa }x} . $$
(20)

where \(c_0\) is the integration constant. Comparing Eq. (20) with Eq. (14) suggests the density of dark energy as

$$ \rho_X = - \frac{{\rho_{m0} \kappa \left( {3\alpha - 2\beta } \right)}}{{6 + \kappa \left( {3\alpha - 2\beta } \right)}}e^{ - 3x} + \frac{{{{\mathcal{E}}}_0 \kappa \left( {\alpha \gamma + 2\beta } \right)}}{{6 - \kappa \left( {\alpha \gamma + 2\beta } \right)}}e^{\gamma x} + \frac{3c_0 }{\kappa }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\alpha \kappa }x} . $$
(21)

It shows density of dark energy includes three parts: first part is function of matter evolution while second part is depending on non-conservation term and third part can be proposed as the interior interaction between matter and non-conservation term.

Calculating continuity equation from Eqs. (14) and (15) can help us to find corresponding pressure for density (21). In this case, taking derivative with respect to e-folding number from first Friedmann Eq. (14) and plugging its result into Eq. (15) gives continuity equation as follows:

$$ \rho_m^{\prime} + {{\mathcal{E}}}_{tt}^{[e]^{\prime} } + \rho_X^{\prime} + 3\left( {\rho_m + {{\mathcal{E}}}_{tt}^{\left[ e \right]} + \rho_X + p_X } \right) = 0, $$
(22)

where prime denotes derivative with respect to \(x\).

To reconstruct standard density of matter, one may decouple above equation like

$$ \rho_m^{\prime} + 3\rho_m = Q, $$
(23)
$$ {{\mathcal{E}}}_{tt}^{[e]^{\prime} } + \rho_X^{\prime} + 3\left( {{{\mathcal{E}}}_{tt}^{\left[ e \right]} + \rho_X + p_X } \right) = - Q. $$
(24)

where \(Q\) represents the mutual interaction between dark energy and matter field. With some computations, one finds:

$$ p_X = - \frac{1}{3}\left( {Q + {{\mathcal{E}}}_{tt}^{\left[ e \right]^{\prime} } + \rho_X^{\prime} } \right) - {{\mathcal{E}}}_{tt}^{\left[ e \right]} + \rho_X . $$
(25)

As shown, pressure of dark energy depends on interaction term \(Q\). In this level of our study, it is worthwhile to explore model in two different scenarios, non-interaction and interaction models in two following subsections.

3.1 Non-interaction model

In the lack of enough microscopic evidences around interaction term, one may attempt to consider field Eqs. (14) and (15) when \(Q = 0\), non-interaction model. Hence, when density (21) is used, the pressure of dark energy given by

$$ p_X = - \frac{{c_0 \left( {6 + \kappa \left( {3\alpha - 2\beta } \right)} \right)}}{\alpha \kappa^2 }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\alpha \kappa }x} - \frac{{2{{\mathcal{E}}}_0 \left( {3 + \gamma } \right)}}{{6 - \kappa \left( {\alpha \gamma + 2\beta } \right)}}e^{\gamma x} . $$
(26)

while using Eq. (23) yields \(\rho_m = \rho_{m0} e^{ - 3x}\).

In cosmology context, there are three essential parameters play key roles at late-time. One of these parameters is the dimensionless one calculating through dividing pressure of dark energy by its corresponded density, i.e., \(\omega_X = p_X /\rho_X\). This parameter so-called ‘equation of state’ illustrates general behavior of dark energy during expansion of the Universe,

$$ \omega_X = \frac{{ - \frac{{c_0 \left( {6 + \kappa \left( {3\alpha - 2\beta } \right)} \right)}}{\alpha \kappa^2 }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\alpha \kappa }x} - \frac{{2{{\mathcal{E}}}_0 \left( {3 + \gamma } \right)}}{{6 - \kappa \left( {\alpha \gamma + 2\beta } \right)}}e^{\gamma x} }}{{ - \frac{{\rho_{m0} \kappa \left( {3\alpha - 2\beta } \right)}}{{6 + \kappa \left( {3\alpha - 2\beta } \right)}}e^{ - 3x} + \frac{{{{\mathcal{E}}}_0 \kappa \left( {\alpha \gamma + 2\beta } \right)}}{{6 - \kappa \left( {\alpha \gamma + 2\beta } \right)}}e^{\gamma x} + \frac{3c_0 }{\kappa }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\alpha \kappa }x} }}. $$
(27)

Recent observations reveals that this parameter for current time, \(x = 0\), is around \(\omega_{X0} \approx - 1\) [40]. Moreover, defining fractional density

$$ {\Omega }_m = \frac{\kappa \rho_m }{{3H^2 }}, $$
(28)

and Eq. (27) let us to constraint our model with current values. Hence, with aid of Eq. (17), we find out

$$ \beta = \frac{{{{\mathcal{E}}}_0 \left( {\alpha \kappa - 2} \right)}}{2H_0^2 } + \frac{{3\left( {2 + {\Omega }_{m0} \left( {\alpha \kappa - 2} \right)} \right)}}{2\kappa }, $$
(29)
$$ c_1 = \frac{\alpha \kappa H_0^2 \Xi }{{\Sigma {\Pi }}}, $$
(30)

where we define

$$ {\Xi } = \alpha {{\mathcal{E}}}_0^2 \kappa^3 - {{\mathcal{E}}}_0 \kappa^2 \left( {\alpha H_0^2 \left( {3 - \gamma - 6{\Omega }_{m0} } \right) + 2{{\mathcal{E}}}_0 } \right) + \kappa H_0^2 \left( {3\left( {{\Omega }_{m0} - 1} \right)\left( {\gamma + 3{\Omega }_{m0} } \right)H_0^2 - 2{{\mathcal{E}}}_0 \left( {\gamma + 6{\Omega }_{m0} } \right)} \right) - 18{\Omega }_{m0} H_0^4 \left( {{\Omega }_{m0} - 1} \right), $$
(31)
$$ {\Sigma } = \alpha {{\mathcal{E}}}_0 \kappa^2 + \left( {\alpha \left( {\gamma + 3{\Omega }_{m0} } \right)H_0^2 - 2{{\mathcal{E}}}_0 } \right)\kappa - 6{\Omega }_{m0} H_0^2 , $$
(32)
$$ {\Pi } = \alpha {{\mathcal{E}}}_0 \kappa^2 + (3\alpha \left( {{\Omega }_{m0} - 1} \right)H_0^2 - 2{{\mathcal{E}}}_0 )\kappa - 6{\Omega }_{m0} H_0^2 , $$
(33)

In Fig. 1 the evolution of equation of state \(\omega_X\) versus redshift \(z\) for \(H_0 = 67.4\), \({\Omega }_{m0} = 0.315\), \({{\mathcal{E}}}_0 = \gamma = 1\) and different values of \(\alpha\) is plotted. As shown dark energy for non-interaction scenario behaves like dust matter in past Universe, coincides with the cosmological constant at present, \(z = 0,\) and evolves like phantom field in future Universe. Comparing this model with standard Granda–Oliveros dark energy shows that the non-interaction term gives no tangible effects on the general behavior of dark energy for non-interaction scenario (see and compare this study results with Refs. [26, 27]). Hence, the non-conservation term does not play role in non-interaction scenario.

Fig. 1
figure 1

The equation of state of dark energy as function of redshift for \({\mathcal{E}}_{0}=\gamma =1\) and \(\alpha =0.075\) (solid curve), \(0.07\) (dashed curve), \(0.065\) (dash-dotted curve) and \(0.06\) (dotted curve). We set \({H}_{0}=67.4\) and \({\Omega }_{m0}=0.315\)

Full size image

The second parameter is debugged ‘deceleration parameter’ and defied as follows:

$$ q = - 1 - \frac{1}{2H^2 }\frac{dH^2 }{{dx}}. $$
(34)

which measures the cosmic acceleration rate of expanded Universe. This parameter is plotted in Fig. 2 with same sets of free parameters. Since \(q \to 0.5\) for \(z \gg 0\), there is no deviations in matter structure formation during matter-dominated era in our model. Moreover, the model shows acceleration era for these sets of constants onsets at \(z_T \approx 0.5 - 0.6\) which is not in conflict with joint analysis of SNe + CMB data and the \({\Lambda }\)CDM theory, \(z_T = 0.52 - 0.73\) [41].

Fig. 2
figure 2

Deceleration parameter for non-interaction scenario when \({H}_{0}=67.4\), \({\Omega }_{m0}=0.315\), \({\mathcal{E}}_{0}=\gamma =1\) and \(\alpha =0.075\) (solid curve), \(0.07\) (dashed curve), \(0.065\) (dash-dotted curve) and \(0.06\) (dotted curve)

Full size image

As the third parameter, one may attempt to consider stability of model, classically. In this case, the speed of sound squared

$$ \nu_c^2 = \frac{dp_X }{{d\rho_X }} = \frac{\partial p_X }{{\partial x}}\left( {\frac{\partial \rho_X }{{\partial x}}} \right)^{ - 1} . $$
(35)

should be positive. As discussed in Refs. [42, 43], the stability of the system involving entropic quantities could affect the effective speed of sound squared. However, considering density (21) and pressure (26) reveals that both of these parameters are linear function of entropic term when one finds, namely

$$ \begin{aligned} \rho_X & = \rho_{g - o} + \rho_{en} \\ p_X & = p_{g - o} + p_{en} \\ \end{aligned} $$

here subscript \(g - o\) and \(en\) denote Granda–Oliveros and entropy (non-interaction) parts, respectively. Therefor \(p_X = \omega_X \rho_X\) implies that \(\delta p_X = \omega_X \delta \rho_X\) [43]. Also, this linearity shows that due to entropy (non-conservation term) there is no deviation from Eq. (35) in investigating the speed of sound squared and thus Eq. (35) is valid for our model.

Plotting evolution of speed of sound square is given in Fig. 3. As shown dark energy is the stable fluid in our model.

Fig. 3
figure 3

The speed of sound square versus redshift for non-interaction scenario when \({\mathcal{E}}_{0}=\gamma =1\) and \(\alpha =0.075\) (solid curve), \(0.07\) (dashed curve), \(0.065\) (dash-dotted curve) and \(0.06\) (dotted curve). We set \({H}_{0}=67.4\) and \({\Omega }_{m0}=0.315\)

Full size image

Till now, we have studied non-interaction scenario of Granda–Oliveros dark energy in non-conserved theory of gravity. As discussed, due to effects of non-conservation term on evolution of dark energy, it behaves as dust matter in past Universe and thus there is no more matter regime during matter-dominated era. Consequently, we have no deviations in matter structure formation in our model. However, it is worthwhile to explore interaction scenario to see effects of interaction term on this model.

3.2 Interaction model

Among all plausible forms for interaction term, one may use \(Q = \zeta \left( {\rho_m + {{\mathcal{E}}}_{tt}^{\left[ e \right]} } \right)\) in which \(\zeta\) is an arbitrary constant. As result and by using Eqs. (19) and (23) the density of matter given by (\(c_1\) is the integration constant)

$$ \rho_m = c_1 e^{\left( {\zeta - 3} \right)x} + \frac{{\zeta {{\mathcal{E}}}_0 }}{3 + \gamma - \zeta }e^{\gamma x} , $$
(36)

With aid of this form of matter density and first Friedmann Eq. (17), the Hubble parameter and thus density of dark energy in interaction scenario become (\(c_2\) is another integration constant)

$$ H^2 = \frac{{2\kappa c_1 e^{x\left( {\zeta - 3} \right)} }}{{6 + \kappa \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)}} - \frac{{2\kappa {{\mathcal{E}}}_0 \left( {3 + \gamma } \right)e^{\gamma x} }}{{\left( {3 + \gamma - \zeta } \right)\left( {\kappa \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)} \right)}} + c_2 e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\kappa \alpha }x} , $$
(37)
$$ \rho_X = - \frac{{\kappa c_1 \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)e^{x\left( {\zeta - 3} \right)} }}{{6 + \kappa \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)}} - \frac{{\kappa {{\mathcal{E}}}_0 \left( {\alpha \gamma + 2\beta } \right)e^{\gamma x} }}{{\left( {3 + \gamma - \zeta } \right)\left( {\kappa \left( {\alpha \gamma + 2\beta } \right) - 6} \right)}} + \frac{3c_2 }{\kappa }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\kappa \alpha }x} . $$
(38)

where Eq. (16) is used.

Also using Eq. (24) and or Eq. (25) yields pressure \(p_X\) as:

$$ p_X = - \frac{{2\zeta c_1 e^{x\left( {\zeta - 3} \right)} }}{{6 + \kappa \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)}} - \frac{{2{{\mathcal{E}}}_0 \left( {3 + \gamma } \right)^2 e^{\gamma x} }}{{\left( {3 + \gamma - \zeta } \right)\left( {\kappa \left( {\alpha \gamma + 2\beta } \right) - 6} \right)}} - \frac{{c_2 \left( {6 + \kappa \left( {3\alpha - 2\beta } \right)} \right)}}{\alpha \kappa^2 }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\kappa \alpha }x} , $$
(39)

Thus, the equation of state for such model given by

$$ \omega_X = \frac{{ - \frac{{2\zeta c_1 e^{x\left( {\zeta - 3} \right)} }}{{6 + \kappa \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)}} - \frac{{2{{\mathcal{E}}}_0 \left( {3 + \gamma } \right)^2 e^{\gamma x} }}{{\left( {3 + \gamma - \zeta } \right)\left( {\kappa \left( {\alpha \gamma + 2\beta } \right) - 6} \right)}} - \frac{{c_2 \left( {6 + \kappa \left( {3\alpha - 2\beta } \right)} \right)}}{\alpha \kappa^2 }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\kappa \alpha }x} }}{{ - \frac{{\kappa c_1 \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)e^{x\left( {\zeta - 3} \right)} }}{{6 + \kappa \left( {\alpha \left( {3 - \zeta } \right) - 2\beta } \right)}} - \frac{{\kappa {{\mathcal{E}}}_0 \left( {\alpha \gamma + 2\beta } \right)e^{\gamma x} }}{{\left( {3 + \gamma - \zeta } \right)\left( {\kappa \left( {\alpha \gamma + 2\beta } \right) - 6} \right)}} + \frac{3c_2 }{\kappa }e^{ - \frac{{2\left( {\beta \kappa - 3} \right)}}{\kappa \alpha }x} }}. $$
(40)

Constraining model by current values of parameters, one obtains

$$ \beta = \frac{3}{\kappa } - \frac{{\left( {2 - \alpha \kappa } \right)\left( {\rho_{m0} + {{\mathcal{E}}}_0 } \right)}}{2H_0^2 }, $$
(41)
$$ c_1 = \rho_{m0} - \frac{{\zeta {{\mathcal{E}}}_0 }}{3 + \gamma - \zeta }, $$
(42)
$$ c_2 = \frac{{\alpha H_0^2 \left( {{{\mathcal{A}\mathcal{B}}}\alpha - 2H_0^2 \left( {\zeta {{\mathcal{C}}} + {{\mathcal{E}}}_0 \gamma - 3\rho_{m0} } \right) - 2\kappa {{\mathcal{C}}}^2 } \right)}}{{\left( {{{\mathcal{B}}}\alpha - 2{{\mathcal{C}}}} \right)\left( {{{\mathcal{A}}}\alpha - 2{{\mathcal{C}}}} \right)}}, $$
(43)

when

$$ {{\mathcal{A}}} = \gamma H_0^2 + \kappa {{\mathcal{C}}}, $$
(44)
$$ {{\mathcal{B}}} = - \left( {3 - \zeta } \right)H_0^2 + \kappa {{\mathcal{C}}}, $$
(45)
$$ {{\mathcal{C}}} = \rho_{m0} + {{\mathcal{E}}}_0 . $$
(46)

are defined.

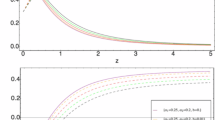
The equation of state (40), deceleration parameter (35) and the speed of sound square (34) are plotted in Figs. 4, 5 and 6 when \({{\mathcal{E}}}_0 = \gamma = 1\). As shown model gives quintessence dark energy field; it behaves like matter with positive pressure in matter-dominated era, evolves like cosmological constant theory at present time and treats as phantom fluid in near future. Using same values of \(\alpha\) reveals that model is stable, classically and acceleration phase onsets around \(z_T \approx 0.49 - 0.59\), which is not in conflict with observations. It should note that interaction parameter \(\zeta\) must be negative to have stable model.

Fig. 4
figure 4

Evolution of equation of state for interaction scenario as function of redshift \(z\) for \(\zeta =-0.02\) and \(\alpha =0.075\) (solid curve), \(0.07\) (dashed curve), \(0.065\) (dash-dotted curve) and \(0.06\) (dotted curve)

Full size image
Fig. 5
figure 5

The diagram of deceleration parameter for interaction model when \(\zeta =-0.02\) and \(\alpha =0.075\) (solid curve), \(0.07\) (dashed curve), \(0.065\) (dash-dotted curve) and \(0.06\) (dotted curve)

Full size image
Fig. 6
figure 6

The speed of sound square for \(\zeta =-0.02\) and \(\alpha =0.075\) (solid curve), \(0.07\) (dashed curve), \(0.065\) (dash-dotted curve) and \(0.06\) (dotted curve)

Full size image

In comparison with the standard Granda–Oliveros model when interaction \(Q = \zeta \rho_m\) is used (in the absence of non-conservation term), our theory yields valuable model, supports observations while the standard Granda–Oliveros for different values of \(\alpha\) gives unstable model at present time and dark energy behaves like matter fluid with the positive pressures for \(z \gg 1\). Futhremore, investigating the deceleration parameter shows that acceleration era for best values of free parameter \(\alpha\) onsets around \(z \approx 3.2\)–4.5 in interaction scenario of Granda–Oliveros theory which is in conflict with observations (see Fig. 7) [41].

Fig. 7
figure 7

The evolution of deceleration parameter (left panel) and equation of state of Granda–Oliveros Holographic dark energy in standard Einstein Field Equations (in absence of non-conservation effects) versus redshift for \(\zeta =-0.02\) for different values of \(\alpha \)

Full size image

Although, our model satisfies observations in interaction scenario, since dark energy behaves as matter with positive pressure in past, there is more matter pressure in interaction scenario with respect to non-interaction one and or the cosmological constant model during matter-dominated era. Hence, there is some deviations in matter structure formation (see for instance Ref. [27]). In this level of our consideration, it is worthwhile to check whether this extra matter influences on matter formation or not.

Exploring Fig. 4 shows that dark energy for \(\alpha = 0.075\) gives most matter pressure for \(z \gg 1\),

$$ {\mathop {\lim }\limits_{z \to \infty }} \omega_X \approx 0.202. $$
(47)

while corresponded value for \(\alpha < 0.075\) is less than \(0.08\). As result, in follows we just investigate matter formation for \(\alpha = 0.075\) (Fig. 8).

Fig. 8
figure 8

The \({\upsilon }_{c}^{2}\) for Granda–Oliveros Holographic dark energy in standard Einstein Field Equations (in absence of non-conservation effects) versus redshift for \(\zeta =-0.02\) for different values of \(\alpha \)

Full size image

In Fig. 9, we have compared the theoretical angular spectrum of the \({\Lambda }\)CDM theory with \({\Lambda }\)CDM theory. In this context and in order to get more details, we calculated CMB TT, EE and TE in Fig. 9. The largest errors are approximately \(\ 4\%\) for CMB TT, \(\% 10\) for CMB EE and \(30\%\) for CMB TE when \(\alpha = 0.075\). In comparison with Granda–Oliveros model studied in Ref. [27], our model alleviates these corresponded errors that shows how non-conservation term alleviates these errors.Footnote 1 It should be noted to calculate CMB the effects of such dark energy (that behaves as the matter with positive pressure) is added to matter field during matter-dominated era (see Ref. [27] as instance).

Fig. 9
figure 9

The theoretical CMB TT (top panel), EE (middle panel) and TE (bottom panel) for our model (dashed red curves) compared with the corresponding parameters in the \(\Lambda \)CDM theory (solid black curves) when we set \(\alpha =0.075\), \({\mathcal{E}}_{0}=\gamma =1\) and \(\zeta =-0.02\)

Full size image

The studying matter power spectrum also shows that extra regimes of matter pressure due to dark energy evolution in high redshift gives no strong error; the largest error occurs around \(K = 10^{ - 2}\) and is about \(1\%\) (Fig. 10).

Fig. 10
figure 10

The matter power spectra for redshift \(z=0\) for our model (dashed red curve) compared with \(\Lambda \)CDM theory (solid black curve) when we set \(\alpha =0.075\)

Full size image

4 Remarks

Understanding nature and origin of current acceleration phase is one of the opening issues in modern cosmology. Among different approaches to investigate current time, and following holographic principle, one may assume that energy density of dark energy given by cut-off length, i.e., \(\rho_X \sim \ell^{ - 2}\).

In this study, we apply Granda–Oliveros infrared cut-off length \(\ell = \left( {\alpha H^2 + \beta \dot{H}} \right)^{ - 1/2}\) to investigate holographic dark energy in new modified theory of gravity so-called ‘non-conserved theory’. To have better insight, we have explored this holographic dark energy through two different scenarios (non-interaction and interaction).

As first step we assume that dark energy and matter evolve independently (non-interaction model). In this case and due to effects of non-conservation term the model presents holographic dark energy which behaves as dust matter in high redshifts. Also, such dark energy coincides with the cosmological constant and evolves like phantom field in future. However, in this scenario non-conservation term does not play key role and one finds general behavior found in Granda–Oliveros holographic dark energy in standard field equations when non-conservation term is vanished.

As the second scenario we have investigated model when dark energy interacts with matter. In this context and as shown the non-conservation term shows its effects on evolution of dark energy. the transition redshift \(z_T\) and stability while in absence of the non-conservation term there is some inconsistencies with observations in stability of dark energy and \(z_T\) (Figs. 7, 8).