1 Introduction

One of the most generalization of the flat universe is Friedman Robertson–Walker (FRW) universe. Similarly the most simplest spatially homogeneous and anisotropic flat universe is the Bianchi type-I universe. FRW universe has the same scale factor for each of the three spatial directions where as Bianchi type-I universe has different scale factors. Near the singularity Bianchi type-I universe behave like Kanser universe. It has been observed that a universe filled with matter, the initial anisotropy in Bianchi type-I universe quickly dies away and evolves into a FRW universe. It has simple mathematical form and interesting because of the ability to explain the cosmic evolution of the early universe. Due to its importance several authors have studied Bianchi type-I universe from different aspects.

In recent years, there has been a lot of work in astrophysics and cosmology based on the observational evidence that the present universe is undergoing in a phase of accelerated expansion. From Ia supernova (Bennet et al. 2003, Spergel et al. 2003, 2007) observations, cosmic microwave background (CMB) anisotropies (Perlmutter et al. 1997, 1999, Riess et al. 2004, 2007) and large scale structure (Tegmark et al. 2004; Cole et al. 2005) indicate that most of the cosmic energy density is dominated by dark energy (DE). This DE is responsible for the cosmic acceleration. There are many candidates of DE, such as the cosmological constant or vacuum energy, quintessence, phantom, tachyon, quantum, Chaplygin gas and many more (Padmanabhan 2002, 2008, Bento et al. 2002; Nojiri and Odintsov 2003; Feng et al. 2005). Among all the candidates, the ΛCDM (Λ-cold dark matter) model is the best one due to its success and fine-tuning (Peebles 2003; Astier et al. 2006).

In view of the late time acceleration and existence of dark energy modified theories of general relativity have been developed and drawn much attention. The modifications are based on the Einstein–Hilbert action to obtain alternative theories of Einstein such as f(R) gravity (Carroll et al. 2004, Nojiri et al. 2006, 2007, 2011, Bertolami et al. 2007; Sotiriou and Faraoni 2010), f(T) gravity (Bengocheu et al. 2009; Linder 2010) and f(G) gravity (Bamba et al. 2010a, 2010b; Rodrigues et al. 2014; Nojiri and Odintsov 2010a) where R, T and G are the scalar curvature, the torsion scalar and the Gauss–Bonnet scalar respectively. The maximal extension of the Hilbert–Einstein action have been proposed by Harko and Lobo (2010) by considering the gravitational Lagrangian as a arbitrary function of Ricci scalar R and of the matter Lagrangian L m . The relativistic covariant model of interacting DE based on the principle of least action is given in f(R,L m ) gravity (Poplawski 2006). In this theory, the cosmological constant is a function of trace of the energy tensor and hence the model was denoted “Λ(T) gravity”. This is more general than the f(R) gravity as it reduces to the latter when we neglect the pressure. A detailed review of f(R) gravity and their properties with different models are discussed in detail by many authors (Lobo 2008; Felice and Tsujikawa 2010, Nojiri and Odintsov 2010a, 2011).

Harko et al. (2011) have developed a new modified theory of gravity known as f(R,T) gravity. In this theory, the gravitational Lagrangian is given by an arbitrary function of the scalar curvature R and the trace T of the energy tensor. The field equations are derived in the metric formalism as well as the equations of motion for test particles. They have presented the field equations corresponding to FRW metric for forms of the function f(R,T). Adhav (2012) constructed LRS Bianchi type cosmological model in f(R,T) gravity with perfect fluid. Sharif and Zubir (2012) studied the anisotropic behavior of perfect fluid and massless scalar field for Bianchi type-I space time in this theory. The negative constant deceleration parameter in presence of perfect fluid is studied in Bianchi type-III cosmological model (Reddy et al. 2012). Bianchi type-III dark energy model is derived in presence of perfect fluid using special law of variation for Hubble’s parameter (Reddy et al. 2013). Chaubey and Shukla (2013) constructed Bianchi type-III, V, VI0 and VI h cosmological models by using linearly varying deceleration parameter. Yadav (2013) constructed Bianchi type-V string cosmological model with power law expansion in this theory. Mishra and Sahoo (2014) solved the field equations of Bianchi type-VI h cosmological model in presence of perfect fluid in f(R,T) gravity. Sahoo and Mishra (2014) studied Kaluza–Klein dark energy model in form of wet dark fluid in this theory. Sahoo et al. (2014) constructed an axially symmetric cosmological model in f(R,T) theory in the presence of a perfect fluid source. In particular Ahmed and Pradhan (2014) constructed Bianchi type-V cosmological model for a specific choice of f(R,T)=f 1(R)+f 2(T). They considered the cosmological constant Λ as a function of the trace of the energy-momentum-tensor T and called the model as “Λ(T) gravity”.

Inspired by the above discussion we plan to study LRS Bianchi type-I space time with perfect fluid source in f(R,T) gravity. We solved the field equations satisfying the linearly varying deceleration parameter q. The paper is organized as follows: In Sect. 1, a brief introduction about f(R,T) gravity is given. The detail derivations of the field equations of f(R,T) is given in Sect. 2. In Sect. 3, the explicit field equations are derived in f(R,T) gravity for LRS Bianchi type-I space time using f(R,T)=λ(R+T). The solutions of the field equations are obtained using the linearly varying deceleration parameter q and also discuss the physical properties of the models in Sect. 4. The field equations and solutions corresponding to f(R,T)=λ(R+T 2) are given in Sect. 5. In Sect. 6, we discuss the jerk parameter which deals with the physical and geometrical behaviour of the universe. The State-finder diagnostic approach to these models is discussed in Sect. 7. The summery and conclusions of the models are given in Sect. 8.

2 Gravitational field equations of f(R,T) gravity

The field equations of f(R,T) gravity are obtained from Hilbert–Einstein variational principle. The modified gravity action is given as

$$ S=\frac{1}{16\pi}\int{f(R,T)\sqrt{-g}d^{4}x}+\int{L_{m} \sqrt{-g}d^{4}x} $$
(1)

where f(R,T) is an arbitrary function of Ricci scalar (R), T be the trace of energy-momentum tensor (T ij ) of the matter, L m is the matter Lagrangian density. The energy momentum tensor T ij of matter is defined as

$$ T_{ij}= - \frac{2}{\sqrt{-g}} \frac{\delta(\sqrt{-g})L_{m}}{\delta g^{ij}} $$
(2)

and its trace by T=g ij T ij . We have assumed that the matter Lagrangian L m depends only on the metric tensor g ij rather than its derivatives. In this case, we obtain

$$ T_{ij}= g_{ij}L_{m} - \frac{\partial L_m}{\partial g^{ij}} $$
(3)

The field equations of f(R,T) gravity are obtained by varying the action S with respect to metric tensor g ij .

$$\begin{aligned} &f_R(R,T)R_{ij}-\frac{1}{2} f(R,T) g_{ij} + (g_{ij}\Box-\nabla_i\nabla_j)f_R(R,T) \\ &\quad{}=8\pi T_{ij}-f_T(R,T) T_{ij} -f_T(R,T) \varTheta_{ij} \end{aligned}$$
(4)

where

$$ \varTheta_{ij}= -2T_{ij}+g_{ij}L_{m} - 2g^{lm} \frac{\partial^2 L_m}{\partial g^{ij} \partial g^{lm}} $$
(5)

Here \(f_{R}(R,T)=\frac{\partial f(R,T)}{\partial R}\), \(f_{T}(R,T)=\frac{\partial f(R,T)}{\partial T}\), □≡∇i∇ i where ∇ i denotes the covariant derivative.

Now contraction of equation (4) gives

$$\begin{aligned} &f_R(R,T)R + 3\Box f_R(R,T)- 2f(R,T) \\ &\quad{}=\bigl(8 \pi-f_T(R,T)\bigr)T -f_T(R,T) \varTheta \end{aligned}$$
(6)

where Θ=g ij Θ ij .

From equations (4) and (6), we obtain

$$\begin{aligned} &f_R(R,T) \biggl(R_{ij}-\frac{1}{3}Rg_{ij} \biggr)+\frac{1}{6}f(R,T)g_{ij} \\ &\quad{}=8\pi-f_T(R,T) \biggl(T_{ij}-\frac{1}{3}Tg_{ij} \biggr) \\ &\qquad{}-f_T(R,T) \biggl(\varTheta_{ij}-\frac{1}{3}\varTheta g_{ij} \biggr)+\nabla_i\nabla_jf_R(R,T) \end{aligned}$$
(7)

Using the source of gravitation as perfect fluid, the stress energy tensor of the matter Lagrangian is given by

$$ T_{ij}=(\rho+p)u_iu_j-pg_{ij} $$
(8)

where u i=(0,0,0,1) is the velocity vector in co-moving coordinate system satisfying the condition u i u i =1 and u i∇ j u i =0. Here ρ and p are energy density and pressure of the fluid respectively. Since there is no unique definition of the matter Lagrangian, it can be taken as L m =−p.

Using the variation of the stress-energy as perfect fluid in equation (5), we obtain

$$ \varTheta_{ij}=-2T_{ij}-pg_{ij} $$
(9)

The field equations of f(R,T) gravity also depend on the physical nature of the matter field through the tensor Θ ij . Hence in this case depending on the nature of the matter source, we can obtain several theoretical models corresponding to different matter contributions for f(R,T) gravity. Harko et al. (2011) presented three classes of these models as follows

$$ f(R,T )= \left \{ \begin{array}{lcl} R+2f(T) \\ f_1(R)+f_2(T) \\ f_1(R)+f_2(R)f_3(T) \end{array} \right . $$
(10)

In this paper, we consider the second case i.e. f(R,T)=f 1(R)+f 2(T) for LRS Bianchi type-I space time which is the straight forward generalization of the flat FRW universe. The derived cosmological model here is totally different and new from the other authors mentioned earlier. Till today, the physically important cosmological term Λ which is considered as a candidate for dark energy remains less attended. So, this model may lead to better understanding of the characteristic of Λ in LRS Bianchi type-I metric. Throughout the paper we restrict ourselves to the natural unit system with G=c=1, where G is the Newtonian gravitational constant and c is the speed of light in vacuum.

3 Metric and field equations for f 1(R)=λR and f 2(T)=λT

We consider the spatially homogeneous and anisotropic LRS Bianchi type-I metric as

$$ ds^{2}=dt^{2}-A(t)^{2}\bigl(dx^{2}+dy^{2} \bigr)-B(t)^{2}dz^{2} $$
(11)

The metric having symmetry plane corresponding to xy-plane. The eccentricity of such a universe is given by \(e=\sqrt{1-\frac {B^{2}}{A^{2}}}\). The average scale factor, spatial volume, scalar expansion for this metric (11) are obtained respectively as

$$ \begin{aligned} &a=\bigl(A^2B\bigr)^{\frac{1}{3}},\qquad V=a^3=A^2B,\\ &\theta=u^i_{;i}=2\frac{A^{\prime}}{A}+\frac{B^{\prime}}{B} \end{aligned} $$
(12)

We consider the linear form of the functions f 1(R)=λR and f 2(T)=λT where λ is an arbitrary parameter, so that f(R,T)=λ(R+T). Using this the gravitational field equations of f(R,T) gravity from equation (4) can be written as

$$\begin{aligned} &\lambda R_{ij}-\frac{1}{2} \lambda(R+T)g_{ij}+(g_{ij} \Box-\nabla_i\nabla_j)\lambda \\ &\quad{}=8\pi T_{ij}- \lambda T_{ij} + \lambda(2T_{ij}+pg_{ij}) \end{aligned}$$
(13)

Setting (g ij □−∇ i ∇ j )λ=0, we get

$$ R_{ij}-\frac{1}{2}Rg_{ij}= \biggl(\frac{8\pi+\lambda}{\lambda} \biggr)T_{ij}+ \biggl(p+\frac{1}{2}T \biggr)g_{ij} $$
(14)

Using the Einstein tensor \(G_{ij}\equiv R_{ij}-\frac{1}{2}g_{ij}R\), the above equation can be rearranged as

$$ G_{ij}- \biggl(p+\frac{1}{2}T \biggr)g_{ij}= \biggl( \frac{8\pi+\lambda}{\lambda} \biggr)T_{ij}. $$
(15)

We choose a small negative value for the arbitrary λ to draw a better analogy with the usual Einstein field equations. We intend to keep this choice of λ throughout.

Einstein field equations with cosmological constant term is usually expressed as

$$ G_{ij}-\varLambda g_{ij}=-8\pi T_{ij}. $$
(16)

A comparison of equations (15) and (16) provides us

$$ \varLambda\equiv\varLambda(T)=p+\frac{1}{2}T. $$
(17)

and \(\lambda=-\frac{8\pi}{8\pi+1}\). In other words, \(p+\frac{1}{2}T\) behaves as cosmological constant.

In a co-moving coordinate system the field equations (14), for the metric (11), with help of energy momentum tensor (8), can be explicitly written as

$$\begin{aligned} &\frac{A^{\prime\prime}}{A}+ \frac{A^{\prime}B^{\prime}}{AB} + \frac {B^{\prime\prime}}{B}= \biggl( \frac{8\pi+\lambda}{\lambda} \biggr)p-\varLambda \end{aligned}$$
(18)
$$\begin{aligned} &2\frac{A^{\prime\prime}}{A}+ \biggl(\frac {A^{\prime}}{A} \biggr)^2= \biggl( \frac{8\pi+\lambda}{\lambda} \biggr)p-\varLambda \end{aligned}$$
(19)
$$\begin{aligned} &\biggl(\frac{A^{\prime}}{A} \biggr)^2 + 2 \frac {A^{\prime}B^{\prime}}{AB}=- \biggl( \frac{8\pi+\lambda}{\lambda} \biggr)\rho-\varLambda \end{aligned}$$
(20)

where an overhead prime hereafter, denote ordinary differentiation with respect to cosmic time “t” only. The trace in our model is given by T=−3p+ρ, so that the effective cosmological constant in equation (17) reduces to

$$ \varLambda(T)=\frac{1}{2} (\rho-p). $$
(21)

Subtracting equation (18) from equation (19), we get

$$ \frac{d}{dt} \biggl(\frac{A^{\prime}}{A}- \frac {B^{\prime}}{B} \biggr)+ \biggl(\frac{A^{\prime}}{A}- \frac{B^{\prime}}{B} \biggr) \biggl(2\frac{A^{\prime}}{A}+ \frac{B^{\prime}}{B} \biggr)=0 $$
(22)

which on integration yields

$$ \frac{A^{\prime}}{A}- \frac{B^{\prime}}{B}=\frac{c_1}{A^2B} $$
(23)

where c 1 is a integration constant. Again integrating

$$ \frac{A}{B}=c_2 \exp\biggl[c_1 \int \frac{dt}{A^2B} \biggr]= c_2 \exp\biggl[c_1 \int \frac{dt}{a^3} \biggr] $$
(24)

where c 2 is integration constant.

From equation (24), the values of metric potentials are

$$ A=c_2^{1/3}a \exp\biggl[\frac{c_1}{3} \int \frac{dt}{a^3} \biggr] $$
(25)

and

$$ B=c_2^{-2/3}a \exp\biggl[\frac{-2c_1}{3} \int \frac{dt}{a^3} \biggr] $$
(26)

The directional Hubble parameters along the symmetry plane and symmetry axis are defined as \(H_{1}=\frac{A^{\prime}}{A}\) and \(H_{2}=\frac {B^{\prime}}{B}\) so that the mean Hubble parameter becomes \(H=\frac{1}{3}(2H_{1}+H_{2})\) and θ=3H. The shear scalar σ 2 for the metric (11) is defined as

$$ \sigma^2=\frac{1}{2} \biggl[\sum H^2_i- \frac{1}{3}\theta^2 \biggr]=\frac{1}{3}(H_1-H_2)^2 $$
(27)

In terms of the directional Hubble parameters, we can express the field equations (18)–(20) as

$$\begin{aligned} &H_1^{\prime}+H_2^{\prime}+H_1^2+H_2^2+H_1H_2= \alpha p-\varLambda, \end{aligned}$$
(28)
$$\begin{aligned} &2H_1^{\prime}+3H_1^2=\alpha p- \varLambda, \end{aligned}$$
(29)
$$\begin{aligned} &H_1^2+H_1H_2=-\alpha\rho- \varLambda, \end{aligned}$$
(30)

where \(\alpha=\frac{8\pi+\lambda}{\lambda}\).

Equations (21), (29) and (30) gives us the general formulations for the physical parameters of the f(R,T) model with respect to the Ricci scalar R and

$$ R=-2 \biggl[2\frac{A^{\prime\prime}}{A}+ 2 \frac{A^{\prime}B^{\prime }}{AB} + \frac {B^{\prime\prime}}{B}+ \biggl(\frac{A^{\prime}}{A} \biggr)^2 \biggr] $$
(31)

Pressure, energy density and the cosmological constant for the model can be written in terms of Hubble parameter as

$$\begin{aligned} &p=\frac{(4\alpha+2)H_1^{\prime}+(6\alpha+2)H_1^2-H_1H_2}{2\alpha(\alpha+1)} \end{aligned}$$
(32)
$$\begin{aligned} &\rho=\frac{2H_1^{\prime}+(2-2\alpha)H_1^2-(2\alpha+1)H_1H_2}{2\alpha (\alpha+1)} \end{aligned}$$
(33)
$$\begin{aligned} &\varLambda=-\frac{2H_1^{\prime}+4H_1^2+H_1H_2}{2(\alpha+1)} \end{aligned}$$
(34)

The equation of state parameter i.e. the ratio between pressure and energy density is

$$ \omega=\frac{(4\alpha+2)H_1^{\prime}+(6\alpha +2)H_1^2-H_1H_2}{2H_1^{\prime}+(2-2\alpha)H_1^2-(2\alpha+1)H_1H_2} $$
(35)

4 Solution of the field equations f 1(R)=λR and f 2(T)=λT

This system consists three linearly independent equations (18)–(20) but four unknowns (A,B,ρ and p), hence it is not fully determined. In order to solve the system completely we used a generalized linearly varying deceleration parameter q (Akarsu and Dereli 2012) as

$$ q=-\frac{a^{\prime\prime}a}{a^{\prime2}}=\frac{d}{dt} \biggl(\frac{1}{H} \biggr)-1=-kt+m-1, $$
(36)

where k≥0 and m≥0 are constants. The universe exhibit decelerating expansion if q>0, expand with constant rate if q=0, accelerating power law expansion if −1<q<0 and exponential expansion if q=−1.

Solving equation (36), we obtain three different forms of the scale factor as

$$\begin{aligned} &a=a_1 \exp[l_1t] \quad\text{for } k=0 \text{ and } m=0 \end{aligned}$$
(37)
$$\begin{aligned} &a=a_2(mt+l_2)^{1/m}\quad \text{for } k=0 \text{ and } m>0 \end{aligned}$$
(38)
$$\begin{aligned} &a=a_3 \exp\biggl[\frac{2}{\sqrt{m^2-2l_3k}} \arctan h \biggl( \frac{kt-m}{\sqrt{m^2-2l_3k}} \biggr) \biggr] \\ &\quad \text{for } k>0 \text{ and } m \geq0 \end{aligned}$$
(39)

where a 1, a 2, a 3, l 1, l 2 and l 3 are integrating constants. The first two cases refer to constant deceleration parameters corresponding to an exponential and power law variation of the scale factor.

4.1 Model 1

Using equation (37) in equations (25) and (26), we can get

$$ A=a_1c_2^{1/3} \exp\biggl[l_1t- \frac{c_1}{9l_1a_1^3}e^{-3l_1t} \biggr], $$
(40)

and

$$ B=a_1c_2^{-2/3} \exp\biggl[l_1t+ \frac{2c_1}{9l_1a_1^3}e^{-3l_1t} \biggr]. $$
(41)

We observe that the scale factors have constant values at initial epoch (t→0) which imply that the model has no singularity. The scale factors start increasing with the increase in cosmic time and finally diverge to ∞ when (t→∞). Hence in this case, the volume of the universe is an exponential function which expands with increase in time from a constant to infinitely large.

The directional Hubble’s parameters are

$$\begin{aligned} &H_1=l_1+\frac{c_1}{3a_1^3} e^{-3l_1t} \end{aligned}$$
(42)
$$\begin{aligned} &H_2=l_1-\frac{2c_1}{3a_1^3} e^{-3l_1t} \end{aligned}$$
(43)

The mean Hubble parameter is obtained as

$$ H=l_1 $$
(44)

The mean Hubble parameter is constant whereas the directional Hubble parameters are dynamical. The directional Hubble parameters H 1 and H 2 becomes constant at t=0 as well as (t→∞). The directional Hubble parameters differ from H by some constant at t=0 and coincides at latter times with the universe.

The scalar expansion θ and the shear scalar σ 2 are found as

$$ \theta=3l_1, \qquad \sigma^2=\frac{c_1^2}{3a_1^6} e^{-6l_1t} $$
(45)

The deceleration parameter q=−1 shows accelerating expansion of the universe which is in agreement with current observations of SNe Ia and CMB. The expansion scalar θ remains constant throughout for this model.

The anisotropy parameter of the expansion Δ is defined as

$$ \Delta=\frac{1}{3}\sum_{i=1}^3 \biggl(\frac{H_i-H}{H} \biggr)^2= 6 \biggl(\frac{\sigma}{\theta} \biggr)^2=\frac{2c_1^2}{9a_1^6l_1^2} e^{-6l_1t} $$
(46)

where H i (i=1,2,3) represent the directional Hubble parameters in the directions of x, y and z respectively. The anisotropy parameter is finite for earlier times and vanishes at infinite time of the universe. It shows that the universe expands isotropically at later times.

Using equations (42) and (43) in equations (32)–(34), we obtain the pressure, energy density and cosmological constant for this model as

$$\begin{aligned} &p=\frac{1}{2\alpha(\alpha+1)} \biggl[(6\alpha+1)l_1^2- \frac{c_1l_1}{3a_1^3} e^{-3l_1t} \\ &\phantom{p=\,}+\frac{(6\alpha+4)c_1^2}{9a_1^6} e^{-6l_1t} \biggr] \end{aligned}$$
(47)
$$\begin{aligned} &\rho=\frac{1}{2\alpha(\alpha+1)} \biggl[(1-4\alpha)l_1^2- \frac{(1+2\alpha)c_1l_1}{3a_1^3} e^{-3l_1t} \\ &\phantom{\rho=\,}+\frac{(2\alpha +4)c_1^2}{9a_1^6} e^{-6l_1t} \biggr] \end{aligned}$$
(48)
$$\begin{aligned} &\varLambda=-\frac{1}{2(\alpha+1)} \biggl[5l_1^2+ \frac{c_1l_1}{3a_1^3} e^{-3l_1t}+\frac{2c_1^2}{9a_1^6} e^{-6l_1t} \biggr] \end{aligned}$$
(49)

The pressure and density are constant at early stages of the universe and behaves monotonically in the evolving of cosmic time.

The equation of state ω for this model is given by

$$\begin{aligned} \omega =&\bigl\{ 9(6\alpha+1)a_1^6l_1^2-3c_1l_1a_1^3e^{-3l_1t}+(6\alpha +4)c_1^2e^{-6l_1t}\bigr\} \\ &{}\times\bigl\{ 9(1-4\alpha)a_1^6l_1^2-3(1+2\alpha )c_1l_1a_1^3e^{-3l_1t} \\ &{}+(2\alpha+4)c_1^2e^{-6l_1t}\bigr\} ^{-1} \end{aligned}$$
(50)

Since ω→ constant as t→0 and also ω→ constant when t→∞ it indicates that the equation state ω would remain ideal during the evolution.

In this model, all cosmological parameters are constant at t=0. Hence the universe starts with a non-singular state at initial epoch. The scale factors and the spatial volume increases exponentially as t increases. Since the scalar expansion is a constant, the universe exhibits uniform exponential expansion. The cosmological constant is negative increasing function of time and reaches to a small value at late time.

The Ricci scalar for this model is given by

$$ R=-\frac{2}{3a_1^6} \bigl[18a_1^6l_1^2+c_1^2e^{-6l_1t} \bigr] $$
(51)

The curvature R remains constant through the whole evolution of the universe.

The trace T for this model is given by

$$\begin{aligned} T =&-\frac{1}{\alpha(\alpha+1)} \biggl[(11\alpha+1)l_1^2- \frac{(1+2\alpha)c_1l_1}{3a_1^3} e^{-3l_1t} \\ &{}+\frac{(8\alpha +4)c_1^2}{9a_1^6} e^{-6l_1t} \biggr] \end{aligned}$$
(52)

The function f(R,T)=f 1(R)+f 2(T) for this model is given by

$$\begin{aligned} f(R,T) =&\frac{-\lambda}{9a_1^6\alpha(\alpha+1)} \bigl[\bigl(108\alpha ^2+207\alpha+9 \bigr)a_1^6l_1^2 \\ &{}-(3+6\alpha)a_1^3c_1l_1 e^{-3l_1t} \\ &{}+\bigl(6\alpha^2+14\alpha+4\bigr)c_1^2 e^{-6l_1t} \bigr] \end{aligned}$$
(53)

In this model the negative deceleration parameter indicates that the universe is accelerating which is consistent with the present day observations.

4.2 Model 2

Using equation (38) in equations (25) and (26), we can get the scale factors as

$$\begin{aligned} A =&a_2c_2^{1/3} (mt+l_2)^{1/m} \\ &{}\times\exp\biggl[\frac{c_1}{3a_2^3(m-3)} (mt+l_2)^{\frac{m-3}{m}} \biggr] \end{aligned}$$
(54)

and

$$\begin{aligned} B =&a_2c_2^{-2/3} (mt+l_2)^{1/m} \\ &{}\times\exp\biggl[\frac{-2c_1}{3a_2^3(m-3)} (mt+l_2)^{\frac{m-3}{m}} \biggr] \end{aligned}$$
(55)

From the above set of solutions we observe that the spatial volume is constant at t=0. The metric potentials A(t) and B(t) are also constant at this initial epoch. As t→∞, both the scale factors A(t) and B(t) tend to infinity.

The directional Hubble’s parameter H 1 and H 2 have the values

$$\begin{aligned} &H_1=(mt+l_2)^{-1}+\frac{c_1}{3a_2^3}(mt+l_2)^{\frac{-3}{m}} \end{aligned}$$
(56)
$$\begin{aligned} &H_2=(mt+l_2)^{-1}-\frac{2c_1}{3a_2^3}(mt+l_2)^{\frac{-3}{m}} \end{aligned}$$
(57)

The average generalized Hubble’s parameter H has the value given by

$$ H=(mt+l_2)^{-1} $$
(58)

The directional Hubble parameters and mean Hubble parameter become constant at the initial epoch while the values of these parameters tend to zero as t→∞.

The expansion scalar θ and the shear scalar σ 2 are turns out to be

$$ \theta=3(mt+l_2)^{-1},\qquad \sigma^2=\frac{c_1^2}{3a_2^6}(mt+l_2)^{\frac{-6}{m}}, $$
(59)

and the anisotropy parameter is

$$ \Delta= \frac{2c_1^2}{9a_2^6}(mt+l_2)^{\frac{-4}{m}} $$
(60)

The pressure, density and cosmological constant for this case are given by

$$\begin{aligned} &p=\frac{1}{2\alpha(\alpha+1)} \biggl[(1-4\alpha m+6\alpha-2m) (mt+l_2)^{-2} \\ &\phantom{p=\,}-\frac{c_1}{3a_2^3}(mt+l_2)^{\frac{-3-m}{m}}+\frac{(6\alpha +4)c_1^2}{9a_2^6}(mt+l_2)^{\frac{-6}{m}} \biggr] \end{aligned}$$
(61)
$$\begin{aligned} &\rho=\frac{1}{2\alpha(\alpha+1)} \biggl[(1-4\alpha-2m) (mt+l_2)^{-2} \\ &\phantom{\rho=\,}-\frac{c_1}{3a_2^3}(mt+l_2)^{\frac{-3-m}{m}}+\frac{(2\alpha +4)c_1^2}{9a_2^6}(mt+l_2)^{\frac{-6}{m}} \biggr] \end{aligned}$$
(62)
$$\begin{aligned} &\varLambda=\frac{1}{2(\alpha+1)} \biggl[(2m-5) (mt+l_2)^{-2}- \frac{c_1}{3a_2^3}(mt+l_2)^{\frac{-3-m}{m}} \\ &\phantom{\varLambda=\,}-\frac {2c_1^2}{9a_2^6}(mt+l_2)^{\frac{-6}{m}} \biggr] \end{aligned}$$
(63)

The pressure and energy density becomes infinite at initial epoch (t=0) and tend to zero as t→∞.

The equation of state ω for this model is given by

$$\begin{aligned} \omega =& \bigl\{ 9a_2^6(1-4\alpha m+6\alpha -2m)(mt+l_2)^{-2} \\ &{}-3c_1a_2^3(mt+l_2)^{\frac{-3-m}{m}}+(6\alpha +4)c_1^2(mt+l_2)^{\frac{-6}{m}}\bigr\} \\ &{}\times\bigl\{ 9a_1^6(1-4\alpha -2m)(mt+l_2)^{-2} \\ &{}-3c_1a_2^3(mt+l_2)^{\frac{-3-m}{m}} \\ &{}+(2\alpha +4)c_1^2(mt+l_2)^{\frac{-6}{m}}\bigr\} ^{-1} \end{aligned}$$
(64)

Here ω→ constant as t→0 however ω→∞ when t→∞. The equation of state ω for this model will start from initial epoch and vary according to the time till infinite future.

In this model, the spatial volume V is zero at t=t 0, where \(t_{0}=-\frac{l_{2}}{m}\) and the expansion scalar θ is infinite. This shows that the universe starts evolving with zero volume at t=t 0 with an infinite rate of expansion. The anisotropy parameter becomes infinite at t=t 0. At t=t 0, the scale factors become zero, hence the model has a point type singularity (MacCallum 1971) at the initial epoch. As t increases the scale factors and the spatial volume increase where as the scalar expansion decreases. The pressure, energy density, cosmological constant, Hubble’s parameter and shear scalar decreases as t increases. Hence the model represents shearing, non-rotating and expanding model of the universe.

The scalar curvature R for this model is given by

$$ R=\frac{2}{3a_2^6} \bigl[6a_2^6(m-2) (mt+l_2)^{-2}-c_1^2(mt+l_2)^{\frac{-6}{m}} \bigr] $$
(65)

The scalar curvature R becomes constant as t→∞.

In this model the trace T is given by

$$\begin{aligned} T =&-\frac{1}{\alpha(\alpha+1)} \biggl[(1-6\alpha m+11\alpha+2m) (mt+l_2)^{-2} \\ &{}+\frac{c_1}{3a_2^3}(mt+l_2)^{\frac{-3-m}{m}}+\frac{(8\alpha +4)c_1^2}{9a_2^6}(mt+l_2)^{\frac{-6}{m}} \biggr] \end{aligned}$$
(66)

Using the above R and T, the f(R,T) gravity from equation (10) obtained as

$$\begin{aligned} f(R,T) =&\frac{\lambda}{9a_2^6\alpha(\alpha+1)} \bigl[\bigl\{ 36(m-2)\alpha^2+(90 \alpha-18)m \\ &{}-171\alpha-9\bigr\} a_2^6(mt+l_2)^{-2} \\ &{}+3c_1a_2^3(mt+l_2)^{\frac{-3-m}{m}} \\ &{}+\bigl(6\alpha^2+14\alpha+4\bigr)c_1^2(mt+l_2)^{\frac{-6}{m}} \bigr] \end{aligned}$$
(67)

4.3 Model 3

From equation (39), let us consider k>0, m≥0 and l 3=0 (Akarsu and Dereli 2012). Hence we get

$$ a=a_3 e^{\frac{2}{m}\arctan h(\frac{kt}{m}-1)} $$
(68)

Using equation (65) in (24) and (25), we obtain the values of scale factors as

$$\begin{aligned} A =&a_3c_2^{1/3} \exp\biggl[\frac{2}{m} \arctan h \biggl(\frac{kt}{m}-1 \biggr) \\ &{}-\frac{2c_1}{ka_3^2} \biggl\{ \biggl(\frac{kt}{m}-1 \biggr)\arctan h \biggl(\frac{kt}{m}-1 \biggr) \\ &{}+\frac{1}{2}\ln\biggl|1- \biggl(\frac{kt}{m}-1 \biggr)^2\biggr| \biggr\} \biggr] \end{aligned}$$
(69)

and

$$\begin{aligned} B =&a_3c_2^{-2/3} \exp\biggl[\frac{2}{m} \arctan h \biggl(\frac{kt}{m}-1 \biggr) \\ &{}+\frac{4c_1}{ka_3^2} \biggl\{ \biggl( \frac{kt}{m}-1 \biggr)\arctan h \biggl(\frac{kt}{m}-1 \biggr) \\ &{}+\frac{1}{2}\ln\biggl|1- \biggl(\frac{kt}{m}-1 \biggr)^2\biggr| \biggr\} \biggr] \end{aligned}$$
(70)

Using (69) and (70), we get the mean Hubble parameter as

$$ H=-\frac{2}{kt(t-t_R)}, $$
(71)

and the directional Hubble parameters as \(H_{1}=H-\frac{2c_{1}\xi}{ma_{3}^{3}}\) and \(H_{2}=H+\frac{4c_{1}\xi}{ma_{3}^{3}}\), where, \(t_{R}=\frac{2m}{k}\) and \(\xi =\arctan h (\frac{kt}{m}-1 )\). When t→0 the Hubble parameter H→∞ and it vanishes at infinite future.

The scalar expansion θ and shear scalar σ 2 are obtained as

$$ \theta=-\frac{6}{kt(t-t_R)},\qquad \sigma^2=\frac{12c_1^2}{m^2a_3^6} \xi^2 $$
(72)

The anisotropy parameter of the expansion is found to be

$$ \Delta= \frac{2c_1^2k^2t^2(t-t_R)^2}{m^2a_3^6}\xi^2 $$
(73)

From the above it is observed that the deceleration parameter is positive at the early stage of the universe. This represents the early deceleration phase of the universe. Present observational data (Ade et al. 2013) indicates that the universe is accelerating and the value of the deceleration parameter lies somewhere in the range −1<q<0. Choosing the values of k=0.097 and m=1.6, the universe enters into acceleration phase at t≈6.2 and the present (t=13.798) value of the deceleration parameter is q≅−0.7386. Therefore these values are consistent with observational results.

Using the values of directional Hubble parameters, we obtain the pressure, energy density and cosmological constant as

$$\begin{aligned} &p=\frac{2}{\alpha(\alpha+1)} \biggl[\bigl\{ (2\alpha +1)\bigl[kt\bigl(2a_3^3+c_1t\bigr)-2m\bigl(a_3^3+c_1t\bigr)\bigr] \\ &\phantom{p=\,}+(6\alpha +1)a_3^3\bigr\} \bigl\{ a_3^3t^2k^2(t-t_R)^2\bigr\} ^{-1}+\frac{(6\alpha+4)c_1^2}{m^2a_3^6} \xi^2 \\ &\phantom{p=\,}+\frac{(12\alpha+5)c_1}{ma_3^2kt(t-t_R)} \xi\biggr] \end{aligned}$$
(74)
$$\begin{aligned} &\rho=\frac{2}{\alpha(\alpha+1)} \biggl[\bigl\{ kt\bigl(2a_3^3+c_1t\bigr)-2m\bigl(a_3^3+c_1t\bigr) \\ &\phantom{\rho=\,}+(2-2\alpha )a_3^3\bigr\} \bigl\{ a_3^3k^2t^2(t-t_R)^2\bigr\} ^{-1}+\frac{(4\alpha+3)c_1^2}{m^2a_3^6} \xi^2 \\ &\phantom{\rho=\,}+\frac{(2\alpha+3)c_1}{ma_3^2kt(t-t_R)}\xi\biggr] \end{aligned}$$
(75)

and

$$\begin{aligned} \varLambda =& -\frac{2}{\alpha+1} \biggl[\frac {kt(2a_3^3+c_1t)-2m(a_3^3+c_1t)+4a_3^3}{a_3^3k^2t^2(t-t_R)^2} \\ &{}+\frac{4c_1^2}{m^2a_3^6} \xi^2+\frac{8c_1}{ma_3^2kt(t-t_R)}\xi\biggr]. \end{aligned}$$
(76)

The equation of state parameter ω is given by

$$\begin{aligned} \omega =& \bigl\{ (2\alpha +1)m^2a_3^3\bigl[kt\bigl(2a_3^3+c_1t\bigr)-2m\bigl(a_3^3+c_1t\bigr)\bigr] \\ &{}\times(6\alpha+1)m^2a_3^6+kt(t-t_R)(6\alpha+4)c_1^2\xi^2 \\ &{}+(12\alpha+5)(t-t_R)ktmc_1a_3^4\xi \bigr\} \bigl\{ m^2a_3^3\bigl[kt\bigl(2a_3^3+c_1t\bigr) \\ &{}-2m\bigl(a_3^3+c_1t\bigr)+(2-2\alpha )a_3^3\bigr]-kt(t-t_R)(4\alpha+3) \\ &{}\times c_1^2\xi^2+(2\alpha+3)(t-t_R)ktmc_1a_3^4\xi\bigr\} ^{-1}, \end{aligned}$$
(77)

The assumption of a linearly varying deceleration parameter as in equation (36) with k>0 and m>0 limits the life time of the universe. It starts with a big bang at an initial epoch t i =0 with zero spatial volume and large energy density. With the growth of cosmic time, the scale factor and the energy density of the cosmic fluid diverge very fast leading to a Bip Rip singularity (Caldwell et al. 2003; Nojiri et al. 2005) at a finite time \(t_{R}=\frac{2m}{k}\). At the beginning, we have a deceleration parameter q i =m−1, which for m>1 is positive signifying a decelerating universe. However with the growth of cosmic time, a transition from deceleration to acceleration occurs at \(t_{a}=\frac{m-1}{k}\) when the deceleration parameter becomes negative. At a time, \(t_{R}=\frac{2m}{k}\), when the repulsive phantom energy rips apart the universe by overcoming the binding force (Big Rip), the deceleration parameter becomes q=−(m+1). The mean Hubble parameter and the directional Hubble rates diverge both at the beginning and at the Big Rip. However, in the intermediate phase of cosmic evolution between the Big Bang and Big Rip, the Hubble rates evolve with time. At the time of transition from a deceleration to acceleration (Nojiri et al. 2010b), the mean Hubble rate becomes \(H_{a}=\frac{2k}{m^{2}-1}\).

The equation of state parameter exhibits different behaviour at different phases of cosmic evolution. At Big Bang (t i ), \(\omega=\frac {(2\alpha+1)(6\alpha+1)m^{3} a_{3}^{6}}{m-1+\alpha}\), whereas at Big Rip (\(t_{R}=\frac{2m}{k}\)), it becomes, \(\omega=\frac{(2\alpha+1)(6\alpha +1)m^{3} a_{3}^{6}}{m+1-\alpha}\). If we take m=1.6, as has been considered in Akarsu and Dereli (2012), the equation of state parameter evolves from a positive value at the Big Bang to a negative value at the time of Big Rip. Obviously, at the time of Big Rip, the equation of state is in the phantom region with value less than −1 ( ω<−1).

The Ricci scalar R for this model is obtained as

$$ R=-2 \biggl[\frac{12(kt-m+2)}{k^2t^2(t-t_R)^2}+\frac {8c_1}{ma_3^3kt(t-t_R)}\xi+\frac{12c_1^2}{m^2a_3^6} \xi^2 \biggr] $$
(78)

The trace of the model T is given by

$$\begin{aligned} T =&\frac{-2}{\alpha(\alpha+1)} \biggl[\bigl\{ (6\alpha +2)\bigl[kt\bigl(2a_3^3+c_1t\bigr) \\ &{}+(36\alpha+20)m\bigl(a_3^3+c_1t\bigr)\bigr]+(4\alpha -1)a_3^3\bigr\} \\ &{}\times\bigl\{ a_3^3k^2t^2(t-t_R)^2\bigr\} ^{-1}+\frac{(34\alpha +12)c_1}{ma_3^2kt(t-t_R)}\xi \\ &{}+\frac{(14\alpha+9)c_1^2}{m^2a_3^6}\xi^2 \biggr] \end{aligned}$$
(79)

The reconstruction of the functional f(R,T) in the present model with the assumption f(R,T)=λ(R+T) obtained as

$$\begin{aligned} f(R,T) =&\frac{-2\lambda}{\alpha(\alpha+1)} \biggl[\bigl\{ a_3^3\bigl[kt\bigl(12\alpha ^2+24\alpha+4\bigr) \\ &{}+\bigl(24\alpha^2+28\alpha-1\bigr)+m\bigl(20+24\alpha-12\alpha ^2\bigr)\bigr] \\ &{}+(6\alpha kt+2kt+36\alpha m+20m)c_1t\bigr\} \\ &{}\times\bigl\{ a_3^3k^2t^2(t-t_R)^2\bigr\} ^{-1} \\ &{}+\frac{\{8\alpha(\alpha+1)+(34\alpha+12)a_3\}c_1}{ma_3^3kt(t-t_R)}\xi \\ &{}+\frac{(12\alpha^2+26\alpha+9)c_1^2}{m^2a_3^6}\xi^2 \biggr] \end{aligned}$$
(80)

It is worth to mention here that, this particular f(R,T) model leads to an effective cosmological constant described through the trace of the stress-energy tensor which should evolve with the cosmic expansion. In this third model with a linearly varying deceleration parameter, it is found that, the effective cosmological constant diverges both at the initial phase t i and at Big Rip t R . It may be concluded that, during the Big Bang, obviously the large value of the cosmological constant in the form of vacuum energy density may have triggered the cosmic expansion. Similarly at the time Big Rip, may be the large value of cosmological constant has certain role in accruing the phantom energy that overcomes the usual binding force of the universe to rip it apart.

5 Field equations and its solutions for f 1(R)=λR and f 2(T)=λT 2

In this case we consider the linear for of R as f 1(R)=λR and f 2(T)=λT 2 which yield f(R,T)=λ(R+T 2). Using this the field equations of f(R,T) gravity from equation (4) becomes

$$ R_{ij}-\frac{1}{2}Rg_{ij}= \biggl(\frac{8\pi+2\lambda T}{\lambda} \biggr)T_{ij}+ \biggl(2pT+\frac{1}{2}T^2 \biggr)g_{ij} $$
(81)

This can be rearranged as

$$ G_{ij}- \biggl(2pT+\frac{1}{2}T^2 \biggr)g_{ij}= \biggl(\frac{8\pi+2\lambda T}{\lambda} \biggr)T_{ij} $$
(82)

Comparing the above equation with equation (16), we get

$$ \varLambda_{\mathit{eff}}=2pT+\frac{1}{2}T^2 $$
(83)

and

$$ G_{\mathit{eff}}=\frac{1}{\lambda}+\frac{2T}{8\pi}. $$
(84)

Λ eff and G eff are respectively the time dependent effective cosmological constant and the time dependent effective Newtonian gravitational constant. It is interesting to note here that, the choice f 1(R)=λR and f 2(T)=λT 2 leads to an effective Newtonian gravitational constant which depends on the stress-energy tensor T and obviously become time dependent.

The field equations for this particular model become

$$\begin{aligned} &H_1^{\prime}+H_2^{\prime}+H_1^2+H_2^2+H_1H_2 \\ &\quad{}=\frac{8\pi}{\lambda}p+3p\rho-\frac{9}{2}p^2-\frac{1}{2} \rho^2 \end{aligned}$$
(85)
$$\begin{aligned} &2H_1^{\prime}+3H_1^2= \frac{8\pi}{\lambda}p+3p\rho-\frac{9}{2}p^2-\frac{1}{2} \rho^2 \end{aligned}$$
(86)
$$\begin{aligned} &H_1^2+H_1H_2=- \frac{8\pi}{\lambda}\rho+\frac{3}{2}p^2+7p\rho- \frac{5}{2}\rho^2 \end{aligned}$$
(87)

The above set of field equations give the values of metric potential A and B same as that of equations (25) and (26) respectively. The field equations are highly non-linear in nature and in order get viable models, we assume a barotropic equation of state described through the relationship p=ωρ. Here ω is the equation of state parameter and for the sake of simplicity, it is assumed to be constant quantity.

One can note from the discussion in the previous choice of the functional f(R,T)=λ(R+T) that, the first two cases corresponding to the power law and exponential expansion of the volume scale factor are trivial in the sense that they have been studied widely and does not reproduce the time dependence of the deceleration parameter. The two specific cases, even though, have importance in getting the dynamics of the universe, have a little priority in the context of the linearly varying deceleration parameter. In view of this, in the present section, we restrict ourselves to the third case only. Using equations (69) and (70), the values of ρ and p are obtained as

$$\begin{aligned} \rho =& \frac{\lambda}{8\pi(E+\omega F)} \biggl[\frac{a_3^3\{8(kt-m)+12\} +4c_1kt}{a_3^3k^2t^2(t-t_R)^2}F \\ &{}+\frac{4c_1(6F-E)t\xi -8a_3^3mE}{a_3^3kt^2m(t-t_R)} \\ &{}+\frac{4c_1^2(3F+E)}{m^2a_3^6}\xi^2 \biggr] \end{aligned}$$
(88)

and

$$\begin{aligned} p =& \frac{\omega\lambda}{8\pi(E+\omega F)} \biggl[\frac{a_3^3\{ 8(kt-m)+12\}+4c_1kt}{a_3^3k^2t^2(t-t_R)^2}F \\ &{}+\frac{4c_1(6F-E)t\xi -8a_3^3mE}{a_3^3kt^2m(t-t_R)} \\ &{}+\frac{4c_1^2(3F+E)}{m^2a_3^6}\xi^2 \biggr] \end{aligned}$$
(89)

where

$$ E=3\omega-\frac{9}{2}\omega^2-\frac{1}{2} \quad\text{and}\quad F=7\omega+\frac{3}{2}\omega^2- \frac{5}{2} $$
(90)

Different choice of the equation of state parameter ω will lead to different cosmological phases of the universe. It is clear from the above expressions that, the model provides unphysical results for a radiation dominated era with \(\omega=\frac{1}{3}\) for which both E and F vanish. Also, for a vacuum energy dominated universe with ω=−1, the factor E+ωF vanishes which results in an infinitely large values for the energy density and pressure. However, for \(\omega=-\frac{1}{3}\), \(\omega=-\frac{2}{3}\) and \(\omega=-\frac {1}{2}\), the values of the parameter pair (E,F) becomes \((-2,-\frac {14}{3})\), \((-\frac{9}{2},-\frac{13}{2})\) and \((-\frac{25}{8},-\frac {45}{8})\) respectively. Consequently, the factor E+ωF for these choices of ω becomes \(-\frac{4}{9}, -\frac {1}{6}\) and \(-\frac{5}{16} \). Therefore, we expect that, we can get viable models for these specific choices of the equation of state parameter. If we interpolate the results, we can expect to get reasonably good models within the region dominated by quintessence behaviour.

The trace of the model is obtained as

$$\begin{aligned} T =& \frac{(1-3\omega)\lambda}{8\pi(E+\omega F)} \biggl[\frac{a_3^3\{ 8(kt-m)+12\}+4c_1kt}{a_3^3k^2t^2(t-t_R)^2}F \\ &{}+\frac{4c_1(6F-E)t\xi -8a_3^3mE}{a_3^3kt^2m(t-t_R)} \\ &{}+\frac{4c_1^2(3F+E)}{m^2a_3^6}\xi^2 \biggr] \end{aligned}$$
(91)

It is interesting to note from the above discussion that, although we can get viable models in the region described by \(-\frac{2}{3} \le \omega\le-\frac{1}{3}\), the Big Rip situation can not be avoided. The Big Rip situation may be inherent in the deceleration parameter we have chosen to mimic it to be time dependent simulating a transition from early deceleration to late time acceleration.

6 The jerk parameter

Observations confirm that in the early stages of the universe, the dark energy would have been too small to counteract the gravity of the matter in universe and the expansion would have initially slowed. After the universe grew big enough the dark energy would dominate and the universe would start to accelerate (Capozziello et al. 2006). Cosmologists believe that the universe transitional from deceleration to acceleration in a cosmic jerk. Hence the knowledge of jerk was important step in figuring out just what the dark energy is. The deceleration to acceleration phase of the universe occurs for different models with negative value of deceleration parameter and positive value of jerk parameter. (Sahni 2002; Visser 2004). As we know flat ΛCDM model have a constant jerk j=1. It is defined as a dimensionless third derivative of the scale factor with respect to the cosmic time

$$ j(t)=\frac{1}{H^3}\frac{a^{\prime\prime\prime}}{a} $$
(92)

Now we solve the equation (92) by putting the values of average scale factor a from equations (37)–(39) for three different physically viable cosmologies.

Case (A) When k=0 and m=0, we get

$$ j(t)=1 $$
(93)

This value overlaps with flat ΛCDM models.

Case (B) When k=0 and m>0, we get

$$ j(t)=(m-1) (2m-1) $$
(94)

This value overlaps with flat ΛCDM models for \(m=\frac{3}{2}\).

Case (C) When k>0 and m≥0, we get

$$ j(t)=\frac{3}{2}k^2t^2-3(m-1)kt+2m^2-3m+1 $$
(95)

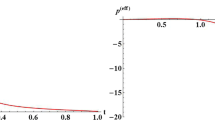
The cases A and B refer to the exponential expansion and power law expansion of the volume scale factor and have been studied widely in literature. However, the third refers to an interesting cosmological model. In view of this, we have plotted the jerk parameter for this third case only as a function of cosmic time in Fig. 1. In the numerical code, we have used the values of k and m to be 0.097 and 1.6 respectively. The jerk parameter initially decreases with the growth of cosmic time upto t=6.2 and then increases with time. It is clear from the figure that the jerk parameter remains in the positive domain throughout the entire history of the universe. For low values as well as large values of cosmic time, the jerk parameter assumes larger value compared to that of ΛCDM model. However, it is interesting to note from the figure that, the present model becomes closer to the ΛCDM model twice in the cosmic evolution i.e. at t≈2.23 and at t≈10.14.

Fig. 1
figure 1

Jerk parameter vs. time

Full size image

7 State-finder diagnosis

To have a geometric view of the dark energy models, Sahni et al. (2003) first introduced a cosmological diagnostic parameter set {r,s} called State-finder pair. The State-finder parameters depend only on the scale factor. The important property of the state-finder pair is that {r,s}={1,0} is a fixed point in the s−r plane for the spatially flat ΛCDM model. The state-finder parameters r and s are defined as follows:

$$\begin{aligned} &r=\frac{a^{\prime\prime\prime}}{aH^3} \end{aligned}$$
(96)
$$\begin{aligned} &s=\frac{r-1}{3(q-\frac{1}{2})} \end{aligned}$$
(97)

For the three different cases of cosmological models as set by the linearly varying deceleration parameter, it is straightforward to calculate the State finder pair by putting the values of average scale factor a from equations (37)–(39).

Case (A): For this case i.e. k=0 and m=0, we get the State finder pair as {1,0} which overlaps with the ΛCDM model. This is obvious because, this case predicts a de Sitter universe where the expansion is exponential and is controlled by a constant Hubble parameter.

Case (B): In this case, i.e. for k=0 and m>0, the State finder parameter pair become

$$\begin{aligned} \begin{aligned} &r = (m-1) (2m-1),\\ &s = \frac{(2m-3)m}{3(m-kt-\frac{3}{2})}. \end{aligned} \end{aligned}$$
(98)

The State finder pair depend on the parameters k and m of the deceleration parameter. Also, r is independent of cosmic time whereas s is time dependent. The magnitude of s decreases with the growth of cosmic time. However, for a specific choice \(m=\frac{3}{2}\), the State-finders parameters overlaps with flat ΛCDM model.

Case (C): For the third case with k>0 and m≥0, the State finder parameters are calculated to be

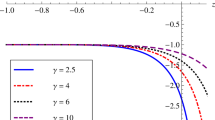
$$\begin{aligned} \begin{aligned} &r = 1+\frac{1}{2}\bigl[6(kt-m)+3kt(kt-2m)+4m^2\bigr],\\ &s = -\frac{2(kt-m)+kt(kt-2m)+\frac{4m^2}{3}}{2(kt-m)+3}. \end{aligned} \end{aligned}$$
(99)

In the present case the State-finder parameters depend on the cosmic time t and the deceleration parameters m and k. The dynamics of the universe as depicted from the geometrical features of the model is shown as the r−s trajectory in the Fig. 2. Here also, we use the value m=1.6 and k=0.097 for our numerical calculation. Fig. 2 shows that within the limits of the present model with a linearly varying deceleration parameter, the universe passes through a phase close to the ΛCDM model at the point (r=1,s=0) at a cosmic time t≈10.13. This clearly imply that at late time cosmic evolution, the dark energy dominates and drives the cosmic acceleration.

Fig. 2
figure 2

s−r vs. time

Full size image

8 Conclusion

In this paper, we have studied spatially homogeneous and anisotropic LRS Bianchi type-I cosmological models with linearly varying deceleration parameter in the framework of a modified gravity theory known as f(R,T) gravity. Following the works of Akarsu and Dereli (2012), we have considered a special law for deceleration parameter which is linear in time with a negative slope. This law covers a wide range of the deceleration parameter including the constant deceleration parameter law proposed by Berman (1983). For different probable combination of the deceleration parameter, we have considered three specific models signifying three different scale factors. The cosmological consequences of first two models that correspond to an exponential expansion and power law expansion have already been discussed earlier by several authors for f(R,T)=R+2f(T).

First of all, the gravitational field equations has been established with f(R,T)=f 1(R)+f 2(T), in particular f(R,T)=λ(R+T). In model 1, it has been found that the cosmological constant is a negative increasing function of time and it converges to a small positive value at late time. In model 2, at \(t=-\frac{l_{2}}{m}\) we have found a point type singularity at initial epoch. It is interesting to note that in the third model the universe ends with a big rip. Expressions for some important cosmological parameters have been obtained and the physical behaviour of the models are discussed in detail. We observed that in case of f(R,T)=λ(R+T), the metric potentials admit the same solution as f(R,T)=f 1(R)+f 2(T). The solutions obtained here are new and useful for a better understanding of the evolution of the universe in LRS Bianchi type-I universe with variable Λ.

Further, one may note that, in the present model of f(R,T), if we consider an isotropic universe such as FRW, we may not get such results. In FRW model, f(R,T)=λ(R+T) leads to a model with an effective cosmological constant where the cosmic fluid behaves fluid with pressure p=−ρ and the equation of state becomes ω=−1. However, in an anisotropic model such as the one considered in the present work, the scenario changes and we get an evolving equation of state parameter.

Secondly, we derive the f(R,T) gravity field equations with f(R,T)=λ(R+T 2). We obtain an exact solution of the field equations by considering the barotropic equation of state for perfect fluid. Physical and kinematical aspects of the universe are studied. With this choice of the functional f(R,T) and the equation of state, the model is dominated by quintessence behaviour. Moreover, our results show that the cosmic jerk parameter of the derived model is positive throughout the entire history of the universe. From the State-finder trajectory in the s−r plane as shown in Fig. 2, we have found that our model cross the ΛCDM fixed point {s=0,r=1} at the cosmic time t≈10.13.

Interestingly, we found from the present study that, the Big Rip situation can not be avoided within the present framework of f(R,T) gravity, what ever may be the functional form chosen for f(R,T). The Big Rip singularity may be inherent in the linearly varying deceleration parameter chosen to mimic the transition of the universe from a decelerated one to an accelerated one at late times of cosmic evolution. We may conclude that, care must be taken, when such parametrization of the deceleration parameter is considered for addressing different issues of cosmology. However, the present issue demands further intensive investigation considering different gravity models and parameter sets.