1 Introduction

In recent years there has been a lot of interest in modified theories of gravity in view of the direct evidence of late time accelerated expansion of the universe which comes from high red shift supernova experiment (Riess et al. [1, 2], Perlmutter et al. [3], Bennett [4]). Among the various modifications of general relativity, f(R) (Akbar and Cai [5]) and f(R,T) (Harko et al. [6]) theories of gravity are treated most seriously during the last decade. These theories are supposed to provide natural gravitational alternatives to dark energy. It has been suggested that cosmic acceleration can be achieved by replacing Einstein-Hilbert action of general relativity with a general function f(R) where R is a Ricci scalar. Chiba et al. [7], Nojiri and Odintsov [8, 9], Multamaki and Vilja [10, 11], and Shamir [12] are some of the authors who have investigated several aspects of f(R) gravity models which show the unification of early time inflation and late time acceleration.

Subsequently, Harko et al. [6] proposed another extension of standard general relativity, f(R,T) modified theory of gravity wherein the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar R and of the trace of the stress-energy tensor T. They have derived the field equations from Hilbert-Einstein type variational principle. The covariant divergence of the stress energy tensor is also obtained. The f(R,T) gravity model depends on a source term, representing the variation of the matter energy tensor with respect to the metric. They have also demonstrated the possibility of reconstruction of arbitrary FRW cosmologies by an appropriate choice of a function (T).

Dark energy and dark energy models in general relativity and in modified theories of gravity have, recently, become an interesting subject of investigation for several authors (Sahni and Starobinsky [13], Padmanabhan [14], Caldwell [15], Nojiri and Odintsov [16], Kamenshchik et al. [17] Wang et al. [18], Setare [19], Naidu et al. [20], Rao et al. [21]). Dark energy is usually characterized by the equation of state (EoS) parameter given by \(\omega(t) = \frac{p}{\rho} \) which is not necessarily constant, where p is the fluid pressure and ρ is energy density. Caroll and Hoffman [22], Ray et al. [23], Akarsu and Kilinc [24], Yadav and Yadav [25], Pradhan et al. [26], Amirhashchi [27] have studied dark energy models with variable EoS parameter.

Spatially homogeneous and anisotropic cosmological models are important in the discussion of large scale structure of the universe and such models have been studied in general relativity to realize the picture of the universe in it’s early stages. Yadav et al. [28], Pradhan et al. [29] have investigated homogeneous and anisotropic Bianchi type-III space time in the context of massive strings. Yadav and Yadav [30] has obtained Bianchi type-II anisotropic dark energy model with constant deceleration parameter. Recently, Pradhan and Amirhashchi [31] have investigated a new anisotropic Bianchi type-III dark energy model, in general relativity, with equation of state (EoS) parameter without assuming constant deceleration parameter. Very recently, Naidu et al. [32–34] have presented Bianchi type-II and III dark energy models in Saez-Bellaster [35] scalar-tensor theory of gravitation. While Reddy et al. [36] have obtained five dimensional Kaluza-Klein cosmological model in f(R,T) gravity. Motivated by the above work’s we have investigated, in this paper Bianchi-III anisotropic dark energy cosmological model with variable EoS parameter in f(R,T) gravity, choosing an appropriate form of f(T) proposed by Harko et al. [6]. This paper is organized as follows. In Sect. 2, the metric and the field equations are obtained in this theory. Section 3 deals with the solution of the field equations. In Sect. 4 some physical properties of the derived dark energy model are discussed. The last section contains conclusions.

2 Metric and Field Equations

We consider spatially homogeneous and anisotropic Bianchi type-III metric given by

$$ ds^2 = dt^2 - A^2 (t) dx^2 - e^{-2 \alpha x} B^2 (t) dy^2 - C^2 (t) dz^2 $$
(1)

where A, B and C are cosmic scale factors and m is a positive constant. The energy momentum tensor for anisotropic dark energy is given by

$$ T^i_j = \mathit{diag}[\rho, -p_x -p_y- p_z] = \mathit{diag}[1 - \omega_x - \omega_y- \omega_z]\rho $$
(2)

where ρ is the energy density of the fluid and p x , p y , p z are the pressures along x, y and z axes respectively. Here ω is the EoS parameter of the fluid and ω x , ω y , and ω z are the EoS parameters in the directions of x, y and z axes respectively. The energy momentum tensor can be parameterized as

$$ T^i_j = \mathit{diag}\bigl[1, -\omega, - (\omega+ \gamma), - (\omega+ \delta)\bigr]\rho. $$
(3)

For the sake of simplicity we choose ω x =ω and the skewness parameters γ and δ are the deviations from ω on y and z axes respectively.

Now varying the action

$$ S = \frac{1}{16 \pi} \int f(R, T) \sqrt{-g} d^4 x + \int L_m \sqrt {-g} d^4 x $$
(4)

Of the gravitational field with respect to the metric tensor components g ij , we obtain the field equations of f(R,T) gravity model as (Harko et al. [6])

(5)

where

$$ \everymath{\displaystyle} \begin{array}{l} T_{ij} = - \frac{2}{\sqrt{-g}} \frac{\delta(\sqrt{-g})}{\delta g^{ij}} L_m, \quad \varTheta_{ij} = - 2T_{ij} -p g_{ij}, \\[10pt] f_R (R, T) = \frac{\partial f (R, T)}{\partial R} \quad\mbox{and}\quad f_T (R, T) = \frac{\partial f (R, T)}{\partial T} \end{array} $$
(6)

Here f(R,T) is an arbitrary function of Ricci scalar R and of the trace T of the stress energy tensor of matter T ij and L m is the matter Lagrangian density and in the present study we have assumed that the stress energy tensor of matter as

$$ T_{ij} = (\rho+ p )u_i u_j - pg_{ij} $$
(7)

Now assuming that the function f(R,T) given by Harko et al. [6]

$$ f(R, T) = R + 2f (T) $$
(8)

where f(T) is an arbitrary function of trace of the stress energy tensor of matter and using Eqs. (6) and (7), the field equations (5) take the form

$$ R_{ij}-\frac{1}{2}Rg_{ij}=8\pi T_{ij}+2f'(T)T_{ij} +\bigl[2pf'(T)+f(T)\bigr]g_{ij} $$
(9)

where the overhead prime indicates differentiation with respect to the argument. We also choose

$$ f(T) = \mu T $$
(10)

where μ is a constant (Harko et al. [6]).

Now assuming commoving coordinate system, the field equations (9) for the metric (1) with the help of (2), (3) and (10) can be written as

(11)
(12)
(13)
(14)
(15)

where an overhead dot denotes differentiation with respect to t.

3 Solution of the Field Equations

Integrating Eq. (15), we obtain

$$ B= \alpha A $$
(16)

where α is a constant of integration which can be taken as unity without loss of generality, so that we have

$$ B= A $$
(17)

Using Eq. (17) in Eqs. (12) and (13) we obtain

$$ \gamma= 0 $$
(18)

Now using Eqs. (17) and (18) in the field equations (11)–(14) we get

(19)
(20)
(21)

The average scale factor a and the spatial volume V are defined as

$$ a = \sqrt[3]{A^2C}, \qquad V= a^3 = A^2 C $$
(22)

The generalized mean Hubble parameter H is given by

$$ H = \frac{1}{3} (H_1 + H_2 +H_3) $$
(23)

where \(H_{1} = \frac{\dot{A}}{A} = H_{2}\), \(H_{3} = \frac{\dot{C}}{C}\) are the directional Hubble’s parameters in the directions of x, y and z axes respectively. Using Eqs. (22) and (23), we obtain

$$ H = \frac{1}{3}(H_1 + H_2 +H_3) = \frac{\dot{a}}{a} $$
(24)

The expansion scalar θ and shear scalar σ are given by

(25)
(26)

The anisotropy parameter A α is given by

$$ A_{\alpha} = \sum\biggl(\frac{\Delta H_{i}}{H}\biggr)^{2} $$
(27)

where ΔH i =H i −H.

The field equations (19)–(21) are three independent equations in six unknowns, A, C, ρ, p, δ and ω. Hence to find a determinate solution three more conditions are necessary. we consider the following conditions:

  1. (i)

    we apply the variation of Hubble’s parameter proposed by Bermann [37] that yields constant deceleration parameter models of the universe defined by

    $$ q = - \frac{a\ddot{a}}{\dot{a}^z} = \mathrm{constant} $$
    (28)

    where the scale factor a is given by Eq. (22).

  2. (ii)

    we assume that the scalar expansion θ is proportional to shear scalar σ which gives us (Collins et al. [38])

    $$ C = A^m $$
    (29)

    where m>1 is a constant.

  3. (iii)

    the EoS parameter ω is proportional to skewness parameter δ (mathematical condition) such that

    $$ \omega+ \delta= 0 $$
    (30)

    The solution of Eq. (28) is given by

    $$ a = (ct + d )^{\frac{1}{1+ q}} $$
    (31)

    where c≠0 and d are constants of integration and 1+q>0 for accelerated expansion of the universe.

Now using Eqs. (22), (29) and (31) the expressions for the metric coefficients in the field equations are

(32)
(33)

Now with a suitable choice of coordinates and constants, the metric (1) with the help of (30) and (31) can be written as

$$ ds^{2}=dt^{2}-t^{\frac{\varepsilon}{(m+z)(1+q)}} \bigl[dx^{2}+e^{-mx}dy^{2}\bigr] -t^{\frac{\varepsilon m}{(m+z)(1+q)}}dz^{2} $$
(34)

This model is similar to the Bianchi type-III dark energy model obtained by Pradhan and Amirhashchi [31].

4 Some Physical Properties of the Model

Equation (34) represents Bianchi type-III dark energy model in f(R,T) gravity with the following physical and kinematical parameters of the model which are important for discussing the physics of the cosmological model.

The spatial volume in the model is

$$ V = t ^{\frac{2}{1+q}} $$
(35)

The generalized Hubble’s parameter is

$$ H = \frac{2}{3(1+q)t} $$
(36)

The scalar expansion in the model is

$$ \theta = \frac{2}{(1+q)t} $$
(37)

The shear scalar in the model is

$$ \sigma^2 = \frac{4 (m-1)^2}{3 [(1+q)(m+2)t]^2} $$
(38)

The mean anisotropy parameter is

$$ A_{\alpha} =\frac{2(m-2)^{2}}{3(m+2)^{2}} $$
(39)

Now with the help of (30) we obtain the following physical parameters in the model (34):

The energy density in the model is

$$ \rho= \frac{1}{(8 \pi+ 2 \mu)} \biggl[ \frac{8(1-m) -4(1+q)(m+2)}{(1+q)^2(m+2)^2} \biggr] \frac{1}{t^2} = -p $$
(40)

Since in the case of accelerated expansion we have ρ+p=0.

The EoS and skewness parameters in the model are

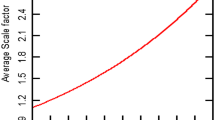
$$ \omega= - 1 + \frac{1}{\rho(8 \pi+ 2 \mu)} \biggl[\frac{8 (1-m)-4(1+q)(m+2)}{(1+q)^2 (m+2)^2} \biggr] \frac{1}{t^2} = -\delta $$
(41)

It may be observed that the cosmological model in f(R,T) gravity is free from initial singularity, i.e. at t=0. The spatial volume in this model increase as t increases confirming accelerated expansion of the universe. It can also be observed that H, θ, σ, δ, ω and p are functions of t and vanish for large t while they diverge for t=0.

Also, \(\frac{\sigma^{2}}{\theta^{2}} = \frac{(m-1)^{2}}{3 (m-2)^{2}}\neq0\) and hence the model does not approach isotropy for large values of t. However the model becomes isotropic for m=1, because in this case, in view of Eqs. (17) and (29), the metric (1) becomes ds 2=dt 2−A 2(t)[dx 2−e −2αx dy 2−dz 2].

It may be mentioned that the behavior of the physical parameters and the dark energy model in this case is quite similar to physical parameters an the Bianchi type-III dark energy model obtained by Pradhan and Amirhashchi [31].

5 Conclusions

It is well known that anisotropic dark energy models with variable EoS parameter in modified theories of gravity play a vital role in the discussion of the accelerated expansion of the universe which is the crux of the problem in the present scenario. In this paper we have investigated homogeneous and anisotropic Bianchi type-III dark energy model in f(R,T) gravity with variable EoS parameter in the presence of perfect fluid source. It is observed that EoS parameter, skewness parameters in the model are all functions of t. It can also be seen that the model is accelerating, expanding, non-rotating and has no initial singularity. This model confirms the high redshift supernova experiment. The dark energy model obtained in this theory, it is observed, is similar to the Bianchi type-III anisotropic dark energy model and its behavior obtained by Pradhan and Amirhashchi [31].