1 Introduction

Recent cosmological observations have revolutionized our understanding on cosmology. It suggests to us that the present observable universe is undergoing an accelerated expansion (Riess et al. 1998; Perlmutter et al. 1999; and Bennet et al. 2003). The source driving this acceleration is known as ‘dark energy’ whose origin is still a mystery in modern cosmology. This is because of the fact that we do not have, so far, a consistent theory of quantum gravity. The accelerated expansion of the universe is driven by the negative pressure of dark energy. The ‘cosmological constant’ is the most simple and natural candidate for explaining cosmic acceleration, but it faces serious problems and a large discrepancy between theory and observations (Copeland et al. 2006; Nojiri and Odintsov 2007).

Recently, new evidence coming from astrophysics and cosmology revealed a quite unexpected picture of the Universe. Our latest datasets coming from different sources, such as the Cosmic Microwave Background Radiation (CMBR) and Supernovae surveys, seem to indicate that the energy budget of the Universe is the following: 4 % ordinary baryonic matter, 22 % dark matter and 74 % dark energy (Riess et al. 2004; Eisenstein et al. 2005; Astier et al. 2006; Spergel et al. 2007). Therefore, in recent years, there has been a lot of interest in constructing dark energy models by modifying the geometrical part of Einstein-Hilbert action of general relativity. This approach is called the modified gravity which can successfully explain the rotation curves of galaxies and the motion of galaxy clusters in the universe. Among the various modifications, f(R) theory of gravity is treated as most suitable due to its cosmological importance. It has been suggested that cosmic acceleration can be achieved by replacing the Einstein-Hilbert action of general relativity with a general function of Ricci scalar, f(R). In view of the late time acceleration of the universe and the existence of dark energy and dark matter, very recently modify theory of gravity has been developed. Noteworthy amongst them are f(R) theory of gravity proposed by Nojiri and Odintsov (2003) and f(R,T) theory of gravity proposed by Harko et al. (2011). Nojiri and Odintsov (2007), Multamaki and Vilja (2006, 2007) and Shamir (2010) are some of the authors who have investigated several aspects of f(R) gravity models which show the unification of early time inflation and late time acceleration.

Moreover, Nojiri and Odintsov (2006a) developed the general scheme for modified f(R) gravity reconstruction from any realistic FRW cosmology. They have shown that the modified f(R) gravity indeed represents the realistic alternative to general relativity, being more consistent in dark epoch. Nojiri and Odintsov (2006b), developed a general program for unification of matter-dominated era with acceleration epoch for scalar-tensor theory of dark fluid. Nojiri and Odintsov (2007) have reviewed various modified gravities considered as gravitational alternative for dark energy. They have considered the version of f(R), f(G) or f(R,G) gravity model with non-linear gravitational coupling or string inspired model with Gauss-Bonnet-dilaton coupling in the late universe.

Very recently, Harko et al. (2011) developed a f(R,T) modified theory of gravity, where the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar R and the trace T of the stress energy tensor. They have obtained the gravitational field equations in the metric formalism, as well as the equations of motion for test particles, which follow from the covariant divergence of the stress energy tensor. The f(R,T) gravity model depends on a source term, representing the variation of the matter stress energy tensor with respect to the metric. A general expression for this source term is obtained as a function of the matter Lagrangian L m so that each choice of L m would generate a specific set of field equations. Some particular models corresponding to specific choices of the function f(R,T) are also presented, they have also demonstrated the possibility of the reconstruction of arbitrary FRW cosmologies by an appropriate choice of a function f(T). In the present model the covariant divergence of the stress energy tensor is nonzero. Hence the motion of test particles is non-geodesic and an extra acceleration due to the coupling between matter and geometry is always present.

The f(R,T) theory of gravity is the modifications of General Relativity (GR). The field equations of f(R,T) gravity are derived from the Hilbert-Einstein type variational principle. The action for the modified f(R,T) gravity is

$$ S=\frac{1}{16\pi}\int{f(R,T)\sqrt{-g}d^{4}x}+\int {L_{m}\sqrt{-g}d^{4}x} $$
(1)

where f(R,T) is an arbitrary function of Ricci scalar (R), T be the trace of stress-energy tensor (T ij ) of the matter. L m is the matter Lagrangian density. The energy momentum tensor T ij is defined as

$$ T_{ij}= - \frac{2}{\sqrt{-g}} \frac{\delta(\sqrt{-g})L_{m}}{\delta g^{ij}} $$
(2)

Here we assume that the dependence of matter Lagrangian is merely on the metric tensor g ij rather than its derivatives. In this case, we obtain

$$ T_{ij}= g_{ij}L_{m} - \frac{\partial L_m}{\partial g^{ij}} $$
(3)

The f(R,T) gravity field equations are obtained by varying the action S with respect to metric tensor g ij .

$$\begin{aligned}& f(R,T)R_{ij}-\frac{1}{2} f(R,T) g_{ij} + (g_{ij}\Box-\nabla_i\nabla_j)f_R(R,T) \\ & \quad=8\pi T_{ij}-f_T(R,T) T_{ij} -f_T(R,T) \theta_{ij} \end{aligned}$$
(4)

where

$$ \theta_{ij}= -2T_{ij}+g_{ij}L_{m} - 2g^{\alpha\beta} \frac{\partial^2 L_m}{\partial g^{ij} \partial g^{\alpha\beta}} $$
(5)

Here \(f_{R}(R,T)=\frac{\partial f(R,T)}{\partial R}\), \(f_{T}(R,T)=\frac{\partial f(R,T)}{\partial T}\), □≡∇i∇ i where ∇ i denotes the covariant derivative.

Now contraction of (4) gives

$$\begin{aligned}& f_R(R,T)R + 3\Box f_R(R,T)- 2f(R,T) \\ & \quad=8\pi T -f_T(R,T)(T+ \theta) \end{aligned}$$
(6)

where \(\theta=\theta^{i}_{i}\). Equation (6) gives a relation between Ricci scalar R and the trace T of energy momentum tensor.

Then with the use of (5), we obtain the variation of stress-energy. Using matter Lagrangian L m , the stress energy tensor of the matter is given by

$$ T_{ij}=(\rho+p)u_iu_j-pg_{ij} $$
(7)

where u i=(0,0,0,1) is the four velocity in comoving coordinates which satisfies the condition u i u i =1 and u i∇ j u i =0. ρ and p are energy density and pressure of the fluid respectively and the matter Lagrangian can be taken as L m =−p since there is no unique definition of the matter Lagrangian.

Then with the use of (5), we obtain for the variation of stress energy of perfect fluid, the following expression

$$ \theta_{ij}=-2T_{ij}-pg_{ij} $$
(8)

On the physical nature of the matter field, the field equations also depend through the tensor θ ij . Hence in the case of f(R,T) gravity depending on the nature of the matter source, we obtain several theoretical models corresponding to different matter contributions for f(R,T) gravity are possible. However, Harko et al. (2011) gave three classes of these models:

$$ f(R,T )= \left\{ \begin{array}{l} R+2f(T) \\ f_1(R)+f_2(T) \\ f_1(R)+f_2(R)f_3(R) \end{array} \right. $$
(9)

In this paper, we are focused to the first class, i.e. f(R,T)=R+2f(T), where f(T) is an arbitrary function of stress-energy tensor of matter. We get the gravitational field equations of f(R,T) gravity from (4) as

$$\begin{aligned}& R_{ij}-\frac{1}{2}Rg_{ij}=8\pi T_{ij}-2f^\prime(T)T_{ij}-2f^\prime (T)\theta_{ij}+ f(T) g_{ij} \end{aligned}$$
(10)

where the prime denotes differentiation with respect to the argument. If the matter source is a perfect fluid then the field equations (in view of Eq. (8)) becomes

$$ R_{ij}-\frac{1}{2}Rg_{ij}=8\pi T_{ij}+2f^\prime (T)T_{ij}+[2pf^\prime(T) + f(T)]g_{ij} $$
(11)

Adhav (2012) has obtained Bianchi type I cosmological model in f(R,T) gravity. Reddy et al. (2012) have discussed Bianchi type III cosmological model in f(R,T) gravity, while Reddy et al. (2013), Reddy and Santikumar (2013) studied Bianchi type III dark energy model and some anisotropic cosmological models, respectively in f(R,T) gravity. Sharif and Shamir (2009, 2010) have studied the solutions of Bianchi types I and V space times in the frame work of f(R) gravity. Shamir (2010) studied the exact vacuum solutions of Bianchi types I, III and Kantowski-Sachs space times in the metric version of f(R) gravity.

Bianchi type cosmological models are important in the sense that these are homogeneous and anisotropic in which a process of isotropization of universe is studied through the passage of time. Moreover, from theoretical point of view anisotropic universes have a greater generality than isotropic models. Space-times admitting a three-parameter group of automorphisms are important in the discussion of cosmological models. The case where group is simply transitive over the three-dimensional, constant-time subspace is particularly useful. Bianchi has shown that there are only nine distinct sets of structure constants for groups of this type so that the algebra may be easily used to classify homogeneous space-times. Thus, Bianchi type space-times admit a three parameter group of motions and hence only a manageable number of degrees of freedom. A complete list of all exact solutions of Einstein’s equations for the Bianchi types I–IX with perfect fluid matter is given by Kramer et al. (1980). Mohanty and Mishra (2002) have studied Bianchi type VI1 cosmological model in scale invariant theory. Also Mohanty and Mishra (2003) have studied Binachi types II, VIII and IX general space-times in scale invariant theory. More cosmological models were studied on Bianchi type cosmology (e.g. Mishra 2003, 2004, 2007; Mishra and Sahoo 2012). Most recently Mishra and Sahoo (2014) have studied Bianchi type VI1 cosmological model with wet dark fluid in scale invariant theory.

Motivated by above discussions and investigations in modified theories and Bianchi type cosmology, we have taken up the study of Bianchi type VI h perfect fluid cosmological model in f(R,T) gravity. This paper is organized as follows: in Sect. 2, we have derived explicit field equations in f(R,T) gravity using the particular form of f(T)=λT used by Harko et al. (2011) with the aid of Bianchi type VI h metric in the presence of perfect fluid. In Sect. 3, we have derived the exact solution to the field equations for Bianchi type VI h , h=1 and the physical properties of the model are discussed in Sect. 3.1. In Sect. 4, the field equations and its solutions for VI h , h=−1 are obtained and studied. Concluding remarks are given in Sect. 5. Finally a list of references are included. Here we have used the natural system of units with G=c=1.

2 Metric and gravitational field equations of f(R,T) gravity

We consider the Bianchi type VI h space-time in the form

$$ ds^{2}=dt^{2}-A^{2}dx^{2}-B^{2}e^{2x}dy^{2}-C^{2}e^{2hx}dz^{2} $$
(12)

with the convention x 1=x, x 2=y, x 3=z and x 4=t and A, B, C are functions of the cosmic time t. The matter tensor for the perfect fluid is

$$ \theta_{ij}=-2T_{ij}-pg_{ij}=(\rho,-p,-p,-p) $$
(13)

Using co-moving coordinates and Eqs. (7)–(8), f(R,T) gravity field equations (11) with a particular choice of the function (Harko et al. 2011)

$$ f(T)=\lambda(T), $$
(14)

where λ is constant, for the metric takes the form

$$\begin{aligned}& \frac{B_{44}}{B}+\frac {C_{44}}{C}+\frac{B_4C_4}{BC} -\frac{h}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(15)
$$\begin{aligned}& \frac{A_{44}}{A}+\frac {C_{44}}{C}+\frac{A_4C_4}{AC} -\frac{h^2}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(16)
$$\begin{aligned}& \frac{A_{44}}{A}+\frac {B_{44}}{B}+\frac{A_4B_4}{AB} -\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(17)
$$\begin{aligned}& \frac{A_4B_4}{AB}+\frac{B_4C_4}{BC}+ \frac{A_4C_4}{AC} -\frac{1+h+h^2}{A^2} \\ & \quad=-(8\pi+3\lambda) \rho+\lambda p \end{aligned}$$
(18)
$$\begin{aligned}& (1+h)\frac{A_4}{A}-\frac{B_4}{B} -h\frac{C_4}{C}=0 \end{aligned}$$
(19)

where the suffix 4 hereafter, denote ordinary differentiation with respect to t.

3 Solutions to the field equations for VI h (h=1)

In this section, we have considered h=1. Then the set of field equations (15–19) reduces to

$$\begin{aligned}& \frac{B_{44}}{B}+\frac {C_{44}}{C}+\frac{B_4C_4}{BC} -\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(20)
$$\begin{aligned}& \frac{A_{44}}{A}+\frac {C_{44}}{C}+\frac{A_4C_4}{AC} -\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(21)
$$\begin{aligned}& \frac{A_{44}}{A}+\frac {B_{44}}{B}+\frac{A_4B_4}{AB} -\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(22)
$$\begin{aligned}& \frac{A_4B_4}{AB}+\frac{B_4C_4}{BC}+ \frac{A_4C_4}{AC} -\frac{3}{A^2} \\& \quad =-(8\pi+3\lambda) \rho+\lambda p \end{aligned}$$
(23)
$$\begin{aligned}& 2\frac{A_4}{A}-\frac{B_4}{B} -\frac{C_4}{C}=0 \end{aligned}$$
(24)

Equation (24) yields A 2=k(BC) where k is the integrating constant. Without loss of generality, we assume that k=1. The set of field equations (20)–(23) after incorporating Eq. (24) reduce to a set of three linear independent equations with four unknowns A, B, p and ρ. In order to solve the system completely, we assume that the expansion scalar is proportional to the shear scalar. This condition leads to

$$ A=B^m,\quad m\neq0 $$
(25)

From Eqs. (20)–(21), we obtain

$$ \frac{B_{44}}{B}-\frac {A_{44}}{A}+3\frac{A_4B_4}{AB} -2\frac{A_4^2}{A^2}-\frac{B_4^2}{B^2} =0 $$
(26)

Using (25) in (26), we obtain two solutions: B=constant, which leads to flat space-time; and

$$ B=A^{\frac{1}{m}}=[3m(k_1t+k_2)]^{\frac{1}{3m}} $$
(27)

Subsequently,

$$ C=\frac{A^2}{B}=[3m(k_1t+k_2)]^{\frac{2m-1}{3m}} $$
(28)

Then the metric (12) can now be written as

$$\begin{aligned}& ds^{2}=dt^{2}-[3m(k_1t+k_2)]^{\frac{2}{3}}dx^{2} \\ & \phantom{ds^{2}=}{}-[3m(k_1t+k_2)]^{\frac {2}{3m}}e^{2x}dy^{2} \\ & \phantom{ds^{2}=}{} -[3m(k_1t+k_2)]^{\frac{2(2m-1)}{3m}}e^{2x}dz^{2} \end{aligned}$$
(29)

where k 1 and k 2 are integrating constants. Subsequently we can obtain the pressure and energy density of the model as in Eqs. (30) and (31) respectively.     

$$\begin{aligned}& p=\frac{[8\pi(2m^2+m)+\lambda(8m^2+5m-1)]k_1^2 + 8\pi[3m(k_1t + k_2)]^{\frac{1}{3}}}{[-(8\pi+3\lambda)^2+\lambda^2][3m(k_1t+k_2)]^2} \end{aligned}$$
(30)
$$\begin{aligned}& \rho=\frac{[8\pi(2m^2+2m-1)+\lambda(8m^2+7m-3)]k_1^2 - 8(3\pi+\lambda )[3m(k_1t + k_2)]^{\frac{1}{3}}}{[-(8\pi+3\lambda)^2+\lambda^2][3m(k_1t+k_2)]^2} \end{aligned}$$
(31)

3.1 Physical parameters for Bianchi type VI h (h=1) model

Equation (29) represents Bianchi type VI1 perfect fluid cosmological model in f(R,T) gravity with the following physical and kinematical parameters which are important in the discussion of cosmological model. Spatial volume of the model obtained as

$$ V=(-g)^{\frac{1}{2}}=ABC=3m(k_1t+k_2) $$
(32)

The scalar expansion θ and shear scalar σ 2 in the model are defined by

$$\begin{aligned}& \theta=\frac{A_4}{A}+\frac{B_4}{B}+\frac{C_4}{C}=\frac{1}{k_1t+k_2} \end{aligned}$$
(33)
$$\begin{aligned}& \sigma^2=\frac{1}{3}\biggl(\frac{A_4}{A}-\frac{B_4}{B}\biggr)^2= \frac {1}{3}\biggl[\frac{k_1(m-1)}{3m(k_1t+k_2)}\biggr]^2 \end{aligned}$$
(34)

Corresponding to the model (29), the Hubble’s parameter H is found to be

$$ H=\frac{1}{3}\biggl(\frac{A_4}{A}+\frac{B_4}{B}+\frac{C_4}{C}\biggr)=\frac{1}{3}\biggl(\frac{1}{k_1t+k_2}\biggr) $$
(35)

which determines the present rate of expansion. The average anisotropy parameter A α defined as

$$\begin{aligned}& A_{\alpha}=\frac{1}{3}\varSigma\biggl(\frac{\Delta H_i}{H}\biggr)^2 \\ & \phantom{A_{\alpha}}=\frac {1}{27m^2}[(13k_1^2-22k_1+11)m^2 \\ & \phantom{A_{\alpha}=}{} -(4k_1^2+16k_1)m+10k_1^2] \end{aligned}$$
(36)

where i=1,2,3. The deceleration parameter (q) is found to be

$$ q=-3 $$
(37)

Also, the ratio of anisotropy to expansion

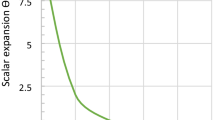
$$ \frac{\sigma^2}{\theta^2}=\frac{k_1}{9}\biggl(\frac{m-1}{m}\biggr)\neq0 $$
(38)

From the above result, we observed that the volume scale factor of the universe increases with the growth of cosmic time. At \(t=-\frac{k_{2}}{k_{1}}\), the volume element of the model vanishes while all the other parameter diverges. The mean isotropy parameter A α ≠0, hence the model does not approach isotropy.

The scalar expansion assumed a constant value as t→0 and assumed infinitely large value at \(t=-\frac{k_{2}}{k_{1}}\). However, with the growth of cosmic time it decreases to null value. The Hubble parameter assumed a constant value at t→0 while decreases in increase of t. It indicates that the rate of expansion is accelerated or decelerated depending on the signature of the parameter.

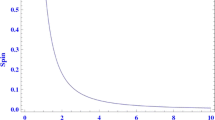
The deceleration parameter is very important vector for understanding cosmic evolution. If q<0, the model accelerates and when q>0, the model decelerates in the standard way. In this work, it is observed that the model accelerates which is in accordance with the present day scenario. For, m≠1, \(\frac{\sigma^{2}}{\theta^{2}}\neq0\), hence the space-time does not approach isotropy for finite t.

The current observations of the large-scale cosmic microwave background suggest that our physical universe is expanding isotropic and homogeneous models with positive cosmological constant. The analysis of CMB fluctuations may confirm this picture. But other analysis reveal some inconsistency. Analysis of WMAP data sets shows that the universe could have a preferred directions. The ILC-WMAP data maps show seven axes well aligned with one another and the direction Virgo. For this reason Bianchi models are important in the study of anisotropies. It may be noted that Bianchi model represents cosmos in its early stage of evolution. The anisotropy disappears only when time increases infinitely. Equation (29) represents Bianchi type VI h ,h=1 perfect fluid model of the universe which describe the early stages of the evolution of the universe with the above physical and kinematical parameters.

4 Solutions to the field equations for VI h (h=−1)

In this section, we have considered h=−1. Then the set of field equations (15–19) reduces to

$$\begin{aligned}& \frac{B_{44}}{B}+\frac {C_{44}}{C}+\frac{B_4C_4}{BC} +\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(39)
$$\begin{aligned}& \frac{A_{44}}{A}+\frac {C_{44}}{C}+\frac{A_4C_4}{AC} -\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(40)
$$\begin{aligned}& \frac{A_{44}}{A}+\frac {B_{44}}{B}+\frac{A_4B_4}{AB} -\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(41)
$$\begin{aligned}& \frac{A_4B_4}{AB}+\frac{B_4C_4}{BC}+ \frac{A_4C_4}{AC} -\frac{1}{A^2} =-(8\pi+3\lambda) \rho+\lambda p \end{aligned}$$
(42)
$$\begin{aligned}& \frac{C_4}{C}-\frac{B_4}{B}=0 \end{aligned}$$
(43)

Equation (41) yields

$$ C=lB $$
(44)

where l is the integrating constant. Without loss of generality, we assume l=1. The set of field equations (39)–(42) after incorporating equation (44) reduce to a set of three linear independent equations with four unknowns A, B, p and ρ as:

$$\begin{aligned}& 2\frac{B_{44}}{B}+\frac{B_4^2}{B^2} +\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(45)
$$\begin{aligned}& \frac{A_{44}}{A}+\frac {B_{44}}{B}+\frac{A_4B_4}{AB} -\frac{1}{A^2} =(8\pi+3\lambda )p-\lambda\rho \end{aligned}$$
(46)
$$\begin{aligned}& 2\frac{A_4B_4}{AB}+\frac{B_4^2}{B^2}-\frac{1}{A^2} =-(8\pi+3\lambda) \rho+\lambda p \end{aligned}$$
(47)

In order to solve the system completely, we assume that the expansion scalar is proportional to the shear scalar. This condition leads to

$$ A=B^m,\quad m\neq0 $$
(48)

On solving the above set of field equations (45)–(47), by using Eq. (48), we obtained

$$ B=[m(c_1t+c_2)]^{\frac{1}{m}} $$
(49)

where \(c_{1}^{2}=\frac{1}{m-1}\) and c 2 is the integrating constant.

$$ A= m(c_1t+c_2) $$
(50)

Then the metric (12) can now be written as

$$\begin{aligned}& ds^{2}=dt^{2}-[m(c_1t+c_2)]^2dx^{2}-[m(c_1t+c_2)]^{\frac {2}{m}}e^{2x}dy^{2} \\& \phantom{ds^{2}=}{} -[m(c_1t+c_2)]^{\frac{2}{m}}e^{-2x}dz^{2} \end{aligned}$$
(51)

This case is same as that of Rao and Neelima (2013), where they have shown that the model some time decelerate in the standard way and later accelerate which is in accordance with the present day scenario.

For λ=0, metric (51) represents an anisotropic Bianchi type VI0 perfect fluid cosmological model in general relativity. However, our case is the general Bianchi type VI h model.

5 Conclusion

We have investigated Bianchi type VI h cosmological models in f(R,T) gravity. We have studied for h=1,−1. For h=1 the exact solution of the field equations has been obtained and involvement of the new function f(R,T) does not affect the geometry of the space time. This model establish the consistency with the present day accelerated expansion of the universe. However for h=−1, the model reduces to Rao and Neelima (2013), where it is shown that the model sometime decelerate in the standard way and later accelerate. However, in spite of the fact that the universe, decelerates in the standard way it will accelerate in finite time due to cosmic re collapse where the universe in turns inflates “decelerates and then accelerates” (Nojiri and Odintsov 2003). Hence, the issues of accelerated expansion of the universe has been explained by taking into account the f(R,T) gravity. In this theory, cosmic acceleration may result not only due to geometric contribution to the matter but also depends on matter contents of the universe. The coupling between matter and geometry in this gravity results in non-geodesic motion of test particles and an extra acceleration is always present.

The recent work of Odintsov and Saez-Gomez (2013) on the new version of modified gravity includes strong coupling of gravitational and matter fields, R ij T ij. Such a covariant power-counting renormalizable theory represents simplest power-law F(R,T,R ij T ij) gravity. Such modified gravity contains extra terms that allow to reconstruct viable cosmological evolution. With this several cosmological solutions have been studied and corresponding gravitational action is reconstructed. They have studied the dynamics of the matter sector, which is a perfect fluid has to be fixed in order to guarantee the same evolution as in general relativity, i.e. to satisfy the continuity equation. Otherwise, a generic F(R,T,R ij T ij) may give a realistic Hubble parameter H(z), but would give rise an anomalous behavior for baryonic, dark matter or any other perfect fluid. Our work based on the matter field perfect fluid and the Hubble parameter depends on the time t indicates that it is in accordance with the work of Odintsov and Saez-Gomez (2013). However, further work is required to generalized for more complicated non-minimal models, which may give some significant results on several issues of current interest on the new modified theories.