1 Introduction

Harko et al. (2011) proposed a general non-minimal coupling between matter and geometry in the framework of an effective gravitational Lagrangian consisting of an arbitrary function of the Ricci scalar \(R\), and the trace \(T\) of the energy-momentum tensor, and introduced \(f(R,T)\) gravitational theory. An extra acceleration in \(f(R,T)\) gravity results not only from a geometrical contribution, but also from the matter content. This extraordinary phenomena of \(f(R,T)\) gravity may provide some significant signatures and effects which could distinguish and discriminate between various gravitational models. Therefore, this theory has attracted many researchers to explore different aspects of cosmology and astrophysics in isotropic and anisotropic space-times (see for example Jamil et al. (2012), Reddy et al. (2013), Azizi (2013), Alvarenga et al. (2013b,a), Sharif et al. (2013), Chakraborty (2013), Houndjo et al. (2013), Pasqua et al. (2013), Ram and Priyanka (2013), Singh and Singh (2015), Baffou et al. (2015, 2018), Santos and Ferst (2015), Noureen et al. (2015), Shamir (2015), Kumar and Singh (2015), Singh and Singh (2016), Alhamzawi and Alhamzawi (2016), Yousaf et al. (2016), Alves et al. (2016), Zubair et al. (2016), Sofuoglu (2016), Momeni et al. (2016), Das et al. (2016), Salehi and Aftabi (2016), Sahoo et al. (2018), Moraes et al. (2018), Singh and Beesham (2018), Srivastava and Singh (2018), Sharif and Anwar (2018), Tiwari and Beesham (2018), Shabani and Ziaie (2018), Rajabi and Nozari (2017), Moraes et al. (2019), Deb et al. (2018, 2019), Lobato et al. (2019), Tretyakov (2018), Elizalde and Khurshudyan (2018), Ordines and Carlson (2019), Maurya and Tello-Ortizb (2019), Esmaeili (2018), Debnath (2019)).

Harko et al. (2011) considered some particular classes of \(f(R, T )\) gravity models, obtained by explicitly specifying the functional form of \(f\). Generally, the field equations in the case of \(f(R, T )\) gravity, depend on the physical nature of the matter field. Hence, for each choice of \(f\) one may obtain several theoretical models, corresponding to different matter sources. In the first example the authors considered \(f(R, T )=R+2f(T)\) and showed that this form is equivalent to a cosmological model with an effective cosmological constant \(\Lambda\propto H^{2}\), where \(H\) is Hubble parameter. They also showed that generally for this choice of \(f(R, T )\) the gravitational coupling becomes an effective and time dependent coupling, of the form \(G_{eff}=G\pm f'(T)\), where the symbols have their usual meaning defined therein. Thus the term \(2f(T )\) in the gravitational action modifies the gravitational interaction between matter and curvature, replacing \(G\) by a running gravitational coupling parameter. Although there is no any fundamental principle behind considering a liner combination of \(R\) and \(T\), the authors showed that the choice \(f(T)=\lambda T\) for the dust matter leads to the power-law expansion of the universe, \(a\propto t^{\alpha}\) where \(\alpha\) depends on parameter \(\lambda\).

The choice \(f(R,T)=R+2\lambda T\) also corresponds to general relativity (GR) with additional matter content on the right side of the field equations. This allows for a wider variety of behavior, which reduces to GR when \(\lambda = 0\). Since the right side of the equations are similar to GR with an imperfect fluid, e.g., bulk viscosity, the theory has the potential to solve the entropy problem which occurs in GR. We will show in Sect. 3 that a variable cosmological parameter arises naturally in \(f(R,T)\) gravity. A dynamic \(\Lambda\) can solve the cosmological constant problem, the coincidence problem as well as the fine tuning problem, whilst being consistent with cosmological observations (Basilakos 2009). The cosmological constant in the gravitational Lagrangian in \(f(R,T)=R+2\lambda T\) gravity is a function of the trace of the stress-energy tensor, and consequently the model can be denoted “\(\Lambda(T )\) gravity” which may be considered a relativistically covariant model of interacting dark energy, based on the principle of least action. Finally, the form \(f(R,T)=R+2\lambda T\) has been criticized in some works (Saha 2015; Fisher and Carlson 2019), but this criticism has been adequately answered by Harko and Moraes (2020) recently.

Moreover, in an earlier work one of the present authors VS with his collaborator (Singh and Singh 2014) when reconstructed \(f(R,T)=R+2f(T)\), found that a de Sitter universe naturally leads to \(f(R,T)=R+\lambda T\). A power-law expansion also gives a similar form of \(f(R,T)\), but that contains some power of \(T\) also. In addition, as we know, the continuity equation does not hold in \(f(R,T)\) gravity, in general. But in one of our recent study Singh and Beesham (2018), when we searched a form of type \(f(R,T)=R+2f(T)\) for which the conservation equation may hold, then for a flat potential of a scalar field we surprisingly found that such form is nothing but \(f(R,T)=R+2\lambda T\). Hence, it is not just an assumption but it has significant mathematical and physical basis. Although it is the simplest form, it has the potential to explore some of the prominent features of \(f(R,T)\) gravity. Certainly, this is the why in most of the studies the researchers have preferred this specific form.

The first work on any anisotropic model in \(f(R,T)\) gravity was carried by Adhav (2012) in a locally-rotationally-symmetric (LRS) Bianchi I space-time. The author considered \(f(R,T)=R+2\lambda T\), and obtained the solutions by assuming a constant expansion rate. The constant expansion rate means the accelerating expansion of the universe. However, a serious shortcoming in his work is that the solutions are mathematically and physically invalid due to an incorrect field equation. Our purpose in this paper is to address the correct field equations and explore the geometrical and physical properties to the paper by Adhav (2012).

If one considers any matter fields in this theory, then due to the coupling between matter and \(f(R,T)\) gravity, some extra terms appear on the right hand side of the field equations. These terms can be treated as matter as well and may be called coupled matter. It may act either as a perfect fluid or DE. Therefore, the effective matter in these models is a sum of primary matter and coupled matter. One may ensure a physically viable scenario by demanding the weak energy condition (WEC)Footnote 1 for the primary matter and coupled matter. We have followed this criteria in our recent study (Singh and Beesham 2020). We shall follow the same criteria in the present work to preserve physical viability of the model.

We extend our solutions to the case of a normal/phantom scalar field model to examine which one is consistent physically. We also depict the behavior of the equation of state (EoS) parameter by using the present values of EoS parameter consistent with observational constraints. We explore the consequences of the introduction of a scalar field and examine the role of \(f(R,T)\) gravity in this model.

The work is organized as follows. In Sect. 2 we show that the geometrical behavior of the model reported by Adhav (2012) is independent of \(f(R,T)\) gravity. In Sect. 3 we present the correct field equations for an LRS Bianchi I spacetime model in \(f(R,T)=R+2f(T)\) gravity, where \(f(T)=\lambda T\), and, ensuring the positivity of the energy density, we find the constraints for a realistic physical scenario. The scalar field model is considered in Sect. 3.1 followed by a study of the behavior of the coupled matter through the energy conditions in Sect. 3.2. The findings are summarized in Sect. 4. Note that the equation numbers in round brackets throughout our discussion refer to the equations of our work, whereas the equation numbers in round brackets, the section numbers and some points in roman mentioned within inverted commas refer to Adhav (2012).

2 The solutions in general relativity

In this section we show that the geometrical behavior in points “(i)–(iv)” addressed by Adhav (2012) in section “4”, is independent from \(f(R,T)\) gravity, and it remains similar to that in GR.

A spatially homogenous and anisotropic LRS Bianchi I space-time metric is given by

$$ ds^{2} =dt^{2}-A^{2}(t)dx^{2}-B^{2}(t)(dy^{2}+dz^{2}), $$
(1)

where \(A\) and \(B\) are the scale factors, and are functions of cosmic time \(t\).

The average scale factor for the metric (1) is defined as

$$ a=(AB^{2})^{\frac{1}{3}}. $$
(2)

The average Hubble parameter (average expansion rate) \(H\), which is the generalization of the Hubble parameter in the isotropic case, is given by

$$ H=\frac{1}{3}\left(\frac{\dot{A}}{A}+2\frac{\dot{B}}{B}\right), $$
(3)

where a dot denotes the derivative with respect to cosmic time \(t\).

Consider the energy-momentum tensor

$$ T_{\mu\nu}=(\rho+p)u_{\mu}u_{\nu}-pg_{\mu\nu}, $$
(4)

where \(\rho\) is the energy density and \(p\) is the thermodynamical pressure of the matter. In comoving coordinates \(u^{\mu}=\delta_{0}^{\mu}\), where \(u_{\mu}\) is the four-velocity of the fluid which satisfies the condition \(u_{\mu}u^{\nu}=1\).

The Einstein field equations read as

$$ R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=T_{\mu\nu}, $$
(5)

where the system of units \(8\pi G=1=c\) are used.

The above field equations for the metric (1) and energy-momentum tensor (4), yield

$$\begin{aligned} &\left(\frac{\dot{B}}{B}\right)^{2}+2\frac{\dot{A}\dot{B}}{A B}=\rho, \end{aligned}$$
(6)
$$\begin{aligned} &\left(\frac{\dot{B}}{B}\right)^{2}+2\frac{\ddot{B}}{ B}=-p, \end{aligned}$$
(7)
$$\begin{aligned} &\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A} \dot{B}}{AB}=-p. \end{aligned}$$
(8)

These are three independent equations with four unknowns, namely \(A\), \(B\), \(\rho\) and \(p\). Therefore, one requires a supplementary constraint to find the exact solutions. Adhav (2012) considered a constant expansion rate

$$ H=k, $$
(9)

where \(k>0\) is a constant. Since \(H=\dot{a}/a\), the average scale factor evolves as

$$ a(t)=a_{0}e^{k t}, $$
(10)

where \(a_{0}\) is an integration constant.

The deceleration parameter, \(q=-a\ddot{a}/\dot{a}^{2}=-1-\dot{H}/ H^{2}\) takes a constant value

$$ q=-1, $$
(11)

which corresponds to an accelerating expansion of the universe.

From (7) and (8), one has

$$ \frac{\dot{A}}{A} -\frac{\dot{B}}{B}=\frac{\beta}{AB^{2}}, $$
(12)

where \(\beta\) is a constant of integration.

From (3) and (12), by the use of (9), one obtains

$$\begin{aligned} &A=c_{1}e^{kt-\frac{2\beta e^{-3kt}}{9k}}, \end{aligned}$$
(13)
$$\begin{aligned} &B=c_{1}e^{kt+\frac{\beta e^{-3kt}}{9k}}, \end{aligned}$$
(14)

where \(c_{1}\) is a constant of integration and another integration constant is taken as unity without any loss of generality. In section “3”, namely, “physical properties”, Adhav (2012) worked out some geometrical parameters and obtained the expressions for the energy density and pressure. The author in his conclusion mentioned that the scale factors are the solutions of the LRS Bianchi I model in \(f(R,T)\) gravity. But here one can see that the scale factors (13) and (14) are obtained in Einstein’s gravity. Hence, the behavior of the geometrical parameters, namely, the expansion scalar, shear scalar, and the anisotropy parameter discussed by Adhav is independent of \(f(R,T)\) gravity and remains the same as in GR. In our recent work (Singh and Beesham 2019), we have explored the features of these parameters.

The main issue in Adhav’s paper is that the expressions for the energy density and pressure are incorrect due to a wrong field equation, namely, equation number “(2.5)”. Therefore, the solutions obtained by him are invalid mathematically. In the next section, we shall reformulate this model. We find the constraints for a viable cosmological scenario and explore the physical behavior of the model. We shall also extend the solutions to a scalar field model.

3 The solutions in \(f(R,T)\) gravity

In Sect. 2, \(\rho\) and \(p\) are, respectively, the energy density and pressure of the effective matter. When one considers the energy-momentum tensor (4) in \(f(R,T)\) gravity, then \(\rho\) and \(p\) no longer correspond to the effective energy density and pressure. As aforementioned in the introduction, due to the coupling between matter and the trace, some extra terms appear on the right hand side of the field equation in \(f(R,T)\) gravity. These terms may be treated as matter. We can call it coupled matter. The matter given by the energy-momentum tensor (4) may be called the primary matter. Therefore, we replace \(\rho\) and \(p\) with \(\rho_{m}\) and \(p_{m}\), respectively, which represent the energy density and pressure of primary matter. The notations for coupled matter are defined in Sect. 3.2. In this way, the old notations \(\rho=\rho_{m}+\rho_{f}\) and \(p=p_{m}+p_{f}\) again represent the effective energy density and pressure, respectively.

The field equations in \(f(R, T)=R+2f(T)\) gravity with the system of units \(8\pi G=1=c\), are obtained as

$$ R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=T_{\mu\nu}+2 (T_{\mu\nu}+p g_{\mu\nu})f'(T)+f(T) g_{\mu\nu}. $$
(15)

Adhav (2012) considered the simplest case \(f(T)=\lambda T\), i.e., \(f(R,T)=R+2\lambda T\), where \(T=g^{\mu\nu}T_{\mu\nu}=\rho_{m}-3p_{m}\), for which the field Eqs. (15) reduce to

$$ R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}=(1+2\lambda) T_{\mu\nu}+\lambda(\rho_{m}-p_{m}) g_{\mu\nu}. $$
(16)

Let us recall Einstein’s equations with cosmological constant (\(\Lambda\)) on the right side

$$ R_{ij}-\frac{1}{2}R g_{ij} = T_{ij} + \Lambda g_{ij}. $$
(17)

By comparing the above two equations, we see that an effective cosmological parameter as a function of \(T\) may be defined as

$$ \Lambda = \Lambda(T) = -(2p_{m}+T)\lambda = (\rho_{m} - p_{m})\lambda. $$
(18)

Hence, we see that a variable cosmological parameter arises naturally in \(f(R,T)=R+2\lambda T\) gravity. This can help resolve the cosmological constant problem, the coincidence problem as well as the fine tuning problem, whilst being consistent with cosmological observations (Basilakos 2009).

The field Eqs. (16) for the metric (1), yield

$$\begin{aligned} &\left(\frac{\dot{B}}{B}\right)^{2}+2\frac{\dot{A}\dot{B}}{A B}=(1+3\lambda)\rho_{m}-\lambda p_{m}, \end{aligned}$$
(19)
$$\begin{aligned} &2\frac{\ddot{B}}{B}+\left(\frac{\dot{B}}{B}\right)^{2}=-(1+3\lambda)p_{m}+\lambda \rho_{m}, \end{aligned}$$
(20)
$$\begin{aligned} &\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A} \dot{B}}{AB}=-(1+3\lambda)p_{m}+\lambda \rho_{m}. \end{aligned}$$
(21)

It is to be noted that the last term of equation “(2.5)” in Ahdav’s paper is “\(+2p\lambda\)”, which is incorrect. Indeed, this should be “\(-\lambda p\)”.

Using (13), (14) in (19) and (20), for \(\lambda\neq-1/2\) and \(\lambda\neq-1/4\), we obtain

$$\begin{aligned} & \rho_{m} =\frac{3 k^{2}}{1+4 \lambda }-\frac{\beta ^{2} e^{-6 k t}}{3(1+2 \lambda) }, \end{aligned}$$
(22)
$$\begin{aligned} & p_{m}=-\frac{3 k^{2}}{1+4 \lambda }-\frac{\beta ^{2} e^{-6 k t}}{3(1+2 \lambda)}. \end{aligned}$$
(23)

These are the correct expressions for the energy density and pressure which are different from those obtained by Adhav (2012). In both of these expressions the variable term decreases with time. Consequently, the energy density and pressure increase with the cosmic evolution and attain a constant value \(\rho_{m}=3 k^{2}/(1+4 \lambda)=-p_{m}\) as \(t\to\infty\), while both physical quantities are infinite in the infinite past.

The energy density for any physically viable cosmological model must be positive. From (22), it is clear that \(\rho_{m}\) could be always positive if \(1+4\lambda>0\) and \(1+2\lambda<0\), but this is not possible. Similarly, the models with \(-1/2<\lambda<-1/4\) also become physically unrealistic as \(\rho_{m}\) always remains negative in this case. However, the energy density can be positive for some restricted periods under the constraints

$$ t\leq\frac{1}{k}\ln\left[\frac{(1+4\lambda) \beta^{2}}{9(1+2\lambda) k^{2}}\right]^{\frac{1}{6}}\text{ if } \lambda< -\frac{1}{2}, $$
(24)

and

$$ t\geq\frac{1}{k}\ln\left[\frac{(1+4\lambda) \beta^{2}}{9(1+2\lambda) k^{2}}\right]^{\frac{1}{6}} \text{ if } \lambda>-\frac{1}{4}. $$
(25)

The model describes an accelerating expansion of the universe (\(q=-1\)). However, the acceleration may be an early inflation or a late time acceleration. Since the model with \(\lambda<-1/2\) is physically viable only during early evolution, the acceleration must be an early inflation in this case, whereas the model with \(\lambda>-1/4\) is physically viable only at late times, hence the acceleration in this case must be the present accelerating expansion.

Our main objective is now to identify the nature of matter. The EoS parameter which is defined as \(\omega_{m}=p_{m}/\rho_{\mathfrak{m}}\), gives

$$ \omega_{m}=-1+\frac{2 }{1+\gamma e^{6 \beta t}}, $$
(26)

where \(\gamma=-9(1+2\lambda)k^{2}/(1+4\lambda)\beta^{2}\). The expression (26) looks similar to the EoS parameter of the effective matter in GR (Singh and Beesham 2019). The only difference here is that \(\gamma\) contains a term \(\lambda\) of \(f(R,T)=R+2\lambda T\) gravity. The constraints obtained in (24) and (25) ensure the positivity of \(\gamma\). Since \(\omega_{m}\to1\) as \(t\to-\infty\), and \(\omega_{m}\to-1\) as \(t\to\infty\), the matter behaves as stiff matter in the infinite past, while it plays the role of a cosmological constant at late times. We see that \(\omega_{m}\) diverges at time \(t=k^{-1}\ln\left[(1+4\lambda) \beta^{2}/(9(1+2\lambda) k^{2})\right]^{1/6}\), so it cannot be used to depict the behavior of the matter during intermediate evolution.

The early and late behavior of primary matter in our model matches with the characteristics of a scalar field. Due to the domination of kinetic energy over the scalar potential at early times, the scalar field acts like stiff matter. A scalar field with a self-interacting potential, due to the domination of the potential term over the kinetic term, gives rise to a negative pressure for driving super fast expansion during inflation. When the field enters into a regime in which the potential energy once again takes over from the kinetic energy, it exerts the same stress as a cosmological constant at late times, which happens however with a different energy density (in comparison to inflation). Therefore, in what follows we substitute the primary matter with a scalar field (quintessence or phantom) for the further investigation.

3.1 Scalar field model

The energy density and pressure of a minimally coupled normal (\(\epsilon=1\)) or phantom (\(\epsilon=-1\)) scalar field, \(\phi\) with self-interacting potential, \(V(\phi)\) are, respectively, given by

$$\begin{aligned} &\rho_{\phi}=\frac{1}{2}\epsilon\dot{\phi}^{2}+V(\phi), \end{aligned}$$
(27)
$$\begin{aligned} & p_{\phi}=\frac{1}{2}\epsilon\dot{\phi}^{2}-V(\phi). \end{aligned}$$
(28)

Replacing \(\rho_{m}\) with \(\rho_{\phi}\) and \(p_{m}\) with \(p_{\phi}\), and using (27) and (28) in (22) and (23), the kinetic energy and scalar potential, respectively, are obtained as

$$\begin{aligned} &\frac{1}{2}\epsilon\dot{\phi}^{2}=-\frac{\beta^{2} e^{-6 k t}}{3(1+2\lambda)}, \end{aligned}$$
(29)
$$\begin{aligned} &V(t)=\frac{3k^{2}}{1+4\lambda}. \end{aligned}$$
(30)

From (29), for physical reality of the solutions, we must have \(\lambda<-1/2\) if \(\epsilon=1\) and \(\lambda>-1/2\) if \(\epsilon=-1\). It is to be noted that the requirement of positive kinetic energy is equivalent to obeying the null energy condition (NEC).Footnote 2 Since we have already ensured the positivity of energy density under the constraints (24) and (25), the WEC is satisfied for \(\lambda<-1/2\) and \(\lambda>-1/2\). In addition, the scalar potential also must be positive for a physically viable model, which is possible only for \(\lambda>-1/4\). Hence, the model is consistent with a phantom scalar field only. It is to be noted that having a negative scalar potential is equivalent to violating the dominant energy condition (DEC).Footnote 3 Furthermore, the energy density for \(\lambda>-1/4\), is positive only after a time given in (25), therefore, the model excludes the possibility of early inflation, and accommodates only late time acceleration.

On integrating (29), we get

$$ \phi=\phi_{0}\pm\frac{\beta }{3k}\left[\frac{2}{3(1+2\lambda)}\right]^{\frac{1}{2}}e^{-3 k t}, $$
(31)

where \(\phi_{0}\) is a constant of integration. Only the positive sign is compatible for physical consistency, so we proceed further with it only.

The energy density and pressure of the phantom scalar field are given by (22) and (23), which can be expressed in terms of red shift, \(z\) via the relation \(a=a_{0}/(1+z)\) as

$$\begin{aligned} &\rho_{\phi}=\frac{3 k^{2}}{1+4 \lambda }-\frac{\beta ^{2} (1+z)^{6}}{3(1+2 \lambda)}, \end{aligned}$$
(32)
$$\begin{aligned} & p_{\phi}=-\frac{3 k^{2}}{1+4 \lambda }-\frac{\beta ^{2} (1+z)^{6}}{3(1+2 \lambda)}, \end{aligned}$$
(33)

respectively, where we have assumed the present scale factor to be unity, i.e., \(a_{0}=1\).

Similarly, the constraints (24) and (25), respectively, can be expressed as

$$\begin{aligned} & z\geq\gamma^{\frac{1}{6}}-1 \text{ for }\lambda< -\frac{1}{2}, \end{aligned}$$
(34)
$$\begin{aligned} & z\leq \gamma^{\frac{1}{6}}-1 \text{ for } \lambda>-\frac{1}{4}. \end{aligned}$$
(35)

The EoS parameter (26), takes the form

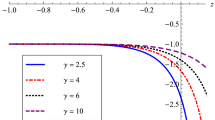
$$ \omega_{\phi}=\left[-1+\frac{2 }{1+\gamma (1+z)^{-6}}\right]^{-1}. $$
(36)

As aforesaid, though \(\gamma\) contains the parameter \(\lambda\) of \(f(R,T) =R+2\lambda T\) gravity, but being a single parameter expression, the above EoS is identical to the EoS of the effective matter of the same model in GR (Singh and Beesham 2019). Hence, the primary matter in this model behaves similar to the effective matter in GR as shown in Fig. 1. An interesting fact here is that though Fig. 1 is identical to one in Ref. Singh and Beesham (2019), it represents a different matter content. In the present study, it describes a part of the matter, while it describes the effective matter in GR. This difference can also be seen in the expression of scalar field (31), which involves the parameter \(\lambda\) of \(f(R,T)=R+2\lambda T\) gravity. So we can examine how \(f(R,T)\) gravity affects the evolution of the scalar field by analyzing its variation against different values of \(\lambda\). We pursue further with the approach that we have adopted in our recent study (Singh and Beesham 2019).

Fig. 1
figure 1

\(\omega_{\phi}\)versus\(z\) for different values of \(\gamma\)

Full size image

The present value of the EoS parameter is

$$ \omega_{\phi}(z=0)=\frac{1+\gamma}{1-\gamma}. $$
(37)

Combined results from the cosmic microwave background (CMB) experiments with large scale structure (LSS) data, the \(H(z)\) measurement from the Hubble Space Telescope (HST) and luminosity measurements of Type Ia Supernovae (SNe Ia), put the following constraints on the EoS: \(-2.68 <\omega_{0}< -0.78\) (Melchiorri et al. 2003). These bounds become more tight, i.e., \(-1.45 <\omega_{0}< -0.74\) (Hannestad and Morstell 2002), when the Wilkinson Microwave Anisotropy Probe (WMAP) data is included (also see Alam et al. (2004); Alcaniz (2004)). For these observational limits from (37), we get \(\gamma>2.19\) for the former bounds, and \(\gamma>5.44\) for the latter. Now we can depict the profile of the EoS parameter for some values of \(\gamma\) consistent with these observational outcomes.

Figure 1 plots the behavior of the EoS parameter against redshift under the constraint (35) for some values of \(\gamma>2.19\). We see that \(\omega_{\phi}<-1\), which confirms the theoretical outcome that the primary matter is of phantom type and mimics the cosmological constant in future evolution.

The phantom scalar field (31) can be given as

$$ \phi=\phi_{0}\pm\left[\frac{2}{3\gamma(1+4\lambda)}\right]^{\frac{1}{2}}(1+z)^{3}. $$
(38)

The evolution of the scalar field against \(z\) for some values of \(\lambda\) with \(\gamma=5\) (this value is consistent with the observational bounds discussed above) and \(\phi_{0}=1\) is shown in Fig. 2. The scalar field decreases from an infinite value with the evolution of the universe, and attains a finite minimum value at late times. If \(\phi_{0}=0\), the scalar field vanishes at late times.

Fig. 2
figure 2

\(\phi(z)\)versus\(z\) for different values of \(\lambda\) with \(\gamma=5\) and \(\phi_{0}=1\)

Full size image

The flat potential (30) can be identified as a cosmological constant. Moreover, if \(\beta=0\) then \(\phi=\phi_{0}\) and \(\rho_{\phi}=3k^{2}=-p_{\phi}\), which essentially corresponds to a cosmological constant. If \(\lambda=0\), the solutions reduces to the model one in GR (Singh and Beesham 2019). One may also readily verify that the standard de Sitter solutions for a flat Friedmann-Lemaitre-Robertson-Walker (FLRW) model of GR are recovered when \(\beta=0\) and \(\lambda=0\).

3.2 The behavior of coupled matter

Separating the energy densities and pressures of primary matter and coupled matter, the field Eqs. (19)–(21) can be written as

$$\begin{aligned} & \left(\frac{\dot{B}}{B}\right)^{2}+2\frac{\dot{A}\dot{B}}{A B}=\rho_{\mathfrak{m}}+\rho_{f}, \end{aligned}$$
(39)
$$\begin{aligned} & 2\frac{\ddot{B}}{ B}+\left(\frac{\dot{B}}{B}\right)^{2}=-(p_{\mathfrak{m}}+p_{f}), \end{aligned}$$
(40)
$$\begin{aligned} & \frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A} \dot{B}}{AB}=-(p_{\mathfrak{m}}+p_{f}), \end{aligned}$$
(41)

where \(\rho_{f}=\lambda(3\rho_{\mathfrak{m}}-p_{\mathfrak{m}})\) and \(p_{f}=\lambda(3p_{\mathfrak{m}}-\rho_{\mathfrak{m}})\), are the energy density and pressure of coupled matter, which are obtained as

$$\begin{aligned} & \rho_{f} =\frac{12 \lambda k^{2} }{1+4 \lambda }-\frac{2 \lambda \beta ^{2} e^{-6 k t}}{3(1+2 \lambda)}, \end{aligned}$$
(42)
$$\begin{aligned} & p_{f}=-\frac{12 \lambda k^{2}}{1+4 \lambda }-\frac{2 \lambda \beta ^{2} e^{-6 k t}}{3(1+2 \lambda)}. \end{aligned}$$
(43)

Although \(\rho_{f}\) always remains positive for \(-1/2<\lambda <-1/4\), the energy density of primary matter becomes negative for these values, and thus we exclude this case. For \(\lambda<-1/2\), \(\rho_{f}\) becomes negative at early times, so we exclude this case too. Similarly, when \(-1/4<\lambda<0\), \(\rho_{f}\) becomes negative at late times. Notwithstanding, \(\rho_{f}\) is positive for \(\lambda>0\) at late times. Hence, the model in this case provides a realistic scenario. The EoS parameter, \(\omega_{f}=p_{f}/\rho_{f}\) diverges at some time, say \(t=t_{\star}\), so it is not worthwhile using it to depict the behavior of coupled matter. Therefore, we shall study the nature of coupled matter through the energy conditions. We require

$$\begin{aligned} & \rho_{f}+p_{f}=-\frac{4 \lambda\beta ^{2} e^{-6 k t}}{3(1+2 \lambda)}, \end{aligned}$$
(44)
$$\begin{aligned} & \rho_{f}-p_{f}=\frac{24 \lambda k^{2} }{1+4 \lambda }. \end{aligned}$$
(45)

The NEC and DEC can be satisfied, respectively, for

$$\begin{aligned} & -\frac{1}{2}< \lambda < 0, \end{aligned}$$
(46)
$$\begin{aligned} & \lambda < -\frac{1}{4} ,\text{ or } \lambda>0. \end{aligned}$$
(47)

Since \(\rho_{f}\) is positive only for \(\lambda>0\), therefore, the coupled matter violates the NEC but holds the DEC. Hence, the behavior of coupled matter is similar to the primary matter, i.e., it also behaves as phantom DE. Thus, the behavior of coupled matter also shows that the model is viable to describe a late time cosmic acceleration in presence of phantom matter.

4 Conclusion

Adhav (2012) studied an LRS Bianchi I model with constant expansion rate in \(f(R,T)=R+2\lambda T\) gravity. Due to an incorrect field equation, the solutions obtained by the author are mathematically and physically invalid. Notwithstanding a wrong field equation, the behavior of the geometrical parameters is not affected. Moreover, the kinematical parameters in such formulation do not depend on \(f(R,T)\) gravity. In the present paper we have reconsidered his work and also extended the solutions to a scalar field (quintessence or phantom) model. Firstly, we have shown that the geometrical behavior of the model remains the same as in GR. We have pointed out that Adhav (2012) misunderstood the time of origin of the universe. He discussed the evolution from \(t=0\) to \(t\to\infty\). He probably understood the origin of the universe at \(t=0\), whereas the model has an infinite past. For details, the readers may refer our recent works (Singh and Beesham 2019, 2020). While Adhav (2012) discussed only the kinematical behavior of the model, we have also explored the physical properties in detail, keeping the physical viability of the solutions at the center. The solutions in \(f(R,T)=R+2\lambda T\) gravity model are valid for all values of \(\lambda\) except \(\lambda\neq-1/2\) and \(\lambda\neq-1/4\). The assumption of constant expansion rate gives a constant value of the deceleration parameter, \(q=-1\). Consequently, the model can describe only an accelerating universe. However, the acceleration may be early inflation or the present acceleration. To ensure this we have obtained the constraints for a physically realistic scenario, and found that the model is viable to describe only the present accelerating phase.

The evolution of the universe is governed by the effective matter. It is important to mention here that \(f(R,T)\) gravity does not alter the behavior of effective matter in the formulations where the kinematical behavior is fixed by some geometrical parameters. Hence the behavior of effective matter in this study remains the same as the one in GR. The effective matter in the present study thus also remains identical to the model in GR. The behavior of the effective matter in GR has been studied by us elsewhere recently (Singh and Beesham 2019). In the present study, an extra matter (other than the primary matter) appears due to the coupling between matter and \(f(R,T)\) gravity. We term this extra matter as “coupled matter”. We have explored the characteristics of primary matter as well as of coupled matter.

The primary matter in this model acts similarly to the effective matter in GR. When primary matter is replaced with a scalar field (normal or phantom), the model has been found consistent only with a phantom scalar field. The phantom field decreases with the cosmic evolution, while the scalar potential remains flat throughout. The scalar potential can be thought of as a cosmological constant. The model can also be consistent with a normal scalar field, but the scalar potential becomes negative in that case, which would be unrealistic. The coupled matter also behaves similarly to primary matter. The viable models are possible only for \(\lambda>0\).

We have also examined the consistency of the behavior of primary matter with the observational data by borrowing some current values of the EoS parameter from some observational outcomes. The dynamics of the EoS parameter supports the observational results and suggests that the phantom field has started dominating over the other energy contents somewhere between \(0.2\lesssim z\lesssim0.5\). The scalar field model also witnesses that if one demands an accelerating cosmic expansion from an anisotropic model, then the model presents a viable cosmological scenario (obeying NEC and WEC) only after a time when the universe enters into an accelerating phase.

It is to be noted that Shamir (2014) obtained solutions of the general Binachi I model with constant expansion rate in \(f(R,T)=R+2\lambda T\) gravity. Those solutions are also valid for late times only as the energy density is negative at early times. Hence, our results can also be interpreted within the general Binachi I spacetime formalism. We believe that only the kinematical behavior would be different, but the physical behavior will remain the same.