1 Introduction

Since the late 90s we consider the universe is currently undergoing a phase of accelerated expansion. The empirical evidence of this non-expected property came from the supernovae Ia observations independently by Riess et al. (1998) and Perlmutter et al. (1999). Thereafter, plenty of models have been created with the purpose of physically and/or mathematically describes the cause of such acceleration, named “dark energy” (DE). The most popular of them is the ΛCDM (Λ-cold dark matter) model which treats the acceleration as due to a quantum vacuum energy mathematically described by the cosmological constant Λ inserted in the Einstein field equations (FEs) and physically described by the exotic equation of state (EoS) ω=p/ρ=−1, with p and ρ being the pressure and the energy density of the universe, respectively. Although this model obtains success in explaining supernovae Ia luminosity distance measures, as shown in Riess et al. (1998), Perlmutter et al. (1999), X-ray spectrum of cluster of galaxies (Allen et al. 2004), baryon acoustic oscillations (Eisenstein et al. 2005; Percival et al. 2010) and galaxy age data (Jimenez et al. 2003), when we compare the value of the quantum vacuum energy obtained via observational cosmology data (Planck Collaboration 2013) with the one obtained via particle physics (Weinberg 1989), the discrepancy between them obligate us to examine another cosmological models. These alternative models might be divided in two categories: those which alters the geometrical part of the Einstein FEs and those in which the physical part of the FEs is modified. In extradimensional models, the terms rising due to such modifications might play the role of the cosmological constant in ΛCDM model, i.e., being responsible for the cosmic acceleration (see, for instance, Dvali et al. 2000; Lue and Starkman 2003; Binetruy et al. 2000; Gogberashvili 2002). The physical importance of the extradimensional part on the Einstein tensor is also explicit in models such as the Randall-Sundrum model (Randall and Sundrum 1999), for which it solves the hierarchy problem, and the Arkani-Hamed-Dimopoulos-Dvali model (Arkani-Hamed et al. 1998) in which the extra dimension predicts radiative corrections in quantum processes. Another alternatives one can find are quintessence models (Linder 2008); Chaplygin gas models (Bilic et al. 2002; Lima et al. 2008); XCDM models (Turner and White 1997; Chiba et al. 1997); Λ(t)CDM models (Ozer and Taha 1986; Freese et al. 1987; Lima 1996; Bessada and Miranda 2013), and f(R) theories (Vollick 2004).

The f(R) theories present the gravitational part of the action as given by a generic function of the Ricci scalar R, generalizing the original Einstein-Hilbert action. Recently, a more generic alternative model has been considered, in which the action depends still on R, but also on the trace T of the energy-momentum tensor, namely the f(R,T) gravity, presented in Harko et al. (2011). The reason to assume that the action depends on T comes from the existence of exotic imperfect fluids or quantum effects. Due to the coupling between matter and geometry predicted by the model, such theory of gravity depends on a source term, which is the variation of the energy-momentum tensor with respect to the metric.

As a broad discussion on DE solutions in a scale invariant theory of gravitation considering the existence of wet dark fluid in Bianchi type VI1 geometry has been given in Mishra and Sahoo (2014), it is interesting to investigate the state of art in what concerns DE in the framework of f(R,T) theories. Bamba et al. (2012) has pointed out that the case f(R,T)=R+2λT, with λ being a constant, for a matter dominated universe (p=0), realizes the accelerated expansion of the universe since it allows exponential solutions for the scale factor a(t). Reddy et al. (2013b) proposed a homogeneous and anisotropic Bianchi type-III model which has resulted in a accelerated universe with time-dependent EoS parameter, similar to the model presented by Pradhan and Amirhashchi (2011). Similarly, Singh and Sharma (2014) have worked with time-dependent EoS parameter in Bianchi type-II model. A cosmological reconstruction of f(R,T) gravity was reported by Houndjo (2012), which has discussed the transition from a matter dominated phase to an accelerated phase and in Houndjo and Piattella (2012), the function f(R,T) was numerically reconstructed from holographic DE. Moreover, Sharif and Zubair (2014) obtained f(R,T) functions corresponding to Ricci DE and new holographic dark DE. They have found an EoS parameter in agreement with WMAP (Wilkinson Microwave Anisotropy Probe) observations.

Still on the observational aspects, Jamil et al. (2012) besides have reproduced ΛCDM cosmology, reconstructed Chaplygin gas and scalar field cosmological models whose numerical simulation for the Hubble parameter have showed good agreement with baryon acoustic oscillations data for z<2. Since in the general f(R,T) gravity model, the energy-momentum tensor is not covariantly conserved, it is presumed that test particles moving in a gravitational field do not follow geodesic lines. Actually, there is an effect of extra acceleration on the objects. From the observational data on the perihelion precession of the planet Mercury, Harko et al. (2011) have constrained the magnitude of the extra acceleration to be a E ≤1.28×10−9 cm/s2.

Furthermore, on the scope of f(R,T) cosmology, Adhav (2012), Reddy et al. (2012a) have derived solutions to Bianchi type-I and type-III space-time, respectively and Ram and Priyanka (2013), Reddy et al. (2012b, 2013a), Samanta and Dhal (2013) obtained solutions for Kaluza-Klein (KK) geometries.

The KK gravitational model (Overduin and Wesson 1997) considers the universe as empty in five dimensions (5D), i.e., described by the FEs G AB =0, with G AB representing the Einstein tensor, and A,B running from 0 to 4. The matter arises as a geometrical manifestation of this empty extra-dimensional space-time. In fact, one can show that from 5D vacuum FEs, it is possible to obtain the Einstein FEs with matter in 4D together with Maxwell equations in the absence of a source (Overduin and Wesson 1997). In this way, KK model is said to unify two of the four fundamental forces: gravitation and electromagnetism, which makes it to be considered a low-energy limit of superstring theories (Salam and Sezgin 1989). To do so, Kaluza imposed an artificial restriction on the coordinates, the “cylindrical condition” (CC), which consists on the annulment of all derivatives with respect to the fifth dimension. Klein’s contribution was to make this restriction less artificial, suggesting a compactification of the fifth dimension. Note that the geometrical terms in the KK FEs which arise due to the existence of an extra dimension might be responsible for describing the accelerated expansion of the universe.

Several cosmological models have been derived from KK space-time set up, for instance: Sharif and Khanum (2011) have derived a KK cosmology with varying G (the Newtonian gravitational constant) and Λ; in Moraes and Miranda (2012) it was obtained a model in which a fifth coordinate parameter simulates the effects of a cosmological constant in 4D; in Samanta et al. (2013), Bianchi geometries with wet dark fluid were considered; Darabi (2010) has proposed that the expansion of the universe may be controlled by the EoS in 5D rather than 4D; Banerjee et al. (1994), Chatterjee et al. (1994), Chatterjee and Banerjee (1993) have considered inhomogeneous models; and Aghmohammad (2009) has treated f(R) theory as unified to KK model. Beyond that, in a series of remarkable works, P.S. Wesson has contributed significantly to the physical interpretation of KK models. For instance: in Wesson (2000), the author explains the origin of matter in terms of the geometry of the bulk space in which our 4D world is embedded, giving rise to the so-called space-time-matter; in Wesson and de Leon (1995), the authors derive the general equation of motion of a (charged or neutral) particle; Wesson (2001) showed that the cosmological constant of general relativity is an artefact of the reduction to 4D of 5D KK theory (or more generally, 10D superstrings and 11D supergravity); and in Wesson (1992a, 1992b), Wesson and de Leon (1992), it is suggested that the density and pressure of the usual 4D energy-momentum tensor are regarded as the extra parts—due to the extra dimension—of the 5D Einstein tensor G AB . This procedure can also be called “induced matter model” (IMM) since the usual matter properties are inducted from an empty 5D space-time. This innovative idea provided some extensions, like in McManus (1994), in which the FRW cosmological models were interpreted as being purely geometrical in origin, while in Halpern (2001, 2002), IMM was applied to anisotropic cosmologies.

As mentioned above, from a 5D KK metric in f(R,T) theory, solutions to the energy density ρ and pressure p have been obtained from usual methods. My proposal in this work is to obtain solutions to 5D f(R,T) theory, considering the case f(R,T)=R+2f(T), in a pioneer form, by applying the IMM, i.e., identifying the extra-dimensional terms in the vacuum FEs as those responsible to induce matter in our observable world. The paper is organized as follows: in Sect. 2 I present a brief review of f(R,T) theory and the FEs which are derived from the specific case of f(R,T) which will be the scope of the present work. In Sect. 3 I obtain the FEs for the KK metric and apply the IMM to them, obtaining the model properties of matter from the extra-dimensional part of the Einstein tensor. The solutions for the energy density and pressure of the universe as well as the Hubble and the deceleration parameter are derived in Sect. 4. Section 5 presents the particular case in which the universe is described by the EoS ω=−1. In Sect. 6 I present some discussion about the CC application in such theory, as well as its consequences. General discussions and prospects are reported in Sect. 7.

2 f(R,T) gravity

Elaborated by Harko et al. (2011), the f(R,T) theory is a model in which the gravitational Lagrangian is given by an arbitrary function of both the Ricci scalar R and the trace T of the energy-momentum tensor T μν . The dependence on T could be interpreted as inducted from the existence of exotic imperfect fluids or quantum effects. In fact, this dependence links with known illustrious proposals such as geometrical curvature inducing matter and geometrical origin of matter content in the universe (Shabani and Farhoudi 2013; Farhoudi 2005). The action of f(R,T) gravity is given by

$$ S=\frac{1}{16\pi}\int f(R,T)\sqrt{-g}d^4x+\int \mathcal{L}_m\sqrt{-g}d^4x, $$
(1)

with f(R,T) representing the arbitrary function of R and T, g the determinant of the metric g μν and \(\mathcal{L}_{m}\) the matter Lagrangian density (note that the author’s original proposal considers a 4D space-time, hence the terms d 4 x).

The variation of the action above yields to the following FEs:

$$ \begin{aligned} &f_R(R,T)R_{\mu\nu}-\frac{1}{2}f(R,T)g_{\mu\nu}+(g_{\mu\nu} \Box-\nabla_\mu\nabla_\nu) \\ & f_R(R,T)=8\pi T_{\mu\nu}-f_T(R,T)T_{\mu\nu}-f_T(R,T) \varTheta_{\mu\nu}, \end{aligned} $$
(2)

with \(\Box\equiv\partial_{\mu}(\sqrt{-g}g^{\mu\nu}\partial_{\nu})/\sqrt{-g}\), Θ μν ≡g αβ δT αβ /δg μν, f R (R,T)≡∂f(R,T)/∂R, f T (R,T)≡∂f(R,T)/∂T, while as usually, \(T_{\mu\nu}=g_{\mu\nu}\mathcal{L}_{m}-2\partial\mathcal{L}_{m}/\partial g^{\mu\nu}\), R μν represents the Ricci tensor and ∇ μ the covariant derivative with respect to the symmetric connection associated to g μν .

Throughout this work, I am going to assume the particular case of the function f(R,T) such that f(R,T)=R+2f(T) with f(T)=λT and λ a constant. Therefore one obtains f R (R,T)=1 and f T (R,T)=2λ. If one assumes the matter source is a perfect fluid, then the matter Lagrangian can be taken as \(\mathcal{L}_{m}=-p\) so that Θ μν =−2T μν −pg μν and the FEs (2) can be rewritten as

$$ G_{\mu\nu}=8\pi T_{\mu\nu}+\lambda Tg_{\mu\nu}+2 \lambda(T_{\mu\nu}+pg_{\mu\nu}), $$
(3)

with T μν =(ρ+p)u μ u ν −pg μν , u μ the four-velocity tensor and throughout this work I am going to assume units such that the fundamental constants c=G=1.

In the next section I develop the vacuum FEs for a KK line element with the coefficients depending on both time and extra spatial coordinate. As it was cited above, the T-dependence of the gravitational Lagrangian in f(R,T) theory refers the geometrical origin of matter content in the universe proposal. Moreover, the function f(R,T) itself suggests a coupling between geometry and matter predicted by the theory. In this way, it is very reasonable to presume that a great interpretation of a 5D f(R,T) gravity rises from Wesson’s IMM, since the matter properties of the model will be obtained from the extra geometrical parts of the Einstein tensor, as it will be demonstrated in the following.

3 Einstein field equations and the induced matter model application

Here, I am going to work with a generalized version of the line element used by Reddy et al. (2012b), Ram and Priyanka (2013), in which the coefficients of the KK metric will depend on both time t and the extra space-like coordinate l:

$$ ds^2=dt^2-A^2(t,l) \bigl(dx^2+dy^2+dz^2\bigr)-B^2(t,l)dl^2. $$
(4)

In the above equation, A(t,l) and B(t,l) are the scale factors; furthermore, I am going to assume that the scalar of expansion of such metric is proportional to its shear scalar, in such a manner that one can write B(t,l)=A(t,l)m, with m≠1 being a constant of integration (see Reddy et al. 2012a; Collins et al. 1980). In this way, the 5D correspondent non-null components of the Einstein tensor are

$$\begin{aligned} G_0^{0} =&\frac{3}{A^{2m}} \biggl[-\frac{A^{**}}{A}+(m-1) \biggl(\frac{A^{*}}{A} \biggr)^{2} \biggr] \\ & {}+3(m+1) \biggl(\frac{\dot{A}}{A} \biggr)^{2}, \end{aligned}$$
(5)
$$\begin{aligned} G_1^{1} =&\frac{1}{A^{2m}} \biggl[-2 \frac{A^{**}}{A}+(2m-1) \biggl(\frac{A^{*}}{A} \biggr)^{2} \biggr] \\ &{}+(m+2)\frac{\ddot{A}}{A}+\bigl(m^{2}+m+1\bigr) \biggl(\frac{\dot{A}}{A} \biggr)^{2}, \end{aligned}$$
(6)
$$\begin{aligned} G_2^{2} =&G_3^{3}=G_1^{1}, \end{aligned}$$
(7)
$$\begin{aligned} G_0^{4} =&3 \biggl(-\frac{\dot{A}^{*}}{A}+m\frac{\dot{A}}{A}\frac{A^{*}}{A} \biggr), \end{aligned}$$
(8)
$$\begin{aligned} G_4^{4} =&3 \biggl[-\frac{1}{A^{2m}} \biggl(\frac{A^{*}}{A} \biggr)^{2}+\frac{\ddot{A}}{A} + \biggl(\frac{\dot{A}}{A} \biggr)^{2} \biggr]. \end{aligned}$$
(9)

Note that I wrote A(t,l)=A for the sake of simplicity, and a dot represents derivation with respect to the time while an asterisk, derivation with respect to the extra coordinate. Equations (5)–(9) must be equal to zero, since from KK gravitational model, G AB =0. In order to obtain properties of matter from the FEs (5)–(9), one should apply the IMM to them, which means to identify the elements that arise due to the extra dimension, i.e., in this case, those that carry the constant m and/or differentiations with respect to l, and characterize them as those responsible for the matter properties in the 4D world. Therefore the FEs (3) assume the form

$$\begin{aligned} &\frac{3}{A^{2m}} \biggl[-\frac{A^{**}}{A}+(m-1) \biggl(\frac{A^{*}}{A}\biggr)^{2} \biggr] +3m \biggl(\frac{\dot{A}}{A} \biggr)^{2} \\ &\quad =(8\pi +3\lambda)\rho -\lambda p, \end{aligned}$$
(10)
$$\begin{aligned} &\frac{m}{A^{2m}} \biggl[-2\frac{A^{**}}{A}+(2m-1) \biggl( \frac{A^{*}}{A} \biggr)^{2} \biggr]+\frac{\ddot{A}}{A} \\ &\quad {}+\bigl(m^{2}+m\bigr) \biggl(\frac{\dot{A}}{A} \biggr)^{2} =-(8 \pi +3\lambda)p+\lambda\rho , \end{aligned}$$
(11)
$$\begin{aligned} &{-}\frac{3}{A^{2m}} \biggl(\frac{A^{*}}{A} \biggr)^{2}=-(8\pi +3\lambda)p+\lambda\rho . \end{aligned}$$
(12)

Note that from Eq. (8), one could also write \(A\dot{A}^{*}=m\dot{A}A^{*}\), but such relation does not contribute with the purposes of the present work. From the FEs above one obtains a second-order partial differential equation for A(t,l) of the form:

$$ \frac{2}{A^{2m}}\bigl[(m+1)A^{*2}-AA^{**} \bigr]+mA\ddot{A}+\bigl(m^{2}+m\bigr)\dot{A}^{2}=0. $$
(13)

To solve Eq. (13) I use the separation of variables method (Butkov 1968; Farlow 1982). Assuming, then, A(t,l)=T(t)L(l), with T(t) and L(l) being functions restrictively dependent on t and l respectively, one can write two ordinary differential equations. Those are

$$\begin{aligned} &mT^{2m-1}\frac{d^{2}T}{dt^{2}}+\bigl(m^{2}+m\bigr)T^{2m-2} \biggl(\frac{dT}{dt} \biggr)^{2}=k, \end{aligned}$$
(14)
$$\begin{aligned} &\frac{2}{L^{2m+1}}\frac{d^{2}L}{dl^{2}}-(m+1)\frac{2}{L^{2m+2}} \biggl( \frac{dL}{dl} \biggr)^{2}=k, \end{aligned}$$
(15)

with k being the separation constant. For k=0, the solution of Eq. (13) becomes

$$ A(t,l)=C_1\frac{\tau(t)^{\frac{1}{m+2}}}{(ml+C_3)^{\frac{1}{m}}}, $$
(16)

with τ(t)=(m+2)t−C 2 and C 1,C 2,C 3 are arbitrary constants.

4 Cosmological solutions

In possession of Eq. (16), some straightforward algebraic calculation with Eqs. (10)–(11) makes one able to write the model solutions for the energy density of the universe ρ and the pressure p. The solutions are

$$\begin{aligned} &\rho=\frac{3}{(\psi_\lambda^{2}-\lambda^{2})} \biggl[C_4\frac{\lambda -2\psi_\lambda}{\tau(t)^{\frac{2m}{m+2}}}+ \frac{m\psi_\lambda}{\tau (t)^{2}} \biggr], \end{aligned}$$
(17)
$$\begin{aligned} &p=\frac{3}{\lambda(\psi_\lambda^{2}-\lambda^{2})} \biggl[C_4\frac{2(2\psi_\lambda^{2}-\lambda^{2})-\lambda \psi_\lambda}{\tau(t)^{\frac{2m}{m+2}}}-\frac{m\lambda^{2}}{\tau(t)^{2}} \biggr], \end{aligned}$$
(18)

with ψ λ ≡8π+3λ and \(C_{4}\equiv C_{1}^{-2m}\). Note that although A(t,l) depends on three arbitrary constants, here, there is no necessity of assuming any value for C 3 since the physical quantities above have no dependence on it. Also, the solutions above do not present any dependence on the fifth coordinate, being restricted then, to the observable world.

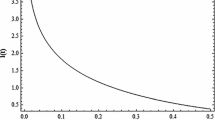
Figures 1 and 2 below show the behaviour of ρ and p with time for a suitable choice of values for the constants of the model. They help us to better interpret the solutions (17)–(18).

Fig. 1
figure 1

Plot of the density of the universe ρ over time for m=3, λ=3, C 1=3, C 2=0

Full size image
Fig. 2
figure 2

Plot of the pressure of the universe p over time for m=3, λ=3, C 1=3, C 2=0

Full size image

From Figs. 1 and 2 it is intuitive that both lim t→0 ρ and lim t→0 p tend to infinity, confirming the expected singularity at t=0.

From the solution (16), one can also derive some important cosmological parameters which are predicted by the present model. The calculation of the mean scale factor a=V 1/4, with V=A 3+m, being the spatial volume of the universe, yields to \(H=\dot{a}/a=0.3t^{-1}\), with H being the Hubble parameter. By taking the second time derivative of a, one obtains the deceleration parameter q to be \(q=-a\ddot{a}/\dot{a}^{2}=2.33\). Note that although the model presents q>0, because of re-collapse, it predicts an accelerated universe within a finite time (Nojiri and Odintson 2003).

The next section is dedicated to the calculation of a solution which describes the late cosmic acceleration of the universe.

5 The accelerated expansion of the universe

Besides the supernovae Ia observations cited above, recent cosmic microwave background observation favours a present accelerated universe, with an EoS of the type p∼−ρ (Planck Collaboration 2013). Let me consider such EoS in the FEs (10)–(12). The separation of variables method yields to the following ordinary differential equations:

$$\begin{aligned} &\frac{2m^{2}-4m+3}{L} \biggl(\frac{dL}{dl} \biggr)^{2}+(-2m+3) \frac{d^{2}L}{dl^{2}}=0, \end{aligned}$$
(19)
$$\begin{aligned} &\frac{m^{2}-2m}{T} \biggl(\frac{dT}{dt} \biggr)^{2}+ \frac{d^{2}T}{dt^{2}}=0. \end{aligned}$$
(20)

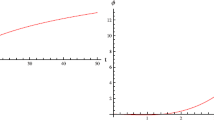
The solutions of Eqs. (19)–(20), with an appropriate choice for the values of the integration constants, yields to the behaviour of the pressure p through time presented in Fig. 3.

Fig. 3
figure 3

Plot of the pressure of the universe p over time for m=2, λ=−6.5

Full size image

Note that the substitution of ω=−1 in the rhs of Eqs. (10)–(12) yields to a consistent behaviour of p, whose negative value represents the vacuum quantum energy in ΛCDM model. Also, the spatial volume of the universe obtained from (19)–(20) yields to q=−0.2, in agreement with an accelerated expansion.

6 The cylindrical condition application and the radiation era description

As it was previously mentioned in Sect. 1, to unify gravitation and electromagnetism, Kaluza applied the so-called cylindrical condition, which consists in neglect all derivations with respect to the extra coordinate. In fact, doing so, the energy-momentum tensor obtained from the 5D empty FEs is considered the energy-momentum tensor of the electromagnetism, defined by \(T_{\mu\nu}^{EM}\equiv g_{\mu\nu}F_{\mu\nu}F^{\zeta\eta}/4-F_{\mu}^{\zeta}F_{\nu\zeta}\), with the electromagnetic tensor F μν ≡∂ μ A ν −∂ ν A μ and A μ is the electromagnetic potential. Moreover, de Leon and Wesson (1993) have shown that the independence on the derivations with respect to the extra coordinate yields to a null trace of the energy-momentum tensor, which is the same as assuming an EoS ρ=3p, i.e., the description of a radiation-dominated universe (indeed described by \(T_{\mu\nu}^{EM}\)).

Note that if one considers the CC application in the present model, one recovers the standard theory of gravity, however, in 5D. In fact, Baffou et al. (2013) have shown that in 4D, the high redshift f(R,T) solutions tend to recover the ΛCDM model, precisely because at very high redshifts, the radiation with EoS parameter ω=1/3 dominates the universe dynamics, making the trace of the energy-momentum tensor to be null.

Now it might be useful to check these features in 5D f(R,T) theory. Let me start by applying the CC to the FEs of the model. First of all, since such application yields to a null trace of the energy-momentum tensor, one re-writes Eq. (3) as G AB =8πT AB . Applying the IMM, the computation of such FEs considering p=ρ/3 results in

$$ A(t,l)=\bigl[(m+1)^{2}t\bigr]^{\frac{1}{(m+1)^{2}}}l $$
(21)

for a suitable choice for the values of the constants involved. Firstly, one should note that the substitution of Eq. (21) in Eq. (4) is useless for low redshifts, since at this era, the length scale of the extra dimension is derisive.

Furthermore, from Eq. (21), the scale factor \(a\sim t^{\frac{m+3}{4(m+1)^{2}}}\). From Friedmann equation, the scale factor of a flat, radiation dominated universe is \(\sim t^{\frac{1}{2}}\). Note that disregarding the negative root, m=0.28 indicates such proportionality. Therefore, such particular case of the model might indeed describe the radiation-dominated era of the universe.

7 Discussion

I have proposed a form of obtaining solutions to f(R,T) cosmology from IMM application. Such model, when elaborated, gave rise to novelties on the physical interpretation of KK gravitational model. It proposes that one should collect all the terms on the 5D vacuum FEs which depends on the extra dimension and relate them with the properties of matter in the observable 4D space-time, which in the present work is indicated in Eqs. (10)–(12).

As a solution to the scale factor A(t,l) I presented Eq. (16), which, apart from the coordinates, depends on four constants: C 1,C 2,C 3 and m (remind that there is no necessity of assuming any value for C 3 since the physical quantities derived from the model does not depend on it). It is convenient to highlight that although the scale factor depends on l, the solutions for the density and pressure of the model does not present any dependence on such coordinate, which constrains those quantities to the observable world and makes it possible to analyse their evolution through time without any sort of assumption for l. Furthermore what is obtained for H is consistent with standard cosmology and despite the positive sign, so is q, since the cosmic re-collapse enables the universe to accelerate within a finite time (Nojiri and Odintson 2003).

In Sect. 5 I presented a particular solution for the case in which the EoS parameter ω=−1. The evolution of the solution p through time presented in Fig. 3 is coherent because it is restricted to an era of the universe in which, from ΛCDM model, it is dominated by an exotic fluid of negative pressure.

I also have applied the CC to the present model. As it is expected, such application recovers the standard theory of gravity in 5D, since in the particular case I have assumed, f(R,T) is linear in R. It was shown that the resulting scale factor indeed might describe the radiation-dominated era of the universe. Also, the linear dependence on l presented in Eq. (21) strengthens such argument, since it makes A(t,l) to be non-negligible only for early times, for which l is still comparable with the other spatial coordinates.

One might wonder what would be the outcome if the CC is dropped in Sect. 6. In such scenario, in order to have the correct time proportionality for a, it is required that \(A(t,l)\sim l^{-\frac{1}{2}}\). Differently from what is predicted by Eq. (21), such solution for A(t,l) does not vanish for low redshifts, what makes advantageous the CC application.

The innovative application of the IMM to 5D f(R,T) theory brought up some interesting cosmological results. Future studies may focus on more general KK metrics and/or other functional forms of f(R,T), objectifying more general solutions for ρ and p.