1 Introduction

Recent astrophysical observations put forward the crucial discovery on the landscape of cosmology by introducing a new vision of the expanding universe. According to these observations, our universe is expanding with an accelerated rate due to the presence of dominant mysterious force dubbed as “dark energy” (DE). The conclusive manifestation of accelerated epoch and puzzling nature of DE motivated many researchers to propose the idea of modified gravitational theories. The simplest modified theory is obtained by replacing Ricci scalar \(R\) with an arbitrary function \(f(R)\) in the Einstein–Hilbert action. This generic function does not appreciate any non-minimal coupling between curvature and matter parts but the effect of minimal curvature and matter coupling yields interesting results (Sotiriou and Faraoni 2010). There is a lot body of literature available about fundamental aspects of this gravity (de Felice and Tsujikawa 2010; Nojiri and Odintsov 2011; Bamba et al. 2012).

Nojiri and Odintsov (2004a) introduced the revolutionary idea of non-minimal coupling between non-linear curvature and matter sectors to identify DE phases of the universe. Harko et al. (2011) studied the effect of non-minimal coupling by a new gravitational theory whose generic function depends on both curvature and matter named as \(f(R,T)\) gravity, where \(T\) represents trace of the energy-momentum tensor. This function evolves gravitational interactions which play a crucial role to study current cosmic acceleration (Harko and Lobo 2014). Sharif and Zubair (2012, 2013a, 2013b, 2013c, 2014a, 2014b) explored different cosmological issues like thermodynamical picture with energy conditions, reconstructed different DE models and established stability criteria as well as exact solutions of anisotropic universe model.

Different researchers investigated exact solutions of non-linear fourth order partial differential equations of \(f(R,T)\) gravity. Sharif and Zubair (2014c) discussed exact solutions to investigate power-law and exponential expansions of Bianchi type I universe model. Harko and Lake (2015) formulated exact solutions for cylindrical spacetime in the presence of non-minimal coupling of curvature and Lagrangian density of matter. Shamir and Raza (2015) found two exact solutions corresponding to cosmic string and non-null electromagnetic field for the same spacetime. Shamir (2015) explored exact solutions and different cosmological parameters to analyze their physical behavior in Bianchi type I universe.

Continuous symmetry plays a significant role to evaluate exact solutions in mathematical physics as it reduces dynamical variables of a non-linear system. On cosmological grounds, Noether symmetry approach is one of the most elegant technique that connects a differentiable symmetry of a physical system to a conserved quantity. For example, the translational and rotational symmetries yield conservation of linear and angular momenta, respectively (Hanc et al. 2004). Capozziello et al. (2007) determined exact solutions of spherically symmetric spacetime via Noether symmetry approach in \(f(R)\) gravity. Hussain et al. (2012) explored Noether symmetry of \(f(R)\) power-law model and found that boundary term of Noether symmetry vanishes for flat FRW universe but Shamir et al. (2012) determined non-zero boundary term for the same model. In modified theories, the presence of Noether symmetry also yields a brief classification of finite time singularities which identifies the points where symmetry is broken (Capozziello et al. 2012).

We have found exact solution of Bianchi I universe model for \(f(R)\) power-law model using Noether symmetry approach (2014). Momeni et al. (2015) discussed the presence of Noether point symmetry for flat FRW universe model in \(f(R,T)\) and mimetic \(f(R)\) gravity. Sharif and Fatima (2016) formulated Noether symmetries and corresponding conserved quantities for both vacuum as well as non-vacuum regions of flat FRW universe model in \(f(G)\) gravity. We have studied exact solution of anisotropic universe model via Noether symmetry approach and established conserved quantities corresponding to Noether point symmetry in \(f(R,T)\) gravity (2017a). The scalar field models play a leading role to explore the evolution as well as current state of the cosmos due to its dynamical nature and tremendous features of spin-0 particles. In this regard, a variety of canonical (quintessence, phantom, k-essence etc) as well as non-canonical scalar field DE models have been proposed (Carroll et al. 2003; de Benedictis et al. 2004; Copeland et al. 2006). The class of non-canonical scalar field models is obtained by modifying the kinetic part of the scalar field which describe both early as well as late-time cosmic expansion. Mamon and Das (2015, 2016) studied cosmic evolution through non-canonical scalar field model and different forms of equation of state (EoS) parameter.

Capozziello and de Ritis (1994) used Noether symmetry approach to formulate different cosmological models as well as to investigate the effect of various scalar field models in scalar-tensor theory. Vakili (2008) found Noether point symmetry as well as conserved quantity of flat FRW universe and studied the behavior of effective EoS parameter relative to quintessence phase in \(f(R)\) gravity. Zhang et al. (2010) discussed multiple scalar field scenario and established a relation of potential function between quintessence and phantom phases through Noether symmetry approach. Jamil et al. (2011) explored the existence of Noether symmetry in the presence of \(f(R)\) tachyon model. Jamil et al. (2012) determined Noether symmetry when matter as well as scalar field minimally incorporates with geometric part and also constructed explicit form of potential function for quintessence as well as phantom phases in \(f(\mathcal{T})\) gravity. Sharif and Shafique (2014) found exact solutions of homogeneous isotropic as well as anisotropic universe models via Noether symmetry approach in scalar-tensor theory non-minimally coupled with torsion scalar. We have studied cosmic evolution with/without canonical scalar field model through anisotropic universe model in \(f(R,T)\) gravity (2017b, 2017c).

In this paper, we study the existence of Noether symmetry of flat FRW universe model in \(f(R,T)\) gravity comprising a minimal coupling with matter and generalized scalar fields. We determine possible symmetries as well as corresponding conserved quantities and evaluate exact solutions for two \(f(R,T)\) models to analyze cosmic evolution through cosmological parameters. The format of this paper is as follows. In Sect. 2, we provide basic construction of \(f(R,T)\) gravity. Section 3 develops Noether symmetry as well as symmetry generators with associated conserved quantities. In the last section, we present final remarks.

2 Basic formalism of \(f(R,T)\) gravity

The action of \(f(R,T)\) gravity is given by (Harko et al. 2011)

$$ \mathcal{I}= \int d^{4}x\sqrt{-g}\biggl[\frac{f(R,T)}{2\kappa ^{2}}+ \mathcal{L}_{m}\biggr], $$
(1)

where \(g\) represents determinant of the metric tensor \(g_{\mu \nu }\) and generic function \(f\) independently introduces a coupling between geometric and matter parts whereas \(\mathcal{L}_{m}\) denotes the matter Lagrangian. The metric variation of action (1) gives non-linear fourth order partial differential equation as

$$\begin{aligned} &f_{R}(R,T) R_{\mu \nu }-\frac{1}{2}f(R,T)g_{\mu \nu } \\ &\qquad {}+(g_{\mu \nu } \Box -\nabla _{\mu }\nabla _{\nu }) f_{R}(R,T)+f_{T}(R,T)T_{\mu \nu } \\ &\qquad {}+f_{T}(R,T)\varTheta _{\mu \nu }=\kappa ^{2}T_{\mu \nu }, \end{aligned}$$
(2)

where \(\nabla _{\mu }\) describes covariant derivative and

$$\begin{aligned} &{\Box =\nabla _{\mu }\nabla ^{\mu },\qquad f_{R}(R,T)=\frac{\partial f(R,T)}{ \partial R},} \\ &{f_{T}(R,T)= \frac{\partial f(R,T)}{\partial T},} \\ &{\varTheta _{\mu \nu } =\frac{g^{\alpha \beta }\delta T_{\alpha \beta }}{ \delta g^{\mu \nu }}=g_{\mu \nu } \mathcal{L}_{m}-2T_{\mu \nu }-2g^{ \alpha \beta } \frac{\partial ^{2}\mathcal{L}_{m}}{\partial g^{\alpha \beta }\partial g^{\mu \nu }}.} \end{aligned}$$

A significant relationship between geometric and matter parts is established from the trace of Eq. (2) as follows

$$\begin{aligned} &{Rf_{R}(R,T)+3\Box f_{R}(R,T)-2f(R,T)+Tf_{T}(R,T)} \\ &{ \quad {}+ \varTheta f_{T}(R,T)= \kappa ^{2}T.} \end{aligned}$$

The action of \(f(R,T)\) gravity incorporating minimal coupling of matter and scalar fields is

$$ \mathcal{I}= \int d^{4}x\sqrt{-g}\biggl[\frac{f(R,T)}{2\kappa ^{2}}+ \mathcal{L}_{m}+\mathcal{L}_{\phi }\biggr], $$
(3)

where \(\mathcal{L}_{\phi }\) represents scalar Lagrangian. For perfect fluid configuration, we consider \(\mathcal{L}_{m}=p_{m}\) and \(\mathcal{L}_{\phi }= \frac{\epsilon }{2}g^{\mu \nu }\partial _{\mu } \phi \partial _{\nu }\phi -V(\phi )\) (\(V(\phi )\) represents potential energy) which reduce the action (3) to

$$ \mathcal{I}= \int d^{4}x\sqrt{-g}\biggl[\frac{f(R,T)}{2\kappa ^{2}}+p_{m}+ \frac{ \epsilon }{2} g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi -V( \phi )\biggr]. $$
(4)

Here \(\epsilon =1\) and −1 correspond to quintessence and phantom models, respectively.

For complete analysis of scalar field model, we explore the effect of positive as well as negative kinetic energy. The negative energy appearing from phantom model emerges some troubles like violation of energy bounds, negative entropy of phantom-dominated universe due to which black holes disappear. At the end, such universe meets a finite time future singularity called big-rip singularity (Nojiri and Odintsov 2004b). Different ideas are introduced to sort out such troubles like considering phantom acceleration as transient phenomenon with different scalar potentials or to modify the gravity, couple DE with dark matter or to use particular forms of EoS interpreting DE era or taking into account some quantum effects (giving rise to the second quantum gravity era) which may delay/stop the singularity occurrence (Elizalde et al. 2004; Nojiri and Odintsov 2004c, 2010, 2011; Bamba et al. 2008).

We consider flat homogeneous and isotropic universe model as

$$ ds^{2}=-dt^{2}+a^{2}(t) \bigl(dx^{2}+dy^{2}+dz^{2}\bigr), $$
(5)

where \(a(t)\) is the scale factor describing expansion of the universe in \(x\), \(y\) and \(z\)-directions. Using Lagrange multiplier approach, the action (4) takes the following form

$$\begin{aligned} \mathcal{I} =& \int \sqrt{-g}\biggl[f(R,T)-\lambda (R-\bar{R})-\chi (T- \bar{T}) +p_{m}(a) \\ &{}+\frac{\epsilon }{2}g^{\mu \nu }\partial _{\mu } \phi \partial _{\nu }\phi -V(\phi )\biggr]dt, \end{aligned}$$
(6)

where \(\sqrt{-g}=a^{3}\), \(\lambda =f_{R}(R,T)\) and \(\chi =f_{T}(R,T)\) are Lagrange multipliers while \(\bar{R}\), \(\bar{T}\) represent dynamical constraints given by

$$\begin{aligned} \bar{R}=6 \biggl( \frac{\ddot{a}}{a}+\frac{\dot{a^{2}}}{a^{2}} \biggr) , \qquad \bar{T}=3p_{m}(a)-\rho _{m}(a). \end{aligned}$$

The corresponding Lagrangian becomes

$$\begin{aligned} &{ \mathcal{L}(a,R,T,\phi ,\dot{a},\dot{R},\dot{T},\dot{\phi })} \\ &{ \quad =a^{3}\biggl[f(R,T)-Rf _{R}(R,T) -Tf_{T}(R,T)} \\ &{ \qquad {} +f_{T}(R,T) \bigl(3p_{m}(a)-\rho _{m}(a)\bigr)+p_{m}(a)} \\ &{ \qquad {} -\frac{\epsilon \dot{\phi }^{2}}{2}-V(\phi )\biggr] -6a\dot{a}^{2}f_{R}(R,T)} \\ &{ \qquad {}-6a^{2}\dot{a}\dot{R}f_{\mathit{RR}}(R,T)-6a^{2} \dot{a}\dot{T}f_{\mathit{RT}}(R,T).} \end{aligned}$$
(7)

The equation of motion of a dynamical system is defined as

$$\begin{aligned} \frac{\partial \mathcal{L}}{\partial q^{i}}-\frac{d}{dt} \biggl( \frac{ \partial \mathcal{L}}{\partial \dot{q}^{i}} \biggr) =0,\qquad p_{i}=\frac{ \partial \mathcal{L}}{\partial q^{i}}, \end{aligned}$$

where \(q_{i}\) and \(p_{i}\) represent \(n\) generalized coordinates and conjugate momenta of configuration space, respectively. Using Eq. (7), the conjugate momenta and equations of motion of configuration space \(Q=\{a,R,T,\phi \}\) become

$$\begin{aligned} &{ p_{a}=-12a\dot{a}f_{R}(R,T)} \\ &{ \hphantom{p_{a}=}{}-6a^{2} \bigl(\dot{R}f_{\mathit{RR}}(R,T)+\dot{T}f _{\mathit{RT}}(R,T)\bigr),} \\ &{ p_{R}= -6a^{2}\dot{a}f_{\mathit{RR}}(R,T), \qquad p_{T}= -6a^{2}\dot{a}f_{\mathit{RT}}(R,T), } \\ &{ p_{\phi }=-\epsilon a^{3}\dot{\phi },} \\ &{ \frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =- \frac{1}{2f_{R}(R,T)} \biggl[f(R,T)-Rf_{R}(R,T)} \\ &{ \hphantom{\frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =} {} -Tf_{T}(R,T)+f_{T}(R,T) \bigl(3p_{m}(a)-\rho _{m}(a) \bigr)} \\ &{ \hphantom{\frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =} {}+p_{m}(a)-\frac{\epsilon \dot{\phi } ^{2}}{2}-V(\phi )} \\ &{\hphantom{\frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =} {} +\frac{a}{3}\bigl\{ f_{T}(3p_{m},_{{a}}-\rho _{m},_{{a}}) +p_{m},_{{a}}\bigr\} } \\ &{\hphantom{\frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =}{} +2\ddot{R}f_{\mathit{RR}}(R,T)+2 \dot{R}^{2}f_{\mathit{RRR}}(R,T) } \\ &{ \hphantom{\frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =}{}+4 \dot{R}\dot{T}f_{\mathit{RRT}}(R,T)+2\ddot{T}f_{\mathit{RT}}(R,T)} \\ &{\hphantom{\frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =} {}+2\dot{T}^{2}f_{\mathit{RTT}}(R,T)+ \frac{4\dot{a} \dot{R}f_{\mathit{RR}}(R,T)}{a}} \\ &{\hphantom{\frac{\dot{a^{2}}}{a^{2}}+\frac{2\ddot{a}}{a} =}{}+\frac{4\dot{a}\dot{T}f_{\mathit{RT}}(R,T)}{a}\biggr],} \end{aligned}$$
(8)
$$\begin{aligned} &{ f_{\mathit{RT}}\bigl(3p_{m}(a)-\rho _{m}(a)\bigr)+6\bigl(\dot{a^{2}}a^{-2} +2 \ddot{a}a^{-1}\bigr)f _{\mathit{RR}}} \\ &{ \qquad {}-Rf_{\mathit{RR}}-Tf_{\mathit{RT}}=0,} \end{aligned}$$
(9)
$$\begin{aligned} &{ Rf_{\mathit{RT}} -6\bigl(\dot{a^{2}}a^{-2} +2\ddot{a}a^{-1}\bigr)f_{\mathit{RT}}} \\ &{ \qquad {}+f_{\mathit{TT}} \bigl(3p_{m}(a)- \rho _{m}(a)\bigr)=0,} \end{aligned}$$
(10)
$$\begin{aligned} &{ a\ddot{\phi }+3\epsilon \dot{a}\dot{\phi }-aV'( \phi )=0.} \end{aligned}$$
(11)

The associated energy function for Lagrangian (7) takes the form

$$\begin{aligned} \mathcal{H} =&\varSigma _{i}\dot{q}^{i}p_{i}- \mathcal{L} \\ =&\frac{6 \dot{a^{2}}f_{R}(R,T)}{a^{2}} +f(R,T)-Rf_{R}(R,T)-Tf_{T}(R,T) \\ &{}+f_{T}(R,T) \bigl(3p_{m}(a)-\rho _{m}(a)\bigr)+p_{m}(a) +\frac{\epsilon \dot{\phi }^{2}}{2} \\ &{}-V(\phi )+ \frac{6\dot{a}\dot{R}f_{\mathit{RR}}(R,T)}{a} +\frac{6\dot{a}\dot{T}f_{\mathit{RT}}(R,T)}{a}. \end{aligned}$$
(12)

3 Noether symmetry approach

In cosmology and theoretical physics, the formalism of Noether symmetry is the most significant strategy to deal with the complexity of non-linear partial differential equations that leads to formulate the corresponding exact solutions. According to remarkable Noether’s theorem, if variational integral remains invariant under a continuous group then group generator provides relative conservation law of equation of motion. If the modified theory of gravity does not possess any conserved quantity then the theory is referred as non-physical. The infinitesimal generator of continuous group is defined as

$$\begin{aligned} K =&\xi \bigl(t,q^{i}\bigr)\frac{\partial }{\partial t}+\eta ^{j}\bigl(t,q^{i}\bigr)\frac{ \partial }{\partial q^{j}}, \end{aligned}$$
(13)

where \(t\) is an affine parameter. For the existence of Noether symmetry, this generator satisfies the invariance condition given by

$$ K^{[1]}\mathcal{L}+(D\xi )\mathcal{L}=\mathit{DB} \bigl(t,q^{i}\bigr), $$
(14)

where \(B\) represents boundary term while the total derivative \(D\) and first order prolongation \(K^{[1]}\) are

$$\begin{aligned} \begin{aligned} &D=\frac{\partial }{\partial t}+\dot{q}^{i}\frac{\partial }{\partial q ^{i}}, \\ & K^{[1]}=K+\bigl(\eta ^{j},_{t}+\eta ^{j},_{i}\dot{q}^{i}-\xi ,_{t} \dot{q}^{j} -\xi ,_{i}\dot{q}^{i} \dot{q}^{j}\bigr)\frac{\partial }{\partial \dot{q}^{j}}. \end{aligned} \end{aligned}$$
(15)

The conserved quantity corresponding to symmetry generator \(K\) takes the form

$$ I=B-\xi \mathcal{L}-\bigl(\eta ^{j}- \dot{q}^{j}\xi \bigr) \frac{\partial \mathcal{L}}{\partial \dot{q}^{j}}. $$
(16)

This quantity also known as Noether integral or first integral. If first order prolongation as well as boundary term of the extended symmetry vanishes, then symmetry generator, invariance condition and corresponding conserved quantity become

$$ \begin{aligned} &K=\beta ^{i}\bigl(q^{i}\bigr) \frac{\partial }{\partial q^{i}}+ \biggl[ \frac{d}{dt}\bigl(\beta ^{i} \bigl(q^{i}\bigr)\bigr) \biggr] \frac{\partial }{\partial \dot{q}^{i}}, \\ &L_{K}\mathcal{L}=K\mathcal{L}=0,\qquad I=-\eta ^{j} \frac{ \partial \mathcal{L}}{\partial \dot{q}^{j}}, \end{aligned} $$
(17)

where \(L\) represents Lie derivative.

In order to evaluate symmetry generator and associated conserved quantity of Lagrangian (7) under invariance condition (14), we consider the vector field with tangent space \(T=\{t,a,\dot{a},R, \dot{R},T,\dot{T},\phi ,\dot{\phi }\}\) for the configuration space \(Q=\{t,a,R,T,\phi \}\) as

$$\begin{aligned} K =&\tau (t,a,R,T,\phi )\frac{\partial }{\partial t}+\alpha (t,a,R,T, \phi ) \frac{\partial }{\partial a} \\ &{}+\beta (t,a,R,T,\phi )\frac{\partial }{\partial R} +\gamma (t,a,R,T,\phi )\frac{\partial }{\partial T} \\ &{}+\delta (t,a,R,T, \phi )\frac{\partial }{\partial \phi }, \end{aligned}$$
(18)

where \(\tau \), \(\alpha \), \(\beta \), \(\gamma \) and \(\delta \) are unknown coefficients of vector field. The prolongation of the vector field up to first order is given by

$$\begin{aligned} K^{[1]} =&\tau \frac{\partial }{\partial t}+\alpha \frac{\partial }{ \partial a}+ \beta \frac{\partial }{\partial R}+\gamma \frac{\partial }{\partial T}+\dot{\alpha } \frac{\partial }{\partial \dot{a}}+ \dot{\beta }\frac{\partial }{\partial \dot{R}} \\ &{}+\dot{\gamma } \frac{ \partial }{\partial \dot{T}}+\dot{\delta }\frac{\partial }{\partial \dot{\phi }}, \end{aligned}$$

where the time derivative of these unknown coefficients are

$$\begin{aligned} \dot{\alpha } =&\frac{\partial \alpha }{\partial t}+\dot{a}\frac{ \partial \alpha }{\partial a}+\dot{R} \frac{\partial \alpha }{\partial R}+\dot{T}\frac{\partial \alpha }{\partial T}\\ &{}-\dot{a} \biggl\{ \frac{ \partial \tau }{\partial t}+ \dot{a}\frac{\partial \tau }{\partial a}+ \dot{R}\frac{\partial \tau }{\partial R} +\dot{T}\frac{\partial \tau }{\partial T} \biggr\} , \\ \dot{\beta } =&\frac{\partial \beta }{\partial t}+\dot{a}\frac{\partial \beta }{\partial a}+\dot{R} \frac{\partial \beta }{\partial R}+\dot{T}\frac{ \partial \beta }{\partial T}\\ &{}-\dot{R} \biggl\{ \frac{\partial \tau }{ \partial t}+ \dot{a}\frac{\partial \tau }{\partial a}+\dot{R}\frac{ \partial \tau }{\partial R} +\dot{T}\frac{\partial \tau }{\partial T} \biggr\} , \\ \dot{\gamma } =&\frac{\partial \gamma }{\partial t}+\dot{a}\frac{ \partial \gamma }{\partial a}+\dot{R} \frac{\partial \gamma }{\partial R}+\dot{T}\frac{\partial \gamma }{\partial T}\\ &{}-\dot{T} \biggl\{ \frac{ \partial \tau }{\partial t}+ \dot{a}\frac{\partial \tau }{\partial a}+ \dot{R}\frac{\partial \tau }{\partial R} +\dot{T}\frac{\partial \tau }{\partial T} \biggr\} , \\ \dot{\delta } =&\frac{\partial \delta }{\partial t}+\dot{a}\frac{ \partial \delta }{\partial a}+\dot{R} \frac{\partial \delta }{\partial R}+\dot{T}\frac{\partial \delta }{\partial T}\\ &{}-\dot{\phi } \biggl\{ \frac{ \partial \tau }{\partial t}+\dot{a}\frac{\partial \tau }{\partial a}+ \dot{R}\frac{\partial \tau }{\partial R} +\dot{T} \frac{\partial \tau }{\partial T} \biggr\} . \end{aligned}$$

Inserting Eq. (18) with its first order prolongation and time derivative of unknown coefficients in invariance condition (14), we obtain the system of equations as follows

$$\begin{aligned} &{ a\tau ,_{{a}}f_{R}=0,\quad a\tau,_{{R}}f_{R}=0,} \\ \end{aligned}$$
(19)
$$\begin{aligned} &{ a\tau ,_{{T}}f_{R}=0, \qquad a\tau ,_{{\phi }}f_{R}=0,} \\ &{6a^{2}\alpha ,_{{R}}f_{\mathit{RR}}=0,} \end{aligned}$$
(20)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{T}}f_{\mathit{RT}}=0,} \end{aligned}$$
(21)
$$\begin{aligned} &{{\epsilon a^{3}\delta ,_{{T}}=-B,_{{\phi }},}} \end{aligned}$$
(22)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{t}}f_{\mathit{RT}}=-B,_{{T}},} \end{aligned}$$
(23)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{t}}f_{\mathit{RR}}=-B,_{{R}},} \end{aligned}$$
(24)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{\phi }}f_{\mathit{RR}}+ \epsilon a^{3}\delta ,_{{R}}=0,} \end{aligned}$$
(25)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{\phi }}f_{\mathit{RT}}+ \epsilon a^{3}\delta ,_{{T}}=0,} \end{aligned}$$
(26)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{T}}f_{\mathit{RR}}+6a^{2} \alpha ,_{{R}}f_{\mathit{RT}}=0,} \end{aligned}$$
(27)
$$\begin{aligned} &{ 12a\alpha ,_{{T}}f_{R}+6a^{2} \beta ,_{{t}}f_{\mathit{RR}} +6a^{2}\gamma ,_{{t}}f_{\mathit{RT}}=-B,_{{a}},} \end{aligned}$$
(28)
$$\begin{aligned} &{ (\alpha -\tau ,_{{t}})-2a^{3}(\delta ,_{{\phi }}-\tau ,_{{t}})=0,} \end{aligned}$$
(29)
$$\begin{aligned} &{ a^{3}\epsilon \delta ,_{{a}}+6a^{2} \gamma ,_{{\phi }}f_{\mathit{RT}} +6a ^{2}\beta ,_{{\phi }}f_{\mathit{RR}}+12a\alpha ,_{{\phi }}f_{R}=0,} \end{aligned}$$
(30)
$$\begin{aligned} &{ \alpha f_{R}+a\beta f_{\mathit{RR}}+a\gamma f_{\mathit{RT}}-a\tau ,_{{t}}+2a\alpha ,_{{a}}f_{R}+a^{2} \beta ,_{{a}}f_{\mathit{RR}}} \\ &{ \quad {}+a^{2}\gamma ,_{{a}} f_{\mathit{RT}}=0,} \end{aligned}$$
(31)
$$\begin{aligned} &{ 2\alpha f_{\mathit{RR}}+a\beta f_{\mathit{RRR}}+a\gamma f_{\mathit{RRT}}+2a\alpha ,_{{R}}f _{R}+a\alpha ,_{{a}}f_{\mathit{RR}}} \\ &{\quad {}+a\beta ,_{{R}}f_{\mathit{RR}} +a\gamma ,_{{R}}f_{\mathit{RT}}-a\tau ,_{{t}}f_{\mathit{RR}}=0,} \end{aligned}$$
(32)
$$\begin{aligned} &{ 2\alpha f_{\mathit{RT}}+a\beta f_{\mathit{RRT}}+a\gamma f_{\mathit{RTT}}+a\alpha ,_{{a}}f_{\mathit{RT}}+2 \alpha ,_{{T}}f_{R}} \\ &{\quad {}+a\beta ,_{{T}}f_{\mathit{RR}} +a\gamma ,_{{T}}f_{\mathit{RT}}-a\tau ,_{{t}}f_{\mathit{RT}}=0,} \end{aligned}$$
(33)
$$\begin{aligned} &{ \alpha \bigl[3a^{2}\bigl(f-Rf_{R}-Tf_{T}+f_{T}(3p_{m}- \rho _{m})+p_{m}} \\ &{\quad {} -V( \phi )\bigr) +a^{3}\bigl\{ f_{T}(3p_{m},_{{a}} -\rho _{m},_{{a}})+p_{m},_{{a}} \bigr\} \bigr]} \\ &{ \quad {} +a^{3}\beta \bigl[-Rf_{\mathit{RR}}-Tf_{\mathit{RT}}+f _{\mathit{RT}}(3p_{m}-\rho _{m})\bigr] } \\ &{ \quad {} +a^{3} \gamma \bigl[-Rf_{\mathit{RT}}-Tf_{\mathit{TT}}+f_{\mathit{TT}}(3p_{m}- \rho _{m})\bigr]} \\ &{ \quad {}-a^{3}V'(\phi ) \delta +a^{3}\tau ,_{{t}}\bigl(f-Rf_{R} -Tf_{T}} \\ &{\quad {}+f_{T}(3p_{m}-\rho _{m})+p_{m}-V(\phi )\bigr)=B,_{{t}}.} \end{aligned}$$
(34)

Equation (19) implies that either \(f_{R}=0\) with \(\tau ,_{{a}}\), \(\tau ,_{{R}}\), \(\tau ,_{{T}}\), \(\tau ,_{{\phi }}\neq 0\) or vice versa.

To evaluate solution of the above system for \(f_{R}=0\), we choose power-law form of unknown coefficients given by

$$\begin{aligned} \alpha =&\alpha _{0}t^{\alpha _{1}}a^{\alpha _{2}}R^{\alpha _{3}}T^{ \alpha _{4}} \phi ^{\alpha _{5}}, \qquad \beta =\beta _{0}t^{\beta _{1}}a ^{\beta _{2}}R^{\beta _{3}}T^{\beta _{4}}\phi ^{\beta _{5}}, \\ \end{aligned}$$
(35)
$$\begin{aligned} \gamma =&\gamma _{0}t^{\gamma _{1}}a^{\gamma _{2}}R^{\gamma _{3}} T^{ \gamma _{4}}\phi ^{\gamma _{5}}, \qquad \delta =\delta _{0}t^{\delta _{1}}a ^{\delta _{2}}R^{\delta _{3}}T^{\delta _{4}}\phi ^{\delta _{5}}, \end{aligned}$$
(36)
$$\begin{aligned} \tau =&\tau _{0}t^{\tau _{1}}a^{\tau _{2}}R^{\tau _{3}}T^{\tau _{4}} \phi ^{\tau _{5}}, \end{aligned}$$
(37)

where \(\alpha _{m}\), \(\beta _{m}\), \(\gamma _{m}\), \(\delta _{m}\) and \(\tau _{m}\) (\(m=0,1,2,3,4,5\)) are unknown constants to be determined. Solving Eqs. (19)–(34) for the above power-law form of symmetry generator coefficients, we obtain trivial solution, i.e., \(\alpha = \beta =\gamma =\delta =0\) with \(B=c_{1}\). Thus, we must have to choose some appropriate model of \(f(R,T)\) gravity to evaluate possible solutions of the above non-linear system. For different choices of matter contribution, Harko et al. (2011) introduced some theoretical models in this gravity given as

  • \(f(R,T)=R+2g(T)\),

  • \(f(R,T)=f(R)+g(T)\),

  • \(f(R,T)=f_{1}(R)+f_{2}(R)g(T)\).

We solve the system of partial differential equations for two models of \(f(R,T)\) gravity to formulate symmetry generator coefficients as well as associated conserved quantities and also evaluate corresponding exact solutions.

3.1 \(f(R,T)=R+2g(T)\)

Here we consider a simple \(f(R,T)\) model that preserves Einstein gravity with some additional matter components, i.e., \(f(R,T)=R+2g(T)\), where the curvature term dominates over the matter part. This model elegantly reduces to standard constant cosmological constant cold dark matter (\(\varLambda \)CDM) model if matter part contains a trace dependent cosmological constant \(\varLambda (T)\) defined as

$$ f(R,T)=R+2\varLambda (T)+h(T). $$
(38)

Inserting this model in Eqs. (19)–(34), we obtain

$$\begin{aligned} &{ B =c_{1}\phi +c_{2}t+c_{3},\qquad \alpha =2c_{4}a^{\frac{-1}{2}}+2c _{5}a,} \\ &{ \beta =\gamma =0,\qquad V(\phi )=c_{7},\qquad \tau =6c_{5}t+c_{6},}\\ &{ \delta =c_{2}a-\frac{c_{1}t}{a^{3}\epsilon }+\phi \bigl\{ a^{-\frac{7}{2}}c_{4}+ \bigl(6a^{3}+a-3\bigr)a^{-3}c_{5}\bigr\} ,} \end{aligned}$$

where \(c_{n}~(n=1,2,\ldots,7)\) are arbitrary constants while Eq. (30) yields

$$ \phi =-\frac{2(\epsilon a^{4}+3c_{1}t)}{\epsilon \{2c_{8}(9-2a)-7c _{9}a^{-\frac{1}{2}}\}}. $$
(39)

For this value of \(\phi \), the boundary term and coefficient of symmetry generator corresponding to scalar field reduce to

$$\begin{aligned} B =&-\frac{2c_{1}(\epsilon a^{4}+3c_{1}t)}{\epsilon \{2c_{8}(9-2a)-7c _{9}a^{-\frac{1}{2}}\}}+c_{2}t+c_{3}, \\ \delta =&c_{2}a-\frac{c_{1}t}{a^{3}\epsilon } \\ &{}-\frac{2(\epsilon a^{4}+3c _{1}t)\{a^{-\frac{7}{2}}c_{4}+(6a^{3}+a-3)a^{-3}c_{5}\}}{\epsilon \{2c _{8}(9-2a)-7c_{9}a^{-\frac{1}{2}}\}}. \end{aligned}$$

In this case, the symmetry generator turns out to be

$$\begin{aligned} K =&(6c_{5}t+c_{6})\frac{\partial }{\partial t}+ \bigl(2c_{4}a^{ \frac{-1}{2}}+2c_{5}a\bigr)\frac{\partial }{\partial a} \\ &{}+ \biggl\{ -\frac{6t(6a ^{3}+a-3)c_{10}}{\epsilon a^{3}\{2c_{8}(9-2a)-7c_{9}a^{-\frac{1}{2}} \}} \\ &{}-\frac{6tc_{11}}{\epsilon a^{\frac{7}{2}}\{2c_{8}(9-2a)-7c _{9}a^{-\frac{1}{2}}\}} \\ &{}-\frac{2a^{\frac{1}{2}}\{(6a^{3}+a-3) a^{ \frac{1}{2}}c_{10}+c_{11}\}}{2c_{8}(9-2a)-7c_{9}a^{-\frac{1}{2}}} \\ &{}+c _{2}a - \frac{c_{1}t}{a^{3}\epsilon } \biggr\} \frac{\partial }{ \partial \phi }, \end{aligned}$$

where \(c_{10}=c_{1}c_{5}\) and \(c_{11}=c_{1}c_{4}\).

The formulated symmetry generator can be split into following Noether point symmetry which leads to the associated Noether integral as follows

$$\begin{aligned} &{ K_{1} =\frac{\partial }{\partial t},} \\ &{ I_{1}=-6a \dot{a}^{2}-a^{3}\biggl(2c _{12}-c_{7}-p_{m}- \frac{3\epsilon \dot{\phi }^{2}}{2}\biggr),} \\ &{ K_{2} =2a^{-\frac{1}{2}}\frac{\partial }{\partial a},\qquad I_{2}=24a ^{\frac{1}{2}}\dot{a},}\\ &{ K_{3}=a \frac{\partial }{\partial \phi }, \qquad I_{3}=t+\epsilon a^{4}\dot{\phi }^{2},} \\ &{ K_{4} =-\frac{t}{a^{3}\epsilon }\frac{\partial }{\partial \phi },} \\ &{ I_{4}=-t\dot{\phi }-\frac{2(\epsilon a^{4}+3c_{1}t)}{\epsilon \{2c_{8}(9-2a)-7c_{9}a^{-\frac{1}{2}}\}},} \\ &{ K_{5} =6t\frac{\partial }{\partial t}+2a\frac{\partial }{\partial a},} \\ &{ I_{5}=24a^{2}\dot{a}-36a\dot{a}^{2}+9\epsilon ta^{3}\dot{\phi } ^{2}-6ta^{3}(2c_{12}-c_{7}-p_{m}),} \\ &{ K_{6} =-\frac{6t(6a^{3}+a-3)}{\epsilon a^{3}\{2c_{8}(9-2a)-7c_{9}a ^{-\frac{1}{2}}\}}\frac{\partial }{\partial \phi },} \\ &{ I_{6}=-\frac{6t \dot{\phi }(6a^{3}+a-3)}{2c_{8}(9-2a)-7c_{9}a^{-\frac{1}{2}}},} \\ &{ K_{7} =-\frac{6t}{\epsilon a^{\frac{7}{2}}\{2c_{7}(9-2a)-7c_{8}a^{- \frac{1}{2}}\}}\frac{\partial }{\partial \phi },}\\ &{ I_{7}=-\frac{6t \dot{\phi }a^{-\frac{1}{2}}}{2c_{8}(9-2a)-7c_{9}a^{-\frac{1}{2}}}.} \end{aligned}$$

The Noether symmetry \(K_{1}\) provides energy conservation with its first integral \(I_{1}\) while \(K_{2}\) yields scaling symmetry. To determine the exact solution, we insert Eq. (39) into (11) and obtain

$$\begin{aligned} a(t) =&\eta _{1}t^{\frac{2}{15}},\qquad \epsilon =1, \\ a(t) =&\eta _{2}t^{\frac{2}{3}},\qquad \epsilon =-1, \end{aligned}$$

where \(\eta _{1}=52l_{1}^{\frac{2}{15}}/410\) and \(\eta _{2}=(3l_{2})^{ \frac{2}{3}}/4^{\frac{1}{3}}\). The Hubble parameter (\(H\)) determines the rate of expansion whereas deceleration parameter (\(q\)) measures that either the universe experiences acceleration (\(q<0\)), or deceleration (\(q>0\)), or constant expansion (\(q=0\)). For isotropic universe model, the Hubble and deceleration parameters are defined as

$$ H=\frac{\dot{a}}{a},\qquad q=-\frac{\dot{H}}{H^{2}}-1. $$

In this case, the corresponding Hubble and deceleration parameters turn out to be \(H=\frac{2t}{15}\), \(q=\frac{13}{2}\) and \(H=\frac{2t}{3}\), \(q= \frac{1}{2}\) for \(\epsilon =1\) and \(\epsilon =-1\), respectively. For late-time cosmic accelerated expansion, the power-law scale factor \(a(t)\) is proportional to \(t^{p}\) (\(p>1\)) but for \(p=\frac{1}{2}\) and \(p=\frac{2}{3}\), it corresponds to radiation and matter dominated universe, respectively. In our case, the solution obtained for \(\epsilon =1\) is not compatible to late-time acceleration of the universe whereas for \(\epsilon =-1\), our solution corresponds to matter dominated era of the universe. The positivity of deceleration parameter ensures decelerating universe for both quintessence and phantom models.

The potential and kinetic energies of the scalar field play a dynamical role to study cosmic expansion. For accelerated expansion, the field \(\phi \) evolves negatively and potential dominates over the kinetic energy (\(\frac{\dot{\phi }^{2}}{2}< V(\phi )\)) whereas negative potential follows the kinetic energy for decelerated expansion of the universe (\(\frac{ \dot{\phi }^{2}}{2}>-V(\phi )\)). Figure 1 analyzes the behavior of scalar field and cosmic expansion via quintessence and phantom models. The left plot shows that the scalar field is negative initially indicating accelerated expansion but gradually, it tends to increase positively which describes decelerated expansion. In case of phantom model, the scalar field grows positively leading to decelerated expansion of the universe.

Fig. 1
figure 1

Plots of scalar field \(\phi (t)\) versus cosmic time \(t\) for \(\epsilon =1\) (left) and \(\epsilon =-1\) (right) with \(c_{1}=0.3\), \(c_{8}=0.002\), \(c_{9}=1\), \(l_{1}=5.5\) and \(l_{2}=0.5\)

Full size image

Next, we determine Noether point symmetry as well as corresponding first integral in the absence of boundary term of extended symmetry and also formulate exact solution of the field equations. In this case, the first order prolongation vanishes and the vector field of configuration space \(Q=\{a,R,T,\phi \}\) with tangent space \(T=\{a,\dot{a},R,\dot{R},T, \dot{T},\phi ,\dot{\phi }\}\) is given by

$$\begin{aligned} K =&\alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial R}+\gamma \frac{\partial }{\partial T}+\delta \frac{\partial }{\partial \phi }+\dot{\alpha }\frac{\partial }{\partial \dot{a}}+\dot{ \beta }\frac{ \partial }{\partial \dot{R}}+\dot{\gamma }\frac{\partial }{\partial \dot{T}} \\ &{}+\dot{\delta } \frac{\partial }{\partial \dot{\phi }}, \end{aligned}$$
(40)

where time derivative of unknown coefficients of the vector field are

$$\begin{aligned} \dot{\alpha } =&\dot{a}\frac{\partial \alpha }{\partial a}+\dot{R}\frac{ \partial \alpha }{\partial R}+ \dot{T}\frac{\partial \alpha }{\partial T}+\dot{\phi }\frac{\partial \alpha }{\partial \phi },\\ \dot{\beta } =&\dot{a} \frac{\partial \beta }{\partial a}+\dot{R}\frac{ \partial \beta }{\partial R}+\dot{T} \frac{\partial \beta }{\partial T}+\dot{ \phi }\frac{\partial \beta }{ \partial \phi }, \\ \dot{\gamma } =&\dot{a}\frac{\partial \gamma }{\partial a}+\dot{R} \frac{ \partial \gamma }{\partial R}+\dot{T}\frac{\partial \gamma }{\partial T}+\dot{\phi }\frac{\partial \beta }{\partial \phi },\\ \dot{\delta } =&\dot{a}\frac{\partial \delta }{\partial a}+\dot{R}\frac{ \partial \delta }{\partial R}+\dot{T} \frac{\partial \delta }{\partial T}+\dot{\phi }\frac{\partial \beta }{\partial \phi }. \end{aligned}$$

Taking the Lie derivative of Lagrangian (7) relative to the vector field (40), we obtain an over determined system of non-linear equations given as

$$\begin{aligned} &{ a^{2}\alpha ,_{{R}}f_{\mathit{RR}}=0,} \end{aligned}$$
(41)
$$\begin{aligned} &{ a^{2}\alpha ,_{{T}}f_{\mathit{RT}}=0,} \end{aligned}$$
(42)
$$\begin{aligned} &{ 3\epsilon \alpha +\epsilon a\delta ,_{{\phi }}=0,} \end{aligned}$$
(43)
$$\begin{aligned} &{ a^{2}\alpha ,_{{T}}f_{\mathit{RR}}+a^{2} \alpha ,_{{R}}f_{\mathit{RT}}=0,} \end{aligned}$$
(44)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{\phi }}f_{\mathit{RR}}+ \epsilon \delta ,_{{R}}=0,} \end{aligned}$$
(45)
$$\begin{aligned} &{ 6a^{2}\alpha ,_{{\phi }}f_{\mathit{RT}}+ \epsilon \delta ,_{{T}}=0,} \end{aligned}$$
(46)
$$\begin{aligned} &{ 12a\alpha ,_{{\phi }}f_{R}+6a^{2} \beta ,_{{\phi }}f_{\mathit{RR}} +6a^{2} \delta ,_{{\phi }}f_{\mathit{RT}}+\epsilon a^{3}\delta ,_{{a}}=0,} \end{aligned}$$
(47)
$$\begin{aligned} &{ a\beta f_{\mathit{RR}}+a\gamma f_{\mathit{RT}}+2a\alpha ,_{{a}}f_{R}+a^{2}\beta ,_{{a}}f_{\mathit{RR}}} \\ &{ \quad {}+a^{2} \gamma ,_{{a}}f_{\mathit{RT}}+\alpha f_{R}=0,} \end{aligned}$$
(48)
$$\begin{aligned} &{ a\beta f_{\mathit{RRR}}+a\gamma f_{\mathit{RRT}}+2a\alpha ,_{{R}}f_{R}+a\alpha ,_{{a}}f_{\mathit{RR}}} \\ &{ \quad {}+a\beta ,_{{R}}f_{\mathit{RR}} +a\gamma ,_{{R}}f_{\mathit{RT}} +2\alpha f_{\mathit{RR}}=0,} \end{aligned}$$
(49)
$$\begin{aligned} &{ a\beta f_{\mathit{RRT}}+a\gamma f_{\mathit{RTT}}+a\alpha ,_{{a}}f_{\mathit{RT}}+2\alpha ,_{{T}}f_{R}+a\beta ,_{{T}}f_{\mathit{RR}}} \\ &{\quad {} +a\gamma ,_{{T}}f_{\mathit{RT}} +2\alpha f_{\mathit{RT}}=0,} \end{aligned}$$
(50)
$$\begin{aligned} &{ \alpha \bigl[3a^{2}\bigl(f-Rf_{R}-Tf_{T}+f_{T}(3p_{m}- \rho _{m})+p_{m}-V( \phi )\bigr) } \\ &{\quad {}+a^{3}\bigl\{ f_{T}(3p_{m},_{{a}} -\rho _{m},_{{a}})+p_{m},_{{a}} \bigr\} \bigr] +a^{3}\beta \bigl[-Rf_{\mathit{RR}}} \\ &{ \quad {}-Tf_{\mathit{RT}}+f _{\mathit{RT}}(3p_{m}-\rho _{m})\bigr] +a^{3} \gamma \bigl[-Rf_{\mathit{RT}}-Tf_{\mathit{TT}}} \\ &{\quad {} +f_{\mathit{TT}}(3p_{m}-\rho _{m})\bigr]-a^{3}V'( \phi ) \delta =0.} \end{aligned}$$
(51)

Solving the system for \(f(R,T)\) model (38), we obtain unknown coefficients and potential function as

$$\begin{aligned} &{ \alpha =d_{1}\sin \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) +d_{2}\cos \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) ,\qquad \beta =0,} \\ &{ \gamma =0,} \\ &{ \delta =-\frac{2\sqrt{3}}{\sqrt{\epsilon }a^{\frac{3}{2}}} \biggl[ -d_{1}\cos \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) +d_{2}\sin \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) \biggr] ,} \\ &{ V(\phi ) =d_{4} \biggl[ -\bigl(d_{1}^{2}-d_{2}^{2} \bigr)\cos \biggl( \frac{\sqrt{3 \epsilon }\phi }{2} \biggr)}\\ &{ \hphantom{V(\phi ) =}{} +2d_{1}d_{2} \sin \biggl( \frac{\sqrt{3 \epsilon }\phi }{2} \biggr) \biggr] .} \end{aligned}$$

Without any loss of generality, we assume \(d_{3}=0\). In this case, the trace dependent cosmological constant, density and pressure of matter part become

$$\begin{aligned} &{ \varLambda (T) =d_{9}(-T+3d_{5}-d_{7})+ \frac{d_{4}(d_{1}^{2}+d_{2}^{2})+d _{5}-h(T)}{2},} \\ &{ p_{m}(a) =d_{5}+\frac{d_{6}}{a^{3}},\qquad \rho _{m}(a)=d_{7}+\frac{d _{8}}{a^{3}},} \end{aligned}$$

where \(d_{k}~(k=1,2,\ldots,8)\) are arbitrary constants.

These solutions satisfy the over determined system (41)–(51) for \(d_{1}=0\) with \(d_{2},~d_{4}\neq 0\). Thus, the symmetry generator of Noether symmetry and corresponding Noether first integral become

$$\begin{aligned} &{ K =d_{2}\cos \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) \frac{ \partial }{\partial a}-2d_{2}\sqrt{3\epsilon ^{-1}a^{-3}} \sin \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) \frac{\partial }{\partial \phi },} \\ &{ I =12a\dot{a}d_{2}\cos \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) -2d_{2}\sqrt{3\epsilon a ^{3}}\dot{\phi }\sin \biggl( \frac{\sqrt{3\epsilon }\phi }{4} \biggr) .} \end{aligned}$$

Without any loss of generality, we assume \(d_{7}=d_{5}\) and \(d_{8}=d_{6}\) which leads to the explicit form of \(f(R,T)\) model given by

$$ f(R,T)=R-2Td_{9}+d_{4}d_{2}^{2}+d_{5}(4d_{9}+1). $$
(52)

In order to establish cosmological analysis of the constructed model experiencing minimal coupling with matter and scalar fields, we evaluate exact solution of equation of motion by using Eq. (52) in (8) and (12) which leads to

$$\begin{aligned} a(t) =&\frac{(d_{2}d_{4}-1)^{-1}}{\sqrt{2.3^{\frac{1}{3}}}d_{2}} \biggl[ d_{2}^{2}(d_{2}d_{4}-1)^{2} \\ &{}\times \biggl\{ 12 \biggl( -d_{10} \sin \biggl( \sqrt{\frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr) \\ &{}+ d_{11} \cos \biggl( \sqrt{ \frac{3d_{2}(d _{2}d_{4}-1)}{2}}t \biggr) \biggr) \sqrt{d_{2}(d_{2}d_{4}-1)} \\ &{}+d _{6}\sqrt{6} (4d_{9}+1) \biggr\} \biggr] ^{\frac{1}{3}}. \end{aligned}$$
(53)

This form of scale factor defines an oscillatory solution of the universe.

To investigate this oscillatory solution, we discuss the behavior of the some significant cosmological parameters, i.e., Hubble, deceleration, EoS and \(r-s\) parameters which play a crucial role to study current accelerated expansion of the universe. For the explicit form of \(f(R,T)\) model (52) and scale factor (53), these parameters become

$$\begin{aligned} H =&2\sqrt{6} \biggl[ d_{10} \cos \biggl( \sqrt{\frac{3d_{2}(d_{2}d _{4}-1)}{2}}t \biggr)\\ &{} +d_{11} \sin \biggl( \sqrt{\frac{3d_{2}(d_{2}d _{4}-1)}{2}}t \biggr) \biggr]d_{2}(d_{2}d_{4}-1) \\ &{}\times \biggl\{ 12 \sqrt{d_{2}(d_{2}d_{4}-1)} \biggl[ d_{10} \sin \biggl( \sqrt{\frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr) \\ &{} -d_{11} \cos \biggl( \sqrt{ \frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr)\! \biggr] +d_{6}\sqrt{6} (4d _{9}+1) \biggr\} ^{-1}\!, \\ q =&-1+ \biggl( 12d_{2}(d_{2}d_{4}-1) \bigl(d_{10}^{2}+d_{11}^{2}\bigr) \\ &{} - \sqrt{6d _{2}(d_{2}d_{4}-1)}d_{6}(4d_{9}+1) \\ &{}\times \biggl[ d_{10} \sin \biggl( \sqrt{ \frac{3d_{2}(d _{2}d_{4}-1)}{2}}t \biggr) \\ &{}-d_{11} \cos \biggl( \sqrt{ \frac{3d_{2}(d _{2}d_{4}-1)}{2}}t \biggr) \biggr] \biggr) \\ &{}\times \biggl[ d_{10} \cos \biggl( \sqrt{ \frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr)\\ &{} +d_{11} \sin \biggl( \sqrt{ \frac{3d _{2}(d_{2}d_{4}-1)}{2}}t \biggr) \biggr] ^{-2} \\ &{}\times \bigl\{ 4d_{2}(d_{2}d_{4}-1) \bigr\} ^{-1}. \end{aligned}$$

The diagnostic pair of \(r-s\) parameters are used to investigate the features of DE candidates as these parameters establish a correspondence between constructed and standard models of the universe. For \((r,s)=(1,0)\), the constructed model corresponds to standard \(\varLambda \)CDM model while \((1,0)\) and \((-\infty ,\infty )\) indicate standard cold dark matter and Einstein universe, respectively whereas the trajectories with \(s>0\) and \(r<1\) correspond to quintessence and phantom phases of DE. In this case, these parameters turn out to be

$$\begin{aligned} r =& \biggl[ d_{2}(d_{2}d_{4}-1)\cos ^{3} \biggl( \sqrt{\frac{3d_{2}(d _{2}d_{4}-1)}{2}}t \biggr) \\ &{}\times\sin \biggl( \sqrt{ \frac{3d_{2}(d_{2}d _{4}-1)}{2}}t \biggr) d_{10}d_{11}\bigl(d_{10}^{2}+d_{11^{2}} \bigr)\\ &{} +\biggl(d_{2}(d_{2}d _{4}-1) \bigl(18d_{10}^{2}+22d_{11^{2}}\bigr)- \frac{3}{4}d_{6}^{2}d_{10}d_{11} \\ &{}\times \bigl(1+8d_{9}(2d_{9}+1)\bigr) \biggr) \cos \biggl( \sqrt{\frac{3d _{2}(d_{2}d_{4}-1)}{2}}t \biggr)\\ &{}\times \sin \biggl( \sqrt{ \frac{3d_{2}(d _{2}d_{4}-1)}{2}}t \biggr) +d_{2}(d_{2}d_{4}-1) \\ &{} \times\bigl(d_{10}^{4}-6d_{2}d_{10}^{2}d_{11}^{2}+d _{11}^{4}\bigr) \cos ^{4} \biggl( \sqrt{ \frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr) \\ &{}+ \biggl\{ d_{2}(d_{2}d_{4}-1) \bigl(9d_{10}^{4}+6d_{10}^{2}d_{11}^{2}-11d _{11}^{4}\bigr)\\ &{} +\frac{3}{8}\bigl(1+8d_{9}(2d_{9}+1) \bigr)d_{6}^{2} \bigl(d_{11}^{2}-d_{10}^{2} \bigr)\biggr\} \\ &{}\times \cos ^{2} \biggl( \sqrt{\frac{3d _{2}(d_{2}d_{4}-1)}{2}}t \biggr) +d_{2}\bigl(9d_{10}^{2}d_{11}^{2}+10d_{11} ^{4}\bigr) \\ &{}\times (d_{2}d_{4}-1)-3d_{11}^{2}d_{6}^{2}d_{9}(2d_{9}+1) \biggr] \\ &{}\times\biggl[ d _{10} \cos \biggl( \sqrt{\frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr) \\ &{}+ d_{11} \sin \biggl( \sqrt{\frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr) \biggr] ^{-4}\bigl\{ d_{2}(d _{2}d_{4}-1) \bigr\} ^{-1}, \\ s =&-\frac{1}{32} \biggl[ 24\bigl(d_{10}^{2}+d_{11}^{2} \bigr) -\frac{d_{6}^{2}(1+8d _{9}(2d_{9}+1))}{d_{2}(d_{2}d_{4}-1)} \biggr]\\ &{}\times \biggl[ 6\bigl(d_{10}^{2}+d _{11^{2}}\bigr) \cos ^{2} \biggl( \sqrt{ \frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr)\\ &{} + \sqrt{6\bigl(d_{2}(d_{2}d_{4}-1) \bigr)^{-1}}d_{6}(d_{10}-d_{11}) \\ &{}\times \biggl[ \cos \biggl( \sqrt{ \frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr)\\ &{} +\sin \biggl( \sqrt{\frac{3d _{2}(d_{2}d_{4}-1)}{2}}t \biggr) \biggr] \\ &{} +12d_{10}d_{11} \cos \biggl( \sqrt{\frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr)\\ &{} \times\sin \biggl( \sqrt{\frac{3d _{2}(d_{2}d_{4}-1)}{2}}t \biggr) -6\bigl(2d_{10}^{2}+d_{11}^{2} \bigr) \biggr] \\ &{}\times \biggl[ d_{10} \cos \biggl( \sqrt{ \frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr)\\ &{} +d_{11} \sin \biggl( \sqrt{ \frac{3d _{2}(d_{2}d_{4}-1)}{2}}t \biggr) \biggr] ^{-4}. \end{aligned}$$

The EoS parameter \((\omega =\frac{p}{\rho })\) characterizes the universe into different eras and also distinguishes DE era into distinct phases like \(\omega =-1\) describes cosmological constant while \(-1<\omega \leq -1/3\) and \(\omega <-1\) correspond to quintessence and phantom phases, respectively. Inserting Eqs. (52) and (53) in (8) and (9), we obtain the effective EoS parameter as follows

$$ \omega _{\mathit{eff}}=\frac{d_{2}(d_{2}d_{4}-1)-\epsilon \frac{\dot{\phi }^{2}}{2}}{d_{2}(d_{2}d_{4}-1)-d_{6}(4d_{9}+1)a^{-3}+ \epsilon \frac{\dot{\phi }^{2}}{2}}, $$

where

$$\begin{aligned} \frac{\dot{\phi }^{2}}{2} =&\epsilon d_{2}(d_{2}d_{4}-1) \bigl\{ 24d _{2}(d_{2}d_{4}-1) \bigl(d_{10}^{2}+d_{11}^{2} \bigr)\\ &{}-d_{6}^{2}\bigl(1+8d_{9}(2d_{9}+1) \bigr) \bigr\} \\ &{}\times \biggl[ \biggl\{ d_{10} \sin \biggl( \sqrt{ \frac{3d_{2}(d _{2}d_{4}-1)}{2}}t \biggr)\\ &{} -d_{11} \cos \biggl( \sqrt{ \frac{3d_{2}(d _{2}d_{4}-1)}{2}}t \biggr) \biggr\} 24\sqrt{d_{2}(d_{2}d_{4}-1)} \\ &{}\times \biggl\{ -\sqrt{d_{2}(d _{2}d_{4}-1)} \biggl\{ d_{10} \sin \biggl( \sqrt{\frac{3d_{2}(d_{2}d _{4}-1)}{2}}t \biggr) \\ &{}-d_{11} \cos \biggl( \sqrt{ \frac{3d_{2}(d_{2}d_{4}-1)}{2}}t \biggr) \biggr\} +d_{6}(4d_{9}+1)\\ &{} - d _{6}^{2} \bigl(1+8d_{9}(2d_{9}+1)\bigr)\biggr\} \biggr] ^{-1}. \end{aligned}$$

For the oscillatory solution of the scale factor, both plots of Fig. 2 show that the universe experiences accelerated expansion as scale factor and Hubble parameter grow continuously. In the left plot of Fig. 3, the negative behavior of deceleration parameter also represents accelerated cosmic expansion while the right plot identifies \(r-s\) parameters trajectories in quintessence and phantom phases as \(s>0\) when \(r<1\). The graphical analysis of Fig. 4 gives different phases of DE era of the universe like the first plot indicates that the universe enters into phantom phase leading to future singularities. The second plot of Fig. 4 shows that the universe possesses an elegant exit from matter dominated era to quintessence phase which leads to phantom phase with the passage of time. Figure 5 analyzes cosmic expansion via scalar field and also compares its kinetic and potential energies. The left plot shows that the scalar field is negatively increasing whereas the right plot ensures \(\frac{\dot{\phi }^{2}}{2}< V(\phi )\) implying that quintessence model yields accelerated expansion.

Fig. 2
figure 2

Plots of scale factor \(a(t)\) (left) for and Hubble parameter \(H(t)\) (right) versus cosmic time \(t\) for \(d_{2}=0.2\), \(d_{4}=5.5\), \(d_{6}=-0.95\), \(d_{9}=-0.1\), \(d_{10}=-5\) and \(d_{11}=0.1\)

Full size image
Fig. 3
figure 3

Plots of deceleration parameter \(q(t)\) (left) and \(r-s\) parameters (right) versus cosmic time \(t\)

Full size image
Fig. 4
figure 4

Plots of EoS parameter \(\omega _{\mathit{eff}}\) for \(\epsilon =1\) (left) and EoS parameter \(\omega _{\mathit{eff}}\) for \(\epsilon =-1\) (right) versus cosmic time \(t\)

Full size image
Fig. 5
figure 5

Plots of scalar field \(\phi (t)\) (left) versus cosmic time \(t\) and potential energy \(V(\phi )\) versus kinetic energy \(\frac{ \dot{\phi }^{2}}{2}\) (right) for \(\epsilon =1\)

Full size image

3.2 \(f(R,T)=f(R)+g(T)\)

Now we study the behavior of an indirect non-minimal curvature and matter coupling interacting with scalar field. For this purpose, we consider a model of \(f(R,T)\) gravity which can be split into curvature and matter parts such as the model can also referred as correction to \(f(R)\) gravity given by

$$ f(R,T)=f(R)+g(T). $$
(54)

To formulate Noether point symmetry of this model under the invariance condition (18), we insert (54) into (19)–(34) which leads to trivial solution with constant boundary term and potential function. To avoid this situation, we consider power-law form, i.e., \(f(R)=f_{0}R^{n}\), \(n\neq 0,1\) which yields

$$ f(R,T)=f_{0}R^{n}+g(T). $$
(55)

Using Eq. (55) in (19)–(34), we obtain the following generator coefficients

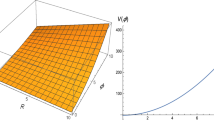
$$\begin{aligned} \tau =&\xi _{4},\qquad \alpha =0,\qquad \gamma =0,\qquad \delta =\xi _{1}+\frac{ \xi _{2}}{a}, \\ \beta =&\frac{1}{aR^{n-2}} \biggl( -\frac{t}{3nf_{0}(n-1)} + \frac{\xi _{2}\epsilon \phi }{nf_{0}(n-1)}+\xi _{3} \biggr) , \end{aligned}$$

where \(\xi _{l}\ (l=1,2,\ldots,5)\) are arbitrary constants while the boundary term and potential function turn out to be

$$\begin{aligned} &{ B =\bigl(\xi _{4}+\xi _{5}a^{2}\bigr)t,}\\ &{ V(\phi )= \bigl\{ -12\phi \bigl(1+a^{2}\bigr)+12 \xi _{6}a^{2}( \xi _{1}a+\xi _{2})+4Rta^{2}\phi} \\ &{\hphantom{ V(\phi )=}{} - \xi _{2}\epsilon a^{2}R\phi ^{2}+12\xi _{3}f_{0}n(n-1)a^{2}R \phi \bigr\} } \\ &{\hphantom{ V(\phi )=}{} \times\bigl\{ 12a^{2}(\xi _{1}a+\xi _{2})\bigr\} ^{-1}.} \end{aligned}$$

This boundary term and symmetry generator coefficients yield Noether point symmetry and Noether first integral of equation of motion which leads to the following conserved quantities

$$\begin{aligned} &{ K_{1} =\frac{\partial }{\partial \phi },\qquad I_{1}=\epsilon a^{3} \dot{\phi },} \\ &{ K_{2} =\frac{1}{a}\frac{\partial }{\partial \phi }+ \frac{\epsilon \phi }{nf_{0}(n-1)}\frac{\partial }{\partial R},\qquad I_{2}=6\epsilon a\dot{a}\phi +\epsilon a^{2}\dot{\phi },} \\ &{ K_{3} =\frac{\partial }{\partial R},\qquad I_{3}=6n(n-1)f_{0}a \dot{a},} \\ &{ K_{4} =\frac{\partial }{\partial t},}\\ &{ I_{4}=t-a^{3} \bigl(f_{0}R^{n}(1-n)+g(T)+g(T),_{{T}}} \\ &{ \hphantom{I_{4}=}{} \times (3p_{m}-\rho _{m}-T)-p_{m}-V(\phi )\bigr)}\\ &{ \hphantom{I_{4}=}{}+6nf_{0}a \dot{a}^{2}R^{n-1}-\frac{\epsilon a^{3} \dot{\phi }^{2}}{2},} \\ &{ K_{5} =-\frac{t}{3nf_{0}(n-1)aR^{n-2}}\frac{\partial }{\partial R}, \qquad I_{5}=a^{2}t-2a\dot{a}t.} \end{aligned}$$

In this case, the Noether symmetry \(K_{4}\) along with first integral \(I_{4}\) yields energy conservation.

Now we discuss the existence of Noether symmetry and corresponding conserved quantities in the absence of boundary term and first order prolongation. For this purpose, we consider the invariance condition (17) and insert the \(f(R,T)\) model (54) along its derivatives relative to \(R\) and \(T\) in Eqs. (41)–(51). On solving the system, we obtain

$$\begin{aligned} &{ \alpha =-\frac{2a\zeta _{1}}{3},\qquad \beta =\frac{R\zeta _{1}}{a}, \qquad \gamma =0,} \\ &{ \delta =\zeta _{1}\phi +\zeta _{2}, \qquad V(\phi ) =\zeta _{4}+\frac{\zeta _{5}(\zeta _{1}\phi +\zeta _{2})^{2}}{ \zeta _{1}^{2}},} \end{aligned}$$

where \(\zeta _{n}\) are arbitrary constants and without any loss of generality, we assume that \(\zeta _{3}=0\). For these symmetry generator coefficients, the Noether symmetry and corresponding conserved quantities turn out to be

$$\begin{aligned} K_{1} =&\frac{\partial }{\partial \phi },\qquad I_{1}=-\epsilon a^{3} \dot{\phi }, \\ K_{2} =&-\frac{2a}{3}\frac{\partial }{\partial a}+ \frac{R}{a}\frac{ \partial }{\partial R}+\phi \frac{\partial }{\partial \phi },\qquad I _{2}=-\epsilon a^{3}\phi \dot{\phi }. \end{aligned}$$

These symmetries appear for \(f(R)=\zeta _{3}\) and \(g(T)=\zeta _{6}T\) implying the dominant effect of matter distribution. Using the field equations (8) and (9), we formulate exact solution of the scale factor and scalar field given as

$$\begin{aligned} &{ a(t)= \biggl[ \frac{\zeta _{7}}{2\zeta _{5}} \biggl( -1+\frac{2\tan ( \lambda )^{2}}{1+\tan (\lambda )^{2}} \biggr) ^{-2} \biggr] ^{ \frac{1}{3}},}\\ &{ \phi =\frac{\zeta _{2}}{\zeta _{1}}+ \frac{\sqrt{\frac{ \zeta _{2}}{2\zeta _{5}}} \tan (\lambda )}{1+\tan (\lambda )^{2}},} \end{aligned}$$

where \(\lambda =\sqrt{2\zeta _{5}/\epsilon }(-t+\zeta _{8})\). For this oscillatory solution, Hubble, deceleration and \(r-s\) parameters become

$$\begin{aligned} &{ H =-\frac{8\sqrt{2\zeta _{5}}}{3\sqrt{\epsilon }} \frac{\sin ( \lambda )\cos (\lambda )}{2\cos (\lambda )^{2}-1},}\\ &{ q=-\frac{ \cos (\lambda )^{4}-\cos (\lambda )^{2}-\frac{3}{8}}{\cos (\lambda )^{2}( \cos (\lambda )^{2}-1)},} \\ &{ r =-\frac{8\cos (\lambda )^{2}\{17\cos (\lambda )^{2} -16\cos ( \lambda )^{4}+8\cos (\lambda )^{6}-9\}+9}{64\cos (\lambda )^{4}\{1-2 \cos (\lambda )^{2}+\cos (\lambda )^{4}\}},} \\ &{ s =\frac{8\cos (\lambda )^{2}\{25\cos (\lambda )^{2}-32\cos (\lambda )^{4} +16\cos (\lambda )^{6}-9\}+9}{72\cos (\lambda )^{2}\{\cos ( \lambda )^{2}(3-8\cos (\lambda )^{2}+\cos (\lambda )^{4})+1\}}.} \end{aligned}$$

In this case, the effective EoS parameter takes the form

$$\begin{aligned} \omega _{\mathit{eff}} =&9\bigl[-\zeta _{6}\zeta _{1}^{2}+4\zeta _{5}\zeta _{2} \zeta _{1}\sqrt{2\zeta _{5}\zeta _{6}} \sin (\lambda ) \cos (\lambda )\\ &{}+2\zeta _{5}\bigl(\zeta _{1}^{2}+4 \zeta _{2}^{2}\bigr)+ (8-\zeta _{5}\zeta _{6}) \zeta _{5}\zeta _{1}^{2}\cos (\lambda )^{4}-\zeta _{5}\zeta _{1}^{2} \\ &{}\times(8- \zeta _{5}\zeta _{6})\cos (\lambda )^{2}\bigr]/ \bigl\{ -\zeta _{6}\zeta _{1}^{2}+4\zeta _{5}\zeta _{2}\zeta _{1}\sqrt{2\zeta _{5}\zeta _{6}} \\ &{}\times \sin (\lambda )\cos (\lambda )+2\zeta _{5}\bigl(3 \zeta _{1}^{2} +4 \zeta _{2}^{2}\bigr)\\ &{}+ \zeta _{5}\zeta _{1}^{2} (24-\zeta _{5} \zeta _{6})\cos ( \lambda )^{4}-\zeta _{5}\zeta _{1}^{2} \\ &{}\times (24-\zeta _{5}\zeta _{6})\cos (\lambda )^{2}\bigr\} . \end{aligned}$$

The graphical behavior of the oscillatory solution and Hubble parameter is shown in Fig. 6. The left plot indicates that the initially increasing behavior of scale factor describes accelerated expansion but with the passage of time, this scale factor leads to decelerated expansion due to its decreasing behavior. The right plot of Fig. 6 identifies decreasing rate of expansion. In Fig. 7, the deceleration parameter experiences a transition from negative to positive region which shows that the universe admits an exit from accelerated to decelerated expansion. The trajectories of \(r-s\) parameters yield \(s>0\) for \(r<1\) initially implying quintessence and phantom phases but after some time, \(s<0\). Figure 8 indicates that the effective EoS parameter is approaching to zero as time goes on implying a transition from quintessence to matter dominated universe. In Fig. 9, the scalar field is found to be positively increasing in left plot while potential and kinetic energies satisfy \(\frac{\dot{\phi }^{2}}{2}< V(\phi )\) initially. With the passage of time, kinetic energy starts dominating over potential energy and consequently representing an epoch of decelerated expansion. Thus, the analysis indicates that the universe experiences a transition from accelerated to decelerated phase.

Fig. 6
figure 6

Plots of scale factor \(a(t)\) (left) and Hubble parameter \(H(t)\) (right) versus cosmic time \(t\) for \(\zeta _{5}=0.05\), \(\zeta _{7}=1\), \(\zeta _{8}=10\)

Full size image
Fig. 7
figure 7

Plots of deceleration parameter \(q(t)\) (left) and \(r-s\) parameters (right)

Full size image
Fig. 8
figure 8

Plot of EoS parameter \(\omega _{\mathit{eff}}\) for \(\zeta _{6}=0.2\)

Full size image
Fig. 9
figure 9

Plots of scalar field \(\phi (t)\) (left) versus cosmic time \(t\) and potential energy \(V(\phi )\) versus kinetic energy \(\frac{\dot{\phi }^{2}}{2}\) (right) for \(\epsilon =1\) when \(\zeta _{1}=0.5\) and \(\zeta_{2} = 0.4\)

Full size image

In order to discuss the effect of curvature appreciating non-minimal curvature matter coupling, we choose power-law form of \(f(R)\) and evaluate the symmetry generator with associated first integrals given by

$$\begin{aligned} &{ K_{1} =a\frac{\partial }{\partial a}-\frac{3R}{n-1}\frac{\partial }{ \partial R}- \frac{3\phi }{2}\frac{\partial }{\partial \phi },} \\ &{ I_{1} =-6nf_{0}a^{2} \dot{a}R^{n-1}+6nf_{0}(n-1)a^{3} \dot{R}R^{n-2}-\frac{3a ^{3}\epsilon \phi \dot{\phi }}{2},} \\ &{ K_{2} =\frac{\epsilon \phi }{6nf_{0}aR^{n-2}(n-1)}\frac{\partial }{ \partial R}+ \frac{1}{a}\frac{\partial }{\partial \phi },}\\ &{ I_{2}=a \dot{a}\epsilon \phi +a^{2}\epsilon \dot{\phi },} \end{aligned}$$

where the Noether symmetry \(K_{1}\) with Noether integral \(I_{1}\) generates scaling symmetry.

4 Final remarks

In this paper, we have studied the existence of Noether symmetry of flat FRW universe model in \(f(R,T)\) gravity admitting minimal coupling of geometric part with generalized scalar field. We have formulated all possible Noether symmetry generators as well as associated conserved quantities for two theoretical models of this gravity in the presence/absence of boundary term. We have studied exact solutions and investigated physical behavior of some well-known cosmological parameters for vanishing first order prolongation.

For the first \(f(R,T)\) model, the invariance condition for the existence of Noether symmetry yields maximum symmetry generators and corresponding conserved quantities. The first symmetry generator provides energy conservation under translational invariance in time, the second generator produces scaling symmetry and the potential function turns out to be constant. We have obtained exact solutions of power-law form corresponding to quintessence and phantom phases. For \(\epsilon =1\), the scale factor is not compatible to late-time acceleration while it corresponds to matter dominated era for \(\epsilon =-1\). The positive behavior of deceleration parameter and positively increasing scalar field also ensure this decelerating phase for both scalar field models.

In the absence of boundary term and first order prolongation, the potential function remains no more constant but is restricted to quintessence phase only as phantom phase leads to non-physical region of the universe. In this case, we have found oscillatory solution of the scale factor whose physical interpretation is established through cosmological parameters like Hubble, deceleration, \(r-s\) and EoS parameters. The graphical analysis of scale factor and rate of expansion is found to be increasing. The deceleration parameter remains negative while \(r-s\) parameters yield quintessence and phantom phases for \(s>0\) and \(r<1\). The EoS parameter characterize phantom phase for \(\epsilon =1\) whereas it appreciates a transition from radiation dominated era to DE era by crossing matter dominated phase. The negatively increasing scalar field and dominating potential energy imply cosmic accelerated expansion.

For the second model, we have found trivial solution under the invariance condition of Noether symmetry. Thus, we have considered \(f(R)=f_{0}R^{n}\), \(n\neq 0,1\) and formulated five symmetry generators with associated first integrals. For this choice of model, the symmetry generator \(K_{4}\) yields energy conservation while the potential function is no more constant. When boundary term of the extended symmetry vanishes, we have obtained again an oscillatory solution of the scale factor for \(f(R)+g(T)\) model. For this oscillatory solution, the graphical interpretation of scale factor, Hubble, deceleration and \(r-s\) parameters identify a transition of the universe from accelerated to decelerated expansion. The EoS parameter determines matter dominated universe by crossing quintessence phase. The scalar field remains positively increasing whereas kinetic and potential energies follow \(\frac{\dot{\phi }^{2}}{2}< V(\phi )\) initially yielding accelerated expansion. With the passage of time, this condition is disturbed as kinetic energy initiates to dominate over potential energy leading to decelerated expansion of the universe. For \(f_{0}R^{n}+g(T)\) model, we have obtained two symmetry generators in which the first generator yields scaling symmetry.

Finally, it is concluded that the symmetry generator and corresponding conserved quantities have appeared for both models. For \(R+2\varLambda (T)+h(T)\) model, the maximum Noether symmetry generators and conserved quantities indicate that this model yields more physical results as compared to the second model. For this model, the exact solution corresponds to accelerated expansion whereas for second model, the exact solution describes a transition from accelerated to decelerated cosmic expansion. It would be interesting to consider a non-canonical scalar field as a candidate for DE component and study cosmic evolution in the background of minimal as well as non-minimal curvature-matter coupling.