1 Introduction

Contemporary observational data on the cosmic expansion history (Fedeli et al. 2009; Perlmutter et al. 1999; Riess et al. 2007; Spergel et al. 2003; Tegmark et al. 2004) affirm the expanding paradigm of the universe. These developments may be considered as indication either for the existence of strange energy component dubbed as dark energy (DE) or for the modification of Einstein-Hilbert action. In the first stance, various representations (Bamba et al. 2012; Sharif and Zubair 2010a, 2010b, 2012a) have been suggested in general relativity to understand the characteristics of DE. In particular, the holographic DE (HDE) appeared as one of the most prominent candidates which has extensively been studied in literature (Huang and Gong 2004; Zhang and Wu 2005). This model has been constructed by incorporating the holographic principle in quantum gravity and its energy density is given by Cohen et al. (1999), Li (2004)

$$ \rho_{\vartheta}=3c^2 M^{2}_pL^{-2}, $$

where L is the infrared (IR) cutoff, c is a constant and \(M_{p}^{-2}=8\pi{G}\) is the reduced Planck mass. The future event horizon is suggested as the most appropriate choice for the IR cutoff to make it consistent with the observational data (Li 2004). Cai (2007) found this proposal as a challenging issue of causality which motivated the modification of IR cutoff. In Gao et al. (2009), the Ricci scalar is intimated as another proposal resulting in new form of HDE termed as Ricci DE (RDE). Granda and Oliveros (2008, 2009) also suggested a new IR cutoff for HDE in terms of H and \(\dot{H}\) which generalizes the RDE known as new HDE (NHDE).

In the second path, the issue of cosmic acceleration can be counted on the basis of modified theories of gravity. In this respect, there are various candidates such as f(R) (Sotiriou and Faraoni 2010), \(f(\mathcal{T})\) (Ferraro and Fiorini 2007), where \(\mathcal{T}\) is the torsion and f(R,T) (Harko et al. 2011) etc. The f(R,T) gravity is a more general modified theory involving coupling between matter and geometry which is described by the action (Harko et al. 2011)

$$ \mathcal{I}=\frac{1}{2{\kappa}^2}\int{f(R,T)\sqrt{-g}dx^4}+\int \mathcal{L}_{m}\sqrt{-g}dx^4, $$
(1)

where κ 2=8πG, and \(\mathcal{L}_{m}\) denotes matter Lagrangian. If we vary the action (1) with respect to the metric tensor then the following field equations can be obtained

$$\begin{aligned} &\kappa^{2}T_{\alpha\beta}-f_{T}(R,T)T_{\alpha\beta}-f_{T}(R,T) \varTheta_{\alpha\beta}-R_{\alpha\beta}f_{R}(R,T) \\ &\qquad {}+\frac{1}{2}g_{\alpha\beta}f(R,T) -(g_{\alpha\beta} {\Box}-{ \nabla}_{\alpha}{\nabla}_{\beta})f_{R}(R,T) \\ &\quad =0, \end{aligned}$$
(2)

where f R and f T denote derivatives of f(R,T) with respect to R and T respectively, □=g μν∇ μ ∇ μ and \(\varTheta_{\alpha\beta}=\frac{g^{\mu\nu}{\delta}T_{\mu\nu}}{ {\delta}g^{\alpha\beta}}\). This theory has drawn significant attention and some valuable results have been explored in literature. We have discussed the validity of thermodynamics laws, existence of power law solutions and energy conditions for FRW universe (Sharif and Zubair 2012b, 2013a, 2013b). The cosmological reconstruction is an important aspect in alternative theories of gravity and is still under consideration. Recently, some explicit models of f(R,T) gravity are presented for anisotropic universe which can produce the phantom era of DE (Sharif and Zubair 2012c). Houndjo (2012) discussed the reconstruction scheme by introducing an auxiliary scalar field and HDE model.

In a recent paper (Sharif and Zubair 2013c), the cosmology of holographic and new agegraphic f(R,T) models is investigated for flat FRW universe. We have found that the reconstructed f(R,T) models can reproduce the quintessence/phantom regimes of the universe satisfying current observations. In this paper, we consider RDE and NHDE models to develop an equivalence between these proposals and f(R,T) gravity without introducing any additional DE component. We reconstruct the f(R,T) models and discuss their future evolution for different values of essential parameters. The paper has the following format. In next section, we reconstruct the function f(R,T) according to RDE and NHDE models and explore future evolution. Section 3 explores Dolgov-Kawasaki stability conditions for this function. Finally, we discuss the results in Sect. 4.

2 Reconstructing f(R,T) gravity

In this study, we consider the Lagrangian as sum of two independent functions of R and T given by

$$ f(R,T)=f_1(R)+f_2(T), $$
(3)

Consequently, the corresponding field equations are found as

$$\begin{aligned} &\kappa^{2}T_{\alpha\beta}-f_{2T}T_{\alpha\beta}-f_{2T} \varTheta_{\alpha\beta}+\frac{1}{2}g_{\alpha\beta}(f_1+f_2) \\ &\qquad {}-R_{\alpha\beta}f_{1R} -(g_{\alpha\beta}{\Box}-{ \nabla}_{\alpha}{\nabla}_{\beta})f_{1R} \\ &\quad =0. \end{aligned}$$
(4)

If the matter content is given by perfect fluid then the effective Einstein field equations can be constituted as

$$ \tilde{\kappa}^{-2} \biggl(R_{\alpha\beta}- \frac{1}{2}Rg_{\alpha\beta} \biggr) =T_{\alpha\beta}+T^{(de)}_{\alpha\beta}, $$
(5)

where \(\tilde{\kappa}^{2}=(\kappa^{2}+f_{2T})/f_{1R}\), T αβ is the matter energy-momentum tensor and

$$\begin{aligned} {T}_{\alpha\beta}^{(de)}&=\frac{\tilde{\kappa}^{-2}}{f_{1R}} \biggl[\frac{1}{2}(f_1+f_2+ 2pf_{2T}-Rf_{1R})g_{\alpha\beta} \\ &\quad {}+({\nabla}_{\alpha}{\nabla}_{\beta}-g_{\alpha\beta}{ \Box})f_{1R} \biggr] \end{aligned}$$

provides the contribution from DE components. In flat FRW background, the 00 component of the field equations can be written as

$$ 3H^2=\kappa^2\rho+\rho_{de}, $$
(6)

where ρ is the matter energy density

$$\begin{aligned} \rho_{de} =&\frac{1}{f_{1R}} \biggl[\bigl((1-f_{1R}) \kappa^2+f_{2T}\bigr)\rho \\ &{}+\frac{1}{2}(f_1+f_2-Rf_{1R}) -3H \dot{R}f_{1RR} \biggr], \end{aligned}$$
(7)

\(H=\dot{a}/{a}\), \(R=-6(\dot{H}+2H^{2})\) and dot represents the time derivative. Likewise, the 11 component implies the pressure of DE contribution as

$$\begin{aligned} p_{de}&=\frac{1}{f_{1R}} \biggl[\frac{1}{2}(Rf_{1R}-f_1-f_2)+( \ddot{R}+2H\dot{R})f_{1RR} \\ &\quad {}+\dot{R}^2f_{1RRR} \biggr]. \end{aligned}$$
(8)

Combining Eqs. (7) and (8), we get the evolution equation in terms of f 1 as

$$\begin{aligned} &\dot{R}^2f_{1RRR}+(\ddot{R}-H\dot{R})f_{1RR}+ \bigl[\kappa^2T \\ &\qquad {}+(1+\omega_{de})\rho_{de}\bigr]f_{1R}+ \bigl(\kappa^2+f_{2T}\bigr)T \\ &\quad =0, \end{aligned}$$
(9)

which is the third order differential equation in f 1 involving contribution both from scalar curvature and matter density.

In this modified theory, the divergence of matter energy-momentum tensor is defined as Harko et al. (2011)

$$\begin{aligned} \nabla^{\alpha}T_{\alpha\beta}&=\frac{f_T}{\kappa^2-f_T} \biggl[(T_{\alpha\beta}+\varTheta_{\alpha\beta}) \nabla^{\alpha} \ln{f}_T \\ &\quad {}+\nabla^{\alpha}\varTheta_{\alpha\beta}- \frac{1}{2}g_{\alpha\beta} \nabla^{\alpha}T \biggr]. \end{aligned}$$
(10)

For the choice of Lagrangian (3) having perfect fluid as a matter source with EoS ω=p/ρ, we get

$$\begin{aligned} \dot{\rho}+3H(\rho+p)&=\frac{-1}{\kappa^2+f_{2T}} \biggl[(\rho+p) \dot{T}f_{2TT} \\ &\quad {}+\dot{p} f_{2T} +\frac{1}{2} \dot{T}f_{2T} \biggr]. \end{aligned}$$
(11)

It is evident that energy-momentum tensor is not covariantly conserved due to the coupling between matter and geometry in this theory. Though it is a general statement where the right side represents the energy transfer but still there is a possibility of conserved energy-momentum tensor. To make the Lagrangian (3) consistent with the standard continuity equation, we need to set an additional constraint so that the right side of the above equation vanishes. In such scenario, we have (Alvarenga et al. 2013)

$$ (1+\omega)Tf_{2TT}+\frac{1}{2}(1-\omega)f_{2T}=0, $$

which results in functional form of f 2(T) as

$$ f_2(T)=\alpha_1T^{\frac{1+3\omega}{2(1+\omega)}}+\alpha_2, $$
(12)

where α i ’s are integration constants.

Another interesting case is to consider f 2 in linear form i.e., f 2(T)=λT even then matter is nonconserved and from Eq. (11), we obtain the relation

$$ \dot{\rho}+3H\zeta(1+\omega)\rho=0, $$

where \(\zeta=\frac{2(1+\lambda)}{2+(3-\omega)\lambda}\). The solution of this equation implies

$$ \rho=\rho_0a^{-3(1+w)\zeta}=\rho_0a^{-3(1+w)+\frac{\lambda(2+\omega)-3}{2+(3-\omega)\lambda}}, $$
(13)

where ρ 0 is an integration constant. The above result is analogous to Eq. (18) discussed in Bisabr (2012), where the nonconserved matter equation is due to the non-minimal coupling in f(R) gravity. The significant difference in these results is the contribution of source term. In our case, matter contents play its role in nonconserved continuity equation while in Bisabr (2012), it involves the curvature correction. In this reconstruction scheme, we shall consider both functional forms of f 2(T) given by (12) as well as f 2(T)=λT and find the curvature contribution term f 1. In the following, we reconstruct the f(R,T) models corresponding to Ricci and modified Ricci DE candidates.

2.1 Model I

First we consider the RDE model whose energy density is defined as Gao et al. (2009)

$$ \rho_{\vartheta}=3\sigma\bigl(\dot{H}+2H^2\bigr), $$
(14)

where ‘σ’ is a constant to be determined by the observational data. In Gao et al. (2009), it is shown that σ=0.46 is the most probable choice for which RDE behaves like dark matter at high redshifts whereas universe evolves into phantom dominated epoch in future evolution. Feng (2009) reconstructed f(R) theory corresponding to RDE and explored the effect of parameter ‘σ’ on f(R) model. The EoS parameter ω ϑ for RDE is given by

$$ \begin{aligned} \omega_{\vartheta}=-1-\frac{1}{3}\frac{d\ln(\varOmega_{\vartheta}H^2)}{d\ln{a}}, \\ \varOmega_{\vartheta}=\sigma\bigl[2-d/dt\bigl(H^{-1}\bigr)\bigr]. \end{aligned}$$
(15)

Modified theories can be reconstructed for a known expansion history in terms of scale factor. We intend to reconstruct the f(R,T) model corresponding to RDE.

Let us consider the scale factor of the form

$$ a(t)=a_0(t_p-t)^{-n},\quad a_0>0 $$
(16)

which represents the phantom phase of the universe resulting in big rip singularity within finite-time. Here n is a positive constant and t<t p , t p is the probable time when finite-time future singularity may appear. The derivatives of R and H are determined as

$$\begin{aligned} \dot{R}^2=\frac{-2R^3}{3n(2n+1)}, \qquad \ddot{R}-H\dot{R}= \frac{(n-3)R^2}{3n(2n+1)}. \end{aligned}$$

Using the above relation (16), matter energy density and (1+ω de )ρ de can be expressed in terms of Ricci scalar as

$$\begin{aligned} \rho_{m}=\frac{[\sigma(2n+1)-n]R}{2(2n+1)}, \quad (1+\omega_{de}) \rho_{de}=\frac{\sigma{R}}{3n}. \end{aligned}$$
(17)

Initially, we consider f 2(T) given by Eq. (12). Substituting the above results in Eq. (9), we obtain a 3rd order differential equation in terms of f 1 whose solution is

$$ f_1(R)=\varepsilon_{+}R^{\varepsilon_{+}} \sigma_3+\varepsilon_{-}R^{\varepsilon_{-}} \sigma_4+\chi_1\sqrt{R}+\chi_2R+ \sigma_5, $$
(18)

where

$$\begin{aligned} &\varepsilon_{\pm}=\frac{1}{4} \bigl[3+n\pm\sqrt{1-8 \sigma-2n(1+14\sigma)+n^2(13-24\sigma)} \bigr], \\ &\chi_1=\frac{3\sqrt{2}n(1+2n)\sigma_1\sqrt{\frac{\sigma+n(-1+2\sigma)}{1+2n}}}{ 2\sigma+n(1+7\sigma)+n^2(-3+6\sigma)}, \\ &\chi_2= \frac{3n[\sigma+n(-1+2\sigma)]}{2\sigma+7n\sigma+n^2(-3+6\sigma)}. \end{aligned}$$

Thus the f(R,T) model

$$\begin{aligned} f(R,T)&=\varepsilon_{+}R^{\varepsilon_{+}}\sigma_3+ \varepsilon_{-}R^{\varepsilon_{-}} \sigma_4+ \chi_1\sqrt{R}+\chi_2R+\sigma_5 \\ &\quad {}+ \sigma_1T^{\frac{1+3\omega}{2(1+\omega)}}+ \sigma_2, \end{aligned}$$
(19)

can reproduce the expansion history corresponding to RDE.

To keep the above function real valued, we set σ=0.5 (otherwise χ 1 would be imaginary) and n⩾17. We plot the function f 1(R) against R and redshift z as shown in Fig. 1. The behavior of NEC is shown in Fig. 2(a) for σ=0.5 and n⩾17. The violation of NEC would imply ω de <−1 which represents phantom DE and is a possible candidate of the present accelerated expansion. The phantom regime favors recent observational cosmology implying accelerated cosmic expansion. We also plot the EoS parameter in Fig. 2(b) which shows that RDE favors the quintom model of DE where the EoS parameter crosses the phantom divide line (ω ϑ =−1). This evolution of ω ϑ is consistent with current observational constraints on RDE (Gao et al. 2009).

Fig. 1
figure 1

Evolution of f 1(R) versus R and redshift for σ=0.5

Full size image
Fig. 2
figure 2

Evolution of NEC and 1+ω de for the model (19) with σ=0.5

Full size image

Now we consider the case of f 2(T)=λT which does not imply the standard continuity equation. Solving Eq. (9), we obtain the functional form of f 1 as

$$\begin{aligned} &f_1(R)=\varepsilon_{+}R^{\varepsilon_{+}} \sigma_3+\varepsilon_{-}R^{\varepsilon_{-}} \sigma_4+\chi_3R+\sigma_5, \\ &\quad \chi_3=(1+\lambda)\chi_2. \end{aligned}$$
(20)

In f(R) gravity, the effective gravitational constant is G eff =G/f R (R) and to make the theory consistent with solar system experiments the present day value of f R is considered as unity (Capozziello et al. 2005). Here, we can find the constants σ i ’s by applying the initial conditions as in f(R) gravity (Capozziello et al. 2005). For this modified theory with f 2(T)=λT, we have G eff =(G+λ)/f 1R and if one assumes f 1R =1 then G eff would be an approximate constant. In this perspective, we make the similar assumption as in Houndjo (2012), Houndjo and Piattella (2012), Sharif and Zubair (2013c) and set the following initial conditions

$$\begin{aligned} \begin{aligned} &\biggl(\frac{df_1}{dt} \biggr)_{t=t_0}= \biggl( \frac{dR}{dt} \biggr)_{t=t_0}, \qquad \biggl(\frac{d^2f_1}{dt^2} \biggr)_{t=t_0}= \biggl(\frac{d^2R}{dt^2} \biggr)_{t=t_0}, \\ &(f_1)_{t=t_0}=R_0+\delta, \quad \delta=6H_0^2\biggl(1-\varOmega_{M0} - \frac{3}{2}{\lambda}\varOmega_{M0}\biggr). \end{aligned} \end{aligned}$$
(21)

Making use of the above conditions, the solution (20) can be rewritten as

$$ f_1(R)=C_{+}R^{\varepsilon_{+}}+C_{-}R^{\varepsilon_{-}}+ \chi_3R+\beta, $$
(22)

where

$$\begin{aligned} \begin{aligned} &C_{+}=\frac{(\chi_3-1)(\varepsilon_{-}-1)}{\varepsilon_{+}(\varepsilon_{+} -\varepsilon_{-})R_0^{\varepsilon_{+}-1}}, \\ &C_{-}=\frac{(\chi_3-1)(\varepsilon_{+}-1)}{\varepsilon_{-}(\varepsilon_{-} -\varepsilon_{+})R_0^{\varepsilon_{-}-1}}, \\ &\beta=\delta+(1-\chi_3)R_0+\frac{1}{\varepsilon_+\varepsilon_-}( \chi_3-1) (\varepsilon_++\varepsilon_--1)R_0. \end{aligned} \end{aligned}$$

The plot of function f 1(R) for different values of σ=0.46,0.48,0.5 and λ=1 is shown in Fig. 3. The parameter σ plays significant role in the evolution of function f 1. The variation in evolution of f 1 corresponding to different values of coupling parameter is shown in Fig. 4. The EoS parameter is analyzed for σ=0.46, n⩾8 and λ=1 as shown in Fig. 5(a). This model favors the phantom era of DE which is also true for other values of λ as depicted in Fig. 5(b).

Fig. 3
figure 3

In plot (a) reconstructed f 1(R) is shown for n=17 and different values of σ and (b) the plot of f 1 in terms of redshift for σ=0.46

Full size image
Fig. 4
figure 4

The left plot shows the effect of coupling parameter λ versus R. The difference in evolution is evident for large values of λ. This evolutionary paradigm is also shown for redshift in the right plot

Full size image
Fig. 5
figure 5

Evolution of 1+ω de for the model (22) with σ=0.46. In left plot, we set λ=1 and n⩾8 whereas for the right plot n=10 is fixed and λ lies in the range {−5,5}

Full size image

2.2 Model II

Here we consider the HDE with Granda-Oliveros cutoff as second model and reconstruct the corresponding f(R,T) function. The energy density of NHDE is given by Granda and Oliveros (2008, 2009)

$$ \rho_{\vartheta}=3M^{2}_p\bigl( \mu{H}^2+\upsilon\dot{H}\bigr), $$
(23)

where μ and υ are positive constants. Granda and Oliveros (2008, 2009) proposed that μ≈0.93 and υ≈0.5 are the best fit values of these parameters so that NHDE is consistent with the theory of big-bang nucleosynthesis. In Wang and Xu (2010), the best fit values of parameters (μ,υ) have been developed from observationally consistent region in both flat and non-flat NHDE models. It is found that the most appropriate parameters for flat model are \(\mu=0.8502^{+0.0984+0.1299}_{-0.0875-0.1064}\) and \(\upsilon=0.4817^{+0.0842+0.1176}_{-0.0773-0.0955}\).

For the choice of scale factor (16), we determine ρ m and (1+ω de )ρ de of NHDE in the following form

$$\begin{aligned} \begin{aligned} &\rho_{m}=\frac{[\upsilon-n(1-\mu)]R}{2(2n+1)}, \\ &(1+\omega_{de}) \rho_{de}=\frac{(\mu{n}+\upsilon)R}{3n(2n+1)}. \end{aligned} \end{aligned}$$
(24)

We first take the function (12) and solve Eq. (9) for NHDE, we obtain f 1 in the form of Eq. (18) with

$$\begin{aligned} \begin{aligned} & \begin{aligned} \varepsilon_{\pm}&=\frac{1}{4} \bigl[3+n \\ &\pm\sqrt{1-8 \upsilon-2n(1+4\mu+6\upsilon)+n^2(13-12\mu)} \bigr], \end{aligned} \\ &\chi_1=\frac{3\sqrt{2}n(1+2n)\sigma_1\sqrt{\frac{\upsilon+n(-1+\mu)}{1+2n}}}{ 2\upsilon+n(1+2\mu+3\upsilon)+3n^2(-1+\mu)}, \\ &\chi_2= \frac{3n[\upsilon+n(-1+\mu)]}{2\upsilon+n(1+2\mu+3\upsilon)+3n^2(-1+\mu)}. \end{aligned} \end{aligned}$$
(25)

It is found that the function f 1(R) corresponding to NADE is real valued for μ=1, υ=0.63 and n⩾18 and its evolution is shown in Fig. 6. The plot of 1+ω de for NHDE reconstructed f(R,T) model is shown in Fig. 7. It can be seen that EoS parameter intersects the phantom divide line representing phantom model of DE in future evolution. This behavior depicts the picture of ω de in NHDE where this choice would result in ω de <−1.

Fig. 6
figure 6

Evolution of f 1(R) versus R and redshift in NHDE for μ=1, υ=0.63

Full size image
Fig. 7
figure 7

Evolution of EoS parameter corresponding to f(R,T) of the type (18) in NHDE

Full size image

If one follows the similar procedure as in the previous case, the f(R,T) model for the choice of f 2(T)=λT can be reconstructed as given in Eq. (22). For this f(R,T) model, ε ± and χ 2 are given by Eq. (25) and χ 3=(1+λ)χ 2. The function f 1(R) corresponding to NHDE is plotted against R and redshift in Fig. 8. We also introduce the variation in coupling parameter λ and results are evident from Fig. 9. It is found that large values of λ modify the behavior of curves in a significant way. In this case, the evolution of EoS parameter and its evolution is shown in Fig. 10. It is quiet evident from this plot that reconstructed f(R,T)=f 1(R)+λT model in NHDE favors the phantom regime of the universe.

Fig. 8
figure 8

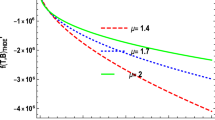
Evolution of reconstructed model f(R,T)=f 1(R)+λT in NHDE. Plot (a) shows the variation in f 1 versus R for three independent values of (μ,υ). Since the variation in evolution of f 1 is quite prominent depending on the values of (μ,υ), so for the redshift case we only consider (μ,υ)=(0.85,0.48) as shown in plot (b). We have set λ=1 and n⩾18

Full size image
Fig. 9
figure 9

Evolution of f 1 versus R and redshift in NHDE for different values of λ. Here, we set (μ,υ)=(0.85,0.48) and n=18

Full size image
Fig. 10
figure 10

Evolution of 1+ω de for f(R,T)=f 1(R)+λT model in NHDE. In (a) and (b) we set {(μ,υ)=(0.85,0.48),λ=1} and {(μ,υ)=(0.85,0.48),n=6} respectively

Full size image

3 Dolgov-Kawasaki stability conditions

The study of stability criteria is a significant issue in modified theories for the viability of such modification to general relativity. One of the important instabilities is Dolgov-Kawasaki instability criterion which was developed to constrain the f(R) theory (Dolgov and Kawasaki 2003; De Felice and Tsujikawa 2010). The viable f(R) models require to satisfy the following stability conditions

$$ f^{'}(R)>0,\qquad f^{''}(R)>0,\quad R{\geq}R_{0}, $$

where R 0 is the Ricci scalar today. This instability criterion is also generalized to f(R) gravity involving coupling between matter and geometry (Bertolami and Sequeira 2005; Wang et al. 2010). Recently, a new modification is introduced to f(R,T) gravity involving the contraction of the Ricci tensor and energy-momentum tensor so that Lagrangian is of the form f(R,T,R μν T μν) (Haghani et al. 2013; Sharif and Zubair 2013d). The authors suggested that Dolgov-Kawasaki instability needs to be modified in this case whereas for f(R,T) gravity, this criteria remains the same as in f(R) gravity. Thus for f(R,T) gravity, we have

$$ f_R(R,T)>0,\qquad f_{RR}(R,T)>0,\quad R{ \geq}R_{0}, $$

We are interested to explore the stability of f(R,T) gravity consistent with the Ricci and modified Ricci DE. The results of these constraints are explained as follows.

  • First consider the model (19) and its second derivative with respect to scalar curvature as given by

    $$\begin{aligned} f_{RR}(R,T)&=\varepsilon_{+}^2( \varepsilon_{+}-1)\sigma_3R^{\varepsilon_{+}-2} \\ &\quad {}+ \varepsilon_{-}^2(\varepsilon_{-}-1) \sigma_4R^{\varepsilon_{-}-2} -\frac{\chi_1}{4R^{3/2}}, \end{aligned}$$
    (26)

    where ε ±, χ 1 depend on parameters m and σ. If f RR >0, then we need to have σ i >0, ε ±>1 and χ 1<0. For the viability of model (19), we set σ=0.5, n⩾17 which clearly implies that the first two terms are positive. To satisfy the condition χ 1<0, we choose σ 1<0 (the parameter involving the contribution from matter part.)

  • The f(R,T) model corresponding to RDE with function f 2(T)=λT is given by

    $$ f(R,T)=C_{+}R^{\varepsilon_{+}}+C_{-}R^{\varepsilon_{-}}+ \chi_3R+\beta+\lambda{T}, $$
    (27)

    Taking the double derivative of this equation with respect to the scalar curvature, we obtain

    $$ f_{RR}=\varepsilon_{+}(\varepsilon_{+}-1)C_+R^{\varepsilon_{+}-2} +\varepsilon_{-}(\varepsilon_{-}-1)C_-R^{\varepsilon_{-}-2}. $$
    (28)

    Now f RR >0 if C ±>0, ε ±>1 and C ± depend on χ 3 and ε ±. For this model, we can set different values of σ and classify other constraints. For σ=0.46, we need to have n⩾8 (to keep the function real valued) and this choice makes ε ±>1, χ 3>1 and C ±>0.

  • Now we consider the f(R,T) model corresponding to NHDE whose curvature derivative is given by Eq. (26) and the parameters (ε ±,χ 1) are represented by Eq. (25). For the viability of this model, we choose (μ,υ)=(1,0.63) and n⩾18. This model would satisfy the stability condition if (σ 3,σ 4)>0, ε ±>1 (which is true for the chosen parameters) and χ 1<0 (or σ 1<0).

  • Finally, we present the stability of f(R,T)=f 1(R)+λT model consistent with NHDE. In this case, double derivative with respect to scalar curvature is given by Eq. (28), where the parameters ε ± and constants C ± are given by

    $$\begin{aligned} & \begin{aligned} \varepsilon_{\pm}&=\frac{1}{4} \bigl[3+n \\ &\pm\sqrt{1-8 \upsilon-2n(1+4\mu+6\upsilon) +n^2(13-12\mu)} \bigr], \end{aligned} \\ &C_{+}=\frac{(\chi_3-1)(\varepsilon_{-}-1)}{\varepsilon_{+}(\varepsilon_{+} -\varepsilon_{-})R_0^{\varepsilon_{+}-1}}, \\ &C_{-}=\frac{(\chi_3-1)(\varepsilon_{+}-1)}{\varepsilon_{-}(\varepsilon_{-} -\varepsilon_{+})R_0^{\varepsilon_{-}-1}}. \end{aligned}$$

    Here we are free to choose the values of (μ,υ) and then constrain n to make the function real valued. We set (μ,υ)=(0.85,0.48) and n⩾6 which imply ε ±>1 and constants C ±>0 i,e., the function f(R,T) satisfies the Dolgov-Kawasaki stability condition.

4 Conclusions

The f(R,T) theory can be regarded as a potential candidate in explaining the role of DE to accelerate the cosmic expansion. Such theory is of great importance as the source of DE components can be seen from an integrated contribution of both curvature and matter Lagrangian part. A suitable form of Lagrangian which can explain the cosmic evolution in a definite way is still under consideration. In recent papers (Sharif and Zubair 2012c, 2013b, 2013c; Houndjo 2012; Houndjo and Piattella 2012), the cosmological reconstruction in f(R,T) gravity has been explored under different scenarios such as power law expansion history, anisotropic universe model and class of HDE models, while the numerical reconstruction scheme is used to develop the correspondence in HDE and this modified theory (Houndjo 2012; Houndjo and Piattella 2012). So far, the reconstruction is executed only for the function (3) with linear form of f 2(T) or f 1(R) that do not imply the standard matter conservation equation in this theory.

Though the strong coupling of curvature and trace of matter tensor violate the usual continuity equation but there exists suitable model to settle this problem as shown in Alvarenga et al. (2013). In this paper, we have applied the reconstruction program (formulated in Sharif and Zubair (2013c) to obtain the f(R,T) functions corresponding to RDE and NHDE models. We have discussed the functional form of f 2 given by Eq. (12) and also f 2(T)=λT. We have presented the evolution of f(R,T) models for both RDE and NHDE depending on the values of parameters. It is found that EoS parameter ω de of the reconstructed models is in agreement with the observational results of WMAP5 (Komatsu et al. 2009). Finally, we have used Dolgov-Kawasaki instability criteria for f(R,T) gravity in similar form as in f(R) gravity and explored the viability of reconstructed models. It is found that the selection of parameters in explaining the evolution of f(R,T) models is consistent with the viability conditions.