Abstract
A five dimensional Kaluza-Klein cosmological model is considered in the frame work of f(R,T) gravity proposed by Harko et al. (Phys. Rev. D 84:024020, 2011) when the source for energy momentum tensor is a bulk viscous fluid containing one dimensional cosmic strings. A barotropic equation of state is assumed to get a determinate solution of the field equations. Also, the bulk viscous pressure is assumed to be proportional to the energy density. The physical behavior of the model is also discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well known that the discovery of the accelerated expansion of the universe has revolutionized modern cosmology (Riess et al. 1998; Perlmutter et al. 1999; Bennet et al. 2003). Astrophysical observations indicate that this cosmic acceleration is driven by exotic energy with a large negative pressure which is known as dark energy (for a general complete review see Nojiri and Odintsov 2007). In recent years modified theories of gravity are attracting much attention to explore the dark energy and late time acceleration of the universe. Among the various modifications of general relativity, f(R) theory of gravity has gained importance during the last decade since it provides a natural gravitational alternative to dark energy. It has been suggested that cosmic acceleration can be achieved by replacing the Einstein-Hilbert action of general relativity with a general function f(R) of Ricci scalar R. The explanation of cosmic acceleration is obtained just by introducing the term 1/R which is essential at small curvatures. The useful aspects of f(R) gravity are that it gives an easy unification of early time inflation and late time acceleration. It also describes the transition phase of the universe from deceleration to acceleration (Nojiri and Odintsov 2007). Capozziello et al. (2007, 2008), Multamaki and Vilja (2006, 2007), Sharif (2010). Azadi et al. (2008), Caroll et al. (2004), Nojiri and Odintsov (2003, 2004, 2007) and Chiba et al. (2007) are some of the authors who have investigated several aspects of f(R) gravity. Copeland et al. (2006) have given a comprehensive review of f(R) gravity.
Recently, Harko et al. (2011) proposed another modification of Einstein’s theory of gravitation which is known as f(R,T) theory of gravity wherein the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar R and of the trace T of the stress energy tensor T ij . They have derived the field equations of f(R,T) gravity from Hilbert-Einstein type variational principle by taking the action
where f(R,T) is an arbitrary function of the Ricci scalar R, T is the trace of energy tensor of the matter T ij and L m is the matter Lagrangian density. By varying the action S of the gravitational field with respect to the metric tensor components g ij, they have obtained the field equations of f(R,T) gravity, with the special choice of f(R,T) (Harko et al. 2011) given by
as (for a detailed derivation of the field equations one can refer to Harko et al. 2011)
where the overhead prime indicates derivative with respect to the argument and T ij is given by
ρ and p being energy density and isotropic pressure respectively.
During the past two decades, string cosmological models have received considerable attention of research workers because of their importance in structure formation in the early stages of evolution of the universe. During the phase transition in the early universe, spontaneous symmetry breaking gives rise to a random network of stable line like topological defects known as cosmic strings. It is well known that massive strings serve as seeds for the large structures like galaxies and cluster of galaxies in the universe. Letlier (1983), Stachel (1980), Vilenkin et al. (1987), Banerjee et al. (1990), Tripathy et al. (2009), Reddy (2003a, 2003b), Katore and Rane (2006) and Sahoo (2008) are some of the authors who have investigated several important aspects of string cosmological models either in the frame work of general relativity or in modified theories of gravitation.
It is well known that viscosity plays an important role in cosmology (Singh and Devi 2011; Singh and Kale 2011; Setare and Sheyki 2010 and Misner 1969). Also, bulk viscosity appears as the only dissipative phenomenon occurring in FRW models and has a significant role in getting accelerated expansion of the universe popularly known as inflationary space. Bulk viscosity contributes negative pressure term giving rise to an effective total negative pressure stimulating repulsive gravity. The repulsive gravity overcomes attractive gravity of matter and gives an impetus for rapid expansion of the universe hence cosmological models with bulk viscosity have gained importance in recent years. Barrow (1986), Pavon et al. (1991), Martens (1995), Lima et al. (1993), and Mohanty and Pradhan (1992) are some of the authors who have investigated bulk viscous cosmological models in general relativity. Johri and Sudharsan (1989), Pimental (1994), Banerjee and Beesham (1996), Singh et al. (1997), Rao et al. (2011, 2012), Naidu et al. (2012) and Reddy et al. (2012a) have studied bulk viscous and bulk viscous string cosmological models in Brans and Dicke (1961) and other modified theories of gravity.
Friedmann-Robertson-Walker (FRW) models being spatially homogeneous and isotropic in nature are best for the representation of large scale structure of the present day universe. However, it is believed that the early universe may not have been exactly uniform. Thus the models with anisotropic background are suitable to describe the early stages of the universe. Bianchi type models are among the simplest models with anisotropic back ground Hence the investigation of Bianchi type models in modified or alternative theories of gravity is also an interesting discussion. Adhav (2012) has obtained Bianchi type-I cosmological model in f(R,T) gravity. Reddy et al. (2012b) have discussed Bianchi type-III cosmological model in f(R,T) gravity while Reddy et al. (2012a), Reddy and Shanthikumar (2013a, 2013b) studied Bianchi type-III dark energy model and some anisotropic cosmological models, respectively, in f(R,T) gravity.
The study of higher dimensional space-time is important at early stages of evolution of the universe. Witten (1984), Applequist et al. (1987), Chodos and Detweller (1980) and Marchiano (1984) have studied higher dimensional cosmology because it has physical relevance to the early times before the universe has undergone compactification transitions. Reddy et al. (2007), Reddy and Naidu (2007) have discussed five dimensional Kaluza-Klein cosmological models in Brans and Dicke (1961) and Saez and Ballester (1985) modified theories of gravitation. Reddy et al. (2012b) studied Kaluza-Klein model in f(R,T) gravity while Reddy et al. (2013a, 2013b) have discussed Kaluza-Klein bulk viscous string cosmological model in Saez and Ballester (1985) scalar-tensor theory of gravitation. Very recently Reddy and Shanthikumar (2013a, 2013b) have obtained LRS Bianchi type-II model in f(R,T) gravity.
Motivated by the above discussion and investigations in modified theories of gravity, we have studied, in this paper, Kaluza-Klein cosmological model in the modified f(R,T) gravity proposed by Harko et al. (2011), in the presence of cosmic strings and bulk viscosity. In Sect. 2, explicit field equations in f(R,T) gravity for Kaluza-Klein metric are obtained in the presence of bulk viscous fluid containing one dimensional strings. In Sect. 3 the cosmological model is presented by solving the field equations. Physical and kinematical properties of the model are discussed in Sect. 4. The last section contains some conclusions.
2 Metric and field equations
We consider five dimensional Kaluza-Klein metric in the form
where A and B are functions of cosmic time t.
We consider the energy momentum tensor for a bulk viscous fluid containing one dimensional cosmic strings as
and
where ρ is the rest energy density of the system, ζ(t) is the coefficient of bulk viscosity, 3ζH is usually known as bulk viscous pressure, H is Hubble’s parameter and λ is string tension density.
Also, \(u ^{i} = \delta _{4} ^{i}\) is a four-velocity vector which satisfies
Here we also consider ρ, \(\overline{p}\) and λ are functions of time t only.
Using co moving coordinates and a particular choice of the function given by (Harko et al. 2011)
the field equations (3), for the metric (5) with the help of Eqs. (6)–(9) can be written, explicitly, as
where an overhead dot indicates differentiation with respect to time t.
The spatial volume is given by
where a(t) is the scale factor of the universe.
The scalar expansion θ and the shear scalar σ 2 in the model are defined by


3 Solutions and the model
The field equations (10)–(12) are a system of three independent equations in five unknowns \(A, B, \overline{p},\rho\) and λ. Also the field equations are highly non-linear in nature and therefore we use the following plausible physical conditions to find determinate solution.
-
(i)
The shear scalar σ 2 is proportional to scalar of expansion θ so that we can take (Collins et al. 1980)
$$ A= B ^{m} $$(16)where m≠1 is a constant and it takes care of the anisotropic nature of the model.
-
(ii)
A more general relationship between the proper rest energy density ρ and string tension density λ is taken to be
$$ \rho=\gamma \lambda $$(17)where γ is an arbitrary constant which can take both positive and negative values. The negative values of γ lead to the absence of strings in the universe and the positive values show the presence of one dimensional strings in the cosmic fluid. The energy density of the particles attached to the strings is
$$ \rho _{p} =\rho- \lambda=( \gamma -1)\lambda $$(18) -
(iii)
For a barotropic fluid, the combined effect of the proper pressure and the bulk viscous pressure can be expressed as
$$ \overline{p} = p-3 \varsigma H = \varepsilon\rho $$(19)where
 (20)
(20)and α is an arbitrary constant.
Now using the above conditions the field equations (10)–(12) reduce to the equation
$$ \frac{\ddot{B}}{B} +d \biggl( \frac{\dot{B}}{B} \biggr) ^{2} =0 $$(21)where we have put the constants
 (22)
(22)Integrating Eq. (21) and using (16) we obtain the metric coefficients as
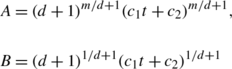 (23)
(23)where c 1≠0 and c 2 are constants of integration. Now by a suitable choice of coordinates and integration constants (i.e. c 1=1 and c 2=0) the metric (5), with the help of Eq. (23), can be written as
 (24)
(24)
4 Physical properties of the model
Equation (24) represents LRS Bianchi type-II bulk viscous string cosmological model in f(R,T) gravity with the following physical and kinematical parameters which are very important for physical discussion of the model.
Spatial volume of the model from Eq. (13) is
Scalar of expansion from Eq. (14) is
Shear scalar from Eq. (15) is
The Hubble’s parameter is
The energy density in the model is
The string tension density is
Coefficient of bulk viscosity

Energy density of the particles attached to the string
Scale factor of the model is
The deceleration parameter in this model is
It is obvious that q depends on the constants d and m and it may be noted that in order to get accelerated expansion model, one should have \(\frac{3 (d-m ) +2}{ 3m+1} <0\).
From the above results it can be observed that the model (24) has no initial singularity and the spatial volume increases as t increases giving the accelerated expansion of the universe. In this model, we also observe that \(\theta, \sigma ^{2}, H, \overline{p}, p,\rho,\lambda,\zeta\) and ρ p all diverge at the initial epoch, i.e. at t=0 while they vanish for infinitely large t. Also \(\frac{\sigma ^{2}}{\theta ^{2}} \neq0\), the model does not approach isotropy throughout the evolution of the universe.
5 Conclusions
It is well known that f(R,T) gravity has been proposed to explain the recent scenario of accelerated expansion of the universe. In spite of the fact the present day universe is well represented by the spatially homogeneous isotropic FRW model, experiments reveal that there is certain amount of anisotropy in our universe. Hence, in this paper, we studied five dimensional cosmological model in f(R,T) gravity proposed by Harko et al. (2011) when the source of energy momentum tensor is a viscous fluid containing one dimensional cosmic strings. A barotropic cosmic fluid is considered for this study. A general equation of state for the energy density is assumed. We have also assumed that the scalar expansion of the space-time is proportional to shear scalar to get a determinate solution. Here the model does not approach isotropy throughout the evolution of the universe. But Nojiri and Odintsov (2003) have investigated Kaluza-Klein cosmology wherein the universe in turns inflates, decelerates and then accelerates in, respectively, early times, radiation dominated era and matter dominated era. This is possible by cosmic recollapse of the universe in the finite future. Thus, even though the early universe is anisotropic it becomes isotropic and will accelerate in finite time establishing consistency with the present day universe. The model presented will, also, help to discuss the role of bulk viscosity in getting an inflationary model and to understand structure formation in the universe.
References
Adhav, K.S.: Astrophys. Space Sci. 339, 365 (2012)
Appelquist, T., et al.: Modern-Klein Theories. Addison-Wesley, Reading (1987)
Azadi, A., et al.: Phys. Lett. B 670, 210 (2008)
Banerjee, A., Sanyal, A.K., Chakrabarty, S.: Pramana—J. Phys. 34, 1 (1990)
Banerjee, N., Beesham, A.: Aust. J. Phys. 49, 899 (1996)
Barrow, J.D.: Phys. Lett. B 180, 335 (1986)
Bennet, C.L., et al.: Astrophys. J. Suppl. Ser. 148, 1 (2003)
Brans, C.H., Dicke, R.H.: Phys. Rev. 124, 925 (1961)
Capozziello, S., et al.: Class. Quantum Gravity 24, 2153 (2007)
Capozziello, S., et al.: Phys. Lett. B 664, 12 (2008)
Caroll, S.M., Duvuri, V., Trpden, M., Turner, M.S.: Phys. Rev. D 70, 043528 (2004)
Chiba, T., Smith, L., Erickcek, A.L.: Phys. Rev. D 75, 124014 (2007)
Chodos, A., Detweller, S.: Phys. Rev. D 21, 2167 (1980)
Copeland, E.J., et al.: Int. J. Mod. Phys. D 15, 1753 (2006)
Harko, T., Lobo, F.S.N., Nojiri, S., Odintsov, S.D.: Phys. Rev. D 84, 024020 (2011)
Johri, V.B., Sudharsan, R.: Aust. J. Phys. 42, 215 (1989)
Katore, S.D., Rane, R.S.: Pramana—J. Phys. 67, 227 (2006)
Letelier, P.S.: Phys. Rev. D 28, 2414 (1983)
Lima, J.A.S., Germano, A.S.M., Abrama, L.R.W.: Phys. Rev. D 53, 4287 (1993)
Marchiano, W.J.: Phys. Lett. 52, 498 (1984)
Martens, R.: Class. Quantum Gravity 12, 1455 (1995)
Misner, C.V.: Astrophys. J. 151, 431 (1969)
Mohanthy, G., Pradhan, B.D.: Int. J. Theor. Phys. 31, 151 (1992)
Multamaki, T., Vilja, I.: Phys. Rev. D 74, 064022 (2006)
Multamaki, T., Vilja, I.: Phys. Rev. D 76, 064021 (2007)
Naidu, R.L., Satyanarayana, B., Reddy, D.R.K.: Int. J. Theor. Phys. 51, 1997–2002 (2012)
Nojiri, S., Odintsov, S.D.: Phys. Rev. D 68, 123512 (2003)
Nojiri, S., Odintsov, S.D.: Phys. Lett. A 19, 627 (2004)
Nojiri, S., Odintsov, S.D.: Int. J. Geom. Methods Mod. Phys. 4, 115 (2007)
Pavon, D., Bafluy, J., Jou, D.: Class. Quantum Gravity 8, 347 (1991)
Perlmutter, S., et al.: Astrophys. J. 517, 565 (1999)
Pimental, L.O.: Int. J. Theor. Phys. 33, 1335 (1994)
Rao, V.U.M., Kumari, S.G., Sirisha, K.V.S.: Astrophys. Space Sci. 335, 635 (2011)
Rao, V.U.M., Kumari, S.G., Neelima, D.: Astrophys. Space Sci. 337, 499 (2012)
Reddy, D.R.K.: Astrophys. Space Sci. 286, 356 (2003a)
Reddy, D.R.K.: Astrophys. Space Sci. 286, 359 (2003b)
Reddy, D.R.K., Naidu, R.L.: Int. J. Theor. Phys. 46, 2788 (2007)
Reddy, D.R.K., et al.: Astrophys. Space Sci. 310, 177 (2007)
Reddy, D.R.K., Santhikumar, R., Naidu, R.L.: Astrophys. Space Sci. 342, 249 (2012a)
Reddy, D.R.K., Naidu, R.L., Satyanarayana, B.: Int. J. Theor. Phys. 51(10), 3222 (2012b)
Reddy, D.R.K., Shanthikumar, R.: Global J. Sci. Frontier Res. A 13 (2013a)
Reddy, D.R.K., Shantikumar, R.: Astrophys. Space Sci. 344, 253 (2013b)
Reddy, D.R.K., Shantikumar, R., Kumar, P.V.P.: Int. J. Theor. Phys. 52(1), 239 (2013a). doi:10.1007/s10773-012-1325-1
Reddy, D.R.K., et al.: Int. J. Theor. Phys. 52, 1214 (2013b)
Riess, A.G., et al.: Astron. J. 116, 1009 (1998)
Saez, D., Ballester, V.J.: Phys. Lett. A 113, 467 (1985)
Sahoo, P.K.: Int. J. Theor. Phys. 47, 3029 (2008)
Setare, M.R., Sheyki, A.: Int. J. Mod. Phys. D 19, 171 (2010)
Shamir, M.F.: Astrophys. Space Sci. 330, 183 (2010)
Singh, N.I., Devi, S.R.: Astrophys. Space Sci. 334, 231 (2011)
Singh, G.P., Kale, A.Y.: Astrophys. Space Sci. 331, 207 (2011)
Singh, J.P., Ghosh, S.G., Beesham, A.: Aust. J. Phys. 50, 1 (1997)
Stachel, J.: Phys. Rev. D 21, 2171 (1980)
Tripathy, S.K., Nayak, S.K., Sahu, S.K., Routray, T.R.: Astrophys. Space Sci. 321, 247 (2009)
Vilenkin, A., Hwaking, S.W., Israel, W. (eds.): Three Hundred Years of Gravitation, p. 499. Cambridge Univ. Press, Cambridge (1987)
Witten, E.: Phys. Lett. B 144, 351 (1984)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Reddy, D.R.K., Naidu, R.L., Dasu Naidu, K. et al. Kaluza-Klein universe with cosmic strings and bulk viscosity in f(R,T) gravity. Astrophys Space Sci 346, 261–265 (2013). https://doi.org/10.1007/s10509-013-1426-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10509-013-1426-1