An improved regularization based Lagrangian asymmetric ν-twin support vector regression using pinball loss function

Abstract

In twin support vector regression (TSVR), one can notice that the samples are having the same importance even they are laying above the up-bound and below the down-bound on the estimation function for regression problem. Instead of giving the same emphasis to the samples, a novel approach Asymmetric ν-twin support vector regression (Asy-ν-TSVR) is suggested in this context where samples are having different influences with the estimation function based on samples distribution. Inspired by this concept, in this paper, we propose a new approach as improved regularization based Lagrangian asymmetric ν-twin support vector regression using pinball loss function (LAsy-ν-TSVR) which is more effective and efficient to deal with the outliers and noise. The solution is obtained by solving the simple linearly convergent approach which reduces the computational complexity of the proposed LAsy-ν-TSVR. Also, the structural risk minimization principle is implemented to make the problem strongly convex and more stable by adding the regularization term in their objective functions. The superiority of proposed LAsy-ν-TSVR is justified by performing the various numerical experiments on artificial generated datasets with symmetric and heteroscedastic structure noise as well as standard real-world datasets. The results of LAsy-ν-TSVR compares with support vector regression (SVR), TSVR, TSVR with Huber loss (HN-TSVR) and Asy-ν-TSVR, regularization on Lagrangian TSVR (RLTSVR) for the linear and Gaussian kernel which clearly demonstrates the efficacy and efficiency of the proposed algorithm LAsy-ν-TSVR.

1 Introduction

In the machine learning computational world, support vector machine (SVM) is a very popular and safe algorithm for binary classification [1]. Later, it is extended for regression problem also that is known as support vector regression (SVR) [2]. According to statistical learning theory, SVM follows the structural risk minimization (SRM) principle that solves a single large size quadratic programming problem (QPP) to get the optimal solution. SRM principle is basically for model selections which broadly explains the details of capacity control of model and maintain balance between VC dimension of function and empirical error.

SVM for regression is globally accepted due to superior forecasting performance in many research fields such as predict the popularity of online video [3], productiveness of higher education system [4], energy utilization in heat equalization [5], software enhancement effort [6], electric load [7], velocity of wind [8], flow of river [9], snow depth [10], neutral profiles from laser induced fluorescence data [11] and stock price [12]. The disadvantage of SVM is high training cost i.e. O(m³). So many significant improvements have been done by the researchers to lessen the training cost and complexity of SVM such as ν-SVR [13], SVMTorch [14], Bayesian SVR [15], geometric approach to SVR [16], active set SVR [17], heuristic training for SVR [18], smooth ε-SVR [19], fuzzy weighted support vector regression with fuzzy partition [20] etc.

A remarkable enhancement has been done in standard SVM by Jayadeva et al. [21] to propose a novel approach termed as twin support vector machine (TWSVM) which finds two non-parallel hyperplanes that are nearer to one of the class either positive or negative and also sustains unit difference between each other. In comparison to SVM, TWSVM has shown good generalization ability and lesser computation time. Motivated by the concept of TWSVM, a non-parallel twin support vector regression (TSVR) is proposed by Peng [22] in which two unknown optimal regression such as ε−insensitive down- and up- bound functions are determined. TSVR has better prediction performance and accelerated training speed over the SVR [22]. Many other variants of TSVR have been suggested such as reduced TSVR [23] which applied the concept of rectangle kernels to obtain significant improvement in learning time on TSVR, weighted TSVR [24] reduces the problem of overfitting by assigned different penalties to each sample. Twin least square SVR [25] takes the concept of TSVR and least square SVR [26] to improve the prediction performance with training speed. Linearly convergent based Lagrangian TSVR [27] has been proposed to improve the generalization performance and learning speed. Unconstrained based Lagrangian TSVR [28] has been suggested to reduce the complexity of model and improve the learning speed via solving the unconstrained minimization problems. Niu et al. [29] has combined the TSVR with Huber loss function (HN-TSVR) for handling the Gaussian noise. Tanveer & Shubham [30] has proposed a new algorithm termed as regularization on Lagrangian twin support vector regression (RLTSVR) which solves the regression problem very effectively. There are many variants of SVM exists in the literature based on pinball loss function for the classification problems like Huang has applied pin ball loss function in SVM and suggested an approach as pin-SVM [31] to handle the noisy data; Huang et al. [32] has proposed sequential minimization optimization for SVM with truncated pinball loss along with its sparse version that enhances the generalization efficiency of pin-SVM; Pin-M³HM [33] has improved the twin hyper-sphere SVM (THSVM) [34] using pin ball loss that avoids noise and error in very effective manner; Xu et al. [35] has proposed a new approach TWSVM with pin ball loss that indulge with quantile distance which is performed well for noisy data and related to this for more study, see [36,37,38,39,40,41,42,43,44]. It actually gives the active research direction in forward way.

One can notice that very few literatures are available on SVR with pinball loss function for the regression problems. In spite of considering ε-insensitive loss function, Huang has proposed a novel approach termed as asymmetric ν-tube support vector regression (Asy-ν-SVR) [45] based on ν-SVR with pinball loss function to divide the outliers asymmetrically over above and below of the tube and improved the computational complexity. Similarly, one can observe that we have assigned same penalties to every point above the up-bound and below the down-bound in TSVR. But each sample may not give same effect in order to determine the regression function. So, asymmetric ν-twin support vector regression (Asy-ν-TSVR) [35] has been suggested to give different effects on the regression function by using the pin-ball loss function. Motivated by the above studies, we propose a new approach as improved regularization based Lagrangian asymmetric ν-twin support vector regression (LAsy-ν-TSVR) using pinball loss function in this paper where the end regression function is determined by solving the linearly convergent iterative approach unlike solve the QPPs in case of SVR, TSVR, HN-TSVR and Asy-ν-TSVR. This approach reduces the computational cost of the model. Another advantage of our proposed LAsy-ν-TSVR is that it follows the SRM principle which yields the existence of global solution and improves the generalization ability. The characteristics of proposed LAsy-ν-TSVR are as follows:

• To make the problem strongly convex and find the unique global solution, 2-norm of vector of slack variables is included in the objective functions of proposed LAsy-ν-TSVR.

• Regularization terms are added in the objective functions of LAsy-ν-TSVR to implement the SRM principle which makes the model well pose.

• The solution of proposed LAsy-ν-TSVR is obtained by using the linearly convergent iterative schemes which improve the computational cost.

Further, to check the effectiveness and applicability of proposed LAsy-ν-TSVR, numerical experiments are conducted on artificial generated datasets having symmetric and asymmetric structure of noise and also on real-world benchmark datasets. The experimental results of proposed LAsy-ν-TSVR are compared with SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR in this paper.

This paper is organised as follows. Section 2 outlines briefly about SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR. The formulation of proposed LAsy-ν-TSVR is described in Section 3. In Section 4, the numerical experiments are performed on artificially generated and real-world datasets in detail. At last, conclusion and future work is presented in Section 5.

2 Background

In this paper, consider the training data as ${\left\{\left({x}_i,{y}_i\right)\right\}}_{i=1}^m$ where i^th -input data sample is shown as x_i = (x_i1, ..., x_in) ∈ Rⁿ and y_i ∈ R is the observed outcome of corresponding input sample. Let consider A is a m × n matrix in which m is the number of input samples and n is the number of attributes in such a way that A = (x₁, ..., x_m)^t ∈ R^m × n and y= (y₁, ..., y_m)^t ∈ R^m. The 2-norm of a vector x will be represented by ‖x‖. The plus function x₊ is given by max{0, x_i} for i = 1, ..., m.

2.1 Support vector regression (SVR)

In the linear regression [2], the main aim is to find the optimal linear regression estimating function of the form as

$$ f(x)={w}^tx+b $$

where, w ∈ Rⁿ, b ∈ R.

The formulation of linear SVR as constrained minimization problem [46] is given as

$$ \min \frac{1}{2}{\left\Vert w\right\Vert}^2+C\left({e}^t{\xi}_1+{e}^t{\xi}_2\right) $$

subject to

$$ {\displaystyle \begin{array}{l}y-\left( Aw+ be\right)\le \varepsilon e+{\xi}_{1i},{\xi}_{1i}\ge 0\\ {}\left( Aw+ be\right)-y\le \varepsilon e+{\xi}_{2i},{\xi}_{2i}\ge 0\;\mathrm{for}\;i=1,...,m\end{array}} $$

(1)

where, the vectors of slack variables ξ₁ ≥ (ξ₁₁, ..., ξ_1m)^t and ξ₂ ≥ (ξ₂₁, ..., ξ_2m)^t; C > 0, ε > 0 are the input parameters and e ∈ R^m is the vector of one’s.

Now introduce the Lagrangian multipliers α₁ = (α₁₁, ..., α_1m)^t,β₁ = (β₁₁, ..., β_1m)^t and further apply the Karush–Kuhn–Tucker (KKT) conditions, the dual QPP of (1) is given as:

$$ \min \frac{1}{2}\sum \limits_{i,j=1}^m\left({\alpha}_{1i}-{\beta}_{1i}\right)\left({x}_i^t{x}_j\right)\left({\alpha}_{1j}-{\beta}_{1j}\right)+\varepsilon \sum \limits_{i=1}^m\left({\alpha}_{1i}+{\beta}_{1i}\right)-\sum \limits_{i=1}^m{y}_i\left({\alpha}_{1i}-{\beta}_{1i}\right) $$

subject to

$$ \sum \limits_{i=1}^m{e}^t\left({\alpha}_{1i}-{\beta}_{1i}\right)=0,0\le {\alpha}_1,{\beta}_1\le Ce. $$

(2)

The decision function f(.) will be obtained from (2) [46] for any test data x ∈ Rⁿ as

$$ f(x)=\sum \limits_{i=1}^m\left({\alpha}_{1i}-{\beta}_{1i}\right)\left({x}^t{x}_i\right)+b $$

For nonlinear SVR, we assume the nonlinear function of the given form as.

f(x) = w^tϕ(x) + b

where, ϕ(.) is a nonlinear mapping which consider the input space into feature space in the high dimension. The formulation of nonlinear constrained QPP [2, 46] is considered as

$$ \min \frac{1}{2}{\left\Vert w\right\Vert}^2+C\left({e}^t{\xi}_1+{e}^t{\xi}_2\right) $$

subject to

$$ {\displaystyle \begin{array}{l}y-\left(\varphi \left({x}_i\right)w+ be\right)\le \varepsilon e+{\xi}_{1i},{\xi}_{1i}\ge 0\\ {}\left(\varphi \left({x}_i\right)w+ be\right)-y\le \varepsilon e+{\xi}_{2i},{\xi}_{2i}\ge 0\;\mathrm{for}\;i=1,...,m\end{array}} $$

(3)

Now, the dual QPP of the primal problem (3) is determined by using the Lagrangian multipliersα₁, β₁ and further apply the KKT conditions. We get

$$ \min \frac{1}{2}\sum \limits_{i,j=1}^m\left({\alpha}_{1i}-{\beta}_{1i}\right)k\left({x}_i,{x}_j\right)\left({\alpha}_{1j}-{\beta}_{1j}\right)+\varepsilon \sum \limits_{i=1}^m\left({\alpha}_{1i}+{\beta}_{1i}\right)-\sum \limits_{i=1}^m{y}_i\left({\alpha}_{1i}-{\beta}_{1i}\right) $$

subject to

$$ \sum \limits_{i=1}^m{e}^t\left({\alpha}_{1i}-{\beta}_{1i}\right)=0,0\le {\alpha}_1,{\beta}_1\le Ce. $$

(4)

where, the kernel function k(x_i, x_j) = ϕ(x_i)^tϕ(x_j). The decision function f(.) will be obtained [46] for any test data x ∈ Rⁿ from (4) as

$$ f(x)=\sum \limits_{i=1}^m\left({\alpha}_{1i}-{\beta}_{1i}\right)k\left(x,{x}_i\right)+b $$

2.2 Twin support vector regression (TSVR)

Twin support vector regression (TSVR) [22] is an effective approach which is influenced from TWSVM [21] to predict the two nonparallel ε-insensitive down-bound function ${f}_1(x)={w}_1^tx+{b}_1$ and ε-insensitive up-bound function ${f}_2(x)={w}_2^tx+{b}_2$. Here, w₁, w₂ ∈ Rⁿ and b₁, b₂ ∈ R are unknowns. In linear TSVR, the regression functions are determined by solving the following QPPs in such a way:

$$ \min \frac{1}{2}{\left\Vert y-{\varepsilon}_1e-\left(A{w}_1+{b}_1e\right)\right\Vert}^2+{C}_1{e}^t{\xi}_1 $$

subject to

$$ y-\left(A{w}_1+{b}_1e\right)\ge {\varepsilon}_1e-{\xi}_1,{\xi}_1\ge 0 $$

(5)

and

$$ \min \frac{1}{2}{\left\Vert y+{\varepsilon}_2e-\left(A{w}_2+{b}_2e\right)\right\Vert}^2+{C}_2{e}^t{\xi}_2 $$

subject to

$$ \left(A{w}_2+{b}_2e\right)-y\ge {\varepsilon}_2e-{\xi}_2,{\xi}_2\ge 0 $$

(6)

where, input parameters are C₁, C₂ > 0 and ε₁, ε₂ > 0; the vectors of slack variables are ξ₁ and ξ₂.

Now introduce the Lagrangian multipliers in the above problems (5) and (6) is shown as

$$ L\left({w}_1,{b}_1,{\xi}_1,{\alpha}_1,{\beta}_1\right)=\frac{1}{2}{\left\Vert \left(y-e{\varepsilon}_1-\left(A{w}_1+e{b}_1\right)\right)\right\Vert}^2+{C}_1{e}^t{\xi}_1-{\alpha}_1^t\left(y-\left(A{w}_1+e{b}_1\right)-e{\varepsilon}_1+{\xi}_1\right)-{\beta}_1^t{\xi}_1 $$

and

$$ L\left({w}_2,{b}_2,{\xi}_2,{\alpha}_2,{\beta}_2\right)=\frac{1}{2}{\left\Vert \left(y+{\varepsilon}_2e-\left(A{w}_2+e{b}_2\right)\right)\right\Vert}^2+{C}_2{e}^t{\xi}_2-{\alpha}_2^t\left(\left(A{w}_2+e{b}_2\right)-y-e{\varepsilon}_2+{\xi}_2\right)-{\beta}_2^t{\xi}_2 $$

where, α₁ = (α₁₁, ..., α_1m)^t, α₂ = (α₂₁, ..., α_2m)^t are the vectors of Lagrangian multipliers. After, we get the Wolfe dual QPPs of the above primal problems by using the KKT conditions as

$$ \max -\frac{1}{2}{\alpha}_1^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_1+{\left(y-{\varepsilon}_1e\right)}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_1-{\left(y-{\varepsilon}_1e\right)}^t{\alpha}_1 $$

subject to

$$ 0\le {\alpha}_1\le {C}_1e $$

(7)

and

$$ \max -\frac{1}{2}{\alpha}_2^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_2+{\left(y+{\varepsilon}_2e\right)}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_2+{\left(y+{\varepsilon}_2e\right)}^t{\alpha}_2 $$

subject to

$$ 0\le {\alpha}_2\le {C}_2e $$

(8)

where, S = [A e] is the augmented matrix.

After solving the above pair of dual QPPs (7) and (8) for α₁ and α₂, one can derive the values as:

$$ \left[\begin{array}{l}{w}_1\\ {}{b}_1\end{array}\right]={\left({S}^tS\right)}^{-1}{S}^t\left(y-{\varepsilon}_1e-{\alpha}_1\right) $$

and

$$ \left[\begin{array}{l}{w}_2\\ {}{b}_2\end{array}\right]={\left({S}^tS\right)}^{-1}{S}^t\left(y+{\varepsilon}_2e+{\alpha}_2\right) $$

Then, the final estimated regression function is obtained as

$$ f(x)=\frac{1}{2}\left({f}_1(x)+{f}_2(x)\right) $$

(9)

In nonlinear case of TSVR, the kernel generating regression functions f₁(x) = K(x^t, A^t)w₁ + b₁ and f₂(x) = K(x^t, A^t)w₂ + b₂ are determined by the following QPPs as

$$ \min \frac{1}{2}{\left\Vert y-{\varepsilon}_1e-\left(K\left(A,{A}^t\right){w}_1+{b}_1e\right)\right\Vert}^2+{C}_1{e}^t{\xi}_1 $$

subject to

$$ y-\left(K\left(A,{A}^t\right){w}_1+{b}_1e\right)\ge {\varepsilon}_1e-{\xi}_1,{\xi}_1\ge 0 $$

(10)

and

$$ \min \frac{1}{2}{\left\Vert y+{\varepsilon}_2e-\left(K\left(A,{A}^t\right){w}_2+{b}_2e\right)\right\Vert}^2+{C}_2{e}^t{\xi}_2 $$

subject to

$$ \left(K\left(A,{A}^t\right){w}_2+{b}_2e\right)-y\ge {\varepsilon}_2e-{\xi}_2,{\xi}_2\ge 0 $$

(11)

Similarly as the linear TSVR, we get the dual QPP from the Eqs. (10) and (11)

$$ \max -\frac{1}{2}{\alpha}_1^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_1+{\left(y-{\varepsilon}_1e\right)}^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_1-{\left(y-{\varepsilon}_1e\right)}^t{\alpha}_1 $$

subject to

$$ 0\le {\alpha}_1\le {C}_1e $$

(12)

and

$$ \max -\frac{1}{2}{\alpha}_2^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_2+{\left(y+{\varepsilon}_2e\right)}^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_2+{\left(y+{\varepsilon}_2e\right)}^t{\alpha}_2 $$

subject to

$$ 0\le {\alpha}_2\le {C}_2e $$

(13)

where, $T=\left[K\left(A,{A}^t\right)\kern0.5em e\right]$ is the augmented matrix; α₁ and α₂ are Lagrangian multipliers.

One can derive the values of w₁, w₂, b₁, b₂ from the Eqs. (12) and (13) as follows:

$$ \left[\begin{array}{l}{w}_1\\ {}{b}_1\end{array}\right]={\left({T}^tT+\sigma I\right)}^{-1}{T}^t\left(y-e{\varepsilon}_1-{\alpha}_1\right) $$

and

$$ \left[\begin{array}{l}{w}_2\\ {}{b}_2\end{array}\right]={\left({T}^tT+\sigma I\right)}^{-1}{T}^t\left(y+e{\varepsilon}_2+{\alpha}_2\right) $$

One can notice that σI is added as extra term in the matrix (T^tT)⁻¹ to make the matrix positive definite, where σ > 0 is the small real positive value. Finally, end regression function is obtained from (9).

2.3 Twin support vector regression with Huber loss (HN-TSVR)

TSVR [22] is based on ε-insensitive loss function but fail to deal for data having Gaussian noise. Motivated by the work of [47, 48], TSVR with Huber loss function (HN-TSVR) [29] has been suggested in order to improve the generalization ability by suppress a variety of noise and outliers. Here, Huber loss function is given by

$$ c(x)=\Big\{{\displaystyle \begin{array}{ll}\frac{x^2}{2},& if\;x\le \varepsilon \\ {}\varepsilon \mid x\mid -\frac{\varepsilon^2}{2},& otherwise\end{array}}. $$

The nonlinear HN-TSVR QPPs are as follows:

$$ \min \frac{1}{2}{\left\Vert y-e{\varepsilon}_1-\left(K\left(A,{A}^t\right){w}_1+e{b}_1\right)\right\Vert}^2+{C}_1\left(\sum \limits_{i\in {U}_1}\frac{1}{2}{\xi}_{1i}^2+\varepsilon \sum \limits_{i\in {U}_2}\left({\xi}_{1i}-\frac{1}{2}\varepsilon \right)\right) $$

subject to

$$ y-\left(K\left(A,{A}^t\right){w}_1+e{b}_1\right)\ge e{\varepsilon}_1-{\xi}_1,{\xi}_1\ge 0 $$

(14)

where, U₁ = {i| 0 ≤ ξ_1i < ε}, U₂ = {i| ξ_1i ≥ ε}.and

$$ \min \frac{1}{2}{\left\Vert y+e{\varepsilon}_2-\left(K\left(A,{A}^t\right){w}_2+e{b}_2\right)\right\Vert}^2+{C}_2\left(\sum \limits_{i\in {V}_1}\frac{1}{2}{\xi}_{2i}^2+\varepsilon \sum \limits_{i\in {V}_2}\left({\xi}_{2i}-\frac{1}{2}\varepsilon \right)\right) $$

subject to

$$ \left(K\left(A,{A}^t\right){w}_2+e{b}_2\right)-y\ge e{\varepsilon}_2-{\xi}_2,{\xi}_2\ge 0 $$

(15)

where, V₁ = {i| 0 ≤ ξ_2i < ε}, V₂ = {i| ξ_2i ≥ ε};ξ₁ = (ξ₁₁, ...ξ_1m)^t and ξ₂ = (ξ₂₁, ...ξ_2m)^t are the slack variables; C₁, C₂ > 0, ε₁, ε₂ > 0 are parameters.

By applying the Lagrange’s multipliers α₁ = (α₁₁, ..., α_1m)^t, α₂ = (α₂₁, ..., α_2m)^t, the dual formulation of problem (14) and (15) are determined as

$$ \min\;\frac{1}{2}{\alpha_1}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_1-{\left(y-{\varepsilon}_1e\right)}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_1+{\left(y-{\varepsilon}_1e\right)}^t{\alpha}_1+\frac{1}{2{C}_1}{\alpha_1}^t{\alpha}_1 $$

subject to:

$$ 0\le {\alpha}_1\le {C}_1{\varepsilon}_1e $$

(16)

and

$$ \min \frac{1}{2}{\alpha_2}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_2+{\left(y+{\varepsilon}_2e\right)}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_2-{\left(y+{\varepsilon}_2e\right)}^t{\alpha}_2+\frac{1}{2{C}_2}{\alpha_2}^t{\alpha}_2 $$

subject to:

$$ 0\le {\alpha}_2\le {C}_2{\varepsilon}_2e $$

(17)

where, $S=\left[K\left(A,{A}^t\right)\kern0.5em e\right].$

The value of corresponding w₁, w₂, b₁, b₂ are

$$ {\displaystyle \begin{array}{l}\left[\begin{array}{l}{w}_1\\ {}{b}_1\end{array}\right]={\left({S}^tS\right)}^{-1}{S}^t\left(y-e{\varepsilon}_1-{\alpha}_1\right)\\ {}\left[\begin{array}{l}{w}_2\\ {}{b}_2\end{array}\right]={\left({S}^tS\right)}^{-1}{S}^t\left(y+e{\varepsilon}_2-{\alpha}_2\right)\end{array}} $$

Finally, the end regression function can be obtained as similar to (9).

2.4 Asymmetric ν-twin support vector regression (Asy-ν-TSVR)

Asymmetric v-twin support vector regression with pinball loss function (Asy-ν-TSVR) [35] has been proposed in order to pursue the asymmetric tube where the different penalties are assigned to the above the up-bound and below the down-bound. Asy-ν-TSVR is highly influenced from Huang et al. [45] whereε-insensitive loss is replaced by pinball loss [40] where points having the different penalties based on their different position. Here, pinball loss function is defined as:

$$ {L}_{\varepsilon}^p(x)=\Big\{{\displaystyle \begin{array}{ll}\frac{1}{2p}\left(x-\varepsilon \right),& x\ge \varepsilon, \\ {}0,& -\varepsilon <x<\varepsilon, \\ {}\frac{1}{2\left(1-p\right)}\left(-x-\varepsilon \right),& x\le -\varepsilon, \end{array}} $$

(18)

where p is the asymmetric penalty parameter. One can be degraded into ε-insensitive loss by choosing the value p = 0.5..

In linear Asy-ν-TSVR case, two nonparallel ε₁-insensitive down-bound ${f}_1(x)={w}_1^tx+{b}_1$ and up-bound ${f}_2(x)={w}_2^tx+{b}_2$ functions are generated by solving the pair of QPPs in the following manner:

$$ \min \frac{1}{2}{\left\Vert y-\left(A{w}_1+{b}_1e\right)\right\Vert}^2+{C}_1{\nu}_1{\varepsilon}_1+\frac{1}{m}{C}_1{e}^t{\xi}_1 $$

subject to

$$ y-\left(A{w}_1+{b}_1e\right)\ge -{\varepsilon}_1e-2\left(1-p\right){\xi}_1,{\xi}_1\ge 0,{\varepsilon}_1\ge 0 $$

(19)

and

$$ \min \frac{1}{2}{\left\Vert y-\left(A{w}_2+{b}_2e\right)\right\Vert}^2+{C}_2{\nu}_2{\varepsilon}_2+\frac{1}{m}{C}_2{e}^t{\xi}_2 $$

subject to

$$ \left(A{w}_2+{b}_2e\right)-y\ge -{\varepsilon}_2e-2p{\xi}_2,{\xi}_2\ge 0,{\varepsilon}_2\ge 0 $$

(20)

where, ξ₁, ξ₂ are the slack variables; C₁, C₂ > 0; ε₁, ε₂ > 0, ν₁, ν₂ are the input parameters.

Apply Lagrangian multipliers α₁, α₂ > 0 ∈ R^m and KKT conditions, we get the dual QPP of Asy-ν-TSVR from the Eqs. (19) and (20)

$$ \min\;\frac{1}{2}{\alpha}_1^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_1-{y}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_1+{y}^t{\alpha}_1 $$

subject to

$$ 0\le {\alpha}_1\le \frac{C_1e}{2\left(1-p\right)m},{e}^t{\alpha}_1\le {C}_1{\nu}_1 $$

(21)

and

$$ \min\;\frac{1}{2}{\alpha}_2^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_2+{y}^tS{\left({S}^tS\right)}^{-1}{S}^t{\alpha}_2-{y}^t{\alpha}_2 $$

subject to

$$ 0\le {\alpha}_2\le \frac{C_2e}{2 pm},{e}^t{\alpha}_2\le {C}_2{\nu}_2 $$

(22)

where, $S=\left[A\kern0.5em e\right]$.

After solving the Eqs. (21) and (22), one can compute the values of w₁, w₂, b₁, b₂ in the following manner:

$$ \left[\begin{array}{l}{w}_1\\ {}{b}_1\end{array}\right]={\left({S}^tS\right)}^{-1}{S}^t\left(y-{\alpha}_1\right) $$

and

$$ \left[\begin{array}{l}{w}_2\\ {}{b}_2\end{array}\right]={\left({S}^tS\right)}^{-1}{S}^t\left(y+{\alpha}_2\right) $$

Finally, the end regression function is obtained as similar to (9).

In the nonlinear case, kernel generating regression functions are f₁(x) = K(x^t, A^t)w₁ + b₁ and f₂(x) = K(x^t, A^t)w₂ + b₂ by solving the pair of QPPs in such a way:

$$ \min \frac{1}{2}{\left\Vert y-\Big(K\left(A,{A}^t\right){w}_1+{b}_1e\right\Vert}^2+{C}_1{\nu}_1{\varepsilon}_1+\frac{1}{m}{C}_1{e}^t{\xi}_1 $$

subject to

$$ y-\left(K\left(A,{A}^t\right){w}_1+{b}_1e\right)\ge -{\varepsilon}_1e-2\left(1-p\right){\xi}_1,{\xi}_1\ge 0,{\varepsilon}_1\ge 0 $$

(23)

and

$$ \min \frac{1}{2}{\left\Vert y-\Big(K\left(A,{A}^t\right){w}_2+{b}_2e\right\Vert}^2+{C}_2{\nu}_2{\varepsilon}_2+\frac{1}{m}{C}_2{e}^t{\xi}_2 $$

subject to

$$ \left(K\left(A,{A}^t\right){w}_2+{b}_2e\right)-y\ge -{\varepsilon}_2e-2p{\xi}_2,{\xi}_2\ge 0,{\varepsilon}_2\ge 0 $$

(24)

Apply Lagrangian multipliers α₁, α₂and KKT necessary conditions, the dual formation of (23) and (24) can be derived as follows:

$$ \min\;\frac{1}{2}{\alpha}_1^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_1-{y}^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_1+{y}^t{\alpha}_1 $$

subject to

$$ 0\le {\alpha}_1\le \frac{C_1e}{2\left(1-p\right)m},{e}^t{\alpha}_1\le {C}_1{\nu}_1 $$

(25)

and

$$ \min\;\frac{1}{2}{\alpha}_2^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_2+{y}^tT{\left({T}^tT\right)}^{-1}{T}^t{\alpha}_2-{y}^t{\alpha}_2 $$

subject to

$$ 0\le {\alpha}_2\le \frac{C_2e}{2 pm},{e}^t{\alpha}_2\le {C}_2{\nu}_2 $$

(26)

where, $T=\left[K\left(A,{A}^t\right)\kern0.5em e\right]$.

After solving the Eqs. (27) and (28) for α₁ and α₂, we can obtain the augmented vectors as

$$ \left[\begin{array}{l}{w}_1\\ {}{b}_1\end{array}\right]={\left({T}^tT\right)}^{-1}{T}^t\left(y-{\alpha}_1\right) $$

and

$$ \left[\begin{array}{l}{w}_2\\ {}{b}_2\end{array}\right]={\left({T}^tT\right)}^{-1}{T}^t\left(y+{\alpha}_2\right) $$

Finally, the end regression estimation function is given as similar to the linear case for any test samplex ∈ Rⁿ.

2.5 A regularization on Lagrangian twin support vector regression (RLTSVR)

By considering the principle of structural risk minimization instead of usual empirical risk in ε-TSVR, recently Tanveer & Shubham [30] proposed a new algorithm termed as regularization on Lagrangian twin support vector regression (RLTSVR) whose solution is obtained by simple linearly convergent iterative approach. The two nonparallel functions f₁(x) = K(x^t, A^t)w₁ + b₁ and f₂(x) = K(x^t, A^t)w₂ + b₂ are determined by using the following constrained minimization problems:

$$ \min \frac{C_3}{2}\left({w}_1^t{w}_1+{b}_1^2\right)+\frac{1}{2}{\left\Vert y-\left(K\right(A,{A}^t\left){w}_1+e{b}_1\right)\right\Vert}^2+\frac{1}{2}{C}_1{\xi_1}^t{\xi}_1 $$

subject to

$$ y-\left(K\left(A,{A}^t\right){w}_1+e{b}_1\right)\ge e{\varepsilon}_1-{\xi}_1 $$

(27)

and

$$ \min \frac{C_4}{2}\left({w}_2^t{w}_2+{b}_2^2\right)+\frac{1}{2}{\left\Vert y-\left(K\right(A,{A}^t\left){w}_2+e{b}_2\right)\right\Vert}^2+\frac{1}{2}{C}_2{\xi_2}^t{\xi}_2 $$

subject to

$$ \left(K\left(A,{A}^t\right){w}_2+e{b}_2\right)-y\ge e{\varepsilon}_2-{\xi}_2 $$

(28)

where, input parameters are C₁, C₂, C₃, C₄ > 0 and ε₁, ε₂ > 0; ξ₁, ξ₂ are slack variables.

Now introduce the Lagrangian multipliers α₁ = (α₁₁, ..., α_1m)^t and α₂ = (α₂₁, ..., α_2m)^t, the dual form of the QPP of (27) and (28) can be written as:

$$ \underset{\alpha_1\ge 0}{\min\;}\frac{1}{2}{\alpha}_1^t\left(\frac{I}{C_1}+S{\left({S}^tS+{C}_3I\right)}^{-1}{S}^t\right){\alpha}_1-\left({y}^tS{\left({S}^tS+{C}_3I\right)}^{-1}{S}^t-{\left(y+e{\varepsilon}_1\right)}^t\right){\alpha}_1 $$

(29)

and

$$ \underset{\alpha_2\ge 0}{\min\;}\frac{1}{2}{\alpha}_2^t\left(\frac{I}{C_2}+S{\left({S}^tS+{C}_4I\right)}^{-1}{S}^t\right){\alpha}_2-\left({\left(y-e{\varepsilon}_2\right)}^t-{y}^tS{\left({S}^tS+{C}_4I\right)}^{-1}{S}^t\right){\alpha}_2 $$

(30)

where, $S=\left[K\left(A,{A}^t\right)\kern0.5em e\right]$ is the augmented matrix.

After solving the above pair of dual QPPs (29) and (30) for α₁ and α₂, one can derive the values as:

$$ \left[\begin{array}{l}{w}_1\\ {}{b}_1\end{array}\right]={\left({S}^tS+{C}_3I\right)}^{-1}{S}^t\left(y-{\alpha}_1\right) $$

and

$$ \left[\begin{array}{l}{w}_2\\ {}{b}_2\end{array}\right]={\left({S}^tS+{C}_4I\right)}^{-1}{S}^t\left(y+{\alpha}_2\right) $$

Finally, the end regression function is obtained as similar to (9). For more details, one can see [30].

3 Proposed improved regularization based Lagrangian asymmetric ν-twin support vector regression using pinball loss (LAsy-ν-TSVR)

Recently, Xu et al., [35] has suggested a novel approach termed as asymmetric ν-twin support vector regression using pinball loss function to handle the asymmetric noise and outliers in challenging real-world problems. In order to further improvement of generalization ability and reduction of computation cost, we propose another approach termed as improved regularization based Lagrangian asymmetric ν-twin support vector regression using pinball loss function (LAsy-ν-TSVR) whose solution is obtained by solving the linearly convergent iterative method in place of solving QPPs. To formulate our proposed LAsy-ν-TSVR formulation, we replace the 1-norm of vector of slack variables ξ₁ and ξ₂, by the square of the vector of slack variables in 2-norm which makes the problem strongly convex and yields the existence of global unique solution. In order to follow the SRM principle unlike in case of TSVR and Asy-ν-TSVR, the regularization terms $\frac{C_3}{2}\left({\left\Vert {w}_1\right\Vert}^2+{b}_1^2\right)$ and $\frac{C_4}{2}\left({\left\Vert {w}_2\right\Vert}^2+{b}_2^2\right)$ are also added in the objective functions of (19) and (20) respectively that improves the stability in the dual formulations as well as makes the model well-posed. In the formulations of linear proposed LAsy-ν-TSVR, the regression functions ${f}_1(x)={w}_1^tx+{b}_1$ and ${f}_2(x)={w}_2^tx+{b}_2$ are obtained by solving the modified QPPs as

$$ \min \frac{C_3}{2}\left({\left\Vert {w}_1\right\Vert}^2+{b}_1^2\right)+\frac{1}{2}{\left\Vert y-\left(A{w}_1+e{b}_1\right)\right\Vert}^2+\frac{1}{m}{C}_1{\xi}_1^t{\xi}_1+{C}_1{\nu}_1{\varepsilon}_1^2 $$

subject to

$$ y-\left(A{w}_1+e{b}_1\right)\ge -e{\varepsilon}_1-2\left(1-p\right){\xi}_1 $$

(31)

and

$$ \min \frac{C_4}{2}\left({\left\Vert {w}_2\right\Vert}^2+{b}_2^2\right)+\frac{1}{2}{\left\Vert y-\left(A{w}_2+e{b}_2\right)\right\Vert}^2+\frac{1}{m}{C}_2{\xi}_2^t{\xi}_2+{C}_2{\nu}_2{\varepsilon}_2^2 $$

subject to

$$ \left(A{w}_2+e{b}_2\right)-y\ge -e{\varepsilon}_2-2p{\xi}_2 $$

(32)

where C₁, C₂, C₃, C₄ > 0, and ν₁, ν₂ are input parameters; ξ₁ = (ξ₁₁, ...ξ_1m)^t, ξ₂ = (ξ₂₁, ...ξ_2m)^t are the slack variables. Here, the non-negative constraints of the slack variables are dropped in (31) and (32). The Lagrangian functions of (31) and (32) are obtained by using the Lagrangian multipliers α₁, α₂ > 0 ∈ R^m as

$$ {L}_1=\frac{C_3}{2}\left({\left\Vert {w}_1\right\Vert}^2+{b}_1^2\right)+\frac{1}{2}{\left\Vert y-\left(A{w}_1+e{b}_1\right)\right\Vert}^2+\frac{1}{m}{C}_1{\xi}_1^t{\xi}_1+{C}_1{\nu}_1{\varepsilon}_1^2-{\alpha}_1^t\left(y-\left(A{w}_1+e{b}_1\right)+e{\varepsilon}_1+2\left(1-p\right){\xi}_1\right) $$

(33)

and

$$ {L}_2=\frac{C_4}{2}\left({\left\Vert {w}_2\right\Vert}^2+{b}_2^2\right)+\frac{1}{2}{\left\Vert y-\left(A{w}_2+e{b}_2\right)\right\Vert}^2+\frac{1}{m}{C}_2{\xi}_2^t{\xi}_2+{C}_2{\nu}_2{\varepsilon}_2^2-{\alpha}_2^t\left(\left(A{w}_2+e{b}_2\right)-y+e{\varepsilon}_2+2p{\xi}_2\right) $$

(34)

Further, apply the KKT conditions in (41), we get

$$ \frac{\partial {L}_1}{\partial {w}_1}={C}_3{w}_1-{A}^t\left(y-\left(A{w}_1+e{b}_1\right)\right)+{A}^t{\alpha}_1=0, $$

(35)

$$ \frac{\partial {L}_1}{\partial {b}_1}={C}_3{b}_1-{e}^t\left(y-\left(A{w}_1+e{b}_1\right)\right)+{e}^t{\alpha}_1=0, $$

(36)

$$ \frac{\partial {L}_1}{\partial {\xi}_1}=\frac{C_1}{m}{\xi}_1-2\left(1-p\right){\alpha}_1=0, $$

(37)

$$ \frac{\partial {L}_1}{\partial {\varepsilon}_1}=2{C}_1{\nu}_1{\varepsilon}_1-{e}^t{\alpha}_1=0. $$

(38)

By combining the Eqs. (35) and (36), we get

$$ \left[\begin{array}{l}{w}_1\\ {}{b}_1\end{array}\right]={\left({S}^tS+{C}_3I\right)}^{-1}{S}^t\left(y-{\alpha}_1\right) $$

(39)

where $S=\left[A\kern0.5em e\right]$ is an augmented matrix.

By using the Eqs. (33), (36), (37) and (38), the dual QPP of primal problem (33) is given as

$$ \min \frac{1}{2}{\alpha}_1^t\left(S{\left({S}^tS+{C}_3I\right)}^{-1}{S}^t+\frac{4m{\left(1-p\right)}^2}{C_1}+\frac{e{e}^t}{2{C}_1{\nu}_1}\right){\alpha}_1-{\left(S{\left({S}^tS+{C}_3I\right)}^{-1}{S}^ty-y\right)}^t{\alpha}_1 $$

(40)

Similarly, we get the following dual QPP of the primal problem (34) as

$$ \min \frac{1}{2}{\alpha}_2^t\left(S{\left({S}^tS+{C}_4I\right)}^{-1}{S}^t+\frac{4m{p}^2}{C_2}+\frac{e{e}^t}{2{C}_2{\nu}_2}\right){\alpha}_2-{\left(-S{\left({S}^tS+{C}_4I\right)}^{-1}{S}^ty+y\right)}^t{\alpha}_2 $$

(41)

The values of α₁ and α₂ are determined by solving the QPPs (40) and (41). The end regression function f(.) is determined by taking the mean of f₁(x) and f₂(x) for any test sample x ∈ Rⁿ:

$$ {f}_1(x)={w}_1^tx+{b}_1=\left[{x}^t\kern0.5em 1\right]\left({\left({S}^tS+{C}_3I\right)}^{-1}{S}^t\left(y-{\alpha}_1\right)\right) $$

(42)

and

$$ {f}_2(x)={w}_2^tx+{b}_2=\left[{x}^t\kern0.5em 1\right]\left({\left({S}^tS+{C}_4I\right)}^{-1}{S}^t\left(y+{\alpha}_2\right)\right). $$

(43)

In the formulation of non-linear LAsy-ν-TSVR, the kernel generated functions f₁(x) = K(x^t, A^t)w₁ + b₁ and f₂(x) = K(x^t, A^t)w₂ + b₂ are determined by the following QPPs as

$$ \min \frac{C_3}{2}\left({\left\Vert {w}_1\right\Vert}^2+{b}_1^2\right)+\frac{1}{2}{\left\Vert y-\left(K\right(A,{A}^t\left){w}_1+e{b}_1\right)\right\Vert}^2+\frac{1}{m}{C}_1{\xi}_1^t{\xi}_1+{C}_1{\nu}_1{\varepsilon}_1^2 $$

subject to

$$ y-\left(K\left(A,{A}^t\right){w}_1+e{b}_1\right)\ge -e{\varepsilon}_1-2\left(1-p\right){\xi}_1 $$

(44)

and

$$ \min \frac{C_4}{2}\left({\left\Vert {w}_2\right\Vert}^2+{b}_2^2\right)+\frac{1}{2}{\left\Vert y-\left(K\right(A,{A}^t\left){w}_2+e{b}_2\right)\right\Vert}^2+\frac{1}{m}{C}_2{\xi}_2^t{\xi}_2+{C}_2{\nu}_2{\varepsilon}_2^2 $$

subject to

$$ \left(K\left(A,{A}^t\right){w}_2+e{b}_2\right)-y\ge -e{\varepsilon}_2-2p{\xi}_2 $$

(45)

respectively, where C₁, C₂, C₃, C₄ > 0; and ν₁, ν₂ are input parameters.

Using the Lagrangian multipliers α₁, α₂ > 0 ∈ R^m, the Lagrangian functions of (44) and (45) are given by

$$ {\displaystyle \begin{array}{l}{L}_1=\frac{C_3}{2}\left({\left\Vert {w}_1\right\Vert}^2+{b}_1^2\right)+\frac{1}{2}{\left\Vert y-\left(K\right(A,{A}^t\left){w}_1+e{b}_1\right)\right\Vert}^2+\frac{1}{m}{C}_1{\xi}_1^t{\xi}_1+{C}_1{\nu}_1{\varepsilon}_1^2\\ {}-{\alpha}_1^t\left(y-\left(K\left(A,{A}^t\right){w}_1+e{b}_1\right)+e{\varepsilon}_1+2\left(1-p\right){\xi}_1\right)\end{array}} $$

(46)

and

$$ {\displaystyle \begin{array}{l}{L}_2=\frac{C_4}{2}\left({\left\Vert {w}_2\right\Vert}^2+{b}_2^2\right)+\frac{1}{2}{\left\Vert y-\left(K\right(A,{A}^t\left){w}_2+e{b}_2\right)\right\Vert}^2+\frac{1}{m}{C}_2{\xi}_2^t{\xi}_2+{C}_2{\nu}_2{\varepsilon}_2^2\\ {}-{\alpha}_2^t\left(\left(K\left(A,{A}^t\right){w}_2+e{b}_2\right)-y+e{\varepsilon}_2+2p{\xi}_2\right)\end{array}} $$

(47)

Further, apply the KKT conditions, the dual QPP of primal problems (46) & (47) are given as

$$ \min \frac{1}{2}{\alpha}_1^t\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^t+\frac{4m{\left(1-p\right)}^2}{C_1}+\frac{e{e}^t}{2{C}_1{\nu}_1}\right){\alpha}_1-{\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^ty-y\right)}^t{\alpha}_1 $$

(48)

and

$$ \min \frac{1}{2}{\alpha}_2^t\left(T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^t+\frac{4m{p}^2}{C_2}+\frac{e{e}^t}{2{C}_2{\nu}_2}\right){\alpha}_2-{\left(-T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^ty+y\right)}^t{\alpha}_2 $$

(49)

where $T=\left[K\left(A,{A}^t\right)\kern0.5em e\right]$ is an augmented matrix.

After computing the values of α₁ and α₂ from (48) and (49), the final estimation function f(.) is determined for non-linear kernel by taking the mean of the following non-linear functions f₁(x) and f₂(x) as

$$ {f}_1(x)=\left[K\left({x}^t,{A}^t\right)\kern0.5em 1\right]\left[\begin{array}{c}{w}_1\\ {}{b}_1\end{array}\right]=\left[\begin{array}{cc}K\left({x}^t,{A}^t\right)& 1\end{array}\right]\left({\left({T}^tT+{C}_3I\right)}^{-1}{T}^t\left(y-{\alpha}_1\right)\right) $$

and

$$ {f}_2(x)=\left[K\left({x}^t,{A}^t\right)\kern0.5em 1\right]\left[\begin{array}{c}{w}_2\\ {}{b}_2\end{array}\right]=\left[\begin{array}{cc}K\left({x}^t,{A}^t\right)& 1\end{array}\right]\left({\left({T}^tT+{C}_4I\right)}^{-1}{T}^t\left(y+{\alpha}_2\right)\right) $$

One can rewrite the problems (48) and (49) in the following form:

$$ \underset{0\le {\alpha}_1\in {R}^m}{\min }{L}_1\left({\alpha}_1\right)=\frac{1}{2}{\alpha}_1^t{D}_1{\alpha}_1-{r}_1^t{\alpha}_1 $$

(50)

and

$$ \underset{0\le {\alpha}_2\in {R}^m}{\min }{L}_2\left({\alpha}_2\right)=\frac{1}{2}{\alpha}_2^t{D}_2{\alpha}_2-{r}_2^t{\alpha}_2 $$

(51)

respectively, where

${D}_1=\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^t+\frac{4m{\left(1-p\right)}^2}{C_1}+\frac{e{e}^t}{2{C}_1{\nu}_1}\right)$, ${D}_2=\left(T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^t+\frac{4m{p}^2}{C_2}+\frac{e{e}^t}{2{C}_2{\nu}_2}\right)$, r₁ = T(T^tT + C₃I)⁻¹T^ty − y and r₂ =  − T(T^tT + C₄I)⁻¹T^ty + y.

The KKT optimality conditions [49] is applied on the QPPs (50) and (51) which lead to the following pair of classical complementary problems as

$$ 0\le \left({D}_1{\alpha}_1-{r}_1\right)\perp {\alpha}_1\ge 0 $$

(52)

and

$$ 0\le \left({D}_2{\alpha}_2-{r}_2\right)\perp {\alpha}_2\ge 0, $$

(53)

respectively. By using the identity 0 ≤ x ⊥ y ≥ 0 if and only if x = (x − ψy)₊ for any vectors x, y and parameter ψ > 0, the equivalent pair of problems [50] of (52) and (53) are rewritten in the following fixed point theorems: for any ψ₁, ψ₂ > 0, the relations

$$ \left({D}_1{\alpha}_1-{r}_1\right)={\left({D}_1{\alpha}_1-{\psi}_1{\alpha}_1-{r}_1\right)}_{+} $$

(54)

and

$$ \left({D}_2{\alpha}_2-{r}_2\right)={\left({D}_2{\alpha}_2-{\psi}_2{\alpha}_2-{r}_2\right)}_{+}. $$

(55)

To solve the above problems (50) and (51), one can propose the following simple iterative approach in the following form:

$$ {\alpha}_1^{i+1}={D}_1^{-1}\left({\left({D}_1{\alpha}_1^i-{\psi}_1{\alpha}_1^i-{r}_1\right)}_{+}+{r}_1\right) $$

(56)

and

$$ {\alpha}_2^{i+1}={D}_2^{-1}\left({\left({D}_2{\alpha}_2^i-{\psi}_2{\alpha}_2^i-{r}_2\right)}_{+}+{r}_2\right) $$

(57)

i.e.

$$ {\displaystyle \begin{array}{l}{\alpha}_1^{i+1}={\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^t+\frac{4m{\left(1-p\right)}^2}{C_1}+\frac{e{e}^t}{2{C}_1{\nu}_1}\right)}^{-1}\Big[\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^t+\frac{4m{\left(1-p\right)}^2}{C_1}+\frac{e{e}^t}{2{C}_1{\nu}_1}\right){\alpha}_1^i\\ {}-{\psi}_1{\alpha}_1^i-\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^ty-y\right)\left){}_{+}+T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^ty-y\right)\Big]\end{array}} $$

(58)

and

$$ {\displaystyle \begin{array}{l}{\alpha}_2^{i+1}={\left(T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^t+\frac{4m{p}^2}{C_2}+\frac{e{e}^t}{2{C}_2{\nu}_2}\right)}^{-1}\Big[\left(T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^t+\frac{4m{p}^2}{C_2}+\frac{e{e}^t}{2{C}_2{\nu}_2}\right){\alpha}_2^i\\ {}-{\psi}_2{\alpha}_2^i-\left(-T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^ty+y\right)\left){}_{+}+\left(-T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^ty+y\right)\right)\Big]\end{array}} $$

(59)

Remark 1

One may notice that we have to compute the inverse of the matrices $\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^t+\frac{4m{\left(1-p\right)}^2}{C_1}+\frac{e{e}^t}{2{C}_1{\nu}_1}\right)$ and $\left(T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^t+\frac{4m{p}^2}{C_2}+\frac{e{e}^t}{2{C}_2{\nu}_2}\right)$ in the above iterative schemes (58) and (59) to find the solution of our proposed LAsy-ν-TSVR. Unlike the Asy-ν-TSVR and TSVR, these matrices are positive definite which can be compute at the very beginning of the algorithm.

Remark 2

Unlike the TSVR and Asy-ν-TSVR, there is not any required additions of extra term δ I to make the matrix positive definite where δ is very small positive number and I is the identity matrix. Our proposed LAsy-ν-TSVR always gives unique global solution since $\left(T{\left({T}^tT+{C}_3I\right)}^{-1}{T}^t+\frac{4m{\left(1-p\right)}^2}{C_1}+\frac{e{e}^t}{2{C}_1{\nu}_1}\right)$ and $\left(T{\left({T}^tT+{C}_4I\right)}^{-1}{T}^t+\frac{4m{p}^2}{C_2}+\frac{e{e}^t}{2{C}_2{\nu}_2}\right)$ both are positive definite matrices.

Remark 3

For any arbitrary vectors ${\alpha}_1^0\in {R}^m$ and ${\alpha}_2^0\in {R}^m$, the iterate ${\alpha}_1^i\in {R}^m$ and ${\alpha}_2^i\in {R}^m$ of iterative schemes (58) and (59) converge to the unique solution ${\alpha}_1^{\ast}\in {R}^m$ and ${\alpha}_2^{\ast}\in {R}^m$ respectively and also satisfying the following conditions as

$$ \left\Vert {D}_1{\alpha}_1^{i+1}-{D}_1{\alpha}_1^{\ast}\right\Vert \le \left\Vert I-{\alpha}_1{D}_1^{-1}\right\Vert\;\left\Vert {D}_1{\alpha}_1^i-{D}_1{\alpha}_1^{\ast}\right\Vert $$

and

$$ \left\Vert {D}_2{\alpha}_2^{i+1}-{D}_2{\alpha}_2^{\ast}\right\Vert \le \left\Vert I-{\alpha}_2{D}_2^{-1}\right\Vert\;\left\Vert {D}_2{\alpha}_2^i-{D}_2{\alpha}_2^{\ast}\right\Vert . $$

One can follow the proof of convergence of above from [50].

4 Numerical experiments

To measure the effectiveness of the proposed LAsy-ν-TSVR, several numerical experiments have been performed on standard benchmark real-world datasets for SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR. To conduct these numerical experiments, MATLAB software version2008b is used. In the formulations of SVR, TSVR, HN-TSVR, Asy-ν-TSVR, the QPPs are solved by using the external MOSEK optimization toolbox [51]. The number of interesting datasets are used in these numerical experiments such as Pollution, Space Ga [52]; Kin900, Demo [53]; the inverse dynamics of a Flexible robot arm [54]; S&P500, IBM, RedHat, Google, Intel, Microsoft [55]; Concrete CS, Boston, Auto-MPG, Parkinson, Gas furnace, Winequality from ([56]), Mg₁₇ from [57]. In this paper, we consider both linear and non-linear case where Gaussian kernel function is taken in case of non-linear as

$$ K\left({x}_i,{x}_j\right)=\exp \left(-\mu {\left\Vert {x}_i-{x}_j\right\Vert}^2\right),\mathrm{for}\;i,j=1,...,m $$

where, kernel parameter μ > 0.

Here, the user input parameter values are described in Table 1. Finally, root mean square error (RMSE) is calculated based on optimal values for measuring the prediction accuracy by using the following formula:

$$ RMSE=\sqrt{\frac{1}{N}\sum \limits_{i=1}^N{\left({y}_i-{\tilde{y}}_i\right)}^2}, $$

where, y_i are the observed values, ${\tilde{y}}_i$ are the predicted values respectively and N is the number of test data samples.

Table 1 Different user define parameters used in numerical experiment

4.1 Artificial datasets

In this subsection, we have performed numerical experiments on 8 artificial generated datasets which are mentioned in Table 2 with their function definitions. In order to check the applicability of proposed LAsy-ν-TSVR for outliers and noise, we added two types of noise level in artificial datasets i.e. symmetric noise and asymmetric noise structure. Function 1 to Function 6 are having symmetric noise to generate artificial datasets in which variability of noise is proceeded from symmetric distribution and Function 7 and Function 8 are using the asymmetric noise such as heteroscedastic noise structure to generate the artificial dataset i.e. the noise is directly dependent on the value of input samples. Further, we use uniform probability distribution Ω ∈ U (a, b) with interval (a, b) for uniform noise and normal distribution Ω ∈ N (μ, σ²) where μ and σ² are the mean and variance respectively for Gaussian noise. Here, artificial dataset is generated by using 200 training samples with the additive noise and 500 testing samples without any addition of noise. To test the efficacy of proposed LAsy-ν-TSVR along with reported algorithms in this paper, a comparative analysis of their corresponding prediction errors for all artificial datasets are presented in Table 3 using linear kernel and Table 5 using Gaussian kernel. One can conclude from Tables 3 and 5 that our proposed LAsy-ν-TSVR performs better or comparable generalization performance in comparison to other methods. Further, Tables 4 and 6 are consisted the average ranks of SVR, TSVR, HN-TSVR, Asy-ν-TSVR, RLTSVR and LAsy-ν-TSVR based on RMSE values for artificial datasets using linear and Gaussian kernel respectively. One can notice that proposed LAsy-ν-TSVR is having lowest rank among SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR in both linear and nonlinear case which shows the usability and effectiveness of proposed LAsy-ν-TSVR.

Table 2 Functions used for generating artificial datasets

Table 3 Performance comparison of LAsy-v-TSVR with SVR, TSVR, HN-TSVR, Asy-v-TSVR and RLTSVR on artificial datasets using linear kernel

Table 4 Average ranks of SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on RMSE values for artificial datasets using linear kernel

Table 5 Performance comparison of LAsy-v-TSVR with SVR, TSVR, HN-TSVR, Asy-v-TSVR and RLTSVR on artificial datasets using Gaussian kernel

Table 6 Average ranks of SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on RMSE values for artificial datasets using Gaussian kernel

Table 7 Performance comparison of LAsy-v-TSVR with SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR using linear kernel on real-world datasets

Table 8 Average ranks of SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on RMSE values for real-world datasets using linear kernel

Table 9 Performance comparison of LAsy-v-TSVR with SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR using Gaussian kernel on real-world datasets

Table 10 Average ranks of SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on RMSE values for real-world datasets using Gaussian kernel

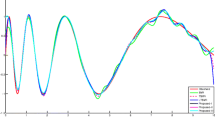
To check the performance for symmetric noise structure, the prediction values are plotted for SVR, TSVR, HN-TSVR, Asy-ν-TSVR, RLTSVR and LAsy-ν-TSVR using Gaussian kernel of Function 5 in Fig. 1 with uniform noise. Similarly, for Function 6 with Gaussian noise, we depict the prediction plots in Fig. 2 respectively. It is easily noticeable that our proposed LAsy-ν-TSVR is having better agreement with final target values in comparison to SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR for symmetric noise structure having both uniform and Gaussian noise.

Fig. 1

Accuracy plot over the test set by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR using Gaussian kernel for Function 5 with uniform noise

Fig. 2

Accuracy plot over the test set by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR using Gaussian kernel for Function 6 with Gaussian noise

Further, to test the applicability of proposed LAsy-ν-TSVR on datasets having asymmetric noise structure i.e. heteroscedastic noise, the prediction plots are drawn in Fig. 3 for Function 7 using uniform noise. Similarly, for Function 8, we depict the prediction plots in Fig. 4 having Gaussian noise. One can observe from these results that LAsy-ν-TSVR is more effective to handle the asymmetric noise structure for both uniform and Gaussian noise.

Fig. 3

Accuracy plot over the test set by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR using Gaussian kernel for Function 7 with uniform noise

Fig. 4

Accuracy plot over the test set by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR using Gaussian kernel for Function 8 with Gaussian noise

4.2 Real world datasets

In this paper, we have shown comparative analysis of our proposed LAsy-ν-TSVR with SVR, TSVR, HN-TSVR, Asy-ν-TSVR, RLTSVR using real world datasets for linear and non-linear case that are tabulated in Tables 7 and 9 respectively. One can notice that the prediction accuracy of proposed LAsy-ν-TSVR is better or equal in 8 out of 18 standard benchmark real world datasets for linear kernel and 11 out of 18 standard real world datasets for Gaussian kernel which justified the applicability and usability. In order to show the performance graphically, we plot prediction values for Auto-MPG, Gas furnace and Intel datasets in Figs. 5, 7 and 9 respectively. Similarity, prediction error of Auto-MPG, Gas furnace and Intel are shown in Figs. 6, 8 and 10 respectively. One can conclude from these results that the prediction values of our proposed LAsy-ν-TSVR is very close to target values in comparison to SVR, TSVR, HN-TSVR, Asy-ν-TSVR, RLTSVR which justify the existence and usability of our approach. Further, to justify the performance statistically of our proposed LAsy-ν-TSVR, the average ranks are depicted based on RMSE values in Tables 8 and 10 for all reported methods using both linear and nonlinear kernel respectively. It is clear form Tables 8 and 10 that proposed LAsy-ν-TSVR is having lowest rank among all in both cases.

Fig. 5

Prediction over the testing dataset by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on the Auto-MPG dataset. Gaussian kernel was used

Fig. 6

Prediction error over the testing dataset by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on the Auto-MPG dataset. Gaussian kernel was used

Fig. 7

Prediction over the testing dataset by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on the Gas furnace dataset. Gaussian kernel was used

Fig. 8

Prediction error over the testing dataset by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on the Gas furnace dataset. Gaussian kernel was used

Fig. 9

Prediction over the testing dataset by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on the Intel dataset. Gaussian kernel was used

Fig. 10

Prediction error over the testing dataset by SVR, TSVR, HN-TSVR, Asy-v-TSVR, RLTSVR and LAsy-v-TSVR on the Intel dataset. Gaussian kernel was used

Now, non-parametric Friedman test is conducted with the corresponding post hoc test [58] on 6 algorithms and 18 datasets in which it is used to detect differences in ranking of RMSE across multiple algorithms.

This test is mainly used for one-way repeated measures analysis of variance by ranks of different algorithms. Let us consider, all methods are equivalent under null hypothesis, the Friedman statistic is determined for linear cases from Table 8 as follows.

$$ {\displaystyle \begin{array}{l}{\chi}_F^2=\frac{12\times 18}{6\times 7}\left[\left(5{.055556}^2+3{.27778}^2+3{.83333}^2+3{.66667}^2+2{.63889}^2+2{.52778}^2\right)-\left(\frac{6\times {7}^2}{4}\right)\right]=22.0873\\ {}{F}_F=\frac{17\times 22.0873}{18\times 5-22.0873}=5.5289\end{array}} $$

According to Fisher–Snedecor F distribution, Friedman expression F_F is distributed with degree of freedom (6 − 1, (6 − 1) ∗ (18 − 1)) = (5, 85) degree of freedom. The critical value of F(5, 85) is 2.321 for α = 0.05. Since F_F > 2.321, we reject the null hypothesis i.e. all algorithms are not equivalent. Now, Nemenyi post hoc test is conducted for pair wise comparison of all methods. This test is applied after Friedman test if it rejects the null hypothesis, for comparison of pair wise performance. For this, we calculate the critical difference (CD) with q_α = 2.589 as

$$ \mathrm{CD}=2.589\sqrt{\frac{6\times 7}{6\times 18}}=1.6145\;\mathrm{for}\;\theta =\mathrm{0.10.} $$

where, the value of q_α is decided on the basis of number of concerned algorithms and the value of θ from Demsar,[58].

The difference of average rank between SVR and proposed LAsy-ν-TSVR (5.055556 − 2.527778 = 2.527778) which is greater than CD i.e. (1.6145). This result assures that the prediction performance of proposed algorithm LAsy-ν-TSVR is better than SVR. Further, the differences of average rank of proposed LAsy-ν-TSVR with TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR are not more than the CD, so there is not any significant differences among them.

Secondly, to apply Friedman test in non linear case for standard real world bench mark datasets on the average ranks of SVR, TSVR, HN-TSVR, Asy-ν-TSVR, RLTSVR and proposed LAsy-ν-TSVR from Table 10 as follows:

$$ {\displaystyle \begin{array}{l}{\chi}_F^2=\frac{12\times 18}{6\times 7}\left[\left(4{.88889}^2+4{.16667}^2+4{.19444}^2+3{.86111}^2+2{.33333}^2+1{.55556}^2\right)-\left(\frac{6\times {7}^2}{4}\right)\right]=41.8016\\ {}{F}_F=\frac{17\times 41.8016}{18\times 5-41.8016}=14.7438\end{array}} $$

The critical value of F(5, 85) is 2.321 forα = 0.05. Since F_F > 2.321, we reject the null hypothesis. Now, we perform the Nemenyi test to compare the methods pair-wise. Here, critical difference (CD) is 1.6145.

• i. The differences between the average rank of SVR and proposed LAsy-ν-TSVR (4.888889 − 1.555556 = 3.333333) is greater than CD ( 1.6145) thus proposed LAsy-ν-TSVR is better than SVR.

• ii. Further, check the dissimilarity between the proposed LAsy-ν-TSVR with TSVR, the difference between the average ranks i.e. (4.166667 − 1.555556 = 2.611111) is larger than( 1.6145), thus the prediction performance of proposed LAsy-ν-TSVR is much effective in comparison to TSVR.

• iii. The average rank difference between HN-TSVR and proposed LAsy-ν-TSVR is (4.194444 − 1.555556 = 2.638889) which is greater than ( 1.6145), it implies that LAsy-ν-TSVR is better than HN-TSVR.

• iv. Since the dissimilarity of average rank between Asy-ν-TSVR and proposed LAsy-ν-TSVR (3.861111 − 1.555556 = 2.305556) is larger than ( 1.6145) which validates the existence and applicability of proposed algorithm LAsy-ν-TSVR in comparison to Asy-ν-TSVR.

5 Conclusions and future work

In this paper, we propose a new approach as improved regularization based Lagrangian asymmetric ν-twin support vector regression (LAsy-ν-TSVR) using pinball loss function that follows the gist of statistical learning theory i.e. SRM principle effectively. The solution of LAsy-ν-TSVR is determined by solving the linearly convergent iterative approach unlike solving the QPPs as used in SVR, TSVR, HN-TSVR and Asy-ν-TSVR. Thus, no external optimization toolbox is required in our case. Another advantage of proposed LAsy-ν-TSVR is that proposed LAsy-ν-TSVR is more effective and usable to handle both symmetric and asymmetric structure having two types uniform and Gaussian noise in comparison to SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR. In order to justify numerically, proposed LAsy-ν-TSVR is tested and validated on various artificial generated datasets having symmetric and heteroscedastic structure of uniform and Gaussian noise. One can conclude that proposed LAsy-ν-TSVR is much more effective to handle the noise in comparison to SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR. On the basis of experimental results for real world datasets, it can be stated that proposed LAsy-ν-TSVR are far better than SVR, TSVR, HN-TSVR, Asy-ν-TSVR and RLTSVR in terms of generalization ability as well as the faster learning ability clearly illustrate its efficacy and applicability. In future, one can apply the heuristic approach to select the optimum parameters and another, a sparse model can be proposed based on asymmetric pinball loss function.