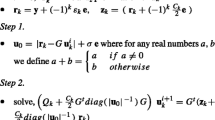1 Introduction

Support vector machines (SVMs) developed by Vapnik [24] are a class of kernel-based supervised learning machines for binary classification and regression. They have shown excellent performance on wide variety of problems [4, 9, 19] due to its method of constructing a hyperplane that partitions the inputs from different classes with maximum margin [6, 24]. Unlike other machine learning methods such as artificial neural networks (ANNs), training of SVMs leads to solving a linearly constrained quadratic programming problem (QPP) having unique optimal solution. Combined with the advantage of having unique optimal solution and better generalization performance, SVM becomes one of the most popular methods for solving classification and regression problems.

Although SVM provides better generalization results in comparison to other machine learning approaches, its training cost is expensive, that is O(m 3) where m is the size of the total training samples [8]. To reduce its time complexity, a family of non-parallel planes learning algorithms has been proposed in the literature [8, 10, 15]. In the sprit of the generalized eigenvalue proximal support vector machine (GEPSVM) proposed in [15], Jayadeva et al. [8] introduced twin support vector machine (TWSVM) wherein two non-parallel planes are constructed by solving two related SVM-type problems of smaller size than the standard SVM. For an improved version named twin bounded support vector machines (TBSVM) based on TWSVM, see [22].

Recently, Peng [20] proposed twin support vector regression (TSVR) similar in sprit to TWSVM wherein a pair of non-parallel functions corresponding to the ɛ-insensitive down- and up- bounds of the unknown regressor is determined. As in TWSVM, this formulation leads to the solution of a pair of dual QPPs of smaller size rather than a single large one as in the standard support vector regression (SVR). This strategy makes TSVR works faster than SVR with the added advantage of better generalization performance over SVR [20]. However, TSVR formulation requires, like TWSVM, the inverse of a positive semi-definite matrix. By reformulating TSVR to become a pair of strongly convex unconstrained minimization problems in primal and employing smooth technique, smooth twin support vector regression (STSVR) has been proposed in [5]. Finally, for the work on the formulation of TSVR as a pair of linear programming problems, we refer the reader to [25].

Motivated by the work of [1, 2, 13], we propose in this paper Lagrangian twin support vector regression (LTSVR) formulation whose solution will be obtained by applying a simple iterative algorithm that converges for any starting point given. In fact, the Karush–Kuhn–Tucker (KKT) necessary and sufficient optimal conditions for the pair of dual QPPs of TSVR are considered and solved using linearly convergent proposed iterative algorithm. Our formulation has the advantage that the ɛ-insensitive down- or up- bound regressor will be determined using an extremely simple iterative method rather than solving a QPP as in SVR and TSVR.

In this work, all vectors are taken as column vectors. The inner product of two vectors x, y in the n-dimensional real space R n will be denoted by: x t y, where x t is the transpose of x. Whenever x is orthogonal to y, we write \( x \bot y \). For \( x = (x_{1} ,\,\ldots ,x_{n} )^{t} \in R^{n} \), the plus function x + is defined as: (x +) i  = max{0, x i }, where i = 1,…, n. The 2-norm of a vector x and a matrix Q will be denoted by \( ||x|| \) and \( ||Q|| \), respectively. We denote the vector of ones of dimension m by e and the identity matrix of appropriate size by I.

The paper is organized as follows. In Sect. 2, the standard SVR and TSVR are reviewed. The proposed LTSVR algorithm for solving the dual QPPs is derived in Sect. 3. Numerical experiments have been performed on a number of interesting synthetic and real-world datasets, and the results obtained are compared with that of SVR and TSVR in Sect. 4 and finally, we conclude our work in Sect. 5.

2 Related work

In this section, we briefly describe the standard SVR and TSVR formulations.

Let a set of input samples \( \{ (x_{i} ,y_{i} )\}_{i = 1,2, \ldots ,m} \) be given where for each training example \( x_{i} \in R^{n} \) its corresponding observed value being \( y_{i} \in R \). Further, let the training examples be represented by a matrix \( A \in R^{m \times n} \) whose ith row is defined to be the row vector \( x_{i}^{t} \) and the vector of observed values be denoted by \( y = (y_{1} , \ldots ,y_{m} )^{t} \).

2.1 Support vector regression (SVR) formulation

In SVM for regression, the estimation function is obtained by mapping the input examples into a higher dimensional feature space via a non-linear mapping \( \varphi (.) \) and learning a linear regressor in the feature space. Assuming that the non-linear regression estimating function \( f:R^{n} \to R \) is taken to be of the form:

$$ f(x) = w^{t} \varphi (x) + b, $$

where w is a vector in the feature space and b is a scalar threshold, the ɛ -insensitive SVR formulation aims at determining w and b as the solution of the following constrained minimization problem [6, 24]:

$$ \mathop {\min }\limits_{{w,b,\xi_{1} ,\xi_{2} }} \frac{1}{2}w^{t} w + C(e^{t} \xi_{1} + e^{t} \xi_{2} ) $$

subject to

$$ \begin{gathered} y_{i} - w^{t} \varphi (x_{i} ) - b \le \varepsilon + \xi_{1i} , \hfill \\ w^{t} \varphi (x_{i} ) + b - y_{i} \le \varepsilon + \xi_{2i} \hfill \\ \end{gathered} $$

and

$$ \xi_{1i} ,\xi_{2i}^{{}} \ge 0\quad {\text{for}}\quad i = 1,2, \ldots ,m, $$

where \( \xi_{1} = (\xi_{11} , \ldots ,\xi_{1m} )^{t} \), \( \xi_{2} = (\xi_{21} , \ldots ,\xi_{2m} )^{t} \) are vectors of slack variables, and C > 0, ɛ > 0 are input parameters.

In practice, rather than solving the primal problem, we solve its dual problem, which can be written in the following form:

$$ \mathop {\min }\limits_{{u_{1} ,u_{2} }} \,\frac{1}{2}\sum\limits_{i,j = 1}^{m} {(u_{1i} - u_{2i} )(u_{1j} - u_{2j} )\varphi (x_{i} )^{t} \varphi (x_{j} ) + } \varepsilon \sum\limits_{i = 1}^{m} {(u_{1i} + u_{2i} ) - } \sum\limits_{i = 1}^{m} {y_{i} (u_{1i} - u_{2i} )} $$

subject to

$$ \sum\limits_{i = 1}^{m} {(u_{1i} - u_{2i} ) = 0} \quad {\text{and}}\quad 0 \le u_{1} ,u_{2} \le Ce, $$

where \( u_{1} = (u_{11} , \ldots ,u_{1m} )^{t} \) and \( u_{2} = (u_{21} , \ldots ,u_{2m} )^{t} \) in R m are Lagrange multipliers.

Applying the kernel trick [6, 24], that is taking:

$$ k(x_{i} ,x_{j} ) = \varphi (x_{i} )^{t} \varphi (x_{j} ), $$

where \( k(.,.) \) is a kernel function, the above dual problem can be rewritten and solved. In this case, the decision function \( f(.) \) will become [6, 24]: for any input example \( x \in R^{n} \), its prediction is given by

$$ f(x) = \sum\limits_{i = 1}^{m} {(u_{1i} - u_{2i} )k(x,x_{i} ) + b} . $$

2.2 Twin support vector regression (TSVR) formulation

Motivated by the work of TWSVM [8], a new regressor called twin support vector regression (TSVR) was proposed in [20] wherein two non-parallel functions are determined as estimators for the ɛ-insensitive down- and up-bounds of the unknown regression function. However, as opposed to solving a single QPP with 2m number of constraints where m is the number of input examples, TSVR formulation leads to solving a pair of QPPs each having m number of linear constraints.

Assume that the down- and up-bound regressors of TSVR in the input space are expressed as: for any \( x \in R^{n} , \)

$$ f_{1} (x) = w_{1}^{t} x + b_{1} \quad {\text{and}}\quad f_{2} (x) = w_{2}^{t} x + b_{2} $$
(1)

respectively, where \( w_{1} ,w_{2} \in R^{n} \) and \( b_{1} ,b_{2} \in R \) are unknowns. The linear TSVR formulation leads to determining the regressors (1) as the solutions of the following pair of QPPs defined by [20]:

$$ \mathop {\min }\limits_{{(w_{1} ,b_{1} ,\xi_{1} ) \in R^{n + 1 + m} }} \,\frac{1}{2}||y - \varepsilon_{1} e - (Aw_{1} + b_{1} e)||^{2} + C_{1} e^{t} \xi_{1} $$

subject to

$$ y - (Aw_{1} + b_{1} e) \ge \varepsilon_{1} e - \xi_{1} ,\,\xi_{1} \ge 0 $$
(2)

and

$$ \mathop {\min }\limits_{{(w_{2} ,b_{2} ,\xi_{2} ) \in R^{n + 1 + m} }} \,\frac{1}{2}||y + \varepsilon_{2} e - (Aw_{2} + b_{2} e)||^{2} + C_{2} e^{t} \xi_{2} $$

subject to

$$ (Aw_{2} + b_{2} e) - y \ge \varepsilon_{2} e - \xi_{2} ,\,\xi_{2} \ge 0 $$
(3)

respectively, where C 1, C 2 > 0; ɛ 1, ɛ 2 > 0 are input parameters and \( \xi_{1} ,\xi_{2} \) are vectors of slack variables in R m. Now using the down- and up-bound regressors, the end regression function f: R n → R is taken as

$$ f(x) = \frac{1}{2}(f_{1} (x) + f_{2} (x))\quad {\text{for}}\,{\text{all}}\quad x \in R^{n} . $$
(4)

By considering the Lagrangian functions for the problems (2), (3) and using the KKT necessary and sufficient optimal conditions, one can obtain the pair of dual QPPs of TSVR as given below [20]:

$$ \mathop {\min }\limits_{{u_{1} \in R^{m} }} \,\frac{1}{2}u_{1}^{t} G(G^{t} G)^{ - 1} G^{t} u_{1} - (y - \varepsilon_{1} e)^{t} (G(G^{t} G)^{ - 1} G^{t} - I)u_{1} $$

subject to

$$ 0 \le u_{1} \le C_{1} e $$
(5)

and

$$ \mathop {\min }\limits_{{u_{2} \in R^{m} }} \,\frac{1}{2}u_{2}^{t} G(G^{t} G)^{ - 1} G^{t} u_{2} - (y + \varepsilon_{2} e)^{t} (I - G(G^{t} G)^{ - 1} G^{t} )u_{2} $$

subject to

$$ 0 \le u_{2} \le C_{2} e $$
(6)

respectively, satisfying

$$ \left[ {\begin{array}{*{20}c} {w_{1} } \\ {b_{1} } \\ \end{array} } \right] = (G^{t} G)^{ - 1} G^{t} (y - \varepsilon_{1} e - u_{1} )\quad {\text{and}}\quad \left[ {\begin{array}{*{20}c} {w_{2} } \\ {b_{2} } \\ \end{array} } \right] = (G^{t} G)^{ - 1} G^{t} (y + \varepsilon_{2} e + u_{2} ), $$
(7)

where u 1, u 2 are Lagrange multipliers and \( G = \left[ {\begin{array}{*{20}c} A & e \\ \end{array} } \right] \) is an augmented matrix.

Following the approach of [13], the TSVR discussed above can be easily extended to kernel TSVR. In fact, for the input matrix \( A \in R^{m \times n} \) define the kernel matrix K = K(A, A t) of order m whose (i, j)th element is given by

$$ K(A,A^{t} )_{ij} = k(x_{i} ,x_{j} ) \in R, $$

where \( k(.,.) \) is a non-linear kernel function. Also for a given vector \( x_{{}} \in R^{n} \), we define

$$ K(x^{t} ,A^{t} ) = (k(x,x_{1} ), \ldots ,k(x,x_{m} )), $$

a row vector in R m. Then, assuming that the down- and up- bound regressors are of the form: for any vector x \(\in\)  R n,

$$ f_{ 1} \left( x \right) = K\left( {x^{t} , A^{t} } \right)w_{ 1} + b_{ 1} \quad {\text{and}}\quad f_{2} (x) = K(x^{t} ,A^{t} )w_{2} + b_{2} $$
(8)

respectively, the non-linear TSVR determines the unknowns \( w_{1} ,w_{2} \in R^{m} \) and \( b_{1} ,b_{2} \in R \) as the solutions of the following pair of minimization problems:

$$ \mathop {\min }\limits_{{(w_{1} ,b_{1} ,\xi_{1} ) \in R^{m + 1 + m} }} \,\frac{1}{2}||y - \varepsilon_{1} e - (K(A,A^{t} )w_{1} + b_{1} e)||^{2} + C_{1} e_{{}}^{t} \xi_{1} $$

subject to

$$ y - (K(A,A^{t} )w_{1} + b_{1} e) \ge \varepsilon_{1} e - \xi_{1} ,\quad \xi_{1} \ge 0 $$

and

$$ \mathop {\min }\limits_{{(w_{2} ,b_{2} ,\xi_{2} ) \in R^{m + 1 + m} }} \frac{1}{2}||y + \varepsilon_{2} e - (K(A,A^{t} )w_{2} + b_{2} e)||^{2} + C_{2} e^{t} \xi_{2} $$

subject to

$$ (K(A,A^{t} )w_{2} + b_{2} e) - y \ge \varepsilon_{2} e - \xi_{2} ,\quad \xi_{2} \ge 0. $$

Now proceeding as in the linear case, the pair of dual QPPs for the kernel TSVR can be obtained. In fact, they are found to be exactly of the same form as (5), (6) satisfying (7) where \( u_{1} ,u_{2} \in R^{m} \) are Lagrange multipliers, but the augmented matrix G is defined by: \( G = \left[ {\begin{array}{*{20}c} {K\left( {A,A^{t} } \right)} & e \\ \end{array} } \right] \). Finally, the end regressor given by (4) is obtained using (7) and (8).

For a detailed discussion on the problem formulation of TSVR and its method of solution, see [20].

3 Lagrangian twin support vector regression (LTSVR)

Since the matrix G t G appearing in the dual object functions of (5), (6) is positive semi-definite, it is possible that its inverse may not exist. Assuming that it is invertible, the objective functions of (5), (6) become merely convex, and therefore, more than one optimal solution to the minimization problems may exist. To make the objective functions become strongly convex, following the approach of Mangasarian et al. [13], we consider the square of the 2-norm of the vector of slack variables instead of the usual 1-norm and propose in this section Lagrangian twin support vector regression (LTSVR) formulation whose solution will be obtained by an extremely simple iterative algorithm. The computational results, given in Sect. 4, clearly show that our proposed 2-norm formulation does not compromise on generalization performance.

The linear TSVR in 2-norm determines the down- and up- bound regressors \( f_{1} (.) \) and \( f_{2} (.) \) of the form (1) as the solutions of the pair of QPPs:

$$ \mathop {\min }\limits_{{(w_{1} ,b_{1} ,\xi_{1} ) \in R^{n + 1 + m} }} \,\frac{1}{2}||y - \varepsilon_{1} e - (Aw_{1} + b_{1} e)||^{2} + \frac{{C_{1} }}{2}\xi_{1}^{t} \xi_{1} $$

subject to

$$ y - (Aw_{1} + b_{1} e) \ge \varepsilon_{1} e - \xi_{1}^{{}} $$
(9)

and

$$ \mathop {\min }\limits_{{(w_{2} ,b_{2} ,\xi_{2} ) \in R^{n + 1 + m} }} \,\frac{1}{2}||y + \varepsilon_{2} e - (Aw_{2} + b_{2} e)||^{2} + \frac{{C_{2} }}{2}\xi_{2}^{t} \xi_{2} $$

subject to

$$ (Aw_{2} + b_{2} e) - y \ge \varepsilon_{2} e - \xi_{2}^{{}} $$
(10)

respectively, where C 1, C 2 > 0; ɛ 1, ɛ 2 > 0 are input parameters and ξ 1, ξ 2 are vectors of slack variables. Note that the non-negativity constraints of the slack variables are dropped in this formulation since they will be satisfied automatically at optimality.

By considering the Lagrangian functions corresponding to (9) and (10) and using the condition that their partial derivatives with respect to the primal variables will be zero at optimality, the dual QPPs of (9) and (10) can be obtained as a pair of minimization problems of the following form:

$$ \begin{gathered} \mathop {\min }\limits_{{0 \le u_{1} \in R^{m} }} \frac{1}{2}(y - \varepsilon_{1} e)^{t} G(G^{t} G)^{ - 1} G^{t} (y - \varepsilon_{1} e) - \frac{1}{2}||y - \varepsilon_{1} e||^{2} \hfill \\ \quad + \frac{1}{2}u_{1}^{t} \left(\frac{I}{{C_{1} }} + G(G^{t} G)^{ - 1} G^{t} \right)u_{1} - (y - \varepsilon_{1} e)^{t} (G(G^{t} G)^{ - 1} G^{t} - I)u_{1} \hfill \\ \end{gathered} $$
(11)

and

$$ \begin{gathered} \mathop {\min }\limits_{{0 \le u_{2} \in R^{m} }} \frac{1}{2}(y + \varepsilon_{2} e)^{t} G(G^{t} G)^{ - 1} G^{t} (y + \varepsilon_{2} e) - \frac{1}{2}||y + \varepsilon_{2} e||^{2} \hfill \\ \quad + \frac{1}{2}u_{2}^{t} \left(\frac{I}{{C_{2} }} + G(G^{t} G)^{ - 1} G^{t} \right)u_{2} - (y + \varepsilon_{2} e)^{t} (I - G(G^{t} G)^{ - 1} G^{t} )u_{2} , \hfill \\ \end{gathered} $$
(12)

respectively, where \( G = \left[ {\begin{array}{*{20}c} A & e \\ \end{array} } \right] \) is an augmented matrix and the Lagrange multipliers u 1, u 2 \(\in\) R m satisfy the conditions: \( u_{1} ,u_{2} \ge 0 \) and (7).

Define the matrix

$$ H = G(G^{t} G)^{ - 1} G^{t} . $$
(13)

Then, dropping the terms that are independent of the dual variables, the above minimization problems (11) and (12) can be rewritten in the following simpler form:

$$ \mathop {\min }\limits_{{0 \le u_{1} \in R^{m} }} L_{1} (u_{1} ) = \frac{1}{2}u_{1}^{t} Q_{1} u_{1} - r_{1}^{t} u_{1} \quad {\text{and}}\quad \mathop {\min }\limits_{{0 \le u_{2} \in R^{m} }} L_{2} (u_{2} ) = \frac{1}{2}u_{2}^{t} Q_{2} u_{2} - r_{2}^{t} u_{2} $$
(14)

respectively, where

$$ Q_{1} = \frac{I}{{C_{1} }} + H,\,Q_{2} = \frac{I}{{C_{2} }} + H,\,r_{1} = (H - I)(y - \varepsilon_{1} e)\quad {\text{and}}\quad r_{2} = (I - H)(y + \varepsilon_{2} e). $$
(15)

Finally, using the solutions of (14) and equations (1), (7), the end regressor (4) will be obtained.

In Sect. 2.2, we briefly described the kernel TSVR in 1-norm initially proposed in [20]. Now we discuss the TSVR for the non-linear case, but in 2-norm.

The non-linear TSVR in 2-norm determines the ɛ-insensitive down- and up-bound regressors in the feature space by solving the following pair of QPPs:

$$ \mathop {\min }\limits_{{(w_{1} ,b_{1} ,\xi_{1} ) \in R^{m + 1 + m} }} \,\frac{1}{2}\left\|y - \varepsilon_{1} e - (K(A,A^{t} )w_{1} + b_{1} e)\right\|^{2} + \frac{{C_{1} }}{2}\xi_{1}^{t} \xi_{1} $$

subject to

$$ y - (K(A,A^{t} )w_{1} + b_{1} e) \ge \varepsilon_{1} e - \xi_{1}^{{}} $$
(16)

and

$$ \mathop {\min }\limits_{{(w_{2} ,b_{2} ,\xi_{2} ) \in R^{m + 1 + m} }} \,\frac{1}{2}\left\|y + \varepsilon_{2} e - (K(A,A^{t} )w_{2} + b_{2} e)\right\|^{2} + \frac{{C_{2} }}{2}\xi_{2}^{t} \xi_{2} $$

subject to

$$ (K(A,A^{t} )w_{2} + b_{2} e) - y \ge \varepsilon_{2} e - \xi_{2} . $$
(17)

Proceeding as in the linear TSVR, the dual QPPs of (16) and (17) can be constructed as a pair of minimization problems of the form (14) where \( u_{1} ,u_{2} \in R^{m} \) are Lagrange multipliers and Q 1, Q 2, r 1, r 2 are determined using (13) and (15) in which the augmented matrix G is defined by: \( G = [ {\begin{array}{*{20}c} K( {A,A^{t} } ) & e \\ \end{array}} ] \). In this case, the kernel regression estimation f: R n → R will be determined using (4) and the down- and up- bound regressors (8), obtained to be: for any vector x \(\in\) R n,

$$ f_{1} (x) = [{\begin{array}{*{20}c} K(x^{t} ,A^{t} ) & 1 \\ \end{array} }](G^{t} G)^{ - 1} G^{t} (y - \varepsilon_{1} e - u_{1} ) $$

and

$$ f_{2} (x) = [{\begin{array}{*{20}c} K(x^{t} ,A^{t} ) & 1 \\ \end{array} }](G^{t} G)^{ - 1} G^{t} (y + \varepsilon_{2} e + u_{2} ). $$

When linear kernel is used, the above down- and up-bound functions will degenerate into linear functions (1) [20].

Now we discuss our iterative LTSVR algorithm for solving the dual QPPs given by (14).

The KKT necessary and sufficient optimal conditions for the pair of dual QPPs (14) will become determining solutions for the classical complementarity problems [12]:

$$ 0 \le u_{1} \bot (Q_{1} u_{1} - r_{1} ) \ge 0\quad {\text{and}}\quad 0 \le u_{2} \bot (Q_{2} u_{2} - r_{2} ) \ge 0, $$
(18)

respectively. However, the optimality conditions (18) are satisfied if and only if for any \( \alpha_{1} ,\alpha_{2} > 0 \), the relations

$$ (Q_{1} u_{1} - r_{1} ) = (Q_{1} u_{1} - \alpha_{1} u_{1} - r_{1} )_{ + } \quad {\text{and}}\quad (Q_{2} u_{2} - r_{2} ) = (Q_{2} u_{2} - \alpha_{2} u_{2} - r_{2} )_{ + } $$
(19)

respectively, must hold [13].

For solving the above pair of problems (19), it is proposed to apply the following simple iterative scheme that constitutes our LTSVR algorithm: i = 0, 1, 2…

$$ u_{1}^{i + 1} = Q_{1}^{ - 1} (r_{1} + (Q_{1} u_{1}^{i} - \alpha_{1} u_{1}^{i} - r_{1} )_{ + } )\quad {\text{and}}\quad u_{2}^{i + 1} = Q_{2}^{ - 1} (r_{2} + (Q_{2} u_{2}^{i} - \alpha_{2} u_{2}^{i} - r_{2} )_{ + } ) $$
(20)

whose global convergence will follow from the result of [13].

Theorem 1 [13]

Assume that the matrix \( (G^{t} G)^{ - 1} \) exists and let the conditions:

$$ 0 < \alpha_{1} < \frac{2}{{C_{1} }}\quad {\text{and}}\quad 0 < \alpha_{2} < \frac{2}{{C_{2} }} $$

be satisfied. Then,

  1. (i)

    The matrices \( Q_{1} ,Q_{2} \) defined by (15) are symmetric and positive-definite;

  2. (ii)

    Starting with any initial vector \( u_{k}^{0} \in R^{m} \) where k = 1, 2, the iterate \( u_{k}^{i} \in R^{m} \) of (20) will converge linearly to the unique solution \( \bar{u}_{k}^{{}} \in R^{m} \) satisfying the condition

    $$ ||Q_{k} u_{k}^{i + 1} - Q_{k} \bar{u}_{k} || \le ||I - \alpha_{k} Q_{k}^{ - 1} ||\,||Q_{k} u_{k}^{i} - Q_{k} \bar{u}_{k} ||. $$

From (20), we immediately notice that our LTSVR algorithm requires at its very beginning the inverse of the matrices Q 1 and Q 2. However, we will show in the next theorem that they need not be computed explicitly since they can be easily obtained once the matrix (G t G)−1 that appears in the original TSVR formulation is known.

Theorem 2

Assume that the matrix (G t G) −1 exists. Then,

  1. (i)

    H = H 2 will be satisfied;

  2. (ii)

    for k = 1, 2,

    $$ Q_{k}^{ - 1} = C_{k} \left( {I - \frac{{C_{k} }}{{1 + C_{k} }}H} \right), $$
    (21)

    where the matrices H and Q 1 , Q 2 are given by (13) and (15) respectively.

Proof

  1. (i)

    The result will follow from the definition of the matrix H.

  2. (ii)

    Using the result (i) and (15), we have: for k = 1, 2, 

    $$ \begin{gathered}Q_{k} C_{k} {\left({I-\frac{{C_{k} }}{{1 + C_{k}}}H}\right)} =C_{k} \left({\frac{I}{{C_{k} }} + H} \right)\left( {I -\frac{{C_{k} }}{{1 + C_{k} }}H} \right) \hfill \\\quad = I + C_{k}\left( {H - \frac{H}{{1 + C_{k}}} - \frac{{C_{k}}}{{1 + C{k}}}H^{2}}\right)= I + C_{k} \left( {H - \frac{H}{{1 + C_{k}}} - \frac{{C_{k}H}}{{1 + C_{k}}}} \right) = I.\hfill \\ \end{gathered}$$

Note that the matrix G t G is positive semi-definite, and therefore, it may not be invertible. However, if G t G is invertible then the dual objective functions of the minimization problems (14) are strongly convex and therefore will have unique solutions since Q 1 and Q 2 are positive-definite. In all our numerical experiments, by introducing a regularization term δI, the inverse of the matrix G t G is computed to be \( (\delta I + G^{t} G)^{ - 1} \) where δ is a very small positive number. Finally, we observe, by Theorem 2, that for the implementation of LTSVR algorithm only the inverse of G t G needs to be known.

4 Numerical experiments and comparison of results

In order to evaluate the efficiency of LTSVR, numerical experiments were performed on eight synthetic and several well-known, publicly available, real-world benchmark datasets, and their results were compared with SVR and TSVR. All the regression methods were implemented in MATLAB R2010a environment on a PC running on Windows XP OS with 2.27 GHz Intel(R) Xeon(R) processor having 3 GB of RAM. The standard SVR was solved by MOSEK optimization toolbox [23] for MATLAB. For TSVR, however, we used the optimization toolbox of MATLAB. In all the examples considered, the Gaussian kernel function with parameter σ > 0, defined by: for \( x_{1} ,x_{2} \in R^{m} \)

$$ k(x_{1} ,x_{2} ) = \exp \left( { - \frac{{||x_{1} - x_{2} ||^{2} }}{{2\sigma^{2} }}} \right), $$

is used. The 2-norm root mean square error (RMSE), given by the following formula:

$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {(y_{i} - \tilde{y}_{i} )^{2} } } , $$

is chosen to measure the accuracy of the results obtained, where y i and \( \tilde{y}_{i} \) are the observed and its corresponding predicted values, respectively, and N is the number of test samples.

Since more parameters need to be selected in both TSVR and LTSVR, this will lead to, however, a slower model selection speed in comparison to SVR, and therefore, in all experiments ɛ 1 = ɛ 2 = 0.01, C 1 = C 2 and \( \delta = 10^{ - 5} \) were assumed. For SVR, we set ɛ = 0.01. The optimal values of the parameters were determined by performing 10-fold cross-validation on the training dataset, where the regularization parameter values C 1 = C 2 = C and the kernel parameter value σ were allowed to vary from the sets {10−5, 10−4,…, 105} and {2−10, 2−9, …, 210}, respectively. Finally, choosing these optimal values, the RMSE on the test dataset was calculated.

4.1 Synthetic datasets

As the first example, we considered the function [11] defined as below:

$$ y = f(x) = \frac{4}{|x| + 2} + \cos (2x) + \sin (3x),\quad x \in [ - 10,10]. $$

Using the function definition, 200 examples for training and 1,000 examples for testing were chosen randomly from the interval [−10, 10]. The observed values were polluted by adding two different kinds of noises: uniform noises over the interval [−0.2, 0.2] and Gaussian noises with mean zero and standard deviation 0.2, that is we have taken:

$$ y = f(x) + \xi , $$

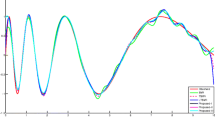
so that ξ is an additive noise. Test data were taken to be free of noises. The plots of the original function and its approximations using SVR, TSVR and LTSVR for uniform and Gaussian noises were shown in Fig. 1a, b, respectively along with the noisy training samples marked by the symbol ‘o’. The optimal values of the parameters were determined by the tuning procedure explained earlier. The 10-fold numerical results of non-linear SVR, TSVR and LTSVR were summarized in Table 2.

Fig. 1
figure 1

Results of approximation of \( \frac{4}{\left| x \right| + 2} + \cos (2x) + \sin (3x) \) with LTSVR, SVR and TSVR when different kinds of additive noises were used. Gaussian kernel was employed. a Uniform noises over the interval [−0.2, 0.2]. b Gaussian noises with mean zero and standard deviation 0.2

Full size image

We performed numerical experiments on another seven synthetic datasets generated by functions listed in Table 1. As in the previous case, 200 examples were generated for training whose observed values were polluted by uniform and Gaussian noises, and a test set consisting of 1,000 examples, free of noises, was considered. By performing 10-fold cross-validation, the numerical results obtained were summarized in Table 2.

Table 1 Functions used for generating synthetic datasets
Full size table
Table 2 Performance comparison of the proposed LTSVR with SVR and TSVR on synthetic datasets for Uniform and Gaussian additive noises
Full size table

4.2 Real-world benchmark datasets

In this sub-section, numerical tests and comparisons were carried out on real-world datasets.

We considered the Box and Jenkins gas furnace example [3] as the first real-world dataset. It consists of 296 input–output pairs of values of the form: \( (u(t),y(t)) \) where u(t) is input gas flow rate whose output y(t) is the CO 2 concentration from the gas furnace. We predict y(t) based on 10 attributes taken to be of the form: \( x(t) = (y(t - 1),y(t - 2),y(t - 3),y(t - 4),u(t - 1),u(t - 2),u(t - 3),u(t - 4),u(t - 5),u(t - 6)) \) [21]. Thus, we get 290 samples in total where each sample is of the form (x(t), y(t)). The first 100 samples for training and the rest for testing were assumed. The performances of SVR, TSVR and LTSVR on the training and test sets were shown in Fig. 2a, b, respectively.

Fig. 2
figure 2

Results of comparison for Gas furnace. Gaussian kernel was employed. a Prediction over the training set. b Prediction over the test set

Full size image

We performed numerical experiments non-linearly on several real-world datasets: Boston housing, Auto-Mpg, Machine CPU, Servo, Auto price, Wisconsin B.C, Concrete CS, Abalone, Kin-fh, Bodyfat, Google, IBM, Intel, Redhat, Microsoft, S&P500, Sunspots, SantaFeA and the data generated by Lorenz and Mackey–glass differential equations.

The Boston housing, Auto-Mpg, Machine CPU, Servo, Auto price, Wisconsin B.C and Concrete CS are popular regression benchmark dataset available at: http://archive.ics.uci.edu/ml/datasets. The details on the number of training and test samples considered for our experiment along with the number of attributes are listed in Table 3.

Table 3 Performance comparison of the proposed LTSVR with SVR and TSVR on real-world datasets
Full size table

We conducted our experiment on Abalone dataset [18] using 1,000 samples for training and the remaining 3,177 samples for testing. The predicted value is the age of an abalone using 8 physical measurements as their features. The Kin-fh dataset [7] represents a realistic simulation of the forward dynamics of eight links all revolute robot arm. The observed value is the prediction of the end-effector from a target with 32 features. The first 1,000 samples were taken for training and the remaining 7,192 samples for testing.

In all the previous real-world examples considered, each attribute of the original data is normalized as follows:

$$ \bar{x}_{ij} = \frac{{x_{ij} - x_{j}^{\min } }}{{x_{j}^{\max } - x_{j}^{\min } }} $$

where x ij is the (i, j)th element of the input matrix \( A \), \( \bar{x}_{ij} \) is its corresponding normalized value and \( x_{j}^{\min } = \min_{i = 1}^{m} (x_{ij} ) \) and \( x_{j}^{\max } = \max_{i = 1}^{m} (x_{ij} ) \) denote the minimum and maximum values, respectively, of the jth column of A. However, in the following examples, the original data are normalized with mean zero and standard deviation equals to 1.

Bodyfat is another benchmark dataset and is taken from the Statlib collection: http://lib.stat.cmu.edu/datasets, where the observed value being the estimation of the body fat from the body density values. It consists of 252 samples with 14 attributes. The first 150 samples were taken for training and the rest for testing.

In the following time series examples considered, five previous values are used to predict the current value.

Google, IBM, Intel, Red Hat, Microsoft and Standard & Poor 500 (S&P500) are financial datasets of stock index taken from the Yahoo website: http://finance.yahoo.com. For our experimental study, we considered 755 closing prices starting from 01–01–2006 to 31–12–2008, and using them, we get 750 samples. For each of the above financial time series examples considered, the first 200 samples were taken for training and the rest 550 for testing.

The sunspots dataset is well-known and is commonly used to compare regression algorithms. It is taken from http://www.bme.ogi.edu/~ericwan/data.html. We considered the annual readings of sunspots from the year 1700 to 1994. With five previous values being used to predict its current value, we get 290 samples in total and from which the first 100 samples were taken for training and the rest for testing. SantaFe-A is a laser time series dataset recorded from a Far-Intrared-Laser in a chaotic state. It consists of 1,000 numbers of time series values, and therefore, we get 995 samples in total. The first 200 samples were considered for training and the rest for testing. This dataset is available at: http://www-psych.stanford.edu/~andreas/Time-Series/SantaFe.html.

Taking the values of the parameters as: ρ = 10, r = 28 and b = 8/3, two datasets ,Lorenz0.05 and Lorenz0.20, corresponding to the sampling rates τ = 0.05 and τ = 0.20, respectively, were generated using the time series values associated to the variable x of the Lorenz differential equation [16, 17]:

$$ \dot{x} = \rho (y - x),\dot{y} = rx - y - xz\quad {\text{and}}\quad \dot{z} = xy - bz, $$

obtained by fourth-order Runge–Kutta method. They consist of 30,000 number of time series values. The first 1,000 values were discarded to avoid the initial transients. The next 3,000 values were taken for our experiment. Among them, the first 500 samples were taken for training and the remaining 2,495 samples for testing.

Finally, for comparing the performance of LTSVR with SVR and TSVR, two time series generated by the Mackey–Glass time delay differential equation [16, 17], given by:

$$ \frac{dx(t)}{dt} = - 0.1x(t) + \frac{0.2x(t - \tau )}{{1 + x(t - \tau )^{10} }}, $$

with respect to the parameters τ = 17, 30, were considered. Let us denote these two time series by MG 17 and MG 30. They are available at: http://www.cse.ogi.edu/~ericwan. Among the total of 1,495 samples obtained, the first 500 were considered for training and the rest for testing.

The 10-fold numerical results obtained by SVR, TSVR and LTSVR on each dataset along with the number of training and test samples taken, the number of attributes, the optimal values of the parameters determined and the training time were summarized in Table 3. Similar or better generalization performance of the proposed method in less execution time for training clearly demonstrates that the proposed algorithm is a powerful method of solution for regression problems.

5 Conclusions

A new iterative Lagrangian support vector machine algorithm for the twin SVR in its dual is proposed. Our formulation leads to minimization problems having their objective functions strongly convex with non-negativity constraints only. Though at the outset, the algorithm requires inverse of matrices, it was shown that they could be obtained by performing a simple matrix subtraction of the identity matrix with a scalar multiple of the inverse of a positive semi-definite matrix that arises in the original twin SVR formulation. Our formulation has the advantage that the unknown regressor is obtained using an extremely simple linearly convergent iterative algorithm rather than solving QPPs as in SVR and twin SVR. Also the proposed algorithm does not need any specialized optimization software. Similar or better generalization performance of the proposed method on synthetic and real-world datasets in less computational time than the standard and twin SVR methods clearly illustrates its effectiveness and suitability. Future work will include the study of implicit Lagrangian formulation [14] for the dual twin SVR problem and its applications.