1 Introduction

Carbon nanotubes (CNTs), discovered by Iijima (1991), have exhibited outstanding application prospects in nanodevice, nanoelectronics, and nanocomposite due to their remarkable physical, mechanical, electrical, thermal, and optical properties (Mattia and Gogotsi 2008). It is essential to understand the physical and mechanical behaviors of CNTs for better guiding its applications in engineering. However, the small size effect of CNTs brings two challenges to the research.

One problem is that the traditional theories and methods will lose effectiveness. Although the molecular dynamic (MD) simulation is widely accepted as an effective method to reflect the size-dependent mechanical behaviors of CNTs, this method is limited to structures with a small number of atoms, and it is also time consuming. In this case, an efficient continuum theory is needed to account for the size-dependent effect of CNTs. Unfortunately, the classical continuum theory is no longer applicable to capture the small-scale effects of CNTs due to the lack of size-scale parameter (Ansari et al. 2015; Li et al. 2016). Recently, the nonlocal continuum theory, which assumes that the stress tensor at any point is dependent on the whole strain field of the continuum, is widely used to characterize the small-scale effects of CNTs. This theory was firstly proposed by Eringen (1972) and was successfully used in solving the vibration (De Rosa and Lippiello 2017; Deng and Yang 2014; Ebrahimi and Nasirzadeh 2015; Hu et al. 2012; Kiani 2013a, b; Xia and Wang 2010; Zhen et al. 2011), wave propagation (Aydogdu 2014; Huang et al. 2013; Narendar and Gopalakrishnan 2010; Narendar et al. 2012; Wang et al. 2006, 2013, 2015), and buckling (Adali 2008; Amara et al. 2010; Khademolhosseini et al. 2010; Robinson and Adali 2016; Setoodeh et al. 2011) problems of CNTs. Several different nonlocal continuum theories, such as the nonlocal Euler–Bernoulli beam (Setoodeh et al. 2011; Wang et al. 2015; Zhen et al. 2011), nonlocal Timoshenko beam (De Rosa and Lippiello 2017; Narendar and Gopalakrishnan 2010; Xia and Wang 2010), and nonlocal shell (Khademolhosseini et al. 2010) theory, were adopted to study the mechanical behaviors of CNTs, in particular, because the CNT comprises a sheet of carbon atoms, which makes it perfect a candidate for nanocontainers to store gases and for nanotubes to convey fluids (Ansari et al. 2016; Bahaadini and Hosseini 2016; Li et al. 2016; SafarPour and Ghadiri 2017). Several different types of fluids such as water (Hanasaki and Nakatani 2006; Mattia and Calabrò 2012; Zhang et al. 2010), methane, ethane, and ethylene molecules (Mao and Sinnott 2000) and light gases (Skoulidas et al. 2002) were reported by many researchers. In this case, the effects of the conveying fluids on mechanical behaviors of CNTs have aroused worldwide academic interests (Mattia and Gogotsi 2008). For instance, Narendar and Gopalakrishnan (2010) proposed a nonlocal Timoshenko beam model to investigate the terahertz wave propagation behavior in fluid-conveying single-walled CNTs. Based on nonlocal Euler–Bernoulli beam theory, Bahaadini and Hosseini (2016) analyzed the divergence and flutter instability of fluid-conveying CNTs under combined effect of elastic foundation and magnetic field. Kiani (2013b) studied the vibration behavior of CNTs subjected to an inside viscous fluid flow by using Eringen’s nonlocal elasticity theory. Other similar analyses also can be found in Refs. (Abbasnejad et al. 2015; Amiri et al. 2016; Chang 2013a, b; Deng and Yang 2014; Wang et al. 2013; Xia and Wang 2010).

The other problem induced by the small size effect is that the uncertainties during the nanoscale system will become much more serious. The model inaccuracies, physical imperfections, material defects, and system complexities are unavoidable, and they both would introduce system uncertainties. Many experimental results have indicated that the Young’s modulus of CNTs has a wide range and shows a great of uncertainties. For instance, Salvetat et al. (1999) used an atomic force microscope experiment to measure the flexural Young’s modulus and shear modulus of CNTs, and 50% of error was found in their test results. Krishnan et al. (1998) measured 27 CNTs and found that the Young’s modulus was in a wide range of 1.3–0.4/+0.6 TPa. Tu and Ou-Yang (2002) summarized several different results presented by different authors and a large varying range of 0.5–5.5 TPa of Young’s modulus was found. Several other experiments, theoretical models and MD simulations, were also carried out to predict the elastic properties of CNTs, and similar phenomena were also reported (Cagliero et al. 2015; Liew et al. 2004; Meo and Rossi 2006; Treacy et al. 1996; Bao et al. 2004; Wong et al. 1997).

Following the available references, it can be easily found that the material properties of CNTs are affected by many factors, and it cannot be set as certain values. Under many circumstances, they should be considered as uncertain parameters with a range. To the authors’ knowledge, the material parameters are sometimes treated as random variables in a few studies. For example, Scarpa and Adhikari (2008) established a stochastic reduced order model to analyze the natural frequencies of CNT terahertz oscillators. In their work, both the thickness and the mass density were defined as random variables, and the predictions calculated by the analytical models were also validated by comparing with FE models. Chang (2013a, b) proposed a stochastic finite element (FE) method to study the nonlinear vibration of the fluid-conveying double-walled CNTs. In his studies, the Young’s modulus of the CNTs was characterized as random parameters. In fact, the influence of uncertain system parameters on the mechanical behaviors of fluid-conveying pipes has aroused widely concern in recent years. For instance, Ritto et al.(2014) studied the stochastic stability and reliability behaviors of the fluid-conveying pipe system by using a probabilistic model with consideration of the modeling errors. Gan et al.(2014) presented a random uncertainty modeling procedure to study the vibration characteristics of a straight pipe conveying fluid. Alizadeh et al.(2016) discussed the vibration and stability of fluid-conveying pipes by considering the structural and fluid parameters as random variables.

Probabilistic model can be used to describe the uncertain parameters. However, a large number of information should be offered to build a precise probability distribution function (PDF) for the uncertain parameters in the probabilistic model (Lv and Qiu 2016). Unfortunately, due to the small size effect, it is often too difficult to collect enough information about the uncertainty of nanostructures. To overcome the weaknesses of the probabilistic model, an interval analysis method is proposed in the present paper. In the interval model, the uncertain parameters can be defined as interval variables with deterministic bounds (Impollonia and Muscolino 2011). Because only the upper and lower bounds of the uncertain parameter are needed, the interval model can be effectively used to represent the uncertain parameters where the sample points are limited. As a matter of fact, the uncertain-but-bounded parameters are widely used in many engineering problems such as vibration, bulking, and static and dynamic characteristics of engineering structures (Impollonia and Muscolino 2011; Koyluoglu and Elishakoff 1998; Neumaier 1990; Rao and Berke 1997; Sofi and Muscolino 2015; Sofi et al. 2015a, b). However, an interval analysis model incorporating the small-scale and uncertain-but-bounded parameters of CNTs has not been reported yet.

The wave dispersion behavior of CNTs has gained extensive attention from scientific communities because many crucial physical characteristics such as optical transition and electrical conductance and many dynamic behaviors of CNTs are directly related to the presence of waves. As far as the authors’ awareness, many works have been reported on deterministic analysis of wave propagation characteristics of fluid-conveying CNTs, such as (Dong et al. 2007, 2008; Li and Hu 2016; Narendar and Gopalakrishnan 2010; Wang et al. 2013). However, no previous work is available in the literature to accomplish the wave propagation analysis of fluid-conveying CNTs with uncertain-but-bounded material and fluid properties. The main objective of this paper is to set up a theoretical model to investigate the influence of the uncertain-but-bounded parameters on wave propagation characteristics of fluid-conveying CNTs.

The paper is organized as follows. In the next section, a theoretical model is presented to characterize the wave propagation behavior of CNTs, and the small-scale effect is also taken into account by using the nonlocal elasticity theory. Besides, an iterative algorithm-based interval analysis method is proposed to account for the uncertain-but-bounded properties of the material and fluid. In Sect. 3, the presented interval analysis method is validated by comparing with the Monte Carlo simulation and the probabilistic model. In Sect. 4, the influence of the uncertain-but-bounded parameters of the material and fluid on wave dispersion behaviors of fluid-conveying CNTs is investigated in detail. Finally, conclusions are drawn in Sect. 5.

2 Problem formulation

2.1 Nonlocal continuum theory

Nonlocal continuum theory has been widely applied to CNTs because it can reflect the small-scale effect of CNTs. This theory assumes that the stress tensor at a reference points x is related to the whole strain field of the object under study. The nonlocal elasticity constitutive relation can be expressed in the differential form as (Eringen 1972)

$$\left( {1 - (e_{0} a)^{2} \nabla^{2} } \right){\varvec{\upsigma}}{\mathbf{(x)}} = {\mathbf{T(x)}},\quad {\mathbf{T(x) = C(x):}}{\varvec{\upvarepsilon}}{\mathbf{(x)}},$$
(1)

where \({\varvec{\upsigma}}{\mathbf{(x)}}\) and \({\mathbf{T(x)}}\) denote the nonlocal and local stress tensor components, respectively, and C(x) represents the fourth-order elasticity tensor, the symbol “:” denotes the “double-dot product,” \({\varvec{\upvarepsilon}}{\mathbf{(x)}}\) denotes the strain tensor component, e 0 a denotes the small-scale coefficient, and \(\nabla^{2}\) is the Laplacian operator. Note that the classical (local) elasticity theory can be recovered from e 0 a = 0.

In the special case of Euler–Bernoulli beams, Eq. (1) reduces to

$$\sigma_{xx} - \left( {e_{0} a} \right)^{2} \frac{{{\text{d}}^{2} \sigma_{xx} }}{{{\text{d}}x^{2} }} = E\varepsilon_{xx}$$
(2)

where E represents Young’s modulus of CNTs, σ xx and ε xx are axial stress and strain of CNTs, respectively.

2.2 Governing equations

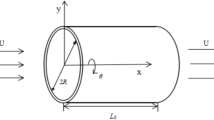
To understand the wave propagation in fluid-conveying CNTs, a CNT with Young’s modulus E, mass density ρ c , outer radius R o , inner radius R i , and cross-sectional area A is considered. The conveying fluid is modeled as a steady flow of mass density ρ f , and flowing with an axial uniform velocity V f , as depicted in Fig. 1. Based on Euler–Bernoulli beam theory, the deformation fields of CNTs are denoted as

$$u(x,t) = - z\frac{\partial w}{\partial x}$$
(3)
$$w(x,t) = w(x,t).$$
(4)
Fig. 1
figure 1

Schematic of flexural wave propagation in a fluid-conveying CNT

Full size image

According to the small deformation assumption, the only nonzero strain of the CNT is

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }}.$$
(5)

The Euler–Bernoulli beam theory with considering the rotary inertia and nonlocal effects of the CNT is used to derive the governing equation of fluid-conveying CNTs, which have been presented by Li and Hu (2016). Neglecting the fluid viscosity and strain gradient effects in their study or based on the Hamilton’s principle derived in “Appendix”, the differential equation of motion of the fluid-conveying CNTs can be given by

$$\left( {1 - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\left[ {\rho_{c} A\frac{{\partial^{2} w}}{{\partial t^{2} }} - \rho_{c} I\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} +\,m_{f} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2V_{f} \frac{{\partial^{2} w}}{\partial x\partial t} + V_{f}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right] + EI\frac{{\partial^{4} w}}{{\partial x^{4} }} = 0.$$
(6)

where m f and I are, respectively, the mass per unit length of the fluid and the moment of inertia of the CNT, which can be determined by

$$m_{f} = \rho_{f} A_{i} ,\quad I = \int_{A} {z^{2} } {\text{d}}A,$$
(7)

where \(A_{i} = \pi R_{i}^{2}\) denotes the inner internal cross-sectional area of the CNT.

In the wave propagation analysis, the transverse displacement of the fluid-conveying CNT is supposed to have the form as follows:

$$w = W\exp \left[ { - j(kx - \omega t)} \right]$$
(8)

where W is the wave amplitude, k and ω are the wave number and the circular frequency, respectively, and \(j = \sqrt { - 1}\). Substituting Eqs. (8) into (6) leads to

$$\left( {1 + \left( {e_{0} a} \right)^{2} k^{2} } \right)\left[ { - \rho_{c} A\omega^{2} - \rho_{c} I\omega^{2} k^{2} - m_{f} \left( {\omega^{2} - 2V_{f} \omega k + V_{f}^{2} k^{2} } \right)} \right] + EIk^{4} = 0.$$
(9)

Then, the frequency can be calculated by

$$\omega = \frac{{c_{2} + \sqrt {c_{2}^{2} + 4c_{1} c_{3} } }}{{2c_{1} }}$$
(10)

where the parameters c 1, c 2, and c 3 are, respectively, given as

$$c_{1} = \left[ {1 + \left( {e_{0} a} \right)^{2} k^{2} } \right]\left( {\rho_{c} A{ + }\rho_{c} Ik^{2} { + }m_{f} } \right)$$
(11a)
$$c_{2} = 2m_{f} V_{f} k\left[ {1 + \left( {e_{0} a} \right)^{2} k^{2} } \right]$$
(11b)
$$c_{3} = EIk^{4} - \left[ {1 + \left( {e_{0} a} \right)^{2} k^{2} } \right]m_{f} V_{f}^{2} k^{2}.$$
(11c)

The phase velocity can be derived by using the following equation

$$c_{p} = \frac{\omega }{k}.$$
(12)

2.3 Interval analysis method

In the above section, the deterministic analysis for the wave propagation characteristics of fluid-conveying CNTs is presented. However, the system uncertainties caused by the manufacturing errors, physical imperfections, and material defects are unavoidable, and many experimental results have shown that the material properties of CNTs have a great of uncertainties. To overcome the massive information needed to build a precise PDF for the uncertain parameters to conduct the probabilistic analysis, the uncertain parameters are defined as interval variables with known bounds in this section. The material and fluid parameters, i.e., the mass density ρ c , Young’s modulus E of the CNT and the small-scale coefficient e 0 a, and the velocity V f and mass density ρ f of the conveying fluid, are all defined as interval parameters. These uncertain parameters can be denoted by an interval vector as follows

$${\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} = \left[ {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} ,\bar{z}}}} \right] = \left[ {{\mathbf{z}}^{{\mathbf{c}}} - {\mathbf{\Delta z}},{\mathbf{z}}^{{\mathbf{c}}} + {\mathbf{\Delta z}}} \right] = \left( {z_{i}^{I} } \right),$$
(13a)
$${\text{or}}\quad z_{i} \in z_{i}^{I} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z}_{i} ,\bar{z}_{i} } \right] = \left[ {z_{i}^{c} - \Delta z_{i} ,z_{i}^{c} + \Delta z_{i} } \right]\quad i = 1,2, \ldots , 5$$
(13b)

where \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} }} = \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z}_{i} } \right)\) and \({\bar{\mathbf{z}}} = \left( {\bar{z}_{i} } \right)\) are, respectively, the lower and upper bounds of the uncertain parameter vector \({\mathbf{z}} = \left( {E,\rho_{c} ,e_{0} a,V_{f} ,\rho_{f} } \right)^{\text{T}}\); \({\mathbf{z}}^{{\mathbf{I}}} = \left( {E^{I} ,\rho_{c}^{I} ,e_{0} a^{I} ,V_{f}^{I} ,\rho_{f}^{I} } \right)^{\text{T}}\) is a five-dimensional interval vector including all uncertain material and fluid parameters; \(z_{i}^{c} = \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z}_{i} + \bar{z}_{i} } \right)/2\) and \(\Delta z_{i} = \left( {\bar{z}_{i} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z}_{i} } \right)/2\) represent the midpoint and the radius of the interval parameters, respectively. For simplicity, the radius of the uncertain-but-bounded parameter also can be represented by \(\Delta z_{i} = \alpha z_{i}^{c}\), where the parameter α stands for the uncertain level. Accordingly, the interval parameter \(z_{i}^{I}\) can be denoted as \(z_{i}^{I} = z_{i}^{c} [1 - \alpha ,1 + \alpha ]\).

An interval analysis method based on the iterative algorithm is proposed to capture the lower and upper bounds of the wave dispersion curve. For the sake of generality, the interval extension of the wave dispersion relation expressed in Eq. (9) takes the form as follows:

$$F(\omega ;{\mathbf{z}}^{{\mathbf{I}}} ) = \left( {1 + \left( {e_{0} a^{I} } \right)^{2} k^{2} } \right)\left[ { - \rho_{c}^{I} A\omega^{2} - \quad \rho_{c}^{I} I\omega^{2} k^{2} - \rho_{f}^{I} A_{i} \left( {\omega^{2} - 2V_{f}^{I} \omega k + \left( {V_{f}^{I} k} \right)^{2} } \right)} \right] + E^{I} Ik^{4} = 0$$
(14)

where F(·) denotes a nonlinear function of the wave frequency ω, \(F\left( {\omega ;{\mathbf{z}}^{{\mathbf{I}}} } \right)\) is the natural interval extension of \(F\left( {\omega ;{\mathbf{z}}} \right)\).

The solution of Eq. (14) can be defined as a set

$$\Lambda = \omega ({\mathbf{z}}^{{\mathbf{I}}} ) = \left\{ {\omega \in R:F(\omega ;{\mathbf{z}}) = 0,{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} } \right\}$$
(15)

where R denotes the real domain. One can notice that a direct solution to the above equation cannot be fulfilled due to the strong nonlinearity. Here, an iterative algorithm-based interval analysis method is proposed to solve the bounds of the wave frequency.

Firstly, we introduce two functions as follows

$$\phi \left( \omega \right) = \bar{F}\left( {\omega ;{\mathbf{z}}^{{\mathbf{I}}} } \right) = \mathop {\hbox{max} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} F\left( {\omega ;{\mathbf{z}}} \right)$$
(16)
$$\varphi \left( \omega \right) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{F} \left( {\omega ;{\mathbf{z}}^{{\mathbf{I}}} } \right) = \mathop {\hbox{min} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} F\left( {\omega ;{\mathbf{z}}} \right)$$
(17)

where \(\phi \left( \omega \right)\) and \(\varphi \left( \omega \right)\) both can be treated as nonlinear functions of the wave frequency ω.

The first-order derivative of Eqs. (16) and (17) can be separately given as

$$\frac{{\text{d}\phi \left( \omega \right)}}{{\text{d}\omega }} = \frac{\text{d}}{{\text{d}\omega }}\left( {\mathop {\hbox{max} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} F\left( {\omega ;{\mathbf{z}}} \right)} \right) = \mathop {\hbox{max} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} \frac{{\partial F\left( {\omega ;{\mathbf{z}}} \right)}}{\partial \omega }$$
(18)
$$\frac{{\text{d}\varphi \left( \omega \right)}}{{\text{d}\omega }} = \frac{\text{d}}{{\text{d}\omega }}\left( {\mathop {\hbox{min} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} F\left( {\omega ;{\mathbf{z}}} \right)} \right) = \mathop {\hbox{min} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} \frac{{\partial F\left( {\omega ;{\mathbf{z}}} \right)}}{\partial \omega }.$$
(19)

Supposing \(\omega = \omega_{a}\) as the solution of \(\partial F\left( {\omega ;{\mathbf{z}}} \right) /\partial \omega { = }0\), from Eq. (14), one has \({{\partial F(\omega ;{\mathbf{z}}^{{\mathbf{I}}} )} \mathord{\left/ {\vphantom {{\partial F(\omega ;{\mathbf{z}}^{{\mathbf{I}}} )} {\partial \omega }}} \right. \kern-0pt} {\partial \omega }} < 0\) when \(\omega > \omega_{a}\), and then, it can be arrived at:

$$\frac{{\text{d}\varphi \left( \omega \right)}}{{\text{d}\omega }} = \frac{\text{d}}{{\text{d}\omega }}\left( {\mathop {\hbox{min} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} F\left( {\omega ;{\mathbf{z}}} \right)} \right) < \frac{{\text{d}\phi \left( \omega \right)}}{{\text{d}\omega }} = \frac{\text{d}}{{\text{d}\omega }}\left( {\mathop {\hbox{max} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} F\left( {\omega ;{\mathbf{z}}} \right)} \right) < 0.$$
(20)

Hence, it can be concluded that both \(\phi \left( \omega \right)\) and \(\varphi \left( \omega \right)\) are monotonically decreasing function with respect to the wave frequency ω when \(\omega > \omega_{a}\).

Assuming that \(\omega = \omega_{ *}\) is the solution of equation \(F\left( {\omega ;{\mathbf{z}}} \right) = 0\) and by using monotonicity, one has

$$F\left( {\omega_{ *} ;{\mathbf{z}}} \right) \in F\left( {\omega_{ *} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)$$
(21)

where \(F\left( {\omega_{ *} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)\) is an interval extension of \(F\left( {\omega_{ *} ;{\mathbf{z}}} \right)\).

Combining \(F\left( {\omega_{ *} ;{\mathbf{z}}} \right) = 0\) with Eqs. (16), (17), and (21), the following inequality can be derived as

$$\varphi \left( {\omega_{*} } \right) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{F} \left( {\omega_{ *} ;{\mathbf{z}}^{{\mathbf{I}}} } \right) \le 0 \le \bar{F}\left( {\omega_{ *} ;{\mathbf{z}}^{{\mathbf{I}}} } \right) = \phi \left( {\omega_{*} } \right).$$
(22)

The above relationship is clearly found in Fig. 2. From this figure, the following two equations also can be obtained

$$\phi \left( {\bar{\omega }} \right) = \mathop {\lim }\limits_{{\omega_{*} \to \bar{\omega }}} \phi \left( {\omega_{*} } \right) = 0$$
(23)
$$\varphi \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega } } \right) = \mathop {\lim }\limits_{{\omega_{*} \to \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega } }} \varphi \left( {\omega_{*} } \right) = 0$$
(24)

where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega } = \mathop {\hbox{min} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} \omega \left( {\mathbf{z}} \right)\) and \(\bar{\omega } = \mathop {\hbox{max} }\limits_{{{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} \omega \left( {\mathbf{z}} \right)\) are the lower and upper bounds of the wave frequency, respectively.

Fig. 2
figure 2

Illustration of interval analysis method based on the iterative algorithm

Full size image

Introducing three interval vectors as follows

$$\omega_{S}^{I} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{S} ,\bar{\omega }_{S} } \right],\quad \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{S} \le \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega } \le \bar{\omega } \le \bar{\omega }_{S}$$
(25)
$$\omega_{U}^{I} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{U} ,\bar{\omega }_{U} } \right],\quad \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{U} \le \bar{\omega } \le \bar{\omega }_{U}$$
(26)
$$\omega_{L}^{I} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{L} ,\bar{\omega }_{L} } \right],\quad \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{L} \le \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega } \le \bar{\omega }_{L}$$
(27)

where \(\omega_{S}^{I}\) denotes an initial interval involving all possible values of the wave frequency set \(\omega^{I}\); \(\omega_{U}^{I}\) and \(\omega_{L}^{I}\) are iterative intervals of the upper and lower bounds of the wave frequency, respectively. \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{b}\) and \(\bar{\omega }_{b}\) (b = S, U and L) denote the lower and upper bounds of the corresponding intervals, respectively.

In Eq. (23), the first-order Taylor series expansion at \(\omega = \omega_{ *}\) can be expressed as

$$\phi \left( {\bar{\omega }} \right) = \phi \left( {\omega_{*} } \right) + \frac{{\text{d}\phi \left( \xi \right)}}{{\text{d}\omega }}\left( {\bar{\omega } - \omega_{*} } \right)$$
(28)

where \(\omega_{*} \le \xi \le \bar{\omega }\). By combining Eqs. (18), (25), and (26), and using monotonicity, and considering \(\xi \in \omega_{S}^{I}\) and \(\bar{\omega } \in \omega_{U}^{I}\), one has

$$\phi \left( {\bar{\omega }} \right) \in \phi \left( {\omega_{U}^{I} } \right) \subset \phi \left( {\omega_{*} } \right) + \frac{{\text{d}\phi \left( \xi \right)}}{{\text{d}\omega }}\left( {\omega_{U}^{I} - \omega_{*} } \right)$$
(29)
$$\frac{{\text{d}\phi \left( \xi \right)}}{{\text{d}\omega }} \in \frac{{\text{d}\phi \left( {\omega_{S}^{I} } \right)}}{{\text{d}\omega }} \subset \frac{{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)}}{\partial \omega }$$
(30)

where \({{\text{d}\phi \left( {\omega_{S}^{I} } \right)} \mathord{\left/ {\vphantom {{\text{d}\phi \left( {\omega_{S}^{I} } \right)} {\text{d}\omega }}} \right. \kern-0pt} {\text{d}\omega }}\) and \({{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)} \mathord{\left/ {\vphantom {{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)} {\partial \omega }}} \right. \kern-0pt} {\partial \omega }}\) represent the interval extensions of \({{\text{d}\phi \left( \omega \right)} \mathord{\left/ {\vphantom {{\text{d}\phi \left( \omega \right)} {\text{d}\omega }}} \right. \kern-0pt} {\text{d}\omega }}\) and \({{\partial F\left( {\omega ;{\mathbf{z}}} \right)} \mathord{\left/ {\vphantom {{\partial F\left( {\omega ;{\mathbf{z}}} \right)} {\partial \omega }}} \right. \kern-0pt} {\partial \omega }}\), respectively.

Inserting Eqs. (23) and (30) into Eq. (29), the following equation can be obtained

$$0 \in \phi \left( {\omega_{*} } \right) + \frac{{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)}}{\partial \omega }\left( {\omega_{U}^{I} - \omega_{*} } \right).$$
(31)

Based on the interval mathematics, it is clear that the width of right-hand side interval given in Eq. (31) depends only on \(\omega_{U}^{I}\) because the widths of both \(\omega_{S}^{I}\) and \({\mathbf{z}}^{{\mathbf{I}}}\) are constants. Then there exists a constant λ c satisfying (Alefeld and Mayer 2000; Moore 1979)

$$\text{Wid}\left( {\phi \left( {\omega_{*} } \right) + \frac{{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)}}{\partial \omega }\left( {\omega_{U}^{I} - \omega_{*} } \right)} \right) \le \lambda_{c} \text{Wid}\left( {\omega_{U}^{I} } \right).$$
(32)

where Wid(·) represents the width of interval vector. Our goal is to obtain the upper bound of the wave frequency \(\bar{\omega } \in \omega_{U}^{I}\) whose width is zero. Based on the interval analysis theory proposed by Moore (1979), if the interval arithmetic evaluation exists, then the width of \(\omega_{U}^{I}\) is approaching zero. Correspondingly, the width of the interval arithmetic evaluation will go linearly to zero (Alefeld and Mayer 2000), i.e.,

$$\text{Wid}\left( {\phi \left( {\omega_{*} } \right) + \frac{{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)}}{\partial \omega }\left( {\omega_{U}^{I} - \omega_{*} } \right)} \right) \to 0.$$
(33)

Equation (33) provides an available method to identify the upper bound of frequency by an iterative algorithm to reduce the width of \(\omega_{U}^{I}\). The iterative algorithm can be established via the following equation

$$\phi \left( {\omega_{*} } \right) + \frac{{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)}}{\partial \omega }\left( {\omega_{U}^{I} - \omega_{*} } \right) = 0.$$
(34)

Because \(\phi \left( {\omega_{*} } \right) \ge 0\) and \({{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)} \mathord{\left/ {\vphantom {{\partial F\left( {\omega_{S}^{I} ;{\mathbf{z}}^{{\mathbf{I}}} } \right)} {\partial \omega }}} \right. \kern-0pt} {\partial \omega }} < 0\), the iterative interval \(\omega_{U}^{I}\) can be obtained by Eq. (34), which can be further expressed as

$$\omega_{U}^{I} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{U} ,\bar{\omega }_{U} } \right] = \left[ {\omega_{*} - \frac{{\phi \left( {\omega_{*} } \right)}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{d} }}, \, \omega_{*} - \frac{{\phi \left( {\omega_{*} } \right)}}{{\bar{d}}}} \right]$$
(35)

where

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{d} = \mathop {\hbox{min} }\limits_{{\omega \in \omega_{S}^{I} ,{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} \frac{{\partial F\left( {\omega ;{\mathbf{z}}} \right)}}{\partial \omega },\quad \bar{d} = \mathop {\hbox{max} }\limits_{{\omega \in \omega_{S}^{I} ,{\mathbf{z}} \in {\mathbf{z}}^{{\mathbf{I}}} }} \frac{{\partial F\left( {\omega ;{\mathbf{z}}} \right)}}{\partial \omega }.$$
(36)

Substituting \(\bar{\omega } \in \omega_{U}^{I}\) into Eq. (35) leads to

$$\omega_{*} - \frac{{\phi \left( {\omega_{*} } \right)}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{d} }} \le \bar{\omega } \le \omega_{*} - \frac{{\phi \left( {\omega_{*} } \right)}}{{\bar{d}}} .$$
(37)

Because \({{\phi \left( {\omega_{*} } \right)} \mathord{\left/ {\vphantom {{\phi \left( {\omega_{*} } \right)} {d}}} \right. \kern-0pt} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{d} }} \le 0\), one can also have

$$\omega_{*} \le \omega_{*} - \frac{{\phi \left( {\omega_{*} } \right)}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{d} }} \le \bar{\omega }.$$
(38)

Based on the above inequality, the iterative algorithm for the upper bound of the wave frequency can be determined by

$$\bar{\omega }_{p + 1} = \bar{\omega }_{p} - \frac{{\phi \left( {\bar{\omega }_{p} } \right)}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{d} }}$$
(39)

where \(\bar{\omega }_{p}\) is the iterative wave frequency of the pth computational cycle during the iterative procedure. The convergent condition is given as follows

$$\left| {\bar{\omega }_{p + 1} - \bar{\omega }_{p} } \right| \le \theta.$$
(40)

The upper bound of the wave frequency can be determined at the point when the above convergent condition is satisfied. The algorithm flowchart for the interval analysis is shown in Fig. 3.

Fig. 3
figure 3

Algorithm flowchart for the interval analysis of wave propagation in fluid-conveying CNTs

Full size image

Similarly, following the steps presented in Eqs. (28)–(39), the iterative algorithm for the lower bound of the wave frequency also can be calculated by

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{q + 1} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{q} - \frac{{\varphi \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{q} } \right)}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{d} }}$$
(41)

where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }_{q}\) denotes the iterative frequency of the qth computational cycle during the iterative procedure. Combining with the convergent condition, the lower bound of the wave frequency can be obtained. The bounds of the phase velocity also can be calculated in the same way.

2.4 Probabilistic analysis method

In this section, a probabilistic model is presented to validate the interval analysis method proposed in the above section. Assume that the uncertain material and fluid parameter vector \({\mathbf{z}} = \left( {E,\rho_{c} ,e_{0} a,V_{f} ,\rho_{f} } \right)^{\text{T}}\) is random variable. Denote the wave frequency expressed in Eq. (10) as a function ω(z). Then, the wave frequency ω(z) is also random. The mean value of the random parameter vector z can be given as

$$E({\mathbf{z}}) = \left( {E(z_{i} )} \right) = {\mathbf{z}}^{E} = \left( {z_{i}^{E} } \right).$$
(42)

Using first-order Taylor series expansion, the wave frequency ω(z) about the mean value z E is developed as

$$\omega ({\mathbf{z}}) = \omega ({\mathbf{z}}^{E} + \delta ) = \omega ({\mathbf{z}}^{E} ) + \sum\limits_{i = 1}^{n} {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}} \left( {z_{i} - z_{i}^{E} } \right).$$
(43)

The mean value of the wave frequency can be obtained by taking the expected value of both sides of Eq. (43). One can arrive at

$$E\left( {\omega ({\mathbf{z}})} \right) = E\left( {\omega ({\mathbf{z}}^{E} )} \right) + E\left( {\sum\limits_{i = 1}^{n} {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}} \left( {z_{i} - z_{i}^{E} } \right)} \right) = \omega ({\mathbf{z}}^{E} ) + \sum\limits_{i = 1}^{n} {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}E} \left( {z_{i} - z_{i}^{E} } \right)$$
(44)

It is noted that \(E(z_{i} - z_{i}^{E} )\) is zero, and thus, one has

$$E\left( {\omega ({\mathbf{z}})} \right) = \omega ({\mathbf{z}}^{E} ).$$
(45)

In a similar way, the variance of the wave frequency can be calculated as follows:

$$D\left( {\omega ({\mathbf{z}})} \right) = \sum\limits_{i = 1}^{n} {\left( {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}} \right)^{2} D} \left( {z_{i} } \right) + \sum\limits_{i = 1}^{n} {\sum\limits_{l = 1}^{n} {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}} \frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{l} }}{\text{Cov}}} \left( {z_{i} ,z_{l} } \right).$$
(46)

where \({\text{Cov}}\left( {z_{i} ,z_{l} } \right)\) is the covariance of the random parameter variables. When the random parameters are independent, one has \({\text{Cov}}\left( {z_{i} ,z_{l} } \right) = 0\), and then Eq. (46) is reduced as

$$D\left( {\omega ({\mathbf{z}})} \right) = \sum\limits_{i = 1}^{n} {\left( {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}} \right)^{2} D} \left( {z_{i} } \right) = \sum\limits_{i = 1}^{n} {\left( {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}\sigma \left( {z_{i} } \right)} \right)^{2} } = \sum\limits_{i = 1}^{n} {\left( {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}\sigma_{i} } \right)^{2} }$$
(47)

where \(\sigma \left( {\mathbf{z}} \right) = \left( {\sigma \left( {z_{i} } \right)} \right)\) is the standard deviation of the random parameter vector z = (z i ), and then, the standard deviation of the wave frequency can be derived as

$$\sigma \left( {\omega ({\mathbf{z}})} \right) = \sqrt {D\left( {\omega ({\mathbf{z}})} \right)} = \sqrt {\sum\limits_{i = 1}^{n} {\left( {\frac{{\partial \omega \left( {{\mathbf{z}}^{E} } \right)}}{{\partial z_{i} }}\sigma_{i} } \right)^{2} } }.$$
(48)

The probabilistic range of g times standard deviations of the mean value of the wave frequency can be denoted as

$$\omega^{I} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega } \left( {\mathbf{z}} \right),\bar{\omega }\left( {\mathbf{z}} \right)} \right] = \left[ {\omega ({\mathbf{z}}^{E} ) - g\sigma \left( {\omega \left( {\mathbf{z}} \right)} \right),\omega ({\mathbf{z}}^{E} ) + g\sigma \left( {\omega \left( {\mathbf{z}} \right)} \right)} \right]$$
(49)

where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega } ({\mathbf{z}})\) and \(\bar{\omega }({\mathbf{z}})\) are, respectively, the probabilistic lower and upper bounds of the wave frequency obtained by the probabilistic method; g is a positive integer and can be determined by the intervals of the uncertain-but-bounded parameters. Similarly, the probabilistic lower and upper bounds of the phase velocity also can be obtained.

3 Model verification

In this section, the Monte Carlo simulation and the probabilistic model are employed to verify the present interval analysis method. The inner and outer radiuses of the CNT are defined as R i  = 3.4 nm and R o  = 3.74 nm, respectively (Zhen et al. 2011). The material parameters (including the Young’s modulus E, mass density ρ c , and the small-scale coefficient e 0 a of the CNTs) and the fluid parameters (including the velocity V f and the mass density ρ f of the fluid) are all treated as uncertain-but-bounded parameters. The midpoints of these interval parameters are, respectively, defined as (Zhen et al. 2011) E c = 1 TPa, \(\rho_{c}^{c}\) = 2300 kg/m3, e 0 a c = 0.5 nm, \(V_{f}^{c}\) = 1000 m/s, and \(\rho_{f}^{c}\) = 1000 kg/m3, while the radiuses of these parameters are expressed as \(\Delta E = \alpha E^{c}\), \(\Delta \rho_{c} = \alpha \rho_{c}^{c}\), \(\Delta e_{0} a = \alpha \cdot e_{0} a^{c}\), \(\Delta V_{f} = \alpha V_{f}^{c}\) and \(\Delta \rho_{f} = \alpha \rho_{f}^{c}\), respectively, where the variable α represents the uncertainty level.

3.1 Comparison with Monte Carlo simulation

The lower bound (LB) and upper bound (UB) of the wave dispersion curves calculated by the present interval analysis method (IAM) and Monte Carlo simulation (MCS) are compared and shown in Fig. 4. Here, the MCS with 3.2 × 106 sample points is introduced as a referenced method, and it can be performed in the following steps. Firstly, we choose 20 equal incremental values for each uncertain parameter from its LB to UB. Then a large number of deterministic wave frequency and phase velocity responses can be obtained by using Eqs. (10) and (12), from which the maximum and minimum of the wave dispersion curves with respect to the interval parameters can be easily obtained. As depicted in Fig. 4, the UB of the wave frequency and the phase velocity predicted by the IAM is a little lower than that predicted by the MCS, while the LB of the frequency and the phase velocity obtained by the IAM is a little larger than that obtained by the MCS. In other words, the wave dispersion curves predicted by the present IAM is completely reliable and can extensively reduce the computational cost for huge samples of MCS.

Fig. 4
figure 4

Bounds of dispersion curves predicted by IAM and MCS: a wave frequency, b phase velocity. Here, the uncertainty level α = 0.05 and the midpoint of the small-scale coefficient e 0 a c = 0.5 nm are adopted

Full size image

3.2 Comparison with probabilistic analysis method

The probabilistic analysis method (PAM) is presented to validate the IAM. We assume that the Young’s modulus E, mass density ρ c , and the small-scale coefficient e 0 a of the CNTs, and the velocity V f and mass density ρ f of the fluid all have normal distributions with the mean values \(\mu_{E}\) = 1 TPa, \(\mu_{{\rho_{c} }}\) = 2300 kg/m3, \(\mu_{{e_{0} a}}\) = 0.5 nm, \(\mu_{{V_{f} }}\) = 1000 m/s and \(\mu_{{\rho_{f} }}\) = 1000 kg/m3, respectively. Based on 3σ principle, the standard deviations of these uncertain variables are set as \(\sigma_{E}\) = 0.03 TPa, \(\sigma_{{\rho_{c} }}\) = 69 kg/m3, \(\sigma_{{e_{0} a}}\) = 0.015 nm, \(\sigma_{{V_{f} }}\) = 30 m/s and \(\sigma_{{\rho_{f} }}\) = 30 kg/m3, respectively, which corresponds to the uncertain-but-bounded parameters with uncertainty level α = 0.09. The comparison between IAM and PAM for the wave dispersion curves is depicted in Fig. 5. It is clear that the ranges of the wave frequency and phase velocity yielded by IAM are basically in well agreement with those predicted by PAM, but the former encloses the latter, which means the present IAM provides more conservative results than PAM.

Fig. 5
figure 5

Bounds of dispersion curves predicted by IAM with uncertainty level α = 0.09 and PAM based on 3σ principle: a wave frequency, b phase velocity. Here, the midpoint of the small-scale coefficient e 0 a c = 0.5 nm is adopted

Full size image

4 Results and discussion

4.1 Parameter sensitivity studies

To identify the most important uncertain parameters which have the highest contributions to the wave propagation behaviors of fluid-conveying CNTs, the parameter sensitivity study is carried out in this section. The sensitivities of the wave frequency to uncertainty can be studied by using the relative sensitivity indices S(z i ) defined as follows (Isukapalli 1999)

$$S(z_{i} ) = \left| {\frac{{\partial \omega ({\mathbf{z}})}}{{\partial z_{i} }}} \right|\frac{{\left| {z_{i}^{c} } \right|}}{{\omega_{c} ({\mathbf{z}})}}$$
(50)

where ω c (z) denotes the normal value of the wave frequency. The sensitivities of the wave frequency with respect to the uncertain variables at several different wave numbers are compared in Table 1. It is observed that \(S(E)\), \(S(\rho_{c} )\), and \(S(e_{0} a)\) monotonically increase, and \(S(\rho_{f} )\) and \(S(V_{f} )\) monotonically decrease with increasing the wave number. The wave frequency is more sensitive to the small-scale coefficient e 0 a than other uncertain parameters. At small wave numbers, the contribution of the small-scale coefficient e 0 a is the lowest, while it shows the largest contribution to the wave frequency when the wave number becomes large. The Young’s modulus E has the largest influence on the wave frequency when the wave number is small, while for larger wave numbers, the sensitivity of the mass density of the fluid is the lowest.

Table 1 Relative sensitivity of wave frequency with respect to uncertain variables at different wave numbers
Full size table

4.2 Effect of conveying fluid

The influences of the conveying fluid on the upper and lower bounds of the wave dispersion behaviors for the classical and nonlocal continuum models are depicted in Figs. 6 and 7, respectively. One can find that the conveying fluid will primarily affect the bounds of the wave frequency and phase velocity at small wave numbers both for the classical and nonlocal continuum models, while the bounds of the frequency and phase velocity are insignificant to the conveying fluid as the wave number is getting larger.

Fig. 6
figure 6

Bounds of dispersion curves for CNTs with or without conveying fluid predicted by the classical continuum model: a wave frequency, b phase velocity. Here, the uncertainty level α = 0.05 and the small-scale coefficient e 0 a = 0 nm are adopted

Full size image
Fig. 7
figure 7

Bounds of dispersion curves for CNTs with or without conveying fluid predicted by the nonlocal continuum model: a wave frequency, b phase velocity. Here, the uncertainty level α = 0.05 and the midpoint of the small-scale coefficient e 0 a c = 0.5 nm are adopted

Full size image

As depicted in Fig. 6a, the upper and lower bounds of the frequency always increase with increasing the wave number when the nonlocal effect is ignored. While from Fig. 7a, the bounds of the frequency increase firstly and then trend to constant values with increasing the wave number once the nonlocal effect is taken into account. Figure 7b gives the phase velocity versus the wave number with considering the small size effect, which shows that the conveying fluid will reduce both the upper and lower bounds of the phase velocity when k < 3 nm−1, while the influence of the conveying fluid on the phase velocity dispersion curve is not much prominent when k > 3 nm−1. The phase velocity has the widest range when the wave number k approaches to 1 nm−1. However, as shown in Fig. 6b, when the small size effect is ignored, the range of the phase velocity will trend to constant values as k > 4 nm−1. The significant deviation shown in Figs. 6 and 7 demonstrates that the small size scale has much effect on the bounds of the wave frequency and phase velocity, and its effect should not be neglected for the wave propagation analysis of the size-dependent fluid-conveying CNTs.

4.3 Effect of size-scale parameter

The bounds of the frequency dispersion curve for CNTs with several different size scales are illustrated in Fig. 8a. Here, e 0 a = 0 nm represents the classical continuum model with no size-scale effect, e 0 a c = 0.5 nm, 1.0 and 2.0 nm denote three different midpoints of the small-scale coefficient. It is clear that the frequency increases dramatically all along the wave number as e 0 a = 0 nm, while the wave frequency increases firstly and then tends to constant values when the size-scale effect is taken into account. The extensive deviation indicates the classical continuum model cannot be used to reflect the physical behavior of nanoscale CNTs. It is also shown that for a fixed e 0 a c, the range of the frequency increases firstly and then remains unchanged with respect to the wave number. As the parameters e 0 a c increases, the range of the frequency will become much narrower.

Fig. 8
figure 8

Bounds of dispersion curves for CNTs with different size scales: a wave frequency, b phase velocity. Here, the uncertainty level is defined as α = 0.05

Full size image

Figure 8b plots the upper and lower bounds of phase velocity dispersion curves for CNTs with uncertain variables at different size scales. The phase velocity is not sensitive to the midpoint of the small-scale coefficient e 0 a c when the wavelength is large (low wave numbers). However, once the wavelength is small (large wave numbers), the parameter e 0 a c will become important. The range of the phase velocity always increases with the wave number as the wavelength is large. However, if the wavelength is small, the bound of the phase velocity will remain unchanged when the size-dependent effect is ignored (e 0 a = 0 nm), while it decreases dramatically when the size-scale effect is taken into consideration. The observed deviation also confirms that the size-scale effect should not be neglected in analysis of CNTs conveying fluids.

4.4 Effect of uncertainty level

The uncertainty level which governs the uncertain-but-bounded variables is discussed in this section. The bounds of the wave frequency and the phase velocity as a function of the uncertain level are presented in Fig. 9. For the classical continuum model, the small-scale coefficient is defined as e 0 a = 0 nm, while the midpoint of small-scale coefficient e 0 a c = 0.5 nm is used for the nonlocal continuum model. It is evident that the UB of the wave frequency and the phase velocity increases with increasing the uncertainty level both for the classical and nonlocal continuum models, while the LB of these characteristic variables shows an opposite tendency. Due to this fact, the range of the wave frequency and the phase velocity will become larger as the uncertainty level increases. Compared with the classical continuum model, the upper and lower bounds of the wave frequency and the phase velocity both will reduce significantly when the size-scale effect is taken into consideration, which indicates the size-scale effect should not be neglected to analyze the wave propagation behaviors of fluid-conveying CNTs.

Fig. 9
figure 9

Bounds of wave frequency and phase velocity at varying uncertain levels for classical and nonlocal continuum models. Here, the wave number is fixed as k = 2 nm−1

Full size image

5 Conclusion

In this paper, an iterative algorithm-based interval analysis method is proposed to study the flexural wave propagation characteristics of fluid-conveying CNTs with system uncertainties. To deal with the uncertainties where few data are available to establish a precise PDF for probabilistic analysis, both the material properties of CNTs and the properties of the conveying fluid are all set as uncertain-but-bounded parameters. The governing equations are derived on the basis of nonlocal Euler–Bernoulli beam theory. Moreover, the upper and lower bounds of the wave dispersion curves are captured by using the proposed interval analysis method.

It can be concluded that both the fluid and the size-scale parameter will affect the upper and upper bounds of the wave frequency and phase velocity significantly. The uncertain level also has considerable influences on the upper and upper bounds of the wave frequency and the phase velocity. The proposed method is also verified by comparing with the Monte Carlo method and probabilistic method, and good agreements are achieved. Comparing with these two traditional uncertain analysis methods, the proposed interval method can reduce the large computational cost of Monte Carlo simulations and can overcome the large prior information needed in probabilistic analyses. The presented interval analysis method presents one useful way to investigate the uncertain effect in small-scale CNTs and also can be used in other nanostructures with uncertain system properties.