1 Introduction

Miniaturized beams and plates have been widely used in various nano- and microscale devices, modulators, resonators, and systems, such as biosensors, atomic force microscopes, Microelectro-mechanical Systems (MEMS), and Nanoelectro-mechanical Systems (NEMS) (see, e.g., Guo and Rogerson 2003; Moser and Gijs 2007; Li et al. 2007). Across these applications, it is necessary to know how the parameters (e.g., the internal fluid flow velocity) affect the physical properties and mechanical properties of microstructures. As reported by Rinaldi et al. (2010), the design parameters of microstructures would meet requirements of several aspects, such as the material properties, size, geometry, boundary conditions, and modal properties. In this article, we focus on a class of microstructures that may be characterized as micromachined pipes containing internal fluid flow (see, e.g., Enoksson et al. 1995, 1997; Westberg et al. 1999; Burg et al. 2007; Najmzadeh et al. 2007; Sparks et al. 2009).

The study of vibration of macroscale pipes containing fluid flow has a fine pedigree (Païdoussis 1998). The dynamics of fluid-containing macroscale pipes has remained of intense interest to dynamicists well in the last several decades. As reported by Rinaldi et al. (2010), the effects of internal fluid flow on the vibration properties and stability of macroscale pipes, with dimensions ranging from a few centimeters to tens of meters, have been extensively studied for over 60 years. For fluid-containing macroscale pipes with supported ends, divergence (buckling) is the expected form of instability, since the system is conservative if the dissipation is absent or neglected. For a cantilevered system, however, the pipe may undergo a flutter instability once the internal fluid velocity exceeds to a critical one. These important conclusions, of course, were obtained using the classical continuum elastic-beam/shell theories.

It ought to be mentioned that, in the past years, the theoretical models for vibration properties of nanoscale pipes/tubes containing internal fluid flow have also attracted many researchers (see, e.g., Yoon et al. 2005; Natsuki et al. 2007; Reddy et al. 2007; Chang and Lee 2009; He et al. 2008; Wang and Ni 2009; Wang et al. 2008; Lee and Chang 2008; Wang 2009; and several other references cited therein). In these studies, the effects of internal fluid flow velocity on the natural frequencies and instability of nanotubes/nanopipes has been analyzed, displaying some fundamental vibration properties of such nanostructures. The available theoretical models developed for vibration analysis of fluid-containing nanopipes may be grouped into two: the classical continuum beam/shell theoretical models (see, e.g., Yoon et al. 2005; Natsuki et al. 2007; Reddy et al. 2007; Chang and Lee 2009; He et al. 2008; Wang and Ni 2009; Wang et al. 2008) and the nonlocal theoretical models (see, e.g., Lee and Chang 2008; Wang 2009). The classical continuum theoretical models, as the name implies, presume that the materials of the nanopipes and the internal fluid are essentially continuous; physically, the continuum models are not able to exactly describe the properties of nanoscale structures, since the material nanostructure becomes increasingly important and its effect can no longer be ignored. The nonlocal theoretical models, on the other hand, provide a possible solution to extend the classical continuum approach to nano-sized by incorporating information regarding the behavior of material nano-structure. Actually, the nonlocal models may be more suitable to characterize the vibration properties of nanoscale pipes conveying fluid. However, the nonlocal models still seem to break down below 10 nm in the case of fluid in nanopipes, since the continuity assumption of the fluid becomes questionable (Mattia and Gogotsi 2008). Smooth fluid interface disappears in pipes with the diameter <8–10 nm and an anomalous behavior of fluid is observed in 1–7 nm carbon nanopipes. The surface chemistry and structure of nanopipes must be controlled with a high precision for controlling flow velocity (Mattia and Gogotsi 2008). When the pipe size is in nano-scale, therefore, how to quantify the effects of internal fluid flow on the vibration characteristics is still a challenging topic in the near future.

Compared with the macro-scale and nanometer-scale structures containing internal fluid flow, the intermediate range of micrometer-scale structures, which is of interest for MEMS and microfluidics devices, remains largely unexplored (Rinaldi et al. 2010). Although Rinaldi et al. (2010) initiated a theoretical analysis of microscale pipes containing internal flow, their theoretical model is still based on the classical continuum beam theory. For microscale beams/plates, size effects on the mechanical properties and vibration properties can not be ignored, as widely reported recently (e.g., McFarland and Colton 2005). Therefore, beam models based on classical elasticity theory are not capable of exactly describing the microstructure-dependent behaviors of micromachined pipes containing internal fluid. This motivates the work presented in this article. More recently, a size-dependent Euler beam model was developed for predicting the vibration properties of fluid-conveying micropipes (Wang 2010). In that model, however, the motions of micropipes are assumed to be governed by a single transverse displacement variable and the Poisson’s effect was neglected.

The objective of the current article is to develop a microstructure-dependent Timoshenko model for the microscale pipes containing internal fluid using the modified couple stress theory and Hamilton’s principle. Unlike the analytical model given by Wang (2010), in the current non-classical model, the motions of micropipes are governed by three displacement variables, and the Poisson’s effect is also included. This new model contains a material length scale parameter and can capture the size effect. We consider the dynamics of a straight micromachined pipes containing internal fluid flow, and present results for the effects of material length scale parameter and internal fluid flow on natural frequencies and stability of the microfluidic system.

2 Formulation of the non-classical Timoshenko model

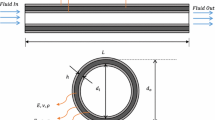
The microscale structures under consideration are modeled as micromachined pipes of mass density ρ p, cross-sectional area A and length L between two positively supported ends (Rinaldi et al. 2010). In this case, there is no motion possible at x = L. The internal flow in the pipe is due to a non-viscous, incompressible, single-phase microfluid of mass density ρ f and cross-sectional area A f flowing with velocity U. The cross-section of the micropipe is symmetric, either circular or rectangular, and may contain one or a set of parallel internal channels, as illustrated in Fig. 1a and b.

Fig. 1
figure 1

a Schematic of a micromachined pipes containing internal fluid flow with circular cross-section. b Schematic of the single rectangular cross-section of a micromachined pipes. c The coordinate system defined in this study

Full size image

The using of modified couple stress theory for microbeams will be reviewed firstly. For more details on this theory, the interested reader is referred to Yang et al. (2002), Ma et al. (2008), and Kong et al. (2008). According to the modified couple stress theory, the strain energy density is a function of both the strain (conjugated with stress) tensor and the curvature (conjugated with couple stress) tensor. Therefore, the strain energy V in a deformed isotropic linear elastic material occupying region Ω can be written as

$$ V = \frac{1}{2}\int\limits_{\Upomega } {(\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} ){\text{d}}v} \quad (i,j = 1,2,3) $$
(1)

where dv denotes a volume element. In the above equation, the stress tensor σ ij , the strain tensor ε ij , the deviatoric part of the couple stress tensor m ij , and the symmetric curvature tensor χ ij , are given by

$$ \sigma_{ij} = \lambda {\text{tr}}(\varepsilon_{ij} )\delta_{ij} + 2G\varepsilon_{ij} $$
(2)
$$ \varepsilon_{ij} = \frac{1}{2}[\nabla \eta_{i} + (\nabla \eta_{i} )^{T} ] $$
(3)
$$ m_{ij} = 2l^{2} G\chi_{ij} $$
(4)
$$ \chi_{ij} = \frac{1}{2}[\nabla \theta_{i} + (\nabla \theta_{i} )^{T} ] $$
(5)

respectively, where λ and G are Lame’s constants (G is also known as the shear modulus), δ ij is Kronecker’s delta function, l is a material length scale parameter, η i is the displacement vector, and θ i is the rotation vector given by

$$ \theta_{i} = \frac{1}{2}{\text{curl}}(\eta_{i} ). $$
(6)

It is noted that both σ ij and ε ij are symmetric. From (4) it can be seen that the square of the length scale parameter l is the ratio of the curvature modulus to the shear modulus. Therefore, l may be viewed as a material property representing the effect of couple stress.

Now, using the rectangular Cartesian coordinate system (X, Y, Z) shown in Fig. 1c, where the X-axis is coincident with the centroidal axis of the undeformed pipe, the Y-axis is the neutral axis and the Z-axis is the symmetry axis, and according to the Timoshenko beam theory, the displacement field may be written as (e.g., Reddy 2007).

$$ \eta_{1} = u(x,t) - z\psi (x,t),\quad \eta_{2} = 0,\quad \eta_{3} = w(x,t) $$
(7)

where η 1, η 2, and η 3 are the components of the displacement vector of a point (x, y, z) on a pipe cross-section in the X-, Y- and Z-directions, respectively; u and w are the components of the displacement vector of the point (x, 0, 0) on the centroidal axis in the X- and Z-directions, respectively; Ψ(x) is the rotation angle (about the Y-axis) of the cross-section with respect to Z-axis.

The combination of (3) and (7) yields

$$ \varepsilon= {\frac{\partial u}{\partial x}} - z{\frac{\partial \psi }{\partial x}},\quad \varepsilon_{yy} = \varepsilon_{zz} = \varepsilon_{xy} = \varepsilon_{yz} = 0,\quad \varepsilon = \frac{1}{2}\left( {{\frac{\partial w}{\partial x}} - \psi } \right) $$
(8)

Similarly, the combination of (6) and (7) yields

$$ \theta_{y} = - \left( {{\frac{\partial w}{\partial x}} + \psi } \right),\quad \theta_{x} = \theta_{z} = 0 $$
(9)

Substitution of the above equation into (5) gives

$$ \chi_{xy} = - \frac{1}{4}\left( {{\frac{{\partial^{2} w}}{{\partial x^{2} }}} + {\frac{\partial \psi }{\partial x}}} \right),\quad \chi_{xx} = \chi_{yy} = \chi_{zz} = \chi_{yz} = \chi_{xz} = 0 $$
(10)

The kinetic energy of the empty pipe can be written as

$$ T_{\text{p}} = {\frac{{\rho_{\text{p}} }}{2}}\int\limits_{\Upomega } {\left[ {\left( {{\frac{{\partial \eta_{1} }}{\partial t}}} \right)^{2} + \left( {{\frac{{\partial \eta_{2} }}{\partial t}}} \right)^{2} + \left( {{\frac{{\partial \eta_{3} }}{\partial t}}} \right)^{2} } \right]{\text{d}}v} $$
(11a)

or

$$ T_{\text{p}} \, = {\frac{{\rho_{\text{p}} }}{2}}\int\limits_{\Upomega } {\left[ {\left( {{\frac{\partial u}{\partial t}}} \right)^{2} + \left( {z{\frac{\partial \psi }{\partial t}}} \right)^{2} + \left( {{\frac{\partial w}{\partial t}}} \right)^{2} } \right]{\text{d}}v} $$
(11b)

For a pipe fixed at both ends, the fluid kinetic energy is given by (Païdoussis 1998)

$$ T_{\text{f}} = {\frac{{\rho_{\text{f}} }}{2}}\int\limits_{\Upomega } {\left[ {\left( {{\frac{{\partial \eta_{3} }}{\partial t}} + U{\frac{{\partial \eta_{3} }}{\partial x}}} \right)^{2} { + }\left( {{\frac{{\partial \eta_{1} }}{\partial t}} + U} \right)^{2} } \right]{\text{d}}v} $$
(12a)

or

$$ T_{\text{f}} = {\frac{{\rho_{\text{f}} }}{2}}\int\limits_{\Upomega } {\left[ {\left( {{\frac{\partial w}{\partial t}} + U{\frac{\partial w}{\partial x}}} \right)^{2} { + }\left( {{\frac{\partial u}{\partial t}} - z{\frac{\partial \psi }{\partial t}} + U} \right)^{2} } \right]{\text{d}}v} . $$
(12b)

Now the first variation of the total kinetic energy on the time internal [t 1, t 2] is given by

$$ \begin{aligned} \delta \int\limits_{{t_{1} }}^{{t_{2} }} {K {\text{d}}t} & = \delta \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {T_{\text{p}} + T_{\text{f}} } \right){\text{d}}t} \\ & = - \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{0}^{L} {\left[ {m_{\text{p}} \left( {{\frac{{\partial^{2} u}}{{\partial t^{2} }}}\delta u + {\frac{{\partial^{2} w}}{{\partial t^{2} }}}\delta w} \right) + \left( {J_{\text{f}} + J_{\text{p}} } \right){\frac{{\partial^{2} \psi }}{{\partial t^{2} }}}\delta \psi } \right]{\text{d}}x{\text{d}}t} } \\ & \quad + \int\limits_{0}^{L} {\left. {\left[ {m_{\text{p}} \left( {{\frac{\partial u}{\partial t}}\delta u + {\frac{\partial w}{\partial t}}\delta w} \right) + \left( {J_{\text{f}} + J_{\text{p}} } \right){\frac{\partial \psi }{\partial t}}\delta \psi } \right]} \right|_{{t = t_{1} }}^{{t = t_{2} }} {\text{d}}x} \\ & \quad - \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{0}^{L} {m_{\text{f}} \left[ {\left( {{\frac{{\partial^{2} u}}{{\partial t^{2} }}}\delta u + {\frac{{\partial^{2} w}}{{\partial t^{2} }}}\delta w} \right) + \left( {2U{\frac{{\partial^{2} w}}{\partial x\partial t}} + U^{2} {\frac{{\partial^{2} w}}{{\partial x^{2} }}}} \right)\delta w} \right]{\text{d}}x{\text{d}}t} } \\ & \quad + \int\limits_{0}^{L} {m_{\text{f}} \left. {\left[ {{\frac{\partial u}{\partial t}}\delta u + \left( {{\frac{\partial w}{\partial t}} + U{\frac{\partial w}{\partial x}}} \right)\delta w} \right]} \right|_{{t = t_{1} }}^{{t = t_{2} }} {\text{d}}x} + \int\limits_{{t_{1} }}^{{t_{2} }} {\left. {\left[ {\left( {m_{\text{f}} U{\frac{\partial w}{\partial t}} + m_{\text{f}} U^{2} {\frac{\partial w}{\partial x}}} \right)\delta w} \right]} \right|_{x = 0}^{x = L} {\text{d}}t} \\ \end{aligned} $$
(13)

where \( J_{\text{f}} = \rho_{\text{f}} \int\nolimits_{{A_{\text{f}} }} {z^{ 2} {\text{d}}A} \) and \( J_{\text{p}} = \rho_{\text{p}} \int\nolimits_{A} {z^{ 2} {\text{d}}A}; \) m p and m f are the mass per unit length of the pipe and the internal fluid, respectively.

From (3) and (8–10), the first variation of the potential energy is given by

$$ \begin{aligned} \delta \int\limits_{{t_{1} }}^{{t_{2} }} {V{\text{d}}t} =& \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{\varvec{\Upomega}} {(\sigma_{ij} \delta \varepsilon_{ij} + m_{ij} \delta \chi_{ij} ){\text{d}}v} } {\text{d}}t= \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{\varvec{\Upomega}} {(\sigma_{xx} \delta \varepsilon_{xx} + 2\sigma_{xz} \delta \varepsilon_{xz} + 2m_{ij} \delta \chi_{ij} ){\text{d}}v} } {\text{d}}t \hfill \\ {\kern 1pt} = &\int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{0}^{L} {\left[ { - {\frac{\partial N}{\partial x}}\delta u - \left( {{\frac{\partial Q}{\partial x}} + \frac{1}{2}{\frac{{\partial Y_{xy} }}{\partial x}}} \right)\delta w + \left( {{\frac{\partial M}{\partial x}} - Q + \frac{1}{2}{\frac{{\partial Y_{xy} }}{\partial x}}} \right)\delta \psi } \right]{\text{d}}x{\text{d}}t} }\\ &+ \int\limits_{{t_{1} }}^{{t_{2} }} {\left. {\left[ {N\delta u + \left( {Q + \frac{1}{2}{\frac{{\partial Y_{xy} }}{\partial x}}} \right)\delta w - \left( {M + \frac{1}{2}Y_{xy} } \right)\delta \psi - \frac{1}{2}Y_{xy} \delta \left( {{\frac{\partial w}{\partial x}}} \right)} \right]} \right|_{x = 0}^{x = L} } {\text{d}}t. \hfill \\ \end{aligned} $$
(14)

where

$$ N = \int\limits_{A} {\sigma_{xx} {\text{d}}A} ,\quad M = \int\limits_{A} {z\sigma_{xx} {\text{d}}A} ,\quad Q = \int\limits_{A} {\sigma_{xz} {\text{d}}A} ,\quad Y_{xy} = \int\limits_{A} {m_{xy} {\text{d}}A} $$
(15)

are the stress resultants. From (2), (4), (8), and (10) it follows that

$$ N = {\frac{E(1 - \upsilon )A}{(1 + \upsilon )(1 - 2\upsilon )}}{\frac{\partial u}{\partial x}},\quad M =\,{\frac{E(1 - \upsilon )I}{(1 + \upsilon )(1 - 2\upsilon )}}{\frac{\partial \psi }{\partial x}} $$
$$ Y_{xy} = \frac{1}{2}l^{2} GA\left( {{\frac{{\partial^{2} w}}{{\partial x^{2} }}} + {\frac{\partial \psi }{\partial x}}} \right),\quad Q = K_{s} GA\left({{\frac{\partial w}{\partial x}} - \psi } \right) $$
(16)

in which E is Young’s modulus, υ is Poisson’s ratio, I is the second moment of cross-sectional area of the pipe about the Y-axis, and K s is the Timoshenko shear coefficient, for a circular micropipe which is approximately given by (Cowper 1966)

$$ K_{\text{s}} = {\frac{{6(1 + \upsilon )(1 + \alpha^{2} )^{2} }}{{(7 + 6\upsilon )(1 + \alpha^{2} )^{2} + (20 + 12\upsilon )\alpha^{2} }}} $$
(17)

where α is the ratio of internal to external diameter of the pipe (i.e., α = d/D).

According to Païdoussis (1998), the Hamilton’s principle for fluid-containing pipes may be written as

$$ \delta \int\limits_{{t_{1} }}^{{t_{2} }} {(\Re - m_{f} U^{2} u_{L} ){\text{d}}t} - \int\limits_{{t_{1} }}^{{t_{2} }} {m_{f} U(\dot{w}_{L} + Uw^{\prime}_{L} )\delta w_{L} {\text{d}}t} = 0 $$
(18)

where \( \Re = K - V \) is the Lagrangian of the closed system. Finally, substituting (13), (14) and (16) into (18), after considerable manipulation, one obtains the equations of motion

$$ (m_{\text{p}} + m_{\text{f}} ){\frac{{\partial^{2} u}}{{\partial t^{2} }}} - {\frac{E(1 - \upsilon )A}{(1 + \upsilon )(1 - 2\upsilon )}}\;{\frac{{\partial^{2} u}}{{\partial x^{2} }}} = 0, $$
(19)
$$ (m_{\text{p}} + m_{\text{f}} ){\frac{{\partial^{2} w}}{{\partial t^{2} }}} - K_{\text{s}} GA\left( {{\frac{{\partial^{2} w}}{{\partial x^{2} }}} - {\frac{\partial \psi }{\partial x}}} \right) + \frac{1}{4}l^{2} GA\left( {{\frac{{\partial^{4} w}}{{\partial x^{4} }}} + {\frac{{\partial^{3} \psi }}{{\partial x^{3} }}}} \right) + 2m_{\text{f}} U{\frac{{\partial^{2} w}}{\partial x\partial t}} + m_{\text{f}} U^{2}\; {\frac{{\partial^{2} w}}{{\partial x^{2} }}} = 0, $$
(20)
$$ (J_{\text{p}} + J_{\text{f}} ){\frac{{\partial^{2} \psi }}{{\partial t^{2} }}} - {\frac{E(1 - \upsilon )I}{(1 + \upsilon )(1 - 2\upsilon )}}\;{\frac{{\partial^{2} \psi }}{{\partial x^{2} }}} - K_{\text{s}} GA\left( {{\frac{\partial w}{\partial x}} - \psi } \right) - \frac{1}{4}l^{2} GA\left( {{\frac{{\partial^{3} w}}{{\partial x^{3} }}} + {\frac{{\partial^{2} \psi }}{{\partial x^{2} }}}} \right) = 0. $$
(21)

It is seen that (19) pertains to the axial vibration, while (20) and (21) are, respectively, associated with the flexural and torsional vibrations. The axial motion can be studied independently, since the axial displacement u(x, t) does not occur in (20) and (21). Equations 20 and 21 display all microscale pipes with both ends supported. In what follows, a micropipe with both ends simply supported will be considered. The corresponding boundary conditions can be written as

$$ u(0,t) = u(L,t) = 0,\quad w(0,t) = {\frac{\partial \psi (0,t)}{\partial x}} = 0,\quad w(L,t) = {\frac{\partial \psi (L,t)}{\partial x}} = 0. $$
(22)

Before closing this section, it is noted that when the current non-classical pipe model is suppressed by letting l = υ = 0, Eqs. 20 and 21 may be reduced to the equations of motion for pipes conveying fluid based on a classical Timoshenko beam theory. Therefore, the classical Timoshenko pipe model may be viewed as a special case of the non-classical Timoshenko pipe model developed in this study.

3 DQ formulation and eigenvalue equation

The differential quadrature method (DQM) (e.g., Wang and Ni 2009; Wang et al. 2008) is used to formulate solutions to (19–22). This method of numerical analysis was introduced to problems of solid mechanics in 1996 (Bert and Malik 1996) and will be used here directly.

The essence of DQM is that the partial derivative of a function with respect to a space variable at a grid point can be approximated at the weighted linear sum of the function values at all grid points in the whole domain. The computational domain of the microscale pipe is \( 0 \le x \le L. \) It is assumed that the pipe is divided into (N-1) intervals by N grid points with the coordinates given as x 1, x 2, …, x N . Here, we adopt the well-accepted mesh point distribution

$$ x_{n} = \frac{1}{2}\left[ {1 - \cos \left( {{\frac{n - 1}{N - 1}}\pi } \right)} \right] \times L,\quad n = 1,2, \ldots ,N. $$
(23)

By applying the DQM to (19–22) in the pipe domain \( 0 \le x \le L, \) one obtains the following discretized formulation of (19–22)

$$ (m_{\text{p}} + m_{\text{f}} ){\frac{{{\text{d}}^{2} u_{n} }}{{{\text{d}}t^{2} }}} - {\frac{E(1 - \upsilon )A}{(1 + \upsilon )(1 - 2\upsilon )}}\sum_{j = 1}^{N} {B_{nj} u_{j} } = 0 $$
(24)
$$ \begin{gathered} (m_{\text{p}} + m_{\text{f}} ){\frac{{{\text{d}}^{2} w_{n} }}{{{\text{d}}t^{2} }}} + 2m_{\text{f}} U\sum_{j = 1}^{N} {A_{nj} {\frac{{{\text{d}}w_{j} }}{{{\text{d}}t}}}} \hfill \\ \quad \quad \quad + \sum_{j = 1}^{N} {\left\{ {\left[ {m_{\text{f}} U^{2} - KGA} \right]B_{nj} + \frac{1}{4}l^{2} GAD_{nj} } \right\}w_{j} } + \sum_{j = 1}^{N} {\left[ {KGAA_{nj} + \frac{1}{4}l^{2} GAC_{nj} } \right]\psi_{j} } = 0 \hfill \\ \end{gathered} $$
(25)
$$ \begin{gathered} (J_{\text{f}} + J_{\text{p}} ){\frac{{{\text{d}}^{2} \psi_{n} }}{{{\text{d}}t^{2} }}} - \sum_{j = 1}^{N} {\left[ {{\frac{E(1 - \upsilon )I}{(1 + \upsilon )(1 - 2\upsilon )}} + \frac{1}{4}l^{2} GA} \right]B_{nj} \psi_{j} } \hfill \\ \quad \quad \quad - \sum_{j = 1}^{N} {\left[ {KGAA_{nj} + \frac{1}{4}l^{2} GAC_{nj} } \right]w_{j} } + KGA\psi_{n} = 0 \hfill \\ \end{gathered} $$
(26)
$$ u_{1} = u_{N} = 0,$$
(27a)
$$w_{1} = \sum_{j = 1}^{N} {A_{1j} \psi_{j} } = 0,$$
(27b)
$$w_{N} = \sum_{j = 1}^{N} {A_{Nj} \psi_{j} } = 0 $$
(27c)

where n = 1,…, N and A nj , B nj , C nj , and D nj are the weighting coefficients for the grid point at x n of the first-, second-, third- and fourth-order derivatives, respectively. The explicit expressions of the weighting coefficients have been given in Ni and Huang (2000) and will be used here directly.

As already stated, only the flexural and torsional vibrations will be studied in this article. Therefore, (25), (26), (27b), and (27c) can be expressed in the following matrix form:

$$ {\mathbf{KU}} + {\mathbf{C}}\dot{\mathbf{U}} + {\mathbf{M}}\ddot{\mathbf{U}} = {\mathbf{0}} $$
(28)

where \( {\mathbf{U}}^{\text{T}} = \left\{ {w_{2} ,w_{3} , \ldots ,w_{N - 1} ,\psi_{2} ,\psi_{3} , \ldots ,\psi_{N - 1} } \right\} \) including the degrees of freedom on the interior points of the domain. For a self-excited vibration, the solutions to (28) may be written in the following form:

$$ {\mathbf{U}} = {\bar{\mathbf{U}}}e^{\omega \,t} $$
(29)

where \( {\bar{\mathbf{U}}} \) is an undetermined function of amplitude, Im(ω) is the natural frequency of the microscale pipes containing fluid flow.

Substituting (29) into (28), one obtains a homogeneous equation corresponding to a generalized eigenvalue problem:

$$ \left( {\omega^{2} {\mathbf{M}} + \omega \,{\mathbf{C}} + {\mathbf{K}}} \right){\bar{\mathbf{U}}} = {\mathbf{0}}. $$
(30)

In order to obtain a non-trivial solution of the above equation, it is required that the determinant of the coefficient matrix vanishes, namely,

$$ {\text{d}}et\left( {\omega^{2} {\mathbf{M}} + \omega \,{\mathbf{C}} + {\mathbf{K}}} \right) = 0. $$
(31)

Therefore, one can compute the eigenvalues numerically from (31) and obtain the natural frequencies of the fluid-containing pipes with various parameter values.

4 Results and discussion

The available data in the literature shows that the flow velocity inside micro- or nano-scale pipes might exceed hundreds of meters per second (see, e.g., Supple and Quirke 2003; Whitby and Quirke 2007). Therefore, the range of 0 m/s ≤ U ≤ 100 m/s will be considered in the present study, which is within the practical range of microfluid flow velocity.

In order to illustrate the new Timoshenko beam model (non-classical model) for microscale pipes containing fluid, numerical calculations have been performed to analyze the free vibrations. In the following analysis, the cross-section of the micropipe is assumed to be circular. For rectangular cross-sectional system, similar results can be easily obtained. Sample results are shown in Figs. 2, 3, and 4. In these figures, the first non-dimensional natural frequencies \(\text{Im} \,(\bar{\omega }) = \text{Im}\,(\omega )L^2[(m_{\text{f}}+m_{\text{p}})/EI]^{1/2}\)for the flexural vibrations predicted by the current non-classical Timoshenko model and by the classical Timoshenko model are given, for various values of the outside diameter, D. Of course, similar diagrams can be constructed for higher-order natural frequencies (e.g., the natural frequencies in the second, third, or fourth mode), but without giving more new insight of the problem. The main reason is that the first (lowest) natural frequencies may represent the principle vibration characteristics of micropipes conveying fluid.

Fig. 2
figure 2

The natural frequencies based on couple stress theory and classical theory, respectively, as functions of the flow velocity, for the first mode of a pinned–pinned micropipe and υ = 0.38

Full size image
Fig. 3
figure 3

The natural frequencies based on couple stress theory and classical theory, respectively, as functions of the flow velocity, for the first mode of a pinned–pinned micropipe and υ = 0.0

Full size image
Fig. 4
figure 4

The critical flow velocities versus D, for υ = 0.38 and υ = 0.0

Full size image

For illustration convenience, the micropipe considered here is taken to be made of epoxy (see, e.g., Lam et al. 2003). The material properties of the micropipe used in the numerical calculations are chosen to be E = 1.44 GPa, ρ f = 1000 kg/m3, ρ p = 1220 kg/m3, υ = 0.38 (or υ = 0.0), and l = 17.6 μm (Lam et al. 2003). For comparison purpose, it is assumed that d/D = 0.8, L/D = 20.

From Fig. 2 (υ = 0.38), it is noted that the flow velocity (U) is the variable parameter. It can be seen that, at U = 0, the natural frequencies predicted by the current non-classical Timoshenko beam theory are about 1.565 times than that predicted by the classical Timoshenko beam theory when the outside diameter of the micropipe is approximately equal to the material length scale parameter (i.e., D = 20 μm). It is also shown that the difference between the two sets of values is diminishing when the outside diameter of the pipe becomes larger (e.g., D = 200 μm), and hence indicating that the size effect is only significant when the outside diameter of the micropipe is comparable to the material length scale parameter.

Figure 3 represents a similar diagram. In this figure, however, the Poisson’s ratio is chosen to be υ = 0.0. In this case, the results based on the non-classical Timoshenko beam model for microscale pipes conveying fluid will get close to those based on the size-dependent Euler beam model (Wang 2010). Again, the natural frequencies predicted by the current non-classical Timoshenko beam theory are generally higher than those predicted by the classical Timoshenko beam theory. When U = 0 and D = 20 μm, the natural frequency predicted by the non-classical theory is about 2.177 times than that obtained by the classical theory. Therefore, the Poisson’s effect on the natural frequencies of fluid-containing micropipes is found to be pronounced. As can be expected, therefore, for natural frequencies predicted with smaller Poisson’s ratio, the difference between the non-classical theory and the classical theory becomes significant, indicating that the Poisson’s effect could not always be neglected.

In Fig. 3, at U = 0, the dimensionless natural frequency predicted by the classical Timoshenko beam model is found to be \( \text{Im} \,(\bar{\omega }) \approx 9.822 \). This value of natural frequency is very close to the value predicted by the classical Euler beam model for macroscale pipes conveying fluid (Païdoussis 1998), since the Poisson’s ratio is assumed to be 0 in this figure. This good agreement demonstrates the validity of the current theoretical model.

From Figs. 2 and 3, it is clearly seen the natural frequencies may become zero with increasing flow velocity. This implies that the micropipe would lose stability at a critical flow velocity (U cr). The form of instability is divergence (buckling), since the system is conservative.

Now, let us turn our attention to the critical flow velocity at which the buckling instability occurs. The results are given in Fig. 4. For comparison convenience, we define a dimensionless flow velocity as \( u = UL\left[ {{{m_{\text{f}} } \mathord{\left/ {\vphantom {{m_{\text{f}} } {(EI}}} \right. \kern-\nulldelimiterspace} {(EI}})} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \). It can be easily found that the critical flow velocity predicted by the classical Timoshenko model is U cr ≈ 45.04 m/s for the case of υ = 0. The corresponding dimensionless value is u cr = 3.13, which is very close to the exact value (u cr = π) predicted by the classical Euler beam theory (Païdoussis 1998). Such a good agreement further demonstrates the validity of the current model. From Fig. 4, it also can be observed that the critical flow velocities predicted by the non-classical Timoshenko beam model are generally higher than those predicted by the classical beam model. The size effects are pronounced, especially for smaller pipe diameter. Therefore, it would seem that the internal material length scale makes the micropipes much stable, which favor them for microfluidic device and resonator applications.

5 Conclusions

Microscale pipes containing internal fluid flow enable novel applications for microfluidic devices and for fundamental studies of the effects of micro-size on fluid–structure interactions. For some reasons, the classical continuum theory and the nonlocal elasticity theory may be inadequate for exactly predicting the vibration properties of pipes containing internal fluid on the micron scale. Up to date, a general theoretical framework on this topic is still missing.

This article performs a theoretical analysis of microscale pipes containing fluid flow, and develops a microstructure-dependent Timoshenko model by using a modified couple stress theory. This new non-classical model for micropipes, motions of which are governed by three displacement variables, has introduced an additional material constant, which enable to capture the size effect on the vibration properties of microscale pipes conveying fluid. The Poisson’s effect is also included in this non-classical Timoshenko pipe model.

The numerical results obtained quantitatively show that the material length scale parameter on the natural frequency and critical flow velocity is large, especially when the outside diameter of the micropipe is comparable to the material length scale parameter. The Poisson ratio is also shown to play an important role in the vibration analysis of such a microfluidic pipe system. These results highlight the importance of considering the effects of microstructure size and Poisson ratio in the design of microscale devices, sensors, and resonators containing internal fluid flow.

Finally, it should be mentioned that the non-classical Timoshenko model developed in this article may be applicable to a wide range of fluid-conveying devices for, either rectangle or circular cross-section, either micro- or nano-scale pipes, different length scales, and various structural materials. The present study might be useful for the design and improvement of microfluidic and nanofluidic device applications.