1 Introduction

The outstanding paper of Iijima in Nature (Iijima 1991) has put carbon nanotubes in center of attention for almost two decades. This has motivated the nanoscientists to propagate further patterns of noncarbon tubular syntheses (Cumings and Zettl 2000; Wu et al. 2003; Goldberger et al. 2003). Of all the fulfilling features of tubular nanomaterials, one can mention their application in nanofluidic systems like the fluid storage, fluid transport and drug delivery (Hummer et al. 2001; Gao and Bando 2002; Adali 1737; Foldvari and Bagonluri 2008).

A major primacy must be given to investigate concerning mechanical phenomena to achieve the apex of the potential of fluid-conveying hollow cylinders. Generally, the mechanical behavior of nanostructures is investigated in two categories: the classical and nonclassical theories. Incapability of the classical theory in capturing the size effect has made the reliability of this analysis doubtful. To overcome this difficulty, different size-dependent nonclassical continuum theories such as the strain gradient elasticity, couple stress elasticity, nonlocal elasticity and the surface elasticity theories have been proposed (Mindlin and Tiersten 1962; Eringen 1972; Lam et al. 2003; Wang 2010); these modified theories have been effectively employed in several papers (Ansari et al. 2012a, b, 2011, 2013a, b, 2015a; b; Wang 2009; Tang et al. 2014; Ghayesh et al. 2013; Zhen and Fang 2015).

The significant effect of the surface stress on the elastic behavior of nanostructures has been demonstrably confirmed by scientists (Wang and Feng 2007; He and Lilley 2008). Based on the continuum mechanics, Gurtin and Murdoch (1975, 1978) introduced a theoretical method capable of including the surface stress effect in the mechanical analysis of nanostructures. They treated the surface as a mathematical layer of tiny thickness with different material properties from the underlying bulk which is totally bonded by the membrane. Wang (2010) studied the vibration behavior of fluid-conveying nanotubes with consideration of surface effects. He showed that for small tubes with large aspect ratios, the surface stress can affect the stability of the nanotubes to a great measure.

Despite the large investigations on the nonlinear vibration behavior of macro- and even microbeams (Ghayesh 2012; Ghayesh et al. 2011; Asghari et al. 2012; Moeenfard et al. 2011; Ramezani 2012; Setoodeh and Afrahim 2014; Xia and Wang 2010; Kural and Özkaya 2015), only a small percentage of literature is concerned with the nonlinear vibration of nanobeams. This phenomenon is due to the induced mid-plane stretching during the transverse deflections and is very often in the large amplitude deflections. Neglecting this nonlinearity completely affects the static and vibration responses, and the model is unable to predict the details of the static or dynamic responses (Khadem and Rezaee 2002; Hassanpour et al. 2010; Zhang et al. 2014; Lü et al. 2015).

Rasekh and Khadem (2009), in the context of the Euler–Bernoulli beam theory, studied the influence of internal moving fluid and compressive axial load on the nonlinear vibration and stability of embedded carbon nanotubes. Ali-Asgari et al. (2013) investigated the nonlinear vibration of carbon nanotube conveying fluid according to the nonlocal theory and von-Karman’s stretching. They examined the effects of mid-plane stretching, nonlocal parameter and their coupling model. Ke and Wang (2011) studied the vibration and instability of fluid-conveying double-walled carbon nanotubes based on the modified couple stress theory and the Timoshenko beam theory. Based on the thermal elasticity theory, the nonlocal Euler–Bernoulli beam model, Zhen et al. (2011) examined the transverse vibration and instability of fluid-conveying double-walled carbon nanotubes embedded in biological soft tissue. According to the Hamilton principle and thermal elasticity theory, Chang (2013) studied the dynamic response variability of nonlinear thermal–mechanical vibration of the fluid-conveying double-walled carbon nanotubes by considering the effects of the temperature change, geometric nonlinearity and nonlinearity of van der Waals force. Arani et al. (2013) studied the nonlinear free vibration and instability of fluid-conveying double-walled boron nitride nanotubes embedded in viscoelastic medium. They also considered the surface stress effects in two earlier works (Arani et al. 2014; Arani and Roudbari 2014). In these papers, linear analyses of surface stress effects on the free vibration of a CNT and the wave propagation of a SWBNNT were presented, respectively. In both cases, the fluid-conveying nanotube was modeled as the Euler–Bernoulli beam, different fields were considered, and the nonlocal elasticity theory was applied. Wang (2012) investigated the nonlinear post-buckling behavior of conveying fluid nanobeams with the consideration of surface effects. The Euler–Bernoulli beam theory was employed, and an analytical method was used to solve the governing equation for both end clamped and both end pinned boundary conditions.

Recently, Ansari et al. (2015c) developed a linear Timoshenko beam model including the surface effect to investigate the linear free vibration and instability of fluid-conveying nanoscale pipes. In this regard and to achieve the nonlinearity effects, the main goal of the authors is to extend their previous study on the linear dynamics of conveying fluid nanoscale pipes with considering surface stress in present work. The present study deals with the geometrically nonlinear vibration and stability of nanoscale pipe conveying fluid incorporating surface stress effect. Hamilton’s principle and the Gurtin–Murdoch continuum elasticity are used in the skeleton of Timoshenko beam theory to derive the governing equations of motion and associated boundary conditions incorporating the surface stress effect. By employing the GDQ and the harmonic balance methods, the nonlinear differential equations are discretized. Then, the Newton–Raphson method is used to numerically solve the discretized equations.

2 Formulation of motion and corresponding boundary conditions

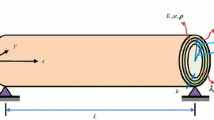
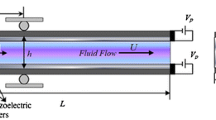
Regarding Fig. 1, a schematic of a flow-induced nanoscale pipe with length L and thickness h is considered with conveying incompressible fluid of the mass density ρ and constant velocity V. To model the internal flow, a continuum-based plug-like flow is employed in which fluid is considered as an infinitely flexible rod-like structure flowing through the nanoscale pipe (Khosravian and Rafii-Tabar 2008). It should be noted that the fluid–structure interaction based on the plug-like flow is according to the assumption of no-slip boundary conditions. Based on the investigations done by Wang and Ni (2009) and Mirramezani and Mirdamadi (2011, 2013), it was observed that the effect of slip boundary condition on the liquid nanobehavior is negligible as compared to that in the case of a continuum flow regime. Considering the slip boundary condition could not change the critical liquid nanoflow velocity noticeably. Therefore, the simple plug-like flow is an acceptable model for the interaction between the fluid and the nanopipes. It is worth to remark that when the diameter of the nanopipe is sufficiently small, the internal fluid flow could not be treated as a continuum. A bulk part and two additional inner and outer surface layers constitute the outside nanoscale pipe. The properties of the bulk part are Young’s modulus E, Poisson’s ratio \(\nu\) and mass density \(\rho\). Two inner and outer surface layers are considered to have Lam’s surface constants \(\lambda_{s}\) and \(\mu_{s}\), mass density \(\rho_{s}\) and the surface residual tension \(\tau_{s}\). Symbols d i and d o are used to denote the inner and outer diameters of the bulk part, respectively.

Fig. 1
figure 1

A schematic of a flow-induced nanoscale pipe

Full size image

The Cartesian coordinate system (x, y, z) is considered with the x-, y- and z-axes along the length of the deflected nanopipe, the neutral axis and the transverse direction, respectively.

Considering the first-order shear deformation and the Timoshenko beam theories, the displacements of an arbitrary point in the nanoscale pipe along the x-, y- and z-axes can be written in a general form as

$$u_{x} = u\left( {x,t} \right) + z\psi \left( {x,t} \right), \quad u_{y} = 0, \quad u_{z} = w\left( {x,t} \right)$$
(1)

where u(x, t), w(x, t) and \(\psi \left( {x,t} \right)\) are the axial displacement of the center of sections, the lateral deflection of the pipe and the rotation angle of the cross section with respect to the vertical direction, respectively. Employing the von-Karman relation, one can represent the nonlinear strain–displacement relations of a nanopipe subjected to large amplitude vibrations as

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} + z\frac{\partial \psi }{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} ,\quad \varepsilon_{xz} = \frac{1}{2}\left( {\frac{\partial w}{\partial x} + \psi } \right)$$
(2)

Additionally, using the linear elasticity, the stress components can be written as

$$\sigma_{xx} = \left( {\lambda + 2\mu } \right)\left[ {\frac{\partial u}{\partial x} + z\frac{\partial \psi }{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right],\quad \sigma_{xz} = \mu \left( {\frac{\partial w}{\partial x} + \psi } \right)$$
(3)

in which \(\lambda = E\nu /\left( {1 - \nu^{2} } \right)\), \(\mu = E/\left( {2\left( {1 + \nu } \right)} \right)\) stand for Lam’s constants.

One can incorporate the size effect into the conventional continuum model through the Gurtin–Murdoch theory. Given the atomic essence of nanostructures, interactions between the elastic surface and bulk material are unavoidable. Accordingly, nanostructures undergo in-plane loads in various directions which lead to the stresses on the surfaces of the bulk of nanopipes. Referring to the Gurtin–Murdoch theory, these surface stresses can be calculated by using surface constitutive equations as

$$\begin{array}{*{20}l} {\sigma_{\alpha \beta }^{s} = \tau_{s} \delta_{\alpha \beta } + (\tau_{s} + \lambda_{s} )\varepsilon_{\gamma \gamma } \delta_{\alpha \beta } + 2(\mu_{s} - \tau_{s} )\varepsilon_{\alpha \beta } + \tau_{s} u_{\alpha ,\beta }^{s} } \hfill \\ {\sigma_{\alpha z}^{s} = \tau_{s} u_{z,\alpha }^{s} } \hfill \\ \end{array} ;\quad ( \alpha , \beta = x,y)$$
(4)

Now, the surface stress components with respect to the displacement constituents can be achieved as follows

$$\sigma_{xx}^{s} = \left( {\lambda_{s} + 2\mu_{s} } \right)\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + z\frac{\partial \psi }{\partial x}} \right] - \frac{{\tau_{s} }}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \tau_{s} ,\quad \sigma_{xz}^{s} = \tau_{s} \frac{\partial w}{\partial x}$$
(5)

In the classical beam theories, the stress component \(\sigma_{zz}\) is small in comparison with the \(\sigma_{xx}\) and \(\sigma_{xz}\) and can be neglected. But when it comes to Gurtin–Murdoch theory, this assumption is not effective to satisfy the surface conditions. To tackle this issue, it is assumed that the stress component \(\sigma_{zz}\) varies linearly through the beam thickness (Lu et al. 2006). Considering this assumption, the stress component \(\sigma_{zz}\) can be achieved as

$$\sigma_{zz} = \frac{{\left( {\frac{{\partial \sigma_{xz}^{s + } }}{\partial x} - \rho_s^+ \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - \left( {\frac{{\partial \sigma_{xz}^{s - } }}{\partial x} - \rho_s^- \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)}}{2} + \frac{{\left( {\frac{{\partial \sigma_{xz}^{s + } }}{\partial x} - \rho_s^+ \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) + \left( {\frac{{\partial \sigma_{xz}^{s - } }}{\partial x} - \rho_s^- \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)}}{h}z$$
(6)

By employing Eq. (5), \(\sigma_{zz}\) can be rewritten as

$$\sigma_{zz} = \frac{2z}{h}\left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)$$
(7)

Introducing Eq. (7) into the components of stress for the bulk of the nanopipe leads to

$$\sigma_{xx} = \left( {\lambda + 2\mu } \right)\left[ {\frac{\partial u}{\partial x} + z\frac{\partial \psi }{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] + \frac{2\nu z}{{\left( {1 - \nu } \right)h}}\left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right),\quad \sigma_{xz} = \mu \left( {\frac{\partial w}{\partial x} + \psi } \right).$$
(8)

Based on the continuum surface elasticity theory, the strain energy of a nanopipe incorporating the surface stress effect would be

$$\begin{aligned} \varPi_{s} & = \frac{1}{2}\mathop \int \limits_{x} \mathop \int \limits_{A} \sigma_{ij} \varepsilon_{ij} {\text{d}}A{\text{d}}x + \frac{1}{2}\left( {\mathop \int \limits_{{S^{ + } }} \sigma_{ij}^{s} \varepsilon_{ij} {\text{d}}S^{ + } + \mathop \int \limits_{{S^{ - } }} \sigma_{ij}^{s} \varepsilon_{ij} {\text{d}}S^{ - } } \right) \\ & = \frac{1}{2}\mathop \int \limits_{x} \left\{ {\left( {N_{xx} + \bar{N}_{xx} } \right)\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] + \left( {M_{xx} + \bar{M}_{xx} } \right)\frac{\partial \psi }{\partial x} + Q_{x} \left( {\frac{\partial w}{\partial x} + \psi } \right) + \bar{Q}_{x} \frac{\partial w}{\partial x}} \right\}{\text{d}}x \\ \end{aligned}$$
(9)

in which

$$\begin{aligned} N_{xx} & = \left( {\lambda + 2\mu } \right)A\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right],\quad Q_{x} = \mu k_{s} A\left( {\frac{\partial w}{\partial x} + \psi } \right), \\ M_{xx} & = \left( {\lambda + 2\mu } \right)I\frac{\partial \psi }{\partial x} + \frac{2\nu I}{{\left( {1 - \nu } \right)h}}\left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }} } \right). \\ \end{aligned}$$
(10a)
$$\begin{aligned} \bar{N}_{xx} & = \mathop \int \limits_{S} \sigma_{xx}^{s} {\text{d}}s = \pi \left( {d_{i} + d_{o} } \right)\left( {\lambda_{s} + 2\mu_{s} } \right)\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] \\ & \quad - \;\frac{{\tau_{s} \pi \left( {d_{i} + d_{o} } \right)}}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \tau_{s} \pi \left( {d_{i} + d_{o} } \right). \\ \bar{M}_{xx} & = \mathop \int \limits_{s} \sigma_{xx}^{s} z{\text{d}}s = \frac{{\left( {\lambda_{s} + 2\mu_{s} } \right)\pi \left( {d_{i}^{3} + d_{o}^{3} } \right)}}{8}\frac{\partial \psi }{\partial x}, \\ \bar{Q}_{x} & = \mathop \int \limits_{s} \sigma_{xz}^{s} {\text{d}}s = \tau_{s} \pi \left( {d_{i} + d_{o} } \right)\frac{\partial w}{\partial x}. \\ \end{aligned}$$
(10b)

in which k s denotes shear correction factor.

The kinetic energy of nanopipe \(\varPi_{T}\) and the kinetic energy of induced fluid \(\varPi_{{T_{f} }}\) can be written as

$$\varPi_{T} = \frac{1}{2}\mathop \int \limits_{x} \left\{ {\left[ {\rho A + \pi \left( {d_{i} + d_{o} } \right)\rho_{s} } \right]\left[ {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right] + \left[ {\rho I + \frac{{\pi \rho_{s} \left( {d_{i}^{3} + d_{o}^{3} } \right)}}{8}} \right]\left( {\frac{\partial \psi }{\partial t}} \right)^{2} } \right\}{\text{d}}x$$
(11a)
$$\begin{aligned} \varPi_{{T_{f} }} & = \frac{1}{2}\mathop \int \limits_{0}^{L} \mathop \int \limits_{{A_{f} }}^{ } \rho_{f} \left\{ {\left( {\frac{\partial w}{\partial t} + V\frac{\partial w}{\partial x}} \right)^{2} + \left( {\frac{\partial u}{\partial t} + z\frac{\partial \psi }{\partial t} + V} \right)^{2} } \right\}{\text{d}}A_{f} {\text{d}}x \\ & = \frac{1}{2}\mathop \int \limits_{0}^{L} \left\{ {\rho_{f} A_{f} \left( {\frac{\partial w}{\partial t} + V\frac{\partial w}{\partial x}} \right)^{2} + \rho_{f} A_{f} \left( {\frac{\partial u}{\partial t}} \right)^{2} + \rho_{f} A_{f} V^{2} + \, 2\rho_{f} A_{f} \frac{\partial u}{\partial t} + \rho_{f} I_{f} \left( {\frac{\partial \psi }{\partial t}} \right)^{2} } \right\}{\text{d}}x \\ \end{aligned}$$
(11b)

In addition, the work \(\varPi_{P}\) done by the transverse force F(x, t) can be written as

$$\varPi_{P} = \mathop \int \limits_{0}^{L} F\left( {x,t} \right){\text{wd}}x$$
(12)

According to the Hamilton principle:

$$\delta \mathop \int \limits_{{t_{1} }}^{{t_{2} }} (\varPi_{T} - \varPi_{s} + \varPi_{P} ){\text{d}}t = 0$$
(13)

By taking the variation of u, w and \(\psi\), integrating by parts and finally setting the coefficients of \(\delta u\), \(\delta w\) and \(\delta \psi\) equal to zero, the governing equations of motion (14a–14c) and the associated boundary conditions (14d–14f) will be attained as

$$\frac{{\partial (N_{xx} + \tilde{N}_{xx} )}}{\partial x} = \left( {\rho A + \rho_{f} A_{f} + \pi \left( {d_{i} + d_{o} } \right)\rho_{s} } \right)\frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(14a)
$$\begin{aligned} & \frac{{\partial (Q + \tilde{Q})}}{\partial x} + \frac{\partial }{\partial x}\left( {\left( {N_{xx} + \tilde{N}_{xx} } \right)\frac{\partial w}{\partial x}} \right) - \rho_{f} A_{f} \left( {2V\frac{{\partial^{2} w}}{\partial t\partial x} + V^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & \quad - \;F(x,t) = \left( {\rho A + \rho_{f} A_{f} + \pi \left( {d_{i} + d_{o} } \right)\rho_{s} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }}; \\ \end{aligned}$$
(14b)
$$\frac{{\partial \left( {M_{xx} + \tilde{M}_{xx} } \right)}}{\partial x} - Q = \left( {\rho I + \rho_{f} I_{f} + \frac{{\pi \rho_{s} \left( {d_{i}^{3} + d_{o}^{3} } \right)}}{8}} \right)\frac{{\partial^{2} \psi }}{{\partial t^{2} }}$$
(14c)
$$\delta u = 0\quad {\text{or}}\quad \delta \left( {N_{xx} + \tilde{N}_{xx} } \right) = 0$$
(14d)
$$\delta w = 0\quad {\text{or}}\quad \delta \left( {\left( {N_{xx} + \tilde{N}_{xx} } \right)\frac{\partial w}{\partial x} + Q + \tilde{Q}} \right) = 0$$
(14e)
$$\delta \psi = 0\quad {\text{or}}\quad \delta \left( {M_{xx} + \tilde{M}_{xx} } \right) = 0$$
(14f)

For the simply supported boundary condition (SS) and clamped boundary condition (C), one can write

$$u = w = M_{xx} + \tilde{M}_{xx} = 0$$
(15a)
$$u = w = \psi = 0$$
(15b)

Let us define stiffness components and inertia-related terms as

$$A_{11} = \left( {\lambda + 2\mu } \right)A + \pi \left( {d_{i} + d_{o} } \right)\left( {\lambda_{s} + 2\mu_{s} } \right),\quad A_{33} = \pi \left( {d_{i} + d_{o} } \right)\tau_{s} ,\quad A_{55} = \mu k_{s} A,$$
$$D_{11} = \left( {\lambda + 2\mu } \right)I + \frac{{\left( {\lambda_{s} + 2\mu_{s} } \right)\pi \left( {d_{i}^{3} + d_{o}^{3} } \right)}}{8},\quad E_{11} = \frac{{2\nu I\tau_{s} }}{{\left( {1 - \nu } \right)h}}$$
$$I_{0} = \rho A + \rho_{f} A_{f} + \pi \rho_{s} \left( {d_{i} + d_{o} } \right), \quad I_{2} = \rho I + \rho_{f} I_{f} + \frac{{\pi \rho_{s} \left( {d_{i}^{3} + d_{o}^{3} } \right)}}{8},\quad G = \frac{{2\nu I\rho_{s} }}{{\left( {1 - \nu } \right)h}}$$
(16)

Substituting above parameters in the governing differential equations of motion leads to

$$A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \left( {A_{11} - A_{33} } \right)\frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }},$$
(17a)
$$\begin{aligned} & A_{55} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial \psi }{\partial x}} \right) + 2A_{33} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{f} A_{f} \left( {2 V\frac{{\partial^{2} w}}{\partial x\partial t} + V^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + A_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\frac{\partial w}{\partial x} \\ & \quad + \;A_{11} \left( {\frac{\partial u}{\partial x} + \frac{1}{2} \left( {\frac{\partial w}{\partial x}} \right)^{2} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} - A_{33} \left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{A_{33} }}{2} \left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}, \\ \end{aligned}$$
(17b)
$$D_{11} \frac{{\partial^{2} \psi }}{{\partial x^{2} }} + E_{11} \frac{{\partial^{3} w}}{{\partial x^{3} }} - A_{55} \left( {\frac{\partial w}{\partial x} + \psi } \right) = I_{2} \frac{{\partial^{2} \psi }}{{\partial t^{2} }} + G\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}.$$
(17c)

Once the following dimensionless quantities are defined

$$\begin{array}{l} u \to \frac{u}{h}, w \to \frac{w}{h}, x \to \frac{x}{L}, \eta = \frac{L}{h}, \tau = \frac{t}{L}\sqrt {\frac{{A_{110} }}{{I_{00} }}} ,I_{0}^{*} = \frac{{I_{0} }}{{I_{00} }},I_{2}^{*} = \frac{{I_{2} }}{{I_{00} h^{2} }},g = \frac{G}{{I_{00} h^{2} }}, \hfill \\ \left\{ {a_{11} ,a_{13} ,a_{33} } \right\} = \left\{ {\frac{{A_{11} }}{{A_{110} }},\frac{{A_{13} }}{{A_{110} }},\frac{{A_{33} }}{{A_{110} }}} \right\},d_{11} = \frac{{D_{11} }}{{A_{110} h^{2} }},e_{11} = \frac{{E_{11} }}{{A_{110} h^{2} }}, \hfill \\ K_{b} = \frac{{2\rho_{f} A_{f} V}}{{\sqrt {A_{110} I_{00} } }},v = \sqrt {\frac{{\rho_{f} A_{f} }}{{A_{110} }}} V, \hfill \\ \end{array}$$
(18)

the governing equations of motion and the associated boundary conditions of the nanopipe can be stated in normalized forms as

$$a_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\left( {a_{11} - a_{33} } \right)}}{\eta }\frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} = I_{0}^{*} \frac{{\partial^{2} u}}{{\partial \tau^{2} }},$$
(19a)
$$\begin{aligned} & a_{55} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \eta \frac{\partial \psi }{\partial x}} \right) + a_{33} \frac{{\partial^{2} w}}{{\partial x^{2} }} - K_{b} \frac{{\partial^{2} w}}{\partial x\partial \tau } - v^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{a_{11} }}{\eta }\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{1}{\eta }\frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\frac{\partial w}{\partial x} \\ & \quad + \;\frac{{a_{11} }}{\eta }\left( {\frac{\partial u}{\partial x} + \frac{1}{2\eta }\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{3a_{33} }}{{2\eta^{2} }} \left( {\frac{\partial w}{\partial x}} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} = I_{0}^{*} \frac{{\partial^{2} w}}{{\partial \tau^{2} }}, \\ \end{aligned}$$
(19b)
$$d_{11} \frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{e_{11} }}{\eta }\frac{{\partial^{3} w}}{{\partial x^{3} }} - a_{55} \eta \left( {\frac{\partial w}{\partial x} + \eta \psi } \right) = I_{2}^{*} \frac{{\partial^{2} \psi }}{{\partial \tau^{2} }} + \frac{g}{\eta }\frac{{\partial^{3} w}}{{\partial x\partial \tau^{2} }}.$$
(19c)

Simply supported boundary condition (SS)

$$u = w = \frac{{e_{11} }}{\eta }\frac{{\partial^{2} w}}{{\partial x^{2} }} + d_{11} \frac{\partial \psi }{\partial x} = 0$$
(20a)

Clamped boundary condition (C)

$$u = w = \psi = 0$$
(20b)

in which \(A_{110} = A\left( {\lambda + 2\mu } \right)\) and \(I_{00} = \rho A\).

3 Numerical solution

In solution procedure, the GDQ method (Shu 2000) is used to discretize the set of the nonlinear equations of motion and boundary conditions. In first step, the grid points are located at the Chebyshev–Gauss–Lobatto points as

$$x_{i} = \frac{1}{2}\left( {1 - \cos \frac{i - 1}{n - 1}\pi } \right);\quad i = 1,2, \ldots ,n$$
(21)

Then, vectors \({\mathbf{u}}\), \({\mathbf{w}}\) and \({\varvec{\Psi}}\) are defined as

$${\mathbf{u}}_{n \times 1} = [u_{1} u_{2} \ldots u_{n} ]^{\text{T}} ,\quad \varvec{ }{\mathbf{w}}_{n \times 1} = [w_{1} w_{2} \ldots w_{n} ]^{\text{T}} ,\quad \varvec{ }{\varvec{\Psi}}_{n \times 1} = [\psi_{1} \psi_{2} \ldots \psi_{n} ]^{\text{T}}$$
(22)

Following are the discretized form of governing equations

$$a_{11} {\mathbf{D}}^{(2)} {\mathbf{u}} + \frac{{a_{11} - a_{33} }}{\eta }\left( {{\mathbf{D}}^{(1)} {\mathbf{w}}} \right)\left( {{\mathbf{D}}^{(2)} {\mathbf{w}}} \right) = I_{0}^{*} {\mathbf{\textit{\"{u}}}}$$
(23a)
$$\begin{aligned} & a_{55} \left( {{\mathbf{D}}^{(2)} {\mathbf{w}} + \eta {\mathbf{D}}^{(1)} {\varvec{\Psi}}} \right) + a_{33} {\mathbf{D}}^{(2)} {\mathbf{w}} - K_{b} {\mathbf{D}}^{(1)} {\dot{\mathbf{w}}} - v^{2} {\mathbf{D}}^{(2)} {\mathbf{w}} \\ & \quad + \;\frac{{a_{11} }}{\eta }\left( {\left( {{\mathbf{D}}^{(2)} {\mathbf{u}}} \right) + \frac{1}{\eta }\left( {{\mathbf{D}}^{(2)} {\mathbf{w}}} \right)\left( {{\mathbf{D}}^{(2)} {\mathbf{w}}} \right)} \right)\left( {{\mathbf{D}}^{(1)} {\mathbf{w}}} \right) \\ & \quad + \;\frac{{a_{11} }}{\eta }\left( {\left( {{\mathbf{D}}^{(1)} {\mathbf{u}}} \right) + \frac{1}{2\eta }\left( {{\mathbf{D}}^{(1)} {\mathbf{w}}} \right)\left( {{\mathbf{D}}^{(1)} {\mathbf{w}}} \right)} \right)\left( {{\mathbf{D}}^{(2)} {\mathbf{w}}} \right) \\ & \quad - \;\frac{{3a_{33} }}{{2\eta^{2} }}\left( {{\mathbf{D}}^{(1)} {\mathbf{w}}} \right)\left( {{\mathbf{D}}^{(1)} {\mathbf{w}}} \right)\left( {{\mathbf{D}}^{(2)} {\mathbf{w}}} \right) = I_{0}^{*} {\mathbf{\textit{\"{w}}}}, \\ \end{aligned}$$
(23b)
$$d_{11} {\mathbf{D}}^{\left( 2 \right)} {\varvec{\Psi}} + \frac{{e_{11} }}{\eta }{\mathbf{D}}^{\left( 3 \right)} {\mathbf{w}} - a_{55} \eta \left( {{\mathbf{D}}^{\left( 1 \right)} {\mathbf{w}} + \eta {\varvec{\Psi}}} \right) = I_{2}^{*}{\ddot{\mathbf{\varPsi}}} + \frac{g}{\eta }{\mathbf{D}}^{\left( 1 \right)} {\mathbf{\textit{\"{w}}}}$$
(23c)

where

$$D_{ij}^{\left( 1 \right)} = \frac{{\mathop \prod \nolimits_{k = 1,k \ne i}^{n} \left( {x_{i} - x_{k} } \right)}}{{\left( {x_{i} - x_{j} } \right)\mathop \prod \nolimits_{k = 1,k \ne j}^{n} \left( {x_{j} - x_{k} } \right)}} ,\quad i = j = 1,2, \ldots ,n,\quad i \ne j$$
(24a)
$$D_{ij}^{\left( r \right)} = r\left( {D_{ii}^{{\left( {r - 1} \right)}} D_{ij}^{\left( 1 \right)} - \frac{{D_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right), \quad i = j = 1,2, \ldots ,n,\quad i \ne j \quad r = 2,3, \ldots ,n - 1;$$
(24b)

Herein, the harmonic balance method (Keller 1977; Doedel et al. 1998) is used to solve the discretized equations. According to this technique, one can assume the solutions as following forms

$${\mathbf{u}} = \mathop \sum \limits_{i = 1}^{n} {\mathbf{x}}_{{1{\text{i}}}} \cos (i\omega t) + \mathop \sum \limits_{i = 1}^{n} {\mathbf{x}}_{{2{\text{i}}}} \sin \left( {i\omega t} \right)$$
(25a)
$${\mathbf{w}} = \mathop \sum \limits_{i = 1}^{n} {\mathbf{y}}_{{1{\text{i}}}} \cos (i\omega t) + \mathop \sum \limits_{i = 1}^{n} {\mathbf{y}}_{{2{\text{i}}}} \sin \left( {i\omega t} \right)$$
(25b)
$${\varvec{\Psi}} = \mathop \sum \limits_{i = 1}^{n} {\mathbf{z}}_{{1{\text{i}}}} \cos (i\omega t) + \mathop \sum \limits_{i = 1}^{n} {\mathbf{z}}_{{2{\text{i}}}} \sin \left( {i\omega t} \right)$$
(25c)

By inserting these solutions in Eq. (23) and using the Fourier series, the governing equations will be obtained with terms of \(\cos (i\omega t)\) and \(\sin \left( {i\omega t} \right)\). By equating similar terms, 6(n) sets of algebraic equations will be attained which can be solved through the Newton–Raphson method with a given value (a) for the middle sample point of y11 as a dimensionless amplitude of vibration.

Moreover, the dynamic stability of nanopipe around the post-buckling configuration is analyzed here. For this purpose, buckled configuration is obtained by dropping time-dependent terms in governing equations and solving the generalized eigenvalue problem in which the flow velocity is the eigenvalue parameter. Then, the dynamic response under post-buckling is considered as below

$$\begin{aligned} u\left( {x,\tau } \right) & = u_{s} \left( x \right) + u_{d} \left( {x,\tau } \right) \\ w\left( {x,\tau } \right) & = w_{s} \left( x \right) + w_{d} \left( {x,\tau } \right) \\ \psi \left( {x,\tau } \right) & = \psi_{s} \left( x \right) + \psi_{d} \left( {x,\tau } \right) \\ \end{aligned}$$
(26)

where u s, w s and \(\psi_{s}\) denote first buckled configuration and \(u_{d}\), \(w_{d}\) and \(\psi_{d}\) are small disturbances around the corresponding static response. Now, by having buckled configurations in hand, dynamic responses are achieved by inserting Eq. (26) in Eq. (19). Similarly, the GDQ method is applied; by vectorizing \({\mathbf{u}}_{s} ,{\mathbf{w}}_{s} ,{\varvec{\uppsi}}_{s} ,{\mathbf{u}}_{d} ,{\mathbf{w}}_{d} ,{\varvec{\uppsi}}_{d}\), new discretized equations are

$$a_{11} {\mathbf{D}}^{\left( 2 \right)} {\mathbf{u}}_{d} + \frac{{a_{11} - a_{33} }}{\eta }{\mathbf{D}}_{{{\mathbf{ww}}}}^{12} = I_{0}^{*}{\mathbf{\textit{\"{u}}}}_{d}$$
(27a)
$$\begin{aligned} & a_{55} \left( {{\mathbf{D}}^{\left( 2 \right)} {\mathbf{w}}_{d} + \eta {\mathbf{D}}^{\left( 1 \right)} {\varvec{\Psi}}_{d} } \right) + a_{33} {\mathbf{D}}^{\left( 2 \right)} {\mathbf{w}}_{d} - K_{b} {\mathbf{D}}^{\left( 1 \right)} {\dot{\mathbf{w}}}_{d} - v^{2} {\mathbf{D}}^{\left( 2 \right)} {\mathbf{w}}_{d} \\ \quad + \;\frac{{a_{11} }}{\eta }\left( {{\mathbf{D}}_{{{\mathbf{uw}}}}^{21} + \frac{1}{\eta }{\mathbf{D}}_{{{\mathbf{www}}}}^{121} } \right) + \frac{{a_{11} }}{\eta }\left( {{\mathbf{D}}_{{{\mathbf{uw}}}}^{12} + \frac{1}{2\eta }{\mathbf{D}}_{{{\mathbf{www}}}}^{112} } \right) - \frac{{3a_{33} }}{{2\eta^{2} }}{\mathbf{D}}_{{{\mathbf{www}}}}^{112} = I_{0}^{*}{\mathbf{\textit{\"{w}}}}_{d} , \\ \end{aligned}$$
(27b)
$$d_{11} {\mathbf{D}}^{\left( 2 \right)} {\varvec{\Psi}}_{d} + \frac{{e_{11} }}{\eta }{\mathbf{D}}^{\left( 3 \right)} {\mathbf{w}}_{d} - a_{55} \eta \left( {{\mathbf{D}}^{\left( 1 \right)} {\mathbf{w}}_{d} + \eta {\varvec{\Psi}}_{d} } \right) = I_{2}^{*}{\ddot{\mathbf{\varPsi}}}_{d} + \frac{g}{\eta }{\mathbf{D}}^{\left( 1 \right)} {\mathbf{\textit{\"{w}}}}_{d}$$
(27c)

in which

$${\mathbf{D}}_{{{\mathbf{xy}}}}^{ij} = \left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{s} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{d} } \right) + \left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{d} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{s} } \right) + \left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{d} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{d} } \right)$$
(28a)
$$\begin{aligned} {\mathbf{D}}_{{{\mathbf{xyz}}}}^{ijk} & = \left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{s} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{d} } \right)\left( {{\mathbf{D}}^{\left( k \right)} {\mathbf{z}}_{s} } \right) + \left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{d} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{s} } \right)\left( {{\mathbf{D}}^{\left( k \right)} {\mathbf{z}}_{s} } \right) \\ & \quad + \;\left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{d} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{d} } \right)\left( {{\mathbf{D}}^{\left( k \right)} {\mathbf{z}}_{s} } \right) + \left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{s} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{s} } \right)\left( {{\mathbf{D}}^{\left( k \right)} {\mathbf{z}}_{d} } \right) \\ & \quad + \;\left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{s} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{d} } \right)\left( {{\mathbf{D}}^{\left( k \right)} {\mathbf{z}}_{d} } \right) + \left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{d} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{s} } \right)\left( {{\mathbf{D}}^{\left( k \right)} {\mathbf{z}}_{d} } \right) \\ & \quad + \;\left( {{\mathbf{D}}^{\left( i \right)} {\mathbf{x}}_{d} } \right)\left( {{\mathbf{D}}^{\left( j \right)} {\mathbf{y}}_{d} } \right)\left( {{\mathbf{D}}^{\left( k \right)} {\mathbf{z}}_{d} } \right) \\ \end{aligned}$$
(28b)

Again, the harmonic balance method is used to determine the dynamic response vectors and \({\varvec{\uppsi}}_{d}\) and corresponding natural frequencies under post-buckling.

4 Results and discussion

In this section, the numerical results concerned with the nonlinear vibration response of nanopipes conveying fluid with boundary conditions predicted by both classical and nonclassical models including surface stress effects are discussed. The results are plotted for nanopipes made of Si and Al with the following material properties (Arani et al. 2014; Arani and Roudbari 2014; Wang 2012):

The bulk and surface elastic material properties of Al: \(\begin{aligned} E & = 68.5 \;{\text{GPa}}, \rho = 2700\;{\text{kg/m}}^{3} , \nu = 0.35, \lambda_{s} = 6.842 \;{\text{N/m}}, \\ \mu_{s} & = - 0.376 \;{\text{N/m}}, \tau_{s} = 0.910 \;{\text{N/m}}, \rho_{s} = 5.46e - 7\;{\text{kg/m}}^{2} \\ \end{aligned}\)

The bulk and surface elastic material properties of Si: \(\begin{aligned} E & = 210\; {\text{GPa}}, \rho = 2331\;{\text{kg/m}}^{3} , \nu = 0.24, \\ \lambda_{s} & = - 4.488\;{\text{N/m}}, \mu_{s} = - 2.774\;{\text{N/m}}, \tau_{s} = 0.605\;{\text{N/m}}, \rho_{s} = 3.17e - 7\;{\text{kg/m}}^{2} \\ \end{aligned}\)

Figures 2 and 3 show variations of the first two modes of frequency of nanoscale pipes made of Si and Al, respectively, with and without considering surface parameters for different thicknesses in two types of boundary conditions with dimensionless amplitude of vibration a = 2. The curves with black color are results predicted by the classical model. The real term of \(\omega\) is connected with the damping, and the imaginary part of \(\omega\) is related to frequency. Once \(\text{Re} \left( \omega \right) > 0\), the system will be unstable, while \(\text{Re} \left( \omega \right) < 0\) signals the stable condition of the system (Amabili and Garziera 2000). It is observed that the frequencies obtained from the present model are higher than those of the classical Timoshenko beam model, especially for small values of thicknesses. For thick nanopipes, the surface effects are negligible and the results are close to classical ones. Also, pointing out the distance between curves in Figs. 2 and 3 indicates that the effects of surface stress on Al nanopipes are more than Si counterparts, especially for pipes with SS–SS end supports. The point where the imaginary part becomes zero is the unset of the static divergence of the system and where the system becomes stable again is known as restabilization point, signifying coupled-mode flutter (Amabili and Garziera 2000). As it is seen in Figs. 2 and 3, in both modes, with considering the surface effects, the velocity that frequency becomes zero increases (static divergence occurs in higher velocities). So, the classical theory underestimates the static divergence.

Fig. 2
figure 2

Surface stress effect on the imaginary and real part of frequency in first and second mode of silicon nanopipe for different values of thickness corresponding to a SS–SS, b C–C boundary conditions, \(d_{i} /d_{o} = 0.8 , L/d_{o} = 20 , a = 2\)

Full size image
Fig. 3
figure 3

Surface stress effect on the imaginary and real part of frequency in first and second mode of aluminum nanopipe for different values of thickness corresponding to a SS–SS, b C–C boundary conditions, \(d_{i} /d_{o} = 0.8 , L/d_{o} = 20 , a = 2\)

Full size image

Figure 4 displays the effects of surface stress on critical flow velocity of the first mode. Graphs are plotted for nanopipes made of Si and Al with different thicknesses. It can be seen that in thin nanopipes, the critical flow velocity is significantly higher than classical result, so the system diverges at larger velocities. This difference is bigger in nanopipes made of aluminum.

Fig. 4
figure 4

Surface stress effect on the critical flow velocity in first mode for different values of thickness corresponding to a SS–SS, b C–C boundary conditions

Full size image

Here, surface stress effects on the instability beyond critical flow velocity are investigated by determining the characteristics of free vibration under post-buckling of nanopipes. In Figs. 5 and 6, the post-buckling paths and fundamental frequencies around post-buckling configuration are presented, respectively, for nanopipes made of Si and Al with different boundary conditions and thicknesses. In the post-buckling analysis, it is apparent that the nanopipe at the first mode buckles and loses stability at the critical flow velocity. In addition to what observed in Figs. 2, 3, 4, it is found that in the stability region of responses of vibration around post-buckling, the frequencies predicted by the classical theory are lower than those of surface stress model, and vice versa in the instability region.

Fig. 5
figure 5

Surface stress effect on the post-buckling configuration in first mode for different values of thickness corresponding to a SS–SS, b C–C boundary conditions, at \(x = 0.5\)

Full size image
Fig. 6
figure 6

Surface stress effect on the natural frequency under post-buckling configuration in first mode for different values of thickness corresponding to a SS–SS, b C–C boundary conditions

Full size image

The effects of the material and surface stress modulus on the imaginary and real parts of the frequency of free vibrations of nanopipes are plotted in Figs. 7 and 8, for those made of Si and Al, respectively. It is observed that the positive surface elastic constant (\(\lambda_{s} + 2\mu_{s}\)) gives larger frequencies and the system diverges in higher velocities, while for the negative one, the behavior is vice versa. As it is expected from previous results, the influence of surface elastic constant on Al nanopipes is more than that on Si counterparts.

Fig. 7
figure 7

Effects of the surface elastic constant on the imaginary and real part of frequency in first and second mode of silicon nanopipe corresponding to a SS–SS, b C–C boundary conditions, \(\rho_{s} = \tau_{s} = 0\), h = 2 nm, \(a = 2\)

Full size image
Fig. 8
figure 8

Effects of the surface elastic constant on the imaginary and real part of frequency in first and second mode of aluminum nanopipe corresponding to a SS–SS, b C–C boundary conditions, \(\rho_{s} = \tau_{s} = 0\), h = 2 nm, \(a = 2\)

Full size image

Figures 9 and 10 imply the effect of the surface density on the frequency of the first two modes of nanopipes with different end supports versus the flow velocity. It is found that the surface density has a significant influence on the frequency of pipe. As the value of the surface density becomes larger, the frequency decreases profoundly. It can be seen that between the critical flow velocity of the first and second modes, the real part of the frequency decreases with the rise of the surface density which means that the instability of the system reduces. Also, it is observed that the surface density has no influence on the critical velocities of first and second modes.

Fig. 9
figure 9

Effects of the surface density on the imaginary and real part of frequency in first and second mode of silicon nanopipe corresponding to a SS–SS, b C–C boundary conditions, \(\lambda_{s} = \mu_{s} = \tau_{s} = 0\), h = 2 nm, \(a = 2\)

Full size image
Fig. 10
figure 10

Effects of the surface density on the imaginary and real part of frequency in first and second mode of aluminum nanopipe corresponding to a SS–SS, b C–C boundary conditions, \(\lambda_{s} = \mu_{s} = \tau_{s} = 0\), h = 2 nm, \(a = 2\)

Full size image

Depicted in Figs. 11 and 12 are the effects of surface residual stress on the frequency in first and second modes for nanopipes made of Si and Al materials, respectively. It can be seen that the positive value of this parameter makes the frequency larger, while the negative one gives smaller frequency than classical beam model. Another important result from Figs. 11 and 12 is that the critical flow velocities are strongly affected by surface residual stress, as the positive value can make the critical velocities of first and second modes higher and negative value makes them lower.

Fig. 11
figure 11

Effects of the residual stress on the imaginary and real part of frequency in first and second mode of silicon nanopipe corresponding to a SS–SS, b C–C boundary conditions, \(\lambda_{s} = \mu_{s} = \rho_{s} = 0\), h = 2 nm, \(a = 2\)

Full size image
Fig. 12
figure 12

Effects of the residual stress on the imaginary and real part of frequency in first and second mode of aluminum nanopipe corresponding to a SS–SS, b C–C boundary conditions, \(\lambda_{s} = \mu_{s} = \rho_{s} = 0\), h = 2 nm, \(a = 2\)

Full size image

Figure 13 reveals the effect of surface stress on nonlinear frequency ratio in silicon and aluminum nanopipes for different amplitudes. It is observed that the large values of thicknesses gives higher frequency ratios. Also it shows that at given amplitude in SS–SS boundary conditions, the frequency ratio is higher than C–C end supports. Furthermore, it is seen that for large values of amplitude, the frequency ratio increases significantly. So it can be concluded that in vibrations with large deflection, the nonlinear analysis should be carried out.

Fig. 13
figure 13

Surface stress effect on the nonlinear frequency ratio of silicon and aluminum nanopipes for different values of thickness at dimensionless velocity v = 0.035

Full size image

5 Conclusion

The geometrically nonlinear free vibration and stability of fluid-conveying nanoscale pipe incorporating surface stress effect were studied in this work. The von-Karman theory in conjunction with the Timoshenko beam theory was employed to model the nanopipe. By means of Hamilton’s principle and the Gurtin–Murdoch continuum elasticity, the governing equations of motion and associated boundary conditions were achieved. In solution procedure, via the GDQ approach, the governing equations were discretized. Then, the harmonic balance method was used to simplify the governing differential equations to algebraic ones, before solving numerically by the Newton–Raphson method. The effects of effective parameters such as the thickness, material and surface stress modulus, residual surface stress, surface density and boundary conditions on the stability and the first two modes of frequency of nanopipes were discussed.

It was observed that both frequencies and static divergence obtained from the present model including the surface stress are higher than those of the classical model, especially for small values of thicknesses; so, the classical theory underestimates both the frequencies and static divergence. Also, it was observed that Al nanopipes are more sensitive to the effects of surface stress rather than Si counterparts, especially for nanopipes with SS–SS boundary conditions. With regard to the effects of surface elastic constant and surface residual stress, it was seen that positive values of either of them give larger frequencies and the system diverge in higher velocities, while for the negative one, a reverse trend occurs. As for the influence of the surface density, once observed that frequencies of nanopipe decrease strongly with the increase in this parameter; however, the surface density has no considerable effect on the critical velocities of first and second modes.