Positive solutions to integral boundary value problems from geophysical fluid flows

Abstract

The mathematical model of the Antarctic Circumpolar Current with integral boundary conditions is established and the explicit expression of green’s function is obtained. The existence and uniqueness of solutions are proved by using the mixed monotone operator theory. The sufficient conditions for the existence of positive solutions of the model are given and the existence of positive solutions with integral boundary is proved by using the fixed point technique in cone.

1 Introduction

The mathematical study of ocean circulation is very important for predicting the characteristics of large-scale natural phenomena in the ocean. The combined forces of gravity and Coriolis forces (due to the earth’s rotation), triggered by wind stress, drive circulating ocean currents, known as gyres. In the gyres, the horizontal velocity is 0.01 m/s, which is about $10^{4}$ times the vertical velocity in [1, 2]. Considering global ocean circulation and global climate, the Antarctic Circumpolar Current (ACC) is probably the most important current of this type. ACC is the most powerful ocean current on earth in [3], which separates Antarctica from the warm subtropical waters. ACC flows clockwise from west to east around the South Pole between about $40^{\circ }$S and $60^{\circ }$S, where there is no large area of land to break down this continuous water. ACC is the only tidal current that completely circles the earth, and its eastward flow is caused by a combination of very strong westerly winds and Coriolis forces. ACC is strongly constrained by the terrain at the bottom, and observed time changes, such as the Antarctic circumpolar wave [4,5,6,7,8,9,10,11,12,13]. ACC carries about 140 million cubic meters of water per second, more than 100 times more than all the world’s rivers combined, and travels about 24,000 km. Nevertheless, ACC is one of the least representative components of global climate models in [14]. Although there are a lot of observations about ACC flow, the pursuit of models that show a high degree of real structure is still the main direction of current research.

The geophysical study of fluid flows involves complex interacting systems from which we attempt to extract the essence of specific physical phenomena. Starting from the inviscid Euler equation and the equation of conservation of mass and energy, a flow function is introduced to encode the horizontal flow component by ignoring the movement in the vertical direction, and the ocean cyclotron flow is modeled as the shallow water on the rotating sphere in [1]. The spherical coordinate model is transformed into an equivalent semilinear plane ellipse boundary value problem by using the stereoscopic projection from the Arctic to the equatorial plane in [1]. Under the ignorance of azimuth angle change of the horizontal velocity that mathematical models of gyres flows with boundary conditions have been studied in the Southern and Northern Hemispheres in [15,16,17,18,19,20,21,22,23,24,25]. Since the projection of ACC flows from the Arctic to the equatorial plane is represented as a circular region on the equatorial plane, we established a new mathematical model of ACC flows, assuming that the circulation boundary is a streamline, which is just represented as the known Riemann-Stieltjes integral $-\int _{t_{1}}^{t_{2}}u(t)d\xi (t)$ and $\int _{t_{1}}^{t_{2}}u(t)d\eta (t)$, and the negative sign indicates that the outer normal direction is opposite to the positive direction selected. This has not been studied in the existing literature, and we try to solve this problem mathematically.

Fig. 1

Azimuthal and polar angular spherical coordinates $\varphi$ and $\theta$ of a point P on the spherical surface of the earth, with $\theta =0$ correspond to the North Pole. Severally, while $\theta =\frac{\pi }{2}$ represents the Equator

2 Preliminaries

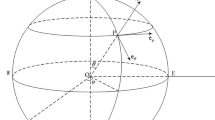
Consider spherical coordinates, $\theta \in [0,\pi )$ is polar angle with $\theta =0$ corresponding to the North Pole, and $\varphi \in [0,2\pi )$ represents the angle of longitude in Fig. 1. In terms of the stereographic projection from the North Pole, which azimuthal and polar velocity components of ACC flows as

$$\begin{aligned} \frac{1}{\sin \theta }\psi _\phi \;~~\text {and}\; ~-\psi _\theta , \end{aligned}$$

In terms of the stream function $\Psi$ associated with the vorticity of the motion of the ocean, and $\Psi$ is not driven by the Earth’s rotation, defining

$$\begin{aligned} \psi (\theta ,\varphi )=-\omega \cos \theta +\Psi (\theta ,\varphi ), \end{aligned}$$

(1)

the governing equation for ACC flows can be given by

$$\begin{aligned} \frac{1}{\sin ^{2}\theta }\Psi _{\varphi \varphi }+\Psi _{\theta }\cot \theta +\Psi _{\theta \theta }=F(\Psi -\omega \cos \theta ), \end{aligned}$$

(2)

where $F(\Psi -\omega \cos \theta )$ is the form of the ACC flows of the vortex that defines the property of the ocean vorticity function. $F(\Psi -\omega \cos \theta )$ is similar to the concept of angular momentum, which is a method of measuring the local spin of a fluid element in [26]. While $\omega >0$ is the non-dimensional Coriolis parameter and $2\omega \cos \theta$ represents the spin vorticity. Ocean vorticity is shown in the form of tidal wave fluctuations, which is mainly due to the influence of wind and the gravitational forces generated by the relative motion of the Earth, the Sun and the Moon. Ebb and tide respectively refer to the horizontal unidirectional movement of water and the vertical movement of water. The oceanic vorticity of the wind-driven current, the vorticity of water current, and the interaction of geophysical wave current can be expressed by non-zero constant in [27, 28]. It is noteworthy that the circulation exists at almost all latitudes except near the Equator and acts as a waveguide, facilitating the flow of current from east to west, driven by Coriolis forces in [29, 30]. Although wave-current interactions in nonzero vorticity flows are a very interesting topic in [31,32,33], we will only discuss the effects of the ACC at large scales. The governing equation (2) is valid in a region where the boundary appears as a streamline.

Fig. 2

The stereographic projection of the unit sphere (center at origin) from the North Pole to the equatorial plane,the point P in the antarctic region, the straight line connecting it to the North Pole intersects the equatorial plane in a point $P'$ belonging to the interior of the circular region delimited by the Equator. The ACC is mapped into a annular region within the equatorial plane

The stereographic projection is used from the North Pole to the equatorial plane on a unit sphere centered at the origin in Fig. 2. The model (2) in spherical coordinates can be transformed into an equivalent semilinear elliptic partial differential equation [1]. Let

$$\begin{aligned} \xi =re^{i\phi }\;~~\text {with}\; ~r=\cot \left( \frac{\theta }{2}\right) =\frac{\sin \theta }{1-\cos \theta }, \end{aligned}$$

(3)

where $(r,\phi )$ represents the polar coordinates on the equatorial plane, and r is a function of $\theta$. After several cancellations by using (3), the Eq. (2) can be simplified as

$$\begin{aligned} \Psi _{\xi \overline{\xi }}=\frac{F(\Psi -\omega ((\xi \overline{\xi }-1)/(\xi \overline{\xi }+1)))}{(1+\xi \overline{\xi })^{2}}. \end{aligned}$$

(4)

Taking the partial derivative of (1), we have

$$\begin{aligned} \Psi _{\xi }=\psi _{\xi }+\frac{2\omega \overline{\xi }}{(1+\xi \overline{\xi })^{2}}, \Psi _{\xi \overline{\xi }}=\psi _{\xi \overline{\xi }}+\frac{2\mu }{(1+\xi \overline{\xi })^{2}}-\frac{4\omega \xi \overline{\xi }}{(1+\xi \overline{\xi })^{3}}. \end{aligned}$$

(5)

By combining (5) and (4), we obtain

$$\begin{aligned} \psi _{\xi \overline{\xi }}+2\omega \frac{1-\xi \overline{\xi }}{(1+\xi \overline{\xi })^{3}}-\frac{F(\psi )}{(1+\xi \overline{\xi }))^{2}}=0, \end{aligned}$$

(6)

using Cartesian coordinates (x, y), Eq. (6) is transformed by

$$\begin{aligned} \Delta \psi +8\omega \frac{1-(x^{2}+y^{2})}{(1+x^2+y^2)^{3}}-\frac{4F(\psi )}{(1+x^2+y^2)^{2}}=0, \end{aligned}$$

(7)

where $\Delta =\partial _{x}^{2}+\partial _{y}^{2}$ is the Laplace operator, expressed in accordance with the Cartesian coordinates on the equatorial plane, in which the unknown function $\psi (x,y)$ represents the stream function. The ACC flows is bounded on the surface of the ocean by the level sets of flow functions, while in spherical projection coordinates, the solution of the ACC flows model (7) in the plane region is determined by these horizontal sets.

Let

$$\begin{aligned} r=\sqrt{x^{2}+y^{2}},~\frac{\partial r}{\partial x}=\frac{x}{\sqrt{x^{2}+y^{2}}}=\frac{x}{r},~\frac{\partial r}{\partial y}=\frac{y}{\sqrt{x^{2}+y^{2}}}=\frac{y}{r}, \end{aligned}$$

therefore, $\psi _{x}=\frac{x}{r}\psi '(r)$, $\psi _{y}=\frac{y}{r}\psi '(r)$, and

$$\begin{aligned} \psi _{xx}=\frac{x^{2}}{r^{2}}\psi ''(r)+\left( \frac{1}{r}-\frac{x^{2}}{r^{3}}\right) \psi '(r),\quad \psi _{yy}=\frac{y^{2}}{r^{2}}\psi ''(r)+\left( \frac{1}{r}-\frac{y^{2}}{r^{3}}\right) \psi '(r), \end{aligned}$$

and so

$$\begin{aligned} \Delta \psi =\psi ''(r)+\frac{1}{r}\psi '(r), \end{aligned}$$

hence, Eq. (7) is transformed into

$$\begin{aligned} \psi ''(r)+\frac{1}{r}\psi '(r)+8\omega \frac{1-r^{2}}{(1+r^{2})^{3}}-\frac{4F(\psi (r))}{(1+r^{2})^{2}}=0. \end{aligned}$$

(8)

Note ACC flows corresponds to the radial symmetric solution of problem (8) with no variations in the azimuthal direction. We introduce

$$\begin{aligned} \psi (r)=u(t),~~~t_{1}<t<t_{2}, \end{aligned}$$

where

$$\begin{aligned} r=e^{\frac{t}{2}}\;~~\text {for}\; ~0<t_1=-2\ln (r_{+})<t_2=-2\ln (r_{-}), \end{aligned}$$

with $0<r_{-}<r_{+}<1$. We obtain

$$\begin{aligned} u'(t)=\frac{1}{2}e^{\frac{t}{2}}\psi '(e^{\frac{t}{2}})=\frac{1}{2}r\psi '(r) \end{aligned}$$

and

$$\begin{aligned} u''(t)=\frac{1}{4}e^{\frac{t}{2}} \psi '(e^{\frac{t}{2}})+\frac{1}{4}e^{t}\psi ''(e^{\frac{t}{2}})=\frac{1}{4}r\psi '(r)+\frac{1}{4}r^{2}\psi ''(r). \end{aligned}$$

As a result, it is convenient to transform (8) equivalently into the second-order ordinary differential equation

$$\begin{aligned} u''(t)=\frac{e^{t}}{(1+e^{t})^{2}}F(t,u(t))+2\omega \frac{e^{t}(e^{t}-1)}{(1+e^{t})^{3}},~~~t_{1}<t<t_{2}, \end{aligned}$$

(9)

with we associate integral boundary conditions

$$\begin{aligned} u(t_1)-\alpha u'(t_1)=-\int _{t_{1}}^{t_{2}}u(t)d\xi (t),~\text {on}\;~r=r_{-}, \end{aligned}$$

(10)

and

$$\begin{aligned} u(t_2)-\beta u'(t_2)=\int _{t_{1}}^{t_{2}}u(t)d\eta (t),~\text {on}\;~r=r_{+}, \end{aligned}$$

(11)

meaning the fact that $r=r_{\pm }$ for ACC as gyre flow are streamlines with $\psi =u(t_{1})$ on $r=r_{-}$ and $\psi =u(t_{2})$ on $r=r_{+}$, $0<r_{-}<r_{+}<1$. ACC flows each particle is always confined within the boundary because ACC flows are stable. In this paper, we assume that ACC flows behavior is a simplified circular region, whose streamline form at the boundary and the linear combination of its velocity are just the Riemann-Stieltjes integral of the streamline with known cyclic boundary, which is mathematically reasonable. Although there have been many good results on the ACC flows boundary value problem, the boundary value problem considering that the circular boundary is the Riemann-Stieltjes integral of the known streamline has not been studied. We obtain sufficient conditions for the existence of positive solutions of such problems by using fixed point technique and mixed monotone operator theory in cone.

Linking (9), (10) and (11), we established the following mathematical model of ACC flows:

$$\begin{aligned} \left\{ \begin{array}{lll} u''(t)=a(t)F(t,u(t))+b(t),~~~t_{1}<t<t_{2},\\ u(t_1)-\alpha u'(t_1)=-\int _{t_{1}}^{t_{2}}u(t)d\xi (t),\\ u(t_2)-\beta u'(t_2)=\int _{t_{1}}^{t_{2}}u(t)d\eta (t), \end{array} \right. \end{aligned}$$

(12)

where $a(\cdot ),b(\cdot ):[t_1,t_2]\rightarrow R$ are continuous, $F(\cdot ,\cdot ):[t_1,t_2]\times R\rightarrow R$ is continuous, and

$$\begin{aligned} a(t)=\frac{e^{t}}{(1+e^{t})^{2}},\quad b(t)=\frac{2\omega e^{t}(e^{t}-1)}{(1+e^{t})^{3}}, \end{aligned}$$

$\alpha$ and $\beta$ are nonnegative real parameters, $\xi (\cdot )$ and $\eta (\cdot )$ are nondecreasing, right continuous on $[t_{1},t_{2})$, left continuous at $t=t_{2}$, $\int _{t_{1}}^{t_{2}}u(t)d\xi (t)$ and $\int _{t_{1}}^{t_{2}}u(t)d\eta (t)$ denote the Riemann-Stieltjes integrals of u with respect to $\xi$ and $\eta$.

3 Main result

We assume the following condition.

(H1):

 $t_{2}-t_{1}+\alpha>\beta >t_{2}$.

Lemma 3.1

Assume that (H1) holds, then for any $y \in C([t_1,t_2],(0,+\infty ))$, the boundary value problem

$$\begin{aligned} \left\{ \begin{array}{lll} u''(t)=y(t),~~~t_{1}<t<t_{2}\\ u(t_1)-\alpha u'(t_1)=-\int _{t_{1}}^{t_{2}}u(t)d\xi (t),\\ u(t_2)-\beta u'(t_2)=\int _{t_{1}}^{t_{2}}u(t)d\eta (t), \end{array} \right. \end{aligned}$$

(13)

has a unique solution given by

$$\begin{aligned} u(t)=\int _{t_{1}}^{t_{2}}G(t,s)y(s)ds+\kappa _{2}(t)\int _{t_{1}}^{t_{2}}u(t)d\xi (t)+\frac{\kappa _{1}(t)}{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\eta (t), \end{aligned}$$

(14)

where

$$\begin{aligned} G(t,s)= \left\{ \begin{array}{lll} \kappa _{1}(t)\cdot \kappa _{2}(s),~~t_{1}\le t\le s\le t_{2},\\ \kappa _{1}(s)\cdot \kappa _{2}(t),~~t_{1}\le s\le t\le t_{2}, \end{array} \right. \end{aligned}$$

(15)

$\kappa _{1}(t)=t+\alpha -t_{1}$ and $\kappa _{2}(t)=\frac{t+\beta -t_{2}}{t_{2}-t_{1}+\alpha -\beta }$, G(t, s) is the Green’s function.

Proof

It is easy to see by integration of (13) that

$$\begin{aligned} u'(t)=u'(t_{1})+\int _{t_{1}}^{t}y(s)ds. \end{aligned}$$

(16)

Integrating again, we have

$$\begin{aligned} u(t)=u(t_{1})+u'(t_{1})(t-t_{1})+\int _{t_{1}}^{t}(t-s)y(s)ds. \end{aligned}$$

(17)

Letting $t=t_{2}$ in (16) and (17), combining this with the boundary conditions in (13), we obtain

$$\begin{aligned} u(t_{2})-\beta u'(t_{2})&=u(t_{1})+u'(t_{1})(t_{2}-t_{1})+\int _{t_{1}}^{t_{2}}(t_{2}-s)y(s)ds \nonumber \\&\quad -\beta u'(t_{1})-\beta \int _{t_{1}}^{t_{2}}y(s)ds=\int _{t_{1}}^{t_{2}}u(t)d\eta (t). \end{aligned}$$

(18)

Since

$$\begin{aligned} u(t_1)-\alpha u'(t_1)=-\int _{t_{1}}^{t_{2}}u(t)d\xi (t), \end{aligned}$$

(19)

thus, it follows from (18) and (19) that

$$\begin{aligned} u'(t_{1})&=\frac{1}{t_{2}-t_{1}+\alpha -\beta }\left[ \int _{t_{1}}^{t_{2}}u(t)d\eta (t)+\int _{t_{1}}^{t_{2}}u(t)d\xi (t)\right. \\&\left. \quad +\,\beta \int _{t_{1}}^{t_{2}}y(s)ds-\int _{t_{1}}^{t_{2}}(t_{2}-s)y(s)ds\right] , \end{aligned}$$

and

$$\begin{aligned} u(t_{1})&=\frac{\alpha }{t_{2}-t_{1}+\alpha -\beta }\left[ \int _{t_{1}}^{t_{2}}u(t)d\eta (t)+\beta \int _{t_{1}}^{t_{2}}y(s)ds-\int _{t_{1}}^{t_{2}}(t_{2}-s)y(s)ds\right] \\&\quad -\frac{t_{2}-t_{1}-\beta }{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\xi (t). \end{aligned}$$

Therefore, BVP (13) has a unique solution

$$\begin{aligned} u(t)= & {} u(t_{1})+u'(t_{1})(t-t_{1})+\int _{t_{1}}^{t}(t-s)y(s)ds \\= & {} \frac{t+\beta -t_{2}}{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\xi (t)+\frac{t+\alpha -t_{1}}{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\eta (t) \\&\quad +\frac{(t+\alpha -t_{1})\beta }{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}y(s)ds-\frac{t+\alpha -t_{1}}{t_{2}-t_{1} +\alpha -\beta }\int _{t_{1}}^{t_{2}}(t_{2}-s)y(s)ds\\&\quad +\int _{t_{1}}^{t}(t-s)y(s)ds \\= & {} \frac{t+\beta -t_{2}}{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\xi (t)+\frac{t+\alpha -t_{1}}{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\eta (t) \\&\quad +\int _{t_{1}}^{t}\frac{(s+\alpha -t_{1})(t+\beta -t_{2})}{t_{2}-t_{1}+\alpha -\beta }y(s)ds+\int _{t}^{t_{2}}\frac{(t+\alpha -t_{1})(s+\beta -t_{2})}{t_{2}-t_{1}+\alpha -\beta }y(s)ds \\= & {} \kappa _{2}(t)\int _{t_{1}}^{t_{2}}u(t)d\xi (t)+\frac{\kappa _{1}(t)}{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\eta (t)+\int _{t_{1}}^{t_{2}}G(t,s)y(s)ds. \end{aligned}$$

The proof is complete. $\square$

Letting

$$\begin{aligned} \gamma _{1}=1-\int _{t_{1}}^{t_{2}}\kappa _{2}(t)d\xi (t),~~~~\gamma _{2}=\int _{t_{1}}^{t_{2}}\frac{\kappa _{1}(t)}{t_{2}-t_{1}+\alpha -\beta }d\xi (t),\\ \gamma _{3}=\int _{t_{1}}^{t_{2}}\kappa _{2}(t)d\eta (t),~~~~\gamma _{4}=1-\int _{t_{1}}^{t_{2}}\frac{\kappa _{1}(t)}{t_{2}-t_{1}+\alpha -\beta }d\eta (t). \end{aligned}$$

Let’s assume that $\gamma _{i}~(i=1,2,3,4)$ satisfies the following conditions:

(H2):

 $\gamma _{1}>0$, $\gamma _{4}>0$, $\gamma =\gamma _{1}\gamma _{4}-\gamma _{2}\gamma _{3}>0$.

Lemma 3.2

Assume that (H2) holds, then (14) can be expressed in the form

$$\begin{aligned} u(t)=\int _{t_{1}}^{t_{2}}H(t,s)y(s)ds, \end{aligned}$$

where

$$\begin{aligned} H(t,s)=G(t,s)+\kappa _{01}(t)\int _{t_{1}}^{t_{2}}G(\tau ,s)d\xi (\tau )+\kappa _{02}(t)\int _{t_{1}}^{t_{2}}G(\tau ,s)d\eta (\tau ), \end{aligned}$$

and

$$\begin{aligned} \kappa _{01}(t)=\gamma ^{-1}\bigg (\gamma _{4}\kappa _{2}(t)+\frac{\gamma _{3}}{t_{2}-t_{1}+\alpha -\beta }\kappa _{1}(t)\bigg ),\\ \kappa _{02}(t)=\gamma ^{-1}\bigg (\gamma _{2}\kappa _{2}(t)+\frac{\gamma _{1}}{t_{2}-t_{1}+\alpha -\beta }\kappa _{1}(t)\bigg ). \end{aligned}$$

Proof

Multiply (14) by $d\xi (t)$ and integrate both sides at $[t_{1},t_{2}]$, we have

$$\begin{aligned} \int _{t_{1}}^{t_{2}}u(t)d\xi (t)&=\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\xi (\tau )+(1-\gamma _{1})\int _{t_{1}}^{t_{2}}u(t)d\xi (t)\\&\quad +\gamma _{2}\int _{t_{1}}^{t_{2}}u(t)d\eta (t), \end{aligned}$$

similarly,

$$\begin{aligned} \int _{t_{1}}^{t_{2}}u(t)d\eta (t)&=\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\eta (\tau )+\gamma _{3}\int _{t_{1}}^{t_{2}}u(t)d\xi (t)\\&\quad +(1-\gamma _{4})\int _{t_{1}}^{t_{2}}u(t)d\eta (t), \end{aligned}$$

hence, we can obtain

$$\begin{aligned}&\gamma _{1}\int _{t_{1}}^{t_{2}}u(t)d\xi (t)-\gamma _{2}\int _{t_{1}}^{t_{2}}u(t)d\eta (t)\\&\quad =\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\xi (\tau ),\\&\qquad -\gamma _{3}\int _{t_{1}}^{t_{2}}u(t)d\xi (t)+\gamma _{4}\int _{t_{1}}^{t_{2}}u(t)d\eta (t)\\&\quad =\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\eta (\tau ). \end{aligned}$$

Solving the two equations, we obtain

$$\begin{aligned} \int _{t_{1}}^{t_{2}}u(t)d\xi (t)&=\gamma ^{-1}\bigg [\gamma _{4}\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\xi (\tau )\nonumber \\&\quad +\gamma _{2}\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\eta (\tau )\bigg ], \end{aligned}$$

(20)

and

$$\begin{aligned} \int _{t_{1}}^{t_{2}}u(t)d\eta (t)&=\gamma ^{-1}\bigg [\gamma _{3}\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\xi (\tau )\nonumber \\&\quad +\gamma _{1}\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\eta (\tau )\bigg ]. \end{aligned}$$

(21)

Linking (20), (21) and (14), we have

$$\begin{aligned} u(t)&=\int _{t_{1}}^{t_{2}}G(t,s)y(s)ds+\kappa _{2}(t)\int _{t_{1}}^{t_{2}}u(t)d\xi (t)+\frac{\kappa _{1}(t)}{t_{2}-t_{1}+\alpha -\beta }\int _{t_{1}}^{t_{2}}u(t)d\eta (t)\\&=\int _{t_{1}}^{t_{2}}G(t,s)y(s)ds+\kappa _{2}(t)\gamma ^{-1}\gamma _{4}\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\xi (\tau )\\&\quad +\kappa _{2}(t)\gamma ^{-1}\gamma _{2}\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\eta (\tau )+\frac{\kappa _{1}(t)}{t_{2}-t_{1}+\alpha -\beta }\gamma ^{-1}\gamma _{3}\\&\quad \int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\xi (\tau )+\frac{\kappa _{1}(t)\gamma ^{-1}\gamma _{1}}{t_{2}-t_{1}+\alpha -\beta }\int _ {t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)y(s)dsd\eta (\tau )\\&=\int _{t_{1}}^{t_{2}}H(t,s)y(s)ds. \end{aligned}$$

This completes the proof. $\square$

Lemma 3.3

There exists continuous function ${\mathfrak {a}}(\cdot ),{\mathfrak {b}}(\cdot ):[t_1,t_2]\rightarrow (0,+\infty )$ such that

$$\begin{aligned} {\mathfrak {a}}(t)G(s,s)\le G(t,s)\le {\mathfrak {b}}(t)G(s,s),~\forall t,s\in [t_{1},t_{2}]. \end{aligned}$$

(22)

Futhermore, $\mathfrak {a_{0}}=\min \limits _{t\in [t_{1},t_{2}]}\mathfrak {a(t)}$, $\mathfrak {b_{0}}=\max \limits _{t\in [t_{1},t_{2}]}\mathfrak {b(t)}$.

Proof

Let

$$\begin{aligned}&\varrho _{{\mathfrak {a}}}=\max \{\Vert \kappa _{1}\Vert ,\Vert \kappa _{2}\Vert \}=\max \left\{ t_{2}-t_{1}+\alpha ,\frac{\beta }{t_{2}-t_{1}+\alpha -\beta }\right\} ,\\&\varrho _{{\mathfrak {b}}}=\min \{\Vert \kappa _{1}\Vert ,\Vert \kappa _{2}\Vert \}=\min \left\{ \alpha ,\frac{t_{1}+\beta -t_{2}}{t_{2}-t_{1}+\alpha -\beta }\right\} . \end{aligned}$$

Define

$$\begin{aligned} {\mathfrak {a}}(t)=\frac{1}{\varrho _{{\mathfrak {a}}}}\cdot \min \{\kappa _{1}(t),\kappa _{2}(t)\},~~{\mathfrak {b}}(t)=\frac{1}{\varrho _{{\mathfrak {b}}}}\cdot \max \{\kappa _{1}(t),\kappa _{2}(t)\}, \end{aligned}$$

(23)

then if $t\le s$, we have

$$\begin{aligned} {\mathfrak {a}}(t)G(s,s)&=\kappa _{1}(s)\kappa _{2}(s){\mathfrak {a}}(t)\le \kappa _{1}(s)\kappa _{2}(s)\frac{\kappa _{1}(t)}{\varrho _{{\mathfrak {a}}}}\\&=\kappa _{1}(t)\kappa _{2}(s)\frac{\kappa _{1}(s)}{\varrho _{{\mathfrak {a}}}}\le \kappa _ {1}(t)\kappa _{2}(s)=G(t,s)\\&\le \kappa _{1}(t)\kappa _{2}(s)\frac{\kappa _{1}(s)}{\varrho _{{\mathfrak {b}}}}=\kappa _{1}(s)\kappa _{2}(s)\frac{\kappa _{1}(t)}{\varrho _{{\mathfrak {b}}}}\le {\mathfrak {b}}(t)G(s,s), \end{aligned}$$

if $s\le t$, we also can obtain

$$\begin{aligned} {\mathfrak {a}}(t)G(s,s)&=\kappa _{1}(s)\kappa _{2}(s){\mathfrak {a}}(t)\le \kappa _{1}(s)\kappa _{2}(s)\frac{\kappa _{2}(t)}{\varrho _{{\mathfrak {a}}}}\\&=\kappa _{1}(s)\kappa _{2}(t)\frac{\kappa _{2}(s)}{\varrho _{{\mathfrak {a}}}}\le \kappa _ {1}(s)\kappa _{2}(t)=G(t,s)\\&\le \kappa _{1}(s)\kappa _{2}(t)\frac{\kappa _{2}(s)}{\varrho _{{\mathfrak {b}}}}=\kappa _{1}(s)\kappa _{2}(s)\frac{\kappa _{2}(t)}{\varrho _{{\mathfrak {b}}}}\le {\mathfrak {b}}(t)G(s,s), \end{aligned}$$

which shows that (22) is correct. $\square$

Lemma 3.4

There exists a constant $\sigma _{0} \in (0,1)$, such that ${\mathfrak {a}}(t)\ge \sigma _{0} {\mathfrak {b}}(t)$ for all $t\in [t_{1},t_{2}]$.

Proof

Since ${\mathfrak {a}}$ and ${\mathfrak {b}}$ can be given by (23), obviously, ${\mathfrak {a}}$ and ${\mathfrak {b}}$ are continuous and positive on $[t_{1},t_{2}]$, the conclusion is easy to prove. $\square$

We give the following assumptions conditions:

(H3):

  Let $F(t,u)=\zeta (t)(g(u)+h(u))$, where $\zeta (\cdot ):[t_{1},t_{2}]\rightarrow [0,+\infty )$ is continuous, $g(\cdot ):(0,+\infty )\rightarrow [0,+\infty )$ is increasing and continuous, $h(\cdot ):(0,+\infty )\rightarrow [0,+\infty )$ is decreasing and continuous;

(H4):

  There exists $\lambda \in (0,1)$ such that

$$\begin{aligned} g(\nu u)\ge \nu ^{\lambda } g(u),~~h(\nu ^{-1} u)\ge \nu ^{\lambda } h(u). \end{aligned}$$

(24)

Let $P_{L_{1}}$ the real Banach space E be partially ordered by a cone $P_{L_{1}}$ of E (see [34]), and it is defined by

$$\begin{aligned} P_{L_{1}}=\{u\in C[t_{1},t_{2}]:C^{-1}L_{1}(t)\le u(t)\le CL_{1}(t) \;~\text {on}\; ~[t_{1},t_{2}]\}, \end{aligned}$$

where the constant $C\ge \max \big \{1,(M_{1})^{\frac{1}{1-\lambda }},(M_{2}\sigma _{0})^{\frac{-1}{1-\lambda }}\big \}$, and the positive constant $M_{1}$, $M_{2}$ and the function $L_{1}(t)$ can be seen in the proof of Theorem 3.5.

Theorem 3.5

Assume that $(H1)-(H4)$ hold, then the integral boundary value problem (12) has a unique solution u(t) in $P_{L_{1}}$ and $u(t)>0$ for all $t \in [t_{1},t_{2}]$.

Proof

For any $u,v\in P_{L_{1}}$, we define the operator $A:P_{L_{1}}\times P_{L_{1}}\rightarrow E$ as following:

$$\begin{aligned} A(u,v)(t)&=\int _{t_{1}}^{t_{2}}H(t,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds\\&=\int _{t_{1}}^{t_{2}}G(t,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds\\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))\\&\quad +b(s)]dsd\xi (\tau )\\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))\\&\quad +b(s)]dsd\eta (\tau ). \end{aligned}$$

We can prove A is a mixed monotone.

In fact, for any $(u_{1},v_{1})\in P_{L_{1}}\times P_{L_{1}}$, $(u_{2},v_{2})\in P_{L_{1}}\times P_{L_{1}}$, let $u_{1}\le u_{2}$, $v_{1}\ge v_{2}$, since g is increasing and h is decreasing on $(0,+\infty )$, then

$$\begin{aligned} A(u_{1},v_{1})(t)&=\int _{t_{1}}^{t_{2}}H(t,s)[a(s)(\zeta (s)(g(u_{1}(s))\\&\quad +h(v_{1}(s))))+b(s)]ds\\&\le \int _{t_{1}}^{t_{2}}H(t,s)[a(s)(\zeta (s)(g(u_{2}(s))+h(v_{2}(s))))\\&\quad +b(s)]ds=A(u_{2},v_{2})(t), \end{aligned}$$

which implies that A is a mixed monotone.

We show that $A:P_{L_{1}}\times P_{L_{1}}\rightarrow P_{L_{1}}$ is well-defined, for any $(u,v)\in P_{L_{1}}\times P_{L_{1}}$ and $t\in [t_{1},t_{2}]$, we have

$$\begin{aligned} A(u,v)(t)&\le \mathfrak {b_{0}}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds\\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))\\&\quad +h(v(s))))+b(s)]ds\\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))\\&\quad +h(v(s))))+b(s)]ds\\&=L_{1}(t)\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds, \end{aligned}$$

where

$$\begin{aligned} L_{1}(t)=\mathfrak {b_{0}}+\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )+\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau ). \end{aligned}$$

Analogously, we also have

$$\begin{aligned} A(u,v)(t)&\ge \mathfrak {a_{0}}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds\\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\xi (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))\\&\quad +h(v(s))))+b(s)]ds\\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\eta (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))\\&\quad +h(v(s))))+b(s)]ds\\&=L_{2}(t)\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds\\&\ge L_{1}(t)\sigma _{0}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds, \end{aligned}$$

where

$$\begin{aligned} L_{2}(t)=\mathfrak {a_{0}}+\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\xi (\tau )+\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\eta (\tau ). \end{aligned}$$

Letting $\nu =\frac{1}{u}$, $u\ge 1$, we can obtain to by using (24) that

$$\begin{aligned} g(u)\le u^{\lambda } g(1), u\ge 1,~~g(\nu )\ge \nu ^{\lambda } g(1), \nu \in (0,1), \end{aligned}$$

(25)

and

$$\begin{aligned} h(\nu ^{-1})\ge \nu ^{\lambda } h(1), \nu \in (0,1),~~h(\nu )\le \nu ^{-\lambda } h(1), \nu \in (0,1). \end{aligned}$$

(26)

Hence, for any $t\in [t_{1},t_{2}]$, by using (25) and (26), we have

$$\begin{aligned} g(u(t))&\le g(C\cdot L_{1}(t))\le (L_{1}(t))^{\lambda }\cdot C^{\lambda }\cdot g(1), \end{aligned}$$

(27)

$$\begin{aligned} g(u(t))&\ge g(C^{-1}\cdot L_{1}(t))\ge g(C^{-1})\ge C^{-\lambda }\cdot g(1), \end{aligned}$$

(28)

and

$$\begin{aligned} h(v(t))&\le h(C^{-1}\cdot L_{1}(t))\le h(C^{-1})\le C^{\lambda }\cdot h(1), \end{aligned}$$

(29)

$$\begin{aligned} h(v(t))&\ge h(C\cdot L_{1}(t))\ge (L_{1}(t))^{-\lambda }\cdot C^{-\lambda }\cdot h(1), \end{aligned}$$

(30)

from (27) and (29), we have

$$\begin{aligned} A(u,v)(t)&\le L_{1}(t)\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds \nonumber \\&\le L_{1}(t)\cdot C^{\lambda }\cdot \int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)((L_{1}(s))^{\lambda }g(1)+h(1)))+b(s)]ds \nonumber \\&=M_{1}C^{\lambda }L_{1}(t)\le C L_{1}(t), \end{aligned}$$

(31)

where

$$\begin{aligned} M_{1}=\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)((L_{1}(s))^{\lambda }g(1)+h(1)))+b(s)]ds, \end{aligned}$$

from (28) and (30), we also have

$$\begin{aligned} A(u,v)(t)&\ge L_{1}(t)\sigma _{0}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds \nonumber \\&\ge L_{1}(t)\cdot \sigma _{0}\cdot C^{-\lambda }\cdot \int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(1)\nonumber \\&\quad +(L_{1}(s))^{-\lambda }h(1)))+b(s)]ds \nonumber \\&=M_{2}C^{-\lambda }\sigma _{0}L_{1}(t)\ge C^{-1} L_{1}(t), \end{aligned}$$

(32)

where

$$\begin{aligned} M_{2}=\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(\zeta (s)(g(1)+(L_{1}(s))^{-\lambda }h(1)))+b(s)]ds, \end{aligned}$$

thus, (31) and (32) show that $A(P_{L_{1}}\times P_{L_{1}})\subseteq P_{L_{1}}$. Letting $(u,v)\in P_{L_{1}}\times P_{L_{1}}$, $\nu \in (0,1)$, we have

$$\begin{aligned} A(\nu u,\nu ^{-1} v)(t)&=\int _{t_{1}}^{t_{2}}H(t,s)[a(s)(\zeta (s)(g(\nu u(s))+h(\nu ^{-1}v(s))))+b(s)]ds\\&\ge \int _{t_{1}}^{t_{2}}H(t,s)[a(s)(\zeta (s)(\nu ^{\lambda }g(u(s))+\nu ^{\lambda }h(v(s))))+b(s)]ds\\&\ge \nu ^{\lambda } \int _{t_{1}}^{t_{2}}H(t,s)[a(s)(\zeta (s)(g(u(s))+h(v(s))))+b(s)]ds\\&= \nu ^{\lambda } A(u,v)(t). \end{aligned}$$

Therefore, we have illuminated that all assumptions of the Lemma 3.4 from [35] are satisfied, consequently, there exists a unique $u\in P_{L_{1}}$ such that $A(u,u)=u$, the integral boundary value problem (12) has a unique solution $u(t)>0$ on $t\in [t_{1},t_{2}]$ by using Lemma 3.3 from [35]. The proof is complete. $\square$

We define a cone P is a subset of the Banach space $E=C[t_{1},t_{2}]$ by

$$\begin{aligned} P=\big \{u\in C[t_{1},t_{2}]: u(t)\ge 0, t\in [t_{1},t_{2}]\big \}, \end{aligned}$$

set

$$\begin{aligned}&K=\big \{u\in P: u(t)~\text {is concave and}\; \min u(t)\ge \delta \Vert u\Vert , ~t\in \big [t_{1}+n^{-1},t_{2}-n^{-1}\big ],\\&~\forall n\in N^{*}\big \}, \end{aligned}$$

where $\delta =\frac{l_{1}\sigma _{0}}{\Vert L_{1}\Vert }$, $l_{1}=\min \nolimits _{t\in [t_{1},t_{2}]}L_{1}(t)$, the norm $\Vert u\Vert =\max \nolimits _{t\in [t_{1},t_{2}]}|u(t)|$, and for any $0<r_{0}<R_{0}<+\infty$, we have ${\overline{K}}_{r_{0},R_{0}}\subseteq K\subseteq P$ , where ${\overline{K}}_{r_{0},R_{0}}=\big \{u\in K: r_{0}\le \Vert u\Vert \le R_{0}\big \}$, and let $K_{r_{0}}=\{u\in K: \Vert u\Vert \le r_{0}\}$, $\partial K_{r_{0}}=\{u\in K: \Vert u\Vert = r_{0}\}$. We give the following lemma:

Lemma 3.6

[36] Let E is a real Banach space, K is a positive cone in E, for arbitrary $0<r_{0}<R_{0}<+\infty$, define the operator $T:{\overline{K}}_{r_{0},R_{0}}\rightarrow K$ is a completely continuous operator, if

(i):

 $\Vert Tu\Vert \le \Vert u\Vert$, $u\in \partial K_{r_{0}}$;

(ii):

 $\exists$ $f\in \partial K_{1}$ such that $u\ne Tu+\mu _{0}f$, $u\in \partial K_{R_{0}}$.

Then T has a fixed point in ${\overline{K}}_{r_{0},R_{0}}$.

We assume that the following condition is satisfied:

(H5):

 Let $\Omega (n)=[t_{1},t_{1}+\frac{1}{n}]\cup [t_{2}-\frac{1}{n},t_{2}]$, $n\in N^{*}$, and for any $0<r_{0}<R_{0}<+\infty$, letting

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\int _{\Omega (n)}G(s,s)[a(s)F(s,u(s))+b(s)]ds=0. \end{aligned}$$

The operator $T: {\overline{K}}_{r_{0},R_{0}}\rightarrow P$ be defined by

$$\begin{aligned} (Tu)(t)&=\int _{t_{1}}^{t_{2}}H(t,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&=\int _{t_{1}}^{t_{2}}G(t,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)[a(s)F(s,u(s))+b(s)]dsd\xi (\tau ) \nonumber \\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}\int _{t_{1}}^{t_{2}}G(\tau ,s)[a(s)F(s,u(s))+b(s)]dsd\eta (\tau ). \end{aligned}$$

(33)

Lemma 3.7

T is a completely continuous operator.

Proof

Since (22) and the define from (33) about T, we have

$$\begin{aligned} (Tu)(t)&\le \mathfrak {b_{0}}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&\le \Vert L_{1}\Vert \int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(t,u(s))+b(s)]ds. \end{aligned}$$

(34)

Since (H5), for $\forall$ $r_{0}>0$, $\exists$ $n_{1}\in N^{*}$ such that

$$\begin{aligned} \sup _{u\in \partial K_{r_{0}}}\int _{\Omega (n_{1})}G(s,s)[a(s)F(s,u(s))+b(s)]ds<1, \end{aligned}$$

for $\forall$ $u\in \partial K_{r_{0}}$, setting $u(t_{0})=\max \limits _{t\in [t_{1},t_{2}]}|u(t)|=r_{0}$, it follows from the concavity of u(t) on $[t_{1},t_{2}]$ that

$$\begin{aligned} u(t)\ge \left\{ \begin{array}{lll} \frac{u(t_{0})(t-t_{1})}{t_{0}-t_{1}},~~t_{1}\le t\le t_{0}\\ \frac{u(t_{0})(t_{2}-t)}{t_{2}-t_{0}},~~t_{0}\le t\le t_{2} \end{array} \right. \ge \left\{ \begin{array}{lll} \frac{r_{0}(t-t_{1})}{t_{2}-t_{1}},~~t_{1}\le t\le t_{0}\\ \frac{r_{0}(t_{2}-t)}{t_{2}-t_{1}},~~t_{0}\le t\le t_{2} \end{array}, \right. \end{aligned}$$

(35)

thus, since (35), for $\forall$ $t\in [t_{1}+\frac{1}{n_{1}},t_{2}-\frac{1}{n_{1}}]$, we obtain $\frac{r_{0}}{n_{1}(t_{2}-t_{1})}\le u(t)\le r_{0}$, and

$$\begin{aligned}&\sup _{u\in \partial K_{r_{0}}}\Vert L_{1}\Vert \int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\quad \le \sup _{u\in \partial K_{r_{0}}}\Vert L_{1}\Vert \int _{\Omega (n_{1})}G(s,s)[a(s)F(s,u(s))\\&\quad +b(s)]ds+\sup _{u\in \partial K_{r_{0}}}\Vert L_{1}\Vert \int _{t_{1}+\frac{1}{n_{1}}}^{t_{2}-\frac{1}{n_{1}}}G(s,s)[a(s)F(s,u(s))+b(s)]ds\le M_{3}, \end{aligned}$$

where

$$\begin{aligned} M_{3}=\Vert L_{1}\Vert +(t_{2}-t_{1})\Vert L_{1}\Vert \frac{(t_{2}-t_{1}+\alpha )\beta }{t_{2}-t_{1}+\alpha -\beta }\bigg [\frac{e^{t_{1}}F_{1}}{(1+e^{t_{1}})^{2}}+\frac{\omega (5+3\sqrt{3})}{27+15\sqrt{3}}\bigg ], \end{aligned}$$

and

$$\begin{aligned} F_{1}=\max \bigg \{F(t,u):(t,u)\in \bigg [t_{1}+\frac{1}{n_{1}},t_{2}-\frac{1}{n_{1}}\bigg ]\times \bigg [\frac{r_{0}}{n_{1}(t_{2}-t_{1})},r_{0}\bigg ]\bigg \}, \end{aligned}$$

which shows that $T:D\subseteq {\overline{K}}_{r_{0},R_{0}}\rightarrow P$ is uniformly bounded.

We prove that $T:{\overline{K}}_{r_{0},R_{0}}\rightarrow P$ is equicontinuous. For $\forall \varepsilon >0$, there exists $n_{2}\in N^{*}$, such that

$$\begin{aligned} \sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\int _{\Omega (n_{2})}G(s,s)[a(s)F(s,u(s))+b(s)]ds<\frac{\varepsilon }{8\Vert L_{1}\Vert }, \end{aligned}$$

since $\kappa _{01}(t)$, $\kappa _{02}(t)$ and G(t, s) is continuous on $[t_{1},t_{2}]$, thus, $\kappa _{01}(t)$, $\kappa _{02}(t)$ and G(t, s) is uniformly continuous on $[t_{1},t_{2}]$, i.e., for $\forall \varepsilon >0$, there exists $\delta >0$, when $|t'-t''|<\delta$ for any $t',t''\in [t_{1},t_{2}]$, we have

$$\begin{aligned}&\big |\kappa _{01}(t')-\kappa _{01}(t'')\big |<\bigg (4M_{4}\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )\bigg )^{-1}\varepsilon ,\\&\big |\kappa _{02}(t')-\kappa _{02}(t'')\big |<\bigg (4M_{4}\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau )\bigg )^{-1}\varepsilon ,\\&\big |G(t',s)-G(t'',s)\big |<(4M_{4})^{-1}G(s,s)\varepsilon , \end{aligned}$$

where

$$\begin{aligned} M_{4}=(t_{2}-t_{1})\frac{(t_{2}-t_{1}+\alpha )\beta }{t_{2}-t_{1}+\alpha -\beta }\bigg [\frac{e^{t_{1}}F_{2}}{(1+e^{t_{1}})^{2}}+\frac{\omega (5+3\sqrt{3})}{27+15\sqrt{3}}\bigg ] \end{aligned}$$

and

$$\begin{aligned} F_{2}=\max \bigg \{F(t,u):(t,u)\in \bigg [t_{1}+\frac{1}{n_{2}},t_{2}-\frac{1}{n_{2}}\bigg ]\times \bigg [\frac{r_{0}}{n_{2}(t_{2}-t_{1})},r_{0}\bigg ]\bigg \}. \end{aligned}$$

Hence, when $|t'-t''|<\delta$ for any $t',t''\in [t_{1},t_{2}]$, we can obtain

$$\begin{aligned} |(Tu)(t')-(Tu)(t'')|&\le 2\mathfrak {b_{0}}\sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\int _{\Omega (n_{2})}G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\quad +\sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\int _{t_{1}+\frac{1}{n_{2}}}^{t_{2}-\frac{1}{n_{2}}}\big |G(t',s)\\&\quad -G(t'',s)\big |[a(s)F(s,u(s))+b(s)]ds\\&\quad +2\Vert \kappa _{01}\Vert \int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )\sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\\&\quad \int _{\Omega (n_{2})}G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\quad +|\kappa _{01}(t')-\kappa _{01}(t'')|\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )\int _{t_{1}+\frac{1}{n_{2}}}^{t_{2}-\frac{1}{n_{2}}}\\&\quad G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\quad +2\Vert \kappa _{02}\Vert \int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau )\sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\\&\quad \int _{\Omega (n_{2})}G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\quad +|\kappa _{02}(t')-\kappa _{02}(t'')|\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau )\int _{t_{1}+\frac{1}{n_{2}}}^{t_{2}-\frac{1}{n_{2}}}\\&\quad G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\le 2\Vert L_{1}\Vert \sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\\&\quad \int _{\Omega (n_{2})}G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\quad +\bigg [|\kappa _{01}(t')-\kappa _{01}(t'')|\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )+|\kappa _{02}(t')\\&\quad -\kappa _{02}(t'')|\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau )\\&\quad +\frac{\varepsilon }{4M_{4}}\bigg ]\cdot \sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\int _{t_{1}+\frac{1}{n_{2}}}^{t_{2}-\frac{1}{n_{2}}}\\&\quad G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&<\varepsilon , \end{aligned}$$

which implies that T is equicontinuous on ${\overline{K}}_{r_{0},R_{0}}$.

By using Arzela-Ascoli theorem, we can prove T is compact on ${\overline{K}}_{r_{0},R_{0}}$.

We prove that $T:{\overline{K}}_{r_{0},R_{0}}\rightarrow P$ is continuous. Assume $u_{n}, u_{0}\in {\overline{K}}_{r_{0},R_{0}}$ and when $n\rightarrow \infty$, we have $\Vert u_{n}-u_{0}\Vert \rightarrow 0$, then $r_{0}<\Vert u_{n}\Vert ,~\Vert u_{0}\Vert <R_{0}$.

Given a fixed $\varepsilon >0$, since (H5), there exists $n_{3}\in N^{*}$ such that

$$\begin{aligned} \sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\int _{\Omega (n_{3})}G(s,s)[a(s)F(s,u(s))+b(s)]ds<\frac{\varepsilon }{4\Vert L_{1}\Vert }, \end{aligned}$$

(36)

since $F(t,u):\big [t_{1}+\frac{1}{n_{3}},t_{2}-\frac{1}{n_{3}}\big ]\times \big [\frac{r_{0}}{n_{3}(t_{2}-t_{1})},R_{0}\big ]\rightarrow R$ is uniformly continuous and $a(t):[t_1,t_2]\rightarrow R$ is continuous, by using the Lebesgue dominated convergence theorem, we have

$$\begin{aligned} \int _{t_{1}+\frac{1}{n_{3}}}^{t_{2}-\frac{1}{n_{3}}}G(s,s)a(s)\big |F(s,u_{n}(s))-F(s,u_{0}(s))\big |ds\rightarrow 0,~~n\rightarrow \infty , \end{aligned}$$

i.e., there exists $N\in N^{*}$, when $n>N$, we have

$$\begin{aligned} \int _{t_{1}+\frac{1}{n_{3}}}^{t_{2}-\frac{1}{n_{3}}}G(s,s)a(s)\big |F(s,u_{n}(s))-F(s,u_{0}(s))\big |ds<\frac{\varepsilon }{2\Vert L_{1}\Vert }, \end{aligned}$$

(37)

by using (36) and (37), we obtain

$$\begin{aligned} |(Tu_{n})(t)-(Tu_{0})(t)|&\le 2\Vert L_{1}\Vert \sup _{u\in {\overline{K}}_{r_{0},R_{0}}}\int _{\Omega (n_{3})}G(s,s)[a(s)F(s,u(s))+b(s)]ds\\&\quad +\Vert L_{1}\Vert \int _{t_{1}+\frac{1}{n_{3}}}^{t_{2}-\frac{1}{n_{3}}}G(s,s)a(s)\big |F(s,u_{n}(s))-F(s,u_{0}(s))\big |ds\\&<\varepsilon . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Vert Tu_{n}-Tu_{0}\Vert \le \varepsilon . \end{aligned}$$

Thus, the operator T is continuous.

As a result, T is a completely continuous operator. $\square$

Lemma 3.8

$T({\overline{K}}_{r_{0},R_{0}})\subseteq K$.

Proof

Let $u\in {\overline{K}}_{r_{0},R_{0}}$, since (22) and (33), we have

$$\begin{aligned} (Tu)(t)&\ge \mathfrak {a_{0}}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\xi (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\eta (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds \nonumber \\&\ge l_{1}\sigma _{0}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(t,u(s))+b(s)]ds. \end{aligned}$$

(38)

Linking (34) and (38), for $t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]$, $n\in N^{*}$, we obtain

$$\begin{aligned} \min _{t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]}(Tu)(t)\ge \min _{t\in [t_{1},t_{2}]}(Tu)(t)\ge \delta \Vert Tu\Vert , \end{aligned}$$

which shows that $T({\overline{K}}_{r_{0},R_{0}})\subseteq K$. $\square$

Theorem 3.9

Assume that (H1), (H2) and (H5) hold, further we assume that the following condition are satisfied:

(H6):

 there exists positive number $F^{0}$ and $F_{\infty }$ such that

$$\begin{aligned} F^{0}=\lim _{u\rightarrow 0}\sup \max _{t\in [t_{1},t_{2}]}\frac{F(t,u)}{u},~F_{\infty }=\lim _{u\rightarrow \infty }\inf \min _{t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]}\frac{F(t,u)}{u}. \end{aligned}$$

Then the integral boundary value problem (12) has at least one positive solution on the interval $[t_{1},t_{2}]$.

Proof

Given a fixed $\epsilon >0$, since (H6), there exists $r_{0}>0$ such that

$$\begin{aligned} F(t,u)\le (F^{0}+\epsilon )u,~~\forall t\in [t_{1},t_{2}], ~0<u<r_{0}, \end{aligned}$$

(39)

and

$$\begin{aligned} \Vert L_{1}\Vert \le \frac{(t_{2}-t_{1}+\alpha -\beta )r_{0}}{(F^{0}+\epsilon )(t_{2}-t_{1})(t_{2}-t_{1}+\alpha )\beta \cdot \big (\frac{e^{t_{1}}r_{0}}{(1+e^ {t_{1}})^{2}}+\frac{\omega (5+3\sqrt{3})}{27+15\sqrt{3}}\big )} \end{aligned}$$

(40)

For arbitrary $u\in \partial K_{r_{0}}$, by using (39) and (40), we have

$$\begin{aligned} |(Tu)(t)|&\le \mathfrak {b_{0}}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(F^{0}+\epsilon )u(s)+b(s)]ds \\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\xi (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(F^{0}+\epsilon )u(s)+b(s)]ds \\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {b}}(\tau )d\eta (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(F^{0}+\epsilon )u(s)+b(s)]ds \\&\le \Vert L_{1}\Vert (F^{0}+\epsilon )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)u(s)+b(s)]ds \\&\le r_{0}, \end{aligned}$$

which implies that $\Vert Tu\Vert \le \Vert u\Vert$.

On the other hand, since (H6), there exists $R'_{0}>0$ such that

$$\begin{aligned} F(t,u)\ge (F_{\infty }-\epsilon )u,~~\forall t\in \bigg [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}\bigg ], ~u\ge R'_{0},~n\in N^{*}. \end{aligned}$$

(41)

and

$$\begin{aligned} l_{1}\ge \frac{(1+e^{t_{2}})^{2}(t_{2}-t_{1}+\alpha -\beta )}{\sigma _{0}\alpha e^{t_{2}}(t_{1}+\beta -t_{2})(t_{2}-t_{1})(F_{\infty }-\epsilon )}. \end{aligned}$$

(42)

Define the function $f(t)\equiv 1$, $\forall$ $t\in [t_{1},t_{2}]$, let $R_{0}=\max \{\delta ^{-1}R'_{0},2r_{0}\}$, then we have $f(t)\in \partial K_{1}$ and $R_{0}>r_{0}$. we prove $u\ne Tu+\mu f(t)$ for arbitrary $u\in \partial K_{R_{0}}$, otherwise, there exists $u_{0}\in \partial K_{R_{0}}$, $\mu _{0}>0$, such that $u_{0}= Tu_{0}+\mu _{0}f(t)$.

For $t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]$, $n\in N^{*}$, we have

$$\begin{aligned} |u_{0}(t)|\ge \min _{t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]}|u_{0}(t)|=u_{0}^{*}\ge \delta \Vert u\Vert \ge R'_{0}, \end{aligned}$$

by using (41) and (42), for $t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]$, we obtain

$$\begin{aligned} u_{0}(t)&\ge \mathfrak {a_{0}}\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(F_{\infty }-\epsilon )u_{0}(s)+b(s)]ds \\&\quad +\kappa _{01}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\xi (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(F_{\infty }-\epsilon )u_{0}(s)+b(s)]ds\\&\quad +\kappa _{02}(t)\int _{t_{1}}^{t_{2}}{\mathfrak {a}}(\tau )d\eta (\tau )\int _{t_{1}}^{t_{2}}G(s,s)[a(s)(F_{\infty }-\epsilon )u_{0}(s)+b(s)]ds\\&\quad +\mu _{0}f(t)\\&\ge l_{1}\sigma _{0}\int _{t_{1}+\frac{1}{n}}^{t_{2}-\frac{1}{n}}G(s,s)[a(s)(F_{\infty }-\epsilon )u_{0}(s)+b(s)]ds+\mu _{0}\\&\ge u_{0}^{*}+\mu _{0}>u_{0}^{*}, \end{aligned}$$

which implies that $u_{0}^{*}>u_{0}^{*}$, this is a contradiction, thus, $u\ne Tu+\mu _{0}f(t)$, $u\in \partial K_{R_{0}}$.

The assumptions of the Lemma 3.6 are satisfied, hence, T has a fixed point $u^{*}$ in K with $r_{0}<\Vert u^{*}\Vert <R_{0}$. i.e., $u^{*}\ge 0$, $t\in [t_{1},t_{2}]$, we obtain

$$\begin{aligned} u^{*}(t)\ge \min _{t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]}u^{*}(t)\ge \delta \Vert u\Vert \ge 0,~t\in \bigg [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}\bigg ], \end{aligned}$$

and since the concavity of $u^{*}$, we also have

$$\begin{aligned} u^{*}(t)&\ge \frac{u^{*}(t_{1}+\frac{1}{n})-u^{*}(t_{1})}{t_{1}+\frac{1}{n}-t_{1}}(t-t_{1})+u^{*}(t_{1})\\&\ge \frac{(t_{1}+\frac{1}{n}-t)u^{*}(t_{1})}{\frac{1}{n}}+\frac{(t-t_{1})u^{*}(t_{1}+\frac{1}{n})}{\frac{1}{n}}\\&>0,~~t\in \big [t_{1},t_{1}+\frac{1}{n}\big ], \end{aligned}$$

and

$$\begin{aligned} u^{*}(t)&\ge \frac{u^{*}(t_{2})-u^{*}(t_{2}-\frac{1}{n})}{t_{2}-t_{2}+\frac{1}{n}}(t-t_{2})+u^{*}(t_{2})\\&\ge \frac{(t-(t_{2}-\frac{1}{n}))u^{*}(t_{2})}{\frac{1}{n}}+\frac{(t_{2}-t)u^{*}(t_{2}-\frac{1}{n})}{\frac{1}{n}}\\&>0,~~t\in \big [t_{2}-\frac{1}{n},t_{2}\big ], \end{aligned}$$

thus, $u^{*}(t)>0$, $t\in [t_{1},t_{2}]$, as a result, the integral boundary value problem (12) has at least one positive solution. $\square$

Theorem 3.10

Assume that (H1), (H2) and (H5) hold, further we assume that the following condition are satisfied:

(H7):

 there exists positive number $F^{\infty }$ and $F_{0}$ such that

$$\begin{aligned} F^{\infty }=\lim _{u\rightarrow +\infty }\sup \max _{t\in [t_{1},t_{2}]}\frac{F(t,u)}{u},~F_{0}=\lim _{u\rightarrow 0}\inf \min _{t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]}\frac{F(t,u)}{u}. \end{aligned}$$

Then the integral boundary value problem (12) has at least one positive solution on the interval $[t_{1},t_{2}]$.

Proof

Given a fixed $\epsilon _{1}>0$, since (H7), there exists $R''_{0}>0$ such that $(1+e^{t_{1}})^{2}(t_{2}-t_{1}+\alpha -\beta )[\Vert L_{1}\Vert \beta (t_{2}-t_{1})e^{t_{1}}(t_{2}-t_{1}+\alpha )]^{-1}-\epsilon _{1}>0$, and

$$\begin{aligned} F(t,u)\le \bigg [\frac{(1+e^{t_{1}})^{2}(t_{2}-t_{1}+\alpha -\beta )}{\Vert L_{1}\Vert \beta (t_{2}-t_{1})e^{t_{1}}(t_{2}-t_{1}+\alpha )}-\epsilon _{1}\bigg ]u, ~u\ge R''_{0},t\in [t_{1},t_{2}], \end{aligned}$$

setting

$$\begin{aligned}&M_{5}=\sup _{u\in \partial K_{R''_{0}}}\Vert L_{1}\Vert \int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(s,u(s))+b(s)]ds,\\&M_{6}=M_{5}+\frac{\beta \omega \Vert L_{1}\Vert (5+3\sqrt{3})(t_{2}-t_{1})(t_{2}-t_{1}+\alpha )}{(27+5\sqrt{3})(t_{2}-t_{1}+\alpha -\beta )}, \end{aligned}$$

and

$$\begin{aligned} R_{0}^{*}>\max \big \{R''_{0},M_{6}(1+e^{t_{1}})^{2}(t_{2}-t_{1}+\alpha -\beta )[\epsilon _{1}\Vert L_{1}\Vert \beta (t_{2}-t_{1})e^{t_{1}}(t_{2}-t_{1}+\alpha )] ^{-1}\big \}. \end{aligned}$$

For any $u\in \partial K_{R_{0}^{*}}$, let

$$\begin{aligned} \Omega (u)=\big \{t\in [t_{1},t_{2}]:u \in [R''_{0},+\infty )\big \}, \end{aligned}$$

which implies that $R''_{0}\le u\le \Vert u\Vert =R_{0}^{*}$, if $u_{1}(t)=\min \{u(t),R''_{0}\}$, then $u_{1}\in \partial K_{R''_{0}}$. Hence, for arbitrary $u\in \partial K_{R_{0}^{*}}$, we obtain

$$\begin{aligned} (Tu)(t)&\le \Vert L_{1}\Vert \int _{\Omega (u)}G(s,s)[a(s)F(t,u(s))+b(s)]ds\\&\quad +\Vert L_{1}\Vert \int _{[t_{1},t_{2}]/\Omega (u)}G(s,s)[a(s)F(t,u(s))+b(s)]ds\\&\le \bigg [\frac{(1+e^{t_{1}})^{2}(t_{2}-t_{1}+\alpha -\beta )}{\Vert L_{1}\Vert \beta (t_{2}-t_{1})e^{t_{1}}(t_{2}-t_{1}+\alpha )}-\epsilon _{1}\bigg ]R_{0}^{*} \Vert L_{1}\Vert \int _{t_{1}}^{t_{2}}G(s,s)a(s)ds\\&\quad +\Vert L_{1}\Vert \int _{t_{1}}^{t_{2}}G(s,s)b(s)ds+\Vert L_{1}\Vert \int _{t_{1}}^{t_{2}}G(s,s)[a(s)F(t,u_{1}(s))+b(s)]ds\\&\le \frac{(1+e^{t_{1}})^{2}(t_{2}-t_{1}+\alpha -\beta )}{\Vert L_{1}\Vert \beta (t_{2}-t_{1})e^{t_{1}}(t_{2}-t_{1}+\alpha )}R_{0}^{*}\Vert L_{1}\Vert \int _{t_{1}} ^{t_{2}}G(s,s)a(s)ds\\&\quad -\epsilon _{1}R_{0}^{*}\Vert L_{1}\Vert \int _{t_{1}}^{t_{2}}G(s,s)a(s)ds+M_{6}\\&\le R_{0}^{*}=\Vert u\Vert , \end{aligned}$$

which shows that $\Vert Tu\Vert \le \Vert u\Vert$ for $u\in \partial K_{R_{0}^{*}}$.

Given a fixed $\epsilon _{2}>0$, since (H7), there exists $0<r'_{0}<R_{0}^{*}$ such that

$$\begin{aligned}&F(t,u)\ge \bigg [\frac{(1+e^{t_{2}})^{2}(t_{2}-t_{1}+\alpha -\beta )}{l_{1}\sigma _{0}\alpha (t_{2}-t_{1})e^{t_{2}}(t_{1}+\beta -t_{2})}+\epsilon _{2}\bigg ]u,\\&~0<u\le r'_{0}, ~t\in \bigg [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}\bigg ], \end{aligned}$$

let $f(t)\equiv 1$, then $f\in \partial K_{1}$, we prove $u\ne Tu+\mu f$, otherwise, $\exists$ $u'_{0}\in \partial K_{r'_{0}}$ and $\mu '_{0}>0$ such that $u'_{0}= Tu'_{0}+\mu '_{0}f$.

Setting $u_{0}^{'*}=\min \big \{u'_{0}(t):t\in [t_{1}+\frac{1}{n},t_{2}-\frac{1}{n}]\big \}$, we have

$$\begin{aligned} u'_{0}(t)&\ge l_{1}\sigma _{0}\int _{t_{1}+\frac{1}{n}}^{t_{2}-\frac{1}{n}}G(s,s)[a(s)F(s,u'_{0}(s))+b(s)]ds+\mu '_{0}f(t) \\&\ge \bigg [\frac{(1+e^{t_{2}})^{2}(t_{2}-t_{1}+\alpha -\beta )}{l_{1}\sigma _{0}\alpha (t_{2}-t_{1})e^{t_{2}}(t_{1}+\beta -t_{2})}+\epsilon _{2}\bigg ]l_{1}\sigma _{0}u_{0}^{'*}\int _{t_{1}+\frac{1}{n}}^{t_{2}-\frac{1}{n}}G(s,s)a(s)ds+\mu '_{0}\\&\ge u_{0}^{'*}+\epsilon _{2}l_{1}\sigma _{0}u_{0}^{'*}\int _{t_{1}+\frac{1}{n}}^{t_{2}-\frac{1}{n}}G(s,s)a(s)ds+\mu '_{0}>u_{0}^{'*}, \end{aligned}$$

which implies that $u_{0}^{'*}>u_{0}^{'*}$, this is a contradiction, thus, $u\ne Tu+\mu f(t)$, $u\in \partial K_{r'_{0}}$.

The assumptions of the Lemma 3.6 are satisfied, hence, T has a fixed point $u^{'*}$ in K with $r'_{0}<\Vert u^{'*}\Vert <R_{0}^{*}$. The conclusion is that the integral boundary value problem (12) has at least one positive solution. $\square$