1 Introduction

Gyres is a circular ocean current driven by wind stress and the rotation of the earth under the Coriolis effect, see [1,2,3,4]. The gyres is deflected clockwise rotation in the Northern Hemisphere and counterclockwise rotation in the Southern Hemisphere due to the Coriolis effect. In ocean current, most of them rely on the equator to present a certain flow pattern in the North and South [5]. It is worth noting that the mid-latitudes do not appear at the equator as the meridional components of the coriolis force disappear, although they do encounter circulations [6].

Mathematical studies of ocean circulation are essential for predicting the characteristics of large-scale natural phenomena in the ocean. In the arctic gyres, the horizontal velocity is 0.01 m/s [7], which is about \(10^4\) times of the vertical velocity [8]. Therefore, in the case of ignoring the vertical velocity, the ocean circulation is approximately regarded as flowing on the rotating sphere by introducing a flow function, and the circulation model in the spherical coordinate system is transformed into a plane elliptic partial differential equation by using the stereographic projection [7]. Since the arctic region is covered by ice, waves do not effect, distinguishing the Southern Ocean (where current and wave interactions are important), see [9, 10], locating in the northern Arctic Ocean (above latitude \(84^{\circ }\)), the circulation is centered roughly to the north and slowly rotates clockwise on an ice surface more than 2 m thick [11].

Recently, Constantin and Johnson [7] transformed the Euler equation expressed in a rotating frame in spherical coordinates coupled with the equation of mass conservation and the appropriate boundary conditions into a second-order ordinary differential equation on a semi-infinite interval under the condition that azimuthal variations is ignored. It’s constrained by asymptotic conditions, the existence of solutions of the equation are studied in [12,13,14,15].

In the present paper, we study the existence and uniqueness of the solution of the nonlinear model of the arctic circulation by using the fixed point method under the mild conditions that the outer boundary is a first-class line and there is no jet. We extend the existence and uniqueness of local solutions in finite interval to a semi-infinite interval by requiring that the North Pole corresponds to a known flow function.

Fig. 1
figure 1

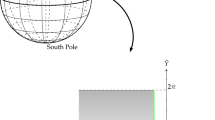
Azimuthal and polar angular spherical coordinates \(\varphi \) and \(\theta \) of a point P on the spherical surface of the Earth,with \(\theta =0\) and \(\theta =\pi \) correspond to the South and North Pole. Respectively, the stereographic projection of the unit sphere (center at origin) from the South Pole to the equatorial plane,the point P in the arctic region,the straight line connecting it to the South Pole intersects the equatorial plane in a point \(P'\) belonging to the interior of the circular region delimited by the Equator. The arctic gyres is mapped into a circular region within the equatorial plane

Full size image

2 Preliminaries

A model for ocean current in spherical coordinates can be described. In terms of the stereographic projection from the South Pole, the azimuthal and polar velocity components of horizontal gyre flow given by

$$\begin{aligned} \frac{1}{\sin \theta }\psi _\phi \quad \text {and}\quad -\psi _\theta , \end{aligned}$$
(1)

where \(\theta \in (0,\pi ]\) is polar angle with \(\theta =\pi \) corresponding to the North Pole,and \(\varphi \in [0,2\pi )\) represents the azimuthal angle (see Fig. 1), and \(\psi (\theta ,\varphi )\) is the stream function. In terms of the stream function \(\Psi \) associated with the vorticity of the motion of the ocean, defined by

$$\begin{aligned} \psi (\theta ,\varphi )=-\,\omega \cos \theta +\Psi (\theta ,\varphi ), \end{aligned}$$

where \(\Psi \) is not driven by the Earth’s rotation, the governing equation of ocean flow can be expressed as

$$\begin{aligned} \frac{1}{\sin ^{2}\theta }\Psi _{\varphi \varphi }+\Psi _{\theta }\cot \theta +\Psi _{\theta \theta }=F(\Psi -\omega \cos \theta ), \end{aligned}$$
(2)

where \(2\omega \cos \theta \) is the planetary vorticity (\(\omega >0\) is the non-dimensional Coriolis parameter), F is the oceanic vorticity which the form of ocean flow dictates the nature of the oceanic vorticity function. For example, the vorticity of water flow, the interaction of geophysical wave-current, and the ocean vorticity of these wind-driven flows can be considered as a fixed non-zero constant. Although the spin vorticity is determined, the vorticity associated with ocean motion can be selected to represent a specific circulation, especially, when the ocean vorticity disappears (that is \(F=0\)), the flow field is irrotational.

Fig. 2
figure 2

In the unit circle, triangle \({ OPS}\) is an isosceles triangle, if G is the middle point of PS, we can get \(\angle PSO=\frac{\pi }{2}-\theta \), through connecting OG, since \(OP=r\), this indicates that (4) is true

Full size image

The stereographic projection is used from the South Pole to the equatorial plane on a unit sphere centered at the origin. Setting

$$\begin{aligned} \xi =re^{i\phi }\quad \text {with}\quad r=\cot \left( \frac{\theta }{2}\right) =\frac{\sin \theta }{1-\cos \theta }, \end{aligned}$$
(3)

where \((r,\phi )\) represents the polar coordinates on the equatorial plane, and r is a function of \(\theta \), whose geometric relationship is shown in Fig. 2, and it transforms (3) into

$$\begin{aligned} \psi _{\xi {\overline{\xi }}}+2\omega \frac{1-\xi {\overline{\xi }}}{(1+\xi {\overline{\xi }})^{3}} -\frac{F(\psi )}{(1+\xi {\overline{\xi }}))^{2}}=0, \end{aligned}$$
(4)

using Cartesian coordinates (x, y), the above equation is equivalent to a semilinear elliptic partial differential equation

$$\begin{aligned} \Delta \psi +8\omega \frac{1-(x^{2}+y^{2})}{(1+x^2+y^2)^{3}}-\frac{4F(\psi )}{(1+x^2+y^2)^{2}}=0. \end{aligned}$$
(5)

where \(\Delta =\partial _{x}^{2}+\partial _{y}^{2}\) is the Laplace operator, expressed in accordance with the Cartesian coordinates on the equatorial plane, in which the unknown function \(\psi (x,y)\) represents the stream function. For a specified \(\omega \) and F, the gyre is obtained by solving (5) in a given plane region \({\mathcal {O}}\), with Dirichlet boundary data

$$\begin{aligned} \psi =u_0\quad \hbox {on}\quad \partial {\mathcal {O}}. \end{aligned}$$
(6)

where \(u_0\) means that the value of the flow function is at the boundary \(\partial {\mathcal {O}}\) of \({\mathcal {O}}\), and the corresponding streamline \(\psi =u_0\). According to the stereographic projection is employed, the plane region \({\mathcal {O}}\) corresponds to the ocean region, and the ocean region is located at the location of the gyre.

In this paper, we study the gyre problem in the Arctic Basin Ecozone which is the core northern part of the Arctic Ocean, and it is covered by more than 2 m of ice thickness. Between the North Pole and 84 degrees north latitude, there is an ocean area about 3.6 km deep, covering an area of about 1.27 million square kilometers, with no coast. The relatively constant ice sheets and floes in the arctic ocean, driven by the circulation of the Arctic Ocean, slowly float in a clockwise direction, roughly the center on North Pole. Setting corresponding to the planar region \({\mathcal {O}}=\{r:~0\le r<r_0\}\), with \(\theta \in [\frac{14\pi }{15},\pi ]\), \(r=\cot (\frac{\theta }{2})<\frac{1}{e}\), therefore \(r_0<\frac{1}{e}\), the considerations made in [3, 4, 6] show that. The flow of the arctic gyre, ignoring the azimuthal variation, corresponds to the radial symmetric solution \(\psi =\psi (r)\) of the problem (5)–(6). Setting \(t_0=-\,\ln (r_0)\ge 1\), the change of variables according to \(r=e^{-t}\) and

$$\begin{aligned} \psi (r)=u(t),\quad t\ge t_0 \end{aligned}$$

we can transforms (5) and (6) as the following second-order ordinary differential equation

$$\begin{aligned} u''(t)=\frac{F(u(t))}{\cosh ^{2}(t)}-\frac{2\omega \sinh (t)}{\cosh ^{3}(t)},\quad t>t_0, \end{aligned}$$
(7)

with the constraint conditions

$$\begin{aligned} u(t_0)=u_0, \end{aligned}$$
(8)

where \(u_0\) represents the stream function on the outer boundary of the ring region, and it expresses that the circle of latitude \(r=r_0\) is a streamline. We seek solutions of (2) in the interior of the circle \(r=r_0\), let \(\nabla _{(\theta ,\varphi )}\psi =(0,0)\) on the circle of latitude \(\theta =2\cot ^{-1}(r_0)\) in consideration of (1), since the component of azimuthal velocity disappears in the whole rotation region, we have equivalent boundary conditions

$$\begin{aligned} u'(t_0)=0. \end{aligned}$$
(9)

which shows that means that there is no jet flow phenomenon on the peripheral boundary.

3 Correlation results of nonlinear ocean vorticity

In this section, we study the existence and uniqueness of a continuous solution for the following nonlinear second order differential equation [arising from (7)]

$$\begin{aligned} u''(t)=a(t)F(t,u(t))+b(t),\quad t\ge t_0 \end{aligned}$$
(10)

where \(a(\cdot ),b(\cdot ):[t_0,+\infty )\rightarrow R\) are continuous, \(F(\cdot ,\cdot ):[t_0,+\infty )\times R\rightarrow R\) is continuous, and by the above case we consider the concrete forms

$$\begin{aligned} a(t):=\frac{1}{\cosh ^{2}(t)},\quad b(t):=-\frac{2\omega \sinh (t)}{\cosh ^{3}(t)}, \end{aligned}$$
(11)

but we form our results for general cases. If u(t) is a solution of the problem (8)–(10), integrating the equation on \([t_0,t)\), we obtain

$$\begin{aligned} u'(t)=\int _{t_0}^{t}a(s)F(s,u(s))ds+\int _{t_0}^{t}b(s)ds, \end{aligned}$$
(12)

then integrating (12) on \([t_0,t)\), which leads to

$$\begin{aligned} u(t)=u_0+\int _{t_0}^{t}(t-s)a(s)F(s,u(s))ds+\int _{t_0}^{t}(t-s)b(s)ds. \end{aligned}$$
(13)

Next, we study the existence and uniqueness for integral Eq. (13).

Theorem 3.1

Assume that \(a(\cdot ):[t_0,+\infty )\rightarrow R\) is continuous, \(b(\cdot ):[t_0,+\infty )\rightarrow R\) is integrable and \(F(\cdot ,\cdot ):[t_0,+\infty )\times R\rightarrow R\) is continuous. Denoted by

$$\begin{aligned} J_1=\int _{t_0}^{T}a(s)ds,\quad J_2=\int _{t_0}^{T}|b(s)|ds\,\text {for some}\, T>t_0, \end{aligned}$$

we suppose that there exists a constant \(h>0\) such that for

$$\begin{aligned} M_h=\max _{(t,u)\in [t_0,T]\times [u_0-h,u_0+h]}|F(t,u)|, \end{aligned}$$

it holds \(M_h\le \frac{h}{2(T-t_0)J_1}\), \(J_2\le \frac{h}{2(T-t_0)}\).Then the integral Eq. (13) has at least one

continuous solution u on the interval \([t_0,T]\) and satisfying \(u(t_0)=u_0\).

Proof

Let U be the space of all continuous functions on \([t_0,T]\). Obviously U is the Banach space with the maximum norm \(\Vert u\Vert =\max \nolimits _{t\in [t_0,T]}|u(t)|\). We define the subset

$$\begin{aligned} U_0=\{u\in C([t_0,T],R):u(t_0)=u_0\} \end{aligned}$$

of the space U. Set

$$\begin{aligned} K=\{u\in U_0:u_0-h\le u(t)\le u_0 +h, t\in [t_0,T]\}. \end{aligned}$$

and the operator \({\mathcal {T}}:K\rightarrow U\) be defined by

$$\begin{aligned} ({\mathcal {T}}u)(t)=u_0+\int _{t_0}^{t}(t-s)a(s)F(s,u(s))ds+\int _{t_0}^{t}(t-s)b(s)ds \end{aligned}$$
(14)

We consider the proof into the following four steps in order to prove that \({\mathcal {T}}\) defined in (14) has a fixed point on K.

Step 1 We prove K is a closed and convex subset on U. In fact, let \(u_i(t)\in K,i=1,2,\ldots ,m\), \(m\in N^{*}\), and

$$\begin{aligned} \sum _{i=1}^{m}\lambda _i=1,\lambda _i\ge 0 \end{aligned}$$

we have

$$\begin{aligned} \left| \sum _{i=1}^{m}\lambda _iu_i(t)-u_0\right| =\left| \sum _{i=1}^{m}\lambda _i(u_i(t)-u_0)\right| \le \sum _{i=1}^{m}\lambda _i h=h. \end{aligned}$$

This gives that

$$\begin{aligned} \sum _{i=1}^{m}\lambda _iu_i(t)\in K. \end{aligned}$$

which shows that K is convex.

Let \({u_n(t)}\subset K,n=1,2,\ldots \), and \(u_n(t)\rightarrow u_*(t)\in U,\quad n\rightarrow \infty \). We have

$$\begin{aligned} |u_*(t)-u_0|\le |u_n(t)-u_*(t)|+|u_n(t)-u_0|\le h,n\rightarrow \infty , \end{aligned}$$

which shows that K is closed.

Step 2 We prove that \({\mathcal {T}}(K)\subset K\). For each \(t\in [t_0,T]\), we have

$$\begin{aligned} |({\mathcal {T}}u)(t)-u_0|&\le \int _{t_0}^{t}(t-s)(|a(s)F(s,u(s))+b(s))|)ds\\&\le (T-t_0)M_h\int _{t_0}^{T}|a(s)|ds+(T-t_0)\int _{t_0}^{T}|b(s)|ds\le h, \end{aligned}$$

which shows that \({\mathcal {T}}:K\rightarrow K\) is well-defined.

Step 3 We prove that \({\mathcal {T}}(K)\) is relatively compact in U. Derive both sides of Eq. (14) with respect to t, we have

$$\begin{aligned} ({\mathcal {T}}u)'(t)=\int _{t_0}^{t}a(s)F(s,u(s))ds+\int _{t_0}^{t}b(s)ds,t\in [t_0,T]. \end{aligned}$$

For all \(t\in [t_0,T]\), we obtain

$$\begin{aligned} |({\mathcal {T}}u)'(t)|\le M_h\int _{t_0}^{T}|a(s)|ds+\int _{t_0}^{T}|b(s)|ds\le \frac{h}{T-t_0}. \end{aligned}$$

Let \(\{u_n\}\) be an arbitrary sequence in K, by using the mean value theorem, we obtain

$$\begin{aligned} |({\mathcal {T}}u_n)(t_1)-({\mathcal {T}}u_n)(t_2)|\le \frac{h}{T-t_0}|t_1-t_2|, t_1,t_2\in [t_0,T],n\in N^{*}, \end{aligned}$$

which implies that \(\{{\mathcal {T}}u_n\}\) is continuous, nondecreasing function in U.

Obviously, it is easy to see from step two that \(\{{\mathcal {T}}u_n\}\) is uniformly bounded in U.

By using the Arzela–Ascoli theorem (see [16]), we obtain that \(\{{\mathcal {T}}u_n\}\) is relatively compact in U.

Step 4 We prove that \({\mathcal {T}}:K\rightarrow K\) is continuous.

Given a fixed \(\varepsilon >0\), since \(F(t,u):[t_0,T]\times [u_0-h,u_0+h]\rightarrow R\) is uniformly continuous, there exists a constant \(\delta >0\) such that if \(u,v\in [u_0-h,u_0+h]\) with \(|u-v|<\delta \), then

$$\begin{aligned} |F(t,u)-F(t,v)|\le \frac{2\varepsilon }{a_*T^2},\quad \text {for all}\, t\in [t_0,T], \end{aligned}$$

where \(a_*=\max \limits _{t\in [t_0,T]}a(t)\). Hence, for arbitrary \(u_1,u_2\in K\) with \(\Vert u_1-u_2\Vert <\delta \), by computations we can have

$$\begin{aligned} |({\mathcal {T}}u_1)(t)-({\mathcal {T}}u_2)(t)|&{=}\left| \int _{t_0}^{t} (t-s)a(s)F(s,u_1(s))ds{-}\int _{t_0}^{t}(t{-}s)a(s)F(s,u_2(s))ds\right| \\&\le \int _{t_0}^{t}(t-s)a(s)(|F(s,u_1(s))-F(s,u_2(s))|)ds\\&\le a_*\frac{2\varepsilon }{a_*T^2}\int _{t_0}^{T}(T-s)ds\\&=a_*\frac{2\varepsilon }{a_*T^2}\cdot \frac{(T-t_0)^2}{2}\\&\le \varepsilon . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Vert {\mathcal {T}}u_1-{\mathcal {T}}u_2\Vert \le \varepsilon . \end{aligned}$$

As a consequence, the operator \({\mathcal {T}}:K\rightarrow K\) is continuous.

We have illuminated that all assumptions of the Schauders fixed point theorem are satisfied. As a result, there exists \(u\in K\) such that \({\mathcal {T}}u=u\), which corresponds to a continuous solution of (13) on \([t_0,T]\). \(\square \)

Note for (11) we have

$$\begin{aligned} \int _{1}^\infty a(s)ds=1-\tanh 1\doteq 0.238406,\quad \int _{1}^\infty |b(s)|ds=\frac{\omega }{\cosh ^21}\doteq 0.419974\omega , \end{aligned}$$

which gives uniform upper bounds for \(J_1\) and \(J_2\). Moreover, we have

$$\begin{aligned} \int _{t_0}^{t}(t-s)b(s)ds=-\,\omega \left( \frac{t-t_0}{\cosh ^2(t_0)}+\tanh (t_0)-\tanh (t)\right) , \end{aligned}$$

which has a linear growth.

Theorem 3.2

Assume that \(a(\cdot ),b(\cdot ):[t_0,+\infty )\rightarrow R^{+}\) and \(F(\cdot ,\cdot ):[0,+\infty )\times R^{+}\rightarrow R^{+}\) are continuous. Suppose further that

$$\begin{aligned} |F(t,u)-F(t,v)|\le L(|u-v|),~ \forall ~ u,v\in [0,+\infty ), \end{aligned}$$

where \(L(\cdot ):[0,+\infty )\rightarrow (0,+\infty )\) is continuous, nondecreasing and satisfies the condition

$$\begin{aligned} \int _{0}^{1}\frac{1}{L(s)}ds=\int _{1}^{+\infty }\frac{1}{L(s)}ds=+\,\infty . \end{aligned}$$
(15)

Then for any \(u_0>0\), Eq. (13) has a unique positive increasing continuous solution u on the interval \([t_0,+\infty )\) and satisfying \(u(t_0)=u_0\).

Proof

It is obviously \(u'(t)>0\) and \(u(t)>0\) because of the integral Eq. (12) and by the assumptions of theorem. We prove the uniqueness result. Let \(u_1(t)\) and \(u_2(t)\) be the two solutions of the integral Eq. (13) on \([t_0,T]\), \(T>t_0\) which are positive. Then we have

$$\begin{aligned} |u_1(t)-u_2(t)|&=\left| \int _{t_0}^{t}(t-s)a(s)F(s,u_1(s))ds -\int _{t_0}^{t}(t-s)a(s)F(s,u_2(s))ds\right| \\&\le \int _{t_0}^{t}(t-s)a(s)|F(s,u_1(s))-F(s,u_2(s))|ds\\&\le T \int _{t_0}^{t}a(s)|F(s,u_1(s))-F(s,u_2(s))|ds\\&\le T \int _{t_0}^{t}a(s)L(|u_1(s)-u_2(s)|)ds. \end{aligned}$$

Let \(\upsilon (t)=|u_1(t)-u_2(t)|\), \(t \in [t_0,T]\), then \(\upsilon (t)\ge 0\) and

$$\begin{aligned} \upsilon (t)\le T \int _{t_0}^{t}a(s)L(\upsilon (s))ds. \end{aligned}$$
(16)

For \(G(r)=\int _{1}^{r}\frac{1}{L(s)}ds\), \(r>0\), we obtain \(G(0_+)=-\,\infty \), \(G(+\infty )=+\,\infty \). Given a fixed \(\varepsilon >0\), it follows from (16) that

$$\begin{aligned} \upsilon (t)\le \varepsilon + T \int _{0}^{t}a(s)L(\upsilon (s))ds. \end{aligned}$$
(17)

By using the Bihary inequality (see [17]), we obtain

$$\begin{aligned} \upsilon (t)\le G^{-1}\left( G(\varepsilon )+T\int _{0}^{t}a(s)ds\right) ,t\in [t_0,T]. \end{aligned}$$
(18)

Letting \(\varepsilon \rightarrow 0\) we have \(G(\varepsilon )\rightarrow -\infty \), since \(G(0_+)=-\,\infty \), hence \(G^{-1}(-\,\infty )=0\). According to the assumptions of the theorem and (19), we obtain \(\upsilon (t)=0\), which shows that \(u_1=u_2\).

Now we show the existence. First, for any \(u_0\ge 0\) we consider

$$\begin{aligned} m_{u_0}=\max _{(t,u)\in [t_0,t_0+1]\times [u_0,u_0+1]}F(t,u), \end{aligned}$$

and Theorem 3.1 is applicable for

$$\begin{aligned} T=t_0+\min \left\{ \frac{1}{2J_2},\frac{1}{2m_{u_0}},1\right\} \end{aligned}$$

with

$$\begin{aligned} K=\{u\in U_0:u_0\le u(t)\le u_0 +1, t\in [t_0,T]\}. \end{aligned}$$

So we have a local existence and uniqueness. Next, assume that this solution is defined on the maximal interval \([u_0,{\hat{T}})\) for \({\hat{T}}\le +\infty \). If \({\hat{T}}<+\infty \) then we use

$$\begin{aligned} F(t,u)\le F(t,0)+L(u) \end{aligned}$$

to get

$$\begin{aligned} u(t)&\le u_0+\int _{t_0}^{{\hat{T}}}({\hat{T}}-s)a(s)F(s,0)ds+\int _{t_0}^{{\hat{T}}}({\hat{T}}-s)b(s)ds+{\hat{T}}\int _{t_0}^{t}a(s)L(u(s))ds. \end{aligned}$$

The Bihary inequality implies

$$\begin{aligned} u(t)&\le G^{-1}\left( G(u_0+\int _{t_0}^{{\hat{T}}}({\hat{T}}-s)a(s)F(s,0)ds +\int _{t_0}^{{\hat{T}}}({\hat{T}}-s)b(s)ds)\right. \nonumber \\&\quad \left. +{\hat{T}}\int _{0}^{{\hat{T}}}a(s)ds\right) , \end{aligned}$$
(19)

so u(t) can be extended to \({\hat{T}}\) and then to \({\hat{T}}+\delta \) for some \(\delta >0\), which is a contradiction. Thus \({\hat{T}}=+\,\infty \). Summarizing we get uniqueness and global existence on \([t_0,+\infty )\). \(\square \)

Remark 3.3

(15) is suitable for some function, for example,

$$\begin{aligned} L(x)= \left\{ \begin{array}{ll} x,&{}\quad x\in [0,1],\\ 1,&{}\quad x\in [1,+\infty ). \end{array} \right. \end{aligned}$$
(20)

Theorem 3.4

Assume that all assumptions in Theorem 3.2 are satisfied, and in the arctic gyres centered at the Arctic Ocean, asymptotic conditions can be considered

$$\begin{aligned} \lim _{t\rightarrow \infty }u(t)=\psi _0, \end{aligned}$$

where \(\psi _0\in R\) is a constant, it can be considered as being fixed since the only role of the stream function at the North Pole and physically. If \(u=u(t)\) is the solution of Eq. (10) on the interval \([t_0,T]\), then the solution \(u=u(t)\) of Eq. (10) pass by \((t_0,u_0)\) can be extended to the interval \([t_0,+\infty ]\).

Proof

We can prove that the conclusion holds by using the continuation theorem of the solution of the differential equation (see [18]), therefore, we omit the detailed proof here. \(\square \)

4 Linear oceanic vorticity

If the ocean vorticity F in the Eq. (10) is linear, i.e.,

$$\begin{aligned} F(t,u(t))=l(t)u(t)+m(t), \end{aligned}$$

where \(l(\cdot ),m(\cdot ):[t_0,+\infty )\rightarrow R\) are continuous, we have

$$\begin{aligned} \left\{ \begin{array}{l} u''(t)=p(t)u(t)+q(t),t\ge t_0,\\ u(t_0)=u_0,\\ u'(t_0)=0, \end{array} \right. \end{aligned}$$
(21)

where

$$\begin{aligned} p(t):=\frac{l(t)}{\cosh ^{2}(t)},\quad q(t):=\frac{m(t)}{\cosh ^{2}(t)}-\frac{2\omega \sinh (t)}{\cosh ^{3}(t)}. \end{aligned}$$

Now we are ready to present the following linear results.

Theorem 4.1

Assume that F is a linear function, \(p(\cdot ),q(\cdot ):[t_0,+\infty )\rightarrow R\) are continuous. If the \(p(\cdot )=p\) is a constant, then the solution of (21) is written as

$$\begin{aligned} u(t)&=\left[ 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-t_0)^{2n}\right] u_{0}+\int _{t_0}^{t}\left[ (t-\tau )\right. \nonumber \\&\quad \left. +\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-\tau )^{2n-1}\right] q(\tau )d\tau . \end{aligned}$$
(22)

On the other hand, if the \(p(\cdot )\) is not a constant, then the solution of (21) is written as

$$\begin{aligned} u(t)&=\bigg (1+\int _{t_0}^{t}\int _{t_0}^{\tau _1}p(\tau _2)d\tau _{2}d\tau _{1}\nonumber \\&\quad +\int _{t_0}^{t}\int _{t_0}^{\tau _1}p(\tau _2)\int _{t_0}^{\tau _{2}} \int _{t_{0}}^{\tau _3}p(\tau _4)d\tau _{4}d\tau _{3}d\tau _{2}d\tau _{1} +\cdots \bigg )u_0\nonumber \\&\quad +\int _{t_0}^{t}\bigg [(t-\tau )+\int _{\tau }^{t}\int _{\tau }^{\tau _{1}} p(\tau _{2})(\tau _{2}-\tau )d\tau _{2}d\tau _{1}+\cdots \bigg ]q(\tau )d\tau . \end{aligned}$$
(23)

Proof

We set \({\mathbb {U}}(t)=(u'(t),u(t))^{T}\), then \({\mathbb {U}}(t_0)=(u'(t_0),u(t_0))^{T}=(0,u_0)^{T}={\mathbb {U}}_0\), (21) can be written as the equivalent form

$$\begin{aligned} {\mathbb {U}}'(t)={\mathbb {P}}(t){\mathbb {U}}(t)+{\mathbb {Q}}(t),\quad t\ge t_0, \end{aligned}$$
(24)

with the constraint conditions

$$\begin{aligned} {\mathbb {U}}(t_0)={\mathbb {U}}_{0}, \end{aligned}$$

where

$$\begin{aligned} {\mathbb {P}}(t)= \begin{bmatrix} 0 &{} \quad p(t)\\ 1 &{} \quad 0 \end{bmatrix}, {\mathbb {Q}}(t)= \begin{bmatrix} q(t)\\ 0 \end{bmatrix}. \end{aligned}$$

The homogeneous one of (24) is

$$\begin{aligned} {\mathbb {U}}'(t)={\mathbb {P}}(t){\mathbb {U}}(t),t\ge t_0. \end{aligned}$$
(25)

We get the state transition matrix

$$\begin{aligned} \Phi _1(t,t_0)=\int _{t_0}^{t}{\mathbb {P}}(\tau )d\tau = \begin{bmatrix} 0 &{} \quad \int _{t_0}^{t}p(\tau )d\tau \\ t-t_0 &{} \quad 0 \end{bmatrix}, \end{aligned}$$

since

$$\begin{aligned} {\mathbb {P}}(t)\Phi _1(t,t_0)= \begin{bmatrix} 0 &{} \quad p(t)\\ 1 &{}\quad 0 \end{bmatrix} \begin{bmatrix} 0 &{} \quad \int _{t_0}^{t}p(\tau )d\tau \\ t-t_0 &{} \quad 0 \end{bmatrix} = \begin{bmatrix} p(t)(t-t_0) &{} \quad 0\\ 0 &{} \quad \int _{t_0}^{t}p(\tau )d\tau \end{bmatrix}, \end{aligned}$$

and

$$\begin{aligned} \Phi _1(t,t_0){\mathbb {P}}(t)= \begin{bmatrix} 0 &{} \quad \int _{t_0}^{t}p(\tau )d\tau \\ t-t_0 &{} \quad 0 \end{bmatrix} \begin{bmatrix} 0 &{} \quad p(t)\\ 1 &{} \quad 0 \end{bmatrix} = \begin{bmatrix} \int _{t_0}^{t}p(\tau )d\tau &{} \quad 0\\ 0 &{} \quad p(t)(t-t_0) \end{bmatrix}. \end{aligned}$$

If the system matrix \({\mathbb {P}}(t)\) and the state transition matrix \(\Phi _1(t,t_0)\) are commutative then \({\mathbb {P}}(t)=p\), p is a constant. Then, the state transition matrix of Eq. (25) is

$$\begin{aligned} \Phi (t,t_0)&=\exp \bigg \{\int _{t_0}^{t} \begin{bmatrix} 0 &{} \quad p\\ 1 &{} \quad 0 \end{bmatrix}d\tau \bigg \}\\&= \begin{bmatrix} 1+\frac{1}{2!}p(t-t_0)^{2}+\frac{1}{4!}p^{2}(t-t_0)^{4}+\cdot \cdot \cdot &{} p(t-t_0)+\frac{1}{3!}p^{2}(t-t_0)^{3}+\frac{1}{5!}p^{3}(t-t_0)^{5}+\cdot \cdot \cdot \\ (t-t_0)+p(t-t_{0})+\frac{1}{3!}p^{2}(t-t_0)^{3}+\frac{1}{5!}p^{3}(t-t_0)^{5}+\cdot \cdot \cdot &{} 1+\frac{1}{2!}p(t-t_0)^{2}+\frac{1}{4!}p^{2}(t-t_0)^{4}+\cdot \cdot \cdot \end{bmatrix}\\&= \begin{bmatrix} 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-t_0)^{2n} &{} \sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-t_0)^{2n-1}\\ (t-t_0)+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-t_0)^{2n-1} &{} 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-t_0)^{2n} \end{bmatrix}. \end{aligned}$$

The solution to the nonhomogeneous Eq. (24) can be obtained, we have

$$\begin{aligned} {\mathbb {U}}(t)= & {} \begin{bmatrix} u'(t)\\ u(t) \end{bmatrix} =\Phi (t,t_0){\mathbb {U}}(t_0)+\int _{t_0}^{t}\Phi (t,\tau ) {\mathbb {Q}}(\tau )d\tau \\= & {} \begin{bmatrix} 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-t_0)^{2n} &{} \sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-t_0)^{2n-1}\\ (t-t_0)+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-t_0)^{2n-1} &{} 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-t_0)^{2n} \end{bmatrix} \begin{bmatrix} u'(t_0)\\ u(t_0) \end{bmatrix}\\&+\int _{t_0}^{t} \begin{bmatrix} 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-\tau )^{2n} &{} \sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-\tau )^{2n-1}\\ (t-\tau )+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-\tau )^{2n-1} &{} 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-\tau )^{2n} \end{bmatrix} \begin{bmatrix} q(\tau )\\ 0 \end{bmatrix}d\tau . \end{aligned}$$

The solution of the Eq. (21) can be expressed as

$$\begin{aligned} u(t)&=\left[ (t-t_0)+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-t_0)^{2n-1}\right] u'(t_0)+\left[ 1+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n)!}(t-t_0)^{2n}\right] u(t_0)\\&+\int _{t_0}^{t}\left[ (t-\tau )+\sum \limits _{n=1}^{\infty }\frac{p^{n}}{(2n-1)!}(t-\tau )^{2n-1}\right] q(\tau )d\tau . \end{aligned}$$

Notice the constraints \(u'(t_0)=0\), \(u(t_0)=u_0\), (22) is verified.

On the other hand, if the system matrix \({\mathbb {P}}(t)\) and the state transition matrix \(\Phi _1(t,t_0)\) are not commutative, then the state transition matrix \(\Phi (t,t_0)\) can be derived by using iterative way in turn, we have

$$\begin{aligned} \Phi (t,t_0)&=E+\int _{t_0}^{t} \begin{bmatrix} 0 &{} \quad p(\tau _1)\\ 1 &{} \quad 0 \end{bmatrix}d\tau _{1}+\int _{t_0}^{t} \begin{bmatrix} 0 &{} \quad p(\tau _1)\\ 1 &{} \quad 0 \end{bmatrix} \int _{t_0}^{\tau _1} \begin{bmatrix} 0 &{} \quad p(\tau _2)\\ 1 &{} \quad 0 \end{bmatrix}d\tau _{2}d\tau _{1}\\&\quad +\int _{t_0}^{t} \begin{bmatrix} 0 &{} \quad p(\tau _1)\\ 1 &{} \quad 0 \end{bmatrix} \int _{t_0}^{\tau _1} \begin{bmatrix} 0 &{} \quad p(\tau _2)\\ 1 &{}\quad 0 \end{bmatrix} \int _{t_0}^{\tau _2} \begin{bmatrix} 0 &{} \quad p(\tau _3)\\ 1 &{} \quad 0 \end{bmatrix}d\tau _{3}d\tau _{2}d\tau _{1}+\cdots \end{aligned}$$

Therefore,

$$\begin{aligned} {\mathbb {U}}(t)= \begin{bmatrix} u'(t) \\ u(t) \end{bmatrix}=\Phi (t,t_0) \begin{bmatrix} 0 \\ u_0 \end{bmatrix}+\int _{t_0}^{t}\Phi (t,\tau ) \begin{bmatrix} q(\tau ) \\ 0 \end{bmatrix}d\tau . \end{aligned}$$

As a result, the solution of the Eq. (21) can be expressed for general linear ocean vorticity F, that is (23). \(\square \)

To end this section, we verify Theorem 4.1 by discussing two examples to which this result is practicable.

Example 4.2

We give a special case where the system matrix is a constant matrix, setting \(t_0=2,u(t_0)=2,p(t)=1\), that is

$$\begin{aligned} {\mathbb {P}}(t)= \begin{bmatrix} 0 &{} \quad 1\\ 1 &{} \quad 0 \end{bmatrix}, \end{aligned}$$

the eigenvalues of the matrix \({\mathbb {P}}(t)\) are \(\lambda _1=1,\lambda _2=-\,1\), in this way, we obtain the transformation matrix \({\mathbb {M}}\) and its inverse \({\mathbb {M}}^{-1}\) of the matrix \({\mathbb {P}}(t)\) into a diagonal linear Jordan canonical form

$$\begin{aligned} {\mathbb {M}}= \begin{bmatrix} 1 &{} \quad 1\\ 1 &{} \quad -\,1 \end{bmatrix}\quad \hbox {and}\quad {\mathbb {M}}^{-1}= \begin{bmatrix} \frac{1}{2} &{} \quad \frac{1}{2}\\ \frac{1}{2} &{} \quad -\frac{1}{2} \end{bmatrix}, \end{aligned}$$

we obtain

$$\begin{aligned} \Phi (t,2)&=\exp ({\mathbb {P}}(t)(t-2))={\mathbb {M}} \begin{bmatrix} e^{\lambda _1(t-2)} &{} \quad 0\\ 0 &{} \quad e^{\lambda _2(t-2)} \end{bmatrix}{\mathbb {M}}^{-1}\\&= \begin{bmatrix} \frac{1}{2}\left( e^{t-2}+e^{2-t}\right) &{} \quad \frac{1}{2}\left( e^{t-2}-e^{2-t}\right) \\ \frac{1}{2}\left( e^{t-2}-e^{2-t}\right) &{} \quad \frac{1}{2}\left( e^{t-2}+e^{2-t}\right) \end{bmatrix}, \end{aligned}$$

the solution of Eq. (24) if \(q(t)=2\), that is

$$\begin{aligned} {\mathbb {U}}(t)&=\Phi (t,2){\mathbb {U}}(2)+\int _{2}^{t}\Phi (2,\tau ) {\mathbb {Q}}(\tau )d\tau \\&= \begin{bmatrix} \frac{1}{2}\left( e^{t-2}+e^{2-t}\right) &{} \quad \frac{1}{2}\left( e^{t-2}-e^{2-t}\right) \\ \frac{1}{2}\left( e^{t-2}-e^{2-t}\right) &{} \quad \frac{1}{2}\left( e^{t-2}+e^{2-t}\right) \end{bmatrix} \begin{bmatrix} 0\\ 2 \end{bmatrix}\\&\quad + \int _{2}^{t} \begin{bmatrix} \frac{1}{2}\left( e^{\tau -2}+e^{2-\tau }\right) &{} \quad \frac{1}{2}\left( e^{\tau -2}-e^{2-\tau }\right) \\ \frac{1}{2}\left( e^{\tau -2}-e^{2-\tau }\right) &{}\quad \frac{1}{2}\left( e^{\tau -2}+e^{2-\tau }\right) \end{bmatrix} \begin{bmatrix} 2\\ 0 \end{bmatrix}d\tau \\&= \begin{bmatrix} 2\left( e^{t-2}-e^{2-t}\right) \\ 2\left( e^{t-2}+e^{2-t}-1\right) \end{bmatrix}. \end{aligned}$$

If \(p(t)=1\) and \(q(t)=2\), the solution to the Eq. (21) can be written as

$$\begin{aligned} u(t)=2\left( e^{t-2}+e^{2-t}-1\right) . \end{aligned}$$

Example 4.3

We assume \(q(t)=e^{t-2}\sqrt{e^{t-2}-1},~t\ge 2\), the conditions are satisfied in Example 4.2, another form of solution of Eq. (24) can be obtained

$$\begin{aligned} {\mathbb {U}}(t)&= \begin{bmatrix} e^{t-2}-e^{2-t} \\ e^{t-2}+e^{2-t} \end{bmatrix}+ \int _{2}^{t} \begin{bmatrix} e^{\tau -2}\sqrt{e^{\tau -2}-1}( e^{\tau -2}+e^{2-\tau }) \\ e^{\tau -2}\sqrt{e^{\tau -2}-1}( e^{\tau -2}-e^{2-\tau }) \end{bmatrix}d\tau \\&= \begin{bmatrix} e^{t-2}{-}e^{2-t}{+}\frac{2}{3}\left( e^{t-2}-1\right) ^{\frac{3}{2}} +\frac{2}{5}\left( e^{t-2}-1\right) ^{\frac{5}{2}}+2\left( e^{t-2}-1\right) ^{\frac{1}{2}} -2\arctan \left[ \left( e^{t-2}-1\right) ^{\frac{1}{2}}\right] \\ e^{t-2}{+}e^{2-t}{+}\frac{2}{3}\left( e^{t-2}-1\right) ^{\frac{3}{2}}+\frac{2}{5} \left( e^{t-2}-1\right) ^{\frac{5}{2}}-2\left( e^{t-2}-1\right) ^{\frac{1}{2}} +2\arctan \left[ \left( e^{t-2}-1\right) ^{\frac{1}{2}}\right] \end{bmatrix}, \end{aligned}$$

which shows that the solution of the Eq. (21)

$$\begin{aligned} u(t)&=e^{t-2}+e^{2-t}+\frac{2}{3}\left( e^{t-2}-1\right) ^{\frac{3}{2}}+\frac{2}{5} \left( e^{t-2}-1\right) ^{\frac{5}{2}}-2\left( e^{t-2}-1\right) ^{\frac{1}{2}}\\&\quad +2\arctan \left[ \left( e^{t-2}-1\right) ^{\frac{1}{2}}\right] . \end{aligned}$$

5 Conclusions

Existence and uniqueness of solutions by a model for the ocean flow in arctic gyres has been studied by means of Schauder’s fixed point techniques and Bihary’s inequality. By adding appropriate boundary conditions, the original equation is transformed into an integral equation, and the existence and uniqueness of the solution is solved when the ocean vorticity is nonlinear. We also have discussed the solutions of the equations in linear cases, which follows two examples for verifying the rationality of the method.