On the nonlocal boundary value problem of geophysical fluid flows

Abstract

This paper proposes a nonlocal formulation regarding the modeling of Antarctic Circumpolar Current by introducing flow functions to encode horizontal flow components without considering vertical motion. Using topological degree, zero exponent theory and fixed point technique, we show the existence of positive solutions to nonlocal boundary value problems with nonlinear vorticity.

1 Introduction

The Antarctic Circumpolar Current (ACC) plays an important role in the global climate and is the main means of water exchange among the Atlantic, Indian and Pacific oceans. A better understanding of ACC transport at the Last Glacial Maximum would allow a better assessment of ACC dynamics and past global climate change. ACC is not a single flow; it is composed of narrow jets about 40-50 km wide with typical velocity exceeding 1 m/s. ACC has remarkably consistent flow characteristics. ACC is a complex and rich structure formed by the combined action of very strong westerly winds and Coriolis forces. It carries about 140 million cubic meters of water per second, more than 100 times the amount of all the world’s rivers, and travels about 24,000 km. ACC is strongly constrained by the terrain at the bottom, so it can be observed as time changes [1,2,3,4,5,6,7,8,9,10].

The problem of the existence of solutions to nonlinear governing equations of geophysical fluid dynamics, initiated by Constantin and Johnson [11,12,13,14,15,16,17,18,19,20], is widely discussed and researched in this field. The mathematical ideas is that, from the inviscid fluid Euler equation and the equation of mass conservation, they introduced spherical pole projection without considering the azimuth change of horizontal velocity to transform spherical coordinate model into an equivalent plane elliptic boundary value problem. In addition, mathematical models of gyres flows with boundary conditions in the southern and northern hemispheres have been studied in [18, 21,22,23,24,25,26,27,28,29,30,31]. Recently, the existence of exact solutions to ACC for the case of varied density has also been discussed in [32, 33]. We try to solve this problem of ACC model with nonlocal boundary conditions which has not been discussed from the existing literature.

2 Preliminaries

We adapt methods from [18] to bear relevance to our setting. By introducing the stream function $\psi (\theta ,\varphi )$ in terms of the stereographic projection from the North Pole, the azimuthal and polar velocity components of ACC flows is given by

$$\begin{aligned} \frac{1}{\sin \theta }\psi _\phi \;~~\text {and}\; ~-\psi _\theta , \end{aligned}$$

Fig. 1

Azimuthal and polar angular spherical coordinates $\varphi$ and $\theta$ of a point P on the spherical surface of the Earth, with $\theta =0$ and $\theta =\pi$ correspond to the North and South Poles

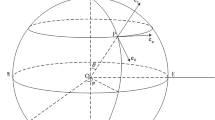
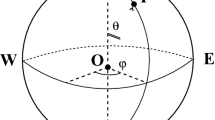
where $\theta \in [0,\pi )$ is polar angle with $\theta =0$ corresponding to the North Pole and $\varphi \in [0,2\pi )$ represents the angle of longitude in Fig. 1. In terms of the stream function $\Psi$ is associated with the vorticity of the motion of the ocean, [18] defined

$$\begin{aligned} \psi (\theta ,\varphi )=-\omega \cos \theta +\Psi (\theta ,\varphi ), \end{aligned}$$

(1)

where $\Psi$ is not driven by the Earth’s rotation. The governing equation of ACC flows can be expressed as

$$\begin{aligned} \frac{1}{\sin ^{2}\theta }\Psi _{\varphi \varphi }+\Psi _{\theta }\cot \theta +\Psi _{\theta \theta }=F(\Psi -\omega \cos \theta ), \end{aligned}$$

(2)

where $F(\Psi -\omega \cos \theta )$ represents the form of the ocean flow of the ocean vortex and defines the property of the ocean vorticity function. $\omega$ in $F(\Psi -\omega \cos \theta )$ is the dimensionless Coriolis parameter and $2\omega \cos \theta$ represents the planetary vorticity. The basic source of ocean vorticity is the gravitational attraction generated by the wind and the relative motion of the Moon, Sun and Earth in the form of tidal currents. Ebb and flow refers to the horizontal unidirectional movement of water, while tide refers to the vertical movement of water. The vorticity of water flows, the interaction of geophysical wave flows and the oceanic vorticity of these wind-driven flows can be regarded as a fixed nonzero constant in [17, 34].

Fig. 2

Stereographic projection of the unit sphere (center at origin) from the North Pole to the equatorial plane, the point P in the Antarctic region, the straight line connecting it to the North Pole intersects the equatorial plane in a point $P'$ belonging to the interior of the circular region delimited by the Equator. The ACC is mapped into a annular region within the equatorial plane

The stereographic projection is used from the North Pole to the equatorial plane on a unit sphere centered at the origin in Fig. 2. The model (2) in spherical coordinates can be transformed into an equivalent semilinear elliptic partial differential equation [18]. Set

$$\begin{aligned} \xi =re^{i\phi }\;~~\text {with}\; ~r=\cot \left( \frac{\theta }{2}\right) =\frac{\sin \theta }{1-\cos \theta }, \end{aligned}$$

(3)

where $(r,\phi )$ represents the polar coordinates on the equatorial plane and r is a function of $\theta$. After several cancellations by using (3), equation (2) is simplified as

$$\begin{aligned} \Psi _{\xi \overline{\xi }}=\frac{F(\Psi -\omega ((\xi \overline{\xi }-1)/(\xi \overline{\xi }+1)))}{(1+\xi \overline{\xi })^{2}}. \end{aligned}$$

(4)

By seeking partial derivatives in (1), we have

$$\begin{aligned} \Psi _{\xi }=\psi _{\xi }+\frac{2\omega \overline{\xi }}{(1+\xi \overline{\xi })^{2}}, \Psi _{\xi \overline{\xi }}=\psi _{\xi \overline{\xi }}+\frac{2\mu }{(1+\xi \overline{\xi })^{2}}-\frac{4\omega \xi \overline{\xi }}{(1+\xi \overline{\xi })^{3}}. \end{aligned}$$

(5)

Linking (5) and (4), we get

$$\begin{aligned} \psi _{\xi \overline{\xi }}+2\omega \frac{1-\xi \overline{\xi }}{(1+\xi \overline{\xi })^{3}}-\frac{F(\psi )}{(1+\xi \overline{\xi }))^{2}}=0. \end{aligned}$$

(6)

According to Cartesian coordinates (x, y), equation (6) is equivalent to a semilinear elliptic partial differential equation

$$\begin{aligned} \Delta \psi +8\omega \frac{1-(x^{2}+y^{2})}{(1+x^2+y^2)^{3}}-\frac{4F(\psi )}{(1+x^2+y^2)^{2}}=0, \end{aligned}$$

(7)

where $\Delta =\partial _{x}^{2}+\partial _{y}^{2}$ is the Laplace operator, expressed by the Cartesian coordinates on the equatorial plane, and the unknown function $\psi (x,y)$ represents the stream function. The circulation on the surface of the ocean is bounded by the horizontal set of flow functions, while in spherical projection coordinates, the solution of the circulation model (7) in the plane region is determined by these horizontal sets. The ACC flows are completely around the Earth [19, 35, 36] in the spherical region between the 56th and 60th latitude south, where there are only oceans and no land [21, 22]. This region is mapped to the circular region of the equatorial plane by the stereographic projection, while the plane projection maps the latitude circles of the southern hemisphere to concentric circles within the unit circle of the equatorial plane.

From

$$\begin{aligned} r=\sqrt{x^{2}+y^{2}}, ~\frac{\partial r}{\partial x}=\frac{x}{\sqrt{x^{2}+y^{2}}}=\frac{x}{r}, ~\frac{\partial r}{\partial y}=\frac{y}{\sqrt{x^{2}+y^{2}}}=\frac{y}{r}, \end{aligned}$$

we obtain

$$\begin{aligned} \psi _{x}&=\frac{x}{r}\psi '(r)\;~~\text {and}\; ~\psi _{y}=\frac{y}{r}\psi '(r),\\ \psi _{xx}&=\frac{x^{2}}{r^{2}}\psi ''(r)+\left( \frac{1}{r}-\frac{x^{2}}{r^{3}}\right) \psi '(r)\;~~\text {and}\; ~\psi _{yy}=\frac{y^{2}}{r^{2}}\psi ''(r)+\left( \frac{1}{r}-\frac{y^{2}}{r^{3}}\right) \psi '(r); \end{aligned}$$

therefore,

$$\begin{aligned} \Delta \psi =\psi ''(r)+\frac{1}{r}\psi '(r). \end{aligned}$$

Thus, by substituting r and $\Delta \psi$ into equation (7), we get

$$\begin{aligned} \psi ''(r)+\frac{1}{r}\psi '(r)+8\omega \frac{1-r^{2}}{(1+r^{2})^{3}}-\frac{4F(\psi (r))}{(1+r^{2})^{2}}=0. \end{aligned}$$

(8)

Noting ACC corresponding to the radial symmetric solution of problem (8) with no variations in the azimuthal direction, we introduce

$$\begin{aligned} \psi (r)=u(t),~~~t_{1}<t<t_{2}, \end{aligned}$$

where

$$\begin{aligned} r=e^{-\frac{t}{2}}\;~~\text {for}\; ~0<t_1=-2\ln (r_{+})<t<t_2=-2\ln (r_{-}), \end{aligned}$$

with $0<r_{-}<r_{+}<1$.

In terms of

$$\begin{aligned} u'(t)=-\frac{1}{2}e^{-\frac{t}{2}}\psi '(e^{-\frac{t}{2}})=-\frac{1}{2}r\psi '(r) \end{aligned}$$

and

$$\begin{aligned} u''(t)=\frac{1}{4}e^{-\frac{t}{2}} \psi '(e^{-\frac{t}{2}})+\frac{1}{4}e^{-t}\psi ''(e^{-\frac{t}{2}})=\frac{1}{4}r\psi '(r)+\frac{1}{4}r^{2}\psi ''(r).\end{aligned}$$

(8) is equivalently turned into the second-order ordinary differential equation

$$\begin{aligned} u''(t)=\frac{e^{t}}{(1+e^{t})^{2}}F(t,u(t))+2\omega \frac{e^{t}(1-e^{t})}{(1+e^{t})^{3}},~~~t_{1}<t<t_{2}, \end{aligned}$$

(9)

with nonlocal boundary conditions

$$\begin{aligned} u(t_1)=\sum _{i=1}^{m-2}\alpha _{i}u(\xi _{i}),~~~~~u(t_2)=\sum _{i=1}^{m-2}\beta _{i}u(\xi _{i}), \end{aligned}$$

(10)

which means the fact that $r=r_{\pm }$ for ACC as gyre flow are streamlines with $\psi =u(t_{1})$ on $r=r_{-}$ and $\psi =u(t_{2})$ on $r=r_{+}$.

In this paper, we assume that at the circulation boundary ACC flows behave as a streamline, which happens to be a linear combination of known streamlines $u(\xi _{i})$, $i=1,2,\cdot \cdot \cdot ,m-2$. This assumption is mathematically reasonable and feasible. Although many researchers have studied the boundary value problem of ACC flows and obtained some very good results, the existence of solutions to nonlocal boundary value problems regarding ACC flows has not been discussed. The ACC model is transformed into an equivalent operator equation by using the knowledge of nonlinear functional analysis. Using the techniques of topological degree theory, zero exponent theory and fixed point, under appropriate conditions, we discuss the existence of solutions to differential equations (9) with boundary conditions (10).

3 An equivalent operator equation for ACC model

In Sect. 2, we establish a new mathematical model of ACC with nonlocal boundary conditions, that is,

$$\begin{aligned} \left\{ \begin{array}{lll} u''(t)=a(t)F(t,u(t))+b(t),~~~t_{1}<t<t_{2},\\ u(t_1)=\sum \limits _{i=1}^{m-2}\alpha _{i}u(\xi _{i}),\\ u(t_2)=\sum \limits _{i=1}^{m-2}\beta _{i}u(\xi _{i}), \end{array} \right. \end{aligned}$$

(11)

where $a(\cdot ),b(\cdot ):[t_1,t_2]\rightarrow R$ are continuous, $F(\cdot ,\cdot ):[t_1,t_2]\times R\rightarrow R$ is continuous,

$$\begin{aligned} a(t)=\frac{e^{t}}{(1+e^{t})^{2}},\quad b(t)=\frac{2\omega e^{t}(1-e^{t})}{(1+e^{t})^{3}}, \end{aligned}$$

and $\xi _{i}$ $(i=1,2,\cdot \cdot \cdot ,m-2)$ satisfies $t_{1}<\xi _{1}<\xi _{2}<\cdot \cdot \cdot<\xi _{m-2}<t_{2}$, $\alpha _{i}$ and $\beta _{i}$ satisfy $\sum \limits _{i=1}^{m-2}\alpha _{i}=\sum \limits _{i=1}^{m-2}\beta _{i}=1$.

Definition 3.1

[37] Let X and Z be normed spaces. $L:domL(\subset X)\rightarrow Z$ is a linear operator, if

• (i)  ImL is the closed subspace of Z,

• (ii)  $dimKerL=codimImL<+\infty$,

then L is called Fredholm operator whose index is zero.

If L is Fredholm operator of index zero, then there are continuous operator $P:X\rightarrow X$ and $Q:Z\rightarrow Z$, such that

$$\begin{aligned} Im P=Ker L,~~Im L=Ker Q,~~X=Ker L\oplus Ker P,~~Z=Im L\oplus Im Q \end{aligned}$$

where the operator $L|_{domL\cap KerP}:domL\cap KerP\rightarrow ImL$ is invertible. We use $K_{P}$ to represent the inverse of $L|_{domL\cap KerP}$ and $K_{P,Q}=K_{P}(I-Q)$ to express $K_{P,Q}:Z\rightarrow domL\cap KerP$, where I is a identity operator. For all $J:ImQ\rightarrow KerL$, there is an isomorphic mapping $JQ+K_{P,Q}:Z\rightarrow domL$ such that $(JQ+K_{P,Q})^{-1}u=(L+J^{-1}P)u$ for $u\in domL$.

Definition 3.2

[37] Let X and Z be normed spaces, $\Omega \subset X$ be open and bounded, $L:domL(\subset X)\rightarrow Z$ is a Fredholm mapping. The operator $N:\overline{\Omega }\rightarrow Z$ is called L-compact on $\overline{\Omega }$ if $QN:\overline{\Omega }\rightarrow Z$ and $K_{P,Q}N:\overline{\Omega }\rightarrow X$ be compact on $\overline{\Omega }$.

Let $X=C^{2}[t_{1},t_{2}]$, $Z=C[t_{1},t_{2}]$, and define

$$\begin{aligned} domL=\left\{ u\in X\bigg |u(t_1)=\sum \limits _{i=1}^{m-2}\alpha _{i}u(\xi _{i}),~u(t_2)=\sum \limits _{i=1}^{m-2}\beta _{i}u(\xi _{i})\right\} , \end{aligned}$$

then domL is a Banach space with the norm

$$\begin{aligned} \Vert u\Vert _{X}=\max \{\Vert u\Vert _{1},\Vert u'\Vert _{1},\Vert u''\Vert _{1}\}, \end{aligned}$$

where $\Vert u\Vert _{1}=\max \limits _{t\in [t_{1},t_{2}]}|u(t)|$. We also introduce the norm $\Vert u\Vert _{2}=\int _{t_{1}}^{t_{2}}|u(t)|dt$ on Z. We put $\Vert u\Vert =\max \{\Vert u\Vert _{1},\Vert u'\Vert _{1}\}$.

Let $L:domL\rightarrow Z$ be given as

$$\begin{aligned} Lu(t)=u''(t), \end{aligned}$$

and $N:X\rightarrow Z$ as

$$\begin{aligned} Nu(t)=a(t)F(t,u(t))+b(t). \end{aligned}$$

Then the nonlocal boundary value problem (11) is transformed into

$$\begin{aligned} Lu=Nu. \end{aligned}$$

(12)

Lemma 3.3

$L:domL(\subset X)\rightarrow Z$ is a Fredholm operator of index zero.

Proof

Let $u\in X$. Since

$$\begin{aligned} \int \limits _{t_{1}}^{t}\int \limits _{t_{1}}^{\tau }u''(s)\hbox {d}s\hbox {d}\tau =u(t)-tu'(t_{1})-u(t_{1})+t_{1}u'(t_{1}), \end{aligned}$$

we have

$$\begin{aligned} u(t)=\int \limits _{t_{1}}^{t}\int \limits _{t_{1}}^{\tau }u''(s)\hbox {d}s\hbox {d}\tau +tu'(t_{1})+u(t_{1})-t_{1}u'(t_{1}). \end{aligned}$$

(13)

There exists a $u\in domL\subset X$ satisfying (10) such that $u''(t)=g(t)$ for every $g\in ImL$. By (13), we have

$$\begin{aligned} u(t_1)=\sum \limits _{i=1}^{m-2}\alpha _{i}u(\xi _{i})=\sum \limits _{i=1}^{m-2}\alpha _{i}\left( \int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau +u(t_{1}) \right) +\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})u'(t_{1}). \end{aligned}$$

Noticing that $\sum \limits _{i=1}^{m-2}\alpha _{i}=1$, we obtain

$$\begin{aligned} u'(t_{1})=-\frac{1}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau . \end{aligned}$$

(14)

Since $u(t_2)=\sum \limits _{i=1}^{m-2}\beta _{i}u(\xi _{i})$, we have

$$\begin{aligned} u(t_{2})&=\int \limits _{t_{1}}^{t_{2}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau +(t_{2}-t_{1})u'(t_{1})+u(t_{1})\nonumber \\&=\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau +\sum \limits _{i=1}^{m-2}\beta _{i}(\xi _{i}-t_{1})u'(t_{1}) +\sum \limits _{i=1}^{m-2}\beta _{i}u(t_{1}). \end{aligned}$$

(15)

Combining (14) and (15), we have

$$\begin{aligned} \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau =\frac{t_{2}-\sum \limits _{i=1}^{m-2}\beta _{i}\xi _{i}}{\sum \limits _ {i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\cdot \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau ; \end{aligned}$$

(16)

therefore,

$$\begin{aligned} ImL\subseteq \left\{ g\in Z\bigg |\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau =0\right\} , \end{aligned}$$

(17)

where

$$\begin{aligned} \gamma =\frac{t_{2}-\sum \limits _{i=1}^{m-2}\beta _{i}\xi _{i}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}. \end{aligned}$$

On the other hand, let $g\in Z$ and

$$\begin{aligned} u(t)=\int \limits _{t_{1}}^{t}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\frac{t}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _ {t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau +C, \end{aligned}$$

where C is an arbitrary constant, $t\in [t_{1},t_{2}]$. Noting that $u(t_1)=\sum \limits _{i=1}^{m-2}\alpha _{i}u(\xi _{i})$,

$$\begin{aligned}&u'(t)=\int \limits _{t_{1}}^{t}g(s)\hbox {d}s-\frac{1}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _ {t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau ,\\&u''(t)=g(t). \end{aligned}$$

Next, (10) is equivalent to

$$\begin{aligned} \int \limits _{t_{1}}^{t_2}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\frac{t_2}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _ {t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau +C\\ =\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\frac{\sum \limits _{i=1}^{m-2}\beta _{i}\xi _{i}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _ {t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau +\sum \limits _{i=1}^{m-2}\beta _{i}C, \end{aligned}$$

which by using $\sum \limits _{i=1}^{m-2}\beta _{i}=1$, gives (16). So (10) is obtained if (16) is true, that is, for $\forall u\in domL$,

$$\begin{aligned} \left\{ g\in Z\bigg |\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau =0\right\} \subseteq ImL. \end{aligned}$$

(18)

From (17) and (18), we have

$$\begin{aligned} \left\{ g\in Z\bigg |\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau =0\right\} =ImL. \end{aligned}$$

Now we define a linear continuous operator $Q:Z\rightarrow Z$ by

$$\begin{aligned} Qg=\frac{1}{C_{1}}\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau \right] \end{aligned}$$

where

$$\begin{aligned} C_{1}=\frac{1}{2}t_{2}^{2}-t_{1}t_{2}-\frac{1}{2}\gamma t_{1}^{2}-\sum \limits _{i=1}^{m-2}\xi _{i}(\beta _{i}+\gamma \alpha _{i})(\frac{1}{2}\xi _{i}-t_{1}). \end{aligned}$$

Here, Q is a projection operator. In fact,

$$\begin{aligned} Q^{2}g&=\frac{1}{C_{1}}\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }Qg\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }Qg\hbox {d}s\hbox {d}\tau \right] \\&=\frac{1}{C_{1}}\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}Qg(\tau -t_{1})d\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}Qg(\tau -t_{1})d\tau \right] \\&=\frac{1}{C_{1}}\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\cdot Qg\cdot \big (\frac{1}{2}t_{2}^{2}-\frac{1}{2}\xi _{i}^{2}-t_{1}t_{2}+t_{1}\xi _{i}\big )-\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\cdot Qg\cdot \big (\frac{1}{2}\xi _{i}^{2}-t_{1}\xi _{i}+\frac{1}{2}t_{1}^{2}\big )\right] \\&=Qg\cdot \frac{1}{C_{1}}\bigg (\frac{1}{2}t_{2}^{2}-\frac{1}{2}\sum \limits _{i=1}^{m-2}\beta _{i}\xi _{i}^{2}-t_{1}t_{2}+t_{1}\sum \limits _{i=1}^{m-2}\beta _{i}\xi _{i} -\frac{1}{2}\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\xi _{i}^{2}+\gamma t_{1}\sum \limits _{i=1}^{m-2}\alpha _{i}\xi _{i}-\frac{1}{2}\gamma t_{1}^{2}\bigg )\\&=Qg, \end{aligned}$$

which implies Q is a projection operator, and $ImL=KerQ$. For $g\in Z$, since $g-Qg\in KerQ=ImL$ and $Qg\in ImQ$, we have $Z=ImL+ImQ$. If $g\in ImL\cap ImQ$, then $g=0$; therefore, $Z=ImL\oplus ImQ$. Because of the definition of domL, it is easy to verify

$$\begin{aligned} KerL=\{u\in X|u(t)=c,~~c\in R\}; \end{aligned}$$

hence,

$$\begin{aligned} dimKerL=codimImL=1. \end{aligned}$$

The proof is finished. $\square$

We define

$$\begin{aligned} Qg=\int \limits _{t_1}^{t_2}q(s)g(s)\hbox {d}s, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} q(s)=\frac{1}{C_{1}}\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\kappa _{1i}(s)-\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\kappa _{2i}(s)\right] ,\\ \kappa _{1i}(s)={\left\{ \begin{array}{ll} t_2-\xi _i, &{} \text{ for } s\in [t_1,\xi _i], \\ t_2-s, &{} \text{ for } s\in [\xi _i,t_2], \end{array}\right. } \\ \kappa _{2i}(s)={\left\{ \begin{array}{ll} s-t_1, &{} \text{ for } s\in [t_1,\xi _i], \\ 0, &{} \text{ for } s\in (\xi _i,t_2]. \end{array}\right. } \end{aligned} \end{aligned}$$

(19)

Considering continuous linear operator $P:X\rightarrow X$ defined by

$$\begin{aligned} P(u(t))=u(t_{1}),~~~t\in [t_{1},t_{2}] \end{aligned}$$

(20)

or

$$\begin{aligned} P(u(t))=\frac{1}{t_{2}-t_{1}}\int \limits _{t_1}^{t_2}u(s)\hbox {d}s,~~~t\in [t_{1},t_{2}], \end{aligned}$$

(21)

we can define $K_{P}:ImL\rightarrow domL\cap KerP$ by

$$\begin{aligned} K_{P}g(t)=\int \limits _{t_{1}}^{t}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau -\frac{t-t_{1}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _ {t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau ; \end{aligned}$$

then,

$$\begin{aligned} (K_{P}g(t))'=\int \limits _{t_{1}}^{t}g(s)\hbox {d}s-\frac{1}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _ {t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)\hbox {d}s\hbox {d}\tau ; \end{aligned}$$

we obtain

$$\begin{aligned}&\max _{t\in [t_{1},t_{2}]}|K_{P}g(t)|\le (t_{2}-t_{1})C_{2}\int \limits _{t_{1}}^{t_{2}}|g(s)|\hbox {d}s,\\&\max _{t\in [t_{1},t_{2}]}|(K_{P}g(t))'|\le C_{2}\int \limits _{t_{1}}^{t_{2}}|g(s)|\hbox {d}s, \end{aligned}$$

where

$$\begin{aligned} C_{2}=1+\frac{t_{2}-t_{1}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}. \end{aligned}$$

Obviously, for every $g\in ImL$, we have

$$\begin{aligned} (LK_{P})g(t)=g(t); \end{aligned}$$

for every $u\in domL\cap KerP$, we have

$$\begin{aligned} (K_{P}L)u(t)&=\int \limits _{t_{1}}^{t}\int \limits _{t_{1}}^{\tau }u''(s)\hbox {d}s\hbox {d}\tau -\frac{t-t_{1}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2} \alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }u''(s)\hbox {d}s\hbox {d}\tau \\&=u(t)-u(t_{1})-u'(t_{1})t+t_{1}u'(t_{1})-\frac{u(t_{1})-\sum \limits _{i=1}^{m-2}\alpha _{i}\xi _{i}u'(t_{1})-u(t_{1})+t_{1}u'(t_{1})}{\sum \limits _{i=1} ^{m-2}\alpha _{i}(\xi _{i}-t_{1})}(t-t_{1})\\&=u(t)-u(t_{1})=u(t), \end{aligned}$$

where P is defined as (20). Since $u\in KerP$, $u(t_{1})=0$; hence,

$$\begin{aligned} K_{P}=(L|_{domL\cap KerP})^{-1}. \end{aligned}$$

Note that

$$\begin{aligned} K_{P}g(t)=\int \limits _{t_1}^{t_2}G(t,s)g(s)\hbox {d}s \end{aligned}$$

for

$$\begin{aligned} G(t,s)=G_1(t,s)-\frac{t-t_{1}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\kappa _{2i}(s),\\ G_1(t,s)={\left\{ \begin{array}{ll} s-t_1, &{} \text{ for } s\in [t_1,t] \\ 0, &{} \text{ for } s\in (t,t_2]. \end{array}\right. } \end{aligned}$$

Then

$$\begin{aligned} K_{P,Q}g(t)=\int \limits _{t_1}^{t_2}G(t,s)\left( g(s)-\int \limits _{t_1}^{t_2}q(\tau )g(\tau )d\tau \right) \hbox {d}s\\ =\int \limits _{t_1}^{t_2}\left( G(t,s)-q(s)\int \limits _{t_1}^{t_2}G(t,\tau )d\tau \right) g(s)\hbox {d}s=\int \limits _{t_1}^{t_2}H(t,s)g(s)\hbox {d}s \end{aligned}$$

for

$$\begin{aligned} H(t,s)=G(t,s)-q(s)\int \limits _{t_1}^{t_2}G(t,\tau )d\tau . \end{aligned}$$

(22)

4 Existence results for positive solutions to ACC model

Set

$$\begin{aligned} M(r)=\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,r)+b(s)\big )\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,r)+b(s)\big )\hbox {d}s\hbox {d}\tau \right] . \end{aligned}$$

(23)

We consider the following assumptions:

(H1):

 There exists a positive constant A such that for every $u\in domL\backslash KerL$ with $QNu=0$, there is a $t_{0}\in [t_{1},t_{2}]$ satisfying $|u(t_{0})|\le A$.

(H2):

 There exist continue functions $p(\cdot ),q(\cdot ):[t_{1},t_{2}]\rightarrow R$ and $p(\cdot )$ satisfying

$$\begin{aligned} \Vert p\Vert _{2}\le \frac{1-(t_{2}-t_{1})}{a^{*}(C_{2}+1)(t_{2}-t_{1})}, \end{aligned}$$

such that

$$\begin{aligned} |F(t,u)|\le p(t)|u|+q(t), \end{aligned}$$

where $a^{*}=\max \limits _{[t_{1},t_{2}]}|a(t)|$, $0<t_{2}-t_{1}<1$.

(H3):

 There exists a positive constant B such that for $\forall ~|c|>B, c\in R$, it holds

$$\begin{aligned} cM(c)<0. \end{aligned}$$

Theorem 4.1

Assume that (H1), (H2) and (H3) hold. Then nonlocal boundary value problem (11) has at least one solution.

Proof

Consider

$$\begin{aligned} \Omega _{1}=\{u\in domL\backslash KerL|~Lu=\lambda Nu,\lambda \in (0,1)\}. \end{aligned}$$

Then for each $u\in \Omega _{1}$, we have $u\notin KerL$, $\lambda \ne 0$; hence, $Nu\in ImL$. Since $KerQ=ImL$, we have $QNu=0$. We know from the condition (H1) that there exists a $t_{0}\in [t_{1},t_{2}]$ satisfying $|u(t_{0})|\le A$; then,

$$\begin{aligned} |u(t_{1})|=\bigg |u(t_{0})-\int \limits _{t_{1}}^{t_{0}}u'(\tau )d\tau \bigg |\le |u(t_{0})|+(t_{2}-t_{1})\Vert u'\Vert _{1}\le A+(t_{2}-t_{1})\Vert u'\Vert _{1}. \end{aligned}$$

(24)

Since

$$\begin{aligned} u'(t)=\int \limits _{t_{1}}^{t}u''(\tau )d\tau +u'(t_{1}), \end{aligned}$$

we have

$$\begin{aligned} |u'(t)|\le \int \limits _{t_{1}}^{t_{2}}|u''(\tau )|d\tau +|u'(t_{1})|=\Vert u''\Vert _{2}+|u'(t_{1})|=\Vert Lu\Vert _{2}+|u'(t_{1})|\le \Vert Nu\Vert _{2}+|u'(t_{1})|. \end{aligned}$$

(25)

Using (24) and (25), we obtain

$$\begin{aligned} |u(t_{1})|\le A+(t_{2}-t_{1})(\Vert Nu\Vert _{2}+|u'(t_{1})|). \end{aligned}$$

(26)

Considering that $(I-P)u\in ImK_{P}=domL\cap KerP$ for all $u\in \Omega _{1}$, we have

$$\begin{aligned} \Vert (I-P)u\Vert&=\Vert K_{P}L(I-P)u\Vert \le (t_{2}-t_{1})C_{2}\Vert L(I-P)u\Vert _{2}\nonumber \\&=(t_{2}-t_{1})C_{2}\Vert Lu\Vert _{2}\le (t_{2}-t_{1})C_{2}\Vert Nu\Vert _{2}. \end{aligned}$$

(27)

Using (26), (27) and (20), we obtain

$$\begin{aligned} \Vert u\Vert =\Vert Pu+(I-P)u\Vert&\le \Vert Pu\Vert +\Vert (I-P)u\Vert \le |u(t_{1})|+(t_{2}-t_{1})C_{2}\Vert Nu\Vert _{2}\\&\le A+(C_{2}+1)(t_{2}-t_{1})\Vert Nu\Vert _{2}+(t_{2}-t_{1})\Vert u'\Vert _{1}; \end{aligned}$$

that is,

$$\begin{aligned} \Vert u\Vert _{1},\Vert u'\Vert _{1}&\le A+(C_{2}+1)(t_{2}-t_{1})\Vert Nu\Vert _{2}+(t_{2}-t_{1})\Vert u'\Vert _{1}\\&\le A+(t_{2}-t_{1})\Vert u'\Vert _{1}+(C_{2}+1)(t_{2}-t_{1})(a^{*}\Vert p\Vert _{2}\Vert u\Vert _{1}+a^{*}\Vert q\Vert _{2}+\Vert b\Vert _{2}); \end{aligned}$$

consequently, we have

$$\begin{aligned} \Vert u\Vert _{1}\le \frac{A+(t_{2}-t_{1})\Vert u'\Vert _{1}+(C_{2}+1)(t_{2}-t_{1})(a^{*}\Vert q\Vert _{2}+\Vert b\Vert _{2})}{1-a^{*}(C_{2}+1)(t_{2}-t_{1})\Vert p\Vert _{2}}, \end{aligned}$$

(28)

and

$$\begin{aligned} \Vert u'\Vert _{1}\le \frac{A+(C_{2}+1)(t_{2}-t_{1})(a^{*}\Vert p\Vert _{2}\Vert u\Vert _{1}+a^{*}\Vert q\Vert _{2}+\Vert b\Vert _{2})}{1-(t_{2}-t_{1})}. \end{aligned}$$

(29)

Linking (28) and (29), we obtain

$$\begin{aligned} \Vert u'\Vert _{1}\le \frac{A+(C_{2}+1)(t_{2}-t_{1})(a^{*}\Vert q\Vert _{2}+\Vert b\Vert _{2})}{1-(t_{2}-t_{1})-a^{*}(C_{2}+1)(t_{2}-t_{1})\Vert p\Vert _{2}}; \end{aligned}$$

therefore, there exist positive number $M_{u'}$ and $M_{u}$, such that $\Vert u'\Vert _{1}\le M_{u'}$ and $\Vert u\Vert _{1}\le M_{u}$ for all $u\in \Omega _{1}$, which shows that $\Omega _{1}$ is bounded.

Let $\Omega _{2}=\{u\in KerL|~Nu\in ImL\}$. For each $u\in \Omega _{2}$, we have $u=c\in R$ and $Nu\in ImL=KerQ$, i.e.,

$$\begin{aligned} \frac{1}{C_{1}}\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,c)+b(s)\big )\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,c)+b(s)\big )\hbox {d}s\hbox {d}\tau \right] =0. \end{aligned}$$

Thus, by (H3), we obtain $\Vert u\Vert =\Vert c\Vert <B$, which implies that $\Omega _{2}$ is bounded.

Define the mapping $J:ImQ\rightarrow KerL$ by $Jc=c$. Let

$$\begin{aligned} \Omega _{3}=\{u\in KerL|~-\lambda J^{-1}u+(1-\lambda )QNu=0,~\lambda \in [0,1]\}, \end{aligned}$$

then $u=c\in R$ for all $u\in \Omega _{3}$, and we have

$$\begin{aligned}&\frac{1-\lambda }{C_{1}}\bigg [\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,c)+b(s)\big )\hbox {d}s\hbox {d}\tau -\nonumber \\&\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,c)+b(s)\big )\hbox {d}s\hbox {d}\tau \bigg ]=\lambda c. \end{aligned}$$

(30)

Using the condition (H3) and (30), we obtain $\lambda c^{2}<0$, which is a contradiction. Thus, $\Vert u\Vert =|c|\le B$, which shows that $\Omega _{3}$ is bounded.

Let $\Omega$ be an open and bounded set satisfying $\overline{\Omega }_{1}\cup \overline{\Omega }_{2}\cup \overline{\Omega }_{3}\subseteq \Omega$, then we can obtain

$$\begin{aligned}&Lu\ne \lambda Nu,~~(u,\lambda )\in ((domL\backslash KerL)\cap \partial \Omega )\times (0,1),\\&Nu\notin ImL,~~u\in KerL\cap \partial \Omega . \end{aligned}$$

Next, let us show that N is L-compact on $\overline{\Omega }$.

We notice the fact that to prove that N is L-compact on $\overline{\Omega }$ just need to prove that $QN(\overline{\Omega })$ is bounded and $K_{P,Q}N:\overline{\Omega }\rightarrow X$ is compact. In fact, we have

$$\begin{aligned} |QNu|&\le \frac{1}{C_{1}}\bigg (\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }(|a(s)||p(s)||u(s)|+|a(s)||q(s)|+|b(s)|)\hbox {d}s\hbox {d}\tau \\&\quad +|\gamma |\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }(|a(s)||p(s)||u(s)|+|a(s)||q(s)|+|b(s)|)\hbox {d}s\hbox {d}\tau \bigg )\\&\le \frac{|\gamma |+1}{C_{1}}(t_{2}-t_{1})(a^{*}\Vert p\Vert _{2}\Vert u\Vert _{1}+a^{*}\Vert q\Vert _{2}+\Vert b\Vert _{2}), \end{aligned}$$

which shows that $QN(\overline{\Omega })$ is bounded.

We now show that $K_{P,Q}N(\overline{\Omega })$ is compact in X. In fact,

$$\begin{aligned} |(K_{P,Q}Nu)(t)|&=\bigg |\int \limits _{t_{1}}^{t}\int \limits _{t_{1}}^{\tau }(I-Q)Nu(s)\hbox {d}s\hbox {d}\tau -\frac{t-t_{1}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }(I-Q)Nu(s)\hbox {d}s\hbox {d}\tau \bigg |\\&\le \left( 1+\frac{t_{2}-t_{1}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}+\frac{|\gamma |+1}{C_{1}}(t_{2}-t_{1})^{2}+\frac{|\gamma |+1}{C_{1}\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}(t_{2}-t_{1})^{3}\right) \\&\quad \cdot (t_{2}-t_{1})(a^{*}\Vert p\Vert _{2}\Vert u\Vert _{1}+a^{*}\Vert q\Vert _{2}+\Vert b\Vert _{2}):=M_{K}, \end{aligned}$$

which implies that $K_{P,Q}N(\overline{\Omega })$ is uniformly bounded in X.

For all $t\in [t_{1},t_{2}]$, we have

$$\begin{aligned} |(K_{P,Q}Nu)'(t)|&=\bigg |\int \limits _{t_{1}}^{t}(I-Q)Nu(s)\hbox {d}s\hbox {d}\tau -\frac{1}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}\sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }(I-Q)Nu(s)\hbox {d}s\hbox {d}\tau \bigg |\\&\le \left( 1+\frac{t_{2}-t_{1}}{\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}+\frac{|\gamma |+1}{C_{1}}(t_{2}-t_{1})^{2}+\frac{|\gamma |+1}{C_{1}\sum \limits _{i=1}^{m-2}\alpha _{i}(\xi _{i}-t_{1})}(t_{2}-t_{1})^{3}\right) \\&\quad \cdot (a^{*}\Vert p\Vert _{2}\Vert u\Vert _{1}+a^{*}\Vert q\Vert _{2}+\Vert b\Vert _{2})=\frac{M_{K}}{t_{2}-t_{1}}. \end{aligned}$$

Let $\{u_n\}$ be an arbitrary sequence in $\overline{\Omega }$ , then by using the mean value theorem, we obtain

$$\begin{aligned} \big |(K_{P,Q}Nu_{n})(t'_{1})-(K_{P,Q}Nu_{n})(t'_{2})\big |\le \frac{M_{K}}{t_{2}-t_{1}}\big |t'_{1}-t'_{2}\big |,~t'_{1},t'_{2}\in [t_{1},t_{2}],n\in N^{*}. \end{aligned}$$

Hence, by using the Arzela–Ascoli theorem (see [38]), we obain that $K_{P,Q}N(\overline{\Omega })$ is compact, which shows that N is L-compact on $\overline{\Omega }$.

Let $H(u,\lambda )=\lambda Ju+(1-\lambda )JQNu$ for all $u\in KerL\cap \partial \Omega$. Then by using the homotopy invariance of Leray–Schauder degree, we have

$$\begin{aligned} deg(JQN|_{KerL\cap \partial \Omega },\Omega \cap KerL,0)=deg(J,\Omega \cap KerL,0)\ne 0. \end{aligned}$$

On the other hand, $L:domL(\subset X)\rightarrow Z$ is Fredholm operator of index zero by Lemma 3.3; therefore, we have illuminated that all assumptions of [37, Theorem 1.5] are satisfied. As a result, the nonlocal boundary value problem (11) has at least one solution on $\Omega$. The proof is complete. $\square$

Remark 4.2

Assume the existence of two continuous functions $F_\pm (t)\in C[t_1,t_2]$ and positive constants $\kappa$, $r_0$ such that

$$\begin{aligned} |F(t,u)-F_\pm (s)|\le \kappa \end{aligned}$$

(31)

for any $t\in [t_1,t_2]$ and $\pm u\ge r_0$ and

$$\begin{aligned} N_\pm =\pm \left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }\big (a(s)F_\pm (s)+b(s)\big )\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }\big (a(s)F_\pm (s)+b(s)\big )\hbox {d}s\hbox {d}\tau \right] <0, \end{aligned}$$

respectively. Then for any $u\in C[t_1,t_2]$ with $u(t)\ge r_0$, we derive

$$\begin{aligned} \begin{aligned}&\Bigg |\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,u(s))+b(s)\big )\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,u(s))+b(s)\big )\hbox {d}s\hbox {d}\tau -N_+\Bigg |\\&\quad \le \kappa (1+\gamma )(t_2-t_1)^2\le -\frac{N_+}{2}, \end{aligned} \end{aligned}$$

when

$$\begin{aligned} \kappa \le -\frac{N_+}{2(1+\gamma )(t_2-t_1)^2}. \end{aligned}$$

(32)

Thus,

$$\begin{aligned} \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,u(s))+b(s)\big )\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,u(s))+b(s)\big )\hbox {d}s\hbox {d}\tau \le \frac{N_+}{2}<0. \end{aligned}$$

Similarly, if

$$\begin{aligned} \kappa \le -\frac{N_-}{2(1+\gamma )(t_2-t_1)^2}, \end{aligned}$$

(33)

then

$$\begin{aligned} 0<-\frac{N_-}{2}\le \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,u(s))+b(s)\big )\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }\big (a(s)F(s,u(s))+b(s)\big )\hbox {d}s\hbox {d}\tau . \end{aligned}$$

Consequently, (31), (32) and (33) imply (H1) and (H3) of Theorem 4.1 with $A=B=r_0$.

Now we consider (11) with small nonlinearities of the form

$$\begin{aligned} \left\{ \begin{array}{lll} u''(t)=\epsilon \left( a(t)F(t,u(t))+b(t)\right) ,~~~t_{1}<t<t_{2},\\ u(t_1)=\sum \limits _{i=1}^{m-2}\alpha _{i}u(\xi _{i}),\\ u(t_2)=\sum \limits _{i=1}^{m-2}\beta _{i}u(\xi _{i}), \end{array} \right. \end{aligned}$$

(34)

where $\epsilon$ is a small parameter. We show a simple but applicable result, giving also positive solutions, or multiple ones.

Theorem 4.3

If there are $r_1<r_2$ such that $M(r_1)M(r_2)<0$ for a function (23), then (34) has a solution $r_1<u_\epsilon (t)<r_2$, $t_{1}\le t\le t_{2}$ for any $\epsilon$ small.

Proof

We apply Theorem IV.2 of [39]. The operator of (IV.12) of [39] is just (23). This finishes the proof. $\square$

So analyzing the graph of the scalar function (23) over R, we can study solvability of (34). When F(t, u) is $C^1$-smooth in u, then (23) uniquely analyzes solvability of (34). This means for instance that if M(r) does not change the sign over R, then (34) has no solution for $\epsilon \ne 0$ small. Furthermore, the number of sign changes of M(r) over R is a lower number of possible solutions of (34) for $\epsilon \ne 0$ small. To be more concrete, we consider that $F(t,u)=F(u)$ in (9). Then (23) has the form

$$\begin{aligned} \begin{aligned} M(r)=F(r)\sum \limits _{i=1}^{m-2}\left[ \beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }a(s)sd\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }a(s)\hbox {d}s\hbox {d}\tau \right] \\ +\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }b(s)\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }b(s)\hbox {d}s\hbox {d}\tau \right] \\ =M_1F(r)+M_2 \end{aligned} \end{aligned}$$

for

$$\begin{aligned} \begin{aligned} M_1=\sum \limits _{i=1}^{m-2}\left[ \beta _{i}\left( \frac{e^{t_1}(\xi _i-t_2)}{e^{t_1}+1}+\ln \frac{e^{t_1}+1}{e^{\xi _i}+1}\right) -\gamma \alpha _{i}\frac{(\cosh t_1+1)\left( \tanh \frac{t_2}{2}-\tanh \frac{\xi _i}{2}\right) -t_2+\xi _i}{2(\cosh t_1+1)}\right] \\ M_2=\sum \limits _{i=1}^{m-2}\Bigg [\beta _{i}\frac{(\cosh t_1+1)\left( \tanh \frac{t_2}{2}-\tanh \frac{\xi _i}{2}\right) -t_2+\xi _i}{2(\cosh t_1+1)}\\ -\frac{\gamma \alpha _{i}}{4}\left( (t_1-\xi _i)\text {sech}^2\frac{t_1}{2}-2\tanh \frac{t_1}{2}+2\tanh \frac{\xi _i}{2}\right) \Bigg ]. \end{aligned} \end{aligned}$$

(35)

Consequently, if

$$\begin{aligned} M_1\ne 0 \end{aligned}$$

and

$$\begin{aligned} \inf _{r\in R}F(r)<-\frac{M_2}{M_1}<\sup _{r\in R}F(r), \end{aligned}$$

then (34) has a solution for any $\epsilon$ small. In particular, if F(r) is a polynomial of odd degree, then we get existence result. On other hand, if either

$$\begin{aligned} \inf _{r\in R}F(r)>-\frac{M_2}{M_1} \end{aligned}$$

or

$$\begin{aligned} \sup _{r\in R}F(r)<-\frac{M_2}{M_1}, \end{aligned}$$

then (34) has no solutions for any $\epsilon$ small.

Theorem 4.4

Assume that

• (i) $\lim \limits _{u\rightarrow \infty }F(t,u)=F_+$ uniformly for all $t\in [t_{1},t_{2}]$ and $M_1F_++M_2<0$, where $M_{1,2}$ are given by (35).

• (ii) There exists a $\beta \in R$, such that

  $$\begin{aligned} \frac{u}{t_{2}-t_{1}}+(\beta q(s)+H(t,s))(a(s)F(s,u))+b(s))\ge 0\quad \forall (t,s)\in [t_1,t_2]^2, \end{aligned}$$

  where q(s) and H(t, s) are given by (19) and (22), respectively.

Then the nonlocal boundary value problem (11) has at least one nonnegative solution.

Proof

We follow [40, Theorem 1]. We consider now $X=Z=C[t_1,t_2]$ with the norm $\Vert u\Vert _1$. Clearly it holds

$$\begin{aligned} |N(u)(t)|\le |a(t)||F(t,u(t))|+|b(t)|\le M_F+2\omega , \end{aligned}$$

where

$$\begin{aligned} M_F=\sup _{t\in [t_1,t_2],u\ge 0}|F(t,u)|<\infty . \end{aligned}$$

So condition (i) of [40, Theorem 1] is verified for $c_1=M_F+2\omega$ and $c_2=0$. We take Pu(t) given by (21) and a cone

$$\begin{aligned} K=\{u\in X\mid u(t)\ge 0,~t\in [t_{1},t_{2}]\}. \end{aligned}$$

Next, we consider a continuous bilinear form on $Z\times X$

$$\begin{aligned} \langle g,u\rangle =\sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }g(s)z(s)\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }g(s)z(s)\hbox {d}s\hbox {d}\tau \end{aligned}$$

with a property that $g\in Im L$ if and only if $\langle g,u_0\rangle =0$ for every $u_0\in Ker L$. Note

$$\begin{aligned} Qg=\frac{\langle g,1\rangle }{\langle 1,1\rangle },\quad \langle 1,1\rangle =C_1. \end{aligned}$$

If $u=u_0+u_1\in K$, where $u_0=r\in Ker L$, $r>\rho =(M_F+2\omega )\Vert K_{P,Q}\Vert$, $u_1\in Ker P$ and $\Vert u_1\Vert _1\le \rho$, then

$$\begin{aligned} \begin{aligned} \langle QN(u),u_0\rangle =\left\langle \frac{\langle N(u),1\rangle }{\langle 1,1\rangle },r\right\rangle =r\langle N(u),1\rangle \\ =r\left[ \sum \limits _{i=1}^{m-2}\beta _{i}\int \limits _{\xi _{i}}^{t_{2}}\int \limits _{t_{1}}^{\tau }N(u)(s)\hbox {d}s\hbox {d}\tau -\gamma \sum \limits _{i=1}^{m-2}\alpha _{i}\int \limits _{t_{1}}^{\xi _{i}}\int \limits _{t_{1}}^{\tau }N(u)(s)\hbox {d}s\hbox {d}\tau \right] \end{aligned} \end{aligned}$$

and by (i)

$$\begin{aligned} N(u)(s)=N(r+u_1)(s)=a(s)F(s,r+u_1(s))+b(s)\rightrightarrows a(s)F_++b(s)\text { as }r\rightarrow \infty \end{aligned}$$

uniformly for $s\in [t_1,t_2]$. Thus, we obtain

$$\begin{aligned} \frac{1}{r}\langle QN(u),u_0\rangle \rightarrow M_1F_++M_2\text { as }r\rightarrow \infty . \end{aligned}$$

Consequently by (i), we get $\langle QN(u),u_0\rangle <0$ for a large $r>0$. So condition (ii) of [40, Theorem 1] is also verified. Next, we consider a continuous retraction $\gamma : X\rightarrow K$ given by

$$\begin{aligned} \gamma (u)(t)=|u(t)|, \end{aligned}$$

then a mapping $J : Im Q\rightarrow Ker L$, $Jz=\beta z$, and we derive

$$\begin{aligned} \begin{aligned} (P+JQN+K_{P,Q}N)(\gamma (u)(t))\\ =\frac{1}{t_{2}-t_{1}}\int \limits _{t_1}^{t_2}|u(s)|\hbox {d}s+\beta \int \limits _{t_1}^{t_2}q(s)N(|u|)(s)\hbox {d}s+\int \limits _{t_1}^{t_2}H(t,s)N(|u|)(s)\hbox {d}s\\ =\int \limits _{t_1}^{t_2}\left[ \frac{|u(s)|}{t_{2}-t_{1}}+(\beta q(s)+H(t,s))(a(s)F(s,|u(s)|)+b(s))\right] \hbox {d}s\ge 0 \end{aligned} \end{aligned}$$

by (ii). So condition (iii) of [40, Theorem 1] is also verified. The proof is finished. $\square$

Similarly we have the next result.

Theorem 4.5

Assume that

• (i) $\lim \limits _{u\rightarrow \pm \infty }F(t,u)=F_\pm$ uniformly for all $t\in [t_{1},t_{2}]$ and $\pm (M_1F_\pm +M_2)<0$, where $M_{1,2}$ are given by (35).

Then the nonlocal boundary value problem (11) has at least one solution.

Proof

We follow the above proof with a trivial cone $K=X$. Then $\gamma (u)=u$ and (i), (ii) of [40, Theorem 1] are verified by (i) and condition (iii) of [40, Theorem 1] trivially holds. The proof is finished. $\square$

Remark 4.6

Conditions (i) of Theorems 4.4 and 4.5 are Landesman–Lazer type [39]. Condition (ii) of Theorem 4.5 holds, if

$$\begin{aligned} \sup _{u>0,s\in [t_1,t_2]}\frac{|a(s)F(s,u))+b(s)|}{u}\sup _{(t,s)\in [t_1,t_2]^2}|\beta q(s)+H(t,s)|<\frac{1}{t_{2}-t_{1}}. \end{aligned}$$