1 Introduction

In the past few decades, the basic properties of complex dynamical networks have been extensively studied [1,2,3] and have attracted increasing attention, especially on the issues of synchronization [4,5,6], the typical and interesting collective behaviors. Hitherto, the cluster synchronization and the related control problems have become a hot topic [7,8,9]. The main reason lies in that it not only can well explain many natural phenomena, but also has potential applications in the areas of secure communication [10], image processing [11], mechanical engineering [12], etc. Certainly, one has already obtained many important results. Zhang et al. [13] studied the cluster synchronization problem in asymmetric negative coupling networks and found that the couplings of one-node clusters to multi-node clusters have beneficial effects in the cluster synchronization. The authors of [14] investigated the cluster synchronization problem of complex networks with stochastic perturbations and non-identical nodes. Recently, Li et al. [15] studied an attraction region for the frequency synchronization on a class of symmetrically connected power network systems, which was helpful to the insight into the study of the stability of large power grids.

It is worth pointing out that time delay is of great interest to many researchers in recent years [16,17,18]. For instance, the stability of uncertain delayed and time-varying delayed neural networks was investigated in [16] and [17], respectively. Huang et al. [18] analyzed the synchronization of delayed chaotic systems with parameter mismatches, etc. However, in real applications, there are not only the time-varying delays in the self-dynamics but also the transmission delay between the signal source and destination. Namely, the signal received at the time \(t + \sigma\) is always transmitted from the source at the time \(t\). Therefore, the research about cluster lag synchronization has an extremely vital significance in theory and practice. However, hitherto, in previous studies, only a few results have been published.

Besides this, in the history of research on the network control, controllers should be added on all nodes. However, in actual applications, researchers find that it is impossible to implement this requirement since there are a large number of nodes in the super-network. With the gradual development of the network theories, an effective control technology, i.e., pinning control technology, is then put forward and applied with great advantage. The controllers only need to be added on a small percentage of nodes. Chen et al. [19] analyzed the feasibility of the pinning control scheme with the pinned nodes as little as possible and proved that the pinning synchronization can be achieved under some mild conditions. This efficient control technology was also used for solving the cluster synchronization problem in [20, 21]. Liu and Chen [22] studied the exponential synchronization problem with the time-varying delays by the pinning control scheme.

In the real world, it is also too expensive to implement the controllers all the time. Therefore, some optimized control technologies were put forward, for instance, the impulse control technology [23], the sampled-data control technology [24] and the event-triggered and self-triggered technology [5, 25]. All these technologies are discontinuous, which have attracted great interests and have been used in practice widely. For the periodical intermittent control technique, the control interval is assumed to be periodic and each cycle consists of work time and rest time. Liu and Chen [26] studied the problem of cluster synchronization by employing this control technology, and several conditions for synchronization were presented. The authors of [27] discussed the finite-time synchronization between two complex dynamical networks under this periodically intermittent control. Cai et al. [28] investigated the cluster synchronization of the complex networks with the time-varying delays in the self-dynamics under the intermittent pinning control scheme.

To the best of our knowledge, adaptive control has also been used in many systems and applications [29,30,31,32,33]. In recent years, there are a lot of works about this control technology. For instance, an adaptive neural network control was proposed in [31], which succeeds in controlling the desired trajectory robustly to a small neighborhood of zero and guarantees the boundedness of all the closed-loop signals at the same time. In [33], the adaptive control was adopted to handle system uncertainties and disturbances. A common feature of these works is that there are fixed pinned nodes or centralized nodes. Obviously, a more reasonable adaptive approach is decentralized (or distributed), which only relies on local information instead of global information of the whole network. A decentralized adaptive intermittent pinning control scheme was investigated for a class of discrete-time nonlinear hidden leader–follower multi-agent systems in [34]. In [35], this control scheme was adopted for the global synchronization of complex directed dynamical networks. Although some research was done about the synchronization problem in [34,35,36], few works concerned the decentralized pinning intermittent control about the cluster lag synchronization problem. In this paper, we will solve this problem.

Enlightened by the above discussions, this paper aims at investigating the cluster lag synchronization of the delayed heterogeneous dynamical networks. Considering the delayed dynamical complex networks that involve both the transmission delay in communication channels and the time-varying delays in self-dynamics simultaneously. Several criteria are presented to guarantee a cluster lag synchronization without assuming the coupling matrix being symmetric and irreducible, which is very loose. In addition, a decentralized adaptive intermittent pinning control scheme is proposed to reduce the control cost. Then, an effective pinned-cluster selection scheme is also introduced to guide what kind of clusters should be pinned preferentially. It is helpful to improve the cluster lag synchronization efficiency.

The rest of this paper is organized as follows. Section 2 establishes an intermittent pinning-controlled complex directed dynamical network model, which contains the mixed delays we mentioned as above, and gives some definitions, remarks and lemmas. Several criteria are presented in Sect. 3 to ensure the cluster lag synchronization, and then, some theorems and corollaries are derived. Besides this, a pinned-cluster selection scheme is introduced in this section. In Sect. 4, the final control scheme is proposed. Two simulations are provided in Sect. 5 to verify the correctness of the theoretical results. Section 6 closes the paper with a conclusion.

2 Preliminaries

Consider a standard directed complex network model with \(N\) non-identical dynamical nodes, in which each node is an \(n\)-dimensional dynamical system with the time-varying delays in the self-dynamics. For \(i = 1,2, \ldots ,N\), the network can be described as

$$\dot{x}_{i} \left( t \right) = f_{i} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{i} \left( t \right)} \right)} \right) + c\sum\limits_{j = 1,j \ne i}^{N} {b_{ij} \varGamma \left( {x_{j} \left( t \right) - x_{i} \left( t \right)} \right)} ,$$
(1)

where \(x_{i} \left( t \right) = \left( {x_{i1} \left( t \right),x_{i2} \left( t \right), \ldots ,x_{in} \left( t \right)} \right)^{\rm T} \in {\mathbb{R}}^{n}\) is an \(n\)-dimensional state variable of the node \(i\). A continuous vector-valued function \(f_{i} :\left[ {0, + \infty } \right) \times {\mathbb{R}}^{n} \times {\mathbb{R}}^{n} \to {\mathbb{R}}^{n}\) is used to control the evolution of the \(i\)th node. The time-varying delays \(\tau_{i} \left( t \right)\) may be unknown (constant or time varying) but be known by constraints, i.e., \(0 \le \tau_{i} \left( t \right) \le \tau_{i}\), \(i = 1,2, \ldots ,N\). The positive constant \(c\) is the coupling strength. And the coupling matrix \(B = \left( {b_{ij} } \right)_{N \times N}\) represents the network topology structure, and if there is a directed link from the \(j\)th node to the \(i\)th node (\(j \ne i\)), then \(b_{ij} > 0\); otherwise, \(b_{ij} = 0\). This means that the network is directed and \(B\) is an asymmetric coupling matrix. Furthermore, for \(i = 1,2, \ldots ,N\), the definition of the diagonal entry of the matrix \(B\) is: \(b_{ii} = - \sum\nolimits_{j = 1,j \ne i}^{N} {b_{ij} }\) and thus \(\sum\nolimits_{j = 1}^{N} {b_{ij} } = 0\). The inner connecting matrix \(\varGamma = \text{diag} \left( {\gamma_{1} ,\gamma_{2} , \ldots ,\gamma_{n} } \right) > 0\) is used to describe the internal individual coupling between nodes. The initial conditions of network (1) are obtained from \(x_{i} \left( s \right) = \varphi_{i} \left( s \right) \in C\left( {\left[ { - \tau ,0} \right],{\mathbb{R}}^{n} } \right)\), \(i = 1,2, \ldots ,N\), where \(C\left( {\left[ { - \tau ,0} \right],{\mathbb{R}}^{n} } \right)\) represents the collection of all \(n\)-dimensional continuous functions being defined on the range \(\left[ { - \tau ,0} \right]\) with \(\tau = \max_{1 \le i \le N} \tau_{i}\).

Assume that the collection of nodes in the network (1) can be divided into \(m\) clusters with \(1 \le m < N\). Without loss of generality, the \(k\)th cluster is indicated as \(C_{k}\), \(k \in \Im = \left\{ {1,2, \ldots ,m} \right\}\), and let

$$\begin{array}{l} {C_{1} = \left\{ {1,2, \ldots ,r_{1} } \right\},} \hfill \\ {C_{2} = \left\{ {r_{1} + 1,r_{1} + 2, \ldots ,r_{1} + r_{2} } \right\},{\kern 1pt} {\kern 1pt} } \hfill \\ { \ldots ,} \hfill \\ {C_{m} = \left\{ {r_{1} + r_{2} + \cdots + r_{m - 1} + 1,r_{1} + r_{2} + \cdots + r_{m - 1} + 2, \ldots ,r_{1} + r_{2} + \cdots + r_{m - 1} + r_{m} } \right\},} \hfill \\ \end{array}$$

where \(1 \le r_{k} \le N\) and \(\sum\nolimits_{k = 1}^{m} {r_{k} } = N\). In many real-world systems, such as metabolic, neural, gene regulation or software networks, the independent nodes in each group can be considered as functional units, see [2, 37, 38]. According to their functions, any pair of nodes in different clusters is essentially different. Assume that the nodes from the same cluster have the same dynamical behavior, while the nodes from different clusters show the distinct behaviors. In this case, the dynamical behavior of each node from the \(k\)th cluster can be expressed by

$$\dot{x}_{i} \left( t \right) = \tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right),\quad i \in C_{k} .$$
(2)

Then, the directed delayed dynamical network (1) can be described as

$$\dot{x}_{i} \left( t \right) = \tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right) + c\sum\limits_{j = 1}^{N} {b_{ij} \varGamma x_{j} \left( t \right)} ,\quad i \in C_{k} .$$
(3)

In this paper, we pay attention driving network (3) to the cluster lag synchronization by employing the intermittent pinning control scheme. For this purpose, a definition about the cluster lag synchronization of a dynamical network is given.

We first give some notations that will be used. A positive constant \(\sigma\) is the transmission delay, and let \(s_{k} \left( {t - \sigma } \right)\) denote the lag synchronous state for the cluster \(C_{k}\). Then, the desired cluster lag synchronous state of network (3) denotes by \(s\left( t \right) = \left( {s_{1} \left( t \right),s_{2} \left( t \right), \ldots s_{m} \left( t \right)} \right)\).

Definition 1

We say the cluster lag synchronization of network (3) is realized, if the nodes of network (3) can be divided into \(m\) clusters as mentioned above, such that, for any node \(i \in C_{k}\), \(k \in \Im\), one has

$$\begin{aligned} & \mathop {\lim }\limits_{t \to + \infty } \left\| {x_{i} \left( t \right) - s_{k} \left( {t - \sigma } \right)} \right\| = 0\quad {\text{and}} \\ & \mathop {\lim }\limits_{t \to + \infty } \left\| {s_{k} \left( t \right) - s_{j} \left( t \right)} \right\| \ne 0,\quad j \ne k. \\ \end{aligned}$$

According to the network (3), we know that each \(s_{k} \left( t \right)\) satisfies

$$\begin{aligned} \dot{s}_{k} \left( t \right) & = \tilde{f}_{k} \left( {t,s_{k} \left( t \right),s_{k} \left( {t - \tau_{k} \left( t \right)} \right)} \right) \\ & \quad +\,c\sum\limits_{p = 1}^{m} {\sum\limits_{{j \in C_{p} }} {b_{ij} \varGamma s_{p} \left( t \right)} } ,\quad i \in C_{k} ,\;\;k \in \Im . \\ \end{aligned}$$
(4)

Apparently, for each \(i \in C_{k}\), the lag synchronous state \(s_{k} \left( t \right)\) in the same cluster should be uniform, see [38]. In order to achieve the cluster lag synchronization of network (3), we put forward the following assumption.

Assumption 1

Assume that the coupling matrix \(B = \left( {b_{ij} } \right) \in {\mathbb{R}}^{N \times N}\) of network (3) can be expressed by

$$B = \left( {\begin{array}{llll} {B_{11} } \hfill & {B_{12} } \hfill & \ldots \hfill & {B_{1m} } \hfill \\ {B_{21} } \hfill & {B_{22} } \hfill & \ldots \hfill & {B_{2m} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {B_{m1} } \hfill & {B_{m2} } \hfill & \ldots \hfill & {B_{mm} } \hfill \\ \end{array} } \right).$$

Each block \(B_{uv} = \left( {b_{ij} } \right) \in {\mathbb{R}}^{{r_{u} \times r_{v} }} \left( {u,v \in \Im } \right)\) is a matrix that has the same sum of row, which means there exist some constants \(\beta_{uv} ,u,v \in \Im\), such that \(\sum\nolimits_{{j \in C_{v} }} {b_{ij} } = \beta_{uv}\), \(i \in C_{u}\).

Remark 1

Based on Assumption 1, the cluster lag synchronous manifold diagram of the network (3) satisfies

$$M = \left\{ \begin{aligned} &\left( {x_{1}^{\rm T} \left( t \right),x_{2}^{\rm T} \left( t \right), \ldots ,x_{N}^{\rm T} \left( t \right)} \right)^{\rm T} \in {\mathbb{R}}^{nN} : \hfill \\ & x_{1} \left( t \right) = x_{2} \left( t \right) = \cdots = x_{{r_{1} }} \left( t \right), \hfill \\ & x_{{r_{1} + 1}} \left( t \right) = x_{{r_{1} + 2}} \left( t \right) = \cdots = x_{{r_{1} + r_{2} }} \left( t \right), \hfill \\ & \ldots \hfill \\ &x_{{r_{1} + r_{2} + \cdots + r_{m - 1} + 1}} \left( t \right) = x_{{r_{1} + r_{2} + \cdots + r_{m - 1} + 2}} \left( t \right) = \cdots = x_{N} \left( t \right) \hfill \\ \end{aligned} \right\}.$$

It is an invariant manifold of network (3) and is a precondition for the cluster synchronization [38]. Additionally, the information communication in the same cluster is represented by each diagonal block in the matrix \(B\), and the information communication among different clusters is expressed by each non-diagonal block, respectively.

Remark 2

In the traditional literature about the cluster lag synchronization of the complex dynamical networks, each block unit in the coupling matrix of the network is supposed to be a zero-row-sum matrix. This condition is introduced to ensure the cluster synchronization of the network, see [39, 40]. This requests that the average of the influence from the other cluster for each node is equal to zero. In fact, it is relatively conservative. In this paper, we assume that each block of the coupling matrix is an equal-row-sum matrix; furthermore, the sum of each block can be different. Therefore, the hypothesis is less conservative than that in [39, 40].

Under Assumption 1, we can reduce formula (4) to

$$\dot{s}_{k} \left( t \right) = \tilde{f}_{k} \left( {t,s_{k} \left( t \right),s_{k} \left( {t - \tau_{k} \left( t \right)} \right)} \right) + c\sum\limits_{p = 1}^{m} {\beta_{kp} \varGamma s_{p} \left( t \right)} ,\quad k \in \Im .$$
(5)

Formula (5) is referred to as the cluster lag synchronous form of network (3). One can clearly see that the values of the cluster lag synchronous states are sets of un-decoupled trajectories instead of decoupled ones. This is different mostly from previous works [37, 39, 40], where the cluster lag synchronous states were selected as the particular solutions of the decoupled node systems when they worked on the problems of synchronization, i.e., \(\dot{s}_{k} \left( t \right) = \tilde{f}_{k} \left( {t,s_{k} \left( t \right),s_{k} \left( {t - \tau_{k} \left( t \right)} \right)} \right)\).

To achieve the cluster lag synchronization of the delayed dynamical network (3), an intermittent pinning control scheme will be used. As is known, the nodes that in the same cluster usually have the same properties. Thus, while studying the cluster lag synchronization, each cluster can naturally be seen as a whole [37]. According to this, we put each cluster of the network (3) as a whole and control part of them intermittently to achieve the cluster lag synchronization. Let the first \(l\left( {1 \le l < m} \right)\) clusters to be pinned, without loss of generality, and then, we have the delayed dynamical network under pinning control as

$$\left\{ \begin{aligned} &\dot{x}_{i} \left( t \right) = \tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right) + c\sum\nolimits_{p = 1}^{m} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma x_{j} \left( t \right)} } + u_{i} \left( t \right),\quad i \in C_{k} ,\;\;1 \le k \le l, \hfill \\ & \dot{x}_{i} \left( t \right) = \tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right) + c\sum\nolimits_{p = 1}^{m} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma x_{j} \left( t \right)} } ,\quad i \in C_{k} ,\;\;1 + l \le k \le m. \hfill \\ \end{aligned} \right.$$
(6)

The intermittent controllers \(u_{i} \left( t \right) \in {\mathbb{R}}^{n}\) are defined as

$$u_{i} \left( t \right) = cd_{k} \left( t \right)\varGamma \left( {s_{k} \left( {t - \sigma } \right) - x_{i} \left( t \right)} \right),\quad i \in C_{k} ,1 \le k \le l,$$
(7)

where the intermittent feedback control gain \(d_{k} \left( t \right)\) of the cluster \(C_{k}\) is described by

$$d_{k} \left( t \right) = \left\{ {\begin{array}{lll} {d_{k} ,} \hfill & {\omega T \le t < \omega T + \delta ,} \hfill & {i \in C_{k} ,\;1 \le k \le l,} \hfill \\ {0,} \hfill & {\omega T + \delta \le t < \left( {\omega + 1} \right)T,} \hfill & {i \in C_{k} ,\;1 \le k \le l.} \hfill \\ \end{array} } \right.$$
(8)

where \(d_{k} > 0\) is a constant, the control period \(T > 0\), the control width \(\delta > 0\), and \(T - \delta\) is the non-control width, where \(\omega = 0,1,2, \ldots\). It is found that the control time of controllers (7) is cyclical, and each period \(T\) is composed by the work time \(\delta\) and the rest time \(T - \delta\). As a result, the control behavior is intermittent rather than continuous and it can reduce the cost of control.

For \(i \in C_{k}\), \(k \in \Im\), define the synchronous errors as \(e_{ik} \left( t \right) = x_{i} \left( t \right) - s_{k} \left( {t - \sigma } \right)\). Let \(\theta = {\delta \mathord{\left/ {\vphantom {\delta T}} \right. \kern-0pt} T}\) be the ratio of the control width \(\delta\) to the control period \(T\), which is also referred to as the control rate. From the control law (8), the error dynamical system is obtained as

$$\left\{ {\begin{array}{llll} {\dot{e}_{ik} \left( t \right) = \tilde{f}_{k}^{{\tau_{k} ,\sigma }} \left( {t,x_{i} ,s_{k} } \right) + c\sum\nolimits_{p = 1}^{m} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma e_{jp} \left( t \right)} } - cd_{k} \varGamma e_{ik} \left( t \right),} \hfill & {\omega T \le t < \left( {\omega { + }\theta } \right)T,} \hfill & {i \in C_{k} ,} \hfill & {1 \le k \le l,} \hfill \\ {\dot{e}_{ik} \left( t \right) = \tilde{f}_{k}^{{\tau_{k} ,\sigma }} \left( {t,x_{i} ,s_{k} } \right) + c\sum\nolimits_{p = 1}^{m} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma e_{jp} \left( t \right)} } ,} \hfill & {\left( {\omega { + }\theta } \right)T \le t < \left( {\omega + 1} \right)T,} \hfill & {i \in C_{k} ,} \hfill & {1 \le k \le m,} \hfill \\ {\dot{e}_{ik} \left( t \right) = \tilde{f}_{k}^{{\tau_{k} ,\sigma }} \left( {t,x_{i} ,s_{k} } \right) + c\sum\nolimits_{p = 1}^{m} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma e_{jp} \left( t \right)} } ,} \hfill & {\omega T \le t < \left( {\omega { + }\theta } \right)T,} \hfill & {i \in C_{k} ,} \hfill & {l + 1 \le k \le m,} \hfill \\ \end{array} } \right.$$
(9)

where \(\tilde{f}_{k}^{{\tau_{k} ,\sigma }} \left( {t,x_{i} ,s_{k} } \right) = \tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right) - \tilde{f}_{k} \left( {\left( {t - \sigma } \right),s_{k} \left( {t - \sigma } \right),s_{k} \left( {t - \tau_{k} \left( t \right) - \sigma } \right)} \right)\). For the error dynamical system (9), if the zero solution is globally exponentially stable, then obviously, for the pinning-controlled delayed dynamical network (6), the global cluster lag synchronization is achievable.

According to the above, the following assumption is needed.

Assumption 2

For the vector-valued function \(\tilde{f}_{k} \left( {t,x\left( t \right),x\left( {t - \tau_{k} \left( t \right)} \right)} \right)\), supposing that there exist some constants \(L_{k}^{0}\) and \(L_{k}^{\tau } \ge 0\), such that, for any \(x\left( t \right),y\left( t \right) \in {\mathbb{R}}^{n}\) and \(k \in \Im\),

$$\begin{aligned} & \left( {x\left( t \right) - y\left( t \right)} \right)^{\rm T} \left( {\tilde{f}_{k} \left( {t,x\left( t \right),x\left( {t - \tau_{k} \left( t \right)} \right)} \right) - \tilde{f}_{k} \left( {t,y\left( t \right),y\left( {t - \tau_{k} \left( t \right)} \right)} \right)} \right) \\ & \quad \le L_{k}^{0} \left( {x\left( t \right) - y\left( t \right)} \right)^{\rm T} \varGamma \left( {x\left( t \right) - y\left( t \right)} \right) \\ & \quad \quad + L_{k}^{\tau } \left( {x\left( {t - \tau_{k} \left( t \right)} \right) - y\left( {t - \tau_{k} \left( t \right)} \right)} \right)^{\rm T} \varGamma \left( {x\left( {t - \tau_{k} \left( t \right)} \right) - y\left( {t - \tau_{k} \left( t \right)} \right)} \right). \\ \end{aligned}$$

Remark 3

Some requirements about the dynamical change in the nodes in the cluster \(C_{k}\) are given in Assumption 2. If the function \(\tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right)\) of each node in the cluster \(C_{k}\) satisfies the Lipschitz condition [41, 42], then

$$\begin{aligned} & \left\| {\left( {\tilde{f}_{k} \left( {t,x\left( t \right),x\left( {t - \tau_{k} \left( t \right)} \right)} \right) - \tilde{f}_{k} \left( {t,y\left( t \right),y\left( {t - \tau_{k} \left( t \right)} \right)} \right)} \right)} \right\| \\ & \quad \le \varLambda_{k}^{0} \left\| {x\left( t \right) - y\left( t \right)} \right\| + \varLambda_{k}^{\tau } \left\| {x\left( {t - \tau_{k} \left( t \right)} \right) - y\left( {t - \tau_{k} \left( t \right)} \right)} \right\|. \\ \end{aligned}$$

We can choose \(L_{k}^{0} = \frac{{2\varLambda_{k}^{0} + \varLambda_{k}^{\tau } }}{{2\lambda_{\hbox{min} } \left( \varGamma \right)}}\) and \(L_{k}^{\tau } = \frac{{\varLambda_{k}^{\tau } }}{{2\lambda_{\hbox{min} } \left( \varGamma \right)}}\) to satisfy Assumption 1. In addition, almost all the famous chaotic systems with or without delay also satisfy Assumption 1. Such as Lorenz system, Chen system, Rössler system, Chua’s circuit, as well as delayed Ikeda equations, delayed cellular neural networks, and so on, see [41, 42].

Lemma 1

(Gershgorin disk theorem [43]) Let\(A = \left( {a_{ij} } \right)_{n \times n}\)be a complex matrix. For\(i = 1,2, \ldots ,n\), define\(R^{\prime}_{i} \left( A \right) = \sum\nolimits_{j = 1,j \ne i} {\left| {a_{ij} } \right|}\)as the absolute row sums of\(A\)besides the diagonal elements, and consider the\(n\)Gershgorin disks as

$$\left\{ {z \in {\mathbb{C}}\left| {\left| {z - a_{ii} } \right| \le R^{\prime}_{i} \left( A \right)} \right.} \right\}.$$

All the eigenvalues of \(A\) are included in the Gershgorin disks set as

$$G\left( A \right) = \mathop \bigcup \limits_{i = 1}^{n} \left\{ {z \in {\mathbb{C}}\left| {\left| {z - a_{ii} } \right| \le R^{\prime}_{i} \left( A \right)} \right.} \right\}.$$

Lemma 2

(Schur complement [41]) The linear matrix inequality

$$\left( {\begin{array}{ll} {Q\left( x \right)} & {U\left( x \right)} \\ {U\left( x \right)^{\rm T} } & {R\left( x \right)} \\ \end{array} } \right) < 0,$$

where\(Q\left( x \right) = Q\left( x \right)^{\rm T}\), \(R\left( x \right) = R\left( x \right)^{\rm T}\)and\(U\left( x \right)\)is a matrix with suitable dimensions, can be represented by one of the following situations.

$$\begin{array}{lll} {\left( 1 \right)\quad Q\left( x \right) < 0,} \hfill & {\quad R\left( x \right) - U\left( x \right)^{\rm T} Q\left( x \right)^{ - 1} U\left( x \right) < 0;} \hfill \\ {\left( 2 \right)\quad R\left( x \right) < 0,} \hfill & {\quad Q\left( x \right) - U\left( x \right)R\left( x \right)^{ - 1} U\left( x \right)^{\rm T} < 0.} \hfill \\ \end{array}$$

3 Intermittent pinning criteria for cluster lag synchronization

We explore the stability condition of the delayed dynamical network (6) under pinning control in this section and introduce some criteria, which can be used to ensure that the globally exponential stability with an intermittent pinning control scheme is realizable. With Lemma 2, we will show how to set the appropriate control parameters \(d_{k} \left( {k = 1,2, \ldots ,l} \right)\), \(\delta\) and \(T\) in the delayed dynamical network (6) such that the cluster lag synchronization is reachable. For convenience, we will introduce the following notations.

Let \(r_{0} = 0\), and for each \(i \in C_{k}\), \(k \in \Im\), let \(a_{i}^{k} = \sum\nolimits_{{j \in C_{k} }} {\left( {b_{ji} + b_{ij} } \right)}\), \(\xi_{i}^{k} = \sum\nolimits_{j = 1}^{N} {b_{ji} }\), \(A_{k} = \text{diag} \left( {a_{{r_{0} + r_{1} + \cdots + r_{k - 1} + 1}}^{k} , \ldots ,a_{{r_{0} + r_{1} + \cdots + r_{k - 1} + r_{k} }}^{k} } \right)\quad {\text{and}}\quad \varPsi_{k} = \text{diag} \left( {\xi_{{r_{0} + r_{1} + \cdots + r_{k - 1} + 1}}^{k} , \ldots ,\xi_{{r_{0} + r_{1} + \cdots + r_{k - 1} + r_{k} }}^{k} } \right).\)

Define two block diagonal matrices \(Z \in {\mathbb{R}}^{N \times N}\) and \(D \in {\mathbb{R}}^{N \times N}\) as

$$\begin{aligned} Z & = \left( {\begin{array}{lllllll} {Z_{11} } & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 & {Z_{22} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & \cdots & {Z_{ll} } & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 & {Z_{l + 1,l + 1} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & 0 & \cdots & {Z_{mm} } \\ \end{array} } \right)\quad {\text{and}} \\ D & = \left( {\begin{array}{lllllll} {d_{1} I_{{r_{1} }} } & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 & {d_{2} I_{{r_{2} }} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & \cdots & {d_{l} I_{{r_{l} }} } & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \end{array} } \right), \\ \end{aligned}$$

where \(Z_{kk} = \left( {z_{ij} } \right) \in {\mathbb{R}}^{{r_{k} \times r_{k} }} = B_{kk}^{s} + \frac{1}{2}\varPsi_{k} + \left( {\frac{{L_{k}^{0} }}{c}} \right)I_{{r_{k} }} - \frac{1}{2}A_{k}\), \(B_{kk}^{s} = \frac{1}{2}\left( {B_{kk} + B_{kk}^{\rm T} } \right)\), \(k \in \Im\) and \(I_{{r_{j} }}\) represents the \(r_{j}\)-dimensional identity matrix, \(j = 1,2, \ldots ,l\).

Theorem 1

Suppose that Assumptions 1 and 2 hold. If there are two positive constants\(a_{1}\)and\(a_{2}\)such that

$$\begin{array}{ll} {(\text{i})\quad a_{1} I_{N} + cZ - cD < 0,} \hfill \\ {(\text{ii}){\kern 1pt} \quad cZ - a_{2} I_{N} \le 0,} \hfill \\ {(\text{iii})\quad q - p_{1} < 0,} \hfill \\ {(\text{iv}){\kern 1pt} \quad \varpi = \lambda - \left( {p_{1} + p_{2} } \right)\left( {1 - \theta } \right) > 0,} \hfill \\ \end{array}$$

where\(p_{1} = 2a_{1} \lambda_{\hbox{min} } \left( \varGamma \right)\), \(p_{ 2} = 2a_{ 2} \lambda_{\hbox{max} } \left( \varGamma \right)\), \(q = 2\left( {\max_{1 \le k \le m} L_{k}^{\tau } } \right)\lambda_{\hbox{max} } \left( \varGamma \right)\), and the unique positive solution of the equation\(\lambda - p_{1} + qe^{\lambda \tau } = 0\)is\(\lambda > 0\), then the cluster lag synchronization of the delayed dynamical network (6) can be realized.

Proof

See “Appendix 1.”□

Remark 4

For a directed complex network with non-identical time-varying delayed dynamical nodes, Theorem 1 presents a novel cluster lag synchronous condition by combining the intermittent control technique with pinning scheme. As far as we know, there is a little work concerning the cluster lag synchronization of the heterogeneous complex dynamical networks with intermittent pinning control. It should be emphasized that in this paper, we discuss the cluster lag synchronization with both the time-varying delays and transmission delay and treat each cluster as a whole. Moreover, the desired cluster lag synchronous states are chosen as a collection of uncoupled trajectories instead of the particular solutions of the decoupled node systems. Most of the existing researches on the cluster lag synchronization problems are different with the precondition that we set [37, 39, 40]. In addition, from Theorem 1, we can see that the cluster lag synchronous specification relies mostly on the control rate \(\theta\) rather than the control width \(\delta\) or the control period \(T\). With regard to the actual problems, the cluster lag synchronization can be realized by randomly selecting the control period \(T\).

Theorem 1 provides a general control standard to ensure that the cluster lag synchronization of the delayed dynamical network (3) can be realized. However, how to choose an appropriate control gain matrix \(D\) and a control rate \(\theta\) is still not clear. Using Lemma 2 and the matrix decomposition method [41, 44], some simplified versions of Theorem 1 are constructed (see below). These simplified versions are more convenient when estimating the control rate and the control gains.

Let \(Q = a_{1} I_{N} + cZ\), \(a_{1} I_{N} + cZ - cD = Q - cD = \left( {\begin{array}{ll} {G - c\tilde{D}} & 0 \\ {0^{\rm T} } & {\tilde{Q}} \\ \end{array} } \right)\), \(d = \min_{1 \le k \le l} d_{k}\), where \(G\) and \(\tilde{D}\) are two block diagonal matrices. The definitions of \(E\) and \(\tilde{D}\) are

$$\begin{aligned} G & = \left( {\begin{array}{llll} {cZ_{11} + a_{1} I_{{r_{1} }} } & 0 & \cdots & 0 \\ 0 & {cZ_{22} + a_{1} I_{{r_{2} }} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {cZ_{ll} + a_{1} I_{{r_{l} }} } \\ \end{array} } \right)\quad {\text{and}} \\ \tilde{D} & = \left( {\begin{array}{llll} {d_{1} I_{{r_{1} }} } & 0 & \cdots & 0 \\ 0 & {d_{2} I_{{r_{2} }} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {d_{l} I_{{r_{l} }} } \\ \end{array} } \right). \\ \end{aligned}$$

Obviously, the real matrix \(Q\) is symmetric, and by removing its first \(\left( {r_{1} + r_{2} + \cdots + r_{l} } \right)\) row–column pairs, the matrix \(\tilde{Q}\) is obtained. In virtue of Lemma 2, we can verify that \(\tilde{Q} < 0\) and \(d > \frac{{a_{1} }}{c} + \max_{1 \le k \le l} \left( {\lambda_{\hbox{max} } \left( {Z_{kk} } \right)} \right)\) is equivalent to \(Q - cD < 0\). If \(d\) can be large enough (we can set \(d_{i} > \frac{{a_{1} }}{c} + \max_{1 \le k \le l} \left( {\lambda_{\hbox{max} } \left( {Z_{kk} } \right)} \right)\), \(i = 1,2, \ldots ,l\)), then \(Q - cD < 0\) is equivalent to \(\tilde{Q} < 0\).

Let \(\varTheta_{kk} = \left( {\vartheta_{ij}^{k} } \right) \in {\mathbb{R}}^{{r_{k} \times r_{k} }} = B_{kk}^{s} + \frac{1}{2}\varPsi_{k} - \frac{1}{2}A_{k} = Z_{kk} - \frac{{L_{k}^{0} }}{c}I_{{r_{k} }}\) and \(\varUpsilon_{k} = \lambda_{\hbox{max} } \left( {\varTheta_{kk} } \right) + \frac{{L_{k}^{0} }}{c},\;\;k \in \Im\).

Noticing that

$$\tilde{Q} = \left( {\begin{array}{llll} {cZ_{l + 1,l + 1} + a_{1} I_{{r_{l + 1} }} } & 0 & \cdots & 0 \\ 0 & {cZ_{l + 2,l + 2} + a_{1} I_{{r_{l + 2} }} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {cZ_{m,m} + a_{1} I_{{r_{m} }} } \\ \end{array} } \right)$$

and \(\lambda_{\hbox{max} } \left( {\varTheta_{kk} } \right) \le \varUpsilon_{k} ,\quad k \in \Im\), the following corollary can be concluded from Theorem 1.

Corollary 1

Suppose that Assumptions 1 and 2 hold. If the intermittent feedback control gains\(d_{i} \left( {1 \le i \le l} \right)\)are large enough, and there exists a positive constant\(a_{1} > \frac{q}{{2\lambda_{\hbox{min} } \left( \varGamma \right)}}\)such that

$$\begin{aligned} & \left( {{\text{i}}^{\prime } } \right)\quad \varUpsilon_{k} < - \frac{{a_{1} }}{c},\quad l + 1 \le k \le m, \\ & \left( {{\text{ii}}^{\prime } } \right)\quad 1 - \frac{\lambda }{{p_{1} + p_{2} }} < \theta < 1, \\ \end{aligned}$$

then the cluster lag synchronization of the delayed dynamical network (6) is realizable.

An explanation of the notations in Corollary 1 is given. The definitions of \(\lambda\), \(p_{1}\) and \(q\) are the same as Theorem 1, and \(p_{2} = 2c\lambda_{\hbox{max} } \left( Z \right)\lambda_{\hbox{max} } \left( \varGamma \right)\). We set \(d_{i} > \frac{{a_{1} }}{c} + \max_{1 \le k \le l} \left( {\lambda_{\hbox{max} } \left( {Z_{kk} } \right)} \right)\).

Furthermore, assume that \(a_{1}\) is given as \(a_{1}^{0} > \frac{q}{{2\lambda_{\hbox{min} } \left( \varGamma \right)}}\). We substitute \(a_{1} = a_{1}^{0}\) into the equation \(\lambda - p_{1} + qe^{\lambda \tau } = 0\), where \(\lambda = \phi \left( {a_{1}^{0} } \right)\). Let \(d_{i} > \frac{{a_{1}^{0} }}{c} + \max_{1 \le k \le l} \left( {\lambda_{\hbox{max} } \left( {Z_{kk} } \right)} \right)\) and \(p_{1} = 2a_{1}^{0} \lambda_{\hbox{min} } \left( \varGamma \right)\). Besides this, the variables \(p_{2}\) and \(q\) are the same with Corollary 1. Then, we can put the above corollary in the following way.

Corollary 2

Suppose that Assumptions 1 and 2 hold. If the intermittent feedback control gains\(d_{i} \left( {1 \le i \le l} \right)\)are large enough, and there exists a positive constant\(a_{1}^{0} > \frac{q}{{2\lambda_{\hbox{min} } \left( \varGamma \right)}}\)such that

$$\begin{aligned} & \left( {{\text{i}}^{\prime \prime } } \right)\quad \varUpsilon_{k} < - \frac{{a_{1}^{0} }}{c},\quad l + 1 \le k \le m, \\ & \left( {{\text{ii}}^{\prime \prime } } \right)\quad 1 - \frac{{\phi \left( {a_{1}^{0} } \right)}}{{p_{1} + p_{2} }} < \theta < 1, \\ \end{aligned}$$

then the cluster lag synchronization of the delayed dynamical network (6) is realizable.

Remark 5

Corollary 2 allows us to simply determine the control rate \(\theta\) and the feedback control gains \(d_{i} \left( {1 \le i \le l} \right)\), thus, the intermittent controller (7)–(8) can be conveniently designed.

Remark 6

An undirected delayed dynamical network can be regarded as a special case of the directed delayed dynamical network with symmetrically coupling matrix, i.e., \(B = B^{\rm T}\). Therefore, the theoretical results that we obtained in this paper establish the appropriate conditions for the cluster lag synchronization of the undirected complex dynamical delayed networks under the intermittent pinning control.

In the above, we regard the each cluster as a whole and put forward some low-dimensional specifications to ensure that we can implement the cluster lag synchronization by intermittently controlling a part of clusters of the delayed dynamical network (3). But, how to choose these pinned clusters? We make use of an effective scheme, which was originally proposed in [28]. To facilitate the applications, we give the selection scheme as follows. At first, the following notations are given.

\({\text{Intra-InDeg}}\left( {i,k} \right)\) denotes the sum weights of the directed edges \(e\left( {i,j} \right)\) with \(j \in C_{k}\) into \(i \in C_{k}\), i.e., the intra-in-degree of the \(i\)th node of the cluster \(C_{k}\) [38]. \({\text{Extra-InDeg}}\left( {i,k} \right)\) denotes the sum weights of the directed edges \(e\left( {i,j} \right)\) with \(j \notin C_{k}\) into \(i \in C_{k}\), i.e., the extra-in-degree of the \(i\)th node in the cluster \(C_{k}\) [38]. Similarly, \({\text{Intra - OutDeg}}\left( {i,k} \right)\) denotes the sum weights of the directed edges \(e\left( {j,i} \right)\) with \(j \in C_{k}\) from \(i \in C_{k}\), i.e., the intra-out-degree of the \(i\)th node in the cluster \(C_{k}\) [38]. \({\text{Extra-OutDeg}}\left( {i,k} \right)\) denotes the sum weights of the directed edges \(e\left( {j,i} \right)\) with \(j \notin C_{k}\) from \(i \in C_{k}\), i.e., the extra-out-degree of the \(i\)th node in the cluster \(C_{k}\) [38]. In addition, \({\text{InDeg}}\left( {i,k} \right)\) and \({\text{OutDeg}}\left( {i,k} \right)\), respectively, denote the in-degree and the out-degree of the \(i\)th node of the cluster \(C_{k}\) [38]. According to the definition about the coupling matrix \(B\) of network (1), for any \(i \in C_{k}\), one has

  • \({\text{Intra-InDeg}}\left( {i,k} \right) = \sum\nolimits_{{j \in C_{k} ,j \ne i}} {b_{ij} } \quad {\text{and}}\quad {\text{Extra-InDeg}}\left( {i,k} \right) = \sum\nolimits_{p = 1,p \ne k}^{m} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} } } ,\)

  • \({\text{Intra-OutDeg}}\left( {i,k} \right) = \sum\nolimits_{{j \in C_{k} ,j \ne i}} {b_{ji} } \quad {\text{and}}\quad {\text{Extra-OutDeg}}\left( {i,k} \right) = \sum\nolimits_{p = 1,p \ne k}^{m} {\sum\nolimits_{{j \in C_{p} }} {b_{ji} } } ,\)

  • \({\text{InDeg}}\left( {i,k} \right) = {\text{Intra-InDeg}}\left( {i,k} \right) + {\text{Extra-InDeg}}\left( {i,k} \right) = \sum\nolimits_{j = 1,j \ne i}^{N} {b_{ij} } = - b_{ii} ,\)

  • \({\text{OutDeg}}\left( {i,k} \right) = {\text{Intra-OutDeg}}\left( {i,k} \right) + {\text{Extra-OutDeg}}\left( {i,k} \right) = \sum\nolimits_{j = 1,j \ne i}^{N} {b_{ji} } .\)

Furthermore, \({\text{Intra-InDeg}}\left( k \right)\) stands for the sum of the intra-in-degree for all nodes of the cluster \(C_{k}\), i.e., the intra-in-degree of the cluster \(C_{k}\) in network (1) [38]. \({\text{Extra-InDeg}}\left( k \right)\) denotes the sum of the extra-in-degree for all nodes of the cluster \(C_{k}\), i.e., the extra-in-degree of the cluster \(C_{k}\) in network (1) [38]. Similarly, define \({\text{Intra-OutDeg}}\left( k \right)\) (\({\text{Extra-OutDeg}}\left( k \right)\)) as the intra(extra)-out-degree of the cluster \(C_{k}\) in network (1). This means the sum of the intra(extra)-out-degree for all nodes of the cluster \(C_{k}\) [38]. Additionally, define \({\text{InDeg}}\left( k \right)\) and \({\text{OutDeg}}\left( k \right)\) as the in-degree and the out-degree of the cluster \(C_{k}\) in network (1), respectively [38]. Then, we have

$$\begin{aligned} {\text{InDeg}}\left( k \right) & = \sum\limits_{{i \in C_{k} }} {{\text{InDeg}}\left( {i,k} \right)} \\ & = \sum\limits_{{i \in C_{k} }} {\left( {{\text{Intra-InDeg}}\left( {i,k} \right) + {\text{Extra-InDeg}}\left( {i,k} \right)} \right)} \\ & = {\text{Intra-InDeg}}\left( k \right) + {\text{Extra-InDeg}}\left( k \right), \\ \end{aligned}$$
$$\begin{aligned} {\text{OutDeg}}\left( k \right) & = \sum\limits_{{i \in C_{k} }} {{\text{OutDeg}}\left( {i,k} \right)} \\ & = \sum\limits_{{i \in C_{k} }} {\left( {{\text{Intra-OutDeg}}\left( {i,k} \right) + {\text{Extra-OutDeg}}\left( {i,k} \right)} \right)} \\ & = {\text{Intra-OutDeg}}\left( k \right) + {\text{Extra-OutDeg}}\left( k \right) \\ \end{aligned}$$

and

$$\begin{aligned} & {\text{OutDeg}}\left( k \right) - {\text{InDeg}}\left( k \right) = \sum\limits_{{i \in C_{k} }} {\left( {{\text{OutDeg}}\left( {i,k} \right) - {\text{InDeg}}\left( {i,k} \right)} \right)} \\ &\quad = \sum\limits_{{i \in C_{k} }} {\left( {\sum\limits_{j = 1,j \ne i}^{N} {b_{ji} } - \sum\limits_{j = 1,j \ne i}^{N} {b_{ij} } } \right)} = \sum\limits_{{i \in C_{k} }} {\sum\limits_{j = 1}^{N} {b_{ji} } } . \\ \end{aligned}$$

Obviously, the information about the intra-cluster communication is represented by the intra-in-degree and the intra-out-degree of the cluster, and the information about the inter-clusters communication is represented by the extra-in-degree and the extra-out-degree of the cluster.

In order to meet the control condition \(\left( {{\text{i}}^{\prime \prime } } \right)\), at least we need to choose some pinned nodes to make \(\varUpsilon_{k} < 0,\;l + 1 \le k \le m\). To achieve this purpose, based on the degree information of each cluster defined as above, we give the following theorem.

Theorem 2

For any\(k \in \Im\),

$$\lambda_{\hbox{max} } \left( {\varTheta_{kk} } \right) \le \frac{{\max_{{i \in C_{k} }} \left( {{\text{OutDeg}}\left( {i,k} \right) - {\text{InDeg}}\left( {i,k} \right)} \right)}}{2}.$$
(10)

In particular, for some\(k\), if\(\max_{{i \in C_{k} }} \left( {{\text{OutDeg}}\left( {i,k} \right) - {\text{InDeg}}\left( {i,k} \right)} \right) < 0\), then\(\lambda_{\hbox{max} } \left( {\varTheta_{kk} } \right) < 0\).

Proof

Noting \(\varTheta_{kk} = \left( {\vartheta_{ij}^{k} } \right) \in {\mathbb{R}}^{{r_{k} \times r_{k} }} = B_{kk}^{s} + \frac{1}{2}\varPsi_{k} - \frac{1}{2}A_{k}\), then for any \(i \in C_{k}\),

$$\begin{aligned} \vartheta_{ii}^{k} + \sum\nolimits_{{j \in C_{k} ,j \ne i}} {\left| {\vartheta_{ij}^{k} } \right|} & = \left( {\sum\limits_{{j \in C_{k} }} {\frac{{b_{ij} + b_{ji} }}{2}} } \right) + \frac{{\xi_{i}^{k} }}{2} - \frac{{a_{i}^{k} }}{2} \\ & = \frac{1}{2}\left( {\sum\limits_{j = 1,j \ne i} {b_{ji} } } \right) + \frac{1}{2}b_{ii} \\ & {\kern 1pt} = \frac{{{\text{OutDeg}} \left( {i,k} \right) - {\text{InDeg}} \left( {i,k} \right)}}{2}. \\ \end{aligned}$$
(11)

Let \(\lambda^{k}\) be an eigenvalue of \(\varTheta_{kk}\). According to Lemma 1, we get

$$\lambda^{k} \le \mathop \bigcup \limits_{{i \in C_{k} }} \left\{ {z \in {\mathbb{R}}\left| {\left| {z - \vartheta_{ii}^{k} } \right| \le \sum\nolimits_{{j \in C_{k} ,j \ne i}} {\left| {\vartheta_{ij}^{k} } \right|} } \right|} \right\}.$$
(12)

With (12), we have

$$\lambda ^{k} \le \mathop {\max }\limits_{{i \in C_{k} }} \left( {{\text{OutDeg}}\left( {i,k} \right) - {\text{InDeg}}\left( {i,k} \right)} \right)/2,$$
(13)

and if \(\mathop {\hbox{max} }\nolimits_{{i \in C_{k} }} \left( {{\text{OutDeg}} \left( {i,k} \right) - {\text{InDeg}} \left( {i,k} \right)} \right) < 0\), then \(\lambda^{k} < 0\). The proof is thus completed.□

Remark 7

Theorem 2 provides some useful guidance about how to set up the pinned clusters to achieve the cluster lag synchronization. For \(k \in \Im\), define

$${\text{DiffDeg}} \left( k \right) = {\text{OutDeg}} \left( k \right) - {\text{InDeg}} \left( k \right)$$

as the difference between the out-degree and the in-degree of the cluster \(C_{k}\). Noticing that for any \(k \in \Im\), one has \(\mathop {\hbox{max} }\nolimits_{{i \in C_{k} }} \left( {{\text{OutDeg}} \left( {i,k} \right) - {\text{InDeg}} \left( {i,k} \right)} \right) \ge {{{\text{DiffDeg}} \left( k \right)} \mathord{\left/ {\vphantom {{{\text{DiffDeg}} \left( k \right)} {r_{k} }}} \right. \kern-0pt} {r_{k} }}\). Thus, if the out-degrees of some unpinned clusters are bigger than their in-degrees, then according to Theorem 2, for those clusters which are not be pinned, we have \(\lambda_{\hbox{max} } \left( {\varTheta_{kk} } \right) > 0\). Namely, condition \(\left( {{\text{i}}^{\prime \prime } } \right)\) may not be met. This means that, to satisfy condition \(\left( {{\text{i}}^{\prime \prime } } \right)\), these clusters whose out-degrees are bigger than their in-degrees should be chosen as pinned candidates preferentially. Based on Theorem 2 and condition \(\left( {{\text{i}}^{\prime \prime } } \right)\), we adopt the following special pinned scheme to choose the pinned clusters for the delayed dynamical networks:

  1. 1.

    Define a cluster information vector

    $$\text{CluInf} \left( k \right) = \frac{{L_{k}^{0} }}{c} + \frac{1}{2}\mathop {\hbox{max} }\limits_{{i \in C_{k} }} \left( {{\text{OutDeg}} \left( {i,k} \right) - {\text{InDeg}} \left( {i,k} \right)} \right),\quad k \in \Im .$$
  2. 2.

    Select the cluster which has zero-in-degrees as the clusters be pinned firstly.

  3. 3.

    According to the value of \(\text{CluInf} \left( k \right)\), rearrange the rest of the clusters in descending order. For those clusters having the same \(\text{CluInf} \left( k \right)\), rearrange them in descending order according to their out-degrees. According to the sequence of the cluster information to increase the number of clusters to be pinned until the restrain condition \(\left( {{\text{i}}^{\prime \prime } } \right)\) holds. In addition, from condition \(\left( {{\text{i}}^{\prime \prime } } \right)\), we know that the number of clusters being selected and pinned to achieve the cluster lag synchronization of the delayed dynamical network (6) is at least equal to \(l_{0}\) which is bounded by

    $$\varUpsilon_{{l_{0} - 1}} \ge - \frac{{a_{1}^{0} }}{c}\quad {\text{and}}\quad \varUpsilon_{{l_{0} }} < - \frac{{a_{1}^{0} }}{c}.$$

4 Adaptive intermittent pinning control scheme

In order to realize the cluster lag synchronization of the dynamical delayed network (6), we can set the intermittent feedback control gains according to the following condition.

$$d_{i} > \frac{{a_{1}^{0} }}{c} + \mathop {\hbox{max} }\limits_{1 \le k \le l} \left( {\lambda_{\hbox{max} } \left( {Z_{kk} } \right)} \right),\quad i = 1,2, \ldots ,l.$$
(14)

Unfortunately, the theoretical values, i.e., the intermittent feedback control gains given by condition (14), are usually bigger than the actual need. In practice, however, it cannot be realized if the control gains are too large [19]. To make the control gains as small as possible for practical applications, a better way is to adjust the gains by an adaptive intermittent feedback control approach. In this section, by introducing a local adaptive strategy for the intermittent feedback control gains, a decentralized adaptive intermittent pinning control scheme is proposed in order to realize the cluster lag synchronization of the delayed dynamical network (3).

Theorem 3

Suppose that Assumptions 1 and 2 hold, and there are\(l\)clusters being pinned such that condition\(\left( {{\text{i}}^{\prime \prime } } \right)\)satisfies. With the adaptive intermittent pinning control (16), if

$$1 - \frac{{\phi \left( {a_{1}^{0} } \right)}}{{p_{1} + p_{2} }} < \theta < 1 ,$$
(15)

then the cluster lag synchronization of the network (6) with transmission delay\(\sigma\)can be realized.

Proof

See “Appendix 2.”□

The variables \(a_{1}^{0}\), \(p_{1}\) and \(p_{2}\) are the same as that in Corollary 2, and Eq. (16) is given in the following:

$$u_{i} \left( t \right) = \left\{ {\begin{array}{ll} { - cd_{k} \left( t \right)\varGamma e_{ik} \left( t \right),} & \quad{\omega T \le t < \left( {\omega + \theta } \right)T,\;\;i \in C_{k} ,\;\;1 \le k \le l,} \\ {0,} &\quad {\text{otherwise,}} \\ \end{array} } \right.$$
(16)

where \(e_{ik} \left( t \right) = x_{i} \left( t \right) - s_{k} \left( {t - \sigma } \right)\), with the adaptive rules

$$\dot{d}_{k} \left( t \right) = h_{k} \sum\limits_{{i \in C_{k} }} {e_{ik} \left( t \right)^{\text{T}} \varGamma e_{ik} \left( t \right)} ,\quad \omega T \le t < \left( {\omega + \theta } \right)T,$$
(17)

where for \(k = 1,2, \ldots ,l\), the initial conditions \(d_{k} \left( 0 \right) \ge 0\) and constants \(h_{k} > 0\). Assume that \(d_{k} \left( {t_{\omega }^{ - } } \right) = \lim_{{t \to t_{\omega }^{ - } }} d_{k} \left( t \right)\) exists and \(d_{k} \left( {\left( {\omega + 1} \right)T} \right) = d_{k} \left( {t_{\omega }^{ - } } \right)\), where \(t_{\omega } = \left( {\omega + \theta } \right)T\).

When the transmission delay \(\sigma = 0\), the values of \(a_{1}^{0}\), \(p_{1}\) and \(p_{2}\) keep the same with Theorem 3. Theorem 3 reduces to the following result.

Theorem 4

Suppose that Assumptions 1 and 2 hold, and there are\(l\)clusters being pinned such that condition\(\left( {{\text{i}}^{\prime \prime } } \right)\)satisfies. With the adaptive intermittent pinning control (19), if

$$1 - \frac{{\phi \left( {a_{1}^{0} } \right)}}{{p_{1} + p_{2} }} < \theta < 1 ,$$
(18)

then the cluster synchronization of the network (6) can be realized.

Equation (19) is given in the following:

$$u_{i} \left( t \right) = \left\{ {\begin{array}{ll} { - cd_{k} \left( t \right)\varGamma \left( {x_{i} \left( t \right) - s_{k} \left( t \right)} \right),} & {\omega T \le t < \left( {\omega + \theta } \right)T,i \in C_{k} ,1 \le k \le l,} \\ {0,} & {{\text{otherwise}},} \\ \end{array} } \right.$$
(19)

with the adaptive rules

$$\dot{d}_{k} \left( t \right) = h_{k} \sum\nolimits_{{i \in C_{k} }} {\left( {x_{i} \left( t \right) - s_{k} \left( t \right)} \right)^{\rm T} \varGamma \left( {x_{i} \left( t \right) - s_{k} \left( t \right)} \right)} ,\quad \omega T \le t < \left( {\omega + \theta } \right)T,$$
(20)

where for\(k = 1,2, \ldots ,l\), the initial conditions\(d_{k} \left( 0 \right) \ge 0\)and constants\(h_{k} > 0\). Assume that\(d_{k} \left( {t_{\omega }^{ - } } \right) = \lim_{{t \to t_{\omega }^{ - } }} d_{k} \left( t \right)\)exists and\(d_{k} \left( {\left( {\omega + 1} \right)T} \right) = d_{k} \left( {t_{\omega }^{ - } } \right)\), where\(t_{\omega } = \left( {\omega + \theta } \right)T\).

Remark 8

In [28], the cluster synchronization under the intermittent pinning control has been studied; however, the authors ignored the transmission delay in the process of communication. In this paper, we analyze a more general network model with non-identical dynamical nodes containing both time-varying delays and transmission delay. And an intermittent adaptive control strategy is discussed. The adaptive update rules for the controlled clusters only determined by the state information of the controlled cluster itself and the information of the desired cluster synchronous state of the cluster. Namely, the intermittent adaptive control strategy only depends on some local information rather than the global information of the entire network. Therefore, the results obtained in the paper are more practically applicable.

5 Numerical simulations

In this section, we present two numerical examples to verify the validity of the theoretical results in the previous section.

5.1 Example A: cluster lag synchronization of a directed network with 15 nodes

We design a directed network consisting of 15 non-identical delayed dynamical nodes, and suppose it can be divided into three clusters: \(C_{1} = \left\{ {1,2,3,4,5} \right\}\), \(C_{2} = \left\{ {6,7,8,9,10} \right\}\), \(C_{3} = \left\{ {11,12,13,14,15} \right\}\). The network state equation is

$$\left\{ \begin{aligned}& \dot{x}_{i} \left( t \right) = - 1.5x_{i} \left( t \right) + 0.75\tanh \left( {x_{i} \left( {t - \tau_{1} \left( t \right)} \right)} \right) + c\sum\nolimits_{p = 1}^{3} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma x_{j} \left( t \right)} } ,\quad i \in C_{1} , \hfill \\ & \dot{x}_{i} \left( t \right) = - 2.5x_{i} \left( t \right){ + }\tanh \left( {x_{i} \left( {t - \tau_{2} \left( t \right)} \right)} \right) + c\sum\nolimits_{p = 1}^{3} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma x_{j} \left( t \right)} } ,\quad i \in C_{2} , \hfill \\ & \dot{x}_{i} \left( t \right) = 0.375x_{i} \left( t \right) + \tanh \left( {x_{i} \left( {t - \tau_{3} \left( t \right)} \right)} \right) + c\sum\nolimits_{p = 1}^{3} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma x_{j} \left( t \right)} } ,\quad i \in C_{3} , \hfill \\ \end{aligned} \right.$$
(21)

where \(x_{i} \left( t \right) \in {\mathbb{R}}^{3}\), \(\varGamma = I_{3}\), \(\tau_{1} \left( t \right) = \tau_{2} \left( t \right) = \tau_{3} \left( t \right) = 0.02\frac{{e^{t} }}{{1 + e^{t} }}\), the transmission delay \(\sigma = 0.5\), and the coupling strength \(c = 8\). It can be verified that \(L_{1}^{0} = - 1.5\), \(L_{1}^{\tau } { = 0} . 7 5\), \(L_{2}^{0} = - 2.5\), \(L_{2}^{\tau } { = 1}\), \(L_{3}^{0} { = 0} . 3 7 5\), \(L_{3}^{\tau } { = 1}\), and thus, Assumption 2 is satisfied. We assume that the characteristics of the coupling matrix \(B = \left( {b_{ij} } \right)_{15 \times 15} = \left( {\begin{array}{lll} {B_{11} } & {B_{12} } & {B_{13} } \\ {B_{21} } & {B_{22} } & {B_{23} } \\ {B_{31} } & {B_{32} } & {B_{33} } \\ \end{array} } \right)\) are as follows:

$$\begin{aligned} B_{11} & = \left( {\begin{array}{lllll} { - 16} & 1 & 0 & 1 & 1 \\ 0 & { - 16} & 1 & 1 & 1 \\ 1 & 0 & { - 16} & 1 & 1 \\ 1 & 1 & 1 & { - 16} & 0 \\ 1 & 1 & 1 & 0 & { - 16} \\ \end{array} } \right),\quad B_{12} = \left( {\begin{array}{lllll} 0 & 6 & 0 & 0 & 0 \\ 0 & 0 & 6 & 0 & 0 \\ 6 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 0 & 6 \\ \end{array} } \right),\quad B_{13} = \left( {\begin{array}{lllll} 0 & 0 & 5 & 0 & 2 \\ 5 & 0 & 0 & 2 & 0 \\ 0 & 5 & 0 & 0 & 2 \\ 5 & 0 & 2 & 0 & 0 \\ 0 & 5 & 0 & 2 & 0 \\ \end{array} } \right), \\ B_{21} & = \left( {\begin{array}{lllll} 0 & 0 & 5 & 0 & 2 \\ 5 & 0 & 0 & 2 & 0 \\ 0 & 5 & 0 & 0 & 2 \\ 5 & 0 & 2 & 0 & 0 \\ 0 & 5 & 0 & 2 & 0 \\ \end{array} } \right),\quad B_{22} = \left( {\begin{array}{lllll} { - 16} & 1 & 0 & 1 & 1 \\ 0 & { - 16} & 1 & 1 & 1 \\ 1 & 0 & { - 16} & 1 & 1 \\ 1 & 1 & 1 & { - 16} & 0 \\ 1 & 1 & 1 & 0 & { - 16} \\ \end{array} } \right),\quad B_{23} = \left( {\begin{array}{lllll} 0 & 6 & 0 & 0 & 0 \\ 0 & 0 & 6 & 0 & 0 \\ 6 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 0 & 6 \\ \end{array} } \right) \\ B_{31} & = \left( {\begin{array}{lllll} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ \end{array} } \right),\quad B_{32} = \left( {\begin{array}{lllll} 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ \end{array} } \right),\quad B_{33} = \left( {\begin{array}{lllll} { - 5} & 0 & 1 & 1 & 1 \\ 1 & { - 5} & 0 & 1 & 1 \\ 1 & 1 & { - 5} & 0 & 1 \\ 1 & 1 & 1 & { - 5} & 0 \\ 1 & 1 & 1 & 1 & { - 6} \\ \end{array} } \right). \\ \end{aligned}$$

Obviously, \(\beta_{11} = - 13\), \(\beta_{12} = 6\), \(\beta_{13} = 7\), \(\beta_{21} = 7\), \(\beta_{22} = - 13\), \(\beta_{23} = 6\), \(\beta_{31} = 1\), \(\beta_{32} = 1\), \(\beta_{33} = - 2\). Therefore, the cluster lag synchronous equations of network (21) can be described as

$$\left\{ \begin{aligned}& \dot{s}_{1} \left( t \right) = - 105.5s_{1} \left( t \right) + 48s_{2} \left( t \right) + 56s_{3} \left( t \right) + 0.75\tanh \left( {s_{1} \left( {t - \tau_{1} \left( t \right)} \right)} \right), \hfill \\ & \dot{s}_{2} \left( t \right) = 56s_{1} \left( t \right) - 106.5s_{2} \left( t \right) + 48s_{3} \left( t \right){ + }\tanh \left( {s_{2} \left( {t - \tau_{2} \left( t \right)} \right)} \right), \hfill \\ & \dot{s}_{3} \left( t \right) = 8s_{1} \left( t \right) + 8s_{2} \left( t \right) - 15.625s_{3} \left( t \right) + \tanh \left( {s_{3} \left( {t - \tau_{3} \left( t \right)} \right)} \right). \hfill \\ \end{aligned} \right.$$
(22)

Through calculation, the network (22) has three equilibrium points described by

$$S_{1}^{*} = \left( { - 5.7456, - 5.7007, - 5.9245} \right),\quad S_{2}^{ * } = \left( {0,0,0} \right),\quad S_{3}^{*} = \left( {5.7456,5.7007,5.9245} \right).$$

We choose \(S_{3}^{*}\) as the desired cluster lag synchronous state. By calculation, we get \(q = 2\) and \(\lambda_{\hbox{max} } \left( Z \right) = 6.0366\). Let \(a_{1}^{0} = 12\), from conditions \(\left( {{\text{i}}^{\prime \prime } } \right)\) and \(\left( {{\text{ii}}^{\prime \prime } } \right)\), we have

$$\varUpsilon_{k} < - 1.5,\quad l + 1 \le k \le 3,\quad 0.8215 < \theta < 1.$$
(23)

Since \(\text{CluInf} \left( 1 \right) = - 1.1875\), \(\text{CluInf} \left( 2 \right) = - 3.3125\) and \(\text{CluInf} \left( 3 \right) = 7.5469\), according to the descending order of the values, the rearranging order of cluster is \(C_{3}\), \(C_{1}\), \(C_{2}\). Noticing that \(\varUpsilon_{3} = 6.0366\), \(\varUpsilon_{2} = - 3.3125\) and \(\varUpsilon_{1} = - 2.3095\), then the cluster lag synchronization of the network (21) can be realized by controlling the first rearranged cluster, i.e., \(C_{3}\). Moreover, from condition (14), we get the lower bound of \(d_{i}\) is \(7.5366\).

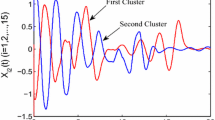
Setting \(\theta = 0.85\) and \(d_{3} = 8\), conditions (14) and (23) are satisfied. Select the control period \(T = 0.01\). The network with the intermittent controllers (7)–(8) can realize the desired cluster lag synchronization by pinning the first rearranged cluster, which uses the parameters chosen as above. Figure 1 shows the time evolutions of \(x_{i} \left( t \right)\left( {1 \le i \le 15} \right)\) with different initial values under the intermittent controllers (7)–(8). It can be seen that the cluster lag synchronization is realized with the nodes in the \(k\)th cluster converges to the \(k\)th component of \(S_{3}^{*} \left( {k = 1,2,3} \right)\).

Fig. 1
figure 1

Time evolutions of \(x_{i} \left( t \right)\left( {1 \le i \le 15} \right)\) for network (21) under the intermittent pinning control schemes (7)–(8), where \(\sigma = 0. 5\), \(\theta = 0. 8 5\), \(T = 0. 0 1\) and \(d_{3} = 8\)

Full size image

We apply the adaptive intermittent pinning control schemes (16)–(17) to network (21) based on Theorem 3. Select \(\theta = 0.85\), \(T = 0. 1\), \(h_{3} = 0.2\) and \(\sigma = 0. 5\). The time evolutions of \(x_{i} \left( t \right)\left( {1 \le i \le 15} \right)\) and \(d_{3} \left( t \right)\) are, respectively, illustrated in Figs. 2 and 3. We can see that the cluster lag synchronization of network (21) is realized and the adaptive intermittent feedback gain \(d_{3} \left( t \right)\) converges to 0.4741 finally, which is smaller than the fixed intermittent feedback gain we select as above. When the set \(S_{1}^{*}\) is chosen as the desired cluster lag synchronous state, we can get the similar simulation results, not shown here.

Fig. 2
figure 2

Time evolutions of \(x_{i} \left( t \right)\left( {1 \le i \le 15} \right)\) for network (21) under the adaptive intermittent pinning control schemes (16)–(17), where \(\sigma = 0. 5\), \(\theta = 0. 8 5\), \(T = 0. 1\) and \(h_{3} = 0.2\)

Full size image
Fig. 3
figure 3

Time evolutions of \(d_{3} \left( t \right)\) for network (21) under the adaptive intermittent pinning control schemes (16)–(17), where \(\sigma = 0. 5\), \(\theta = 0. 8 5\), \(T = 0. 1\) and \(h_{3} = 0.2\)

Full size image

5.2 Example B: cluster lag synchronization of a directed scale-free network

In this case, we consider the cluster lag synchronization of the directed scale-free network which consists of 300 non-identical delayed dynamical nodes. We suppose that the nodes can be divided into three clusters: \(C_{1} = \left\{ {1,2, \ldots ,100} \right\},\)\(C_{2} = \left\{ {101,102, \ldots ,200} \right\}\), \(C_{3} = \left\{ {201,202, \ldots ,300} \right\}\). The network state equations are as follows:

$$\dot{x}_{i} \left( t \right) = \tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right) + c\sum\nolimits_{p = 1}^{3} {\sum\nolimits_{{j \in C_{p} }} {b_{ij} \varGamma x_{j} \left( t \right)} } ,\quad i \in C_{k} ,\quad k \in \Im = \left\{ {1,2,3} \right\},$$
(24)

where \(\varGamma = I_{3}\), \(B = \left( {b_{ij} } \right)_{300 \times 300}\) is an asymmetrical coupling matrix, and the coupling strength \(c = 15\). The node dynamics of the three clusters are chosen as the delayed Chua oscillators with different system parameters, i.e.,

$$\begin{aligned} \dot{x}_{i} \left( t \right) & = \tilde{f}_{k} \left( {t,x_{i} \left( t \right),x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right) \\ & = \varOmega_{k} x_{i} \left( t \right) + \tilde{f}_{k}^{1} \left( {x_{i} \left( t \right)} \right) + \tilde{f}_{k}^{2} \left( {x_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right),\quad i \in C_{k} , \\ \end{aligned}$$
(25)

where

$$\begin{aligned} x_{i} \left( t \right) & = \left( {x_{i1} \left( t \right),x_{i2} \left( t \right),x_{i3} \left( t \right)} \right)^{\rm T} \in {\mathbb{R}}^{3} , \\ \tilde{f}_{k}^{1} \left( {x_{i} \left( t \right)} \right) & = \left( { - \frac{1}{2}\alpha_{k} \left( {a - b} \right)} \right)\left( {\left( {\left| {x_{i1} \left( t \right) + 1} \right| - \left| {x_{i1} \left( t \right) - 1} \right|} \right),0,0} \right)^{\rm T} \in {\mathbb{R}}^{3} , \\ \tilde{f}_{k}^{2} \left( {x_{i} \left( t \right)} \right) & = \left( {0,0, - \psi_{k} \varsigma \sin \left( {\upsilon x_{i1} \left( {t - \tau_{k} \left( t \right)} \right)} \right)} \right)^{\rm T} \in {\mathbb{R}}^{3} ,\quad \varOmega_{k} = \left( {\begin{array}{lll} { - \alpha_{k} \left( {1 + b} \right)} & {\alpha_{k} } & 0 \\ 1 & { - 1} & 1 \\ 0 & { - \psi_{k} } & { - \omega_{k} } \\ \end{array} } \right), \\ \end{aligned}$$

\(a = - 1.4325\), \(b = - 0.7831\), \(\upsilon = 0.5\), \(\varsigma = 0.2\), \(\tau_{k} \left( t \right) = 0.02\) and the transmission delay \(\sigma = 0.2\). In this simulation, we select \(\alpha_{1} = 10\), \(\psi_{1} = 19.53\), \(\omega_{1} = 0.1636\) for the cluster \(C_{1}\), \(\alpha_{2} = 10.5\), \(\psi_{2} = 20.53\), \(\omega_{2} = 0.2636\) for the cluster \(C_{2}\), \(\alpha_{3} = 11\), \(\psi_{3} = 18.53\), \(\omega_{3} = 0.3636\) for the cluster \(C_{3}\). We verify Assumption 2 as

$$\begin{aligned} {\kern 1pt} & \left( {x\left( t \right) - y\left( t \right)} \right)^{\rm T} \left( {\tilde{f}_{k} \left( {t,x\left( t \right),x\left( {t - \tau_{k} \left( t \right)} \right)} \right) - \tilde{f}_{k} \left( {\left( t \right),y\left( t \right),y\left( {t - \tau_{k} \left( t \right)} \right)} \right)} \right) \\ & \quad \le \frac{1}{2}\left( {x\left( t \right) - y\left( t \right)} \right)^{\rm T} \left( {\varOmega_{k} + \varOmega_{k}^{\rm T} } \right)\left( {x\left( t \right) - y\left( t \right)} \right) + \left| {\alpha_{k} \left( {a - b} \right)} \right|\left( {x_{1} \left( t \right) - y_{1} \left( t \right)} \right)^{2} \\ & \quad \quad + \psi_{k} \varsigma \upsilon \left| {x_{3} \left( t \right) - y_{3} \left( t \right)} \right|\left| {x_{1} \left( {t - \tau_{k} \left( t \right)} \right) - y_{1} \left( {t - \tau_{k} \left( t \right)} \right)} \right| \\ & \quad \le \lambda_{\hbox{max} } \left( {\tilde{\varOmega }_{k} } \right)\left( {x\left( t \right) - y\left( t \right)} \right)^{\rm T} \left( {x\left( t \right) - y\left( t \right)} \right) \\ & \quad \quad + {{\left( {\psi_{k} \varsigma \upsilon } \right)} \mathord{\left/ {\vphantom {{\left( {\psi_{k} \varsigma \upsilon } \right)} {\left( {2\varpi } \right)}}} \right. \kern-0pt} {\left( {2\varpi } \right)}}\left( {x\left( {t - \tau_{k} \left( t \right)} \right) - y\left( {t - \tau_{k} \left( t \right)} \right)} \right)^{\rm T} \left( {x\left( {t - \tau_{k} \left( t \right)} \right) - y\left( {t - \tau_{k} \left( t \right)} \right)} \right) \\ & \quad = L_{k}^{0} \left( {x\left( t \right) - y\left( t \right)} \right)^{\rm T} \varGamma \left( {x\left( t \right) - y\left( t \right)} \right) + L_{k}^{\tau } \left( {x\left( {t - \tau_{k} \left( t \right)} \right) - y\left( {t - \tau_{k} \left( t \right)} \right)} \right)^{\rm T} \varGamma \left( {x\left( {t - \tau_{k} \left( t \right)} \right) - y\left( {t - \tau_{k} \left( t \right)} \right)} \right). \\ \end{aligned}$$

Here, \(\tilde{\varOmega }_{k} = \left( {{{\left( {\varOmega_{k} + \varOmega_{k}^{\rm T} } \right)} \mathord{\left/ {\vphantom {{\left( {\varOmega_{k} + \varOmega_{k}^{\rm T} } \right)} 2}} \right. \kern-0pt} 2} + \text{diag} \left( {\left| {\alpha_{k} \left( {a - b} \right)} \right|,0,{{\varpi \left( {\psi_{k} \varsigma \upsilon } \right)} \mathord{\left/ {\vphantom {{\varpi \left( {\psi_{k} \delta \upsilon } \right)} 2}} \right. \kern-0pt} 2}} \right)} \right)\), \(L_{k}^{0} = \lambda_{\hbox{max} } \left( {\tilde{\varOmega }_{k} } \right)\) and \(L_{k}^{\tau } = {{\left( {\psi_{k} \varsigma \upsilon } \right)} \mathord{\left/ {\vphantom {{\left( {\psi_{k} \varsigma \upsilon } \right)} {\left( {2\varpi } \right)}}} \right. \kern-0pt} {\left( {2\varpi } \right)}}\) can be determined by selecting the proper parameter \(\varpi > 0\). Therefore, Assumption 2 is satisfied.

For convenience, we take the coupling matrix \(B\) as

$$B = \left( {b_{ij} } \right)_{300 \times 300} = \left( {\begin{array}{lll} {\varPhi_{1} - 15I_{100} } & {8I_{100} } & {7I_{100} } \\ {6I_{100} } & {\varPhi_{2} - 15I_{100} } & {9I_{100} } \\ {4I_{100} } & {2I_{100} } & {\varPhi_{3} - 6I_{100} } \\ \end{array} } \right),$$

where \(\varPhi_{1}\), \(\varPhi_{2}\) and \(\varPhi_{3}\) represent the intra-coupling matrices of the three scale-free characteristics clusters. And \(\beta_{11} = - 15\), \(\beta_{12} = 8\), \(\beta_{13} = 7\), \(\beta_{21} = 6\), \(\beta_{22} = - 15\), \(\beta_{23} = 9\), \(\beta_{31} = 4\), \(\beta_{32} = 2\), \(\beta_{33} = -\,6\). Hence, the cluster lag synchronous equations of network (24) can be characterized by

$$\dot{s}_{k} \left( t \right) = \tilde{f}_{k} \left( {t,s_{i} \left( t \right),s_{i} \left( {t - \tau_{k} \left( t \right)} \right)} \right) + c\sum\nolimits_{p = 1}^{3} {\beta_{kp} s_{p} \left( t \right)} ,\quad {\kern 1pt} k \in \Im .$$
(26)

Setting \(\varpi = 2\), then we can get that \(L_{1}^{0} { = 11} . 3 9 3 1\), \(L_{1}^{\tau } { = 0} . 4 8 8 3\), \(L_{2}^{0} { = 11} . 9 6 5 4\), \(L_{2}^{\tau } { = 0} . 5 1 3 3\), \(L_{3}^{0} { = 11} . 4 4 4 2\), \(L_{3}^{\tau } { = 0} . 4 6 3 3\), therefore \(q = 1.0266\). We have \(\text{CluInf} \left( 1 \right) = - 1.7405\), \(\text{CluInf} \left( 2 \right) = - 1.7023\), \(\text{CluInf} \left( 3 \right) = 5.7629\) and \(\lambda_{\hbox{max} } \left( Z \right) = 5.7629\) through computation. According to the descending order of values, the rearranging order of the cluster is \(C_{3}\),\(C_{2}\),\(C_{1}\). Choosing \(a_{1}^{0} = 25\), under conditions \(\left( {{\text{i}}^{\prime \prime } } \right)\) and \(\left( {{\text{ii}}^{\prime \prime } } \right)\), we have

$$\varUpsilon_{k} < - 1.6667,\quad l + 1 \le k \le 3,\quad {\text{and}}\quad 0.7802 < \theta < 1.$$
(27)

Due to \(\varUpsilon_{3} = 5.7629\), \(\varUpsilon_{2} = - 1.7023\), \(\varUpsilon_{1} = - 1.7405\), then the cluster lag synchronization of network (24) can be realized by controlling the first rearranged cluster, i.e., \(C_{3}\).

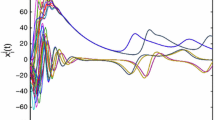
Considering Theorem 3, we use the adaptive intermittent pinning control schemes (16)–(17) to achieve the cluster lag synchronization of network (24). Setting \(\theta = 0.8\), conditions (15) and (27) are satisfied. Select a control period \(T = 0.1\) and \(h_{3} = 0.01\). Figures 4, 5, 6 and 7, respectively, show the time evolutions of the synchronous errors \(E_{ij}^{k} \left( t \right)\left( {k \in \Im } \right)\) and the adaptive intermittent feedback gain \(d_{3} \left( t \right)\). Define the lag synchronous errors as \(E^{k} \left( t \right)\), \(k \in \Im\), i.e., \(E_{j}^{1} \left( t \right) = \sqrt {\sum\nolimits_{i = 1}^{100} {{{\left\| {x_{ij} \left( t \right) - s_{1j} \left( {t - \sigma } \right)} \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {x_{ij} \left( t \right) - s_{1j} \left( {t - \sigma } \right)} \right\|^{2} } { 1 0 0}}} \right. \kern-0pt} { 1 0 0}}} }\), \(E_{j}^{2} \left( t \right) = \sqrt {\sum\nolimits_{i = 101}^{200} {{{\left\| {x_{ij} \left( t \right) - s_{2j} \left( {t - \sigma } \right)} \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {x_{ij} \left( t \right) - s_{2j} \left( {t - \sigma } \right)} \right\|^{2} } {100}}} \right. \kern-0pt} {100}}} }\), \(E_{j}^{3} \left( t \right) = \sqrt {\sum\nolimits_{i = 201}^{300} {{{\left\| {x_{ij} \left( t \right) - s_{3j} \left( {t - \sigma } \right)} \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {x_{ij} \left( t \right) - s_{3j} \left( {t - \sigma } \right)} \right\|^{2} } {100}}} \right. \kern-0pt} {100}}} }\), where \(j = 1,2,3\). Then, Figs. 8, 9 and 10 show the time evolutions of the lag synchronous errors \(E^{k} \left( t \right)\). We can see that the cluster lag synchronization is realized and the feedback gain \(d_{3} \left( t \right)\) converges to 0.3258 at last.

Fig. 4
figure 4

Time evolutions of the synchronous errors \(E_{ij}^{1} \left( t \right) = \left| {x_{ij} \left( t \right) - s_{1j} \left( {t - \sigma } \right)} \right|,\left( {i \in C_{1} ,j = 1,2,3} \right)\) for the first cluster of network (24) under the adaptive intermittent pinning control schemes (16)–(17), where \(\theta = 0. 8\), \(T = 0. 1\), \(\sigma = 0. 2\) and \(h_{3} = 0.01\)

Full size image
Fig. 5
figure 5

Time evolutions of the synchronous errors \(E_{ij}^{ 2} \left( t \right) = \left| {x_{ij} \left( t \right) - s_{ 2j} \left( {t - \sigma } \right)} \right|,\left( {i \in C_{ 2} ,j = 1,2,3} \right)\) for the second cluster of network (24) under the adaptive intermittent pinning control schemes (16)–(17), where \(\theta = 0. 8\), \(T = 0. 1\), \(\sigma = 0. 2\) and \(h_{3} = 0.01\)

Full size image
Fig. 6
figure 6

Time evolutions of the lag synchronous errors \(E_{ij}^{ 3} \left( t \right) = \left| {x_{ij} \left( t \right) - s_{ 3j} \left( {t - \sigma } \right)} \right|,\left( {i \in C_{ 3} ,j = 1,2,3} \right)\) for the third cluster of network (24) under the adaptive intermittent pinning control schemes (16)–(17), where \(\theta = 0. 8\), \(T = 0. 1\), \(\sigma = 0. 2\) and \(h_{3} = 0.01\)

Full size image
Fig. 7
figure 7

Time evolutions of the adaptive intermittent feedback gain \(d_{3} \left( t \right)\) for the network (24) under the adaptive intermittent pinning control schemes (16)–(17), where \(\theta = 0. 8\), \(T = 0. 1\), \(\sigma = 0. 2\) and \(h_{3} = 0.01\)

Full size image
Fig. 8
figure 8

Time evolutions of the lag synchronous error \(E_{j}^{1} \left( t \right) = \sqrt {{{\sum\nolimits_{i = 1}^{100} {\left\| {x_{ij} \left( t \right) - s_{1j} \left( {t - \sigma } \right)} \right\|^{2} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{100} {\left\| {x_{ij} \left( t \right) - s_{1j} \left( {t - \sigma } \right)} \right\|^{2} } } {100}}} \right. \kern-0pt} {100}}} ,\left( {j = 1,2,3} \right)\) for the network (24) under the adaptive intermittent pinning control schemes (16)–(17), where \(\theta = 0. 8\), \(T = 0. 1\), \(\sigma = 0. 2\) and \(h_{3} = 0.01\)

Full size image
Fig. 9
figure 9

Time evolutions of the lag synchronous error \(E_{j}^{ 2} \left( t \right) = \sqrt {{{\sum\nolimits_{i = 1 01}^{ 200} {\left\| {x_{ij} \left( t \right) - s_{ 2j} \left( {t - \sigma } \right)} \right\|^{2} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1 01}^{ 200} {\left\| {x_{ij} \left( t \right) - s_{ 2j} \left( {t - \sigma } \right)} \right\|^{2} } } {100}}} \right. \kern-0pt} {100}}} ,\left( {j = 1,2,3} \right)\) for the network (24) under the adaptive intermittent pinning control schemes (16)–(17), where \(\theta = 0. 8\), \(T = 0. 1\), \(\sigma = 0. 2\) and \(h_{3} = 0.01\)

Full size image
Fig. 10
figure 10

Time evolutions of the lag synchronous error \(E_{j}^{ 3} \left( t \right) = \sqrt {{{\sum\nolimits_{i = 2 01}^{ 300} {\left\| {x_{ij} \left( t \right) - s_{ 3j} \left( {t - \sigma } \right)} \right\|^{2} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 2 01}^{ 300} {\left\| {x_{ij} \left( t \right) - s_{ 3j} \left( {t - \sigma } \right)} \right\|^{2} } } {100}}} \right. \kern-0pt} {100}}} ,\left( {j = 1,2,3} \right)\) for the network (24) under the adaptive intermittent pinning control schemes (16)–(17), where \(\theta = 0. 8\), \(T = 0. 1\), \(\sigma = 0. 2\) and \(h_{3} = 0.01\)

Full size image

6 Conclusion

In this paper, we investigated the cluster lag synchronization of the intermittent pinning-controlled directed complex dynamical networks, which have the non-identical dynamical nodes with time-varying delays in the self-dynamics. Each cluster was regarded as a whole in the study of the cluster lag synchronization. The desired cluster lag synchronous states were chosen as a collection of the un-decoupled trajectories rather than the particular solutions of the systems with decoupled nodes. We generalized the intermittent control scheme from the cluster synchronization without the transmission delay to the cluster lag synchronization involving both the time-varying delays in the self-dynamics and the transmission delay in the communication channels. By making some mild assumptions, we proposed the main theorems and the criteria for the cluster lag synchronization. Two numerical simulations were given to verify the correctness of the theoretical results.

As a more general case, the cluster lag synchronization of general delayed dynamical networks under the pinning control technology is worth studying in the near future. Topic of the work time of controller being time-varying is also interesting.