Cluster synchronization of overlapping uncertain complex networks with time-varying impulse disturbances

Abstract

This paper addresses the scheme of cluster synchronization of overlapping uncertain complex networks with time-varying impulse disturbances. Many existing works on cluster synchronization focus on synchronizing and desynchronizing impulses separately, but the effects of two types of impulses are rarely observed. Here, we present the analysis of the two types (time-varying impulses) in complex networks. Furthermore, by means of stochastic stability theorem, sufficient conditions for guaranteeing the realization of cluster synchronization are derived. The network topology is assumed to be overlapping community, which includes an overlapping sub community with different dynamic behavior due to its identity (community). Finally, numerical examples are exploited to verify the correctness and effectiveness of theoretical results.

1 Introduction

Complex networks have aroused compelling attention among scientists as the facts that they are successfully introduced to describe and study many nature and artificial systems [1, 2]. It should be noted that mounting studies are given to investigate various issues existing in complex networks such as analysis of network dynamics, scale-free property and others [3, 4]. In particular, synchronization in complex networks has been a longstanding hot research topic due to its potential application ranging from mechanics, neural networks and secure communications [2–5]. In general, synchronization can be divided into different categories: complete synchronization, phase synchronization, lag synchronization, cluster synchronization and so on [4–7].

Cluster synchronization among these synchronization methods is considered to be of high relevance in engineering control, social and ecological science [7]. It requires that the coupled oscillators split into subgroups called clusters, which is achieved when the oscillator synchronizes with one other in the same cluster but desynchronizes among the different clusters [7–13]. Till now, many related results can be obtained on studying the cluster stability of complex network. Wang et al. [8] studied cluster synchronization in nonlinearly coupled delayed networks of nonidentical dynamic systems. Tang et al. [9] discussed cluster synchronization of non-delayed and delayed coupling complex networks with nonidentical nodes via adaptive control. In addition, Wu et al. [10] investigated cluster projective synchronization between community networks with nonidentical nodes. Su et al. [11] considered decentralized adaptive pinning control for cluster synchronization of complex dynamical networks. Ma et al. [12] studied cluster synchronization for directed complex dynamical networks with pinning control. Moreover, Zhang et al. [13] investigated exponential cluster synchronization of coupled impulsive genetic oscillators with external disturbances and communication delay.

Significant progress through their efforts has been made in cluster synchronization of complex networks. However, the models used in these works [7–13] always involve directed topology, general community and topology. They sometimes do not simulate more realistic and special situations which motivates current study. In addition, some important phenomena and problems in real world have not been concerned, which also stimulate us to further investigate cluster synchronization of complex networks.

In this present manuscript, we concentrate on the effects of uncertainties in complex networks. As we all know, parameter fluctuation, external disturbance and parameter uncertainty in many practical situations are unavoidable and may destroy the networks stability or can make synchronization more difficult due to measure errors. There exist ‘partially’ or ‘even’ fully uncertain parameters in ‘either’ or ‘both’ drive system ‘and’ or ‘or’ response system [14]. Thus, it is extremely important and significant to study the effects of uncertainties on cluster synchronization.

On the other hand, we extensively discuss the effects of time-varying impulses. The states of electronic network and biological network are often subjected to instantaneous disturbances and experience abrupt changes at certain instant, which may be caused by switching phenomenon, frequency change or other sudden noise, i.e., they exhibit impulsive effects [13–17]. Notably, it is indispensable to consider the effects of impulses on cluster synchronization. In most existing literatures, the synchronizing and desynchronizing impulses are considered separately. But, in practice, many electronic or biological networks are often subjected to instantaneous disturbances, and both synchronizing and desynchronizing impulses might exist simultaneously, which are widely overlooked in the existing results [16]. However, to our knowledge, cluster synchronization of complex dynamic networks via both synchronizing and desynchronizing impulses has not been reported.

Motivated by the above discussions, this paper aims at studying the problem of cluster synchronization of overlapping uncertain dynamical networks with time-varying impulses. Analytical results show the correctness of the proposed theorem, and numerical examples are given to illustrate the validity of the derived theoretical analysis. The most important highlights of this paper: (i) we study the complex networks with uncertainties instead of known or estimated parameters in the cluster synchronization. Meanwhile, the theoretical analysis of uncertain networks is based on stochastic stability analysis rather than classical Lyapunov stability theorem; (ii) the time-varying impulses but not a type of synchronizing and desynchronizing impulses are considered to achieve cluster synchronization; (iii) unlike the general and special topology in the existing works, the overlapping networks are applied to mimic more realistic and special situations.

The remaining part of this paper is outlined as follows. In Sect. 2, we give the description of an uncertain complex network. In addition, some conditions are employed to guarantee the uncertain complex network converging to a desired state. In Sect. 3, the main theory for cluster synchronization is presented. A network with an overlapping community is given to illustrate the effectiveness of proposed theorem in Sect. 4. At last, conclusions are drawn in Sect. 5.

2 Problem statement

Throughout this paper, let $(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_\mathrm{t} \}_{\mathrm{t}\ge 0} ,{\mathbb {P}})$ be a complete probability space with a filtration $\{{\mathcal {F}}_\mathrm{t}\}_{\mathrm{t}\ge 0}$ that is right continuous and ${\mathcal {F}}_0$ contains all ${\mathbb {P}}$-null sets. Let ${\mathbb {Z}}^{+}$ denote the set of positive integers, ${\mathbb {R}}^{n}$ denote the n-dimensional real Euclidean space, ${\mathbb {R}}_+$ denote the set of nonnegative real numbers and ${\mathbb {R}}^{n\times m}$ denote the $n \times m$ real matrix. Meanwhile, $\lambda (\cdot )$ denotes the eigenvalue of a matrix.

Let $\tau >0$ be a positive real number and $\hbox {PC}([-\tau ,0];{\mathbb {R}}^{n})$ denote the family of piecewise continuous functions from $[-\tau ,0]$ to ${\mathbb {R}}^{n}$, i.e., $\hbox {PC}([-\tau ,0];{\mathbb {R}}^{n})=\{\varphi :[-\tau ,0]\rightarrow {\mathbb {R}}^{n}|\varphi (t^{+})=\varphi (t)$ for all $t\in [-\tau ,0),\varphi (t^{-})$ exists and $\varphi (t^{-})=\varphi (t)$ for all but at most a finite number of points $t\in [-\tau , 0)\}$ is with the norm $\left\| \varphi \right\| =\sup _{-\tau \le \theta \le 0} \left| {\varphi (\theta )} \right| ,$ where $\varphi (t^{+})$ and $\varphi (t^{-})$ denote the right-hand and left-hand limits of function $\varphi (t)$ at $t$, respectively.

For $p>0$ and $t\ge 0$, let $\hbox {PC}_{{\mathcal {F}}_t}^p ([-\tau ,0];{\mathbb {R}}^{n})$ denote the family of all ${\mathcal {F}}_{\mathrm{t}}$—measurable $\hbox {PC}([-\tau ,0];{\mathbb {R}}^{n})$—valued random variables $\varphi$ such that $\sup _{-\tau \le \theta \le 0}{\mathbb {E}}\left| {\varphi (\theta )}\right| ^{p}\!<\!\infty$, where ${\mathbb {E}}$ stands for the mathematical expectation operator with respect to the given probability measure ${\mathbb {P}}$. And $\hbox {PC}_{{\mathcal {F}}_{t_0 }}^p ([-\tau ,0];{\mathbb {R}}^{n})$ denotes the family of all ${\mathcal {F}}_{\mathrm{t}_0}$ measurable bounded $\hbox {PC}([-\tau ,0];{\mathbb {R}}^{n})$—valued functions.

In this section, we consider an uncertain complex network consisting of $n$ linearly and diffusively coupled identical nodes:

$$\begin{aligned} \dot{x}_i(t)=F_i (t,x_i (t),\alpha _i)+\sum _{j=1}^n {c_{ij} Tx_j (t),\quad i\in \mathop {U}\limits ^{\frown }},\nonumber \\ \end{aligned}$$

(1)

where $x_i (t)=(x_{i1} (t),x_{i2} (t),\ldots ,x_{in} (t))^{\mathrm{T}}\in {\mathbb {R}}^{n}$ is the state vector of the $i$th node, and $\mathop {U}\limits ^{\frown } =\left\{ {k_{l-1}+1,\ldots ,k_l}\right\}$ denotes the index set of all the nodes in the $k$th cluster, $k=1,2,\ldots ,m,k_m =n,k_{l-1}<k_l$. The matrix $C=(c_{ij})_{n\times n}$ is the zero-row-sum outer-coupling matrix, which denotes the networks topology. If there is a connection from node $i$ to node $j(i\ne j)$, then $\hbox {c}_{ij} \ne 0$, otherwise, $\hbox {c}_{ij} =0$. $T$ is the inner connecting matrix. $F_i (t,x_i(t),\alpha _i)$ indicates the node dynamic behavior, where $\alpha _i$ is the uncertain parameter, and defined as $f_i (t,x_i (t))+\sigma _i (t,x_1(t),x_2 (t),\ldots ,x_n (t))\xi _i (t)$ so as to show the effects of noises or disturbances. In addition, $f_i (\cdot ):\hbox {PC}_{{\mathcal {F}}_t }^2 ([-\tau ,0];{\mathbb {R}}^{n}) \times {\mathbb {R}}\rightarrow {\mathbb {R}}^{n}$ and $\sigma _i(\cdot ):\hbox {PC}_{{\mathcal {F}}_t }^2 ([-\tau ,0];{\mathbb {R}}^{n})\times {\mathbb {R}}\rightarrow {\mathbb {R}}^{n}$ are Borel measurable and continuous for almost all $t\in [t_0,\infty )$, and $\xi _i(t)$ indicates a standard white noise in the dynamic behavior. As we all know, the time derivative of a Wiener process (or Brownian motion) is a white noise process in the stochastic theory [18, 19]. Then, the network (1) can be re-expressed as following:

$$\begin{aligned} \hbox {d}x_i (t)&= \left( f_i (t,x_i(t))+\sum _{j=1}^n {c_{ij}} Tx_j (t)\right) \hbox {d}t\\&\quad +\,\sigma _i \left( t,x_1(t),x_2(t), \ldots ,x_n (t) \right) \hbox {d}\omega _i, \quad i \in \mathop {U}\limits ^{\frown },\nonumber \end{aligned}$$

(2)

where $\omega _i=(\omega _{i1} ,\omega _{i2},\ldots ,\omega _{in} )\in {\mathbb {R}}^{n}$ is a bounded vector form Weiner process defined on a complete probability space $(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_\mathrm{t}\}_{\mathrm{t}\ge 0} ,{\mathbb {P}})$,which satisfies ${\mathbb {E}}[\hbox {d}\omega _i (t)]=0$ and ${\mathbb {E}}\{[\hbox {d} \omega _i(t)]^{2}\}=\hbox {d}t$.

Now we introduce the impulse expression in order to study the effects of disturbances. There are “sudden changes” (or “jumps”) at time instants $t_k$ in the state variables such that

$$\begin{aligned} \Delta x_i\left| {_{t=t_k}}\right.&= x_i (t_k^+ )-x_i (t_k^- )=B_i x_i(t_k^-), \quad k \in {\mathbb {Z}}^{+}, \nonumber \\&\quad i=1,2,\ldots ,n, \end{aligned}$$

(3)

where $x(t_k^+)=\lim \nolimits _{t\rightarrow t_k^+}x(t), x(t_k^-)= \lim \nolimits _{t\rightarrow t_k^-}x(t_k)$ and the impulse instant sequence $\left\{ t_k\right\}$ satisfies $0<t_1 <t_2 < \cdots <t_k < \cdots ,\lim \nolimits _{t \rightarrow \infty }t_k =\infty$ and $t_k -t_{k-1} <\infty$. Let $B_i=\hbox {diag}(b_1 ,b_2,\ldots , b_{n_i})$ be the impulse feedback matrix of node $i$ received at moment $t_k$. For the sake of analytical simplification, we assume $B_i =b_i I_{n_i \times n_i},b_i =\max \{b_k\},k=1,\ldots ,n_i$. Hence, the following stochastic dynamical network with impulse disturbances is obtained:

$$\begin{aligned} \left\{ {\begin{array}{l} \hbox {d}x_i(t)=(f_i (t,x_i (t))+\sum _{j=1}^n {c_{ij} Tx_j (t))\hbox {d}t+\sigma _i (t,x_1 (t),x_2 (t),\ldots ,x_n (t))\hbox {d}\omega _i ,}\\ \;t\ne t_k ,\;\;t\ge t_0 ,\;\;t\in \mathop {U}\limits ^{\frown } \\ \Delta x_i =x_i(t_k^+ )-x_i (t_k^- )=b_i (x_i (t_k^- )),t=t_k ,k \in {\mathbb {Z}}^{+},i=1,2,\ldots ,l, \\ \end{array}}\right. \end{aligned}$$

(4)

with initial value $x(t_0 )=\xi =\{\xi (\theta )|-\tau \le \theta \le 0\}\in \hbox {PC}_{{\mathcal {F}}_{t_0 } }^2 ([-\tau ,0];{\mathbb {R}}^{n})$.

Throughout this paper, the following basic and useful definitions, assumptions and lemmas are required for achieving cluster synchronization.

Definition 1

[20]. A stochastic network with $n$ nodes is said to realize cluster synchronization if the $n$ nodes are divided into $k$ clusters $U_1 ,U_2,\ldots ,U_k ,$ where $\{U_1 =(1,2,\ldots ,k_1 ),U_2 =(k_1 +1,\ldots ,k_2),\ldots ,U_m =(k_{m-1} +1,\ldots ,k_m )(k_m =n)\}$, such that the nodes in the same cluster synchronize with one another, i.e., for the states $x_i ,x_j$ of the arbitrary nodes $i$ and $j$ in the same cluster, $\lim \nolimits _{t\rightarrow \infty } {\mathbb {E}}\left\| {x_i(t)-x_j(t)}\right\| ^{2}=0$ holds.

Definition 2

Consider an $n$-dimensional stochastic differential equation:

$$\begin{aligned} \hbox {d}x_i(t)=f(t,x_i(t))\hbox {d}t+\sigma _i (t,x_1 (t),x_2 (t),\ldots ,x_n (t))\hbox {d}\omega ,\nonumber \\ \end{aligned}$$

(5)

Let $C^{2,1}({\mathbb {R}}^{n}\times [t_0 -\uptau ,\infty );{\mathbb {R}}_+)$ denotes the family of all nonnegative functions $V(t,x)$ on ${\mathbb {R}}^{n}\times [t_0 -\uptau ,\infty )$, which is twice continuously differentiable in $x$ and once differentiable in $t$. For each $V\in C^{2,1}({\mathbb {R}}^{n}\times [t_0-\uptau ,\infty );{\mathbb {R}}_+)$, the stochastic derivative of $V$ along trajectories of (5) can be expressed as follows:

$$\begin{aligned} \hbox {d}V(t,x)&= {\mathcal {L}} V(t,x(t))\hbox {d}t+V_x (t,x(t))\nonumber \\&\quad \times \, \sigma _i(t,x_1 (t),x_2 (t),\ldots ,x_n (t))\hbox {d}\omega , \end{aligned}$$

(6)

where ${\mathcal {L}}V:\hbox {PC}([-\tau ,0];{\mathbb {R}}^{n})\times [t_0 ,\infty )\rightarrow {\mathbb {R}}$ is an operator, defined by

$$\begin{aligned} {\mathcal {L}}V(t,x)&= V_t (t,x)\hbox {d}t+V_x (t,x)f(t,x)\nonumber \\&\quad +\,\frac{1}{2}tr\left[ \sigma (t,x)^{\mathrm{T}}V_{xx} (t,x)\sigma (t,x)\right] ,\nonumber \\ V_t (t,x)&= \partial V(t,x)/\partial t,V_x (t,x)\nonumber \\&= \left( \partial V(t,x)/ \partial x_1 ,\ldots ,\partial V(t,x)/\partial x_n \right) ,\nonumber \\ V_{xx}(t,x)&= \left( \partial ^{2}V(t,x)/\partial x_i \partial x_j \right) _{n\times n}. \end{aligned}$$

(7)

Definition 3

[21]. The trivial solution of system (4) is said to be exponentially synchronized in mean square if for every $\phi \in \hbox {PC}_{{\mathcal {F}}_t }^2 ([-\tau ,0];{\mathbb {R}}^{n})$, there exist $K>0$ and $\lambda >0$ such that the following inequality holds:

$$\begin{aligned} {\mathbb {E}}\left| {x(t;\phi )} \right| ^{2}\le Ke^{-\lambda (t-t_0 )}, t>t_0. \end{aligned}$$

Assumption 1

The vector function $f(\cdot )$ satisfies Lipschitz condition with respect to $t$, i.e., for any $x(t),\;y(t)\in \hbox {PC}_{{\mathcal {F}}_t }^2 ([-\tau ,0];{\mathbb {R}}^{n})$, there exist positive constants $l_i >0(i=1,2,\ldots , n)$ such that

$$\begin{aligned} \left\| {f(x(t))-f(y(t))}\right\| \le L\left\| {x(t)-y(t)} \right\| , \end{aligned}$$

(8)

where $L =\hbox {diag}(l_1,l_2 ,\ldots ,l_n)$.

Assumption 2

There exists a constant matrix $M$ such that

$$\begin{aligned}&\hbox {tr}\left\{ \sigma _i^\mathrm{T} (t,e_1 (t),e_2 (t),\ldots ,e_n (t))\sigma _i (t,e_1 (t),\right. \\&\quad \left. \times \, e_2 (t),\ldots ,e_n (t))\right\} \le \sum _{j=1}^n {\left\| {Me_j (t)}\right\| ^{2}} , \end{aligned}$$

where $\sigma _i(t,e_1 (t),e_2 (t),\ldots ,e_n (t))=\sigma _i (t,x_1(t),x_2 (t),\ldots ,x_n (t))-\sigma _i (t,s_1 (t),s_2 (t),\ldots ,s_n (t))$.

Assumption 3

[22]. The coupling matrix $C=(c_{ij} )_{n\times n}$ of network (2) satisfies

$$\begin{aligned} C=\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {C_{11} }&{} {C_{12} } &{} \cdots &{} {C_{1m} } \\ {C_{21} }&{} {C_{22} } &{} \cdots &{} {C_{2m} } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {C_{m1} }&{} {C_{m2}} &{} \cdots &{} {C_{mm} } \\ \end{array} }} \right] , \end{aligned}$$

where $(C_{kk})_{(l_k -l_{k-1} )\times (l_k -l_{k-1} )}$ belongs to $C_1$, and $(C_{kq} )_{(l_k -l_{k-1} )\times (l_q -l_{q-1})}$ belongs to $C_2$, $k$ and $q=1,2,\ldots ,m$.

Lemma 1

[23]. For any two $n$-dimensional real vectors $X,Y$ and a positive definite matrix $U\in R^{n\times n}$, the matrix inequality $2X^{\mathrm{T}}Y\le X^{\mathrm{T}}UX+Y^{\mathrm{T}}U^{-1}Y$ holds.

Define the error vector as $e_i (t)=x_i(t)-s_{\vartheta _i}(t)$. The key point in this letter mainly focuses on that the uncertain complex network (4) with impulse disturbances synchronize with $s_{\vartheta _i}(t)$ in an overlapping network. That is

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } \left\| {x_i (t)-s_{\vartheta _i}(t)}\right\| =0, \quad i\in \mathop {U}\limits ^{\frown } , \end{aligned}$$

(9)

where $s_{\vartheta _i } (t)\in R^{n}$ is a dynamic solution of the isolated node $\dot{s}_{\vartheta _i}(t)=F_i (t,s_{\vartheta _i } (t),\alpha _i )$ $(i=1,2,\ldots ,n)$, or even an equilibrium point, a limit cycle, a chaotic attractor, which describes the identical local dynamics of the nodes in the $\vartheta _i$th cluster (community).

Remark 1

It is worth being pointed out that the synchronizing (or beneficial) and desynchronizing (or non-beneficial) impulses for cluster synchronization are discussed in this paper. It is different from the former research almost considering the synchronizing or desynchronizing impulses, separately. In other words, when $\left| {\lambda _i(1+b_i)}\right| <1$, the impulses are beneficial for the cluster synchronization. That is $-2<\lambda _i (b_i )<0$, the impulses help cluster synchronization. Conversely, $\left| {\lambda _i (1+b_i)}\right| >1$ or $\lambda _i (b_i )<-2,\lambda _i (b_i )>0$, the impulses destroy the synchronization so that the absolute values of the synchronization errors are enlarged. When $\left| {\lambda _i (1+b_i )} \right| =1$, the impulses do not generate neither beneficial nor harmful actions to cluster synchronization. So, this type of impulses is often not considered for its little impact on cluster synchronization.

3 Main result

In this section, we present our main results about how to employ both synchronizing and desynchronizing impulses to realize globally exponential cluster synchronization in mean square. For simplicity and clarity in the process of proof, some notations are required, and given as follows.

Throughout this paper at interval $[t_0 ,t)$, let $b_i^\mathrm{sy}$ and $b_i^\mathrm{desy}$ denote synchronizing and desynchronizing impulse strengths, respectively. And they take values from the finite matrix sets $\left\{ {b_1^\mathrm{sy} ,b_2^\mathrm{sy}, \mathrm{L}, b_M^\mathrm{sy}} \right\}$ and $\left\{ {b_1^\mathrm{desy} ,b_2^\mathrm{desy} ,\mathrm{L}, b_N^\mathrm{desy} } \right\}$ respectively, where $-2<\lambda (b_i^\mathrm{sy} )\!<\!0$, $\lambda (b_j^\mathrm{desy} )\!<\!-2,$ or $\lambda (b_j^\mathrm{desy} )\!>\!0$ for $i=1,2,\ldots ,M$, $j=1,2,\ldots ,N$. Assume that there exist $o_i >0$ impulse times, $\psi _i$ synchronizing impulse times and $\psi _j$ desynchronizing impulse times. Meanwhile, assume that $t_{i_\varsigma }^\mathrm{sy}$ and $t_{j_\sigma }^\mathrm{desy} (\varsigma ,\sigma =1,2,\ldots )$ signify the activation time of synchronizing impulses and that of desynchronizing impulses, respectively, and assume that $b_0^\mathrm{sy} =\mathop {\lambda _{\max } }\nolimits _{1\le i\le M} (b_i^\mathrm{sy})$, $b_0^\mathrm{desy} =\mathop {\lambda _{\max } }\nolimits _{1\le j\le N} (b_j^\mathrm{desy} )$, $T_{\max }^\mathrm{sy} =\sup \{t_{i_\varsigma }^\mathrm{sy} -t_{i_\varsigma -1}^\mathrm{sy} \}<\infty$, $T_{\min }^\mathrm{desy}= \quad \inf \{t_{j_\sigma }^\mathrm{desy} -t_{j_\sigma -1}^\mathrm{desy} \}>0$. Then, we derive that $(\psi _i +1)T_{\max }^\mathrm{sy} \ge t-s$ and $(\psi _j-1)T_{\min }^\mathrm{desy} \le t-s$.

Theorem 1

Suppose that Assumptions 1–3 hold. The uncertain complex network (4) will achieve globally exponentially cluster synchronization in mean square if there are constant matrices $M,L$ and positive definition matrix $P=\hbox {diag}(p_1 ,p_2 ,\ldots ,p_n)$ such that

$$\begin{aligned} \eta =\lambda +2 \left( \frac{\ln (1+b_0^\mathrm{sy} )}{T_{\max }^\mathrm{sy} }\right) +2\left( \frac{\ln (1+b_0^\mathrm{desy} )}{T_{\min }^\mathrm{desy} }\right) <0, \end{aligned}$$

where $\lambda =\lambda _{\max } \{(PP^{\mathrm{T}}+LL^{\mathrm{T}}+2MM^{\mathrm{T}})\otimes I+2C \otimes (TP)\}>0$.

Proof

Consider the Lyapunov–Krasovskii function:

$$\begin{aligned} V(t)=\frac{1}{2}e^{T}(t)Pe(t)=\frac{1}{2}\sum _{i=1}^n{e_i^\mathrm{T}(t) Pe_i (t)}, \end{aligned}$$

where $P=\hbox {diag}(p_1 ,p_2 ,\ldots ,p_n )$ is a positive definition matrix. $\square$

Based on Assumption 3,we can get $\sum \nolimits _{j\in \mathop {U}\limits ^{\frown }} a_{ij}y_\kappa (t)\!=\! 0$ for $i=1,2,\ldots ,n$ and $\kappa =1,2,\ldots ,m$.

$$\begin{aligned} \hbox {Thus} \sum \limits _{j=1}^n {a_{ij} x_j(t)}&= \sum \limits _{\kappa =1}^m {\sum \limits _{j\in \mathop {U}\limits ^{\frown }} {a_{ij} x_j(t)} } -\sum \limits _{\kappa =1}^m {\sum \limits _{\kappa \in \mathop {U}\limits ^{\frown }} {a_{ij} y_\kappa (t)}}\\&= \sum \limits _{\kappa =1}^m {\sum \limits _{j\in \mathop {U}\limits ^{\frown }} {a_{ij}e_j (t)}}=\sum \limits _{j=1}^n {a_{ij} e_j (t)}. \end{aligned}$$

When $t\in [t_{k-1} ,t_k)$, taking the time derivative of $V(t)$ along the error trajectories, we have

$$\begin{aligned} \hbox {d}V(t)={\mathcal {L}}V(t)\hbox {d}t+\sum _{i=1}^n {e_i (t)} P\sigma _i (t,e_1 (t),e_2 (t), \ldots , e_n (t))\hbox {d}\omega , \end{aligned}$$

where

$$\begin{aligned} {\mathcal {L}}V(t)&= \sum _{i\in \mathop {U}\limits ^{\frown }} e_i^\mathrm{T} P\left[ f_i (t,x_i (t))-f_i (t,s_i (t))\right. \\&\quad \left. +\sum _{j=1}^N {c_{ij} Te_j (t)}\right] +tr\left[ \sigma _i (t,e_1 (t),e_2 (t)\right. \\&\quad \left. \!\times \! \ldots , e_n (t))^{\mathrm{T}}\sigma _i (t,e_1 (t),e_2 (t), \ldots , e_n (t))\right] . \end{aligned}$$

Then, it is easy to get

$$\begin{aligned}&{\mathbb {E}}[{\mathcal {L}}V(t)]={\mathbb {E}}\left\{ \sum _{i\in \mathop {U}\limits ^{\frown }} e_i^\mathrm{T} P\left[ f_i(t,x_i (t))-f_i (t,s_i (t))\right] \right. \\&\quad +\sum _{i=1}^n{e_i^\mathrm{T} P\sum _{j=1}^n {c_{ij} Te_j (t)} }+tr\left[ \sigma _i(t,e_1 (t),e_2 (t),\right. \\&\quad \left. \left. \times \ldots ,e_n (t))^{\mathrm{T}}\sigma _i (t,e_1 (t),e_2 (t),\ldots ,e_n (t))\right] \right\} . \end{aligned}$$

Based on the Assumptions 1–2, the following inequalities can be derived.

$$\begin{aligned}&\sum _{i\in \mathop {U}\limits ^{\frown }}{e_i^\mathrm{T} P\left[ f_i (t,x_i (t))-f_i (t,s_i (t))\right] }\\&\quad \le \frac{1}{2}\sum _{i\in \mathop {U}\limits ^{\frown }}{e_i^\mathrm{T} (PP^{\mathrm{T}}+LL^{\mathrm{T}})e_i} \end{aligned}$$

and

$$\begin{aligned}&tr\left[ \sigma _i (t,e_1 (t),e_2 (t),\ldots ,e_n (t))^{\mathrm{T}}\sigma _i (t,e_1(t),e_2 (t) \right. \\&\quad \left. \times \ldots , e_n (t))\right] \le \sum _{j=1}^n {e_i^\mathrm{T} MM^{\mathrm{T}}e_i}. \end{aligned}$$

Hence,

$$\begin{aligned}&{\mathcal {L}} V(t)\le \frac{1}{2}e^{\mathrm{T}}\left[ \left( PP^{\mathrm{T}}+LL^{\mathrm{T}}+2MM^{\mathrm{T}} \right) \otimes I\right. \\&\quad \left. +\, 2C\otimes (TP)\right] e\le \lambda V(t). \end{aligned}$$

Using Definition 2, we have

$$\begin{aligned}&V(t)-V(t_0 )=\int _{t_0 }^t {{\mathcal {L}}V(s)\hbox {d}t}+\int _{t_0 }^t \sum _{i=1}^n {e_i^\mathrm{T} (s)P}\nonumber \\&\quad \times \sigma _i (t,e_1 (s),e_2 (s), \ldots ,e_n (s))\hbox {d}\omega (s). \end{aligned}$$

(10)

Taking the expectation of both sides of the Eq. (10), we have

$$\begin{aligned} {\mathbb {E}}V(t)-{\mathbb {E}}V(t_0)= {\mathbb {E}}\int _{t_0 }^t {{\mathcal {L}}V(s)\hbox {d}s}\le \lambda \int _{t_0}^t {{\mathbb {E}}V(s)\hbox {d}s}. \end{aligned}$$

In light of Gronwall inequality, we get

$$\begin{aligned} {\mathbb {E}}V(t)\le {\mathbb {E}}V(t_0)\exp (\lambda (t-t_0)). \end{aligned}$$

(11)

On the other hand, when $t=t_k$, it can be obtained from the construction of $V(t)$

$$\begin{aligned} V(t_k )=(1+b_k )^{2}V(t_k^-). \end{aligned}$$

(12)

According to Eqs. (11)–(12), we obtain the following equivalent inequality for $t\in [t_{k-1} ,t_k)$:

Since ${\mathbb {E}}V(t)\le {\mathbb {E}}V(t_0 )e^{\lambda (t-t_0 )}$ for $t\in [t_0 ,t_1 )$, one has ${\mathbb {E}}V(t_1^- )\le {\mathbb {E}}V(t_0 )e^{\lambda (t-t_0)}$. Then, we can obtain ${\mathbb {E}}V(t_1 )=(1+b_1 )^{2}{\mathbb {E}}V(t_1^- )\le (1+b_1 )^{2}{\mathbb {E}}V(t_0 )e^{\lambda (t_1 -t_0 )}$. Similarly, for $t\in [t_1 ,t_2 ),$ we have ${\mathbb {E}}V(t)\le {\mathbb {E}}V(t_1 )e^{\lambda (t-t_1 )}$, which implies ${\mathbb {E}}V(t_2^-)\le {\mathbb {E}}V(t_1)e^{\lambda (t-t_1 )}$. So ${\mathbb {E}}V(t_2 )=(1+b_2 )^{2}{\mathbb {E}}V(t_2^- )\le [\prod \limits _{i=1}^2 {(1+b_i )^{2}]} V(t_0 )e^{\lambda (t_2 -t_0 )}$. In general, for $t\in [t_{k-1} ,t_k )$, we obtain

$$\begin{aligned} {\mathbb {E}}V(t_k )&= (1+b_k )^{2}{\mathbb {E}}V(t_k^- )\nonumber \\&\le \left[ \prod _{i=1}^k (1+b_i )^{2}\right] {\mathbb {E}}V(t_0 )e^{\lambda (t-t_0 )}. \end{aligned}$$

(13)

Consequently, for each $t\in (t_0 ,t],$ it follows from Eq. (13) that

$$\begin{aligned} {\mathbb {E}}V(t) \le \;\mathop \prod \limits _{i=1}^{o_i } \left( 1+b_i \right) ^{2}{\mathbb {E}}V(t_0)e^{\lambda (t-t_0)}. \end{aligned}$$

From the supposing parameters, we can obtain

$$\begin{aligned}&{\mathbb {E}}V(t)\le \left( \prod _{i=1}^{\psi _i } {(1+b_i )^{2}} \prod _{j=1}^{\psi _j } {(1+b_j )^{2}} \right) {\mathbb {E}}V(t_0 )e^{\lambda (t-t_0 )}\\&\quad \!\le \! \left| {(1\!+\!b_0^\mathrm{sy} )} \right| ^{2(\frac{t-t_0 }{T_{\max }^\mathrm{sy} }-1)}\left| {(1\!+\!b_0^\mathrm{desy} )} \right| ^{2(\frac{t-t_0 }{T_{\min }^\mathrm{desy} }\!+\!1)}{\mathbb {E}}V(t_0 )e^{\lambda (t-t_0 )}. \end{aligned}$$

Furthermore, detailed calculations show

$$\begin{aligned} {\mathbb {E}}V(t)&\le \left| {\left( 1+b_0^\mathrm{sy} \right) } \right| ^{-2}\left| {\left( 1+b_0^\mathrm{desy} \right) } \right| ^{2}{\mathbb {E}}V(t_0 )\\&\quad \times \exp \left( \left( \lambda +2\left( \frac{\ln \left( 1+b_0^\mathrm{sy} \right) }{T_{\max }^\mathrm{sy} }\right) \right. \right. \\&\quad \left. \left. +\, 2\left( \frac{\ln \left( 1+b_0^\mathrm{desy} \right) }{T_{\min }^\mathrm{desy} }\right) \right) (t-t_0 )\right) . \end{aligned}$$

There exists a constant $\eta <0$ under the conditions in Theorem 1 such that

$$\begin{aligned}&{\mathbb {E}} V(t) \le \left| {\left( 1+b_0^\mathrm{sy} \right) } \right| ^{-2}\left| {\left( 1+b_0^\mathrm{desy} \right) } \right| ^{2}{\mathbb {E}}V(t_0 )\exp \left\{ \eta \left( t-t_0 \right) \right\} .\\&\hbox {Therefore},\;\sum \nolimits _{i=1}^n {\mathbb {E}}\left\| {e_i (t)} \right\| ^{2}\le \left| {(1+b_0^\mathrm{sy} )} \right| ^{-2}\left| {(1+b_0^\mathrm{desy})}\right| ^{2}\\&\quad ({\mathbb {E}}V(t_0 )/p^{*})\exp \{\eta (t-t_0)\}, \end{aligned}$$

where $p^{*}=\min \{p_1 ,p_2 ,\ldots ,p_n\}>0$. Notably, the trivial solution of system (4) is exponentially stable in mean square. In other words, the cluster synchronization of uncertain complex networks with time-varying impulses is achieved. The proof is complete.

4 Numerical simulation

To demonstrate the validity of the proposed theory, two effective examples will be given. And they can be applied to many networks with different topologies, such as neural networks, colored networks, etc. In this section, Let $b_0^\mathrm{sy} =b_i^\mathrm{sy}$, $b_0^{\mathrm{desy}} =b_j^\mathrm{desy}$, $i=1,2,\ldots ,M$, $j=1,2,\ldots ,N$. Meanwhile, synchronizing and desynchronizing impulses have the same time interval, and the impulse strength $d_k^{*}(k\in {\mathbb {Z}}^{+})$ meets the following condition:

$$\begin{aligned} d_k^{*} =\left\{ {\begin{array}{ll} b_0^\mathrm{sy} ,&{}\quad \hbox {if}\; \hbox {mod} (k,2)=0, \\ b_0^\mathrm{desy} ,&{}\quad \hbox {if}\; \hbox {mod} (k,2)\ne 0. \\ \end{array}} \right. \end{aligned}$$

Example 1

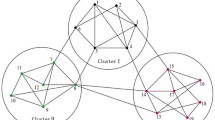
We analyze a complex network with 22 nodes shown in Fig. 1. In particular, different community having different dynamical behavior is considered. The unified chaotic system [24] with stochastic disturbances is described as follows:

$$\begin{aligned} \hbox {d}x(t)=f(t,x(t))\hbox {d}t +\sigma (t,x(t))\hbox {d}\omega , \end{aligned}$$

where $x(t)=(x_1(t),x_2 (t),x_3 (t))^{\mathrm{T}}\in \mathrm{R}^{3}$ is the state vector, $\sigma (t,x(t))=\sqrt{5}x_i \sin t$, $f(\cdot )$ $=\left[ \begin{array}{l} \hbox {25}\kappa +10(x_2 -x_1 )\\ -x_1 x_3 +(29\kappa -1)x_2 +(\hbox {28-35}\kappa )x_1 \\ x_1 x_2 +-(8+\kappa )/3)^\mathrm{T}x_3 \\ \end{array} \right] , \kappa$ is a system parameter.

In numerical simulation, the initial values of drive-response system are chosen as $x_i (0)=(0.3+0.1i,0.3+0.1i,0.3+0.1i)^{\mathrm{T}}$, $s_i (0)=(2.0+0.7i, 2.0+0.7i, 2.0+0.7i)^{\mathrm{T}}$.

For brevity, we always assume $T=\hbox {diag}(1,1,1)$, and the desynchronizing impulse strength is $b_0^\mathrm{desy} =0.2$. The impulse time interval is 0.01s. From Theorem 1, we obtain $-2<b_0^\mathrm{sy} <\frac{e^{(-\eta T)}}{1+b_0^\mathrm{desy}}-1=-0.28$, and then $b_0^\mathrm{sy} =-0.5$ is selected in this simulation.

Fig. 1

The topology of overlapping community networks with three communities

Remark 2

In foregoing works [7–13], cluster synchronization always involves directed topology, general community and general topology. Different from the previous models used in cluster synchronization, there is a cross region between community I and II in Fig. 1, marked by the red dotted line. The dynamic behavior of overlapping sub community is variable due to its identity. In other words, the individual behavior in cross region is easily subjected to the impacts from neighboring community. More precisely, the individual in cross region generates different behaviors when they communicate with different community, or the individual in cross region has dual or multiple identities which shows different behaviors in communication. For instance, in biological networks, proteins are the results of gene expression which is regulated by gene regulatory networks. Proteins interact with one another to form protein interaction networks. Also, special proteins known as enzymes help transforming metabolites to another, hence, they are also part of the metabolic networks. That is, These networks share common elements [25]. The communication messages between these networks, and common elements are often different, which are referred to as different dynamic behaviors in this paper.

Figure 2 gives a description of the dynamic behavior of certain system when $\kappa =0.5$. However, when certain system is affected by noises or disturbances, we can get that the trajectory of certain system is not stable (see Fig. 3). Figures 4, 5 and 6 show the time evolution of synchronization errors in Communities I–III, respectively. Figure 7 describes the time-varying impulsive sequence. Then, the numerical simulations conclusively demonstrate the correctness of Theorem 1, which means that even the desynchronizing and synchronizing impulses occur simultaneously, it is possible to guarantee the uncertain dynamical networks (1) to the desired heterogeneous stationary states in the same cluster. Namely appropriate synchronizing impulses can prevent the effects of desynchronizing impulse.

Fig. 2

The dynamic behavior of certain system when $\kappa =0.5$

Fig. 3

The dynamic behavior of uncertain system when $\kappa =0.5$

Fig. 4

The time evolution of $e _{i}=x _{i}(t)-s(t),\, i=1,2,\ldots ,8$ in Community I with $\kappa =0.1$

Fig. 5

The time evolution of $e_{i}=x _{i}(t)-s(t),\, i=6,7,\ldots ,14$ in Community II with $\kappa =0.5$

Fig. 6

The time evolution of $e_{i}=x _{i}(t)-s(t),\, i=15,16,\ldots ,22$ in Community III with $\kappa =0.8$

Fig. 7

Time-varying impulsive sequence

Example 2

In this example, we consider Chua system with stochastic disturbances:

$$\begin{aligned} \hbox {d}x(t)=(Ax(t)+h_1 (x(t)))\hbox {d}t+\sigma (t,x(t))\hbox {d}\omega , \end{aligned}$$

where $x(t)=(x_1 ,x_2 ,x_3 )^{{\mathrm{T}}}$, $h_1 (x(t))=(-1/2\alpha (m_1 -m_2 ))(\left| {x_1 (t)\!+\!1} \right| -\left| {x_1 (t)-1} \right| ),0,$ $-\beta \rho _0 \sin (\nu x_1 (t)))^{\mathrm{T}} A=\left( {{\begin{array}{l@{\quad }l@{\quad }l} {\alpha (1+m_2 )}&{} \alpha &{} 0 \\ 1&{} {-1}&{} 1 \\ 0&{} {-\beta }&{} {-\omega } \\ \end{array}}}\right)$, and $\alpha =10, \beta =19.53, \omega =0.1636,$ $m_1 =-14.325,m_2 =-0.7831,\upsilon =0.5,\rho _0 =0.2, \sigma (t,x(t))=x_i .$ In order to mimic bigger networks, the number of nodes we choose is 200. They are also suitable to the Example 1. And the region of overlapping community is from the node 61 to 100. The impulse time interval is 0.1 s. By $-2<b_0^\mathrm{sy} <\frac{e^{(-\eta T)}}{1+b_0^\mathrm{desy}}-1=-0.79,$ we shall select impulse strength $b_0^\mathrm{sy}=-0.8$.

Figures 8 and 9 give a description of the state trajectory of certain system and uncertain system variables. We can easily obtain the effects of uncertainty from figures. Figures 10, 11 and 12 show the time evolution of synchronization errors in Communities I–III, respectively. Therefore, from these results, we can conclude that the uncertain dynamical networks (1) successfully achieve cluster synchronization.

Fig. 8

The $x_{1}(t)$ state trajectory of the certain system and uncertain system

Fig. 9

The $x _{2}(t)$ state trajectory of the certain system and uncertain system

Fig. 10

The time evolution of $e _{i}=x_{i}(t)-s(t),\, i=1,2,\ldots ,100$ in Community I

Fig. 11

The time evolution of $e _{i}=x _{i}(t)-s(t),\, i=61,62,\ldots ,140$ in Community II

Fig. 12

The time evolution of $e _{i}\!\!=\!\!x _{i}(t)-s(t),\, i\!\!=\!\!141,142,\ldots ,200$ in Community III

5 Conclusion

In this paper, we have investigated the problem of cluster synchronization of overlapping uncertain dynamic networks with the effects of time-varying impulses. In the proposed model, uncertainties are considered as disturbances. In addition, both synchronizing and desynchronizing impulses are discussed. Moreover, sufficient conditions are derived analytically for cluster synchronization of uncertain dynamic networks by stochastic stability analysis of the impulsive functional differential equation. At last, an overlapping community has been applied to simulate realistic and special model, which few works on cluster synchronization have focused on this model, and simulations have shown the effectiveness of theoretical analysis.