1 Introduction

Cluster synchronization is a particular synchronization phenomenon, requiring that the coupled oscillators split into subgroups called clusters and that synchronization occurs in each cluster. Since the first observation of synchronization phenomenon was made by Huygens [1] in the seventeenth century, this phenomenon has been widely discovered in social networks, food webs, biological networks, and the World Wide Web (see [2,3,4,5,6,7]). In 1990, controlling chaos have been proposed and show that one can convert a chaotic attractor to any one of a large number of possible attracting time-periodic motions by making only small time-dependent perturbations of an available system parameter [8]. Recently, the effects of cluster structures on cluster synchronization have been studied in different types of networks, such as networks composed of coupled Josephson equations, networks composed of impulsive delayed genetic oscillators with external disturbances, networks with cooperative and competitive weight-couplings, and networks with noise and interaction delays. Many researches have indicated that cluster synchronization can be induced by suitable cluster structures (see [9,10,11,12]).

From the control strategy point of view, all kinds of control approaches have been proposed in the field of the synchronization of complex networks. These approaches can be divided into two classes in general. On the one hand, it is based on the continuous updating feedback signals, for instance time-delay feedback control [13], linear feedback control [14], adaptive control [15, 16], nonlinear feedback control [17, 18]. On the other hand, it is based on the discrete signals updated at instant times, such as sampled-data control [19], impulsive control [20,21,22]. The traditional method to synchronize a complex network is to add a controller to each of the network nodes to tame the dynamics to approach a desired synchronization trajectory. However, a complex network is normally composed of a large number of high-dimensional nodes, and it is expensive and infeasible to control all the neurons. Motivated by this practical consideration, the idea of controlling a small portion of nodes, named pinning control, was introduced in [23], and many pinning algorithms have been reported for the synchronization of dynamical networks(see [24,25,26]). Obviously, the pinning control method reduces the control cost to a certain extent by reducing the amount of controllers added to the nodes.

Time delay is important phenomenon in many practical systems such as biological networks, finite chemical reaction times, and memory effects. It is well known that time delay can destabilize the dynamical behavior. This implies that a system with time delay becomes more complicated and interesting. There are a great number of research reports considered time-delay systems [19, 24, 27,28,29,30,31,32,33,34,35,36,37,38]. Generally, there are two types of time delays in dynamical networks. One is internal delay occurring inside the dynamical node [28,29,30]. The internal delay comes from intrinsic factor associated with the dynamical node or oscillator, and it is usually called response or processing time delay, for instance the time delay associated with autapse connected to neuron [28]. Another one is coupling delay caused by the exchange of information between dynamical nodes [31, 32]. The coupling delay is regarded as transmission (or propagation) delay between dynamical nodes of network; for example, time delay with diversity is involved in the neuronal network and the effect of time delay is considered in biological systems [32]. In this paper, synchronization of complex networks with coupling delay will be considered.

The researches on the complete synchronization of networked multi-agent systems, with the aim to reach an agreement regarding a certain quantity of interest that depends on the state of all agents, have received much attention in the past decades [13, 15, 17,18,19,20, 27, 39, 40]. However, a real-world complex network may be composed of interacting smaller subnetworks and such a network in general exhibits richer scenarios than just synchronization. The phenomenon of cluster synchronization is observed when an ensemble of oscillators splits into several subgroups, called clusters throughout the paper, of synchronized elements. Cluster synchronization is considered to be significant in biological sciences and communication engineering. To start with the pioneer work in understanding the mutual synchronization between different neighboring visual columns [41], increasing attention has been paid to cluster synchronization during the past few decades [9,10,11,12, 42]. In [10], a scheme with the presence of negative couplings among different clusters is employed to consider the clustering for full-state coupled identical oscillators via pinning control techniques. Cluster synchronization with intermittent control was investigated in [11]. The work in [12] investigated the cluster synchronization in network of linear systems via pinning control technique in a general framework that the couplings among nodes are of partial state and directed.

Until now, some topics for cluster synchronization have not been studied in detail. In this paper, we will focus on the following two problems:

  1. 1.

    Time delay usually leads the system to be unstable. Will the cluster synchronization be obtained for systems with delay coupling under linear pinning control?

  2. 2.

    In [10,11,12], the coupling matrix is assumed to be symmetric. What will happen when the coupling matrix is asymmetric? Can the cluster synchronization be realized for networks with asymmetric coupling?

Motivated by the above discussions, in this paper, we will study the cluster synchronization of linearly coupled complex dynamical networks with nondelayed and delayed couplings under pinning control. Combining nonlinear pinning and adaptive feedback control methods, some sufficient conditions for the cluster synchronization of complex networks are derived. Moreover, the lower bounds of the coupling strengths are designed within clusters which are necessary to guarantee the cluster synchronization. Finally, two numerical examples are presented to demonstrate the effectiveness and advantages of the theoretical results.

The main contributions of this paper are as follows: (1) compared with [10,11,12], a more general delayed coupling term involving the transmission delay is introduced in the network model; (2) we reduce constraint about coupling matrices; coupling matrix is defined as symmetric and irreducible; (3) the solutions \(s_l, l=1,\ldots ,q\) satisfied \(\lim \limits _{t\rightarrow \infty }\Vert s_l(t)-s_k(t)\Vert \ne 0\) for \(l,k=1,\ldots ,q\); then, \(s_l(t)\) and \(s_k(t)\) have same dimension in [10,11,12]; however, we can consider solutions with different dimension; (4) linear pinning control is only considered by [10,11,12], which makes the derived cluster synchronization criteria less conservative. Therefore, it is interesting and challenging issue to study further pinning and adaptive feedback control methods.

This paper is organized as follows. The network model is introduced, and some necessary lemmas are given in Sect. 2. Section 3 discusses cluster synchronization of the complex dynamical networks with nondelayed and delayed couplings via linear pinning and adaptive feedback controller. The theoretical results are verified numerically by two representative examples in Sect. 4. Finally, this paper is concluded in Sect. 5.

Notation: Throughout this paper, \(\mathfrak {R}^n\) denotes n-dimensional Euclidean space, and \(\mathfrak {R}^{n \times \ n}\) is the set of all \(n \times \ n\) real matrices. \({\text {Rank}}(X)\) is the rank of matric X. For symmetric matrices X and Y, the notation \(X> Y\) (\(X\ge Y\)) means that the matrix \(X-Y\) is positive definite (nonnegative).

2 Preliminaries

Let \(P=\,\{P_1,\ldots ,P_q\}\) be a partition of the index set \({1,2,\ldots ,N}\) into q nonempty subsets, i.e., \(P_l\ne \phi \) and \(\cup _{l=1}^q P_l=P\), where \(P_1=\{1,2,\ldots ,m_1\}\), \(P_2=\{m_1+1,\ldots ,m_1+m_2\},\ldots \),\(P_q=\{m_1+\ldots +m_{q-1}+1,\ldots ,m_1+\ldots +m_q\}, 1<q<N, 1\le m_l<N\), \(\sum \limits _{l=1}^qm_l=N\). Let \(G_l\) denote the underlying topology of cluster \(P_l, l=1,\ldots ,q\), i.e., \(P_l=P(G_l)\). For \(i\in P\), let \(\hat{i}\) denote the subscript of the subset to which the integer i belongs, i.e., \(i\in P_{\hat{i}}\).

Consider a complex dynamical network consisting of N identical nodes with linearly diffusive couplings [5,6,7, 11], which is described by

$$\begin{aligned} \begin{aligned} \dot{x}_i(t)=f(x_i(t))+c\sum \limits _{j=1}^{N}a_{ij}(x_j(t)-x_i(t)), \end{aligned} \end{aligned}$$
(1)

where \(i=1,2, \ldots , N\), \(x_i(t)=(x_{i1}(t),\ldots , x_{in}(t))^\mathrm{{T}} \in \mathfrak {R}^n\) is the state vector of node i, \(f:\mathfrak {R}^n \rightarrow \mathfrak {R}^n\) is continuously differentiable. \(c>0\) is the coupling strength. \(A=(a_{ij})_{N\times \ N}\) is the coupling matrices defined to satisfy the following conditions: \(a_{ij}=a_{ji}=1\) if node i has connection with node j; otherwise, \(a_{ij}=a_{ji}=0\) (\(i\ne j\)). The diagonal elements of matrix A are defined by \(a_{ii}=-\sum \limits _{j=1}^N a_{ij}=-\sum \limits _{j=1}^N a_{ji}\).

Although model (1) reflects the complexity from the networks structure, it is a simple uniform dynamical network without coupling delay. However, in reality, there usually are some time delays in influence and response due to the finite speeds of transmission and spreading as well as traffic congestions. So, time delays should be modeled in order to simulate more realistic networks. In this section, we introduce coupled complex dynamical network consisting of N identical nodes with nondelayed and delayed couplings:

$$\begin{aligned} \dot{x}_i(t)= & {} Bx_i(t)+f(x_i(t))+\sum \limits _{j=1}^{N}c_{ij}a_{ij}^1(x_j(t)-x_i(t))\nonumber \\&+\,c_\tau \sum \limits _{j=1}^Na_{ij}^2x_j(t-\tau )+u_i(t), \end{aligned}$$
(2)

where \(i=1,2,...,N\), \(x_i(t)=(x_{i1}(t),\ldots , x_{in}(t))^\mathrm{{T}} \in \mathfrak {R}^n\) is the state vector of node i, \(f:\mathfrak {R}^n \rightarrow \mathfrak {R}^n\) is continuously differentiable. \(B \in \mathfrak {R}^{n\times \ n}\). \(c_{ij}=c_l\) if \(\hat{i}=\hat{j}=l\), \(c_{ij}=1\) if \(\hat{i}\ne \hat{j}\). \(c_l>0\) measures the intra-cluster coupling strength in cluster l. \(A^1=(a_{ij}^1)_{N\times \ N}\) and \(A^2=(a_{ij}^2)_{N\times \ N}\) are the coupling configuration matrices representing the coupling strength and topological structure of the network, defined to satisfy the following conditions: \(a_{ij}^m\ne 0\) if and only if there exists a directed edge from node j to node i; in particular, \(a_{ij}^m\le 0\) if \(\hat{i}=\hat{j}, m=1,2\) (i.e., nodes i and j are within the same cluster) and \(a_{ij}^m\in \mathfrak {R}\) otherwise. In general, \(A^1\) and \(A^2\) are the asymmetric and may not be identical. \(c_{\tau }>0\) is the coupling strength, \(\tau \) is constant time delay, \(u_i(t)\) is the pinning controller.

Suppose the dynamical behavior of uncoupled system is described by

$$\begin{aligned} \dot{s}_l(t)=Bs_l(t)+f(s_l(t)), \end{aligned}$$

where \(s_l(t), l=1,2,\ldots ,q\), are the particular solutions of the uncoupled system. There is no consensus between any two different clusters with different dimension.

Definition 1

The dynamical networks (2) with the partition \(\{P_1,\ldots ,P_q\}\) are said to achieve cluster synchronization if

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert \mathrm{{e}}_i(t)\Vert {=}\lim _{t\rightarrow \infty }\Vert x_i(t)-s_{\hat{i}}(t)\Vert =0, \ i=1,2,...,N, \end{aligned}$$

where \(\Vert \cdot \Vert \) stands for the Euclidean vector norm, \(s_{\hat{i}}(t)\) is the isolate solution of the \(\hat{i}\)th cluster, \(s_{\hat{i}}(t)=s_l(t)\) if node \(i\in P_{l}\), that is to say, \(\lim \limits _{t\rightarrow \infty }\Vert x_l(t)-s_l(t)\Vert =0, \ \ l=1,2,...,q.\)

The pinning controller \(u_i(t)\) takes the following form:

$$\begin{aligned} u_i(t)=c_{\hat{i}}d_i(s_{\hat{i}}(t)-x_i(t)), \end{aligned}$$
(3)

where \(d_i>0\) if node i is pinned and \(d_i=0\) otherwise. \(c_{\hat{i}}=c_l, l=1,2,\dots ,q\) if node \(i\in P_{l}\).

Assumption 1

(QUAD)There exists a diagonal matrix \(\varDelta ={\text {diag}}(\delta _1,\ldots ,\delta _n)\) and a constant \(w>0\), such that

$$\begin{aligned} (u-v)^\mathrm{{T}}[f(u)-f(v)-\varDelta (u-v)]\le -w(u-v)^\mathrm{{T}}(u-v) \end{aligned}$$

holds for any \(u,v\in \mathfrak {R}^n\) .

Lemma 1

Let \(\forall x,y\in \mathfrak {R}^n\), then

$$\begin{aligned} 2x^\mathrm{{T}}y\le x^\mathrm{{T}}x+y^\mathrm{{T}}y. \end{aligned}$$

Lemma 2

For matrices \(A,B,C,D\in \mathfrak {R}^{n\times n}\),the properties of Kronecker product \(\otimes \):

  1. 1.

    \(A\otimes (B+C)=A\otimes B+A\otimes C\);

  2. 2.

    \((A+B)\otimes C=A\otimes C+B\otimes C\);

  3. 3.

    \((k A)\otimes B=A\otimes (k B)=k(A\otimes B)\);

  4. 4.

    \((A\otimes B)C=A\otimes (B\otimes C)\);

  5. 5.

    \((A\otimes B)(C\otimes D)=(AC)\otimes (BD)\).

According to the partition P, rewrite the coupling matrix as follows:

$$\begin{aligned} A^m=\left( \begin{array}{cccc} A_{11}^m &{} A_{12}^m &{} \cdots &{} A_{1q}^m \\ A_{21}^m &{} A_{22}^m &{} \cdots &{} A_{2q}^m \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_{q1}^m &{} A_{q2}^m &{} \cdots &{} A_{qq}^m \\ \end{array} \right) , \end{aligned}$$

where \(m=1,2.\)

Assumption 2

\(A_{ij}^m\) is zero-row-sum matrix, \(i,j=1,\ldots ,q\). And \(a_{ii}^m\) is equal to negative sum of nondiagonal entry of \(A_{ii}^m\). Then, we say that \(A^m\in M\), \(m=1,2\).

Let \(D={\text {diag}}\{D_1,\ldots ,D_q\}={\text {diag}}\{d_1,\ldots ,d_N\}\); then, let

$$\begin{aligned} \tilde{A}=\left( \begin{array}{cccc} c_1\bar{A}_{11}^1 &{} A_{12}^1 &{} \cdots &{} A_{1q}^1 \\ A_{21}^1 &{} c_2\bar{A}_{22}^1 &{} \cdots &{} A_{2q}^1 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_{q1}^1 &{} A_{q2}^1 &{} \cdots &{} c_q\bar{A}_{qq}^1 \\ \end{array} \right) \end{aligned}$$

where \(\bar{A}_{ii}^1=A_{ii}^1-D_i, i=1,\ldots ,q\). Denote \(\tilde{A}={\text {diag}}\{c_1\bar{A}_{11}^1,c_2\bar{A}_{22}^1,\ldots ,c_q\bar{A}_{qq}^1\}+A_0^1\). Let \(\bar{A}_{11}^1\) be symmetric.

Remark 1

Assumption 2 shows that the inter-cluster couplings may be either positively or negatively weighted. The nodes in the same cluster only have cooperative relationships, while nodes belonging to different clusters can have both cooperative and competitive relationships. The positively weighted coupling between nodes is functioned as the synchronizing scheme for such nodes, while the coupling among nodes from different clusters, which may be negatively weighted, are functioned as a scheme to desynchronize the motions of such nodes from different clusters. In recent research [9,10,11,12], they only considered positively weighted couplings.

3 Main results

In this section, the cluster synchronization of complex network with nondelayed and delayed coupling is investigated. With the help of linear pinning control and Lyapunov functional method, the following theorem can be derived:

Theorem 1

Under Assumptions 1 and 2, the complex system (2) can achieve cluster synchronization if there exist positive constant w and \(\gamma \), such that the following inequalities hold:

$$\begin{aligned}&B+\gamma I_n+\varDelta +\frac{c_{\tau }}{2}I_n\le \frac{w}{2}I_n, \end{aligned}$$
(4)
$$\begin{aligned}&\frac{c_{\tau }}{2}\lambda _{\max }[(A^2)^\mathrm{{T}}A^2]\le \gamma \end{aligned}$$
(5)

and

$$\begin{aligned} c_l\ge \frac{\frac{w}{2}-\lambda _{\max }(A_0^1)}{\lambda _{\max }(\bar{A}_{ll}^1)},\quad l=1,2,\ldots ,q, \end{aligned}$$
(6)

where \(\lambda _{\max }(A)\) is the largest eigenvalue of matrix A, \(\tilde{A}=\mathrm{{diag}}\{c_1\bar{A}_{11}^1,c_2\bar{A}_{22}^1,\ldots ,c_q\bar{A}_{qq}^1\}+A_0^1\).

Proof

Define the error system \(\mathrm{{e}}_i(t)=x_i(t)-s_{\hat{i}}(t), i=1,\ldots ,N\). \(\square \)

Since \(A^1\in M\), then

$$\begin{aligned} \begin{aligned} \sum \limits _{j=1}^Na_{ij}^1x_j(t)=&\sum \limits _{l=1}^q\sum \limits _{j\in P_l}a_{ij}^1x_j(t)\\ =&\sum \limits _{l=1}^q\sum \limits _{j\in P_l}a_{ij}^1[x_j(t)-s_l(t)+s_l(t)]\\ =&\sum \limits _{l=1}^q\sum \limits _{j\in P_l}a_{ij}^1[\mathrm{{e}}_j(t)+s_l(t)]\\ =&\sum \limits _{l=1}^q\sum \limits _{j\in P_l}a_{ij}^1\mathrm{{e}}_j(t)+\sum \limits _{l=1}^q\sum \limits _{j\in P_l}a_{ij}^1s_l(t)\\ =&\sum \limits _{l=1}^q\sum \limits _{j\in P_l}a_{ij}^1\mathrm{{e}}_j(t)=\sum \limits _{j=1}^Na_{ij}^1\mathrm{{e}}_j(t). \end{aligned} \end{aligned}$$
(7)

Similarly, Since \(A^2\in M\), one has

$$\begin{aligned} \sum \limits _{j=1}^Na_{ij}^2x_j(t)=\sum \limits _{j=1}^Na_{ij}^2\mathrm{{e}}_j(t). \end{aligned}$$

Therefore, the error system is

$$\begin{aligned} \begin{aligned} \dot{e}_i(t)=&B\mathrm{{e}}_i(t)+f(x_i(t))-f(s_{\hat{i}}(t))\\&+\sum \limits _{j=1}^Nc_{ij}a_{ij}^1(\mathrm{{e}}_j(t)-\mathrm{{e}}_i(t))\\&+c_{\tau }\sum \limits _{j=1}^Na_{ij}^2\mathrm{{e}}_j(t-\tau )-c_{\hat{i}}d_i\mathrm{{e}}_i(t). \end{aligned} \end{aligned}$$
(8)

Construct a Lyapunov functional as follows:

$$\begin{aligned} V(\mathrm{{e}}_t)=\,\frac{1}{2}\sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t) +\gamma \sum \limits _{i=1}^N\int _{t-\tau }^t\mathrm{{e}}_i^\mathrm{{T}}(s)\mathrm{{e}}_i(s)\mathrm{{d}}s. \end{aligned}$$
(9)

The derivative of \(V(\mathrm{{e}}_t)\) along the trajectories of Eq. (8) is

$$\begin{aligned} \begin{aligned} \dot{V}(\mathrm{{e}}_t)=&\sum \limits _{i=1}^N\mathrm{{e}}_i(t)\dot{e}_i(t)+ \gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t)\\&-\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t-\tau )\mathrm{{e}}_i(t-\tau )\\ =&\sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)[B\mathrm{{e}}_i{(t)}+f(x_i(t))-f(s_{\hat{i}}(t))\\&+\sum \limits _{j=1}^Nc_{ij}a_{ij}^1(\mathrm{{e}}_j(t)-\mathrm{{e}}_i(t))\\&+c_{\tau }\sum \limits _{j=1}^Na_{ij}^2\mathrm{{e}}_j(t-\tau )-c_{\hat{i}}d_i\mathrm{{e}}_i(t)]\\&+\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t)\\&-\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t-\tau )\mathrm{{e}}_i(t-\tau ) \end{aligned} \end{aligned}$$

Due to Assumption 1, one has

$$\begin{aligned} \dot{V}(\mathrm{{e}}_t)= & {} \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)[B\mathrm{{e}}_i{(t)}+f(x_i(t))-f(s_{\hat{i}}(t))\nonumber \\&-\varDelta \mathrm{{e}}_i(t)] +\sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\varDelta \mathrm{{e}}_i(t)\nonumber \\&+\sum \limits _{i=1}^N\sum \limits _{j=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)c_{ij}a_{ij}^1(\mathrm{{e}}_j(t)-\mathrm{{e}}_i(t))\nonumber \\&+\,c_{\tau }\sum \limits _{i=1}^N\sum \limits _{j=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)a_{ij}^2\mathrm{{e}}_j(t-\tau )\nonumber \\&-\sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)c_{\hat{i}}d_i\mathrm{{e}}_i(t) +\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t)\nonumber \\&-\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t-\tau )\mathrm{{e}}_i(t-\tau )\nonumber \\\le & {} \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)(B+\gamma I_n+\varDelta )\mathrm{{e}}_i(t)\nonumber \\&-w\sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t)+\sum \limits _{i=1}^N\sum \limits _{j=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)c_{ij}a_{ij}^1\mathrm{{e}}_j(t)\nonumber \\&+c_{\tau }\sum \limits _{i=1}^N\sum \limits _{j=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)a_{ij}^2\mathrm{{e}}_j(t-\tau )\nonumber \\&-\sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)c_{\hat{i}}d_i\mathrm{{e}}_i(t)\nonumber \\&-\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t-\tau )\mathrm{{e}}_i(t-\tau ). \end{aligned}$$
(10)

Denote \(\mathrm{{e}}(t)=[\mathrm{{e}}_1^\mathrm{{T}}(t),\mathrm{{e}}_2^\mathrm{{T}}(t),\ldots ,\mathrm{{e}}_N^\mathrm{{T}}(t)]^\mathrm{{T}}\), applying to Lemma 2 and the form of \(\tilde{A}\); then,

$$\begin{aligned} \begin{aligned} \dot{V}(\mathrm{{e}}_t)\le&\,\mathrm{{e}}^\mathrm{{T}}(t)I_N\otimes (B+\gamma I_n+\varDelta )\mathrm{{e}}(t)\\&-w\mathrm{{e}}^\mathrm{{T}}(t)(I_N\otimes I_n)\mathrm{{e}}(t)\\&+\mathrm{{e}}^\mathrm{{T}}(t)(\tilde{A}\otimes I_n)\mathrm{{e}}(t)\\&{+}\,c_{\tau }\mathrm{{e}}^\mathrm{{T}}(t)(A^2\otimes I_n)\mathrm{{e}}(t-\tau )\\&-\gamma \mathrm{{e}}^\mathrm{{T}}(t-\tau )\mathrm{{e}}(t-\tau ). \end{aligned} \end{aligned}$$
(11)

Using Lemma 1, one has

$$\begin{aligned} \begin{aligned} \dot{V}(\mathrm{{e}}_t)\le&\,\mathrm{{e}}^\mathrm{{T}}(t)[I_N\otimes (B+\gamma I_n+\varDelta )]\mathrm{{e}}(t)\\&-\frac{1}{2}\mathrm{{e}}^\mathrm{{T}}(t)(I_N\otimes wI_n)\mathrm{{e}}(t)\\&-\frac{1}{2}\mathrm{{e}}^\mathrm{{T}}(t)(wI_N\otimes I_n)\mathrm{{e}}(t)\\&+\mathrm{{e}}^\mathrm{{T}}(t)(\tilde{A}\otimes I_n)\mathrm{{e}}(t)+\frac{c_{\tau }}{2}\mathrm{{e}}^\mathrm{{T}}(t)\mathrm{{e}}(t)\\&+\frac{c_{\tau }}{2}\mathrm{{e}}^\mathrm{{T}}(t-\tau )(A^2\otimes I_n)^\mathrm{{T}}(A^2\otimes I_n)\\&\times \mathrm{{e}}(t-\tau ) -\gamma \mathrm{{e}}^\mathrm{{T}}(t-\tau )\mathrm{{e}}(t-\tau )\\ \le&\mathrm{{e}}^\mathrm{{T}}(t)\left[ I_N\otimes \left( B+\gamma I_n+\varDelta -\frac{w}{2}I_n+\frac{c_{\tau }}{2}I_n\right) \right] \\&\times \mathrm{{e}}(t) +\mathrm{{e}}^\mathrm{{T}}(t)\left[ \left( -\frac{w}{2}I_N+\tilde{A}\right) \otimes I_n\right] \mathrm{{e}}(t)\\&+\mathrm{{e}}^\mathrm{{T}}(t-\tau )\left[ \frac{c_{\tau }}{2}(A^2)^\mathrm{{T}}A^2\otimes I_n-\gamma I_N\otimes I_n\right] \\&\times \mathrm{{e}}(t-\tau ). \end{aligned} \end{aligned}$$
(12)

Since \(A^1\in M\), then \(\lambda _{\max }\{\bar{A}_{ll}^1\}\le 0\). According to condition (6), one has

$$\begin{aligned} c_l \lambda _{\max }(\bar{A}_{ll}^1)+\lambda _{\max }(A_0^1)\le \frac{w}{2}, \end{aligned}$$

where \(\tilde{A}={\text {diag}}\{c_1\bar{A}_{11}^1,c_2\bar{A}_{22}^1,\ldots ,c_q\bar{A}_{qq}^1\}+A_0^1\); let \(\tilde{A}_d={\text {diag}}\{c_1\bar{A}_{11}^1,c_2\bar{A}_{22}^1,\ldots ,c_q\bar{A}_{qq}^1\}\), then

$$\begin{aligned} \lambda _{\max }(\tilde{A}_d)+\lambda _{\max }(A_0^1)\le \frac{w}{2}. \end{aligned}$$
(13)

Together with (4), (5) and (13), one can obtain \(V(\mathrm{{e}}_t)\le 0\). According to Lyapunov stability theory [43], the controlled system (2) can cluster synchronize.

The proof is completed. \(\square \)

Remark 2

In [7,8,9], select q particular solutions \(s_1(t),s_2(t),\ldots ,s_q(t)\) of the homogeneous system

\(\dot{s}(t)=f(s(t),t)\), such that \(\lim _{t\rightarrow \infty }\Vert s_l(t)-s_k(t)\Vert \ne 0\) for \(l,k=1,\ldots ,q, l\ne k\). Although they investigated two different clusters, the clusters have the same dimension, i.e., \({\text {rank}}(s_l(t))={\text {rank}}(s_k(t))\). Here, we consider clusters of different dimension, that is to say, the each cluster has different nodes; for example, \(s_1(t)\) has 3 nodes and \(s_2(t)\) has 5 nodes. The situation that the clusters have the same dimension is special case in this paper.

Remark 3

Theorem 1 shows that the cluster synchronization can be achieved under linear pinning control. Further, the lower bounds of the coupling strengths are designed within clusters which are necessary to guarantee the cluster synchronization.

Next we consider the complex network with adaptive feedback control; by using similar method, we can obtain cluster synchronization of complex network under adaptive feedback control. The dynamical behavior is described as follows:

$$\begin{aligned} \dot{x}_i(t)= & {} Bx_i(t)+f(x_i(t))+\sum \limits _{j=1}^{N}c_{ij}a_{ij}^1(x_j(t)-x_i(t))\nonumber \\&+c_\tau \sum \limits _{j=1}^Na_{ij}^2x_j(t-\tau )+u_i(t), \end{aligned}$$
(14)
$$\begin{aligned} u_i(t)= & {} c_{\hat{i}}d_i(t)(s_{\hat{i}}(t)-x_i(t))\nonumber \\ \dot{d}_i(t)= & {} \eta _i \mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t). \end{aligned}$$
(15)

where \(\eta _i>0\) if node i is pinned and \(\eta =0\) otherwise.

The error system is

$$\begin{aligned} \begin{aligned} \dot{e}_i(t)=\,&B\mathrm{{e}}_i(t)+f(x_i(t))-f(s_{\hat{i}}(t))\\&+\sum \limits _{j=1}^Nc_{ij}a_{ij}^1(\mathrm{{e}}_j(t)-\mathrm{{e}}_i(t))\\&+c_{\tau }\sum \limits _{j=1}^Na_{ij}^2\mathrm{{e}}_j(t-\tau )-c_{\hat{i}}d_i(t)\mathrm{{e}}_i(t). \end{aligned} \end{aligned}$$
(16)

Theorem 2

Under Assumptions 1 and 2, the complex system (14) can achieve cluster synchronization if there exist positive constant w and \(\gamma \) and positive diagonal matrix \(d^*={\text {diag}}\{d_1^*, \ldots ,d_N^*\}\), such that the following inequalities hold:

$$\begin{aligned}&B+\gamma I_n+\varDelta +\frac{c_{\tau }}{2}I_n\le \frac{w}{2}I_n, \end{aligned}$$
(17)
$$\begin{aligned}&\frac{c_{\tau }}{2}\lambda _{\max }[(A^2)^\mathrm{{T}}A^2]\le \gamma \end{aligned}$$
(18)

and

$$\begin{aligned} \bar{A}^*\le \frac{w}{2}I_N, \end{aligned}$$
(19)

where \(\lambda _{\max }(A)\) is the largest eigenvalue of matrix A,

$$\begin{aligned} \bar{A}^*=\left( \begin{array}{cccc} c_1\bar{A}_{11}^{1*} &{} A_{12}^1 &{} \cdots &{} A_{1q}^1 \\ A_{21}^1 &{} c_2\bar{A}_{22}^{2*} &{} \cdots &{} A_{2q}^1 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_{q1}^1 &{} A_{q2}^1 &{} \cdots &{} c_q\bar{A}_{qq}^{l*} \\ \end{array} \right) , \end{aligned}$$

\(\bar{A}_{ii}^{1*}=A_{ii}^1-D^*_i, i=1,\ldots ,q, d^*={\text {diag}}(D_1^*,\ldots ,D_q^*)=\mathrm{{diag}}\{d_1^*,\ldots ,d_N^*\}.\)

Proof

Construct a Lyapunov functional as follows:

$$\begin{aligned} \begin{aligned} V(\mathrm{{e}}_t)=&\frac{1}{2}\sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t) +\sum \limits _{i=1}^N\frac{c_{\hat{i}}(d_i(t)-d_i^*)^2}{2\eta _i}\\&+\gamma \sum \limits _{i=1}^N\int _{t-\tau }^t\mathrm{{e}}_i^\mathrm{{T}}(s)\mathrm{{e}}_i(s)\mathrm{{d}}s. \end{aligned} \end{aligned}$$
(20)

The derivative of \(V(\mathrm{{e}}_t)\) along the trajectories is

$$\begin{aligned} \dot{V}(\mathrm{{e}}_t)= & {} \sum \limits _{i=1}^N\mathrm{{e}}_i(t)\dot{e}_i(t) +\sum \limits _{i=1}^Nc_{\hat{i}}\mathrm{{e}}_i^\mathrm{{T}}(t)(d_i(t)-d_i^*)\mathrm{{e}}_i(t)\nonumber \\&+\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t)-\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t-\tau )\mathrm{{e}}_i(t-\tau )\nonumber \\= & {} \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)[B\mathrm{{e}}_i{(t)}+f(x_i(t))-f(s_{\hat{i}}(t))\nonumber \\&+\,\sum \limits _{j=1}^Nc_{ij}a_{ij}^1(\mathrm{{e}}_j(t)-\mathrm{{e}}_i(t)) +\,c_{\tau }\sum \limits _{j=1}^Na_{ij}^2\mathrm{{e}}_j(t-\tau )\nonumber \\&-\,c_{\hat{i}}d_i^*\mathrm{{e}}_i(t)]+\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t)\mathrm{{e}}_i(t)\nonumber \\&-\,\gamma \sum \limits _{i=1}^N\mathrm{{e}}_i^\mathrm{{T}}(t-\tau )\mathrm{{e}}_i(t-\tau ). \end{aligned}$$
(21)

Similar to Theorem 1, it follows that

$$\begin{aligned} \dot{V}(\mathrm{{e}}_t)\le & {} \, \mathrm{{e}}^\mathrm{{T}}(t)\left[ I_N\otimes \left( B+\gamma I_n+\varDelta -\frac{w}{2}I_n+\frac{c_{\tau }}{2}I_n\right) \right] \mathrm{{e}}(t)\nonumber \\&+\mathrm{{e}}^\mathrm{{T}}(t)\left[ \left( -\frac{w}{2}I_N+\bar{A}^*\right) \otimes I_n\right] \mathrm{{e}}(t)\nonumber \\&+\mathrm{{e}}^\mathrm{{T}}(t-\tau )\left[ \frac{c_{\tau }}{2}(A^2)^\mathrm{{T}}A^2\otimes I_n-\gamma I_N\otimes I_n\right] \nonumber \\&\times \mathrm{{e}}(t-\tau ), \end{aligned}$$
(22)

where

$$\begin{aligned} \bar{A}^*=\left( \begin{array}{cccc} c_1\bar{A}_{11}^{1*} &{} A_{12}^1 &{} \cdots &{} A_{1q}^1 \\ A_{21}^1 &{} c_2\bar{A}_{22}^{2*} &{} \cdots &{} A_{2q}^1 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_{q1}^1 &{} A_{q2}^1 &{} \cdots &{} c_q\bar{A}_{qq}^{l*} \\ \end{array} \right) , \end{aligned}$$

\(\bar{A}_{ii}^{1*}=A_{ii}^1-D^*_i, i=1,\ldots ,q, d^*={\text {diag}}(D_1^*,\ldots , D_q^*)={\text {diag}}\{d_1^*,\ldots ,d_N^*\}.\)

Substituting (17–19) into (22), \(\dot{V}(\mathrm{{e}}_t)\le 0.\) According to Lyapunov stability theory [43], the controlled system (14) can cluster synchronize.

The proof is completed. \(\square \)

4 Numerical examples

In this section, we use two numerical examples to illustrate the effectiveness of the proposed methods.

Fig. 1
figure 1

Network topology among the 6 nodes

Full size image

Example 1

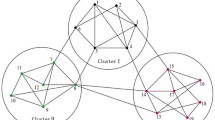
Consider a complex network of \(N=6\) nodes with three clusters \(P_1=\{1\}, P_2=\{2,3\}, P_3=\{4,5,6\}\). Here we choose that the three clusters are different dimension. Each cluster is pinned as shown in Fig. 1. Figure 1 shows that the node 1 is pinned in cluster \(P_1\), the node 3 is pinned in cluster \(P_2\), and the node 6 is pinned in cluster \(P_3\).

According to Fig. 1, we can get the coupling matrices to be

$$\begin{aligned} A^1= & {} \left( \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} -1 \\ 0 &{} -1 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} -1 &{} -1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} -2 &{} 1 &{} 1 \\ 0 &{} -1 &{} 1 &{} 0 &{} -1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1&{} 1 &{} -2 \\ \end{array} \right) ,\\ A^2= & {} \left( \begin{array}{cccccc} 0 &{} -1 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} -1 &{} 1 &{} 1 &{} -1 &{} 0 \\ 0 &{} 1 &{} -1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} -2 &{} 1 \\ 0 &{} 1 &{} -1 &{} 1 &{} 1 &{} -1 \\ \end{array} \right) . \end{aligned}$$

We consider the nodes in complex network with the form of Lorenz system and described as:

$$\begin{aligned} f(x_i(t))=\left( \begin{array}{ccc} -5 &{} 5 &{} 0 \\ 4/3 &{} -1 &{} 0 \\ 0 &{} 0 &{} -14 \\ \end{array} \right) \left( \begin{array}{c} x_{i1} \\ x_{i2} \\ x_{i3} \\ \end{array} \right) + \left( \begin{array}{c} 0 \\ -x_{i1}x_{i3} \\ x_{i1}x_{i2} \\ \end{array} \right) . \end{aligned}$$
(23)

Let

$$\begin{aligned} B=\left( \begin{array}{ccc} -5.6 &{} 1.1 &{} 0 \\ 0.7 &{} -3.5 &{} 1.2 \\ 0.2 &{} 0 &{} 7.2 \end{array} \right) , \end{aligned}$$

and \(c_\tau =0.3\), \(\tau =1.5\), the initial values of state vector \(s_i(t), i=1,2,3\) are chosen in (0,2) randomly. \(d_1=30, d_3=20, d_5=10\) and \(d_2=d_4=d_6=0\), the intra-cluster coupling strength \(c_1=0.1, c_2=0.2, c_3=0.3\). Figure 2 shows trajectory of error vectors \(\mathrm{{e}}_{i1}(t)\), \(\mathrm{{e}}_{i2}(t)\) and \(\mathrm{{e}}_{i3}(t)(i=1,\ldots ,6)\), respectively. We can see that error vectors \(\mathrm{{e}}_{i1}(t)\), \(\mathrm{{e}}_{i2}(t)\) and \(\mathrm{{e}}_{i3}(t)(i=1,\ldots ,6)\) tend to 0. That is to say, the complex network (2) with pinning controller (3) achieves cluster synchronization. We only pin three nodes to lead the whole network to be cluster synchronized. Compared with traditional control method, pinning control method can improve efficiency.

Compared with [10], we not only consider linearity, but also investigate adaptive feedback control. The result of [10] is a special case of this paper.

Fig. 2
figure 2

Time evolution of \(\mathrm{{e}}_i(t)(i=1,\ldots ,6)\) in system (2) under controller (3)

Full size image
Fig. 3
figure 3

Network topology among the 8 nodes

Full size image

Example 2

Consider a complex network (2) of \(N=8\) nodes under adaptive pinning controller (15) with three clusters \(P_1=\{1,2,3\}, P_2=\{4,5,6\}, P_3=\{7,8\}\). Here we choose that the three clusters are different dimension. Each cluster is pinned as shown in Fig. 3. Figure 3 shows that the node 1 is pinned in cluster \(P_1\), the node 5 is pinned in cluster \(P_2\), and the node 7 is pinned in cluster \(P_3\).

According to Fig. 3, we can get the coupling matrices to be

$$\begin{aligned} A^1= & {} \left( \begin{array}{cccccccc} -1 &{} 1 &{} 0 &{} -1 &{} 0 &{} 1 &{} 0 &{} 0 \\ 1 &{} -2 &{} 1 &{} 0 &{} 0 &{} 0 &{} -1 &{} 1 \\ 0 &{} 1 &{} -1 &{} 0 &{} -1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 &{} 1 &{} 0 &{} -1 &{} 1 \\ -1 &{} 1 &{} 0 &{} 1 &{} -1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -2 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 &{} 0 &{} 1 &{} -1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 \\ \end{array} \right) ,\\ A^2= & {} \left( \begin{array}{cccccccc} -1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 \\ 1 &{} 1 &{} -2 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 \\ 0 &{} 0 &{} 0 &{} -1 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} -1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} -2 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 &{} -1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 \\ \end{array} \right) \end{aligned}$$

Let

$$\begin{aligned} B=\left( \begin{array}{cc} -4.5 &{} 1..2 \\ 0.3 &{} -2.8 \end{array} \right) , \,f(x_i(t))=\left( \begin{array}{c} \tanh (x_{i1}(t)) \\ \tanh (x_{i2}(t)) \\ \end{array} \right) \end{aligned}$$

and \(c_\tau =0.5\), \(\tau =3\), the initial values of state vector \(s_i(t), i=1,2,3\) are chosen in (\(-2,2\)) randomly. \(d_1(0)=3, d_5(0)=2, d_7(0)=1\), \(\eta _1=3, \eta _5=2, \eta _7=1\), and \(d_l=\eta _l=0, l=2,3,4,8\), the intra-cluster coupling strength \(c_1=0.1, c_2=0.2, c_3=0.3\). Figure 2 shows trajectory of error vectors \(\mathrm{{e}}_{i1}(t)\), \(\mathrm{{e}}_{i2}(t)\) and \(\mathrm{{e}}_{i3}(t)(i=1,\ldots ,8)\), respectively. We can see that error vectors \(\mathrm{{e}}_{i1}(t)\), \(\mathrm{{e}}_{i2}(t)\) and \(\mathrm{{e}}_{i3}(t)(i=1,\ldots ,8)\) tend to 0. That is to say, the complex network (14) with pinning controller (15) achieves cluster synchronization. We only pin three nodes to lead the whole network to be cluster synchronized. Compared with traditional control method, pinning control method can improve efficiency (Fig. 4). The evolution of \(d_i(t)\) in the system (14) is illustrated in Fig. 5.

Fig. 4
figure 4

Time evolution of \(\mathrm{{e}}_i(t)(i=1,\ldots ,8)\) in system (2) under controller (15)

Full size image
Fig. 5
figure 5

Time evolution of \(d_i(t)\) in the pinning controlled networks

Full size image

From these two simulations, one can conclude that using the proposed two methods in this paper, cluster synchronization of network (2) under pinning controller (3) and adaptive pinning controller (15) can be achieved.

5 Conclusion

In this paper, the linear pinning and adaptive feedback controllers have been designed, and some sufficient conditions for the cluster synchronization of complex networks are derived. The clusters of different dimension are considered. We have also obtained the lower bounds for the strengths of the couplings within clusters which guarantee the cluster synchronization. Finally, the feasibility and effectiveness of the proposed methods have been demonstrated by numerical simulation examples. In future work, we will consider to extend the proposed methods for solving complex dynamical networks with the internal delay and coupling delay. This kind of dynamical network is ubiquitous in the real world, especially in many biological networks and neural networks. It is a challenging and interesting problem.