Synchronization of coupled memristive chaotic circuits via state-dependent impulsive control

Abstract

This paper investigates the synchronization of two memristive chaotic circuits via state-dependent impulsive control. Different from most existing publications, impulses occurring is not at fixed instants but depends on the states of systems. Furthermore, the state variables of the driving system (driving system which does not involve the impulses) are transmitted to the response system, and then the state variables of response system are subjected to jumps at the state-dependent impulsive instants, and ultimately to achieve synchronization. Based on the Lyapunov stability theory, impulsive differential equation, and inequality techniques, the sufficient conditions with theoretical demonstration ensuring every solution of error system intersects each surface of the discontinuity exactly once are derived. Then, by applying B-equivalence method, the error system with state-dependent impulses can be reduced to the case of fixed-time impulses. Finally, the numerical simulations are carried out to demonstrate the effectiveness of the obtained results.

1 Introduction

The memristor was postulated as a new two-terminal circuit element by Chua in 1971 [1] and was realized by Williams’s Team in 2008 [2]. Recently, a lot of works have been done to analyze the memristive chaotic circuits, in which the Chua’s diode was replaced by various memristors with different nonlinearities [3,4,5,6,7,8]. The above memristive chaotic circuits produce chaotic behaviors due to the nonlinear equations. We have studied the stabilization and synchronization of memristor-based chaotic circuit via fixed-time impulsive control in [6]. Furthermore, the impulsive synchronization and initial value effect for memristor-based chaotic system have been investigated in [9]. However, there has been no relevant published results in the literature effectively applied to the synchronization on coupled memristive chaotic circuits via state-dependent impulsive control. Due to the extensive applications of memristor, more and more researchers have been working to study the dynamic behavior of memristive system, investigating its properties and functions, which are becoming the active research topics.

Over the past years, synchronization have been extensively investigated and applied to secure communications, signal processing, image processing, pattern classification, and associative memory by [10,11,12,13,14,15,16,17,18,19,20,21]. Meanwhile, many control approaches have been proposed to synchronize chaotic networks and nonlinear systems such as impulsive control [15,16,17,18] (state-independent impulsive control), sampled data control [20], and intermittent control [21]. Many important results have been reported on the synchronization control of nonlinear systems [13,14,15,16,17,18,19,20,21]. Based on the impulsive theory and linear matrix inequality technique, Li et al have been obtained impulsive synchronization of chaotic systems in [13] and the chaotic delay systems in [14]. Based on the impulsive control theory, the authors in [15] have been established the global exponential synchronization of complex networks. The exponential synchronization of fractional-order complex networks via pinning impulsive control have been investigated in [16]. By applying switching Lyapunov function method, the synchronization of coupled delayed switched neural networks with impulsive time window have been studied in [18]. By using a convex combination technique, the problems of the novel impulsive synchronization scheme have been proposed in [19], which allowed to synchronize two identical discrete-time neural networks (DDNNs) with unknown delays. It is noted that there are few results about the synchronization of state-dependent impulsive control, where the state is included in the impulsive moment.

Generally, impulsive control has been widely recognized as a powerful control approach for stabilizing linear and nonlinear systems, and synchronizing two chaotic systems, or driving the system to a limit cycle [10,11,12,13,14,15,16,17,18,19, 22,23,24,25,26]. According to different switching rule, impulsive system can be classified into two types: impulsive systems with fixed-time impulses and impulsive systems with variable-time impulses, that is, impulsive systems with state-dependent impulses. If the impulsive instants are absolutely predetermined and independent of state, then we get an impulsive system with fixed-time impulses. If the impulses occur when the trajectory hits a hypersurface in the extended phase space, then the impulsive instants are dependent on state, that is, state-dependent impulsive systems. Recently, the impulsive systems with fixed-time impulses analysis problem for nonlinear system or linear system has received increasing research attention and many relevant results have been reported in the literature [10,11,12,13,14,15,16,17,18,19, 22,23,24,25,26]. For example, the impulsive effects on stability of discrete-time complex-valued neural networks with both discrete and distributed time-varying delays have been investigated in 2015 [24]. In [25], the authors researched the synchronization of memristor-based bidirectional associative memory (BAM) neural networks with time-varying delays by applying impulsive control. In [26], the authors proposed a novel impulsive control law for synchronization of stochastic discrete complex networks with time delays and switching topologies.

To our knowledge, the most existing publications focus on the fixed-time impulsive systems, and the readers are referred to the references [10,11,12,13,14,15,16,17,18,19, 22,23,24,25,26]. But only a few results on dynamics for state-dependent impulsive systems have been published. Recently, series significant theoretical results are the generalization of the studies with fixed-time impulses to state-dependent impulse time $t=\theta _k+\tau _k(x)$ [27,28,29,30,31,32,33,34,35]. However, in [27,28,29,30,31,32,33,34,35], the authors investigated the dynamics of state-dependent impulsive control system via comparison system method, and the established comparison systems yet also be variable-time impulsive systems but with one dimension. Therefore, it is still difficult to analyze the dynamics for such comparison systems. The critical challenge for the research on state-dependent impulsive system is that the dwell time is completely indeterminate, and the moments of impulses are arbitrary in $R_+$, that is, solutions with different initial data have different impulse time. Recently, Akhmet in [37] proposed a powerful analytical tool for discontinuous ystems: B-equivalence method. By applying this method, the global robust asymptotic stability of variable-time impulsive BAM neural networks have been obtained in [36]. Unfortunately, in [36, 37], the relationship between the original jump operator in variable-time impulsive system and new jump operator in corresponding fixed-time impulsive system have not been obtained. It is noted that the authors in [36] just simply assumed that new jump operator is linear with respect to system state. However, we have successfully handled these problems through our analysis in this paper. Although there are many results concerning the state-dependent impulsive control for nonlinear systems, one should underline that there have no relevant published results in literature where the reduction principle based on B-equivalence is effectively applied to synchronization on memristive chaotic circuit via state-dependent impulsive control.

Motivated by the above discussions, the main objective of this paper is to find the sufficient conditions which ensure the synchronization of two memristive chaotic circuit system via state-dependent impulsive control by means of B-equivalence method. Moreover, we will establish several assumptions that guarantee every solution of the error system intersects each surface of discontinuity exactly once. Based on the Lyapunov stability theory and inequality techniques, the state-dependent impulsive error systems can be reduced to the fixed-time impulsive ones, which can be regarded as the comparison systems of the original impulsive system. The numerical simulations are carried out to demonstrate that the driving system without impulses can be synchronized by state-dependent impulsive control, and finally establish a set of stability criteria of error system by using of B-equivalent comparison system. Therefore, investigating the synchronization on the system with non-fixed moments of impulses is necessary and more general than the fixed-time impulsive system.

This paper is organized as follows: In following section, the theoretical model for memristive chaotic system, some definitions and lemmas are presented. In Sect. 3, the conditions of absence of beating and the corresponding B-equivalence method are introduced. The synchronization via state-dependent impulsive control are established in Sect. 4. The numerical simulations are carried out to demonstrate the effectiveness of the obtained results in Sect. 5, and the conclusion is drawn in Sect. 6.

2 Model description and some preliminaries

Notations The notations used in this paper are quite and fairly standard. Throughout this paper, $R^n$ and $R^{n\times n}$denote, respectively, the n-dimensional Euclidean space and the set of all $n\times n$ real matrices. $\Vert x\Vert =\sqrt{x^\mathrm {T}x}$ refers to the Euclidean vector norm. $A^T$ represents the transpose of matrix A. Matrices, if not explicitly specified, are assumed to have compatible dimensions. Let $R_+=[0,+\infty ),~Z_+={1, 2, 3,\ldots }$, and $G=\bigcup _{i=1}^\infty G_i$. We further denote $\varGamma _i=\{(t,x(t))\in R_+\times G:t=\theta _i+\tau _i(x(t)),t\in R_+,x\in G, G\subset R^n\}$ the $i-$th surface of discontinuity, and the sequence $\theta =\{\theta _i\}_{i=1}^\infty$ satisfies $0=\theta _0<\theta _1<\theta _2<\cdots<\theta _i<\theta _{i+1}<\cdots$ with $\lim _{i\rightarrow \infty }\theta _i=\infty$.

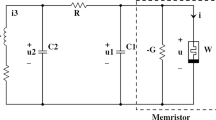
In this section, some preliminaries including the memristive chaotic circuit model, some necessary definitions and lemmas are presented, which are used throughout this paper. In 2010, Muthuswamy [5] proposed the possible nonlinear circuits as shown in Fig. 1, which replaces the Chua’s diode with a flux-controlled memristor. The equations of the memristor-based chaotic circuit in Fig. 1 can be written as following:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{{\text {d}}v_1 (t)}{{\text {d}}t}=\frac{1}{\mathop C\nolimits _1 }\left( \frac{v_2 (t)-v_1 (t)}{R}-i(t)\right) ,\\ \frac{{\text {d}}v_2 (t)}{{\text {d}}t}=\frac{1}{C_2 }\left( \frac{v_1 (t)-v_2 (t)}{R}- i_L (t)\right) ,\\ \frac{{\text {d}} i_L (t)}{{\text {d}}t}=\frac{v_2 (t)}{L},\\ \frac{{\text {d}}\varphi }{{\text {d}}t}=v_1 (t). \end{array}\right. } \end{aligned}$$

(1)

where i(t) is defined as:

$$\begin{aligned} i(t)=W(\varphi (t))\upsilon _1 (t)=\frac{{\text {d}}q}{{\text {d}}\varphi }\upsilon _1 (t), \end{aligned}$$

(2)

Fig. 1

The memristor chaotic circuit, which is derived from Chua’s circuit by replacing the Chua diode with the flux-controlled memristor

Fig. 2

Several projections of the chaotic attractor codified by Eq. (1)

We choose a cubic nonlinearity for the $q-\varphi$ function [5]:

$$\begin{aligned} q(\varphi )=\alpha \varphi +\beta \varphi ^3, \end{aligned}$$

(3)

Then, the memductance function $W(\varphi )$ is given by:

$$\begin{aligned} W(\varphi )=\frac{dq}{d\varphi }=\alpha +3\beta \varphi ^2. \end{aligned}$$

(4)

In order to obtain the chaos generation, we then settled the parameter values of Eq. (1) which yield chaotic dynamics are: $R =2\,k\varOmega ,~ L =15.5\,mH,~ C_1 =8\,uF, ~C_2=200\,uF$ potentiometer. Letting $\alpha =-0.663\times 10^{-3}$ and $\beta =0.004\times 10^{-3}$ in Eq. (4), similar to values in [38]. Choosing the initial conditions $(\upsilon _1(0),\upsilon _2(0),i_L(0),\varphi (0))=(0.132,0.147,0.691,0)$ the attractor generated by means of numerical integration is illustrated in Fig. 2.

For convenience, we let $\upsilon _1 =x_1 ,~ \upsilon _2 =x_2,~ i_L =x_3,~ \varphi =x_4; ~a_1=1/C_1, ~a_2=1/C_2,~a_3=1/R,~a_4=1/L$. Then the memristor-based chaotic circuit system is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}_{1} =a_1(a_3(x_2 -x_1)-W(x_4 )x_1 ),\\ \dot{x}_{2}=a_2(a_3(x_1 -x_2) -x_3),\\ \dot{x}_{3} =a_4x_2,\\ \dot{x}_{4} =x_1.\\ \end{array}\right. } \end{aligned}$$

(5)

By decomposing the linear and nonlinear parts of the memristor-based chaotic circuit system in (5), we can rewrite it as

$$\begin{aligned} \dot{x}=Ax+\varPhi (x), \end{aligned}$$

(6)

where $x^{\mathrm {T}} =( x_1, x_2, x_3, x_4 ), A= \left[ {{\begin{array}{cccc} {-a_1a_3} &{} a_1a_3 &{} 0 &{} 0\\ a_2a_3 &{} -a_2a_3 &{} {-a_2} &{} 0\\ 0 &{} a_4 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 0\\ \end{array} }} \right] , \varPhi (x)=\left[ {{\begin{array}{c} {-a_1W(x_4 )\mathop x\nolimits _1 }\\ 0\\ 0\\ 0\\ \end{array} }} \right]$.

In order to synchronize the memristive chaotic system (6) (called the driving system) via state-dependent impulsive control, another system (called the response system) is designed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{y}=Ay+\varPhi (y)+u,~~~~~~t\ne \theta _i+\tau _i(y-x)\\ \Delta y\mid _{t=\theta _i+\tau _i(y-x)}=J_i(y-x),~~~~~~~~~i\in Z_+ \end{array}\right. } \end{aligned}$$

(7)

where $y^{\hbox {T}} =( y_1 , y_2 , y_3 , y_4 ), A$ is the same as in Eq. (6), and $\varPhi (y)=\left[ {{\begin{array}{c} {-a_1W(y_4 )\mathop y\nolimits _1 }\\ 0\\ 0\\ 0\\ \end{array} }} \right] . u=(u_1,u_2,u_3,u_4)^T$ is the state feedback controller to be designed. $J_i(y-x)$ denotes the jump operator function with $J_i(0)=0$.

Let the error between the states of system (6) and (7) be $e=y-x$. Then, we can easily obtain the following impulsive error system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{e}=Ae+f(x,y)+u,~~~~~~t\ne \theta _i+\tau _i(e)\\ \Delta e\mid _{t=\theta _i+\tau _i(e)}=J_i(e),~~~~~~~~i\in Z_+ \end{array}\right. } \end{aligned}$$

(8)

where $f(x,y)\triangleq \varPhi (y)-\varPhi (x)=\left[ {{\begin{array}{c} {-a_1W(y_4 )y_1+a_1W(x_4)x_1}\\ 0\\ 0\\ 0\\ \end{array} }} \right]$.

In this paper, we shall choose a state feedback controller which is defined by:

$$\begin{aligned} u=-K(y-x), \end{aligned}$$

where $K={\text {diag}}(k_1,k_2,k_3,k_4)$ and $k_i>0~(i=1,2,3,4)$. The impulsive controller is designed as $J_i(e)$.

Then the error system are governed by

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{e}=(A-K)e+f(x,y),~~~~~~t\ne \theta _i+\tau _i(e)\\ \Delta e\mid _{t=\theta _i+\tau _i(e)}=J_i(e),~~~~~~~~~i\in Z_+ \end{array}\right. } \end{aligned}$$

(9)

where $e^{\mathrm {T}} =( e_1 , e_2 , e_3 , e_4 )\in G\subseteq R^n$ stands for the state vector of the error system at time $t, \triangle e\mid _{t=\xi _k}=e(\xi _k+)-e(\xi _k)$ with $e(\xi _k+)=\lim _{t\rightarrow \xi _k+0}e(t)$ stands for the state jump at moment $\xi _k$, satisfying $\xi _k=\theta _k+\tau _k(e(\xi _k))$. Without loss of generality, we assume that the solution e(t) is left continuous at impulse point, that is, $e(\xi _k-)=\lim _{t\rightarrow \xi _k-0}e(\xi _k)$.

Remark 1

In [10,11,12,13,14,15,16,17,18,19, 22,23,24,25,26], the authors investigated the dynamic behaviors of fixed-time impulsive systems. In real-world problems, the impulses of many systems do not occur at fixed time, for example, population control systems, saving rates control systems, ecological systems, and some circuit control systems. These types of systems are called state-dependent impulsive differential systems or impulsive systems with variable-time impulses. The fixed-time impulsive control can not deal with these problems. Compared with them, our results are generalization of the studies with fixed-time impulses to the state-dependent impulse time $t =\theta _i+\tau _i(x)$. In other words, the results obtained in the previous articles are just the specific case of our results with $\tau _i(x)=0$. Therefore, the results of this paper are more practically and more advanced version of the previously constructed results.

Definition 1

[28] Let $V:R_+\times R^n\rightarrow R_+$, then V is said to belong to class $\varOmega$ if

• 1. V is continuous in $(\tau _{i-1},\tau _i]\times R^n$ and for each $x\in R^n,~i=1,2,\cdots ,$

  $$\begin{aligned} \lim \limits _{(t,y)\rightarrow (\tau _i^+,x)}V(t,y)=V(\tau _i^+,x) \end{aligned}$$

  exists, and $V(\tau _i^-,x)=V(\tau _i,x)$.

• 2. V is locally Lipschizian in x.

From this definition, one can see that a function V associated with the impulsive system (9) is similar to a Lyapunov function for stability analysis of an ordinary differential equation. Because these Lyapunov-like functions are generally discontinuous, we then need the following definition of the right and upper Dini’s derivative.

Definition 2

[28] For $(t,x)\in (\tau _{i-1},\tau _i]\times R^n$, the right and upper Dini’s derivative $V\in \varOmega$ with respect to time variable is defined as

$$\begin{aligned} D^+V(t,x)\equiv \lim \limits _{h\rightarrow 0^+}\sup \frac{1}{h}\{V[t+h,x+hf(t,x)]-V(t,x)\}. \end{aligned}$$

Definition 3

The origin of system (9) is said to be globally exponentially stable if there exist some constants $\alpha >0$ and $M>0$ such that $\Vert e(t,t_0,e(t_0))\Vert \le Me^{-\alpha (t-t_0)}$, for any $t\ge t_0.$

To prove the global exponential stability of the error system (9), the following lemma is necessary.

Lemma 1

[39] Given any real matrices $\varSigma _1,\varSigma _2,\varSigma _3$ of appropriate dimensions and a scalar $s>0$, such that $0<\varSigma _3=\varSigma _3^T$, then the following inequality holds:

$$\begin{aligned} \varSigma _1^T\varSigma _2+\varSigma _2^T\varSigma _1\le s\varSigma _1^T\varSigma _3\varSigma _1+s^{-1}\varSigma _2^T\varSigma _3^{-1}\varSigma _2. \end{aligned}$$

Throughout this paper, we further make the following assumption.

(H) $J_i(e):G\rightarrow G,\tau _i(e):G\rightarrow R$ with $J_i(0)=0,\tau _i(0)=0$ are continuous functions, for all $i\in Z_+$, and there exist positive numbers $l_J$ and $l_{\tau }$ such that

$$\begin{aligned}&\Vert e+J_i(e)\Vert \le l_J\Vert e\Vert ,\\&\Vert \tau _i(\alpha )-\tau _i(\beta )\Vert \le l_{\tau }\Vert \alpha -\beta \Vert \end{aligned}$$

for all $i\in Z_+,~\alpha ,\beta \in R^n$.

3 Absence of beating and B-equivalent system

The task of investigation of the globally exponentially stable for system (9) with state-dependent impulses is more complex than that of systems with impulses acting at prescribed moments. A reason for this is the possibility of the ‘beating’ of solutions against the surfaces of discontinuity. Therefore, our goal is to reduce state-dependent impulsive system (9) to fixed-time impulsive analog as its comparison system by means of B-equivalence method.

3.1 Absence of beating phenomena

Throughout this paper, we will present a new of conditions that ensure that each solution of (9) intersects each surface of discontinuity exactly once. For this purpose, we make the following assumptions.

• (H1) There exists a positive number $\nu$ such that $0\le \tau _i(e)<\nu$, therefore, $\theta _i\le \theta _i+\tau _i(e)\le \theta _i+\nu$.

• (H2) There exist two positive numbers $\underline{\theta },\bar{\theta }$ such that $\underline{\theta }+\nu<\theta _{i+1}-\theta _i<\bar{\theta }-\nu$ for all $i\in Z_+, e\in G$.

• (H3) Fix j, and let $e(t):[\theta _j,\theta _j+\nu ]\rightarrow G$ is a solution of (9) in time interval $[\theta _j,\theta _j+\nu ]$. One of the following two conditions is satisfied:

  $$\begin{aligned}&(i) {\left\{ \begin{array}{ll} \frac{{\text {d}}\tau _j(e)}{{\text {d}}e}\cdot [(A-K)e+f(x,y)]>1,~~ for ~all ~e\in G,\\ \tau _j(e(\xi ))+J_j(e(\xi ))\ge \tau _j(e(\xi )),~~t=\xi \end{array}\right. }\\&(ii) {\left\{ \begin{array}{ll} \frac{{\text {d}}\tau _j(e)}{{\text {d}}e}\cdot [(A-K)e+f(x,y)]<1,~~ for ~all ~e\in G,\\ \tau _j(e(\xi ))+J_j(e(\xi ))\le \tau _j(e(\xi )),~~t=\xi \end{array}\right. } \end{aligned}$$

  where $t=\xi$ is the discontinuity point of (9), i.e., $\xi =\theta _j+\tau _j(e(\xi )).$

From assumptions (H1)–(H3), the following lemmas could be obtained.

Lemma 2

Assume that (H1) and (H2) hold, then each solution of system (9) which intersects surfaces $\varGamma _j$ and $\varGamma _k, j<k-1$, must intersects all surfaces $\varGamma _i, j<i<k$, between the two.

Proof

Let e(t) be a solution of system (9), which intersects $\varGamma _j$ and $\varGamma _k$. Then, there exist $\xi _j$ and $\xi _k~(\xi _j<\xi _k)$, such that $\xi _j=\theta _j+\tau _j(e(\xi _j))$ and $\xi _k=\theta _k+\tau _k(e(\xi _k))$.

Define a function $\Delta (t)=t-\theta _i-\tau _i(e(t)),~(j<i<k)$. Notably, $\Delta (t)$ is continuous with respect to t by virtue of the continuity of $\tau _i(e(t))$. Note that assumptions (H1) and (H2) implies

$$\begin{aligned} \underline{\theta }<[\theta _{i+1}+\tau _{i+1}(e)]-[\theta _i+\tau _i(e)]<\bar{\theta }, \end{aligned}$$

and

$$\begin{aligned}&[\theta _i+\tau _i(e)]-[\theta _j+\tau _j(e)]=[\theta _i-\theta _{i-1}+\tau _i(e)-\tau _{i-1}(e)],\\&\quad +[\theta _{i-1}-\theta _{i-2}+\tau _{i-1}(e)-\tau _{i-2}(e)]+\cdots \\&\quad +[\theta _{j+1}-\theta _j+\tau _{j+1}(e)-\tau _j(e)], \end{aligned}$$

hence

$$\begin{aligned} (i-j)\underline{\theta }<\theta _i-\theta _j+\tau _i(e)-\tau _j(e)<(i-j)\bar{\theta }. \end{aligned}$$

Then we have

$$\begin{aligned} \Delta (\xi _j)= & {} \xi _j-\theta _i-\tau _i(e(\xi _j))<\theta _j-\theta _i+\tau _j(e(\xi _j))\\&-\tau _i(e(\xi _j))<-(i-j)\underline{\theta }\le 0,\\ \Delta (\xi _k)= & {} \xi _k-\theta _i-\tau _i(e(\xi _k))<\theta _k-\theta _i+\tau _k(e(\xi _k))\\&-\tau _i(e(\xi _k))<(k-i)\bar{\theta }\ge 0. \end{aligned}$$

Then there exists a positive number $\xi _i,~\xi _j<\xi _i<\xi _k$, such that $\Delta (\xi _i)=0$, that is $\xi _i=\theta _i+\tau _i(e(\xi _i))$. Then e(t) intersects all surfaces $\varGamma _i,~j<i<k$, between $\varGamma _j$ and $\varGamma _k$. This completes the proof. $\square$

Lemma 3

Assume that (H1) and (H2) hold, and $e(t):R_+\rightarrow G$ is a solution of system (9). Then e(t) intersects all surfaces $\varGamma _i, i\in Z_+$.

Proof

The proof of this lemma is similar to Lemma 5.3.2 in [24], thus we omit it. $\square$

Lemma 4

Assume that (H3) holds. Then every solution $e(t):R_+\rightarrow G$ of system (9) intersects each of the surfaces $\varGamma _i, i\in Z_+$ at most once.

Proof

Assume on the contrary there exists a solution e(t) intersects the surface $\varGamma _j$ at points $(s_1,e(s_1))$ and $(s_2,e(s_2))$, where we assume that $s_1<s_2$, and there exists no discontinuity point of e(t) between $s_1$ and $s_2$. Then, $s_1=\theta _j+\tau _j(e(s_1)), s_2=\theta _j+\tau _j(e(s_2))$. For the case (i) in (H3), we have, by the differential mean value theorem,

$$\begin{aligned} s_2-s_1&=\tau _j(e(s_2))-\tau _j(e(s_1))\\&\ge \tau _j(e(s_2))-\tau _j(e(s_1)+J_j(e(s_1)))\\&= \tau _j(e(s_2))-\tau _j(e(s_1+))\\&= \left\{ \frac{{\text {d}}\tau _j(e)}{{\text {d}}e}\cdot [(A-K)e+f(x,y)]\right\} (s_2-s_1)\\&> s_2-s_1 \end{aligned}$$

This is a contradiction. Similarly, for the case (ii) in (H3), we have

$$\begin{aligned} s_2-s_1&=\tau _j(e(s_2))-\tau _j(e(s_1))\\&\le \tau _j(e(s_2))-\tau _j(e(s_1)+J_j(e(s_1)))\\&= \tau _j(e(s_2))-\tau _j(e(s_1+))\\&= \left\{ \frac{{\text {d}}\tau _j(e)}{{\text {d}}e}\cdot [(A-K)e+f(x,y)]\right\} (s_2-s_1)\\&< s_2-s_1 \end{aligned}$$

This is also a contradiction (H3), and thus, Lemma 4 holds. The proof is completed. $\square$

Based on Lemmas 2–4, we obtain the following result immediately.

Theorem 1

Assume that (H1)–(H3) hold, then every solution $e(t):R_+\rightarrow G$ of system (9) intersects each of the surfaces $\varGamma _i,i\in Z_+$ exactly once.

Fig. 3

Construction principle of map $W_i(e)$

3.2 B-equivalent system

In this subsection, we will introduce the B-equivalent system for (9).

Let $e^0(t)=e(t,\theta _i,e)$, that is $e^0(\theta _i)=e$, be a solution of the first equation in Eq. (9) in $[\theta _i,\xi _i]$. Denote $\xi _i$ the meeting moment of the solution with the surface $\varGamma _i$ of discontinuity so that $\xi _i=\theta _i+\tau _i(e^0(\xi _i))$. Let $e^1(t)$ also be the a solution of the first equation in Eq. (9) in $[\theta _i,\xi _i]$, such that $e^1(\xi _i)=e^0(\xi _i+)=e^0(\xi _i)+J_i(e^0(\xi _i)).$

Define the following map (as shown in Fig. 3):

$$\begin{aligned} W_i(e)= & {} e^1(\theta _i)-e\nonumber \\= & {} e^1(\xi _i)-\int _{\theta _i}^{\xi _i}[(A-K)e^1(s)\nonumber \\&+f(x^1(s),y^1(s))]{\text {d}}s-e\nonumber \\= & {} e^0(\xi _i)+J_i(e^0(\xi _i))-\int _{\theta _i}^{\xi _i}[(A-K)e^1(s)\nonumber \\&+f(x^1(s),y^1(s))]{\text {d}}s-e\nonumber \\= & {} \int _{\theta _i}^{\xi _i}[(A-K)e^0(s)+f(x^0(s),y^0(s))]{\text {d}}s\nonumber \\&+e+J_i(e^0(\theta _i)+\int _{\theta _i}^{\xi _i}[(A-K)e^0(s)\nonumber \\&+f(x^0(s),y^0(s))]{\text {d}}s)\nonumber \\&-\int _{\theta _i}^{\xi _i}[(A-K)e^1(s)+f(x^1(s),y^1(s))]{\text {d}}s-e\nonumber \\= & {} \int _{\theta _i}^{\xi _i}[(A-K)e^0(s)+f(x^0(s),y^0(s))]{\text {d}}s\nonumber \\&+J_i(e^0(\theta _i)+\int _{\theta _i}^{\xi _i}[(A-K)e^0(s)\nonumber \\&+f(x^0(s),y^0(s))]{\text {d}}s)\nonumber \\&-\int _{\theta _i}^{\xi _i}[(A-K)e^1(s)+f(x^1(s),y^1(s))]{\text {d}}s\nonumber \\ \end{aligned}$$

(10)

Fig. 4

The impulsive synchronization between two memristor chaotic circuits

The impulsive synchronization between two memristor chaotic circuits is depicted in Fig. 4. In this implementation, we have determined the circuit parameters for each memristor chaotic circuits are same as Fig. 1. Because the occurrence of the impulses is determined by the statement of the system, we know that the impulsive intervals of the system also depend on the statement of the memristive chaotic circuits, as shown in Fig. 3.

From the definition of $W_i(e)$ together with Fig. 3, we get the following observations:

Observation 1

$e^0(t)=e(t,\theta _i,e)$ can be extended as the solution of (9) in $R_+$;

Observation 2

$e^1(t)=e(t,\xi _i,e^0(\xi _i+))$ can be extended as the solution of the following fixed-time impulsive system in $R_+$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{e}(t)=(A-K)e(t)+f(x(t),y(t)),~~~~t\ne \theta _i,\\ \triangle e|_{t=\theta _i}=W_i(e). \end{array}\right. } \end{aligned}$$

(11)

Observation 3

For all $i\in Z_+$, on time internal $(\xi _{i-1},\theta _i]$ with $\xi _0=t_0$,

$$\begin{aligned} {\left\{ \begin{array}{ll} e^0(t)=e^1(t),\\ e^1(\theta _i+)=e^0(\theta _i)+W_i(e^0(\theta _i)),\\ e^1(\xi _i)=e^0(\xi _i+)=e^0(\xi _i)+J_i(e^0(\xi _i)).\\ \end{array}\right. } \end{aligned}$$

Observation 4

For all $i\in Z_+$, on time internal $(\theta _i,\xi _i]$,

$$\begin{aligned}&e^1(t)-e^0(t)=e+W_i(e)+\int _{\theta _i}^t[(A-K)e^1(s)\nonumber \\&\qquad +f(x^1(s),y^1(s))]{\text {d}}s\nonumber \\&\qquad -e-\int _{\theta _i}^t[(A-K)e^0(s)+f(x^0(s),y^0(s))]{\text {d}}s\nonumber \\&\quad =W_i(e)+\int _{\theta _i}^t[(A-K)e^1(s)+f(x^1(s),y^1(s))]{\text {d}}s\nonumber \\&\qquad -\int _{\theta _i}^t[(A-K)e^0(s)+f(x^0(s),y^0(s))]{\text {d}}s \end{aligned}$$

(12)

Then for all $t\in (\theta _i,\xi _i]$, we have,

$$\begin{aligned}&\Vert e^1(t)-e^0(t)\Vert \le \Vert W_i(e)\Vert +\int _{\theta _i}^t\Vert (A-K)e^1(s)\nonumber \\&\qquad +f(x^1(s),y^1(s))\Vert {\text {d}}s\nonumber \\&\qquad +\int _{\theta _i}^t\Vert (A-K)e^0(s)+f(x^0(s),y^0(s))\Vert {\text {d}}s\nonumber \\&\quad \le \Vert W_i(e)\Vert +2M_e(t-\theta _i)\nonumber \\&\quad =\Vert W_i(e)\Vert +2M_e\tau _i(e^0(t)) \end{aligned}$$

(13)

where $M_e=\sup \limits _{(t,e)\in R_+\times G}\Vert (A-K)e(t)+f(x(t),y(t))\Vert$, and

$$\begin{aligned}&\Vert W_i(e)\Vert \nonumber \\&\quad =\Vert \int _{\theta _i}^{\xi _i}[(A-K)e^0(s)+f(x^0(s),y^0(s))]{\text {d}}s\nonumber \\&\qquad +J_i(e^0(\theta _i)+\int _{\theta _i}^{\xi _i}[(A-K)e^0(s)\nonumber \\&\qquad +f(x^0(s),y^0(s))]{\text {d}}s)\nonumber \\&\qquad -\int _{\theta _i}^{\xi _i}[(A-K)e^1(s)+f(x^1(s),y^1(s))]{\text {d}}s\Vert \nonumber \\&\quad \le \Vert \int _{\theta _i}^{\xi _i}(A-K)e^0(s)+f(x^0(s),y^0(s)){\text {d}}s\Vert \nonumber \\&\qquad +\Vert J_i(e^0(\theta _i)+\int _{\theta _i}^{\xi _i}[(A-K)e^0(s)\nonumber \\&\qquad +f(x^0(s),y^0(s))]{\text {d}}s)\Vert \nonumber \\&\qquad +\Vert \int _{\theta _i}^{\xi _i}(A-K)e^1(s)+f(x^1(s),y^1(s)){\text {d}}s\Vert \nonumber \\&\quad \le M_e(\xi _i-\theta _i)+l_J\Vert e\Vert +l_JM_e(\xi _i-\theta _i)+M_e(\xi _i-\theta _i)\nonumber \\&\quad =(2M_e+l_JM_e)\tau _i(e^0(\xi _i))+l_J\Vert e\Vert \end{aligned}$$

(14)

and

$$\begin{aligned} \tau _i(e^0(\xi _i))&\le l_{\tau }\Vert e^0(\xi _i)\Vert =l_{\tau }\Vert e+\int _{\theta _i}^{\xi _i}[(A-K)e^0(s)\\&\quad +f(x^0(s),y^0(s))]{\text {d}}s\Vert \\&\le l_{\tau }\Vert e\Vert +l_{\tau }M_e(\xi _i-\theta _i)\\&=l_{\tau }\Vert e\Vert +l_{\tau }M_e\tau _i(e^0(\xi _i)) \end{aligned}$$

which implies that

$$\begin{aligned} \tau _i(e^0(\xi _i))\le (1-l_{\tau }M_e)^{-1}l_{\tau }\Vert e\Vert . \end{aligned}$$

(15)

Therefore,

$$\begin{aligned} \Vert W_i(e)\Vert&\le [(2M_e+l_JM_e)(1-l_{\tau }M_e)^{-1}l_{\tau }+l_J]\Vert e\Vert . \end{aligned}$$

(16)

Thus,

$$\begin{aligned} \Vert e^1(t)-e^0(t)\Vert&\le [M_e(4+l_J)(1-l_{\tau }M_e)^{-1}l_{\tau }+l_J]\Vert e\Vert . \end{aligned}$$

(17)

4 Synchronization via state-dependent impulsive control

In this section, we shall present that the global exponential stability property of system (11) implies the same stability property of (9) under the previous discussion.

Theorem 2

Assume that (H1)–(H3) hold. Suppose that there exist $V\in \varOmega$ such that:

$$\begin{aligned} \nu _1\Vert e(t)\Vert ^p\le V(e(t))\le \nu _2\Vert e(t)\Vert ^p,~~~~~for~any~e\in R^n, \end{aligned}$$

(18)

and

$$\begin{aligned} D^+V(e(t))\le \alpha V(e(t)),~~~~~~~~~~~~~~~~~~for~any~t\in (\theta _i,\xi _i], \end{aligned}$$

(19)

where $\nu _1>0,\nu _2>0,\alpha>0,p>0$, and e(t) is a solution of (9) in $(\theta _i,\xi _i]$. Then it holds that

• 1. $\Vert e+W_i(e)\Vert \le \mu _1\Vert e\Vert ,~~~~~~for~any~e\in G,$

• 2. $\Vert e^1(t)-e^0(t)\Vert \le \mu _2\Vert e\Vert ,~~~for~any~t\in (\theta _i,\xi _i],$

where

$$\begin{aligned} \mu _1&=l_J\root p \of {\nu _1^{-1}\nu _2}e^{\alpha \nu /p}+M_e(1-l_{\tau }M_e)^{-1}l_{\tau }\\ \mu _2&=M_e(4+l_J)(1-l_{\tau }M_e)^{-1}l_{\tau }+l_J \end{aligned}$$

$e^0(t)=e(t,\theta _i,e)$ is an any solution of (9), which intersects the surface $\varGamma _i$ of discontinuity at $\xi _i,~\xi _i=\theta _i+\tau _i(e^0(\xi _i))$. And $e^1(t)$ is a solution of (11) such that $e^1(\theta _i+)=e+W_i(e),e^1(\xi _i)=e^0(\xi _i+)=e^0(\xi _i)+J_i(e^0(\xi _i)),W_i(e)$ is defined by (10).

Proof

It follows from (18), (19) that:

$$\begin{aligned}{}[\nu _2^{-1}V(e(t))]^{\frac{1}{p}}\le \Vert e(t)\Vert \le [\nu _1^{-1}V(e(t))]^{\frac{1}{p}}, \end{aligned}$$

(20)

Integrate both side of inequality (19) from $\theta _i$ to t, where $t\in (\theta _i,\xi _i]$, we get

$$\begin{aligned} V(e(t))\le V(e(\theta _i+))e^{\alpha (t-\theta _i)} \end{aligned}$$

(21)

From Eqs. (20)–(21) that

$$\begin{aligned} \Vert e(t)\Vert&\le [\nu _1^{-1}V(e(\theta _i+))e^{\alpha (t-\theta _i)}]^{\frac{1}{p}}\nonumber \\&\le \root p \of {\nu _1^{-1}\nu _2}e^{\frac{\alpha }{p}(t-\theta _i)}\Vert e(\theta _i+)\Vert , \end{aligned}$$

(22)

Therefore,

$$\begin{aligned} \Vert e^0(t)\Vert&\le \root p \of {\nu _1^{-1}\nu _2}e^{\frac{\alpha }{p}(t-\theta _i)}\Vert e\Vert ,\\ \Vert e^1(t)\Vert&\le \root p \of {\nu _1^{-1}\nu _2}e^{\frac{\alpha }{p}(t-\theta _i)}\Vert e+W_i(e)\Vert . \end{aligned}$$

Because $0<t-\theta _i=\tau _i(e(t))\le \nu$, then we can get

$$\begin{aligned} \Vert e^0(t)\Vert&\le \root p \of {\nu _1^{-1}\nu _2}e^{\frac{\alpha }{p}\nu }\Vert e\Vert . \end{aligned}$$

(23)

Therefore, from Eqs. (15) and (23), we have

$$\begin{aligned}&\Vert e+W_i(e)\Vert = \Vert e^1(\theta _i+)\Vert \nonumber \\&\quad =\Vert e^1(\xi _i)+\int _{\theta _i}^{\xi _i}[(A-K)e^1(s)\nonumber \\&\qquad +f(x^1(s),y^1(s))]{\text {d}}s\Vert \nonumber \\&\quad \le \Vert e^1(\xi _i)\Vert +\Vert \int _{\theta _i}^{\xi _i}[(A-K)e^1(s)\nonumber \\&\qquad +f(x^1(s),y^1(s))]{\text {d}}s\Vert \nonumber \\&\quad \le \Vert e^0(\xi _i)+J_i(e^0(\xi _i))\Vert +M_e(\xi _i-\theta _i)\nonumber \\&\quad \le l_J\Vert e^0(\xi _i)\Vert +M_e\tau _i(e^0(\xi _i))\nonumber \\&\quad \le \left( l_J\root p \of {\nu _1^{-1}\nu _2}e^{\alpha \nu /p}+M_e(1-l_{\tau }M_e)^{-1}l_{\tau }\right) \Vert e\Vert \nonumber \\&\quad =\mu _1\Vert e\Vert . \end{aligned}$$

(24)

The proof of condition (b) has been obtained in Eq. (17), and thus we omit it.

Then, we complete the proof. $\square$

Remark 2

Assume that (H1)–(H3) hold; the Theorem 2 implies that the state-dependent impulsive error system (9) has the same stability property with the fixed-time impulsive error system (11).

Theorem 3

Assume that all the assumptions hold. Suppose that there exist $V\in \varOmega$ such that:

• 1.  $\nu _1\Vert e(t)\Vert ^p\le V(e(t))\le \nu _2\Vert e(t)\Vert ^p$

• 2. ${\left\{ \begin{array}{ll} D^+V(e(t))\le \alpha V(e(t)),~~~~t\ne \theta _k,~~~k\in Z_+\\ V(e(\theta _k+))\le d_k V(e(\theta _k)),\\ \end{array}\right. }$

• 3.  $\alpha (\bar{\theta }-\nu )+\ln d_k<-\delta$ where $\nu _1>0,\nu _2>0,p>0,d_k>0,\delta >0$, and $\theta _k$ is the impulsive moments of (11).

Then the origin of system (11) is globally exponentially stable, and therefore, the origin of system (9) is globally exponentially stable.

Proof

From condition (b), by taking the mathematical induction, we have

• 1. When $t\in (0,\theta _1]$, we get

  $$\begin{aligned} V(e(t))\le V(e(t_0))e^{\alpha t}. \end{aligned}$$

  (25)

  then we can get,

  $$\begin{aligned} V(e(\theta _1))\le V(e(t_0))\exp \{\alpha \theta _1\}. \end{aligned}$$

• 2. When $t\in (\theta _1,\theta _2]$, we have

  $$\begin{aligned} V(e(t))&\le V(e(\theta _1+))e^{\alpha (t-\theta _1)}\nonumber \\&\le d_1 V(e(\theta _1))e^{\alpha (t-\theta _1)}\nonumber \\&= d_1V(e(t_0))\exp \{\alpha \theta _1\}\exp \{\alpha (t-\theta _1)\}.\nonumber \\&\le V(e(t_0))\exp \{\alpha t+\ln d_1\}. \end{aligned}$$

  (26)

  and

  $$\begin{aligned} V(e(\theta _2))\le V(e(t_0))\exp \{\alpha \theta _2+\ln d_1\}. \end{aligned}$$

• 3. Assume that the inequality also holds for $t\in (\theta _k,\theta _{k+1}],~k\ge 1$, that is,

  $$\begin{aligned} V(e(t))&\le V(e(t_0))\exp \left\{ \alpha t+\sum _{i=1}^k\ln d_i\right\} . \end{aligned}$$

  (27)

  and

  $$\begin{aligned} V(e(\theta _k))\le V(e(t_0))\exp \left\{ \alpha \theta _k+\sum _{i=1}^k\ln d_i\right\} . \end{aligned}$$

• 4. Note that, if $t\in (\theta _{k+1},\theta _{k+2}],$ repeat the same process, and hence we have

  $$\begin{aligned}&V(e(t))\le V(e(\theta _k+))e^{\alpha (t-\theta _k)}\nonumber \\&\quad \le d_{k+1} V(e(\theta _k))e^{\alpha (t-\theta _k)}\nonumber \\&\quad = d_{k+1}V(e(t_0))\exp \left\{ \alpha \theta _k+\sum _{i=1}^k\ln d_i\right\} \exp \{\alpha (t-\theta _k)\}\nonumber \\&\quad =V(e(t_0))\exp \{\alpha t+\sum _{i=1}^{k+1}\ln d_i\}. \end{aligned}$$

  (28)

Therefore, for $t\in (\theta _k,\theta _{k+1}],k\in Z_+$,

$$\begin{aligned} V(e(t))&\le V(e(t_0))\exp \left\{ \alpha t+\sum _{i=1}^k\ln d_i\right\} . \end{aligned}$$

(29)

and we also have

$$\begin{aligned} t&\le \theta _{k+1}=\theta _{k+1}-\theta _k+\theta _k-\theta _{k-1}\\&\quad +\cdots +\theta _1-\theta _0+0\\&\le \sum _{i=1}^{k+1}(\theta _i-\theta _{i-1})\\&\le (k+1)(\bar{\theta }-\nu ) \end{aligned}$$

Therefore,

$$\begin{aligned} k\ge \frac{t}{\bar{\theta }-\nu }-1, \end{aligned}$$

and

$$\begin{aligned}&V(e(t))\le V(e(t_0))\exp \left\{ \alpha t+\sum _{i=1}^k\ln d_i\right\} .\nonumber \\&\quad \le V(e(t_0))\exp \left\{ \alpha \sum _{i=1}^{k+1}(\theta _i-\theta _{i-1})+\sum _{i=1}^k\ln d_i\right\} .\nonumber \\&\quad = V(e(t_0))\exp \{\alpha (\bar{\theta }-\nu )\}\nonumber \\&\qquad \exp \left\{ \sum _{i=1}^{k}(\ln d_i+\alpha (\theta _i-\theta _{i-1})\right\} .\nonumber \\&\quad \le V(e(t_0))\exp \{\alpha (\bar{\theta }-\nu )\}\exp \{-k\delta \}\nonumber \\&\quad <V(e(t_0))\exp \{\alpha (\bar{\theta }-\nu )+\delta \}\exp \left\{ -\frac{\delta }{\bar{\theta }-\nu }t\right\} . \end{aligned}$$

(30)

Then, from condition 1, we get

$$\begin{aligned} \Vert e(t)\Vert&\le M\Vert e(t_0)\Vert \exp \left\{ -\frac{\delta }{\bar{\theta }-\nu }t\right\} \end{aligned}$$

(31)

where $M=\root p \of {\nu _1^{-1}\nu _2}\exp \{\alpha (\bar{\theta }-\nu )+\delta \}$.

This completes the proof. $\square$

Theorem 4

Assume that all the assumptions hold. Suppose that $\chi =\{x\in R^n,y\in R^n\mid \Vert f(x,y)\Vert \le \gamma \Vert y-x\Vert \}$, then there exist symmetric and positive definite matrix $P>0$, and positive scalars $\alpha>0,s>0$ such that:

• 1.  $\varOmega =(A-K)^TP+P(A-K)+sP^2+s^{-1}\gamma ^2 I-\alpha P\le 0$

• 2.  $d_k=\frac{\lambda _M\mu _1^2}{\lambda _m}\le 1$

• 3.  $\alpha (\bar{\theta }-\nu )+\ln d_k<-\delta$

Then the origin of system (11) is globally exponentially stable.

Proof

Consider the following Lyapunov functional:

$$\begin{aligned} V(e(t))=e^T(t)Pe(t) \end{aligned}$$

When $t\ne \theta _k$, calculate the derivative $\dot{V}$ of t along the solution of system (11), and then we get

$$\begin{aligned} \dot{V}(e(t))= & {} \dot{e}^T(t)Pe(t)+e^T(t)P\dot{e}(t)\nonumber \\= & {} [(A-K)e(t)+f(x(t),y(t))]^TPe(t)\nonumber \\&+\,e^T(t)P[(A-K)e(t)+f(x(t),y(t))]\nonumber \\\le & {} e^T(t)[(A-K)^TP+P(A-K)]e(t)\nonumber \\&+\,se^T(t)PP^Te(t)\nonumber \\&+\,s^{-1}f^T(x(t),y(t))f(x(t),y(t))\nonumber \\\le & {} e^T(t)[(A-K)^TP+P(A-K)+sP^2\nonumber \\&+\,s^{-1}\gamma ^2 I-\alpha P]e(t)+\alpha e^T(t)Pe(t)\nonumber \\\le & {} \alpha V(e(t)) \end{aligned}$$

(32)

When $t=\theta _k$, we have,

$$\begin{aligned}&V(\theta _k,e(\theta _k)+W_k(e(\theta _k)))\nonumber \\&\quad =[e+W_k(e)]^TP[e+W_k(e)]\nonumber \\&\quad \le \lambda _M\mu _1^2\Vert e(\theta _k)\Vert ^2\nonumber \\&\quad \le \frac{\lambda _M\mu _1^2}{\lambda _m}V(e(\theta _k))\nonumber \\&\quad =d_kV(e(\theta _k)) \end{aligned}$$

(33)

$\square$

Therefore, according to Theorem 3, together with (32) and (33), we know that the origin of system (11) is globally exponentially stable, which implies the same stability property of system (9). Then the proof is completed.

When P is identity matrix, assume that all the assumptions hold. Then we have the following corollary by Theorems 2–4.

Corollary 1

Let $\alpha , s, \gamma$ be as in Theorem 4. If there exists positive number $\delta$ such that, for all $k\in Z_+$,

• 1.  $(A-K)^T+A-K+sI+s^{-1}\gamma ^2 I-\alpha I\le 0$

• 2.  $-1\le \mu _1\le 1$

• 3.  $\alpha (\bar{\theta }-\nu )+2\ln \mu _1<-\delta$

where $\mu _1=l_Je^{\alpha \nu /2}+M_e(1-l_{\tau }M_e)^{-1}l_{\tau }$. Then, the origin of system (11) is globally exponentially stable, that is, the memristive chaotic circuit (6) can be synchronized follow the response system (7) under the state-dependent impulsive control.

When there is no impulsive controller and only a state feedback controller, the error system (9) reduces to

$$\begin{aligned} \dot{e}=(A-K)e+f(x,y). \end{aligned}$$

(34)

Then we obtain the following result.

Corollary 2

Let $s, \gamma$ be as in Theorem 4. If there exists positive number $\alpha$ such that,

$$\begin{aligned} \varOmega =(A-K)^T+A-K+sI+s^{-1}\gamma ^2 I+\alpha I\le 0 \end{aligned}$$

Then, the origin of system (34) is globally stable, that is, the memristive chaotic circuit (6) can be synchronized follow the response system (7) when the impulsive controller $J_i(e)=0$.

Proof

Consider the following Lyapunov functional:

$$\begin{aligned} V(e(t))=e^T(t)e(t) \end{aligned}$$

Calculate the derivative $\dot{V}$ of t along the solution of system (34), we get

$$\begin{aligned} \dot{V}(e(t))&=\dot{e}^T(t)e(t)+e^T(t)\dot{e}(t)\\&=[(A-K)e(t)+f(x(t),y(t))]^Te(t)\\&\qquad +e^T(t)[(A-K)e(t)+f(x(t),y(t))]\\&\le e^T(t)[(A-K)^T+(A-K)]e(t)\\&\qquad +se^T(t)e(t)+s^{-1}f^T(x(t),y(t))f(x(t),y(t))\\&\le e^T(t)[(A-K)^T+(A-K)+sI\nonumber \\&\qquad +s^{-1}\gamma ^2 I+\alpha I]e(t)-\alpha e^T(t)e(t)\\&\le -\alpha V(e(t)) \end{aligned}$$

$\square$

The proof is completed.

Remark 3

References [10,11,12,13,14,15,16,17,18,19, 22,23,24,25,26] have investigated the dynamics of nonlinear systems with fixed-time impulse. Different from the previous results, the B-equivalence method allows us to consider equations with fixed-time impulsive systems instead of state-dependent impulsive systems. In addition, a novel B-map for synchronization analysis of the addressed models has been formulated, and the reduction process is explained in Theorems 2–4.

Remark 4

In Theorems 2–4 and Corollaries 1–2, the results obtained in [10,11,12,13,14,15,16,17,18,19, 22,23,24,25,26] have been extended to the state-dependent impulsive case in this paper. In other words, the time sequence is differential systems with fixed-time impulses can be viewed as special impulsive differential systems with state-dependent impulses. If $\tau _i(\cdot )=0$, Eqs. (7) and (8) can be reduced to the fixed-time impulsive system, which is same as [6], then it is easy to analyze its dynamic behavior via fixed-time impulsive control.

Remark 5

Theorems 2–4 imply that the effectiveness of state-dependent impulsive control has been successfully analyzed theoretically, and the effective electrical design scheme of memristive chaotic circuits has been proposed in [5], and the impulsive synchronization circuit is devised as shown in Fig. 4.

5 Numerical simulations

In this section, we will give the numerical simulation to imply the impulsive synchronization of the two memristive chaotic circuit by applying the theory presented in the previous section. The error system is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{e}(t)=(A-K)e(t)+f(x(t),y(t)),\quad t\ne \theta _i+\tau _i(e(t))\\ \Delta e\mid _{t=\theta _i+\tau _i(e(t))}=J_i(e(t)),\quad i\in Z_+ \end{array}\right. } \end{aligned}$$

(35)

Let $A= \left[ {{\begin{array}{*{20}c} {-a_1a_3} &{} a_1a_3 &{} 0 &{} 0\\ a_2a_3 &{} -a_2a_3 &{} {-a_2} &{} 0\\ 0 &{} a_4 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 0\\ \end{array} }} \right] \approx \left[ {{\begin{array}{*{20}c} -62.5 &{} 62.5 &{} 0 &{} 0\\ 2.5 &{} -2.5 &{} {-5\times 10^{-3}} &{} 0\\ 0 &{} 65 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 0\\ \end{array} }} \right]$, the state feedback control gain can be defined by $K={\text {diag}}(0.8,0.8,0.8,0.8)$. Then Eq. (34) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{e}_{1} =a_1(a_3(e_2 -e_1)-W(y_4 )y_1+W(x_4 )x_1 ),~~~t\ne \theta _i+\tau _i(e(t))\\ \dot{e}_{2}=a_2(a_3(e_1 -e_2) -e_3),~~~~~~~~~~~~~~~~~~~~~~~~~~~t\ne \theta _i+\tau _i(e(t))\\ \dot{e}_{3} =a_4e_2,~~~~~~~~~~~t\ne \theta _i+\tau _i(e(t))\\ \dot{e}_{4} =e_1,~~~~~~~~~~~~~~t\ne \theta _i+\tau _i(e(t))\\ \Delta e_1=J_1(e(t)),~~~~t=\theta _i+\tau _i(e(t))\\ \Delta e_2=J_2(e(t)),~~~~t=\theta _i+\tau _i(e(t))\\ \Delta e_3=J_3(e(t)),~~~~t=\theta _i+\tau _i(e(t))\\ \Delta e_4=J_4(e(t)),~~~~t=\theta _i+\tau _i(e(t))\\ \end{array}\right. } \end{aligned}$$

(36)

In the following simulation, We take $\theta _i=0.2i,\tau _i(e(t))=\frac{1}{75\pi }[{\text {arcsin}}(e_1)]^2, J_i(e(t))=B_ie(t)=-0.5e(t)$ in this paper. By simple calculation, we can obtain that $l_{\tau }=\frac{1}{75\pi },l_J=|1+B_i|<1,0\le \tau _i(e(t))\le \pi l_{\tau }=\frac{1}{75}=\nu$. Note that

Fig. 5

The time response curve of the error system without state-dependent impulsive controller and state feedback controller

Fig. 6

The time response curve of the error system using state-dependent impulsive controller and state feedback controller

Fig. 7

The norm of synchronization error with the initial value $(x_1(0),x_2(0),x_3(0),x_4(0))^T=(0.132,0.147,0.691,0)^T$ and $(y_1(0),y_2(0),y_3(0),y_4(0))^T=(6.285,1.652,3.731,0.001)^T$

Fig. 8

The time response curve of the error system with state feedback controller

$$\begin{aligned}&\frac{\partial \tau _i(e)}{\partial e}[(A-K)e(t)+f(x(t),y(t))]\nonumber \\&\quad =2l_{\tau }\arcsin (e_1)\left[ {{\begin{array}{cccc} {\frac{1}{\sqrt{1-e_1^2}}}&{}~~0&{}~~0&{}~~0\\ \end{array} }} \right] \nonumber \\&\quad \quad \left[ {{\begin{array}{c} {a_1(a_3(e_2-e_1)-W(y_4 )y_1+W(x_4)x_1)}\\ a_2(a_3(e_1-e_2)-e_3)\\ a_4e_2\\ e_1\\ \end{array} }} \right] \nonumber \\&\quad =2l_{\tau }\arcsin (e_1)\frac{a_1(a_3(e_2-e_1)-W(y_4 )y_1+W(x_4)x_1)}{\frac{1}{\sqrt{1-e_1^2}}}\nonumber \\&\quad \le 2l_{\tau }\arcsin (e_1)\frac{|a_1(a_3(e_2-e_1)-W(y_4 )y_1+W(x_4)x_1)|}{\frac{1}{\sqrt{1-e_1^2}}}\nonumber \\&\quad \le \frac{1}{5}\times 10^{-5}<1\end{aligned}$$

(37)

$$\begin{aligned}&\tau _i(e+J_i(e))-\tau _i(e)=\frac{1}{75\pi }[\arcsin ((1+B_i)e_1)]^2\nonumber \\&\qquad -\frac{1}{75\pi }[\arcsin (e_1)]^2\nonumber \\&\quad =\frac{1}{75\pi }{[\arcsin (|(1+B_i)e_1|)]^2-\frac{1}{75\pi }[\arcsin (|e_1|)]^2}\nonumber \\&\quad =\frac{1}{75\pi }[\arcsin (|(1+B_i)e_1|)\nonumber \\&\qquad +\arcsin (|e_1|)][\arcsin (|(1+B_i)e_1|)-\arcsin (|e_1|)]\nonumber \\&\quad \le 0 \end{aligned}$$

(38)

That is $\frac{\partial \tau _i(e)}{\partial e}[(A-K)e(t)+f(x(t),y(t))]<1, \tau _i(e+J_i(e))\le \tau _i(e)$. Then all the assumptions hold. Therefore, every solution $e(t):R_+\rightarrow G$ of (34) intersects each surface $\varGamma _i=\{(t,e(t))\in R_+\times G:t\ne 0.2i+\frac{1}{75\pi }[{\text {arcsin}}(e_1)]^2\},i\in Z_+$ exactly once.

Using the impulsive control scheme and the state feedback control scheme proposed in Corollary 1, we take $s=10,\alpha =25.6$. By simple computation, we have $\gamma =172.2656, \mu _1=0.6183, \mu _2=0.613, d_k=0.3822, \delta =11.8516$. Then Theorem 2 and Theorem 3 are satisfied. Therefore, by Corollary 1, the origin of error system (9) is globally exponentially stable, that is, the memristive chaotic circuit (6) can be synchronized following the response system (7) and it becomes ultimately the same under the state-dependent impulsive control, as shown in Fig. 6. Figure 7 is the norm of synchronization error with the initial value $(x_1(0),x_2(0),x_3(0),x_4(0))^T=(0.132,0.147,0.691,0)^T$ and $(y_1(0),y_2(0),y_3(0),y_4(0))^T=(6.285,1.652,3.731,0.001)^T$, which is globally exponentially stable.

In this numerical simulation, when the parameters of driving system are the same as those in response system, the initial conditions of two systems are different, the time-response curve of the error system without state-dependent impulsive control and state feedback control (with K = diag(0.8)) as shown in Fig. 5, from which we can see the error system is unstable. When the state-dependent impulsive controller and state feedback controller are added to system, the memristive chaotic circuit (6) can be synchronized with the response system (7). Figure 6 shows the time response curve of error system using state-dependent impulsive control and state feedback control, where the impulsive controller is $J_i(e(t))=-0.5e(t)$.

In order to compare the performance of state-dependent impulsive control, next, when we take $s=2$, the parameters of error system are the same as the first equation of (35), we choose the another group of initial conditions of driving system and response system are $(x_1(0),x_2(0),x_3(0),x_4(0))^T=(0.132,0.147,0.691,0)^T$ and $(y_1(0),y_2(0),y_3(0),y_4(0))^T=(0.022,0.21,0.7,0.001)^T$, respectively. Figure 7 shows the time response curve of the error system without the state-dependent impulsive control. It can be seen that the synchronization performance is poor, and thus, the necessity of using suitable controller is inevitable.

In this example, when we choose $s=2$ and the state feedback controller $K={\text {diag}}(1.2)$, by applying Corollary 2, we can get $\alpha =43.9107$. Figure 8 shows the time response curve of the error system with initial value $(x_1(0),x_2(0),x_3(0),x_4(0))^T=(0.132,0.147,0.691,0)^T$ and $(y_1(0),y_2(0),y_3(0),y_4(0))^T=(0.022,0.21,0.7,0.001)^T$, which are free of impulsive control.

6 Conclusions

This paper is focuses on the synchronization analysis of two memristive chaotic circuits via state-dependent impulsive control by using a series of analysis technique. By adding state-dependent impulsive controllers, the general stability criterion conditions of the error system, together with its simplified versions has been obtained. Moreover, several necessary assumptions have been proposed to ensure each solution of the error system intersects each of the discontinuity exactly once. In addition, based on B-equivalence method and inequality techniques, we have reduced state-dependent impulsive error system to the fixed-time impulses (which is state-independent impulses), and corresponding proofs have been proposed to imply that the state-dependent impulsive error system has the same stability property with the fixed-time impulsive system. Finally, numerical simulations are carried to demonstrate the effectiveness of the obtained results. As we know, there are few works (if any) have been reported to control the TS fuzzy systems and higher-order memristive circuit via state-dependent impulsive control in the existing literature, so one of the future tasks will be to improve the stability criteria for TS fuzzy model systems and higher-order memristive circuit under state-dependent impulsive control by B-equivalence method.