A novel solver for multi-objective optimization: dynamic non-dominated sorting genetic algorithm (DNSGA)

Abstract

Non-dominated sorting is a critical component of all multi-objective evolutionary algorithms (MOEAs). A large percentage of computational cost of MOEAs is spent on non-dominated sorting. So, the complexity of non-dominated sorting method in a large extent decides the efficiency of the MOEA. In this paper, we present a novel non-dominated sorting method called the dynamic non-dominated sorting (DNS). It is based on the sorting of real number sequence instead of dominance comparisons. The computational complexity of DNS is $O(mN\log N)$ (m is the number of objectives, N is the population size), which equals to the best record so far. In the numerical experiments, we verify the outperformance of DNS comparing with other non-dominated sorting methods. Based on DNS, we introduce a novel multi-objective genetic algorithm called the dynamic non-dominated sorting genetic algorithm (DNSGA). Numerical experiments on DNSGA are also given. The results show that DNSGA outperforms some other MOEAs on both general-scale and large-scale multi-objective problems.

1 Introduction

Multi-objective optimization has extensive application in engineering and management. Many optimization problems in the real-world can be modeled as multi-objective optimization problems (MOPs) (Guo et al. 2019; Passos et al. 2019; Zhang et al. 2019). However, due to the theoretical and computational challenges, it is not easy to solve MOPs. Therefore, numerical multi-objective optimization attracts a wide range of research over the last decades.

One popular way to solve MOP is to reformulate it into a single-objective optimization problem. We call this technique the indirect method. Typical indirect methods are weighted sum method (Wang et al. 2016), $\varepsilon$-constraint method (Du et al. 2014) and their variations (Gutjahr and Pichler 2016). One difficulty for the weighted sum method is the selection of proper weights so as to satisfy the decision-maker’s preference. Since the weighted sum is a linear combination of the objective functions, the concave part of the Pareto frontier cannot be obtained using the weighted sum method. The $\varepsilon$-constraint method converts multiple objectives, except one, to constraints. However, it is difficult to determine the upper bounds of these objectives. On the one hand, small upper bounds could exclude some Pareto solutions; on the other hand, large upper bounds could enlarge the searching area, which yields some sub-Pareto solutions. Additionally, indirect method can only obtain a single Pareto solution in each run, but in the real-world application, decision-makers often prefer a number of optional strategies so that they can choose one according to their preference.

Another strategy to solve MOP is to explore the entire objective function value space directly in order to obtain its Pareto frontier. We call this strategy the direct method. Population-based heuristic methods are ideal direct methods, because their iterative units are populations instead of a single point, so they can obtain a set of solutions in a single run. In the past few years, many heuristic methods were applied to solve MOP, such as the evolutionary algorithm (Ma et al. 2016; Ruiz et al. 2015; Zhang et al. 2015), genetic algorithm (Yang et al. 2017) and differential evolution (Mlakar et al. 2015; Qiu et al. 2016). Among them, genetic algorithm attracted a great deal of attention and lots of good methods has been presented (Deb et al. 2002; Hei et al. 2019; Long 2014; Long et al. 2015).

A combination of direct and indirect methods is another strategy to solve MOP. We call this type the hybrid method (Nikhil et al. 2017, 2018, 2019, 2020). A representative of this type is MOEA/D (Zhang and Li 2007). It combines the evolutionary algorithm and three scalarization methods.

When solving MOP using direct methods, two important issues (Zitzler et al. 2000) need to be addressed:

• Elitism: In the process of multi-objective evolutionary algorithm (MOEA), we always prefer solutions whose function values are closer to the real Pareto frontier. In the selection procedure, these solutions should be selected as parents for the next generation, which leads the task of non-dominated sorting in each iteration. According to the definition of efficient point, numerous amount of comparisons are needed to identify the non-dominated state of each point. Therefore, reasonably reducing the computational cost is one of the key research issues in designing MOEA.

• Diversity: Diversity reflects the distribution of the obtained Pareto frontier. Obviously, a uniformly distributed Pareto frontier is preferred than a unevenly distributed one. In other words, a good algorithm should avoid obtaining solutions which are excessively concentrate on one or two isolated areas.

Among them, elitism is realized by non-dominated sorting whose core operation is comparison. Since non-dominated sorting is needed in each iteration, the efficiency of non-dominated sorting method is very important for the performance of MOEA. In this paper, we first propose a novel non-dominated sorting method called the dynamic non-dominated sorting (DNS) and then a new multi-objective genetic algorithm (MOGA) based on DNS.

The rest of the paper is organized as follows: In Sect. 2, we review some existing non-dominated sorting methods and the framework of genetic algorithm. In Sect. 3, we propose DNS and a new MOGA based on DNS. In Sect. 4, we compare DNS with other existing non-dominated sorting methods. In Sect. 5, we test the proposed MOGA using some numerical benchmarks and compare its numerical performance with other MOEAs. Section 6 concludes the paper.

2 Related works

In this section, we first review some basic definitions of multi-objective optimization, then some existing non-dominated sorting methods, and finally propose the framework of genetic algorithm.

2.1 Some basic definitions of MOP

The general mathematical model of MOP is

$$\begin{aligned} \text{(MOP) }\quad \left\{ \begin{array}{ll} \text{ Minimize }&{}F(\varvec{x})\\ \text{ Subject } \text{ to } &{}\varvec{x}\in X. \end{array}\right. \end{aligned}$$

(1)

Here $F:\mathbb {R}^n\mapsto \mathbb {R}^m$ is a vector function and $X\subseteq \mathbb {R}^n$ is a box constraint. In this paper, we also call X the decision variable space, and its image set $F(X)=\{F(\varvec{x})|\varvec{x}\in X\}$ the objective function value space.

Given two vectors $\varvec{y}=(y_1,y_2,\ldots ,y_m)^T$ and $\varvec{z}=(z_1,z_2,\ldots ,z_m)^T\in \mathbb {R}^m,$ define:

• (1) $\varvec{y}=\varvec{z}\Leftrightarrow y_i=z_i$ for all $i=1,2,\ldots ,m$;

• (2) $\varvec{y}\prec \varvec{z}\Leftrightarrow y_i< z_i$ for all $i=1,2,\ldots ,m$;

• (3) $\varvec{y}\preceq \varvec{z}\Leftrightarrow y_i\le z_i$ for all $i=1,2,\ldots ,m$, and $\varvec{y}\ne \varvec{z}$.

Obviously, if $\varvec{y}\prec \varvec{z}$, then $\varvec{y}\preceq \varvec{z}$. In this paper, if $\varvec{y}\preceq \varvec{z}$, we say $\varvec{y}$ dominates $\varvec{z}$ or $\varvec{z}$ is dominated by $\varvec{y}$; if $\varvec{y}\npreceq \varvec{z}$ and $\varvec{z}\npreceq \varvec{y}$, we say $\varvec{y}$ and $\varvec{z}$ are non-dominated.

Let $Y\subseteq \mathbb {R}^m$ and $\varvec{y}^*\in Y$, if there is no $\varvec{y}\in Y$ such that $\varvec{y}\preceq \varvec{y}^*$ (or $\varvec{y}\prec \varvec{y}^*$), then $\varvec{y}^*$ is called an efficient point (or weakly efficient point) of Y. Suppose that $\varvec{x}^*\in X$, if there is no $\varvec{x}\in X$ such that $F(\varvec{x})\preceq F(\varvec{x}^*)~(\text{ or } F(\varvec{x})\prec F(\varvec{x}^*)),$ i.e., $F(\varvec{x}^*)$ is an efficient point (or weakly efficient point) of the objective function value space F(X), then $\varvec{x}^*$ is called an efficient solution (or weakly efficient solution) of Problem (1).

Efficient and weakly efficient solutions can also be defined using cone or partial order. Another name of the efficient solution is Pareto solution. The meaning of Pareto solution is that, if $\varvec{x}^*$ is a Pareto solution, there is no feasible solution $\varvec{x}\in X$, such that $f_i(\varvec{x})\le f_i(\varvec{x}^*)$ for all $i\in \{1,2,\ldots ,m\}$ and there is at least one $i_0\in \{1,2,\ldots ,m\}$ such that $f_{i_0}(\varvec{x})<f_{i_0}(\varvec{x}^*)$. In other words, $\varvec{x}^*$ is the best solution in the sense of “$\preceq$”. Another intuitive interpretation of Pareto solution is that it cannot be improved with respect to any objective without worsening at least one of the others. Weakly efficient solution means that if $\varvec{x}^*$ is a weakly efficient solution, then there is no feasible solution $\varvec{x}\in X$, such that any $f_i(\varvec{x})$ of $F(\varvec{x})$ is strictly better than that of $F(\varvec{x}^*)$. In other words, $\varvec{x}^*$ is the best solution in the sense of “$\prec$”. Obviously, an efficient solution is also a weakly efficient solution. The set of efficient solutions is denoted by $\mathcal {P}^*$; its image set $F(\mathcal {P}^*)$ is called the Pareto frontier, denoted by $\mathcal {PF}^*$.

2.2 Existing non-dominated sorting methods

Non-dominated sorting is a critical step in MOEAs. A large percentage of computational cost is spent on non-dominated sorting for it involves numerous comparisons. Until now, there are more than ten different non-dominated sorting methods (Long et al. 2020). The earliest one is the naive non-dominated sorting (Srinivas and Deb 1994). In this method, in order to find whether a solution is dominated, the solution has to do dominance comparisons with all the other solutions, which leads a numerical complexity of $O(mN^3)$ in the worst case. Here, m stands for the number of objectives, N stands for the population size, the same below. The naive approach does not record any dominance comparison result, which in return cause a lot of repeated computation. The fast non-dominated sorting (Deb et al. 2002) overcomes this drawback by calculating two entities for each solution p: (1) domination count $n_p$, the number of solutions which dominate the solution p; and (2) dominate set $S_p$, a set of solutions that the solution p dominates. This modification reduces the computational complexity of the naive non-dominated sorting to $O(mN^2)$.

McClymont and Keedwell (2012) proposed climbing sorting and deductive sorting. The climbing sorting is similar to the bubble sorting for real number sequence. In order to locate a non-dominated solution, the candidate is shifted from dominated solution to the dominating one until all the solutions in the current population are visited. The final candidate must be a non-dominated solution. The deductive sorting is similar to the selection sorting for real number sequence. In the deductive sorting, one successively check each solution; once the current solution is found to be dominated, abandon it. If the current solution dominates all the other solutions, or is non-dominated with the others, then it is identified as a non-dominated solution. The climbing sorting works well on populations with large number of Pareto frontiers. On the contrary, the deductive sorting is good at sorting population with small number of Pareto frontiers. The average computational complexity of the climbing sorting and deductive is both $O(mN^2)$.

Another idea to save dominance comparisons is to discard the identified non-dominated solutions, Corner sorting (Wang and Yao 2013) applies this idea. Some of the non-dominated sorting method consider the partial order of the solutions in the populations. For example, the efficient non-dominated sorting (Zhang et al. 2014) first sorts solutions using the common partial order of m-dimensional vector. This sorted population has a very important feature: solution $\varvec{p}_m$ will never be dominated by a solution $\varvec{p}_n$ if $m<n$. As shown in Table (III) in Zhang et al. (2014), computational complexity of the efficient non-dominated sorting is $O(mN^2)$ in the worst case, while $O(mN\sqrt{N})$ or $O(mN\log N)$ in the best case (depends on the different methods used in partial order.)

In order to avoid repeated dominance comparisons, one can record the results of dominance comparisons in a matrix. This idea is applied in the dynamic non-dominated sorting (Long et al. 2020) where a $N\times N$ matrix with entries $1,-1,0$ is used to record the dominance relationships between solutions. The computational complexity of the dynamic non-dominated sorting is $O(mN^2)$. Another method applying this idea is the dominance degree sorting (Zhou et al. 2017). This method first calculates a comparison matrix for each objective, then builds a dominance degree matrix by adding these comparison matrices together. The dominance relationship can be found in the dominance degree matrix. In the dominance degree sorting, only the real number sequence sorting is needed. This makes it much faster than the method based on dominance comparison. In this paper, we improve the dynamic non-dominated sorting by hybridizing it with the dominance degree sorting. The computational complexity of the improved dynamic non-dominated sorting will decrease to $O(mN\log N)$.

2.3 Genetic algorithm

In computer science and operations research, genetic algorithm (GA), which is inspired by the process of natural selection, is one of the most popular evolutionary algorithms. It is introduced by John Holland in 1960s, and then developed by his students and colleagues at the University of Michigan between 1960s and 1970s (Goldberg 1989). Over the last two decades, GA was increasingly enriched by plenty of literatures (Harik et al. 1999; Mirjalili 2019; Whitley 1994). Nowadays, GA are applied in a wide range of areas, such as mathematical programming, combinational optimization, automatic control, image processing, etc..

Suppose P(t), O(t) and S(t) represent parents, offsprings and selection pool of the $t^{th}$ generation, respectively. The general structure of GA is described in Algorithm 1.

The implementation of GA may be various in different situations. For example, some implementation generate $O_c(t)$ and $O_m(t)$ independently based on P(t), while some implementation first generates $O_c(t)$ based on P(t) and then yields $O_m(t)$ based on $O_c(t)$. Furthermore, crossover, mutation and selection operators are alterable in GA. Different designs of these operators lead to different numerical performance of GA.

It is worth to notice that, for notation P(t), O(t) and S(t), we do not specify whether they are decision variables (i.e., $P(t)/O(t)/S(t)\subset X$) or objective function values (i.e., $P(t)/O(t)/S(t)\subset F(X)$) since they are bijection through objective function $F(\varvec{x})$. One can distinguish them according to the contexts. For example, when calculating the Pareto frontier, they are seen as objective function values; when running crossover and mutation, they are seen as decision variables.

3 Dynamic non-dominated sorting genetic algorithm

In this section, we first propose an improved dynamic non-dominated sorting; then based on the improved dynamic non-dominated sorting, we design a novel multi-objective optimization genetic algorithm titled the dynamic non-dominated sorting genetic algorithm.

3.1 Dynamic non-dominated sorting

According to the definition of efficient point, in order to detect the non-dominated points in a selection pool, each solution must compare with the others in the selection pool to find if it is dominated. In the naive sorting (Deb 1999), the non-dominated points in different Pareto frontiers are detected one by one, so there exist numerous repetitive dominance comparisons between some candidate pairs, which in a large extent increases the computational complexity of native sorting. In this subsection, we tackle this shortage by recording the result of dominance comparison between each candidate pairs, which in return, avoids any repeated comparison. This idea is inspired by the dynamic programming, so we call it the dynamic non-dominated sorting, abbreviated as DNS.

Suppose S(t) is the current selection pool who has N solutions. The aim of non-dominated sorting is to identify all the Pareto frontiers in S(t). We denote the $i^{th}$ Pareto frontier $l_i$ ($1\le i\le i_{max}$). Obviously, we have $1\le i_{max}\le N$, $i_{max}=1$ means that all the solutions in S(t) are non-dominated, $i_{max}=N$ means that each Pareto frontier has only one solution. We use a $N\times N$ matrix D to record the dominance relationship in S(t), where

$$\begin{aligned} d_{ij(i\ne j)}=\left\{ \begin{array}{ll} 1,&{} \text{ if } \varvec{y}_i \text{ dominates } \varvec{y}_j, \text{ i.e. },\varvec{y}_i\preceq \varvec{y}_j;\\ -1,&{} \text{ if } \varvec{y}_i \text{ is } \text{ dominated } \text{ by } \varvec{y}_j, \text{ i.e. }, \varvec{y}_i\succeq \varvec{y}_j;\\ 0,&{} \text{ if } \varvec{y}_i \text{ and } \varvec{y}_j \text{ are } \text{ non-dominated }. \end{array}\right. \end{aligned}$$

(2)

The diagonal entries of D are set to be 0, i.e., $d_{ii}=0,~i=1,2,\ldots ,N$. The non-dominated solutions can be detected using D. Each row of D stands for a solution. If there is no $-1$ in the $i^{th}$ row, that means $\varvec{y}_i$ is not dominated by any other solution, i.e., $\varvec{y}_i$ is non-dominated. Finding all rows with this feature, we can detect all the non-dominated solutions. These solutions consist the first Pareto frontier of the selection pool S(t). Assign $l_i=1$ to these points. When detecting the second Pareto frontier, solutions on the first Pareto frontier (already identified) should not be involved any more. So, we shrink D by discarding the rows and columns whose solutions are already identified as in the first Pareto frontier. Then, repeat the same process to detect the second Pareto frontier and so forth, until all the solutions are identified, i.e., the matrix D becomes empty.

The procedure of the dynamic non-dominated sorting is presented in Algorithm 2. The input is the current selection pool S(t); its size is N; the output is the Pareto frontier index $l_i,~i=1,2,\ldots ,N$. Step 1 computes the $N\times N$ dynamic matrix D. Step 2 detects the current non-dominated solution using the current D. Step 3 shrinks the matrix D by ignoring rows and columns corresponding to the detected non-dominated solutions in Step 2. Then if D is not empty, go back to Step 2 to detect non-dominated solution in the next Pareto frontier; otherwise, the process of non-dominated detection finishes.

The index $l_i$ is called the Pareto frontier index. The smaller $l_i$ is, the better elitism $\varvec{y}_i$ is, i.e., the solution with smaller Pareto frontier index is closer to the real Pareto frontier.

In Algorithm 2, computing the dynamic matrix D (Step 1) is a key step. We present a novel efficient method to address this issue in the next subsection.

3.2 Dynamic matrix

The computation of the dynamic matrix D is the core step of the dynamic non-dominated sorting; most of the computational cost is spent on this step. If we use the dominance comparison to calculate the dynamic matrix D, $N(N-1)/2$ times of dominance comparisons are needed, which makes the computational complexity of the dynamic non-dominated sorting $O(mN^2)$. Through the transitivity of dominating can be used in practice, it still cannot reduce the computational complexity dramatically. In this subsection, we apply the idea presented in the dominance degree sorting (Zhou et al. 2017), introducing a faster method to calculate the dynamic matrix.

The process of calculating the dominance matrix is as follows. Firstly, for each objective, we calculate a $N\times N$ comparison matrix $C^{f_k}~(1\le k\le m)$ which records the comparison relationship of solutions on this objective. Take the first objective, for example; suppose vector $\varvec{w}^{f_1}=(\varvec{p}_1^{f_1},\varvec{p}_2^{f_1},\ldots ,\varvec{p}_N^{f_1})$, where $\varvec{p}_j^{f_1}$ is the first objective value of solution $\varvec{p}_i~(0\le i\le N)$, then the entry of $C^{f_1}$ is

$$\begin{aligned}C_{ij}^{f_1}=\left\{ \begin{array}{ll} 1,&{}\text {if } \varvec{p}_i^{f_1}< \varvec{p}_j^{f_1},\\ 0,&{}\text {otherwise}. \end{array}\right. \end{aligned}$$

$C^{f_1}$ can be obtained very fast by sorting the entries of $\varvec{w}^{f_1}$. Here, $\varvec{w}^{f_1}$ is a real number sequence; we can use any real number sorting method, such as quick sorting, to sort it. Without loss of generality, suppose $\varvec{w}^{f_1}=(\varvec{p}_1^{f_1},\varvec{p}_2^{f_1},\ldots ,\varvec{p}_N^{f_1})$ is already sorted in ascending order, then all the entries except the first one in the first row (when $i=1$) are 1, since $\varvec{p}_j^{f_1}>\varvec{p}_1^{f_1}$ holds for all $j=2,3,\ldots ,N$. Similarly, entries except the first and second ones in the second row (when $i=2$) are all 1. Inferring in this way, we will finally obtain

$$\begin{aligned} C^{f_1}=\left( \begin{array}{lllll} 0&{}1&{}1&{}\cdots &{}1\\ 0&{}0&{}1&{}\cdots &{}1\\ &{}&{}\cdots &{}\cdots &{}\\ 0&{}0&{}0&{}\cdots &{}0 \end{array}\right) . \end{aligned}$$

Secondly, adding all the comparison matrix together to get a dominance degree matrix C, i.e.,

$$\begin{aligned} C=C^{f_1}+C^{f_2}+\cdots +C^{f_m}. \end{aligned}$$

To eliminate the effect of these solutions with identical values for all objectives, we set the corresponding element of C to be zero. For example, if $\varvec{p}_i$ and $\varvec{p}_j$ are identical respect to all objectives, we set $C_{ij}=0$. Obviously, according to this rule, $C_{ii}=0$ for all $i=1,2,\ldots ,N$.

Thirdly, the elements of C reflect the dominance relationship between solutions. For example, $\varvec{p}_i$ dominates $\varvec{p}_j$ means $\varvec{p}_i^{f_k}\le \varvec{p}_j^{f_k}$ (i.e., $C_{ij}^{f_k}=1$) for any $k\in \{1,2,\ldots ,m\}$, which yields $C_{ij}=m$. So, we have $\varvec{p}_i$ dominates $\varvec{p}_j$ if and only if $C_{ij}=m$. The dynamic matrix can be directly obtained according to the dominance degree matrix C. That is, if $C_{ij}=m$, set $D_{ij} =1$ and $D_{ji}=-1$; otherwise, reset $D_{ij}=0$.

The pseudocode of calculating the dynamic matrix is presented in Algorithm 3

The main computational effort of the dynamic matrix is on the computation of the comparison matrices $C^{f_k}~(k=1,2,\ldots ,m)$. Intuitively, for each objective, function values are compared with each other, so $N(N-1)/2$ real number comparisons are needed, which makes the numerical complexity of dynamic matrix $O(mN^2)$. However, this process can be improved by applying a real number sequence sorting method, such as quick sort (Zhou et al. 2017). The computational complexity of the quick sort is $O(N\log N)$, so the computational complexity of dynamic matrix is $O(mN\log N)$.

3.3 Dynamic non-dominated sorting genetic algorithm (DNSGA)

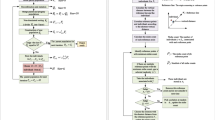
In this subsection, we present a novel multi-objective genetic algorithm. Non-dominated sorting in this algorithm applies the dynamic non-dominated sorting presented above, so we call this algorithm the dynamic non-dominated sorting genetic algorithm, abbreviated as DNSGA. The process of DNSGA is presented in Fig. 1.

Fig. 1

DNSGA algorithm

In the step of crossover and mutation, self-adaptive simulated binary crossover operator (SSBX) (Deb et al. 2007) and power mutation operator (PM) (Deep and Thakur 2007) are applied. The SSBX operator is a real-parameter recombination operator which is commonly used in the evolutionary algorithm (EA) literature. The operator involves a parameter which dedicates the spread of offspring solutions vis-a-vis that of the parent solutions. The PM operator is based on the power distribution. It is proved to have the same performance as the widely used non-uniform mutation operator (Deep and Thakur 2007).

For the selection step, the binary tournament selection operator used in NSGA-II is still applied in DNSGA. The binary tournament selection operator is mainly constituted by the fast non-dominated sorting and the crowded-comparison operator. In DNSGA, we replace the fast non-dominated sorting by the dynamic non-dominated sorting proposed above.

4 Comparison of non-dominated sorting methods

In order to clarify the improvement of the dynamic non-dominated sorting (DNS), this subsection compares it with other non-dominated sorting methods. Except DNS proposed in this paper, four other referential non-dominated sorting methods are considered: the fast non-dominated sorting (FNS) (Deb et al. 2002), climbing sorting (CS) (McClymont and Keedwell 2012), deductive sorting (DS) (McClymont and Keedwell 2012) and the dominance degree non-dominated sorting (DDNS) (Zhou et al. 2017). FNS is one of the earliest Pareto sorting approaches. It is updated from the naive non-dominated sorting (Deb 1999). The computational complexity of FNS is $O(mN^2)$. CS follows dominating relationships between solutions and climbs up the graph toward the Pareto frontier. The key process of CS is to change the considering solution from any dominated one to dominating one until a non-dominated solution (at the current Pareto frontier) has been identified. The computational complexity of CS is $O(mN^2)$. DS accesses each solution based upon the natural order of the population. The candidate solution compares with all its following solutions but not with its previous ones. The average numerical complexity of DS is $O(mN^2)$, but in the best case that each Pareto frontier has only one solution, it decreases to O(mN). DDNS is one of the state-of-the-art non-dominated sorting algorithms. Differently from the other non-dominated sorting algorithms, DDNS does not compare two solutions to identify dominating relationship. Instead, it constructs a comparison matrix which stores the relationship of all solutions with respect to each objective. Then a dominance degree matrix can be obtained by adding these comparison matrices together. Finally, Pareto ranking of the population can be obtained by analyzing the dominance degree matrix. If we use quick sort in ranking each objective, the computational complexity of DDNS is $O(mN\log N)$.

We compare DNS with these referential non-dominated sorting methods introduced above. For metrics of numerical performance, time consumption and number of comparisons are considered. Experiments are divided into three groups: (1) performance with respect to the variation of the population size, (2) performance with respect to the variation of the number of Pareto frontiers and (3) performance with respect to the variation of the number of objectives. We use the fixed features population generator (Long et al. 2020) to generate test populations. This generator can generate test populations with certain features, such as having prefixed number of points, prefixed number of Pareto frontier and prefixed number of points in each Pareto frontier. The generated test populations are listed in Table 1 where m stands for the number of objectives, k stands for the number of Pareto frontiers and N is a vector standing for the number of points in each Pareto frontiers. In the series (1) test populations, the number of objectives and Pareto frontiers is fixed, while the number of points in each Pareto frontier is even and increases from 12 to 30 with a step of 2. In the series (2) test populations, the number of objectives is fixed, while the number of Pareto frontiers increases from 1 to 10 with step of 1, each test population has 150 points in total evenly distributed in each Pareto frontier. In the series (3) test populations, the number of Pareto frontiers and number of points in each Pareto frontier are fixed, while the number of objectives arises from 2 to 10 with step of 1.

Table 1 Three series of test populations

Results of the numerical experiments are illustrated in Figs. 2, 3 and 4. In Fig. 2b, FNS needs much more comparisons than the other four methods, CS and DS need exact the same amount of comparisons, DDNS and DNS too but less than CS and DS. As with the increase of population size, the number of comparisons for FNS increases much faster than the other four methods, then DS and CS, the increasing trend of DDNS and DNS is relatively gentle. The same features demonstrated in Fig. 2a for time consumption. It is worth to note that DDNS spent slightly less time than DNS.

Figure 3 shows that, as the number of Pareto frontiers increases, the time consumption and the number of comparisons decrease for CS and DS. DDNS and DNS stay in a lower level stably, while FNS stably appears in a very high level.

It is shown in Fig. 4 that the time consumption and the number of comparisons increase with the rise in the number of objectives. This is reasonable because the increase in the number of objectives must increase the number of comparisons, which in return increases the time consumption. But the increase rates are different. FNS has the steepest trend, CS and DS are less, and DDNS and DNS only have a slight increase.

In summary, the computation complexity of DNS keeps stable if the population size is fixed, and has a slight increase if the population size and number of objectives increase. This statement agrees with the theoretical complexity analysis of DNS. DNS outperforms FNS, CD and DS and performs the same as DDNS which is considered as the most efficient non-dominated sorting method (Zhou et al. 2017).

Fig. 2

Numerical performance with respect to the variation of population size. In this test, the number of objectives $m=3$, the number of Pareto frontiers $k=5$, the population size is from 60 to 150 with increment 10, and each Pareto frontier has the same number of solutions

Fig. 3

Numerical performance with respect to the variation of Pareto frontiers. In this test, the number of objectives $m=3$, the number of Pareto frontiers increases from 1 to 10, the population size $N=150$, and each Pareto frontier has almost the same number of solutions

Fig. 4

Numerical performance with respect to the variation of objectives. In this test, the number of objectives increases from 2 to 10, the number of Pareto frontiers $k=5$, the population size is $N=150$, and each Pareto frontier has the same number of solutions

5 Numerical experiments

In this section, we investigate the numerical performance of DNSGA. Firstly, we further compare the sorting methods FNS and DNS by embedding them into the same MOEA (NSGAII Deb et al. 2002). Secondly, we compare DNSGA with some of the other popular MOEAs, including MOEA/D (Zhang and Li 2007), SparseEA (Tian et al. 2019a), PPS (Fan et al. 2019) and LSMOF (Tian et al. 2019b). Finally, we investigate the numerical performance of DNSGA when scaling the number of variables.

5.1 Test problems

We use five series of test problems in the numerical experiments. They are ZDT series (Zitzler et al. 2000), DTLZ series (Deb et al. 2005), UF series (Zhang et al. 2008), BT series (Li et al. 2016) and LSMOP series (Cheng et al. 2016). Features of these test problems including number of objective functions m, number of dimensions n, variable bounds X and references are demonstrated in Table 2. All test problems are scalable respect to the number of dimensions; the DTLZ series is also scalable respect to the number of objective functions. Numbers in the brackets are the number of dimensions or the number of objectives we set in our experiments. Details of the objective functions, referential Pareto frontiers and Pareto solutions refer to the references.

Table 2 Test problems

5.2 Referential algorithms and parameter setting

We use five referential MOEAs in the numerical experiments. They are NSGAII (Deb et al. 2002), MOEA/D (Zhang and Li 2007), SparseEA (Tian et al. 2019a), PPS (Fan et al. 2019) and LSMOF (Tian et al. 2019b). Among them, NSGAII is one of the most popular MOEAs based on genetic algorithm. In the past decades, NSGAII got thousands of citations. MOEA/D is a successful multi-objective optimization method based on decomposition; it is often used as a standard in numerical experiments. SparseEA, PPS and LSMOF are three of the latest MOEAs; note that SparseEA and LSMOF are originally designed for solving large-scale multi-objective optimization problems. Among the five referential algorithms, NSGAII is used to verify the improvement of the sorting method DNS comparing with the traditional one FNS, while the other four referential algorithms are used to investigate the numerical performance of the proposed method DNSGA. The implementation of these algorithms is based on the PlatEMO (Tian et al. 2017).

For the sake of fair comparison, parameters for all algorithms are uniformly set as far as possible. To be specific, the population size is set to be 100, the maximum number of objective function evaluations is set to be 100,000, and the maximum number of iterations is set to be 500. The maximum number of objective function evaluations and iterations is taken as stop criteria for all algorithms. In order to achieve statistic performance, all the test are run 30 times independently, and the mean and standard deviation of the performance metrics are recorded. The other parameters for certain algorithms are set as the default in PlatEMO.

5.3 Performance metrics

Many performance metrics have been proposed to evaluate the numerical performance of MOGAs (Zhou et al. 2011). There are two goals for evaluation metrics: (1) measure the convergence of the obtained Pareto frontier, and (2) measure the diversity of the obtained Pareto frontier.

We use the performance metric IGD (Long et al. 2015) to evaluate the numerical performance. Suppose that $P^*$ is a set of uniformly distributed points belonging to the real Pareto frontier. It can be taken as a standard representation of the real Pareto frontier. Let A be a set of solutions obtained by a certain solver, then IGD is defined as the average distance from $P^*$ to A:

$$\begin{aligned} IGD(A,P^*)=\frac{\sum _{v\in P^*} d(\varvec{v},A)}{|P^*|}, \end{aligned}$$

where d(v, A) is the minimum Euclidean distances between v and the points in A, i.e.,

$$\begin{aligned} d(\varvec{v},A)=\min _{y\in A}\parallel \varvec{v}-\varvec{y}\parallel \quad \varvec{v}\in P^*. \end{aligned}$$

In fact, $P^*$ is a sample set of the real Pareto frontier. If $|P^*|$ is large enough to approximate the Pareto frontier very well, ${{IGD}}(A,P^*)$ could measure both the diversity and convergence of A. This is also the reason that we choose IGD as the evaluation metric for this paper. A smaller ${{IGD}}(A,P^*)$ means the set A is closer to the real Pareto frontier and has better diversity.

5.4 NSGAII with FNS and DNS

In this subsection, we compare FNS and DNS by embedded them into the same MOEA. Since FNS is originally used in NSGAII, we replace FNS in NSGAII by DNS to build a new MOEA. In the following, we call the NSGAII with FNS NSGAII-FNS, and call the NSGAII with DNS NSGAII-DNS. Note that NSGAII-FNS and NSGAII-DNS are only different in the non-dominated sorting method.

In order to achieve fair competition and statistical performance, all the tests are run for 30 times independently, and the mean and standard deviation of two performance metrics, CPU time and IGD value, are recorded. In the following tables, the best record for a certain performance metric is marked as in gray cell. Besides, the Wilcoxon rank sum test with a significant level of 0.05 is adopted to perform statistical analysis of the experimental results, where the symbols “+”,“-” and “=” indicate that the result by NSGAII-FNS are significantly better, significantly worse and statistically similar to that obtained by NSGAII-DNS, respectively.

As shown in Table 3, NSGAII-DNS spends significantly less CPU time than NSGAII-FNS on all test problems, which further verifies that DNS is faster than FNS. As for the IGD value, Table 3 shows that 38 out of the total 39 test problems are statistically similar. This is reasonable for that NSGAII-FNS and NSGAII-DNS are only different in the non-dominated sorting method, which affects the CPU time but not the final solutions.

In Fig. 5, we demonstrate the decrease curve of IGD of the first test problem in each series. Because inside a series, the test problems have more or less the same structure, the IGD curve of one problem can represent the others. For each test problem, 10 samples of IGD value are taken evenly from 1000 to 10,000 times of objective function evaluations. From Fig. 5, the IGD value of NDGAII-DNS and NSGAII-FNS converges to almost the same value for problems ZDT1 and DTLZ1. Figs. 5d, e shows that NSGAII-DNS outperforms NSGAII-FNS for problems BT1 and LSMOP1. For problem UF1, Fig. 5c shows that NSGAII-FNS outperforms NSGAII-DNS.

Table 3 Numerical comparison between NSGAII-FNS and NSGAII-DNS

Fig. 5

The decreasing trend of IGD

In order to verify whether the numerical results of 30 runs are normally distributed, Chi-square test with confidential level $\alpha =0.1$ is applied. The results is positive; normal distribution of the numerical results of 30 runs holds for all test problems. We also use Kruskal–Wallis test (H-test) to see whether the difference between NSGAII-FNS and NSGAII-DNS is significant. Results show that the difference with respect to CPU time is significant, but not significant respect to IGD value.

5.5 Compare DNSGA with other MOEAs

In this subsection, we compare the numerical performance of the proposed method DNSGA with other existing MOEAs. The referential MOEAs are MOEA/D, SparseEA, PPS and LSMOF. We investigate average and standard deviation of CPU time and IGD value. Each test problem runs 30 time independently. The statistical results are shown in Tables 4 and 5. Gray cell represents the best values of a certain performance metric.

Table 4 illustrates the CPU time of comparing DNSGA with other MOEAs. It can be seen that DNSGA outperforms the other MOEAs on all test problems except LSMOF on problem ZDT2. This indicates that DNS indeed accelerates the speed of non-dominated sorting. Table 5 illustrates the IGD value of comparing DNSGA with other MOEAs. It can be observed that SparseEA performs the best on the ZDT series and PPS performs the best on most problems of the LSMOP series. The proposed DNSGA outperforms the others on DTLZ6, UF1-2, UF6-7, BT1-5 and BT9. Statistically, in terms of the Wilcoxon rank sum test, the proportion of the test instances where DNSGA performs significantly better than MOEA/D, SparseEA, PPS and LSMOF is 25/39, 25/39, 26/39 and 19/39, respectively.

Fig. 6

The decreasing trajectory of IGD

H tests of CPU time and IGD value show the same conclusion as the above analysis. For CPU time, DNSGA has significant difference with the other methods, but for IGD value, the difference is not significant.

Table 4 CPU time of comparing DNSGA with other MOEAs

Table 5 IGD value of comparing DNSGA with other MOEAs

For further observation, Fig. 6 depicts the decrease trajectory of IGD value on the first case of each test problem series. Ten samples are recorded after every 1000 times of objective function evaluation. It can be seen from the figures that the IGD value of DNSGA may start at a high value, but can dramatically decrease to a promising zone. For all the test problems, IGD value obtained by DNSGA can converge to a competitively small value. For problem BT1, DNSGA outperforms the other MOEAs.

5.6 Scalability with respect to the number of variables

In this subsection, we investigate the performance of DNSGA with respect to the scaling of decision variables. In this experiment, only SparseEA and LSMOF are selected as referential algorithms for they are originally designed for large-scale multi-objective optimization, test problems are also restricted in the LSMOP series (Cheng et al. 2016). There are 9 problems in the LSMOP series, the number of subcomponent in each variable group $n_k$ is set to be 5, the number of objectives is set to be 2 and 3, and the number of decision variables is set to be 10, 30, 50, 100, 300, 500, and 1000. Test problems in the LSMOP series can be categories into three groups (LSMOP 1-4, LSMOP5-8 and LSMOP9) according to their structure of Pareto frontiers. So, for the sake of saving space, we demonstrate the performance of LSMOP1, LSMOP5 and LSMOP9 for 2 objectives and the performance of LSMOP2, LSMOP6 and LSMOP9 for 3 objectives.

Table 6 CPU time for scaling the number of decision variables (2 objectives)

Table 7 IGD value for scaling the number of decision variables (2 objectives)

Table 8 CPU time for scaling the number of decision variables (3 objectives)

Table 9 IGD value for scaling the number of decision variables (3 objectives)

Table 6 illustrates the CPU time of SparseEA, LSMOF and DNSGA on solving 2-objective LSMOP1, LSMOP5 and LSMOP9. From the table, DNSGA outperforms SparseEA on all cases except LSMOP9 with 10 decision variables. Comparing between LSMOF and DNSGA, for LSMOP1 and LSMOP9, DNSGA is faster when dimension is small and LSMOF is faster when dimension becomes large. However, for LSMOP5, DNSGA is always faster than LSMOF except when dimension is 10. Statistically, the proportion of test instances where DNSGA performs significantly faster than SparseEA and LSMOF is 20/21 and 14/21, respectively. Table 8 illustrates the CPU time of the three compared MOEAs on solving 3-objective LSMOP2, LSMOP6 and LSMOP9. From the table, DNSGA is still faster than SparseEA for all cases except when dimension is 10. Except LSMOP9 with dimension equals 100, 500 and 1000, DNSGA is also faster than LSMOF. In terms of the Wilcoxon rank test, the proportion of test cases where DNSGA performs significant faster than SparseEA and LSMOF are both 18/21. Tables 6 and 8 verify that DNSGA outperforms SparseEA and LSMOF in terms of CPU time.

Tables 7 and 9 illustrate the IGD value of solving 2-objective LSMOP1, LSMOP5, LSMOP9 and 3-objective LSMOP2, LSMOP6, LSMOP9, respectively. From Table 7, DNSGA outperforms the other two MOEAs on problem LSMOP1 with dimension of 30 and 50 and problem LSMOP5 with dimensions of 30, 50 and 100. From Table 9, DNSGA outperforms the other two MOEAs only on problem LSMOP2. Tables 7 and 9 reveal that, for solving large-scale MOPs, the solution obtained by DNSGA is not as good as LSMOF and SparseEA. This is reasonable for LSMOF and SparseEA which are originally designed for large-scale MOPs. So, some modifications need to be made before NSGA can be used to efficiently solve large-scale MOPs.

Finally, Fig. 7 depicts the trend of CPU time and IGD value for DNSGA solving LSMOP9 with different numbers of decision variables. It is obvious that both CPU time and IGD value increase with the rise in dimensions. The CPU time spent on 2-objective problems and 3-objective problems is very close, while the IGD values are dramatically different, and the gap increases as the number of dimension rises. This means that, for scaling the number of objectives, DNSGA is not sensitivity on CPU time but on IGD value.

6 Conclusion

In this work, we have proposed a novel non-dominated sorting method, and based on it, a novel multi-objective genetic algorithm. The computational complexity of the proposed non-dominated sorting method is $O(mN\log N)$, which is the same as the current best. The numerical comparison between the proposed non-dominated sorting method and some other existing ones still shows its efficiency and outperformance. The novel multi-objective genetic algorithm is obtained by embedding the proposed non-dominated sorting method into the framework of NSGAII. Numerical experiments show that the proposed multi-objective genetic algorithm is efficient and promising.

Fig. 7

CPU time and IGD value for scaling decision variables

For large-scale multi-objective optimization problem, the proposed method has no obvious advantage comparing with some methods specially designed for large-scale multi-objective optimization problem. The future work of the research is to extend the proposed method to large-scale multi-objective optimization problems.