Abstract
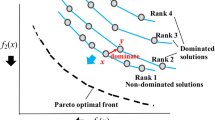
Dominance resistance is a challenge for Pareto-based multi-objective evolutionary algorithms to solve the high-dimensional optimization problems. The Non-dominated Sorting Genetic Algorithm III (NSGA-III) still has such disadvantage even though it is recognized as an algorithm with good performance for many-objective problems. Thus, a variation of NSGA-III algorithm based on fine final level selection is proposed to improve convergence. The fine final level selection is designed in this way. The θ-dominance relation is used to sort the solutions in the critical layer firstly. Then ISDE index and favor convergence are employed to evaluate convergence of individuals for different situations. And some better solutions are selected finally. The effectiveness of our proposed algorithm is validated by comparing with nine state-of-the-art algorithms on the Deb-Thiele-Laumanns-Zitzler and Walking-Fish-Group test suits. And the optimization objectives are varying from 3 to 15. The performance is evaluated by the inverted generational distance (IGD), hypervolume (HV), generational distance (GD). The simulation results show that the proposed algorithm has an average improvement of 55.4%, 60.0%, 63.1% of 65 test instances for IGD, HV, GD indexes over the original NSGA-III algorithm. Besides, the proposed algorithm obtains the best performance by comparing 9 state-of-art algorithms in HV, GD indexes and ranks third for IGD indicator. Therefore, the proposed algorithm can achieve the advantages over the benchmarks.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In engineering practice, people often face problems with multiple objectives, which are called multi-objective problems (MOPs). The MOPs with at least four objectives are informally known as many-objective problems (MaOPs) [1]. And there always exists MaOPs in real life, such as water distribution system design [2], intrusion detection [3], green vehicle routing problem [4]. Multi-objective evolutionary algorithms (MOEAs) is usually used to solve MOPs and MaOPs, which can be divided into decomposition-based [5,6,7,8], indicator-based [9, 10] and Pareto-based [11,12,13] algorithms. However, it should be pointed that the MOEAs confront three challenges when handling MaOPs, namely dominance resistance (DR) phenomenon, dimensional curse and visualization difficulty [1]. To solve the first challenge efficiently, three methods are introduced, including modification on Pareto-dominance relation, indicator-based approach and the enhanced diversity management. The first method suggests modifying the Pareto-dominance relation. The examples include grid dominance [14], θ-dominance [15], fuzzy Pareto-dominance [16], angle dominance [17]. Besides, Bao et al. [18] presented an augmented penalty boundary intersection (APBI) dominance-relation to reach the balance between convergence and diversity. The second way is to replace the Pareto-dominance relation with indicator function for evaluating the quality of solutions. And this method is called the indicator-based approach, including Hypervolume-based MOEAs (SMS-EMOA) [19]. Recently, Li et al. [20] proposed a two-stage algorithm and R2 indicator was used for the first selection with noticeable success. Moreover, the inverted generational distance was used to evaluate the quality of solutions [21]. Even though these methods can deal with MOPs effectively, there are still high computational burdens. The third approach for MaOPs is to enhance diversity management. For example, the NSGA-II [22] algorithm managed the activation and deactivation of the crowding distance to maintain diversity. Another example is the shift-based density estimation (SDE) strategy [23], which utilizes penalties for the non-dominated solutions with poor convergence. In addition, Cai et al. [24] proposed a diversity indicator based on reference vectors to estimate the diversity. The Two-Archive algorithm 2 [25] increased convergence and diversity by adopting two separate archives. And here are some recent solutions [26,26,27,28,30].
As one of the Pareto-based algorithms, NSGA-III [31] had achieved great success in practical application, which replaced the crowding distance operator in the NSGA-II with a clustering operator and used a set of well-distributed reference points to guarantee diversity. Although the NSGA-III algorithm can achieve good diversity, the performance needs to be improved by remedying deficiency or expanding application. Hence, many related studies have been developed. For example, not all reference points may be associated with a well-dispersed Pareto-optimal set in the search process of NSGA-III algorithm. The selection of these reference points with a number of solutions may not take account of all solutions uniformly over the entire Pareto-fronts [32]. Therefore, Jain and Deb proposed A-NSGA-III [32] to overcome this drawback and extended it to solve the constrained problems. θ-DEA [15] based a new dominance relation were presented, aiming to balance the convergence and diversity in many-objective optimization. Moreover, Cai et al. [33] combined clustering with NSGA-III to build a clustering-ranking evolutionary algorithm (crEA). The convergence and diversity of solutions were guaranteed by two archives respectively in NSGA-III-UE and achieved good results [34]. NSGA-III-SE [35] adopted selection and elimination operator to maintain convergence and diversity. Maha [36] integrated ISC-Pareto dominance into C-NSGA-III algorithm to solve the constrained optimization problems. In addition, a novel niche preservation procedure was used in NSGA-III to alleviate the imbalance problem with higher classification accuracy for classes having fewer instances [3]. Yi et al. [37] introduced an improved NSGA-III algorithm with adaptive mutation operator to deal with big data optimization problems. Tavana [38] combined NSGA-III with MOPSO to settle X-bar control charts. Furthermore, a niche-elimination operation and worse-elimination were introduced in NSGA-III to improve convergence [39]. An elimination operator was presented to promote the convergence of NSGA-III algorithm [40].
Although these above algorithms have been successful in some respects, further study is still needed. The NSGA-III algorithm still faces the problem that Pareto dominance cannot provide enough selection pressure. To solve this problem, mating selection and environmental selection (or diversity maintenance mechanism) are two important factors that needed to be considered. For the former condition, the behind idea is that individuals with better convergence should have a better chance of producing offspring. For the latter case, since most individuals are non-dominated solutions in the evolutionary process, it is necessary to weaken the original diversity information or consider other convergence information. Therefore, how to determine the convergence and diversity of individuals and how to integrate convergence information into the diversity maintenance mechanism are two key issues. This paper promotes the convergence of NSGA-III by modifying the environmental selection. We improve NSGA-III algorithm based on fine final level selection and propose NSGA-III-FS algorithm. In the modified algorithm, non-dominated sorting is used to divide the population firstly in environmental selection. Next, a new dominance relation is utilized to classify the individuals in the critical layer. Then the favor convergence and shift-based density estimation are exploited to assess individuals, and some individuals with good performance are selected finally. Compared with the improvement of NSGA-III algorithm in existing literatures, the improved algorithm in this paper has such innovation. Since most algorithms still use fast non-dominant sorting, critical layer selection becomes very important. A more detailed and rigorous solution selection process is adopted, and the solutions are associated with the reference point only at the critical layer, resulting in less computation. Then, a more elaborate case selection process is used to ensure the quality of the solution. Choosing a suitable solution mechanism for each case from different aspects is not well studied by the above developed algorithms. Although more calculations are possible in the selection process, combined with the reference point correlation part, the overall algorithm will not be too many calculations.
The innovation and contribution of this paper are as follows:
-
(1)
The integration of θ-dominance, favor convergence and density estimation ISDE index form a fine final level selection mechanism to optimize solutions. In the fine final level selection, the θ-dominance relation mainly subdivides the solutions in the critical layer. The favor convergence and density estimation ISDE are used for selecting solutions when the number of candidate solutions does not meet or exceeds the demand. The solutions with good convergence are preserved by such a careful solution selection process.
-
(2)
The fine final level selection mechanism is applied to NSGA-III algorithm to improve convergence. A variant of NSGA-III algorithm is formed by combining fine final level selection with a different normalization process. And the effectiveness of the proposed algorithm is evaluated against multiple experiments.
The rest of this paper is organized as follows. Section 2 reviews the NSGA-III algorithm and certain knowledge that will be used later. Section 3 describes the framework of the proposed algorithm together with details. Experimental designs are listed in Section 4. Experimental results and analysis on many-objective optimization are given in Section 5. Section 6 concludes this paper and describes the future work.
2 Preliminary work
2.1 NSGA-III
Compared to NSGA-II, one major difference of NSGA-III is that a uniform set of reference points is selected to maintain diversity. Figure 1 shows the detailed flow of NSGA-III. During the evolution process, the NSGA-III firstly generates a random initial parent population Pt(size = N) and a set of uniform reference points. The offspring population Qt(size = N) is obtained through recombination and mutation. Next, the parent population Ptand offspring populationQt are combined to get a new population Rt(size = 2 N). The NSGA-III algorithm divides Rt into different non-dominated levels (F1, F2, ⋯Fl) using the non-dominated sorting method. Then, it chooses individuals from F1 layer, and continues withF2, ⋯, until the size of St is equal to or greater than N for the first time. After the selection, a new population St (size = N) is constructed, which serves as the parent population Pt + 1 for the next iteration. Generally, St only accepts some individuals in the critical layer (i.e. Fl layer) after storing individuals from F1, ⋯Fl − 1 levels. Finally, the algorithm chooses K = N − |Pt + 1| individuals from Fl level. The following steps are the process of choosing K individuals. (1) The first step is to normalize the objective values of individuals in St. (2) It defines reference lines, which are the origin connecting to reference points on the hyperplane. (3) It calculates the perpendicular distances between the individuals in St and reference lines. (4) Each individual in St is associated with a reference point according to the minimum perpendicular distance. (5) It calculates the niche count for each reference point (i.e. the number of individuals in St associated with each reference point). (6) It selects K individuals based on the calculated niche count [31].
2.2 θ-Dominance relation
In this section, some figures and several basic definitions are utilized to describe the θ-dominance relation. Figure 2 shows the process of θ-dominance and Figure 3 shows the dj, 1(x) and dj, 2(x) of θ-dominance visually. Concepts of θ-dominance are defined as follows:
-
Definition 1:
two solutions x, y ∈ St, x is said to θ-dominate y, denoted by x ≺ θy, iff x ∈ Cj, y ∈ Cj and Fj(x) < Fj(y).
-
Definition 2:
solution x∗ ∈ St is θ-optimal iff there is no other solution x ∈ St dominate x∗.
-
Definition 3:
all the solutions are θ-optimal in St to form the θ-optimal solution set (θ-OS), and the corresponding mapping of θ-OS to the objective space is the θ-optimal front (θ-OF).
Each reference direction is assigned a θ-value if the reference direction exists only one-dimension value greater than 10−4, and then the θ-value of this reference direction is set to 106. Otherwise, the θ-value is 5. Characteristics of the θ-dominance relationship and more details are available in [15].
3 The proposed NSGA-III-FS algorithm
Algorithm 1 describes the main loop of NSGA-III-FS. The proposed algorithm is different from NSGA-III in Step 6–7 as shown in Algorithm 1, and the remaining steps are consistent with the original NSGA-III algorithm. To describe the proposed algorithm in detail, we introduce the proposed algorithm step by step in the following.

Step 1: Reference-point generation
In this paper, the reference-point generation is divided into inner layer and outer layer. And this generation method is the same as the original algorithm, so the original NSGA-III [31] can be referred for the detailed descriptions.
-
Step 2:
Initialization
Like most algorithms, the random population is produced in the first generation and then optimize the population through effective strategies.
-
Step 3:
Identify ideal point and nadir point
The initialized ideal point and nadir point are assigned the minimum and maximum objective values, and these two points are updated by Step 6.
-
Step 4:
Produce offspring
The offspring is generated by a generic operator. It contains adaptive simulate binary crossover and polynomial mutation.
-
Step 5:
Combined population
A combined population is consisting of a parent population and its offspring. Then its size becomes 2 N.
-
Step 6:
Update the ideal point and the nadir point
The essence of normalization process is to solve the inconsistency of objectives. However, the normalization process of the original NSGA-III is to construct a hyperplane on the transformed objective space. This does not fully reflect the entire Pareto front. Thus, the normalization process used in the proposed algorithm is to construct a hyperplane on the original objective space, this is more reflective for the whole Pareto front.
The main difference between NSGA-III-FS and NSGA-III is the identification of nadir point Znad in the normalization. The ideal point Z∗ represents the minimum objective value found so far. The Znad is difficult to be estimated because it takes into account the whole information of Pareto front. Suppose individuals in the population S are needed to be optimized, the extreme point ej on the objective axis fj is found by finding the minimum achievement scalarizing function of the solution x ∈ S. The calculation method is the formula (1) [11].
Where the Wj = (Wj, 1, Wj, 2, ⋯Wj, m)T is the axis direction of objective axisfj, if i ≠ j, Wj, i = 0, else Wj, i = 1 in the formula (1), then theWj, i = 0is replaced byWj, i = 10−6. The \( {Z}_i^{nad} \) is estimated in the previous generation, the extreme pointej = f(x). Finally, m extreme points{e1, e2, ⋯, em}can be obtained after considering m objective axes; and a m-dimensional hyperplane is constructed by those extreme points; a1, a2, ⋯, amrepresent the intercepts on the hyperplane with directions\( {\left(1,{Z}_1^{\ast },\cdots, {Z}_m^{\ast}\right)}^T,{\left({Z}_1^{\ast },1,\cdots, {Z}_m^{\ast}\right)}^T,\cdots, {\left({Z}_1^{\ast },\cdots, {Z}_{m-1}^{\ast },1\right)}^T \). The \( {Z}_i^{nad} \) is updated with the calculated intercept ai.
To have an intuitive understanding of the normalization process differences between NSGA-III and NSGA-III-FS. In addition to the detailed description of Step 6 above, the Fig. 4 shows the comparison of the specific calculation and flow chart of NSGA-III, NSGA-III-FS. The Fig. 5 is a schematic diagram of three-dimensional hyperplane for NSGA-III and NSGA-III-FS algorithms.
-
Step 7:
Environmental selection process
This paper proposes a fine final level selection mechanism for the environmental selection. The design motivation of new selection method is that: For NSGA-III algorithm, the correlation is first made by the shortest distance between solution and reference point after the non-dominated sorting of populationRt. Then it selects solutions mainly considers the least number of solutions closest to the reference point. This does not take full advantage of individual information. While modifying the environmental selection is a way to improve convergence. Thus, this study designs final level selection to improve the convergence of NSGA-III.
More details about the environmental selection of the proposed NSGA-III-FS algorithm can be found in Algorithm 2. In environmental selection, the non-dominated sorting method is also utilized to sort the populationRt firstly. The following steps are constructing a populationStstarting from F1until the size of Stis equal to or greater than N for the first time. If the size of St is equal to N, Stis outputted as the next generation. Otherwise, the fine final level selection is performed from Step 7–7 to Step7–21 in Algorithm 2. The key steps of fine final level selection are described in detail. Principle of fine final-level selection in environmental selection is as follows: To guarantee the quality of solutions, θ-non-dominated sorting is adopted in the critical layer (Fllayer). When the number of candidate solutions in the first θ-non-dominated layer does not meet the requirements, all the individuals in the first θ-non-dominated layer are kept and some solutions with better favor convergence in the rest θ-non-dominated layers are chosen. If the number of candidate solutions exceeds the requirements, the solutions with balance performance in first θ-non-dominated layer are selected. Figure 6 visually illustrates an example of the solution selection about the fine final level selection.
Example of the proposed fine final level selection mechanism. An example of the fine final level selection: Suppose there are 13 solutions associated with 5 reference points in the critical layer. According to the vertical distance from the solution to the reference line (the line between the reference point and the origin), the solutions are divided into 5 clusters, namely C1, C2, C3, C4, C5 (Fig. a); The solutions with Rank1 are stored in first θ – dominance layer (The green dots in Figures); If the number of individuals in the first layer is greater than the required number, the ISDE index is used to select solutions in the first layer (Fig. b); If the number of individuals in the first layer is less than the required number, all the individuals in the first layer are retained, the favor convergence is used to select solutions from the individuals that are not in the first layer (Fig. c).
The solutions that using the θ-non-dominated sorting method in the critical layer take advantage of the guidance of reference points. Then, favor convergence fully considers the convergence information and ISDEconsiders the solution with equilibrium properties. This makes our mechanism more likely to retain better solutions and output satisfactory results.

-
Step 7-8:
The normalization of population members
For a solution x, the normalized objective value\( {f}_i^{\prime }(x) \)can be calculated by the formula (2), fi(x) is the objective value, \( {Z}_i^{\ast } \) is the ideal point and\( {Z}_i^{nad} \)is the nadir point as mentioned above, m is the objective dimension [11].
-
Step 7-9:
θ-non-dominated sorting
The principle of θ-dominance relation has already introduced in Section 2. The θ-non-dominated sorting method is based on this relationship.
-
Step 7-13:
ISDE indicator calculation
As is known to all, shift-based density estimation (SDE) [23] is a successful strategy to solve the phenomenon of dominance resistance in high-dimensional optimization for the Pareto-based algorithms. Therefore, this advantage is incorporated in the process of choosing solutions. And in order to reduce the calculation, a slight calculation change is made based on the original SDE strategy to form the indicator ISDE. The ISDE can be calculated by the formula (3)–(5) [9].
Where y precedes x means the original position of y in the population P is smaller than x. x and y are two different solutions.fi(x),fi(y)represent the objective value of x, y respectively. The solution with largerISDEvalue is selected potentially.
-
Step 7-16:
Favor convergence calculation
The favor convergence (FC) function is based on Chebyshev and preference weights. It is designed to measure the convergence of individuals. For an individual x, the favor convergence value is calculated by the formula (6) [41].
Where M is the number of objectives,\( {z}^{\mathrm{min}}=\left({z}_1^{\mathrm{min}},{z}_2^{\mathrm{min}},\cdots, {z}_M^{\mathrm{min}}\right) \) is the ideal point for a population, wx = (wx, 1, wx, 2, ⋯, wx, M) is the favorable weight for x and see the formula (7) [41] for the calculation. Small FC value means better convergence.
4 Experimental designs
4.1 Test problems
The widely used Deb-Thiele-Laumanns-Zitzler (DTLZ) [42] and the Walking-Fish-Group (WFG) [43] test suits are selected for experiment. Table 1 lists the main characteristics of all benchmark functions. Tables 2 and 3 list the mathematical formulas of DTLZ and WFG test suits respectively.
4.2 Comparing algorithms and parameter settings
NSGA-III-FS is compared with three types of algorithms: with reference points without parameters, with reference points (or weight vector) and parameters, without reference points and parameters, i.e., hpaEA [44], RPD-NSGAII [45], θ-DEA [15], NSGA-III [31], MOEA/D-DU [11], RVEA [46], 1by1EA [47], VaEA [48] and PDMOEAWS [13].
Table 4 lists the number of decision variables n and max evaluations. Due to the difficulty for solving the problem with different number of objectives, the setting of evaluations is different. Hence each evaluation corresponds to an objective M and the setting of evaluations refers to NSGA-III algorithm. The tests are started for the same test function with objective numbers M = {3,5,8,10,15}. Table 5 lists the number of reference points and population sizes for all algorithms, which keep the same as literature [15]. Refer to literature [11, 46], some parameters that used in the algorithms are listed in Table 6.
4.3 Performance metrics and experimental environment
In this study, the following widely used performance metrics are adopted.
-
1).
Inverted generational distance (IGD) [49] can measure both convergence and diversity of a solution set. And the smaller the IGD value, the better the algorithm.
-
2).
Hypervolume (HV) [50] is equal to the volume of the region dominated by P and bounded by z to evaluate convergence and uniformity, where P is a set of non-dominated points obtained in the objective space and z is a reference point. Higher values represent better solutions.
-
3).
Generational distance (GD) [51] is an index for evaluating convergence by calculating the distance between the obtained Pareto front and true Pareto front, smaller values represent better solutions.
The experimental environment is PC with 1.8 GHz Inter (R) Core (TM) i7-8550UCPU and Windows 10 64-bit operating system with 16GB RAM. All the algorithms are implemented in the PlatEMO [52] platform with 2.5 version, which is a general multi-objective optimization tool. To compare the performance of algorithms, the mean value and standard deviation of indicators are acquired by running 50 times independently. The Wilcoxon rank-sum test [53] with a significance level of 0.05 is adopted to perform statistical analysis on the experimental results, where the symbols’+’,’−’ and’=’ indicate that the result obtained by this algorithm is significantly better, significantly worse and statistically similar to that obtained by NSGA-III-FS algorithm respectively. Detailed process of the statistical test can be referred to literature [45]. The best results between all algorithms are highlighted in bold.
5 Experimental results and analysis
5.1 Strategies validation and analysis
The method of updating nadir point in the proposed algorithm is different from the original NSGA-III algorithm, which results in different normalization. Furthermore, the environmental selection in the proposed algorithm is different from the original algorithm, because a fine final level selection mechanism is introduced. DTLZ1–4, WFG 1–9 problems are selected to test the strategies between original NSGA-III algorithm and the proposed NSGA-III-FS algorithm, and IGD metric is used to evaluate the results.
Table 7 shows the comparison of IGD indicator for the original and modified normalization processes. It can be observed from the Table 7 that the normalization process in the proposed algorithm can obtain better results than the original algorithm on 47 of the 65 test cases. This indicates the effectiveness of the normalization process.
The performance of fine final level selection is verified in Table 8. The original NSGA-III algorithm achieves the best IGD on 24 of the 65 test instances, while that of the proposed algorithm is 41. The overall results show that the modified environment selection is advantageous.
5.2 Algorithm performance analysis
Tables 9, 10 and 11 show the IGD results of all algorithms on DTLZ1–4, WFG1-WFG9 problems. As we can see from these tables, the overall performance of VaEA and hpaEA algorithms are remarkable in ten algorithms, while the effectiveness of NSGA-III-FS comes third. To be more specific, DTLZ1 and DTLZ3 introduce a large number of local Pareto fronts while DTLZ2 presents a spherical Pareto front. The hpaEA algorithm is the best when the number of objectives is 3–5. Furthermore, 1by1EA are better on DTLZ2, DTLZ3, DTLZ4 with 10–15 objectives and DTLZ1 with 15-objective. NSGA-III-FS can obtain the best value on DTLZ1 with 10-objective and DTLZ2 with 8-objective, RVEA is superior to other algorithms on DTLZ1 and DTLZ3 problems with 8-objective. In contrast, the VaEA algorithm is outstanding on WFG2 problem with 8–15 objectives, WFG4-WFG9 problems with 10–15 objectives. In comparison, hpaEA shows excellent performance on 3–5 objectives of WFG5, WFG7-WFG9 problems, PDMOEAWS performs well on all of the objectives of WFG3 problem. The proposed NSGA-III-FS algorithm is more inclined to solve the WFG test problems of 3 or 8 objectives.
Tables 12, 13 and 14 show the HV values for the comparisons of algorithm performances on DTLZ1–4, WFG1-WFG9 problems. The MOEA/D-DU algorithm demonstrates superiority over other algorithms on DTLZ1–4 problems. The PF of WFG1 problem has flat bias and mixed structure. The capability of NSGA-III-FS is satisfactory if there are 5-objective while the MOEA/D-DU algorithm is better than the rest of algorithms if there are 8 and10 objectives. WFG2 tests the abilities of algorithms to handle the disconnected Pareto front. The MOEA/D-DU algorithm exceeds other algorithms if there are 5–10 objectives. NSGA-III performs well on 15 objectives and NSGA-III-FS surpasses other algorithms on 3 objectives. WFG3 problem is difficult to solve due to the PF is degenerate and decision variables are non-separable. PDMOEAWS obtains higher HV values on 3–8 objectives, NSGA-III-FS performs better than other algorithms if there are 10–15 objectives. The RPD-NSGA-II is advantageous than other algorithms on 5–15 objectives of WFG4 problem. For WFG6 and WFG7 problems, the difficulty is that the decision space is multimodal or deceptive or inseparable, and so on. NSGA-III-FS is superior to other algorithms in most cases. This shows that NSGA-III-FS has better capacity in these problems according to the HV indicator. hpaEA and RPD-NSGA-II algorithms are more likely to solve WFG8 problem, while PDMOEAWS is better on WFG9 problem with 5–10 objectives.
Since we aim to improve the convergence of NSGA-III algorithm, a convergence indicator (GD) is used to evaluate algorithms performance. Tables 15, 16 and 17 are the convergence evaluation results of ten algorithms on DTLZ1–4, WFG1-WFG9 problems. The hpaEA algorithm can achieve smaller values on 5-objective of DTLZ1 and DTLZ3 problems as well as 3–5 objectives of DTLZ4 problem. MOEA/D-DU obtains best results on 3–8 objectives of DTLZ1 and 3-,8-,15- objective of DTLZ3 problem. NSGA-III-FS is better than other algorithms on the 15- objective of DTLZ2 and DTLZ4 problems. RVEA has demonstrated superiority on the DTLZ 1 problem with 10–15 targets. PDMOEAWS has good convergence on the DTLZ2 problem with 5–8 objectives. 1by1EA performs well on WFG2 problem with 5–15 objectives and 5–8 objectives of WFG1 problem. Besides, NSGA-III-FS can obtain entire convergence on all objectives of WFG3 test problem. The PDMOEAWS algorithm is superior to other algorithms in 3 and 8 objectives of WFG4-WFG7, WFG9 problems. In addition, PDMOEAWS also performs well in 8 targets of WFG8 problem. The NSGA-III-FS obtains incomparable convergence performance in WFG5 and WFG6 problems with 10–15 objectives, WFG7 problem with 15 objectives. In contrast, RVEA is more likely to obtain better convergence in WFG9 problem.
The statistical analysis results between the comparing algorithms and the proposed NSGA-III-FS algorithm are shown in Table 18. VaEA performs better on 18 out of 65 test instances and hpaEA obtains 15 best results for IGD index. And NSGA-III-FS get 8 best values for IGD indicator. The NSGA-III-FS and MOEA/D-DU algorithms perform the best view from HV results. The statistical analysis results indicate that 1by1EA and VaEA are worse than NSGA-III-FS up to 58 test instances about HV. hpaEA, PDMOEAWS, RPD-NSGA-II, NSGA-III, RVEA, MOEA/D-DU and θ-DEA have 46, 43, 39, 39, 34, 34 and 15 poor HV values compared with NSGA-III-FS, these data highlight the excellence of NSGA-III-FS in HV indicator. As can be observed, NSGA-III-FS is competitive than the remaining algorithms by achieving best values on 16 out of 65 test instances for GD indicator. It is shown that the convergence performance of NSGA-III-FS is predominant and testified that the proposed algorithm improves the convergence. In short, the statistical analysis results show the superiority of NSGA-III-FS algorithm.
To further explain the results directly, figures on DTLZ1 with 3-objective and WFG7 with 8 objectives are drawn. The reasons for choosing these two representations are as follows. We can see that DTLZ1 and WFG3 problems have linear common characteristics from the Table 1. Concave is a common feature of DTLZ2-DTLZ4、WFG4-WFG9 problems. Scaled is the commonality of WFG1-WFG9 problems. DTLZ4、WFG1、WFG5- WFG9 problems have biased feature in common. The characteristic of DTLZ1 problem is linear, and the characteristics of WFG7 problem are concave, biased, scaled. Through the above analysis, DTLZ1 and WFG7 can represent these problems respectively, so the results of these two examples are shown.
Figure 7 shows that non-dominated solutions are obtained by each algorithm on DTLZ1 with 3-objective. The obtained sparse solutions of 1by1EA show poor distribution. And the range of solutions is very far from true Pareto front, which proves that the convergence is very poor. The solutions obtained by RPD-NSGA-II, VaEA and PDMOEAWS algorithms are very aggregated, it turns out that the distribution is bad. The effectiveness of hpaEA, RVEA, θ-DEA, MOEA/D-DU, NSGA-III, NSGA-III-FS is almost equivalent. However, hpaEA algorithm has more solutions at the corners.
Figure 8 shows that results of each algorithm on 8-objective of WFG7 problem. The objective range of all algorithms is consistent. Parallel coordinates map an M-dimensional graph onto a 2D graph cannot fully reflect the coverage of solution sets to some extent. The hpaEA might be uniform due to the curve looks dense. The RPD-NSGA-II, θ-DEA, NSGA-III, NSGA-III-FS, PDMOEAWS may have good convergence because the cartesian curve is flat compared to other algorithms. It is known from the convergence index (GD values) that PDMOEAWS converges best and NSGA-III-FS has the best comprehensive performance (IGD and HV), but it is hardly told the difference from the graph. So, it is only when the gap in the graphs are particularly obvious that some conclusions can be drawn. The difficulty of visualization has always been a major challenge for many-objective optimization.
To show the performance of the proposed algorithm in many aspects, the CPU time of all algorithms are shown in Tables 21, 22 and 23 of Appendix 1. It is obvious that RPD-NSGA-II takes the shortest time on almost all objectives of DTLZ1-DTLZ3 problems. The RVEA algorithm has the shortest running time on almost all the test instances of DTLZ4, WFG1-WFG9 problems. This demonstrates RVEA algorithm has a great time advantage among all algorithms. However, the evaluation results of this algorithm are not superior. Generally speaking, the solution quality is firstly pursued, and the solution speed is improved as far as possible under the premise of ensuring the solution quality. In the 65 test cases, the proposed algorithm takes slightly longer than NSGA-III, we can observe that except for the time difference of the WFG3 problem is large between NSGA-III and NSGA-III-FS algorithms, the difference is comparatively small for other problems. Although the runtime of NSGA-III-FS is not the shortest in all algorithms but not bad, for example, hapEA, MOEA/D-DU, 1by1EA and VaEA, PDMOEAWS spend more time on most test cases than the proposed NSGA-III-FS algorithm. The time cost of NSGA-III-FS is within an acceptable range combined with the previously obtained indicator results in all the contrast algorithms. It is proved that NSGA-III-FS has certain advantages.
5.3 Comparison of existing modified NSGA-III algorithms
To further verify the performance of the proposed algorithm in many aspects, the proposed algorithm and the existing improved NSGA-III algorithm are compared. Bi et al. [40] proposed a NSGA-III-EO algorithm. This algorithm used elimination operator, penalty distance and the idea of eliminating inferior solution to improve the convergence of NSGA-III. After studying and analyzing, NSGA-III-EO algorithm is chosen to compare with NSGA-III-FS algorithm proposed in this paper. The purpose of NSGA-III-EO algorithm and the proposed NSGA-III-FS are to improve the convergence of NSGA-III. Thus, the GD index that evaluates the convergence and a comprehensive performance evaluation index (IGD) are used to estimate the performance of these two algorithms.
Tables 19 and 20 show the GD and IGD values of NSGA-III-EO and NSGA-III-FS algorithms severally. For GD results, NSGA-III-EO obtains 18 best values on 65 test cases. In contrast, NSGA-III-FS gets 47 best values on 65 test instances. Comparing the comprehensive performance of these two algorithms, NSGA-III-EO and NSGA-III-FS obtain 20, 45 best IGD values respectively. The results show that the proposed NSGA-III-FS algorithm in this paper is competitive.
6 Conclusion and future work
This paper introduces a modified version of Non-dominated Sorting Genetic Algorithm III that alters environmental selection to improve the convergence for many-objective optimization. A fine final level selection is implemented in the proposed NSGA-III-FS algorithm. Experiments are conducted on the DTLZ1–4 and WFG1–9 benchmark problems with the objective number varying from 3 to 15. And the experiment results show superiority of the proposed algorithm over the selected comparison algorithms.
Based on the evaluation indicator results on problem sets, the proposed algorithm shows competitiveness in the IGD, HV and GD indexes compared to the nine selected algorithms. For the IGD index, the proposed algorithm is comparable to hpaEA, RPD-NSGA-II, RVEA, θ-DEA, MOEA/D-DU, VaEA, 1by1EA, NSGA-III and PDMOEAWS in 56.9%, 84.6%, 47.7%, 15.4%, 76.9%, 56.9%, 81.5%, 55.4%,73.8% of 65 cases. The proposed algorithm also has an average improvement of 70.8%, 60.0%, 52.3%, 23.1%, 52.3%, 89.2%, 89.2%, 60.0%, 66.2% of 65 cases over the compared nine algorithms about HV results. For the GD indicator, the proposed algorithm is better than hpaEA, RPD-NSGA-II, RVEA, θ-DEA, MOEA/D-DU, VaEA, 1by1EA, NSGA-III and PDMOEAWS in 56.9%, 69.2%, 61.5%, 38.5%, 52.3%, 89.2%, 73.8%, 63.1%, 66.2% of 65 cases. Consequently, it makes us to be more convinced that the proposed method can be very helpful in dominance resistance.
In the future, we will focus on the computational speed of the algorithm on the basis of the excellent performance, such as designing an effective way to generate new individuals. In addition, we expect to extend the algorithm for solving practical problems and the solutions of practical problems are also a challenging work.
References
Li B, Li J, Tang K, Yao X (2015) Many-objective evolutionary algorithms: a survey. ACM Comput Surv 48(1):1–35. https://doi.org/10.1145/2792984
Fu G, Kapelan Z, Kasprzyk JR, Reed P (2013) Optimal design of water distribution systems using many-objective visual analytics. J Water Resour Plan Manag 139(6):624–633. https://doi.org/10.1061/(asce)wr.1943-5452.0000311
Zhu Y, Liang J, Chen J, Ming Z (2017) An improved NSGA-III algorithm for feature selection used in intrusion detection. Knowl-Based Syst 116:74–85
Zulvia FE, Kuo RJ, Nugroho DY (2020) A many-objective gradient evolution algorithm for solving a green vehicle routing problem with time windows and time dependency for perishable products. J Clean Prod 242:118428
Li K, Deb K, Zhang Q, Kwong S (2014) An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans Evol Comput 19(5):694–716
Zheng W, Tan Y, Meng L, Zhang H (2018) An improved MOEA/D design for many-objective optimization problems. Appl Intell 48(10):3839–3861
Asafuddoula M, Ray T, Sarker R (2014) A decomposition-based evolutionary algorithm for many objective optimization. IEEE Trans Evol Comput 19(3):445–460
Wang R, Zhou Z, Ishibuchi H, Liao T, Zhang T (2016) Localized weighted sum method for many-objective optimization. IEEE Trans Evol Comput 22(1):3–18
Li B, Tang K, Li J, Yao X (2016) Stochastic ranking algorithm for many-objective optimization based on multiple indicators. IEEE Trans Evol Comput 20(6):924–938
Pamulapati T, Mallipeddi R, Suganthan PN (2018) $ I_ {\text SDE} $+—an Indicator for multi and many-objective optimization. IEEE Trans Evol Comput 23(2):346–352
Yuan Y, Xu H, Wang B, Zhang B, Yao X (2015) Balancing convergence and diversity in decomposition-based many-objective optimizers. IEEE Trans Evol Comput 20(2):180–198
Jiang S, Yang S (2017) A strength Pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization. IEEE Trans Evol Comput 21(3):329–346
Palakonda V, Mallipeddi R (2017) Pareto dominance-based algorithms with ranking methods for many-objective optimization. IEEE Access 5:11043–11053
Yang S, Li M, Liu X, Zheng J (2013) A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 17(5):721–736
Yuan Y, Xu H, Wang B, Yao X (2015) A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 20(1):16–37
He Z, Yen GG, Zhang J (2013) Fuzzy-based Pareto optimality for many-objective evolutionary algorithms. IEEE Trans Evol Comput 18(2):269–285
Liu Y, Zhu N, Li K, Li M, Zheng J, Li K (2020) An angle dominance criterion for evolutionary many-objective optimization. Inf Sci 509:376–399
Bao C, Xu L, Goodman ED (2019) A new dominance-relation metric balancing convergence and diversity in multi-and many-objective optimization. Expert Syst Appl 134:14–27
Beume N, Naujoks B, Emmerich M (2007) SMS-EMOA: multiobjective selection based on dominated hypervolume. Eur J Oper Res 181(3):1653–1669
Li F, Cheng R, Liu J, Jin Y (2018) A two-stage R2 indicator based evolutionary algorithm for many-objective optimization. Appl Soft Comput 67:245–260
Sun Y, Yen GG, Yi Z (2018) IGD indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans Evol Comput 23(2):173–187
Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197
Li M, Yang S, Liu X (2013) Shift-based density estimation for Pareto-based algorithms in many-objective optimization. IEEE Trans Evol Comput 18(3):348–365
Cai X, Sun H, Fan Z (2018) A diversity indicator based on reference vectors for many-objective optimization. Inf Sci 430:467–486
Wang H, Jiao L, Yao X (2014) Two_Arch2: An improved two-archive algorithm for many-objective optimization. IEEE Trans Evol Comput 19(4):524–541
Lin Q, Liu S, Wong K-C, Gong M, Coello CAC, Chen J, Zhang J (2018) A clustering-based evolutionary algorithm for many-objective optimization problems. IEEE Trans Evol Comput 23(3):391–405
Dai G, Zhou C, Wang M, Li X (2018) Indicator and reference points co-guided evolutionary algorithm for many-objective optimization problems. Knowl-Based Syst 140:50–63
Liu C, Zhao Q, Yan B, Elsayed S, Ray T, Sarker R (2018) Adaptive sorting-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 23(2):247–257
Sun Y, Xue B, Zhang M, Yen GG (2018) A new two-stage evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 23(5):748–761
Xu H, Zeng W, Zeng X, Yen GG (2018) An evolutionary algorithm based on Minkowski distance for many-objective optimization. IEEE Trans Cybern 49(11):3968–3979
Deb K, Jain H (2013) An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints. IEEE Trans Evol Comput 18(4):577–601
Jain H, Deb K (2013) An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: handling constraints and extending to an adaptive approach. IEEE Trans Evol Comput 18(4):602–622
Cai L, Qu S, Yuan Y, Yao X (2015) A clustering-ranking method for many-objective optimization. Appl Soft Comput 35:681–694
Ding R, Dong H, He J, Li T (2019) A novel two-archive strategy for evolutionary many-objective optimization algorithm based on reference points. Appl Soft Comput 78:447–464
Cui Z, Chang Y, Zhang J, Cai X, Zhang W (2019) Improved NSGA-III with selection-and-elimination operator. Swarm Evol Comput 49:23–33
Elarbi M, Bechikh S, Said LB (2018) On the importance of isolated infeasible solutions in the many-objective constrained NSGA-III. Knowl-Based Syst 104335. https://doi.org/10.1016/j.knosys.2018.05.015
Yi J-H, Deb S, Dong J, Alavi AH, Wang G-G (2018) An improved NSGA-III algorithm with adaptive mutation operator for big data optimization problems. Futur Gener Comput Syst 88:571–585
Tavana M, Li Z, Mobin M, Komaki M, Teymourian E (2016) Multi-objective control chart design optimization using NSGA-III and MOPSO enhanced with DEA and TOPSIS. Expert Syst Appl 50:17–39
Bi X, Wang C (2018) A niche-elimination operation based NSGA-III algorithm for many-objective optimization. Appl Intell 48(1):118–141
Bi X, Wang C (2017) An improved NSGA-III algorithm based on elimination operator for many-objective optimization. Memetic Computing 9(4):361–383
Cheng J, Yen GG, Zhang G (2015) A many-objective evolutionary algorithm with enhanced mating and environmental selections. IEEE Trans Evol Comput 19(4):592–605
Deb K, Thiele L, Laumanns M, Zitzler E (2005) Scalable test problems for evolutionary multiobjective optimization. Evolutionary multiobjective optimization. Springer, In, pp 105–145. https://doi.org/10.1007/1-84628-137-7_6
Huband S, Hingston P, Barone L, While L (2006) A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans Evol Comput 10(5):477–506
Chen H, Tian Y, Pedrycz W, Wu G, Wang R, Wang L (2019) Hyperplane assisted evolutionary algorithm for many-objective optimization problems. IEEE transactions on cybernetics, Hyperplane Assisted Evolutionary Algorithm for Many-Objective Optimization Problems
Elarbi M, Bechikh S, Gupta A, Said LB, Ong Y-S (2017) A new decomposition-based NSGA-II for many-objective optimization. IEEE Trans Syst, Man, Cybernetics: Syst 48(7):1191–1210
Cheng R, Jin Y, Olhofer M, Sendhoff B (2016) A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 20(5):773–791. https://doi.org/10.1109/tevc.2016.2519378
Liu Y, Gong D, Sun J, Jin Y (2017) A many-objective evolutionary algorithm using a one-by-one selection strategy. IEEE Trans Cybernet 47(9):2689–2702
Xiang Y, Zhou Y, Li M, Chen Z (2016) A vector angle-based evolutionary algorithm for unconstrained many-objective optimization. IEEE Trans Evol Comput 21(1):131–152
Coello CAC, Cortés NC (2005) Solving multiobjective optimization problems using an artificial immune system. Genet Program Evolvable Mach 6(2):163–190
Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput 3(4):257–271
Van Veldhuizen DA (1999) Multiobjective evolutionary algorithms: classifications, analyses, and new innovations. Air Force Inst Tech Wright-Pattersonafb oh School of Eng
tian y, cheng r, Zhang X, Jin Y (2017) PlatEMO: a MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput Intell Mag 12(4):73–87
Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18
Acknowledgments
This work was supported by the National Natural Science Foundation of China [Grant No.51774228].
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1
Appendix 1
Rights and permissions
About this article
Cite this article
Gu, Q., Wang, R., Xie, H. et al. Modified non-dominated sorting genetic algorithm III with fine final level selection. Appl Intell 51, 4236–4269 (2021). https://doi.org/10.1007/s10489-020-02053-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-020-02053-z