A novel $\hbox {CACO}_{\mathrm{R}}$-SVR multi-objective optimization approach and its application in aerodynamic shape optimization of high-speed train

Abstract

A chaos ant colony optimization algorithm for continuous domain is proposed based on chaos optimization theory and ant colony optimization algorithm. The searching abilities of optimization algorithms with different coding methods are compared, and the results indicate that the proposed algorithm has better performance than genetic algorithm and particle swarm optimization algorithm. Based on the non-dominated sorting concept and niching method, a multi-objective chaos ant colony optimization algorithm is also constructed and numerical results show that the improved algorithm performs well at solving multi-objective optimization problems. An optimal support vector regression model based on radial basis kernel function is developed for the small sample size and nonlinear characteristics of streamlined head optimization. On the basis of the above work, a multi-objective optimization design for the aerodynamic head shape of high-speed train is developed using a modified vehicle modeling function parametric approach. The optimization results demonstrate that the new optimization design method has exceptional searching abilities and high prediction accuracy. After optimization, the aerodynamic drag of the simplified train with three carriages is reduced by 10.52% and the aerodynamic lift of the tail car is reduced by 35.70%. The optimization approach proposed in the present paper is simple yet efficient and sheds light on the engineering design of aerodynamic shape of high-speed trains.

1 Introduction

In recent years, metaheuristics have been improved rapidly and have been applied to numerous problems in fields of engineering design, pattern recognition, scientific computation, economics, and so on. Different kinds of biological-inspired algorithms have been proposed to solve optimization problems with single objective or multiple objectives. For single-objective optimization problems, genetic algorithm (GA) (Holland 1975), particle swarm optimization (PSO) (Kennedy and Eberhart 1995) and ant colony optimization (ACO) algorithm (Dorigo 1992) are some of the competitive algorithms that attract a lot of attention. The above basic algorithms have good performance over many optimization problems; however, these algorithms have deficiencies of low searching efficiency and local optimum in optimizing some problems. Therefore, a number of variations have been developed to improve performance of the basic algorithms. Prominent examples of the variations include AGA (Srinivas and Patnaik 1994), HGA (Gonçalves et al. 2005), CLPSO (Liang et al. 2006), APSO (Zhan et al. 2009) and $\hbox {ACO}_{\mathrm{R}}$ (Socha and Dorigo 2008). However, when devising optimization models for a problem, it is frequently the case that there is not one but several objectives that we would like to optimize. These problems with two or more objective functions are called multi-objective optimization problems (MOP). There are two general approaches to multiple-objective optimization. One is to combine the individual objective functions into a single composite function or move all but one objective to the constraint set. The second general approach is to determine an entire Pareto optimal solution set or a representative subset (Coello 2006; Konak et al. 2006). The most representative multi-objective optimization algorithms include NPGA (Horn et al. 1994), NSGA-II (Deb et al. 2002) and NSPSO (Li 2003).

In the field of engineering optimization design, algorithms are usually combined with surrogate models to reduce the design cost (so-called surrogate-based optimization, SBO). In surrogate-based optimization, direct evaluations of the expensive high-fidelity simulation models are replaced by function approximation surrogate models which can be created by approximating sampled high-fidelity model data. Therefore, the design cost can be greatly reduced. SBO methods differ mostly in the optimization algorithm it adopted and how the surrogate model is created. The most popular surrogate modeling techniques include polynomial approximation, neural networks (Lee et al. 2011), Kriging (Simpson et al. 2001), radial basis function (RBF) interpolation (Forrester and Keane 2009) and support vector regression (SVR) (Smola and Schölkopf 2004; Bourinet 2016). During the modeling process, a certain number of simulation data training samples are required to ensure the reasonable accuracy. Currently, SBO methods have received more and more attention for the reason that it has shorter design cycle and lower investment than traditional design method (Koziel and Leifsson 2012; Koziel et al. 2014; Datta and Regis 2016). In the past decades, various engineering optimization design based on surrogate models has been performed. Bellman et al. (2009) employed a GA-ANN optimization technique for shape optimization of low Reynolds number airfoils to generate maximum lift. Muñoz-Paniagua et al. (2014) extracted three design variables and conducted the shape optimization of a high-speed train entering a tunnel with the unconstrained single-objective genetic algorithm. Lee and Geem (2005) proposed a new meta-heuristic algorithm and applied it into pressure vessel design and welded beam design.

In the present paper, on the basis of the above literature, a chaos ant colony optimization algorithm for continuous domain ($\hbox {CACO}_{\mathrm{R}})$ is proposed based on chaos optimization theory and $\hbox {ACO}_{\mathrm{R}}$. Meanwhile, an optimal SVR model is established for the reason that it performs well at response accuracy when the number of training samples is limited. Combined with $\hbox {CACO}_{\mathrm{R}}$ and SVR surrogate model, a multi-objective efficient optimization method $\hbox {CACO}_{\mathrm{R}}$-SVR is developed. In order to verify the efficiency of the $\hbox {CACO}_{\mathrm{R}}$-SVR approach in engineering design problems, aerodynamic shape optimization for high-speed trains is performed using $\hbox {CACO}_{\mathrm{R}}$-SVR. The aerodynamic drag and aerodynamic lift are treated as optimization objectives and a modified vehicle modeling function (VMF) (Ku et al. 2010) is devised to generate 3-D nose shapes of high-speed trains. After optimization, the Pareto optimal solutions are obtained and the aerodynamic performance of the optimized shape and the original shape of high-speed train with three carriages is comparatively analyzed.

2 Chaos ant colony optimization algorithm

2.1 General ant colony optimization algorithm

The ant colony optimization algorithm is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. It was initially proposed by Dorigo in 1992, and it has become a promising approach in solving a wider class of numerical issues. The first algorithm was used to solve the traveling salesman problem (TSP), a well-known NP-Hard problem. While searching for food, the ants deposit a chemical substance called pheromone in the ground and they will return and reinforce the pheromone trail if they eventually find food. Meanwhile, the pheromones evaporate over time and the more time it takes for the ant to travel from the nest to the food source, the more time the pheromones have to evaporate. As a result, a short path gets marched over more frequently, and thus the pheromone density becomes higher on shorter paths than the longer ones. If the path has a large concentration of pheromone, this is probably due to its shorter length that allowed ants to travel faster, resulting in a larger number of ants depositing pheromone on it. Ants are more likely to follow the path that contains more pheromones, and this positive feedback mechanism will lead to all the ants following a single path eventually. The mathematical model of ACO is given by:

$$\begin{aligned} P_{ij}^k \left( t \right) =\left\{ {\begin{array}{l} \frac{\tau _{ij}^\alpha \left( t \right) \eta _{ij}^\beta \left( t \right) }{\sum \limits _{s\in \mathrm{allowed}_k } {\tau _{is}^\alpha \left( t \right) \eta _{is}^\beta \left( t \right) } },\hbox { }j\in \mathrm{allowed}_k \\ 0\hbox { , }\mathrm{otherwise}, \\ \end{array}} \right. \end{aligned}$$

(1)

where $P_{ij}^k \left( t \right)$ is the probability of ant k, positioned at city i, traveling to city j at the moment t. The pheromone quantity is given by $\tau _{ij}, \eta _{ij}$ is the heuristic information of the problem and is given by the inverse of the distance between city i and city $j:\eta _{ij} =1/{d_{ij} }.\mathrm{allowed}_k$ is the set of cities not yet visited by ant k while at city i, $\alpha >0$ and $\beta >0$ are parameters weighting the relative importance of the pheromone and of the heuristic information, respectively. The pheromone evaporation is performed according to the following update function:

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{ij} \left( {t+\Delta t} \right) =\rho \cdot \tau _{ij} \left( t \right) +\Delta \tau _{ij} \\ \Delta \tau _{ij} =\sum _{k=1}^m {\Delta \tau _{ij}^k }, \\ \end{array}} \right. \end{aligned}$$

(2)

where $\rho \in \left[ {0,1} \right]$ is the persistence parameter for the pheromone. $\Delta \tau _{ij}^k$ represents the pheromone quantity to be deposited by ant k, and it is given by:

$$\begin{aligned} \Delta \tau _{ij}^k =\left\{ {\begin{array}{l} \frac{Q}{F^{k}\left( t \right) }\quad \hbox {if arc}\left( {i,j} \right) \hbox { used by ant }k\hbox {,} \\ 0\quad \hbox {otherwise}, \\ \end{array}} \right. \end{aligned}$$

(3)

where Q is a positive proportionality parameter and $F^{k}\left( t \right)$ is the length of the tour constructed by ant k at iteration t.

According to the existing references (Socha and Dorigo 2008; Liu et al. 2014), general ant colony algorithm can be applied to continuous domain by either discretizing the continuous domain into several regions or shifting from using a discrete probability distribution to using a continuous one such as a Gaussian probability density function (PDF). The research results show that probability density function could improve searching efficiency significantly compared with basic ACO. As a result, in the present paper, the $\hbox {ACO}_{\mathrm{R}}$ approach is adopted for continuous optimization.

For a D-dimensional real-valued minimization problem, $\hbox {ACO}_{\mathrm{R}}$ initializes k solutions at random firstly: $\mathbf{S}_j^i \big ( i=1,2,3,\ldots ,D\hbox { };j=1,2,3,\ldots ,k \big )$ and the k solutions are kept sorted according to their objective values (from minimum to maximum) and each solution $\mathbf{S}_j$ has a weight $\omega _j$ which is defined by Gaussian function:

$$\begin{aligned} \omega _j =\frac{1}{qk\sqrt{2\pi }}e^{\frac{-\left( {\hbox {rank}\left( j \right) -1} \right) ^{2}}{2q^{2}k^{2}}}, \end{aligned}$$

(4)

where rank(j) is the rank of $\mathbf{S}_j$ in the sorted archive and q is a positive parameter of the algorithm. Obviously, $\omega _1 \ge \omega _2 \ge \cdots \omega _j \ge \cdots \omega _k$. The probability of choosing solution $\mathbf{S}_j$ as guiding solution is given by:

$$\begin{aligned} P_j =\frac{\omega { }_j}{\sum _{r=1}^k {\omega { }_r} }. \end{aligned}$$

(5)

Therefore, the better solution has higher chances to be chosen as the guiding solution. Population updating is accomplished by generating a certain number of new solutions near $\mathbf{S}_{{\text {guide}}}$ and adding them to the solution set; meanwhile, remove the same number of worst solutions so that the size of solution set does not change. However, the mechanism of pheromone updating tends to induce a potential problem of trapping into local optimum in case that $\mathbf{S}_{\mathrm{guide}}$ is near the local minimum point. In the present paper, a chaotic disturbance is introduced into the algorithm to avoid this problem.

2.2 Construction of $\hbox {CACO}_{\mathrm{R}}$ algorithm

Chaos is a kind of universal nonlinear phenomena in many areas of science. It is highly sensitive to the changes in initial conditions that small differences in initial conditions yield widely diverging outcomes for the system. Chaos theory studies the behavior of systems that follow deterministic laws but appear random and unpredictable (May 1976; Cong et al. 2010). There are three main properties of the chaotic map: randomness, ergodicity and regularity. The ergodicity property of chaos can ensure chaotic variables to go through every state in certain scale. As a result, it could be introduced into the optimization strategy to avoid falling into local minimum solution. Meanwhile, the randomness and ergodicity can accelerate the optimum seeking operation (Ikeguchi et al. 2011).

Fig. 1

Randomness and ergodicity for logistic map

Chaotic behavior can arise from very simple nonlinear dynamical models. The logistic map is generally used in chaos optimization algorithm, and it was popularized by the biologist Robert May in 1976. The map is written by:

$$\begin{aligned} X_{n+1} =L\left( {\mu ,X_n } \right) =\mu X_n (1-X_n ),n=0,1,2\ldots \end{aligned}$$

(6)

Here the initial value of X is chosen between 0 and 1, and $\mu \in \left[ {0,4} \right]$ is the control parameter. In theory, $X_{n}$ will traverse all values non-repeatedly in $\left[ {0,1} \right]$ in condition that n is large enough. When $n=1000$, the initial value of X is 0.6, the randomness and ergodicity for logistic map are shown in Fig. 1. By varying the parameter $\mu$, different behavior of the dynamic model can be observed, and when $\mu =4.0$, the system is in the state of complete chaos. Figure 2 illustrates the amplitude and frequency content of some logistic map iterates in phase space.

Fig. 2

a Logistic map for different parameter $\mu$ in phase space. b Logistic map with 4 iterations ($\mu =4.0$) in phase space

The $\hbox {CACO}_{\mathrm{R}}$ is proposed based on the problem that traditional ACO is easy to fall in local best, and its searching speed is slow in some special optimization problems. The main idea of $\hbox {CACO}_{\mathrm{R}}$ is to generate the initial ant colony by the logistic map and update the population with chaotic disturbance. For a D-dimensional real-valued minimization problem, the initial colony is given by:

$$\begin{aligned} \text {Ant } j:\left\{ {\begin{array}{ll} X_i =\mu _1 X_{i-1} (1-X_{i-1} ),&{}i=1,2,\ldots ,D \\ S_j^i =\left( {b_i -a_i } \right) X_i +a_i ,&{}j=1,2,\ldots ,k, \\ \end{array}} \right. \end{aligned}$$

(7)

where $S_j^i$ is the component of $\mathbf{S}_j$, the i-th component definitional domain of $\mathbf{S}_j$ is [$a_{i}$, $b_{i}$]. $X_i$ is the logistic map with $\mu _1 =4.0$ and $X_0 =0.6$, and k is the population number of ant colony. Hence, a randomly generated initial population is obtained. When updating the population at each iteration, sort all the individuals according to their quality (from best to worst) and calculate the weight $\omega _j$ for each solution $\mathbf{S}_j$. Choose the individual with highest $\omega _j$ as the guiding solution $\mathbf{S}_\mathrm{guide}$, and then, remove $m\left( {m<k} \right)$ worst solutions and generate the same number of new solutions by introducing the chaos perturbation to the current population:

$$\begin{aligned} \left\{ {\begin{array}{l} S_l^i =\rho \cdot S_\mathrm{guide}^i +\lambda \left( {S_\mathrm{guide}^i -a_i } \right) Y_l ,\hbox { }i=1,2,\ldots D \\ Y_l =\mu _2 Y_{l-1} \left( {1-Y_{l-1} } \right) ,\hbox { }l=1,2,\ldots m, \\ \end{array}} \right. \end{aligned}$$

(8)

where $\rho \in \left[ {0,1} \right]$ represents how much the new individual inherited from the guiding solution, $\lambda \in \left[ {0,1} \right]$ is the coefficient related to the chaos perturbation quantity, and $Y_l$ is the logistic map with $\mu _2 =4.0$ and $Y_0 =0.5$. In general, the $\hbox {CACO}_{\mathrm{R}}$ is described as follows:

Step 1 Initialize the ant colony: generate a certain number of ants with logistic map and compute objective values of every ant. Initialize the parameters of the program, set the value of stop iteration number N and weighting coefficients $\rho$ and $\lambda$.

Step 2 Sort the solutions by objective values, calculate $\omega _j$, $P_j$ and choose the guiding solution $\mathbf{S}_\mathrm{guide}$. Save $\mathbf{S}_\mathrm{guide}$ and the corresponding best value Jbest of the current generation.

Step 3 Generate m new solutions using chaotic theory according to equation (8) and remove the same number of worst solutions. Calculate the current objective values of every solution.

Step 4 Compute the difference of best values between neighboring generations and check the current iteration number n, if the precision or iteration number is not be satisfied, then loop Step 2–Step 4.

Step 5 If the termination conditions are satisfied, stop iteration and put out the best solution.

2.3 Single-objective optimization test

To examine the performance of the proposed $\hbox {CACO}_{\mathrm{R}}$ algorithm, 5 test functions are adopted in this paper; meanwhile, the $\hbox {CACO}_{\mathrm{R}}$ algorithm is compared with the standard GA and PSO, the original $\hbox {ACO}_{\mathrm{R}}$ and the CLPSO algorithms. All the test functions are minimization problems, as shown in Table 1.

Table 1 Test functions

Perform three optimizing searches to find out the minimum solution of the functions in Table 1 and each algorithm was run by 30 times. Besides, the mean, max and min (best) value of the solution are calculated. In GA algorithm, the population size is set to 100, crossover rate is set to 0.75, and mutation rate is set to 0.2. For PSO algorithm, 100 particles are generated and the acceleration coefficients $c_{1}$ and $c_{2}$ are both set to 2.0. Meanwhile, linearly decreasing inertia weight$\omega$ is adopted and the maximal and minimal weights are set to 0.9 and 0.4. For CLPSO, algorithm, we adopt the learning probability $Pc_i =0.05+0.45\times \frac{\exp \left( {\frac{5\left( {i-1} \right) }{S-1}} \right) -1}{\exp \left( 5 \right) -1}$. In the proposed $\hbox {CACO}_{\mathrm{R}}$ algorithm and the original $\hbox {ACO}_{\mathrm{R}}$ algorithm, ant colony population is set to 30, parameter $\rho$ is set to 0.9. The default number of generation N of all algorithms is set to 200. The numerical results and the comparison of performance differences between traditional GA, PSO, $\hbox {ACO}_{\mathrm{R}}$, CLPSO and $\hbox {CACO}_{\mathrm{R}}$ are summarized in Table 2.

Table 2 Numerical results

It can be concluded that the $\hbox {CACO}_{\mathrm{R}}$ algorithm gets a better performance at optimization precision and reliability compared to GA, PSO, original $\hbox {ACO}_{\mathrm{R}}$ and CLPSO algorithms. Furthermore, the original $\hbox {ACO}_{\mathrm{R}}$ was trapped into the local optimum when solving the Rastrigin function while the $\hbox {CACO}_{\mathrm{R}}$ algorithm could get the correct minimum. Figure 3 gives two examples of convergence curves ($f_1 (x)$,$f_2 (x))$ for different algorithms in logarithmic coordinate. Obviously, the convergence rate of the $\hbox {CACO}_{\mathrm{R}}$ is faster than the other algorithms.

Fig. 3

a Convergence curves for $f_1 \left( x \right)$, b convergence curves for $f_2 \left( x \right)$

2.4 Non-dominated sorting technique and niching method

When applied to multi-objective optimization problems, the main difficulties come from how to obtain a set of non-dominated solutions as closely as possible to the true Pareto front and to maintain a well-distributed solution set along the Pareto front. The non-dominated sorting concept which originated from NSGA-II (Deb et al. 2002) is widely used in multi-objective optimization algorithms. It solves the problem of selecting the better individuals by sorting the entire population into different non-domination levels. Hence, it is introduced into the $\hbox {CACO}_{\mathrm{R}}$ algorithm to obtain a series of solutions on the Pareto front. Besides, to preserve diversity in the final group of solutions, the niching method (Li 2003) is adopted in the present paper. Niching methods have been successfully used in GA and PSO algorithms, Goldberg and Richardson (1987) proposed a sharing function model for GA and Li (2003) introduced the $\upsigma _{\mathrm{share}}$ distance into NSPSO. Figure 4 shows the non-dominated sorting concept and niche counts method.

Fig. 4

a Non-dominated fronts of different levels, b niche counts for two-objective optimization

The dynamically updated $\sigma _{\mathrm{share}}$ is defined as follows:

$$\begin{aligned} \sigma _{\mathrm{share}} =\frac{\sum \limits _{i=1}^m {\left( {u_i -l_i } \right) } }{n-1}, \end{aligned}$$

(9)

where $u_{i}$ and $l_{i}$ are the upper and lower bounds for every objective value, n is the size of the ant population, and m is the number of objectives. Calculate the niche count of each candidate solution within the $\sigma _{\mathrm{share}}$ distance, and select the one with smaller niche count as a new front solution. Obviously, A will be preferred over B in Fig. 4b. In addition, to illustrate the key steps of the algorithm, Fig. 5 shows the construction process of the multi-objective $\hbox {CACO}_{\mathrm{R}}$.

Fig. 5

Flowchart of the multi-objective $\hbox {CACO}_{\mathrm{R}}$ algorithm

Fig. 6

a Pareto solution of Test 1, b Pareto solution of Test 2

Fig. 7

Soft margin loss setting for a nonlinear SVR

2.5 Multi-objective optimization test

In order to verify the multi-objective optimization efficiency of the algorithm, two test functions are used. Test1 function was proposed by Kursawe (1991), and Test2 function was proposed by Zitzler et al. (2000), these functions have been widely used in algorithm testing because of disconnectedness of Pareto front and multiple local fronts.

$$\begin{aligned} \hbox {Test1: }\left\{ {\begin{array}{l} f_1 ({\varvec{x}})=\sum _{i=1}^2 {[-10\exp (-0.2\sqrt{x_i^2 +x_{i+1}^2 })]} \\ f_2 ({\varvec{x}})=\sum _{i=1}^3 {(|x_i |^{0.8}+5\sin (x_{_i }^3 ))} \\ \end{array}} \right. \end{aligned}$$

(10)

where $-5\le x_i \le 5,i=1,2,3$.

$$\begin{aligned} \hbox {Test2: }\left\{ {\begin{array}{l} f_1 ({\varvec{x}})=x_1 \\ f_2 ({\varvec{x}})=g\left( {\varvec{x}} \right) h\left( {f_1 \left( {\varvec{x}} \right) ,g\left( {\varvec{x}} \right) } \right) \\ g\left( {\varvec{x}} \right) =1+\frac{9}{29}\sum _{i=2}^{30} {x_i } \\ h\left( {f_1 \left( {\varvec{x}} \right) ,g\left( {\varvec{x}} \right) } \right) =1-\sqrt{\frac{f_1 \left( {\varvec{x}} \right) }{g\left( {\varvec{x}} \right) }}\\ \qquad -\left( {\frac{f_1 \left( {\varvec{x}} \right) }{g\left( {\varvec{x}} \right) }} \right) \sin \left( {10\pi f_1 ({\varvec{x}})} \right) \\ \end{array}} \right. \end{aligned}$$

(11)

where $0\le x_1 ,x_2 \le 1,1\le i\le 30$.

For all test functions, the initial ant population is 150 and the number of iterations is 500. Figure 6 shows comparison between the true Pareto front and $\hbox {CACO}_{\mathrm{R}}$ front for each test function, and both results illustrate good multi-objective search ability of the improved algorithm.

3 Support vector regression

Support vector machine (SVM), which is based on statistical learning theory and characterized by usage of kernel tricks and support vectors, is a standard classification technique that has been widely used in many classification problems. It was developed by Vapnik in 1995 and has been extensively developed during the past two decades (Vladimir and Vapnik 1995; Iosifidis and Gabbouj 2016). The main idea of the SVM is to minimize classification errors by maximizing the margin between the separating hyperplane and the data sets. Smola and Vapnik (1997) developed the SVR method to solve nonlinear regression problems by introducing an $\varepsilon$-insensitive loss function into SVM. A number of studies have indicated that SVR has advantages of high-dimensional input space, few irrelevant features and good accuracy. As a result, SVR has been successfully applied to various problems: regression estimation (Bourinet 2016), signal processing, pattern recognition, medical diagnosis, forecasting problems, etc.

3.1 Construction of SVR model

The training set is defined as $\left\{ {\left( {\varvec{x}}_{\varvec{i}} ,y_i \right) ,i=1,2,\ldots ,l} \right\}$, where l is the number of samples, ${\varvec{x}}_{\varvec{i}} \left( {{\varvec{x}}_{\varvec{i}} \in {\varvec{R}}^{d}} \right)$ is the ith input, ${\varvec{x}}_{\varvec{i}} =\left[ {x_i^1 ,x_i^2 ,\ldots x_i^d } \right] ^{\mathrm{T}},d$ is the dimension of input space and $y_i \in {\varvec{R}}$ is the ith output, correspondingly. Kernel trick uses a classifier algorithm to solve a nonlinear problem by mapping data from the input space into a higher-dimensional space. Define the linear discriminant function

$$\begin{aligned} f\left( {\varvec{x}} \right) ={\varvec{w}}\Phi \left( {\varvec{x}} \right) +b, \end{aligned}$$

(12)

where $\Phi \left( {\varvec{x}} \right)$ is the nonlinear mapping function and $\left( {{\varvec{w}},b} \right)$ is the functional margin. Define the $\varepsilon$-insensitive loss function

$$\begin{aligned} L\left( {f\left( {\varvec{x}} \right) ,y,\varepsilon } \right) =\left\{ {\begin{array}{ll} 0,&{}\left| {y-f\left( {\varvec{x}} \right) } \right| \le \varepsilon \\ \left| {y-f\left( {\varvec{x}} \right) } \right| -\varepsilon ,&{}\left| {y-f\left( {\varvec{x}} \right) } \right| >\varepsilon \\ \end{array}} \right. \end{aligned}$$

(13)

where y is the true value and $f\left( {\varvec{x}} \right)$ is the corresponding prediction. Analogously to the soft margin loss function which was adapted to SVM, positive-valued slack variables $\xi _i ,\xi _i^*$ can be introduced and the problem of searching $\left( {{\varvec{w}},b} \right)$ can be written as an optimization problem:

$$\begin{aligned} \left\{ {\begin{array}{l} \min \hbox { }\frac{1}{2}\left\| {\varvec{w}} \right\| ^{2}+C\sum _{i=1}^l {\left( {\xi _i +\xi _i^*} \right) ,\hbox { }C>0} \\ \hbox {s. t. }\left\{ {\begin{array}{l} y_i -{\varvec{w}}\Phi \left( {{\varvec{x}}_i } \right) -b\le \varepsilon +\xi _i \hbox { , }i=1,2,\ldots ,l \\ -y_i +{\varvec{w}}\Phi \left( {{\varvec{x}}_i } \right) +b\le \varepsilon +\xi _i^*\\ \hbox { }\xi _i \ge 0,\xi _i^*\ge 0. \\ \end{array}} \right. \\ \end{array}} \right. \end{aligned}$$

(14)

Parameter C determines the trade-off between the model complexity (flatness) and the amount to which deviations larger than $\varepsilon$ are tolerated in optimization formulation. If C is too large, then the objective is to minimize the empirical risk only, without regard to model complexity part in the optimization formulation. Parameter $\varepsilon$ controls the width of the $\varepsilon$-insensitive zone, used to fit the training data, as shown in Fig. 7.

The main idea to solve the above optimization problem is to construct a Lagrange function from the objective function and the corresponding constraints, by introducing a dual set of variables:

$$\begin{aligned} L:= & {} \frac{1}{2}{\left\| {\varvec{w}} \right\| ^2} + C\sum \limits _{i = 1}^l {\left( {{\xi _i} + \xi _i^*} \right) - } \sum \limits _{i = 1}^l {\left( {{\eta _i}{\xi _i} + \eta _i^*\xi _i^*} \right) } \nonumber \\&-\sum \limits _{i = 1}^l {{\alpha _i}\left( {\varepsilon + {\xi _i} - {y_i} + {\varvec{w}}\Phi \left( {{{\varvec{x}}_i}} \right) + b} \right) } \nonumber \\&-\sum \limits _{i = 1}^l {\alpha _i^*\left( {\varepsilon + \xi _i^* + {y_i} - {\varvec{w}}\Phi \left( {{{\varvec{x}}_i}} \right) - b} \right) } \end{aligned}$$

(15)

where $\alpha _i ,\eta _i ,\alpha _i^*,\eta _i^*\ge 0$ are Lagrange multipliers. The saddle point condition is given by:

$$\begin{aligned} \left\{ \begin{array}{l} {\partial _b}L = \sum \limits _{i = 1}^l {\left( {\alpha _i^* - {\alpha _i}} \right) } = 0\\ {\partial _w}L = {\varvec{w}} - \sum \limits _{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right) \Phi \left( {{{\varvec{x}}_i}} \right) } = 0\\ {\partial _{{\xi _i}}}L = C - {\alpha _i} - {\eta _i} = 0\\ {\partial _{\xi _i^*}}L = C - \alpha _i^* - \eta _i^* = 0. \end{array} \right. \end{aligned}$$

(16)

Eliminate the dual variables $\eta _i ,\eta _i^*$ and we can get:

$$\begin{aligned} \left\{ \begin{array}{l} \mathop {\max }\limits _{{\varvec{\alpha }} ,{{\varvec{\alpha }} ^*}} \Bigg [ - \frac{1}{2}\sum \limits _{i = 1}^l \sum \limits _{j = 1}^l \left( {{\alpha _i} - \alpha _i^*} \right) \left( {{\alpha _j} - \alpha _j^*} \right) K\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right) \\ \qquad \qquad \left. - \sum \limits _{i = 1}^l \left( {{\alpha _i} + \alpha _i^*} \right) \varepsilon + \sum \limits _{i = 1}^l \left( {{\alpha _i} - \alpha _i^*} \right) {y_i} \Bigg ] \right. \\ \mathrm{{s}}\mathrm{{. t}}\mathrm{{. }}\left\{ \begin{array}{l} \sum \limits _{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right) = 0} \\ 0 \le {\alpha _i} \le C\\ 0 \le \alpha _i^* \le C, \end{array} \right. \end{array} \right. \end{aligned}$$

(17)

where $K\left( {{\varvec{x}}_i, {\varvec{x}}_j } \right) =\Phi \left( {{\varvec{x}}_i } \right) \Phi \left( {{\varvec{x}}_j } \right)$ is the kernel function. Define ${\varvec{N}}_{{\varvec{nsv}}}$ as the number of support vectors and the solution can be written as:

$$\begin{aligned} \left\{ \begin{array}{l} {{\varvec{w}}^*} = \sum \limits _{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right) \Phi \left( {{\varvec{x}_i}} \right) } \\ {b^*} = \frac{1}{{{N_{nsv}}}}\\ \qquad \times \,\left\{ \sum \limits _{0< {\alpha _i}< C} {y_i} - \left[ \sum \limits _{{x_i} \in SV} \left( {{\alpha _i} - \alpha _i^*} \right) K\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right) - \varepsilon \right] \right. \\ \qquad \left. + \sum \limits _{0< {\alpha _i} < C} {y_i} - \left[ \sum \limits _{{x_j} \in SV} \left( {{\alpha _i} - \alpha _i^*} \right) K\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right) + \varepsilon \right] \right\} . \end{array} \right. \nonumber \\ \end{aligned}$$

(18)

Finally, we get the regression function

$$\begin{aligned} f\left( {\varvec{x}} \right) = {{\varvec{w}}^*}\Phi \left( {\varvec{x}} \right) + {b^*} = \sum \limits _{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right) K\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right) + } {b^*}.\nonumber \\ \end{aligned}$$

(19)

It is well known that SVR performance (estimation accuracy) depends on a good setting of parameters $C, \varepsilon$ and the kernel parameters. Selecting a particular kernel type and kernel function parameters is usually based on characteristics of the training data. Common kernel functions include:

D-th-order polynomial function:

$$\begin{aligned} K\left( {{\varvec{x}}_i ,{\varvec{x}}_j } \right) =\left( {{\varvec{x}}_i \cdot {\varvec{x}}_j } \right) ^{d} \end{aligned}$$

(20)

Gaussian radial basis function (RBF):

$$\begin{aligned} K\left( {{\varvec{x}}_i ,{\varvec{x}}_j } \right) =\exp \left( {-\gamma \left\| {{\varvec{x}}_i -{\varvec{x}}_j } \right\| ^{2}} \right) \end{aligned}$$

(21)

Hyperbolic tangent function (Sigmoid):

$$\begin{aligned} K\left( {{\varvec{x}}_i ,{\varvec{x}}_j } \right) =\tanh \left( {\gamma {\varvec{x}}_i \cdot {\varvec{x}}_j +c} \right) . \end{aligned}$$

(22)

3.2 Regression accuracy analysis

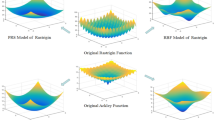
According to existing studies, RBF kernel function is widely used in SVM classification and regression for the reason that it has better generalization performance. As a result, RBF kernel function is adopted in the present paper. Meanwhile, SVR model is sensitive to the input parameters and only obtain suitable parameters can the model perform well enough. Hence, the input parameters are optimized with $\hbox {CACO}_{\mathrm{R}}$ before use. Figure 8 shows the regression and prediction test results of SVR mode, and Table 3 gives the mean squared error (mse) and squared correlation coefficient $(\hbox {R}^{2})$ for different cases. Here $f_1 \left( x \right)$ is an exponential function, $f_2 \left( x \right)$ is a polynomial function, $f_3 \left( x \right)$ is a two-dimensional projection transform of Ackley function:

$$\begin{aligned} f_3 \left( x \right)= & {} -20\exp \left( {-0.2\sqrt{0.5x^{2}}} \right) \nonumber \\&-\exp \left( {0.5\cos \left( {2\pi x} \right) } \right) +e+20. \end{aligned}$$

(23)

And $f_4 \left( x \right)$ is Schwefel function:

$$\begin{aligned} f_4 \left( x \right) =418.9829-x\sin \left( {\sqrt{\left| x \right| }}. \right) \end{aligned}$$

(24)

It can be concluded from Fig. 8 and Table 3 that SVR model constructed with RBF kernel is sufficiently accurate.

Fig. 8

Test results of SVR model

4 Optimization of high-speed train nose shape

Optimization design of aerodynamic shape is a research focus in the field of fluid mechanics, especially in the design of aircraft. In recent years, optimization of the streamlined head of high-speed trains has attracted more and more attention as the aerodynamic problems become more serious with the increasing running speed. The aerodynamic drag of high-speed trains can be up to 80% of the total drag (Yang et al. 2012) at the speed of 300 km/h. Resistance characteristics of the trains are directly related to the ability of energy saving and environmental protection (Raghunathan et al. 2002; Baker 2010; Tian 2009). In aerodynamic lift research, the wheel-track force is significantly reduced while excessive positive lift act on the train, which affects the operation safety. Meanwhile, negative aerodynamic lift increases the dynamic axle load and aggravates rail abrasion. For high-speed maglev trains, the time difference between the change in electromagnetic suspension force and aerodynamic lift causes server vibration and affects the amenity of the train. Therefore, to reduce aerodynamic drag and lift of the train becomes the key issue of optimization design of head shape of high-speed trains (Tian 2007).

In the initial stage of optimization design, the parametric method to efficiently represent the shape with significantly less data should be developed. It plays an important role in aerodynamic optimal design for the reason that an efficient parametric method can not only describe the changes of shape completely, but also reduce the optimization cycle and improve optimization efficiency. For airfoil optimization, various parametric approaches have been investigated since the 1970s. Free form deformation (FFD), class function transformation (CST), Hicks-Henne approach and B-spline representation method are widely used in airfoil design. The head shape of a high-speed train is much more complicated than the airfoil, and there are much fewer references on parametric methods for high-speed trains. Rho et al. (2009) proposed a vehicle modeling function in the form of an exponential function to smoothly express the complex shapes of an automobile. Ku et al. (2010) applied the VMF method in the optimization design of high-speed trains to reduce the micro-pressure wave and aerodynamic drag. In the present paper, a modified VMF parametric approach for high-speed train nose shape is adopted.

4.1 Vehicle modeling function parametric approach

The basic VMF proposed by Rho and Ku is given by:

$$\begin{aligned} F\left( {\frac{x}{c}} \right) =\left( {\frac{x}{c}} \right) ^{A_1 }\left( {1-\frac{x}{c}} \right) ^{A_2 }S\left( {\frac{x}{c}} \right) +\left( {1-\frac{x}{c}} \right) Y_1 +\left( {\frac{x}{c}} \right) Y_2, \end{aligned}$$

(25)

where $Y_{1}$ and $Y_{2}$ are the heights of the starting and finishing points and x and c are the dimension and length of each section box. S(x / c) can be defined by the simple polynomial functions. In order to generate outline curves of the streamlined nose shape, the equation is modified by:

$$\begin{aligned} F\left( {\frac{x}{c}} \right) =\left( {\frac{x}{c}} \right) ^{A_1 }\left( {1-\frac{x}{c}} \right) ^{A_2 }a_k +g\left( {\frac{x}{c}} \right) , \end{aligned}$$

(26)

where S(x / c) and g(x / c) are given by:

$$\begin{aligned} g\left( {\frac{x}{c}} \right) =2\left( {Y_2 -Y_1 } \right) \frac{x}{c}-\left( {Y_2 -Y_1 } \right) \left( {\frac{x}{c}} \right) ^{2} \end{aligned}$$

(27)

$A_{1}$, $A_{2}$ and $a_{k}$ are design variables. $A_{1}$ and $A_{2}$ control the basic curve shapes, and $a_{k}$ affects the amplitude of F(x / c). Using the modified function, we can define different complex shapes by varying the design variables. Figure 9 illustrates how the shape changes with the exponent $A_{1}$ and $A_{2}$ in the modified VMF equation.

Table 3 Regression accuracy of SVR

Fig. 9

a Curves variation with the parametric $A_{1}$. b Curves variation with the parametric $A_{2}$

The basic shape of streamlined head of high-speed trains is controlled by the critical two-dimensional line, and surface configuration is generated by means of interpolation between different profile lines. According to the common nose shapes of high-speed trains, basic lines and control points are extracted, as shown in Fig. 10.

Fig. 10

Basic lines and control points in VMF design

L1 is the upper longitudinal section profile line, L2 is horizontal section profile, L3 is the bottom horizontal section profile, L4 is the cowcatcher profile line, and L5 is the maximum cross-sectional profile line. According to the functional requirements, the shape of cowcatcher profile line cannot be changed too much; therefore, L4 adopts realistic geometric structure. In addition, L5 has a fixed shape since it should matches with the carriage of high-speed train. Equation of L1 is given by:

$$\begin{aligned} z\left( x \right)= & {} \left( {\frac{x-x_{11} }{x_{12} -x_{11} }} \right) ^{A_{11} }\left( {1-\frac{x-x_{11} }{x_{12} -x_{11} }} \right) ^{A_{12} }a_{k1} \nonumber \\&\hbox {+2}\left( {z_{12} -z_{11} } \right) \frac{x-x_{11} }{x_{12} -x_{11} }\nonumber \\&-\left( {z_{12} -z_{11} } \right) \left( {\frac{x-x_{11} }{x_{12} -x_{11} }} \right) ^{2}, \end{aligned}$$

(28)

where $\left( {x_{11} ,z_{11} } \right) ,\left( {x_{12} ,z_{12} } \right)$ are the coordinate values of P1 and P2. Analogously, equation of L2 is given by:

$$\begin{aligned} y\left( x \right)= & {} \left( {\frac{x-x_{11} }{x_{22} -x_{11} }} \right) ^{A_{21} }\left( {1-\frac{x-x_{11} }{x_{22} -x_{11} }} \right) ^{A_{22} }a_{k2} \nonumber \\&\hbox {+\,2}\left( {z_{22} -z_{11} } \right) \frac{x-x_{11} }{x_{22} -x_{11} }\nonumber \\&-\,\left( {z_{22} -z_{11} } \right) \left( {\frac{x-x_{11} }{x_{22} -x_{11} }} \right) ^{2}, \end{aligned}$$

(29)

where $\left( {x_{22} ,z_{22} } \right)$ is the coordinate value of P3. For L3, the equation is given by:

$$\begin{aligned} y\left( x \right)= & {} \left( {\frac{x-x_{31} }{x_{32} -x_{31} }} \right) ^{A_{21} }\left( {1-\frac{x-x_{31} }{x_{32} -x_{31} }} \right) ^{A_{22} }a_{k3} \nonumber \\&\hbox {+\,2}\left( {z_{32} -z_{31} } \right) \frac{x-x_{31} }{x_{32} -x_{31} }\nonumber \\&-\,\left( {z_{32} -z_{31} } \right) \left( {\frac{x-x_{31} }{x_{32} -x_{31} }} \right) ^{2}, \end{aligned}$$

(30)

where $\left( {x_{31} ,z_{31} } \right) ,\left( {x_{32} ,z_{32} } \right)$ are the coordinate values of P4 and P5. During the process of shape construction, control points P1 to P5 are unchanged, as a result, the basic design parameters are $a_{ki}, A_{i1}$ and $A_{i2}$, $\left( {i=1,2,3} \right)$.

Table 4 Design variables and their ranges

Table 4 shows the ranges of design parameters, and Fig. 11 shows different types of streamlined nose shapes obtained by adjusting the design parameters.

Fig. 11

Different shapes obtained by adjusting design parameters

Fig. 12

Computational domain

4.2 Computational domain and CFD algorithm

In the present paper, a mixture spatial mesh that combines with Cartesian grid and prism mesh is adopted. The total length of the train is about 78 m, in which the length of the head car and the tail car is about 26 m. The height H of the train is 3.5 m, while the width of the car-body is 3.38 m. Take the height H as the characteristic length, and the computational domain extends 30H ahead of the train nose and 60H from the train tail to the exit of the computational domain. The top of the computational domain is at a distance 30H from the bottom of the rail and the sides are at a distance of 30H from the center axis of the train, the outline of computational domain and the model are shown in Fig. 12.

In this paper, the speed of high-speed train is 350 km/h, so the Mach number was 0.2859. In this condition, the air compression characteristic had an obvious effect on the aerodynamic drag of the train. Therefore, the steady compressible Reynolds-averaged Navier-Stokes equation (Blazek 2015) that is based on the finite volume method was used to predict the aerodynamic drag. Roe’s FDS scheme was used to calculate convective fluxes, and lower-upper symmetric Gauss-Seidel (LU-SGS) was chosen for temporal discretization. The k-$\omega$ SST model was selected as the turbulence model. The standard wall functions were used near the wall so that the accuracy of the CFD results could be ensured with a limited amount of mesh. The flow velocity is 97.222 m/s, the far-field pressure is 1 atm, the temperature is 288 K, and the reference area is the maximum cross-sectional area of the train. As a result of the compressibility calculation model, one-dimensional inviscid flow of the Riemann invariants is introduced as the far-field boundary conditions, which are also known as non-reflective boundary conditions. Inflow, outflow and the top boundaries are all set as far-field boundary conditions and the train body is nonslip solid wall boundary condition. The ground is treated as the moving wall so as to simulate the ground effect, and the moving speed is equal to the train speed.

4.3 Optimization process

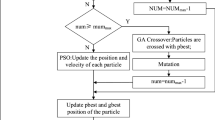
In order to improve the optimization efficiency, a reasonable optimization process is designed in the present paper, as shown in Fig. 13.

Fig. 13

Optimization process

All the steps are listed as follows:

• (1) Modify the VMF equation and extract the design parameters.

• (2) Determine baselines composing the streamlined surface and then determine the range of design parameters.

• (3) Generate a certain number of sample points using Latin hypercube sampling (LHS) method.

• (4) Obtain the accurate value of the aerodynamic drag and lift for every sample point using the CFD simulation. Train the SVR model constructed with RBF kernel. Because there are two objectives, two sets of SVR models need to be constructed. On the premise of sufficient precision, two sets of models share the same parameters $C,\varepsilon$ and $\gamma$ in the present paper. The sum of the squares of the two errors is defined as the final prediction error. If the prediction error is greater than limited value $\Delta$, then use the proposed algorithm to find the optimal values of correlation coefficients $C,\varepsilon$ and $\gamma$.

• (5) Construct multi-objective $\hbox {CACO}_{\mathrm{R}}$ algorithm using non-dominated sorting concept and niche counts method, test the performance with different functions and then get the $\hbox {CACO}_{\mathrm{R}}$-SVR model.

• (6) Based on the $\hbox {CACO}_{\mathrm{R}}$-SVR model, perform the optimization for 3D nose shape of high-speed trains, obtain the optimal Pareto solutions.

• (7) Chose one of the solutions as the design point and generate the optimal shape correspondingly. Verify their performance using the CFD approach.

4.4 Sample points and training of SVR

A uniform distribution of samples is essential for training the SVR model, and reasonable sampling method could provide the detailed information with fewer samples in the design space. Latin hypercube sampling is a recent development in sampling technology designed to accurately recreate the input distribution through sampling in a few iterations. References (Joseph and Hung 2008) have shown that LHS offers great benefits in terms of increased sampling efficiency and better reflects the underlying distribution for a smaller number of samples. As a result, LHS is adopted in the present paper to generate initial samples according to the design variables and their ranges listed in Table 4. Twenty-two initial sampling points have been generated for training the SVR model, of which the first 20 points are chosen as training points while the last two are chosen as the test points. For all the sampling points, the aerodynamic drag of the whole train (Cd) and the lift of the tail car (Cl) are calculated and designed as optimization objectives, as shown in Table 5.

Table 5 Training points and test points

In general, the essence of training the SVR model based on RBF kernel is to find the most appropriate value of C, $\varepsilon$ and $\gamma$. A basic SVR model could be firstly constructed from the initial 20 training points. If the average prediction error for the other two test points is greater than 5%, then optimize the key parameters $C,\varepsilon$ and $\gamma$ with $\hbox {CACO}_{\mathrm{R}}$ until the accuracy requirement is satisfied. For the selection of the most appropriate values of SVR model parameters, take $C,\varepsilon$ and $\gamma$ as the vector of independent variables and mean square error as the optimization objective, then the appropriate parameters could be obtained by the $\hbox {CACO}_{\mathrm{R}}$ algorithm. Table 6 compares the prediction error of the initial parameters and the optimal parameters. The initial values of $C,\varepsilon$ and $\gamma$ are 2.0, 0.1 and 3.0, while after optimization the parameters are changed to 45.6238, 0.0101 and 2.4630, respectively.

It can be observed that aerodynamic lift coefficient of the tail car is more sensitive to the input parameters of SVR model. Prediction error of the initial $C,\varepsilon$ and $\gamma$ for aerodynamic drag coefficient is about 3.0, while the error of the optimal $C,\varepsilon$ and $\gamma$ is reduced to 0.31%. For aerodynamic lift of the tail car, prediction error declines from about 26% to 3.0% after optimization. Hence, the optimal SVR models have met the accuracy requirement.

Table 6 Prediction error comparison

5 Results and discussion

Based on the constructed SVR model, the Pareto optimal solution of the aerodynamic drag of the train and the aerodynamic lift of the tail car is found. For the setting of parameters in CACO$_{\mathrm{R}}$ algorithm, ant colony population is set to 100, parameter $\rho$ is set to 0.9. The default number of generation N is set to 300.

Figure 14 shows the Pareto solution of the Cd-Cl optimization based on $\hbox {CACO}_{\mathrm{R}}$-SVR. The result shows that a suitable Pareto front is obtained after iterations. Theoretically, the objective values of each point on the Pareto frontier are better than those of the original one. In the shape design for high-speed train, when the aerodynamic parameters are balanced, the running stability of the train is the best. As a result, points near the center of the Pareto frontier are more likely to be the final design point. In the present paper, a specific individual as the red star shows in Fig. 14 is chosen as the design point for comparison.

Fig. 14

Pareto solution based on $\hbox {CACO}_{\mathrm{R}}$-SVR

Table 7 shows aerodynamic forces comparison between original and optimal shape. After optimization, the aerodynamic drag of the whole train is reduced by 10.52%, while the aerodynamic lift of the tail car is reduced by 35.70%. The results indicate that the aerodynamic lift of the tail car is more sensitive to the change of nose shape.

Table 7 Aerodynamic forces reduction after $\hbox {CACO}_{\mathrm{R}}$-SVR optimization

Figure 15 illustrates the transformation of L1, L2 and L3 after optimization. It can be seen from Fig.15 that L1 changes a little near P1 and almost remains unchanged near P2. Curvature of L2 and the first half of L3 decreases significantly, while curvature of the second half of L3 increases slightly.

Fig. 15

Comparison for section profile lines

Fig. 16

Pressure distribution of head car and the iso-surface of $Q=80$ in the wake flow

In order to better understand the influence on aerodynamic performance due to the change of nose shape of high-speed train, pressure distribution of head car and the iso-surface of the second invariant of the velocity gradient Q in the wake flow are shown in Figure 16. It can be concluded that the high-pressure area of the head car is reduced after optimization. Meanwhile, the strengths of two steady vortices which were developed along the surface of the tail car are reduced; hence, negative pressure in the wake region is weaker. The results indicate that decreasing the curvature of horizontal section profile and the curvature of bottom horizontal section profile of the nose can be beneficial to local pressure distribution of the train.

6 Conclusions

In the present paper, a chaos ant colony optimization algorithm for continuous domain $(\hbox {CACO}_{\mathrm{R}})$ is proposed based on chaos optimization theory and ant colony optimization algorithm. Five single-objective test functions and two multi-objective functions are used to verify the searching efficiency and global optimization capability of the proposed algorithm. Meanwhile, the proposed algorithm is improved for multi-objective optimization by introducing the non-dominated sorting concept and niche counts method. The results show that $\hbox {CACO}_{\mathrm{R}}$ algorithm gets a good performance at single-objective optimization as well as searching for Pareto front in multi-objective optimization.

With limited sample points, an optimal-parameter SVR surrogate model based on RBF kernel function is constructed. Both results of test functions and test points demonstrate sufficient prediction accuracy of the SVR model.

According to common shape of high-speed trains, a modified VMF parametric method is improved and 9 design variables are extracted. Combined with the proposed $\hbox {CACO}_{\mathrm{R}}$-SVR approach, optimization for nose shape of high-speed train has been performed, the aerodynamic drag coefficient is reduced by 10.52%, and the aerodynamic lift of the tail car is reduced by 35.70%. The results can be beneficial to the shape design of high-speed trains.