An approach to construct entropies on interval-valued intuitionistic fuzzy sets by their distance functions

Abstract

The main contribution of this paper is to give a new axiomatic definition of entropy measure and provide a constructing approach in the context of interval-valued intuitionistic fuzzy set (IVIFS). We give a new idea to define entropy on IVIFS: From the graphical representation, we consider the difference between a given IVIFS and its corresponding two interval fuzzy sets (IVFSs) by introducing a distance function that meets some specific conditions. The relationship between the distance function and the distance measure has also been illustrated. Based on distance functions, we give an approach to construct entropy measures on IVIFS. Then, a plenty of new entropies on IVIFS are introduced. Furthermore, we use a comparative example to show the proposed measures outperform the existing measures and utilize a demonstrative example to explain the application of the entropy measure in the multi-criteria decision making (MCDM), which verify the feasibility of our entropy construction method.

1 Introduction

In the classical set theory, the concepts expressed by the set attributes are clear and well defined. Therefore, the membership of each object to the classical set is also clear. But there are still many vague concepts in real life, such as “young”, “old”, “warm”, “cold”, and so on. The object attributes described by these concepts cannot be simply answered as “yes” or “no”. Fuzzy set theory, founded by Zadeh (1965) in 1965, is a method to describe fuzzy phenomena, which takes the object and the corresponding fuzzy concept as a fuzzy set, and establishes a membership function between the fuzzy object and the fuzzy set. The difference between classical set theory and fuzzy set theory is that in classical set theory, the membership of elements in a set evaluates “whether the element belongs to the set”. On the other hand, in fuzzy theory, a more fuzzy way of “degree” is used to describe the relationship between elements and sets.

Fuzzy set (FS) and interval-valued fuzzy set (IVFS) were proposed by Zadeh (1965), Zadeh (1975). The membership of fuzzy set is a real number in [0, 1], while the membership of interval-valued fuzzy set is a closed subinterval of [0, 1]. In order to better describe the fuzzy variables in real life, Atanassov (1986) proposed the notion of intuitionistic fuzzy sets (IFS) in 1986. That is to say, IFS contains two variables, representing the membership and the non-membership, respectively. The more the element conforms to the set’s attribute, the closer the membership value is to 1. The more the element does not conform to the set’s attribute, the closer the membership value is to 0, while the non-membership is exactly the opposite. Moreover, these two variables satisfy the constraint that their sum is less than or equal to one. The difference between one and the sum of these two variables is referred to as the hesitation index, indicating that there is the lack of information to determine the relationship between the element and the set. Later, interval-valued intuitionistic fuzzy set (IVIFS) extended by Atanassov and Gargov (1989) in 1989 generalized the membership and non-membership of each element from real numbers to closed subintervals of [0, 1]. Due to its better description for fuzzy variables, IVIFS has been widely studied and put into various fields (Nguyen 2016; De Miguel et al. 2016; Park et al. 2009; Düğenci 2016; Chen 2013; Jin et al. 2014; Li 2010; Ye 2013).

Since Zadeh (1965) proposed the fuzzy entropy theory firstly in 1965, entropy is an important research object in fuzzy theory, which is used to characterize the uncertainty of the information of fuzzy sets (Suo et al. 2021a; Li et al. 2020; Deng 2020). Let us briefly review some existing research results on entropy measure in the context of IFS, IVFS and IVIFS here. Burillo and Bustince (1996) introduced the concepts of entropy on IVFS and IFS with the consideration of the degree of intuitionism. An intuitionistic fuzzy non-probabilistic-type entropy had been advanced by Szmidt and Kacprzyk (2001) from the geometric interpretation. Hung and Yang (2006) based on the concept of probability gave their own axiomatic definitions of entropies of IFS and IVFS. Liu et al. (2005) generalized the axioms of intuitionistic fuzzy entropy introduced by Szmidt and Kacprzyk (2001), and proposed a set of axiomatic conditions which entropy measures should satisfy in the context of IVIFS. Wei et al. (2011) also extended entropy to IVIFS based on the result of Szmidt and Kacprzyk (2001), and presented a method to generate similarity measure through entropy measure. Besides, many scholars put forward different entropy formulae for IFSs (Hung and Yang 2006; Xia and Xu 2012; Ye 2010b; Vlachos and Sergiadis 2006, 2007; Xue et al. 2020), IVFSs (Zeng and Li 2006; Zhang et al. 2009; Suo et al. 2021b), and IVIFSs (Ye 2010a; Zhang et al. 2010; Zhang and Jiang 2010).

Compared with FS and IFS, there are not so many studies on the entropy of IVIFS. Different from some existing studies, this paper not only gives the formula of entropy, but also gives a new idea of constructing entropy. Under the guidance of this idea, we can propose a family of entropy measure formulae and then select one that best meets the intuitive expectations. Inspired by the entropy proposed by Burillo and Bustince that we abbreviate it to BB entropy (Burillo and Bustince 1996), we shall give a new idea to define entropy on IVIFS in this paper. For each IVIFS, the membership and the non-membership can be considered as IVFS, respectively. The graphically representation will be given below. Since then, we can measure the entropy by calculating the distance between the given IVIFS and its corresponding two IVFSs. In this paper, we introduce the distance function to consider the difference between IVIFS and its corresponding two IVFSs, which should satisfy some specific conditions. Based on these distance functions, we give an approach to construct entropy measures on IVIFS. Then, a plenty of new entropies on IVIFS are introduced. Our goal is to solve this critical issue and provide new ideas for the study of entropy measures on IVIFS.

To illustrate the construction process we mentioned before, the background knowledge required in this paper is given in Sect. 2. The new axiomatic definition and concrete form of entropy are shown in Sect. 3. Moreover, the proposed specific entropy measure is reasonably as illustrated in the numerical example of multi-criteria decision making in Sect. 4. Conclusion is presented in Sect. 5.

2 Preliminaries

We briefly review several notions about fuzzy set theory which we will use in this paper. Let $X=\{x_1,x_2,\ldots ,x_n\}$ be a universe of discourse.

Definition 2.1

(Zadeh 1965) A fuzzy set (FS) A in X is defined as the following form:

$$\begin{aligned} A=\left\{ \left\langle x, \mu _{A}(x)\right\rangle | x \in X\right\} , \end{aligned}$$

where $\mu _A(x): X \rightarrow [0,1]$ is the membership degree of $x \in X$.

Interval-valued fuzzy sets expand the membership of fuzzy sets to interval forms.

Definition 2.2

(Zadeh 1975) An interval-valued fuzzy set (IVFS) $A^{\prime }$ in X is defined as the following form:

$$\begin{aligned} A^{\prime }= & {} \left\{ \langle x, \mu _{A^{\prime }}(x)\rangle | x \in X\right\} \\= & {} \left\{ \langle x, [\mu _{A^{\prime }}^{-}(x),\mu _{A^{\prime }}^{+}(x)]\rangle | x \in X\right\} , \end{aligned}$$

where $\mu _{A^{\prime }}(x): X\rightarrow L([0,1])$ are the membership degree intervals of $x \in X$, $\mu ^-_{A^{\prime }}, \mu ^+_{A^{\prime }}: X\rightarrow [0,1]$ are two membership of $A^{\prime }$ such that $\mu ^-_{A^{\prime }}(x)\le \mu ^+_{A^{\prime }}(x)$ for any x, and $\mu _{A^{\prime }}(x)=[ \mu ^-_{A^{\prime }}(x), \mu ^+_{A^{\prime }}(x)]$. Here, L([0, 1]) represents the set of closed subintervals on [0, 1].

Suo et al. (2021b) explored the relative properties of polygonal interval-value fuzzy sets approximating to general interval-valued fuzzy sets in recent work.

Due to the lack of information, the intuitionistic fuzzy set adds a parameter of non-membership on the basis of the fuzzy set to measure the degree that x does not conform to the attribute of $A^{\prime }$.

Definition 2.3

(Atanassov 1986) An intuitionistic fuzzy set(IFS) ${\bar{A}}$ in X is defined as the following form:

$$\begin{aligned} {\bar{A}}=\left\{ \left\langle x, \mu _{{\bar{A}}}(x), \nu _{{\bar{A}}}(x)\right\rangle | x \in X\right\} , \end{aligned}$$

where $\mu _{{\bar{A}}}: X \rightarrow [0,1]$ and $\nu _{{\bar{A}}}: X \rightarrow [0,1]$ are the membership and the non-membership, respectively, satisfying $\mu _{{\bar{A}}}(x)+\nu _{{\bar{A}}}(x) \le 1$ for any $x \in X$.

In addition, we define another parameter of IFS to measure the hesitation as $\pi _{{\bar{A}}}(x)=1-\mu _{{\bar{A}}}(x)-\nu _{{\bar{A}}}(x)$ and name it the intuitionistic fuzzy index, which indicates the lack of information about whether x belongs to ${\bar{A}}$. Obviously, for any $x\in X$, $0\le \pi _{{\bar{A}}}(x)\le 1$. When $\mu _{{\bar{A}}} (x)= 1-\nu _{{\bar{A}}}(x)$ for each element of X, A is reduced to FS.

Definition 2.4

(Atanassov 1986) For an intuitionistic fuzzy set (IFS) ${\bar{A}}$ in X, the complement of ${\bar{A}}$ is defined as ${{\bar{A}}}^c=\left\{ \left\langle x, \nu _{{\bar{A}}}(x), \mu _{{\bar{A}}}(x)\right\rangle | x \in X\right\}$.

Subsequently, interval-valued intuitionistic fuzzy set is extended from intuitionistic fuzzy set. At this time, the degree of membership and non-membership is not a real value on [0, 1], but a real number interval.

Definition 2.5

(Atanassov and Gargov 1989) An interval-valued intuitionistic fuzzy set (IVIFS) ${\tilde{A}}$ in X is defined as the following form:

$$\begin{aligned} {\tilde{A}}=\left\{ \left\langle x, {\tilde{\mu }}_{{\tilde{A}}}(x), {\tilde{\nu }}_{{\tilde{A}}}(x)\right\rangle | x \in X\right\} , \end{aligned}$$

where ${\tilde{\mu }}_{{\tilde{A}}}(x)=[\mu ^L_{{\tilde{A}}}(x),\mu ^U_{{\tilde{A}}}(x)]\subseteq [0,1]$ and ${\tilde{\nu }}_{{\tilde{A}}}(x)=[\nu ^L_{{\tilde{A}}}(x),\nu ^U_{{\tilde{A}}}(x)]\subseteq [0,1]$ are intervals, satisfying $\mu ^U_{{\tilde{A}}}(x)+\nu ^U_{{\tilde{A}}}(x)\le 1$ for any $x\in X$. For the interval hesitation margin ${\tilde{\pi }}_{{\tilde{A}}}(x)=[\pi ^L_{{\tilde{A}}}(x),\pi ^U_{{\tilde{A}}}(x)]$, we have $\pi ^L_{{\tilde{A}}}(x)=1-\mu ^U_{{\tilde{A}}}(x)-\nu ^U_{{\tilde{A}}}(x)$ and $\pi ^U_{{\tilde{A}}}(x)=1-\mu ^L_{{\tilde{A}}}(x)-\nu ^L_{{\tilde{A}}}(x)$. If $\mu ^L_{{\tilde{A}}}(x)=\mu ^U_{{\tilde{A}}}(x)$ and $\nu ^L_{{\tilde{A}}}(x)=\nu ^U_{{\tilde{A}}}(x)$, then the IVIFS ${\tilde{A}}$ is reduced to an IFS. In addition, $\left( {\tilde{\mu }}_{{\tilde{A}}}(x), {\tilde{\nu }}_{{\tilde{A}}}(x)\right)$ is named interval-valued intuitionistic fuzzy value (IVIFV).

Fig. 1

Graphical representation of IVIFS

In order to better understand IVIFS and the following discussion, here we present its graphical representation. When the universe X is a singleton space, an IVIFS ${\tilde{A}}$ can be represented by the image as a rectangular region in Fig. 1. The three vertices of the triangle are (0, 0), (0, 1), and (1, 0), where (0, 0) corresponds to $\pi _{{\tilde{A}}}(x)=1$, and (0, 1), (1, 0) represent the cases of classic sets. The hypotenuse of the triangle, that is, the segment from (0, 1) to (1, 0), corresponds to $\nu _{{\tilde{A}}}(x)=1-\mu _{{\tilde{A}}}(x)$, i.e., $\pi _{{\tilde{A}}}(x) = 0$. Because of the limitation of IVIFS $\mu _{{\tilde{A}}}(x) + \nu _{{\tilde{A}}}(x)\le 1$, we can know that the upper right vertex of the rectangular area in Fig. 1 must not exceed the hypotenuse of the triangle.

In order to express more simply in the following definitions, use FS(X) to represent the set of FSs on X, IVFS(X) to represent the set of IVFSs on X, IFS(X) to represent the set of IFSs on X, IVIFS(X) to represent the set of IVIFSs on X.

Definition 2.6

(Xu 2007) For any two IVIFSs ${\tilde{A}}=\{\langle x,[{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)],[\nu _{{\tilde{A}}}^L(x)$, $\nu _{{\tilde{A}}}^U(x)]\rangle |x\in X\}$ and ${\tilde{B}}=\{\langle x,[{\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x)],[\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x)]\rangle |x\in X\}$,

• (1) ${\tilde{A}} \subseteq {\tilde{B}}$ iff $\mu _{{\tilde{A}}}^{L}(x) \le \mu _{{\tilde{B}}}^{L}(x), \mu _{{\tilde{A}}}^{U}(x) \le \mu _{{\tilde{B}}}^{U}(x), \nu _{{\tilde{A}}}^{L}(x) \ge \nu _{{\tilde{B}}}^{L}(x)$ and $\nu _{{\tilde{A}}}^{U}(x) \ge \nu _{{\tilde{B}}}^{U}(x)$ for any $x \in X$,

• (2) ${\tilde{A}}={\tilde{B}}$ iff ${\tilde{A}} \subseteq {\tilde{B}}$ and ${\tilde{A}} \supseteq {\tilde{B}}$,i.e., $\mu _{{\tilde{A}}}^{L}(x) = \mu _{{\tilde{B}}}^{L}(x), \mu _{{\tilde{A}}}^{U}(x) = \mu _{{\tilde{B}}}^{U}(x), \nu _{{\tilde{A}}}^{L}(x)= \nu _{{\tilde{B}}}^{L}(x)$, $\nu _{{\tilde{A}}}^{U}(x) = \nu _{{\tilde{B}}}^{U}(x)$ for any $x \in X$,

• (3) ${\tilde{A}}^{c}=\left\{ \left\langle x, {\tilde{\nu }}_{{\tilde{A}}}(x), {\tilde{\mu }}_{{\tilde{A}}}(x)\right\rangle | x \in X\right\} .$

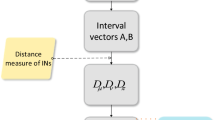
Here, we review the definition of distance measure and some widely used distance measures of IVIFSs.

Definition 2.7

(Liu and Jiang 2020) For any ${\tilde{A}},{\tilde{B}},{\tilde{C}}\in IVIFS(X)$, let D be a mapping $D: IVIFS(X) \times IVIFS(X)\rightarrow [0,1]$. $D({\tilde{A}}, {\tilde{B}})$ is called a distance measure if it satisfies the following properties:

• (1) $D({\tilde{A}}, {\tilde{B}})=0$ iff ${\tilde{A}} = {\tilde{B}}$,

• (2) $D({\tilde{A}}, {\tilde{B}})=D({\tilde{B}},{\tilde{A}})$,

• (3) $D({\tilde{A}},{\tilde{C}})\le D({\tilde{A}}, {\tilde{B}})+D({\tilde{B}},{\tilde{C}})$,

• (4) If ${\tilde{A}}\subseteq {\tilde{B}}\subseteq {\tilde{C}}$, then $\max \{D({\tilde{A}}, {\tilde{B}}),D({\tilde{B}},{\tilde{C}})\}\le D({\tilde{A}},{\tilde{C}})$.

For any two IVIFSs A and B on X, the following distance measures were discussed in Zhang et al. (2014). Let ${\tilde{A}}=\{\langle x,[{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)],[\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)]\rangle |x\in X\}$ and ${\tilde{B}}=\{\langle x,[{\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x)],[\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x)]\rangle |x\in X\}$.

1. Hamming distance

$$\begin{aligned} D_{H}({{\tilde{A}}},{\tilde{B}})= & {} D_{H}\left( ({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),\right. \nonumber \\&\left. ({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x))\right) \nonumber \\= & {} \frac{1}{4n}\sum _{i=1}^{n}\left[ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-{\mu }^L_{{\tilde{B}}}(x_{i})\right| \right. \nonumber \\&+\left| {\mu }^U_{{\tilde{A}}}(x_i)-{\mu }^U_{{\tilde{B}}}(x_{i})\right| \nonumber \\&\left. +\left| {\nu }^L_{{\tilde{A}}}(x_{i})-{\nu }^L_{{\tilde{B}}}(x_{i})\right| +\left| {\nu }^U_{{\tilde{A}}}(x_{i})-{\nu }^U_{{\tilde{B}}}(x_{i})\right| \right] .\nonumber \\ \end{aligned}$$

(1)

2. Normalized Hamming distance induced by Hausdorff metric

$$\begin{aligned} D_{NH}({{\tilde{A}}},{\tilde{B}})= & {} D_{NH}\left( ({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),\right. \nonumber \\&\left. ({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x))\right) \nonumber \\= & {} \frac{1}{2n} \sum _{i=1}^{n}\left[ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-{\mu }^L_{{\tilde{B}}}(x_{i})\right| \right. \nonumber \\&\vee \left| {\mu }^U_{{\tilde{A}}}(x_i)-{\mu }^U_{{\tilde{B}}}(x_{i})\right| \nonumber \\&\left. +\left| {\nu }^L_{{\tilde{A}}}(x_{i})-{\nu }^L_{{\tilde{B}}}(x_{i})\right| \vee \left| {\nu }^U_{{\tilde{A}}}(x_{i})-{\nu }^U_{{\tilde{B}}}(x_{i})\right| \right] .\nonumber \\ \end{aligned}$$

(2)

3. Normalized distance induced by Hausdorff metric

$$\begin{aligned} D_{N}({\tilde{A}},{\tilde{B}})= & {} D_{N}\left( ({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),\right. \nonumber \\&\left. ({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x))\right) \nonumber \\= & {} \frac{1}{2n} \sum _{i=1}^{n}\max \left\{ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-{\mu }^L_{{\tilde{B}}}(x_{i})\right| \right. \nonumber \\&+\left| {\mu }^U_{{\tilde{A}}}(x_i)-{\mu }^U_{{\tilde{B}}}(x_{i})\right| ,\nonumber \\&\left. \left| {\nu }^L_{{\tilde{A}}}(x_{i})-{\nu }^L_{{\tilde{B}}}(x_{i})\right| +\left| {\nu }^U_{{\tilde{A}}}(x_{i})-{\nu }^U_{{\tilde{B}}}(x_{i})\right| \right\} .\nonumber \\ \end{aligned}$$

(3)

3 Entropy measure for IVIFS

The main content of this section is divided into two subsections. The first subsection gives a new axiomatic definition of entropy, and the second subsection shows the specific entropy measure construction method.

3.1 A new axiomatic definition of entropy on IVIFS

Firstly, we recall the definition of entropy on IFS proposed by Burillo and Bustince.

Definition 3.1

(Burillo and Bustince 1996) For any ${\bar{A}}$, ${\bar{B}}\in IFS(X)$, a mapping $I:IFS(X)\rightarrow [0,1]$ is called an entropy on IFS(X), if I satisfies the following conditions:

• (IP1) $I({\bar{A}})=0$ iff ${\bar{A}}\in FS(X)$,

• (IP2) $I({\bar{A}})=1$ iff $\mu _{{\bar{A}}}(x)=\nu _{{\bar{A}}}(x)=0$ for all $x \in X$,

• (IP3) $I({\bar{A}})=I({{\bar{A}}}^c)$,

• (IP4) $I({\bar{A}}) \ge I({\bar{B}})$ if $\mu _{{\bar{A}}}(x) \le \mu _{{\bar{B}}}(x)$ and $\nu _{{\bar{A}}}(x) \le \nu _{{\bar{B}}}(x)$ for all $x \in X$.

We abbreviate this entropy to BB entropy (Burillo and Bustince 1996). It measures the intuitive degree of IFS, that is, the difference between IFS and FS. In the definition of BB entropy, we can see that (IP1) means the entropy is zero if and only if IFS degrades to FS, i.e., the hesitation index is zero. The second condition indicates that the entropy reaches the maximum if and only if the hesitation index is one, i.e., the complete lack of information. Moreover, (IP3) states that the entropy is symmetric under complementary conditions, while (IP4) means the more hesitant, the higher the entropy value.

Inspired by BB entropy of IFS, we can give the similar axiomatic definition of entropy on IVIFS, which is used to measure the difference between IVIFS and IVFS.

Definition 3.2

For any ${\tilde{A}}$, ${\tilde{B}}\in IVIFS(X)$, a mapping $E:IVIFS(X)\rightarrow [0,1]$ is called entropy on IVIFS(X), if E satisfies the following conditions:

• (E1) $E({\tilde{A}})=0$ iff ${\tilde{A}}\in IVFS(X)$,

• (E2) $E({\tilde{A}})=1$ iff ${\widetilde{\mu }}_{{\tilde{A}}}(x)={\widetilde{\nu }}_{{\tilde{A}}}(x)=[0,0]$ for all $x \in X$,

• (E3) $E({\tilde{A}})=E({{\tilde{A}}}^c)$,

• (E4) $E({\tilde{A}})\ge E({\tilde{B}})$ if ${\widetilde{\mu }}_{{\tilde{A}}}(x) \le {\widetilde{\mu }}_{{\tilde{B}}}(x)$, ${\widetilde{\nu }}_{{\tilde{A}}}(x) \le {\widetilde{\nu }}_{{\tilde{B}}}(x)$, i.e., ${\mu }_{{\tilde{A}}}^L(x)\le {\mu }_{{\tilde{B}}}^L(x)$, ${\mu }_{{\tilde{A}}}^U(x)\le {\mu }_{{\tilde{B}}}^U(x)$, $\nu _{{\tilde{A}}}^L(x)\le {\nu }_{{\tilde{B}}}^L(x)$, $\nu _{{\tilde{A}}}^U(x)\le \nu _{{\tilde{B}}}^U(x)$ for all $x \in X$.

Accordingly, the first property (E1) indicates that the entropy is zero if and only if IVIFS degenerates to IVFS. (E2), (E3) and (E4) have the same meaning as BB-entropy expression on IFS(X).

Fig. 2

Graphical relationship between ${\tilde{A}}$ and ${\tilde{A}}^+$, ${\tilde{A}}^-$

In this part, we will propose an approach to construct entropy measures using the distance function of IVIFSs. Given ${\tilde{A}}\in IVIFS(X)$, in the light of the image representation of the IVIFS discussed in the previous section, the closer the rectangular area of ${\tilde{A}}$ to the hypotenuse of the triangle, the smaller the entropy value $E({\tilde{A}})$, the closer to the point (0, 0), the greater the entropy $E({\tilde{A}})$. The rectangular area represented by IVIFS ${\tilde{A}}$ is projected vertically on the hypotenuse of the triangle to get the set ${{\tilde{A}}}^+$, and projected horizontally on the hypotenuse of the triangle to obtain the set ${{\tilde{A}}}^-$, as shown in Fig. 2. Because the hypotenuse means ${\tilde{\mu }}(x)+{\tilde{\nu }}(x)=1$, and the sets ${{\tilde{A}}}^+$, ${{\tilde{A}}}^-$ satisfy ${\widetilde{\mu }}_{{{\tilde{A}}}^+}(x)={\widetilde{\mu }}_{{\tilde{A}}}(x)$, ${\widetilde{\nu }}_{{{\tilde{A}}}^-}(x)={\widetilde{\nu }}_{{\tilde{A}}}(x)$, so

$$\begin{aligned} {{\tilde{A}}}^+= & {} \{\langle x, {\tilde{\mu }}(x) ,1-{\tilde{\mu }}(x)\rangle | x \in X\}\\= & {} \{\langle x,[\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x)], [1-\mu _{{\tilde{A}}}^U(x) , 1-\mu _{{\tilde{A}}}^L(x)]\rangle | x \in X\},\\ {{\tilde{A}}}^-= & {} \{\langle x ,1-{\tilde{\nu }}(x),{\tilde{\nu }}(x)\rangle | x \in X\}\\= & {} \{\langle x ,[1-\nu _{{\tilde{A}}}^U(x), 1-\nu _{{\tilde{A}}}^L(x)],\\&[\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x)]\rangle | x \in X\}. \end{aligned}$$

Obviously, the sets ${{\tilde{A}}}^+$ and ${{\tilde{A}}}^-$ are IVFSs. The entropy value of ${\tilde{A}}$ is related to the distance between ${\tilde{A}}$ and two IVFSs ${{\tilde{A}}}^+$ and ${{\tilde{A}}}^-$.

To facilitate the calculation of the distance between IVIFS and IVFS, we write the parameters of ${{\tilde{A}}}$, ${{\tilde{A}}}^+$, ${{\tilde{A}}}^-$ as vector form, i.e., the parameters of ${{\tilde{A}}}$ are $(\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x))$, then the parameters of ${{\tilde{A}}}^+$ are $(\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x), 1-\mu _{{\tilde{A}}}^U(x) , 1-\mu _{{\tilde{A}}}^L(x))$, and the parameters of ${{\tilde{A}}}^-$ are $(1-\nu _{{\tilde{A}}}^U(x), 1-\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x))$.

Example 3.3

Given ${\tilde{A}}\in IVIFS(X)$, ${{\tilde{A}}}=\{\langle x,[0.1,0.2],[0.3,0.4]\rangle | x \in X\}\}$, then the corresponding IVFSs ${{\tilde{A}}}^+=\{\langle x,[0.1,0.2], [0,8, 0.9]\rangle | x \in X\}$, ${{\tilde{A}}}^-=\{\langle x ,[0.6, 0.7], [0.3,0.4] \rangle | x \in X\}$. Expressed as a vector form: ${{\tilde{A}}}=(0.1,0.2,0.3,0.4)$, ${{\tilde{A}}}^+=(0.1,0.2, 0,8, 0.9)$, and ${{\tilde{A}}}^-=(0.6, 0.7, 0.3,0.4)$.

So we use a function g to measure the distances from ${\tilde{A}}$ to ${{\tilde{A}}}^+$ and ${\tilde{A}}$ to ${{\tilde{A}}}^-$, respectively, then an external binary function f aggregates these two distances to describe the entropy of ${\tilde{A}}$. Here we give the definitions of the distance function g and the external binary function f.

The domain I of the function g to be used in the following construction is given by:

$$\begin{aligned} I= & {} \left\{ ({\tilde{A}},{{\tilde{A}}}^+),({\tilde{A}},{{\tilde{A}}}^-)\right\} \\= & {} \left\{ \left( (\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x)),\right. \right. \\&\left. \left. (\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x), 1-\mu _{{\tilde{A}}}^U(x) , 1-\mu _{{\tilde{A}}}^L(x))\right) ,\right. \\&\left. \left( (\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x)),\right. \right. \\&\left. \left. (1-\nu _{{\tilde{A}}}^U(x), 1-\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x))\right) \right\} , \end{aligned}$$

where ${\tilde{A}}\in IVIFS(X)$, ${{\tilde{A}}}^+$, ${{\tilde{A}}}^-\in IVFS(X)$.

Definition 3.4

For any ${\tilde{A}}\in IVIFS(X)$, a function $g:I\rightarrow [0,1]$ is called a distance function, if g satisfies the following conditions:

• (i) $g({\tilde{A}},{{\tilde{A}}}^+)=0$ and $g({\tilde{A}},{{\tilde{A}}}^-)=0$ iff ${\mu }_{{\tilde{A}}}^L(x)=1-{\nu }_{{\tilde{A}}}^U(x)$, $\mu _{{\tilde{A}}}^U(x)=1-\nu _{{\tilde{A}}}^L(x)$,

• (ii) $g({\tilde{A}},{{\tilde{A}}}^+)=1$ and $g({\tilde{A}},{{\tilde{A}}}^-)=1$ iff $\mu _{{\tilde{A}}}^L(x)=\mu _{{\tilde{A}}}^U(x)=\nu _{{\tilde{A}}}^L(x)=\nu _{{\tilde{A}}}^U(x)=0$,

• (iii) The membership and non-membership in g are commutative, i.e.,

  $$\begin{aligned}&g((\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x)),(\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x),\\&\qquad 1-\mu _{{\tilde{A}}}^U(x) , 1-\mu _{{\tilde{A}}}^L(x)))\\&\quad =g((\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x),\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x)),(1-\mu _{{\tilde{A}}}^U(x) ,\\&\qquad 1-\mu _{{\tilde{A}}}^L(x),\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x))),\\&\qquad g((\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x)),(1-\nu _{{\tilde{A}}}^U(x),\\&\qquad 1-\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x)))\\&\quad =g((\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x),\mu _{{\tilde{A}}}^L(x), \mu _{{\tilde{A}}}^U(x)),\\&\qquad (\nu _{{\tilde{A}}}^L(x), \nu _{{\tilde{A}}}^U(x),1-\nu _{{\tilde{A}}}^U(x), 1-\nu _{{\tilde{A}}}^L(x))), \end{aligned}$$

  (iv) $g({\tilde{A}},{{\tilde{A}}}^+)$ and $g({\tilde{A}},{{\tilde{A}}}^-)$ decrease with respect to $\mu _{{\tilde{A}}}^L(x)$, $\mu _{{\tilde{A}}}^U(x)$, $\nu _{{\tilde{A}}}^L(x)$, $\nu _{{\tilde{A}}}^U(x)$.

Condition (i) states that if the distances from ${\tilde{A}}$ to ${\tilde{A}}^+$ and ${\tilde{A}}$ to ${\tilde{A}}^-$ are 0, it means that ${\tilde{A}}$, ${\tilde{A}}^+$, and ${\tilde{A}}^-$ overlap in Fig. 2. At this time, ${\tilde{A}}$ is an IVFS. Condition (ii) shows that when the distances from ${\tilde{A}}$ to ${{\tilde{A}}}^+$ and ${\tilde{A}}$ to ${{\tilde{A}}}^-$ reach 1, the distance between IVIFS ${\tilde{A}}$ and two IVFSs ${{\tilde{A}}}^+$, ${{\tilde{A}}}^-$ is the farthest, which ${\tilde{A}}$ is at point (0, 0) in Fig. 2. Condition (iii) shows that the position of ${\tilde{\mu }}$ and ${\tilde{\nu }}$ is equal when measuring the distance between ${\tilde{A}}$ and ${\tilde{A}}^+$, so the position of membership and non-membership is commutative in the formula, the same as the distance between ${\tilde{A}}$ and ${\tilde{A}}^-$. Moreover, condition (iv) indicates that when the membership and non-membership parameters increase, that is, when the rectangular area represented by ${\tilde{A}}$ in Fig. 2 becomes larger or close to the hypotenuse of the triangle, the distance between IVIFS ${\tilde{A}}$ and two IVFSs ${{\tilde{A}}}^+$, ${{\tilde{A}}}^-$ becomes smaller, that is, the distance is related to the parameters of membership degree and non-membership degree decrease.

Definition 3.5

(Bustince et al. 2019) A function ${f}:[0,1]^{2} \rightarrow [0,1]$ is called a binary aggregation function if it satisfies the following conditions:

• (I) f is component-wise increasing,

• (II) ${f(0, 0)=0}$,

• (III) ${f(1, 1)=1}$,

• (IV) ${f\left( x, y\right) ={f}\left( y, x\right) }$.

We provide a detailed discussion about the construction process and present it in the form of theorem in the context of these concepts.

Theorem 3.6

Let $g:I\rightarrow [0,1]$ be a distance function and $f:[0,1]\times [0,1]\rightarrow [0,1]$ be a binary aggregation function. For any ${\tilde{A}}\in IVIFS(X)$, the function $E:IVIFS(X)\rightarrow [0,1]$ defined by:

$$\begin{aligned} \begin{aligned} E({\tilde{A}})=\frac{1}{n}\sum _{x\in X}f(g({\tilde{A}},{{\tilde{A}}}^+),g({\tilde{A}},{{\tilde{A}}}^-)) \end{aligned} \end{aligned}$$

(4)

is an entropy on IVIFS(X).

Proof

In the following, we will prove the proposed formula satisfies four conditions in Definition 3.2.

(1) Let $E({\tilde{A}})=0$, i.e., for any $x\in X$

$$\begin{aligned} \begin{aligned}&f(g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\\&\quad 1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^L(x))),\\&\quad g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),(1-\nu _{{\tilde{A}}}^U(x),\\&\quad 1-\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)))=0. \end{aligned} \end{aligned}$$

From (II), it is equivalent to

$$\begin{aligned}&g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\\&\quad \nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^L(x)))=0 \end{aligned}$$

and

$$\begin{aligned}&g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\\&\quad \nu _{{\tilde{A}}}^U(x)),(1-\nu _{{\tilde{A}}}^U(x),1-\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)))=0, \end{aligned}$$

which by (i) is equivalent to ${\mu }_{{\tilde{A}}}^L(x)=1-{\nu }_{{\tilde{A}}}^U(x)$ and $\mu _{{\tilde{A}}}^U(x)=1-\nu _{{\tilde{A}}}^L(x)$. So ${{\tilde{A}}}$ is an IVFS.

(2) We can find that

$$\begin{aligned} \begin{aligned}&E({{\tilde{A}}})=1{\Leftrightarrow }f(g({\tilde{A}},{{\tilde{A}}}^+),g({\tilde{A}},{{\tilde{A}}}^-))\\&\quad =1\Leftrightarrow g({\tilde{A}},{{\tilde{A}}}^+)=g({\tilde{A}},{{\tilde{A}}}^-)=1\\&\qquad {\Leftrightarrow } g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^L(x)))=1,\\&\qquad g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),(1-\nu _{{\tilde{A}}}^U(x),\\&\qquad 1-\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)))=1.\\&\qquad {\Leftrightarrow }{\mu }_{{\tilde{A}}}^L(x)={\mu }_{{\tilde{A}}}^U(x)=\nu _{{\tilde{A}}}^L(x)=\nu _{{\tilde{A}}}^U(x)=0.\\ \end{aligned} \end{aligned}$$

(3) From (iii), we have

$$\begin{aligned} \begin{aligned}&f(g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^L(x))),\\&\qquad g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),\\&\qquad (1-\nu _{{\tilde{A}}}^U(x),1-\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)))) \\&\quad =f(g((\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)),\\&\qquad (1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x))),\\&\qquad g((\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)),(\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),\\&\qquad 1-\nu _{{\tilde{A}}}^U(x),1-\nu _{{\tilde{A}}}^L(x)))). \end{aligned} \end{aligned}$$

Therefore, taking (iv) into account, it follows that:

$$\begin{aligned} \begin{aligned}&f(g((\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)),\\&\qquad (1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x))),\\&\qquad g((\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)),(\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),\\&\qquad 1-\nu _{{\tilde{A}}}^U(x),1-\nu _{{\tilde{A}}}^L(x))))\\&\quad =f(g((\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)),(\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),\\&\qquad 1-\nu _{{\tilde{A}}}^U(x),1-\nu _{{\tilde{A}}}^L(x))),\\&\qquad g((\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)),(1-{\mu }_{{\tilde{A}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x)))). \end{aligned} \end{aligned}$$

Thus, $E({\tilde{A}})=E({\tilde{A}}^c)$.

(4) Take ${\tilde{A}}, {\tilde{B}}\in IVIFS(X)$ such that ${\widetilde{\mu }}_{{\tilde{A}}}(x)\le {\widetilde{\mu }}_{{\tilde{B}}}(x)$, ${\widetilde{\nu }}_{{\tilde{A}}}(x)\le {\widetilde{\nu }}_{{\tilde{B}}}(x)$. By condition (iv), it holds that:

$$\begin{aligned} \begin{aligned}&g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{A}}}^L(x)))\\&\quad \ge g(({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{A}}}^U(x),1-{\mu }_{{\tilde{B}}}^L(x)))\\&\quad \ge g(({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{B}}}^U(x),1-{\mu }_{{\tilde{B}}}^L(x)))\\&\quad \ge g(({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{A}}}^U(x)),({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{B}}}^U(x),1-{\mu }_{{\tilde{B}}}^L(x)))\\&\quad \ge g(({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x)),({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\\&\qquad 1-{\mu }_{{\tilde{B}}}^U(x),1-{\mu }_{{\tilde{B}}}^L(x))). \end{aligned} \end{aligned}$$

Similarly, it can be proved that

$$\begin{aligned} \begin{aligned}&g(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),\\&\qquad (1-\nu _{{\tilde{A}}}^U(x),1-\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)))\\&\quad \ge g(({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x)),\\&\qquad (1-\nu _{{\tilde{B}}}^U(x),1-\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x))). \end{aligned} \end{aligned}$$

Hence, from (I), we conclude $E({\tilde{A}})\ge E({\tilde{B}})$. $\square$

3.2 Construct entropy with distance function on IVIFS

In this part, we first give the relationship between the distance function and the distance measure, and then give the concrete method of constructing the entropy of the distance function.

If $D({\tilde{A}}, {\tilde{B}})$ is a distance measure, then the relationship between distance function g and distance measure D is:

$$\begin{aligned} \begin{aligned} D({\tilde{A}}, {\tilde{B}})&=\frac{1}{n} \sum _{x\in X}g({\tilde{A}},{\tilde{B}})\\&=\frac{1}{n} \sum _{x\in X} g\left( ({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),\right. \\&\left. ({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x))\right) \end{aligned} \end{aligned}$$

for any ${\tilde{A}}$, ${\tilde{B}}\in IVIFS(X)$.

From Theorem 3.6, a plenty of formulae of entropy measure can be derived by using different distance functions g and binary aggregation functions f with the aforementioned conditions. Next, we review some well-known distance measures of IVIFSs that can help understand the process of our entropy construction clearly.

Example 3.7

For any ${\tilde{A}}$, ${\tilde{B}}\in IVIFS(X)$, from the distance functions $g_H$, $g_{NH}$, $g_N$ given below:

$$\begin{aligned} g_H({\tilde{A}},{\tilde{B}})= & {} g_H(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x)),\\&({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x)))\\= & {} \frac{1}{2}\left[ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-{\mu }^L_{{\tilde{B}}}(x_{i})\right| \right. +\left| {\mu }^U_{{\tilde{A}}}(x_i)-{\mu }^U_{{\tilde{B}}}(x_{i})\right| \\&\left. +\left| {\nu }^L_{{\tilde{A}}}(x_{i})-{\nu }^L_{{\tilde{B}}}(x_{i})\right| +\left| {\nu }^U_{{\tilde{A}}}(x_{i})-{\nu }^U_{{\tilde{B}}}(x_{i})\right| \right] ,\\ g_{NH}({\tilde{A}},{\tilde{B}})= & {} g_{NH}(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),v_{{\tilde{A}}}^L(x),v_{{\tilde{A}}}^U(x)),\\&({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x)))\\= & {} \left[ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-{\mu }^L_{{\tilde{B}}}(x_{i})\right| \right. \vee \left| {\mu }^U_{{\tilde{A}}}(x_i)-{\mu }^U_{{\tilde{B}}}(x_{i})\right| \\&\left. +\left| {\nu }^L_{{\tilde{A}}}(x_{i})-{\nu }^L_{{\tilde{B}}}(x_{i})\right| \vee \left| {\nu }^U_{{\tilde{A}}}(x_{i})-{\nu }^U_{{\tilde{B}}}(x_{i})\right| \right] ,\\ g_N({\tilde{A}},{\tilde{B}})= & {} g_{N}(({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),v_{{\tilde{A}}}^L(x),v_{{\tilde{A}}}^U(x)),\\&({\mu }_{{\tilde{B}}}^L(x),{\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x)))\\= & {} \frac{1}{2}\max \left\{ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-{\mu }^L_{{\tilde{B}}}(x_{i})\right| \right. \\&+\left| {\mu }^U_{{\tilde{A}}}(x_i)-{\mu }^U_{{\tilde{B}}}(x_{i})\right| ,\\&\left. \left| {\nu }^L_{{\tilde{A}}}(x_{i})-{\nu }^L_{{\tilde{B}}}(x_{i})\right| +\left| {\nu }^U_{{\tilde{A}}}(x_{i})-{\nu }^U_{{\tilde{B}}}(x_{i})\right| \right\} . \end{aligned}$$

Combined with the relationship between distance function g and distance measure D, we can get the corresponding distance measures $D_H$, $D_{NH}$, $D_N$, that is, Eqs. (1)–(3) mentioned in Sect. 2.

In addition, it is easy to prove that the formulae $g_H$ and $g_N$ satisfy conditions $(i)-(iv)$, but $g_{NH}$ does not satisfy (ii). When $g_{NH}({\tilde{A}},{{\tilde{A}}}^+)=1$ and $g_{NH}({\tilde{A}},{{\tilde{A}}}^-)=1$, the result of $\mu _{{\tilde{A}}}^L(x)=\mu _{{\tilde{A}}}^U(x)=\nu _{{\tilde{A}}}^L(x)=\nu _{{\tilde{A}}}^U(x)=0$ cannot be derived.

Next, we use $g_H$ and $g_N$ to calculate the distances from ${\tilde{A}}$ to ${{\tilde{A}}}^+$ and ${\tilde{A}}$ to ${{\tilde{A}}}^-$, respectively.

Example 3.8

Consider two distance functions $g_H$ and $g_N$, for any ${\tilde{A}}\in IVIFS(X)$,

$$\begin{aligned}&g_H({\tilde{A}},{{\tilde{A}}}^+) =\frac{1}{2}\left[ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-{\mu }^L_{{\tilde{A}}}(x_{i})\right| \right. +\left| {\mu }^U_{{\tilde{A}}}(x_i)-{\mu }^U_{{\tilde{A}}}(x_{i})\right| \\&\qquad \left. +\left| {\nu }^L_{{\tilde{A}}}(x_{i})-(1-{\mu }^U_{{\tilde{A}}}(x_i))\right| +\left| {\nu }^U_{{\tilde{A}}}(x_{i})-(1-{\mu }^L_{{\tilde{A}}}(x_{i}))\right| \right] \\&\quad =\frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2},\\&\qquad g_H({\tilde{A}},{{\tilde{A}}}^-) =\frac{1}{2}\left[ \left| {\mu }^L_{{\tilde{A}}}(x_{i})-(1-{\nu }^U_{{\tilde{A}}}(x_{i}))\right| \right. \\&\qquad +\left| {\mu }^U_{{\tilde{A}}}(x_i)-(1-{\nu }^L_{{\tilde{A}}}(x_{i}))\right| \\&\qquad \left. +\left| {\nu }^L_{{\tilde{A}}}(x_{i})-{\nu }^L_{{\tilde{A}}}(x_{i})\right| +\left| {\nu }^U_{{\tilde{A}}}(x_{i})-{\nu }^U_{{\tilde{A}}}(x_{i})\right| \right] \\&\quad =\frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2}, \end{aligned}$$

In the same way,

$$\begin{aligned} g_N({\tilde{A}},{{\tilde{A}}}^+) =g_N({\tilde{A}},{{\tilde{A}}}^-)=\frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2}. \end{aligned}$$

In the above calculation, we have shown that the distance between IVIFS ${{\tilde{A}}}$ and the corresponding two IVFSs ${{\tilde{A}}}^+$ and ${{\tilde{A}}}^-$ based on $g_H$ and $g_N$, respectively, is the same. Thus, we can draw a conclusion: combined with binary aggregation function $f:[0,1]\times [0,1]\rightarrow [0,1]$, the distance functions $g_H$ and $g_N$ induce the same entropy, given by:

$$\begin{aligned} \begin{aligned} E_H({\tilde{A}}){=}\frac{1}{n}\sum _{x\in X}f\left( \frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2},\frac{\pi _{{\tilde{A}}}^L(x){+}\pi _{{\tilde{A}}}^U(x)}{2}\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(5)

In particular, we consider f as:

• (1) $\displaystyle f_1(u,v)=\frac{u+v}{2}$,

• (2) $\displaystyle f_2(u,v)=\root p \of {\frac{u^p+v^p}{2}}$ $(p>1)$,

• (3) $\displaystyle f_3(u,v)=1-(1-\frac{u+v}{2})^k$ $(k>0)$,

• (4) $\displaystyle f_4(u,v)=\frac{u+v}{2e} exp(\sqrt{\frac{u+v}{2}})$.

Then, we get the following four entropies:

$$\begin{aligned} E_{H_1}({\tilde{A}})= & {} \frac{1}{n}\sum _{x\in X}\frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2}, \end{aligned}$$

(6)

$$\begin{aligned} E_{H_2}({\tilde{A}})= & {} \frac{1}{n}\sum _{x\in X}\frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2}, \end{aligned}$$

(7)

$$\begin{aligned} E_{H_3}({\tilde{A}})= & {} 1-\frac{1}{n}\sum _{x\in X}\frac{\left[ {\mu }_{{\tilde{A}}}^L(x)+{\mu }_{{\tilde{A}}}^U(x)+\nu _{{\tilde{A}}}^L(x)+\nu _{{\tilde{A}}}^U(x)\right] ^k}{\nonumber }\\&{2^k} (k>0), \end{aligned}$$

(8)

$$\begin{aligned} E_{H_4}({\tilde{A}})= & {} \frac{1}{n}\sum _{x\in X}\frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2e} exp(\sqrt{\frac{\pi _{{\tilde{A}}}^L(x)+\pi _{{\tilde{A}}}^U(x)}{2}}).\nonumber \\ \end{aligned}$$

(9)

In the next example, we give a more general distance function.

Example 3.9

For any ${\tilde{A}}$, ${\tilde{B}}\in IVIFS(X)$, consider a distance function $g_\lambda :I\rightarrow [0,1]$,

$$\begin{aligned} \begin{aligned} g_\lambda ({\tilde{A}},{\tilde{B}})&=g_{\lambda }({\mu }_{{\tilde{A}}}^L(x),{\mu }_{{\tilde{A}}}^U(x),\nu _{{\tilde{A}}}^L(x),\nu _{{\tilde{A}}}^U(x),{\mu }_{{\tilde{B}}}^L(x),\\&\quad {\mu }_{{\tilde{B}}}^U(x),\nu _{{\tilde{B}}}^L(x),\nu _{{\tilde{B}}}^U(x))\\&=\left| \lambda \left( \mu ^U_{{\tilde{A}}}(x)-{\mu }^U_{{\tilde{B}}}(x) \right) \right. \\&\quad \left. +(1-\lambda )\left( \mu ^L_{{\tilde{A}}}(x)-\mu ^L_{{\tilde{B}}}(x)\right) \right| \\&\quad +\left| \lambda \left( {\nu }^U_{{\tilde{A}}}(x)-{\nu }^U_{{\tilde{B}}}(x)\right) \right. \\&\quad \left. +(1-\lambda )\left( {\nu }^L_{{\tilde{A}}}(x)-{\nu }^L_{{\tilde{B}}}(x)\right) \right| , \end{aligned} \end{aligned}$$

and a binary aggregation function $f:[0,1]\times [0,1]\rightarrow [0,1]$, they induce an entropy, given by: for any ${\tilde{A}}\in IVIFS(X)$,

$$\begin{aligned} \begin{aligned} E_\lambda ({\tilde{A}})&=\frac{1}{n}\sum _{x\in X} f\left( \lambda \left( 1-{\mu }^L_{{\tilde{A}}}(x)-{\nu }^U_{{\tilde{A}}}(x)\right) \right. \\&\quad \left. +(1-\lambda )\left( 1-{\mu }^U_{{\tilde{A}}}(x)-{\nu }^L_{{\tilde{A}}}(x)\right) ,\right. \\&\quad \left. \lambda \left( 1-{\mu }^U_{{\tilde{A}}}(x)-{\nu }^L_{{\tilde{A}}}(x)\right) \right. \\&\quad \left. +(1-\lambda )\left( 1-{\mu }^L_{{\tilde{A}}}(x)-{\nu }^U_{{\tilde{A}}}(x)\right) \right) . \end{aligned} \end{aligned}$$

(10)

For $E_\lambda$, we can reflect the difference in the distance calculation method by transforming the value of the parameter $\lambda$, or we can transform the external aggregation function to reflect the difference between these two distance normalization methods. Through our discussion on the geometric representation of IVIFS, a series of entropy measures of IVIFS can be proposed under this method.

If $\lambda =1/2$, Eq. (5) is recovered. If we consider $f(u,v)=\root p \of {\frac{u^p+v^p}{2}}$ $(p>1)$ we mentioned previously, then we get the following entropy:

$$\begin{aligned} \begin{aligned} E_{\lambda _2}({\tilde{A}})&=\frac{1}{n}\sum _{x\in X}\frac{1}{\root p \of {2}}\Big [ \left[ \lambda \left( 1-{\mu }^L_{{\tilde{A}}}(x)-{\nu }^U_{{\tilde{A}}}(x)\right) \right. \\&\quad \left. +(1-\lambda )\left( 1-{\mu }^U_{{\tilde{A}}}(x)-{\nu }^L_{{\tilde{A}}}(x)\right) \right] ^p\\&\quad +\left[ \lambda \left( 1-{\mu }^U_{{\tilde{A}}}(x)-{\nu }^L_{{\tilde{A}}}(x)\right) \right. \\&\quad \left. +(1-\lambda )\left( 1-{\mu }^L_{{\tilde{A}}}(x)-{\nu }^U_{{\tilde{A}}}(x)\right) \right] ^p\Big ]^{1/p}. \end{aligned} \end{aligned}$$

For instance, if $\displaystyle \lambda =1/4$, $p=2$, then

$$\begin{aligned} \begin{aligned} E^*_{\lambda _2}({\tilde{A}})&=\frac{1}{4n}\sum _{x\in X} \left[ 5\left( 1-{\mu }^L_{{\tilde{A}}}(x)-{\nu }^U_{{\tilde{A}}}(x)\right) ^2\right. \\&\quad \left. +5\left( 1-{\mu }^U_{{\tilde{A}}}(x)-{\nu }^L_{{\tilde{A}}}(x)\right) ^2\right. \\&\quad \left. +9\left( 1-{\mu }^L_{{\tilde{A}}}(x)-{\nu }^U_{{\tilde{A}}}(x)\right) \left( 1-{\mu }^U_{{\tilde{A}}}(x)-{\nu }^L_{{\tilde{A}}}(x)\right) \right] ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

(11)

In the following, we will use some proposed entropy formulae as examples and apply them to numerical examples to prove that the newly entropy construction method is effective.

4 Demonstrative example

In this part, we first present a comparison with the existing IVIFS entropy measures, which is adapted from Nguyen (2016), to demonstrate the effectiveness of the newly proposed measures.

Example 4.1

Three pairs of singleton IVIFSs are given below:

We compare the performance between the proposed measures $E_{H1}$, $E_{H2}$, $E_{H3}$, $E_{H4}$, $E^*_{\lambda _2}$, that is, Eqs. (6)–(9), (11), and the existing measures $E_Y$ (Ye 2010b), $E_{ZJJL}$ (Zhang et al. 2010), $E_{Z}$ (Zhang et al. 2014), $E_{WZ}$ (Wei and Zhang 2015) with the above three pairs of IVIFSs. The calculation results are presented in Table 1.

Table 1 Comparison results of entropy measures

It is obvious in Table 1 that from the perspective of entropy, all proposed measures are superior to the listed existing measures. Compared with the measures we proposed, $E_Y$, $E_{ZJJL}$, $E_{Z}$, $E_{WZ}$ cannot achieve the desired results. ${{\tilde{A}}}_{i}$ is more fuzzy than ${{\tilde{B}}}_{i}$ in each pair of IVIFSs, i.e., the entropy of ${{\tilde{A}}}_i$ should be greater than the entropy of ${{\tilde{B}}}_i$ for $i=1,2,3$. In the first pair of IVIFSs, $E_Y$ provides the same value for different IVIFSs, while the results of H and $E_{Z}$ are contrary to our expectations. A similar situation happens in the second pair of comparison, in which $E_Y$, $E_{ZJJL}$, $E_{Z}$ do not work well. ${{\tilde{A}}}_{2}$, ${{\tilde{B}}}_{2}$ and ${{\tilde{B}}}_{3}$ are reverted to IFSs, when $\mu ^{L}(x_{i})=\mu ^{U}(x_{i})$, $\nu ^{L}(x_{i})=\nu ^{U}(x_{i})$. In particular, ${{\tilde{B}}}_3$ is a classic set, that is, its entropy should be 0. All of the models except $E_{ZJJL}$ perform well, meeting the requirement mentioned before, while $E_{ZJJL}$ cannot distinguish between ${{\tilde{A}}}_3$ and ${{\tilde{B}}}_3$. Obviously, our proposed measures all produce the intuitive and persuading results that they can reasonably distinguish these IVIFSs.

In the next example, we will introduce the practical application of entropy measure and put our outcomes into a multi-criteria decision making (MCDM) problem. We utilize the example adapted from Das et al. (2016) to clarify the applicability of entropy in solving criteria weights.

Example 4.2

A couple wants to buy a house in a certain place. They have selected four sets. Now they have to choose one of the four houses that best meets their requirements. These four sets they selected are not in the same housing estate, denoted as $A_1$, $A_2$, $A_3$ and $A_4$, respectively. The couple’s four criteria for the house are: $C_1$: house prices, $C_2$: school district, $C_3$: location, $C_4$: transport facilities. They are hesitant about the preferences of the alternatives, so they can use IVIFSs to score. The weight vector written as $w = (w_1 ,w_2 ,w_3 ,w_4 )^T$ is unknown. According to the above criteria, the four houses are rated to obtain the matrix D below:

Since the weights of criteria are estimated based on knowledge measures in Das et al. (2016), we will modify the part of the knowledge measure in the original method to the entropy-based criteria weight determination method as shown below (Montes et al. 2018):

Step 1 We compute the amount of entropy $E(C_j)$ with D for each $C_j$.

Step 2 The weight of each criterion is obtained by normalizing the difference between one and the entropy value $E(C_j)$.

$$\begin{aligned} w_{j}=\frac{1-E(C_{j})}{ \sum _{j=1}^{4}\left( 1-E(C_{j})\right) } w_{j} \in [0,1], \sum _{j=1}^{4} w_{j}=1. \end{aligned}$$

By using the proposed entropy formulae, the entropy value of each criterion can be easily calculated. Generally, if a criterion has a small entropy value among all alternatives, decision makers can obtain more useful information from this criterion. Therefore, the criterion which has the minimum entropy value should be given priority as the most important criterion for decision makers. And then further calculate the weighted average value of IVIFS for each alternative, and finally get the alternative ranking, as shown in Table 2.

Table 2 Weights of criteria and alternatives’ ranking of entropy measures

It is observed from Table 2 that in terms of the weights of criteria, $E_{LZX}$ (Liu et al. 2005), $E_{ZJJL}$ (Zhang et al. 2010), $E_{WWZ}$ (Wei et al. 2011), $E_{JPCZ}$ (Jin et al. 2014), and $E^*_{\lambda _2}$ all get the similar result that the weight of $C_2$ is largest , while $E_{H_1}$, $E_{H_2}$, $E_{H_3}$, $E_{H_4}$ get that the weight of $C_4$ is largest. Additionally, the rankings of the alternatives we obtained are exactly the same, and all entropy measures indicate that $A_4$ is the most ideal choice, which ensures the entropy measures we proposed is reasonable. Therefore, from the above numerical problems, it is feasible and meaningful to construct a new entropy measure by distance functions.

In summary, in Example 4.1, the performance of the proposed entropy measures is preferable to that of some existing measures in the comparison of the entropy values of the three pairs of IVIFSs. From Example 4.2, we can see the proposed entropy measures perform well and can reach the ranking level of the existing entropy measures, where $E^*_{\lambda _2}$ obtains the analogous result both in weight value and alternatives ranking. As a consequence, combining two examples, $E^*_{\lambda _2}$ is the best performer that best fits the intuitive expectation among the entropy measures listed under our construction method.

5 Conclusions

This paper introduces a newly method to construct some entropy measures on IVIFS. Specifically, we give a set of new axiomatic definitions that entropy measures need to meet and then build some models that follow these axioms to implement measures. The construction of our proposed new entropy measure is based on the geometric representation of IVIFS, obtained by the distance aggregation of IVIFS ${\tilde{A}}$ with its two IVFSs ${{\tilde{A}}}^+$ and ${{\tilde{A}}}^-$. Since then, we can construct entropy measures using distance functions. Finally, an example is used to show that our proposed entropy measures perform better in the comparison of some special IVIFSs, and a demonstrative example is utilized to explain the application of entropy measure in MCDM. In future, we will continue to explore more reasonable and better entropy measures.