Parameterized utility functions on interval-valued intuitionistic fuzzy numbers with two kinds of entropy and their application in multi-criteria decision making

Abstract

In this study, the entropy of interval-valued intuitionistic fuzzy numbers (IVIFNs) is analyzed, and two kinds of entropy factors are proposed. By using the normalized score function, normalized Type-1 entropy factor, and normalized Type-2 entropy factor, a series of utility functions on IVIFNs are proposed. In particular, one of the proposed utility functions is structured based on integral. By using the proposed utility functions, IVIFNs can be compared and ranked. The characteristic of these proposed utility functions is that they are objective on comparing IVIFNs from the point of probability. Thereafter, two kinds of fuzzy multi-criteria decision-making methods in interval-valued intuitionistic fuzzy setting are introduced by using the proposed entropy functions. Finally, an example is given to demonstrate the effectiveness of the proposed utility functions and the fuzzy multi-criteria decision-making methods.

1 Introduction

Atanassov (1986) introduced the concept of intuitionistic fuzzy sets (IFSs), where the relationship between an element and a set is described by two values, i.e., the membership degree and non-membership degree of the element to the set. Three years later, Antanassov and Gargov (1989) proposed a notion as interval-valued intuitionistic fuzzy sets (IVIFSs). Thereafter, Pap (1997) presented a mathematical background for treating problems with uncertainty in soft computing, which includes fuzzy sets. For more than 20 years, regulations on IVIFSs have been studied from multiple perspectives, such as entropy function, similarity measure, score function, accuracy function, and aggregation function (see Liang and Shi 2003; Xu and Cai 2010; Liang and Wei 2014; Song and Wang 2017; Grabisch et al. 2009, 2011). Among these pioneering researches, ranking of intuitionistic fuzzy numbers (IFNs) or IVIFNs plays a main role in modeling many real-life problem and attracted many scholars’ attentions. For example, Chen and Tan (1994) proposed the score function of IFNs, by which IFNs can be ranked. However, there are some situations where some of IFNs produce same score values. Later, Hong and Choi (2000) proposed the accuracy function of IFNs. Mitchell (2004) adopted a statistical viewpoint and interprets each IFN as an ensemble of ordinary fuzzy numbers, and then, one method is proposed to rank IFNs. Xu and Yager (2006) proposed a method for ranking IFNs by using both the score function and the accuracy function. Moreover, Nehi (2010) proposed a method to rank trapezoidal IFNs based on integral.

Recently, some scholars use accuracy functions solely to compare IFNs or IVIFNs (see, Xu 2007a, b, c; Ye 2009; Nayagam et al. 2011; Zhao et al. 2017). However, Şahin (2016) indicated that there are some difficulties arising from the proposed accuracy functions on ranking IFNs or IVIFNs. Specifically, the comparison between two IFNs or IVIFNs needs to consider two factors, one is score values, and the other is accuracy values. How to coordinate the two factors? There are infinite possibilities. From the point of probability theory, the existing accuracy functions are all the moment estimation functions of the relationship between the two factors. Therefore, they can only be used in certain applicable environments. Besides, the mentioned two factors can also be dealt with form the viewpoint of utility theories. More details on utility function, please refer to Dubois et al. (2000). Referring the above analyses, the comparison between IVIFNs is studied based on utility theory in this study. Different from IFNs setting, the comparison between IVIFNs should consider three factors. On careful consideration, a series of novel utility functions to compare IVIFNs are proposed.

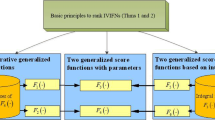
The rest part of this study is organized as follows. In Sect. 1, the definitions of IFSs and IVIFSs, some score functions and accuracy functions, as well as arithmetic and geometric aggregation operators on IVIFSs are introduced. In Sect. 2, a series of utility functions for ranking IVIFNs are proposed. Section 3 proposes two kinds of multi-criteria decision-making methods. Section 4 provides an example to demonstrate the effectiveness of the newly proposed utility functions and the novel decision-making methods. Finally, some innovation points are concluded in Sect. 5.

2 Preliminaries

In this section, classical concepts of IFSs, IVIFSs, some classical score functions and accuracy functions, as well as some classical arithmetic and geometric aggregation operators on IVIFSs are introduced.

Definition 1

(Atanassov 1986) Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a given set. An IFS $A$ in $X$ is defined as $A = \left\{ {\left\langle {x,\mu_{A} \left( x \right),\nu_{A} \left( x \right)} \right\rangle \left| {x \in X} \right.} \right\},$ where $X \ne \varPhi ,$$\mu_{A} \left( x \right):X \to \left[ {0,1} \right]$ and $\nu_{A} \left( X \right):$$X \to \left[ {0,1} \right]$ with condition $0 \le \mu_{A} \left( x \right) + \nu_{A} \left( x \right) \le 1.$ Denote $\pi_{A} \left( x \right) = 1 - \mu_{A} \left( x \right) - \nu_{A} \left( x \right),$$x \in X.$ Obviously, $0 \le \pi_{A} \left( x \right) \le 1.$ Then, the values $\mu_{A} \left( x \right),$$\nu_{A} \left( x \right),$ and $\pi_{A} \left( x \right)$ represent the membership degree, the non-membership degree, and the intuitionistic index of the element $x$ to the set $A$, respectively.

Definition 2

(Atanassov and Gargov 1989) Let $X\left( { \ne \varPhi } \right)$ be a given set. For any $x \in X,$ an IVIFS $A$ in the universe of discourse $X$ is defined as.

$$ A = \left\{ {\left\langle {x,\left[ {\mu_{AL} \left( x \right),\mu_{AU} \left( x \right)} \right]} \right.} \right. ,\left. {\left. {\left[ {\nu_{AL} \left( x \right),\nu_{AU} \left( x \right)} \right]} \right\rangle \left| {x \in X} \right.} \right\}, $$

(1)

where $0 \le \mu_{AU} \left( x \right) + \nu_{AU} \left( x \right) \le 1,$ and $0 \le \mu_{AL} \left( x \right),$$0 \le \nu_{AL} \left( x \right).$ For any $x \in X,$ denote

$$ \pi_{A} \left( x \right) = \left[ {1 - \mu_{AU} \left( x \right) - \nu_{AU} \left( x \right),} \right.\left. {1 - \mu_{AL} \left( x \right) - \nu_{AL} \left( x \right)} \right]. $$

(2)

Then, the intervals $\mu_{A} \left( x \right)$, $\nu_{A} \left( x \right)$ and $\pi_{A} \left( x \right)$ represent the membership degree, the non-membership degree, the intuitionistic index of the element $x$ to the set $A$, respectively.

Definition 3

(Xu 2007) Let $A = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$ be an IVIFN, then the score function is defined by $S_{xu} \left( A \right) = \frac{1}{2}\left( {a + b - c - d} \right),$ the accuracy function is defined by $H_{xu} \left( A \right) = \frac{1}{2}\left( {a + b + c + d} \right).$

Definition 4

(Xu 2007) Let $A_{j} \in {\text{IVIFS}}\left( X \right)$$\left( {j = 1,2, \ldots ,n} \right)$. The weighted arithmetic average operator is defined by

$$ F_{\omega } \left( {A_{1} ,A_{2} , \ldots ,A_{n} } \right) = \left( {\left[ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{A_{j} L}} \left( x \right)} \right)^{{\omega_{j} }} ,1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{A_{j} U}} \left( x \right)} \right)^{{\omega_{j} }} } } } \right],} \right.\left. {\left[ {\prod\limits_{j = 1}^{n} {\left( {\nu_{{A_{j} L}} \left( x \right)} \right)^{{\omega_{j} }} ,\prod\limits_{j = 1}^{n} {\left( {\nu_{{A_{j} U}} \left( x \right)} \right)^{{\omega_{j} }} } } } \right]} \right), $$

(3)

The weighted geometric average operator is defined by

$$ G_{\omega } \left( {A_{1} ,A_{2} , \ldots ,A_{n} } \right) = \left( {\left[ {\prod\limits_{j = 1}^{n} {\left( {\mu_{{A_{j} L}} \left( x \right)} \right)^{{\omega_{j} }} ,\prod\limits_{j = 1}^{n} {\left( {\mu_{{A_{j} U}} \left( x \right)} \right)^{{\omega_{j} }} } } } \right],} \right.\left. {\left[ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \nu_{{A_{j} L}} \left( x \right)} \right)^{{\omega_{j} }} ,1 - \prod\limits_{j = 1}^{n} {\left( {1 - \nu_{{A_{j} U}} \left( x \right)} \right)^{{\omega_{j} }} } } } \right]} \right), $$

(4)

where $\omega_{j}$ is the weight of $A_{j}$$\left( {j = 1,2, \ldots ,n} \right)$. In particular, assume $\omega_{j} = \frac{1}{n},$ then $F_{\omega }$ and $G_{\omega }$ are called arithmetic average operator and geometric average operator of IVIFSs, respectively.

Most recently, some scholars tried to describe IVIFSs by generalized score function, and to compare different IVIFNs by using solely index. This is also the target of this study. The core task in this study is to propose comparing methods on IVIFNs by using utility functions, but what needs to be explained is that the tool of this study is probability knowledge, which decides that this study has some unique application features.

3 Utility functions on IVIFNs with entropy index

3.1 Analysis on IVIFNs

Let $X\left( { \ne \varPhi } \right)$ be a given set, Let $A_{i} = \left( {\left[ {a_{i} ,b_{i} } \right],\left[ {c_{i} ,d_{i} } \right]} \right)\left( {i = 1,2} \right)$ be two IVIFNs on $X$, and let $E\left( {A_{i} } \right) = 1 - \left( {b_{i} - a_{i} } \right) + \left( {d_{i} - c_{i} } \right).$ it knows that $S_{xu} \left( \cdot \right)$ is an index to describe the score value that $A$ belongs to $X;$$H_{xu} \left( \cdot \right)$ is an index to describe the accuracy or clearness degree of the information that $A$ holds. Meanwhile, the index $E\left( \cdot \right)$ is also an accuracy index of $A$. Take $A_{1} = \left( {\left[ {a_{1} ,b_{1} } \right],\left[ {c_{1} ,d_{1} } \right]} \right)$ for example, practically, the smaller the value $b_{1} - a_{1}$ or $d_{1} - c_{1}$ is, the information of $A_{1}$ is more trusted; conversely, the bigger is the value $b_{1} - a_{1}$ or $d_{1} - c_{1}$, the bigger the entropy of $A_{1}$ is. By summarizing the above analyses, it gets that there are two indexes, i.e., $H_{xu} \left( \cdot \right)$ and $E\left( \cdot \right)$ are two independent indicators describing the accuracy (entropy) of $A$. Therefore, to compare $A_{1}$ and $A_{2} ,$ the aforementioned three indexes $S_{xu} \left( \cdot \right)$, $H_{xu} \left( \cdot \right)$ and $E\left( \cdot \right)$ all should be used.

3.2 A series of novel utility functions on IVIFNs

To propose the novel utility function on IVIFNs, this study firstly normalizes $S_{xu} \left( \cdot \right)$, $H_{xu} \left( \cdot \right)$ and $E\left( \cdot \right)$ as follows

Definition 10

Let $A = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$ be an IVIFN, then a normalized score function on $A$ is defined as

$$ S^{{\prime }} \left( A \right) = \frac{1}{2}\left( {\frac{{\left( {a - c} \right) + \left( {b - d} \right)}}{2} + 1} \right). $$

(5)

A normalized Type-1 entropy function on $A$ is defined as

$$ H^{{\prime }} \left( A \right) = 1 - \frac{1}{2}\left( {\frac{{\left( {a + c} \right) + \left( {b + d} \right)}}{2} + 1} \right). $$

(6)

A normalized Type-2 entropy function on $A$ is defined as

$$ E^{{\prime }} \left( A \right) = \left( {b - a} \right) + \left( {d - c} \right). $$

(7)

It is noteworthy that $S^{{\prime }} \left( A \right) \in \left[ {0,1} \right],$$H^{{\prime }} \left( A \right) \in \left[ {0,1} \right],$$E^{{\prime }} \left( A \right) \in \left[ {0,1} \right],$ whereas they are extensions of the classical score and accuracy functions proposed in Xu (2007c). In the following, by using these three key functions, a series of utility function on IVIFNs are proposed.

Definition 11

Let $A = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$ be an IVIFN. A utility function on $A$ is defined as

$$ F_{1} \left( A \right) = \frac{{S^{{\prime }} \left( A \right)^{{H^{{\prime }} \left( A \right) \cdot E^{{\prime }} \left( A \right)}} - S^{{\prime }} \left( A \right)}}{{1 - S^{{\prime }} \left( A \right)}} \cdot S^{{\prime }} \left( A \right). $$

(8)

There are infinite possibilities to describe the relationship between $S^{{\prime }} \left( A \right),$$H^{{\prime }} \left( A \right),$ and $E^{{\prime }} \left( A \right).$ When the importance of these three indexes is taken into account, a weighted utility function is proposed as follows.

Definition 12

Let $A = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$ be an IVIFN. A weighted utility function on $A$ is defined as

$$ F_{2} \left( A \right) = \frac{{\left( {S^{{\prime }} \left( A \right)^{{\left( {1 - w_{1} } \right)}} } \right)^{{H^{{\prime }} \left( A \right)^{{\left( {1 - w_{2} } \right)}} \cdot E^{{\prime }} \left( A \right)^{{\left( {w_{1} + w_{2} } \right)}} }} - S^{{\prime }} \left( A \right)}}{{1 - S^{{\prime }} \left( A \right)}} \cdot S^{{\prime }} \left( A \right). $$

(9)

where $w_{i} \in \left[ {0,1} \right], \, i = 1,2,0 \le w_{1} + w_{2} \le 1.$ It is noteworthy that $w_{1} ,$$w_{2} ,$ and $1 - w_{1} - w_{2}$ are the weights of $S^{{\prime }} \left( A \right),$$H^{{\prime }} \left( A \right)$, and $E^{{\prime }} \left( A \right)$, respectively.

From the point of probability theory, there are infinite possibilities to describe the relationship between $S^{{\prime }} \left( A \right),$$H^{{\prime }} \left( A \right)$ and $E^{{\prime }} \left( A \right)$ When probability factor is taken into account, a probability-based utility function is proposed as follows.

Definition 13

Let $A = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$ be an IVIFN. A probability-based utility function on $A$ is defined as

$$ F_{3} \left( A \right) = \int_{0}^{1} {\int_{0}^{{1 - w_{2} }} {\frac{{\left( {S^{\prime } \left( A \right)^{{\left( {1 - w_{1} } \right)}} } \right)^{{H^{\prime } \left( A \right)^{{\left( {1 - w_{2} } \right)}} \cdot E^{\prime } \left( A \right)^{{\left( {w_{1} + w_{2} } \right)}} }} - S^{\prime } \left( A \right)}}{{1 - S^{\prime } \left( A \right)}} \cdot S^{\prime } \left( A \right){\text{d}}w_{1} {\text{d}}w_{2} } } . $$

(10)

where $w_{i} \in \left[ {0,1} \right], \, i = 1,2,0 \le w_{1} + w_{2} \le 1.$

In the following, some important theorems are introduced.

• (1) There is a boundary feature on Eqs. (8), (9), and (10) as follows.

Theorem 1

Let $A = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$ be an IVIFN. Then, it gets that $0 \le F_{1} \left( A \right),F_{2} \left( A \right),F_{3} \left( A \right) \le S^{{\prime }} \left( A \right).$

• (2) There are some monotonical features on Eqs. (8), (9), and (10) as follows.

Theorem 2

In Eq. (8), $F_{1}$is a monotonically increasing function of$S^{{\prime }} \left( A \right),$is a monotonically decreasing function of$H^{{\prime }} \left( A \right)$and$E^{{\prime }} \left( A \right)$.

Theorem 3

In Eq. (9), $F_{2}$is a monotonically increasing function of$w_{1} ,$is a monotonically decreasing function of$w_{2}$and$1 - w_{1} - w_{2}$.

• (3) In classical fuzzy environment, Eqs. (8), (9), and (10) can be simplified as follows.

Theorem 4

Let$A = \left( {\left[ {a,b} \right],\left[ {c,d} \right]} \right)$be an IVIFN. When$a = b,$$c = d,$$b + d = 1,$then, Eqs. (8), (9), and (10) all can be reduced, where$F_{1} \left( A \right) = S^{{\prime }} \left( A \right),$$F_{2} \left( A \right) = S^{{\prime }} \left( A \right),$$F_{3} \left( A \right) = S^{{\prime }} \left( A \right).$

• (4) In classical intuitionistic fuzzy environment, Eqs. (8), (9), and (10) can be simplified as follows.

Theorem 5

Let$A = \left( {\mu ,\nu } \right),$be an IFN, where$0 \le \mu ,\nu ,\mu + \nu \le 1.$Then Eq. (8) is reduced to

$$ F_{1} \left( A \right) = \frac{{S^{{\prime }} \left( A \right)^{{H^{{\prime }} \left( A \right) \cdot }} - S^{{\prime }} \left( A \right)}}{{1 - S^{{\prime }} \left( A \right)}} \cdot S^{{\prime }} \left( A \right). $$

Equation (9) is reduced to

$$ F_{2} \left( A \right) = \frac{{\left( {S^{{\prime }} \left( A \right)^{{\left( {1 - w_{1} } \right)}} } \right)^{{H^{{\prime }} \left( A \right)^{{\left( {1 - w_{2} } \right)}} }} - S^{{\prime }} \left( A \right)}}{{1 - S^{{\prime }} \left( A \right)}} \cdot S^{{\prime }} \left( A \right). $$

Equation (10) is reduced to

$$ F_{3} \left( A \right) = \int_{0}^{1} {\int_{0}^{{1 - w_{2} }} {\frac{{\left( {S^{{\prime }} \left( A \right)^{{\left( {1 - w_{1} } \right)}} } \right)^{{H^{{\prime }} \left( A \right)^{{\left( {1 - w_{2} } \right)}} }} - S^{{\prime }} \left( A \right)}}{{1 - S^{{\prime }} \left( A \right)}} \cdot S^{{\prime }} \left( A \right){\text{d}}w_{1} {\text{d}}w_{2} } } . $$

Besides, it is noteworthy that Eq. (10) is proposed based on integral. In Eq. (10), every possibility of the relationship between normalized score function, normalized Type-1 entropy, and normalized Type-2 entropy is considered. Therefore, from the point of probability theory, Eq. (10) is objective on comparing IVIFNs.

3.3 Multi-criteria decision-making method

3.3.1 Problem introduction

Assume that there are m alternatives $A = \left( {A_{1} ,A_{2} , \ldots ,A_{m} } \right)$ and n decision-making criteria $C = \left( {C_{1} ,C_{2} , \ldots ,C_{n} } \right)$. Assume that the weight of criterion $C_{j}$$\left( {j = 1,2, \ldots ,n} \right)$, stated by the decision maker, is $\omega_{j}$, where $\omega_{j} \in \left[ {0,1} \right],$$\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1.$ The characteristic of alternative $A_{i} \left( {i = 1,2, \ldots ,m} \right)$ is expressed as

$$ A_{i} = \left\{ {\left\langle {C_{j} ,\left[ {\mu_{{A_{i} L}} \left( {C_{j} } \right),\mu_{{A_{i} U}} \left( {C_{j} } \right)} \right],} \right.} \right.\left. {\left. {\left[ {\nu_{{A_{i} L}} \left( {C_{j} } \right),\nu_{{A_{i} U}} \left( {C_{j} } \right)} \right]} \right\rangle \left| {C_{j} \in C} \right.} \right\}, $$

where $0 \le \mu_{{A_{i} U}} \left( x \right) + \nu_{{A_{i} U}} \left( x \right) \le 1,$$0 \le \mu_{{A_{i} L}} \left( x \right),$$0 \le \nu_{{A_{i} L}} \left( x \right),$ and $i = 1,2, \ldots ,m,$$j = 1,2, \ldots ,n.$ The IVIFN, which is the pair of values for $C_{j}$, is denoted by $\beta_{ij} = \left( {\left[ {a_{ij} ,b_{ij} } \right],\left[ {c_{ij} ,d_{ij} } \right]} \right),$ where $\left[ {a_{ij} ,b_{ij} } \right]$ indicates the degree that $A_{i}$ satisfies the criterion $C_{j}$, whereas $\left[ {c_{ij} ,d_{ij} } \right]$ indicates the degree that $A_{i}$ does not satisfy the criterion $C_{j}$. Then, the problem is how to rank $A_{i} \left( {i = 1,2, \ldots ,m} \right).$

3.3.2 Fuzzy decision-making methods

To solve the problem introduced in Sect. 3.1, two decision-making methods are proposed. Details of method 1 are as follows.

• Step 1 aggregate the information $\beta_{ij}$$\left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n} \right)$ by Eq. (3). For any attribute $A_{i}$, denote its result as $\beta_{i}$.

• Step 2 For any $\beta_{i} ,$ calculate the utility value $F_{2} \left( {\beta_{i} } \right)$ by using Eq. (9) and draw images for them.

• Step 3 For any $\beta_{i} ,$ calculate the utility value $F_{3} \left( {\beta_{i} } \right)$ by using Eq. (10).

• Step 4 rank all the alternatives by $F_{2} \left( {\beta_{i} } \right)$ and $F_{3} \left( {\beta_{i} } \right)$$\left( {i = 1,2, \ldots ,m} \right)$. Then, the alternatives are ranked, and the optimal alternative is obtained.

Method 2 is the same as method 1, except that Eq. (3) is replaced by Eq. (4). It is noted that the different emphasis points between method 1 and method 2 are that method 2 is more sensitive to the score value or the accuracy value, whereas method 1 is less sensitive to the score value or the accuracy value.

In the following, an illustrative numerical example is introduced to show the effectiveness of the proposed utility functions and the decision-making methods.

4 Numerical example

In this section, the authors adapt an example discussed in Chen et al. (2013) to demonstrate the effectiveness of the new method. Suppose that a lending expert in a financial management firm is assessing the entrepreneurship orientation of four online P2P lending platforms, $A = \left\{ {A_{1} ,A_{2} ,A_{3} ,A_{4} } \right\}.$ Three evaluated criteria are considered, which include innovativeness $C_{1}$, risk-taking $C_{2}$, and proactiveness $C_{3}$. In addition, the lending expert is only comfortable with providing his assessment of each alternative on each attribute as an IVIFS and the evaluation matrix is $D = \left( {D_{1} ,D_{2} ,D_{3} } \right),$ where

By calculation, it gets that the weight vector for $\left\{ {C_{1} ,C_{2} ,C_{3} } \right\}$ is $W = \left( {0.30,0.35,0.35} \right).$ On the above conditions, the task is to select the optimal alternative. Firstly, method 1 is used to choose the optimal alternative.

Step 1 Compute the weighted geometric average value $\beta_{i}$ for $A_{i} (i = 1,2,3,4)$; by using Eq. (3), the results are obtained as

$$ \begin{aligned} \beta_{1} = \left( {\left[ {0.4276,0.5421} \right],\left[ {0.2697,0.4446} \right]} \right),\beta_{2} = \left( {\left[ {0.3911,0.6094} \right],\left[ {0.2890,0.3906} \right]} \right), \hfill \\ \beta_{3} = \left( {\left[ {0.3667,0.4929} \right],\left[ {0.2550,0.3583} \right]} \right),\beta_{4} = \left( {\left[ {0.4329,0.5464} \right],\left[ {0.2851,0.3672} \right]} \right). \hfill \\ \end{aligned} $$

Step 2 By using Eq. (9), four utility functions $F_{3} \left( {\beta_{1} } \right),$$F_{3} \left( {\beta_{2} } \right),$$F_{3} \left( {\beta_{3} } \right),$ and $F_{3} \left( {\beta_{4} } \right)$ are obtained, and their corresponding images are shown in Figs. 1, 2, 3, and 4, respectively.

Fig. 1

Utility function $F_{3} \left( {\beta_{1} } \right)$

Fig. 2

Utility function $F_{3} \left( {\beta_{2} } \right)$

Fig. 3

Utility function $F_{3} \left( {\beta_{3} } \right)$

Fig. 4

Utility function $F_{3} \left( {\beta_{4} } \right)$

Step 3 By using Eq. (10), it gets that $F_{3} \left( {\beta_{1} } \right) = 0.2568,$$F_{2} \left( {\beta_{2} } \right) = 0.2627,$$F_{3} \left( {\beta_{3} } \right) = 0.2523,$$F_{3} \left( {\beta_{4} } \right) = 0.2692.$

Step 4 Rank all the alternatives according to the obtained utility values, and the results are $\underline{{A_{4} \succ A_{2} \succ A_{1} }} \succ A_{3} .$

In the following, method 2 is used to solve the given problem.

Step 1 Compute the weighted arithmetic average value $\beta_{i}^{{\prime }}$ for $A_{i} (i = 1,2,3,4)$; by using Eq. (4), the results are obtained as

$$ \begin{aligned} \beta_{1}^{{\prime }} \left( {\left[ {0.4360,0.5677} \right],\left[ {0.2307,0.4056} \right]} \right),\beta_{2}^{{\prime }} = \left( {\left[ {0.4371,0.6503} \right],\left[ {0.2307,0.3497} \right]} \right), \hfill \\ \beta_{3}^{{\prime }} = \left( {\left[ {0.4667,0.5918} \right],\left[ {0.2001,0.3034} \right]} \right),\beta_{4}^{{\prime }} = \left( {\left[ {0.4777,0.5689} \right],\left[ {0.2551,0.3497} \right]} \right). \hfill \\ \end{aligned} $$

Step 2 By using Eq. (9), four utility functions $F_{3} \left( {\beta_{1}^{{\prime }} } \right),$$F_{3} \left( {\beta_{2}^{{\prime }} } \right),$$F_{3} \left( {\beta_{3}^{{\prime }} } \right),$ and $F_{3} \left( {\beta_{4}^{{\prime }} } \right)$ are obtained, and their corresponding images are shown in Figs. 5, 6, 7, and 8, respectively.

Fig. 5

Utility function $F_{3} \left( {\beta_{1}^{{\prime }} } \right)$

Fig. 6

Utility function $F_{3} \left( {\beta_{2}^{{\prime }} } \right)$

Fig. 7

Utility function $F_{3} \left( {\beta_{3}^{{\prime }} } \right)$

Fig. 8

Utility function $F_{3} \left( {\beta_{4}^{{\prime }} } \right)$

Step 3 By using Eq. (10), it gets that $F_{3} \left( {\beta_{1}^{{\prime }} } \right) = 0.2672,$$F_{2} \left( {\beta_{2}^{{\prime }} } \right) = 0.2833,$$F_{3} \left( {\beta_{3} } \right) = 0.2917,$$F_{3} \left( {\beta_{4} } \right) = 0.2843.$

Step 4 Rank all the alternatives according to the obtained utility values, and the results are $A_{3} \succ \underline{{A_{4} \succ A_{2} \succ A_{1} }} .$

It is noteworthy that $A_{4} \succ A_{2} \succ A_{1}$ holds in the solutions obtained by using the two proposed methods. Meanwhile, $A_{3}$ varies greatly. That is because that there are different emphasis points in Eqs. (3) and (4), where Eq. (3) indicates the group’s influence, whereas Eq. (4) indicates the individual influence (see Xu 007). With respect to the above calculation results, this study prefers that the optimal alternative is $A_{4}$. It is noteworthy that the decision-making results obtained by Chen et al. (2013) are $A_{3} \succ A_{2} \succ \underline{{A_{4} \succ A_{1} }} ,$ which is inconsistent with the results obtained by this study. This is because the internal mechanism of Eq. (3) is different with the method proposed by Chen et al. (2013).

In particular, Figs. 1, 2, 3, 4, 5, 6, 7, and 8 show that the difference between each alternative is small; therefore, it is not surprising that different decision makers can get different decision results by using different methods. This phenomenon tells us it is a matter thing to choose suitable decision-making method according to decision makers’ specific requirement when making decision.

5 Conclusion

In this study, the entropy of interval-valued intuitionistic fuzzy numbers (IVIFNs) is explored, and the main innovations on this study are as follows.

• (1) As for IVIFNs, two kinds of entropy are summed up, where one is refined to describe the intuitionistic fuzzy feature, whereas the other one is refined to describe the interval feature of IVIFNs.

• (2) By using the normalized score function, normalized Type-1 entropy, and normalized Type-2 entropy, a series of utility functions on IVIFNs are proposed. In particular, one of the proposed utility functions is structured based on integral.

• (3) By using the proposed utility functions, IVIFNs can be compared and ranked. The characteristic of these proposed utility functions is that they are objective on comparing IVIFNs from the point of probability theory.

• (4) Two kinds of fuzzy multi-criteria decision-making methods in interval-valued intuitionistic fuzzy setting are proposed by using the proposed entropy functions.

Finally, the effectiveness of the proposed utility functions and the fuzzy multi-criteria decision-making methods is illustrated by using a numerical example. In future, we will consider applying the multi-criteria decision-making methods to solve some transportation problems, such as maximizing the probability of arriving on time (Cao et al. 2016a, b, 2017) and traffic light setting in congestion alleviation (Cao et al. 2016c).