A new distance measure of interval-valued intuitionistic fuzzy sets and its application in decision making

Abstract

Interval-valued intuitionistic fuzzy sets are widely used in multi-attribute decision-making problems to select the optimal alternative, but how to measure uncertainty is an open and significant problem. In this paper, a new distance measure of interval-valued intuitionistic fuzzy sets is proposed based on the distance of interval numbers. With the advantages of taking account of the whole number in the interval and having definite physical meaning, the proposed distance measure of interval-valued intuitionistic fuzzy sets shows superiority in measuring uncertainty and imprecision. In addition, the proposed distance measure is compared with some recent research works and classical distances through numerical examples. Graphs are drawn to visually display the variation characteristics and analyze the properties of the distance measures. The results prove that the proposed distance measure of interval-valued intuitionistic fuzzy sets outperforms other metrics in measuring uncertainty and avoiding counterintuitive cases. Some illustrative examples of multi-attribute decision making under real life are conducted, which demonstrates the strong discrimination capability and effectiveness of the proposed distance measure.

1 Introduction

Decision making has been widely applied in many fields in recent years and receives increasing attention (Deng and Deng 2019), like industrial engineering (Ayhan et al. 2015; Ling et al. 2016; Zhang and Deng 2018b), medical treatment (Deem 2016; Garg 2016; Xiao 2018) and so on (Chen et al. 2016; Deng et al. 2019c). The first step of decision is establishing mathematical structures to describe the characteristics of uncertain information from different levels. The second step is designing corresponding algorithms to address fuzzy data based on the decision-making goals. Therefore, finding an appropriate description model and a reasonable method to deal with data are two fundamental topics.

There are many models to describe uncertainty such as rough set (Pawlak 1982), evidence theory (Deng et al. 2016; Dong et al. 2019; Gao and Deng 2019; Sun and Deng 2019), and D number theory (Mo and Deng 2019; Zhao and Deng 2019; Deng and Jiang 2019a). Since a crisp number cannot describe uncertainty and imprecision properly, Zadeh proposed fuzzy set (FS) (Zadeh 1965). Afterward, many extended approaches and theories were proposed. Interval-valued fuzzy set (IVFS) (Zadeh 1975), presented by Zadeh, generalized the membership degree from exact number to interval number. Atanassov conceived intuitionistic fuzzy set (IFS) (Atanassov 1986), which considered simultaneously the membership degree and non-membership degree of the element to a set. Hesitant fuzzy sets (Torra 2010) was defined by Torra in terms of a function that returns a set of membership values for each element in the domain. Different extended fuzzy sets depict the uncertainty of complex things from different aspects. As a combination of IFS and IVFS, interval-valued intuitionistic fuzzy set (IVIFS) was introduced by Atanassov (Atanassov 1994), which describes membership degree and non-membership degree via interval numbers and provides a more reasonable mathematical model to deal with uncertain events and fuzzy information. However, these theories have inherent defects, namely lack of parametrization as pointed in (Molodtsov 1999). Molodtsov proposed soft set theory as a parameterized tool for dealing with uncertainty. By integrating soft set theory with classical fuzzy set theory, a lot of extensions of fuzzy set theory have been presented (Majumdar and Samanta 2010). For instance, interval-valued fuzzy soft set (Yang et al. 2009) is a combination of interval-valued fuzzy set and soft set. In the same way, vague soft set (Xu et al. 2010), generalized interval-valued intuitionistic fuzzy soft rough set (He and Xiong 2017), etc., were proposed successively. Jiang et al. (2010) proposed interval-valued intuitionistic fuzzy soft set (IVIFSS), which is widely applied in dealing with decision-making issues with multiple participations and different decision metrics. Due to an appropriate description of uncertainty and imprecision, fuzzy theories and soft computing theories are widely used in practical application: life sciences (Carmona et al. 2013; Uslan and Seker 2016), data fusion (Xu and Deng 2019; Song and Deng 2019; Zhang and Deng 2018a), decision making (Chen and Huang 2017; Gou and Xu 2017; Oztaysi et al. 2017; Tao et al. 2017; Wang and Chen 2017a; Wang 2017), evaluation (Marasini et al. 2017; Ren et al. 2017; Song and Wang 2017; Kang et al. 2019), categorization (He and Jiang 2018a), etc. For example, a fuzzy linguistic RFM (recency, frequency and monetary value) model was proposed by Alberto Carrasco et al. (2019) and applied to campaign management.

As a significant topic in the theory of fuzzy sets, uncertainty measures are used to deal with fuzzy data and have been developed from different views, such as distance measure (Merigo and Casanovas 2010), similarity measure (Ren and Wei 2017; Fei and Deng 2019), inclusion measure, entropy measure (Huang et al. 2019; Li and Deng 2018; Xiao 2019; Zhao et al. 2016) and correlation coefficient (Jiang et al. 2019). For example, Hu and Li (2013) researched the relationship between entropy and similarity of interval-valued intuitionistic fuzzy sets in detail. Deng and Jiang (2019b) introduced a novel method to evaluate green supply chain management practices under fuzzy environment based on D number theory. Song and Wang (2017) proposed a new similarity measure between IFSs and illustrated its superiority of avoiding counterintuitive cases. In Jiang (2018), a novel correlation coefficient is proposed to measure the similarity of two basic probability assignments (BPAs). Selvachandran et al. (2017) defined similarity measure and intuitionistic entropy by means of the distance measure and discussed relationship among these information measures. Meantime, these uncertainty measures of extended fuzzy soft sets are widely applied in practical engineering and have achieved effective results, such as pattern recognition (Han and Deng 2018; Zhang and Deng 2019; Uslan et al. 2014), optimization problems (Deng et al. 2019b, 2017a, b) cluster analysis (Rahim et al. 2016), etc., especially in decision making (Han and Deng 2019; He and Xiong 2017; Oztaysi et al. 2017; Zhou et al. 2016). For example, Morente-Molinera et al. (2017) proposed fuzzy ontologies and multi-granular linguistic modeling methods to solve multi-criteria group decision-making problems under environments with a high number of alternatives. In He and Jiang (2018b), an evidential Markov decision-making model based on Dempster-Shafer (D-S) evidence theory and Markov modeling is proposed to model the real human decision-making process. A damage degree identification method based on high-order difference mathematical morphology gradient spectrum entropy is proposed by Zhao et al. (2018). Liu et al. (2017) presented the interval-valued intuitionistic fuzzy-ordered weighted cosine similarity (IVIFOWCS) measure and introduced its application in group decision making. Tang (2017) investigated an approach to interval-valued intuitionistic fuzzy soft sets in decision making by means of grey relational analysis and D-S theory of evidence. A metamodel and its corresponding domain-specific language were presented by Rojas et al. (2018), which supported decision making from open government data. Wang and Chen (2017b) proposed a new multi-attribute decision-making (MADM) method based on IVIFSs, the linear programming (LP) methodology, and the extension of the technique for order preference by similarity to ideal solution (TOPSIS) method. Deng et al. (2018) presented a new motor bearing fault diagnosis method based on integrating empirical wavelet transform, fuzzy entropy, and support vector machine. A new interval-valued information entropy measure for interval-valued intuitionistic fuzzy sets (IVIFSs) was constructed by Nguyen (2016) to handle with the increasing complexity of the decision-making problems. Morente-Molinera et al. (2018) used fuzzy ontologies to manage multi-criteria group decision-making environments with high number of alternatives. Feng and Guo (2017) discussed relationships among distance measures, similarity measures and inclusion measures of interval-valued intuitionistic fuzzy soft sets (IVIFSSs) and applied them in decision making.

Due to the increasing complexity of the decision-making problems in engineering and the lack of precise information, the IVIFSs is more applicable to represent uncertain information. There has been little investigation on the distance measure of interval-valued intuitionistic fuzzy sets; therefore, it is highly necessary and significant to construct an appropriate distance measure for IVIFSs. But how to measure the distance of IVIFSs is an open issue. Dugenci (2016) introduced a novel generalized distance measure for interval-valued intuitionistic fuzzy sets. Singh and Garg (2017) proposed a family of distance measures based on Hamming, Euclidean and Hausdorff metrics under the environment of type-2 intuitionistic fuzzy set to rank the alternatives. Nevertheless, the constructions of some formulas are complicated and have no definite physical meaning. Most existing uncertainty measures are obtained based mainly on particular points (Zhang and Yu 2013), such as midpoints or endpoints on the intervals of IVIFSs, which inevitably leads to information loss and even ineffectiveness of the distance measures in some cases. In practical applications, these distance measures defined on the basis of general distance metrics have poor discrimination capability or even cause counterintuitive results. In order to solve these problems, a new distance measure of IVIFSs is presented in this paper and applied in multi-attribute decision-making problems. The main contributions of this work are the following:

• A new distance measure of IVIFSs is presented based on the distance of interval numbers, which takes into account of all the numbers in the interval and considers hesitancy degree as a component in distance measure.

• The proposed distance measure of IVIFSs is comprehensively compared and analyzed with some recent research works and classical distance measures through numerical examples. The results demonstrate that the proposed distance outperforms other metrics to measure uncertainty and avoid counterintuitive cases.

• Some real-life applications are provided to prove the strong discrimination capability of the proposed distance measure in addressing decision-making problems.

This article is organized as follows. Some notions and properties about interval-valued intuitionistic fuzzy sets and distance measures discussed in this paper are briefly introduced in Sect. 2. Section 3 introduces the new distance measure of interval-valued intuitionistic fuzzy sets. In Sect. 4, the new distance measure of interval-valued intuitionistic fuzzy sets is compared with some recent works and classical distance measures through numerical examples, also their properties are discussed in detail. Section 5 illustrates real-life applications in decision making based on the new distance measure of IVIFSs. Finally, this paper is concluded in Sect. 6.

2 Preliminaries

In this section, some necessary definitions are briefly introduced.

Let U be an initial universe of objects, E be the set of parameters in relation to objects in U.

$$\begin{aligned} U = \left\{ {{x_1},{x_2}, \ldots ,{x_n}} \right\} ,E = \left\{ {{e_1},{e_2}, \ldots ,{e_m}} \right\} \end{aligned}$$

Definition 1

(Interval-valued intuitionistic fuzzy set) (Atanassov 1994; Liu et al. 2017) An interval-valued intuitionistic fuzzy set on a universe U is an object of the form

$$\begin{aligned} A= & {} \left\{ {\left\langle {x,{\mu _A}\left( {{x_i}} \right) ,{\nu _A}\left( {{x_i}} \right) } \right\rangle \left| {{x_i} \in U} \right. } \right\} \\= & {} \left\{ {\left\langle {x,[{{{\underline{\mu }} }_A}({x_i}),{{{\overline{\mu }} }_A}({x_i})],[{{{\underline{\nu }} }_A}({x_i}),{{{\overline{\nu }} }_A}({x_i})]} \right\rangle \left| {{x_i} \in U} \right. } \right\} \end{aligned}$$

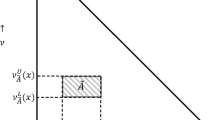
where interval membership degree ${\mu _A}\left( {{x_i}} \right) \in [0,1]$, interval non-membership degree ${\nu _A}\left( {{x_i}} \right) \in [0,1]$ and satisfy the following condition: $\forall {x_i} \in U, 0 \le {{\overline{\mu }} _A}\left( {{x_i}} \right) + {{\overline{\nu }} _A}\left( {{x_i}} \right) \le 1$. For each ${x_i} \in U$, the interval hesitancy degree of an interval intuitionistic fuzzy set A is defined as follows:

$$\begin{aligned} {\pi _A}({x_i})= & {} \left[ {{{{\underline{\pi }} }_A}({x_i}),{{{\bar{\pi }} }_A}({x_i})} \right] \\= & {} \left[ {1 - {{{\bar{\mu }} }_A}({x_i}) - {{{\bar{\nu }} }_A}({x_i}),1 - {{{\underline{\mu }} }_A}({x_i}) - {{{\underline{\nu }} }_A}({x_i})} \right] . \end{aligned}$$

The class of all interval-valued intuitionistic fuzzy sets on U can be denoted by $IVIFS\left( U \right)$.

The term “intuitionistic,” which was used by Atanassov, has a specific meaning in logic. It captures the separate handling of positive and negative aspects of information. Specifically, ${ \mu _A}\left( x \right)$ is the membership degree which represents the positive aspect of an element to a set, while ${\nu _A}\left( x \right)$ is non-membership degree which represents the negative aspects of an element to a set. ${ \pi _A}\left( x \right)$ is a measure of the hesitation of the expert to assign a numerical value to ${ \mu _A}\left( x \right)$ and ${ \nu _A}\left( x \right)$. Actually, the term “intuitionistic” works very well in problems in which we have to represent the difference between the positive and the negative representation of something, in particular, in cognitive psychology and medicine (Bustince et al. 2016).

Definition 2

(Interval-valued intuitionistic fuzzy soft set) Let U be a universe set, E be s set of parameters, and $A \subseteq E$. A pair $\left( {F,A} \right)$ is called an interval-valued intuitionistic fuzzy soft set over U, where F is a mapping given by

$$\begin{aligned} F:A \rightarrow \hbox {IVIFS}\left( U \right) \end{aligned}$$

From the definition, an interval-valued intuitionistic fuzzy soft set is a parameterized family of interval-valued intuitionistic fuzzy subsets of U. Every set $F\left( e \right)$$\left( {e \in E} \right)$ may be considered as the interval-valued intuitionistic fuzzy value set of parameter e, and it can be written as: $F\left( e \right) = \left\{ {\left\langle {x,{\mu _{F\left( e \right) }}\left( x \right) ,{\nu _{F\left( e \right) }}\left( x \right) } \right\rangle } \right.$$\left. {\left| {x \in U} \right. } \right\}$. Here, ${\mu _{F\left( e \right) }}\left( x \right)$ is the interval-valued fuzzy membership degree of object x to parameter e; ${\nu _{F\left( e \right) }}\left( x \right)$ is the interval-valued fuzzy non-membership degree of object x to parameter e.

Definition 3

(Tran and Duckstein 2002) Let $F\left( R \right)$ be the set of interval numbers in R, and the distance between two interval numbers $A\left( {{a_1},{a_2}} \right)$ and $B\left( {{b_1},{b_2}} \right)$ is defined as:

$$\begin{aligned} {D^2}\left( {A,B} \right)= & {} \int _{{{ - 1} / 2}}^{{1/2}} \left\{ \left[ {\frac{1}{2}\left( {{a_1} + {a_2}} \right) + x\left( {{a_2} - {a_1}} \right) } \right] \right. \nonumber \\&\left. - \left[ {\frac{1}{2}\left( {{b_1} + {b_2}} \right) + x\left( {{b_2} - {b_1}} \right) } \right] \right\} ^2 \mathrm{d}x \end{aligned}$$

(1)

$$\begin{aligned}= & {} {\left[ \frac{1}{2}({a_1} + {a_2}) - \frac{1}{2}({b_1} + {b_2})\right] ^2} \nonumber \\&+ \frac{1}{3}{\left[ \frac{1}{2}({a_2} - {a_1}) - \frac{1}{2}({b_2} - {b_1})\right] ^2} \end{aligned}$$

(2)

Definition 4

For any $A,B,C \in \hbox {IVIFSs}\left( U \right)$, Let d be a mapping $d:IVIFSs\left( U \right) \times \hbox {IVIFSs}\left( U \right) \rightarrow \left[ {0,1} \right]$. If $d\left( {A,B} \right)$ satisfies the following properties:

• (1) $0 \leqslant d\left( {A,B} \right) \leqslant 1$

• (2) $d\left( {A,B} \right) = 0$ if and only if $A = B$.

• (3) $d\left( {A,B} \right) = d\left( {B,A} \right)$

• (4) if $A \subseteq B \subseteq C$, then $d\left( {B,C} \right) \leqslant d\left( {A,C} \right)$ and $d\left( {A,B} \right) \leqslant d\left( {A,C} \right)$

• (5) $d\left( {A,C} \right) \leqslant d\left( {A,B} \right) + d\left( {B,C} \right)$

Then, $d\left( {A,B} \right)$ is a distance measure between IVIFSs A and B.

Definition 5

Introductions of some recent works and classical distance measures of interval-valued intuitionistic fuzzy sets.

In this section, we review some recent research works and widely used distance measures of interval-valued intuitionistic fuzzy sets, which is necessary to help understand the construction of IVIFS distance. Additionally, in Sects. 4 and 5, these distances will be compared with the proposed distance measure of IVIFSs and detailedly investigated through numerical examples.

Let A and B be two interval-valued intuitionistic fuzzy sets on $U = \left\{ {{x_1},{x_2},\ldots ,{x_n}} \right\}$, where

$$\begin{aligned} A= & {} \left\{ {\left\langle {x,[{{{\underline{\mu }} }_A}({x_i}),{{{\bar{\mu }} }_A}({x_i})],[{{{\underline{\nu }} }_A}({x_i}),{{{\bar{\nu }} }_A}({x_i})]} \right\rangle \left| {{x_i} \in U} \right. } \right\} \\ B= & {} \left\{ {\left\langle {{x_i},[{{{\underline{\mu }} }_B}({x_i}),{{{\bar{\mu }} }_B}({x_i})],[{{{\underline{\nu }} }_B}({x_i}),{{{\bar{\nu }} }_B}({x_i})]} \right\rangle \left| {{x_i} \in U} \right. } \right\} \end{aligned}$$

• 1. In Dugenci (2016), Muharrem proposed a new distance measure for IVIFSs:

  $$\begin{aligned}&D_p^t\left( {A,B} \right) \\&\qquad = \root p \of {\begin{array}{l} \frac{1}{{4n{{\left( {t + 1} \right) }^p}}}\sum \limits _{i = 1}^n {\left\{ {{{\left| {t\left( {{{{\underline{\mu }} }_A}\left( {{x_i}} \right) - {{{\underline{\mu }} }_B}\left( {{x_i}} \right) } \right) - \left( {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) } \right) } \right| }^P}} \right. } \\ + {\left| {t\left( {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) } \right) - \left( {{{{\underline{\mu }} }_A}\left( {{x_i}} \right) - {{{\underline{\mu }} }_B}\left( {{x_i}} \right) } \right) } \right| ^P}\\ + {\left| {t\left( {{{{\overline{\mu }} }_A}\left( {{x_i}} \right) - {{{\overline{\mu }} }_B}\left( {{x_i}} \right) } \right) - \left( {{{{\overline{\nu }} }_A}\left( {{x_i}} \right) - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) } \right) } \right| ^P}\\ \left. { + {{\left| {t\left( {{{{\overline{\nu }} }_A}\left( {{x_i}} \right) - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) } \right) - \left( {{{{\overline{\mu }} }_A}\left( {{x_i}} \right) - {{\overline{\mu }}_B}\left( {{x_i}} \right) } \right) } \right| }^P}} \right\} \end{array}} \end{aligned}$$

  where $t = 2,3,4, \ldots$ and $p = 1,2,3, \ldots$, in which, parameter p is the $L_p$ norm and t identifies the level of uncertainty. When calculating, $t=2$, $p=1$ in this paper.

• 2. Zhou et al. (2016) proposed continuous intuitionistic fuzzy-ordered weighted distance (C-IFOWD) measure. A C-IFOWD measure is a mapping $C - IFOWD:\sum \nolimits _{}^n { \times \sum \nolimits _{}^n { \rightarrow R} }$ that has an associated weighting vector $\overrightarrow{\omega }$ of dimension n, such that $\sum \nolimits _{j = 1}^n {{\omega _j}} = 1$ and ${\omega _j} \in \left[ {0,1} \right]$.

  $$\begin{aligned}&{d_{C - IFOWD}}\left( {A,B} \right) = \left( \sum \limits _{~j = 1}^n {{\omega _j}{d_\lambda }{{\left( {{A_{\sigma \left( j \right) }},{B_{\sigma \left( j \right) }}} \right) }^r}} \right) ^{{1/ r}}\\&{d_\lambda }\left( {A,B} \right) = \frac{1}{2}\left( \Big | \lambda \left( {{{{\overline{\mu }} }_A}\left( {{x_i}} \right) - {{{\overline{\mu }} }_B}\left( {{x_i}} \right) } \right) \right. \\&\quad + \left( {1 - \lambda } \right) \Big ({{{\underline{\mu }}}_A\left( {{x_i}} \right) - {{{\underline{\mu }} }_B}\left( {{x_i}} \right) } \Big ) \Big | + \big | \lambda \left( {{{\overline{\nu }} }_A}\left( {{x_i}} \right) \right. \\&\quad \left. - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) \right) + \left( {1 - \lambda } \right) \left( {{\underline{\nu }}_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) \right) \big |\Big ) \end{aligned}$$

  where $\sigma \left( 1 \right) ,\sigma \left( 2 \right) , \ldots ,\sigma \left( n \right)$ is any permutation of $\left( {1,2, \ldots ,n} \right)$, such that:

  $$\begin{aligned}&{d_\lambda }\left( {{A_{\sigma \left( {j - 1} \right) }},{B_{\sigma \left( {j - 1} \right) }}} \right) \\&\quad \ge {d_\lambda }\left( {{A_{\sigma \left( j \right) }},{B_{\sigma \left( j \right) }}} \right) ,j = 2,3, \ldots ,n \end{aligned}$$

  ${d_\lambda }\left( {{A_j},{B_j}} \right)$ is the continuous intuitionistic fuzzy distance between ${A_j}$ and ${B_j}$ based on the continuous interval-valued intuitionistic fuzzy-ordered weighted averaging (C-IVIFOWA) operator and parameter $r > 0$. When calculating, $\lambda = {1/3}$ in this paper. If $r=1$, then the C-IFOWD measure reduces to the C-IFOWHD measure:

  $$\begin{aligned} {d_{C - IFOWHD}}\left( {A,B} \right) = \left( {\sum \limits _{~j = 1}^n {{\omega _j}{d_\lambda }\left( {{A_{\sigma \left( j \right) }},{B_{\sigma \left( j \right) }}} \right) } } \right) \end{aligned}$$

  If $r=2$, then the C-IFOWD measure becomes the C-IFOWED measure:

  $$\begin{aligned} {d_{C - IFOWED}}\left( {A,B} \right) = {\left( {\sum \limits _{~j = 1}^n {{\omega _j}{d_\lambda }{{\left( {{A_{\sigma \left( j \right) }},{B_{\sigma \left( j \right) }}} \right) }^2}} } \right) ^{{1/2}}} \end{aligned}$$

• 3. Hamming distance

  $$\begin{aligned} \begin{aligned}&{d_H}\left( {A,B} \right) = \frac{1}{{4n}}\sum \limits _{i = 1}^n {[|{{{\underline{\mu }} }_A}\left( {{x_i}} \right) - {{{\underline{\mu }} }_B}\left( {{x_i}} \right) |} \\&\quad + \left| {{{{\bar{\mu }} }_A}\left( {{x_i}} \right) - {{{\bar{\mu }} }_B}\left( {{x_i}} \right) } \right| \\&\quad \left. { + \left| {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) } \right| + \left| {{{{\overline{\nu }} }_A}\left( {{x_i}} \right) - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) } \right| } \right] \end{aligned} \end{aligned}$$

• 4. Euclidean distance

  $$\begin{aligned} \begin{aligned}&{d_E}\left( {A,B}\right) = \left\{ \frac{1}{{4n}}\sum \limits _{i = 1}^n [{{({{{\underline{\mu }} }_A}({x_i}) - {{{\underline{\mu }} }_B}({x_i}))}^2} \right. \\&\quad + {{({{{\bar{\mu }} }_A}({x_i}) - {{{\bar{\mu }} }_B}({x_i}))}^2}\\&\quad \left. \left. + {{\left( {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) } \right) }^2} + {{\left( {{{{\overline{\nu }} }_A}\left( {{x_i}} \right) - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) } \right) }^2} \right] \right\} ^{\frac{1}{2}} \end{aligned} \end{aligned}$$

• 5. Normalized hamming distance induced by Hausdorff metric

  $$\begin{aligned} \begin{aligned}&{d_{NH}}\left( {A,B} \right) = \frac{1}{{2n}}\sum \limits _{i = 1}^n {[|{{{\underline{\mu }} }_A}({x_i}) - {{{\underline{\mu }} }_B}({x_i})|} \\&\quad \vee \left| {{{{\bar{\mu }} }_A}({x_i}) - {{{\bar{\mu }} }_B}({x_i})} \right| \\&\quad \left. { + \left| {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) } \right| \vee \left| {{{{\overline{\nu }} }_A}\left( {{x_i}} \right) - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) } \right| } \right] \end{aligned} \end{aligned}$$

• 6. Normalized distance induced by Hausdorff metric

  $$\begin{aligned} \begin{aligned}&{d_{N}}\left( {A,B} \right) = \frac{1}{{2n}}\sum \limits _{i = 1}^n \max \left\{ |{{{\underline{\mu }} }_A}({x_i}) - {{{\underline{\mu }} }_B}({x_i})| \right. \\&\quad + \left| {{{{\bar{\mu }} }_A}({x_i}) - {{{\bar{\mu }} }_B}({x_i})} \right| , \\&\quad \left. {\left| {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) } \right| + \left| {{{{\overline{\nu }} }_A}\left( {{x_i}} \right) - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) } \right| } \right\} \end{aligned} \end{aligned}$$

3 The new distance measure of interval-valued intuitionistic fuzzy sets

Interval-valued intuitionistic fuzzy set is a flexible mathematical tool to depict and handle uncertainty, which is the inherent characteristic of multi-attribute decision-making (MADM) problems. Hence, several uncertainty measures such as distance measure have been generalized in interval-valued intuitionistic fuzzy environment. Nevertheless, the constructions of some formulas are complicated and have no definite physical meaning. Additionally, these distance measures defined on the basis of general distance metrics have poor distinguishing ability or even cause counterintuitive results. Therefore, a rational and effective distance measure of IVIFSs is desirable from the theoretical and practical points of view.

3.1 The new distance measure of interval-valued intuitionistic fuzzy sets

In this section, a new distance measure of interval-valued intuitionistic fuzzy sets is proposed inspired by the distance of interval numbers in Definition 3. A conversion between interval-valued intuitionistic fuzzy set and interval vector is established, so that the distance of IVIFSs can be investigated from an interval number perspective. The process of constructing the distance measure of IVIFSs is that convert IVIFS to a set of interval vector firstly, and then construct the distance of interval vectors by means of the distance of interval numbers. Simultaneously that is the distance measure of interval-valued intuitionistic fuzzy sets. The concrete steps are shown as follows.

For each ${x_i} \in U$, IVIFS A, B are defined as

$$\begin{aligned} A= & {} \left\{ {\left\langle {x,[{{{\underline{\mu }} }_A}(x),{{{\bar{\mu }} }_A}(x)],[{{{\underline{\nu }} }_A}(x),{{{\bar{\nu }} }_A}(x)]} \right\rangle \left| {{x_i} \in U} \right. } \right\} \\ B= & {} \left\{ {\left\langle {x,[{{{\underline{\mu }} }_B}(x),{{{\bar{\mu }} }_B}(x)],[{{{\underline{\nu }} }_B}(x),{{{\bar{\nu }} }_B}(x)]} \right\rangle \left| {{x_i} \in U} \right. } \right\} \end{aligned}$$

Step 1:

Convert IVIFS to interval vector.

The elements of interval vectors are interval membership degree, interval non-membership degree and interval hesitancy degree, respectively.

$$\begin{aligned}&\left\langle {\left[ {{\underline{\mu }} ,{\overline{\mu }} } \right] ,\left[ {{\underline{\nu }} ,{\overline{\nu }} } \right] } \right\rangle \rightarrow \left( {\begin{array}{*{20}{c}} {\left[ {{\underline{\mu }} ,{\overline{\mu }} } \right] } \\ {\left[ {{\underline{\nu }} ,{\overline{\nu }} } \right] } \\ {\left[ {{\underline{\pi }} ,{\overline{\pi }} } \right] } \end{array}} \right) \end{aligned}$$

For A and B, the vectors can be expressed by:

$$\begin{aligned} \overrightarrow{A}= & {} \left( {\begin{array}{*{20}{c}} {\left[ {{{{\underline{\mu }} }_A}\left( x \right) ,{{{\overline{\mu }} }_A}\left( x \right) } \right] }\\ {\left[ {{{{\underline{\nu }} }_A}\left( x \right) ,{{{\overline{\nu }} }_A}\left( x \right) } \right] }\\ {\left[ {{{{\underline{\pi }} }_A}\left( x \right) ,{{{\overline{\pi }} }_A}\left( x \right) } \right] } \end{array}} \right) \\ {\overrightarrow{B}}= & {} \left( {\begin{array}{*{20}{c}} {\left[ {{{{\underline{\mu }} }_B}\left( x \right) ,{{{\overline{\mu }} }_B}\left( x \right) } \right] }\\ {\left[ {{{{\underline{\nu }} }_B}\left( x \right) ,{{{\overline{\nu }} }_B}\left( x \right) } \right] }\\ {\left[ {{{{\underline{\pi }} }_B}\left( x \right) ,{{{\overline{\pi }} }_B}\left( x \right) } \right] } \end{array}} \right) \end{aligned}$$

Now, the distance of IVIFSs can be regarded as the distance between vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ . Based on the distance measure of interval numbers, the distance between the corresponding elements in the vector can be obtained.

Step 2:

Calculate the distance of vectors elements.

According to the distance of interval numbers which has been introduced in Definition 3. ${D_\mu }$ is the distance between the degree of interval membership. ${D_\nu }$ is the distance between the degree of interval non-membership. ${D_\pi }$ is the distance between the degree of interval hesitancy. And their formulas are as follows:

$$\begin{aligned}&{D_\mu }^2\left( {A,B} \right) \\&\quad = {\left[ {\left( {\frac{{{{{\underline{\mu }} }_A}\left( x \right) + {{{\bar{\mu }} }_A}\left( x \right) }}{2}} \right) - \left( {\frac{{{{{\underline{\mu }} }_B}\left( x \right) + {{{\bar{\mu }} }_B}\left( x \right) }}{2}} \right) } \right] ^2} \\&\qquad + \frac{1}{3}{\left[ {\left( {\frac{{{{{\bar{\mu }} }_A}\left( x \right) - {{{\underline{\mu }} }_A}\left( x \right) }}{2}} \right) - \left( {\frac{{{{{\bar{\mu }} }_B}\left( x \right) - {{{\underline{\mu }} }_B}\left( x \right) }}{2}} \right) } \right] ^2} \\&{D_\nu }^2\left( {A,B} \right) \\&\quad = {\left[ {\left( {\frac{{{{{\underline{\nu }} }_A}\left( x \right) + {{{\bar{\nu }} }_A}\left( x \right) }}{2}} \right) - \left( {\frac{{{{{\underline{\nu }} }_B}\left( x \right) + {{{\bar{\nu }} }_B}\left( x \right) }}{2}} \right) } \right] ^2} \\&\qquad + \frac{1}{3}{\left[ {\left( {\frac{{{{{\bar{\nu }} }_A}\left( x \right) - {{{\underline{\nu }} }_A}\left( x \right) }}{2}} \right) - \left( {\frac{{{{{\bar{\nu }} }_B}\left( x \right) - {{{\underline{\nu }} }_B}\left( x \right) }}{2}} \right) } \right] ^2} \\&{D_\pi }^2\left( {A,B} \right) \\&\quad = {\left[ {\left( {\frac{{{{{\underline{\pi }} }_A}\left( x \right) + {{{\bar{\pi }} }_A}\left( x \right) }}{2}} \right) - \left( {\frac{{{{{\underline{\pi }} }_B}\left( x \right) + {{{\bar{\pi }} }_B}\left( x \right) }}{2}} \right) } \right] ^2} \\&\qquad + \frac{1}{3}{\left[ {\left( {\frac{{{{{\bar{\pi }} }_A}\left( x \right) - {{{\underline{\pi }} }_A}\left( x \right) }}{2}} \right) - \left( {\frac{{{{{\overline{\pi }} }_B}\left( x \right) - {{{\underline{\pi }} }_B}\left( x \right) }}{2}} \right) } \right] ^2} \end{aligned}$$

In order to represent the difference between corresponding interval elements, the following rules are formulated:

1.:

$$\begin{aligned} {D_\mu } = \sqrt{{D_\mu }^2} , \hbox { when } {{\underline{\mu }} _A} + {{\overline{\mu }} _A} \geqslant {{\underline{\mu }} _B} + {{\overline{\mu }} _B};\\ {D_\mu } = - \sqrt{{D_\mu }^2} , \hbox { when } {{\underline{\mu }} _A} + {{\bar{\mu }} _A} < {{\underline{\mu }} _B} + {{\bar{\mu }} _B}. \end{aligned}$$

2.:

$$\begin{aligned} {D_\nu } = \sqrt{{D_\nu }^2} , \hbox { when } {{\underline{\nu }} _A} + {{\overline{\nu }} _A} \geqslant {{\underline{\nu }} _B} + {{\overline{\nu }} _B};\\ {D_\nu } = - \sqrt{{D_\nu }^2} , \hbox { when } {{\underline{\nu }} _A} + {{\overline{\nu }} _A} < {{\underline{\nu }} _B} + {{\overline{\nu }} _B}. \end{aligned}$$

3.:

$$\begin{aligned} {D_\pi } = \sqrt{{D_\pi }^2} , \hbox { when } {{\underline{\pi }} _A} + {{\overline{\pi }} _A} \geqslant {{\underline{\pi }} _B} + {{\overline{\pi }} _B};\\ {D_\pi } = - \sqrt{{D_\pi }^2} , \hbox { when } {{\underline{\pi }} _A} + {{\overline{\pi }} _A} < {{\underline{\pi }} _B} + {{\overline{\pi }} _B}. \end{aligned}$$

Step 3:

The distance measure between interval vectors.

Based on the distance of interval numbers, a new distance measure between vector $\overrightarrow{A}$ and $\overrightarrow{B}$ is introduced as follows.

$$\begin{aligned}&d\left( {A,B} \right) \nonumber \\&\quad = \sqrt{\frac{1}{2}\left( {{D_\mu }^2 + {D_\nu }^2 + {D_\pi }^2 + {D_\pi }{D_\mu } + {D_\pi }{D_\nu }} \right) } {\text { }}\nonumber \\ \end{aligned}$$

(3)

The distance measure between interval vectors consists of the distance between each pair of corresponding elements in two vectors. The elements of interval vectors are interval numbers, hence the distance between elements ${D_\mu }$, ${D_\nu }$, ${D_\pi }$ can be obtained by means of distance of interval numbers.

Step 4:

The distance measure of interval-valued intuitionistic fuzzy sets.

The interval vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ are transformed from the IVIFSs A and B. A conclusion can be safely reached that an interval-valued intuitionistic fuzzy set is equivalent to a vector. Meanwhile, the distance between interval vectors is the distance between IVIFSs. As mentioned above, the distance of the interval-valued intuitionistic fuzzy sets is the sum of the distance of the interval-valued intuitionistic fuzzy numbers for each ${x_i} \in U$. Therefore, the new distance measure of IVIFSs is proposed as follows:

$$\begin{aligned}&{d_\mathrm{IVIFS}}\left( {A,B} \right) \nonumber \\&\quad = \frac{1}{n}\sum \limits _{i = 1}^n {\sqrt{\frac{1}{2}\left( {{D_\mu }^2 + {D_\nu }^2 + {D_\pi }^2 + {D_\pi }{D_\mu } + {D_\pi }{D_\nu }} \right) }}\nonumber \\ \end{aligned}$$

(4)

The proposed distance measure of IVIFSs is constructed by ${D_\mu }$, ${D_\nu }$ and ${D_\pi }$ through square and multiplication, which considers not only the difference of membership degree and non-membership degree, but also takes into account of hesitancy degree. The hesitancy degree plays a role in measuring the uncertainty of information, which is superior to other widely used distance measures of IVIFSs, as illustrated in the examples in Sect. 4. In addition, the coefficient $\frac{1}{2}$ is to keep the distance between 0 and 1.

The novelty of this distance measure is that a conversion between interval-valued intuitionistic fuzzy set and interval vector is established, and the distance measure of IVIFSs is proposed based on the distance of interval numbers, which takes into account of all the points in the interval and is theoretically reasonable. The flowchart of constructing the novel distance measure of interval-valued intuitionistic fuzzy sets is shown in Fig. 1.

Fig. 1

Flowchart of novel distance measure

Example 1

Suppose there are two interval-valued intuitionistic fuzzy sets, A and B.

$$\begin{aligned} A= & {} \left\{ \left\langle {\left[ {0.55,0.67} \right] ,\left[ {0.1,0.28} \right] } \right\rangle ,\left\langle \left[ {0.26,0.37} \right] ,\right. \right. \\&\left. \left. \left[ 0.55,0.63 \right] \right\rangle \right\} \\ B= & {} \left\{ {\left\langle {\left[ {0.7,0.8} \right] ,\left[ {0.15,0.2} \right] } \right\rangle ,\left\langle {\left[ {0.61,0.71} \right] ,\left[ {0,0.1} \right] } \right\rangle } \right\} \end{aligned}$$

Use the proposed new distance of IVIFSs to calculate the distance of them. Firstly, the distance of the two IVIFSs corresponding to element ${x_1}$ is calculated as follows:

$$\begin{aligned}&\overrightarrow{{A_1}} = \left( {\begin{array}{*{20}{c}} {\left[ {0.55,0.67} \right] }\\ {\left[ {0.1,0.28} \right] }\\ {\left[ {0.05,0.35} \right] } \end{array}} \right) \overrightarrow{{B_1}} = \left( {\begin{array}{*{20}{c}} {\left[ {0.7,0.8} \right] }\\ {\left[ {0.15,0.2} \right] }\\ {\left[ {0,0.15} \right] } \end{array}} \right) \\&{D_{\mu 1}}^2\left( {A,B} \right) = {\left[ {\left( {\frac{{0.55 + 0.67}}{2}} \right) - \left( {\frac{{0.7 + 0.8}}{2}} \right) } \right] ^2} \\&\quad + \frac{1}{3}{\left[ {\left( {\frac{{0.67 - 0.55}}{2}} \right) - \left( {\frac{{0.8 - 0.7}}{2}} \right) } \right] ^2} =0.0196\\&{D_{\nu 1}}^2\left( {A,B} \right) = {\left[ {\left( {\frac{{0.1 + 0.28}}{2}} \right) - \left( {\frac{{0.15 + 0.2}}{2}} \right) } \right] ^2} \\&\quad + \frac{1}{3}{\left[ {\left( {\frac{{0.28 - 0.1}}{2}} \right) - \left( {\frac{{0.2 - 0.15}}{2}} \right) } \right] ^2} =0.0016\\&{D_{\pi 1}}^2\left( {A,B} \right) = {\left[ {\left( {\frac{{0.05 + 0.35}}{2}} \right) - \left( {\frac{{0 + 0.15}}{2}} \right) } \right] ^2} \\&\quad + \frac{1}{3}{\left[ {\left( {\frac{{0.35 - 0.05}}{2}} \right) - \left( {\frac{{0.15 - 0}}{2}} \right) } \right] ^2} =0.0175\\&0.55 + 0.67 < 0.7 + 0.8, \hbox { then }\\&{D_{\mu 1}} = - \sqrt{{D_{\mu 1}}^2} = - 0.1401\\&0.1 + 0.28 \geqslant 0.15 + 0.2, \hbox { then } {D_{\nu 1}} = \sqrt{{D_{\nu 1}}^2} = 0.0404\\&0.05 + 0.35 \geqslant 0 + 0.15, \hbox { then } {D_{\pi 1}} = \sqrt{{D_{\pi 1}}^2} = 0.1323 \end{aligned}$$

$$\begin{aligned}&{d_{\mathrm{IVIF}{S_1}}} = \sqrt{\frac{1}{2} \times \left( {0.0196 + 0.0016 + 0.0175 - 0.1401 \times 0.1323 + 0.0404 \times 0.1323} \right) } \\&\quad = 0.1131 \end{aligned}$$

In the same way, the distance of the two IVIFSs corresponding to element ${x_2}$ is calculated as follows:

$$\begin{aligned}&{D_{\mu 2}}^2\left( {A,B} \right) = 0.1190 , {D_{\nu 2}}^2\left( {A,B} \right) = 0.2916 ,{D_{\pi 2}}^2\left( {A,B} \right) = 0.0380\\&{D_{\mu 2}} = - 0.3450 , {D_{\nu 2}} = 0.5400 , {D_{\pi 2}} = - 0.1950 \\&{d_{IVIF{S_2}}} = \sqrt{\frac{1}{2} \times \left( {0.1190 + 0.2916 + 0.0380 + 0.3450 \times 0.1950 - 0.5400 \times 0.1950} \right) } \\&\quad = 0.4531 \end{aligned}$$

Finally, the distance between IVIFSs A and B is obtained:

$$\begin{aligned} {d_\mathrm{IVIFS}}\left( {A,B} \right) = \frac{{0.1131 + 0.4531}}{2} = 0.2831 \end{aligned}$$

Example 2

Assume there are two interval-valued intuitionistic fuzzy sets A and B, the distance of A and B is calculated as follows:

$$\begin{aligned} A= & {} \left\{ {\left\langle {\left[ {0,0} \right] ,\left[ {1,1} \right] } \right\rangle } \right\} \\ B= & {} \left\{ {\left\langle {\left[ {1,1} \right] ,\left[ {0,0} \right] } \right\rangle } \right\} \\ {D_\mu }^2\left( {A,B} \right)= & {} 1, {D_\nu }^2\left( {A,B} \right) = 1, {D_\pi }^2\left( {A,B} \right) = 0\\ {D_\mu }\left( {A,B} \right)= & {} - 1, {D_\nu }\left( {A,B} \right) = 1, {D_\pi }\left( {A,B} \right) = 0\\ {d_\mathrm{IVIFS}}= & {} \sqrt{\frac{1}{2} \times \left( {1 + 1 + 0 - 1 \times 0 + 1 \times 0} \right) } = 1 \end{aligned}$$

When the distance of interval-valued intuitionistic fuzzy sets arrives at maximum 1, the membership degree of A is the complement of B, meanwhile the non-membership of A is the complement of B. That means, when we make sure x not belongs to A (the value of membership is 0), while x surely belongs to B (the value of membership is 1), the distance between IVIFSs A and B is the largest. That is, A is the complement of B.

Example 3

Given two interval-valued intuitionistic fuzzy sets A and B, the distance of A and B is proved as follows.

$$\begin{aligned} A= & {} \left\{ {\left\langle {\left[ {{a_1},{a_2}} \right] ,\left[ {{b_1},{b_2}} \right] } \right\rangle } \right\} \\ B= & {} \left\{ {\left\langle {\left[ {{a_1},{a_2}} \right] ,\left[ {{b_1},{b_2}} \right] } \right\rangle } \right\} \\ {D_\mu }^2\left( {A,B} \right)= & {} 0, {D_\nu }^2\left( {A,B} \right) = 0, {D_\pi }^2\left( {A,B} \right) = 0\\ {D_\mu }\left( {A,B} \right)= & {} 0, {D_\nu }\left( {A,B} \right) = 0, {D_\pi }\left( {A,B} \right) = 0\\ {d_\mathrm{IVIFS}}= & {} \sqrt{\frac{1}{2} \times \left( {0 + 0 + 0 - 0 \times 0 + 0 \times 0} \right) } = 0 \end{aligned}$$

When the interval-valued intuitionistic fuzzy sets A and B own the same membership degree $\left[ {{a_1},{a_2}} \right]$ and same non-membership degree $\left[ {{b_1},{b_2}} \right]$, the distance of membership degree ${D_\mu }\left( {A,B} \right)$ is 0, also ${D_\nu }\left( {A,B} \right) = 0$ and ${D_\pi }\left( {A,B} \right) = 0$. According to Eq. (4) , the distance between A and B is 0.

Therefore, the essence of the distance measure is to measure the difference between sets by dealing with the membership or non-membership of the elements to the sets. Obviously, Examples 2 and 3 have shown that the maximum value of ${d_\mathrm{IVIFS}}$ is 1 if and only if A is the complement of B, and the minimum value of ${d_\mathrm{IVIFS}}$ is 0 on condition that $A = B$, which satisfies the requirements of distance in Definition 4.

3.2 The new distance measure of interval-valued intuitionistic fuzzy soft sets

The soft set theory is widely used to deal with uncertainty information, which describes objects by a set of parameters. Therefore the novel distance measure of IVIFSs can be generalized to distance of interval-valued intuitionistic fuzzy soft sets to address multi-attribute decision-making problems. The distance of the interval-valued intuitionistic fuzzy soft sets is the sum of the distance of interval-valued intuitionistic fuzzy numbers for each ${x_i} \in U$ to each ${e_j} \in E$. Therefore, based on the new distance measure of interval-valued intuitionistic fuzzy sets, the new distance measure of interval-valued intuitionistic fuzzy soft sets can be obtained as follows:

$$\begin{aligned}&{d_\mathrm{IVIFSS}}\left( {\left( {F,E} \right) ,\left( {G,E} \right) } \right) \nonumber \\&\quad = \frac{1}{{mn}}\sum \limits _{i = 1}^m {\sum \limits _{j = 1}^n {\sqrt{\frac{1}{2}\left( {{D_\mu }^2 + {D_\nu }^2 + {D_\pi }^2 + {D_\pi }{D_\mu } + {D_\pi }{D_\nu }} \right) } } }\nonumber \\ \end{aligned}$$

(5)

It can also be proved that the generalized distance measure of interval-valued intuitionistic fuzzy soft sets conforms to the axioms of distance measurement.

4 Comparison of the proposed distance measure with recent works and classical distance measures

4.1 Numerical examples

In this part, the novel distance measure is compared with $D_p^t$, C-IFOWD, Hamming distance, Euclidean distance, normalized Hamming distance induced by Hausdorff metric and normalized distance induced by Hausdorff metric through numerical examples. Meanwhile, some properties of the formulas are discussed and the counterintuitive cases of the other widely used distances will be pointed out, where the proposed distance of IVIFSs performs well.

As mentioned above, the distance measures of IVIFSs and IVIFSSs are based on the distance measure of interval-valued intuitionistic fuzzy numbers. For interval-valued intuitionistic fuzzy sets, its distance is the sum of interval-valued intuitionistic fuzzy numbers for each ${x_i} \in U$. For interval-valued intuitionistic fuzzy soft sets, its distance is the sum of interval-valued intuitionistic fuzzy numbers for each ${x_i} \in U$ to each ${e_j} \in E$. Therefore, when it refers to the comparison of seven distances of IVIFSs, choose the interval-valued intuitionistic fuzzy sets with just one element x in U, which has two advantages:

• The distance of IVIFSs and IVIFSSs are made up of distance of interval-valued intuitionistic fuzzy numbers; therefore, the distance of IVIFNs is opposed to be investigated firstly.

• Analyzing the IVIFS with one element helps to visually study the distance changed by membership and non-membership, which avoids the impact caused by other elements in the IVIFS.

Example 4

Given IVIFSs A and B as follows, in accordance with the definition: $0 \le {\overline{\mu }} \left( x \right) + {\overline{\nu }} \left( x \right) \le 1$, x could change continuously in the interval $\left[ {0.1,0.9} \right]$. Draw Hamming distance $d_H$, Euclidean distance $d_E$, $D_p^t$, $d_\mathrm{C-IFOWD}$, normalized Hamming distance induced by Hausdorff metric $d_{NH}$, normalized distance induced by Hausdorff metric $d_N$ and the novel proposed distance measure $d_\mathrm{IVIFS}$ with function curve, which is graphically shown in Fig. 2.

$$\begin{aligned} A= & {} \left\{ {\left\langle {\left[ {0.1,0.8} \right] ,\left[ {0,0.1} \right] } \right\rangle } \right\} \\ B= & {} \left\{ {\left\langle {\left[ {0.1,x} \right] ,\left[ {0,0.1} \right] } \right\rangle } \right\} \end{aligned}$$

Fig. 2

Comparison between novel distance measure and other distance measures by using Example 4

From Fig. 2, all of the distance get to the minimum when $x = 0.8$, where $A = B$ and the distance of interval-valued intuitionistic fuzzy sets A and B is 0, which indicates that the proposed distance measure have the same tendency with other widely used distances of IVIFSs and can measure the distance of interval-valued intuitionistic fuzzy sets in common cases. What’s more, the curve of the proposed distance has the highest slope; hence, a slight change of IVIFS will lead to more obvious numerical change than other distance measures, which can distinguish the difference between similar IVIFSs. On the other hand, the proposed distance measure will not lead to an overestimation of distance between two IVIFSs. Firstly, the numerical values of all the distances belong to interval $\left[ {0,1} \right]$. Then, in Fig. 2, all the distances vary linearly, which means there is merely a coefficient difference between them. What’s more, distance measure is usually applied in ranking problem, the proposed distance appears sensitivity in measuring uncertainty and can distinguish different objects easily. Hence, the overestimation of dissimilarity can be avoided through the proposed distance measure.

Fig. 3

Comparison between novel distance measure and $d_{NH}$, $d_N$ by using Example 5

Example 5

Given IVIFSs A and B as follows, according to the definition: $0 \le {\overline{\mu }} \left( x \right) + {\overline{\nu }} \left( x \right) \le 1$, x could change continuously in the interval $\left[ {0.1,0.9} \right]$. We have drawn normalized Hamming distance induced by Hausdorff metric $d_{NH}$, normalized distance induced by Hausdorff metric $d_N$ and the proposed distance $d_\mathrm{IVIFS}$, which is graphically shown in Fig. 3.

$$\begin{aligned} A= & {} \left\{ {\left\langle {\left[ {0.1,x} \right] ,\left[ {0,0.1} \right] } \right\rangle } \right\} \\ B= & {} \left\{ {\left\langle {\left[ {0.8,0.9} \right] ,\left[ {0,0.1} \right] } \right\rangle } \right\} \end{aligned}$$

Example 6

Given IVIFSs A and B as follows, according to the definition: $0 \le {\overline{\mu }} \left( x \right) + {\overline{\nu }} \left( x \right) \le 1$, x could change continuously in the interval $\left[ {0.2,0.8} \right]$. We have drawn normalized Hamming distance induced by Hausdorff metric $d_{NH}$, normalized distance induced by Hausdorff metric $d_N$ and the proposed distance $d_\mathrm{IVIFS}$, which is graphically shown in Fig. 4.

$$\begin{aligned} A= & {} \left\{ {\left\langle {\left[ {0.7,0.8} \right] ,\left[ {0.1,0.2} \right] } \right\rangle } \right\} \\ B= & {} \left\{ {\left\langle {\left[ {0.1,0.2} \right] ,\left[ {0.2,x} \right] } \right\rangle } \right\} \end{aligned}$$

Fig. 4

Comparison between novel distance measure and $d_{NH}$, $d_N$ by using Example 6

From Fig. 3, as the value of x changes, the interval-valued intuitionistic fuzzy set A also changes. The distance between IVIFSs A and B are supposed to change accordingly. The result demonstrates that the proposed distance decreases with the rise of the value of x. The tendency of proposed distance can characterize the difference between A and B appropriately. However, normalized Hamming distance induced by Hausdorff metric keeps the constant 3.5 from $x = 0.2$, which is obviously irrational. From Fig. 4, as x increases, the distance between interval non-membership degree of A and B is increasing intuitively. Therefore, the distance between interval-valued intuitionistic fuzzy set A and B should increase accordingly. In Fig. 4, the value of the proposed distance measure of IVIFSs rises smoothly. Nevertheless, the value of normalized distance induced by Hausdorff metric keeps the 0.6 constant, which is also inappropriate. In Example 5 and Example 6, the results of normalized Hamming distance induced by Hausdorff metric and normalized distance induced by Hausdorff metric are counterintuitive when measuring the distance between IVIFSs, while the proposed distance measure has an effective and rational performance in the situations.

From a theoretical point of view, membership degree and non-membership degree are equally weighted, the upper and lower limits are equally weighted, as well. Consider the structure of $d_{NH}$ and $d_N$ as shown in Definition 5. In the equation of $d_{NH}$, for each ${x_i} \in U$, the larger one between $\left| {{{{\underline{\mu }} }_A}\left( {{x_i}} \right) - {{\underline{\mu }}_B}\left( {{x_i}} \right) } \right|$ and $\left| {{{\overline{\mu }}_A}\left( {{x_i}} \right) - {{{\overline{\mu }} }_B}\left( {{x_i}} \right) } \right|$, together with the larger one between $\left| {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{\underline{\nu }}_B}\left( {{x_i}} \right) } \right|$ and $\left| {{{\overline{\nu }}_A}\left( {{x_i}} \right) - {{{\overline{\nu }} }_B}\left( {{x_i}} \right) } \right|$ is preserved to calculate the distance of IVIFSs. In a similar way, for equation $d_N$, the larger one between $\left| {{{{\underline{\mu }} }_A}\left( {{x_i}} \right) - {{\underline{\mu }}_B}\left( {{x_i}} \right) } \right| + \left| {{{{\overline{\mu }} }_A}\left( {{x_i}} \right) - {{{\overline{\mu }} }_B}\left( {{x_i}} \right) } \right|$ and $\left| {{{{\underline{\nu }} }_A}\left( {{x_i}} \right) - {{{\underline{\nu }} }_B}\left( {{x_i}} \right) } \right| + \left| {{{{\overline{\nu }} }_A}\left( {{x_i}} \right) - {{\overline{\nu }}_B}\left( {{x_i}} \right) } \right|$ is retained to calculate the distance between IVIFSs. They abandon the part of the data in the process of calculating, which destroys the equal weight between the membership degree and the non-membership degree, also the upper and lower limits of intervals. This partly leads to the loss of information and emerges poor sensitivity of measuring. Here, sensitivity refers to the degree of change of response quantity caused by the change of input quantity in a certain method. Specifically, when the input quantities, i.e., interval membership degree, interval non-membership degree and interval hesitancy degree change, the response quantity namely the distance of IVIFSs is expected to change with a reasonable trend, and the magnitude of the change should be observable. Compared with $d_{NH}$ and $d_N$, the proposed distance measure takes into account lower and upper limits of membership and non-membership equally. Therefore, it appears sensitively as x changes and demonstrates better metric performance.

Example 7

Given IVIFSs A and B as follows, in accordance with the definition: $0 \le {\overline{\mu }} \left( x \right) + {\overline{\nu }} \left( x \right) \le 1$, x could change continuously in the interval $\left[ {0.1,0.9} \right]$, We have drawn Hamming distance $d_H$, Euclidean distance $d_E$, $D_t^p$, $d_\mathrm{C-IFOWD}$ and the proposed distance $d_\mathrm{IVIFS}$ with function curve, which is graphically shown in Fig. 5.

$$\begin{aligned} A= & {} \left\{ {\left\langle {\left[ {0.1,0.8} \right] ,\left[ {0,0.2} \right] } \right\rangle } \right\} \\ B= & {} \left\{ {\left\langle {\left[ {0.1,x} \right] ,\left[ {0,0.1} \right] } \right\rangle } \right\} \end{aligned}$$

Fig. 5

Comparison by using Example 7

Fig. 6

Comparison between novel distance measure and Euclidean distance by using Example 8

When $x = 0.8$, the membership degree of IVIFSs A and B is the same, meanwhile the distance between A and B should be minimized. From Fig. 5, it can be observed that other distances take the minimum value at $x = 0.8$, while the minimum of $D_p^t$ is between $x=0.7$ and $x=0.8$, which indicates that $D_p^t$ appears unreasonably when measuring the distance of IVIFSs in this example.

Example 8

Given IVIFSs A and B as follows, in accordance with the definition: $0 \le {\overline{\mu }} \left( x \right) + {\overline{\nu }} \left( x \right) \le 1$, x could change continuously in the interval $\left[ {0.1,0.9} \right]$, We have drawn Hamming distance $d_H$, Euclidean distance $d_E$, $D_t^p$, $d_\mathrm{C-IFOWD}$ and the proposed distance $d_\mathrm{IVIFS}$ with function curve, which is graphically shown in Fig. 6.

$$\begin{aligned} A= & {} \left\{ {\left\langle {\left[ {0.1,x} \right] ,\left[ {0,0.1} \right] } \right\rangle } \right\} \\ B= & {} \left\{ {\left\langle {\left[ {0.8,0.9} \right] ,\left[ {0.1,0.1} \right] } \right\rangle } \right\} \end{aligned}$$

Table 1 Example 9

From Fig. 6, as x increases, the tendency of other distances measure and Euclidean distance are similar. However, approximately from $x=0.6$ to $x=0.9$, the slope of Euclidean distance is slowing down. In particular, at the end of the x, Euclidean distance can hardly measure change in the distance of IVIFSs when x changes, while the proposed distance can distinguish the change of interval-valued intuitionistic fuzzy set.

Example 9

As shown in Table 1, the distances of two groups of interval-valued intuitionistic fuzzy sets are calculated by $D_p^t$, C-IFOWD, Hamming distance, Euclidean distance, normalized hamming distance induced by Hausdorff metric and normalized distance induced by Hausdorff metric and the proposed distance measure of IVIFSs.

The numbers in bold are counterintuitive cases. The distances in Group 1 should not be equal to each other, where $d_\mathrm{C-IFOWD}$ and $d_H$ show counterintuitive cases. In contrast, the proposed distance measure can distinguish the difference because of the superior property. The novel proposed distance measures the interval-valued intuitionistic fuzzy sets by means of distance measure of interval numbers. According to Definition 3, the integral in Eq. (1) shows that this distance takes into account each point in both intervals when computing the distance between those two interval numbers. So the novel distance measure contains all data in the interval, while other widely used distance measures merely use the lower and upper bound values. Therefore, the novel proposed distance measure appears more perfectly and effectively when measuring the distance of IVIFSs. In addition, the new distance measure put the hesitancy degree as a part of the formula, which is an uncertainty measure belonging to IVIFSs. Consequently, the novel distance has an advantage in measuring uncertainty of IVIFSs and avoiding counterintuitive cases comparing with other widely used distance measures. Comparing the distances in Group 2, the distance between $\left\langle {\left[ {0.35,0.4} \right] ,\left[ {0.25,0.35} \right] } \right\rangle$ and $\left\langle {\left[ {0.5,0.55} \right] ,\left[ {0.3,0.35} \right] } \right\rangle$ should be smaller than the distance between $\left\langle {\left[ {0.35,0.4} \right] ,\left[ {0.25,0.35} \right] } \right\rangle$ and $\left\langle \left[ {0.5,0.55} \right] ,\left[ {0.25,0.35} \right] \right\rangle$. However, the result of $D_p^t$ is 0.0625 < 0.0750, which is unreasonable and different from other distance measures.

4.2 A brief comparison with Intuitionistic Fuzzy Entropy Feature Selection method (Revanasiddappa and Harish 2018)

In Revanasiddappa and Harish (2018), Revanasiddappa and Harish proposed a new feature selection method based on intuitionistic fuzzy entropy. Firstly, based on the membership degree, non-membership degree and hesitancy degree of intuitionistic fuzzy set, intuitionistic fuzzy C-Means clustering method is employed to compute the intuitionistic membership values. Then, intuitionistic fuzzy entropy is constructed via the computed intuitionistic membership values. Further, features with lower entropy values are selected to categorize the text documents.

In this paper, a new distance measure of interval-valued intuitionistic fuzzy sets is proposed and applied in multi-attribute decision-making problem. Firstly, the distance measure is inspired by the distance of interval numbers and copes with interval membership degree, interval non-membership degree and interval hesitancy degree. Then, the distances between the objects to be evaluated and the ideal object are calculated respectively. Object with lower distance is superior object selected.

Table 2 Interval-valued intuitionistic fuzzy soft sets over U

Comparing the above methods, different extended fuzzy sets are employed to handle uncertain and vague information. Revanasiddappa and Harish’s work is based on the intuitionistic fuzzy set, while this paper is based on the interval-valued intuitionistic fuzzy set. It is worth noting that intuitionistic fuzzy set is a special case of interval-valued intuitionistic fuzzy set, in which the interval membership degree satisfies ${{\underline{\mu }} _A}\left( x \right) = {{\overline{\mu }} _A}\left( x \right)$, interval non-membership degree satisfies ${{\underline{\nu }} _A}\left( x \right) = {{\overline{\nu }} _A}\left( x \right)$, interval hesitancy degree satisfies ${{\underline{\pi }} _A}\left( x \right) = {{\overline{\pi }} _A}\left( x \right)$. In addition, Revanasiddappa and Harish proposed an intuitionistic fuzzy entropy to measure the features, while this paper introduced a distance measure to choose the optimal object.

5 The application of the proposed distance in decision making

Decision making under uncertainty environment is an open issue. The membership information of alternatives to attributes is represented through interval-valued intuitionistic fuzzy soft set and integrated in a decision-making matrix firstly. Then, the distance measure of IVIFSSs is utilized to evaluate the degree of the alternatives in line with the ideal object. The essence of the distance measure to make decision is that the difference of two sets is measured by means of calculating the distance between the membership functions of the same element to two sets. In this section, the problem of decision making is solved using the new proposed distance measure of interval-valued intuitionistic fuzzy soft sets.

Table 3 Interval-valued intuitionistic soft set of ideal house

Table 4 Interval-valued intuitionistic fuzzy set of ${h_k}$

Example 10

(Qin et al. 2011) Consider an interval-valued intuitionistic fuzzy soft set $\left( {F,A} \right)$ which describes the “attractiveness of houses” that Mr. X is considering for purchase. Suppose that there are six houses under consideration, namely the universes $U = \left\{ {{h_1},{h_2},{h_3},{h_{4,}}{h_5},{h_6}} \right\}$, and the parameter set $A = \left\{ {{e_1},{e_2},{e_3},{e_4},{e_5}} \right\}$, where ${e_i}$ stand for “beautiful,” “large,” “cheap,” “modern” and “in green surroundings,” respectively. The tabular representation of $\left( {F,A} \right)$ is shown in Table 2. Obviously, the precise evaluation for each objects on each parameter is unknown, while the lower and upper limits of such an evaluation are given.

Use the proposed distance measure of IVIFSSs to evaluate the houses and make decisions. Firstly, assuming the Mr. X’s ideal house ${h_0}$ completely conforms to these five parameters. IVIFSS $\left( {{F_0},A} \right)$ is denoted in Table 3. Then, divide IVIFSS $\left( {F,A} \right)$ into IVIFSS $\left( {{F_k},A} \right) \left( {k = 1,2,3,4,5,6} \right)$; each $\left( {{F_k},A} \right)$ represents the interval membership degree and interval non-membership degree for each house ${h_k}$ to each attribute. The tabular representation of $\left( {{F_k},A} \right)$ is shown in Table 4.

Evaluate each house by calculating the distance between each $\left( {{F_k},A} \right)$ and $\left( {{F_0},A} \right)$. A small distance means that the house is more in line with the properties of the ideal house, and it is the optimal solution. Six distances are calculated by means of the new distance measure of IVIFSSs, and the result is shown in Table 5.

From Table 5, the ranking of the degree of satisfaction is ${h_2}> {h_1}> {h_5}> {h_3}> {h_4} > {h_6}$. Therefore, Mr. X should choose house ${h_2}$ in preference to other houses. Compared with the result in Qin et al. (2011) ${h_2}> {h_1} = {h_5} > {h_3} = {h_4} = {h_6}$, there is a fuzzy priority of identifying ${h_1}$ and ${h_5}$; ${h_3}$, ${h_4}$ and ${h_6}$. Therefore, the order of the distances of the six houses calculated by proposed distance is more clear, the new distance measure appears accurately and effectively in multi-attribute decision making.

Table 5 Distance between ${h_k}$ and ideal house based on IVIFSS

Table 6 Comparison of the distance measures for Example 10

For the sake of comparing and verifying the performance of the proposed distance $D_p^t$, C-IFOWHD, C-IFOWED, Hamming distance, Euclidean distance, normalized Hamming distance induced by Hausdorff metric and normalized distance induced by Hausdorff metric are also utilized in this example to decide which house for Mr.X to choose. The results are calculated as shown in Table 6. The rankings calculated by other distances almost have the same order with the result obtained by the proposed distance measure except C-IFOWED. As shown in bold, C-IFOWED has an abnormal result when measuring and comparing house $h_3$ and $h_4$.

Furthermore, partial values of Table 2 are changed to test the performance of each distance measure as shown in Table 7. The changed numbers are bold. Actually, the membership degree of $h_4$ to parameters are improved overall, which leads to slight optimization of $h_4$; the membership degree of $h_5$ to parameters are reduced overall, which leads to slight deterioration of $h_5$. Now, all the distance measure are reused to evaluated the situation of houses. The results are shown in Table 8.

Table 7 The changed interval-valued intuitionistic fuzzy soft sets over U

Table 8 Comparison of the distance measures for Table 7

As expected, the distances between $h_4$ and ideal object are reduced and the distances between $h_5$ and ideal object are increased overall. However, $D_p^t$ and Hamming distance are ambiguous in distinguishing ${h_3}$ from ${h_5}$; C-IFOWHD shows difficulty to distinguish ${h_3}$ and ${h_4}$. The ranking of houses obtained by the proposed distance measure is ${h_2}> {h_1}> {h_3}> {h_4}> {h_5} > {h_6}$, which is the same as the results of Euclidean distance and normalized Hamming distance induced by Hausdorff metric. However, in the previous examples, ${d_E}$ shows poor degree of discrimination when measuring the slight change in Example 8, and ${d_{NH}}$ performs counterintuitively in Example 5 and Example 6. From a performance point of view, the proposed distance measure ${d_\mathrm{IVIFS}}$ is reasonable and effective in all cases. From a theoretical point of view, the proposed distance measure is based on the distance of interval numbers, which takes into account each point in the interval and considers hesitancy degree as a component in the equation. In conclusion, the proposed distance measure is preferable to measuring distance accurately and distinguishing objects in decision-making problems.

Table 9 Interval-valued intuitionistic fuzzy decision matrix ${A^{\left( 1 \right) }}$ of expert 1

Table 10 Interval-valued intuitionistic fuzzy decision matrix ${A^{\left( 2 \right) }}$ of expert 2

Table 11 Interval-valued intuitionistic fuzzy decision matrix ${A^{\left( 3 \right) }}$ of expert 3

Table 12 Ideal strategy of three experts

In the following, a brief example of group decision-making problem under interval-valued intuitionistic fuzzy environment is illustrated.

Example 11

(Zhou et al. 2016) There is a human resource management problem where a university wants to introduce oversea outstanding teachers. The university has brought together a group of decision makers. The group is constituted by three persons including university president $e_1$, dean of management school $e_2$ and human resource officer $e_3$. After careful review of the information, they made strict evaluation for five candidates $x_i(i=1,2,3,4,5)$ and summarized the abilities of candidates with four aspects $U = \left\{ {{u_1},{u_2},{u_3},{u_4}} \right\}$: namely morality($u_1$), research capabilities($u_2$), teaching skills($u_3$), educational background($u_4$).

Three decision makers evaluate the candidates $x_i(i=1,2,3,4,5)$ with respect to the attributes $u_j(j=1,2,3,4)$ and construct three interval-valued intuitionistic fuzzy decision matrices ${A^{\left( k \right) }} = {\left( {{a_{ij}}^{\left( k \right) }} \right) _{5 \times 4}}\left( {k = 1,2,3} \right)$, which are shown in Tables 9,10,11. According to the objectives of the university, each expert establishes his/her own ideal strategy as shown in Table 12.

Table 13 Collective distance matrix R

Table 14 The results of the decision by proposed distance

Table 15 Comparison of the distances for Example 11

With these information, the proposed distance of interval-valued intuitionistic fuzzy sets can be utilized to obtain the ranking of the candidates. The following steps are involved:

Step 1:

Calculate the distance of each preference value $a_{ij}^{\left( k \right) }$ provided by the decision maker $e_k$ and his/her ideal preference value with Equation (3). Use the proposed distance measure of interval-valued intuitionistic fuzzy soft sets (Equation (5)) to combine the four aspects, where the weight of aspects is $\omega = \left( {0.3,0.2,0.4,0.1} \right)$.

Step 2:

Aggregate the whole distance into a collective distance matrix $R = {\left( {{r_{ik}}} \right) _{5 \times 3}}$, as shown in Table 13. The collective distance matrix describes the distance between each candidate $x_i$ and the expectation of each expert.

Step 3:

Use the proposed distance measure of interval-valued intuitionistic fuzzy soft sets to combine the evaluation of the three experts and derive the comprehensive preference value of the alternative $x_i$, where the weight of the experts is $v = \left( {0.4,0.3,0.3} \right)$.

The results are shown in Table 14. The priority relationship of the candidates is ${x_1}> {x_5}> {x_2}> {x_3} > {x_4}$, which means that candidate $x_1$ is the best person after considering experts’ assessment and multi-factors. Furthermore, in order to verify the calculation result of the proposed distance measure, the candidate-selecting problem is calculated in the same way using the other distances of interval-valued intuitionistic fuzzy soft sets introduced in Definition 5, as shown in Table 15. Comparing the ranking of the candidates calculated by these distances, C-IFOWED displays different orders when measuring candidates $x_2$ and $x_5$, while other distance measures have the same order.

In this paper, a new proposed distance measure of IVIFSs and some classical or recent works are tested and analyzed through numerical examples. From Examples 5 to 11, other distances all appear counterintuitive cases in different occasions, while the proposed distance measure performs well in measuring distance between interval-valued intuitionistic fuzzy sets and shows strong discrimination capability in MADM problems. Therefore, it can be safely concluded that the proposed distance of IVIFSs provides an effective methodology to solve multi-attribute group decision-making problem.

6 Conclusions

In this paper, a new distance measure of interval-valued intuitionistic fuzzy sets is proposed to handle multi-attribute decision-making problems. To begin with, the novel distance measure of IVIFSs is constructed based on the distance of interval numbers. Our proposed distance measure contains all data in the interval; hence, it can avoid information loss and handle uncertain information effectively. Additionally, the proposed distance measure of IVIFSs is compared with some recent works, such as Muharrem’s distance, C-IFOWD, and classical distance measures, such as Hamming distance, Euclidean distance, normalized Hamming distance induced by Hausdorff metric and normalized distance induced by Hausdorff metric through numerical examples. With the advantages of considering all the numbers in the interval and taking hesitancy degree as a part of the formula, the proposed distance of IVIFSs shows predominant sensitivity and avoids counterintuitive cases. What’s more, the proposed distance measure can give the effective solution which can be accepted by decision makers in MCDM problems. Two illustrative real-life applications of decision making are conducted to demonstrate the effectiveness of the proposed distance measure, which can not only obtain the best choice, but also accurately rank the alternatives in order of preference.