Intuitionistic fuzzy entropy-based knowledge and accuracy measure with its applications in extended VIKOR approach for solving multi-criteria decision-making

Abstract

The study of unclear phenomena has been facilitated by fuzzy sets. Fuzzy set extensions have allowed for a more detailed investigation of these kinds of research. Finding quantitative measures for ambiguity and other characteristics of these occurrences thus becomes a challenge. As a fuzzy set extension, several researchers proposed intuitionistic fuzzy (IF) sets and used them in many contexts since they were first described by Atanassov. One such use is to solve multi-criteria decision-making issues. This study measure the amount of knowledge linked with an IF-set. An IF-knowledge measure is proposed. Using numerical examples, its utility and validity are examined. Besides this, the IF-accuracy measure, IF-information measure, similarity measure, and dissimilarity measure, are the four new measures that are derived from the proposed IF-knowledge measure. All these measures are checked for their validation and their properties are discussed. Pattern detection is taken as an application of the proposed accuracy measure. Finally, a modified VIKOR approach depending upon the proposed similarity and dissimilarity measure is proposed to deal with an MCDM issue in an intuitionistic fuzzy environment. The efficiency of the proposed approach is demonstrated by using a numerical example. A comparative study is also provided to assess the feasibility of the proposed approach.

1 Introduction

Based on Zadeh’s fuzzy set (Zadeh 1965), Atanassov (1986) gave the notion of intuitionistic fuzzy (IF) set. The requirement that the non-membership degree and membership degree after adding give one is relaxed by Atanassov’s IF-sets. We can say that an IF-set is a general form of fuzzy sets as described in Bustince et al. (2015), Couso and Bustince (2018). For an IF-set, the hesitation degree is calculated by subtracting the sum of the non-membership and membership degrees from one. Due to its benefit in modelling uncertain information systems, Bustince (2000) has given the IF-set theory a lot of attention. Numerous areas, including decision-making (Ye 2010b; Xia and Xu 2012) and uncertainty reasoning (Papakostas et al. 2013) have effectively used the concept of IF-sets.

To quantify the fuzziness of a fuzzy set, Zadeh (1968) initially established the concept of entropy. In certain ways, the Shannon entropy idea (Shannon 1948), which was first introduced in probability theory, is related to the fuzzy entropy concept proposed for fuzzy sets. Luca and Termini (1972) developed the axiomatic idea of entropy. The measure of intuitionistic entropy was first axiomatically established by Burillo and Bustince (1996), and it was just based on hesitation degree. The ratio of two distance values served as the basis for the definition of IF-sets provided by Szmidt and Kacprzyk (2001); Szmidt et al. (2014a). Many authors including Wang and Xin (2005), Song et al. (2017), Garg and Kaur (2018), Garg (2019) etc. gave attention to the definition of entropy of an IF-set. Find entropy of IF-sets and use this in evaluating attribution weighting vectors have also been focused on by some researchers. According to Szmidt et al. (2014a), the entropy cannot properly describe the uncertainty present in an IF-set. As a result, using an entropy measure alone may not be sufficient to create an acceptable uncertainty estimate for IF-sets. In computing the uncertainty of IF-sets, Pal et al. (2013) have underlined the distinction between entropy and hesitation. Entropy and hesitation together may provide a useful technique to calculate the entire quantity of uncertainty associated with an IF-set.

In general, the IF-knowledge measure is connected to the usable data that an IF-set provides. According to information theory, having a lot of information means having a lot of knowledge, which is beneficial for making decisions. Accordingly, rather than the entropy measure, the concept of knowledge measure may be seen as a complementary idea to the total uncertainty measure. (see Arya and Kumar 2021) This indicates that more knowledge is always accompanied by less overall uncertainty. Szmidt et al. (2014a) proposed an IF-knowledge measure by taking into account both entropy and hesitation of an IF-set to differentiate between different types of intuitionistic fuzzy information. In order to resolve challenges with multi-criteria decision-making (MCDM), Das et al. (2016) found that each attribute’s weight has been estimated by using the knowledge measure. By calculating the separation between an IF-set and the most uncertain IF-set, Nguyen (2015) has created a novel knowledge measure. Guo (2015) offered a new notion of knowledge measure for IF-set. The model studied by Guo (2015) has been widely utilized to establish the intuitionistic fuzzy entropy by calculating the difference between an IF-set and its complement. A detailed inspection of the axiomatic definitions of IF-information measures was also carried out by Das et al. (2017).

In an MCDM issue, we try to find out a particular alternative from given alternatives that meets the greatest number of predetermined criteria. Numerous scholars including Hwang and Yoon (1981), Mareschal et al. (1984), Gomes and Lima (1991), Opricovic (1998), Yager (2020), Dutta and Saikia (2021), Ohlan (2022), Gupta and Kumar (2022) etc. have looked at various strategies for selecting a most preferable alternative from all available alternatives. Every solution to an MCDM issue has a key term attached to it like criteria weights. By using the justified criteria weights, we may identify the best alternative. Therefore, extra attention must be given while evaluating the weights of each criterion. Criteria weights are calculated by several approaches. For the evaluation of criteria, Chen and Li (2010) provided the following two ways-

• Objective Evaluation approach: The criterion weights in this approach are determined using mathematical formulas. The most acceptable objective evaluation approach is the calculation of criterion weights using information and knowledge measures (see Diakoulaki et al. 1995; Fan 2002; Odu 2019).

• Subjective Evaluation approach: In this approach, resource persons directly assess the criteria weights. Subjective weights are determined by the preferences indicated by resource persons (see Chu et al. 1979; Ginevičius and Podvezko 2005; Zoraghi et al. 2013).

When dealing with MCDM issues, Opricovic (1998) suggested an approach, called VIKOR¹ approach, which can offer a compromise solution in an MCDM issue. In this approach, the precise assessment of “Closeness” to the positive ideal solution is employed to select the best alternative. Many researchers extended the traditional VIKOR approach to finding the solutions of MCDM, MADM, and MCGDM problems. Chen and Chang (2016) proposed IF-geometric averaging operator to solve MADM issues. Wang and Chang (2005) solved the MCGDM problem by using the VIKOR approach in a fuzzy environment. Sanayei et al. (2010) took the problem of supplier selection and solve it with help of the fuzzy VIKOR approach. Shemshadi et al. (2011) solved the supplier selection method by entropy-based fuzzy VIKOR approach. By using triangular intuitionistic fuzzy numbers, Wan et al. (2013) extended the Concept of the VIKOR approach to solving multi-attribute group decision-making problems. Chang (2014) studied a case to find the best hospital in Taiwan. By using triangular fuzzy numbers, Rostamzadeh et al. (2015) found the solution to the green supply chain management problem by using the VIKOR approach. Gupta et al. (2016) extended the VIKOR approach for the selection of plant location. Zeng et al. (2019) used the novel score function in the VIKOR approach to finding the best alternative. Ravichandran et al. (2020) solved the personnel selection problem by extended VIKOR approach. Hu et al. (2020) gave a ranking to the doctors by using the VIKOR approach. Gupta and Kumar (2022) proposed VIKOR approach based on IF-scale-invariant information measure with correlation coefficients for solving MCDM. Most of the researchers used the distance measure in calculating maximum group utility and the minimum individual regret in the VIKOR approach. But in the proposed approach, we use the proposed similarity as well as dissimilarity measure and find the results are highly encouraging.

According to the study presented above, there is still space for debate about IF-knowledge measures. The majority of studies on the IF-knowledge and information measures primarily concentrate on the distinction between IF-sets and their complement. Even though Nguyen (2015) pioneered this novel approach to analysing IF-knowledge measures, further research is required to enhance this type of measure and provide a suitable measure that will find the total amount of knowledge for an IF-set. Some of the valuable conclusions from the study on IF-information and knowledge measures cannot fully address some problems in intuitionistic fuzzy environment and run into different difficulties, including the following:

$\checkmark$:

The vast majority of IF-knowledge and information measures do not follow the order required for linguistic comparison. But, the proposed IF-knowledge measure fulfils the desired order (see Example 1).

$\checkmark$:

The bulk of the IF-knowledge and information measures that are documented in the literature provide absurd results when calculating the ambiguity between different IF-sets (see Example 2).

$\checkmark$:

The majority of IF-knowledge and information measures compute the same criteria weights for various alternatives, while the criteria weights calculated by the proposed IF-knowledge measure are different for different alternatives (see Example 3).

$\checkmark$:

The vast majority of similarity and dissimilarity measures in intuitionistic fuzzy environment are not able to detect a pattern from the available patterns. But, the proposed IF-accuracy measure clearly detects the pattern from the given patterns (see Example 4).

This inspires us to provide a fresh way to gauge one’s understanding of IF-sets. From these facts, we proposed an effective IF-knowledge measure in this study. The main highlights of this study are as follows

$\checkmark$:

An IF-knowledge measure, together with its properties, is proposed.

$\checkmark$:

We provide numerical examples to show how the proposed IF-knowledge measure overcomes the drawbacks of some current IF-knowledge and information measures.

$\checkmark$:

Based on the proposed knowledge measure, we derived a new accuracy measure, information measure, similarity measure, and dissimilarity measure in intuitionistic fuzzy environment. Some properties are also discussed.

$\checkmark$:

The proposed accuracy measure is used in pattern detection. A comparison with various measures is provided to demonstrate the efficacy of the proposed accuracy measure in pattern detection.

$\checkmark$:

To address an MCDM issue, a modified VIKOR approach is presented. In the proposed approach, we use proposed IF-similarity and dissimilarity measures in place of the distance measure.

$\checkmark$:

We also show how effective the proposed approach is for selecting the best university for a student in the MCDM issue.

This study’s primary points are as follows: Sect. 1 covered the primary objective of this article and related literature. The requirement and main contribution of this study are discussed. In Sect. 2, some of the basic definitions are discussed. In Sect. 3, an IF-knowledge measure is suggested and is checked for validation. Some of its properties are mentioned and a comparison with some other measures is given. In Sect. 4, we developed four additional measures based on the proposed IF-knowledge measure: accuracy measure, information measure, similarity measure, and dissimilarity measure in intuitionistic fuzzy environment. They are validated, and it is discussed what properties they have. The proposed accuracy measure is used in pattern detection and is compared with some existing measures for detecting patterns. Section 5 discusses a modified VIKOR approach depending upon proposed similarity and dissimilarity measures to solve MCDM issues. By employing a numerical example to tackle the MCDM issues, the proposed approach is compared with previously published approaches in the literature. The conclusion and recommendations for more study are given in Sect. 6.

2 Preliminaries

In the present section, we quickly recap a few pieces of background information on IF-sets to make the upcoming exposition easier.

Assume that

$$\begin{aligned} \Omega _{t}= & {} \left\{ \Lambda =(\lambda _1,\lambda _2,\lambda _3,\dots ,\lambda _t) | \sum _{i=1}^{t} \lambda _i =1 \right. \nonumber \\{} & {} \quad \left. \text { where } 0 \le \lambda _i \le 1 \forall i=1,2, \dots t \right\} , \end{aligned}$$

(1)

is the collection of total probability distributions for t $\ge$ 2. Shannon’s definition of the information measure is

$$\begin{aligned} E(\Lambda ) = -\sum _{i=1}^t \lambda _i \log \lambda _i; \end{aligned}$$

(2)

where $\Lambda$ $\in$ $\Omega _{t}$. There are many generalizations of Shannon entropy (Shannon 1948) given by many researchers including Rényi (1961), Havdra and Charvat (1967), Tsallis (1988), Boekee and Vander Lubbe (1980) etc. The r-norm entropy explored by Boekee and Vander Lubbe (1980) is provided by

$$\begin{aligned} E_{r}(\Lambda )=\frac{r}{r-1}\left[ 1-\left( \sum _{i=1}^{t} \lambda _i^r \right) ^{\frac{1}{r}}\right] ; r \in \left( 0, \infty \right) , r \ne 1. \end{aligned}$$

(3)

Furthermore, the r-norm entropy is equivalent to the Shannon entropy when $r \rightarrow 1$ and $E_{r}(\Lambda ) \rightarrow (1-\max (\lambda _i))$ when $r \rightarrow \infty$. The r-norm entropy was further generalized by Hooda (2004), Kumar (2009), Kumar et al. (2014), Joshi and Kumar (2018).

Now, we provide the necessary background information on IF-sets and their generalizations.

Definition 1

(Zadeh 1965) Let D($\ne$ $\phi$) be a finite set. A Fuzzy set ${\bar{R}}$ defined on D is given by

$$\begin{aligned} {\bar{R}}=\left\{ \langle d_i, \mu _{{\bar{R}}}(d_i) \rangle : d_i \in D\right\} ; \end{aligned}$$

(4)

where $\mu _{{\bar{R}}}$: D $\rightarrow$ $\left[ 0,1\right]$ represents membership function for the fuzzy set ${\bar{R}}$.

Definition 2

(Atanassov 1986) Let D($\ne$ $\phi$) be a finite set. An IF-set R defined on D is given by

$$\begin{aligned} R=\left\{ \langle d_i, \mu _{R}(d_i), \nu _{R}(d_i) \rangle : d_i \in D\right\} ; \end{aligned}$$

(5)

where $\mu _{R}$: D $\rightarrow$ $\left[ 0,1\right]$ is membership function and $\nu _{R}$: D $\rightarrow$ $\left[ 0,1\right]$ is non-membership function with condition that

$$\begin{aligned} 0 \le \mu _{R}(d_i)+\nu _{R}(d_i) \le 1, \forall d_i \in D. \end{aligned}$$

(6)

For an IF-set R described on D, the hesitation degree ($\pi _R$) is computed by the formula given below

$$\begin{aligned} \pi _R(d_i)=1-\mu _{R}(d_i)-\nu _{R}(d_i); \forall d_i \in D. \end{aligned}$$

(7)

Clearly, $\pi _R(d_i)$ $\in$ [0,1]. Hesitation degree can also be regarded as an intuitionistic index and is used to represent the degree of the hesitance of the element $d_i$ $\in$ D in IF-set R. Higher value of $\pi _R(d_i)$ corresponds to high vagueness. Also, when $\pi _R(d_i)=0$, then the IF-set R decays into a simple fuzzy set. The most IF-set is an IF-set in which the membership and non-membership function values are identical for every element of the set. Every element of most IF-set is called a crossover element.

Note: From this point forward, the term IFS(D) shall refer to the collection of all the IF-sets.

Definition 3

Consider two IF-sets $R,S \in$ IFS(D) defined by

$$\begin{aligned} \begin{aligned} R&=\left\{ \langle d_i, \mu _{R}(d_i), \nu _{R}(d_i) \rangle : d_i \in D\right\} ,\\ S&=\left\{ \langle d_i, \mu _{S}(d_i), \nu _{S}(d_i) \rangle : d_i \in D\right\} , \end{aligned} \end{aligned}$$

then following are the basic operations on IF-sets:

$$\begin{aligned} \begin{aligned}&R\cup S = \left\{ \langle d_i, max\left( \mu _{R}\left( d_i\right) ,\mu _{S}\left( d_i\right) \right) ,\right. \\&\quad \left. min\left( \nu _{R}\left( d_i\right) ,\nu _{S}\left( d_i\right) \right) \rangle : d_i \in D\right\} ; \\&R\cap S = \left\{ \langle d_i, min\left( \mu _{R}\left( d_i\right) ,\mu _{S}\left( d_i\right) \right) ,\right. \\&\quad \left. max\left( \nu _{R}\left( d_i\right) ,\nu _{S}\left( d_i\right) \right) \rangle : d_i \in D\right\} ; \\&R^c =\left\{ \langle d_i, \nu _{R}(d_i), \mu _{R}(d_i) \rangle : d_i \in D\right\} ;\\&R \subseteq S \Leftrightarrow {\left\{ \begin{array}{ll} \mu _{R}\left( d_i\right) \le \mu _{S}\left( d_i\right) \text { and } \nu _{R}\left( d_i\right) \ge \nu _{S}\left( d_i\right) &{} if \text { } \mu _{R}(d_i) \le \nu _{S}(d_i) \\ \mu _{R}\left( d_i\right) \ge \mu _{S}\left( d_i\right) \text { and } \nu _{R}\left( d_i\right) \le \nu _{S}\left( d_i\right) &{} if \text { } \mu _{R}(d_i) \ge \nu _{S}(d_i) \\ \end{array}\right. }, \forall d_i \in D; \\&R = S \Leftrightarrow S \subseteq R \text { and } R \subseteq S. \end{aligned} \end{aligned}$$

(8)

Definition 4

(Szmidt and Kacprzyk 2001) To define a function E: IFS(D) $\rightarrow$ $\left[ 0,1\right]$ as an IF-information measure, it must satisfy the following four axioms:

(E1):

E(R)=1 $\Leftrightarrow$ $\mu _{R}(d_i)=\nu _{R}(d_i)$ $\forall$ $d_i \in D$, i.e., R is most IF-set.

(E2):

E(R)=0 $\Leftrightarrow$ $\mu _{R}(d_i)=0$, $\nu _{R}(d_i)=1$ or $\mu _{R}(d_i)=1$, $\nu _{R}(d_i)=0$ $\forall$ $d_i \in D$, i.e., R is a crisp set.

(E3):

E(R) $\le$ E(S) $\Leftrightarrow$ R $\subseteq$ S.

(E4):

If $R^{c}$ represents complement of a fuzzy set R, then $E(R)=E(R^{c})$.

The fuzzy entropy calculates the Fuzziness of a fuzzy set. In addition, a knowledge measure determines the total quantity of knowledge. According to Singh et al. (2019), these two theories are complimentary to one another.

Definition 5

(Singh et al. 2019) The following four axioms must be met to define a function K: IFS(D) $\rightarrow$ $\left[ 0,1\right]$ as an IF-knowledge measure:

(K1):

K(R)=1 $\Leftrightarrow$ $\mu _{R}(d_i)=0$, $\nu _{R}(d_i)=1$ or $\mu _{R}(d_i)=1$, $\nu _{R}(d_i)=0$ $\forall$ $d_i \in D$, i.e., R is a crisp set.

(K2):

K(R)=0 $\Leftrightarrow$ $\mu _{R}(d_i)=\nu _{R}(d_i)$ $\forall$ $d_i \in D$, i.e., R is most IF-set.

(K3):

K(R) $\ge$ K(S) $\Leftrightarrow$ R $\subseteq$ S.

(K4):

If $R^{c}$ represents complement of a fuzzy set R, then $K(R)=K(R^{c})$.

Definition 6

(Hung and Yang 2004; Chen and Chang 2015) Let $R,S,T \in IFS(D)$. A mapping $S_m: IFS(D) \times IFS(D) \rightarrow [0,1]$ is considered to be an IF-similarity measure if it meets the four axioms listed below:

(S1):

$0 \le S_m(R,S) \le 1$.

(S2):

$S_m(R,S)=S_m(S,R)$.

(S3):

$S_m(R,S)=1$ $\Leftrightarrow$ $R=S$.

(S4):

If $R \subseteq S \subseteq T$, then $S_m(R,S) \ge S_m(R,T)$ & $S_m(S,T) \ge S_m(R,T)$.

Definition 7

(Wang and Xin 2005) Let $R,S,T \in IFS(D)$. A mapping $D_m: IFS(D) \times IFS(D) \rightarrow [0,1]$ is considered to be a dissimilarity/distance measure if it meets the four axioms listed below:

(D1):

$0 \le D_m(R,S) \le 1$.

(D2):

$D_m(R,S)=D_m(S,R)$.

(D3):

$D_m(R,S)=0$ $\Leftrightarrow$ $R=S$.

(D4):

If $R \subseteq S \subseteq T$, then $D_m(R,S) \le D_m(R,T)$ & $D_m(S,T) \le D_m(R,T)$.

Definition 8

Let $R,S \in IFS(D)$. A mapping $A_m: IFS(D) \times IFS(D) \rightarrow [0,1]$ is said to be accuracy measure in S w.r.t. R, if it fulfils the following four axioms:

(A1):

$A_m(R,S) \in [0,1]$.

(A2):

$A_m(R,S)=0$ $\Leftrightarrow$ $\mu _{R}(d_i)=\nu _{R}(d_i)$.

(A3):

$A_m(R,S)=1$ if $\mu _{R}(d_i) =\mu _{S}(d_i)=0$, $\nu _{R}(d_i) =\nu _{S}(d_i)=1$ or $\mu _{R}(d_i) =\mu _{S}(d_i)=1$, $\nu _{R}(d_i) =\nu _{S}(d_i)=0$, i.e., Both R and S are equal and crisp IF-sets.

(A4):

$A_m(R,S)=K(R)$ if $R=S$, where K(R) is knowledge measure.

As briefly described below, Szmidt and Kacprzyk (1998) provided a technique for converting IF-sets into fuzzy sets.

Definition 9

(Szmidt and Kacprzyk 1998) Let R $\in$ IFS(D), then the fuzzy membership function $\mu _{{\bar{R}}}(d_i)$ corresponding to fuzzy set ${\bar{R}}$ is given as follow

$$\begin{aligned} \begin{aligned} \mu _{{\bar{R}}}(d_i)&=\mu _{R}(d_i)+\frac{\pi _R(d_i)}{2}; \\&=\frac{\mu _{R}(d_i)+1-\nu _{R}(d_i)}{2}, \forall d_i \in D. \end{aligned} \end{aligned}$$

(9)

In the next section, we proposed an IF-knowledge measure.

3 Proposed intuitionistic fuzzy knowledge measure

3.1 Definition

Let R $\in$ IFS(D). Based on the concept of r-norm information measure proposed by Hooda (2004), Verma and Sharma (2011), and Bajaj et al. (2012), we define a new IF-knowledge measure for IF-set R as follow

$$\begin{aligned}{} & {} K^A_{I}(R)=\frac{\left( \sqrt{2}-1\right) ^{-1}}{t}\nonumber \\{} & {} \quad \sum _{i=1}^{t}\left[ \sqrt{2\left( \left( \frac{\mu _{R}(d_i)+1 -\nu _{R}(d_i)}{2}\right) ^2+\left( \frac{\nu _{R}(d_i)+1 -\mu _{R}(d_i)}{2}\right) ^2\right) }-1\right] ; \end{aligned}$$

(10)

for some R $\in$ IFS(D). Further on solving, we can write Eq. (10) as follows

$$\begin{aligned} K^A_{I}(R)= & {} \frac{(\sqrt{2}-1)^{-1} }{t} \nonumber \\{} & {} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] . \end{aligned}$$

(11)

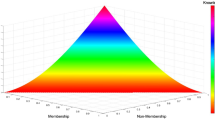
Further, if $\nu _R(d_i)=1-\mu _R(d_i), \forall d_i \in D$ then Eq. (11) becomes a fuzzy knowledge measure which is studied by Joshi (2023) and is slightly different from the knowledge measure studied by Singh and Kumar (2023). Figure 1 represents the total quantity of the knowledge passed by the proposed IF-knowledge measure.

Fig. 1

Knowledge passed by proposed IF-knowledge measure

Now, we test the validity of the proposed IF-knowledge measure $K^A_{I}$.

Theorem 1

Let $R=\left\{ \langle d_i, \mu _{R}(d_i), \nu _{R}(d_i) \rangle : d_i \in D\right\}$ and $S=\left\{ \langle d_i, \mu _{S}(d_i), \nu _{S}(d_i) \rangle : d_i \in D\right\}$ are two members of IFS(D) for a finite set D$\left( \ne \phi \right)$. Define a mapping $K^A_I$:IFS(D) $\rightarrow$ $\left[ 0,1\right]$ given in Eq. (11). Then, $K^A_I$ is a valid IF-knowledge measure if it fulfils the following axioms, (K1)-(K4):

(K1):

$K^A_I(R)=1 \Leftrightarrow \mu _{R}(d_i)=0$, $\nu _{R}(d_i)=1$ or $\mu _{R}(d_i)=1$, $\nu _{R}(d_i)=0$ $\forall$ $d_i \in D$, i.e., R is a crisp set.

(K2):

$K^A_I(R)=0 \Leftrightarrow \mu _{R}(d_i)=\nu _{R}(d_i)$ $\forall$ $d_i \in D$, i.e., R is most IF-set.

(K3):

$K^A_I(R) \ge K^A_I(S) \Leftrightarrow$ R $\subseteq$ S.

(K4):

If $R^{c}$ represents complement of a fuzzy set R, then $K^A_I(R)=K^A_I(R^c)$.

Proof

(K1). First, we consider

$$\begin{aligned} \begin{aligned} K^A_I(R)=1&\Leftrightarrow \frac{(\sqrt{2}-1)^{-1} }{t}\\&\sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] =1,\\&\Leftrightarrow \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}=\sqrt{2}, \quad \forall d_i \in D, \\&\Leftrightarrow \left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2=1, \quad \forall d_i \in D, \\&\Leftrightarrow \mu _{R}(d_i)=0, \nu _{R}(d_i)=1 \text { or } \mu _{R}(d_i)=1,\\&\quad \nu _{R}(d_i)=0, \forall d_i \in D. \end{aligned} \end{aligned}$$

This proves axiom K1.

(K2). Let us take $K^A_I$(R)=0. Then, from Eq. (11), we have

$$\begin{aligned} \frac{(\sqrt{2}-1)^{-1} }{t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] =0; \end{aligned}$$

which gives

$$\begin{aligned} \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}=1, \forall d_i \in D, \end{aligned}$$

i.e.,

$$\begin{aligned} \left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2=0, \forall d_i \in D. \end{aligned}$$

Thus, we get $\mu _{R}(d_i)=\nu _{R}(d_i)$ $\forall$ $d_i \in D.$

Conversely, Let $\mu _{R}(d_i)=\nu _{R}(d_i)$ $\forall$ $d_i \in D,$ then Eq. (11) implies $K^A_I$(R)=0.

This proves axiom K2.

(K3). To prove this axiom, first, we prove that function

$$\begin{aligned} f(s,t)=\sqrt{1+\left( s-t\right) ^2}-1, \end{aligned}$$

(12)

is an increasing function w.r.t. t and decreasing function w.r.t. s, where $s,t \in [0,1]$. Partially differentiate function f w.r.t. s, we have

$$\begin{aligned} \frac{\partial f(s,t)}{\partial s}= \frac{s-t}{\sqrt{1+\left( s-t\right) ^2}}. \end{aligned}$$

(13)

Now, critical points of s can be found by putting

$$\begin{aligned} \frac{\partial f(s,t)}{\partial s}=0; \end{aligned}$$

which gives $s=t$.

Here, two cases arise given below:

$$\begin{aligned} \frac{\partial f(s,t)}{\partial s} = {\left\{ \begin{array}{ll} Positive &{} \text {if } s \ge t\\ Negative &{} \text {if } s \le t\\ \end{array}\right. } \end{aligned}$$

(14)

i.e., function f is increasing function for $s \ge t$ and is decreasing function for $s \le t$.

Similarly, we have

$$\begin{aligned} \frac{\partial f(s,t)}{\partial t} = {\left\{ \begin{array}{ll} Negative &{} \text {if } s \ge t\\ Positive &{} \text {if } s \le t\\ \end{array}\right. } \end{aligned}$$

(15)

i.e., function f is decreasing function for $s \ge t$ and is increasing function for $s \le t$.

Now, take R,S $\in$ IFS(D) s.t. $R \subseteq S$. Let $D_1$ and $D_2$ are two partitions of D s.t. $D=D_1\cup D_2$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{R}(d_i) \le \mu _{S}(d_i) \le \nu _{S}(d_i) \le \nu _{R}(d_i) &{} \forall d_i \in D_1\\ \mu _{R}(d_i) \ge \mu _{S}(d_i) \ge \nu _{S}(d_i) \ge \nu _{R}(d_i) &{} \forall d_i \in D_2 \\ \end{array}\right. } \end{aligned}$$

Thus, from the monotonic behaviour of function f and from Eq. (11), it is easy to prove that $K^A_I(R)$ $\ge$ $K^A_I(S)$. This proves axiom (K3).

(K4). It is easy to see that $R^c =\left\{ \langle d_i, \nu _{R}(d_i), \mu _{R}(d_i) \rangle : d_i \in D\right\}$,

i.e.,

$$\begin{aligned} \mu _{R^c}(d_i)=\nu _{R}(d_i) \text { and } \nu _{R^c}(d_i)=\mu _{R}(d_i), \forall d_i \in D. \end{aligned}$$

Thus, from Eq. (11), we get $K^A_I(R)=K^A_I(R^c)$. This proves axiom (K4).

Thus, $K^A_I$(R) is a valid IF-knowledge measure. $\square$

3.2 Properties

Now, we study about some of the characteristics of the suggested knowledge measure  $K^A_I$(R).

Theorem 2

Some following properties are fulfilled by the proposed IF-knowledge measure $K^A_I$:

• (1) For an IF-set R, $K^A_I$(R) $\in$ [0,1].

• (2) $K^A_I(R)=K^A_I(R^c)$.

• (3) $K^A_I(R \cup S)+K^A_I(R \cap S)=K^A_I(R)+K^A_I(S)$ for any two arbitrary IF-sets R, S.

• (4) $K^A_I(R)$ attains its highest value for crisp set R and attains its lowest value for most IF-set R.

Proof

(1). Since, $\mu _{R}(d_i)$, $\nu _{R}(d_i) \in \left[ 0,1\right]$ $\forall d_i \in \hbox {D}$, therefore, $-1 \le \mu _{R}(d_i)-\nu _{R}(d_i) \le 1$ $\forall d_i \in D.$

$\Rightarrow$ $0 \le \left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2 \le 1$ $\forall d_i \in D$,

$\Rightarrow$ $1 \le \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2} \le \sqrt{2}$ $\forall d_i \in D$,

$\Rightarrow$ $0 \le \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1 \le \sqrt{2}-1$ $\forall d_i \in D$,

$\Rightarrow 0 \le \frac{(\sqrt{2}-1)^{-1} }{t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] \le 1$,

$\Rightarrow 0 \le K^A_I(R) \le 1$.

$\Rightarrow K^A_I(R) \in [0,1]$.

(2). Proof is obvious from axiom (K4).

(3). Let R, S $\in$ IFS(D). We take the partition of D as follows:

$$\begin{aligned} \begin{aligned} D_1&= \left\{ d_i \in D | R \subseteq S \right\} , \\ D_2&= \left\{ d_i \in D | S \subseteq R \right\} , \end{aligned} \end{aligned}$$

(16)

i.e.,

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{R}\left( d_i\right) \le \mu _{S}\left( d_i\right) \text { and } \nu _{R}\left( d_i\right) \ge \nu _{S}\left( d_i\right) &{} \forall d_i \in D_1 \\ \mu _{R}\left( d_i\right) \ge \mu _{S}\left( d_i\right) \text { and } \nu _{R}\left( d_i\right) \le \nu _{S}\left( d_i\right) &{} \forall d_i \in D_2 \\ \end{array}\right. } \end{aligned}$$

where $\mu _{R}(d_i)$ and $\mu _{S}(d_i)$ are the membership functions and $\nu _{R}(d_i)$ and $\nu _{S}(d_i)$ are the non-membership functions for the IF-set R and S, respectively.

Now, $\forall d_i \in D$,

$$\begin{aligned}{} & {} K^A_I(R \cup S)+K^A_I(R \cap S)\\{} & {} \quad = \frac{(\sqrt{2}-1)^{-1} }{t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R \cup S}(d_i)-\nu _{R \cup S}(d_i)\right) ^2}-1\right] \\{} & {} \qquad + \frac{(\sqrt{2}-1)^{-1} }{t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R \cap S}(d_i)-\nu _{R \cap S}(d_i)\right) ^2}-1\right] ; \end{aligned}$$

which gives

$$\begin{aligned} \begin{aligned}&K^A_I(R \cup S)+K^A_I(R \cap S) \\&\quad = \frac{\left( \sqrt{2}-1 \right) ^{-1}}{t}\sum _{D_1}\left[ \sqrt{1+\left( \mu _{S}(d_i) -\nu _{S}(d_i)\right) ^2}-1\right] \\&\qquad + \frac{\left( \sqrt{2}-1\right) ^{-1}}{t}\sum _{D_2} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] \\&\qquad + \frac{\left( \sqrt{2}-1\right) ^{-1}}{t}\sum _{D_1} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] \\&\qquad + \frac{\left( \sqrt{2}-1\right) ^{-1}}{t}\sum _{D_2} \left[ \sqrt{1+\left( \mu _{S}(d_i)-\nu _{S}(d_i)\right) ^2}-1\right] . \\ \end{aligned} \end{aligned}$$

On solving, we get

$$\begin{aligned} K^A_I(R \cup S)+K^A_I(R \cap S)=K^A_I(R)+K^A_I(S). \end{aligned}$$

(17)

(4). Proof is obvious from axioms (K1) and (K2). $\square$

3.3 Comparative study

Now, we contrast the suggested IF-knowledge measure with the other measures that are already in use. The benefits of new knowledge measure are explored by this comparison. We examine these benefits in relation to the estimation of ambiguity content of IF-sets, the estimation of attribute weights in MCDM issues, and the manipulation of structured linguistic variables. Among the available measures in the literature are

$$\begin{aligned} E_{ZL}(R)= & {} 1-\frac{1}{t} \sum _{i=1}^{t} |\mu _{R}(d_i)-\nu _{R}(d_i)|;\nonumber \\{} & {} (\text {Zeng and Li 2006}). \end{aligned}$$

(18)

$$\begin{aligned} E_{BB}(R)= & {} \frac{1}{t} \sum _{i=1}^{t} (1-\mu _{R}(d_i)-\nu _{R}(d_i));\nonumber \\{} & {} (\text {Burillo and Bustince 1996}). \end{aligned}$$

(19)

$$\begin{aligned} E_{SK}(R)= & {} \frac{1}{t} \sum _{i=1}^{t} \frac{\min {(\mu _{R}(d_i),\nu _{R}(d_i))}+\pi _{R}(d_i)}{\max {(\mu _{R}(d_i),\nu _{R}(d_i))}+\pi _{R}(d_i)};\nonumber \\{} & {} (\text {Szmidt and Kacprzyk 2001}). \end{aligned}$$

(20)

$$\begin{aligned} E_{HY}(R)= & {} \frac{1}{t} \sum _{i=1}^{t} (1-\mu ^2_{R}(d_i)-\nu ^2_{R}(d_i)-\pi ^2_{R}(d_i));\nonumber \\{} & {} (\text {Hung and Yang 2006}). \end{aligned}$$

(21)

$$\begin{aligned} E_{ZJ}(R)= & {} \frac{1}{t} \sum _{i=1}^{t} \frac{\min {(\mu _{R}(d_i),\nu _{R}(d_i))}}{\max {(\mu _{R}(d_i),\nu _{R}(d_i))}};\nonumber \\{} & {} (\text {Zhang and Jiang 2008}). \end{aligned}$$

(22)

$$\begin{aligned} E_{Z}^p(R)= & {} 1-\frac{1}{2t} \sum _{i=1}^{t} \left( |\mu _{R}(d_i)-\nu _{R}(d_i)|^p + |\mu _{R}(d_i)-\nu _{R}(d_i)|^{3p} \right) , p>0;\nonumber \\{} & {} (\text{Li et al. 2012}). \end{aligned}$$

(23)

$$\begin{aligned} E^r_{B}(R)= & {} \frac{r}{t(1-r)} \sum _{i=1}^{t} (1-\left( \mu ^r_{R}(d_i)+\nu ^r_{R}(d_i)+\pi ^r_{R}(d_i)\right) ^{\frac{1}{r}});\nonumber \\{} & {} (\text {Bajaj et al. 2012}). \end{aligned}$$

(24)

$$\begin{aligned} K_{S}(R)= & {} 1-\frac{1}{2t} \sum _{i=1}^{t} \left[ \frac{\min {(\mu _{R}(d_i),\nu _{R}(d_i))}+\pi _{R}(d_i)}{\max {(\mu _{R}(d_i),\nu _{R}(d_i))}+\pi _{R}(d_i)} + \pi _{R}(d_i) \right] ; \nonumber \\{} & {} ({\text{Szmidt et al. } 2014}{b}). \end{aligned}$$

(25)

$$K_{N} (R) = {\text{ }}\frac{1}{{t\sqrt 2 }}\sum\limits_{{i = 1}}^{t} {\sqrt {\mu _{R}^{2} (d_{i} ) + \nu _{R}^{2} (d_{i} ) + \left( {\mu _{R} (d_{i} ) + \nu _{R} (d_{i} )} \right)^{2} } } ;({\text{Nguyen 2015}}).$$

(26)

$$\begin{aligned} K_{G}(R)= & {} 1-\frac{1}{2t} \sum _{i=1}^{t} \left( 1- |\mu _{R}(d_i)-\nu _{R}(d_i)|\right) \left( 1+\pi _{R}(d_i)\right) ; \nonumber \\{} & {} (\text {Guo 2015}).\end{aligned}$$

(27)

$$\begin{aligned} K^A_{I}(R)= & {} \frac{(\sqrt{2}-1)^{-1} }{t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] ;\nonumber \\{} & {} \text {(Proposed one)} \end{aligned}$$

(28)

3.3.1 Structured linguistic computation

The idea of an IF-set is utilized to represent linguistic variables, and the linguistic hedges are used to represent the operations on an IF-Set. The linguistic hedges, which are used to reflect linguistic variables, include “MORE”, “LESS”, “VERY”, “FEW”, “SLIGHTLY” and “LESS”. In this situation, we investigated these linguistic hedges and compared the suggested IF-knowledge measure’s performance to existing measures.

Let us take an IF-set $R=\left\{ \langle d_i, \mu _{R}(d_i), \nu _{R}(d_i) \rangle : d_i \in D\right\}$ defined on a finite set D($\ne \phi$) and treat this IF-set as “Wide” on D. For $k>0$, De et al. (2000) define the modifier of IF-set R as follow

$$\begin{aligned} R^k=\left\{ \langle d_i, \left( \mu _{R}(d_i)\right) ^k,1-\left( 1- \nu _{R}(d_i)\right) ^k \rangle : d_i \in D\right\} . \end{aligned}$$

(29)

De et al. (2000) define the concentration and dilatation for an IF-set R as follow

$$\begin{aligned} \begin{aligned} CON(R)&=R^2, \\ DIL(R)&=R^{0.5}. \end{aligned} \end{aligned}$$

(30)

Concentration and dilatation are used for modifiers. For the sake of clarity, we shorten the following terms: W stands for WIDE, V.W. stands for VERY WIDE, M.L.W. stands for MORE/LESS WIDE, Q.V.W. stands for QUITE VERY WIDE and V.V.W. stands for VERY VERY WIDE. Hedges for the IF-set R are defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} M.L.W. &{} \text { stands for } R^{0.5}\\ W &{} \text { stands for } R \\ V.W. &{} \text { stands for } R^2 \\ Q.V.W. &{} \text { stands for } R^3 \\ V.V.W. &{} \text { stands for } R^4 \end{array}\right. } \end{aligned}$$

(31)

It makes intuitive sense that as we move from set $R^{0.5}$ to set $R^4$, the uncertainty concealed in them decreases and the knowledge amount they express grows. For top performance, the information measure E(R) of an IF-set R must match the following criteria:

$$\begin{aligned} E(V.V.W.)< & {} E(Q.V.W.)< E(V.W.) \nonumber \\< & {} E(W) < E(M.L.W.); \end{aligned}$$

(32)

where E(R) is the information measure of an IF-set R. On the other hand, a knowledge measure must adhere to the following criteria:

$$\begin{aligned} K(V.V.W.)> & {} K(Q.V.W.)> K(V.W.) \nonumber \\> & {} K(W) > K(M.L.W.); \end{aligned}$$

(33)

where $K^A$(R) is knowledge measure of IF-set R.

Now, to assess the efficacy of the suggested knowledge measure $K^A_I$(R), consider the following example:

Example 1

Let us consider a set $\hbox {D}= \left\{ d_i, 1\le i \le 5\right\}$ and let R is an IF-set defined on D defined as follows:

$$\begin{aligned} R= & {} \left\{ \left( d_1,0.105,0.809\right) , \left( d_2,0.297,0.492\right) ,\right. \nonumber \\{} & {} \left( d_3,0.509,0.482\right) , \left( d_4,0.906,0.005\right) ,\nonumber \\{} & {} \left. \left( d_5,0.997,0.001\right) \right\} . \end{aligned}$$

(34)

Considering an IF-set “R” on D as “WIDE” and assuming the linguistic variables according to Eq. (31). Using Eq. (29), we may produce the following IF-sets:

$$\begin{aligned} \begin{aligned} R^{0.5}&=\left\{ \left( d_1,0.3240,0.5630\right) , \left( d_2,0.5450,0.2873\right) ,\right. \\&\quad \left( d_3,0.7134,0.2803\right) , \left( d_4,0.9518,0.0025\right) , \\&\quad \left. \left( d_5,0.9985,0.0005\right) \right\} ; \\ R&=\left\{ \left( d_1,0.1050,0.8090\right) , \left( d_2,0.2970,0.4920\right) ,\right. \\&\quad \left( d_3,0.5090,0.4820\right) , \left( d_4,0.9060,0.0050\right) , \\&\quad \left. \left( d_5,0.9970,0.0010\right) \right\} ; \\ R^2&=\left\{ \left( d_1,0.0110,0.9635\right) , \left( d_2,0.0882,0.7419\right) ,\right. \\&\quad \left( d_3,0.2591,0.7317\right) , \left( d_4,0.8208,0.0100\right) , \\&\quad \left. \left( d_5,0.9940,0.0020\right) \right\} ; \\ R^3&=\left\{ \left( d_1,0.0012,0.9930\right) , \left( d_2,0.0262,0.8689\right) ,\right. \\&\quad \left( d_3,0.1319,0.8610\right) , \left( d_4,0.7437,0.0149\right) , \\&\quad \left. \left( d_5,0.9910,0.0030\right) \right\} ; \\ R^4&=\left\{ \left( d_1,0.0001,0.9987\right) , \left( d_2,0.0078,0.9334\right) ,\right. \\&\quad \left( d_3,0.0671,0.9280\right) , \left( d_4,0.6738,0.0199\right) , \\&\quad \left. \left( d_5,0.9881,0.0040\right) \right\} . \\ \end{aligned} \end{aligned}$$

(35)

Now, we compared the suggested IF-knowledge measure’s performance to existing measures described in the literature. The values of the existing measures and the proposed IF-knowledge measure are compared and shown in Table 1.

Table 1 Comparison of the proposed IF-knowledge measure with some current measures

Following observations are made from Table 1:

$$\begin{aligned} \begin{aligned} E_{ZL}(V.V.W.)&< E_{ZL}(Q.V.W.)< E_{ZL}(V.W.) \\&< E_{ZL}(W)> E_{ZL}(M.L.W.); \\ E_{BB}(V.V.W.)&> E_{BB}(Q.V.W.)< E_{BB}(V.W.) \\&< E_{BB}(W)> E_{BB}(M.L.W.); \\ E_{SK}(V.V.W.)&< E_{SK}(Q.V.W.)< E_{SK}(V.W.) \\&< E_{SK}(W)> E_{SK}(M.L.W.); \\ E_{HY}(V.V.W.)&< E_{HY}(Q.V.W.)< E_{HY}(V.W.) \\&< E_{HY}(W)< E_{HY}(M.L.W.); \\ E_{ZJ}(V.V.W.)&< E_{ZJ}(Q.V.W.)< E_{ZJ}(V.W.) \\&< E_{ZJ}(W)> E_{ZJ}(M.L.W.); \\ E_{Z}^3(V.V.W.)&< E_{Z}^3(Q.V.W.)< E_{Z}^3(V.W.) \\&< E_{Z}^3(W)> E_{Z}^3(M.L.W.); \\ E_{B}^5(V.V.W.)&< E_{B}^5(Q.V.W.)< E_{B}^5(V.W.) \\&< E_{B}^5(W)> E_{B}^5(M.L.W.); \\ K_S(V.V.W.)&> K_S(Q.V.W.)> K_S(V.W.) \\&> K_S(W)< K_S(M.L.W.); \\ K_N(V.V.W.)&> K_N(Q.V.W.)> K_N(V.W.) \\&> K_N(W)< K_N(M.L.W.); \\ K_G(V.V.W.)&> K_G(Q.V.W.)> K_G(V.W.) \\&> K_G(W) < K_G(M.L.W.); \\ K_I^A(V.V.W.)&> K_I^A(Q.V.W.)> K_I^A(V.W.) \\&> K_I^A(W) > K_I^A(M.L.W.). \\ \end{aligned} \end{aligned}$$

(36)

Now, we found that, except $E_{HY}(R)$ and $K_I^A(R)$, none of the information and knowledge measures follow the sequence indicated in Eqs. (32) and (33). It suggests that they are not performing well. Then, we solely compare information measure $E_{HY}(R)$ and knowledge measure $K_I^A(R)$.

To do this, we use another IF-set provided by

$$\begin{aligned} R= & {} \left\{ \left( d_1,0.110,0.798\right) , \left( d_2,0.280,0.502\right) ,\right. \nonumber \\{} & {} \left( d_3,0.475,0.423\right) , \left( d_4,0.920,0.019\right) ,\nonumber \\{} & {} \left. \left( d_5,0.981,0.005\right) \right\} . \end{aligned}$$

(37)

The observed values are computed in Table 2 and the following observations are made from it:

$$\begin{aligned} \begin{aligned} E_{HY}(V.V.W.)&< E_{HY}(Q.V.W.)< E_{HY}(V.W.) \\&< E_{HY}(W)> E_{HY}(M.L.W.); \\ K_I^A(V.V.W.)&> K_I^A(Q.V.W.)> K_I^A(V.W.) \\&> K_I^A(W) > K_I^A(M.L.W.). \\ \end{aligned} \end{aligned}$$

(38)

Table 2 Computed values of measures defined in Eqs. (21) and (28)

In this case, we see that the information measure $E_{HY}(R)$ does not match the order stated in Eq. (32). But the proposed knowledge measure goes in the right order. Consequently, the efficacy of the proposed knowledge measure is really amazing.

3.3.2 Ambiguity computation

Two separate IF-sets have different levels of ambiguity. However, some knowledge measures provide the same ambiguity values corresponding to various IF-sets. As a result, a new knowledge measure that generalizes previously recognized knowledge measures is required. The effectiveness of the proposed measure is illustrated in the following example:

Example 2

Define a set D=$\left\{ d_1,d_2,d_3,d_4\right\}$ and take $R_1,R_2,R_3,R_4 \in$ IFS(D) as follows

$$\begin{aligned} \begin{aligned} R_1&=\left\{ (d_1,0.423,0.529),(d_2,0.219,0.421),\right. \\&\quad \left. (d_3,0.231,0.480),(d_4,0.421,0.368)\right\} ; \\ R_2&=\left\{ (d_1,0.320,0.480),(d_2,0.410,0.390),\right. \\&\quad \left. (d_3,0.480,0.320),(d_4,0.319,0.481)\right\} ; \\ R_3&=\left\{ (d_1,0.623,0.077),(d_2,0.619,0.080),\right. \\&\quad \left. (d_3,0.613,0.065),(d_4,0.725,0.002)\right\} ; \\ R_4&=\left\{ (d_1,0.423,0.019),(d_2,0.214,0.523),\right. \\&\quad \left. (d_3,0.329,0.112),(d_4,0.298,0.397)\right\} . \\ \end{aligned} \end{aligned}$$

(39)

We now determine the ambiguous content of given IF-sets using some previously established knowledge measures and suggested knowledge measure. Table 3 displays the results of the calculations.

Table 3 Ambiguity computation corresponding to different IF-sets defined in Example 2

We can observe from Table 3 that the ambiguity content as determined by existing knowledge measures is the same for various IF-sets. However, the proposed knowledge measure clearly distinguishes between these IF-sets. Therefore, a fresh approach is constantly needed.

3.3.3 Attribute weights evaluation

The attribute weights are significant in an MCDM issue. Here, we calculate attribute weights using both the proposed measure and the previously existing knowledge measures defined for IF-sets. Take a look at an example of this.

Example 3

Let D is a decision matrix corresponding to a set of alternatives $\left\{ L_1,L_2,L_3,L_4\right\}$ and a set of attributes $\left\{ T_1,T_2,T_3,T_4\right\}$ established in an intuitionistic fuzzy environment.

$$\begin{aligned} D= \begin{bmatrix}<0.623,0.077>&{}<0.320,0.480>&{}<0.423,0.019>&{}<0.423,0.529>\\<0.619,0.080>&{}<0.410,0.390>&{}<0.214,0.523>&{}<0.219,0.421>\\<0.613,0.065>&{}<0.480,0.320>&{}<0.329,0.112>&{}<0.231,0.480>\\<0.725,0.002>&{}<0.319,0.481>&{}<0.298,0.397>&{} <0.421,0.368>\end{bmatrix} \end{aligned}$$

The attribute weights can be determined using one of two approaches given below:

(A).:

Approach depending upon information measures - We can determine the weights corresponding to various attributes by using the formula given as follows:

$$\begin{aligned} w_j=\frac{1-E(T_j)}{q-\sum _{j=1}^{q}E(T_j)}, j=1,2,3,\dots ,q; \end{aligned}$$

(40)

where E denotes information measures corresponding to an IF-set.

(B).:

Approach depending upon knowledge measures - We can determine the weights corresponding to various attributes by using the formula given as follows:

$$\begin{aligned} w_j=\frac{K(T_j)}{\sum _{j=1}^{q} K(T_j)}, j=1,2,3,\dots ,q; \end{aligned}$$

(41)

where K denotes knowledge measures corresponding to an IF-set.

In this example, we calculate weights calculated by knowledge measures only. The attribute weights are computed in the Table 4.

Table 4 Attributes weights corresponding to Example 3

Table 4 demonstrates that the attribute weights determined by some existing knowledge measures are inconsistent. In some cases, the weights assigned to different attributes are the same. However, the weights assigned by the proposed knowledge measure are different for different attributes. Thus, it is necessary to develop a new knowledge measure for IF-sets.

4 Deduction of some new measures

In the present section, some more measures that are derived from the proposed IF-knowledge measure, are suggested.

4.1 IF-accuracy measure

The quantity of intuitionistic fuzzy accuracy can be equated with the quantity of intuitionistic fuzzy knowledge. The notion of IF-accuracy measure is used when we wish to know how accurate IF-set S is in comparison to another IF-set R. Verma and Sharma (2014) expanded the notion of inaccuracy measure for IF-sets from fuzzy sets and gave Intuitionistic Fuzzy Inaccuracy measure as follows:

$$\begin{aligned} I(R,S)= & {} - \frac{1}{t} \sum _{i=1}^{t} \Bigg [ \Bigg . \mu _{R}\log \left( \frac{\mu _{R}+\mu _{S}}{2}\right) \nonumber \\{} & {} +\nu _{R}\log \left( \frac{\nu _{R}+\nu _{S}}{2}\right) + \pi _{R}\log \left( \frac{\pi _{R}+\pi _{S}}{2}\right) \nonumber \\{} & {} - \pi _{R}\log \pi _{R} -\left( 1 - \pi _{R}\right) \log \left( 1 - \pi _{R}\right) - \pi _{R} \Bigg . \Bigg ]; \end{aligned}$$

(42)

where $R,S \in IFS(D)$.

Now, depending upon proposed IF-knowledge measure $K_I^A(R)$, we define a new IF-accuracy measure $K^{I}_{accy}(R,S)$ of IF-set S w.r.t. IF-set R as follows:

$$\begin{aligned} \begin{aligned}&K^{I}_{accy}(R,S)\\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{i=1}^{t} \left[ \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)|\times |\mu _{S}(d_i)-\nu _{S}(d_i)|}-1\right] . \end{aligned} \end{aligned}$$

(43)

Now we check for the validation of the proposed accuracy measure $K^{I}_{accy}$.

Theorem 3

Let $R=\left\{ \langle d_i, \mu _{R}(d_i), \nu _{R}(d_i) \rangle : d_i \in D\right\}$ and $S=\left\{ \langle d_i, \mu _{S}(d_i), \nu _{S}(d_i) \rangle : d_i \in D\right\}$ are two members of IFS(D) for a finite set D$\left( \ne \phi \right)$. Define a mapping $K^{I}_{accy}:IFS(D) \times IFS(D)$ $\rightarrow$ $\left[ 0,1\right]$ given in Eq. (43). Then, $K^{I}_{accy}(R,S)$ is a valid accuracy measure for IF-set S relative to R if it fulfils the following axioms, (A1)-(A4):

(A1):

$K^{I}_{accy}(R,S) \in [0,1]$.

(A2):

$K^{I}_{accy}(R,S)=0$ $\Leftrightarrow$ $\mu _{R}(d_i)=\nu _{R}(d_i)$.

(A3):

$K^{I}_{accy}(R,S)=1$ if $\mu _{R}(d_i) =\mu _{S}(d_i)=0$, $\nu _{R}(d_i) =\nu _{S}(d_i)=1$ or $\mu _{R}(d_i) =\mu _{S}(d_i)=1$, $\nu _{R}(d_i) =\nu _{S}(d_i)=0$, i.e., R and S both are equal crisp IF-sets.

(A4):

$K^{I}_{accy}(R,S)=K^A_I(R)$ if $R=S$, where $K^A_I(R)$ is the proposed knowledge measure.

Proof

(A1). It is easy to prove this from Eq. (43).

(A2). Let $K^{I}_{accy}(R,S)=0$,

i.e.,

$$\begin{aligned}{} & {} \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] \\{} & {} \quad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\{} & {} \quad \sum _{i=1}^{t} \left[ \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)|\times |\mu _{S}(d_i)-\nu _{S}(d_i)|}-1\right] =0. \end{aligned}$$

Since the above summation contains only positive terms, therefore above-mentioned equation is true only if $\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) =0$ and $|\mu _{R}(d_i)-\nu _{R}(d_i)|\times |\mu _{S}(d_i)-\nu _{S}(d_i)|=0, \forall d_i \in D$; which gives $\mu _{R}(d_i)=\nu _{R}(d_i), \forall d_i \in D$.

Conversely, let us consider $\mu _{R}(d_i)=\nu _{R}(d_i), \forall d_i \in D$; which clearly implies $K^{I}_{accy}(R,S)=0$.

(A3). Let R, S are two crisp sets in IFS(D) and are equal. It implies that $\mu _{R}(d_i) =\mu _{S}(d_i)=0$, $\nu _{R}(d_i) =\nu _{S}(d_i)=1$ or $\mu _{R}(d_i) =\mu _{S}(d_i)=1$, $\nu _{R}(d_i) =\nu _{S}(d_i)=0$. Clearly, $K^{I}_{accy}(R,S)=1$ from both cases.

(A4). It is simple to demonstrate $K^{I}_{accy}(R,S)=K^A_I(R)$ for $R=S$ from definition given in Eq. (43).

Hence, $K^{I}_{accy}(R,S)$ is a valid IF-accuracy measure. $\square$

Theorem 4

For $R,S,T \in IFS(D)$, then $K^{I}_{accy}$ satisfy the following properties:

(1):

$K^{I}_{accy}(R,S \cup T) + K^{I}_{accy}(R,S \cap T) = K^{I}_{accy}(R,S) + K^{I}_{accy}(R,T)$.

(2):

$K^{I}_{accy}(R \cup S, T) + K^{I}_{accy}(R \cap S, T) = K^{I}_{accy}(R,T) + K^{I}_{accy}(S,T)$.

(3):

$K^{I}_{accy}(R \cup S, R \cap S) + K^{I}_{accy}(R \cap S, R \cup S) = K^{I}_{accy}(R,S) + K^{I}_{accy}(S,R)$.

(4):

If $R^c$ and $S^c$ represents complements of R and S respectively then

(a):

$K^{I}_{accy}(R,R^c)=K^{I}_{accy}(R^c,R)$.

(b):

$K^{I}_{accy}(R,S^c)=K^{I}_{accy}(R^c,S)$.

(c):

$K^{I}_{accy}(R,S)=K^{I}_{accy}(R^c,S^c)$.

(d):

$K^{I}_{accy}(R,S) + K^{I}_{accy}(R^c,S) = K^{I}_{accy}(R^c,S^c) + K^{I}_{accy}(R,S^c)$.

Proof

Let $R,S,T \in$ IFS(D) for a non-empty finite set D, are given as follows:

$$\begin{aligned} \begin{aligned} R&=\left\{ \langle d_i, \mu _{R}(d_i), \nu _{R}(d_i) \rangle : d_i \in D\right\} ; \\ S&=\left\{ \langle d_i, \mu _{S}(d_i), \nu _{S}(d_i) \rangle : d_i \in D\right\} ; \\ T&=\left\{ \langle d_i, \mu _{T}(d_i), \nu _{T}(d_i) \rangle : d_i \in D\right\} , \end{aligned} \end{aligned}$$

where $\mu _{R}(d_i),\mu _{S}(d_i),\mu _{T}(d_i)$ are membership functions and $\nu _{R}(d_i),\nu _{S}(d_i),\nu _{T}(d_i)$ are non-membership functions corresponding to sets R, S, T, respectively.

(1). Consider two sets

$$\begin{aligned} \begin{aligned} \Phi _1&=\left\{ d_i \in D: \mu _{S}(d_i) \ge \mu _{T}(d_i), \nu _{S}(d_i)< \nu _{T}(d_i) \right\} , \\ \Phi _2&=\left\{ d_i \in D: \mu _{S}(d_i) < \mu _{T}(d_i), \nu _{S}(d_i) \ge \nu _{T}(d_i) \right\} . \\ \end{aligned} \end{aligned}$$

Now,

$$\begin{aligned} \begin{aligned}&K^{I}_{accy}(R,S \cup T) \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{i=1}^{t} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{S \cup T}(d_i)-\nu _{S \cup T}(d_i)|}-1\right) , \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \\&\qquad + \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t}\\&\qquad \sum _{d_i \in \Phi _1} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{S}(d_i)- \nu _{S}(d_i)|}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Phi _2} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{T}(d_i)- \nu _{T}(d_i)|}-1\right) \Bigg . \Bigg ], \\ \end{aligned} \end{aligned}$$

(44)

and

$$\begin{aligned} \begin{aligned}&K^{I}_{accy}(R,S \cap T) \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{i=1}^{t} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{S \cap T}(d_i)-\nu _{S \cap T}(d_i)|}-1\right) , \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \\&\qquad + \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Phi _1} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{T}(d_i)- \nu _{T}(d_i)|}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t}\\&\qquad \sum _{d_i \in \Phi _2} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{S}(d_i)- \nu _{S}(d_i)|}-1\right) \Bigg . \Bigg ]. \end{aligned} \end{aligned}$$

(45)

On adding Eqs. (44) and (45), we get

$$\begin{aligned}{} & {} K^{I}_{accy}(R,S \cup T) + K^{I}_{accy}(R,S \cap T) \\{} & {} \quad = K^{I}_{accy}(R,S) + K^{I}_{accy}(R,T). \end{aligned}$$

(2). Consider two sets

$$\begin{aligned} \begin{aligned} \Psi _1&=\left\{ d_i \in D: \mu _{R}(d_i) \ge \mu _{S}(d_i), \nu _{R}(d_i)< \nu _{S}(d_i) \right\} , \\ \Psi _2&=\left\{ d_i \in D: \mu _{R}(d_i) < \mu _{S}(d_i), \nu _{R}(d_i) \ge \nu _{S}(d_i) \right\} . \\ \end{aligned} \end{aligned}$$

Now,

$$\begin{aligned} \begin{aligned}&K^{I}_{accy}(R \cup S,T) \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R \cup S}(d_i)-\nu _{R \cup S}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{i=1}^{t} \left( \sqrt{1+|\mu _{R \cup S}(d_i)-\nu _{R \cup S}(d_i)| \times |\mu _{T}(d_i)|-\nu _{T}(d_i)}-1\right) , \\&\quad = \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _1} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{d_i \in \Psi _2} \left( \sqrt{1+\left( \mu _{S}(d_i)-\nu _{S}(d_i)\right) ^2}-1\right) \Bigg . \Bigg ] \\&\qquad + \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _1} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{T}(d_i)- \nu _{T}(d_i)|}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _2} \left( \sqrt{1+|\mu _{S}(d_i)-\nu _{S}(d_i)| \times |\mu _{T}(d_i)- \nu _{T}(d_i)|}-1\right) \Bigg . \Bigg ], \end{aligned} \end{aligned}$$

(46)

and

$$\begin{aligned} \begin{aligned}&K^{I}_{accy}(R \cap S,T) \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R \cap S}(d_i)-\nu _{R \cap S}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{i=1}^{t} \left( \sqrt{1+|\mu _{R \cap S}(d_i)-\nu _{R \cap S}(d_i)| \times |\mu _{T}(d_i)-\nu _{T}(d_i)|}-1\right) , \\&\quad = \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _1} \left( \sqrt{1+\left( \mu _{S}(d_i)-\nu _{S}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{d_i \in \Psi _2} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \Bigg . \Bigg ] \\&\qquad + \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _1} \left( \sqrt{1+|\mu _{S}(d_i)-\nu _{S}(d_i)| \times |\mu _{T}(d_i)- \nu _{T}(d_i)|}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _2} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{T}(d_i)- \nu _{T}(d_i)|}-1\right) \Bigg . \Bigg ]. \end{aligned} \end{aligned}$$

(47)

On adding Eqs. (46) and (47), we get

$$\begin{aligned} K^{I}_{accy}(R \cup S, T) + K^{I}_{accy}(R \cap S, T) = K^{I}_{accy}(R,T) + K^{I}_{accy}(S,T). \end{aligned}$$

(3). Consider the same two sets

$$\begin{aligned} \begin{aligned} \Psi _1&=\left\{ d_i \in D: \mu _{R}(d_i) \ge \mu _{S}(d_i), \nu _{R}(d_i)< \nu _{S}(d_i) \right\} , \\ \Psi _2&=\left\{ d_i \in D: \mu _{R}(d_i) < \mu _{S}(d_i), \nu _{R}(d_i) \ge \nu _{S}(d_i) \right\} . \\ \end{aligned} \end{aligned}$$

Now,

$$\begin{aligned} \begin{aligned}&K^{I}_{accy}(R \cup S,R \cap S) \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R \cup S}(d_i)-\nu _{R \cup S}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{i=1}^{t} \left( \sqrt{1+|\mu _{R \cup S}(d_i)-\nu _{R \cup S}(d_i)| \times |\mu _{R \cap S}(d_i)-\nu _{R \cap S}(d_i)|}-1\right) , \\&\quad = \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{d_i \in \Psi _1} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _2} \left( \sqrt{1+\left( \mu _{S}(d_i)-\nu _{S}(d_i)\right) ^2}-1\right) \Bigg . \Bigg ] \\&\qquad + \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _1} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{S}(d_i)- \nu _{S}(d_i)|}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _2} \left( \sqrt{1+|\mu _{S}(d_i)-\nu _{S}(d_i)| \times |\mu _{R}(d_i)- \nu _{R}(d_i)|}-1\right) \Bigg . \Bigg ], \end{aligned} \end{aligned}$$

(48)

and

$$\begin{aligned} \begin{aligned}&K^{I}_{accy}(R \cap S,R \cup S) \\&\quad = \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{i=1}^{t} \left( \sqrt{1+\left( \mu _{R \cap S}(d_i)-\nu _{R \cap S}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{i=1}^{t} \left( \sqrt{1+|\mu _{R \cap S}(d_i)-\nu _{R \cap S}(d_i)| \times |\mu _{R \cup S}(d_i)-\nu _{R \cup S}(d_i)|}-1\right) , \\&\quad = \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \sum _{d_i \in \Psi _1} \left( \sqrt{1+\left( \mu _{S}(d_i)-\nu _{S}(d_i)\right) ^2}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _2} \left( \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right) \Bigg . \Bigg ] \\&\qquad + \Bigg [ \Bigg . \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _1} \left( \sqrt{1+|\mu _{S}(d_i)-\nu _{S}(d_i)| \times |\mu _{R}(d_i)- \nu _{R}(d_i)|}-1\right) \\&\qquad + \frac{(\sqrt{2}-1)^{-1} }{2t} \\&\qquad \sum _{d_i \in \Psi _2} \left( \sqrt{1+|\mu _{R}(d_i)-\nu _{R}(d_i)| \times |\mu _{S}(d_i)- \nu _{S}(d_i)|}-1\right) \Bigg . \Bigg ]. \end{aligned} \end{aligned}$$

(49)

Adding Eqs. (48) and (49), we get

$$\begin{aligned}{} & {} K^{I}_{accy}(R \cup S, R \cap S) + K^{I}_{accy}(R \cap S, R \cup S)\\{} & {} \quad = K^{I}_{accy}(R,S) + K^{I}_{accy}(S,R). \end{aligned}$$

(4). The definition given in Eq. (43) is used as the direct proof for this part. $\square$

4.1.1 Application of proposed accuracy measure in pattern detection

Now, the pattern detection issue with IF-set is addressed by the following application of the accuracy measure.

Problem: Let us consider m patterns, represented by IF-sets $P_j=\left\{ \langle d_i, \mu _{P_j}(d_i), \nu _{P_J}(d_i) \rangle :d_i \in D\right\}$ $(j=1,2,3,\dots ,m)$ defined on a non-empty finite set $D=\left\{ d_1,d_2,\dots ,d_n\right\}$. Let $C=\left\{ \langle d_i, \mu _{C}(d_i), \nu _{C}(d_i) \rangle : d_i \in D\right\}$ is any unknown pattern. The goal is to categorize pattern C into one of the recognized patterns $P_j$.

There are three approaches to finding the solution to the above problem as folows:

• Similarity measure approach: (Chen et al. 2016b) If S(R,S) represents the similarity between pattern R and S, then C is recognized as pattern $P_{{\bar{j}}}$, where

  $$\begin{aligned} S(C,P_{{\bar{j}}})=\max _{j=1,2,3,\dots ,m} (S(C,P_j)). \end{aligned}$$

• Dissimilarity measure approach: (Kadian and Kumar 2021) If D(R,S) represents the dissimilarity between pattern R and S, then C is recognized as pattern $P_{{\bar{j}}}$, where

  $$\begin{aligned} D(C,P_{{\bar{j}}})=\min _{j=1,2,3,\dots ,m} (D(C,P_j)). \end{aligned}$$

• Accuracy measure approach: If A(R,S) represents the accuracy of pattern R from S, then C is recognized as pattern $P_{{\bar{j}}}$, where

  $$\begin{aligned} A(C,P_{{\bar{j}}})=\max _{j=1,2,3,\dots ,m} (A(C,P_j)). \end{aligned}$$

Boran and Akay (2014) investigated pattern detection using similarity measures, whereas Xiao (2019) investigated pattern detection using dissimilarity measures. We notice from the comparative studies of similarity and dissimilarity measures that neither a similarity measure nor a dissimilarity measure is suitable for every problem of pattern detection. Therefore, for issues involving pattern detection, an alternative model is required. In some pattern detection problems, the proposed accuracy measure may work as an improvement over the existing similarity and dissimilarity measures. In the pattern detection issue, we compare the examples from Boran and Akay (2014) and illustrate the usefulness of the proposed IF-accuracy measure.

Example 4

Let us consider a non-empty finite set $D=\left\{ d_1,d_2,d_3,d_4\right\}$. Let $A_1,A_2,A_3$ be three patterns defined as follows:

$$\begin{aligned} \begin{aligned} A_1&=\left\{ (d_1,0.6,0.1),(d_2,0.7,0.2),(d_3,0.2,0.5),(d_4,0.6,0.3)\right\} ; \\ A_2&=\left\{ (d_1,0.5,0.5),(d_2,0.5,0.3),(d_3,0.6,0.1),(d_4,0.8,0.1)\right\} ; \\ A_3&=\left\{ (d_1,0.0,0.0),(d_2,0.4,0.2),(d_3,0.3,0.3),(d_4,0.5,0.4)\right\} . \\ \end{aligned} \end{aligned}$$

Let the unknown pattern C be defined as follows:

$$\begin{aligned} C=\left\{ (d_1,0.1,0.0),(d_2,0.5,0.2),(d_3,0.4,0.3),(d_4,0.7,0.2)\right\} . \end{aligned}$$

Our current goal is to classify the unknown pattern C as one of the patterns $A_1,A_2$ or $A_3$.

Boran and Akay (2014) used a similarity-measure approach to solve this problem of pattern detection. Results are computed in Table 5.

Table 5 Measures of similarity between known and unknown patterns given in Example 4

From Table 5, we found that the similarity measures $S_C$ (Fan and Zhangyan 2001), $S_{HB}$ (Mitchell 2003), $S_{HY}^1$ (Hung and Yang 2004), $S_{HY}^2$ (Hung and Yang 2004) and $S_{HY}^3$ (Hung and Yang 2004) are not able to recognize the pattern C, but similarity measures $S_H$ (Hong and Kim 1999), $S_O$ (Li et al. 2002) and $S_e^P$ (Liang and Shi 2003) easily recognize the pattern C.

Further, Xiao (2019) used a dissimilarity measure approach to find the solution of the same example. Results are computed in Table 6.

Table 6 Measures of dissimilarity between known and unknown patterns given in Example 4

From Table 6, we found that the dissimilarity measures $l_{eh}$ (Yang and Chiclana 2012), $l_h$ (Grzegorzewski 2004) and $d^2_Z$ (Zhang and Yu 2013) are not able to classify pattern C, but dissimilarity measures $d_E$ (Wang and Xin 2005), $d^1_Z$ (Zhang and Yu 2013) and $d_1$ (Wang and Xin 2005) easily classify the pattern C.

Now, we use the accuracy measure approach and apply the proposed accuracy measure to the given patterns. The values calculated are: $K^{I}_{accy}(C,A_1)=0.2914$, $K^{I}_{accy}(C,A_2)=0.2406$ and $K^{I}_{accy}(C,A_3)=0.1932$. Pattern C is categorized into the pattern $\hbox {A}_1$ using the proposed accuracy measure. As a result, the proposed accuracy measure technique works well for this pattern detection problem.

4.2 IF-information measure

For any IF-set R, we can define an IF-information measure $E^A_I$ as follows:

$$\begin{aligned} \begin{aligned} E^A_I(R)&= 1 - K^A_I(R), \\&= 1 - \frac{(\sqrt{2}-1)^{-1} }{t} \sum _{i=1}^{t} \left[ \sqrt{1+\left( \mu _{R}(d_i)-\nu _{R}(d_i)\right) ^2}-1\right] . \end{aligned} \end{aligned}$$

(50)

We now test the proposed IF-information measure’s validity.

Theorem 5

Let $R=\left\{ \langle d_i, \mu _{R}(d_i), \nu _{R}(d_i) \rangle : d_i \in D\right\}$ is a member of IFS(D) for a finite set D$\left( \ne \phi \right)$. Define a mapping $E^A_I:IFS(D)$ $\rightarrow$ $\left[ 0,1\right]$ given in Eq. (50). Then, $E^A_I$ is a valid IF-information measure if it satisfies the following axioms, (E1)-(E4):

(E1):

$E^A_I(R)=1$ $\Leftrightarrow$ $\mu _{R}(d_i)=\nu _{R}(d_i)$ $\forall$ $d_i \in D$, i.e., R is most IF-set.

(E2):

$E^A_I(R)=0$ $\Leftrightarrow$ $\mu _{R}(d_i)=0$, $\nu _{R}(d_i)=1$ or $\mu _{R}(d_i)=1$, $\nu _{R}(d_i)=0$ $\forall$ $d_i \in D$, i.e., R is a crisp set.

(E3):

$E^A_I(R)$ $\le$ $E^A_I(S)$ $\Leftrightarrow$ R $\subseteq$ S.

(E4):

If $R^{c}$ represents the complement of R, then $E^A_I(R)=E^A_I(R^{c})$.

Proof

It is simple to confirm that the information measure given in Eq. (50) adheres to the aforementioned axioms. $\square$

4.3 Similarity measure in intuitionistic fuzzy environment

For $R,S \in$ IFS(D), we can define a similarity measure as follows:

$$\begin{aligned} \Im _m(R,S)=1-|K^A_I(R)-K^A_I(S)|. \end{aligned}$$

(51)

Now we examine the proposed similarity measure’s validity in an intuitionistic fuzzy environment.

Theorem 6

Let $R,S,T \in$ IFS(D) for a finite set D$\left( \ne \phi \right)$. Define a mapping $\Im _m:IFS(D) \times IFS(D)$ $\rightarrow$ $\left[ 0,1\right]$ given in Eq. (51). Then, $\Im _m$ is considered to be an IF-similarity measure if it meets the four axioms (S1)-(S4) listed below:

(S1):

$0 \le \Im _m(R,S) \le 1$.

(S2):

$\Im _m(R,S)=\Im _m(S,R)$.

(S3):

$\Im _m(R,S)=1 \Leftrightarrow R=S$.

(S4):

If $R \subseteq S \subseteq T$, then $\Im _m(R,S) \ge \Im _m(R,T)$ and $\Im _m(S,T) \ge \Im _m(R,T)$.

Proof

We verify the axioms (S1)-(S4) as follows:

(S1).:

Since, we know that values of proposed knowledge measures $K^A_I(R)$ and $K^A_I(S)$ lies in [0,1], therefore, $0 \le |K^A_I(R)-K^A_I(S)| \le 1$, and hence the axiom (S1).

(S2).:

From Eq. (51), we can say that $\Im _m(R,S)=\Im _m(S,R)$.

(S3).:

From Eq. (51), we have

$$\begin{aligned} \begin{aligned} \Im _m(R,S)=1&\Leftrightarrow 1-|K^A_I(R)-K^A_I(S)|=1,\\&\Leftrightarrow |K^A_I(R)-K^A_I(S)|=0, \\&\Leftrightarrow K^A_I(R)=K^A_I(S), \\&\Leftrightarrow \mu _{R}(d_i)=\mu _{S}(d_i) \text { and } \nu _{R}(d_i)=\nu _{S}(d_i), ~\forall d_i \in D, \\&\Leftrightarrow R=S. \end{aligned} \end{aligned}$$

(S4).:

Let $R,S,T \in$ IFS(D) be s.t. $R \subseteq S \subseteq T$,

$$\begin{aligned} \begin{aligned}\Rightarrow & \mu _{R}(d_i) \le \mu _{S}(d_i) \le \mu _{T}(d_i) \text { and } \\ & \nu _{R}(d_i) \ge \nu _{S}(d_i) \ge \nu _{T}(d_i), \text { } \forall d_i \in D, \\ \Rightarrow & K^A_I(R) \ge K^A_I(S) \ge K^A_I(T), \\ \Rightarrow & K^A_I(R)-K^A_I(T) \ge K^A_I(R)-K^A_I(S), \\ \Rightarrow & |K^A_I(R)-K^A_I(T)| \ge |K^A_I(R)-K^A_I(S)|, \\ \Rightarrow & 1- |K^A_I(R)-K^A_I(T)| \le 1-|K^A_I(R)-K^A_I(S)|, \\ \Rightarrow & \Im _m(R,T) \le \Im _m(R,S). \end{aligned} \end{aligned}$$

Similarly, we can prove that $\Im _m(S,T) \ge \Im _m(R,T)$.

$\square$

Thus, the measure defined in Eq. (51) is a valid similarity measure. If two IF-sets provide equal knowledge, then the proposed similarity measure attains its maximum value, i.e., 1. This set up the potency of the proposed similarity measure.

Example 5

If D={d} and $R,S \in$ IFS(D) s.t. $R= \left\{ d, \mu _{R}(d), \nu _{R}(d) \right\}$ and $S= \left\{ d, 0.5, 0.5\right\}$, where $\mu _R$ is the membership and $\nu _R$ is non membership function, respectively. Thus, Fig. 2 represents the amount of similarity in IF-sets R and S corresponding to different values of $\mu$ and $\nu$. From Fig. 2, the following points are easy to understand:

• Boundedness i.e., $0 \le \Im _m(R,S) \le 1$.

• $\Im _m(R,S)=1$ when $R=S$.

• Symmetry i.e., $\Im _m(R,S)=\Im _m(S,R)$.

Fig. 2

Proposed Similarity measure

4.4 Dissimilarity/distance measure in intuitionistic fuzzy environment

For $R,S \in$ IFS(D), we can define a dissimilarity measure as follows:

$$\begin{aligned} \zeta _m(R,S)=|K^A_I(R)-K^A_I(S)|. \end{aligned}$$

(52)

Now we examine the proposed dissimilarity measure’s validity in an intuitionistic fuzzy environment.

Theorem 7

Let $R,S,T \in$ IFS(D) for a finite set D$\left( \ne \phi \right)$. Define a mapping $\zeta _m:IFS(D) \times IFS(D)$ $\rightarrow$ $\left[ 0,1\right]$ given in Eq. (52). Then, $\zeta _m$ is considered to be an IF-dissimilarity/distance measure if it meets the four axioms (D1)-(D4) listed as follows:

(D1):

$0 \le \zeta _m(R,S) \le 1$.

(D2):

$\zeta _m(R,S)=\zeta _m(S,R)$.

(D3):

$\zeta _m(R,S)$=0 $\Leftrightarrow$ $R=S$.

(D4):

If $R \subseteq S \subseteq T$, then $\zeta _m(R,S) \le \zeta _m(R,T)$ and $\zeta _m(S,T) \le \zeta _m(R,T)$.

Proof

We verify the axioms (D1)-(D4) as follows:

(D1).:

Since, $K^A_I(R) \in [0,1] \forall R \in$ IFS(D), therefore,  $0 \le |K^A_I(R)-K^A_I(S)| \le 1$, and hence the axiom (D1).

(D2).:

From Eq. (52), it is easy to say that $\zeta _m(R,S)=\zeta _m(S,R)$.

(D3).:

From Eq. (52), we have

$$\begin{aligned} \begin{aligned} \zeta _m(R,S)=0&\Leftrightarrow |K^A_I(R)-K^A_I(S)|=0,\\&\Leftrightarrow K^A_I(R)=K^A_I(S), \\&\Leftrightarrow \mu _{R}(d_i)=\mu _{S}(d_i) \text { and } \nu _{R}(d_i)=\nu _{S}(d_i), \text { } \forall d_i \in D, \\&\Leftrightarrow R=S. \end{aligned} \end{aligned}$$

(S4).:

Let $R,S,T \in$ IFS(D) are s.t. $R \subseteq S \subseteq T$,

$$\begin{aligned} \begin{aligned}&\Rightarrow \mu _{R}(d_i) \le \mu _{S}(d_i) \le \mu _{T}(d_i) \text { and } \nu _{R}(d_i) \ge \nu _{S}(d_i) \ge \nu _{T}(d_i), \text { } \forall d_i \in D, \\&\Rightarrow K^A_I(R) \ge K^A_I(S) \ge K^A_I(T), \\&\Rightarrow K^A_I(R)-K^A_I(T) \ge K^A_I(R)-K^A_I(S), \\&\Rightarrow |K^A_I(R)-K^A_I(T)| \ge |K^A_I(R)-K^A_I(S)|, \\&\Rightarrow \zeta _m(R,T) \ge \zeta _m(R,S). \end{aligned} \end{aligned}$$

Similarly, we can prove that $\zeta _m(S,T) \le \zeta _m(R,T)$.

$\square$

Thus, the measure defined in Eq. (52) is a valid dissimilarity measure. If two IF-sets provide equal knowledge, then the proposed dissimilarity measure attains its minimum value, i.e., 0. This set up the potency of the proposed dissimilarity/distance measure.

Example 6

If D={d} and $R,S \in$ IFS(D) s.t. $R= \left\{ d, \mu _{R}(d), \nu _{R}(d) \right\}$ and $S= \left\{ d, 0.5, 0.5\right\}$, where $\mu _R$ is the membership and $\nu _R$ is non membership function, respectively. Thus, Fig. 3 represents the amount of dissimilarity in IF-sets R and S corresponding to different values of $\mu$ and $\nu$. From Fig. 3, the following points are easy to understand:

• Boundedness i.e., $0 \le \zeta _m(R,S) \le 1$.

• $\zeta _m(R,S)=0$ when $R=S$.

• Symmetry i.e., $\zeta _m(R,S)=\zeta _m(S,R)$.

Fig. 3

Proposed Dissimilarity measure

5 Proposed intuitionistic fuzzy knowledge, similarity and dissimilarity measure-based modified VIKOR approach

In the present section, applications of the proposed IF-knowledge measure, similarity, and dissimilarity measure are provided in MCDM issues.

In MCDM problems, we try to choose the best alternative out of all those that are accessible. Multiple criteria are used to describe a variety of real-world issues. This model must meet the following requirements:

• (i). A group of all the alternatives.

• (ii). A defined group of criterions.

• (iii). Weights of the defined Attributes/Criteria weights.

• (iv). Variables that might change the priority given to each alternative.

5.1 The proposed approach

Opricovic (1998) studied an approach, named VIKOR approach to tackle MCDM issues. In terms of aggregation function and normalizing technique, VIKOR differs from TOPSIS. In the TOPSIS approach, an alternative that is nearer to the positive ideal solution and farthest from the negative ideal solution is chosen as the best alternative (see Chen et al. 2016a). This could prefer to make a choice that maximizes the profit and minimize the cost. Furthermore, in the VIKOR, the precise assessment of “Closeness” to the positive ideal solution is employed to select the best alternative.

Fig. 4

Flowchart representing steps of the proposed approach

5.2 Proposed IF-similarity and dissimilarity measure-based modified VIKOR approach

The similarity and dissimilarity-based modified VIKOR technique for the MCDM issue with the IF-knowledge measure may be provided. It is inspired by the traditional VIKOR approach and its extensions. Consider a MCDM issue in which ${\mathcal {M}}_L=\left\{ L_i\right\} _{i=1}^r$ is a collection of all the alternatives and ${\mathcal {M}}_T=\left\{ T_j\right\} _{j=1}^s$ is a collection of criteria. Let ${\mathcal {R}}_P=\left\{ P_d\right\} _{d=1}^n$ is a set of resource persons that are involved to give their opinion for an alternative under certain criteria. Let ${\mathcal {W}}_C=\left\{ c_j\right\} _{j=1}^s$ represent the criteria weight corresponding to the attributes $T_j$ s.t. $\sum _{j=1}^{s} c_j =1$. Figure 4 represents the working steps of the proposed approach. The proposed VIKOR approach includes the following steps:

• Step 1: Create assessment information: We may create the following decision matrix (Table 7) in an intuitionistic fuzzy environment after receiving the resource person’s responses for a criterion of a certain alternative:

  Table 7 Decision matrix in Intuitionistic Fuzzy environment $DM_{r \times s}$

  where $\mu _{ij}$ is the degree with which $L_i$ alternative satisfy $T_j$ criteria and $\nu _{ij}$ is the degree with which $L_i$ alternative do not satisfy $T_j$ criteria.

• Step 2: Compute normalized decision matrix: We can normalize the fuzzy decision matrix as follows

  $$\begin{aligned} \begin{aligned} M&= \left\{ m_{ij}\right\} , \\&={\left\{ \begin{array}{ll} \langle \mu _{ij}, \nu _{ij} \rangle &{}\quad \text {Benefit criteria} \\ \langle \nu _{ij}, \mu _{ij} \rangle &{}\quad \text {Cost criteria} \end{array}\right. } \end{aligned} \end{aligned}$$

  (53)

  Also, the amount of knowledge passed is estimated by using Eq. (11).

• Step 3: Compute criteria weights: Criteria weights are calculated by following two approaches:

  (A).:

  For unknown criteria weights: Chen and Li (2010) provided the following approach for determining the criterion weights:

  $$\begin{aligned} c^E_j=\left( 1-FE_{j}\right) /\left( s-\sum _{j=1}^{s}FE_{j}\right) ,\forall j=1,2,\dots ,s; \end{aligned}$$

  (54)

  where $FE_{j}= \sum _{i=1}^{r}E(L_i,T_j)$ $(\forall j=1,2,\dots ,s)$. In this case, $E(L_i,T_j)$ stands for the fuzzy information measure of the alternative $L_i$ equivalent to the criteria $T_j$. Knowing that the ideas of fuzzy information measure and fuzzy knowledge measure complement each other, we apply the following formula to get the criteria weights:

  $$\begin{aligned} c^K_{j}=\frac{FK_{ij}}{\sum _{j=1}^{s}FK_{ij}}, \forall j=1,2,\dots ,s; \end{aligned}$$

  (55)

  where $FK_{ij}=\sum _{i=1}^{r} K(L_i,T_j)$ and $K(L_i,T_j)$ is the knowledge obtained from the alternative $L_i$ analogous to criteria $T_j$.

  (B).:

  For partially known criteria weights: Resource persons may not always be able to offer their opinions in the form of exact statistics in real-world circumstances. This could be as a result of lack of time, inability to understand the issue domain, etc. So, resource persons like to give their opinions in the form of intervals in this sort of difficult circumstance. We compile the information delivered by resource persons in the set ${\bar{I}}$. Also, the total quantity of knowledge is found by the formula given as follows

  $$\begin{aligned} FK_{j}= \sum _{i=1}^{r} K(m_{ij}); \end{aligned}$$

  (56)

  where

  $$\begin{aligned} \begin{aligned} K(m_{ij})&= K^A_I (L_i,T_j), \\&= \frac{{(\sqrt{2}-1)^{-1}} {\left[ \sqrt{1+\left( \mu _{ij}-\nu _{ij}\right) ^2}-1\right] }}{t},\\&\qquad \forall i=1,2,3,\dots ,r,j=1,2,3,\dots ,s. \\ \end{aligned} \end{aligned}$$

  (57)

  Thus, optimum criteria weights are calculated as follows

  $$\begin{aligned} \begin{aligned} max({\mathcal {F}})&= \sum _{j=1}^{s} (c^K_j)(FK_{j}), \\&= \sum _{j=1}^{s}\left( c^K_j\sum _{i=1}^{r} K(m_{ij})\right) , \\&= \left( \sqrt{2}-1\right) ^{-1} \\&\quad \sum _{i=1}^{r} \sum _{j=1}^{s} \left[ c^K_j\left( \frac{\sqrt{1+\left( \mu _{ij}-\nu _{ij}\right) ^2}-1}{t}\right) \right] ; \end{aligned} \end{aligned}$$

  (58)

  where $c^K_j \in {\bar{I}}$ and $\sum _{j=1}^{s} c^K_j=1.$

  Hence, the criteria weights obtained by Eq. (58) are given as follows

  $$\begin{aligned} \arg \max ({\mathcal {F}})= \left( C_1,C_2,\dots ,C_s\right) ^{{\mathcal {T}}}; \end{aligned}$$

  (59)

  where $^{\mathcal {T}}$ represents the transpose of the matrix.

• Step 4: Compute Best and Worst ideal solutions: Now, we find the ideal solutions. Let ${\mathcal {B}}=\left\{ {\mathcal {B}}_1,{\mathcal {B}}_2,\dots , {\mathcal {B}}_s\right\}$ and ${\mathcal {W}}=\left\{ {\mathcal {W}}_1,{\mathcal {W}}_2,\dots ,{\mathcal {W}}_s\right\}$ are two sets of best and worst ideal solutions respectively. We can find the values of the best and worst ideal solutions as follows

  $$\begin{aligned} {\mathcal {B}}_j= & {} {\left\{ \begin{array}{ll} \langle \max \nolimits _{\{i\}} \mu _{ij}, \min \nolimits _{\{i\}} \nu _{ij} \rangle &{} \text { Benefit criteria} \\ \langle \min \nolimits _{\{i\}} \mu _{ij}, \max \nolimits _{\{i\}} \nu _{ij} \rangle &{} \text { Cost criteria} \end{array}\right. } \end{aligned}$$

  (60)
  $$\begin{aligned} {\mathcal {W}}_j= & {} {\left\{ \begin{array}{ll} \langle \min \nolimits _{\{i\}} \mu _{ij}, \max \nolimits _{\{i\}} \nu _{ij} \rangle &{} \text { Benefit criteria} \\ \langle \max \nolimits _{\{i\}} \mu _{ij}, \min \nolimits _{\{i\}} \nu _{ij} \rangle &{} \text { Cost criteria} \end{array}\right. } \end{aligned}$$

  (61)

• Step 5: Compute best and worst ideal similarity matrices: By using the formula of similarity measure given in Eq. (51), we can find the value of similarity measure of the best ideal solution ${\mathcal {B}}$ and normalized decision matrix M for each attribute, find the value of similarity measure of the worst ideal solution ${\mathcal {W}}$ and normalized decision matrix M for each attribute, and compute the best ideal matrix B and worst ideal matrix W under similarity measure as follows

  $$\begin{aligned} B= \left\{ b_{ij}\right\} _{r \times s} \text { and } W= \left\{ w_{ij}\right\} _{r \times s} \end{aligned}$$

  (62)

  where $b_{ij}=\Im _m({\mathcal {B}}_j,m_{ij}), w_{ij}=\Im _m({\mathcal {W}}_j,m_{ij})$.²

• Step 6: Compute similarity measure solutions: We can find the similarity measure solution $Y^+$ which is nearest to the best ideal solution and similarity measure solution $Y^-$ which is farthest to the best ideal solution and find the similarity measure solution $Z^+$ which is nearest to worst ideal solution and similarity measure solution $Z^-$ which is farthest to worst ideal solution as follows

  $$\begin{aligned} \begin{aligned} Y^+=\left\{ y^+_1,y^+_2,\dots ,y^+_s\right\} , Y^-=\left\{ y^-_1,y^-_2,\dots ,y^-_s\right\} ,\\ Z^+=\left\{ z^+_1,z^+_2,\dots ,z^+_s\right\} , Z^-=\left\{ z^-_1,z^-_2,\dots ,z^-_s\right\} ; \end{aligned} \end{aligned}$$

  (63)

  where $y^+_j=\max _{\{i\}}b_{ij}$, $y^-_j=\min _{\{i\}}b_{ij}$, $z^+_j=\max _{\{i\}}w_{ij}$, $z^-_j=\min _{\{i\}}w_{ij}, (j=1,2,3,\dots ,s)$.

• Step 7: Compute normalized best & worst group utility and individual regret values: We can find the values of normalized nearest best ideal group utility $\mathcal{B}\mathcal{U}_i$ and normalized nearest best ideal individual regret $\mathcal{B}\mathcal{R}_i$ as follows

  $$\begin{aligned} \mathcal{B}\mathcal{U}_i= & {} \sum _{j=1}^s c^K_j \frac{y^+_j-b_{ij}}{y^+_j-y^-_j},\nonumber \\ \mathcal{B}\mathcal{R}_i= & {} \max _{\{j\}}\left( c^K_j \frac{y^+_j-b_{ij}}{y^+_j-y^-_j}\right) , \forall i=1,2,3,\dots , r. \end{aligned}$$

  (64)

  Similarly, we can find the values of normalized nearest worst ideal group utility $\mathcal{W}\mathcal{U}_i$ and normalized nearest worst ideal individual regret $\mathcal{W}\mathcal{R}_i$ as follows

  $$\begin{aligned} \mathcal{W}\mathcal{U}_i= & {} \sum _{j=1}^s c^K_j \frac{z^+_j-w_{ij}}{z^+_j-z^-_j},\nonumber \\ \mathcal{W}\mathcal{R}_i= & {} \max _{\{j\}}\left( c^K_j \frac{z^+_j-w_{ij}}{z^+_j-z^-_j}\right) , \forall i=1,2,3,\dots , r. \end{aligned}$$

  (65)

• Step 8: Compute nearest best and worst ideal VIKOR indices: we can find the values of VIKOR indices ${\mathcal {V}}^P_i$ that are nearest to best ideal solutions and VIKOR indices ${\mathcal {V}}^N_i$ that are nearest to worst ideal solutions as follows

  $$\begin{aligned} \begin{aligned} {\mathcal {V}}^P_i&= \lambda \frac{\mathcal{B}\mathcal{U}_i-\min _{\{i\}}\mathcal{B}\mathcal{U}_i}{\max _{\{i\}}\mathcal{B}\mathcal{U}_i-\min _{\{i\}}\mathcal{B}\mathcal{U}_i} \\&\quad + (1-\lambda ) \frac{\mathcal{B}\mathcal{R}_i-\min _{\{i\}}\mathcal{B}\mathcal{R}_i}{\max _{\{i\}}\mathcal{B}\mathcal{R}_i-\min _{\{i\}}\mathcal{B}\mathcal{R}_i}, \forall i=1,2,3,\dots , r, \\ {\mathcal {V}}^N_i&= \lambda \frac{\mathcal{W}\mathcal{U}_i-\min _{\{i\}}\mathcal{W}\mathcal{U}_i}{\max _{\{i\}}\mathcal{W}\mathcal{U}_i-\min _{\{i\}}\mathcal{W}\mathcal{U}_i} \\&\quad + (1-\lambda ) \frac{\mathcal{W}\mathcal{R}_i-\min _{\{i\}}\mathcal{W}\mathcal{R}_i}{\max _{\{i\}}\mathcal{W}\mathcal{R}_i-\min _{\{i\}}\mathcal{W}\mathcal{R}_i}, \forall i=1,2,3,\dots , r. \end{aligned} \end{aligned}$$

  (66)

  In general, the value of weightage ($\lambda$) is used to be 0.5.

• Step 9: Compute Correlation factor for proximity: We can find the value of correlation factor ${\mathcal {C}}^c_i$ for each alternative $L_i$ as follows

  $$\begin{aligned} {\mathcal {C}}^c_i=\frac{{\mathcal {V}}^P_i}{{\mathcal {V}}^P_i+{\mathcal {V}}^N_i}, \forall i=1,2,3,\dots ,r. \end{aligned}$$

  (67)

  After calculating the value of the correlation factor, we arrange the list of correlation factors of each alternative in increasing order. Smaller the value of the correlation factor for an alternative, the better the performance of that alternative.

  ${{\textbf {Note:}}}$ Also, if we use the proposed dissimilarity measure in place of the similarity measure, then the greater the value of the correlation factor for an alternative, the better the performance of that alternative.

5.3 Numerical example

University selection for higher education: Take an example of a student looking for the best university for his higher education. After initial scrutiny, a student has shortlisted five universities as alternatives say $L_1,L_2,L_3,L_4$ and $L_5$. He has established twelve criteria’s $T_1,T_2,\dots ,T_{12}$ defined in Table 8. In Fig. 5, a basic framework is given.

Table 8 Definitions of Criteria

Fig. 5

Basic framework of MCDM

The student has taken the help of ten resource persons $P_1,P_2,P_3,\dots , P_{10}$ from various education-related fields to choose the best alternative. Table 9 provides the details about the profession and experiences of the resource persons involved in the proposed MCDM issue. The basic framework of the MCDM issue is shown in Fig. 6.

Fig. 6

Framework of the proposed MCDM issue

Table 9 Profession and Experiences of Resource persons

Now, we solve the given MCDM issue by using the proposed model. There are the following steps involved:

• Case 1. For unknown criteria weights

  • Step 1: We collect the responses from all the resource persons about a criterion corresponding to a particular alternative. Table 10 provides the details about the responses collected from the resource persons.

    Compile the responses supplied by all resource persons, and the resulting decision matrix is displayed in Table 11.

    In this matrix, M = $m_{ij}=\langle \mu _{ij}, \nu _{ij} \rangle$, $\mu _{ij}$ represents the ratio of total number of all the resource persons that support alternative $L_i$ w.r.t. criteria $T_j$ to the total resource persons involved and $\nu _{ij}$ represents the ratio of total number of all the resource persons that don’t support alternative $L_i$ w.r.t. criteria $T_j$ to the total resource persons involved. The amount of knowledge passed by each individual criteria is also provided in Table 11.

  • Step 2: Because all of the criteria involved are benefit criteria, therefore normalized matrix is the same as presented in Table 11.

  • Step 3: The criterion weights are calculated. Let us say that the criterion weights are unknown. Then, by using Eq. (55), we have

    $$\begin{aligned} {\mathcal {W}}_C= & {} \left\{ 0.0441,0.0899, 0.0414, 0.1035, 0.0417,\right. \\{} & {} 0.0849, 0.0876, 0.1104, 0.0780, 0.0479, \\{} & {} \left. 0.1202, 0.1504\right\} . \end{aligned}$$

  • Step 4: We can determine the best and worst ideal solutions provided by Eqs. (60) and (61) as given below:

    $$\begin{aligned} \begin{aligned} {\mathcal {B}}&=\{ \langle 0.6,0.3 \rangle , \langle 0.7,0.1 \rangle , \langle 0.6,0.3 \rangle , \langle 0.7,0.1 \rangle , \\&\quad \langle 0.6,0.3 \rangle , \langle 0.6,0.2 \rangle , \langle 0.8,0.2 \rangle , \langle 0.7,0.2 \rangle ,\\&\quad \langle 0.6,0.2 \rangle , \langle 0.6,0.2 \rangle , \langle 0.8,0.1 \rangle , \langle 0.7,0.2 \rangle \}.\\ {\mathcal {W}}&=\{ \langle 0.3,0.5 \rangle , \langle 0.3,0.6 \rangle , \langle 0.4,0.5 \rangle , \langle 0.4,0.4 \rangle , \\&\quad \langle 0.3,0.5 \rangle , \langle 0.3,0.5 \rangle , \langle 0.3,0.4 \rangle , \langle 0.3,0.4 \rangle , \\&\quad \langle 0.3,0.6 \rangle , \langle 0.3,0.4 \rangle , \langle 0.4,0.5 \rangle , \langle 0.2,0.5 \rangle \}. \end{aligned} \end{aligned}$$

  • Step 5: Using the Eq. (62), we calculate best ideal matrices ${\mathcal {B}}$ and worst ideal matrices ${\mathcal {W}}$ under similarity measure as follows

    $$\begin{aligned} B= \left[ \begin{array}{cccccccccccc} 0.9057 &{} 0.6108 &{} 0.8937 &{} 0.8837 &{} 0.9415 &{} 1 &{} 0.6108 &{} 0.9010 &{} 0.8261 &{} 1 &{} 1 &{} 0.8213 \\ 0.9415 &{} 1 &{} 1 &{} 0.6108 &{} 1 &{} 0.9203 &{} 1 &{} 0.7629 &{} 1 &{} 0.8618 &{} 0.4793 &{} 1 \\ 1 &{} 0.5988 &{} 1 &{} 0.6466 &{} 0.8937 &{} 0.8618 &{} 0.6108 &{} 0.7629 &{} 0.8618 &{} 0.8140 &{} 0.4793 &{} 0.7629 \\ 0.9415 &{} 0.6466 &{} 0.8937 &{} 0.7848 &{} 0.9057 &{} 0.8618 &{} 0.6108 &{} 1 &{} 0.9203 &{} 0.8261 &{} 0.4793 &{} 1 \\ 0.9057 &{} 0.5988 &{} 0.8937 &{} 0.5988 &{} 0.9415 &{} 0.8618 &{} 0.6108 &{} 0.7150 &{} 0.8618 &{} 0.8140 &{} 0.5151 &{} 0.7629 \\ \end{array}\right] \end{aligned}$$

    and

    $$\begin{aligned} W= \left[ \begin{array}{cccccccccccc} 0.9642 &{} 0.9057 &{} 0.9880 &{} 0.7150 &{} 1 &{} 0.8618 &{} 1 &{} 0.8261 &{} 0.9057 &{} 0.8261 &{} 0.4793 &{} 1 \\ 1 &{} 0.7051 &{} 0.9057 &{} 0.9880 &{} 0.9415 &{} 0.9415 &{} 0.6108 &{} 0.9642 &{} 0.9203 &{} 0.9642 &{} 1 &{} 0.8213 \\ 0.9415 &{} 0.8937 &{} 0.9057 &{} 0.9522 &{} 0.9522 &{} 1 &{} 1 &{} 0.9642 &{} 0.9415 &{} 0.9880 &{} 1 &{} 0.9415 \\ 1 &{} 0.9415 &{} 0.9880 &{} 0.8140 &{} 0.9642 &{} 1 &{} 1 &{} 0.7271 &{} 1 &{} 1 &{} 1 &{} 0.8213 \\ 0.9642 &{} 0.8937 &{} 0.9880 &{} 1 &{} 1 &{} 1 &{} 1 &{} 0.9880 &{} 0.9415 &{} 0.9880 &{} 0.9642 &{} 0.9415 \\ \end{array}\right] \end{aligned}$$

  • Step 6: The similarity measure solutions $Y^+,Y^-,Z^+,Z^-$ can be found by using Eq. (63) and their values are given as below

    $$\begin{aligned} \begin{aligned} Y^+&= \left\{ 1,1,1,0.8837, 1, 1, 1,1, 1, 1, 1, 1 \right\} , \\ Y^-&= \left\{ 0.9057, 0.5988, 0.8937, 0.5988, \right. \\&\quad 0.8937, 0.8618, 0.6108, 0.7150, 0.8261, \\&\quad \left. 0.8140, 0.4793, 0.7629 \right\} , \\ Z^+&=\left\{ 1, 0.9415, 0.9880, 1, 1, 1, 1, 0.9880, 1, 1, 1, 1 \right\} , \\ Z^-&=\left\{ 0.9415, 0.7051, 0.9057, 0.7150, \right. \\&\quad 0.9415, 0.8618, 0.6108, 0.7271, 0.9057,\\&\quad \left. 0.8261, 0.4793, 0.8213 \right\} . \end{aligned} \end{aligned}$$

  • Step 7: By using Eq. (64), the calculated values of normalized nearest best ideal group utility $\mathcal{B}\mathcal{U}_i$ and normalized nearest best ideal individual regret $\mathcal{B}\mathcal{R}_i$ for each alternative, are shown below

    $$\begin{aligned} \begin{aligned} \mathcal{B}\mathcal{U}_1&= 0.5129, \mathcal{B}\mathcal{U}_2 =0.4231, \mathcal{B}\mathcal{U}_3 =0.8626,\\ \mathcal{B}\mathcal{U}_4&=0.5941, \mathcal{B}\mathcal{U}_5 =0.9570; \\ \mathcal{B}\mathcal{R}_1&= 0.1133, \mathcal{B}\mathcal{R}_2 =0.1202, \mathcal{B}\mathcal{R}_3 =0.1504, \\ \mathcal{B}\mathcal{R}_4&= 0.1202, \mathcal{B}\mathcal{R}_5 = 0.1504. \end{aligned} \end{aligned}$$

    Similarly, by using Eq. (65), the calculated values of normalized nearest worst ideal group utility $\mathcal{W}\mathcal{U}_i$ and normalized nearest worst ideal individual regret $\mathcal{W}\mathcal{R}_i$ for each alternative, are shown below

    $$\begin{aligned} \begin{aligned} \mathcal{W}\mathcal{U}_1&= 0.5435, \mathcal{W}\mathcal{U}_2 = 0.5372, \mathcal{W}\mathcal{U}_3 = 0.2661, \\ \mathcal{W}\mathcal{U}_4&= 0.3539, \mathcal{W}\mathcal{U}_5 =0.1543; \\ \mathcal{W}\mathcal{R}_1&= 0.1202, \mathcal{W}\mathcal{R}_2 = 0.1504, \mathcal{W}\mathcal{R}_3 = 0.0493, \\ \mathcal{W}\mathcal{R}_4&= 0.1504, \mathcal{W}\mathcal{R}_5 = 0.0493. \end{aligned} \end{aligned}$$

  • Step 8: By using Eq. (66), the values of VIKOR indices ${\mathcal {V}}^P$ and ${\mathcal {V}}^N$ for each alternative, are shown below

    $$\begin{aligned} \begin{aligned} {\mathcal {V}}^P_1&= 0.0841, {\mathcal {V}}^P_2 = 0.924, {\mathcal {V}}^P_3 = 0.9116, \\ {\mathcal {V}}^P_4&= 0.2525, {\mathcal {V}}^P_5 = 1, \\ {\mathcal {V}}^N_1&= 0.8505, {\mathcal {V}}^N_2 = 0.9918, {\mathcal {V}}^N_3 = 0.1436, \\ {\mathcal {V}}^N_4&= 0.7564, {\mathcal {V}}^N_5 = 0. \end{aligned} \end{aligned}$$

  • Step 9: From Eq. (67), the calculated values of correlation factors ${\mathcal {C}}^c_i$ for each alternative, are shown below

    $$\begin{aligned} {\mathcal {C}}^c_1= & {} 0.09, {\mathcal {C}}^c_2 = 0.0852, {\mathcal {C}}^c_3 = 0.8639, \\ {\mathcal {C}}^c_4= & {} 0.2503, {\mathcal {C}}^c_5 = 1. \end{aligned}$$

    Fig. 7 represents the graphical representation of the values of correlation factors ${\mathcal {C}}^c_i$ w.r.t. each alternative

    We compile the values of nearest best ideal VIKOR indices ${\mathcal {V}}^P_i$, nearest worst ideal VIKOR indices ${\mathcal {V}}^N_i$, correlation factor ${\mathcal {C}}^c_i$ and ranks for each alternative by using proposed similarity measure and proposed dissimilarity measure in Table 12. Figure 8 and Fig. 9 represent these values under similarity measure and dissimilarity measure respectively.

    The preference order of the alternatives is given by

    $$\begin{aligned} {\left\{ \begin{array}{ll} L_2 \succ L_1 \succ L_4 \succ L_3 \succ L_5 &{} \text {for proposed similarity measure} \\ L_2 \succ L_4 \succ L_1 \succ L_3 \succ L_5 &{} \text {for proposed dissimilarity measure} \end{array}\right. } \end{aligned}$$

    (68)

    In both cases, we get $L_2$ as the most preferable alternative.

  Now, we take a sensitivity analysis for the different values of weightage ($\lambda$). The value of $\lambda$ lies between 0 and 1. We take the different values of $\lambda$ starting from 0 and ending with 1 with step interval 0.1. The values of correlation factor under the proposed similarity measure for different values of $\lambda$’s are shown in Table 13 and diagrammatical representation is given in Fig. 10. Further, The values of the correlation factor under the proposed dissimilarity measure for different values of $\lambda$’s are shown in Table 14, and diagrammatical representation is given in Fig. 11.

• Case 2. For partially known criteria weights

  Resource persons are not in a position to assign criterion weights in the form of numbers since there are so many real-world issues involved. Under these circumstances, intervals are used to distribute the weights of the criterion. Let us have a look at the MCDM issue mentioned above with partially known criterion weights. Let the following details be provided for the weights of the criteria:

  $$\begin{aligned} \bar{I}= {\left\{ \begin{array}{ll} 0.02 \le c^K_1 \le 0.06, 0.05 \le c^K_2 \le 0.10, 0.02 \le c^K_3 \le 0.06, 0.08 \le c^K_4 \le 0.12, \\ 0.02 \le c^K_5 \le 0.06, 0.05 \le c^K_6 \le 0.10, 0.05 \le c^K_7 \le 0.10, 0.10 \le c^K_8 \le 0.14, \\ 0.05 \le c^K_9 \le 0.10, 0.02 \le c^K_{10} \le 0.06, 0.10 \le c^K_{11} \le 0.14, 0.13 \le c^K_{12} \le 0.18. \\ \end{array}\right. } \end{aligned}$$

  (69)

  The data in Eq. (69) should be interpreted as follow

  $$\begin{aligned} \begin{aligned} {\mathcal {F}}_{max}&= 0.0452 c^K_1 + 0.0922 c^K_2 + 0.0425 c^K_3 + 0.1062 c^K_4 + 0.0428 c^K_5 + 0.0871c^K_6 + 0.0899 c^K_7 + 0.1133 c^K_8 \\&\quad + 0.0800 c^K_9 + 0.0492 c^K_{10} + 0.1233 c^K_{11} + 0.1544 c^K_{12}; \\&\quad \text {subjected to conditions} {\left\{ \begin{array}{ll} 0.02 \le c^K_1 \le 0.06, \\ 0.05 \le c^K_2 \le 0.10, \\ 0.02 \le c^K_3 \le 0.06, \\ 0.08 \le c^K_4 \le 0.12, \\ 0.02 \le c^K_5 \le 0.06, \\ 0.05 \le c^K_6 \le 0.10, \\ 0.05 \le c^K_7 \le 0.10, \\ 0.10 \le c^K_8 \le 0.14, \\ 0.05 \le c^K_9 \le 0.10, \\ 0.02 \le c^K_{10} \le 0.06, \\ 0.10 \le c^K_{11} \le 0.14, \\ 0.13 \le c^K_{12} \le 0.18. \\ \sum _{i=1}^{12} c^K_i=1. \end{array}\right. } \end{aligned} \end{aligned}$$

  (70)

  Using MATLAB software to solve Eq. (70), the following result is obtained:

  $$\begin{aligned} \begin{aligned} c^K_1&=0.06, c^K_2= 0.10, c^K_3= 0.06, c^K_4= 0.1, \\ c^K_5&=0.05, c^K_6=0.08, c^K_7=0.06, c^K_8= 0.1, \\ c^K_9&= 0.1, c^K_{10}= 0.06, c^K_{11}=0.1, c^K_{12}=0.13. \end{aligned} \end{aligned}$$

  (71)

  We again acquire $L_2$ as a more preferred alternative by solving in the same way that case ${\textbf {(}}1)$ was solved.

Table 10 Responses given by the Resource persons for each alternative

Table 11 Intuitionistic fuzzy decision matrix $D_{5 \times 12}$

Fig. 7

Correlation factors for proximity for each alternative

Table 12 Computed VIKOR indices, Correlation factors, and Ranks

Fig. 8

Nearest best & worst ideal VIKOR indices, correlation factor and ranks in case of the proposed Similarity measure

Fig. 9

Nearest best & worst ideal VIKOR indices, correlation factor and ranks in case of proposed Dissimilarity measure

Table 13 Sensitive analysis for different values of $\lambda$ under proposed similarity measure

Fig. 10

Sensitive analysis under proposed similarity measure

Table 14 Sensitive analysis for different values of $\lambda$ under proposed dissimilarity measure

Fig. 11

Sensitive analysis under proposed dissimilarity measure

The aforementioned technique may be used to resolve a variety of MCDM issues that occur in real-world contexts, including the following:

• (I). A person wants to pick a restaurant in a city for a party. The selection criteria are (A) Costs, (B) Location, (C) Quality of food, (D) Comfort, and (E) Other services.

• (II). A student wishes to pick one of the six offered subjects. Student selection factors include (A) The availability of the teacher, (B) The number of seats available, (C) the Student’s interest in the subject, and (D) the Topic’s future.

• (III). A principal wants to choose a teacher for his school. There are the following criteria that the principal created: (A) Education, (B) Experience, (D) Communication skill, (D) Age, (E) Previous record (if any).

• (IV). A company wants to develop tourism in India. Some factors might have an impact on it. They are (A) Community interest, (B) Funds availability, (C) Development of infrastructure, and (D) Support of government.

5.4 Comparison and discussion

To test the usefulness of the proposed approach, we solve the example described in Table 11 utilizing other approved methodologies from the literature. Among the popular techniques are as follows:

$\checkmark$:

Hwang and Yoon (1981) proposed TOPSIS (Technique for Order Preference by Similarity to Ideal Solutions) approach.

$\checkmark$:

Ye (2010a) proposed Decision-making approach (DMA).

$\checkmark$:

Verma and Sharma (2014) proposed DMA.

$\checkmark$:

Singh et al. (2020) proposed DMAs by using three knowledge measures.

$\checkmark$:

Farhadinia (2020) proposed DMAs by using four knowledge measures.

$\checkmark$:

Farhadinia (2020) proposed DMA by using knowledge measure studied by Nguyen (2015).

$\checkmark$:

Farhadinia (2020) proposed DMA by using knowledge measure studied by Guo (2015).

To compare the outcomes of several approaches with the outcomes of the proposed approach in intuitionistic fuzzy environment, we generate Table 15 and Fig. 12.

Table 15 Comparison of proposed modified VIKOR approach with other known approaches in the literature

Fig. 12

Comparison of the proposed approach with other known approaches

According to the TOPSIS approach, the best alternative is the one that is the furthest away from the worst solution and closest to the best solution. Opricovic and Tzeng (2004) contrasted the VIKOR approach to the TOPSIS approach, arguing that it is not always correct that the alternative closest to the best solution is likewise the alternative farthest from the worst solution. Ye (2010a) merely took into account the relationships between alternatives and the optimal alternative. In certain specific situations, being close to the optimum answer may be advantageous, but not always, as this might result in the loss of crucial information. As a result, the output suggested by Ye (2010a) technique is not particularly trustworthy. Verma and Sharma (2014) developed an approach to solve MCDM issues in an intuitionistic fuzzy environment based on the weighted intuitionistic fuzzy inaccuracy measure. Singh et al. (2020) gave an approach to tackle MCDM issues by utilizing three different knowledge measures. Farhadinia (2020) gave an approach to finding the solution to the MCDM issue by using four different measures. He also uses the measures proposed by Nguyen (2015) and Guo (2015) to solve the same MCDM issue. The proposed problem suggests five different alternatives out of which the $L_2$ alternative is the best alternative by all given approaches as suggested by Table 15. As a result, the output of the proposed approach is trustworthy.

6 Conclusion

In this study, an IF-knowledge measure is suggested and is checked for validation. The IF-knowledge measure proposed in this work is found to be an effective option for handling problems with structured linguistic variables, the calculation of ambiguity for two different IF-sets, and the computation of objective weights. To show the efficacy of the proposed IF-knowledge measure, its comparison with several well-known IF-information and knowledge measures is taken. Three examples are provided in the current study to evaluate the efficacy of the proposed IF-knowledge measure. In addition, four new measures are proposed and validated namely accuracy measure, information measure, Similarity measure, and Dissimilarity measure in intuitionistic fuzzy environment. We use the proposed IF-accuracy measures in pattern detection. Also, an example of pattern detection is given to compare the performance of some other measures with the proposed accuracy measure. To tackle MCDM issues, proposed knowledge measure, similarity measure, and dissimilarity measure based modified VIKOR approach based is proposed, and it is discovered that the results were quite encouraging. To illustrate its efficacy, a numerical example with a comparison is given. The proposed approach has great promise since it can find the best alternative that almost perfectly meets all the criteria. It also gives professionals advice on what factors make a particular alternative less successful. Further, the proposed approaches make it simple to see why some alternatives are preferable to others in terms of making decisions. The proposed approach does not require more complex calculations and may be assessed and used for a wide range of intuitionistic fuzzy scenarios. Hesitant Fuzzy set; Interval-valued Intuitionistic Fuzzy set; Picture Fuzzy set; and Neutrosophic Fuzzy set are all included in the scope of expansion of the proposed measure. The suggested knowledge, accuracy, similarity, and dissimilarity measures may be applied to many areas including feature recognition, voice recognition, and image thresholding.