SChoA: a newly fusion of sine and cosine with chimp optimization algorithm for HLS of datapaths in digital filters and engineering applications

Abstract

The Chimp optimization algorithm (ChoA) inspired by the individual intelligence and sexual motivation of chimps in their group hunting, which is separate from the another social predators. Generally, it is developed for trapping in local optima on the complex functions and alleviate the slow convergence speed. This algorithm has been widely applied to find the best optima solutions of complex global optimization tasks due to its simplicity and inexpensive computational overhead. Nevertheless, premature convergence is easily trapped in the local optimum solution during search process and is ineffective in balancing exploitation and exploration. In this paper, we have developed a modified novel nature inspired optimizer algorithm based on the sine–cosine functions; it is called as sine–cosine chimp optimization algorithm (SChoA). During this research, the sine–cosine functions have been applied to update the equations of chimps during the search process for reducing the several drawbacks of the ChoA algorithm such as slow convergence rate, locating local minima rather than global minima, and low balance amid exploitation and exploration. Experimental solutions based on 23-standard benchmark and 06 engineering functions such as welded beam, tension/compression spring, pressure vessel, multiple disk clutch brake, planetary gear train and digital filters design, etc. demonstrate the robustness, effectiveness, efficiency, and convergence speed of the proposed algorithm in comparison with others.

1 Introduction

In the last few decades, optimization is a hot topic in each and every field of research. Researchers are developing the best-to-best optimizer algorithms for complex issues of engineering, statistics, mathematics, computer science, medical fields, and many more [1,2,3,4,5,6,7]. In general, the optimization is identified as the process of selecting the best possible optima solutions for a given function/or problem globally or almost globally. Most issues in the real world can be seen as problems of optimization [8,9,10,11,12]. Day by day, the demand of every field faces several complex issues related to real-world optimization problems [13,14,15,16]. Frankly, the high performing algorithms are required for fulfilling the future complex issues. Therefore, the researchers are trying to develop highly effective optimization algorithms for these kinds of issues. So that these algorithms fulfill the future complex issue requirements. In general, the optimization method has been applied to find the accurate best solution of the optimization problems which are mostly deterministic that suffer from various drawbacks or major issues like that unbalanced exploitation or exploration, local optima, slow convergence, premature convergence, and the need to derivate search space [17].

The interest of the researcher of the different fields is growing in the nature inspired techniques in the last few years due to these drawbacks [18, 19]. Often, mainly of the real applications in dissimilar fields/or domain like that tuning of machine learning parameters, engineering, pattern recognition, clustering, bio-medical, digital filtering, computer science, statistics, applied mathematics, image processing, etc., are severely non-linear, linear, not continuous, so it includes complex constraints and many design variables. Furthermore, there is no guarantee of searching a best and possible optima solution in the search space as well as often failing to solve such kinds of complex functions [20]. Being these reasons, the real-world problems motivate the scientists to originate an effective and alternative highly robust optimization algorithm to find the solutions of these. In this regard, the various robust optimizer algorithms suffer from some drawbacks in finding the solution for complex functions, and hence, nature inspired algorithms [21, 22] is considered as the most widely used among the algorithms for solving the optimization problems recently.

With the advantage of the different nature inspired techniques, merge/modified two or various techniques while enhancing their constraints. Several algorithms have failed to prove better convergence performance without modified or hybridization to apply on complex function and enhance its competence. With the strategy of hybridization [23] or modification [24] of the algorithms could be fully improved the exploitation and exploration parts of the algorithm.

A hybrid SSA–PSO algorithm has been developed by Ibrahim et al. [25] to enhance SSA’s exploration and exploitation capacity. The algorithm implemented makes apply of the attributes of the particle swarm optimization algorithm to enhanced the feasibility of the Salp swarm optimization algorithm in searching the best or possible optima solutions. Therefore, the performance of the convergence is increased.

Luis and Arribas [26] have proposed a new approach for the design of digital frequency selective FIR filters using an flowers pollination algorithm (FPA), with a novel multiple fitness function, to get optimized filter coefficients that best approximate ideal specifications.

Ibrahim et al. [27] introduced a segmentation approach using SSA to select the Perfect Threshold for multi-level image segmentation thresholds.

Saha et al. [28] applied Cat Swarm optimization (CSO) approach to determine the best optimal impulse response coefficients of FIR band stop filters, band pass, low pass, high pass, and trying to meet the respective ideal frequency response characteristics.

Liu et al. [29] developed a novel approach merging the salp swarm optimizer algorithm with a local search strategy to classify the passive location of the non-linear Time-Difference-Of-Arrival (TDOA) problem. Numerical and statistical results have proven that salp swarm optimizer has significantly enhanced position precision, fewer control parameters, and more reliable performance verified to particle swarm optimization.

In [30], the effectiveness of employing the swarm intelligence (SI) based and nature inspired algorithm is investigated for determining the optimal global best solutions to the Finite Impulse Response filter design problem.

[31] have been designed a new modified approach and framework for retiming the DSP blocks based on evolutionary computation processes. During this study, the authors have used various algorithms for fair comparison.

In [32], SSA is utilized to train Feed-Forward Neural Networks (FNNs). The planned strategy applies to various conventional classification and regression datasets. Results also appreciate the better and balanced exploitation–exploration properties of the SSA optimization algorithm, making the algorithm favorable for neural network training.

Sahu et al. [33] have been presented a modified version of sine–cosine algorithm-based fuzzy-aided PID controller which is called M-SCA algorithm. In this methodology, the SCA version by improving and updating few mathematical equations which is able of making the balance between exploitation and exploration phase of this version and enhancing the updating quality of generation. On the basis of experiential results has been showed the superior ability in fast convergence rate performance outperform than others.

However, the merits of Chimp optimization algorithm (ChoA) have satisfied the convergence performance, and it has a best balance amid exploitation and exploration. However, this version is not able to solve each type of complex problem during the search process. This algorithm also faces several drawbacks such as premature convergence, slow convergence rate, locating local minima rather than global minima, and low balance amid exploitation and exploration etc.

Considering the above, it is necessary to improve the ChoA algorithm to hide its limitations. Therefore, during this research, the proposed method is introduced from its original Chimp Optimization Algorithm by updating and improving the various mathematical equations by sine–cosine functions, which is able of enhancing the quality of optima outputs, updating quality of iteration, and is also capable to making the balance amid exploitation and exploration phases of the original ChoA algorithm. This concept is helpful in optimization, because they help to generate accurate solutions. The inclusion of these functions in optimization methods helps to increase the diversity of the solutions avoiding the local solutions.

This research introduces a modified version of Chimp Optimizer that combines the features of sine–cosine functions with original ChoA called SChoA algorithm. The idea is to enhance the search process of the original version of ChoA to find the optimal solutions. Different comparisons and experiments are performed between the version to select the one that provide the most accurate solutions. It is noted that, in terms of numerical results, statistical measurements, and convergence curves, the SChoA algorithm trapped the best optima solutions verified with the competitor versions. To sum up, the major contributions of this work are:

• 1. Sine–cosine functions are applied to tackle with the drawbacks of original ChoA algorithm to enhance its convergence performance.

• 2. SChoA is developed for solving complex single objective optimization problems.

• 3. The experimental solutions and convergence graphs are demonstrate the superiority of the proposed algorithm in solving single objective complex optimization problems.

The rest of the paper is organized as follows: In Sect. 2, the literature review is presented. In Sect. 3, preliminaries of various methods including the basic of Chimp Optimization Algorithm Salp swarm algorithm (SSA) are introduced. Section 4 explains the proposed SChoA algorithm. Section 5 discusses and analyzes the obtained experimental results. In Sect. 6, the proposed algorithm is tested on engineering problems. Finally, Sect. 7 provides conclusion and future work for this paper.

2 Literature review

In the literature, the meta-heuristic techniques are classified in different phases such as (1) evolutionary Algorithms (EA), but not SI, (2) swarm intelligence (SI), includes nature inspired optimizer algorithms that mimic the social behavior of groups of birds, human, animals and plants, (3) natural phenomenon algorithms (NP), imitates the chemistry and physical principles also, includes methods inspired by human behavior but neither SI nor EA [34].

For fulfilling the demand of the complex issues of different fields, the researchers are developing the robust modified or hybrid nature nature techniques [35], such as genetic algorithm (GA) [36], and particle swarm optimization (PSO) [37], Salp swarm optimization [38] , sine cosine algorithm [39], Harris Hawks Optimization (HHO) [40], suggested chaotic SSA (CSSA) [41], binary version of the SSA named BSSA [42], and many more [43]. Furthermore, the recently hybrid and modified version has been reported.

Alresheedi et al. [44] combined the SSA and sine cosine algorithm (SCA) with the means of improving MOPS techniques (MOSSASCA) to find a suitable solution for virtual machine location problem. The main purpose of the proposed MOSSASCA is to mitigate infringements of service quality, reduce power usage, and increase the average time before an agent termination, as well as minimize tension between the three goals. In SCA, a local search technique is followed to increase SSA’s performance to increase convergence speed and avoid being trapped in a local optimum solution. In a set of experiments, there were different digital and physical devices to test the performance of the combined algorithm. Well-known methods of MOP were compared with MOSSASCA’s findings. Results show a compromise between achieving the three goals.

In [45], a least-squares support vector machine (LS-SVM) model was suggested by Zhao et al. to predict carbon dioxide emissions ($\text {CO}_2)$using the principles of SVM. Compared to the other selected models, the proposed model showed more predictive performance. The numerical results showed the great superiority and ability of the SSA–LSSVM model to improve the accuracy and reliability of predicting emissions of $\text {CO}_2$.

SSA can approximate the optimum solution with high convergence, but the search for the optimum solution that affects the efficiency of the algorithm is not yet advantageous to SSA. To that this impact and boost its capacity and efficacy, Sayed et al. [41] suggested chaotic SSA (CSSA) by combining SSA with chaos algorithm. Chaos has recently been used a novel numerical approach to improve the execution of meta-heuristic approaches. Chaos is described as a simulation for non-linear [46] self-motivated conduct. Meta-heuristic method populations have the same advantages as scalable approach, simplicity, and reduced computational time. However, there are two intrinsic weaknesses in these approaches; low convergence rate and local optima recession.

Features selection (FS) problems with binary parameters are considering binary problems. Al-Zoubi and Mirjalili [47] introduced two versions of binary SSA. The SSA is transformed from continuous to binary in the first iteration using eight separate transfer functions (TFs). SSA is built into a crossover operator in the second version. In addition, the best search agent (leader) of SSA is updated to facilitate exploration using the crossover operator while maintaining the main mechanism of this algorithm.

Qu et al. [48] have been proposed improved SCA algorithm by Greedy Levy mutation. This algorithm adopts the method of linear decreasing inertia weight to better balance the global searching and both exponential decreasing conversion parameter and local development ability of the algorithm. On the basis of simulation results prove that existing method can it has faster convergence speed and effectively avoid falling into the local optimum, and higher optimization accuracy.

While the original study of Salp algorithm was proposed to solve continuous problems, and it cannot be applied to binary problems directly, Rizk and Hassanien [42] proposed a new binary version of the SSA named BSSA to enhance the exploration and exploitation capabilities by modifying Arctan transformation. This modification has two features regarding the transfer function, namely multiplicity and mobility. The proposed BSSA is compared among four variants of transfer functions for solving global optimization problems. Furthermore, the non parametric statistical test based on Wilcoxon’s rank-sum is carried out to judge statistically the significant of the obtained results among the different algorithms. The results affirm the superior performance of the modified BSSA variant over the other variants as well as the existing approaches regarding solution quality.

A novel method based on the new moth flame optimizer technique has been developed by Mohammad Reza Esmaeili et al. [49]. After applying this method in synthesizing digital filters, it was observed that compared to the genetic algorithm-based and the Particle Swarm Optimization-based techniques, it exhibited a higher ability to reach an optimal solution under the same initial conditions (the initial population and the same number of iteration)

Gholizadeh and Sojoudizadeh [50] have developed a modified version of the SCA algorithm known as Modified SCA algorithm (MSCA). The proposed strategy combines with two computational strategies during its search process, such that, first, a kind of elitism is utilized by substituting a number of worst solutions of the current population with some variants of the global best optima solution, and second, a mutation operation is performed to increase the probability of searching the best global optimum solution. Experimental results showed that the proposed algorithm is able to give the highly accurate or fast convergence results than others.

3 Chimp optimization algorithm (ChoA)

A new nature inspired algorithm known as Chimp optimization algorithm (ChoA) has been developed by Khishe et al. [51]. This strategy is inspired by individual intelligence and sexual motivation of chimps in their group hunting. It is different from the other social predators. During this methodology, four different phases have been used for simulating diverse intelligence such as attacker, barrier, chaser, and driver, etc.

The mathematical model of this proposed algorithm has been described as following step by step:

The driving and chasing the target or prey is illustrated by the following mathematical equations (Eqs. ((1)–(2)):

$$\begin{aligned}&D=\left| c.a_{\mathrm{prey}} (n) -ma_{\mathrm{chimp}} (n)\right| \end{aligned}$$

(1)

$$\begin{aligned}&a_{\mathrm{chimp}} (n+1)=a_{\mathrm{prey}}-a.d, \end{aligned}$$

(2)

where n is represented the total number of iterations, and c, m, and a are the coefficient vectors. The coefficients c, m, and a are calculated by Eqs. [(3)–(4)]:

$$\begin{aligned} a= & {} 2.l.r_1-l \end{aligned}$$

(3)

$$\begin{aligned} c= & {} 2.r_2 \end{aligned}$$

(4)

$$\begin{aligned} m= & {} \mathrm{chotic}_{\mathrm{value}}, \end{aligned}$$

(5)

where $r_1$ and $r_2$ are random values in range of $\left[ 0,1 \right]$, m is represented the chotic vector, and l is reduced non-linearly from 2.5 to 0 through the iteration process.

During this step has been implemented the behavior of the chimps mathematically. Here, it assumes that the initial solution is available by the attacker, driver, barrier, and chaser which are better informed about the location of the target. In the next iteration, four of the other optima solutions yet obtained are stored and the rest of the chimps are forced to update their own location according to the best chimp locations. This process have been illustrated by the following mathematical Eqs. (6)–(9):

$$\begin{aligned}&d_{\mathrm{attacker}}=\left| c_1a_{\mathrm{attacker}}-m_1.x \right| \end{aligned}$$

(6)

$$\begin{aligned}&d_{\mathrm{barrier}}=\left| c_2a_{\mathrm{barrier}}-m_2.x \right| \end{aligned}$$

(7)

$$\begin{aligned}&d_{\mathrm{chaser}}=\left| c_3a_{\mathrm{chaser}}-m_3.x \right| \end{aligned}$$

(8)

$$\begin{aligned}&d_{\mathrm{driver}}=\left| c_4a_{\mathrm{driver}}-m_4.x \right| . \end{aligned}$$

(9)

When the random vectors are lie between the range of $\left[ -1,1 \right]$, then the next location of a chimp can be in any location amid its present location and the location of the target or prey:

$$\begin{aligned}&x_1=a_{\mathrm{attacker}}-a_1.d_{\mathrm{attacker}} \end{aligned}$$

(10)

$$\begin{aligned}&x_2=a_{\mathrm{barrier}}-a_2.d_{\mathrm{barrier}} \end{aligned}$$

(11)

$$\begin{aligned}&x_3=a_{\mathrm{chaser}}-a_3.d_{\mathrm{chaser}} \end{aligned}$$

(12)

$$\begin{aligned}&x_4=a_{\mathrm{driver}}-a_4.d_{\mathrm{driver}}. \end{aligned}$$

(13)

From the overall equations, the position of the chimps during the search process is updated by the following mathematical Eq. (14):

$$\begin{aligned} x_{n+1}=\frac{x_1+x_2+x_3+x_4}{4}. \end{aligned}$$

(14)

Finally, for the update of the location of the chimps during the search process in the search domain has been applied to the following mathematical equation 15:

$$\begin{aligned} a_{\mathrm{chimp}}\left( n+1 \right) =\left\{ \begin{array}{ll} a_{\mathrm{prey}}\left( n \right) -x.d,&{}\quad \mathrm{if} \; \phi <0.5 \\ \mathrm{chaotic}_{\mathrm{value}}&{}\quad \mathrm{if} \;\phi >0.5. \end{array}\right. \end{aligned}$$

(15)

3.1 3.0.1 Pseudocode of ChoA

The pseudocode of CHoA algorithm is reported in Algorithm 1.

4 The proposed sine–cosine Chimp optimization algorithm (SChoA)

The complex optimization application is challenges for the optimization meta-heuristics. According to the literature, each optimization method could not be able to shows the best solution of all type of complex problems. All algorithms may be faced some drawbacks, so due to these weakness these could failure to find the solution of complex functions.

Therefore, due to the present competitive situations, we are needed most powerful optimization techniques, so that these could tackle complex problems easily. However, these techniques could be tackle complex functions easily if the exploration and exploitation phase of these techniques will be too strong.

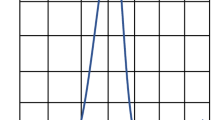
After learning the initial phase of chimp optimization algorithm, here, we are trying to present a newly modified algorithm with the help of sine–sine function functions for the complex optimization functions. The sine and cosine function are helped by the algorithm in fluctuating outward or toward finding the optimal solutions. These functions help to ignore the local optima and force the algorithm for trapping the global optima fastly. The performance of the sine and cosine functions in the search space is illustrated by Fig. 1.

Fig. 1

The performance graph of sine and cosine function

Figure 1 illustrates the present solution which will be away from the target and explore the search domain when the search member moves in $[-2,-1)$ or (1, 2]. Additionally, the present solution will be toward the target and exploit the search domain when the search member moves in $[-1,1]$.

However, the ChoA algorithm is capable to solve various complex optimization functions; nevertheless, it face various drawbacks for trapping the local, global, and explore optima values in the search domain. It could not be fitted for highly complex optimization problems and cannot tackle their several drawbacks such as slow diversity, premature convergence, slow convergence speed, etc. For improving exploitation phase of the standard chimp optimization algorithm, we are trying to incorporate the sine–cosine functions in the position updation equations of the ChoA algorithm, and to improve the weaknesses of standard ChoA version.

In the search domain for identify the accurate and best global optimum for complex optimization functions have been applied this modified algorithm. The chimp optimization algorithm (ChoA) phases operate in the directions of exploration of the optima solution and modified phases have been applied for exploitation of the optima in the search domain. The modification has helped for getting the best global outputs fastly and ignoring the local optima. Due to the impact of this, we have enhanced the convergence rate of the standard ChoA algorithm through this modification.

Furthermore, the mathematical formulation of the SChoA algorithm has been illustrated by the following steps:

• Constants  During the runs of the Matlab code of the algorithms have applied the various parameter settings such as search agents is 30, total number of iterations are 500, and dimension as per Table 15.

• Initialization  In this stage, first, we are initializing the population of the search agents and these are initialized randomly as per the given functions. Where the algorithms assigns a random vector of n dimensional for the ith chimp; $X_i (i=1,2,...,n)$.

• Evaluation  In this stage, the search members of the population are evaluated according to the superiority of the own position in the search space during the search process. After that, the fitness value of each search member is tested through the given objective function and each search member of the crowd during the search process is used these fitness values for locating the new positions in the search space.

• Exploration phase  In this state, the chimps are update their position for the purpose of searching next nearest position of his prey. These position are updated through Eqs. 1–5.

• Exploitation phase  In this phase, the search agent position has been evaluated through modified mathematical equations (Eqs. 16–20). These equations have played an important role for enhancing the exploitation phase for chimps for trapping the best optima values in the search domain during the search process and ignoring the local optima solutions. With the help of this modification chimps could be easily trapped in the optima solutions in the complex space in at least a number of iterations. Additionally, it also helps in reducing the computational time in searching the next best position for the search agents:

  $$\begin{aligned} r_2= & {} (2 \pi )\times rand \end{aligned}$$

  (16)
  $$\begin{aligned} x_1= & {} a_{\mathrm{attacker}}-\cos (r_2)\times a_1.d_{\mathrm{attacker}} \end{aligned}$$

  (17)
  $$\begin{aligned} x_2= & {} a_{\mathrm{barrier}}-\sin (r_2)\times a_2.d_{\mathrm{barrier}} \end{aligned}$$

  (18)
  $$\begin{aligned} x_3= & {} a_{\mathrm{chaser}}-\cos (r_2)\times a_3.d_{\mathrm{chaser}} \end{aligned}$$

  (19)
  $$\begin{aligned} x_4= & {} a_{\mathrm{driver}}-\sin (r_2)\times a_4.d_{\mathrm{driver}}, \end{aligned}$$

  (20)

  where $r_2$ represents the rand number lies between 0 and 1, $x_1$, $x_2$, $x_3$, $x_4$ are update positions of the chimps, and $a_1$, $a_2$, $a_3$, $a_4$ are coefficient vectors, respectively.

• Leader Chimp position The leader chimp position updated through Eq. 14.

• Stopping conditions  Finally, the stopping conditions have been implemented for searching the best possible optima value in the search domain. These conditions have been applied for evaluating the assessment process of the all search agents of the group and replacing the position according to best search agent’s positions. It is repeated again and again until it satisfies the criteria of prevention for example it reaches the highest maximum iterations or the solution is earliest found.

4.1 4.0.1 Pseudocode of modified SChoA algorithm

The pseudocode of SCHoA algorithm is reported in Algorithm 2.

5 Complexity

The complexity of the proposed method is illustrated in the two different following forms;

5.1 Time complexity of SChoA

The computational complexity of the proposed algorithm (SChoA) can be represented as:

$$\begin{aligned} R(v(M(sd+cs+ms^2))), \end{aligned}$$

(21)

where v, s, d, c, m, and L illustrate the number of runs, number of solutions, dimension, cost of objective function, number of objective function, and number of iterations.

5.2 Search space complexity of SChoA

The search space complexity of SChoA algorithm in terms of the memory space depends on the constants or parameters of both the dimension of the given function and the search members. This identifies the amount of space that proposed method needs during the initialization process. Therefore, the search space complexity of proposed method can be illustrated by the mathematical equation as follows:

$$\begin{aligned} R(sd). \end{aligned}$$

(22)

Here, the proposed algorithm also requires additional search space for other constants. However, this extra search space is not critical, and hence, the search space complexity of the proposed algorithm remains within the range of above mathematical equation (Eq. (22)).

6 Results and discussion

To evaluate the convergence and accuracy performance of the proposed SChoA algorithm, a experiential analysis has been performed in this section. For comparison, various robust population-based algorithms, such as MPSO, SCA, PSO, TACPSO, and Chimp, have been used.

Table 1 The optimal solutions obtained on 23-benchmark functions by the SChoA algorithm and the competitors

Fig. 2

Convergence graphs of algorithms on uni-modal functions

Fig. 3

Convergence graphs of algorithms on multi-modal functions

Fig. 4

Convergence graphs of algorithms on fixed dimension multi-modal functions

6.1 Parameter setting and standard benchmark functions

The Matlab 2015a software has been applied for the coding of all algorithms for verifying the performance with each others. In this implementation, have been applied different parameters settings, like total number of iterations 500, search chimps 30, dim, and upper and lower bounds as per as standard functions, respectively.

It is always beneficial to use a set of standard testbeds with different characteristics to conveniently and confidently test the performance of any new optimization algorithm on different standard benchmark problems and compare it with other nature inspired algorithms. The diversity of test problems or functions allows observing and testing the ability of any new optimizer algorithm from different perspectives.

A set of 23-standard functions are applied to demonstrate the performance and efficiency of the SChoA algorithm compared to other existing optimization techniques in the literature. These functions can be divided into three different phases: uni-modal [52], multi-modal [53], and fixed dimension multi-modal [52] functions, respectively. The mathematical details of these functions have been illustrated in “Appendix”. A detailed description of the characteristics of the unimodal ($F_1$–$F_7$), multi-modal ($F_8$–$F_{13}$), and fixed dimension multi-modal functions ($F_{14}$–$F_{23}$) are reported in Table 15 in “Appendix” .

The unimodal problems have only one global optimum with no local optima. These problems are highly suitable to explore the exploitative efficiency and convergence behavior of the new proposed optimization algorithm. Multimodal and fixed-dimension multimodal benchmark test problems face the existence of several local optimum solutions and more than one global optimum.

The landscapes of these benchmark test functions have been showed in 2-D versions through figures, respectively.

To verify the accuracy of the proposed SChoA algorithm have been tested on these 23-test functions as comparison with the other recent algorithms: MPSO, PSO, TACPSO, Chimp, etc. Furthermore, the more analysis of the results of algorithms on these functions has been illustrated through the following sections.

6.2 Experiment and comparison

The simulation must be required to done multiple n-times to evaluate stable numerical and statistical efforts for the performance of the optimizer methods. And for evaluating the stability of the algorithms, every run must be carried out to m number of generations or iterations [54]. In this work, has been applied the same experimental procedure for testing the performance of proposed method. And the accuracy of the results obtained by algorithms has been verified through different categories such as least best minima value, max best value, standard deviation, and mean. Experimental solutions of the algorithms are reported in Table 1, and convergence graphs are illustrated by Figs. 2, 3 and 4.

Here, the accuracy and performance of the SChoA algorithm has been compared with recent algorithms MPSO, PSO, TACPSO, Chimp, etc. in terms of best numerical and statistical outputs.

6.3 Discussion

The standard deviation (SD) and mean measures were used to verify the result output performance of SChoA to those of the Standard ChoA or Chimp and other nature inspired techniques on 23-standard test benchmark problems. All algorithms has run 30 independent times with at least 500 number of iterations on every test suite, to evaluate meaningful solutions. The statistical solutions are computed at the last iteration of each nature inspired approach on each test suite to get the best optimal result and give a highly fair comparison among all comparative nature inspired algorithms.

Furthermore, in the following sections have been illustrated the comparison of proposed algorithm with other algorithms in three different phases; evaluation of uni-modal, multi-modal, and fixed dimension multi-modal test suites.

6.3.1 Assessment of exploitation capability

The uni-modal ($F_1$–$F_7$) functions of 23-test suites have only one global compatibility, so these functions have been used to evaluate the exploitation phase. In Table 1, it can be seen that the SChoA algorithm gives better optimal solutions on these test suites as comparison to others. Experimental solutions of these test suites reveals that the SChoA algorithm has demonstrated better exploitation capabilities than the others. The main motive for these global optima solutions is that the modification by sine–cosine functions in standard chimp optimization algorithm allowed the test suites to reach the best optimum global point. Hence, all simulations have proven that the SChoA algorithm strategy has a robust exploitation behavior which is important for most issues of compatibility that need to be addressed. As mentioned earlier, these functions are most suitable for these standard test suits. The solutions prove that the SChoA algorithm is highly functional.

Additionally, superior to the global results of ChoA algorithm, it is revealed that modification is most successful and effective in providing the best and accurate solutions for complex optimization functions with a single objective phase and reaching best global optima.

6.3.2 Capability assessment

In multimodal ($F_8$–$F_{13}$) and fixed dimension multimodal ($F_{14}$–$F_{23}$) test suits are contains many local optima and the number of design variables increases exponentially with the size of the problem compared to the unimodal function. These functions have the ability to assess the exploration capability of algorithms.

In general, these functions are used to indicate the suitability of the suit meta-heuristics. Here, all outputs in Table 1 show that the SChoA method achieves a higher detection capability and better exploitation capabilities.

6.3.3 Accuracy of the algorithms

The average values obtained by the algorithms are discussed in Table 2. These values has been divided into two different phases, such as (B) is best value and (W) is indicate the worse average value of the algorithm. In general, the least mean values of the algorithm denoted accuracy of the algorithm for the best optimal score. On the basis of table, we notice that the proposed algorithm is providing the least mean values at the maximum number of standard test suits. Hence, SChoA algorithm could be capable to provide the best global optima outputs for complex optimization functions.

Table 2 Comparison of average values of algorithms on 23-benchmark functions

6.3.4 Stability of SChoA algorithm

In this section has been verified the performance of the proposed algorithm through standard deviation (SD) outputs, as shown in the table and illustrated through Fig. 5.

Through Fig. 5, we could be analyzed that the proposed algorithms on the 23-standard benchmark functions are near to zero, and it means that the SChoA algorithm is stable on the given functions that were performed. Furthermore, the least standard scores show the fast convergence performance of the algorithms. Here, it could easily be seen that the SChoA algorithm is able to give the least standard score at maximum test suites outperform than the others. Therefore, it can be concluded that SChoA algorithm convergence speed is faster than others for trapping the best global optimum value during the search process in the search domain.

Fig. 5

The SD values of SChoA algorithm on 23-standard benchmark functions

6.3.5 Convergence graphs analysis and discussion

The convergence performance graphs of uni-modal, multi-modal, and fixed dimension multi-modal test suites have been plotted through Figs. 2, 3 and 4. Please keep in mind that the average best solution for each iteration represents the average best solution found so far in each iteration.

In these graphs, Figs. 2, 3 and 4 could be seen easily that the convergence performance of the SChoA algorithm fall in two categories, such as if trapped the best optima value of the functions at least number of iterations and next, it tends to be accelerated as generation increases. Furthermore, as per Berg et al. [55], this behavior can assurance that a optimization algorithms ultimately converges to a point and finds locally. Therefore, SChoA algorithm is able to improve the fitness of all search chimps in the search domain and guarantee finding superior quality of global optima scores for complex optimization application as iteration increases.

Here, with this reasons, it can be discussed and as per reasoned to the modification of the chimp optimization algorithm. As the search agents move from higher values to global minimum values, so with the assumption of growth in ChoA, the overall chimps and their fitness are improved during the iterations.

Additionally, with the help of this strategy, we save the best value and this value helps to find the next best value to enhance the fitness of entire agents of the group during the search process. Here, we also observed that the SChoA algorithm is capable of getting the higher success rate in searching the optima solution in the complex space during the search space than sine–cosine functions and ChoA algorithm and it finds these goals fast with least number of iterations.

With this modified strategy, which can help the search agents in the initial stages of the iteration to find new regions in the complex space during the search process and enhance the speed for searching the best optima goal with a least number of the iterations.

7 The SChoA algorithm for engineering designs

In this section has been tested the performance of the proposed SChoA algorithm on six-engineering real-world applications such as Welded beam, tension or compression spring, pressure vessel, multiple disk clutch brake, planetary gear train, and digital filters design problems, etc. To optimize the restricted issues of these functions have been compared the proposed method with various recent algorithms. These engineering designs are restricted in equal and in inequality measure. In the proposed methodology during the search process in the search domain the position updated through chimps.

However, between the fitness function of these designs and chimps, no any immediate relationship. On the basis of these designs have been verified the work performance of the proposed algorithm through recent optimizer.

7.1 Welded beam design problem

The objective of this design is decreasing the cost of manufacturing a welded beam, it is shown in Fig. 6. This graph represents a rigid component which is welded on a beam. At the end of the member, a load is applied. Here, we have been finding the values of thickness of weld (h), length of attached part of bar (l), the height of the bar (t), and thickness of the bar (b) for evaluating the minimum price of this function (see Sect. 9.1 in “Appendix”).

The performance of the proposed method has been verified with recent optimization techniques on this design like that CPSO [56], Random [57], GA [58], RO [59], GWO [60], MVO [61], GSA [62] Chimp [51], HSSAHHO [63], and WOA [62]. The experimental solutions of this design are reported in Table 3. All these numerical solutions reveal that the proposed version is capable of giving the highly accurate and least optimal scores as compared to others.

Table 3 The optimal solutions of the algorithms on welded beam design problem

Fig. 6

Welded beam design

7.2 Tension/compression spring design problem

The main objective of this design (see Sect. 9.4 in “Appendix” ) is decreasing the pressure/voltage source weight, as shown in Fig. 7. The subject to constraints of this design has contain some restrictions such as shear stress, floating frequency, and minimum floating deflections. During this research have been applied various recent optimization techniques for the best or accurate possible solution of this design. By literature can be easily analysis that the meta-heuristic most useful for giving the accurate solutions of these kinds of designs. All the simulation outputs obtained through algorithms are reported in Table 4.

During this study, the convergence performance of the proposed method has been verified with various recent techniques such as RO, DE, ES, GA, PSO, GWO, MFO, WOA, GSA, Halton-PSO [64], HSSAHHO [63], and Chimp [51] algorithms, which demonstrates that this algorithm can highly be effective in solving real problems outperform than others.

Table 4 The optimal solutions of the algorithms on tension/compression spring design problem

Fig. 7

Tension/compression spring design

7.3 Pressure vessel design

The main motive of this design (see Sect. 9.3 in “Appendix”) is reducing the construction cost of pressure vessel design, as seen in Fig. 8. This design cost include; associate with geometric parameters of the pressure vessel, shaping, materials, and welding. Therefore, for reaching the least cost for this function, calculations of the optima solutions of the geometric constants are necessary. The mathematical formulation of this design is provided in “Appendix”.

Table 5 provides the optimal solutions of SChoA algorithm and the other meta-heuristics CGA [65], DGA [66], CPSO [67], HPSO [68], CDE [69], CSA [70], WOA-DE [71], WOA-BSA [72], and Chimp [51] algorithm, respectively, for this design.

The solution accuracy of the proposed algorithm is clearly revealed in this design by giving the best or accurate result among the other recent meta-heuristics and is capable of evaluating the best design with the minimum cost.

Table 5 The optimal solutions of the algorithms on pressure vessel design problem

Fig. 8

Pressure vessel design

7.4 Multiple disk clutch brake design

The main objective of this design is to minimize the weight of a multiple disc clutch brake (see Sect. 9.2 in “Appendix” ) by considering various discrete variables such as inner radius, number of friction surfaces outer radius, actuating force, and thickness of discs. This design includes eight different constraints based on operating conditions and the geometry. The global optima solution for this design is f(x) at $X=(70,90,1,810,3)$ with one active constant. This design is represented by Fig. 9.

This design has been compared with various recent optimization algorithms like NSGA-II, TLBO, WCA, APSO [73], SCA [39], FSO [73], EGWO [74], TACPSO [75], MPSO [76], and Chimp [51] algorithms. The comparison to discover the best scores, given by such meta-heuristics, is reported in Table 6, respectively. Simulation results have proven that the proposed algorithm is able to find the best minima solution for this design outperform than others.

Table 6 The optimal solutions of the algorithms on multiple disk clutch brake design problem

Fig. 9

Multiple disk clutch brake design

7.5 Planetary gear train design

The main motive of this design (see Sect. 9.5 in “Appendix”) is to synthesize the gear-teeth number for an automatic planetary transmission system, as shown in Fig. 10: which is used in automobiles to reduce the errors in the gear ratio, Which involved 6 design variables based on the number of teeth in the gears ($N_1$, $N_2$, $N_3$, $N_4$, $N_5$, and $N_6$), respectively, and which can only take specified integer constant values. There are three more design variables such as modules of the gears ($m_1$ and $m_2$) and number of planets gears (P), which can only take specific discrete constant values. In this design, 11 restrictions are considered in subject to constraints.

The numerical and statistical solutions of this design are reported in Tables 7 and 8. In these tables, has been compared the performance of the algorithms in different forms such as best optimal value, minima, maxima, mean, standard deviation and median, respectively. All these simulation results reveal that the proposed algorithm gives the best or accurate solutions for this design than others.

Table 7 The optimal solutions of the algorithms on planetary gear train design problem

Table 8 The statistical solutions of the algorithms on planetary gear train design problem

Fig. 10

Planetary gear train design

7.6 HLS of digital filter design

In this section, we are implementing the proposed strategy for datapaths in digital filters. During designing, the digital filters HLS is highly paramount stage for this. In general, high-level optimization reduces design time at lower levels, leading to better circuit indices [77]. HLS is a stage of very-large-scale integration (VLSI) design where in behavioral description (here the filter’s behavioral characteristic) is converted into a structural characteristic [78, 79].

The high-level synthesis (HLS) is the first step in synthesizing a circuit and data flow graph (DFG) is used to display the behavioral description, which describes the operators’ type and the relationships between them. The hypothetical data flow graph is illustrated by the mathematical Eq. (23):

$$\begin{aligned} Y=(((a+b) \times (c\times d))+((e+f)\times (g\times h)))+((e+f)\times (g\times h)). \end{aligned}$$

(23)

Fig. 11

Data flow graph for Eq. (23)

In Fig. 11, 04 adder and 04 multiplier operators have been used for evaluating the given function (23). Here, 1, 2 and 3, 4 output operators are considered as the inputs operator 5 and 6. Similarly, 5 and 6 output operators are considered as the inputs operator 7 and 7, 8. At the end, 7 output operator is considered as the input operator 8, respectively.

In general, the digital filters are most used for images, videos, digital signal processing, process signals, communication applications, and so on. The finite impulse response (FIR), the infinite impulse response (IIR), the band-pass filter (BPF), the auto regressive filter (ARF), the wave digital filter (WDF), and the elliptic wave filter (EWF) are the digital filters used in this article. The data flow graph of the ARF used in this article is illustrated by Fig. 12 [80].

Fig. 12

The ARF data flow graph

In this phase, the proposed strategy is applying for optimizing chip area, power, and delay in HLS of datapaths in digital filters. The obtained results of the proposed algorithm have been compared with the literature results of MFO [49] and PSO [49]. The working steps of the proposed strategy are illustrated by the following.

• The decision variables of the function are the same as the position of the chimps in the search domain. The position of the chimps can be defined by Eq. (24):

  $$\begin{aligned} C= \begin{bmatrix} c_{1,1} &{} c_{1,2} &{}, ... , &{} c_{1,d}\\ c_{2,1} &{} c_{2,2} &{}, ... , &{} c_{2,d}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ c_{n,1} &{} c_{n,2} &{}, ... , &{} c_{n,d}\\ \end{bmatrix}, \end{aligned}$$

  (24)

  Where n is the number of chimps or search agents and d is a dimension. The fitness values of the chimps or search agents in the search domain can be stored by Eq. (25):

  $$\begin{aligned} FC=\begin{bmatrix} fc_{1} \\ fc_{2} \\ \vdots \\ fc_{n} \\ \end{bmatrix}, \end{aligned}$$

  (25)

  where n is number of search agents or chimps in search domain and $fc_{i}$ represents the fitness values of the $i{\mathrm{th}}$ chimp. In the same way, the other two matrices can be defined for preys by the following equations:

  $$\begin{aligned} P= & {} \begin{bmatrix} p_{1,1} &{} p_{1,2} &{}, ... , &{} p_{1,d}\\ p_{2,1} &{} p_{2,2} &{}, ... , &{} p_{2,d}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ p_{n,1} &{} p_{n,2} &{}, ... , &{} p_{n,d}\\ \end{bmatrix} \end{aligned}$$

  (26)
  $$\begin{aligned} FP= & {} \begin{bmatrix} fp_{1} \\ fp_{2} \\ \vdots \\ fp_{n} \\ \end{bmatrix}, \end{aligned}$$

  (27)

  where n is number of preys, d is the dimension of the function, and $fp_{i}$ is the fitness value of $i^{th}$ prey.

• In the next phase, the new location and distance of the given node is evaluated by Eqs. (16)–(20); these equations denote the new positions of variables of chimp and (1)–(5); these equations indicate the distance amid the position decision variables of the prey and the position of variables of chimp.

• For updating the number of search agents or chimps in each iterations with the objective of enhancing the extractability of the algorithm has used Eq. (28):

  $$\begin{aligned} C_{N}= \left( N-I \right) \times \frac{N}{M_{I}}, \end{aligned}$$

  (28)

  where N is the number of search agents or chimps, I is the current iteration, and $M_{I}$ is the maximum number of iterations. Hence, the search agents or chimps update their positions in the search domain w.r.t. the best prey or goal in the last iterations.

• Fitness function for DFG: For evaluating the area, power, and delay in the proposed hybrid algorithm and verifying its accuracy performance against the results of MFO [49] and PSO [49] algorithms, the following fitness functions are applied:

  $$\begin{aligned} F=w_{1} \times \frac{l_{t}}{l_{\max }}+w_{2} \times \frac{a_{t}}{a_{\max }}+w_{3} \times \frac{p_{t}}{p_{\max }}, \end{aligned}$$

  (29)

  where F denotes the fitness function, $w_{1}$,$w_{2}$,$w_{3}$ represent the weights of the power, delay, and area terms, $l_{t}$ denotes the schedule length of sample evaluated, $a_(t)$ denotes the total number of registers and transistors in the operators, $p_{t}$ denotes the power consumption of operators, $l_{\max }$ denotes the long scheduled length in the current crowd, $a_{\max }$ denotes the largest area in the current crowd, and $p_{\max }$ denotes the highest power in the current crowd, respectively.

Table 9 Results of algorithms on IIR DFG

Table 10 Results of algorithms on FIR DFG

Table 11 Results of algorithms on ARF DFG

Table 12 Results of algorithms on EWF DFG

Table 13 Results of algorithms on BPF DFG

Table 14 Results of algorithms on WDF DFG

Fig. 13

The best solutions for delay, occupied area, and power in HLS of digital filter problem

Further meticulously elaborates on the solutions obtained by the proposed algorithm in the next phase of this section. These solutions have been verified through the literature results obtained by MFO [49] and PSO [49]. The program of the proposed algorithm has been runned on Matlab-R2015a under the system with Intel (R) Core (TM) i3-8130 U processor and 8GM of RAM. During this process, various constant settings have been applied for obtaining the solutions such as number search agents or chimps is 30, maximum number of iterations are 100, and maximum number of sources and operational units are 5, respectively.

The obtained experimental solutions of the HLS of the digital filters are illustrated in Tables 9, 10, 11, 12, 13 and 14. And the best solutions of the proposed algorithm for lowest delay, occupied area, and power are illustrated in Fig. 13. These results have been categorized into three different phases like delay, area, and power. Additionally, all these results evaluated on three different modes $w_1=0.8$, $w_2=1$,$w_3=1$, and $w_1=1$, $w_2=0.8$,$w_3=1$, and $w_1=1$, $w_2=1$,$w_3=0.8$, respectively. For each mode, the mean of the acquired response for a 50-times execution for the proposed method has been tabulated along with their relevant the standard deviation(sd). The point to keep in mind is that, here, the sd for the proposed method has been reported for a comparison and superior presentation of the result due to the power consumption and largeness of the occupied area.

In Tables 9, 10, 11, 12, 13 and 14, all results are represent the best response in terms of the area, power, and delay in the three algorithms . All the results of IIR, FIR, ARF, EWF, BPF, and WDF-DFG have been obtained by replacing the parameter values of the weight ($w_1$, $w_2$, $w_3$) and a significant improvement in the optimal responses of the algorithms observed. For instance, the best delay will be achieved, compared to the other two modes, when assuming a weight of 0.8 for $w_{1}$; this factor is connected to the delay, and assuming a coefficient of 0.1 for $w_{2}$ and $w_{1}$ as the coefficients of the occupied area and power. The same is true for the other two modes.

The proposed hybrid algorithm is a superior than the MFO [49] and PSO [49] algorithms with average values 2899.56 and 3078.4 for the lowest power consumption and occupied area. Similarly, in Table 10, the lowest average values for the delay 8.70, 0.0219, 13.45, 0.4734, 12.26, and 0.213 have been obtained by proposed algorithm than others. These results prove that the proposed method is able to reduced the delay time as comparison to MFO and PSO algorithm for digital filter problem.

Hence, the proposed method is able to provide the best output response in terms of delay, area, and power consumption for high-level synthesis of VLSI circuits.

8 Conclusion

The Chimp optimization algorithm is a most recent population-based meta-heuristic. Chimp optimization (ChoA) could be widely applied to solve complex tasks of different domains due to its inexpensive computational and implementation simplicity overhead. Nevertheless, ChoA is also faced several drawbacks during search process in the search domain like ineffective in balancing exploitation and exploration, premature convergence, and complex multipeak search problems, especially in easily trapped in the local optima results. To overcome the shortcomings of ChoA, a modified chimp optimization algorithm with sine cosine functions is developed to solve single objective functions. In this work, we developed as new update position equations with sine–cosine functions to improving the convergence performance of the search agents during to search process in the search domain. So that, this algorithm could be effectively controlled the local search and convergence to the global optimum result during the search process.

During this extensive investigational research efforts, a huge number of simulations have been carried out for verifying the performance and results accuracy of the proposed SChoA method. Its performance has been verified through 23-benchmark and 06-engineering designs. Experiential solutions proved that SChoA algorithm possesses some superior performance in terms of numerical results, statistical measurements and convergence curves, stability, and robustness, as compared to state-of-the-art PSO and others, such as MPSO, SCA, PSO, TACPSO, and Chimp. Hence, the proposed algorithm can be a good alternative for tackling various complex applications.

Additionally, the proposed strategy is able to successfully solve the HLS of datapaths in digital filters problem in terms of lowest delay, area, and power, respectively, than the other two algorithms.

In future direction, the SChoA can be implemented on complex real-life application problems. The constrained and multi-objective version of SChoA or based feature selection approach for high dimensional with small instance to simultaneously maximize the classification performance and minimize the number of features can be developed also.

Appendix

See Table 15.

1.1 Welded beam design problem

$$\begin{aligned}&\text {Consider }\mathbf {x}=\left[ {{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}} \right] =\left[ h\,l\,t\,b \right] \\&\text {Minimize } f\left( {\mathbf {x}} \right) =1.10471x_{1}^{2}{{x}_{2}}+0.04811{{x}_{3}}{{x}_{4}}\left( 14.0+{{x}_{2}} \right) \\&\text {Subject to: } \\&{{g}_{1}}\left( {\mathbf {x}} \right) =\tau \left( {\mathbf {x}} \right) -13600\le 0 \\&{{g}_{2}}\left( {\mathbf {x}} \right) =\sigma \left( {\mathbf {x}} \right) -30000\le 0 \\&{{g}_{3}}\left( {\mathbf {x}} \right) ={{x}_{1}}-{{x}_{4}}\le 0 \\&{{g}_{4}}\left( {\mathbf {x}} \right) =0.10471\left( x_{1}^{2} \right) +0.04811{{x}_{3}}{{x}_{4}}\left( 14+{{x}_{2}} \right) -5.0\le 0 \\&{{g}_{6}}\left( {\mathbf {x}} \right) =\delta \left( {\mathbf {x}} \right) -0.25\le 0 \\&{{g}_{7}}\left( {\mathbf {x}} \right) =6000-{{p}_{c}}\left( {\mathbf {x}} \right) \le 0 \\&\text {where} \\&\tau \left( {\mathbf {x}} \right) =\sqrt{\left( {{\tau }'} \right) +\left( 2{\tau }'{\tau }'' \right) \frac{{{x}_{2}}}{2R}+{{\left( {{\tau }''} \right) }^{2}}} \\&{\tau }'=\frac{6000}{\sqrt{2}{{x}_{1}}{{x}_{2}}} \\&{\tau }''=\frac{MR}{J} \\&M=6000\left( 14+\frac{{{x}_{2}}}{2} \right) \\&R=\sqrt{\frac{x_{2}^{2}}{4}+{{\left( \frac{{{x}_{1}}+{{x}_{3}}}{2} \right) }^{2}}} \\&j=2\left\{ {{x}_{1}}{{x}_{2}}\sqrt{2}\left[ \frac{x_{2}^{2}}{12}+{{\left( \frac{{{x}_{1}}+{{x}_{3}}}{2} \right) }^{2}} \right] \right\} \\&\sigma \left( {\mathbf {x}} \right) =\frac{504000}{{{x}_{4}}x_{3}^{2}} \\&\delta \left( {\mathbf {x}} \right) =\frac{65856000}{\left( 30\times {{10}^{6}} \right) {{x}_{4}}x_{3}^{3}} \\&{{p}_{c}}\left( {\mathbf {x}} \right) =\frac{4.013\left( 30\times {{10}^{6}} \right) \sqrt{\frac{x_{3}^{2}x_{4}^{6}}{36}}}{196}\left( 1-\frac{{{x}_{3}}\sqrt{\frac{30\times {{10}^{6}}}{4\left( 12\times {{10}^{6}} \right) }}}{28} \right) \\&\text {with } 0.1\le {{x}_{1}},{{x}_{4}}\le 2.0\,and\,0.1\le {{x}_{2}},{{x}_{3}}\le 10.0. \end{aligned}$$

1.2 Tension/compression spring design problem

Consider:

$$\begin{aligned}&\mathbf {x}=\left[ {{x}_{1}}{{x}_{2}}{{x}_{3}} \right] =\left[ d\,D\,N \right] \\&\text {Minimize } f\left( {\mathbf {x}} \right) =\left( {{x}_{3}}+2 \right) {{x}_{2}}x_{1}^{2} \\&\text {subject to: } \\&{{g}_{1}}\left( {\mathbf {x}} \right) =1-\frac{x_{2}^{3}{{x}_{3}}}{71785x_{1}^{4}}\le 0 \\&{{g}_{2}}\left( {\mathbf {x}} \right) =\frac{4x_{2}^{2}-{{x}_{1}}{{x}_{2}}}{12566\left( {{x}_{2}}x_{1}^{3}-x_{1}^{4} \right) }+\frac{1}{5108x_{1}^{2}}-1\le 0 \\&{{g}_{3}}\left( {\mathbf {x}} \right) =1-\frac{140.45{{x}_{1}}}{x_{2}^{2}{{x}_{3}}}\le 0 \\&{{g}_{4}}\left( {\mathbf {x}} \right) =\frac{{{x}_{1}}+{{x}_{2}}}{1.5}-1\le 0 \\&\text {with } 0.05\le {{x}_{1}}\le 2.0,0.25\le {{x}_{2}}\le 1.3,and\,2.0\le {{x}_{3}}\le 15.0. \end{aligned}$$

1.3 Pressure vessel design problem

$$\begin{aligned}&\text {Minimize }f(x)=0.6224{{x}_{1}}{{x}_{3}}{{x}_{4}}+1.7781{{x}_{2}}x_{3}^{2}+3.1661x_{1}^{2}{{x}_{4}}+19.84x_{1}^{2}{{x}_{3}} \\&\text {Subject to: }\\&{{g}_{1}}(x)=-{{x}_{1}}+0.0193x \\&{{g}_{2}}(x)=-{{x}_{2}}+0.00954{{x}_{3}}\,\le 0 \\&{{g}_{3}}(x)=-\pi x_{3}^{2}{{x}_{4}}-(4/3)\pi x_{3}^{3}+1,296,000\le 0 \\&{{g}_{4}}(x)={{x}_{4}}-240\le 0 \\&0\le {{x}_{i}}\le 100,\,\,i=1,2 \\&10\le {{x}_{i}}\le 200,\,\,i=3,4. \end{aligned}$$

1.4 Multiple disk clutch brake design problem

$$\begin{aligned}&\quad \text {Minimize}f(x)=\pi (x_{2}^{2}-x_{1}^{2})x_3(x_5+1)\rho \\&\text {Variable range} \\&x_1 \varepsilon \left\{ 60,61,...,79,80 \right\} \\&x_2 \varepsilon \left\{ 90,91,...,109,110 \right\} \\&x_3 \varepsilon \left\{ 1,1.5,...,3 \right\} \\&x_4 \varepsilon \left\{ 600,610,...,990,1000 \right\} \\&x_5 \varepsilon \left\{ 2,3,...,8,9 \right\} \\&\text {Subject to;} g_1(x)=x_2-x_1-\Delta r \le 0 \\&g_2(x)=L_{\max }-(x_5+1)(x_3+\delta ) \le 0 \\&g_3(x)=p_{\max }-p_{rz}\le 0 \\&g_4(x)=p_{\max }v_{\mathrm{sr},\, \max }-p_{rz}v_{sr}\le 0 \\&g_5(x)=v_{\mathrm{sr}, \max }-v_{sr}\le 0 \\&g_6(x)=M_h-sM_s \le 0 \\&g_7(x)=T \le 0 \\&g_8(x)=T_{\max }-T \le 0 \\&\Delta r =20\,(\mathrm{mm}), I_z = 55\,(\mathrm{kg},\,\mathrm{mm}^2), p_{\max }=1\,(\mathrm{MPa}), T_{max}=15 (\mathrm{s}), \mu =0.50 \\&s=1.50. M_s=40\,(\mathrm{Nm}), M_f=3\,(\mathrm{Nm}), n=250\,(\mathrm{rpm}),v_{\mathrm{sr},\, \mathrm{max}}=10(\frac{m}{s}), L_{\max }=30(mm). \end{aligned}$$

1.5 Planetary gear train design problem

$$\begin{aligned}&\quad \text {Maximize }f(x)=\max \left| i_k-i_{ok} \right| ; k=\left\{ 1,2,R \right\} \\&\mathrm{where} \\&i_1=N_6/N_4 \\&i_{01}=3.11 \\&i_2=\frac{N_6(N_1N_3+N_2N_4)}{N_1N_3(N_6-N_4)} \\&i_{02}=1.84 \\&i_R=-\frac{N_2N_6}{N_1N3} \\&i_{0R}=-3.11 \\&X= \left\{ N_1,N_2,N_3,N_4,N_5,p,m_1,m_2 \right\} , \\&\text {Subject to: }\\&g_1(X)=m_3(N_6+2.5)\le D_{\max } \\&g_2(X)=m_1(N_1+N_2)+m_1(N_2+2) \le D_{\max } \\&g_3(X)=m_3(N_4+N_5)+m_3(N_5+2) \le D_{\max } \\&g_4(X)=\left| m_1(N_1+N_2)-m_3(N_6-N_3) \right| \le m_1+m_3 \\&g_5(X)=(N_1+N_2)\sin \left( \frac{\pi }{p}\right) -N_2-2-\delta _{22} \ge 0 \\&g_6(X)=(N_6-N_3)\sin \left( \frac{\pi }{p}\right) -N_3-2-\delta _{33} \ge 0 \\&g_7(X)=(N_4+N_5)\sin \left( \frac{\pi }{p}\right) -N_5-2 -\delta _{55} \ge 0 \\&g_8(X)=(N_6-N_3)^2+(N_4+N_5)^2-(N_6-N_3)(N_4+N_5)cos(\frac{2\pi }{p}-\beta )\le (N+3+N_5+2+\delta _{35})^2 \\&\mathrm{where} \\&\beta = \frac{\cos ^{-1}(N_6-N_3)^2+(N_4+N-5)^2-(N_3+N_5)^2}{2(N_6-N_3)(N_4+N_5)} \\&g_9(X) = N_6-2N_3-N_4-4-2\delta _{34} \ge 0 \\&g_10(X)=N_6-N_4-2N_5-4-2\delta _{56} \ge 0 \\&h(X)=\frac{N_6-N_4}{p}\,=\, \mathrm{integer},\\&\mathrm{where} \\&D_{\max }=220, p=(3,4,5), m_1,m_3=(1.75,2.0,2.25,2.5,2.75,3.0), \delta _{22},\delta _{33},\delta _{55},\delta _{35},\delta _{56},=0.5\\&17\le N_1 \le 96, 14\le N_2 \le 54, 14\le N_3 \le 51, 17\le N_4 \le 46, \\&14\le N_5 \le 51, 48\le N_6 \le 124, N_i=integer. \end{aligned}$$

Table 15 23-standard benchmark test functions