1 Introduction

Recently, meta-heuristic algorithms have become surprisingly very popular. This is due to proving their superiority in solving many optimization problems. Some of the most popular meta-heuristic algorithms are Particle Swarm Optimization (PSO) [1], Artificial Bee Colony (ABC) [2] and Ant Colony Optimization [3]. Regardless of the different structure of meta-heuristic algorithms, they are divided into two main phases. These phases are exploitation and exploration phases. In exploration phase, an optimizer algorithm can efficiently discover the search space, mostly by randomization. However, during this phase, the population may face abrupt changes. In exploitation phase, an optimizer algorithm converges toward the most promising region. But, in most of the cases, there is no clear boundary between these two phases, which makes meta-heuristic algorithms trapped into local optima. This is due to their stochastic nature and improper balancing between exploration and exploitation. Thus, many studies have been presented to improve the performance of meta-heuristic algorithms and to overcome this problem. Most of these studies used chaotic theory in their system [4,5,6,7].

Chaos is one of the most common mathematical approaches recently employed to boost the performance of meta-heuristic algorithms. It is defined as the simulation of the dynamic behavior of nonlinear systems [8]. Over the years, chaos has attracted a great attention and has been applied in different sciences such as chaos control [9], synchronization [10], optimization researches [11, 12] and so on. Each hyperchaotic system has its own dynamic behavior characteristics, which can be applied on certain applications [13]. Authors in [14] proposed a new chaotic complex model, namely cutting edge chaotic complex L\(\ddot {u}\) system, where a complex nonlinear expression is added to the third equation of the L\(\ddot {u}\) system. Also, the authors present complex antilag synchronization (CALS) schema. They applied their proposed CALS for two indistinguishable chaotic complex systems with different introductory qualities. The results show the effectiveness of their proposed complex system. Authors in [15] proposed another hyperchaotic system, where fractional-order is used. The experimental results show that the effectiveness of their proposed system in terms of equilibrium points, Lyapunov spectrum, and attractor forms. Moreover, the results show that their system exhibits larger Lyapunov exponents compared with other hyperchaotic systems. Authors in [16] applied the ten-term chaotic system without equilibrium on multimedia security application including image encryption and sound steganography. The results show that their system is able to encrypt 128kbit data and hide in sound files. Also, the properties of chaos is embedded with the searching mechanism of meta-heuristic algorithms and applied in different applications. Authors in [17] employed logistic chaotic map with Genetic Algorithm (GA) for encrypting the image. In this approach, the logistic chaotic map is used to encode the initial image, after that GA is applied to improve the encryption results. The simulation results reveal the capability of their approach in avoiding the frequent attacks. Authors in [5] hybridized chaos optimization algorithm (COA) and PSO. The experimental results show that embedding logistic chaotic map can significantly improve the performance of PSO in terms of convergence rate and time oscillation. Another approach based on hybridization with chaotic maps is proposed in [6]. In this approach, the authors employed ten chaotic maps with Biogeography-Based Optimization (BBO). These maps are gauss/mouse, Chebyshev, logistic, iterative, piecewise, sine, singer, circle, sinusoidal and tent chaotic maps. The simulation results show that the proposed chaotic biogeography-based optimization is able to improve the performance of original BBO for both exploration and exploitation. Authors in [18] employed piecewise chaotic map with search iteration of Harmony Search (HS). Their main objective is to minimize makespan for the permutation flow shop scheduling problem with limited buffers. The experimental results show the efficiency of their proposed chaotic harmony search algorithm compared with the original HS and other meta-heuristic algorithms in terms of solution quality and robustness. A modified version of Antlion Optimization Algorithm (ALO) based on chaotic maps, namely Chaotic Antlion Optimization Algorithm (CALO) is proposed in [19]. The authors applied CALO for feature selection problem, where five chaotic maps are employed. These maps are the singer, piecewise, logistic, tent and sinusoidal. The experimental results reveal the capability of CALO to find better feature subset than original ALO and other meta-heuristic algorithms. Authors in [7] proposed Chaotic Crow Search Algorithm (CCSA) for solving feature selection problem. In this approach, ten chaotic maps are employed. The experimental results show that the efficiency of CCSA in finding an optimal feature subset, which maximizes the classification performance, while minimizing the number of selected features.

Feature selection is an essential task for machine learning tasks. Recently, data obviously increases in both number of features and number of instances. Thus, removing irrelevant and noisy features is considered a challenging task especially for large dataset. Feature selection algorithms have proved their efficiency in removing redundant features, reducing computational cost, improving the performance of a classifier and reducing the required storage [20]. Additionally, they have been successfully applied in many applications including image retrieval [21], text categorization [22], customer relationship management [23] and diagnostic medical support systems [24, 25]. Also, feature selection can influence the clustering performance [20]. Moreover, it can further help for better data interpretation and understanding than using all features. Thus, several studies have been presented in literature applying feature selection such as in [20, 26]. From studies, it has been proved that building cluster with relevant features is more interpretable and practical in use than building a cluster with all features, which can include noise and irrelevant features. Feature selection algorithms are divided into two families; wrapper-based and filter-based algorithms. In wrapper-based algorithms, machine learning algorithms are used in evaluation, while statistical methods are used for filter-based algorithms [27]. However, it has been proven that wrapper-based algorithms provide better results compared with filter-based algorithms. However, wrapper-based algorithms are computationally expensive. In addition, filter-based algorithms such as sequential forward selection (SFS) and sequential backward selection (SBS) suffer from entrapment at local optima [27]. On the other hand, meta-heuristic algorithms can find the optimal feature subset through using their agents. Recently, meta-heuristic algorithms are applied for feature selection problem such as Moth-Flame Optimization (MFO) [28], Gray Wolf Algorithm (GWO) [29], Particle Swarm Optimization (PSO) [30] and Artificial Bee Colony (ABC) [31].

In this work, a novel hybridization approach based on Salp Swarm Algorithm (SSA) and chaos theory is proposed. SSA is one of most recently proposed algorithm. It is proposed in 2017 by Mirjalili [32]. The main inspiration of the algorithm came from the swarming behavior of salps. Salps are kind of Salpidae with transparent barrel-shaped body. The inventor of original SSA algorithm, showed that the efficiency of this algorithm compared with other well-know meta-heuristics algorithms. Although, slow convergence speed and entrapment in local optima are two possible problems, similar to other meta-heuristic algorithms. As it is previously mentioned, chaos theory is one of most common methods used to improve the performance of evolutionary algorithms. Currently, to the best of our knowledge, there is no work proposed in literature to improve the exploitation and the exploration of SSA. The main contributions of this paper summarized as follows:

  • A novel hybridization approach based on SSA and chaos theory is proposed.

  • The proposed approach is applied for 14 global optimization problem

  • A binary version of CSSA is proposed and applied for feature selection problem, where 20 benchmark datasets are employed.

  • Ten most popular chaotic maps proposed in literature are employed and compared.

  • Several evaluation criteria are used in evaluation. These criteria are; mean, standard deviation, p-values of the Wilcoxon rank sum, trajectory, search history, average fitness of whole population, convergence curves and average length of the selected feature subset.

  • The performance of the proposed approach is compared with original SSA and five other well-known meta-heuristic algorithms; artificial bee colony (ABC), moth flame optimization (MFO), particle swarm optimization (PSO), chicken swarm optimization (CSO) and gray wolf optimizer (GWO)

The rest of this paper is organized as follow. Section 2 provides a full description of the original SSA algorithm concerning its nature inspiration and mathematical model. Also, the basics of chaotic concepts are illustrated in this section. The novel Chaotic Salp Swarm Algorithm (CSSA) is described in Section 3. Section 4 provides simulation results and discussions along with the used benchmark datasets. Finally, conclusions are presented in Section 5.

2 Basics and background

In this section, the basic knowledge about salp behavior and optimization algorithms based on salp behavior are proposed. In addition, the basic knowledge of chaotic maps is discussed as well.

2.1 Salp swarm algorithm (SSA)

Inspiration analysis

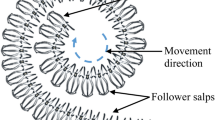
Salp Swarm Algorithm (SSA) is one of meta-heuristic algorithms recently proposed by Mirjalili [32] in 2017. The main inspiration of this algorithm came from the swarming behavior of salps. Salps are kind of Salpidae. They have a transparent barrel-shaped body and similar tissues like jellyfishes. In addition, they move like jellyfish, as the water is pumped through the body as propulsion to move forward. Sometimes, they form a swarm, namely salp chain. However, till now, the reason behind this behavior is not obvious. Some studies refer to this behavior when salps are searching for optimal locomotion based on rapid foraging and coordinated changes.

Mathematical model of SSA

The population of SSA is divided into two groups. These two groups are leader and followers. The leader is the one that taking the position at the front of the chain, while the remainder of salps is known as followers. Let, dim is the number of variables or number of dimensions for a given problem. y is defined as the position of a salp. F denotes the food source, which is the target of the swarm in the search space. The leader updates his position according to the following equation:

$$ {y}_{i}^{1} = \left\{ \begin{array}{ll} F_{i} + r_{1}((ub_{i}-lb_{i})r_{2}+lb_{i}), &\quad r_{3}\geq 0\\ F_{i}-r_{1}((ub_{i}-lb_{i})r_{2}+lb_{i}), &\quad r_{3}< 0 \end{array}\right. $$
(1)

where \({y}_{i}^{1}\) denotes as first salp’s position in i − th dimension, known as leader, lbi,ubi are the lower boundary and upper boundary at i − th dimension, respectively, Fi is the food’s position in i − th dimension and r1, r2 and r3 are random numbers. r1 is responsible for balancing between exploitation and exploration. It is mathematically defined as follows:

$$ r_{1} = 2e^{-\left( \frac{4t}{T}\right)^{2}} $$
(2)

where t is the current iteration number, and T is the maximum number of iterations. r2 and r3 are two random numbers uniformly generated in range [0,1]. r3 is responsible for indicating whether the next position should to be toward negative infinity or positive infinity. The followers update their position according to Newton’s law of motion using the following equation:

$$ {y}_{i}^{j} = \frac{1}{2} \alpha l^{2}+\beta_{0}l $$
(3)

where \({y}_{i}^{j}\) shows the position of j − th follower in i − th dimension, i ≥ 2, β0 is the initial speed, \(\alpha =\frac {\beta _{final}}{\beta {0}}\), \(\beta =\frac {y-y_{0}}{t}\) and l is time. As the time is called an iteration in the optimization process, the discrepancy within iteration equals to one. Let β0 = 0, the updating position of followers in i − th dimension can be represented as follows:

$$ {y}_{i}^{j} = \frac{1}{2}\left( {y}_{i}^{j}+{y}_{i}^{j-1}\right) $$
(4)

2.2 Chaotic maps

Most meta-heuristic algorithms have randomness parameters. These parameters are using probability distribution, usually Gaussian or uniform distributions. Recently, chaos theory used to enhance these parameters [33]. It has the same characteristics as randomness, with better dynamical and statistical characteristics [34]. Chaos is known as a phenomenon. Any change of the initial condition of chaos may lead to non-linear change for the future behavior. Three main properties are describing the chaos; (1) quasi-stochastic, (2) ergodicity and (3) sensitivity to initial conditions. Mixing these characteristics can guarantee the diversity of the generated solutions. Thus, this diversity can be enough to reach every mode of the multi-modal problem [35]. Quasi-stochastic is defined as the ability to replace random variables with values of chaotic maps. Ergodic property refers to the ability of chaotic variables to search non-repeatedly all states within a certain range. Finally, sensitivity to initial condition property is defined as any small change, in the initial starting points, may lead to different behavior. Combining all these properties can significantly boost the performance of meta-heuristic optimization algorithms [36].

In this study, ten distinguished non-invertible maps with different characteristics are used. Table 1 shows these maps, where os denotes the s − th number in the chaotic sequence and s is defined as the index of the chaotic sequence o. The other parameters including c, d, and μ are the control parameters. These parameters are used to determine the chaotic behavior of the dynamic system. From this table, it can be observed that chaotic maps have a determinate form without including random factors. In this work, the initial point (o0) for all adopted chaotic maps is initially set to 0.7. This value is same value used for the same ten chaotic maps in [37].

Table 1 Definition of the ten adapted chaotic maps
Full size table

3 The novel chaotic salp swarm algorithm

In this section, a novel chaotic salp swarm algorithm (CSSA) is proposed where chaotic maps are employed to replace random variables with chaotic variables. The original has mainly three main parameters which affect its performance. These parameters are r1, r2 and r3. As it is shown in (2), r1 is linearly decreased through the iterations, while r3 is responsible for determining whether the next position should to be toward negative or positive infinity. As it can be seen from (1), r2 and r1 are the two main parameters influencing the updating position of a salp. Thus, they significantly impact on balancing between exploration and exploitation. Exploration concentrates on finding new better solutions by investigating the search space on a large scale, while exploitation concentrates on exploiting the data in the local region [7]. An algorithm should properly balance these two components to approximate the global optima. In this study, chaotic maps are employed to adjust a r2 parameter of SSA. Equation (5) shows the updating of r2 parameter according to the chaotic map. Equation (5) shows the updated position of a salp according to the chaotic map, where ot is the obtained value of chaotic map at t − th iteration.

$$ r_{2}=o_{s} $$
(5)
$$ {y}_{i}^{t} = \left\{\begin{array}{ll} F_{i}+r_{1}((ub_{i}-lb_{i})o^{t}+lb_{i}), &\quad r_{3}\geq 0\\ F_{i}-r_{1}((ub_{i}-lb_{i})o^{t}+lb_{i}), &\quad r_{3}< 0 \end{array}\right. $$
(6)

Such embedding chaotic maps into updating position of salp can improve the performance and the convergence rate of SSA as it will be demonstrated later in the following section. The mathematical formula of each used chaotic maps is previously defined at Table 1. In this study, the proposed CCSA is applied not only on 14 unimodal and multimodal benchmark optimization problems but also on feature selection problem. In CSSA feature selection algorithm, the solution pool is restricted to discrete binary form, where positions of salps are restricted to {0,1} [38]. Let a salp position (solution in the search space) y expressed by a i − th-dimensional variable y = [x1,x2,…,xdim], where dim is the maximum number of dimensions. When the value of variable equals to 1, then it means that the corresponding feature is selected and when the value equals to 0, then it means that the corresponding feature is not selected. For example, the feature representation for data have 5 features can be as [1, 0, 0, 1, 1] or [0, 0, 1, 1, 1] and so on. From previous two examples, it can be observed that each solution has different features and each solution has different length. Equation (7) shows how each agent transfers from continues to discrete binary space, where B is random number in range [0,1].

$$ {y}_{i}^{t} = \left\{\begin{array}{ll} 1 &\quad if (s({y}_{i}^{t})) \geq B\\ 0 &\quad otherwise \end{array}\right. $$
(7)

where

$$ s({y}_{i}^{t}) = \frac{1}{1+e^{10\left( {y}_{i}^{t}-0.5\right)}} $$
(8)

Next, the detailed description of the proposed chaotic version of SSA algorithm is presented as follows:-

3.1 Parameters initialization

In the beginning, CSSA starts with randomly initialized salps positions. Then, it initially sets the initial parameters. The lower boundary and upper boundary are initially set respect to the used benchmark function, while for the used benchmark dataset, it initially set the lower boundary to 0 and the upper boundary to 1 for given data. The maximum number of iterations is set for global optimization problem to 500, while 30 for feature selection problem. Finally, the population size is set to 50 for global optimization problem and 20 for feature selection problem. The values of population size and number of iterations are set low for feature selection problem, due to the complexity of the search space.

3.2 Fitness function

Fitness function is used to evaluate each solution (salp position). All the used global benchmark problems are minimization problems. Thus, the solution with the minimum fitness value min(f(X)) is selected as the best solution obtained so far. While for feature selection problem, the optimal solution is the one, which maximizes the classification accuracy, while minimizing the number of selected features. Equation (9) shows the used fitness function for feature selection problem, where these two objectives are combined into one by setting a weight factor. In this equation, Acc is the classification accuracy obtained from K-nearest neighbor (KNN) classifier, where k equals to 3 with mean absolute distance. KNN is one of supervised machine learning algorithms. It classifies the new instance based on distance from the new instance to the training instances [38]. In this work, KNN classifier is used to indicate the goodness of the selected features subset. The selection of K and distance method are based on trial and error method. wf is the weight factor, which used to control the importance of the number of selected features and the classification accuracy. In this study, our goal is to maximize the classification accuracy in the first place then to minimize the number of selected features. Thus, wf is set to 0.8. Lf denotes the length of selected features subset, while Lt denotes the total number of features for a given dataset.

$$ Fn_{t} = maximize \left( w_{f} \times Acc + (1-w_{f}) \times \left( 1-\frac{L_{f}}{L_{t}}\right)\right) $$
(9)

3.3 Positions updating

After evaluating the fitness function of each salp and selecting the best salp position. The best salp position updates its position according to (6), (7), (3) and (4).

3.4 Termination criteria

The process of evaluating each salp and updating the position of best salp will repeat again and again until it reaches to the maximum number of iterations or the optimal solution is early found. In our case, the optimization process terminates when we the maximum number of iteration is met; 50 for global optimization problem and 30 for feature selection problem.

The pseudo code of the proposed CSSA is defined at Algorithm 1.

figure a

4 Simulation results and discussions

In this section, the proposed CSSA algorithm is applied for two problems; global optimization problem and feature selection problem. Section 4.1 discusses the performance of the proposed CSSA for solving the global optimization problem. Moreover, in this section, a comparison between CSSA with different chaotic maps is presented. Section 4.2 compares the performance of the proposed CSSA as feature selection algorithm with other meta-heuristic feature selection algorithms. All the conducted experiments are performed on the same PC with the same specification including Core i3 and RAM 2 GB on OS Windows 7. Moreover, all the experiments are reported on average 30 independent runs.

4.1 CSSA for global optimization problem

This subsection aims to evaluate the performance of the proposed CSSA, to compare CSSA with different chaotic maps and to select the optimal chaotic map. Several measurements are used in this study. These measurements are mean, standard deviation (SD) and p-values of the Wilcoxon rank sum. Also, the search history, the trajectory, the average fitness of all group and the convergence curve are used.

Due to the stochastic behavior of meta-heuristic optimization algorithms, there is a need to employ a set of test function to prove the superiority and efficiency of an algorithm [39]. In this work, several experiments are conducted to evaluate the performance of the proposed CSSA, where two benchmark categories are employed. The mathematical definition and characteristic of the benchmark functions are presented in Tables 12, 13, 14 and 15 in the Appendix section. In these tables, lb denotes the lower boundary of search space, while ub denotes the upper boundary of the search space, opt is defined for the optimal value of a function, and finally, dim is the number of dimensions. For more information of these function, the authors refer to [40,41,42]. The first category, namely unimodal benchmark functions have no local optima and one global optima. This category is used to evaluate the exploitation of the algorithm. The second category known as multimodal benchmark functions has multiple local optima and multi-global optima, despite unimodal function. The properties of this category are used to evaluate the exploration of the algorithm. Also, it is used to evaluate the capability of the algorithm in avoiding the local optima.

Table 2 compares the performance of the original SSA with different versions of CSSA for unimodal benchmark functions in terms of mean and standard deviation. The notations of CSSA1 till CSSA10 are previously defined in Table 1. In Table 2, the best results are underlined. As it can be observed, CSSA with logistic chaotic map obtained the best mean values for three out of six benchmark functions. These functions are F1, F2 and F4. Also, it can be observed that CSSA with Gauss, piecewise and chebychev are in second place. Additionally, it can be seen that the proposed CSSA algorithms have high stability compared with original SSA. This is due to the stochastic behavior of SSA meta-heuristic algorithm, where random variables are included. Moreover, it can be seen that all versions of CSSA obtained better results than original SSA. Table 3 shows p-values obtained from Wilcoxon’s rank sum test for the pair-wise comparison of the best value obtained from whole iterations with a 5% significance level. This test is used to determine whether the proposed CSSA algorithms provide a significant improvement compared to the original SSA. As it can be observed, all CSSA versions are statistically significant. From these two tables, it can be concluded that embedding chaotic variables during optimization process of SSA can significantly boost the performance of original SSA in terms of exploitation and stability.

Table 2 Comparison of statistical results obtained using SSA and different version of CSSA for unimodal benchmark functions
Full size table
Table 3 Comparison of p-values of the Wilcoxon ranksum test obtained using SSA and different version of CSSA over unimodal benchmark functions
Full size table

Table 4 compares mean and standard deviation values of SSA with the proposed CSSA algorithms for multimodal benchmark functions. As it can be observed, again, CSSA with logistic chaotic map obtained the best results for most of the multimodal functions. As it obtained the best mean values for four functions out of seven functions; F9,F10,F12 and F13. While CSSA with Gauss chaotic map obtained the optimal results for F13 and F14. Also, the results from embedding different chaotic maps in optimization process of SSA obtained better results than SSA. Moreover, it can be observed the high stability of the proposed CSSA algorithms compared with SSA. Table (5) shows the p-values of Wilcoxon’s rank-sum test. As it can be seen, most of the obtained values are less than 0.05, which means that the proposed CSSA algorithms are statistically significant. From these two tables, it can be concluded that embedding the characteristics of chaotic maps able to obviously avoid local optima and obtain global optima with a small number of iterations. This is due to a proper balance between exploitation and exploration when employing chaotic variables during optimization process of SSA. Based on all the produced results, we select logistic chaotic map as the most appropriate map. Thus, in next, this map will be further evaluated in more details.

Table 4 Comparison ofstatistical results obtained using SSA and different version of CSSA for multimodal benchmark functions
Full size table
Table 5 Comparison of p-values of the Wilcoxon ranksum test obtained using SSA and different version of CSSA over multimodal benchmark functions
Full size table

Figure 1a shows the mathematical representation of three unimodal benchmark functions including F1, F3 and F7 and three multimodal benchmark functions including F9, F13 and F14. Also, Fig. 1 the search history, the trajectory of the first salp in the first dimension and the average fitness of all group of CSSA with logistic chaotic map. As it can be observed from Fig. 1b, the salps positions are scattered around the optimal solution in the search space during the course of iterations. Also, from Fig. 1c, it can be observed that salp individuals faced abrupt changes of their trajectories in the initial iterations. After that, these abrupt changes are gradually decreased during the optimization process. Based on this behavior, a population-based algorithm can guarantee to converge to some point and search locally in a search space [43]. Figure 1d shows another evidence of the significant improvement and fast convergence rate of salps individuals. As it can be observed, average fitness values are gradually decreased. From this behavior, it can be concluded the improvement of the fitness value of all individuals through iterations. This is due to a proper balance between exploration and exploitation phases. In Fig. 1e, the convergence curves of original SSA and the proposed CSSA is drawn. As it can be observed, CSSA converges faster than original SSA. Also, the proposed CSSA obtains better results than SSA. This can be an evidence of the superiority of the proposed CSSA in terms of the stability and the performance.

Fig. 1
figure 1

a Graphical representations of benchmark mathematical functions, b Search history of CSSA, c trajectory of CSSA in first dimension, d the average fitness of all group of CSSA, and e the convergence curve of CSSA and SSA

Full size image

4.2 CSSA for feature selection

In this subsection, the performance of CSSA as feature selection algorithm is evaluated and compared with other meta-heuristic feature selection algorithms. All these algorithms are applied to twenty benchmark datasets with different types. The used datasets are collected from UCI machine learning repository [44]. Table 6 shows a brief description of each used dataset. From this table, it can be observed that some of the adopted datasets contain missing values in their records. In this work, the median method is used to solve this problem by replacing the missing value with the median value of known values of a feature given class. Equation (10) shows the mathematical representation of the median method, where Qi,j is the missing value at i − th iteration given j − th feature for class C. However, in case of missing categorical values, the most repeated value is replaced with the missing value.

$$\begin{array}{@{}rcl@{}} \overline{Q}_{i,j} = median_{i:Q_{i,j}\in C_{r}}{Q_{i,j}} \end{array} $$
(10)
Table 6 Datasets description
Full size table

Also, four evaluation criteria are used in this work. These criteria are mean, standard deviation (SD), average feature subset length, p-values of the Wilcoxon rank sum test and convergence curve.

Table 8 shows the statistical results of the proposed CCSA with logistic chaotic map and five other meta-heuristic algorithms, previously proposed in the literature as feature selection algorithms. The optimal results are underlined. These related algorithms are artificial bee colony (ABC) [45], moth flame optimization (MFO) [28], particle swarm optimization (PSO) [46], chicken swarm optimization (CSO) [47], gray wolf optimizer (GWO) [48], bird swarm algorithm [49], crow search algorithm [7], whale optimization algorithm [50] and sine cosine algorithm [51]. In all the experiments, we used the same fitness function with same population size, number of dimensions, search boundary and the maximum number of iteration. Moreover, all the algorithms start with same initial population. The reason behind this, we would like to make a fair comparison. Table 7 shows the rest of parameters set for the competitor algorithms. In this table, the best results are underlined. As it can be observed from Table 8, the proposed CSSA feature selection algorithm is very competitive algorithm. CSSA obtains the highest mean fitness value for 12 benchmark datasets out of 20, with WOA in the second place. WOA obtains the top results for 6 benchmark datasets out of 20. However, it can be seen that embedding chaos theory in the searching mechanism of SSA achieves the higher mean fitness values with higher stability compared with the original SSA and the other meta-heuristic algorithms. Also, it can be observed that in all cases, CSSA can find better feature subset, which maximizes the classification accuracy, while minimizing the length of the selected feature subset.

Table 7 Meta-heuristic algorithms parameters settings
Full size table
Table 8 Comparison of statistical results obtained using CSSA and most recent and popular meta-heuristics feature selection algorithms for 20 Datasets
Full size table

Moreover, it can be observed that ABC and PSO in most cases obtain the worst results. The reason behind this can be referred to (1) improper balancing between exploitation and exploration and (2) improper setting of parameters values. Also, as we mentioned before, meta-heuristic algorithms are stochastic. Thus they have random parameters, which have a great influence on their performance. These random parameters can lead agents such as bee and moth to be stuck at local optima with high probability. Therefore, these algorithms such as PSO and ABC need to be tuned first to get better results. Several studies have been proposed in literature to improve the performance of these algorithms such as in [52,53,54]. Authors in [55] proposed a new initialization method and new updating mechanism of PSO. They applied their modified PSO based their new initialization and updating mechanism on feature selection problem. The results showed that their proposed algorithm can overcome the drawbacks of original PSO. Moreover, the results showed that the modified PSO obtain better feature subset compared with original PSO, which maximizing the classification accuracy while minimizing the number of selected features. Authors in [56] proposed a modified version of PSO, where an adaptive factor, namely fa is adopted to avoid the local optima and prevent the premature convergence. The authors applied their modified particle swarm optimization (MPSO) on fractional-order proportional integral derivative (FOPID) controller. Table (9) shows the best controller parameters tuned from MPSO for two control design case studies. The description for both cases are described in [56]. Also, the authors compared their algorithm with the original PSO. The results prove the stability and robustness of the MPSO based FOPID controller regarding tracking errors for both smooth and a non smooth cart trajectory.

Table 9 The best controller parameters for two case studies
Full size table

Authors in [57] applied their modified version of PSO on multilevel thresholding problem. They used two-dimensional (2D) Kullback–Leibler(K–L) divergence as the fitness function to find the optimal thresholds. Figure 2 summarized the mean fitness values obtained for number of segmentation levels equal to 3 and 5 in terms of Boundary Displacement Error (BDE), Probability Rand Index (PRI), Global Consistency Error (GCE) and Variation of Information (VOI). The authors adopted Berkeley Segmentation Dataset and Benchmark (BSDS300) in their experiments. The simulation results showed that their hybrid 2D K-L divergence with MPSO (2DKLMPSO) can efficiently overcome the premature convergence of PSO and can reduce the time complexity of multilevel thresholding segmentation. In this work, the authors used the default parameters setting of all competitor algorithms, as we are mainly focused on improving the performance of only SSA.

Fig. 2
figure 2

Average performance indices of 2DKLMPSO over BSDS300 with 3-level and 5-level segmentation

Full size image

Table 10 compares the length of the selected feature subset on average 30 independent runs. Equation (11) shows the mathematical formulation of average feature subset length (ASS), where ybest is the best position obtained so far at i − th iteration and L is the number of features in the original dataset.

$$ ASS = \frac{1}{tMax} \sum\limits_{i = 1}^{tMax} \frac{length({y}_{best}^{i})}{L} $$
(11)

As it can be observed from Table 10, CSSA yields the minimum feature subset on four cases, however in the rest of cases, it takes place on second or third. From the obtained results at Table 10, it can be observed that the proposed CSSA is very competitive algorithm compared with other popular and most recent feature selection algorithm. Table 11 shows p-values of the Wilcoxon rank sum test of CSSA with other meta-heuristic feature selection algorithms for twenty benchmark datasets. As it can be observed, the proposed CSSA is statistically significant compared with the other algorithms. This is because most of the obtained results are less than 0.05. Thus, it can be considered a sufficient evidence against the null hypothesis.

Table 10 CSSA vs other meta-heuristics feature selection algorithms for 20 Datasets in terms of average feature vector length
Full size table
Table 11 CSSA vs other meta-heuristics feature selection algorithms for 20 Datasets in terms of p-values of the Wilcoxon ranksum test
Full size table

For further evaluation of the proposed CSSA with logistic chaotic map, the graphical representation of the convergence curve for single run is drawn for the twenty benchmark datasets as shown in Fig. 3. In this figure, the proposed CSSA is marked with black circles on the yellow line. As it can be observed, the proposed CSSA is superior. As it obtained the highest fitness value for most of cases. In case of the rest of cases, WOA In addition, it can be observed that the proposed CSSA converges faster than the other algorithms toward the optimal results. Moreover, it can be obviously noticed that the proposed CSSA always obtains better results compare with the original SSA. Such improvement of the performance came from embedding chaotic sequence in optimization process of SSA, which highly impact on the performance of SSA.

Fig. 3
figure 3figure 3figure 3

Performance comparison on D1 to D20

Full size image

5 Conclusion

In this paper, a novel hybridization approach is proposed based on SSA and chaos theory. The effectiveness of ten chaotic maps is analyzed and compared regarding enhancing the performance of the original SSA. Fourteen benchmark global optimization functions and twenty benchmark datasets were employed. The experimental results show that the proposed chaotic version of SSA can significantly boost the performance of SSA in terms of both exploitation and exploration. Moreover, the results suggest that logistic chaotic map is the optimal map. Another finding of this paper was that embedding chaotic maps in optimization process of SSA can find optimal feature subset, which maximizes the classification accuracy, while minimizes the number of selected features. Also, the performance of CSSA as feature selection algorithm is compared with ten other meta-heuristic feature selection algorithms. These algorithms are SSA, ABC, PSO, GWO, MFO, CSO, BSA, CSA, WOA and SCA. The results show the superiority of the proposed CSSA algorithm.

In the future, more complex science and real-world problems will be considered for evaluating CSSA. Additionally, more chaotic maps are also worth employed to CSSA.