1 Introduction

In the last few decades, researchers have developed a number of new Evolutionary based Multiobjective Optimization (EMO) algorithms for solving problems that have two or three objectives [3,4,5]. Evolutionary Algorithms (EA) are population based heuristic algorithms that are capable for obtaining the set of solutions [63,64,65,66,67,68, 72]. However, many real-life problems such as automotive engine calibration [6], water distribution systems [7], fuzzy systems [69, 70, 73], software engineering [71], and land use management [8] problems, often require a number of objectives. Therefore, Multiobjective Evolutionary Algorithms (MOEA) face some challenges to handle large number of objectives. Most of MOEAs are unable to produce optimal solution due to their selection strategies. This strategy is helpful to converge the solutions towards the Pareto front. When the number of objectives increases, it is difficult to maintain the diversity as the solutions will allocate very sparsely in the objective search space.

The two well-known multi-objective evolutionary algorithms are Non-dominated Sorting Genetic Algorithm 2 (NSGA-II) [9] and Strength Pareto Evolutionary Algorithm 2 (SPEA2) [42]. Both of these algorithms use dominance based selection strategy which fails to solve more than three objective problems because the non-dominated candidate solutions lie in limited range of population. To solve this problem, researchers have developed new optimization algorithm named as Many-objective Optimization (MaOP) to handle a large number of objectives [50]. The main challenges in MaOP are as follows:

  • The visualization of Pareto front in a given search space requires special techniques [54].

  • The number of solutions has increased exponentially to describe the Pareto front of multi dimensional problems [1, 2].

Diversity maintenance and convergence improvement are the main focus of MOEAs. However, these algorithms do not consider the use of preferences for many-objective problems. This is so because the researchers may be focused on Pareto optimal solutions and less computational efforts to achieve a demonstrative subset of the Pareto front using evolutionary approaches [50].

Apart from this, there are various performance indicator based algorithms that have been developed to improve the efficiency of algorithms for many-objective optimization problems [10,11,12]. One of the most popular hypervolume indicator based algorithms is the Hypervolume Estimation Algorithm (HypE) [13] which uses Monte Carlo simulation to estimate the exact hypervolume values. Unfortunately, when the number of objective increases, then computational complexity of the algorithm also increases [15].

The main contribution of this paper is to propose a hybrid algorithm that utilizes the concepts of Knee Point Driven Evolutionary Algorithm (KnEA) and Reference Vector Guided Evolutionary Algorithm (RVEA). The algorithm is named as a hybrid evolutionary algorithm based on knee points and reference vector adaptation strategies (KnRVEA). The proposed KnRVEA algorithm has five main strategies namely mating selection, variation, finding knee point, environmental selection, and knee adaptation strategy. The mating selection strategy is used to exchange the information between individuals and pick the most promising optimal solution from the current population. The variation utilizes simulated binary crossover (SBX) [59] and the polynomial mutation [60] operators to produce new offspring. The knee points are helpful to improve the search ability of the algorithm. The solutions are decomposed and merged into non-dominated fronts using environmental selection strategy. The knee adaptation strategy is used to decompose the many-objective optimization problem into a sub-problems for handling irregular Pareto front.

The performance of KnRVEA has been evaluated on thirteen well established benchmark test problems with respect to two performance measures namely Inverted Generational Distance (IGD) and Hypervolume (HV ).

The results have been compared with five well-known techniques such as Reference Vector Guided Evolutionary Algorithm (RVEA) [14], Hypervolume Estimation Algorithm (HypE) [13], Niche-elimination Operation based Non-dominated Sorting Genetic Algorithm (NSGA-III-NE) [56], Improved many-objective Optimization Algorithm based on Decomposition (I-MOEA/D) [44], and Knee Point Driven Evolutionary Algorithm (KnEA) [31]. KnRVEA has further been applied on three real-life many-objective problems.

The rest of the paper is structured as follows: Section 2 presents the related work done in the field of many-objective optimization techniques. Brief description of KnEA and RVEA is presented in Section 3. Section 4 presents motivation and description of proposed KnRVEA algorithm. Section 5 discusses benchmark test problems, experimental setup, and results. Section 6 discusses the performance of KnRVEA on three real-life problems followed by conclusions in Section 7.

2 Related work

In the last few decades, the number of the evolutionary algorithms have been developed to solve multi-objective optimization problems. These algorithms are broadly classified into two categories such as decomposition based algorithms and performance indicator based algorithms.

2.1 Decomposition based approaches

Ishibuchi and Murata [40] proposed a Multi-objective Genetic Local Search (MOGLS) algorithm which was further improved by Jaszkiewicz [41]. MOGLS algorithm transformed the optimization problem into the collection of weighted Tchebycheff functions. However, the performance of MOGLS is greatly affected from recombination operator. The another popular algorithm is Non-dominated Sorting Genetic Algorithm 2 (NSGA-II) [9]. NSGA-II has been widely used in many real-life applications with small number of objectives. Hence, it is unable to solve the problems that have a large number of objectives. ∈-NSGA-II utilized the concepts of NSGA-II and epsilon-dominance for solving multi-objective problems [16, 18]. Bi and Wang [56] proposed an improved version of NSGA-III based on niche-elimination operation. In the proposed algorithm, an adaptive penalty distance (APD) function is presented to consider the importance of convergence and diversity in the different stages of the evolutionary process. MOEA/D [23] used a decomposition approach to divide the optimization problem into a number of sub-problems. These problems are further optimized using an evolutionary approach. Li et al. [39] proposed an extended version of MOEA/D which is based on the combination of dominance and decomposition approaches. However, the performance of MOEA/DD is greatly affected from neighborhood size and selection probability. Zheng et al. [44] proposed a new decomposition based approach that uses weighted mixture style method. It utilized two approaches namely weighted sum decomposition and Tchebycheff decomposition. This approach is known as I-MOEA/D that improves the effectiveness of the algorithm.

Hadka and Reed [19, 20] proposed a multi-objective evolutionary algorithm for handling many-objective problems using auto-adaptive recombination operators to improve the search process. Asafuddoula et al. [25, 26] proposed a evolutionary technique based on decomposition with adaptive epsilon (DBEA-Eps) that employs the reference directions to adjust the search space and maintain the balance between convergence and diversity. However, DBEA-Eps’s performance is greatly depends upon input parameters and adaptive rules. Xiao et al. [49] proposed a novel immune dominance selection multi-objective optimization algorithm (IDSMOA) to solve multi-objective problems. The main idea of IDSMOA is to promote two populations, i.e., population B and population T to co-evolve through immune selection, immune clone, immune gen, and memory selection operators to produce a satisfying Pareto front.

Deb and Jain [24] proposed NSGA-III algorithm which utilizes a reference point based approach for many-objective optimization. These reference points are same as the population size in which each population member is assisted with a reference point. There are number of improved versions has been proposed for NSGA-III. Jain and Deb [28] proposed an adaptive-NSGA-III (A-NSGA-III) technique that has an ability to add and remove the reference points. The same authors also presented an improved version of adaptive-NSGA-III algorithm (A2-NSGA-III) to remove the limitations of A-NSGA-III [27] with improvements in replacement strategy of reference points. Another extension of NSGA-III is the unified evolutionary algorithm (U-NSGA-III) [29] which is able to solve single-objective, multi-objective, and many-objective optimization problems.

Zhang et al. [31] proposed a knee point driven evolutionary algorithm (KnEA) which adopts a neighbor punishment density estimation strategy. An adaptive strategy was proposed for identifying the knee points in a small neighbourhood. The purpose of this strategy is to combine the parent and offspring populations to improve the convergence and promote diversity. The main drawback of KnEA is that the knee points are sensitive towards the given problem. Recently, Roy et al. [51] proposed an Evolutionary Path Control Strategy (EPCS) based algorithm to handle many-objective optimization problems. A reference vector strategy was introduced to reduce the number of non-dominated solutions. A novel fitness assignment procedure was proposed for survival selection which uses classical methods, aggregation methods or combination of these two methods. The main advantages of EPCS algorithm are low computational complexity and better diversity. Cheng et al. [14] proposed a Reference Vector Guided Evolutionary Algorithm (RVEA) for many-objective optimization problems. In RVEA, Angle Penalized Distance (APD) is used to balance both convergence and diversity. APD used adaptive strategy to adjust the reference vectors that ensure uniform distribution of solution in the given search space. Therefore, RVEA is able to handle irregular Pareto fronts.

2.2 Indicator based approaches

Zitzler and Künzli [43] proposed an Indicator-based Evolutionary Algorithm (IBEA) which utilizes a binary performance indicator in selection process. The main drawback of IBEA is high computational cost. There are several extended versions of IBEA such as IBMOLS that uses local search operator [45]. Wagner et al. [46] reported that IBEA algorithm is able to solve MaOPs. Emmerich et al. [47] proposed S Metric Selection based Evolutionary Multi-objective Algorithm (SMS-EMOA) that uses non-dominated sorting as a ranking criterion. They used hypervolume indicator to remove the individuals that have lowest hypervolume. The computational cost of S-Metric is high for large number of objective functions. Bader and Zitzler [13] proposed a fast hypervolume indicator based evolutionary algorithm known as Hypervolume Estimation Algorithm (HypE). The main concept of behind this algorithm is the ranking of solutions done through hypervolume. It uses Monte-Carlo simulation to estimate the hypervolume values. Three main components of HypE are mating selection, variation, and environmental selection. The binary tournament selection is proposed to select the offsprings. The variation used mutation and recombination operators to produce offspring. In environmental selection, the parent and children population are combined and decomposed into non-dominated fronts. Thereafter, the best fronts are included in new population. HypE suffers from overhead of maintaining necessary information. Bringmann et al. [21] proposed a Approximation-Guided Evolution (AGE) technique which uses the concept of approximation. However, it suffers from high computational cost. To reduce this problem, Wagner et al. [22] proposed fast approximation-guided evolutionary algorithm (AGE-II). AGE-II used archive for storing additive ∈-approximation of non-dominated solutions. Gomez and Coello Coello [48] introduced a Many-objective Metaheuristic based on R2 Indicator (MOMBI) algorithm. The fundamental concept behind this algorithm is utility functions. These are used to group the solutions and provide them rank. The whole process is run until each member of the population is ranked. The ranking procedure is done by R2-ranking strategy. They used binary tournament selection to select the individuals based on their ranks. However, it suffers from loss of diversity for high dimensionality problems. Wang et al. [30] proposed an improved version of two-archive algorithm known as Two-Arch2 for handling many-objective optimization. They used Convergence Archive (CA) and Diversity Archive (DA). I∈+ indicator and Pareto dominance concepts are used to improve the convergence and diversity. However, it does not provide optimal solution for some WFG test instances because it does not consider extreme points.

3 Background

The basic concepts of Multi-objective Problems (MOPs) are presented in this section. Thereafter, the brief description of KnEA and RVEA algorithms are presented.

3.1 Basic concepts

Multi-objective Optimization Problems (MOPs) involve more than one objective which is to be optimized. The MOPs can be formulated as follows [17]:

$$ Minimize: F(z) = [f_{1}(z), f_{2}(z),\ldots,f_{n}(z)] $$
(1)
$$ \begin{array}{ll} &\text{Subject to:} \\ &g_{i}(z) \geq 0, i = 1,2,\ldots,m \end{array} $$
(2)
$$ h_{i}(z)= 0, i = 1,2,\ldots,p $$
(3)

where z = [z1, z2,…, zk]T is the vector of decision variables, m is the number of inequality constraints, p is the number of equality constraints, gi is the ith inequality constraints, hi is the ith equality constraints, and n is the number of objective functions \(f_{i} : \mathbb {R}^{n} \rightarrow \mathbb {R}\).

There is a possibility that an optimal solution may not optimize all the objectives simultaneously. Whereas, Pareto optimal solutions representing the trade-offs between the objectives. In objective search space, the Pareto solutions are known as Pareto front (PF) and these solutions are known as Pareto set (PS) [55, 57] in the decision space.

Definition 1

Pareto Dominance: Assume there are two vectors such as: y=(y1, y2,…, yr) and x=(x1, x2,…, xr). Vector y is said to dominate vector x (such as y ≻ x) if and only if:

$$\begin{array}{@{}rcl@{}} &&\forall i \in \{1,2,\ldots,r\},\\&& [f(y_{i})\geq f(x_{i})]\wedge[\exists i \in 1,2,\ldots,r : f(y_{i})] \end{array} $$
(4)

Definition 2

Pareto Optimality:

A solution x ∈ X is called Pareto optimal if and only if:

$$ \nexists x \in X \mid f(x) \succ f(y) $$
(5)

Definition 3

Pareto optimal set:

The set of all Pareto-optimal solutions including all non-dominated solutions of a problem is called Pareto optimal set if and only if:

$$ P_{s}=\{y,x \in X \mid \exists f(x) \succ f(y)\} $$
(6)

Definition 4

Pareto optimal front: A set containing the objective values corresponding to Pareto optimal solutions in Pareto optimal set is called Pareto optimal front and it is defined as follows:

$$ P_{f}=\{ f(y) \mid y \in P_{s}\} $$
(7)

Definition 5

Knee point:

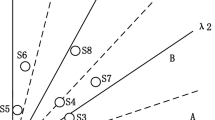
It is defined as the Pareto-optimal point that have maximum reflex angle computed from its neighbors. It means that if small improvement is done in one objective, then there will be severe degradation in at least one other objective [37]. Figure 1 shows the knee points and boundary points.

Fig. 1
figure 1

Relation between Knee point and Boundary point

Full size image

3.2 Knee Point Driven Evolutionary Algorithm (KnEA)

Multi-objective Evolutionary Algorithms (MOEAs) suffers from two major problems. These speed up the convergence performance and enhance the diversity. To resolve these problems, several evolutionary algorithms have been proposed. Knee Point Driven Evolutionary Algorithm (KnEA) is a recently developed many-objective evolutionary algorithm [31]. The knee points are used as secondary selection criteria to improve the search ability in MOEAs. The main components of KnEA are described as follows:

  • An initial population is randomly generated of size N.

  • A binary tournament selection strategy is used to select the individuals and generate N number of individual offsprings using variation method. The selection strategy adopts three tournament metrics such as dominance relationship, knee point, and a weighted distance measure.

  • The non-dominated sorting method is applied on population to identify the solutions located in knee regions.

  • An environmental selection strategy is performed to select N number of individuals.

The above-mentioned components of KnEA are described in Algorithm 1.

The mating selection in KnEA uses binary tournament selection strategy that comprises of three tournament strategies such as dominance comparison, knee point criterion, and weighted distance (see Algorithm 2). Two individuals are randomly selected from the given population. If one solution dominates the other, then the dominated solution is selected. If both solutions are non-dominated, then determine whether they are knee points or not. If one of them is knee point, then the knee points is selected. If both of these are knee points or neither of them is a knee point, then a weighted distance method is used to compare the solutions. A weighted distance DW is used to select a winner solution if neither the knee point criterion nor dominance comparison can differentiate the two solution participated in selection strategy [31]. An efficient non-dominated sorting (ENS) algorithm [61] is used to sort the non-dominated solutions present in the population.

An adaptive strategy is used to find knee points present in the population. Algorithm 3 describes the main steps of adaptive strategy for finding knee points. The same procedure is repeated for all non-dominated fronts in the combined population until knee points are detected for all non-dominated fronts.

Environmental selection process is used to select fitter solutions as parents for the next generation. KnEA selects parents for next generation from the combination of parent and offspring populations of this generation. The main steps of environmental selection in KnEA are presented in Algorithm 4.

3.3 Reference Vector Guided Evolutionary Algorithm (RVEA)

Reference Vector Guided Evolutionary Algorithm (RVEA) is a recently developed evolutionary algorithm for solving many-objective optimization problems [14]. The main components of RVEA are offspring creation, reference vector guided selection, and reference vector adaptation. The genetic operators are used to generate the offspring population. The reference vector guided selection has four sub-steps such as objective value translation, population partitions, computation of Angle Penalized Distance (APD), and elitism selection [14]. It adopts a set of reference vectors for their selection strategy. In RVEA, Angle Penalized Distance (APD) is used to balance the both convergence and diversity dynamically. It uses adaptive strategy to adjust the reference vectors that ensure uniform distribution of solution in the search space. The preference articulation approach is used to generate the distributed Pareto optimal solution in a search space. Algorithm 5 describes the main components of RVEA [14].

3.3.1 Reference vector guided selection

Reference vector guided selection strategy consists of four main steps. These are objective value translation, population partition, angle penalized distance calculation, and elitism selection. The objective values of individuals in population are translated into RVEA to guide the search process. To generate a uniformly distributed set of reference vectors, a set of uniformly distributed reference points is generated on a unit hyperplane using the canonical simplex lattice design method [58].

3.3.2 Assignment of individuals to reference vectors

After the generation of the reference vectors, individuals are assigned to them. An individual is assigned to a reference vectors if and only if the angle between it and the reference vector is minimum among all reference vectors. In this way, assignment of individuals to the reference vectors partitions the population into sub-populations.

3.3.3 Selection mechanism in each sub-population

After the generation of reference vectors and the assignment of individuals then, one individual is selected from each sub-population. The selection criterion consists of two sub-criteria that are meant for managing convergence and diversity, respectively. Convergence is taken care of by the distance between the translated objective vector and the origin. Diversity is accounted by the angle between the translated objective vector and the reference vector. The individual with the smallest angle is preferred over other individuals.

3.3.4 Adaptation of reference vectors

For some optimization problems where objective functions are scaled to different ranges, a uniformly distributed set of reference vectors is not best suited as shown in Fig. 2.

Fig. 2
figure 2

Uniformly distributed reference vectors in 3D search space. In this case, nine uniformly distributed reference points are generated and then mapped to generate the nine reference vectors

Full size image

To tackle this issue, one possible solution is to adapt the reference vectors. In RVEA, reference vectors are adaptive. In other words, they change their position according to the location of individuals in the objective space.

4 Proposed Knee Point and Reference Vector Adaptation based Evolutionary Algorithm (KnRVEA)

This section first describe the motivation behind proposed algorithm followed by a detailed description of proposed algorithm.

4.1 Motivation

The main contribution of this paper is to propose a hybrid many objective optimization algorithm that utilizes the knee points and reference vector adaption strategies. The primary intention to combine these strategies is to minimize the each other’s weakness and promote respective strengths. It is worth mentioning that the knee points are designated for exploratory search and reference vector adaption strategy is assigned for uniform distribution of solutions even the objective functions are not normalized same range. In the proposed algorithm, only reference vector adaption strategy is used for uniform distribution of knee points. The collaboration between knee point and reference vector adaption strategy enhances the exploratory search capability such that reference vector adaptation strategy tune the knee points according to the distribution of candidate solutions which makes the exploration process more directive. Hence, a novel knee adaption strategy is proposed which is inspired from reference vector adaption strategy.

4.2 Proposed algorithm

The basic procedure of proposed KnRVEA algorithm is described in Algorithm 6. KnRVEA algorithm is inspired from knee points and reference vector adaptation strategies. KnRVEA consists of six main steps such as mating selection, variation, non-dominated sorting, identifying knee points, environmental selection, and knee adaptation strategy. Initially, parent population P is randomly initialized with N number of individuals. The mating selection procedure is used to select the promising solutions in a given search space. The variation uses simulated binary crossover (SBX) [59] and polynomial mutation [60] operators to generate N offspring individuals. Non-dominated sorting is applied on both parent and offspring population followed by a search strategy to identify knee points in each non-dominated front. The environmental selection is used to select N individuals. Finally, knee adaptation strategy is performed to obtain uniformly distributed Pareto optimal solutions set.

4.2.1 Binary tournament mating selection

There are three tournament selection strategies are employed in KnEA algorithm such as dominance comparison, knee point criterion and a weighted distance.

The two random solutions are selected in binary tournament selection. If one solution dominates the other one then the former solution is selected. If both of these two solutions are non-dominated with each other, then the proposed algorithm check if they are knee points or not. If only one solution is knee point, then the knee point is chosen. If both of these solutions are knee point or none of them is a knee point then a weighted method is used for comparing these solutions. The solution which has the large weighted distance can win the tournament. If both of these solutions have the same distance then the solution will be chosen randomly for reproduction.

An important component of KnEA algorithm is a weighted distance measurement for choosing a winning solution in the binary tournament mating selection if both the dominance comparison and the knee points criterion are not able to distinguish the two solutions in the tournament. The weighted distance of a solution is described as follows based on the k −nearest neighbors:

$$ DW(p)=\sum\limits_{i = 1}^{k}w_{p_{i}} d_{pp_{i}}\\ $$
(8)
$$ w_{pi}=\frac{r_{p_{i}}}{{\sum}_{i = 1}^{k}r_{p_{i}}}\\ $$
(9)
$$ r_{p_{i}}=\frac{1}{\mid d_{pp_{i}} - \frac{1}{k}{\sum}_{i = 1}^{k}d_{pp_{i}} \mid} $$
(10)

where pi indicates the i th neighbor of population p, \(w_{p_{i}}\) represents the weight of pi, \(d_{pp_{i}}\) is the Euclidean distance between p and pi, and \(r_{p_{i}}\) represents the rank of distance \(d_{pp_{i}}\).

4.2.2 Variation

The proposed approach uses simulated binary crossover (SBX) [59] and polynomial mutation [60] operators for variation to generate N offspring individuals. These operators are responsible for better exploration and exploitation between the individuals. The normal boundary insertion method is used for offsprings which lies outside the boundary [62].

4.2.3 Non-dominated sorting

KnRVEA performs non-dominated sorting to select the non-dominated solutions from the first front, i.e., PF1. If the number of solutions in PF1 is greater than the size of population N, then knee points in PF1 are firstly selected as parents for the next population. Let the number of knee points in PF1 be NPF1. In case NPF1 is larger than N, then the knee points that have larger distance to the hyperplane are selected. Otherwise, NPF1 knee points are selected together with other solutions in PF1 that have a larger distance to the hyperplane of PF1.

4.2.4 Adaptive strategy for identifying knee points

In KnEA, an adaptive strategy is proposed for finding the knee points in a population. There is a extreme line L having the maximum of f1 and f2 functions. Then, the distance of each solution is identified as a knee point if its distance is maximum with respect to the extreme line (see Fig. 1). Here, L can be defined by ax + by + c = 0 for a bi-objective minimization problem. The solution is also considered as a knee point if there is only one solution in its neighbourhood. The distance from a solution A(xA, yA) to extreme line L with more than two objectives is computed as follows:

$$ ds(A,L)= \left\{\begin{array}{ll} \frac{|ax_{A}+by_{A}+c|}{\sqrt{a^{2}+b^{2}}}, & \text{if } ax_{A}+by_{A}+c < 0 \\ -\frac{|ax_{A}+by_{A}+c|}{\sqrt{a^{2}+b^{2}}}, & \text{otherwise} \end{array}\right. $$
(11)

A strategy to tune the size of neighborhood solutions is proposed in KnEA algorithm if all the solutions lie in a same neighbourhood. However, the proposed adaptive strategy is able to find the knee points in its neighbourhood.

4.2.5 Environmental selection

KnEA uses elitist approach to selects the parents for the next generation. KnEA prefers knee points rather than the non-dominated solutions in environmental selection. It performs non-dominated sorting before environmental selection to select the non-dominated solutions in the first non-dominated front. If these solutions are larger than the population size, then knee points are selected first for the next generation of population.

4.2.6 Knee adaptation strategy

The proposed knee adaptation strategy utilizes the concept of reference vector adaptation [14] strategy to obtain a set of Pareto optimal solutions. This strategy is mentioned in Algorithm 7. These solutions are the points that are intersection between knee points and Pareto front. However, these knee points will not produce uniformly distributed solutions when the objective function values are normalized in the same range. To remove this conflict, the range of the knee points will be adapted as follows:

$$ v_{k + 1,j}= \frac{ v_{0,j}\circ(O_{k + 1}^{max}-O_{k + 1}^{min})} {\mid\mid v_{0,j}\circ(O_{k + 1}^{max}-O_{k + 1}^{min})\mid\mid} $$
(12)

where j = 1,2,…, N, vk+ 1, j represents the jth knee point adapted for generation k + 1, v0, j represents the jth uniformly distributed knee point. \(O_{k + 1}^{min}\) and \(O_{k + 1}^{max}\) are the minimum and maximum values of objective function, respectively. The ∘ operator indicates the Hadamard product that element-wise multiply the two knee points of same size [14]. The knee adaptation strategy has obtained the uniformly distributed solutions even if the objective functions are not normalized.

There is a controlling parameter Fc that control the frequency of employing the adaptation strategy. It ensures that knee adaptation strategy have to be performed in selected generation because there is no need to employ this strategy very frequently [52]. Example 2 illustrates the workings of control parameter Fc in adaptation strategy. Example 2: (Control parameter) For instance, the value of Fc is set to 0.4. The knee point will be adapted only at k = 0, k = 0.4 × Maxiteration, k = 0.8 × Maxiteration, k = 0.12 × Maxiteration and so forth.

4.3 Computational complexity

In this subsection, the computational complexity of proposed algorithm is discussed. Both time and space complexities of the proposed algorithm are given below.

4.3.1 Time complexity

  1. 1.

    Initialization of KnRVEA population needs \(\mathcal {O}(M \times N)\) time where M and N represent the number of objectives and population size, respectively.

  2. 2.

    Mating selection procedure requires \(\mathcal {O}(M \times N \times N)\), i.e., \(\mathcal {O}(M \times N^{2})\) time.

  3. 3.

    Variation procedure uses \(\mathcal {O}(N)\) time.

  4. 4.

    Non-dominated sorting procedure requires \(\mathcal {O}(MN^{2})\).

  5. 5.

    Knee point identification requires \(\mathcal {O}(MN^{2})\).

  6. 6.

    Environmental selection needs \(\mathcal {O}(NlogN)\).

  7. 7.

    Knee adaptation strategy requires \(\mathcal {O}(MN/F_{c} \times Max_{iteration})\), where Fc represents control parameter and Maxiteration represents the maximum number of iterations.

Therefore, summing up the complexities of all the above steps and the total time complexity of KnRVEA for maximum number of generations is \(\mathcal {O}(M \times N^{2} \times Max_{iteration})\).

4.3.2 Space complexity

The space complexity of KnRVEA algorithm is the maximum amount of space which is considered at any one time during its initialization process. Thus, the total space complexity of KnRVEA algorithm is \(\mathcal {O}(M \times N)\).

5 Experimentation and results

In order to demonstrate the effectiveness of proposed KnRVEA, thirteen benchmark test problems have been used for experimentation which are taken from two well-known test suites such as DTLZ [32] and WFG [33]. The performance of KnRVEA has been compared with five well-established algorithms such as Reference Vector Guided Evolutionary Algorithm (RVEA) [14], Hypervolume Estimation Algorithm (HypE) [13], Niche-elimination Operation based Non-dominated Sorting Genetic Algorithm (NSGA-III-NE) [56], Improved many-objective Optimization Algorithm based on Decomposition (I-MOEA/D) [44], and Knee Point Driven Evolutionary Algorithm (KnEA) [31]. The results are evaluated and compared with two well-known performance measures such as Inverted Generational Distance (IGD) [36] and Hypervolume (HV ) [38].

5.1 Benchmark test problems

All the algorithms have been tested over four DTLZ test problems (DTLZ1-DTLZ4) [32] and nine WFG test problems (WFG1-WFG9) [33]. For each benchmark test suite, the number of objectives is to be varied from 3 to 15, i.e., {3, 5, 10, 15}. Table 1 represents the description of these test problems. According to [32], the decision variables are set to n = m + r − 1 for DTLZ test problems. The value of r is fixed for DTLZ1 (r = 5) and for DTLZ2-DTLZ4(r = 10). The decision variables are set to n = k + l for WFG test problems, where variable k = 2 × (m − 1) and l is set to 20 as suggested by [33].

Table 1 The characteristics of benchmark test problems
Full size table

5.2 Parameter setting

The parameters of the above-mentioned algorithms are set as they are recommended in their original work. The parameters setting of these algorithms are reported in Table 2. In addition to these parameters, the population size and maximum iterations for all above-mentioned algorithms are set to 100 and 3000, respectively. Due to the stochastic nature of these algorithms, the results are averaged over 30 independent runs under 30 random seeds. The mean and median solutions obtained in final iteration are reported in tables. The simulations are carried out in Matlab R2017a environment operating on Core i5 processor and 2.40 GHz processor with 4 GB RAM.

Table 2 Parameters values of algorithms
Full size table

5.3 Experimentation 1: Performance evaluation on DTLZ test suite

Tables 3 and 4 show the values of IGD and HV obtained from above-mentioned six algorithms on DTLZ test suite with 3, 5, 10, and 15 objectives (i.e., 16 test instances). It can be seen from these tables that KnRVEA provides better values of IGD and HV for DTLZ1 test instances. After the proposed KnRVEA, RVEA and I-MOEA/D provide the better value of IGD and HV than the others. RVEA and I-MOEA/D are the second best performing algorithms. NSGA-III-NE performs almost similar to HypE algorithm in all the test instances of DTLZ1.

Table 3 The IGD values obtained by proposed KnRVEA and other competitor algorithm in DTLZ test suite
Full size table
Table 4 The HV values obtained by proposed KnRVEA and other competitor algorithm in DTLZ test suite
Full size table

For DTLZ2 test instances, KnRVEA provides better value of IGD for 3- and 15-objective test instances. After the proposed KnRVEA, RVEA provides better results than the other algorithms for these test instances. For 5- and 10-objective test instances, KnRVEA is the second best algorithm in terms of IGD. For these instances, RVEA provides better results than KnRVEA. For HV, KnRVEA provides better results for all test instances of DTLZ2. While, the performance of RVEA and HypE algorithms is similar to each other for HV measure.

For DTLZ3 test instances, KnRVEA is significantly better than other competitor algorithms in terms of IGD and HV. For IGD, I-MOEA/D and NSGA-III-NE are the second and third best algorithm after KnRVEA, respectively. For HV performance measure, NSGA-III-NE is the second best algorithm after KnRVEA.

For DTLZ4 test instances, the results obtained from KnRVEA are better than the competitor algorithms in terms of IGD and HV. The I-MOEA/D and NSGA-III-NE are the second and third best algorithms after KnRVEA for IGD and HV performance measures.

It has been observed from the results presented in Tables 3 and 4 that KnRVEA is able to find the optimal solution for most of test instances. For IGD, KnRVEA provides best results on 12 out of 16 test instances. For HV values, KnRVEA provides best results on all test instances.

For the visualization of solutions distribution, Figs. 3 and 4 show the non-dominated fronts obtained from KnRVEA and other competitor algorithms for 15- and 3-objective DTLZ test functions, respectively. For 15-objective DTLZ test functions, RVEA and I-MOEA/D provide uniform convergence but fails to reach some regions of Pareto front. HypE, NSGA-III-NE, and KnEA provide good convergence over all Pareto front. It can be seen from Fig. 3 that the non-dominated front obtained from KnRVEA provides better convergence and diversity than the other competitor algorithms. For 3-objective DTLZ test functions, it is observed that the Pareto front obtained from KnRVEA, RVEA, NSGA-III-NE, and I-MOEA/D has uniform convergence and better diversity (see Fig. 4). However, HypE and KnEA fail to provide a good coverage over the Pareto front.

Fig. 3
figure 3

The non-dominated fronts obtained from six algorithms on 15-objectives for DTLZ1, DTLZ2, DTLZ3, and DTLZ4 test instances

Full size image
Fig. 4
figure 4

The non-dominated solutions obtained from six algorithms on 3-objectives for DTLZ1, DTLZ2, DTLZ3, and DTLZ4 test instances

Full size image

5.4 Experimentation 2: Performance evaluation on WFG test suite

Table 5 shows the IGD values obtained from KnRVEA and other algorithms for WFG test suite with 3, 5, 10, and 15 objectives (36 test instances). For WFG1 test function, KnRVEA provides better results than the other five algorithms for all test instances. I-MOEA/D is the second best algorithm. The results obtained from KnEA are better than HypE algorithm.

Table 5 The IGD values obtained by proposed KnRVEA and other competitor algorithm in WFG test suite
Full size table

For WFG2 benchmark test function, the best IGD value is obtained from KnRVEA for all test instances. RVEA and I-MOEA/D are the second and third best algorithms for this benchmark test function, respectively. KnEA outperforms HypE in terms of IGD for all test instances.

The results obtained from KnRVEA are better than other algorithms for WFG3 benchmark test function. For 5-, 10-, and 15-objective test instances, I-MOEA/D is the second best algorithm. For 3-objective test instance, RVEA is the second best performing algorithm after KnRVEA. For 3- and 5-objective test instances, HypE performs better than KnEA. Whereas, KnEA performs better than HypE for 10- and 15-objective test instances.

For WFG4 test function, KnRVEA performs better results as compared to the other algorithms for all test instances. After KnRVEA, the results obtained from I-MOEA/D are better than others for 3-, 5-, and 10-objective test instances. For 15-objective test instance, RVEA is the second best algorithm. KnEA performs better than HypE algorithm.

The results obtained from KnRVEA for WFG5 test problem are superior than the other competitor algorithms for all test instances. For 3- and 5-objective test instances, I-MOEA/D provides better results than other algorithms except KnRVEA. For 10- and 15-objective test instances, RVEA is the second best algorithm after KnRVEA. The results obtained from HypE and KnEA are not competitive for this test problem.

WFG6 is a non-separable problem. For this problem, NSGA-III-NE outperforms the other algorithms in all test instances. The results obtained from RVEA and I-MOEA/D are very much similar. Therefore, these are the second best algorithms. KnRVEA is the third best algorithm for all test instances while the results obtained from KnEA are better than HypE.

For WFG7 test problem, KnRVEA outperforms the other algorithm in terms of IGD for all test instances. For 3-objective test instance, RVEA is the second best algorithm. For 5−, 10−, and 15-objective test instances, I-MOEA/D provides better results after KnRVEA. Whereas, KnEA performs better than HypE for all test instances.

For WFG8 test problem, KnRVEA performs better than the above-mentioned algorithms for all WFG8 test instances. For 3-, 5-, and 10-objective test instances, I-MOEA/D is the second best algorithm. For 15-objective test instance, RVEA is the second best optimization algorithm. KnEA performs better than HypE for all test instances.

For WFG9 test problem, KnRVEA outperforms the other competitor algorithms for all test instances. RVEA is the second best algorithm for all instances. KnEA provides better results than HypE for 5-, 10-, and 15-objective test instances. Whereas, I-MOEA/D performs better than NSGA-III-NE for all test instances.

Figures 5, 6, 7, 8 and 9 show the non-dominated fronts obtained from KnRVEA and other competitor algorithms for 15- and 3-objective WFG benchmark test functions, respectively. For 15-objective WFG test functions, RVEA, NSGA-III-NE, and MOEA/ DD provide uniform convergence while HypE and KnEA provide good convergence over all Pareto front. For 3-objective WFG test functions, KnRVEA, RVEA, and NSGA-III-NE algorithms provide good Pareto front while the Pareto fronts of HypE, I-MOEA/D, and KnEA provide good uniform distribution. The results reveal that the KnRVEA, RVEA, and NSGA-III-NE provide better coverage over the Pareto front. On the other hand, the performance of HypE, I-MOEA/D, and KnEA are challenging but they fail to provide better converge in most test instances. After analysing the results, it has been concluded that KnRVEA outperforms on high dimensional objective search space in terms of performance measures.

Fig. 5
figure 5

The non-dominated fronts obtained from six algorithms on 15-objectives for WFG1, WFG2, WFG3, WFG4, WFG5, and WFG6 test instances

Full size image
Fig. 6
figure 6

The non-dominated fronts obtained from six algorithms on 15-objectives for WFG7, WFG8, and WFG9 test instances

Full size image
Fig. 7
figure 7

The non-dominated solutions obtained from six algorithms on 3-objectives for WFG1, WFG2, WFG3, and WFG4 test instances

Full size image
Fig. 8
figure 8

The non-dominated solutions obtained from six algorithms on 3-objectives for WFG5, WFG6, WFG7, and WFG8 test instances

Full size image
Fig. 9
figure 9

The non-dominated solutions obtained from six algorithms on 3-objectives for WFG9 test instance

Full size image

5.5 Experimentation 3: Wilcoxon signed-rank test

In the literature [51], it has been observed that IGD and HV do not provide any guarantee for better convergence and diversity because sometimes the obtained solutions are not close to the Pareto optimal front. To resolve this problem, Wilcoxon signed-rank test [53] has been conducted on the average value of IGD and HV. It is used to compare KnRVEA with other algorithms in pair-wise manner. The positive rank is given to proposed algorithm if it is better than the competitor algorithms with respect to a particular metric measure (i.e., IGD and HV ). Otherwise, the negative rank is assigned. For comparison, a significance level is set to 0.10 and summed up all the positive and negative rank [53]. The TH should be less than or equal to 100 to reject the null hypothesis. The results of Wilcoxon test are tabulated in Table 6 where +, -, and = indicate that the performance of KnRVEA is superior (+), inferior (-), and equal (=) to the competitor algorithms, respectively. It is observed from Table 6 that the KnRVEA outperforms over all the competitor algorithms in terms of IGD and HV performance measures except NSGA-III-NE.

Table 6 Wilcoxon signed-rank test results between proposed KnRVEA and other algorithms based on average IGD and HV
Full size table

5.6 Experimentation 4: Statistical significance test

Besides the basic statistical analysis (i.e., mean and median), ANOVA test has been performed for comparison of RVEA, HypE, NSGA-III-NE, I-MOEA/D, KnEA, and proposed KnRVEA. ANOVA is used to test whether the results obtained from proposed KnRVEA differ from the results of other competitive algorithms in a statistical significant way. A p −value determines the statistical significance level of KnRVEA. The 95% confidence interval is used for ANOVA testing. Therefore, algorithm is statistically significant if and only if the p −value is less than 0.05. ANOVA test results for DTLZ benchmark test suite on performance measures, i.e., IGD and HV, are reported in Tables 7 and 8. It is observed from these tables that KnRVEA is statistically different from the other algorithms. p −value obtained from KnRVEA is much smaller than 0.05. Table 9 shows the ANOVA test results for WFG test suite on performance measure IGD. The p −value obtained from KnRVEA is much smaller than 0.05 for all WFG test instances. The results demonstrate that the p −value obtained from KnRVEA is much smaller than 0.05 for all benchmark test problems. Therefore, KnRVEA is statistically different from the other competitor algorithms.

Table 7 ANOVA results for IGD values on DTLZ benchmark test functions
Full size table
Table 8 ANOVA results for HV values on DTLZ benchmark test functions
Full size table
Table 9 ANOVA results for IGD values on WFG benchmark test functions
Full size table

5.7 Sensitivity analysis

The parameter tuning of many-objective algorithms is one of the major challenge. Different values of parameter might yield different results as reported from the exiting literature. KnRVEA algorithm involves three parameters namely Threshold (T), Crossover (nc), and Mutation (nm). The sensitivity investigation of these parameters has been discussed by varying their values.

  1. 1.

    Threshold (T): KnRVEA algorithm was run for different value of T. The values of T used in experimentation are 0.2, 0.5, 0.8, and 1.0. Figure 10a reveals that KnRVEA converges towards the optimum when the value of T is 0.5.

  2. 2.

    Crossover (nc): To investigate the effect of crossover, KnRVEA algorithm was executed for 10, 20, 30, and 40. For brevity, the DTLZ1 test function is chosen for analysis. Figure 10b shows the effect of number of search agents on the performance of the above-mentioned algorithms. For most of these functions, it was found that KnRVEA provides best optimal solutions when the number of search agent is set to 20.

  3. 3.

    Mutation (nm): KnRVEA algorithm was run for different values of parameter nm. The values of nm used in experimentation are 10, 20, 30, and 40. Figure 10c shows that the function DTLZ1 obtains best optimal solution when the value of nm is set to 20.

Fig. 10
figure 10

Sensitivity analysis of proposed KnRVEA algorithm

Full size image
Fig. 11
figure 11

The convergence analysis of non-dominated solutions on 3-, 5-, 10-, and 15-objectives for DTLZ2 and DTLZ4 test functions in terms of HV and IGD

Full size image

5.8 Discussion

This subsection explains why KnRVEA provides better results than the other algorithms. KnRVEA maintains diversity among solutions. This is achieved by utilizing hypervolume indicator. It is evident from results that the solutions are very close to Pareto optimal solution. The solutions are distributed in whole region of Pareto front. Whereas, the above-mentioned algorithms do not maintain uniform Pareto front solutions (i.e., diversity). Besides this, KnRVEA also converges the solutions very fast. Figure 11 shows the evolutionary progress over number of generations. It can be seen that the number of non-dominated solutions decrease with an increase in number of objectives. This shows applicability of KnRVEA on many-objective optimization problems.

KnRVEA maintains the information about non-dominated solutions. This can be achieved by utilizing the knee adaptation strategy. This strategy adjusts the solutions according to objective functions. It ensures uniform distribution of solution, even if objective functions are not well normalized or Pareto fronts are in irregular shape.

6 Real-life applications

In this section, the performance of the proposed KnRVEA has been tested on three real-life problems such as Multi-objective Travelling Salesman Problem (MOTSP), Multi-objective 0/1 Knapsack Problem (MOKP), and Water Resource Planning Problem (WRPP). These problems are used to show the effectiveness of proposed KnRVEA in real-life problems.

6.1 Multi-objective travelling salesman problem

The mathematical formulation of multi-objective travelling salesman problem (MOTSP) is as follows [34]: Given a set n cities and p cost \(c_{ij}^{k}, \quad k = 1,2,\ldots , p\) (travel from city i to j). The main objective of this problem is to find a tour, i.e., a cyclic permutation R of n cities.

$$ \text{Minimize} \sum\limits_{i = 1}^{n-1} c_{R(i),R(i + 1)}^{k} + c_{R(n),R(1)}^{k} , \quad k = 1,2,\ldots,p $$
(13)

In this paper, p is set to 3, 5, 10, and 15.

Table 10 shows IGD value obtained from KnRVEA and and other competitor algorithms on MOTSP. It can be seen that KnRVEA performs better than other algorithms for all test instances (i.e., 3, 5, 10, 15). For 3- and 5-objective instances, KnRVEA provides best IGD value. RVEA is the second best algorithm for 3-objective test instance. For 5-objective test instance, I-MOEA/D is the second best performing algorithm. For 10- and 15-objective test instances, KnRVEA outperforms the other five algorithms. RVEA is the second best algorithm for these test instances. It is worth mentioning that KnRVEA consistently performing better than other algorithms for all four MOTSP instances.

Table 10 The IGD values obtained by proposed KnRVEA and other competitor algorithms on MOTSP
Full size table

6.2 Multi-objective 0/1 knapsack problem

Multi-objective 0/1 knapsack problem (MOKP) is a combinatorial optimization problem. In multi-objective 0/1 knapsack problem, there are q knapsacks and a set of n items. The objective of this problem is to find the vector z = (z1, z2,…, zn) ∈{0,1}n, where zk = 1 indicates the item k is in all knapsacks and zk = 0 represents the item k is not in any knapsacks [38]. The mathematical formulation of multi-objective 0/1 knapsack problem is defined as follows [38]:

$$ \begin{array}{ll} &\text{Maximize} f_{k}(z) = \sum\limits_{j = 1}^{n}p_{kj} \times z_{j}, \quad k = 1,2,\ldots,q\\ &\text{Subject to:} \end{array} $$
(14)
$$ \sum\limits_{j = 1}^{n}w_{kj}\times z_{j} \leq c_{k} $$
(15)

where pkj is the profit of item j placed in knapsack k, wkj is the weight of item j placed in knapsack k, and ck is the capacity of knapsack k. zq is the selected item q in the knapsack. According to [38], the value of pkj and wkj lies in the interval of [10,100].

Table 11 shows the results obtained from KnRVEA and other competitive algorithms on MOKP. It is observed from table that KnRVEA provides better results than the other algorithms for 3- and 5-objective test instances. KnRVEA always provides lower IGD value than the other algorithms. For these instances, RVEA is the second best performing algorithm. For 10- and 15-objective test instances, KnRVEA provides lowest value of IGD as compared to other algorithms. RVEA and KnEA are the second best algorithm for these instances. The results reveal that KnRVEA maintains a good balance between convergence and diversity.

Table 11 The IGD values obtained by proposed KnRVEA and other competitor algorithms on MOKP
Full size table

6.3 Water resource planning problem

Water resource planning (WRPP) involves optimal planning for storm drainage systems in urban area which is described by Musselman and Talavage [35]. It consists of three variables such as local detention storage capacity (z1), maximum treatment rate (z2), and maximum allowable overflow rate (z3). It uses five objectives functions (f1 − f5) and seven constraints (g1 − g7).

Table 12 shows the IGD values obtained from six algorithms on four WRPP instances. From this table, it is observed that KnRVEA provides better results than other algorithms for 3- and 5-objective test instances. The IGD value obtained from KnRVEA is much smaller than the others. RVEA is the second best algorithm for these test instances. For 10- and 15-objective test instances, the proposed KnRVEA always provides smaller value of IGD. The results reveal that KnRVEA is able to solve a problem with many objectives and constraints.

Table 12 The IGD values obtained by proposed KnRVEA and other competitor algorithms on WRPP
Full size table

7 Conclusions

In this paper, a hybrid many-objective optimization algorithm, named KnRVEA, has been proposed. KnRVEA utilizes the features of knee points and reference vector adaptation strategies. The knee points are used to improve the search performance when the number of objectives increases. The knee points are used to increase the selection pressure for improving the convergence performance of proposed algorithm. The proposed knee adaption strategy is used to obtain a set of uniformly distributed solutions. KnRVEA has been implemented and tested on thirteen benchmark test functions. On comparing the results of KnRVEA with other algorithms, it has been observed that KnRVEA outperformes five recently developed MOEAs such as RVEA, HypE, NSGA-III-NE, I-MOEA/D, and KnEA. KnRVEA has further been applied on three well-known real-life problems. The results reveal that KnRVEA provides better results among all the competitive algorithms.