1 Introduction

Due to its significant applications in optical communications, remote sensing, and optical imaging, the generation of laser beams and the study of their properties of propagation through the turbulent atmosphere has attracted a lot of attention (Andrews and Philips 1998; Cai and He 2006; Khannous et al. 2016; Ez-Zariy et al. 2016; Saad et al. 2017; Yaalou et al. 2019; Boufalah et al. 2018; Hricha et al. 2020, 2022; Ebrahim and Belafhal 2021; Chib et al. 2022). It is well known that the atmospheric turbulence changes depending on the geographical setting, season, weather, and other factors. However, terrestrial environments, where temperature difference dominates the behaviors of the air’s refractive index fluctuations in maritime environments, humidity fluctuation is another significant factor that affects optical turbulence. This makes the beam propagation more complicated (Friehe et al. 1975). What it will limit the performance and the propagation of the laser beams in some practical situations for example vessel-to-vessel communications. So, understanding how optical beams interact with the marine atmosphere is crucial. In the literature, a few models that describe the marine atmospheric spectrum have been investigated and created. In 2008, Grayshan et al. developed a new analytical marine atmospheric spectrum about similar to Hill’s Salton Sea numerical spectrum (Grayshan et al. 2008). Several studies have been developed using this spectrum (Cheng et al. 2015; Baykal 2016; Zhang et al. 2017; Cui et al. 2018). Later, Khannous and Belafhal have proposed an improvement of the atmospheric spectral model for the marine environment (Khannous and Belafhal 2018). The analytical expression of this spectrum is formulated to fit the numerical spectrum of Hill’s Salton Sea by the expression of the spectrum proposed in the literature. The spectrum of Khannous and Belafhal is wide and applicable to marine atmospheric turbulence in various spaces. Recently, Chib et al. have studied the propagation properties of a partially coherent Generalized Flattened Hermite-Cosh-Gaussian beam in maritime atmospheric turbulence using the newly created spectrum (Chib et al. 2023).

Many theoretical models have been introduced to describe dark-hollow beams, such as the TEM*01 beam which is the most popular model (Balykin and Letokhov 1987), the hollow Gaussian beams (Cai et al. 2003), and the controllable dark beams (Mei and Zhao 2005). These beams have attracted interests because of their increasing applications in many fields, mainly atomic optics, binary optics, optical trapping of particles and medical sciences (Ping et al. 2002).

More recently, Saad and Belafhal have investigated a new light beam of Hollow higher-order cosh-Gaussian (HhCG) as a generalized beam of cosh Gaussian (Saad and Belafhal 2021). In this paper, it is reported that the normalized intensity distribution of this beam varies periodically during propagation in a quadratic index medium from dark hollow to central light spot in the first half of the period reversely to the second half. Also, the spatial characteristics of this beam through a fractional Fourier transform system have been examined (Saad and Belafhal 2021). The parametric characterization of HhCG beam has been developed in detail (Saad et al. 2022; Ebrahim et al. 2022). Recently, a general form of HhCG, whatever the order of cosh function, was introduced by Ebrahim et al. (2023). It is referred to as General Model vortex higher-order cosh-Gaussian beam (GMvHchGB). The propagation properties of this new hollow family of beams in a turbulent atmosphere have been studied. They found that, at large values of the turbulence, this beam is converted into a flat-top Gaussian-like beam in the far-field region. However, to our knowledge, the propagation of such beams through the turbulent maritime atmosphere has not been reported up to now. On the other hand, the study of the propagation of the GMvHchGB in a turbulent maritime atmosphere allows describing the propagation characteristics of some particular beams travelling through medium turbulent such as a fundamental Gaussian, Cosh-Gaussian, vortex Cosh-Gaussian and higher-order Cosh-Gaussian beams not treated before in the literature. Here our study will be more general and interesting. From this study, the intensity of the central area of GMvHchGB can be controlled by altering the beam parameters.

So, the present work is aimed at investigating the propagation of GMvHchGB in maritime turbulence. The rest of the paper is organized: in Sect. 2, the analytical expression of the intensity of GMvHchGB, in a marine environment, is derived by using the Huygens–Fresnel diffraction integral. Then, the intensity distribution features GMvHchGB are discussed with numerical examples in Sect. 3. The main results are summarized in the conclusion part.

2 Theoretical results

The source field of GMvHchGB can be expressed in Cartesian coordinates as (Ebrahim et al. 2023)

$$E\left( {x_{0} ,y_{0} ,0} \right) = A_{0} \cosh^{N} \left( {\Omega x_{0} } \right)\,\cosh^{N} \left( {\Omega y_{0} } \right)\exp \left( { - \frac{{x_{0}^{2} + y_{0}^{2} }}{{\omega_{0}^{2} }}} \right)\left( {x_{0} + iy_{0} } \right)^{l} ,$$
(1)

where (x0, y0) are the transverse coordinates of an arbitrary point at the source plane and ω0 is the beam waist radius of the Gaussian beam. In Eq. (1), \(\Omega\) is the decentered parameter of the cosh (.), it takes a real value, l being an integer that denotes the topological charge of the vortex, \(A_{0}\) is the amplitude of the GMvHchGB at the origin of the source plane and N represented the beam-order of the considered beams. The source field in Eq. (1) can be re-organized in the form as follows

$$\begin{aligned} E\left( {x_{0} ,y_{0} ,0} \right) = & \frac{{A_{0} }}{{2^{2N} }}\,\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \exp \left( {a_{m}^{2} + a_{n}^{2} } \right) \\ & \times \exp \left[ { - \left( {\frac{{x_{0} }}{{\omega_{0} }} - a_{m} } \right)^{2} } \right]\exp \left[ { - \left( {\frac{{y_{0} }}{{\omega_{0} }} - a_{n} } \right)^{2} } \right]\,\left( {x_{0} + iy_{0} } \right)^{l} , \\ \end{aligned}$$
(2)

where

\(a_{m} = \left( {m - \frac{N}{2}} \right)\sqrt \delta\), and \(a_{n} = \left( {n - \frac{N}{2}} \right)\sqrt \delta\), with \(\delta = \Omega^{2} \omega_{0}^{2} .\)

Within the frame of the paraxial approximation, a light beam propagating through the maritime atmospheric turbulence along the z-axis can be formulated by the extended Huygens–Fresnel diffraction integral (Born and Wolf 1999)

$$E\left( {\overrightarrow {r} ,z} \right) = - \frac{ik}{{2\pi z}}\exp \left( {ikz} \right)\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E\left( {\overrightarrow {{r_{0} }} ,0} \right)} } \exp \left\{ { - \frac{ik}{{2z}}\left( {\overrightarrow {{r_{0} }} - \overrightarrow {r} } \right)^{2} + \psi \left( {\overrightarrow {{r_{0} }} ,\overrightarrow {r} ,z} \right)} \right\}d\overrightarrow {{r_{0} }} ,$$
(3)

where \(\overrightarrow {{r_{0} }} = \left( {x_{0} ,y_{0} } \right)\) and \(\overrightarrow {r} = \left( {x,y} \right)\) are the transverse coordinates in the source and the receiver planes, respectively, z is the distance between the initial plane z = 0 and the receiver plane, and \(k = \frac{2\pi }{\lambda }\) is the wavenumber with \(\lambda\) is the wavelength of the source radiation in a vacuum. \(\psi \left( {\overrightarrow {{r_{0} }} ,\overrightarrow {r} ,z} \right)\) denotes the random part for the complex phase of a spherical wave spreading from the source plane to the output plane,

The average intensity of a GMvHchGB through maritime atmospheric turbulence is given by

$$\begin{aligned} \left\langle {I\left( {\overrightarrow {r} ,z} \right)} \right\rangle = & \frac{{k^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E\left( {x_{01} ,y_{01} ,0} \right)} } } } E^{*} \left( {x_{02} ,y_{02} ,0} \right) \\ & \times \exp \left\{ { - \frac{ik}{{2z}}\left[ {\left( {x_{01} - x} \right)^{2} + \left( {y_{01} - y} \right)^{2} - \left( {x_{02} - x} \right)^{2} - \left( {y_{01} - y} \right)^{2} } \right]} \right\} \\ & \times \left\langle {\exp \left[ {\psi \left( {\overrightarrow {{r_{01} }} ,\overrightarrow {r} } \right) + \psi^{ * } \left( {\overrightarrow {{r_{02} }} ,\overrightarrow {r} } \right)} \right]} \right\rangle d\overrightarrow {{r_{01} }} d\overrightarrow {{r_{02} }} , \\ \end{aligned}$$
(4)

where * and 〈 〉 denote the complex conjugation and the ensemble average over the medium statistics, respectively. Within the Rytov theory, the ensemble average in Eq. (4) is given by Andrews and Philips (1998)

$$\left\langle {\exp \left[ {\psi \left( {x_{01} ,y_{01} ,x,y} \right) + \psi^{*} \left( {x_{02} ,y_{02} ,x,y} \right)} \right]} \right\rangle = \exp \left[ { - \frac{{\left( {x_{01} - x_{02} } \right)^{2} + \left( {y_{01} - y_{02} } \right)^{2} }}{{\rho_{0}^{2} }}} \right],$$
(5)

where \(\rho_{0}\), which is the spatial coherence length of spherical wave propagation, is expressed in terms of the spatial power spectrum of the refractive index fluctuations \(\Phi_{n} \left( \kappa \right)\) in the integral form (Belafhal et al. 2021)

$$\rho_{0} = \left[ {\frac{{\pi^{2} }}{3}k^{2} z\int\limits_{0}^{ + \infty } {\kappa^{3} \Phi_{n} \left( \kappa \right)d\kappa } } \right]^{ - 1/2} ,$$
(6)

with κ is the spatial wavenumber and z being the axial distance between the source and the output planes. In the present study, we will adopt the model developed by Khannous and Belafhal (2018)

$$\Phi_{n} \left( \kappa \right) = 0.033C_{n}^{2} e^{{ - \frac{{\kappa^{2} }}{{\kappa_{Hn}^{2} }}}} \left( {1 + b\frac{\kappa }{{\kappa_{Hn} }}e^{{ - \alpha^{\prime } \frac{{\kappa^{2} }}{{\kappa_{Hn}^{2} }}}} + c\left( {\frac{\kappa }{{\kappa_{Hn} }}} \right)^{\frac{7}{6}} e^{{ - \beta \frac{{\kappa^{2} }}{{\kappa_{Hn}^{2} }}}} } \right)\frac{1}{{\left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{\frac{11}{6}} }},$$
(7)

where \(b = - 3.930,\) \(\,c = 6.109,\) \(\alpha^{\prime } = 204.278,\) \(\beta = 4.623,\) \(\kappa_{Hn} = {{6.262} \mathord{\left/ {\vphantom {{6.262} {l_{0} }}} \right. \kern-0pt} {l_{0} }}\) and \(\kappa_{0} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {L_{0} }}} \right. \kern-0pt} {L_{0} }},\) with \(l_{0}\) and \(L_{0}\) as the inner scale size and outer scale size of the turbulence and \(C_{n}^{2}\), which describes the turbulence level, is the constant of the refraction index structure.

Substituting Eq. (7) into Eq. (6), the integral part takes the following form

$$\begin{aligned} \int\limits_{0}^{ + \infty } {\kappa^{3} \Phi_{n} \left( \kappa \right)} d\kappa &= 0.033C_{n}^{2} \left[ {\int\limits_{0}^{ + \infty } {\kappa^{3} \frac{{e^{{ - {{\kappa^{2} } \mathord{\left/ {\vphantom {{\kappa^{2} } {\kappa_{Hn}^{2} }}} \right. \kern-0pt} {\kappa_{Hn}^{2} }}}} }}{{\left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{{{{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0pt} 6}}} }}d\kappa + \frac{b}{{\kappa_{Hn} }}\int\limits_{0}^{ + \infty } {\kappa^{4} \frac{{e^{{ - {{\kappa^{2} \left( {1 + \alpha ^{\prime}} \right)} \mathord{\left/ {\vphantom {{\kappa^{2} \left( {1 + \alpha ^{\prime}} \right)} {\kappa_{Hn}^{2} }}} \right. \kern-0pt} {\kappa_{Hn}^{2} }}}} }}{{\left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{{{{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0pt} 6}}} }}d\kappa } } } \right. \\ &\quad + \left. {\frac{c}{{\kappa_{Hn}^{{{7 \mathord{\left/ {\vphantom {7 6}} \right. \kern-0pt} 6}}} }}\int\limits_{0}^{ + \infty } {\kappa^{{{{25} \mathord{\left/ {\vphantom {{25} 6}} \right. \kern-0pt} 6}}} \frac{{e^{{ - {{\kappa^{2} \left( {1 + \beta } \right)} \mathord{\left/ {\vphantom {{\kappa^{2} \left( {1 + \beta } \right)} {\kappa_{Hn}^{2} }}} \right. \kern-0pt} {\kappa_{Hn}^{2} }}}} }}{{\left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{{{{11} \mathord{\left/ {\vphantom {{11} 6}} \right. \kern-0pt} 6}}} }}d\kappa } } \right], \\ \end{aligned}$$
(8)

and by recalling the integral formula (Belafhal et al. 2021)

$$\int\limits_{0}^{ + \infty } {\frac{{t^{2\mu - 1} e^{{ - \varepsilon t^{2} }} }}{{\left( {1 + ct^{2} } \right)^{\nu } }}} dt = \frac{\Gamma \left( \mu \right)}{{2c^{\mu } }}U\left( {\mu ;\mu + 1 - \nu ;\frac{\varepsilon }{c}} \right),$$
(9)

with \(c \ne 0\) and \(U\left( {a;b;z} \right)\) denoting the confluent hypergeometric of the second kind, the expression of the spatial coherence length is given by

$$\begin{aligned} \rho_{0} = & \left\{ {0.011\frac{{\pi^{2} k^{2} z}}{2}C_{n}^{2} \kappa_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} \left[ {U\left( {2;\frac{7}{6};\frac{{\kappa_{0}^{2} }}{{\kappa_{Hn}^{2} }}} \right) + \Gamma \left( \frac{5}{2} \right)b\left( {\frac{{\kappa_{0} }}{{\kappa_{Hn} }}} \right)U\left( {\frac{5}{2};\frac{5}{3};\frac{{\left( {1 + \alpha^{\prime } } \right)\kappa_{0}^{2} }}{{\kappa_{Hn}^{2} }}} \right)} \right.} \right. \\ & \left. {\left. { + \Gamma \left( {\frac{31}{{12}}} \right)c\left( {\frac{{\kappa_{0} }}{{\kappa_{Hn} }}} \right)^{{{7 \mathord{\left/ {\vphantom {7 6}} \right. \kern-0pt} 6}}} U\left( {\frac{31}{{12}};\frac{7}{4};\frac{{\left( {1 + \beta } \right)\kappa_{0}^{2} }}{{\kappa_{Hn}^{2} }}} \right)} \right]} \right\}^{ - 1/2} . \\ \end{aligned}$$
(10)

By using the binomial expansion (Gradshteyn and Ryzhik 1994)

$$(x_{0} + iy_{0} )^{l} = \sum\limits_{s = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ s \\ \end{array} } \right)x_{0}^{s} \left( {iy_{0} } \right)^{l - s} } ,$$
(11)

and these integrals and identities formulas (Belafhal et al. 2020; Gradshteyn and Ryzhik 1994)

$$\int\limits_{ - \infty }^{ + \infty } {x^{n} e^{{ - px^{2} + 2qx}} dx} = \sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right),$$
(12a)
$$\int\limits_{ - \infty }^{ + \infty } {x^{l} H_{m} (\alpha x)e^{{ - px^{2} + 2qx}} dx} = \frac{1}{{2^{l} }}\sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\sum\limits_{k = 0}^{{\left[ {m/2} \right]}} {\frac{{( - 1)^{k} m!}}{{k!\left( {m - 2k} \right)!}}} \left( {\frac{1}{i\sqrt p }} \right)^{m + l - 2k} H_{m + l - 2k} \left( {\frac{iq}{{\sqrt p }}} \right),$$
(12b)

with Re(p) > 0.

$$H_{n} (x + y) = \frac{1}{{2^{n/2} }}\sum\limits_{k = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)H_{k} \left( {\sqrt 2 x} \right)H_{n - k} \left( {\sqrt 2 y} \right),}$$
(12c)

and

$$H_{n} (x) = \sum\limits_{k = 0}^{{\left[ {n/2} \right]}} {\frac{{( - 1)^{k} n!}}{{k!\left( {n - 2k} \right)!}}} \left( {2x} \right)^{n - 2k} ,$$
(12d)

we can deduce, by substituting Eqs. (2) and (5) into Eq. (4), the analytical expression of the intensity distribution of GMvHchGB in turbulent maritime atmosphere as follows

$$\begin{aligned} \left\langle {I\left( {x,y,z} \right)} \right\rangle = & \frac{{k^{2} }}{{4z^{2} }}\frac{1}{{2^{{4N + {{3l} \mathord{\left/ {\vphantom {{3l} 2}} \right. \kern-0pt} 2}}} }}\frac{1}{{\sqrt {\alpha_{1,x} \alpha_{2,x} \alpha_{1,y} \alpha_{2,y} } }}\sum\limits_{m = 0}^{N} {\sum\limits_{n = 0}^{N} {\left( {\begin{array}{*{20}c} N \\ m \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)} \sum\limits_{s = 0}^{l} {\left( {\begin{array}{*{20}c} l \\ s \\ \end{array} } \right)\,\sum\limits_{{m^{\prime} = 0}}^{N} {\sum\limits_{{n^{\prime} = 0}}^{N} {\left( {\begin{array}{*{20}c} N \\ {m^{\prime } } \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} N \\ {n^{\prime } } \\ \end{array} } \right)} \sum\limits_{{s^{\prime} = 0}}^{l} {\left( {\begin{array}{*{20}c} l \\ {s^{\prime } } \\ \end{array} } \right)} } \\ & \times i^{{2l - s - s^{\prime } }} \exp \left( {\frac{{\gamma_{1,x}^{2} }}{{\alpha_{1,x} }} + \frac{{\gamma_{2,x}^{2} }}{{\alpha_{2,x} }}} \right)\left( {\frac{1}{{2i\sqrt {\alpha_{1,x} } }}} \right)^{s} \sum\limits_{h = 0}^{s} {\left( {\begin{array}{*{20}c} s \\ h \\ \end{array} } \right)} H_{s - h} \left( {\frac{{i\sqrt 2 \gamma_{1,x} }}{{\sqrt {\alpha_{1} } }}} \right) \\ & \times \sum\limits_{\mu = 0}^{{\left[ {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{\left( { - 1} \right)^{\mu } h!}}{{\mu !\left( {h - 2\mu } \right)!}}} \,\left( {\frac{\sqrt 2 }{{\rho_{0}^{2} \sqrt {\alpha_{1,x} \alpha_{2,x} } }}} \right)^{{h + s^{\prime } - 2\mu }} H_{{h + s^{\prime } - 2\mu }} \left( {\frac{{i\gamma_{2,x} }}{{\sqrt {\alpha_{2,x} } }}} \right) \\ & \times \exp \left( {\frac{{\gamma_{1,y}^{2} }}{{\alpha_{1,y} }} + \frac{{\gamma_{2,y}^{2} }}{{\alpha_{2,y} }}} \right)\,\left( {\frac{1}{{2i\sqrt {\alpha_{1,y} } }}} \right)^{l - s} \,\sum\limits_{{h^{\prime } = 0}}^{l - s} {\left( {\begin{array}{*{20}c} {l - s} \\ {h^{\prime } } \\ \end{array} } \right)} H_{{l - s - h^{\prime } }} \left( {\frac{{i\sqrt 2 \gamma_{1,y} }}{{\sqrt {\alpha_{1,y} } }}} \right) \\ & \times \sum\limits_{{\mu^{\prime } = 0}}^{{\left[ {{{h^{\prime } } \mathord{\left/ {\vphantom {{h^{\prime } } 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{\left( { - 1} \right)^{{\mu^{\prime } }} h^{\prime } !}}{{\mu^{\prime } !\left( {h^{\prime } - 2\mu^{\prime } } \right)!}}} \left( {\frac{\sqrt 2 }{{\rho_{0}^{2} \sqrt {\alpha_{1,x} \alpha_{2,y} } }}} \right)^{{h^{\prime } + l - s^{\prime } - 2\mu^{\prime } }} H_{{h^{\prime } + l - s^{\prime } - 2\mu^{\prime } }} \left( {\frac{{i\gamma_{2,y} }}{{\sqrt {\alpha_{2,y} } }}} \right), \\ \end{aligned}$$
(13)

where

$$\alpha_{1,x} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{ik}{{2z}},$$
(14a)
$$\alpha_{1,y} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{ik}{{2z}},$$
(14b)
$$\gamma_{1,x} = \frac{{a_{m} }}{{\omega_{0} }} + \frac{ikx}{{2z}},$$
(14c)
$$\gamma_{1,y} = \frac{{a_{n} }}{{\omega_{0} }} + \frac{iky}{{2z}},$$
(14d)
$$\alpha_{2,x} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}} - \frac{1}{{\alpha_{1,x} \rho_{0}^{4} }},$$
(14e)
$$\alpha_{2,y} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}} - \frac{1}{{\alpha_{1,y} \rho_{0}^{4} }},$$
(14f)
$$\gamma_{2,x} = \frac{{a_{{m^{\prime } }} }}{{\omega_{0} }} - \frac{ikx}{{2z}} + \frac{{\gamma_{1,x} }}{{\alpha_{1,x} \rho_{0}^{2} }},$$
(14g)

and

$$\gamma_{2,y} = \frac{{a_{{n^{\prime } }} }}{{\omega_{0} }} - \frac{iky}{{2z}} + \frac{{\gamma_{1,y} }}{{\alpha_{1,y} \rho_{0}^{2} }}.$$
(14h)

Equation (13) is the main result of the present study and represents the output field of the average intensity of the GMvHchGB in a medium turbulence maritime.

3 Numerical results

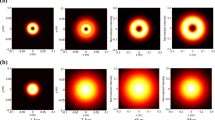
Based on the analytical expression obtained in Eq. (13), several numerical calculations were performed to illustrate the propagation features GMvHchGB propagating in maritime atmospheric turbulence as a function of the involved parameters. Figure 1 illustrates the normalized average intensity distribution of GMvHchGB in maritime atmospheric turbulence at several propagation distances and for three values of the constant of refraction index structure (\(C_{n}^{2} = 5.10^{ - 16} \,{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\), \(C_{n}^{2} = 10^{ - 15} \,{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\) and \(C_{n}^{2} = 10^{ - 14} \,{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\)).

Fig. 1
figure 1

Transversal intensity distribution of GMvHchGB propagating in maritime atmospheric turbulence at different propagation distances for a \(C_{n}^{2} = 5 \times 10^{ - 16} \;{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\), b \(C_{n}^{2} = 10^{ - 15} \;{\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\) and c \(C_{n}^{2} = 10^{ - 14} \;{\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\). With \(\lambda = 0.8\;\mu {\text{m}}\), \(\omega_{0} = 0.02\;{\text{m}}\), \(\Omega = 100\;{\text{m}}^{ - 1}\), N = 2 and l = 1

Full size image

These parameters are chosen to analyze the effect of the turbulence strength on the beam propagation. For all these figures, we chose the calculation parameters as \(A_{0} = 1\), \(L_{0} = 1\;{\text{m}}\) and \(l_{0} = 1\;{\text{mm}}\). It is seen from the plots of Fig. 1 that the GMvHchGB keeps its first profile invariant, until a certain propagation distance and then the beam gradually changes profile with two lobes then flat-topped to a Gaussian form in a far field, with the increasing of the propagation distance. We try to find the distance that corresponds to each profile change. The reason that GMvHchGB beam converts into Gaussian-like beam is because at long-distance propagation the output beam changes into a completely incoherent light due to the effect of the turbulent medium (\(\rho_{0} \to 0\) as z increases) (Eyyuboğlu et al. 2006). In addition, the graphs of Fig. 1 show that the central peak rises more quickly as the turbulence strength increases, i.e., the change of the profile of GMvHchGB is faster when the turbulence strength is stronger.

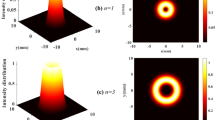
Figure 2 presents the influence of the decentered parameter Ω and the topological charge l on the evolution of the intensity distribution of GMvHchGB in maritime atmospheric turbulence at the propagation distance z = 1km and for N = 2.

Fig. 2
figure 2

Normalized intensity distribution of GMvHchGB propagating in maritime atmospheric turbulence with: z = 1 km, \(\lambda = 0.8\;\mu {\text{m}}\), \(C_{n}^{2} = 10^{ - 14} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\), \(\omega_{0} = 0.02\;{\text{m}}\) for: a \(l = 0\), b \(l = 1\), c \(l = 2\), d \(l = 3\), e \(l = 4\) and f \(l = 5\)

Full size image

From the illustrations in Fig. 2, one can clearly see that the GMvHchGB gradually turns into a dark hollow beam from a Gaussian beam like with an increase of Ω for l = 0. And for l > 0, the dark and the deep hollow area of GMvHchGB are wider with the increase of Ω. Also, one can clearly see that increasing the value of l increases the hollowness of the beam. The findings can be interpreted as follows. For a small value of the parameter Ω, the influence of the cosh function lessens.

In Fig. 3, we investigate the effect of Gaussian waist parameter on the normalized intensity distribution of GMvHchGB propagating in the maritime atmosphere. From this figure, it is found that the evolution speed of dark hollows is faster with the increase of the beam waist.

Fig. 3
figure 3

Normalized intensity distribution of GMvHchGB propagating in maritime atmospheric turbulence with: z = 1 km, \(\lambda = 0.8\;\mu {\text{m}}\), \(C_{n}^{2} = 10^{ - 14} \;{\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\), \(\Omega = 80\;{\text{m}}^{ - 1}\), \(N = 2\) and for: a \(l = 0\), b \(l = 1\), c \(l = 2\), d \(l = 3\), e \(l = 4\), f and \(l = 5\)

Full size image

Figure 4 gives the behavior of the normalized intensity distribution of GMvHchGB propagating in a maritime atmosphere for different values of the beam order N(= 0, 2, 4) and the topological charge l. We can see that the central bright region of GMvHchGB for N = l = 0 slowly turns into a dark hollow with the increase of the beam order. It was found that with the increase of N, the beam becomes hollowed. It is to be noted that the order of a laser beam refers to its spatial coherence. Spatial coherence is a property of light that describes the degree to which the phases of different parts of the beam are correlated with each other. The central dip of the GMvHchGB can be sustained for a large value of the beam waist and the beam order. This may be caused by the fluctuation of the source field increasing as the topological charge increases.

Fig. 4
figure 4

Normalized intensity distribution of GMvHchGB propagating in maritime atmospheric turbulence, with: z = 1 km, \(\lambda = 0.8\;\mu {\text{m}}\), \(\Omega = 80\;{\text{m}}^{ - 1}\), \(C_{n}^{2} = 10^{ - 14} \;{\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}\), \(\omega_{0} = 0.02\;{\text{m}}\) and for: a \(l = 0\), b \(l = 1\), c \(l = 2\), d \(l = 3\), e \(l = 4\), and f \(l = 5\)

Full size image

Figure 5 is plotted to see the variation of the intensity distribution of GMvHchGB by changing the hollowness parameters (l = 0, 1 and 2) for different values of \(C_{n}^{2}\).

Fig. 5
figure 5

Normalized intensity distribution of GMvHchGB propagating in maritime atmospheric turbulence, with: z = 1 km, \(\lambda = 0.8\;\mu {\text{m}}\), \(\Omega = 60\;{\text{m}}^{ - 1}\), \(N = 2\), \(\omega_{0} = 0.02\;{\text{m}}\) and for: a \(l = 0\), b \(l = 1\) and c \(l = 2\)

Full size image

From this figure, we can observe that the studied beam changes its shape slowly when the medium is more turbulent as the hollowness parameters increase. The results can be physically interpreted as follows. The higher turbulent strength leads to more significant and unpredictable changes in the refractive index of the medium. This affects the propagation of this laser beam which will lead to a fast transformation in its form.

4 Conclusions

In the present study, we have investigated the spreading features of GMvHchGB in maritime atmospheric turbulence. Based on the extended Huygens-Fresnel diffraction integral, the analytical expression of the average intensity is established for this family of laser beams in a marine environment. To study the impact of turbulent maritime environment on the properties of this beam, some numerical simulations are performed based on the derived formula and in terms of beam parameter settings. It is shown that GMvHchGB changes the profile shape at several propagation distances. This conversion is faster when the structure constant increases. In addition, the effect of the beam order, hollowness, decentered, and Gaussian waist parameters on the distribution intensity of GMvHchGB is discussed. It is to be noted that the results obtained in the present paper would be helpful for the optical-communications and remote sensing.