A climate-based malaria model with the use of bed nets

Abstract

Insecticide-treated bed nets (ITNs) are among the most important and effective intervention measures against malaria. In order to investigate the impact of bed net use on disease control, we formulate a periodic vector-bias malaria model incorporating the juvenile stage of mosquitoes and the use of ITNs. We derive the vector reproduction ratio $R_v$ and the basic reproduction ratio $R_0$. We show that the global dynamics of the model is completely determined by these two reproduction ratios. More precisely, the mosquito-free periodic solution is globally attractive if $R_v<1$; the unique disease-free periodic solution is globally attractive if $R_v>1$ and $R_0<1$; and the model admits a unique positive periodic solution and it is globally attractive if $R_v>1$ and $R_0>1$. Numerically, we study the malaria transmission case in Port Harcourt, Nigeria. Our findings show that the use of ITNs has a positive effect on reducing $R_0$, and that malaria may be eliminated from this area if over 75% of the human population were to use ITNs. The simulation about the long term behavior of solutions has good agreement with the obtained analytic result. Moreover, we find that the ignorance of the vector-bias effect may result in underestimation of the basic reproduction ratio $R_0$. Another notable result is that the infection risk would be underestimated if the basic reproduction ratio $[R_0]$ of the time-averaged autonomous system were used.

1 Introduction

Malaria is an infectious disease caused by five species of Plasmodium protozoan parasites and it is transmitted among humans by female Anopheles mosquitoes. Malaria remains the most severe and complex health challenge facing the vast majority of the countries in the sub-Saharan Africa (Uneke 2009). The World Health Organization estimated that there were 214 million malaria cases in 2015, resulting in about 438 thousand deaths (WHO 2015). Some commonly used strategies in combatting malaria include antimalarial drugs, larvicides, insecticides and intermittent preventive treatment. Insecticide-treated bed nets (ITNs) is the preferred tool for reducing malaria transmission and alleviating disease burden (D’Alessandro et al. 1995; Lengeler 2004). In addition to providing a physical barrier between humans and mosquitoes, the insecticide used to treat the bed nets repels mosquitoes, and if a mosquito fails to be repelled, it will often rest on the bed net, and may then be killed by contacting the insecticide (Birget and Koella 2015). A number of studies in Africa have demonstrated that high coverage of ITNs benefits not only the users but also the whole local community. Since the pioneering work of Ross (1911), who proved that malaria is transmitted by mosquitoes and proposed the first malaria model, much modeling work has been done to study malaria transmission dynamics (see, e.g., Arino et al. 2012; Aron and May 1982; Koella 1991; Lou and Zhao 2010; Macdonald 1957; Wang et al. 2014 and the references therein). In recent years, several models have been proposed to investigate the impact of bed net use (see, e.g., Agusto et al. 2013; Chitnis et al. 2010; Killeen and Smith 2007; Ngonghala et al. 2014, 2016 and the references therein).

Climate factors such as temperature, rainfall, humidity and wind patterns have great impact on mosquito reproduction and development and the parasite survival in mosquito. The development of the three aquatic stages of mosquitoes and their emergence to adulthood are strongly dependent on temperature (Ngarakana-Gwasira et al. 2014). For example, a change in temperature from 12 to $31\,^{\circ }$C reduces the number of days required for breeding from 65 to 7.3 days (Li et al. 2002). The development of the parasite within the mosquito (sporogonic cycle) also depends on temperature. It takes about 9–10 days at $28\,^{\circ }$C, but stops at temperatures below $16\,^{\circ }$C (Abebe et al. 2011). Thus, it is necessary to incorporate seasonality into a mathematical model of malaria transmission.

As mentioned in Ai et al. (2012), most of the existing malaria models include only adult mosquitoes. Indeed, mosquitoes undergo four distinct development stages during a lifetime: egg, larva, pupa, and adult. Quite a few researchers have incorporated the different stages of mosquitoes into their models (see, e.g., Ai et al. 2012; Li 2009; Lou and Zhao 2011; Ngarakana-Gwasira et al. 2014; Wonham et al. 2004). While it is appropriate to assume that only adult mosquitoes are involved in the malaria transmission, the dynamics of the juvenile stage have significant effects on the dynamics of the mosquito population, and hence the disease transmission dynamics (Ai et al. 2012). In particular, since larval control is a hot recommended strategy in fighting against malaria, it is necessary to develop a mathematical model which includes the two key stages of mosquitoes (juvenile and adult) so that we can better understand the mosquito population dynamics and gain some insights into the design of disease control strategies.

Recent experimental and field study results indicate that malaria parasites manipulate a host to be more attractive to mosquitoes via chemical substances (see, e.g., Lacroix et al. 2005). Only a few mathematical models have accounted for the greater attractiveness of infectious humans to mosquitoes (see, e.g., Chamchod and Britton 2011; Kingsolver 1987; Ngonghala et al. 2016; Wang and Zhao 2017; Xu and Zhao 2012 and the references therein). Incorporating such vector-bias effect in malaria models will give us a better description and a more accurate quantification of the disease dynamics.

The purpose of this paper is to develop an ordinary differential equations model that, for the first time, incorporates the juvenile mosquito stage, the impact of ITNs use, the vector-bias effect and seasonality simultaneously. We use the theory of dynamical systems to obtain the qualitative properties of human and mosquito population sizes.

The rest of the paper is organized as follows. In the next section, we formulate the model and give the underlying assumptions. In the following section, we establish the threshold dynamics of the model in terms of the vector reproduction ratio and the basic reproduction ratio. In Sect. 4, we do a case study for Port Harcourt, Nigeria. A brief discussion concludes the paper.

2 Model formulation

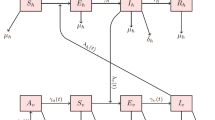
In order to formulate the model, we consider two stages of mosquitoes: the juvenile stage and the adult one. By juvenile, we mean any of the three aquatic stages: egg, larva and pupa. Let $L_v(t)$ be the number of juvenile mosquitoes at time t. The adult mosquito population is grouped into two compartments, susceptible and infectious, the numbers of which at time t are denoted by $S_v(t)$ and $I_v(t)$, respectively. Letting $N_v(t)$ be the number of all adult mosquitoes at time t, we have $N_v(t)=S_v(t)+I_v(t)$. Let $I_h(t)$ be the number of infectious humans at time t. We assume that the total human population size $N_h$ remains constant for a specified region. Then the number of susceptible humans at time t is $N_h-I_h(t)$. To study the human population dynamics we only need to know how $I_h(t)$ changes with time t. Thus, for the human population we only consider the equation for $I_h(t)$ in our model. Let $d_h$ be the human natural death rate. We use $\rho$ to denote the recovery and disease-induced death rate of humans. Let $\lambda _L(t)$ and $\mu _L(t)$ be the birth rate and the natural death rate of juvenile mosquitoes, respectively. According to Li (2009) and Reiskind and Lounibos (2009), larval crowding and competition for limited resources are quite common in some breeding sites. To account for such a phenomenon, we also incorporate the density-dependent mortality rate of juvenile mosquitoes, denoted by $\alpha$. We use $\lambda _v(t)$ to denote the birth rate of adult mosquitoes.

Following Agusto et al. (2013), we model the biting rate of mosquitoes by the linearly decreasing function of the proportion of ITNs use k:

$$\begin{aligned} \beta (t,k)=\beta _v(t)-k(\beta _v(t)-\beta _r(t)), \quad 0\le k\le 1, \end{aligned}$$

where $\beta _v(t)$ is the natural biting rate of mosquitoes, and $\beta _r(t)$ is the reduced biting rate of mosquitoes due to the physical barrier provided by ITNs between the human and the mosquito. If $k=0$, which means that no one uses ITNs, then the biting rate would remain at its natural level $\beta _v(t)$. The biting rate will be reduced to a minimum value $\beta _r(t)$ if $k=1$, when everyone uses ITNs. We model the death rate of adult mosquitoes by the following linearly increasing function of k:

$$\begin{aligned} \mu (t,k)=\mu _v(t)+\bar{\mu }k,\quad 0\le k\le 1, \end{aligned}$$

where $\mu _v(t)$ is the natural death rate of adult mosquitoes and $\bar{\mu }k$ is mosquitoes’ death rate due to their contact with the insecticide on bed nets.

Let p and l be the probabilities that a mosquito arrives at a human at random and picks the human if he is infectious and susceptible, respectively. Since infectious humans are more attractive to mosquitoes, we assume that $p\ge l$. We denote the biting rate of mosquitoes by $\beta (t,k)$, which is the number of bites per mosquito per unit time at time t. Then $\beta (t,k)I_v(t)$ is the number of bites by all infectious mosquitoes per unit time at time t. We assume that a mosquito does not bite the same person for more than once. Since the total number of bites made by mosquitoes equals to the number of bites received by humans (Bowman et al. 2005), $\beta (t,k)I_v(t)$ is also the number of humans that are bitten by infectious mosquitoes per unit time at time t . Among all the humans that are bitten by infectious mosquitoes, only those originally susceptible ones may contribute to the increase of $I_h(t)$. Hence, we need to derive the probability that a human is susceptible under the condition that a mosquito picks him. Obviously, this probability equals to $\frac{l[N_h-I_h(t)]}{pI_h(t)+l[N_h-I_h(t)]}$, the ratio between the total bitten susceptible humans and the total bitten humans. For simplicity, we neglect both the intrinsic incubation period within humans and the extrinsic incubation period within mosquitoes. Thus, the number of newly occurred infectious humans per unit time at time t is

$$\begin{aligned} c\beta (t,k)\frac{l[N_h-I_h(t)]}{pI_h(t)+l[N_h-I_h(t)]}I_v(t), \end{aligned}$$

where c is the probability of transmission of infection from an infectious mosquito to a susceptible human given that the contact between the two occurs. Similarly, $\frac{pI_h(t)}{pI_h(t)+l[N_h-I_h(t)]}$ is the probability that a human is infectious under the condition that a mosquito picks him. Then the number of newly occurred infectious mosquitoes per unit time at time t is

$$\begin{aligned} b\beta (t,k)\frac{pI_h(t)}{pI_h(t)+l[N_h-I_h(t)]}S_v(t), \end{aligned}$$

where b is the transmission probability per bite from infectious humans to susceptible mosquitoes. The model system is governed by

$$\begin{aligned} \frac{dL_v(t)}{dt}= & {} \lambda _L(t)(S_v(t)+I_v(t))-\mu _L(t)L_v(t)-\alpha L_v(t)^2-\lambda _v(t)L_v(t),\nonumber \\ \frac{dS_v(t)}{dt}= & {} \lambda _v(t)L_v(t)-b\beta (t,k)\frac{pI_h(t)}{pI_h(t)+l(N_h-I_h(t))}S_v(t) -\mu (t,k)S_v(t), \nonumber \\ \frac{dI_v(t)}{dt}= & {} b\beta (t,k)\frac{pI_h(t)}{pI_h(t)+l(N_h-I_h(t))}S_v(t) -\mu (t,k)I_v(t),\nonumber \\ \frac{dI_h(t)}{dt}= & {} c\beta (t,k)\frac{l(N_h-I_h(t))}{pI_h(t)+l(N_h-I_h(t))} I_v(t)-(d_h+\rho )I_h(t), \end{aligned}$$

(1)

where all constant parameters are positive, and $\lambda _L(t)$, $\mu _L(t)$, $\lambda _v(t)$, $\beta (t,k)$, $\mu (t,k)$ are positive, continuous functions $\omega$-periodic in time t for some $\omega >0$. For reader’s convenience, we list all the parameters and their biological interpretations in Table 1.

Table 1 Biological interpretations for parameters of model (1)

3 Threshold dynamics

Basic reproduction ratio is an important threshold parameter in epidemiology. It measures the effort to control the disease. The works of $R_0$ by Diekmann et al. (1990) and van den Driessche and Watmough (2002) have found numerous applications in the study of infectious disease models. There are also some investigations on $R_0$ for population models in a periodic environment (see, e.g., Bacaër and Ait Dads 2012; Bacaër and Guernaoui 2006; Inaba 2012; Thieme 2009; Wang and Zhao 2008; Zhao 2017 and the references therein). In what follows, we use the theory developed in Wang and Zhao (2008) to derive two threshold parameters for the model: the vector reproduction ratio $R_v$ and the basic reproduction ratio $R_0$.

Note that system (1) is equivalent to the following one:

$$\begin{aligned} \frac{dL_v(t)}{dt}= & {} \lambda _L(t)N_v(t)-\mu _L(t)L_v(t)-\alpha L_v(t)^2-\lambda _v(t)L_v(t), \nonumber \\ \frac{dN_v(t)}{dt}= & {} \lambda _v(t)L_v(t) -\mu (t,k)N_v(t), \nonumber \\ \frac{dI_v(t)}{dt}= & {} b\beta (t,k)\frac{pI_h(t)}{pI_h(t)+l(N_h-I_h(t))} (N_v(t)-I_v(t))-\mu (t,k)I_v(t),\nonumber \\ \frac{dI_h(t)}{dt}= & {} c\beta (t,k)\frac{l(N_h-I_h(t))}{pI_h(t)+l(N_h-I_h(t))} I_v(t)-(d_h+\rho )I_h(t). \end{aligned}$$

(2)

Then the mosquito population is described by

$$\begin{aligned} \begin{aligned} \frac{dL_v(t)}{dt}&= \lambda _L(t)N_v(t)-\mu _L(t)L_v(t)-\alpha L_v(t)^2-\lambda _v(t)L_v(t), \\ \frac{dN_v(t)}{dt}&= \lambda _v(t)L_v(t) -\mu (t,k)N_v(t). \end{aligned} \end{aligned}$$

(3)

Linearizing system (3) at (0, 0), we get the following linear cooperative system:

$$\begin{aligned} \begin{aligned} \frac{dL_v(t)}{dt}&= \lambda _L(t)N_v(t)-(\mu _L(t)+\lambda _v(t))L_v(t), \\ \frac{dN_v(t)}{dt}&= \lambda _v(t)L_v(t) -\mu (t,k)N_v(t). \end{aligned} \end{aligned}$$

(4)

We rewrite system (4) as $\frac{dv}{dt}=(\tilde{F}(t)-\tilde{V}(t))v$, where

$$\begin{aligned} \tilde{F}(t)=\begin{bmatrix} 0&\quad \lambda _L(t)\\ 0&\quad 0 \end{bmatrix},\quad \tilde{V}(t)=\begin{bmatrix} \mu _L(t)+\lambda _v(t)&\quad 0\\ -\lambda _v(t)&\quad \mu (t,k)\end{bmatrix}. \end{aligned}$$

Let $\tilde{Y}(t,s), t\ge s$, be the evolution operator of the linear periodic system

$$\begin{aligned} \frac{dy}{dt}=-\tilde{V}(t)y. \end{aligned}$$

That is, for each $s\in \mathbb {R}$, the $2\times 2$ matrix $\tilde{Y}(t,s)$ satisfies

$$\begin{aligned} \frac{d}{dt}\tilde{Y}(t,s)=-\tilde{V}(t)\tilde{Y}(t,s),\quad \forall t\ge s,\quad \tilde{Y}(s,s)=I, \end{aligned}$$

where I is the $2\times 2$ identity matrix.

Let $C_\omega$ be the ordered Banach space of all $\omega$-periodic functions from $\mathbb {R}$ to $\mathbb {R}^2$, equipped with the maximum norm and the positive cone $C_\omega ^+:=\{\phi \in C_\omega : \phi (t)\ge 0, \forall t\in \mathbb {R}\}$. According to Wang and Zhao (2008, Sect. 2), we assume that $\phi (s)\in C_\omega$ is the initial distribution of juvenile and adult mosquitoes. Then $\tilde{F}(s)\phi (s)$ is the distribution of new juvenile mosquitoes produced by the adult ones who were introduced at time s. Given $t\ge s$, then $\tilde{Y}(t,s)\tilde{F}(s)\phi (s)$ gives the distribution of those mosquitoes who were newly born into the juvenile mosquito compartment at time s and remain alive (either as juvenile mosquitoes or as adult ones) at time t. It follows that

$$\begin{aligned} \psi (t):=\int _{-\infty }^t\tilde{Y}(t,s)\tilde{F}(s)\phi (s)ds=\int _0^{\infty }\tilde{Y}(t,t-a)\tilde{F}(t-a)\phi (t-a)da \end{aligned}$$

is the distribution of accumulative new juvenile and adult mosquitoes at time t produced by all those juvenile and adult mosquitoes $\phi (s)$ introduced at previous time to t.

We define a linear operator $\tilde{L} : C_\omega \rightarrow C_\omega$ by

$$\begin{aligned} (\tilde{L}\phi )(t)=\int _0^{\infty }\tilde{Y}(t,t-a)\tilde{F}(t-a)\phi (t-a)da,\quad \forall t\in \mathbb {R},\quad \phi \in C_\omega . \end{aligned}$$

It then follows from Wang and Zhao (2008) that the vector reproduction ratio is $R_v:=\rho (\tilde{L})$, the spectral radius of $\tilde{L}$. Let $r_1$ be the principal Floquét multiplier of system (4), that is, the spectral radius of the Poincaré map associated with system (4). By Wang and Zhao (2008, Theorem 2.2), $R_v-1$ has the same sign as $r_1-1$. As a straightforward consequence of Zhao (2003, Theorem 3.1.2), we have the following result.

Lemma 1

The following statements are valid:

• (i) If $R_v\le 1$, then (0, 0) is globally attractive for system (3) in $\mathbb {R}_+^2$;

• (ii) If $R_v>1,$ then system (3) admits a unique positive $\omega$-periodic solution $(L_v^*(t), N_v^*(t))$, which is globally attractive for system (3) in $\mathbb {R}_+^2{\setminus }\{(0,0)\}$.

Let $W:=\mathbb {R}_+^3\times [0,N_h]$. We then have the following result for system (2).

Lemma 2

For any $\varphi \in W$, system (2) has a unique nonnegative bounded solution $u(t,\varphi )$ on $[0,\infty )$ with $u(0)=\varphi$, and $u(t,\varphi )\in W$ for all $t\ge 0$.

Proof

For any $\varphi =(\varphi _1,\varphi _2,\varphi _3,\varphi _4)\in W$, we define

$$\begin{aligned} \hat{f}(t,\varphi )= \left( \begin{array}{c} \lambda _L(t)\varphi _2-\mu _L(t)\varphi _1 -\alpha \varphi _1^2-\lambda _v(t)\varphi _1 \\ \lambda _v(t)\varphi _1-\mu (t,k)\varphi _2 \\ b\beta (t,k)\frac{p\varphi _4(\varphi _2-\varphi _3)}{p\varphi _4+l(N_h-\varphi _4)}-\mu (t,k)\varphi _3 \\ c\beta (t,k)\frac{l(N_h-\varphi _4)\varphi _3}{p\varphi _4+l(N_h-\varphi _4)}-(d_h+\rho )\varphi _4 \end{array} \right) . \end{aligned}$$

Since $\hat{f}(t,\varphi )$ is continuous in $(t,\varphi )\in \mathbb {R}_+\times W$, and $\hat{f}(t,\varphi )$ is Lipschitz in $\varphi$ on each compact subset of W, it follows that system (2) has a unique solution $u(t,\varphi )$ on its maximal interval $[0,\sigma _\varphi )$ of existence with $u(0)=\varphi$ (see, e.g., Hale and Verduyn Lunel 1993, Theorems 2.2.1 and 2.2.3).

Let $\varphi =(\varphi _1,\varphi _2,\varphi _3,\varphi _4)\in W$ be given. If $\varphi _i=0$ for some $i\in \{1,2,3,4\}$, then $\hat{f}_i(t,\varphi )\ge 0$. If $\varphi _4=N_h$, then $\hat{f}_4(t,\varphi )\le 0$. By Smith (1995, Theorem 5.2.1 and Remark 5.2.1), it follows that for any $\varphi \in W$, the unique solution $u(t,\varphi )$ of system (2) with $u(0)=\varphi$ satisfies $u(t,\varphi )\in W$ for all $t\in [0,\sigma _\varphi )$.

Clearly, $0\le u_4(t,\varphi )\le N_h$ for all $t\in [0,\sigma _\varphi )$. It follows from Lemma 1 that there exists $B_1>0$ and $B_2>0$ such that $u_1(t,\varphi )\le B_1$, $u_2(t,\varphi )\le B_2, \forall t\in [0,\sigma _\varphi )$. In view of the third equation of system (2), we have

$$\begin{aligned} \frac{du_3(t,\varphi )}{dt}\le b\beta (t,k)B_2 -(b\beta (t,k)+\mu (t,k))u_3(t,\varphi ). \end{aligned}$$

Hence, $u_3(t,\varphi )$ is also bounded on $[0,\sigma _\varphi )$. Then Hale and Verduyn Lunel (1993 Theorem 2.3.1) implies that $\sigma _\varphi =\infty$. $\square$

If $\lim _{t\rightarrow \infty }(L_v(t)-L_v^*(t))= \lim _{t\rightarrow \infty }(N_v(t)-N_v^*(t))=0$, the last two equations in system (2) give rise to the following limiting system:

$$\begin{aligned} \begin{aligned} \frac{dI_v(t)}{dt}&= b\beta (t,k)\frac{pI_h(t)}{pI_h(t)+l(N_h-I_h(t))} (N_v^*(t)-I_v(t))-\mu (t,k)I_v(t),\\ \frac{dI_h(t)}{dt}&= c\beta (t,k)\frac{l(N_h-I_h(t))}{pI_h(t)+l(N_h-I_h(t))} I_v(t)-(d_h+\rho )I_h(t). \end{aligned} \end{aligned}$$

(5)

The following result implies that the domain $G(t):=[0,N_v^*(t)]\times [0,N_h]$ is positively invariant for system (5).

Lemma 3

For any $\varphi =(\varphi _1,\varphi _2)\in G(0)$, system (5) has a unique solution $v(t,\varphi )$ with $v(0)=\varphi$ and $(I_v(t,\varphi ),I_h(t,\varphi ))\in G(t), \forall t\ge 0$.

Proof

For any $\varphi \in G(0)$, define

$$\begin{aligned} \tilde{f}(t,\varphi )= \left( \begin{array}{c} b\beta (t,k)\frac{p\varphi _2(N_v^*(t)-\varphi _1)}{p\varphi _2+l(N_h-\varphi _2)}-\mu (t,k)\varphi _1 \\ c\beta (t,k)\frac{l(N_h-\varphi _2)\varphi _1}{p\varphi _2+l(N_h-\varphi _2)}-(d_h+\rho )\varphi _2 \end{array} \right) . \end{aligned}$$

Since $\tilde{f}$ is continuous in $(t,\varphi )\in \mathbb {R}\times G(0)$ and $\tilde{f}$ is Lipschitz in $\varphi$ on each compact subset of G(0), it follows that system (5) has a unique solution $v(t,\varphi )$ with $v(0)=\varphi$ on its maximal interval $[0,\sigma _\varphi )$ of existence.

Let $\varphi =(\varphi _1,\varphi _2)\in G(0)$ be given. If $\varphi _1=0$, then $\tilde{f}_1(t,\varphi )\ge 0$. If $\varphi _2=0$, then $\tilde{f}_2(t,\varphi )\ge 0$. If $\varphi _2=N_h$, then $\tilde{f}_2(t,\varphi )\le 0$. By Smith (1995, Theorem 5.2.1 and Remark 5.2.1), it follows that the unique solution $v(t,\varphi )$ of system (5) with $v(0)=\varphi$ satisfies $v(t,\varphi )\in \mathbb {R}_+\times [0,N_h]$.

It remains to prove that $v_1(t)\le N_v^*(t), \forall t\in [0,\sigma _\varphi )$. Suppose this does not hold. Then there exists $t_0\in [0,\sigma _\varphi )$ and $\epsilon _0>0$ such that

$$\begin{aligned} v_1(t_0)=N_v^*(t_0)\quad \text {and}\quad v_1(t)>N_v^*(t),\quad \forall t\in (t_0,t_0+\epsilon _0). \end{aligned}$$

Since

$$\begin{aligned} \frac{dv_1(t_0)}{dt}=-\mu (t_0,k)v_1(t_0)= -\mu (t_0,k)N_v^*(t_0)<\frac{dN_v^*(t_0)}{dt}, \end{aligned}$$

there exists $\epsilon _1\in (0,\epsilon _0)$ such that $v_1(t)\le N_v^*(t), \forall t\in (t_0,t_0+\epsilon _1)$, which is a contradiction. This proves that $v(t,\varphi )\in G(t), \forall t\in [0,\sigma _\varphi )$. Clearly, $v(t,\varphi )$ is bounded on $[0,\sigma _\varphi )$, and hence, Haleand Verduyn Lunel (1993, Theorem 2.3.1) implies that $\sigma _\varphi =\infty$. $\square$

Linearizing system (5) at (0, 0), we get the following linear system

$$\begin{aligned} \begin{aligned} \frac{dI_v(t)}{dt}&= -\mu (t,k)I_v(t)+b\beta (t,k)\frac{pN_v^*(t)}{lN_h}I_h(t),\\ \frac{dI_h(t)}{dt}&= c\beta (t,k)I_v(t)-(d_h+\rho )I_h(t). \end{aligned} \end{aligned}$$

(6)

We rewrite system (6) as $\frac{du}{dt}=(F(t)-V(t))u$, where

$$\begin{aligned} F(t)=\begin{bmatrix} 0&b\beta (t,k)\frac{pN_v^*(t)}{lN_h}\\ c\beta (t,k)&0 \end{bmatrix},\quad V(t)=\begin{bmatrix} \mu (t,k)&0\\ 0&d_h+\rho \end{bmatrix}. \end{aligned}$$

Let $Y(t,s), t\ge s$, be the evolution operator of the linear periodic system

$$\begin{aligned} \frac{dy}{dt}=-V(t)y. \end{aligned}$$

That is, for each $s\in \mathbb {R}$, the $2\times 2$ matrix Y(t, s) satisfies

$$\begin{aligned} \frac{d}{dt}Y(t,s)=-V(t)Y(t,s),\quad \forall t\ge s,\quad Y(s,s)=I, \end{aligned}$$

where I is the $2\times 2$ identity matrix.

We assume that $\varphi (s)\in C_\omega$ is the initial distribution of infectious mosquitoes and infectious humans. Then $F(s)\varphi (s)$ is the distribution of new infections produced by the infectious mosquitoes and infectious humans who were introduced at time s. Given $t\ge s$, then $Y(t,s)F(s)\varphi (s)$ gives the distribution of those infectious mosquitoes and infectious humans who were newly infected at time s and remain in the infectious compartments at time t. It follows that

$$\begin{aligned} \int _{-\infty }^tY(t,s) F(s)\varphi (s)ds=\int _0^{\infty }Y(t,t-a) F(t-a)\varphi (t-a)da \end{aligned}$$

is the distribution of accumulative new infections at time t produced by all those infectious mosquitoes and infectious humans $\varphi (s)$ introduced at previous time to t.

We define a linear operator $L: C_\omega \rightarrow C_\omega$ by

$$\begin{aligned} (L\varphi )(t)=\int _0^{\infty }Y(t,t-a) F(t-a)\varphi (t-a)da,\quad \forall t\in \mathbb {R},\quad \varphi \in C_\omega . \end{aligned}$$

It then follows from Wang and Zhao (2008) that the basic reproduction ratio is $R_0:=\rho (L)$, the spectral radius of L. The following lemma gives a threshold type result for the limiting system (5).

Lemma 4

The following statements are valid:

• (i) If $R_0\le 1$, then (0, 0) is globally attractive for system (5) in G(0);

• (ii) If $R_0>1,$ then system (5) admits a unique positive $\omega$-periodic solution $(I_v^*(t), I_h^*(t))$, which is globally attractive for system (5) in $G(0){\setminus }\{(0,0)\}$.

Proof

Let S(t) be the time-t map of system (5), that is, $S(t)(I_v(0), I_h(0))=(I_v(t), I_h(t)), t\ge 0$, where $(I_v(t), I_h(t))$ is the unique solution of system (5) with $(I_v(0), I_h(0))\in G(0).$ It follows from Lemma 3 that S(t) maps G(0) into G(t), and $S:=S(\omega ): G(0)\rightarrow G(\omega )=G(0)$ is the Poincaré map associated with system (5).

Let $(\bar{y}_1(0), \bar{y}_2(0))\ge (y_1(0), y_2(0))$. Let $(\bar{y}_1(t), \bar{y}_2(t))$ and $(y_1(t), y_2(t))$ be the solutions of system (5) with initial values $(\bar{y}_1(0), \bar{y}_2(0))$ and $(y_1(0), y_2(0))$, respectively. Then the comparison theorem for cooperative ordinary differential systems implies that $(\bar{y}_1(t),\bar{y}_2(t))\ge (y_1(t),y_2(t)), \forall t\ge 0,$ that is, $S(t): G(0)\rightarrow G(t)$ is monotone for each $t\ge 0$.

Next, we show that $S(t): G(0)\rightarrow G(t)$ is strongly monotone for each $t>0$. Suppose $(\bar{y}_1(0), \bar{y}_2(0))>(y_1(0), y_2(0))$. Then the comparison theorem for cooperative ordinary differential systems implies that

$$\begin{aligned} (\bar{y}_1(t), \bar{y}_2(t))>(y_1(t), y_2(t)), \quad \forall t\ge 0. \end{aligned}$$

We proceed with two cases.

Case 1. $\bar{y}_1(0)>y_1(0).$

Let

$$\begin{aligned} g_1(y):=b\beta (t,k)\frac{py_2(t)}{(p-l)y_2(t)+lN_h}(N_v^*(t)-y) -\mu (t,k)y. \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \frac{d\bar{y}_1(t)}{dt}&= b\beta (t,k)\frac{p\bar{y}_2(t)}{(p-l)\bar{y}_2(t)+lN_h}(N_v^*(t)-\bar{y}_1(t))-\mu (t,k)\bar{y}_1(t)\\&\ge b\beta (t,k)\frac{py_2(t)}{(p-l)y_2(t)+lN_h} (N_v^*(t)-\bar{y}_1(t))-\mu (t,k)\bar{y}_1(t)\\&= g_1(\bar{y}_1(t)), \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \frac{d\bar{y}_1(t)}{dt}-g_1(\bar{y}_1(t))\ge 0=\frac{dy_1(t)}{dt}-g_1(y_1(t)), \quad \forall t\ge 0. \end{aligned}$$

Since $\bar{y}_1(0)>y_1(0)$, Walter (1997, Theorem 4) implies that $\bar{y}_1(t)>y_1(t), \forall t\ge 0$.

To prove $\bar{y}_2(t)>y_2(t), \forall t>0$, we first prove that for any $\epsilon >0$, there exists an open interval $(a,b)\subset [0,\epsilon ]$ such that $N_h>\bar{y}_2(t), \forall t\in (a,b)$. Otherwise, there exists $\epsilon _0>0$ such that $N_h=\bar{y}_2(t), \forall t\in (0,\epsilon _0)$. It then follows from the second equation of system (5) that $0=-(d_h+\rho )N_h$, which is a contradiction. Let

$$\begin{aligned} f_1(y):=c\beta (t,k)\frac{l(N_h-y)}{(p-l)y+lN_h}y_1(t) -(d_h+\rho )y. \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned} \frac{d\bar{y}_2(t)}{dt}&= c\beta (t,k)\frac{l(N_h-\bar{y}_2(t))}{(p-l)\bar{y}_2(t)+lN_h}\bar{y}_1(t)-(d_h+\rho )\bar{y}_2(t)\\&> c\beta (t,k)\frac{l(N_h-\bar{y}_2(t))}{(p-l)\bar{y}_2(t)+lN_h}y_1(t)-(d_h+\rho )\bar{y}_2(t)\\&= f_1(\bar{y}_2(t)),\quad \forall t\in (a,b), \end{aligned} \end{aligned}$$

and hence,

$$\begin{aligned} \frac{d\bar{y}_2(t)}{dt}-f_1(\bar{y}_2(t))>0= \frac{dy_2(t)}{dt}-f_1(y_2(t)), \quad \forall t\in (a,b). \end{aligned}$$

Since $\bar{y}_2(0)\ge y_2(0)$, it follows from Walter (1997, Theorem 4) that $\bar{y}_2(t)>y_2(t), \forall t>0.$

Case 2. $\bar{y}_1(0)=y_1(0).$

Since $(\bar{y}_1(0),\bar{y}_2(0))>(y_1(0),y_2(0))$ and $\bar{y}_1(0)=y_1(0)$, we must have $\bar{y}_2(0)>y_2(0)$. By similar arguments to those in Case 1, we see that for any $\epsilon >0$, there exists an open interval $(a,b)\subset [0,\epsilon ]$ such that $N_h>\bar{y}_2(t), \forall t\in (a,b)$. Then we have

$$\begin{aligned} \begin{aligned} \frac{d\bar{y}_2(t)}{dt}&= c\beta (t,k)\frac{l(N_h-\bar{y}_2(t))}{(p-l)\bar{y}_2(t)+lN_h}\bar{y}_1(t)-(d_h+\rho )\bar{y}_2(t)\\&\ge c\beta (t,k)\frac{l(N_h-\bar{y}_2(t))}{(p-l)\bar{y}_2(t)+lN_h}y_1(t)-(d_h+\rho )\bar{y}_2(t)\\&= f_1(\bar{y}_2(t)),\quad \forall t\in (a,b), \end{aligned} \end{aligned}$$

and hence,

$$\begin{aligned} \frac{d\bar{y}_2(t)}{dt}-f_1(\bar{y}_2(t))\ge 0= \frac{dy_2(t)}{dt}-f_1(y_2(t)), \quad \forall t\in (a,b). \end{aligned}$$

Since $\bar{y}_2(0)> y_2(0)$, it follows from Walter (1997, Theorem 4) that $\bar{y}_2(t)>y_2(t), \forall t>0.$

To prove $\bar{y}_1(t)>y_1(t), \forall t>0$, we first prove that for any $\epsilon >0$, there exists $(a_1,b_1)\subset [0,\epsilon ]$ such that $\bar{y}_1(t)<N^*_v(t), \forall t\in (a_1,b_1)$. Otherwise, there exists $\epsilon _1>0$ such that $\bar{y}_1(t)=N_v^*(t), \forall t\in (0,\epsilon _1)$. By the first equation of system (5), we have

$$\begin{aligned} \frac{d\bar{y}_1(t)}{dt}=\frac{dN_v^*(t)}{dt}=-\mu (t,k)N_v^*(t),\quad t\in (0,\epsilon _1), \end{aligned}$$

which contradicts the fact that

$$\begin{aligned} \frac{dN_v^*(t)}{dt}=\lambda _v(t)L_v^*(t)-\mu (t,k)N_v^*(t). \end{aligned}$$

Let

$$\begin{aligned} g_1(t):=b\beta (t,k)\frac{py_2(t)}{(p-l)y_2(t)+lN_h}(N_v^*(t)-y)-\mu (t,k)y. \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \frac{d\bar{y}_1(t)}{dt}&= b\beta (t,k)\frac{p\bar{y}_2(t)}{(p-l)\bar{y}_2(t)+lN_h}(N_v^*(t)-\bar{y}_1(t))-\mu (t,k)\bar{y}_1(t)\\&> b\beta (t,k)\frac{p y_2(t)}{(p-l) y_2(t)+lN_h}(N_v^*(t)-\bar{y}_1(t))-\mu (t,k)\bar{y}_1(t)\\&= g_1(\bar{y}_1(t)),\quad \forall t\in (a_1,b_1), \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \frac{\bar{y}_1(t)}{dt}-g_1(\bar{y}_1(t))>0=\frac{dy_1(t)}{dt}-g_1(y_1(t)), \quad \forall t\in (a_1,b_1). \end{aligned}$$

Since $\bar{y}_1(0)=y_1(0)$, Walter (1997, Theorem 4) implies that $\bar{y}_1(t)>y_1(t), \forall t>0$.

Consequently, $S(t): G(0)\rightarrow G(t)$ is strongly monotone for each $t>0$.

For any given $x=(x_1, x_2)\in G(0), \lambda \in [0,1]$, let v(t, x) and $v(t,\lambda x)$ be the solutions of system (5) satisfying $v(0)=x$ and $v(0)=\lambda x$, respectively. Denote $u(t)=\lambda v(t,x)$ and $z(t)=v(t,\lambda x)$. Define f by

$$\begin{aligned} f(t,x)=\begin{bmatrix} b\beta (t,k)\frac{px_2}{(p-l)x_2+lN_h}(N_v^*(t)-x_1)-\mu (t,k)x_1 \\ c\beta (t,k)\frac{l(N_h-x_2)}{(p-l)x_2+lN_h}x_1-(d_h+\rho )x_2 \end{bmatrix}. \end{aligned}$$

Note that for any $\psi \in G(t)$ and $\lambda \in [0,1]$, we have $f(t,\lambda \psi )\ge \lambda f(t,\psi )$. Then

$$\begin{aligned} \frac{du(t)}{dt}=\lambda \frac{dv(t,x)}{dt}=\lambda f(t,v(t,x))\le f(t,\lambda v(t,x))=f(t,u(t)). \end{aligned}$$

Clearly, $\frac{dz(t)}{dt}=f(t,z(t))$ and $u(0)=\lambda v(0,x)=\lambda x=z(0)$. By the comparison principle we have $u(t)\le z(t), \forall t\ge 0$, that is, $\lambda v(t,x)\le v(t,\lambda x), \forall t\ge 0.$ This shows that the solution map $S(t): G(0)\rightarrow G(t)$ is subhomogeneous.

Next, we prove that for any $t>0$, $S(t): G(0)\rightarrow G(t)$ is strictly subhomogeneous. For any given $x\in G(0)$ with $x\gg 0$ and $\lambda \in (0,1)$, let

$$\begin{aligned} \begin{aligned} f_2(r)&:= c\beta (t,k)\frac{l(N_h-r)}{(p-l)r+lN_h}z_1(t)-(d_h+\rho )r,\\ g_2(r)&:= c\beta (t,k)\frac{l(N_h-r)}{(p-l)r+lN_h}. \end{aligned} \end{aligned}$$

Since $g_2(r)$ is strictly decreasing in r and $\lambda v_1(t,x)\le v_1(t,\lambda x), v_2(t,x)>\lambda v_2(t,x), \forall \lambda \in (0,1), \forall t>0$, it follows that

$$\begin{aligned} \begin{aligned} \frac{du_2(t)}{dt}&= \lambda \frac{dv_2(t,x)}{dt}\\&= \lambda c\beta (t,k)\frac{l(N_h-v_2(t,x))}{(p-l)v_2(t,x)+lN_h}v_1(t,x)-(d_h+\rho )\lambda v_2(t,x)\\&<c\beta (t,k)\frac{l(N_h-\lambda v_2(t,x))}{(p-l)\lambda v_2(t,x)+lN_h}z_1(t)-(d_h+\rho )\lambda v_2(t,x)\\&= c\beta (t,k)\frac{l(N_h-u_2(t))}{(p-l)u_2(t)+lN_h}z_1(t)-(d_h+\rho )\lambda v_2(t,x)\\&= g(u_2(t))z_1(t)-(d_h+\rho )u_2(t)\\&= f_2(u_2(t)), \end{aligned} \end{aligned}$$

and hence,

$$\begin{aligned} \frac{du_2(t)}{dt}-f_2(u_2(t))<0=\frac{dz_2(t)}{dt}-f_2(z_2(t)), \quad \forall t>0. \end{aligned}$$

Note that $u_2(0)=\lambda v_2(0,x)=\lambda x=v_2(0,\lambda x)=z_2(0)$. By Walter (1997, Theorem 4), we then obtain $u_2(t)<z_2(t), \forall t>0.$ Thus, $\lambda v(t,x)<v(t,\lambda x), \forall t>0$.

Let P be the Poincaré map associated with system (6) on $\mathbb {R}^2$ and r(P) be its spectral radius. By the continuity and differentiability of solutions with respect to initial values, it follows that S is differentiable at zero and the Frechét derivative $DS(0)=P.$ By Zhao (2003, Theorem 2.3.4), as applied to S, we have the following result:

• (a) If $r(P)\le 1$, then (0, 0) is globally attractive for (5) in G(0);

• (b) If $r(P)>1,$ then system (5) admits a unique positive $\omega$-periodic solution $(I_v^*(t), I_h^*(t))$, which is globally attractive for system (5) in $G(0){\setminus }\{(0,0)\}$.

By Wang and Zhao (2008, Theorem 2.2), $R_0-1$ has the same sign as $r(P)-1$. Therefore, we have the desired threshold type result in terms of $R_0$. $\square$

Next, we use the theory of chain transitive sets (see Hirsch et al. 2001; Zhao 2003, Chapter 1) to lift the threshold type result for system (5) to system (2).

Theorem 1

The following statements are valid:

• (i) If $R_v\le 1$, then (0, 0, 0, 0) is globally attractive for system (2) in W;

• (ii) If $R_v>1$ and $R_0\le 1$, then $(L_v^*(t), N_v^*(t), 0, 0)$ is globally attractive for system (2) in $W {\setminus }\{(0,0,0,0)\}$;

• (iii) If $R_v>1$ and $R_0> 1$, then $(L_v^*(t), N_v^*(t), I_v^*(t), I_h^*(t))$ is globally attractive for system (2) in $W{\setminus } \mathbb {R}_+^2\times \{(0,0)\}$.

Proof

Let $\{\varPsi (t)\}_{t\ge 0}$ be the periodic semiflow associated with system (2) on W, that is,

$$\begin{aligned} \varPsi (t)(x):= (L_v(t,x), N_v(t,x), I_v(t,x), I_h(t,x)) \end{aligned}$$

is the unique solution of system (2) with initial value $x\in W$. Then $\varPsi :=\varPsi (\omega )$ is the Poincaré map of system (2), and $\{\varPsi ^n\}_{n\ge 0}$ defines a discrete-time dynamical system on W. For any given $x\in W$, let $\mathcal {L}$ be the omega limit set of the discrete-time orbit $\{\varPsi ^n(x)\}_{n\ge 0}$. It follows from Hirsch et al. (2001, Lemma 2.1) (see also Zhao 2003, Lemma 1.2.1) that $\mathcal {L}$ is an internally chain transitive set for $\varPsi ^n$ on W.

In the case where $R_v\le 1$, by Lemma 1(i), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }((\varPsi ^n(x))_1, (\varPsi ^n(x))_2, (\varPsi ^n(x))_3)=(0, 0, 0). \end{aligned}$$

Then there exists a subset $\mathcal {L}_1$ of $\mathbb {R}$ such that

$$\begin{aligned} \mathcal {L}=\{(0,0,0)\}\times \mathcal {L}_1. \end{aligned}$$

For any given $y=(y_1,y_2,y_3,y_4)\in \mathcal {L}$, there exists a sequence $n_k\rightarrow \infty$ such that $\varPsi ^{n_k}(x)\rightarrow y$ as $k\rightarrow \infty$. Since $0\le (\varPsi ^{n_k}(x))_4=I_h(n_k\omega ,x)\le N_h$ for all $x\in W$, letting $n_k\rightarrow \infty$, we obtain $0\le y_4\le N_h$. It then follows that $\mathcal {L}_1\subset [0,N_h]$. It is easy to see that

$$\begin{aligned} \varPsi ^n|_\mathcal {L}(0,0,0,y_4)=\{(0,0,0)\}\times \varPsi _1^n|_{\mathcal {L}_1}(y_4), \end{aligned}$$

where $\{\varPsi _1(t)\}_{t\ge 0}$ is the solution semiflow associated with the following system:

$$\begin{aligned} \begin{aligned} \frac{dI_h(t)}{dt}&= -(d_h+\rho )I_h(t). \end{aligned} \end{aligned}$$

(7)

Since $\mathcal {L}$ is an internally chain transitive set for $\varPsi ^n$, it follows that $\mathcal {L}_1$ is an internally chain transitive set for $\varPsi _1^n$. Since 0 is globally attractive for system (7) in $\mathbb {R}$, it follows from Hirsch et al. (2001, Theorem 3.1) (see also Zhao 2003, Theorem 1.2.1) that $\mathcal {L}_1=\{0\}$, and hence, $\mathcal {L}=\{(0, 0, 0, 0)\}$. This implies that statement (i) is valid.

In the case where $R_v>1$, by Lemma 1(ii), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }((\varPsi ^n(x))_1, (\varPsi ^n(x))_2)=(L_v^*(0), N_v^*(0)). \end{aligned}$$

Then there exists a subset $\mathcal {L}_2$ of $\mathbb {R}^2$ such that

$$\begin{aligned} \mathcal {L}=\{(L_v^*(0), N_v^*(0))\}\times \mathcal {L}_2. \end{aligned}$$

For any given $z=(z_1,z_2,z_3,z_4)\in \mathcal {L}$, there exists a sequence $n_j\rightarrow \infty$ such that $\varPsi ^{n_j}(x)\rightarrow z$ as $j\rightarrow \infty$. Since $0\le (\varPsi ^{n_j}(x))_3=I_v(n_j\omega ,x)\le N_v(n_j\omega ,x)$ and $0\le (\varPsi ^{n_j}(x))_4=I_h(n_j\omega ,x)\le N_h$ for all $x\in W$, letting $n_j\rightarrow \infty$, we obtain $0\le z_3\le N_v^*(0)$, $0\le z_4\le N_h$. It then follows that $\mathcal {L}_2\subset [0,N_v^*(0)]\times [0,N_h]=G(0)$. It is easy to see that

$$\begin{aligned} \varPhi ^n|_{\mathcal {L}}(L_v^*(0), N_v^*(0), z_3, z_4)=\{(L_v^*(0), N_v^*(0))\}\times S^n|_{\mathcal {L}_2}(z_3,z_4). \end{aligned}$$

Since $\mathcal {L}$ is an internally chain transitive set for $\varPsi ^n$, it follows that $\mathcal {L}_2$ is an internally chain transitive set for $S^n$.

In the case where $R_v>1$ and $R_0\le 1$, by Lemma 4 (i), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }((\varPsi ^n(x))_3,(\varPsi ^n(x))_4)=(0,0),\quad \forall x\in G(0). \end{aligned}$$

It then follows from Hirsch et al. (2001, Theorem 3.1) (see also Zhao 2003, Theorem 1.2.1) that $\mathcal {L}_2=\{(0,0)\}$, and hence, $\mathcal {L}=\{(L_v^*(0), N_v^*(0), 0, 0)\}$. This implies that statement (ii) is valid.

In the case where $R_v>1$ and $R_0>1$, by Lemma 4 (ii), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }((\varPsi ^n(x))_3,(\varPsi ^n(x))_4) =(I_v^*(0),I_h^*(0)),\quad \forall x\in G(0){\setminus }\{(0,0)\}. \end{aligned}$$

It follows from Hirsch et al. (2001, Theorem 3.2) (see also Zhao 2003, Theorem 1.2.2) that

$$\begin{aligned} \text {either}\quad \mathcal {L}_2=\{(0,0)\}\quad \text {or}\quad \mathcal {L}_2=\{(I_v^*(0),I_h^*(0))\}. \end{aligned}$$

We further claim that $\mathcal {L}_2\ne \{(0,0)\}$. Suppose, by contradiction, that $\mathcal {L}_2=\{(0,0)\}$. Then we have $\lim _{t\rightarrow \infty }(I_v(t,x), I_h(t,x))=(0,0)$ uniformly for $x\in G(0)$, and for any $\epsilon >0$, there exists $T=T(\epsilon )>0$ such that

$$\begin{aligned} |(L_v(t,x), N_v(t,x))-(L_v^*(t),N_v^*(t))|<\epsilon \end{aligned}$$

for all $t\ge T$ and $x\in G(0)$. Then for any $t\ge T$, we have

$$\begin{aligned} \begin{aligned} \frac{dI_v(t)}{dt}&\ge b\beta (t,k)\frac{pI_h(t)}{(p-l)I_h(t)+lN_h} (N_v^*(t)-\epsilon -I_v(t))-\mu (t,k)I_v(t), \\ \frac{dI_h(t)}{dt}&= c\beta (t,k)\frac{l(N_h-I_h(t))}{(p-l)I_h(t)+lN_h} I_v(t)-(d_h+\rho )I_h(t). \end{aligned} \end{aligned}$$

(8)

Let $r_\epsilon$ be the spectral radius of the Poincaré map associated with the following linear system:

$$\begin{aligned} \begin{aligned} \frac{d\bar{I}_v(t)}{dt}&= b\beta (t,k)\frac{p\bar{I}_h(t)}{lN_h} (N_v^*(t)-\epsilon )-\mu (t,k)\bar{I}_v(t), \\ \frac{d\bar{I}_h(t)}{dt}&= c\beta (t,k)\bar{I}_v(t)-(d_h+\rho )\bar{I}_h(t). \end{aligned} \end{aligned}$$

Since $\lim _{\epsilon \rightarrow 0^+}r_\epsilon =r(P)>1$, we can fix $\epsilon$ small enough such that $r_\epsilon >1$ and $\epsilon <\min _{t\in [0,\omega ]}N_v^*(t)$. By a result similar to Lemma 1 (ii), it follows that the Poincaré map of the following system

$$\begin{aligned} \begin{aligned} \frac{d\bar{I}_v(t)}{dt}&= b\beta (t,k)\frac{p\bar{I}_h(t)}{(p-l)\bar{I}_h(t)+lN_h} (N_v^*(t)-\epsilon -\bar{I}_v(t))-\mu (t,k)\bar{I}_v(t), \\ \frac{d\bar{I}_h(t)}{dt}&= c\beta (t,k)\frac{l(N_h-\bar{I}_h(t))}{(p-l)\bar{I}_h(t)+lN_h} \bar{I}_v(t)-(d_h+\rho )\bar{I}_h(t) \end{aligned} \end{aligned}$$

(9)

admits a globally attractive fixed point $(\bar{I}_v^*(0), \bar{I}_h^*(0))\gg 0$. Since $x\in W{\setminus }\mathbb {R}_+^2\times \{(0,0)\}$, $(I_v(t,x), I_h(t,x))>0$ for all $t>0$. In view of (8) and (9), the comparison principle implies that

$$\begin{aligned} \liminf _{n\rightarrow \infty }(I_v(n\omega ,x), I_h(n\omega ,x))\ge (\bar{I}_v^*(0),\bar{I}_h^*(0))\gg 0, \end{aligned}$$

which contradicts $\lim _{t\rightarrow \infty }(I_v(t,x), I_h(t,x))=(0,0)$. It then follows that $\mathcal {L}_2=\{(I_v^*(0),I_h^*(0))\}$, and hence, $\mathcal {L}=\{(L_v^*(0),N_v^*(0),I_v^*(0),I_h^*(0))\}$. This implies that statement (iii) is valid. $\square$

Since system (1) is equivalent to (2), we have the following result on the global dynamics of our model system.

Theorem 2

The following statements are valid:

• (i) If $R_v\le 1$, then (0, 0, 0, 0) is globally attractive for system (1) in W;

• (ii) If $R_v>1$ and $R_0\le 1$, then $(L_v^*(t), N_v^*(t), 0, 0)$ is globally attractive for system (1) in $W {\setminus }\{(0,0,0,0)\}$;

• (iii) If $R_v>1$ and $R_0> 1$, then $(L_v^*(t), N_v^*(t), I_v^*(t), I_h^*(t))$ is globally attractive for system (1) in $W{\setminus } \mathbb {R}_+^2\times \{(0,0)\}$.

To finish this section, we remark that when all coefficients are constants, the model system (1) reduces to the following autonomous system:

$$\begin{aligned} \begin{aligned} \frac{dL_v(t)}{dt}&= \lambda _LN_v(t)-\mu _LL_v(t)-\alpha L_v(t)^2-\lambda _vL_v(t), \\ \frac{dS_v(t)}{dt}&= \lambda _vL_v(t)-b\beta (k)\frac{pI_h(t)}{pI_h(t)+l(N_h-I_h(t))}S_v(t) -\mu (k)S_v(t), \\ \frac{dI_v(t)}{dt}&= b\beta (k)\frac{pI_h(t)}{pI_h(t)+l(N_h-I_h(t))}S_v(t) -\mu (k)I_v(t),\\ \frac{dI_h(t)}{dt}&= c\beta (k)\frac{l(N_h-I_h(t))}{pI_h(t)+l(N_h-I_h(t))} I_v(t)-(d_h+\rho )I_h(t), \end{aligned} \end{aligned}$$

(10)

where

$$\begin{aligned} \begin{aligned} \beta (k)&= \beta _v-k(\beta _v-\beta _r),\quad 0\le k\le 1,\\ \mu (k)&= \mu _v+\bar{\mu }k,\quad 0\le k\le 1. \end{aligned} \end{aligned}$$

Then the matrices $\tilde{F}(t)$, $\tilde{V}(t)$, F(t) and V(t), respectively, become

$$\begin{aligned} \tilde{F}= & {} \begin{bmatrix} 0&\lambda _L\\ 0&0 \end{bmatrix},\quad \tilde{V}=\begin{bmatrix} \mu _L+\lambda _v&0\\ -\lambda _v&\mu (k)\end{bmatrix},\\ F= & {} \begin{bmatrix} 0&\frac{b\beta (k)N_v^*p}{lN_h}\\ c\beta (k)&0 \end{bmatrix},\quad V=\begin{bmatrix} \mu (k)&0\\ 0&d_h+\rho \end{bmatrix}. \end{aligned}$$

For any given $\omega >0$, we can regard system (10) as an $\omega$-periodic system. By Wang and Zhao (2008, Lemma 2.2 (ii)), we obtain the vector reproduction ratio $R_v$ and the basic reproduction ratio $R_0$ for system (10) as follows:

$$\begin{aligned} R_v= & {} \rho (\tilde{F}\tilde{V}^{-1})=\frac{\lambda _L\lambda _v}{\mu (k)(\mu _L+\lambda _v)},\nonumber \\&\begin{aligned} R_0&= \rho (FV^{-1})=\sqrt{\frac{c\beta (k)}{\mu (k)}\frac{b\beta (k)p}{lN_h(d_h+\rho )}\frac{\lambda _v}{\alpha \mu (k)}\left( \frac{\lambda _L\lambda _v}{\mu (k)}-(\mu _L+\lambda _v)\right) }. \end{aligned}\nonumber \\ \end{aligned}$$

(11)

By the global attractivity in Theorem 2, we can easily obtain its analog for autonomous system (10), where the $\omega$-periodic solutions are replaced by the corresponding equilibria.

4 A case study

In this section, we study the malaria transmission case in Port Harcourt, Nigeria. Nigeria accounts for a quarter of all malaria cases in the 45 malaria endemic countries in Africa (WHO 2015). Port Harcourt is the capital and largest city of Rivers State, Nigeria. The topography of Port Harcourt is that of flat plains with a network of rivers, tributaries and creeks which have a high potential for breeding of mosquitoes. Malaria transmission is intense year round with a peak during months of March to November and a nadir during months of December to February (George et al. 2013).

We do numerical simulations by using ode45 and CFTOOL in Matlab. First, we need to estimate the constant and periodic parameter values. Port Harcourt has a population of 1, 230, 000 (see https://en.wikipedia.org/wiki/List_of_metropolitan_areas_in_Africa), which can be chosen as the value of $N_h$. The life expectancy of Nigeria is 52.11 years (see http://data.worldbank.org). Using this number we estimate the human natural death rate as $d_h$ $=$ $\frac{1}{52.11\times 12}$ $=0.0016$ month$^{-1}$. The values of p and l may vary from 0 to 1 and $p\ge l$ (Chamchod and Britton 2011, Kesavan and Reddy 1985 and Lacroix et al. 2005). Unless otherwise stated, we use the values listed in Table 2 for constant parameters in the simulation.

Table 2 Parameter values

Since temperature plays a major role in the life cycle of mosquitoes, we evaluate the periodic parameters by using the monthly mean temperatures of Port Harcourt from 1990 to 2012 (obtained from Climate Change Knowledge Portal website: http://sdwebx.worldbank.org/climateportal), as shown in Table 3.

Table 3 Monthly mean temperatures for Port Harcourt (in $^{\circ }$C)

According to Paaijmans et al. (2009), the temperature-dependent mosquito biting rate can be expressed as

$$\begin{aligned} \beta _v(T)=30.4\times 0.000203T(T-11.7)\sqrt{42.3-T}\text {month}^{-1}, \end{aligned}$$

where and hereinafter T is the temperature in $^{\circ }$C. The biting rate of mosquitoes in Port Harcourt can then be fitted by

$$\begin{aligned} \begin{aligned} \beta _v(t)&= 0.1554\cos (\pi t/6) +0.9065\sin (\pi t/6)-0.2284\cos (2\pi t/6)\\&\quad -0.2764\sin (2\pi t/6) -0.0578\cos (3\pi t/6)-0.1473\sin (3\pi t/6)\\&\quad -0.0208\cos (4\pi t/6)-0.1573\sin (4\pi t/6) -0.0118\cos (5\pi t/6)\\&\quad -0.0510\sin (5\pi t/6) +9.6794\,\text { month}^{-1}. \end{aligned} \end{aligned}$$

Since ITNs are only used at night, even if the entire human population uses ITNs, they can still be bitten by mosquitoes at daytime. We assume that

$$\begin{aligned} \beta _r(t)=\xi \beta _v(t),\quad \xi \in (0,1), \end{aligned}$$

and we take $\xi =0.1$ in the simulation.

It follows from Rubel et al. (2008) that the birth rates of juvenile and adult mosquitoes and the death rate of juvenile mosquitoes can be respectively given by

$$\begin{aligned} \lambda _L(T)=2.325\beta _v(T), \quad \lambda _v(T)=\frac{\lambda _L(T)}{10}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \mu _L(T)&= 30.4\times (0.0025T^2-0.094T+1.0257) \text { month}^{-1}.\nonumber \end{aligned} \end{aligned}$$

Then the birth rates of juvenile and adult mosquitoes and the death rate of juvenile mosquitoes in Port Harcourt can be fitted respectively by

$$\begin{aligned} \lambda _L(t)=2.325\beta _v(t), \quad \lambda _v(t)=\frac{\lambda _L(t)}{10}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \mu _L(t)&=0.2240\cos (\pi t/6)+1.5699\sin (\pi t/6)-0.4849\cos (2\pi t/6)\\&-0.4268\sin (2\pi t/6)-0.0835\cos (3\pi t/6) -0.3016\sin (3\pi t/6)\\&-0.0210\cos (4\pi t/6) -0.2684\sin (4\pi t/6)-0.0051\cos (5\pi t/6)\\&-0.0845\sin (5\pi t/6) +9.0288\,\text {month}^{-1}. \end{aligned} \end{aligned}$$

According to Martens et al. (1995) and Ngarakana-Gwasira et al. (2014), the death rate of adult mosquitoes is evaluated as

$$\begin{aligned} \mu _v(T)=\frac{30.4}{-0.03T^2+1.31T-4.4} \text {month}^{-1}. \end{aligned}$$

Then the death rate of adult mosquitoes in Port Harcourt can be approximated by

$$\begin{aligned} \begin{aligned} \mu _v(t)&= 0.0168\cos (\pi t/6) +0.1406\sin (\pi t/6)-0.0503\cos (2\pi t/6)\\&-0.0343\sin (2\pi t/6) -0.0064\cos (3\pi t/6)-0.0307\sin (3\pi t/6)\\&-0.0003\cos (4\pi t/6)-0.0235\sin (4\pi t/6) +0.0007\cos (5\pi t/6)\\&-0.0070\sin (5\pi t/6) +3.3136 \text {month}^{-1}. \end{aligned} \end{aligned}$$

Fig. 1

Long term behavior of the solutions of system (1). Here the birthrate of juvenile mosquitoes is set to be $0.8\lambda _L(t)$, $k=0.5$. In this case, $R_v=0.9041<1$

Fig. 2

Long term behavior of the solutions of system (1). Here $k=0.8$ and $R_v=1.3549>1$, $R_0=0.8620<1$

The long term behavior of solutions of system (1) are shown in Figs. 1, 2 and 3. Based on Wang and Zhao (2008, Theorem 2.1 (ii)), we can numerically calculate the vector reproduction ratio $R_v$ and the basic reproduction ratio $R_0$. Larval source deduction will reduce the rate at which gravid female mosquitoes encounter oviposition sites (Yakob and Yan 2009), leading to a decrease in the recruitment rate of larval mosquitoes. In Fig. 1, we suppose the birth rate of juvenile mosquitoes to be $0.8\lambda _L(t)$, which can be achieved by spraying or eliminating mosquito breeding sites. We also assume that 50% of the humans use ITNs effectively. In this case, $R_v=0.9041<1$ and all compartments converge to 0 eventually, which means that mosquitoes are eliminated from this region. In Fig. 2, we keep the birth rate of juvenile mosquitoes as $\lambda _L(t)$ and suppose that $80\%$ of the humans use ITNs. We calculate $R_v=1.3549>1$ and $R_0=0.8620<1$. In this case, the juvenile mosquito and susceptible adult mosquito populations exhibit periodic fluctuations. And both the infectious mosquito and infectious human populations converge to 0, which means that malaria is eliminated from this area. In Fig. 3, we suppose that 50% of the humans use ITNs and keep other parameter values the same as those in Fig. 2. In this case, we obtain $R_v=1.3561>1$ and $R_0=1.6979>1$. All compartments fluctuate periodically, which means that the disease will persist. The simulation results shown in Figs. 1, 2 and 3 are consistent with the conclusion of Theorem 2.

Fig. 3

Long term behavior of the solutions of system (1). Here $k=0.5$ and $R_v=1.3561>1$, $R_0=1.6979>1$

Figure 4a shows the relationship between $R_0$ and k. Clearly, $R_0$ is a decreasing function of k. We also see that if over $75\%$ of the humans use ITNs in Port Harcourt, then $R_0$ can be reduced to less than 1, and hence, malaria can be eliminated from this area. To study the impact of the vector-bias effect, we simulate the relationships between $R_0$ and k under three different vector-bias levels. As shown in Fig. 4b, for each vector-bias level, $R_0$ is a decreasing function of k. It is worthwhile to note that the ignorance of the vector-bias effect (i.e., $p=l$) underestimates $R_0$. Following Wang and Zhao (2008), given a continuous periodic function g(t) with the period $\omega$, we define its average as

$$\begin{aligned}{}[g]:=\frac{1}{\omega }\int _0^\omega g(t)dt. \end{aligned}$$

Then the time-averaged parameter values of system (1) are $[\beta _v]=9.6794$, $[\beta _r]=0.1[\beta _v]$, $[\mu _v]=3.3136$, $[\mu _L]=9.0288$, $[\lambda _L]=2.325[\beta _v]$, $[\lambda _v]=[\lambda _L]/10$. Using these parameter values and formula (11), we can calculate the basic reproduction ratio $[R_0]$ of the time-averaged autonomous system (10). As can be seen from Fig. 4c, compared with $R_0$, the basic reproduction ratio $[R_0]$ of the time-averaged autonomous system underestimates the infection risk a little bit. Although the difference between the values of $R_0$ and $[R_0]$ in Fig. 4c seems little, sometimes it may lead to great difference in designing disease control strategies, especially when applied to a large community of people.

Fig. 4

a The basic reproduction ratio $R_0$ versus the proportion of bed net use k; b $R_0$ versus k under different vector-bias levels; c $R_0$ versus k and $[R_0]$ versus k

5 Discussion

An important issue in developing mathematical models is to identify which biological factors are necessary to include and which can be omitted. Usually this is determined by the purpose of a study. Considering that climate factors have a great impact on the mosquito life cycle and the parasite survival in mosquitoes, we incorporated seasonality by using an ordinary differential equations model with some parameters being periodic functions. In our model we considered the juvenile stage of mosquitoes in addition to the adult one. This enables us to better understand the mosquito population dynamics, and hence, the malaria transmission dynamics. The incorporation of such juvenile stage may also provide some insights into designing larval control strategies. Insecticide-treated bed net use is one of the effective measures in malaria control. To investigate the effect of ITNs, we modeled the biting rate and the death rate of mosquitoes as functions of the proportion of bed net use. To better understand malaria transmission dynamics and to provide more accurate information for the design of control measures, we also incorporated the effects of different feeding biases by mosquitoes towards humans.

By appealing to the theory of monotone and subhomogeneous systems and the theory of chain transitive sets, we have obtained a complete classification of global dynamics of the model in terms of the vector reproduction ratio $R_v$ and the basic reproduction ratio $R_0$: (i) If $R_v<1$, then mosquitoes will die out eventually; (ii) If $R_v>1$ and $R_0<1$, then malaria will be eliminated; (iii) If $R_v>1$ and $R_0>1$, then the disease will persist and exhibit seasonal fluctuation.

By using some published data about Port Harcourt, Nigeria and formula related to mosquito life cycle, we estimated all the constant and periodic parameters. The analytic results are well verified by numerical simulations. Our findings show that if $75\%$ of the human population in Port Harcourt were to use ITNs, then malaria could be eliminated from this area. We have also found that the basic reproduction ratio may be underestimated if we ignore the vector-bias effect. Compared with $R_0$, the basic reproduction ratio $[R_0]$ of the time-averaged autonomous system underestimates the risk of infection, which confirms the necessity of incorporating seasonality.

In our model, we neglected both the extrinsic incubation period in mosquitoes and the intrinsic incubation period in human hosts. Upon infection, human individuals will move to the exposed compartment, where parasites in their bodies are still in the asexual stages. Since individuals in the exposed class do not have gametocytes in their blood, they are not able to transmit the disease to susceptible mosquitoes until they enter into the infectious class. Susceptible mosquitoes that feed on infectious humans will take gametocytes in blood meals and enter into the exposed class. After fertilisation, sporozoites are produced and migrate to the salivary glands ready to infect any susceptible host, the mosquito is then considered as infectious (Ngarakana-Gwasira et al. 2014). As a future work, it would be interesting to modify our model by incorporating such exposed classes of human hosts and mosquitoes.