Long-lasting insecticidal nets and the quest for malaria eradication: a mathematical modeling approach

Abstract

Recent dramatic declines in global malaria burden and mortality can be largely attributed to the large-scale deployment of insecticidal-based measures, namely long-lasting insecticidal nets (LLINs) and indoor residual spraying. However, the sustainability of these gains, and the feasibility of global malaria eradication by 2040, may be affected by increasing insecticide resistance among the Anopheles malaria vector. We employ a new differential-equations based mathematical model, which incorporates the full, weather-dependent mosquito lifecycle, to assess the population-level impact of the large-scale use of LLINs, under different levels of Anopheles pyrethroid insecticide resistance, on malaria transmission dynamics and control in a community. Moreover, we describe the bednet-mosquito interaction using parameters that can be estimated from the large experimental hut trial literature under varying levels of effective pyrethroid resistance. An expression for the basic reproduction number, ${\mathcal {R}}_0$, as a function of population-level bednet coverage, is derived. It is shown, owing to the phenomenon of backward bifurcation, that ${\mathcal {R}}_0$ must be pushed appreciably below 1 to eliminate malaria in endemic areas, potentially complicating eradication efforts. Numerical simulations of the model suggest that, when the baseline ${\mathcal {R}}_0$ is high (corresponding roughly to holoendemic malaria), very high bednet coverage with highly effective nets is necessary to approach conditions for malaria elimination. Further, while >50% bednet coverage is likely sufficient to strongly control or eliminate malaria from areas with a mesoendemic malaria baseline, pyrethroid resistance could undermine control and elimination efforts even in this setting. Our simulations show that pyrethroid resistance in mosquitoes appreciably reduces bednet effectiveness across parameter space. This modeling study also suggests that increasing pre-bloodmeal deterrence of mosquitoes (deterring them from entry into protected homes) actually hampers elimination efforts, as it may focus mosquito biting onto a smaller unprotected host subpopulation. Finally, we observe that temperature affects malaria potential independently of bednet coverage and pyrethroid-resistance levels, with both climate change and pyrethroid resistance posing future threats to malaria control.

1 Introduction

Malaria, a deadly disease caused by protozoan Plasmodium parasites that spread between humans via the bite of infected adult female Anopheles mosquitoes (World Health Organization 2016, 2017a), remains a major public health burden affecting many parts of the globe. Over 2.5 billion people live in areas whose local epidemiology permits transmission of P. falciparum, responsible for the most life-threatening form of malaria (Gething et al. 2011; Johnston et al. 2013). The disease is endemic in 91 countries, and caused 219 million cases and 435,000 deaths in 2017 Camara et al. (2018), Global-Health/Malaria (2019), World Health Organization (2018). Disease burden is concentrated in the African Region, accounting for about 90% of cases and mortality, with the majority of deaths in children under the age of five (World Health Organization 2017a). Other populations at high risk of malaria include pregnant women and those living with HIV/AIDS (owing to their weakened immune systems) (Mohammed-Awel and Numfor 2017; World Health Organization 2016). Malaria transmission dynamics is greatly affected by numerous abiotic and biotic factors, such as the increased mobility of people (the reservoir for the malaria parasite), the altered distribution of disease vectors (Anopheles mosquitoes) due to climate and environmental changes, and malaria’s incursions into new areas [e.g., East African tropical highlands Himeidan and Kweka (2012)].

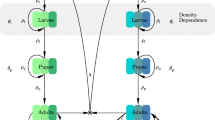
The lifecycle of the ectothermal Anopheles mosquito, which consists of three aquatic juvenile stages (eggs, larva and pupa) and an adult stage, is intimately connected to local weather conditions (Eikenberry and Gumel 2018; Okuneye et al. 2019; Paaijmans et al. 2010), and is fundamental to the spread of malaria. In sub-Saharan Africa, favorable environmental conditions (a warm tropical climate) and the relatively long lifespans and strong human biting habits of the major local Anopheles species, along with broader socioeconomic conditions, and agricultural and land-use practices, make this region particularly vulnerable to malaria transmission. Adult female Anopheles mosquitoes take blood meals from vertebrate hosts (needed for egg development) every few days, with the exact interval depending strongly upon temperature (Beck-Johnson et al. 2017). The mosquito acquires Plasmodium infection by taking blood meals from an infected human, and subsequently passes the disease to a susceptible human, once parasite maturation within the mosquito is complete. As mosquitoes must routinely survive the time interval from initial infection to infectivity [which could range from 8 to 30 days, depending on ambient temperature (Detinova et al. 1962)] for malaria to be transmitted, this explains why the relatively long lifespans of African Anopheles is so important for effective malaria transmission.

Great success has been recorded in the fight against malaria since about the year 2000, largely owing to concerted global public health efforts, such as the Roll Back Malaria initiative and the United Nations Millennium Development Goals (MDGs) (Huijben and Paaijmans 2017; World Health Organization 2015c). However, malaria remains a major public health challenge for about half of the world’s population (Gething et al. 2016; World Health Organization 2012, 2015b). New concerted global efforts, such as The Global Technical Strategy for Malaria 2016–2030 [approved by the World Health Assembly in May 2015 (World Health Organization 2015c)] and the Zero by 40 Initiative [an initiative of five chemical companies with the support of the Bill & Melinda Gates Foundation and the Innovative Vector Control Consortium [Global-Health/Malaria 2019), (Willis and Hamon 2018)], aimed at eradicating malaria by 2030 or 2040, respectively, are currently underway. Central to these laudable malaria eradication efforts is the widespread use of insecticide-based vector control interventions, including pyrethroid-based insecticide-treated nets (ITNs; later replaced by long-lasting insecticidal nets (LLINs)), indoor residual spraying (IRS) and larvacides (Barbosa and Hastings 2012; Huijben and Paaijmans 2017; Okumu and Moore 2011; World Health Organization 2015a), complemented by artemisinin-based combination drug therapy. Five major classes of insecticide are used in malaria control efforts, namely pyrethroids, organochlorines, organophosphates, carbamates and the recent addition of neonicotinoids, with all five used for IRS (World Health Organization 2019). Only the pyrethroids, however, owing to their low mammalian toxicity and irritant effect on mosquitoes, are recommended for ITNs/LLINs (Kabula et al. 2014). It is notable that the earlier WHO’s (World Health Organization’s) Global Malaria Eradication Programme (1955–1969) relied almost exclusively on the use of DDT (Dichlorodiphenyltrichloroethane) and other insecticidal compounds for vector control, with the theoretical goal of interrupting malaria transmission via decreasing adult survival times, rather than decreasing mosquito abundance per se, a goal largely based on the mathematical model of the malariologist George Macdonald (Macdonald 1957; Nájera et al. 2011). Long-lasting insecticidal bednets have been used to great success in reducing the global malaria burden (Bhatt et al. 2015). This success is partly attributed to community protection. In particular, if the coverage of bednet usage exceeds a certain threshold level, overall mosquito densities and malaria transmission are impacted sufficiently to also protect those individuals not using a bednet (Killeen and Smith 2007; Levitz et al. 2018; Okumu and Moore 2011).

It has been estimated that bednets and IRS accounted for 81% of the reduction in malaria burden recorded in the past 15 years [with most of the benefits resulting from the use of bednets (Bhatt et al. 2015)]. The dramatic success of pyrethroid-based LLINs (over IRS) is likely due to multiple factors, including the fact that LLINs target indoor-biting mosquitoes, are effective as a physical barrier to biting, and pyrthroids have an excito-repellent effect that may diverting mosquitoes before they feed on the (protected) human host. However, at the most basic level, the success of LLINs is likely simply due to the enormous scale of implementation in endemic areas, especially in sub-Saharan Africa: Nearly 1.5 billion pyrethroid-based bednets have been deployed in endemic areas since 2010, with 1.25 billion distributed in sub-Saharan Africa (Huijben and Paaijmans 2017; The Alliance for Malaria Prevention 2018). Unfortunately, this widespread and heavy use of insecticides has resulted in the emergence of vector resistance to nearly every currently-available agent used in the insecticides (Alout et al. 2017; Dondorp et al. 2009; Imwong et al. 2017; World Health Organization 2017b) with pyrethroid resistance via multiple molecular mechanisms now widely observed across the African continent (Hemingway et al. 2016). Given this, and the dominant role of LLINs in malaria mortality reductions, any threat to their efficacy via resistance is of foremost importance.

Perhaps most significantly, a recent and very large observational cohort study across five countries found that while LLIN users had lower rates of malaria infection and disease, no relationship between laboratory-assessed insecticide resistance and malaria epidemiology was detected (Kleinschmidt et al. 2018). Nevertheless, at least some data does suggest that resistance can undermine the control of malaria disease. One recent study suggests that insecticide resistance has led to a rebound in malaria incidence in South Africa (Alout et al. 2017). A large, factorial randomized clinical trial (Protopopoff et al. 2018) comparing LLINs, LLINs treated with a piperonyl butoxide (PBO) synergist, and IRS, showed benefit to malaria control with either IRS or a PBO synergist in addition to an LLIN, suggesting that pyrethroid resistance decreased the efficacy of the standard LLIN alone. A recent experimental hut trial (Toe et al. 2018) also suggested benefit to LLINs with PBO synergists in an area with highly pythrethroid-resistant Anopheles.

Some prior mathematical work has examined the impact of insecticide resistance on malaria transmission dynamics. For example, Barbosa and Hastings (2012) developed a genetic model to predict changes in mosquito fitness and resistance allele frequency (parameters that describe insecticide selection, fitness cost as well as LLINs and synergist (PBO) are incorporated). The results of their investigation suggested that resistance was most sensitive to selection coefficients, fitness cost and dominance coefficients. Chitnis et al. (2009) developed and analysed a linear difference equation model for the dynamics of host-seeking adult female mosquitoes in a heterogeneous population of hosts in a community where ITNs are used. In addition to incorporating the gonotrophic cycle of the malaria vector and the aforementioned host heterogeneity, other notable features of the model in Chitnis et al. (2009) include stage-structure in Anopheles feeding cycle and that such cycle varies across mosquitoes as well as allowing for the assessment of various mosquito control interventions. Consistent with previous studies for the impact of ITNs on malaria epidemiology in both ITN-protected and unprotect hosts, Chitnis et al. (2009) shows beneficial effects to unprotected humans at both, low and high, ITN coverage levels. Birget and Koella (2015a) developed a population-genetic model of the spread of insecticide-resistance in Anopheles mosquitoes in response to ITNs and larvicides, which suggested indoor ITNs were less likely to select for resistance. Brown et al. (2013) developed a mathematical model to investigate optimal (cost-effective) strategies for mosquito control in the presence of insecticide resistance. Consistent with previous studies, their results show that fitness costs are the key elements in the computation of economically optimal resistance management strategies. Mohammed-Awel et al. (2018) designed a novel deterministic model for assessing the population-level impact of mosquito insecticide resistance on malaria transmission dynamics and to evaluate the community-wide impact of the use ITNs, IRS and their combination. Their study showed that the prospect of the effective control of malaria spread in endemic settings (while minimizing the risk of insecticide resistance in the female adult mosquito population), using ITNs and IRS, is quite promising (provided the effectiveness and coverage levels are at optimal levels). Birget and Koella (2015b) proposed a model to assess the relative importance in different epidemiological contexts of repellent and insecticidal properties of ITNs. Weidong and Robert (2009) used an agent-based model that incorporated the killing and avoidance of individual mosquitoes exposed to ITNs in a hypothetical village setting with 50 houses and 90 aquatic habitats. Smith et al. (2009) used a mathematical model to establish the relationship between P. falciparum parasite rate (PfPR) and ITNs coverage. Killeen and Smith (2007) proposed a model that describes the interaction of a blood-seeking mosquito with either bednet-protected or unprotected hosts as a two-stage process, whereby mosquito are either diverted from the attempt, or engage in an attempt and then either die or succeed in taking a bloodmeal. Similar bednet-human interaction and feeding cycle models are described in Glunt et al. (2018), Killeen et al. (2011), Le Menach et al. (2007), Okumu et al. (2013).

The main objective of the current study has been to develop a mathematical model for assessing the impact of insecticide resistance on malaria epidemiology in malaria-endemic areas that adopt wide-scale use of LLINs. The main motivation is twofold. First is the fact that LLINs are the core intervention (due to their superior success over IRS) for National Malaria Prevention Programs (World Health Organization 2017c, 2015d). Second is the fact that the impact of pyrethroid resistance on malaria transmission/epidemiology is not well-understood and remains a subject for considerable debate within the malaria control community (Alout et al. 2017; Kleinschmidt et al. 2018; Protopopoff et al. 2018; Toe et al. 2018). The developed model, which takes the form of a deterministic system of nonlinear differential equations, incorporates key features of aquatic and adult mosquito dynamics (including the aquatic developmental stages, adult mosquito gonotrophic cycle, parasite sporogony and schizogony in the hosts population), disease transmission in humans, and the use of bednets as the sole control strategy. The human population is stratified based on whether or not they use LLINs. We partly adapt the prior weather-dependent malaria model of Okuneye et al. (2019), and previous bednet-mosquito interaction models, such as those proposed in Glunt et al. (2018), Killeen and Smith (2007), Killeen et al. (2011), Le Menach et al. (2007), Okumu et al. (2013). We have reviewed the experimental hut trial literature, and the relationships between key parameters describing bednet efficacy have been extracted from a large number of experimental studies. Thus, the model quantitatively represents resistance in a realistic manner.

The ultimate goal is to determine whether effective disease control (or elimination) is feasible, using LLINs, despite insecticide resistance. The paper is organized as follows. The model is formulated in Sect. 2, and analysed for its qualitative features in Sect. 3. The effect of local temperature variability on the effectiveness of LLINs (and, hence, on disease dynamics and control) is assessed in Sect. 4. Discussion and concluding remarks are reported in Sect. 5.

2 Model formulation

The model describes the temporal dynamics of immature and adult mosquitoes and humans. The total immature mosquito population is split into compartments for eggs (E(t)), four larval instar stages ($L_i(t)$; $i=1,2,3,4$ and pupae (P(t)). The dynamics of the adult female mosquitoes is governed by the gonotrophic cycle. Following Okuneye et al. (2019), the adult female mosquito gonotrophic cycle is divided into three stages (Corbel et al. 2004; Okuneye et al. 2019):

Stage I:

host-seeking and taking of a bloodmeal

Stage II:

digestion of bloodmeal and egg maturation

Stage III:

search for, and oviposition into, a suitable body of water (breeding site)

The populations of vectors in Stages I, II and III of the gonotrophic cycle at time t are denoted by X(t), Y(t) and Z(t), respectively. With respect to Plasmodium infection and the sporogonic cycle, vectors in each gonotrophic stage is further subdivided into susceptible ($S_{X}(t), S_{Y}(t), S_{Z}(t)$), exposed (i.e., infected but not yet infectious) ($E_{X}(t), E_{Y}(t), E_{Z}(t)$) and infectious ($I_{X}(t), I_{Y}(t), I_{Z}(t)$) compartments. Thus, the total number of adult female Anopheles mosquitoes at time t, denoted by $N_M(t)$, is given by

$$\begin{aligned} \begin{aligned} N_{M}(t) = S_{X}(t)+E_{X}(t)+I_{X}(t)+S_{Y}(t)+E_{Y}(t)+I_{Y}(t)+S_{Z}(t)+E_{Z}(t)+I_{Z}(t). \end{aligned} \end{aligned}$$

The total human population at time t, denoted by $N_H(t)$, is split into the total number of humans who are protected by bednets (i.e., those who consistently sleep under an LLIN), denoted by $N_{H_p}(t)$, and those who are not protected, denoted by $N_{H_u}(t)$. The population of protected and unprotected individuals is further subdivided into susceptible $S_{H_p}(t)(S_{H_u}(t))$, exposed $E_{H_p}(t)(E_{H_u}(t))$, infectious $I_{H_p}(t)(I_{H_u}(t))$ and recovered $R_{H_p}(t)(R_{H_u}(t))$ humans, so that

$$\begin{aligned} \begin{aligned} N_H(t)&=N_{Hp}(t)+N_{Hu}(t),\\&=S_{H_p}(t)+S_{H_u}(t)+E_{H_p}(t)+E_{H_u}(t)+I_{H_p}(t)+I_{H_u}(t)+R_{H_p}(t)+R_{H_u}(t). \end{aligned} \end{aligned}$$

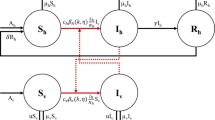
The flow diagram of the model to be developed is depicted in Fig. 1.

Fig. 1

Flow diagram of the model (2.1), (2.2), (2.4)

2.1 Equations for the dynamics of immature mosquitoes

It is convenient to define $L=\displaystyle \sum \nolimits _{j=1}^4L_j$. The equations for the dynamics of immature mosquitoes are given by (where a dot represents differentiation with respect to time t):

$$\begin{aligned} \begin{aligned} {\dot{E}}&=\psi _E\varphi _Z{\left( 1-\frac{E}{K_E} \right) }_+(S_Z+E_Z+I_Z) -[\sigma _E(T_W)+\mu _E(T_W)]E, \\ {\dot{L}}_{1}&= \sigma _E(T_W) E-[\sigma _{L_1}(T_W)+\mu _L(T_W)+{\delta _L L} ]L_1, \\ {\dot{L}}_{j}&= \sigma _{L{j-1}}(T_W)L_{j-1}-[\sigma _{L_j}(T_W) +\mu _L(T_W)+{\delta _L L}]L_{j};\quad j=2,3,4, \\ {\dot{P}}&= \sigma _{ L_{4}}(T_W)L_4-[\sigma _P(T_W) +\mu _P(T_W) ]P, \\ \end{aligned} \end{aligned}$$

(2.1)

where $T_A$ and $T_W$ represent air and water, temperature, respectively. In (2.1), $\psi _E$ is the number of eggs laid per oviposition, $\varphi _Z$ is the rate at which female mosquitoes transition from Stage III to Stage I of the gonotrophic cycle (i.e., the rate of oviposition for mosquitoes in Stage III) and $K_E$ is the environmental carrying capacity of eggs (the notation $r_+ = \max \{0, r \}$ is used to ensure the non-negativity of the logistic term). The quantity $\delta _L L$ represents the density-dependent larval mortality rate (Agusto et al. 2015). Further, $\mu _i$ and $\sigma _i$ ($i=E,L,P$) represent the natural death and maturation rates of immature mosquitoes of type i, respectively. The temperature-dependence of the developmental and survival parameters is presented in Sect. 2.4.

2.2 Equations for the dynamics of adult female Anopheles mosquitoes

As stated above, the dynamics of the adult female Anopheles mosquitoes is governed by the gonotrophic cycle. The total vector population is split into the aforementioned nine compartments ($S_{X},E_{X},I_{X},S_{Y},E_{Y},I_{Y},S_{Z},E_{Z},I_{Z}$) corresponding to the three gonotrophic cycle stages (Okuneye et al. 2019). We let $\pi _p$ represent the proportion of humans that are protected by a bednet (i.e. consistently sleep under an LLIN), while $\pi _u=1-\pi _p$ is the unprotected portion. In other words, $0<\pi _p\le 1$ is the bednet coverage. Bednet-mosquito interactions are defined by three basic parameters: $\varepsilon _{deter}$, $\varepsilon _{die,i}$, and $\varepsilon _{bite,i}$, as described now. We let $\varepsilon _{deter}$ represent the probability that an adult female mosquito is deterred from entering an LLIN-protected hut (or house), relative to an unprotected hut (or house). That is,

$$\begin{aligned}&\varepsilon _{\mathrm{{deter}}}\\&\quad =\frac{{\mathrm {Number\,\, of\,\, mosquitoes\,\, in\,\, control\,\, group-Number\,\, of\,\, mosquitoes\,\, in \,\,the \,\,protected\,\, hut }}}{{\mathrm {Number\,\, of\,\, mosquitoes\,\, in\,\, the\,\, control\,\, group}}}. \end{aligned}$$

It should be emphasized that, in the context of this study, “deterrence” (as measured by the parameter $\varepsilon _{deter}$) means that the mosquito is deterred from entering the house before any attempt is made to take a bloodmeal. Thus, the parameter $\varepsilon _{deter}$ does not include any direct “barrier” property of the net.

We let $\varepsilon _{die,i}$ (with $i=\{p,u\}$; p=protected; u=unprotected) represent the probability that an adult female mosquito dies following entry into a protected (unprotected) house. The parameters $\varepsilon _{bite|die, i}$ and $\varepsilon _{bite|\sim die, i}$ represent, respectively, the probability that an adult female mosquito successfully takes a bloodmeal from the human host, given that the mosquito did or did not die, with i (p or u) indicating the bednet protection status of the targeted human. Figure 2 depicts the associated decision tree of the aforementioned probabilities).

Fig. 2

A decision tree of probabilities of the model (2.1), (2.2), (2.4)

The (temperature-dependent) equations for adult female mosquito dynamics are given by:

$$\begin{aligned} {\mathrm{Stage}} \,\,\text {I} {\left\{ \begin{array}{ll} {\dot{S}}_{X} &{}=f\sigma _P(T_W) P+\varphi _Z S_Z+ b_H (Q_2+Q_3) S_X-[b_H Q_1+{\mu _{\mathbf{X}}}+\mu _M(T_A)]S_{X}, \\ {\dot{E}}_{X} &{}= \varphi _Z E_Z+ b_H (Q_2+Q_3) E_X -[b_H Q_1+\kappa _V(T_A)+{\mu _{\mathbf{X}}}+\mu _M(T_A)]E_{X}, \\ {\dot{I}}_{X} &{}=\varphi _Z I_Z+\kappa _V(T_A) E_{X}+ b_H (Q_2+Q_3) I_X-[b_H Q_1+{\mu _{\mathbf{X}}}+\mu _M(T_A)]I_{X}, \end{array}\right. } \end{aligned}$$

(2.2)

$$\begin{aligned} {\mathrm{Stage}}\,\, \text {II} {\left\{ \begin{array}{ll} {\dot{S}}_{Y} &{}=b_H [(1 - \beta _V \omega _p) R_1 + (1 - \beta _V \omega _u) R_2] S_{X} -[\theta _Y(T_A)+\mu _M(T_A)]S_{Y}, \\ {\dot{E}}_{Y} &{}= b_H (\beta _V \omega _p R_1 + \beta _V \omega _u R_2) S_{X} + b_H (R_1+R_2) E_X\\ &{}\quad -[\theta _Y(T_A)+\kappa _V(T_A)+\mu _M(T_A)]E_{Y}, \\ {\dot{I}}_{Y} &{}=\kappa _V(T_A) E_Y+b_H(R_1+R_2) I_X-[\theta _Y(T_A)+\mu _M(T_A)]I_{Y}, \end{array}\right. } \end{aligned}$$

$$\begin{aligned} {\mathrm{Stage}}\,\, \text {III} {\left\{ \begin{array}{ll} {\dot{S}}_{Z} &{}=\theta _Y(T_A)S_{Y} -[\varphi _Z+\mu _M(T_A)]S_{Z}, \\ {\dot{E}}_{Z} &{}= \theta _Y(T_A) E_{Y}-[\varphi _Z+\kappa _V(T_A)+\mu _M(T_A)]E_{Z}, \\ {\dot{I}}_{Z} &{}=\theta _Y(T_A) I_{Y}+\kappa _V(T_A) E_Z-[\varphi _Z+\mu _M(T_A)]I_{Z}. \end{array}\right. } \end{aligned}$$

where,

$$\begin{aligned} Q_1= & {} \pi _p(1-\varepsilon _{deter})+\pi _u, \nonumber \\ Q_2= & {} \pi _p (1 - \varepsilon _{deter}) (1 - \varepsilon _{die,p}) (1 - \varepsilon _{bite|\sim die,p}),\ \nonumber \\ Q_3= & {} \pi _u (1 - \varepsilon _{die,u}) (1 - \varepsilon _{bite|\sim die,u}),\nonumber \\ R_1= & {} \pi _p (1 - \varepsilon _{deter}) (1 - \varepsilon _{die,p}) \varepsilon _{bite|\sim die,p}, \nonumber \\ R_2= & {} \pi _u (1 - \varepsilon _{die,u}) \varepsilon _{bite|\sim die,u},\nonumber \\ \omega _p= & {} \frac{I_{H_p}}{N_{H_p}}, \nonumber \\ \omega _u= & {} \frac{I_{H_u}}{N_{H_u}}, \end{aligned}$$

(2.3)

with $\omega _p$ ($\omega _u$) representing the fractions of protected (unprotected) humans that are infectious.

In (2.2) and (2.3), the term $f \sigma _{P}$ ($0< f <1$) represents the proportion of new adult mosquitoes that are females. Susceptible adult mosquitoes in Stage I of the gonotrophic cycle encounter hosts at a rate $b_H Q_1$ (where $b_H$ is the mosquito-host encounter rate per unit time, and $Q_1$ is defined above). The rate $b_H (Q_2+Q_3)$ represents failure to take a bloodmeal ending in survival (and thus a return to stage I of the gonotrophic cycle), while $b_H (R_1+R_2)$ is the rate at which encounters result in successful bloodmeals and survival. It should be emphasized that, in the formulation of the model (2.2) questing adult female mosquitoes that do not succeed in biting bednet-protected humans will not necessarily have to bite an unprotected human. They will simply look for a bloodmeal from another human who may be protected or not (see Fig. 1). The parameter $\kappa _V$ represents the maturation rate of malaria parasite in the mosquito (i.e., $\frac{1}{\kappa _V}$ is the average duration of the sporogonic cycle), while the parameter $\theta _Y$ is the progression rate from Stage II to Stage III of the gonotrophic cycle. Susceptible adult female mosquitoes in Stage II of the gonotrophic cycle acquire malaria infection at the rate $b_H (\beta _V \omega _p R_1 + \beta _V \omega _u R_2)$, where $\beta _V$ is the transmission probability from infectious human to a susceptible mosquito, $\omega _p$ and $\omega _u$ are the fractions of protected and unprotected infectious humans, respectively, and $\mu _M$ is the natural mortality rate of adult female mosquitoes. Following Chitnis et al. (2009), we assume an additional mortality rate, $\mu _X$, for adult female mosquitoes in the host-seeking stage, as this stage of the gonotrophic cycle is expected to be most hazardous to the adult female mosquitoes. Moreover, this helps account for a survival cost potentially incurred when the adult female mosquitoes are deterred from protected hosts and, thus, must expend more energy in questing for bloodmeal. Furthermore, as noted by Cator et al. (2012), sporozoite-infected Anopheles gambiae females are more likely than uninfected females to take bloodmeal from multiple hosts in the same night, and they suffer higher feeding-associated mortality. It should, however, be mentioned that very little is known about adult mosquito mortality in the field, and the degree that mortality is associated with bloodfeeding events is unknown. Such data, when available, will be very valuable in malaria modeling studies.

From the above formulation, the (time-varying) entomological inoculation rates [EIRs; the average numbers of infectious bites per human per unit time (Eikenberry and Gumel 2018)] for protected and unprotected hosts are given, respectively, by

$$\begin{aligned} \begin{aligned} \text {EIR}_p(t)&= b_H \frac{I_X(t)}{N_{H_p}(t)} \pi _p(1 - \varepsilon _{deter}) \left[ \varepsilon _{bite|die,p} \,\varepsilon _{die,p} + \varepsilon _{bite|\sim die,p} (1 - \varepsilon _{die,p})\right] , \\ \text {EIR}_u(t)&= b_H \frac{I_X(t)}{N_{H_u}(t)}\pi _u \left[ \varepsilon _{bite|die,u} \,\varepsilon _{die,u} + \varepsilon _{bite|\sim die,u} (1 - \varepsilon _{die,u})\right] . \end{aligned} \end{aligned}$$

Similarly, the biting (infectious or uninfectious) rates for protected and unprotected host are given, respectively, by

$$\begin{aligned} \begin{aligned} \text {biting}_p(t)&= b_H \frac{[S_X(t) + E_X(t) + I_X(t)]}{{N_{H_p}(t)}}\pi _p (1 - \varepsilon _{deter})\\&\quad \left[ \varepsilon _{bite|die,p}\, \varepsilon _{die,p} + \varepsilon _{bite|\sim die,p} (1 - \varepsilon _{die,p})\right] , \\ \text {biting}_u(t)&= b_H \frac{[S_X(t) + E_X(t) + I_X(t)]}{{N_{H_u}(t)}}\pi _u \left[ \varepsilon _{bite|die,u}\, \varepsilon _{die,u} + \varepsilon _{bite|\sim die,u} (1 - \varepsilon _{die,u})\right] . \end{aligned} \end{aligned}$$

The parameters related to the use of LLINs in the community (i.e., $b_H,$$\pi _p,$$\pi _u,$$\varepsilon _{deter},$$\varepsilon _{bite|\sim die,p},$$\varepsilon _{bite|\sim die,u},$$\varepsilon _{bite|die,p},$$\varepsilon _{bite|die,u},$$\varepsilon _{die,p}$ and $\varepsilon _{die,u}$) have been estimated for various mosquito-bednet pairings using experimental hut trial data conducted in various parts of sub-Saharan Africa. We assume, for this work, that $\varepsilon _{bite|\sim die,i}$ = $\varepsilon _{bite,i}$, for $i = u, p$. In brief, such trials typically include a control net and several treated nets that may be of different classes (conventional ITN vs. LLIN), subject to different degrees of wear (e.g. washing and/or artificial holing), and conducted in areas with different levels of local anopheline pyrethroid resistance (or employ lab strains). Volunteers sleep under nets in these trials, and the total number of mosquitoes collected in each hut, the total bloodfed, and the total dead are typically reported. We identified 26 publications conducted in Africa that reported sufficient detail to calculate the above metrics (Asale et al. 2014; Asidi et al. 2004, 2005; Bayili et al. 2017; Camara et al. 2018; Chandre et al. 2000; Corbel et al. 2004, 2010; Djènontin et al. 2015, 2018; Fanello et al. 1999; Ketoh et al. 2018; Koffi et al. 2015; Kweka et al. 2017; Malima et al. 2008, 2013; N’Guessan et al. 2001, 2007, 2010; Ngufor et al. 2014, 2011, 2016; Oxborough et al. 2013; Pennetier et al. 2013; Randriamaherijaona et al. 2015; Tungu et al. 2010).

Fig. 3

Data-points showing probability of death ($\varepsilon _{die,p}$) and blood feeding ($\varepsilon _{bite,p}$) for various mosquito-net pairings drawn from experimental hut trial data. Each point is coded according to net type by symbol shape, and according to mosquito resistance class (either pyrethroid resistant or sensitive). Additionally, representative points on the exponential curve fit relating $\varepsilon _{bite,p}$ to $\varepsilon _{die,p}$ are marked, signifying parameters for a highly effective ($\varepsilon _{die,p} = 0.9$, $\varepsilon _{bite,p} = 0.1$), moderately effective ($\varepsilon _{die,p} = 0.5$, $\varepsilon _{bite,p} = 0.2$), and weakly effective ($\varepsilon _{die,p} = 0.25$, $\varepsilon _{bite,p} = 0.33$) bednet. Data for the curves is drawn from the references (Asale et al. 2014; Asidi et al. 2004, 2005; Bayili et al. 2017; Camara et al. 2018; Chandre et al. 2000; Corbel et al. 2004, 2010; Djènontin et al. 2015, 2018; Fanello et al. 1999; Ketoh et al. 2018; Koffi et al. 2015; Kweka et al. 2017; Malima et al. 2008, 2013; N’Guessan et al. 2001, 2007, 2010; Ngufor et al. 2014, 2011, 2016; Oxborough et al. 2013; Pennetier et al. 2013; Randriamaherijaona et al. 2015; Tungu et al. 2010), as described further in the text

Every mosquito-hut pairing reported in these trials gives a value for $\varepsilon _{die,p}$, $\varepsilon _{bite,p}$, and $\varepsilon _{deter}$. Moreover, each pairing represents some “effective” level of insecticide resistance (i.e. an ineffective net and a sensitive mosquito and effective net but highly resistant mosquito may both represent pairings of high effective resistance). These pairings can be used to estimate how $\varepsilon _{die,p}$ and $\varepsilon _{bite,p}$ systematically co-vary as effective resistance changes, and a functional relationship between $\varepsilon _{die,p}$ (the probability of death following encounter with a protected host) and $\varepsilon _{bite,p}$ (the probability of taking a bloodmeal from a protected host) can been estimated, as depicted in Fig. 3. We choose the exponential relation,

$$\begin{aligned} \varepsilon _{bite,p}=\displaystyle {a_0\,\,{\mathrm{exp}\left( -b_0\,\, \displaystyle {\varepsilon _{die,p}}\right) }}, \end{aligned}$$

where the best-fit values of the constants $a_0$ and $b_0$ are found, using weighted nonlinear least squares (weighting by number of mosquitoes collected in each trial), to be $a_0=0.55$ and $b_0=2$. The value of this relationship is that it allows effective bednet resistance to be described by a single parameter, $\varepsilon _{die,p}$, with $\varepsilon _{bite,p}$ determined as a function of $\varepsilon _{die,p}$. Following Randriamaherijaona et al. (2015), we estimate the probability that a mosquito takes a bloodmeal from a person sleeping without a net or under an extremely holed untreated net is on the order of 70-80%, while the probability of death is $\le$ 5%. Hence, we take $\varepsilon _{bite,u}$ = 0.7 and $\varepsilon _{die,u}$ = 0.05 as baseline parameters for encounters with unprotected hosts. The parameter $\varepsilon _{deter}$ is assumed to vary between 0.01 to 0.4.

In this study, the following three effectiveness levels of the LLINs are considered (given in Table 4), as also highlighted in Fig. 3:

• (i) Weakly-effective net: this is a net that has low killing efficacy and high biting probability. For this setting, we choose $\varepsilon _{die,p}=0.25, \varepsilon _{bite,p}=0.33$. Here, the adult mosquitoes are highly resistant to the net.

• (ii) Moderately-effective net: this is a net with moderate killing efficacy and moderate biting probability. Here, we set $\varepsilon _{die,p}=0.5, \varepsilon _{bite,p}=0.2$, and the adult mosquitoes are moderately resistant to the net.

• (iii) Highly-effective net: this is a net with very high killing efficacy and very low biting probability. Here, we set $\varepsilon _{die,p}=0.9, \varepsilon _{bite,p}=0.1$. This corresponds to the case where the adult mosquitoes are weakly resistant to the net.

2.3 Equations for the dynamics of human population

The equations for the dynamics of the human population are given by:

$$\begin{aligned} \begin{aligned} {\dot{S}}_{H_p}&=\Pi \, \pi _p +\eta _H R_{H_p}- (\lambda _{VH_p}+\mu _{H})S_{H_p}, \\ {\dot{E}}_{H_p}&=\lambda _{VH_p}S_{H_p}-(\gamma _H+\mu _H)E_{H_p}, \\ {\dot{I}}_{H_p}&=\gamma _HE_{H_p}-(\alpha _H+\mu _H+\delta _H)I_{H_p}, \\ {\dot{R}}_{H_p}&=\alpha _HI_{H_p}-(\eta _H+\mu _{H})R_{H_p}, \\ {\dot{S}}_{H_u}&=\Pi \, \pi _u+\eta _H R_{H_u} - (\lambda _{VH_u}+\mu _{H})S_{H_u}, \\ {\dot{E}}_{H_u}&=\lambda _{VH_u}S_{H_u}-(\gamma _H+\mu _H)E_{H_u}, \\ {\dot{I}}_{H_u}&=\gamma _HE_{H_u}-(\alpha _H+\mu _H+\delta _H)I_{H_u}, \\ {\dot{R}}_{H_u}&=\alpha _HI_{H_u}-(\eta _H+\mu _{H})R_{H_u}, \\ \end{aligned} \end{aligned}$$

(2.4)

where, $\lambda _{VH_p}(t)={\beta _M\,\text {EIR}_p}(t)$ and $\lambda _{VH_u}(t)=\beta _M\,\text {EIR}_u(t)$.

In (2.4), $\Pi$ represents the recruitment rate of individuals (by birth or immigration) into the population (with $\pi _p$ and $\pi _u$ as defined in Sect. 2). The parameter $\eta _H$ represents the loss of immunity by individuals who recovered from malaria. Susceptible protected humans acquire malaria infection from infectious mosquitoes at a rate $\lambda _{VHp} \,(\lambda _{VHu})$, with $\beta _M$ being the probability of infection per bite and $EIR_p$ (${EIR_u}$) as defined in Sect. 2. Natural mortality occurs in all human compartments at a rate $\mu _H$. Infected individuals develop clinical symptoms of malaria at a rate $\gamma _H$, and recover at a rate $\alpha _H$. Finally malaria-induced death occurs in the infectious human population at a rate $\delta _H$.

The model (2.1), (2.2), (2.4) is a modification of the model in Okuneye et al. (2019) by:

• (a) Explicitly including the dynamics of the adult mosquitoes under the influence of bednet usage (in Stages I and II of the gonotrophic cycle);

• (b) Stratifying the human population in terms of bednets usage [only one class for susceptible, exposed, infectious and recovered humans was used in Okuneye et al. (2019)].

The 23-dimensional nonlinear continuous-time model (2.1), (2.2), (2.4) is also an extension of the 3-dimenisonal, linear, difference equation model developed by Chitnis et al. (2009) by:

• (i) Explicitly including the dynamics of the immature mosquitoes [i.e., adding equations for the dynamics of eggs, the four larval instars and the pupal stages of the aquatic cycle; this was not included in Chitnis et al. (2009)];

• (ii) Explicitly incorporating the deterrence property of the bednet [this was not explicitly included in Chitnis et al. (2009)];

• (iii) Explicitly including the dynamics of the adult mosquitoes under the influence of bednet usage (in Stages I and II of the gonotrophic cycle);

• (iv) Including the dynamics of humans vis a vis malaria transmission, and stratifying the human population in terms of bednets usage (the dynamics of humans is not explicitly incorporated in the model in Chitnis et al. (2009), making the model linear);

• (v) Explicitly incorporating the effect of temperature variability on the population ecology of immature and adult mosquitoes [this was not considered in Chitnis et al. (2009)].

Furthermore, unlike in the case of the model in Chitnis et al. (2009), the model developed in this study is simulated subject to three effectiveness levels (low, moderate and high) of the bednets used in the community. This allows for the assessment of various levels of insecticide resistance in the community [these bednets effectiveness levels are not considered in Chitnis et al. (2009)].

The state variables and parameters of the model (2.1), (2.2), (2.4) are described in Tables 1, 2, and 3. Baseline values and ranges of the parameters of the model are tabulated in Table 4 [more detailed descriptions may be found in Okuneye et al. (2019)]. All bednet-related parameters vary with net effectiveness, as described above, with the sole exception of $\varepsilon _{deter}$, which we fix at 0.1 for all simulation results, unless otherwise stated.

Table 1 Description of state variables for the model (2.1), (2.2), (2.4)

Table 2 Description of bednet-independent parameters of the model (2.1), (2.2), (2.4)

Table 3 Description of bednet-related parameters of the model (2.1), (2.2), (2.4)

Table 4 Parameters for bednet effectiveness levels with deterrence $\epsilon _{deter}$ set to zero

Table 5 Ranges and baseline values of temperature-independent parameters of the model (2.1), (2.2), (2.4). The estimate for $K_E$ is defined in terms of the total human population at the disease-free equilibrium $(\frac{\Pi }{\mu _H})$ to ensure that the mosquito: host ratio falls within the realistic range of 0.1 to 10 mosquitoes per person per day typically encountered in the field Macdonald (1957)

2.4 Temperature-dependent parameters

Both vector and parasite are ectothermal (dependent on ambient temperature). Thus, their life histories are significantly affected by temperature. For instance, adult and immature aquatic mosquito survival is maximized for temperature values in the mid-20s ($^{\circ }{\mathrm{C}}$), with survival tailing off rather symetrically at higher and lower temperatures (Eikenberry and Gumel 2018). Further, the development rates of Plasmodium parasites, immature anophelines and mosquito eggs generally increase with increasing temperature to, at least, about 30 $^{\circ }{\mathrm{C}}$ (Paaijmans et al. 2010; Eikenberry and Gumel 2018). Thermal response functions for temperature-dependent parameters are determined from experimental lab data as follows.

Death rate of adult female mosquitoes ($\mu _M(T_A)$) The mean survival times for adult Anopheles gambiae under laboratory conditions, and under constant ambient temperatures ranging from 5 to 40 $^{\circ }$C (5 $^{\circ }$C intervals), are taken from Bayoh (2001).

$$\begin{aligned} \frac{1}{\mu _M(T_A)} = \max (0.01, a + b T_A + c T_A^2), \end{aligned}$$

(2.5)

where $a = -11.8239$, $b = 3.3292$ and $c = -0.0771$.

Transition rate from stage II to stage III of gonotrophic cycle ($\theta _Y(T_A)$) We describe the rate at which mosquitoes complete Stage II of the gonotrophic cycle (that is, the transition from the Y to Z compartment(s)), using a Briere function (Briere et al. 1999), such that

$$\begin{aligned} \theta _Y(T_A) = {c T_A (T_A - T^0_A) (T^m_A - T_A)^{\frac{1}{2}}}, \end{aligned}$$

(2.6)

and parameter values are adopted from Mordecai et al. (2013), with c = 0.000203, $T^m_A$ = 42.3 $^{\circ }$C and $T^0_A$ = 11.7 $^{\circ }$C .

Sporogony ($\kappa (T_A)$) We follow Paaijmans et al. (2010) and use a Briere function for $\kappa (T_A)$, given by the right-hand side of (2.6) with parameters c = 0.000112, $T^m_A$ = 35 $^{\circ }$C , and $T^0_A$ = 15.384 $^{\circ }$C .

Death rate of immature mosquitoes ($\mu _E(T_W)$, $\mu _L(T_W)$, $\mu _P(T_W)$) We assume that temperature-dependent death rates are equal for eggs, larvae, and pupae, and use laboratory larval survival times reported by Bayoh and Lindsay (2004), to fit a per-capita death rate (inverse of survival time) with the fourth-order polynomial,

$$\begin{aligned} \mu _{i}(T_W)= & {} 8.929 \times 10^{-6} T_W^4 - 0.0009271 T_W^3 + 0.03536 T_W^2 \nonumber \\&- 0.5814 T_W + 3.509, \quad i = E, L, P. \end{aligned}$$

(2.7)

Development rate of immature mosquitoes ($\sigma _E(T_W)$, $\sigma _L(T_W)$, $\sigma _P(T_W)$) We adopt the relationship between water temperature and overall time from egg to adult, $l(T_W)$, given by Bayoh and Lindsay (2003) (based on laboratory data),

$$\begin{aligned} l(T_W) = (a + b T_W + c e^{T_W} + d e^{-T_W})^{-1}, \end{aligned}$$

(2.8)

with a = $-0.05$, b = 0.005, c = $-2.139$$\times$ 10$^{-16}$ and d = $-281357.656$. We assume that the duration of all six immature stages (egg, four larval instars, and pupa) is equal, giving (Okuneye et al. 2019). We determined stage-specific development times as a function of temperature from Fig. 1 of Bayoh and Lindsay (2003), as shown in Fig. 4. Development times are similar across all immature stages, with appreciable overlap in the temperature-dependent curves. Therefore, we simply assume all stages have the same duration, and the uniform temperature-dependent development rates are given as

$$\begin{aligned} \sigma _E(T_W) = \sigma _P(T_W) = \sigma _L(T_W) = 6 \frac{1}{l(T_W)}. \end{aligned}$$

(2.9)

We have assumed, for this study, that near the surface of the water, air and water temperature are approximately equal (Agusto et al. 2015; Iboi and Gumel 2018), giving $T_A = T_W$ (unless otherwise stated, a default value of $T_A$ = $T_W$ = 25 $^\circ$C will be used to compute each of the aforementioned temperature-dependent parameters of the model). Further, since (by using fixed temperature values) the aforementioned temperature-dependent parameters take constant values, the model (2.1), (2.2), (2.4) is autonomous. This assumption is made for mathematical tractability.

2.5 Basic qualitative properties of the model

The basic qualitative properties of the model (2.1), (2.2), (2.4) in the absence of density-dependent mortality rate in the larvae stage ($\delta _L=0$) are explored in this section, with the positivity and boundedness of the solutions of the model established.

Fig. 4

Development times of the dynamics of the immature mosquitoes

Let $A_X=S_X+E_X+I_X,$$A_Y=S_Y+E_Y+I_Y$, $A_Z=S_Z+E_Z+I_Z$ and $N_M(t)=A_X(t)+A_Y(t)+A_Z(t)$. Further, define

$$\begin{aligned} {\mathcal {X}}= & {} \left( E,L_1,L_2,L_3,L_4,P,S_X,E_X,I_X,S_Y,E_Y,I_Y,S_Z,E_Z,I_Z,S_{H_p}, E_{H_p},\right. \\&\left. I_{H_p}, R_{H_u}, S_{H_u}, E_{H_u}, I_{H_u}, R_{H_u} \right) . \end{aligned}$$

It is convenient to group the variables of the model (2.1), (2.2), (2.4) as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {B}}_1&= \left( E,L_1, L_2, L_3, L_4, P\right) ,\\ {\mathcal {B}}_2&= \left( S_X, E_X, I_X, S_Y, E_Y, I_Y, S_Z, E_Z, I_Z\right) ,\\ {\mathcal {B}}_3&= \left( S_{H_p}, E_{H_p}, I_{H_p}, R_{H_u}, S_{H_u}, E_{H_u}, I_{H_u}, R_{H_u}\right) . \end{aligned} \end{aligned}$$

(2.10)

Consider the feasible region $\Omega =\Omega _1\times \Omega _2\times \Omega _3$ for the model (2.1), (2.2), (2.4), where:

$$\begin{aligned} \Omega _1= & {} \left\{ {\mathcal {B}}_1\in {\mathbb {R}}^{6}_+:E(t)\le K_E,L_1(t)\le L^\diamond _{1},L_2(t)\le L^{\diamond }_2,L_3(t)\le L^{\diamond }_3,L_4(t)\nonumber \right. \\&\left. \quad \le L^{\diamond }_4,P(t)\le P^{\diamond } \right\} ,\nonumber \\ \Omega _2= & {} \left\{ {\mathcal {B}}_2\in {\mathbb {R}}^{9}_+:N_M(t)\le \frac{f\sigma _P P^{\diamond }}{\mu _M}\right\} ,\quad \Omega _3=\left\{ {\mathcal {B}}_3\in {\mathbb {R}}^{8}_+:N_H(t)\le \frac{\Pi }{\mu _H}\right\} ,\nonumber \\ \end{aligned}$$

(2.11)

with, $L^{\diamond }_1=\frac{\sigma _E K_E}{\sigma _{L_1}+\mu _L},\, L^{\diamond }_2=\frac{\sigma _{L_1} L^{\diamond }_1}{\sigma _{L_2}+\mu _L},\, L^{\diamond }_3=\frac{\sigma _{L_2}L^{\diamond }_2}{\sigma _{L_3}+\mu _L},\, L^{\diamond }_4=\frac{\sigma _{L_3}L^{\diamond }_3}{\sigma _{L_4}+\mu _L}$ and $P^{\diamond }=\frac{\sigma _{L_4}L^{\diamond }_4}{\sigma _P +\mu _P}.$

We claim the following result.

Lemma 2.1

Consider the model (2.1), (2.2), (2.4).

• (a) Each component of the solution of the model, with non-negative initial conditions, remains positive and bounded for all time $t>0$.

• (b) The set $\Omega$ is positively-invariant and attracting region for the model.

The proof of Lemma 2.1 is given in “Appendix A”.

3 Mathematical analysis

In this section, the model (2.1), (2.2), (2.4) is rigorously analysed to show the existence and asymptotic stability of its disease-free equilibrium, and to characterize the bifurcation structure of the model. We define the threshold quantity, ${\mathcal {N}}_0$, as

$$\begin{aligned} {\mathcal {N}}_0=\frac{\psi _E\varphi _Z\sigma _Ef\sigma _P\theta _YC_2\prod \nolimits ^4_{i=1}\sigma _{L_{i}}}{\left( C_1K_9K_{11}-C_2\theta _Y\varphi _Z\right) \prod \nolimits ^6_{i=1} K_i}, \end{aligned}$$

(3.1)

where ${C}_{{1}}={K}_{{7}}-{{b}}_{{H}}({Q}_{{2}}+{Q}_{{3}})$, $\,\,C_2=b_H(R_1+R_2)$,$\,\,K_1=\sigma _E+\mu _E$,$\,\,K_j=\sigma _{L_{j-1}}+\mu _L \,(j=2,\ldots ,5$),$\,\,K_6=\sigma _P+\mu _P$,$\,\,{K}_{{7}}={b}_{{H}}{Q}_{{1}} +\mu _{{X}}+\mu _{{M}}$, $K_9=\theta _Y+\mu _M$ and $K_{11}=\varphi _Z+\mu _M$. Furthermore (noting the definitions of $C_9$, $C_{10}$ and $C_{11}$ given in “Appendix B”), $C_1K_9K_{11}-C_2\theta _Y\varphi _Z=\mu ^3_M+\mu ^2_M C_{9}+\mu _M C_{10}+C_{11}>0$. Hence, ${\mathcal {N}}_0>0$.

The quantity ${\mathcal {N}}_0$, which is the extinction threshold for the mosquito population of the model, measures the average number of new adult female mosquitoes produced by one reproductive mosquito during its entire reproductive period (Eikenberry and Gumel 2018; Okuneye et al. 2019).

3.1 Existence of the disease-free equilibrium

The existence and asymptotic stability of the disease-free equilibrium (DFE) of the model (2.1), (2.2), (2.4) is demonstrated here, and we examine the following equilibria:

• (i) The model (2.1), (2.2), (2.4) has a trivial disease-free equilibrium ($TDFE$), given by:

  $$\begin{aligned} \begin{aligned} {\mathcal {T}}_1&=\left( 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,S^*_{H_p},0,0,0,S^*_{H_u},0,0,0\right) ,\\&=\left( 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,\frac{\Pi \,\pi _p}{\mu _H},0,0,0,\frac{\Pi \,\pi _u}{\mu _H},0,0,0\right) . \end{aligned} \end{aligned}$$

  The equilibrium ${\mathcal {T}}_1$ is ecologically unrealistic (since it is associated with the total absence of mosquitoes in the community). Hence, it is not analysed.

• (ii) The model (2.1), (2.2), (2.4) has a unique non-trivial disease-free equilibrium ($NDFE$), given by:

  $$\begin{aligned} {\mathcal {T}}_2=\left( E^*,L^*_1,L^*_2,L^*_3,L^*_4,P^*,S^*_X,0,0,S^*_Y,0,0,S^*_Z,0,0,\frac{\Pi \,\pi _p}{\mu _H},0,0,0,\frac{\Pi \,\pi _u}{\mu _H},0,0,0\right) , \end{aligned}$$

  where,

  $$\begin{aligned} \begin{aligned} E^*&=K_E\left( 1-\frac{1}{{\mathcal {N}}_0}\right) ,\quad L^*_1=\frac{\sigma _E E^*}{K_2},\quad L^*_2=\frac{\sigma _{L_1} L_1^*}{K_3},\quad L^*_3=\frac{\sigma _{L_2} L_2^*}{K_4},\\ L^*_4&=\frac{\sigma _{L_3} L_3^*}{K_5},\quad P^*=\frac{\sigma _{L_4} L_4^*}{K_6},\quad S^*_X=\frac{\left[ f\sigma _E\sigma _PK_E\left( 1-\frac{1}{{\mathcal {N}}_0}\right) K_9K_{11}\right] \prod \limits ^4_{i=1}\sigma _{L_{i}}}{(C_1K_9K_{11}-C_2\theta _Y\varphi _Z)\prod \limits ^6_{i=2} K_i},\\ S^*_Y&=\frac{C_2S^*_X}{K_9},\quad S^*_Z=\frac{\theta _Y S^*_Y}{K_{11}}. \end{aligned}\nonumber \\ \end{aligned}$$

  (3.2)

It is clear from Eq. (3.2) that the equilibrium ${\mathcal {T}}_2$ exists if and only if ${\mathcal {N}}_0>1$ (it is assumed from here on that ${\mathcal {N}}_0>1$, so that the non-trivial disease-free equilibrium, ${\mathcal {T}}_2$, exists). It is worth noting that the NDFE (${\mathcal {T}}_2$) is the non-extinction equilibrium for the mosquito population coupled with the trivial disease-free equilibrium (${\mathcal {T}}_1$) for the human population. Hence, in the absence of the vectors and the disease, the two subsystems (${\mathcal {T}}_1$ and ${\mathcal {T}}_2$) are uncoupled.

3.2 Asymptotic stability of the NDFE

Consider the model (2.1), (2.2), (2.4). It can be shown, using the next generation operator method van den Driessche and Watmough (2002), that the associated reproduction number ${\mathcal {R}}_0$ of the model is given by:

$$\begin{aligned} {\mathcal {R}}_0=\sqrt{({\mathcal {R}}_{H_pV}+{\mathcal {R}}_{H_uV})\times {\mathcal {R}}_{VH}}, \end{aligned}$$

(3.3)

where,

$$\begin{aligned} {\mathcal {R}}_{H_pV}=\frac{\gamma _H\beta _VN^*_{Hu}Q_pR_1}{K_{13}K_{14}},\quad {\mathcal {R}}_{H_uV}=\frac{\gamma _H\beta _VN^*_{Hp}Q_uR_2}{K_{13}K_{14}}, \end{aligned}$$

(3.4)

and,

$$\begin{aligned} {\mathcal {R}}_{VH}=\frac{b_H\beta _M S^*_X}{N^*_{Hp}N^*_{Hu}} \frac{\kappa _V \varphi _Z \theta _Y[(K_9+K_{12})C_3+K_9K_{11}]}{\left( C_3K_{10}K_{12}-C_2\theta _Y\varphi _Z\right) \left( C_1K_9K_{11}-C_2\theta _Y\varphi _Z\right) }, \end{aligned}$$

(3.5)

with,

$$\begin{aligned} Q_p= & {} b_H \pi _p(1 - \varepsilon _{deter}) \left[ \varepsilon _{bite|die,p}\, \epsilon _{die,p} + \varepsilon _{bite|\sim die,p} (1 - \varepsilon _{die,p})\right] , \\ Q_u= & {} b_H \pi _u \left[ \varepsilon _{bite|die,u} \,\varepsilon _{die,u} + \varepsilon _{bite|\sim die,u} (1 - \varepsilon _{die,u})\right] , \end{aligned}$$

$N^*_{Hp}=\frac{\Pi \,\pi _p}{\mu _H}$,   $N^*_{Hu}=\frac{\Pi \,\pi _u}{\mu _H}$,   ${C}_{{3}}={K}_{{8}}-{b}_{{H}}({Q}_{{2}}+{Q}_{{3}})$,$\,\,{K}_{{8}}={b}_{{H}}{Q}_{{1}}+\kappa _{{V}}+\mu _{{X}}+\mu _{{M}}$, $\,\,K_{10}=\theta _Y+\kappa _V+\mu _M$,$\,\,K_{12}=\varphi _Z+\kappa _V+\mu _M$,$\,\,K_{13}=\gamma _H+\mu _H$ and $\,\,K_{14}=\alpha _H+\delta _H+\mu _H$. It can be shown that $C_3K_{10}K_{12}-C_2\theta _Y\varphi _Z=b_H[C_4\kappa ^2_V+2\kappa _V\left( \mu _M+\frac{\theta _Y}{2}+\frac{\varphi _Z}{2}\right) C_5+C_6+C_7]+C_8>0$ (where the coefficients $C_i \,(i = 2, . . . , 8)$ are constants, and are given in “Appendix D”). Hence, ${\mathcal {R}}_{VH}>0$ (and thus ${\mathcal {R}}_0$ is also automatically positive).

Theorem 3.1

Let ${\mathcal {N}}_0>1$. The NDFE, ${\mathcal {T}}_2$, of the model (2.1), (2.2), (2.4) is locally-asymptotically stable (LAS) in $\Omega \setminus {\mathcal {T}}_1$ if ${\mathcal {R}}_0< 1$, and unstable if ${\mathcal {R}}_0>1$.

The epidemiological implication of Theorem 3.1 is that malaria is eliminated from the population if the initial sizes of the subpopulations of the model (2.1), (2.2), (2.4) are in the basin of attraction of the non-trivial disease-free equilibrium (${\mathcal {T}}_2$ ). Hence, a small influx of malaria-infected individuals into the community will not generate large outbreaks, though larger influxes may.

It is notable that the value of the reproduction number $({\mathcal {R}}_{0})$ for the worst-case scenario (i.e., bednet coverage is zero), denoted by $\tilde{{\mathcal {R}}}_{0*}$ and computed using the baseline parameter values in Table 4, is $\tilde{{\mathcal {R}}}_{0*}\simeq$ 11.4 (see “Appendix C” for the formulation of the special case of the model (2.1), (2.2),(2.4) with no bednet coverage). This high value of the reproduction number is typically seen in holo-endemic malaria regions (Gething et al. 2010). It should be mentioned that, for the computation of the value of the reproduction number for this (holo-endemic) setting, we assumed (in Table 4) that there are, on average, 100 eggs per human (which translates to about 10 adult mosquitoes per human). When we reduce the number of eggs per human to 10 per human, so that we have one mosquito per human [which is more typically the case in meso-endemic regions (Gething et al. 2010)], the value of ${\mathcal {R}}_0$ reduces to $\tilde{{\mathcal {R}}}_{0*}\simeq$ 3.6. Hence, these computations (together with Theorem 3.1) show that, for the worst-case scenario (with no bednets used in the community), the disease will persist in both the holoendemic and the mesoendemic regions (since $\tilde{{\mathcal {R}}}_{0*}>1$ in both cases), as expected.

3.3 Existence of backward bifurcation

The phenomenon of backward bifurcation has been observed in numerous models [such as those in Blayneh et al. (2010), Feng et al. (2015), Garba et al. (2008), Garba and Gumel (2010), Iboi and Gumel (2018), Iboi et al. (2018)] for spread of malaria and other vector-borne diseases that incorporated disease-induced death in the host population. A backward bifurcation is characterized by the co-existence of two asymptotically-stable equilibria when ${\mathcal {R}}_0 < 1$: an endemic equilibrium point (EEP) and a disease-free equilibrium point (DFE). Thus, the classical epidemiological requirement that ${\mathcal {R}}_0$ be less than one for elimination of the disease, while necessary, is no longer sufficient to eliminate malaria when it already exists in the population. That is, while ${\mathcal {R}}_0 \ge 1$ remains a condition for malaria to spread within a previously unexposed population, pushing ${\mathcal {R}}_0 < 1$ via control measures does not necessarily guarantee elimination of the disease.

Theorem 3.2

The model (2.1), (2.2), (2.4) undergoes a backward bifurcation at ${\mathcal {R}}_0=1$ whenever a bifurcation coefficient, denoted by a (given in “Appendix D”), is positive.

Proof

The proof of Theorem 3.2, based on using Center Manifold theory Carr (1981); Castillo-Chavez and Song (2004), is given in “Appendix D”. The result given by Theorem 3.2 is numerically illustrated by simulating the model (2.1), (2.2), (2.4) using parameter values such that the backward bifurcation condition, given in “Appendix D”, is satisfied (Fig. 5). $\square$

Fig. 5

Backward bifurcation diagram of the model (2.1), (2.2), (2.4), showing a plot of $I_{Hp}(t)$ as a function of the reproduction number ${\mathcal {R}}_0$, where $\beta _M$ is the chosen bifurcation parameter. Parameter values used are as given in Table 5 with: $\pi _p=0.5,\pi _u=0.5,\varepsilon _{deter}=0.75,\varepsilon _{bite|\sim die,p}=0.1,\varepsilon _{bite|\sim die,u}=0.7,\varepsilon _{bite|die,p}=0.1,\varepsilon _{bite| die,u}=0.7,\varepsilon _{die,p}=0.9,\varepsilon _{die,u}=0.05,b_H=2, \mu _{{X}}={0}.{{005}},\psi _E=5,\delta _H=0.0005,{\eta _H=1/14},\beta _V=0.5,\Pi =1$ and $K_E=\frac{\Pi }{\mu _H}$ (so that the bifurcation coefficient, a (defined in “Appendix D”), is given by a=$5.42\times 10^{-6}>0$ and ${\mathcal {R}}_0=1$). It should be mentioned that in order to generate this figure, the values of seven parameters ($\mu _X,\psi _E, K_E, \eta _H, \delta _H, \beta _V\,\, \mathrm{and}\,\, \Pi$) have to be chosen outside their biologically-feasible ranges given in Table 5

The range for backward bifurcation for a weakly-effective net (i.e., a net with $\varepsilon _{die,p}=0.25$, $\varepsilon _{bite,p}=0.33$) is $\beta _M\in (0.526394,\infty )$, a moderately-effective net (i.e., a net with $\varepsilon _{die,p}=0.5$, $\varepsilon _{bite,p}=0.2$) is $\beta _M\in (0.503682,\infty )$ and that for a highly- effective net (i.e., a net with $\varepsilon _{die,p}=0.9$, $\varepsilon _{bite,p}=0.1$) is $\beta _M\in (1.4009823,\infty )$, where $\beta _M$ is the chosen backward bifurcation parameter (see “Appendix D”). Hence, this study shows that the phenomenon of backward bifurcation is more likely to occur using a moderately-effective net than when either a weak or highly-effective net is used.

Theorem 3.2 shows that elimination is dependent on the initial sizes of the infected vector and human populations. For elimination to be independent of the size of the infected populations, a global asymptotic stability property must be explored for the non-trivial disease-free equilibrium (${\mathcal {T}}_2$). It is convenient to define the associated reproduction number of the model (2.1), (2.2), (2.4) in the absence of disease-induced mortality in the host population ($\delta _H$) by

$$\begin{aligned} \tilde{{\mathcal {R}}}_0={\mathcal {R}}_0|_{\delta _H=0}. \end{aligned}$$

(3.6)

We claim the following.

Theorem 3.3

The NDFE, ${\mathcal {T}}_2$, of the model (2.1), (2.2), (2.4), with $\delta _H=0$ and ${\mathcal {N}}_0> 1$, is globally-asymptotically stable (GAS) in $\Omega \setminus {\mathcal {T}}_1$ if $\tilde{{\mathcal {R}}}_0<1$.

The proof of Theorem 3.3, based on using Lyapunov function theory and LaSalle’s Invariance Principle, is given in “Appendix E”. The epidemiological implication of Theorem 3.3 is that, for the special case of the model (2.1), (2.2), (2.4) with no disease-induced mortality in the host population (i.e., $\delta _H=0$), bringing and maintaining the associated reproduction threshold ($\tilde{{\mathcal {R}}}_0$) to a value less than one is necessary and sufficient for complete elimination of malaria in the community, regardless of initial conditions.

Fig. 6

Relationships among EIR, fraction of infected humans, bednet coverage level, and $\tilde{{\mathcal {R}}}_0$, at the endemic equilibrium, as determined from numerical simulation of the model (2.1), (2.2), (2.4), and for fixed temperature (25 $^\circ$C). Results are disaggregated between the protected, unprotected, and overall (bednet-protected and unprotected human) populations. Results are determined using baseline parameter values with a highly effective net in a holoendemic setting ($K_E=100\frac{\Pi }{\mu _H}$, $\tilde{{\mathcal {R}}}_{0*} = {11.4}$ with no bednet coverage)

4 Numerical simulations: populations at equilibrium

4.1 Interaction between bednet coverage and bednet efficacy parameters

To assess the population-level impact of bednets on malaria transmission dynamics in the community under equilibrium conditions (i.e., the model is numerically simulated until an endemic equilibrium is reached), the model (2.1), (2.2), (2.4) is simulated using various bednet coverage and effectiveness levels, where bednet effectiveness is jointly defined by $\varepsilon _{bite,p}$ and $\varepsilon _{die,p}$. Unless otherwise stated, all simulations use the baseline parameter values in Table 5, and temperature is fixed at $25\,^\circ \hbox {C}$ (i.e., the values of all the temperature-dependent parameters of the model are obtained by evaluating each of the functional forms in Sect. 2 at the fixed temperature T=25 $^\circ$C). Figure 6 illustrates the nonlinear relationships between bednet coverage fraction, $\pi _p$, disease prevalence in the two human populations (bednet-protected and unprotected), $\tilde{{\mathcal {R}}_0}$ (i.e., ${\mathcal {R}}_0$ for the case when the disease-induced mortality in the human population, $\delta _H$, is set to zero), and EIR (again, in the bednet-protected and unprotected populations), at endemic equilibrium and for baseline parameters. Notably, this figure shows that EIR decreases with increasing bednet coverage (top right panel). This result is consistent with that reported in the modeling study by Chitnis et al. (2009), which used data relevant to malaria transmission dynamics in Ifakara, Tanzania (i.e., data for Anopheles gambiae feeding on a heterogenous human population, with no cattle), to show that bednets are effective in reducing malaria transmission. Our result is also consistent with the results of the field trials on permethrin-treated bednets in western Kenya reported by Hawley et al. (2003).

Further, as evident from the graph in the lower left panel of Fig. 6, human disease prevalence varies hyperbolically with EIR (i.e., prevalence increases with increasing EIR), such that, for a high baseline EIR, a large reduction in EIR is required before any meaningful malaria control is realized. A five-fold reduction in overall EIR, however, is achieved with roughly 20% bednet coverage (see upper right panel of Fig. 6). Thus, although even a relatively low bednet coverage can aid somewhat in malaria control, the simulations in Fig. 6 show that much higher bednet coverage (and a decrease in EIR of two orders of magnitude) is needed to achieve malaria elimination. Finally, there is a similar, although less marked, hyperbolic relationship between increasing $\tilde{{\mathcal {R}}_0}$ and increasing disease prevalence (bottom right panel).

Fig. 7

Contour plots of the $\tilde{{\mathcal {R}}}_0$ of the model (2.1), (2.2), (2.4), as a function of $\varepsilon _{die,p}$ and $\varepsilon _{bite,p}$ (the respective probabilities that a mosquito dies or takes a blood meal upon encountering a protected human), for four different permutations of bednet coverage and baseline $\tilde{{\mathcal {R}}}_0$. The top panels use $K_E=100\frac{\Pi }{\mu _H}$ to approximate a holoendemic baseline, while the bottom panels use $K_E=10\frac{\Pi }{\mu _H}$ as an approximation of a mesoendemic baseline. Bednet coverage is either 20% (left) or 80% (right). The inscribed curve shows the approximate relationship between $\varepsilon _{die,p}$ and $\varepsilon _{bite,p}$ derived from experimental hut trial data (using the exponential relation given in Sect. 2.2), with three qualitative net effectiveness levels highlighted

We explore how changes in $\varepsilon _{bite,p}$ and $\varepsilon _{die,p}$ (i.e. net effectiveness) affect $\tilde{{\mathcal {R}}}_0$, starting from either a baseline $\tilde{{\mathcal {R}}}_0$ value of 11.7, presumably representing holoendemic malaria, or 3.7, which is more appropriate for mesoendemic malaria. In particular, we generate contour plots of $\tilde{{\mathcal {R}}}_0$ as a function of $\varepsilon _{bite,p}$ and $\varepsilon _{die,p}$, for either low (20%) or high (80%) bednet coverage levels (Fig. 7). The inscribed curve on each contour plot of Fig. 7 shows how $\varepsilon _{bite,p}$ and $\varepsilon _{die,p}$ co-vary, based upon the experimental hut data discussed in Sect. 2.2. In these plots, the highlighted points indicate highly, moderately, and weakly effective nets. It follows from Fig. 7 that, for the mesoendemic baseline, even a moderately effective net is capable of pushing $\tilde{{\mathcal {R}}}_0$ to a value less than one when bednet coverage is high (80%). Further, for this (mesoendemic baseline scenario) even low bednet coverage (20%) may substantially improve malaria control. In the holoendemic baseline, on the other hand, only a highly effective net with high coverage can have a chance to approach malaria elimination. Thus, these simulations show that our study only supports the claim in the malaria modeling study by Chitnis et al. (2009) (based on data relevant to malaria dynamics in Ifakara, Tanzania) and the permethrin-treated bednets field trial in western Kenya by Hawley et al. (2003) that bednets reduce malaria transmission if the malaria region being considered is mesoendemic. For holoendemic malaria regions, our study shows that only a highly-effective net, coupled with very high coverage, can lead to effective control of malaria. Ifakara and western Kenya are considered regions of high malaria endemicity (Githeko et al. 1992; Holzer et al. 1993).

Fig. 8

Numerically determined relationship between overall EIR and $\tilde{{\mathcal {R}}}_0$ at the endemic equilibrium, where variability in EIR is generated by changing bednet coverage, $\pi _p$. For larger EIR, $\tilde{{\mathcal {R}}}_0$ decreases nearly linearly with falling EIR, while for very small EIR, $\tilde{{\mathcal {R}}}_0$ decreases dramatically with falling EIR. Thus, EIR must be pushed very close to zero for malaria elimination. Results are generating using baseline parameter values with a highly effective net in a holoendemic setting ($K_E=100\frac{\Pi }{\mu _H}$)

Fig. 9

Contour plots showing $\tilde{{\mathcal {R}}}_0$ as a function of $\varepsilon _{deter}$ and $\pi _p$ (bednet coverage), for weakly, moderately, and highly effective nets. For this figure, we use $K_E=100\frac{\Pi }{\mu _H}$ to approximate a holoendemic baseline

Figure 7 also suggests that high coverage of weakly effective (i.e. low killing efficiency) nets is better than low coverage with highly effective (i.e. high killing efficiency) nets. For example, in the holoendemic setting, 20% coverage with a highly effective net pushe $\tilde{{\mathcal {R}}}_0$ from 11.7 to 5.5, while 80% coverage with a weakly effective net gives $\tilde{{\mathcal {R}}}_0$ of 3.6. Given the nonlinear relationship between $\tilde{{\mathcal {R}}}_0$ and disease prevalence, widespread use of even marginally effective bednets may better control malaria than lower coverage rates with better (more effective) nets.

Finally, Fig. 8 shows the nonlinear relationship between $\tilde{{\mathcal {R}}}_0$ and EIR, such that EIR must be pushed very close to zero before $\tilde{{\mathcal {R}}}_0$ drops below one. In other words, Fig. 8 shows that a significant reduction in EIR is needed in order to bring the reproduction number $\tilde{{\mathcal {R}}_0}$ to a value less than 1 (so that, by Theorem 3.3, malaria elimination can be achieved).

We also examine how deterrence, as measured in the model by $\varepsilon _{deter}$, interacts with bednet coverage and net effectiveness to determine $\tilde{{\mathcal {R}}}_0$, as shown in the contour plots in Fig. 9. Perhaps surprisingly, increasing deterrence generally results in an increase in $\tilde{{\mathcal {R}}}_0$. This is likely because increasing $\varepsilon _{deter}$ focuses mosquito biting upon the unprotected subpopulation, resulting in more intense malaria transmission among this subpopulation and an overall increase in $\tilde{{\mathcal {R}}}_0$. It should be emphasized here that this increased biting on unprotected persons is not an assumption directly imposed on the model, but is a natural consequence of the fact that, if a mosquito does not attempt a bloodmeal on a net-protected human she has encountered, due to deterrence, she will continue in her search and likely ultimately encounter an unprotected person (although this comes at an increased mortality, denoted by $\mu _X$ in the model 2.2).

4.2 Effects of temperature

We examine the effect of changing mean ambient temperature (assumed equal to water temperature) upon $\tilde{{\mathcal {R}}}_0$ and EIR, as shown in Fig. 10. We see an asymmetric increase in $\tilde{{\mathcal {R}}}_0$ and EIR from low temperatures to peaks around 29–30 $^\circ$C, followed by rapid drop-offs at higher temperatures. In other words, malaria burden is maximized for temperature values in the range 29–30 $^\circ$C, and such burden decreases for increasing temperatures thereafter. This peak is similar to that reported by Okuneye et al. (2019), but higher than the reported value by the well-known Mordecai et al. (2013) study. Furthermore, although the results in Fig. 10 are obtained using a highly effective net with $K_E=100 \times \Pi / \mu _H$, it should be stated that qualitatively similar results are obtained regardless of net type and $K_E$ value.

To determine if temperature alters the qualitative interaction between bednet efficacy, bednet coverage, and control, we have generated a series of contour plots showing $\tilde{{\mathcal {R}}}_0$ as a function of $\varepsilon _{die,p}$ and $\varepsilon _{bite,p}$, for different ambient temperatures; several surfaces are given in Fig. 11. While altering the maximum $\tilde{{\mathcal {R}}}_0$ value, changes in temperature have no meaningful effect upon the qualitative contour shape. That is, while maximum $\tilde{{\mathcal {R}}}_0$ varies between about 1.3 and 4.5 in the contours shown in Fig. 11, the surface shapes are essentially invariant. Mirroring Fig. 10, maximum $\tilde{{\mathcal {R}}}_0$ increases up to nearly 30 $^\circ$C and then falls off. Thus, it is concluded that bednet coverage and temperature independently affect malaria risk.

Fig. 10

The left panel shows how $\tilde{{\mathcal {R}}}_0$ varies with mean temperature, using a fixed $\pi _p = 0.5$, $K_E=100\frac{\Pi }{\mu _H}$, and a highly effective net. The right shows the numerically determined equilibrium values of EIR for protected, unprotected, and overall human populations as a function of temperature (and for the same parameter values). Both $\tilde{{\mathcal {R}}}_0$ and EIR, across populations, peak around 29 $^\circ$C

Fig. 11

Contours of $\tilde{{\mathcal {R}}}_0$ as a function of $\varepsilon _{die,p}$ and $\varepsilon _{bite,p}$ for four different ambient temperatures, and for different net at 50% bednet coverage (with $K_E=100\frac{\Pi }{\mu _H}$). The qualitative shape of the contour plots does not appreciably vary with temperature

5 Discussion and conclusions

Great success has been recorded in the concerted global effort against malaria over the past 15 years, thanks largely to the large-scale use of long-lasting insecticidal bednets (LLINs) and indoor residual spraying (IRS) in malaria-endemic regions within sub-Saharan Africa. There is now a strong global push to eradicate malaria [particularly the “Zero by 40” initiative of five chemical companies, with support of the Bill & Melinda Gates Foundation and the Innovative Vector Control Consortium (Global-Health/Malaria 2019), Willis and Hamon (2018)]. Given the widespread emergence of vector resistance to pyrethroid-based insecticides (the only chemical agent approved for use in LLINs), and the uncertainty surrounding how this affects (and will affect) malaria epidemiology, mathematical modeling studies are a promising to examine the interaction between bednet resistance and malaria epidemiology.

This paper presents a novel mathematical model, of the form of deterministic system of nonlinear differential equations, for gaining insight into the transmission dynamics of malaria in a population where a certain percentage of the populace use LLINs (consistently and correctly). In addition to incorporating many critical features of malaria disease (e.g., the four main cycles associated with malaria disease, namely immature mosquito life cycle, adult mosquito gonotrophic cycle, parasite sporogony in the mosquito and schizogony in humans; stratifying human population according to bednet usage; etc.), the model allows for the assessment of the killing and deterrence properties of the LLINs (in particular, in addition to killing adult mosquitoes (with some efficacy) upon encounter, the nets can also deter the mosquito from entering the house and/or from biting the human host). The model has been parametrized using ecological data and parameter values relevant to malaria transmission dynamics in holo- and meso-endemic regions of sub-Saharan Africa, and was used to evaluate the population-level impact of various LLINs coverage and effectiveness levels. For numerical simulation purposes, the effectiveness levels of the bednets described in Sect. 2.2 are considered.

The developed model was rigorously analysed to gain insight into its dynamical features (thereby allowing for the determination of important ecological and epidemiological thresholds that govern the persistence, effective control and/or elimination of the disease in a population). It is, first of all, shown, using the theory of center manifold (LaSalle and Lefschetz 1976), that the model undergoes the phenomenon of backward bifurcation, when the reproduction number of the model is less than 1, whenever a certain bifurcation coefficient attains positive values. This condition is associated with the disease-induced mortality in the host population being set to zero (Iboi and Gumel 2018; Iboi et al. 2018). The epidemiological implication of this phenomenon is that the usual epidemiological requirement of having the reproduction number of the model being less than 1, while necessary, is no longer sufficient for the effective control of the disease. Thus, when a backward bifurcation exists, greater control effort is needed to eradicate disease.

However, the phenomenon of backward bifurcation does not exist in the model developed in this study if all the values of the parameters are chosen from their biologically realistic ranges in Table 5, for a holoendemic setting, with five parameter values chosen outside the given range to illustrate a backward bifurcation. Thus, this study shows that, for a holoendemic malaria setting, the backward bifurcation phenomenon in the developed model is essentially a mathematical artifact which may not be realizable using realistic data (or set of parameter values). This result is consistent with those reported in Garba et al. (2008), Garba and Gumel (2010), Iboi and Gumel (2018), Iboi et al. (2018), which also showed that backward bifurcation is not realizable using realistic parameters.

The backward bifurcation phenomenon is known to exist in vector-borne disease models that incorporate disease-induced death in the host(s) population(s). This is confirmed, in the current study, by showing that such bifurcation does not occur in the special case of the model with no disease-induced death in the human population (we showed, using Lyapunov function theory together with LaSalle’s Invariance Principle, that the disease-free equilibrium of the special case of the model with no disease-induced death rate is, indeed, globally-asymptotically stable whenever the associated reproduction number is less than 1).

The impact of coverage level of the LLINs is monitored by simulating the model using various coverage levels. The simulation results obtained show, expectedly, that the disease prevalence in the host population (including those protected, by sleeping under a net, and the unprotected ones who do not sleep under a net) decreases with increasing coverage levels.

We observe LLINs at 20% coverage to reduce the reproduction number, at the holoendemic baseline (approximated by $K_E=100 \times \Pi /\mu _H$), from a baseline value of about 11.7 to either 9.2, 7.3, or 5.5, under weakly, moderately, or highly effective bednets, respectively. Increasing coverage to 80% yields $\tilde{{\mathcal {R}}}_0$ values of 3.6, 1.6, and 0.6, for the same respective net efficacies. Thus, malaria elimination in holoendemic regions will require highly effective nets at high coverage levels. At the mesoendemic baseline, approximated by $K_E=10 \times \Pi /\mu _H$ and giving $\tilde{{\mathcal {R}}}_0 = {{3}}.{{7}}$ without bednets, we see similar relative reductions in $\tilde{{\mathcal {R}}}_0$. However, given the lower baseline $\tilde{{\mathcal {R}}}_0$, even weakly effective nets give $\tilde{{\mathcal {R}}}_0$ = 1.1 under 80% bednet coverage, near the elimination threshold, and both moderately and highly effective nets push $\tilde{{\mathcal {R}}}_0$ well below zero. Bednet coverage of 20%, in this case, improves malaria control, but is insufficient for elimination.

The widespread use of insecticide-based vector control interventions, including pyrethroid based insecticide-treated nets (ITNs; later replaced by long-lasting insecticidal nets (LLINs)) has resulted in the emergence of vector resistance to nearly every currently-available agent used in the insecticides (Alout et al. 2017; Dondorp et al. 2009; Imwong et al. 2017; World Health Organization 2017b) with pyrethroid resistance now widely observed across the African continent (Hemingway et al. 2016). Most nets distributed to-date are pyrethroid-only nets (although pyrethroid nets with the synergist PBO and pyrethroid nets with a second active ingredient are now available), and pyrethroid-only nets will likely remain a core vector control intervention over the next few years. As such it is critical to understand their current impact—now resistance to their active ingredients is so widespread—on malaria epidemiology. This study suggests that high coverage of weakly effective (i.e. low killing efficiency) nets is better than low coverage with highly effective (i.e. high killing efficiency) nets.

The impact of the deterrence property of LLINs to repel mosquitoes from entering protected house has also been examined, and we find, perhaps unexpectedly, that higher deterrence almost uniformly increases $\tilde{{\mathcal {R}}}_0$. This is likely because mosquitoes repelled from protected persons now focus their efforts on the unprotected subpopulation, thus increasing transmission within this group and potentially hampering elimination efforts.

The transmission cycle of malaria is greatly affected by changes in the environment. In particular, the life-cycles of the malaria vector (adult female Anopheles mosquito) and parasites (Plasmodium) are both strongly affected by changes in ambient temperature, while suitable aquatic habitat is necessary for immature mosquito development. Therefore, we have examined how malaria burden changes with mean ambient temperature, and how this interacts with bednet coverage. We find $\tilde{{\mathcal {R}}}_0$ and EIR to both peak at just under 30 $^{\circ }$C, with this true regardless of bednet coverage levels. Indeed, we observe bednet coverage and temperature to essentially independently influence $\tilde{{\mathcal {R}}}_0$. Thus, somewhat colder regions, such as the eastern African highlands, may see an increase in malaria potential with climate change, while warmer western regions may be little affected.

Appendices

Appendix A: Proof of Lemma 2.1

Proof

(a) It should be noted, first of all, that the right-hand side of each of the equations of the model (2.1), (2.2),(2.4) is continuous and locally-Lipschitz at $t=0$. Hence, a solution of the model with non-negative initial conditions exists and is unique in $\Omega =\Omega _1\times \Omega _2\times \Omega _3$ for all time $t>0$ (see also Iboi et al. 2018; Okuneye et al. 2019). Furthermore, since ${\left( 1-\frac{E}{K_E} \right) }_+\ge 0,$ it follows from the first equation of the sub-system (2.1) that $E(t)\le K_E$ for all time $t>0$. Similarly, it follows from the second equation of the sub-system (2.1) that

$$\begin{aligned} {\dot{L}}_{1}= \sigma _E E-\left( \sigma _{L_1}+\mu _L \right) L_1\le \sigma _E K_E-\left( \sigma _{L_1}+\mu _L \right) L_1, \end{aligned}$$

so that $\displaystyle \limsup _{t\rightarrow \infty }L_1(t)\le \frac{\sigma _E K_E}{\sigma _{L_1}+\mu _L}=L^{\diamond }_1.$ Using a similar approach, it can be shown that $\displaystyle \limsup _{t\rightarrow \infty }L_2(t)\le \frac{\sigma _{L_1} L^{\diamond }_1}{\sigma _{L_2}+\mu _L}=L^{\diamond }_2$, $\displaystyle \limsup _{t\rightarrow \infty }L_3(t)\le \frac{\sigma _{L_2}L^{\diamond }_2}{\sigma _{L_3}+\mu _L}=L^{\diamond }_3$, $\displaystyle \limsup _{t\rightarrow \infty }L_4(t)\le \frac{\sigma _{L_3}L^{\diamond }_3}{\sigma _{L_4}+\mu _L}=L^{\diamond }_4$ and $\displaystyle \limsup _{t\rightarrow \infty }P(t)\le \frac{\sigma _{L_4}L^{\diamond }_4}{\sigma _P +\mu _P}=P^{\diamond }.$ That is, all solutions of the sub-system (2.1) are bounded for all time $t>0$.

For the boundedness of the solutions of the sub-system (2.2), we consider the following equation (for the rate of change of the total adult mosquito population):

$$\begin{aligned} {\dot{N}}_M= & {} f\sigma _P P-{\mu _{\mathbf{X}}} S_X-{\mu _{\mathbf{X}}} E_X-{\mu _{\mathbf{X}}} I_X-\mu _M N_M\nonumber \\&+b_H(Q_2+Q_3-Q_1+R_1+R_2) A_X, \end{aligned}$$

(A-1)

where, $N_M=A_X+A_Y+A_Z$ (with $A_X, A_Y, A_Z, Q_1, Q_2, Q_3, R_1$ and $R_2$ are as defined in Sect. 2). It can be shown that $Q_2+Q_3-Q_1+R_1+R_2<0$. Hence, Eq. (A-1) can be re-written as

$$\begin{aligned} {\dot{N}}_M= & {} f\sigma _P P-{\mu _{\mathbf{X}}} S_X-{\mu _{\mathbf{X}}} E_X-{\mu _{\mathbf{X}}} I_X-\mu _M N_M\nonumber \\&+b_H(Q_2+Q_3-Q_1+R_1+R_2) A_X\le f\sigma _P P-\mu _MN_M, \end{aligned}$$

(A-2)

so that,

$$\begin{aligned} \displaystyle \limsup _{t\rightarrow \infty } N_M(t)\le \frac{f\sigma _P P^{\diamond }}{\mu _M}. \end{aligned}$$

Hence, the solutions of the equations of the sub-system (2.2) are bounded for all time $t>0$. Similarly, consider the equation for the rate of change of the total human population, given by:

$$\begin{aligned} {\dot{N}}_H=\Pi -\mu _H N_H-\delta _H (I_{H_p}+I_{H_u})\le \Pi -\mu _H N_H, \end{aligned}$$

(A-3)

from which it follows that $\displaystyle \limsup _{t\rightarrow \infty } N(t)\le \frac{\Pi }{\mu _H}.$ Thus, the solutions of the sub-system (2.4) are bounded for all $t>0$. Since the solutions of the three sub-systems of the model (2.1), (2.2),(2.4) are bounded, it follows that the solutions of the model are bounded. This concludes the proof of Item (a).

(b) The proof for the invariance of the region $\Omega _1$ follows from the bounds established in Item (a) (i.e., $0<\displaystyle \limsup _{t\rightarrow \infty }L_1(t)\le L^{\diamond }_1$, $0<\displaystyle \limsup _{t\rightarrow \infty }L_j(t)\le L^{\diamond }_j$ and $0<\displaystyle \limsup _{t\rightarrow \infty }P(t)\le P^{\diamond }$) and the fact that ${\dot{E}}(t)<0$ whenever $E(t)>K_E$, ${\dot{L}}_1(t)<0$ whenever $L_1(t)>L^{\diamond }_1$ and ${\dot{L}}_j(t)<0$ whenever $L_j(t)>L^{\diamond }_1$ ($j=2,3,4$), respectively.

For the invariance of the region $\Omega _2$, it is convenient to consider the following equation for the rate of change of the total mosquito population given by:

$$\begin{aligned} {\dot{N}}_M= & {} f\sigma _P P-{\mu _{\mathbf{X}}} S_X-{\mu _{\mathbf{X}}} E_X-{\mu _{\mathbf{X}}} I_X-\mu _M N_M\\&+b_H(Q_2+Q_3-Q_1+R_1+R_2) A_X\le f\sigma _P P-\mu _M N_M. \end{aligned}$$

It follows that ${\dot{N}}_M<0$ whenever $N_M(t)> \frac{f\sigma _P P^{\diamond }}{\mu _M}$. Thus, the region $\Omega _2$ is invariant with respect to the sub-system (2.2) of the model (2.1), (2.2),(2.4).

Finally, consider the equation for the total human population given by

$$\begin{aligned} {\dot{N}}_H=\Pi -\mu _H N_H-\delta _H(I_{Hp}+I_{Hu})\le \Pi -\mu _H N_H. \end{aligned}$$

It follows that ${\dot{N}}_H<0$ whenever $N_H(t)> \frac{\Pi }{\mu _H}$. Thus, the region $\Omega _3$ is invariant with respect to the sub-system (2.4) of the model (2.1), (2.2),(2.4). Since the regions $\Omega _1$, $\Omega _2$ and $\Omega _3$ are positively-invariant and attracting, it follows that $\Omega =\Omega _1\times \Omega _2\times \Omega _3$ is positively-invariant and attracting for the model (2.1), (2.2),(2.4). This concludes the proof of Item (b). $\square$

Appendix B: Coefficients of Eq. (3.5)

$$\begin{aligned} C_1= & {} b_H\left\{ \pi _p(1 - \varepsilon _{deter})[(1 - \varepsilon _{die,p})\varepsilon _{bite|\sim die,p}+\varepsilon _{die,p}]\right. \\&\left. +\pi _u[(1 - \varepsilon _{die,u}) \varepsilon _{bite|\sim die,u}+\varepsilon _{die,u}]\right\} +{\mu _{\mathbf{X}}}+\mu _M>0, \\ C_2= & {} b_H[\pi _p(1 - \varepsilon _{deter})(1 - \varepsilon _{die,p}) \varepsilon _{bite|\sim die,p}+\pi _u(1 - \varepsilon _{die,u}) \varepsilon _{bite|\sim die,u}]>0, \\ C_3= & {} b_H\left\{ \pi _p(1 - \varepsilon _{deter})[(1 - \varepsilon _{die,p}) \varepsilon _{bite|\sim die,p}+\varepsilon _{die,p}]\right. \\&\left. +\pi _u[(1 - \varepsilon _{die,u}) \varepsilon _{bite|\sim die,u}+\varepsilon _{die,u}]\right\} +\kappa _V+{\mu _{\mathbf{X}}}+\mu _M>0, \\ C_4= & {} \left\{ \pi _p (1 - \varepsilon _{deter})[\varepsilon _{die,p} (1 - \varepsilon _{bite|\sim die,p})+\varepsilon _{bite|\sim die,p}]\right. \\&\left. +\pi _u [\varepsilon _{die,u} (1 - \varepsilon _{bite|\sim die,u})+\varepsilon _{bite|\sim die,u}]\right\} \kappa ^2_V>0, \\ C_5= & {} 2\kappa _V\left( \mu _M+\frac{\theta _Y}{2}+\frac{\varphi _Z}{2}\right) C_4>0, \\ C_6= & {} \pi _p(1 - \varepsilon _{deter})\left\{ [\varepsilon _{die,p} (1 - \varepsilon _{bite|\sim die,p})+\varepsilon _{bite|\sim die,p}]\mu ^2_M\right. \\&\left. +(\theta _Y+\varphi _Z)[\varepsilon _{die,u} (1 - \varepsilon _{bite|\sim die,u})+\varepsilon _{bite|\sim die,u}]\mu _M+\varepsilon _{bite|\sim die,p}\theta _Y\varphi _Z\right\}>0, \\ C_7= & {} \pi _u\left\{ [\varepsilon _{die,u} (1 - \varepsilon _{bite|\sim die,u})+\varepsilon _{bite|\sim die,u}]\mu ^2_M\right. \\&\left. +(\theta _Y+\varphi _Z)[\varepsilon _{die,u} (1 - \varepsilon _{bite|\sim die,u})+\varepsilon _{bite|\sim die,u}]\mu _M+\varepsilon _{bite|\sim die,u}\theta _Y\varphi _Z\right\}>0, \\ C_8= & {} (\mu _M+\kappa _V)K_{10}K_{12}, \\ C_{9}= & {} \varphi _Z+\theta _Y+b_H\left\{ \pi _p(1 - \varepsilon _{deter})[1-(1 - \varepsilon _{die,p}) (1 - \varepsilon _{bite|\sim die,p})]\right. \\&\left. +\pi _u[1-(1 - \varepsilon _{die,u}) (1 - \varepsilon _{bite|\sim die,u})]\right\}>0,\\ C_{10}= & {} \theta _Y\varphi _Z+b_H(\theta _Y+\varphi _Z)\left\{ \pi _p(1 - \varepsilon _{deter})[1-(1 - \varepsilon _{die,p}) (1 - \varepsilon _{bite|\sim die,p})]\right. \\&\left. +\pi _u[1-(1 - \varepsilon _{die,u}) (1 - \varepsilon _{bite|\sim die,u})]\right\}>0 , \\ C_{11}= & {} b_H\theta _Y\varphi _Z[\pi _p\varepsilon _{die,p}(1 - \varepsilon _{deter})+\varepsilon _{die,u}\pi _u]>0. \end{aligned}$$

Appendix C: Equations of the model (2.1), (2.2), (2.4) without bednets intervention

In the absence of the bednet-based intervention, the sub-systems of the model involving the adults and human dynamics, given by Eqs. (2.2) and (2.4), reduce, respectively, to the following sub-systems:

$$\begin{aligned} \begin{aligned} {\mathrm{Stage}} \,\,\,\,\text {I} {\left\{ \begin{array}{ll} {\dot{S}}_{X} &{}=f\sigma _P P+\varphi _Z S_Z+ b_H Q_3 S_X-\left( b_H+{\mu _{\mathbf{X}}}+\mu _M\right) S_{X}, \\ {\dot{E}}_{X} &{}= \varphi _Z E_Z+ b_H Q_3 E_X -\left( b_H+\kappa _V+{\mu _{\mathbf{X}}}+\mu _M\right) E_{X}, \\ {\dot{I}}_{X} &{}=\varphi _Z I_Z+\kappa _V E_{X}+ b_H Q_3 I_X-\left( b_H+{\mu _{\mathbf{X}}}+\mu _M\right) I_{X}.\\ \end{array}\right. }\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\mathrm{Stage}}\,\,\,\, \text {II} {\left\{ \begin{array}{ll} {\dot{S}}_{Y} &{}= (1 - \beta _V \omega ) R_2 S_{X} -\left( \theta _Y+\mu _M\right) S_{Y}, \\ {\dot{E}}_{Y} &{}= b_H \beta _V \omega R_2 S_{X} + b_H R_2 E_X-\left( \theta _Y+\kappa _V+\mu _M\right) E_{Y}, \\ {\dot{I}}_{Y} &{}=\kappa _V E_Y+b_H R_2 I_X-\left( \theta _Y+\mu _M\right) I_{Y}.\\ \end{array}\right. }\quad \end{aligned} \end{aligned}$$

(C-1)

$$\begin{aligned} \begin{aligned} {\mathrm{Stage}}\,\,\,\, \text {III} {\left\{ \begin{array}{ll} {\dot{S}}_{Z} &{}=\theta _YS_{Y} -\left( \varphi _Z+\mu _M\right) S_{Z}, \\ {\dot{E}}_{Z} &{}= \theta _Y E_{Y}-\left( \varphi _Z+\kappa _V+\mu _M\right) E_{Z}, \\ {\dot{I}}_{Z} &{}=\theta _Y I_{Y}+\kappa _V E_Z-\left( \varphi _Z+\mu _M\right) I_{Z},\\ \end{array}\right. } \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\mathrm{Human}}\,\,\,\, {\left\{ \begin{array}{ll} {\dot{S}}_{H} &{}=\Pi - (\lambda _{VH}+\mu _{H})S_{H}+\eta _H R_{H}, \\ {\dot{E}}_{H} &{}=\lambda _{VH}S_{H}-(\gamma _H+\mu _H)E_{H}, \\ {\dot{I}}_{H} &{}=\gamma _HE_{H}-(\alpha _H+\delta _H+\mu _H)I_{H}, \\ {\dot{R}}_{H} &{}=\alpha _HI_{H}-(\eta _H+\mu _{H})R_{H}. \\ \end{array}\right. } \end{aligned} \end{aligned}$$

(C-2)

The equations for the aquatic dynamics, given by (2.1), remain unchanged. Hence, the reduced (no-bednets) model consist of the Eqs. (2.1), (C-1), (C-2).

It can be shown, using the next generation operator method (as in Sect. 3), that the basic reproduction number of the reduced model (2.1), (C-1), (C-2) is given by

$$\begin{aligned} \tilde{{\mathcal {R}}}_{0*}=\sqrt{\frac{b_H\beta _VJ_1J_3S^0_X\beta _M\gamma _H\theta _Y\varphi _Z\kappa _V[(K_9+K_{12})J_5+K_9K_{11}]}{K_{13}K_{14}N^*_H(J_5K_{10}K_{12}-J_6\theta _Y\varphi _Z)(J_4K_{9}K_{11}-J_6\theta _Y\varphi _Z)}}, \end{aligned}$$

(C-3)

where,

$$\begin{aligned} \begin{aligned} J_1&= b_H\left[ \varepsilon _{bite|die,u} \,\varepsilon _{die,u} + \varepsilon _{bite|\sim die,u} (1 - \varepsilon _{die,u})\right] ,\,\,\\ J_2&= (1 - \varepsilon _{die,u}) (1 - \varepsilon _{bite|\sim die,u}),\,\,N^*_H=\frac{\Pi }{\mu _H},\\ J_3&= (1 - \varepsilon _{die,u}) \varepsilon _{bite|\sim die,u},\,\,J_4=(b_H+{\mu _{\mathbf{X}}}+\mu _M)-b_HJ_2,\,\,\\ J_5&=(b_H+\kappa _V+{\mu _{\mathbf{X}}}+\mu _M)-b_HJ_2,\\ J_6&=b_HJ_3,\,\, {\mathcal {N}}_{0*}=\frac{(\psi _E\varphi _Z\sigma _Ef\sigma _P\theta _YJ_6)\prod \limits ^4_{i=1}\sigma _{L_{i}}}{\left( J_4K_9K_{11}-J_6\theta _Y\varphi _Z\right) \prod \limits ^6_{i=1} K_i},\,\,\\ S^0_X&=\frac{\left[ f\sigma _E\sigma _PK_E\left( 1-\frac{1}{{\mathcal {N}}_{0*}}\right) K_9K_{11}\right] \prod \limits ^4_{i=1}\sigma _{L_{i}}}{(J_4K_9K_{11}-J_6\theta _Y\varphi _Z)\prod \limits ^6_{i=2} K_i}. \end{aligned} \end{aligned}$$

Substituting the baseline parameter values in Table 4 (for the holo-endemic setting) shows that the worst-case scenario basic reproduction number $(\tilde{{\mathcal {R}}}_0)$ of the model (2.1), (2.2), (2.4), or, equivalently, the reduced model (C-1), (C-2), given by (C-3), is $\tilde{{\mathcal {R}}}_{0*}$ $=$ 11.4.

Appendix D: Proof of Theorem 3.2

Proof

The proof of Theorem 3.2 is based on using center manifold theory (Carr 1981; Castillo-Chavez and Song 2004). It is convenient to define the following change of variables for the model (2.1), (2.2), (2.4): $E=x_1$, $L_{1}=x_2$, $L_{2}=x_3$, $L_{3}=x_4$, $L_{4}=x_5$, $P=x_6$, $S_{X}=x_7$, $E_{X}=x_8$, $I_{X}=x_9$, $S_{Y}=x_{10}$, $E_{Y}=x_{11}$, $I_{Y}=x_{12}$, $S_{Z}=x_{13}$, $E_{Z}=x_{14}$, $I_{Z}=x_{15}$, $S_{Hp}=x_{16}$, $E_{Hp}=x_{17}$, $I_{Hp}=x_{18}$, $R_{Hp}=x_{19}$, $S_{Hu}=x_{20}$, $E_{Hu}=x_{21}$, $I_{Hu}=x_{22}$, $R_{Hu}=x_{23}$. Using the vector notation $X=(x_1,\ldots x_{23})^T$ and $F=(f_1,\ldots f_{23})^T$, the model can then be written in the form $\frac{dX}{dt} = (f_1,\ldots f_{23})^T$, as follows:

$$\begin{aligned} \begin{aligned} {\dot{x}}_1 \equiv f_1&=\psi _E\varphi _Z{\left( 1-\frac{x_1}{K_E} \right) }_+(x_{13}+x_{14}+x_{15}) -\left( \sigma _E+\mu _E\right) x_1,\\ {\dot{x}}_2 \equiv f_2&= \sigma _E x_1-\left( \sigma _{L_1}+\mu _L \right) x_2,\\ {\dot{x}}_3 \equiv f_3&= \sigma _{L_1}x_2-\left( \sigma _{L_2}+\mu _L \right) x_3,\\ {\dot{x}}_4 \equiv f_4&= \sigma _{L_2}x_3-\left( \sigma _{L_3}+\mu _L \right) x_4, \\ {\dot{x}}_5 \equiv f_5&= \sigma _{L_3}x_4-\left( \sigma _{L_4}+\mu _L \right) x_5,\\ {\dot{x}}_6 \equiv f_6&= \sigma _{ L_{4}}x_5-\left( \sigma _P +\mu _P \right) x_6,\\ {\dot{x}}_7 \equiv f_7&= f\sigma _P x_6+\varphi _Z x_{13}+ b_H (Q_2+Q_3) x_7-\left( b_H Q_1+{\mu _X}+\mu _M\right) x_{7},\\ {\dot{x}}_8 \equiv f_8&= \varphi _Z x_{14}+ b_H (Q_2+Q_3) x_8 -\left( b_H Q_1+\kappa _V+{\mu _X}+\mu _M\right) x_{8}, \\ {\dot{x}}_9 \equiv f_9&= \varphi _Z x_{15}+\kappa _V x_{8}+ b_H (Q_2+Q_3) x_9-\left( b_H Q_1+{\mu _X}+\mu _M\right) x_{9},\\ {\dot{x}}_{10} \equiv f_{10}&= b_H [(1 - \beta _V \omega _p) R_1 + (1 - \beta _V \omega _u) R_2] x_{7} -\left( \theta _Y+\mu _M\right) x_{10}, \\ {\dot{x}}_{11 } \equiv f_{11}&= b_H (\beta _V \omega _p R_1 + \beta _V \omega _u R_2) x_{7}\\&\quad + b_H (R_1+R_2) x_8-\left( \theta _Y+\kappa _V+\mu _M\right) x_{11}, \\ {\dot{x}}_{12} \equiv f_{12}&= \kappa _V x_{11}+b_H(R_1+R_2) x_9-\left( \theta _Y+\mu _M\right) x_{12},\\ {\dot{x}}_{13} \equiv f_{13}&= \theta _Y x_{10} -\left( \varphi _Z+\mu _M\right) x_{13}, \\ {\dot{x}}_{14} \equiv f_{14}&= \theta _Y x_{11}-\left( \varphi _Z+\kappa _V+\mu _M\right) x_{14}, \\ {\dot{x}}_{15} \equiv f_{15}&= \theta _Y x_{12}+\kappa _V x_{14}-\left( \varphi _Z+\mu _M\right) x_{15},\\ {\dot{x}}_{16} \equiv f_{20}&= \Pi \pi _p - (\lambda _{VH_p}+\mu _{H})x_{16}+\eta _H x_{19}, \\ {\dot{x}}_{17} \equiv f_{21}&= \lambda _{VH_p}x_{16}-(\gamma _H+\mu _H)x_{17}, \\ {\dot{x}}_{18} \equiv f_{22}&= \gamma _H x_{17}-(\alpha _H+\delta _H+\mu _H)x_{18}, \\ {\dot{x}}_{19} \equiv f_{23}&=\alpha _H x_{18}-(\eta _H+\mu _{H})x_{19}, \\ {\dot{x}}_{20} \equiv f_{24}&= \Pi \pi _u - (\lambda _{VH_u}+\mu _{H})x_{20}+\eta _H x_{23}, \\ {\dot{x}}_{21} \equiv f_{25}&= \lambda _{VH_u}x_{20}-(\gamma _H+\mu _H)x_{21}, \\ {\dot{x}}_{22} \equiv f_{26}&= \gamma _Hx_{21}-(\alpha _H+\delta _H+\mu _H)x_{22}, \\ {\dot{x}}_{23} \equiv f_{27}&= \alpha _Hx_{22}-(\eta _H+\mu _{H})x_{23}, \end{aligned} \end{aligned}$$

(D-1)

where,

$$\begin{aligned} \text {EIR}_p= & {} b_H \frac{x_9}{N_{H_p}} \pi _p(1 - \varepsilon _{deter}) \left[ \varepsilon _{bite|die,p} \varepsilon _{die,p} + \epsilon _{bite|\sim die,p} (1 - \varepsilon _{die,p})\right] , \\ \text {EIR}_u= & {} b_H \frac{x_9}{N_{H_u}}\pi _u \left[ \varepsilon _{bite|die,u} \varepsilon _{die,u} + \varepsilon _{bite|\sim die,u} (1 - \varepsilon _{die,u})\right] ,\\ \lambda _{VH_p}= & {} {\beta _M\,\text {EIR}_p},\\ \lambda _{VH_u}= & {} \beta _M\,\text {EIR}_u,\\ \omega _p= & {} \frac{x_{18}}{N_{H_p}},\quad \omega _u= \frac{x_{22}}{N_{H_u}}. \\ \end{aligned}$$

Let ${\mathcal {R}}_0=1$ and suppose, further, that $\beta _M=\beta _M^*$ is chosen as a bifurcation parameter. Solving for $\beta _M=\beta _M^*$ from ${\mathcal {R}}_0=1$ gives

$$\begin{aligned} \beta _M=\beta _M^*=\frac{\Pi \pi _p\pi _u\left( C_3K_{10}K_{12}-C_2\theta _Y\varphi _Z\right) \left( C_1K_9K_{11}-C_2\theta _Y\varphi _Z\right) }{\mu ^2_Hb_H x^*_7\kappa _V \varphi _Z \theta _Y[(K_9+K_{12})C_3+K_9K_{11}]({\mathcal {R}}_{H_pV}+{\mathcal {R}}_{H_uV})}. \end{aligned}$$

The Jacobian of the transformed system (D-1), evaluated at the DFE $({\mathcal {T}}_2)$ with $\beta _M=\beta _M^*$, is given by

$$\begin{aligned} {J(\beta _M^*)}= \left[ \begin{array}{*{20}c} J_1&{}\quad J_2\\ J_3&{}\quad J_4\ \end{array} \right] , \end{aligned}$$

where,

$$\begin{aligned} {J_1}= & {} \left[ \begin{array}{*{20}c} -\frac{\psi _E\varphi _Zx^*_{13}}{K_E}-K_1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \sigma _E&{}\quad -K_2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \sigma _{L_1}&{}\quad -K_3&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \sigma _{L_2}&{}\quad -K_4&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \sigma _{L_3}&{}\quad -\mu _H&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \sigma _{L_4}&{}\quad -K_5&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad f\sigma _{P}&{}\quad -C_1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -C_3&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \kappa _V&{}-C_1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad C_2&{}\quad 0&{}\quad 0&{}\quad -K_9&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad C_2&{}\quad 0&{}\quad 0&{}\quad -K_{10}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad C_2&{}\quad 0&{}\quad \kappa _V&{}\quad -K_9\ \end{array} \right] ,\\ {J_2}= & {} \left[ \begin{array}{*{20}c} \psi _E\varphi _Z(1-\frac{x^*_1}{K_E})&{}\quad \psi _E\varphi _Z(1-\frac{x^*_1}{K_E})&{}\quad \psi _E\varphi _Z(1-\frac{x^*_1}{K_E})&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \varphi _Z&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \varphi _Z&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \varphi _Z&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -\frac{b_HR_1\beta _V x^*_7}{x^*_{16}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -\frac{b_HR_2\beta _V x^*_7}{x^*_{20}}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \frac{b_HR_1\beta _V x^*_7}{x^*_{16}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \frac{b_HR_2\beta _V x^*_7}{x^*_{20}}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\ \end{array} \right] ,\\ {J_3}= & {} \left[ \begin{array}{*{20}c} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \theta _Y&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \theta _Y&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \theta _Y\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -\beta _MQ_p&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \beta _MQ_p&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -\beta _MQ_u&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \beta _MQ_u&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\ \end{array} \right] , \end{aligned}$$

and,

$$\begin{aligned} {J_4}= \left[ \begin{array}{*{20}c} -K_{11}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -K_{12}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \kappa _V&{}\quad -K_{11}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -\mu _H&{}\quad 0&{}\quad 0&{}\quad \eta _H&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -K_{13}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _H&{}\quad -K_{14}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \alpha _H&{}\quad -K_{15}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -\mu _H&{}\quad 0&{}\quad 0&{}\quad \eta _H\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -K_{13}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _H&{}\quad -K_{14}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \alpha _H&{}\quad -K_{15}\ \end{array} \right] . \end{aligned}$$

The Jacobian $J(\beta _M^*)$ has a simple zero eigenvalue (and all other eigenvalues having negative real parts). Hence, the center manifold theory Carr (1981); Castillo-Chavez and Song (2004) can be used to analyse the dynamics of (D-1) near $\beta _M=\beta _M^*$. This entails carrying out the following computations.

Eigenvectors of$J({\mathcal {T}}_2)\mid _{\beta _M=\beta _M^*}$ The Jacobian of the transformed system (D-1), evaluated at the DFE $({\mathcal {T}}_2)$ with $\beta _M=\beta _M^*$, has a right and left eigenvectors (associated with the zero eigenvalue) (the expression for the eigenvector $w_i$ and $v_i$, $i=1,2,..,23$, are given in the Supplementary Material).

Computations of bifurcation coefficients of a and b

By computing the associated non-zero partial derivatives of F(x) evaluated the the DFE, it follows from Theorem 4.1 in Castillo-Chavez and Song (2004) that the associated bifurcation coefficients, a and b, are given, respectively, by

$$\begin{aligned} \begin{aligned} a=&-2 b_H \left[ \frac{\left( -w_{{22}}R_{{2}}w_{{7}}v_{{11}}\beta _{{V}}+v_{{21}}Q_{{u}} \beta _{{M}}w_{{9}} \left( w_{{22}}+w_{{21}}+w_{{23}} \right) \right) x^*_{{20}}+w_{{22}}\beta _{{V}}R_{{2}}x^*_{{7}}v_{{11}} \left( w_{{20}}+w_{ {21}}+w_{{22}}+w_{{23}} \right) }{(x^*_{20})^2}\right] \\&-2 b_H \left[ \frac{\left( -w_{{18}}\beta _{{V}}R_{{1}}w_{{7}}v_{{11}}+Q_{{p}}\beta _{{M}}w _{{9}} \left( w_{{18}}+w_{{19}}+1 \right) \right) x^*_{{16}}+w_{{18}}{(x^* _{{20}}})^2\beta _{{V}}R_{{1}}x^*_{{7}}v_{{11}} \left( w_{{16}}+w_{{18}} +w_{{19}}+1 \right) }{(x^*_{16})^2}\right] , \end{aligned}\nonumber \\ \end{aligned}$$

(D-2)

and,

$$\begin{aligned} b=b_{{H}}w_{{9}} \left( Q_{{u}}v_{{21}}+Q_{{p}} \right) >0. \end{aligned}$$

(D-3)

Hence, it follows from Theorem 4.1 of Castillo-Chavez and Song (2004) that the transformed model (D-1) undegoes a backward bifurcation at ${\mathcal {R}}_0=1$ if the bifurcation coefficient a (given by (D-2)) is positive. This concludes the proof. $\square$

Appendix E: Proof of Theorem 3.3.

Proof

Consider the special case of the model (2.1), (2.2), (2.4) without disease-induced mortality in the host population (i.e., $\delta _H=0$). Further, let ${\mathcal {N}}_0>1$ (so that the NDFE, ${\mathcal {T}}_2$, exists) and $\tilde{{\mathcal {R}}}_0\le 1$. Setting $\delta _H=0$ in the model (2.1), (2.2), (2.4) gives $N_H(t)\rightarrow \frac{\Pi }{\mu _H}$ as $t \rightarrow \infty$, and ${\bar{K}}_{14}=\alpha _H+\mu _H$. Hence, from now on, $N_H(t)$ is replaced by its limiting value, $\frac{\Pi }{\mu _H}$. Furthermore, consider the following linear Lyapunov function:

$$\begin{aligned} \mathcal {{F}}= & {} g_1 E_{Hp}+g_2 {I}_{Hp}+g_3 {E}_{Hu}+g_4 {I}_{Hu}+g_5 {E}_{X}+g_6 {I}_{X}\\&+g_7 {E}_{Y}+g_8 {I}_{Y}+g_9 {E}_{Z}+g_{10} {I}_{Z}, \end{aligned}$$

where,

$$\begin{aligned} \begin{aligned} g_1&=\beta _{{V}}N_{{{ Hu}}}\gamma _{{H}}b_{{H}}R_{{1}}S_{{X}}\kappa _{{V}} \varphi _{{Z}}\theta _{{Y}} \left( C_{{3}} \left( K_{{9}}+K_{{12}} \right) +K_{{9}}K_{{11}} \right) ,\\ g_2&=\beta _{{V}}N_{{{ Hu}}}b_{{H}}R_{{1}}S_{{X}}\kappa _{{V}}\varphi _{{Z} }\theta _{{Y}} \left( C_{{3}} \left( K_{{9}}+K_{{12}} \right) +K_{{9}}K _{{11}} \right) K_{{13}} ,\\ g_3&=\beta _{{V}}N_{{{ Hp}}}\gamma _{{H}}b_{{H}}R_{{2}}S_{{X}}\kappa _{{V}} \varphi _{{Z}}\theta _{{Y}} \left( C_{{3}} \left( K_{{9}}+K_{{12}} \right) +K_{{9}}K_{{11}} \right) ,\\ g_4&=\beta _{{V}}N_{{{ Hp}}}b_{{H}}R_{{2}}S_{{X}}\kappa _{{V}}\varphi _{{Z} }\theta _{{Y}} \left( C_{{3}} \left( K_{{9}}+K_{{12}} \right) +K_{{9}}K _{{11}} \right) K_{{13}} ,\\ g_5&={\frac{C_{{2}}\beta _{{M}}\gamma _{{H}}{\theta ^2_{{Y}}}{\varphi ^2_{{Z}} }{\kappa ^2_{{V}}}S_{{X}}\beta _{{V}} \left( C_{{3}} \left( K_{{9} }+K_{{12}} \right) +K_{{9}}K_{{11}} \right) ^{2} \left( N_{{{ Hp}}} Q_{{u}}R_{{2}}S_{{{ Hu}}}+N_{{{ Hu}}}Q_{{p}}R_{{1}}S_{{{ Hp}} } \right) }{ \left( C_{{3}}K_{{10}}K _{{12}}-C_{{2}}\theta _{{Y}}\varphi _{{Z}} \right) \left( C_{{1}}K_{{9}}K_{{11}}-C_{{2}}\theta _{{Y}} \varphi _{{Z}} \right) C_{{3}}}}\\&\quad +{\frac{K_{{9}}K_{{11}}K_{{13}}{\bar{K}}_{{14}}N_{{{ Hp}}}N_{{{ Hu}}} \left( C_{{3}}K_{{10}}K_{{12}}-C_{{2}}\theta _{{Y}}\varphi _{{Z}} \right) \kappa _{{V}}}{C_{{3}}}} ,\\ g_6&=K_{{9}}K_{{11}}K_{{13}}{\bar{K}}_{{14}}N_{{{ Hp}}}N_{{{ Hu}}} \left( C_{{3}}K_{{10}}K_{{12}}-C_{{2}}\theta _{{Y}}\varphi _{{Z}} \right) ,\\ g_7&={\frac{\beta _{{M}}\gamma _{{H}}{\theta ^2_{{Y}}}{\varphi ^2_{{Z}}}{ \kappa ^2_{{V}}}S_{{X}}\beta _{{V}} \left( C_{{3}} \left( K_{{9}}+K_{{ 12}} \right) +K_{{9}}K_{{11}} \right) ^{2} \left( N_{{{ Hp}}}Q_{{u} }R_{{2}}S_{{{ Hu}}}+N_{{{ Hu}}}Q_{{p}}R_{{1}}S_{{{ Hp}}} \right) }{ \left( C_{{3}}K_{{10}}K_ {{12}}-C_{{2}}\theta _{{Y}}\varphi _{{Z}} \right) \left( C_{{1}}K_{{9}}K_{{11}}-C_{{2}}\theta _{{Y}} \varphi _{{Z}} \right) }} ,\\ g_8&=\theta _{{Y}}K_{{13}}{\bar{K}}_{{14}}\varphi _{{Z}}N_{{{ Hp}}}N_{{{ Hu}}} \left( C_{{3}}K_{{10}}K_{{12}} -C_{{2}}\theta _{{Y}}\varphi _{{Z}}\right) ,\\ g_9&={\frac{C_{{2}}\beta _{{M}}\gamma _{{H}}{\theta ^{2}_{{Y}}}{\varphi ^{3}_{{Z}} }{\kappa ^{2}_{{V}}}S_{{X}}\beta _{{V}} \left( C_{{3}} \left( K_{{9} }+K_{{12}} \right) +K_{{9}}K_{{11}} \right) ^{2} \left( N_{{{ Hp}}} Q_{{u}}R_{{2}}S_{{{ Hu}}}+N_{{{ Hu}}}Q_{{p}}R_{{1}}S_{{{ Hp}} } \right) }{ \left( C_{{3}}K_{{10}}K _{{12}}-C_{{2}}\theta _{{Y}}\varphi _{{Z}} \right) \left( C_{{1}}K_{{9}}K_{{11}}-C_{{2}}\theta _{{Y}} \varphi _{{Z}} \right) K_{{12}}C_{{3}}}}\\&\quad +{\frac{\varphi _{{Z}}K_{{9}}K_{{13}}{\bar{K}}_{{14}}N_{{{ Hp}}}N_{{{ Hu }}} \left( C_{{3}}K_{{10}}K_{{12}}-C_{{2}}\theta _{{Y}}\varphi _{{Z}} \right) \kappa _{{V}} \left( K_{{11}}+C_{{3}} \right) }{K_{{12}}C_{{3} }}} ,\,\,\\ \mathrm{and,}\,\, g_{10}&=\varphi _{{Z}}K_{{9}}K_{{13}}{\bar{K}}_{{14}}N_{{{ Hp}}}N_{{{ Hu}}} \left( C_{{3}}K_{{10}}K_{{12}}-C_{{2}}\theta _{{Y}}\varphi _{{Z}} \right) . \end{aligned} \end{aligned}$$

The Lyapunov derivative of ${\mathcal {F}}$ (where a dot represents differentiation with respect to t) is given by:

$$\begin{aligned} \mathcal {{\dot{F}}}&=g_1 {\dot{E}}_{Hp}+g_2 {\dot{I}}_{Hp}+g_3 {\dot{E}}_{Hu}+g_4 {\dot{I}}_{Hu}+g_5 {\dot{E}}_{X}+g_6 {\dot{I}}_{X}\\&\quad +g_7 {\dot{E}}_{Y}+g_8 {\dot{I}}_{Y}+g_9 {\dot{E}}_{Z}+g_{10} {\dot{I}}_{Z},\\&=g_1 (\lambda _{VH_p}S_{H_p}-K_{13}E_{H_p})+g_2 (\gamma _HE_{H_p}-{\bar{K}}_{14}I_{H_p})+g_3 (\lambda _{VH_u}S_{H_u}-K_{13}E_{H_u})\\&\quad +g_4 (\gamma _HE_{H_u}-{\bar{K}}_{14}I_{Hu})+g_5 (\varphi _Z E_Z-C_3E_{X})+g_6 (\varphi _Z I_Z+\kappa _V E_{X}-C_1I_{X})\\&\quad +g_7 [(b_H\beta _V \omega _p R_1 +b_H \beta _V \omega _u R_2) S_{X} + C_2 E_X-K_{10}E_{Y}]\\&\quad +g_8 (\kappa _V E_Y+C_2 I_X-K_9I_{Y})\\&\quad +g_9 (\theta _Y E_{Y}-K_{12}E_{Z})+g_{10} (\theta _Y I_{Y}+\kappa _V E_Z-K_{11}I_{Z}),\\&=\left( \frac{g_1\beta _MQ_pS_{Hp}}{N_{Hp}}+\frac{g_3\beta _MQ_uS_{Hu}}{N_{Hu}}-g_6C_1+g_8C_2\right) I_X\\&\quad +\left( \frac{g_7b_H\beta _VR_1S_X}{N_{Hp}}-g_2{\bar{K}}_{14}\right) I_{Hp}\\&\quad +\left( \frac{g_7b_H\beta _VR_2S_X}{N_{Hu}}-g_4{\bar{K}}_{14}\right) I_{Hu}+\left( -g_1K_{13}+g_2\gamma _H\right) E_{Hp}\\&\quad +\left( -g_3K_{13}+g_4\gamma _H\right) E_{Hu}\\&\quad +\left( -g_5C_3+g_6\kappa _V+g_7C_2\right) E_{X}+\left( -g_7K_{10}+g_8\kappa _V+g_9\theta _Y\right) E_{Y}\\&\quad +\left( -g_9K_{12}+g_{10}\kappa _V+g_5\varphi _Z\right) E_{Z}\\&\quad +(-g_8K_9+g_{10}\theta _Y)I_Y+(-g_{10}K_{11}+g_6\varphi _Z)I_Z.\\ \end{aligned}$$

Since $S_{Hp}(t)\le N_{Hp}$, $S_{Hu}(t)\le N_{Hu}$, $N_{Hp}(t)=\frac{\Pi \,\pi _p}{\mu _H}$ and $N_{Hu}(t)=\frac{\Pi \,\pi _u}{\mu _H}$ in $\Omega$ for all $t>0$, it follows that:

$$\begin{aligned} \begin{aligned} \mathcal {{\dot{F}}}&=\le K_{13}{\bar{K}}_{14}N_{Hp}N_{Hu}(C_1K_9K_{11}-C_2\theta _Y\varphi _Z)(C_3K_{10}K_{12}-C_2\theta _Y\varphi _Z)(\tilde{{\mathcal {R}}}^2_0-1)I_X\\&\quad +\beta _{{V}}N_{{{ Hu}}}b_{{H}}R_{{1}}S_{{X}}\kappa _{{V}}\varphi _{{Z} }\theta _{{Y}} \left( C_{{3}} \left( K_{{9}}+K_{{12}} \right) +K_{{9}}K _{{11}} \right) K_{{13}}K_{{14}} (\tilde{{\mathcal {R}}}^2_0-1)I_{Hp}\\&\quad +\beta _{{V}}N_{{{ Hp}}}b_{{H}}R_{{2}}S_{{X}}\kappa _{{V}}\varphi _{{Z} }\theta _{{Y}} \left( C_{{3}} \left( K_{{9}}+K_{{12}} \right) +K_{{9}}K _{{11}} \right) K_{{13}}K_{{14}} (\tilde{{\mathcal {R}}}^2_0-1)I_{Hu}\\&\quad +{\frac{{\varphi ^{2}_{{Z}}} \left( N_{{{ Hp}}}Q_{{u}}R_{{2}}S_{{{ Hu}}}+N_{{{ Hu}}}Q_{{p}}R_{{1}}S_{{{ Hp}}} \right) {\kappa ^{2}_{ {V}}}\beta _{{V}} \left( C_{{3}} \left( K_{{9}}+K_{{12}} \right) +K _{{9}}K_{{11}} \right) ^{2}{\theta ^{2}_{{Y}}}S_{{X}}\gamma _{{H}}\beta _ {{M}}}{b_HK_{{12}}C_{{3}} \left( C_{{1}}K_{{9}}K_{{11}}-C_{{2}}\theta _{{Y }}\varphi _{{Z}} \right) }}\\&\quad \left( 1-\frac{1}{\tilde{{\mathcal {R}}}^2_0}\right) E_{Y}. \end{aligned} \end{aligned}$$

Hence, ${\dot{\mathcal {F}}}\le 0$ if $\tilde{{\mathcal {R}}}_0<1$ with ${\dot{\mathcal {F}}}= 0$ if and only if $I_X=I_{Hp}=I_{Hu}=E_Y=0.$ Therefore, $\mathcal {{F}}$ is a Lyapunov function in $\Omega$ and it follows from LaSalle’s Invariance Principle (1976) that every solution to the equations in (2.1), (2.2), (2.4) (with $\delta _H=0$ and initial conditions in $\Omega$) converges to ${\mathcal {T}}_2$ as $t\rightarrow \infty$ That is,

$$\begin{aligned}&(E_X(t),I_X(t),E_Y(t),I_Y(t),E_Z(t),I_Z(t),E_{Hp}(t),I_{Hp}(t),R_{Hp}(t),\\&\quad E_{Hu}(t),I_{Hu}(t),R_{Hu}(t))\\&\quad \rightarrow (0,0,0,0,0,0,0,0,0,0,0,0)\,\,\mathrm{as}\,\, \mathrm{t}\rightarrow \infty .\\&\mathrm{Thus},\,\,{\mathcal {X}}(t) \rightarrow \left( E^*,L^*_1,L^*_2,L^*_3,L^*_4,P^*,S^*_X,0,0,S^*_Y,0,0,S^*_Z,0,0,\right. \\&\qquad \left. \frac{\Pi \,\pi _p}{\mu _H},0,0,0,\frac{\Pi \,\pi _u}{\mu _H},0,0,0\right) \end{aligned}$$

as $t\rightarrow \infty$ for $\tilde{{\mathcal {R}}}_0\le 1$. Hence, the NDFE, ${\mathcal {T}}_2$, is globally-asymptotically stable in $\Omega$ if $\tilde{{\mathcal {R}}}_0\le 1$ for the special case of the model (2.1), (2.2), (2.4) with $\delta _H=0$. This completes the proof. $\square$