1 Introduction

Malaria is a major cause of morbidity and mortality, with an estimated 216 million cases worldwide and at least 655,000 deaths in 2011 [1]. Understanding the role of temperature in malaria transmission is of particular importance in light of climate change. The global mean temperature has increased by 0.7\(~{}^{\circ }\mathrm{C}\) during the past 100 years and is predicted to increase by an additional 1.1–\(6.4~{}^{\circ }\mathrm{C}\) during the twenty-first century [2]. This additional warming is likely to affect malaria transmission because temperature changes can alter vector development rates, shift their geographical distribution and alter transmission dynamics.

Temperature is known to play a major role in the life cycle of the malaria vector. The development of the three aquatic stages and their emergence to adulthood are strongly dependent on temperature. It takes 1, 3 and 10 days for eggs of some mosquitoes to hatch at temperatures of \(30,~20\) and \(10~{}^{\circ }\mathrm{C}\), respectively and water temperature regulates the speed of mosquito breeding [3]. The development of the parasite within the mosquito (sporogonic cycle) depends on temperature. It takes about 9–10 days at temperatures of \(28~{}^{\circ }\mathrm{C}\), but stops at temperatures below \(16~{}^{\circ }\mathrm{C}\) [4]. The minimum temperature for parasite development of P. falciparum approximates \(18~{}^{\circ }\mathrm{C}\) and the daily survival of the vector is dependent on temperature. At temperatures between \(16\) and \(36~{}^{\circ }\mathrm{C}\), the daily survival is about 90 % [4].

Incorporating climate effects into models of disease dynamics is now very crucial as the evidence for climate impacts on disease transmission and potential vector distribution increases. Climate change is known to affect several parameters in the epidemiology of malaria and hence predicting climate change effects on disease transmission requires a framework that specifically incorporates the role of each climate sensitive parameter. Some models examining the contribution of climate change have been explored [5–9]. However, this study incorporates the juvenile stage of the mosquito into malaria transmission dynamics.

We begin by formulating the model and illustrating some of its basic properties in Sect. 2. The equilibria points are determined and stability analysis performed. The effect of temperature on the dynamics of malaria is presented. A discussion of the results is presented in Sect. 3.

2 Model description

In developing a framework for understanding the impact of temperature on malaria dynamics, a deterministic transmission model is developed. The human population is subdivided into four classes: susceptible \((S_H\)), exposed or incubating \(E_H\), infectious \((I_H)\) and recovered individuals who become partially immune \((R_H )\). The rate of infection of a susceptible individual is dependent on the mosquito’s biting rate \(a(T)\) and the proportion of bites by infectious mosquitoes on susceptible humans that produce infection \(b_H\). Blood meal taken by an infectious female anopheles mosquito on a susceptible human will cause sporozoites to be injected into the human bloodstream and will be carried to the liver.

Upon infection, individuals will then move to the exposed class \(E_H\), where parasites in their bodies are still in the asexual stages. We assume that exposed individuals are not capable of transmitting the disease to susceptible mosquitoes as they do not have gametocytes. Exposed humans progress at a rate \(\kappa _H\) to the infectious class, in which they now have gametocytes in their bloodstream making them capable of infecting the susceptible anopheles mosquitoes. Treated individuals recover at a rate \(\alpha \). A proportion \(p\) recovers with temporary immunity and the compliment \((1-p)\) recovers with no temporary immunity. Temporarily immune individuals lose immunity at a rate \(\gamma \). Infected individuals who do not seek treatment die from infection at a rate \(\eta \). The birth rate for humans is \(\theta \) and individuals die naturally at a rate \(\mu _H\). Both human and mosquito infections take time to develop into an infectious state. Within host parasite dynamics are weather independent, but within vector parasite dynamics, as well as the mosquito life cycle are weather dependent.

The mosquito population is divided into the juvenile \((J_M(t))\) and adult population of which the adult population is subdivided into three classes: susceptible \((S_M(t))\), exposed \(E_M(t)\) and infectious \((I_M(t))\). The juvenile stages describe the development of the aquatic stages which mature to become susceptible adult mosquitoes at a rate \(\beta _M\). The rate of infecting a susceptible mosquito depends on the mosquitoes’ biting rate \(a\) and the proportion of bites by susceptible mosquitoes on infected humans that produce infection \(b _M\). Susceptible mosquitoes that feed on infectious humans will take gametocytes in blood meals, but as they do not have sporozoites in their salivary glands, they enter into the exposed class. After fertilisation, sporozoites are produced and migrate to the salivary glands ready to infect any susceptible host, the vector is then considered as infectious. Mosquitoes die at a rate \(\mu _M\) which is independent of infection status. Infected mosquitoes are not harmed by the infection, never clear their infection and the infective period of the mosquito ends with its death.

A coupled mosquito–human compartmental model of malaria dynamics is presented in Fig. 1.

Fig. 1
figure 1

Mosquito–human model of malaria dynamics

Full size image

The following system of differential equations describe the model.

$$\begin{aligned} S_H ^{\prime }&= \theta -\lambda _H (T)S_H-\mu _HS_H+ p \alpha I_H +\gamma R_H\nonumber \\ E_H^\prime&= \lambda _H(T) S_H-(\kappa _H +\mu _h)E_H\nonumber \\ I_H ^{\prime }&= \kappa E_H-( \mu _ H + \alpha +\eta ) I_H\nonumber \\ R_H ^{\prime }&= (1-p) \alpha I_H - (\gamma + \mu _H)R_H \nonumber \\ J_M ^{\prime }&= [\beta _J(T) N_M- \mu _J(T)~~J_M]\left( 1-\frac{J_M}{K}\right) -\beta _M(T)J_M\nonumber \\ S_M ^{\prime }&= \beta _M(T)J_M -\lambda _M (T)S_M -\mu _M (T) S_M\nonumber \\ E_M ^{\prime }&= \lambda _M(T) S_M -(\kappa _M (T) +\mu _M (T))E_M\nonumber \\ I_M ^{\prime }&= \kappa _M (T) E_M -\mu _M (T) I_M \end{aligned}$$
(1)

where \({\lambda _H = \frac{a(T)b_H I_M}{N_M}}\) and \({\lambda _M = \frac{a(T)b_M I_H}{N_H}}\).

All parameters and state variables for model system (1) are assumed to be non-negative to be consistent with human and mosquito juvenile and adult populations. All feasible solutions of model system (1) are positive and eventually enter the invariant attracting region

$$\begin{aligned} \Omega&= \Bigg \{(S_H, E_H,I_H,R_H)\in \mathbb{R }_+ ^4,~~~J_M \in \mathbb{R }_+ ,~~~(S_M,E_M,I_M)\in \mathbb{R }_+ ^3: \\&N_H \le \frac{\theta }{\mu _H};~~~\displaystyle {J_M \le \frac{K(\beta _J \beta _M -\mu _J \mu _M -\beta _M \mu _M)}{\beta _J \beta _M\!-\!\mu _J \mu _M }},~~~ N_M \le \frac{\beta _M K(\beta _J \beta _M -\mu _J \mu _M \!-\!\beta _M \mu _M)}{\mu _M(\beta _J \beta _M-\mu _J \mu _M))}\Bigg \} \end{aligned}$$

Predicting the effect of climate change on malaria dynamics requires a framework that specifically incorporates the role of each climate sensitive parameter. The functional forms of temperature dependent parameters are presented in Table 1.

Table 1 Parameters of the basic malaria model in Eq. (1)
Full size table

2.1 Disease-free equilibrium and stability analysis

The disease-free equilibrium of model 1 is given by,

$$\begin{aligned} \mathcal{E } _0&= \left( S_H ^0,E_H ^0, I_H ^0,R_H ^0, J_M ^0,S_M ^0, E_M ^0, I_M ^0\right) \nonumber \\&= \bigg (\frac{\theta }{\mu _H},0,0,0,\frac{K(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\beta _J \beta _M -\mu _J \mu _M}, \frac{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\mu _M(\beta _J \beta _M -\mu _J \mu _M)},0,0\bigg ). \nonumber \\ \end{aligned}$$
(2)

The next generation operator approach as described by Diekmann 1990 is used to define the basic reproductive number, \(\mathcal{R }_m\), as the number of new infections (in mosquitoes or humans) from one infectious individual (human or mosquito) over the duration of the infectious period, given that all other members of the population are susceptible [16].

$$\begin{aligned} \begin{array}{ll} \mathcal{R }_m=\sqrt{\dfrac{ab_H \kappa _H}{\mu _M (\kappa _M +\mu _M)}\dfrac{ab_M \kappa _M}{(\kappa _H +\mu _H)(\mu _H + \alpha + \eta )}} \end{array} \end{aligned}$$
(3)

2.2 Local stability of the Disease-free Equilibrium \(\mathcal{E }_0\)

The local stability of the disease free equilibrium can be discussed by examining the linearised form of the system (1) at the steady state \(\mathcal{E }_0\).

Theorem 1

The disease-free equilibrium \(\mathcal{E }_0\) is locally asymptotically stable whenever \(\mathcal{R }_m < 1\), and unstable otherwise.

Proof

The Jacobian matrix of the model (1) evaluated at the disease free equilibrium point is given by

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -\mu _H &{}0 &{}\nu &{}\gamma &{}0 &{}0 &{}0 &{} -a b_H Q_3\\ 0&{} -(\kappa _H +\mu _H) &{}0&{}0&{}0&{}0 &{} 0 &{} a b_H Q_3\\ 0&{} \kappa _H &{} -Q_1&{} 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}\alpha &{}-(\gamma +\mu _H)&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{} Q_2&{}0&{}0&{}0\\ 0&{}0&{}-ab_M Q_4&{}0&{}\beta _M&{}-\mu _M &{}0&{}0\\ 0&{}0&{} ab_M Q_4 &{}0&{}0&{}0&{}-(\kappa _M +\mu _M)&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}\kappa _M &{} -\mu _M\\ \end{array}\right] . \end{aligned}$$

where \(Q_1=(\nu +\mu _H +\alpha +\eta )\) and \(Q_2=-(\mu _J +\beta _M)+2\mu _J \frac{(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\beta _J \beta _M -\mu _J \mu _M}\)

\(Q_3= \frac{\theta }{\mu _H}\frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}\) and \(Q_4 =\frac{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\mu _M(\beta _J \beta _M -\mu _J \mu _M)} \frac{\mu _H}{\theta }=\frac{1}{Q_3}\).

The first and the sixth columns have diagonal entries resulting in the diagonal entries being two of the eigenvalues of the Jacobian. Now excluding these columns and the corresponding rows we calculate the remaining eigenvalues.

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -(\kappa _H +\mu _H) &{}0&{}0&{}0 &{} 0 &{} a b_HQ_3 \\ \kappa _H &{} -Q_1&{} 0&{}0&{}0&{}0\\ 0&{}\alpha &{}-(\gamma +\mu _H)&{}0&{}0&{}0\\ 0&{}0&{}0&{} Q_2&{}0&{}0\\ 0&{} ab_M Q_4 &{}0&{}0&{}-(\kappa _M +\mu _M)&{}0\\ 0&{}0&{}0&{}0&{}\kappa _M &{} -\mu _M\\ \end{array}\right] . \end{aligned}$$

Again the third and fourth columns have diagonal entries making them two other eigenvalues. Excluding these columns and the corresponding rows we calculate the remaining eigenvalues from

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -(\kappa _H +\mu _H) &{}0&{}0 &{} a b_H Q_3 \\ \kappa _H &{} -Q_1&{} 0&{}0\\ 0&{} ab_M Q_4 &{}-(\kappa _M +\mu _M)&{}0\\ 0&{}0&{}\kappa _M &{} -\mu _M\\ \end{array}\right] . \end{aligned}$$

Let \(a_1=\kappa _H +\mu _H,~~~a_2=0,~~a_3=0,~~a_4=ab_H\)

In the same manner,

\(b_1=\kappa _H,~~~ b_2 =\mu _H +\alpha +\eta ,~~~ c_2 = ab_M,~~~ c_3= \kappa _M +\mu _M,~~~ d_3 =\kappa _M,~~~ d_4 =\mu _M\)

The eigenvalues are solutions of the characteristic equation of the reduced matrix of dimension four which is given by

$$\begin{aligned} (\kappa _H +\mu _H +\lambda )[(\mu _H +\alpha +\eta +\lambda )(\kappa _M +\mu _M +\lambda )(\mu _M +\lambda )]-ab_H(\kappa _H ab_M \kappa _M)=0 \end{aligned}$$

which is simplified to

$$\begin{aligned} \lambda ^4 +A_3 \lambda ^3 +A _2 \lambda ^ 2 +A_1 \lambda +A_0=0, \end{aligned}$$
(4)

where

$$\begin{aligned} \begin{array}{ll} A_3=a_1+b_2+c_3+d_4\\ A_2=(a_1+d4)(b_2+c_3)+a_1d_4+b_2c_3\\ A_1=c_3d_4(b_2+a_1)+a_1b_2(c_3+d_4)\\ A_0=a_1b_2c_3d_4-a^2b_H\kappa _H \kappa _M b_M \end{array} \end{aligned}$$
(5)

The Routh–Huwirtz conditions are sufficient and necessary conditions on the coefficients of the polynomial (4). These conditions ensure that all roots of the polynomial given by (4) have negative real parts. For this polynomial, the Routh–Hurwitz conditions are \(A_3>0,~~A_2 >0,~~A_1 >0, ~~A_0 >0\) and

$$\begin{aligned} H_1&= A_3 >0, \\ H_2&= \left| \begin{array}{lllllllll} A_3 &{} 1\\ A_1 &{}A_2 \end{array}\right| >0,\\ H_3&= \left| \begin{array}{lllllllll} A_3 &{} 1&{}0\\ A_1 &{}A_2&{}A_3\\ 0&{}A_0&{}A_1 \end{array}\right| >0, \\ H_4&= \left| \begin{array}{lllllllll} A_3 &{} 1&{}0&{}0\\ A_1 &{}A_2&{}A_3&{}1\\ 0&{}A_0&{}A_1&{}A_2\\ 0&{}0&{}0&{}A_0 \end{array}\right| >0, \end{aligned}$$

Since all \(A_i>0, ~~~i=1,2,3.\)

Note that from \(A_0=a_1b_2c_3d_4-a^2b_H\kappa _H \kappa _M b_M\) the reproduction number reduces to

$$\begin{aligned} \mathcal{R }_m ^2 =\frac{a^2b_H\kappa _H \kappa _M b_M}{a_1b_2c_3d_4} \end{aligned}$$

Hence if \(\mathcal{R }_m <0,~~~ A _0 >0\).

Clearly, \(H_1 =A_3 >0.\)

$$\begin{aligned} H_2&= A_3 A_2 -A_1\nonumber \\&= (b_2+c_3)(b_2+d_4)(c_3+d_4)+a_1 ^2 (b_2+c_3+d_4)+a_1(b_2+c_3+d_4)^2 \end{aligned}$$
(6)

which is positive.

$$\begin{aligned} H_3&= A_1(A_3A_2-A_1)-A_0A_3 ^2\nonumber \\&= a_1^3 (b_2 + c_3) (b_2 + d_4) (c_3 + d_4) + b_2 c_3 (b_2 + c_3) d_4 (b_2 + d_4) (c_3 + d_4) \nonumber \\&+a_4 b_1 c_2 d_3 (b_2 + c_3 + d_4)^2 + a_1^2 (a_4 b_1 c_2 d_3 + b_2^3 (c_3 + d_4) + 2 b_2 ^2 (c_3 + d_4)^2 \nonumber \\&+c_3 d_4 (c_3 + d_4)^2 + b_2 (c_3 ^3 + 4 c_3 ^2 d_4 + 4 c_3 d_4 ^2 + d_4 ^3))+ a_1 (b_2 ^3 (c_3 + d_4)^2 \nonumber \\&+ (c_3 + d_4) (2 a_4 b_1 c_2 d_3 + c_3 ^2 d_4 ^2) + b_2 ^2 (c_3 ^3 + 4 c_3 ^2 d_4 + 4 c_3 d_4 ^2 + d_4 ^3)\nonumber \\&+ 2 b_2 (a_4 b_1 c_2 d_3 + c_3 d_4 (c_3 + d_4)^2)) \end{aligned}$$
(7)

which is also positive.

It can be easily seen that \(H_4 = A_0 H_3\).

Therefore, all eigenvalues of the Jacobian matrix have negative real parts when \(\mathcal{R }_m <1.\) However, \(\mathcal{R }_m >0\) implies that \(A_0 <0\), and since all coefficients of the polynomial (4) are positive, not all roots of this polynomial can have negative real parts. This means that when \(\mathcal{R }_m >1\), the disease free equilibrium point is unstable. \(\square \)

2.2.1 Endemic equilibria and stability analysis

The endemic equilibrium point \(E_1\) is a steady-state solution where the disease persists in the population. The endemic equilibrium of model system (1) is given by

$$\begin{aligned} \mathcal{E }_1 = (S_H ^*,E_H ^*, I_H ^*,R_H ^*,S_M ^*, E_M ^*,I_M ^*), \end{aligned}$$

in terms of the forces of infection \(\lambda _H\) and \(\lambda _M\), where

$$\begin{aligned} S_H ^*=\frac{\theta (\gamma +\mu _H)(\kappa _H+ \mu _H)(\mu _H+ \alpha +\eta )}{\mu _H (\gamma +\mu _H)(\kappa _H+ \mu _H)(\mu _H+ \alpha +\eta )+\lambda _H[\mu _H (\gamma +\mu _H)(+\mu _H+ \alpha +\eta )+\kappa _H(\gamma \eta +\mu _H (\mu _H+ \alpha +\eta ))]} \end{aligned}$$
$$\begin{aligned} E_H ^*= \frac{\theta \lambda _H(\gamma +\mu _H)(\mu _H+ \alpha + \eta )}{\lambda _H [\mu _H (\gamma +\mu _H)(\mu _H+ \alpha + \eta )+\kappa _H(\gamma \eta +\mu _H(\mu _H+ \alpha +\eta ))]+\mu _H (\gamma +\mu _H)(\kappa _H+ \mu _H)(\mu _H+ \alpha + \eta )} \end{aligned}$$
$$\begin{aligned} I_H ^* =\frac{\theta \kappa _H \lambda _H (\gamma +\mu _H)}{\lambda _H [\mu _H (\gamma +\mu _H)(\mu _H+) \alpha +\eta )+\kappa _H(\gamma \eta +\mu _H(\mu _H+) \alpha +\eta ))]+\mu _H (\gamma +\mu _H)(\kappa _H+ \mu _H)(\mu _H+ \alpha + \eta )} \end{aligned}$$
$$\begin{aligned} R_H ^* = \frac{(1-p) \alpha \theta \kappa _H \lambda _H }{\lambda _H [\mu _H (\gamma +\mu _H)(\mu _H+ \alpha +\eta )+\kappa _H(\gamma \eta +\mu _H(\mu _H+ \alpha +\eta ))]+\mu _H (\gamma +\mu _H)(\kappa _H+ \mu _H)(\mu _H+ \alpha +\eta )} \end{aligned}$$
$$\begin{aligned} J_M ^* = \frac{K \beta _M + N_M ^* \beta _J + K \mu _J \pm \sqrt{(K \beta _M + N_M ^* \beta _J +K \mu _J)^2-4KN_M ^* \beta _J \mu _J}}{2\mu _J} \end{aligned}$$
$$\begin{aligned} S_M ^*=\frac{\beta _M[K \beta _M +N_M ^* \beta _j +K \mu _J \pm \sqrt{(K \beta _M + N_M ^* \beta _J +K \mu _J)^2-4KN_M ^* \beta _J \mu _J}]}{2\mu _J(\lambda _M +\mu _M)} \end{aligned}$$
$$\begin{aligned} E_M ^*= \frac{\beta _M \lambda _M[K \beta _M +N_M ^* \beta _j +K \mu _J \pm \sqrt{(K \beta _M + N_M ^* \beta _J +K \mu _J)^2-4KN_M ^* \beta _J \mu _J}]}{2\mu _J(\kappa _M +\mu _M)(\lambda _M +\mu _M)} \end{aligned}$$
$$\begin{aligned} I_M ^*= \frac{\beta _M \kappa _M \lambda _M[K \beta _M +N_M ^* \beta _j +K \mu _J \pm \sqrt{(K \beta _M + N_M ^* \beta _J +K \mu _J)^2-4KN_M ^* \beta _J \mu _J}]}{2\mu _J \mu _M (\kappa _M +\mu _M)(\lambda _M +\mu _M)} \end{aligned}$$
$$\begin{aligned} N_M ^*= \frac{K \beta _M (\beta _J \beta _M -\beta _M \mu _M -\mu _J \mu _M)}{\mu _M (\beta _J \beta _M -\beta _M \mu _M)} \end{aligned}$$
$$\begin{aligned} N_H ^* = \frac{\theta [(\gamma +\mu _H)(\mu _H+ \alpha +\eta )(\lambda _H +\mu _H)+ \kappa _H \{\lambda _H ((1-p) \alpha +\gamma +\mu _H)+(\gamma +\mu _H)(\mu _H+ \alpha +\eta )\}]}{\mu _H (\gamma +\mu _H)(\mu _H+) \alpha +\eta )(\lambda _H +\mu _H)+ \kappa _H[\mu _H (\gamma +\mu _H)(\mu _H+ \alpha +\eta +\lambda _H(\gamma \eta +\mu _H(\mu _H+ \alpha +\eta ))]} \end{aligned}$$
$$\begin{aligned} \lambda _M=\frac{a \theta b_M \kappa _H \lambda _H \mu _M(\gamma +\mu _H)(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M [\mu _H (\gamma \!+\!\mu _H)(\mu _H\!+\! \alpha \!+\!\eta )(\lambda _H \!+\!\mu _H)+\kappa _H\{\mu _H (\gamma +\mu _H)(\mu _H+ \alpha +\eta )+\lambda _H[\gamma \eta +\mu _H (\mu _H+ \alpha +\eta )]\}](\beta _J \beta _M -(\beta _M+ \mu _J )\mu _M)} \end{aligned}$$
$$\begin{aligned} \lambda _H =\frac{a b_H \beta _M \kappa _M \lambda _M [\mu _H (\gamma +\mu _H)(\mu _H+ \alpha +\eta )(\lambda _H +\mu _H)+\kappa _H[\mu _H (\gamma +\mu _H)(\mu _H+ \alpha +\eta +\lambda _H(\gamma \eta +\mu _H(\mu _H+ \alpha +\eta ))]A]}{2\theta [(\gamma +\mu _H)(\mu _H+ \alpha +\eta )(\lambda _H +\mu _H)+\kappa _H \{\lambda _H ((1-p) \alpha +\gamma +\mu _H) +(\gamma +\mu _H)(\mu _H + \alpha +\eta )\}] \mu _J \mu _M (\kappa _M +\mu _M)(\lambda _M +\mu _M)} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{ll} A=\dfrac{2K \mu _J(\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)}{\beta _J \beta _M -\mu _J \mu _M} \end{array} \end{aligned}$$
(8)

From expanding and simplifying the equation of \(\lambda _H\), we obtain third order equation in \(\lambda _H\) as follows

$$\begin{aligned} \lambda _H(B_1 \lambda _H ^2 +B_2 \lambda _H + B_3)=0, \end{aligned}$$

where \(B_1 = 2K \mu _J \mu _M [\kappa _H ((1-p) \alpha +\gamma +\mu _H) +(\gamma +\mu _H)((1-p) \alpha + \eta +p \alpha + \mu _H)](\kappa _M +\mu _M)\{\beta _J \beta _M -(\beta _M +\mu _J)\mu _M\} \displaystyle [a \theta b_M \kappa _H (\gamma + \mu _H)(\beta _J \beta _M -\mu _J \mu _M)+\kappa \beta _M (\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)\displaystyle (\mu _H (\gamma +\mu _H)(\eta + \alpha +\mu _H)+\kappa _H (\gamma \eta + \mu _H ((1-p) \alpha + \eta + \gamma + \mu _H))\displaystyle )],\)

\(B_2 = 2K \mu _J (\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)\bigg [a \theta b_M \kappa _H (\gamma +\mu _H)(\eta + \alpha +\mu _H)(\kappa _H+\mu _H)\mu _M (\kappa _M+\mu _M)(\beta _J \beta _M -\mu _J \mu _M)+a^2 K b_H b_M \beta _M \kappa _H\kappa _M(-\mu _H(\gamma +\mu _H)(\eta + \alpha +\mu _H)-\kappa _H (\gamma \eta +\mu _H((1-p) \alpha +\gamma +\eta +\mu _H)))(\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)+ K\beta _M (\eta + \alpha +\mu _H)\mu _M (\kappa _M +\mu _M)(\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)\{\kappa _H ^2 \mu _H ((1-p) \alpha + \gamma +\mu _H)+\kappa _H \mu _H ^2(\alpha +\gamma +\mu _H)+2\kappa _H \mu _H(\gamma +\mu _H)(\eta + \alpha + \mu _H)+2\mu _H ^2(\gamma +\mu _H)(\eta + \alpha +\mu _H)+2K \kappa _H ^3(\gamma \eta +((1-p) \alpha +\gamma +\eta +\mu _H)\mu _H)^2 \mu _J \mu _M (\kappa _M +\mu _M)(\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)\}\bigg ]\)

\(B_3=2K^2 \beta _M \mu _H \mu _J(\gamma +\mu _H)^2(\eta + \alpha +\mu _H)(\kappa _H +\mu _H)(\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)^2[-a^2b_H\) \( b_M \kappa _H \kappa _M +\mu _M(\kappa _M +\mu _M)(\kappa _H +\mu _H)(\eta + \alpha +\mu _H)]\) which reduces to

$$\begin{aligned} B_3 =C(-\mathcal{R }_m ^2 +1) \end{aligned}$$

where \(C=2K^2 \beta _M \mu _H \mu _J(\gamma +\mu _H)^2(\eta + \alpha + \mu _H)(\kappa _H +\mu _H)(\beta _J \beta _M -(\beta _M +\mu _J)\mu _M)^2\)

Now

$$\begin{aligned} \lambda _H(B_1 \lambda _H ^2 +B_2 \lambda _H + B_3)=0, \end{aligned}$$

gives \(\displaystyle {\lambda _H ^*=0}\) which corresponds to the disease free equilibrium, and

$$\begin{aligned} \lambda _H ^*= \frac{-B_2 \pm \sqrt{B_2 ^2-4B_1B_3}}{2B_1} > 0 \end{aligned}$$

for the endemic equilibrium.

$$\begin{aligned} \begin{array}{ll} -B_2 \pm \sqrt{B_2 ^2-4B_1C(1-\mathcal{R }_m ^2)} > 0 \\ -B_2 \pm \sqrt{B_2 ^2+4B_1C(\mathcal{R }_m ^2-1)} > 0\\ B_2 ^2 < B_2 ^2+4B_1C(\mathcal{R }_m ^2-1)\\ 0 < 4B_1C(\mathcal{R }_m ^2-1)\\ \end{array} \end{aligned}$$
(9)

Clearly, \(B_1\) is always positive or negative and C is always positive. If \(B_1\) is negative, then \(\mathcal{R }_m <1\) and if \(B_1\) is positive, \(\mathcal{R }_m >1\). Thus \(\mathcal{E }_1\) exists for both \(\mathcal{R }_m ~~< ~~~\text{ or }~~>~~1 \) and this result is summarised in lemma below.

Lemma 1.

The endemic equilibrium \(E^*\) exists and is unique whenever \(\mathcal{R }_m > 1\), and there exists a backward bifurcation when \(\mathcal{R }_m <1 \), (\(B_1 <0\)).

2.3 Local stability of the Endemic Equilibrium

The stability of the endemic equilibrium can be determined by computing the eigenvalues of the Jacobian matrix and then evaluate it at the endemic equilibrium. However this approach is mathematically complicated for the system of equations (1). Bifurcation analysis is performed at the disease free equilibrium by using Center Manifold Theory as presented in Chavez and Song [21].

The system (1) is rewritten by introducing the dimensionless state variables; let \(x_1=S_H,~x_2=E_H,~x_3= I_H,~x_4= R_H,~x_5=J_M,~x_6=S_M,~x_7=E_M,~ x_8=I_M.\)

We can write

$$\begin{aligned} \frac{dX_i}{dt}=\mathbf{F}(\mathbf{X}_i) \end{aligned}$$

where \(X_i=(x_1,x_2,...,x_8)^T\), \(\mathbf{F}=(f_1,f_2,...,f_8)^T\) and \((.)^T\) represents the matrices transpose.

The system of equations (1) becomes

$$\begin{aligned} \frac{dx_1}{dt}&= \theta -\frac{a \phi ^* x_8 x_1}{N_M}- \mu _H x_1 +p \alpha x_3 +\gamma x_4 =f_1\nonumber \\ \frac{dx_2}{dt}&= \frac{a \phi ^* x_8 x_1}{N_M}-(\kappa _H +\mu _H)x2=f_2 \nonumber \\ \frac{dx_3}{dt}&= \kappa _H x_2 -(p \alpha +\mu _H +(1-p) \alpha +\eta )x_3 =f_3\nonumber \\ \frac{dx_4}{dt}&= (1-p) \alpha x_3 -(\gamma +\mu _H)x_4 =f_4\nonumber \\ \frac{dx_5}{dt}&= [\beta _J N_M- \mu _J(T)x_5]\left( 1-\frac{x_5}{K}\right) -\beta _Mx_5=f_5\nonumber \\ \frac{dx_6}{dt}&= \beta _M x_5 -\frac{ab_M x_3 x_6}{N_H} -\mu _M x_6=f_6\nonumber \\ \frac{dx_7}{dt}&= \frac{ab_M x_3 x_6}{N_H} -(\kappa _M +\mu _M )x_7=f_7\nonumber \\ \frac{dx_8}{dt}&= \kappa _M x_7 -\mu _M x_8 = f_8 \end{aligned}$$
(10)

where \(N_H= x_1+x_2+x_3+x_4\) and \(N_M= x_6+x_7+x_8\), with \(\phi ^*= b_H \) from (3). Suppose that \(\phi ^*\) is a bifurcation parameter, the system (10) is linearised at disease free equilibrium point \(\mathcal{E }_0\) when \(\phi = \phi ^*\) with \(\mathcal{R }_m =1\). Now solving for \(\mathcal{R }_m =1\) in (3) gives

$$\begin{aligned} \phi ^* =\frac{\mu _M (\kappa _M +\mu _M)(\kappa _H +\mu _H)(p \alpha +\mu _H +(1-p) \alpha +\eta )}{a^2b_M \kappa _M}. \end{aligned}$$

Then zero is a simple eigenvalue of the following Jacobian matrix with the application of the bifurcation parameters.

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -\mu _H &{}0 &{}p \alpha &{}\gamma &{}0 &{}0 &{}0 &{} -a \phi Q_3 \\ 0&{} -(\kappa _H +\mu _H) &{}0&{}0&{}0&{}0 &{} 0 &{} a \phi Q_3 \\ 0&{} \kappa _H &{} -Q_1&{} 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}(1-p) \alpha &{}-(\gamma +\mu _H)&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{} Q_2&{}0&{}0&{}0\\ 0&{}0&{}-ab_M Q_4&{}0&{}\beta _M&{}-\mu _M &{}0&{}0\\ 0&{}0&{} ab_M Q_4&{}0&{}0&{}0&{}-(\kappa _M +\mu _M)&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}\kappa _M &{} -\mu _M\\ \end{array}\right] . \end{aligned}$$

where \(Q_1=(p \alpha +\mu _H +(1-p) \alpha +\eta ),~~~\) \(Q_2=-(\mu _J +\beta _M)+2\mu _J \frac{(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\beta _J \beta _M -\mu _J \mu _M},\) \(Q_3= \frac{\theta }{\mu _H}\frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}~~~\) and \(Q_4 =\frac{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\mu _M(\beta _J \beta _M -\mu _J \mu _M)} \frac{\mu _H}{\theta }=\frac{1}{Q_3}\).

A right eigenvector associated with the eigenvalue zero is \(\omega =(\omega _1, \omega _2,..., \omega _7)\).

Solving gives the system

$$\begin{aligned}&\mu _H \omega _1 +p \alpha \omega _3 +\gamma \omega _4 - a \phi Q_3 \omega _8 =0\nonumber \\&-(\kappa _H +\mu _H) \omega _2 +a \phi Q_3 \omega _8 =0\nonumber \\&\kappa _H \omega _2 -(p \alpha +\mu _H +(1-p) \alpha +\eta ) \omega _3=0\nonumber \\&(1-p) \alpha \omega _3 -(\gamma + \mu _H) \omega _4 =0\nonumber \\&\bigg (-(\mu _J +\beta _M)+2\mu _J \frac{(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\beta _J \beta _M -\mu _J \mu _M}\bigg )\omega _5 =0\nonumber \\&-ab_M Q_4 \omega _3 +\beta _M \omega _5 -\mu _M \omega _6 =0\nonumber \\&ab_M Q_4 \omega _3 -(\kappa _M +\mu _M)\omega _7=0\nonumber \\&\kappa _M \omega _7 -\mu _M \omega _8=0 \end{aligned}$$
(11)

Solving the system (11), gives the following right eigenvector

$$\begin{aligned} \omega _1&= \frac{a \phi Q_3 \omega _8 p \alpha \omega _3 -\gamma \omega _4}{\mu _H}\nonumber \\ \omega _2&= \frac{a \phi Q_3 \omega _8}{\kappa _H +\mu _H}\nonumber \\ \omega _3&= \frac{\kappa _H \omega _2}{p \alpha +\mu _H +(1-p) \alpha +\eta }\nonumber \\ \omega _4&= \frac{(1-p) \alpha \omega _3}{\gamma +\mu _H}\nonumber \\ \omega _5&= 0\nonumber \\ \omega _6&= \frac{ab _M Q_4 \omega _3 +\beta _M \omega _5}{\mu _M}\nonumber \\ \omega _7&= \frac{a b _M Q_4 \omega _3 }{\kappa _M +\mu _M }\nonumber \\ \omega _8&= \frac{\kappa _M \omega _7}{\mu _M} \end{aligned}$$
(12)

The left eigenvector satisfying \(v.\omega =1\) is \(v=(v_1,v_2,...,v_8)\). To find these left eigenvector associated with the eigenvalue \(0\), the matrix should be transposed.

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} -\mu _H &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{} 0 \\ 0&{} -(\kappa _H +\mu _H) &{}\kappa _H&{}0&{}0&{}0 &{} 0 &{} 0 \\ p \alpha &{} 0 &{} -Q_1&{} (1-p) \alpha &{}0&{}-a b_M Q_4&{}a b_M Q_4&{}0\\ \gamma &{}0&{}0&{}-(\gamma +\mu _H)&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}Q_2&{}\beta _M &{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}-\mu _M &{}0&{}0\\ 0&{}0&{} 0 &{}0&{}0&{}0&{}-(\kappa _M +\mu _M)&{}\kappa _M\\ -a \phi Q_3&{}a \phi Q_3&{}0&{}0&{}0&{}0&{}0&{} -\mu _M\\ \end{array}\right] . \end{aligned}$$

From which the following system is calculated

$$\begin{aligned}&-\mu _H v_1=0\nonumber \\&-(\kappa _H +\mu _H ) v_2 +\kappa _H v_3 =0\nonumber \\&p \alpha v_1 -(p \alpha +\mu _H +(1-p) \alpha + \eta )v_3 +(1-p) \alpha v_4 +ab_M Q_4 v_6 -ab_M Q_4v_7 =0\nonumber \\&\gamma v_1 -(\gamma +\mu _H)v_4 =0\nonumber \\&\bigg (-(\mu _J +\beta _M)+2\mu _J \frac{(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}{\beta _J \beta _M -\mu _J \mu _M}\bigg )v_5 +\beta _M v_6=0\nonumber \\&-\mu _M v6=0\nonumber \\&-(\kappa _M +\mu _M)v_7 +\kappa _M v_8=0\nonumber \\&-a \phi Q_3 v_1 + a \phi Q_3 v_2 -\mu _M v_8 =0 \end{aligned}$$
(13)

The left eigenvector is solved and the result is \(\displaystyle {v_1 \!=\!0,~~~v_2 \!=\!v_2 >0,~~~v_3 \!=\!\frac{(\kappa _H +\mu _H)v_2}{\kappa _H},}\)

\(\displaystyle {v_4 =0,~~~v_5=0,~~~v_6=0,~~~v_7 = \frac{\kappa _M }{\kappa _M +\mu _M }v_8,~~~v_8 =\frac{a \phi Q_3 }{\mu _M}v_2}.\)

The theorem in Chavez and Song (2004) is reproduced below for convenience, and will be useful to prove local stability of the endemic equilibrium point near

\({\mathcal{R }_m =1}\) [21].

Theorem 2

Consider the following general system of ordinary differential equations with a parameter \(\phi \)

$$\begin{aligned} \frac{dx}{dt}=f(x,\phi ), f:\mathbb{R } ^n \times \mathbb{R }\rightarrow \mathbb{R }~~ \text{ and }~~ f\in \mathbb{C } ^2 (\mathbb{R } ^n \times \mathbb{R }) \end{aligned}$$

where 0 is an equilibrium point of the system, (that is \(f(0.\phi )=0\) for all \(\phi \)) and assume

\(\displaystyle {A1: A = D_xf(0, 0) =(\frac{df_i}{dx_i}(0,0))}\) is the linearization matrix of System (24) around the equilibrium 0 with evaluated at 0. Zero is a simple eigenvalue of A and all other eigenvalues of A have negative real parts;

\(A2:\) Matrix A has a nonnegative right eigenvector \(\omega \) and a left eigenvector \(v\) corresponding to the zero eigenvalue. Let \(f_k\) be the \(k^{th}\) component of \(f\) and

$$\begin{aligned} a_{cs}= \sum _{k,i,j =1} ^n v_k \omega _i \omega _j \frac{\partial ^2 f_k}{\partial x_i \partial x_j}(0,0) \end{aligned}$$
$$\begin{aligned} b_{cs}= \sum _{k,i =1} ^n v_k \omega _i \frac{\partial ^2 f_k}{\partial x_i \partial \phi } (0,0) \end{aligned}$$

then the local dynamics of the system around 0 are totally determined by the sign of \(a_{cs}\) and \(b_{cs}\).

  1. 1.

    \( a_{cs} > 0,~~~ b_{cs} > 0\). When \(\phi < 0\) with \(|\phi | << 1, 0 \) is locally asymptotically stable, and there exists a positive unstable equilibrium; when \(0 < \phi << 1,~~ 0\) is unstable and there exists a negative and locally asymptotically stable equilibrium;

  2. 2.

    \(a_{cs} < 0,~~~ b_{cs} < 0.\) When \(\phi < 0 \) with \(|\phi | << 1,~~ 0\) is unstable; when \(0 < \phi << 1,~~ 0\) is locally asymptotically stable, and there exists a positive unstable equilibrium;

  3. 3.

    \(a_{cs} > 0,~~~ b_{cs} < 0\). When \(\phi < 0\) with \(|\phi | << 1,~~ 0\) is unstable, and there exists a locally asymptotically stable negative equilibrium; when\( 0 < \phi << 1,~~ 0~\) is stable, and a positive unstable equilibrium appears;

  4. 4.

    \(a_{cs} < 0,~~ b_{cs} > 0\). When \(\phi \) changes from negative to positive, 0 changes its stability from stable to unstable. Correspondingly a negative unstable equilibrium becomes positive and locally asymptotically stable.

Particularly, if \(a_{cs}> 0\) and \(b_{cs}>0\), then, a backward bifurcation occurs at \(\phi =0\).

2.3.1 Computation of \(a_{cs} \,\text{ and } \, b_{cs}\)

For the system (10), the associated non-zero second order partial derivatives at disease free equilibrium are given by

$$\begin{aligned} a_{cs}&= \sum _{k,i,j =2} ^3 v_k \omega _i \omega _j \frac{\partial ^2 f_k}{\partial x_i \partial x_j}(0,0)+\sum _{k,i,j =7} ^8 v_k \omega _i \omega _j \frac{\partial ^2 f_k}{\partial x_i \partial x_j}(0,0)\nonumber \\ b_{cs}&= \sum _{k,i =2} ^3 v_k \omega _i \frac{\partial ^2 f_k}{\partial x_i \partial \phi } (0,0)+ \sum _{k,i =7} ^8 v_k \omega _i \frac{\partial ^2 f_k}{\partial x_i \partial \phi } (0,0) \end{aligned}$$

Since \(\displaystyle {v_1, v_4, v_5, v_6 =0}\), for \(\displaystyle { k=1, 4,5,6}\) then \(\displaystyle {k = 2,3,7,8}\) should be considered.

That is, the following functions will be used to find \(\displaystyle {a_{cs}}\) and \(\displaystyle {b_{cs}}\) from the system (10).

$$\begin{aligned} f_2&= \frac{a \phi x_8 x_1}{N_M}- (\kappa _H +\mu _H)x_2\nonumber \\&= \frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}a \phi x_8 x_1 -(\kappa _H +\mu _H)x_2\nonumber \\ N_H&= x_1+x_2+x_3+x_4 \nonumber \\ f_2&= \frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)} a \phi x_8(N_H \!-\!x_2\!-\!x_3\!-\!x_4)\!-\! (\kappa _H \!+\!\mu _H)x_2\qquad \end{aligned}$$
(14)
$$\begin{aligned} f_7&= \frac{ab_M x_3 x_6}{N_H}-(\kappa _M -\mu _M)x_7\nonumber \\ N_M&= x_6+x_7+x_8\nonumber \\ f_7&= \frac{a \mu _H b_M x_3}{\theta }(N_M -x_7 -x_8)-(\kappa _M -\mu _M)x_7 \end{aligned}$$
(15)

hence

$$\begin{aligned} \displaystyle {\frac{\partial ^2 f_7}{\partial x_7 \partial x_3}=-\frac{a \mu _H b_M}{\theta }}~~~=~~~\displaystyle {\frac{\partial ^2 f_7}{\partial x_8 \partial x_3}}. \end{aligned}$$

Therefore

$$\begin{aligned} a_{cs}=\displaystyle {-\frac{\mu _M(\beta _J \beta _M \!-\!\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M\!-\!\beta _M \mu _M)}a \phi \{v_2 \omega _8\{\omega _2 +\omega _3\}\}- \frac{a \mu _H b_M }{\theta }(v_7 \omega _3 \{\omega _7 +\omega _8\})} \end{aligned}$$

Now simplifying

$$\begin{aligned} \displaystyle {-\frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}a \phi \{v_2 \omega _8(\omega _2 +\omega _3)\}} \end{aligned}$$

gives

$$\begin{aligned} \displaystyle { -\frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}a^2 \phi ^2 v_2 \omega _8 ^2 \left[ \frac{\kappa _H +\mu _H + \alpha +\eta }{(\kappa _H +\mu _H)(\mu _H + \alpha +\eta )}\right] } \end{aligned}$$

On the other hand,

$$\begin{aligned} \displaystyle {-\frac{a b_M \mu _M }{\theta } \{v_7 \omega _3 (\omega _7 +\omega _8)\}}=-\frac{a^2 b_M ^2 \mu _H)}{\theta }v_7 \omega _3 ^2 \end{aligned}$$

Hence

$$\begin{aligned}&\displaystyle {a_{cs}\!=\!-a^2 \phi ^2 v_2 \omega _8 ^2\frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)} \bigg [\frac{\kappa _H +\mu _H + \alpha +\eta }{(\kappa _H +\mu _H)(\mu _H + \alpha +\eta )}\bigg ]}\\&{\!-\!\bigg \{\frac{a^2 b_M ^2 \mu _H}{\theta }v_7 \omega _3 ^2 \bigg \}} \end{aligned}$$

If we let \(\displaystyle {P_1=-a^2 \phi ^2 v_2 \omega _8 ^2\frac{\mu _M(\beta _J \beta _M -\mu _J \mu _M)}{K \beta _M(\beta _J \beta _M -\mu _J \mu _M-\beta _M \mu _M)}\bigg [\frac{\kappa _H +\mu _H + \alpha +\eta }{(\kappa _H +\mu _H)(\mu _H + \alpha +\eta )}\bigg ]}\) and

\(\displaystyle {P_2= \bigg \{\frac{a^2 b_M ^2 \mu _H}{\theta }v_7 \omega _3 ^2 \bigg \}}\)

such the \(\displaystyle {a_{cs}= P_1-P_2}.\)

Table 2 Possibilities of the sign of \(a_{cs}\)
Full size table

Possibilities for the sign of \(\displaystyle {a_{cs}}\) are explored in Table 2 below

$$\begin{aligned} \frac{\partial f_2}{\partial \phi }= ax_8~~\text{ and } ~~~\frac{\partial ^2 f_2}{\partial x_8 \partial \phi }=a \end{aligned}$$

Therefore

$$\begin{aligned} b_{cs}=a v_2 \omega _8 >0 . \end{aligned}$$

Theorem 3

If \(\displaystyle {a_{cs} >0}\), then, model system (1) undergoes a backward bifurcation at \(\mathcal{R } _ m\) close to 1, otherwise \(a_{cs} <0\) and a unique endemic equilibrium \(\mathcal{E }_1\) guaranteed by Theorem 2 is locally asymptotically stable for \(\mathcal{R } _m > 1\), but close to 1.

2.4 Effect of temperature dependant parameters on the reproduction number

The effect of climate change is investigated by examining the effect of climate components on the disease reproduction number. Evidence suggests that the mosquito biting rate \((a)\), mosquito mortality rate \((\mu _M)\) and the parasite development rate \(\kappa _M\) are all sensitive to changes in temperature. The change in \(\mathcal{R }_m\), with a change in mean temperature can be determined by the sum of the effects of temperature on each temperature sensitive component of \(\mathcal{R }_m\) coupled with the corresponding change to \(\mathcal{R }_m\).

$$\begin{aligned} \frac{d\mathcal{R }_m}{dT}=\frac{da}{dT} \frac{d\mathcal{R }_m}{da}+\frac{d \kappa _M}{dT}\frac{d\mathcal{R }_m}{d \kappa _M}+\frac{d \mu _M}{dT}\frac{d\mathcal{R }_m}{d \mu _M} \end{aligned}$$
(16)

The mathematical relationships between \(\mathcal{R }_m\) and the temperature-sensitive biological parameters are as follows:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\frac{d\mathcal{R }_m}{da}= \frac{\mathcal{R }_m}{a}}\\ \displaystyle {\frac{d\mathcal{R }_m}{d\kappa _M}=\frac{\mathcal{R }_m}{2} \bigg (1-\frac{1}{\kappa _M +\mu _M}\bigg )}\\ \displaystyle {\frac{d\mathcal{R }_m}{d\mu _M}=-\frac{\mathcal{R }_m}{2} \bigg [\frac{2\mu _M +\kappa _M}{\mu _M(\kappa _M +\mu _M)} \bigg ]}\\ \end{array} \end{aligned}$$
(17)

The system of equations in 17 shows that an increase in \(a,~\text{ and }~~\kappa _M\) will have a positive effect on \(\mathcal{R }_m,\) while increasing \(\mu _M\) will have a negative effect. The quantitative effect of temperature change on \(\mathcal{R }_m\) will depend on both the individual relationships of these parameters with temperature and their combined impact within the \(\mathcal{R }_m\) equation.

  1. 1.

    Mosquito biting rate \(a(T)\) The biting rate represents the frequency of feeding activity by mosquitoes per day.

    $$\begin{aligned} a(T)=0.000203T(T-11.7)\sqrt{42.3-T}. \end{aligned}$$

    Hence

    $$\begin{aligned} \begin{array}{lll} \displaystyle {\frac{da}{dT}=\frac{0.000406(T-10.7)(42.3-T)-0.000203T(T-11.7)}{2\sqrt{42.3-T}}}\\ \displaystyle {\frac{da}{dT}=\frac{-0.000609T^2+0.023891T-0.18376}{2\sqrt{42.3-T}}} \end{array} \end{aligned}$$
    (18)
  2. 2.

    Mosquito mortality rate \(\mu _M (T)\) \(\mu _M(T)= -\ln p(T)\), where \(p(T)= e ^{\frac{-1}{AT^2+BT+C}}\) is the daily survival rate. Therefore

    $$\begin{aligned} \frac{d \mu _M}{dT}= \frac{-(2AT +B)}{(AT^2+BT+C)^2} \end{aligned}$$
    (19)
  3. 3.

    Progression rate of mosquitoes to infectious class \(\kappa _M= \frac{T-T_{min}}{DD}\) where \(DD\) is the total degree days for the parasite development, \(T\) is the mean temperature in degrees centigrade and \(T_{\text{ min }}\) is the temperature at which parasite development ceases. \(DD=\) 111 while \(T_{\text{ min }}\) is 16 for plasmodium falciparum.

    $$\begin{aligned} \frac{d \kappa _M}{dT} = \frac{1}{DD} \end{aligned}$$
    (20)

Substituting equations (17,18, 19, 20) into equation (16) we have

$$\begin{aligned} \frac{d\mathcal{R }_m}{dT}&= \mathcal{R }_m \left[ \frac{-0.000609T^2+0.023891T-0.18376}{2a\sqrt{42.3-T}} \right. \\&\left. +\frac{2AT+B}{2(AT^2+BT+C)}\bigg (\frac{1}{\mu _M}+\frac{1}{(\kappa _M +\mu _M)}\bigg )+\frac{1}{2DD}\bigg (1- \frac{1}{(\kappa _M +\mu _M)}\bigg )\right] \end{aligned}$$

Let \(\displaystyle {\frac{0.023891T}{2a\sqrt{42.3-T}}=G_1},\, \displaystyle {\frac{2AT+B}{2(AT^2+BT+C)}\bigg (\frac{1}{\mu _M}+\frac{1}{(\kappa _M +\mu _M)}\bigg ) =G_2}\),

$$\begin{aligned} \displaystyle {\frac{1}{2DD}=G_3\,\text{ and }~~\frac{0.000609T^2+0.18376}{2a\sqrt{42.3-T}} +\frac{1}{2DD(\kappa _M +\mu _M)}=G_4} \end{aligned}$$

Then

$$\begin{aligned} \displaystyle {\frac{d\mathcal{R }_m}{dT}=\mathcal{R }_m(G_1+G_2+G_3-G_4)}. \end{aligned}$$

If \(G_1+G_2+G_3-G_4 <0 \) then \(\frac{d\mathcal{R }_m}{dT} <0\) and increase in temperature results in a decrease in \(\mathcal{R }_m,\) typically in regions which experience extremely high temperatures. If \(G_1+G_2+G_3-G_4 >0 \) then \(\frac{d\mathcal{R }_m}{dT} >0\) and \(\mathcal{R }_m\) increases as temperature increases the epidemic also increases.

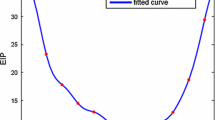
In Fig. 2, the relationship between temperature and mosquito biting rate, parasite development rate, mosquito mortality rate, and malaria reproduction number respectively, are illustrated. The mosquito biting rate is low at lower temperatures but increases to a maximum as temperature increases. Mosquito mortality is high at low temperatures, decreases to a minimum between 20 and \(25 ~{}^{\circ }\mathrm{C}\) before increasing at temperatures beyond \(25^0 C\). The temperature range where \(\mathcal{R }_m > 1\) for malaria is 22.34–\(38.6~{}^{\circ }\mathrm{C}\). A maximum \(\mathcal{R }_m\) of 3.65 occurs at \(31.5~{}^{\circ }\mathrm{C}\).

Fig. 2
figure 2

Simulation of a mosquito biting rate, b mosquito mortality rate, c progression rate of mosquitoes, d \(\mathcal{R }_m\) versus temperature

Full size image

We carry out numerical simulations using a fourth order Runge-Kutta scheme in Matlab with the aim of verifying some of the analytical results on the stability of the system (1). The parameter values that we use for numerical simulations are in Table 1. For numerical simulations, the following initial values are used:

\(S_H=1000,~E_H=300,~I_H=200,~R_H=0,~J_M=30000,~S_M=10000,\)

\(E_M=1000,~~~I_M=1000.\)

In Fig. 3, the effects of varying temperature on the infected human and mosquito populations is illustrated. The simulations reveal both the endemic equilibrium and the disease free equilibrium points as temperature is varied from \(20-40~{}^{\circ }\mathrm{C}\). In Fig. 3, if temperatures are to average \(20 ~{}^{\circ }\mathrm{C}\), the infected human and mosquito population declines to asymptotically low levels as mosquito survives at above \(22~{}^{\circ }\mathrm{C}\) [18]. Furthermore, infected mosquito and human populations tend to decline to asymptotically low levels faster when temperatures average \(40~{}^{\circ }\mathrm{C}\) as compared to temperatures averaging \(20~{}^{\circ }\mathrm{C}\) . This may be due to increased death rate of juvenile mosquitoes as ponds dry up quickly because of high evaporation rates at high temperatures and mosquitoes can not survive above \(40~{}^{\circ }\mathrm{C}\) [19]. Infected humans tend to be more at average temperatures of \(35~{}^{\circ }\mathrm{C}\) as compared to when \(T=30~{}^{\circ }\mathrm{C}\) (the range of optimal temperature for malaria transmission). This is possibly due to increased mosquito biting rate and parasite development rate at higher temperatures.

Fig. 3
figure 3

Simulation of a Exposed humans, b Infectious humans, c Exposed mosquitoes, and d infectious mosquitoes as temperature varies

Full size image

Figure 4 shows that mosquito biting rate plays a more significant role in the increase of \(\mathcal{R }_m\) than any other factor. This suggests that mosquito biting rate promotes malaria transmission than any other factor. Thus intervention strategies should be tailor made to prevent mosquito bites.

Fig. 4
figure 4

Partial rank correlation coefficients showing the effect of parameter variations on \(\mathcal{R }_m\) using ranges in the table. Parameters with positive PRCCs will increase \(\mathcal{R }_m\) when they are increased, whereas parameters with negative PRCCs will decrease \(\mathcal{R }_m\) when they are increased

Full size image

Figure 5 illustrates the effect of varying four sample parameters on the reproductive number \(\mathcal{R }_m\).

Fig. 5
figure 5

Monte Carlo simulations of a mosquito biting rate, b mosquito mortality, c human to mosquito infection, and d recovery rate of humans

Full size image

3 Discussion

In this paper, a mathematical model to explore the impact of temperature on malaria transmission is presented as a system of differential equations and analysed. The model is shown to exhibit backward bifurcation where disease-free and endemic equilibria co-exist when the reproduction number is less than unity. In such a scenario, making the reproduction number less than unity will not be enough to contain the epidemic. Analysis of the model suggests that temperature range 23–\(38~{}^{\circ }\mathrm{C}\) is ideal for malaria transmission. The reproduction number increases as temperature increases to attain a maximum at \(31.5~{}^{\circ }\mathrm{C}\), beyond which the reproduction number starts declining. This result suggests the optimal temperature for malaria transmission is around \(31~{}^{\circ }\mathrm{C}\). The analysed results are also supported by numerical simulations which show an increase in malaria cases as temperature increases to about \(38~{}^{\circ }\mathrm{C}\) and a decrease thereafter. From the PRCCs, it is illustrated that the death rate of mosquitoes have a negative impact on the reproduction number. Thus, results suggest that any factor which contributes to increased mosquito death like spraying, use of treated mosquito nets has potential to reduce malaria transmission. Thus, mosquito spraying, coupled with the use of treated mosquito nets has a great potential to control this deadly tropical scourge. Given high incidences of tuberculosis in Sub-saharan Africa, where malaria is also endemic, this model can be extended to incorporate the malaria and TB coinfection.