A Malaria Transmission Model with Temperature-Dependent Incubation Period

Abstract

Malaria is an infectious disease caused by Plasmodium parasites and is transmitted among humans by female Anopheles mosquitoes. Climate factors have significant impact on both mosquito life cycle and parasite development. To consider the temperature sensitivity of the extrinsic incubation period (EIP) of malaria parasites, we formulate a delay differential equations model with a periodic time delay. We derive the basic reproduction ratio $R_0$ and establish a threshold type result on the global dynamics in terms of $R_0$, that is, the unique disease-free periodic solution is globally asymptotically stable if $R_0<1$; and the model system admits a unique positive periodic solution which is globally asymptotically stable if $R_0>1$. Numerically, we parameterize the model with data from Maputo Province, Mozambique, and simulate the long-term behavior of solutions. The simulation result is consistent with the obtained analytic result. In addition, we find that using the time-averaged EIP may underestimate the basic reproduction ratio.

1 Introduction

Malaria is the most prevalent human vector-borne disease, with an estimated 214 million cases and about 438 thousand deaths worldwide in 2015 (World Health Organisation 2015). Malaria is caused by Plasmodium protozoan parasites and is transmitted among humans by the bites of female Anopheles mosquitoes. More precisely, female Anopheles mosquitoes pick up Plasmodium parasites in a blood meal taken from an infectious human host. The parasites then go through several developmental stages before they migrate to the mosquito salivary glands. Once in the salivary glands, the parasites can be transmitted to a susceptible human host when the mosquito takes another blood meal (Beier 1998; Beck-Johnson et al. 2013). The time parasites spent in completing its development within the mosquito and migrating to the salivary glands is known as the extrinsic incubation period (EIP).

Both the mosquito life cycle and the parasite development are strongly influenced by seasonally varying temperature. Understanding the role of temperature in malaria transmission is of particular importance in light of climate change (Ngarakana-Gwasira et al. 2014). The first mathematical model of malaria transmission was proposed by Ross (1911) and later extended by Macdonald (1957). Since then, a number of malaria models have been developed to study the climate impact on malaria transmission (see, e.g., Craig et al. 1999; Lou and Zhao 2010; Ngarakana-Gwasira et al. 2014; Wang and Zhao 2017; Wang and Zhao, and the references therein). Malaria parasites manipulate a host to be more attractive to mosquitoes via the chemical substances (Lacroix et al. 2005). Kingsolver (1987) proposed the first malaria model to account for the greater attractiveness of infectious humans to mosquitoes. Chamchod and Britton (2011) modeled such vector-bias effect in terms of the different probabilities that a mosquito arrives at a human at random and picks the human if he is infectious or susceptible. Recently, the vector-bias effect has also been incorporated into some climate-based malaria models (see, e.g., Wang and Zhao 2017; Wang and Zhao).

In our recent work, we developed a periodic vector-bias malaria model with incubation period and established the global dynamics in terms of the basic reproduction ratio. We remarked that the constant delay in the model may be modified to a time-dependent delay since the EIP is highly sensitive to temperature, and we left this interesting problem for future investigation (Wang and Zhao 2017). The aim of the current work is to solve this problem. We develop a delay differential equations model of malaria transmission in which the delay is periodic in time. To our knowledge, this is the first mosquito-borne disease model that takes into account the time-dependent delay. Several population models with time-dependent delays have been developed (see, e.g., Beck-Johnson et al. 2013; McCauley et al. 1996; Molnár et al. 2013; Nisbet and Gurney 1983; Omori and Adams 2011; Rittenhouse et al. 2016; Wu et al. 2015). However, little mathematical analysis is carried out to understand the asymptotic behavior of these models. Recently, Lou and Zhao (2017) studied the global dynamics of a host–macroparasite model with seasonal developmental durations by introducing a periodic semiflow on a suitably chosen phase space. We will use the theoretical approach developed in Lou and Zhao (2017) to analyze our model.

The rest of the paper is organized as follows. In the next section, we give the underlying assumptions and formulate the model. In the following section, we establish the threshold dynamics of the model in terms of the basic reproduction ratio. In Sect. 4, we carry out a case study for Maputo Province, Mozambique. A brief discussion concludes the paper.

2 Model Formulation

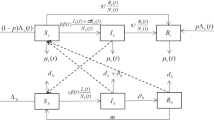
The purpose of this section is to formulate a mathematical model of malaria transmission that incorporates a temperature-dependent delay. We start with a brief introduction of the model of malaria transmission proposed by Wang and Zhao (2017). Since malaria is transmitted among humans by mosquitoes, we consider the dynamics of both human and mosquito populations. Let the state variables $I_h(t)$, $S_m(t)$, $I_m(t)$ be the number of infectious humans, susceptible and infectious adult female mosquitoes at time t, respectively. We suppose that the total number of humans stabilizes at a constant value H. Then the number of susceptible humans at time t is $H-I_h(t)$. We incorporate climate factors into the model by assuming that all the parameters related to mosquitoes are periodic functions. Let $\beta (t)$ be the biting rate of mosquitoes. Let $\mu (t)$ be the recruitment rate at which female adult mosquitoes emerge from larvae, and let $d_m(t)$ be the death rate of mosquitoes. To depict the vector-bias effect, we introduce two parameters p and l, that is, the probabilities that a mosquito arrives at a human at random and picks the human if he is infectious and susceptible, respectively. Let $\tau$ be the length of the EIP. The model of the reference (Wang and Zhao 2017) is governed by the following system of time-delayed differential equations:

$$\begin{aligned} \frac{\mathrm{d}I_h(t)}{\mathrm{d}t}= & {} \frac{c\beta (t) l(H-I_h(t))}{pI_h(t)+l(H-I_h(t))}I_m(t)-(d_{h} +\rho )I_h(t), \nonumber \\ \frac{\mathrm{d}S_m(t)}{\mathrm{d}t}= & {} \mu (t)-\frac{b\beta (t) pI_h(t)}{pI_h(t)+l(H-I_h(t))}S_m(t)-d_{m}(t)S_m(t), \nonumber \\ \frac{\mathrm{d}I_m(t)}{\mathrm{d}t}= & {} -d_{m}(t)I_m(t)+e^{-\int _{t-\tau }^t d_{m}(s)\mathrm{d}s} \frac{b\beta (t-\tau )pI_h(t-\tau )S_m(t-\tau )}{pI_h(t-\tau )+l(H-I_h(t-\tau ))}. \end{aligned}$$

(1)

We refer the readers to Wang and Zhao (2017) for more details about the derivation of model (1). To introduce the temperature-dependent incubation period, we use the arguments similar to those in Nisbet and Gurney (1983), Omori and Adams (2011). We consider the exposed compartment where mosquitoes are infected but not infectious yet. Let $E_m(t)$ be the number of the exposed mosquitoes at time t, and M(t) be the number of newly occured infectious mosquitoes per unit time at time t. Then we have the following system:

$$\begin{aligned} \frac{\mathrm{d}I_h(t)}{\mathrm{d}t}= & {} \frac{c\beta (t)l(H-I_h(t))}{pI_h(t)+l(H-I_h(t))}I_m(t)-(d_h+\rho )I_h(t), \nonumber \\ \frac{\mathrm{d}S_m(t)}{\mathrm{d}t}= & {} \mu (t)-B(t,I_h(t),S_m(t))-d_m(t)S_m(t),\nonumber \\ \frac{\mathrm{d}E_m(t)}{\mathrm{d}t}= & {} B(t,I_h(t),S_m(t))-M(t)-d_m(t)E_m(t),\nonumber \\ \frac{\mathrm{d}I_m(t)}{\mathrm{d}t}= & {} M(t)-d_m(t)I_m(t), \end{aligned}$$

(2)

where $B(t,I_h(t),S_m(t))=\frac{b\beta (t)pI_h(t)S_m(t)}{pI_h(t)+l(H-I_h(t))}$. Let q be the development level of infection such that q increases at a temperature-dependent rate $\gamma (T(t))=\gamma (t)$, $q=q_E=0$ at the transition from $S_m$ to $E_m$, and $q=q_I$ at the transition from $E_m$ to $I_m$. The variable q describes how complete the parasite developmental stages are in the mosquito (in other words, how complete the latency stage is). Let $\rho (q,t)$ be the number of mosquitoes with development level q at time t. Then $M(t)=\gamma (t)\rho (q_I,t)$.

Let J(q, t) be the flux, in the direction of increasing q, of mosquitoes with infection development level q at time t. Then we have the following equation (see, e.g., Kot 2001)

$$\begin{aligned} \frac{\partial \rho }{\partial t}=-\frac{\partial J}{\partial q}-d_m(t)\rho . \end{aligned}$$

Since $J(q,t)=\gamma (t)\rho (q,t)$, we have

$$\begin{aligned} \begin{aligned} \frac{\partial \rho (q,t)}{\partial t} =-\frac{\partial }{\partial q}[\gamma (t)\rho (q,t)]-d_m(t)\rho (q,t). \end{aligned} \end{aligned}$$

(3)

For the $E_m$ state, system (3) has the boundary condition

$$\begin{aligned} \rho (q_E,t)=\frac{B(t,I_h(t),S_m(t))}{\gamma (t)}. \end{aligned}$$

To solve system (3) with this boundary condition, we introduce a new variable

$$\begin{aligned} \eta =h(t):=q_E+\int _0^t\gamma (s)\mathrm{d}s. \end{aligned}$$

Let $h^{-1}(\eta )$ be the inverse function of h(t), and define

$$\begin{aligned} {\hat{\rho }}(q,\eta )=\rho (q,h^{-1}(\eta )),\quad {\hat{d}}_m(\eta )= d_m(h^{-1}(\eta )),\quad \hat{\gamma }(\eta )=\gamma (h^{-1}(\eta )). \end{aligned}$$

In view of (3), we then have

$$\begin{aligned} \begin{aligned} \frac{\partial {\hat{\rho }}(q,\eta )}{\partial \eta } =-\frac{\partial {\hat{\rho }} (q,\eta )}{\partial q}-\frac{{\hat{d}}_m(\eta )}{{\hat{\gamma }}(\eta )}{\hat{\rho }} (q,\eta ). \end{aligned} \end{aligned}$$

(4)

This equation is identical in form to the standard von Foerster equation (see Nisbet and Gurney 1982). Let $V(s)={\hat{\rho }} (s+q-\eta ,s)$. It follows from (4) that

$$\begin{aligned} \frac{\mathrm{d}V(s)}{\mathrm{d}s}=-\frac{{\hat{d}}_m(s)}{{\hat{\gamma }}(s)}V(s). \end{aligned}$$

Since $\eta -(q-q_E)\le \eta$, we have

$$\begin{aligned} V(\eta )=V(\eta -(q-q_E))e^{-\int _{\eta -(q-q_E)}^{\eta } \frac{{\hat{d}}_m(s)}{{\hat{\gamma }}(s)}\mathrm{d}s}, \end{aligned}$$

and hence,

$$\begin{aligned} {\hat{\rho }} (q,\eta )={\hat{\rho }} (q_E,\eta -q+q_E)e^{-\int _{\eta -q+q_E}^{\eta }\frac{{\hat{d}}_m(s)}{{\hat{\gamma }}(s)}\mathrm{d}s}. \end{aligned}$$

Define $\tau (q,t)$ to be the time taken to grow from infection development level $q_E$ to level q by a mosquito who arrives at infection development level q at time t. Since $\frac{\mathrm{d}q}{\mathrm{d}t}=\gamma (t)$, it follows that

$$\begin{aligned} \begin{aligned} q-q_E=\int _{t-\tau (q,t)}^t\gamma (s)\mathrm{d}s, \end{aligned} \end{aligned}$$

(5)

and hence,

$$\begin{aligned} h(t-\tau (q,t))=h(t)-\int _{t-\tau (q,t)}^t\gamma (s)\mathrm{d}s =h(t)-(q-q_E). \end{aligned}$$

By a change of variable $s=h(\xi )$, we then see that

$$\begin{aligned} \int _{\eta -q+q_E}^\eta \frac{{\hat{d}}_m(s)}{{\hat{\gamma }}(s)}\mathrm{d}s=\int _{t-\tau (q,t)}^td_m(\xi )\mathrm{d}\xi . \end{aligned}$$

It follows that

$$\begin{aligned} \begin{aligned} \rho (q,t)=&{\hat{\rho }}(q, h(t))\\ =&\,\rho (q_E,t-\tau (q,t))e^{-\int _{t-\tau (q,t)}^t{d}_m(\xi )\mathrm{d}\xi }\\ =&\,\frac{B(t-\tau (q,t),I_h(t-\tau (q,t)),S_m(t-\tau (q,t)))}{\gamma (t-\tau (q,t))}e^{-\int _{t-\tau (q,t)}^td_m(\xi )\mathrm{d}\xi }. \end{aligned} \end{aligned}$$

Define $\tau (t):=\tau (q_I,t)$. We then obtain

$$\begin{aligned} \gamma (t)\rho (q_I,t)=B(t-\tau (t),I_h(t-\tau (t)),S_m(t-\tau (t)))\frac{\gamma (t)}{\gamma (t-\tau (t))}e^{-\int _{t-\tau (t)}^td_m(\xi )\mathrm{d}\xi }. \end{aligned}$$

Letting $q=q_I$ in (5), we have

$$\begin{aligned} \begin{aligned} q_I-q_E=\int _{t-\tau (t)}^t\gamma (s)\mathrm{d}s \end{aligned} \end{aligned}$$

(6)

Taking the derivative with respect to t on both sides of (6), we obtain

$$\begin{aligned} 1-\tau '(t)=\frac{\gamma (t)}{\gamma (t-\tau (t))}. \end{aligned}$$

Thus, there holds $1-\tau '(t)>0$. In virtue of (6), it easily follows that if $\gamma (t)$ is a periodic function, then so is $\tau (t)$ with the same period. Substituting $M(t)=\gamma (t)\rho (q_I,t)$ into system (2), we arrive at the following model system:

$$\begin{aligned} \frac{\mathrm{d}I_h(t)}{\mathrm{d}t}= & {} \, \frac{c\beta (t)l(H-I_h(t))}{pI_h(t)+l(H-I_h(t))}I_m(t)-(d_h+\rho )I_h(t),\nonumber \\ \frac{\mathrm{d}S_m(t)}{\mathrm{d}t}= & {} \,\mu (t)-B(t,I_h(t),S_m(t))-d_m(t)S_m(t),\nonumber \\ \frac{\mathrm{d}E_m(t)}{\mathrm{d}t}= & {} \,B(t,I_h(t),S_m(t))-d_m(t)E_m(t)\nonumber \\&-\,(1-\tau '(t))B(t-\tau (t),I_h(t-\tau (t)),S_m(t-\tau (t)))e^{-\int _{t-\tau (t)}^{t}d_m(\xi )\mathrm{d}\xi },\nonumber \\ \frac{\mathrm{d}I_m(t)}{\mathrm{d}t}= & {} \,(1-\tau '(t))B(t-\tau (t),I_h(t-\tau (t)),S_m(t-\tau (t)))e^{-\int _{t-\tau (t)}^{t}d_m(\xi )\mathrm{d}\xi }\nonumber \\&-\,d_m(t)I_m(t), \end{aligned}$$

(7)

where all constant parameters are positive, and $\mu (t)$, $\beta (t)$, $d_m(t)$, $\tau (t)$ are positive, continuous and $\omega$-periodic functions t for some $\omega >0$. The biological interpretations for parameters are listed in Table 1. It is easy to see that the function

$$\begin{aligned} a(t):=e^{-\int _{t-\tau (t)}^td_m(\xi )\mathrm{d}\xi } \end{aligned}$$

is also $\omega$-periodic. Thus, model (7) can be written as $u'(t)=F(t,u_t)$ with $F(t+\omega ,\phi )=F(t,\phi )$ (see the proof of Lemma 2), and hence, it is an $\omega$-periodic functional differential system. Note that the term $1-\tau '(t)$ is involved in the development rate from the $E_m$ state to the $I_m$ state, which is different from previous works with constant time delays [see, e.g., system (1) in Wang and Zhao (2017)].

Table 1 Biological interpretations for parameters of model (7)

3 Threshold Dynamics

In this section, we study the global dynamics of system (7). The basic reproduction ratio is a key threshold parameter providing information for disease risk and control (see, e.g., Diekmann et al. 1990; Driessche and Watmough 2002). There have been quite a few investigations on $R_0$ analysis for population models in a periodic environment (see, e.g., Bacaër and Ait Dads 2012; Bacaër and Guernaoui 2006; Inaba 2012; Thieme 2009; Wang and Zhao 2008; Zhao 2017 and the references therein). In what follows, we will use the theory recently developed in Zhao (2017) to derive the basic reproduction ratio $R_0$. Since the third equation of system (7) is decoupled from the other equations, it suffices to study the following system:

$$\begin{aligned} \frac{\mathrm{d}I_h(t)}{\mathrm{d}t}= & {} \frac{c\beta (t)l(H-I_h(t))}{pI_h(t)+l(H-I_h(t))}I_m(t)-(d_h+\rho )I_h(t),\nonumber \\ \frac{\mathrm{d}S_m(t)}{\mathrm{d}t}= & {} \mu (t)-B(t,I_h(t),S_m(t))-d_m(t)S_m(t),\nonumber \\ \frac{\mathrm{d}I_m(t)}{\mathrm{d}t}= & {} (1-\tau '(t))B(t-\tau (t),I_h(t-\tau (t)),S_m(t-\tau (t)))e^{-\int _{t-\tau (t)}^{t}d_m(\xi )\mathrm{d}\xi }\nonumber \\&\,&-d_m(t)I_m(t). \end{aligned}$$

(8)

It is easy to see that the scalar linear periodic equation

$$\begin{aligned} \frac{\mathrm{d}S_m(t)}{\mathrm{d}t} = \mu (t)-d_{m}(t)S_m(t) \end{aligned}$$

(9)

has a unique positive $\omega$-periodic solution

$$\begin{aligned} S_m^*(t)=\bigg [\int _0^t\mu (r)e^{\int _0^rd_m(s)\mathrm{d}s}\mathrm{d}r+ \frac{\int _0^{\omega }\mu (r)e^{\int _0^rd_m(s)\mathrm{d}s}\mathrm{d}r}{e^{\int _0^{\omega }d_m(s)\mathrm{d}s}-1}\bigg ] e^{-\int _0^td_m(s)\mathrm{d}s}, \end{aligned}$$

which is globally attractive in $\mathbb {R}$.

Linearizing system (8) at its disease-free periodic solution $(0,S_m^*(t),0)$, we then obtain the following system of periodic linear equations for the infective variables $I_h$ and $I_m$:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}I_h(t)}{\mathrm{d}t}&= -a_{11}(t)I_h(t)+a_{12}(t)I_m(t),\\ \frac{\mathrm{d}I_m(t)}{\mathrm{d}t}&= a_{21}(t)I_h(t-\tau (t))-a_{22}(t)I_m(t), \end{aligned} \end{aligned}$$

(10)

where $a_{11}(t)=d_h+\rho$, $a_{12}(t)=c\beta (t)$, $a_{22}(t)=d_m(t)$, and

$$\begin{aligned} a_{21}(t)=\frac{(1-\tau '(t))b\beta (t-\tau (t))pS_m^*(t-\tau (t))e^{-\int _{t-\tau (t)}^{t}d_m(\xi )\mathrm{d}\xi }}{lH}. \end{aligned}$$

Let $\hat{\tau }=\max _{0\le t\le \omega }\tau (t),\,\, C=C([-{\hat{\tau }},0],\mathbb {R}^2)$, $C^+=C([-{\hat{\tau }},0],\mathbb {R}_+^2).$ Then $(C,C^+)$ is an ordered Banach space equipped with the maximum norm and the positive cone $C^+$. For any given continuous function $v=(v_1,v_2): [-{\hat{\tau }},\sigma )\rightarrow \mathbb {R}^2$ with $\sigma >0$, we define $v_t\in C$ by

$$\begin{aligned} v_t(\theta )=(v_1(t+\theta ),v_2(t+\theta )), \quad \forall \theta \in [-{\hat{\tau }},0], \end{aligned}$$

for any $t\in [0,\sigma ).$ Let $F:\mathbb {R}\rightarrow \mathcal {L}(C,\mathbb {R}^2)$ be a map and V(t) be a continuous $2\times 2$ matrix function on $\mathbb {R}$ defined as follows:

$$\begin{aligned} F(t)\varphi =\left[ \begin{array}{cc}a_{12}(t)\varphi _2(0)\\ a_{21}(t)\varphi _1(-\tau (t))\end{array}\right] ,\quad V(t)=\left[ \begin{array}{cc}a_{11}(t)&{}0\\ 0&{}a_{22}(t)\end{array}\right] . \end{aligned}$$

Then the internal evolution of the infective compartments $I_h$ and $I_m$ can be expressed by

$$\begin{aligned} \frac{\mathrm{d}v(t)}{\mathrm{d}t}=-V(t)v(t). \end{aligned}$$

Let ${\varPhi }(t,s), t\ge s,$ be the evolution matrix of the above linear system. That is, ${\varPhi }(t,s)$ satisfies

$$\begin{aligned} \frac{\partial }{\partial t}{\varPhi }(t,s)=-V(t){\varPhi }(t,s),\quad \forall t\ge s, \end{aligned}$$

and

$$\begin{aligned} {\varPhi }(s,s)=I,\quad \forall s\in \mathbb {R}, \end{aligned}$$

where I is the $2\times 2$ identity matrix. It then easily follows that

$$\begin{aligned} {\varPhi }(t,s)=\left[ \begin{array}{cc}e^{-\int _s^ta_{11}(r)\mathrm{d}r}&{}0\\ 0&{}e^{-\int _s^ta_{22}(r)\mathrm{d}r}\end{array}\right] . \end{aligned}$$

Let $C_\omega$ be the ordered Banach space of all continuous and $\omega$-periodic functions from $\mathbb {R}$ to $\mathbb {R}^2$, which is equipped with the maximum norm and the positive cone $C_\omega ^+:=\{v \in C_\omega : v(t) \ge 0$ for all $t \in \mathbb {R}\}$.

Suppose that $v\in C_\omega$ is the initial distribution of infectious individuals. Then for any given $s\ge 0$, $F(t-s)v_{t-s}$ is the distribution of newly infectious individuals at time $t-s$, which is produced by the infectious individuals who were introduced over the time interval $[t-s-{\hat{\tau }},t-s]$. Then ${\varPhi }(t,t-s)F(t-s)v_{t-s}$ is the distribution of those infectious individuals who newly became infectious at time $t-s$ and remain in the infectious compartments at time t. It follows that

$$\begin{aligned} \int _0^\infty {\varPhi }(t,t-s)F(t-s)v_{t-s}\mathrm{d}s =\int _0^\infty {\varPhi }(t,t-s)F(t-s)v(t-s+\cdot )\mathrm{d}s \end{aligned}$$

is the distribution of accumulative new infections at time t produced by all those infectious individuals introduced at all previous time to t.

Define a linear operator $L : C_\omega \rightarrow C_\omega$ by

$$\begin{aligned}{}[Lv](t)=\int _{0}^{\infty }{\varPhi }(t,t-s)F(t-s) v(t-s+\cdot )\mathrm{d}s,\quad \forall t \in \mathbb {R},\quad v \in C_\omega . \end{aligned}$$

Following Zhao (2017), we define $R_0=r(L)$, the spectral radius of L. Let ${\hat{P}}(t)$ be the solution maps of system (10), that is, ${\hat{P}}(t)\varphi =u_t(\varphi ), t\ge 0,$ where $u(t,\varphi )$ is the unique solution of (10) with $u_0=\varphi \in C$. Then ${\hat{P}}:={\hat{P}}(\omega )$ is the Poincaré map associated with linear system (10). Let $r({\hat{P}})$ be the spectral radius of ${\hat{P}}$. By Zhao (2017, Theorem 2.1), we have the following result.

Lemma 1

$R_0-1$ has the same sign as $r({\hat{P}})-1$.

Let

$$\begin{aligned} W:=C([-\hat{\tau },0],[0,H])\times C([-\hat{\tau },0],\mathbb {R}_+)\times \mathbb {R_+}. \end{aligned}$$

Then we have the following preliminary result for system (8).

Lemma 2

For any $\varphi \in W$, system (8) has a unique nonnegative bounded solution $u(t,\varphi )$ on $[0,\infty )$ with $u_0=\varphi$, and $u_t(\varphi ):=(u_{1t}(\varphi ),u_{2t}(\varphi ),u_3(t,\varphi ))\in W$ for all $t\ge 0$.

Proof

For any $\varphi =(\varphi _1,\varphi _2,\varphi _3)\in W$, we define

$$\begin{aligned} {\widetilde{f}}(t,\varphi )= \left( \begin{array}{c} \frac{c\beta (t)l(H-\varphi _1(0))}{(p-l)\varphi _1(0)+lH}\varphi _3-(d_h+\rho ) \varphi _1(0)\\ \mu (t)-\frac{b\beta (t)p\varphi _1(0)}{(p-l)\varphi _1(0)+lH}\varphi _2(0)-d_m(t)\varphi _2(0)\\ -d_m(t)\varphi _3+(1-\tau '(t))\frac{b\beta (t-\tau (t))p \varphi _1(-\tau (t))\varphi _2(-\tau (t))}{(p-l)\varphi _1(-\tau (t))+lH}e^{-\int _{t-\tau (t)}^td_m(\xi )\mathrm{d}\xi } \end{array} \right) . \end{aligned}$$

Since ${\widetilde{f}}(t,\varphi )$ is continuous in $(t,\varphi )\in \mathbb {R}_+\times W$, and ${\widetilde{f}}(t,\varphi )$ is Lipschitz in $\varphi$ on each compact subset of W, it then follows that system (8) has a unique solution $u(t,\varphi )$ on its maximal interval $[0,\sigma _\varphi )$ of existence with $u_0=\varphi$ (see, e.g., Hale and Verduyn Lunel (1993, Theorems 2.2.1 and 2.2.3)).

Let $\varphi =(\varphi _1,\varphi _2,\varphi _3)\in W$ be given. If $\varphi _i(0)=0$ for some $i\in \{1,2\}$, then ${\widetilde{f}}_i(t,\varphi )\ge 0$. If $\varphi _3=0$, then ${\widetilde{f}}_3(t,\varphi )\ge 0$. If $\varphi _1(0)=H$, then ${\widetilde{f}}_1(t,\varphi )\le 0$. By Smith (1995, Theorem 5.2.1 and Remark 5.2.1), it follows that for any $\varphi \in W$, the unique solution $u(t,\varphi )$ of system (1) with $u_0=\varphi$ satisfies $u_t(\varphi )\in W$ for all $t\in [0,\sigma _\varphi )$.

Clearly, $0\le u_1(t,\varphi )\le H$ for all $t\in [0,\sigma _\varphi )$. In view of the second and third equations of system (8), we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}u_2(t)}{\mathrm{d}t}&\le \mu (t)-d_m(t)u_2(t), \\ \frac{\mathrm{d}u_3(t)}{\mathrm{d}t}&\le -d_m(t)u_3(t)+(1-\tau '(t))b\beta (t-\tau (t))u_2(t-\tau (t))e^{-\int _{t-\tau (t)}^td_m(\xi )\mathrm{d}\xi }, \end{aligned} \end{aligned}$$

for all $t\in [0,\sigma _\varphi )$. Thus, both $u_2(t)$ and $u_3(t)$ are bounded on $[0,\sigma _\varphi )$, and hence, Hale and Verduyn Lunel (1993, Theorem 2.3.1) implies that $\sigma _\varphi =\infty .$ $\square$

For any given $\varphi \in W,$ let $u(t,\varphi )=(u_1(t),u_2(t),u_3(t))$ be the unique solution of system (8) satisfying $u_0=\varphi$. Let

$$\begin{aligned} w(t):=e^{-\int _{t-\tau (t)}^t d_{m}(s)\mathrm{d}s}u_2(t-\tau (t))+u_3(t). \end{aligned}$$

Then $(u_1(t),u_3(t))$ can be regarded as a solution of the following nonautonomous system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}u_1(t)}{\mathrm{d}t}&= \frac{c\beta (t) l(H-u_1(t) )}{(p-l)u_1(t)+lH}u_3(t)-(d_{h} +\rho )u_1(t),\\ \frac{\mathrm{d}u_3(t)}{\mathrm{d}t}&= -d_{m}(t)u_3(t)+ (1-\tau '(t))\frac{b\beta (t-\tau (t))pu_1(t-\tau (t))}{(p-l)u_1(t-\tau (t))+lH}[w(t)-u_3(t)]. \end{aligned} \end{aligned}$$

(11)

It easily follows that w(t) satisfies

$$\begin{aligned} \frac{\mathrm{d}w(t)}{\mathrm{d}t}=-d_m(t)w(t)+\mu (t-\tau (t))(1-\tau '(t))e^{-\int _{t-\tau (t)}^td_m(s)\mathrm{d}s}, \end{aligned}$$

(12)

and system (12) has a unique positive $\omega$-periodic solution

$$\begin{aligned} K(t):=e^{-\int _{t-\tau (t)}^t d_{m}(s)\mathrm{d}s} S_m^*(t-\tau (t)), \end{aligned}$$

which is globally attractive in $\mathbb {R}$. Thus, system (11) has a limiting system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}v_1(t)}{\mathrm{d}t}&= \frac{c\beta (t) l(H-v_1(t) )}{(p-l)v_1(t)+lH}v_2(t)-(d_{h} +\rho )v_1(t),\\ \frac{\mathrm{d}v_2(t)}{\mathrm{d}t}&= -d_{m}(t)v_2(t)+ (1-\tau '(t))\frac{b\beta (t-\tau (t))pv_1(t-\tau (t))}{(p-l)v_1(t-\tau (t))+lH}(K(t)-v_2(t)). \end{aligned} \end{aligned}$$

(13)

Note that $z(t)=(u_1(t),u_3(t), w(t))$ satisfies the following $\omega$-periodic system:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}u_1(t)}{\mathrm{d}t}&= \frac{c\beta (t) l(H-u_1(t) )}{(p-l)u_1(t)+lH}u_3(t)-(d_{h} +\rho )u_1(t),\\ \frac{\mathrm{d}u_3(t)}{\mathrm{d}t}&= -d_{m}(t)u_3(t)+ (1-\tau '(t))\frac{b\beta (t-\tau (t))pu_1(t-\tau (t))}{(p-l)u_1(t-\tau (t))+lH}(w(t)-u_3(t)),\\ \frac{\mathrm{d}w(t)}{\mathrm{d}t}&= -d_m(t)w(t)+\mu (t-\tau (t))(1-\tau '(t))e^{-\int _{t-\tau (t)}^td_m(s)\mathrm{d}s}. \end{aligned} \end{aligned}$$

(14)

Clearly, system (8) is equivalent to (14). It suffices to study system (14). Let

$$\begin{aligned} {\varOmega }:=C([-{\hat{\tau }},0],[0,H])\times \mathbb {R}^2_+. \end{aligned}$$

We then have the following preliminary result for system (14).

Lemma 3

For any $\varphi \in {\varOmega }$, system (14) has a unique solution $z(t,\varphi )$ with $z_0=\varphi$, and $z_t(\varphi ):=(z_{1t}(\varphi ),z_2(t,\varphi ),z_3(t,\varphi ))\in {\varOmega }$ for all $t\ge 0$.

Proof

For any $\varphi \in {\varOmega }$, define

$$\begin{aligned} \hat{f}(t,\varphi )= \left( \begin{array}{c} \frac{c\beta (t)l(H-\varphi _1(0))}{(p-l)\varphi _1(0)+lH}\varphi _2-(d_h+\rho ) \varphi _1(0)\\ -\,d_m(t)\varphi _2+(1-\tau '(t))\frac{b\beta (t-\tau (t))p\varphi _1(-\tau (t))}{(p-l)\varphi _1(-\tau (t))+lH}(\varphi _3-\varphi _2)\\ -\,d_m(t)\varphi _3+\mu (t-\tau (t))(1-\tau '(t))e^{-\int _{t-\tau (t)}^td_m(s)\mathrm{d}s} \end{array} \right) . \end{aligned}$$

Since $\hat{f}(t,\varphi )$ is continuous in $(t,\varphi )\in \mathbb {R}\times {\varOmega }$, and $\hat{f}(t,\varphi )$ is Lipschitz in $\varphi$ on each compact subset of ${\varOmega }$, it then follows that system (14) has a unique solution $z(t,\varphi )$ with $z_0=\varphi$ on its maximal interval $[0,\sigma _\varphi )$ of existence.

Let $\varphi =(\varphi _1,\varphi _2,\varphi _3)\in {\varOmega }$ be given. If $\varphi _1(0)=0$, then $\hat{f}_1(t,\varphi )\ge 0$. If $\varphi _i=0$ for some $i=2, 3$, then $\hat{f}_i(t,\varphi )\ge 0$. If $\varphi _1(0)=H$, then $\hat{f}_1(t,\varphi )\le 0$. By Smith (1995, Theorem 5.2.1 and Remark 5.2.1), it follows that for any $\varphi \in {\varOmega }$, the unique solution $z(t,\varphi )$ of system (14) with $u_0=\varphi$ satisfies $z_t(\varphi )\in {\varOmega }$ for all $t\in [0,\sigma _\varphi )$.

Since system (12) has a globally attractive periodic solution K(t), it follows that $z_3(t,\varphi )=w(t)$ is bounded on $[0,\sigma _\varphi )$, that is, there exists $B>0$ such that $w(t)\le B$ for all $t\in [0,\sigma _\varphi ).$ In view of the second equation of system (14), we have

$$\begin{aligned} \frac{\mathrm{d}u_3(t)}{\mathrm{d}t}\le -d_m(t)u_3(t)+b(1-\tau '(t))\beta (t-\tau (t))B,\quad \forall t\in [0,\sigma _\varphi ). \end{aligned}$$

Hence, $z_2(t,\varphi )=u_3(t)$ is also bounded on $[0,\sigma _\varphi )$. Then Hale and Verduyn Lunel (1993, Theorem 2.3.1) implies that $\sigma _\varphi =\infty .$ $\square$

Let

$$\begin{aligned} Y(t):=C([-{\hat{\tau }},0],[0,H])\times [0,K(t)],\quad t\ge 0. \end{aligned}$$

Then we have the following result for system (13).

Lemma 4

For any $\varphi \in Y(0)$, system (13) has a unique solution $w(t,\varphi )$ with $w_0=\varphi$, and $w_t(\varphi ):=(w_{1t}(\varphi ),w_2(t,\varphi ))\in Y(t)$ for all $t\ge 0$.

Proof

For any $\varphi \in Y(0)$, define

$$\begin{aligned} f(t,\varphi )= \left( \begin{array}{c} \frac{c\beta (t)l(H-\varphi _1(0))}{(p-l)\varphi _1(0)+lH}\varphi _2-(d_h+\rho ) \varphi _1(0)\\ -d_m(t)\varphi _2+(1-\tau '(t))\frac{b\beta (t-\tau (t))p\varphi _1(-\tau (t))}{(p-l)\varphi _1(-\tau (t))+lH}(K(t)-\varphi _2) \end{array} \right) . \end{aligned}$$

Since f is continuous in $(t,\varphi )\in \mathbb {R}\times Y(0)$, and f is Lipschitz in $\varphi$ on each compact subset of Y(0), it then follows that system (13) has a unique solution $w(t,\varphi )$ with $w_0=\varphi$ on its maximal interval $[0,\sigma _\varphi )$ of existence.

Let $\varphi =(\varphi _1,\varphi _2)\in Y(0)$ be given. If $\varphi _1(0)=0$, then $f_1(t,\varphi )\ge 0$. If $\varphi _2=0$, then $f_2(t,\varphi )\ge 0$. If $\varphi _1(0)=H$, then $f_1(t,\varphi )\le 0$. By Smith (1995, Theorem 5.2.1 and Remark 5.2.1), it follows that the unique solution $w(t,\varphi )$ of system (13) with $w_0=\varphi$ satisfies $w_t(\varphi )\in C([-{\hat{\tau }},0], [0,H])\times \mathbb {R_+}$.

It remains to prove that $w_2(t)\le K(t)$ for all $t\in [0,\sigma _\varphi )$. Suppose this does not hold. Then there exists $t_0\in [0,\sigma _\varphi )$ and $\epsilon _0>0$ such that

$$\begin{aligned} w_2(t_0)=K(t_0)\quad \text {and}\quad w_2(t)>K(t), \quad \forall t\in (t_0,t_0+\epsilon _0). \end{aligned}$$

Since

$$\begin{aligned} \frac{\mathrm{d}w_2(t_0)}{\mathrm{d}t}=-d_m(t_0)w_2(t_0)= -d_m(t_0)K(t_0)<\frac{\mathrm{d}K(t_0)}{\mathrm{d}t}, \end{aligned}$$

there exists $\epsilon _1\in (0,\epsilon _0)$ such that $w_2(t)\le K(t)$ for all $t\in (t_0,t_0+\epsilon _1)$, which is a contradiction. This proves that $w_t(\varphi )\in Y(t)$ for all $t\in [0,\sigma _\varphi ).$ Clearly, $w_t(\varphi )$ is bounded on $[0,\sigma _\varphi ),$ and hence, Hale and Verduyn Lunel (1993, Theorem 2.3.1) implies that $\sigma _\varphi =\infty .$ $\square$

Let

$$\begin{aligned} G(t):=C([-\tau (0),0],[0,H])\times [0,K(t)],\quad t\ge 0. \end{aligned}$$

Lemma 5

For any $\varphi \in G(0)$, system (13) has a unique solution $v(t,\varphi )$ with $v_0=\varphi$, and $v_t(\varphi ):=(v_{1t}(\varphi ),v_2(t,\varphi ))\in G(t)$ for all $t\ge 0$.

Proof

Let ${\bar{\tau }}=\min _{t\in [0,\omega ]}\tau (t)$. For any $t\in [0,{\bar{\tau }}]$, since $t-\tau (t)$ is strictly increasing in t, we have

$$\begin{aligned} -\tau (0)=0-\tau (0)\le t-\tau (t)\le {\bar{\tau }}-\tau (\bar{\tau })\le {\bar{\tau }}-{\bar{\tau }}=0, \end{aligned}$$

and hence,

$$\begin{aligned} v_1(t-\tau (t))=\varphi _1(t-\tau (t)). \end{aligned}$$

Therefore, we have the following ordinary differential equations for $t\in [0,\bar{\tau }]$:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}v_1(t)}{\mathrm{d}t}&= \frac{c\beta (t) l(H-v_1(t))}{(p-l)v_1(t)+lH}v_2(t)-(d_{h} +\rho )v_1(t),\\ \frac{\mathrm{d}v_2(t)}{\mathrm{d}t}&= -d_{m}(t)v_2(t)+ (1-\tau '(t))\frac{b\beta (t-\tau (t))p\varphi _1(t-\tau (t))}{(p-l)\varphi _1(t-\tau (t))+lH}(K(t)-v_2(t)). \end{aligned} \end{aligned}$$

Given $\varphi \in G(0)$, the solution $(v_1(t),v_2(t))$ of the above system exists for $t\in [0,{\bar{\tau }}]$. In other words, we have obtained values of $\psi _1(\theta )=v_1(\theta )$ for $\theta \in [-\tau (0),{\bar{\tau }}]$ and $\psi _2(\theta )=v_2(\theta )$ for $\theta \in [0,{\bar{\tau }}]$. It is easy to see that $v_1(t)\le H$ and $v_2(t)\le K(t)$ for all $t\in [0,\bar{\tau }]$.

For any $t\in [{\bar{\tau }},2\bar{\tau }]$, we have

$$\begin{aligned} -\tau (0)=0-\tau (0)\le \bar{\tau }-\tau (\bar{\tau })\le t-\tau (t)\le 2\bar{\tau }-\tau (2\bar{\tau })\le 2\bar{\tau }-\bar{\tau }=\bar{\tau }, \end{aligned}$$

and hence, $v_1(t-\tau (t))=\psi _1(t-\tau (t))$. Solving the following system of ordinary differential equations for $t\in [{\bar{\tau }},2\bar{\tau }]$ with $v_1({\bar{\tau }})=\psi _1(\bar{\tau })$ and $v_2(\bar{\tau })=\psi _2(\bar{\tau })$:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}v_1(t)}{\mathrm{d}t}&= \frac{c\beta (t) l(H-v_1(t))}{(p-l)v_1(t)+lH}v_2(t)-(d_{h} +\rho )v_1(t),\\ \frac{\mathrm{d}v_2(t)}{\mathrm{d}t}&= -d_{m}(t)v_2(t)+ (1-\tau '(t))\frac{b\beta (t-\tau (t))p\psi _1(t-\tau (t))}{(p-l)\psi _1(t-\tau (t))+lH}(K(t)-v_2(t)). \end{aligned} \end{aligned}$$

We then get the solution $(v_1(t),v_2(t))$ on $[\bar{\tau },2\bar{\tau }]$. We also have $v_1(t)\le H$ and $v_2(t)\le K(t)$ for all $t\in [\bar{\tau },2{\bar{\tau }}]$. Repeating this procedure for $t\in [2\bar{\tau },3\bar{\tau }]$, $[3\bar{\tau },4\bar{\tau }]$,..., it then follows that for any $\varphi \in G(0)$, system (13) has a unique solution $v(t,\varphi )$ with $v_0=\varphi$, and $v_t(\varphi ):=(v_{1t}(\varphi ),v_2(t,\varphi ))\in G(t)$ for all $t\ge 0$. $\square$

Remark 1

By the uniqueness of solutions in Lemmas 4 and 5, it follows that for any $\psi \in Y(0)$ and $\phi \in G(0)$ with $\psi _1(\theta )=\phi _1(\theta )$ for all $\theta \in [-\tau (0),0]$ and $\psi _2=\phi _2$, we have $w(t,\psi )=v(t,\phi )$ for all $t\ge 0$, where $w(t,\psi )$ and $v(t,\phi )$ are solutions of system (13) satisfying $w_0=\psi$ and $v_0=\phi$, respectively. Similarly, we define

$$\begin{aligned} {\varPi }:=C([-\tau (0),0],[0,H])\times \mathbb {R}_+^2, \end{aligned}$$

and

$$\begin{aligned} {\varPsi }:=C([-\tau (0),0],[0,H])\times C([-\tau (0),0],\mathbb {R}_+)\times \mathbb {R}_+. \end{aligned}$$

For any $\psi \in {\varOmega }$ and ${\phi }\in {\varPi }$ with ${\psi }_1(\theta )={\phi }_1(\theta )$ for all $\theta \in [-\tau (0),0]$ and ${\psi }_2={\phi }_2$, ${\psi }_3={\phi }_3$, we have $z(t,{\psi })={\tilde{z}}(t,{\phi })$ for all $t\ge 0$, where $z(t,{\psi })$ and ${\tilde{z}}(t,{\phi })$ are solutions of system (14) satisfying $z_0={\psi }$ and ${\tilde{z}}_0={\phi }$, respectively. It follows that ${\varPi }$ is positively invariant for system (14). For any $\psi \in W$ and ${\phi }\in {\varPsi }$ with ${\psi }_1(\theta )={\phi }_1(\theta ), {\psi }_2(\theta )={\phi }_2(\theta )$ for all $\theta \in [-\tau (0),0]$ and ${\psi }_3={\phi }_3$, we have $u(t,{\psi })={\tilde{u}}(t,{\phi })$ for all $t\ge 0$, where $u(t,{\psi })$ and ${\tilde{u}}(t,{\phi })$ are solutions of system (8) satisfying $u_0={\psi }$ and ${\tilde{u}}_0={\phi }$, respectively. It then follows that ${\varPsi }$ is positively invariant for system (8).

Let S(t) be the solution maps of system (13), that is, $S(t)\varphi =v_t(\varphi )$, $t\ge 0$, where $v(t,\varphi )$ is the unique solution of system (13) with $v_0=\varphi \in G(0)$. By similar arguments to those in Lou and Zhao (2017, Lemma 3.5), we have the following result.

Lemma 6

$S(t): G(0)\rightarrow G(t)$ is an $\omega$-periodic semiflow in the sense that (i) $S(0)=I$; (ii) $S(t+\omega )=S(t)\circ S(\omega )$ for all $t\ge 0$; (iii) $S(t)\varphi$ is continuous in $(t,\varphi )\in [0,\infty )\times G(0)$.

Note that the linearized system of (13) at (0, 0) is

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}v_1(t)}{\mathrm{d}t}&=-(d_h+\rho )v_1(t)+c\beta (t)v_2(t),\\ \frac{\mathrm{d}v_2(t)}{\mathrm{d}t}&=\frac{(1-\tau '(t))b\beta (t-\tau (t))pK(t)}{lH}v_1(t-\tau (t))-d_m(t)v_2(t). \end{aligned} \end{aligned}$$

(15)

Let P be the Poincaré map of the linear system (15) on the space $C([-\tau (0)$, 0], $\mathbb {R})\times \mathbb {R}$, and r(P) be its spectral radius. Then we have the following threshold type result for system (13).

Lemma 7

The following statements are valid:

• (i) If $r(P)\le 1$, then $v^*(t)=(0,0)$ is globally asymptotically stable for system (13) in G(0).

• (ii) If $r(P)>1$, then system (13) admits a unique positive $\omega$-periodic solution ${\tilde{v}}(t)=({\tilde{v}}_1(t),{\tilde{v}}_2(t))$ which is globally asymptotically stable for system (13) in $G(0){\setminus }\{0\}$.

Proof

It follows from Remark 1 that S(t) maps G(0) into G(t), and $S:=S(\omega ): G(0)\rightarrow G(\omega )=G(0)$ is the Poincaré map associated with system (13). By the continuity and differentiability of solutions with respect to initial values, it follows that S is differentiable at zero and the Frechét derivative $DS(0)=P$.

For any given $\varphi , \psi \in G(0)$ with $\varphi \ge \psi$, let ${\bar{v}}(t)=v(t,\varphi )$ and $v(t)=v(t,\psi )$ be the unique solutions of system (13) with $v_0=\varphi$ and $v_0=\psi$, respectively. Let ${\bar{\tau }}=\min _{t\in [0,\omega ]}\tau (t).$ Define

$$\begin{aligned} A(t)=:\frac{{\bar{v}}_1(t-\tau (t))}{(p-l){\bar{v}}_1(t-\tau (t))+lH},\quad B(t):=\frac{ v_1(t-\tau (t))}{(p-l) v_1(t-\tau (t))+lH}. \end{aligned}$$

Since

$$\begin{aligned} -\tau (0)=0-\tau (0)\le t-\tau (t)\le \bar{\tau }-\tau (\bar{\tau })\le \bar{\tau }-\bar{\tau }=0,\quad \forall t\in [0,\bar{\tau }], \end{aligned}$$

we have

$$\begin{aligned} {\bar{v}}_1(t-\tau (t))=\varphi _1(t-\tau (t))\quad \text {and}\quad v_1(t-\tau (t))=\psi _1(t-\tau (t)),\quad \forall t\in [0,\bar{\tau }], \end{aligned}$$

and hence, $A(t)\ge B(t)$ for all $t\in [0,{\bar{\tau }}]$. In view of ${\bar{v}}(0)=\varphi (0)\ge \psi (0)=v(0)$, the comparison theorem for cooperative ordinary differential systems implies that ${\bar{v}}(t)\ge v(t)$ for all $t\in [0,{\bar{\tau }}].$

Repeating this procedure for $t\in [\bar{\tau },2\bar{\tau }], [2\bar{\tau },3\bar{\tau }],...$, it follows that $v(t,\varphi )\ge v(t,\psi )$ for all $t\in [0,\infty )$. This implies that $S(t): G(0)\rightarrow G(t)$ is monotone for each $t\ge 0$. Next we show that the solution map S(t) is eventually strongly monotone. Let $\varphi >\psi$ and denote $v(t,\varphi )=({\bar{y}}_1(t), {\bar{y}}_2(t))$, $v(t,\psi )=(y_1(t),y_2(t))$.

Claim 1

There exists $t_0\in [0,\bar{\tau }]$ such that ${\bar{y}}_2(t)>y_2(t)$ for all $t\ge t_0$.

We first prove that ${\bar{y}}_2(t_0)>y_2(t_0)$ for some $t_0\in [0,{\bar{\tau }}]$. Otherwise, we have ${\bar{y}}_2(t)=y_2(t)$ for all $t\in [0,\bar{\tau }]$, and hence, $\frac{\mathrm{d}{\bar{y}}_2(t)}{\mathrm{d}t}=\frac{\mathrm{d}y_2(t)}{\mathrm{d}t}$ for all $t\in (0,\bar{\tau }).$ Thus, we have

$$\begin{aligned} \begin{aligned} \left[ \frac{b\beta (t-\tau (t))p{\bar{y}}_1(t-\tau (t))}{(p-l){\bar{y}}_1(t-\tau (t))+lH}-\frac{b\beta (t-\tau (t))py_1(t-\tau (t))}{(p-l)y_1(t-\tau (t))+lH}\right] (1-\tau '(t))(K(t)-y_2(t))=0, \forall t\in [0,\bar{\tau }]. \end{aligned} \end{aligned}$$

(16)

Since $\varphi >\psi$ and $\varphi _2={\bar{y}}_2(0)=y_2(0)=\psi _2$, we have $\varphi _1>\psi _1$. Then there exists an open interval $(a,b)\subset [-\tau (0),0]$ such that $\varphi _1(\theta )>\psi _1(\theta )$ for all $\theta \in (a,b)$. Let $h(t)=t-\tau (t)$. Since $h'(t)>0$, the inverse function $h^{-1}(t)$ exists. It follows from (16) that $y_2(t)=K(t)$ for all $t\in (h^{-1}(a), h^{-1}(b))$, and hence,

$$\begin{aligned} \frac{\mathrm{d}K(t)}{\mathrm{d}t}=\frac{\mathrm{d}y_2(t)}{\mathrm{d}t}=-d_m(t)K(t),\quad \forall t\in (h^{-1}(a), h^{-1}(b)), \end{aligned}$$

which contradicts the fact that

$$\begin{aligned} \frac{\mathrm{d}K(t)}{\mathrm{d}t}=-d_m(t)K(t)+\mu (t-\tau (t))(1-\tau '(t))e^{-\int _{t-\tau (t)}^td_m(s)\mathrm{d}s}. \end{aligned}$$

Let

$$\begin{aligned} g_1(t,y):=-d_m(t)y+(1-\tau '(t))\frac{b\beta (t-\tau (t))py_1(t-\tau (t))}{(p-l)y_1(t-\tau (t))+lH}(K(t)-y). \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{y}}_2(t)}{\mathrm{d}t}&=-d_m(t){\bar{y}}_2(t) +(1-\tau '(t))\frac{b\beta (t-\tau (t)) p{\bar{y}}_1(t-\tau (t))}{(p-l){\bar{y}}_1(t-\tau (t))+lH}(K(t)-{\bar{y}}_2(t))\\&\ge -d_m(t){\bar{y}}_2(t) +(1-\tau '(t))\frac{b\beta (t-\tau (t)) py_1(t-\tau (t))}{(p-l)y_1(t-\tau (t))+lH}(K(t)-{\bar{y}}_2(t))\\&= g_1(t,{\bar{y}}_2(t)), \end{aligned} \end{aligned}$$

we have

$$\begin{aligned} \frac{\mathrm{d}{\bar{y}}_2(t)}{\mathrm{d}t}-g_1(t,{\bar{y}}_2(t))\ge 0=\frac{\mathrm{d}y_2(t)}{\mathrm{d}t}-g_1(t,y_2(t)),\, \, \forall t\ge t_0. \end{aligned}$$

Since ${\bar{y}}_2(t_0)>y_2(t_0)$, the comparison theorem for ordinary differential equations (see Walter (1997, Theorem 4)) implies that ${\bar{y}}_2(t)>y_2(t)$ for all $t\ge t_0$.

Claim 2

${\bar{y}}_1(t)>y_1(t)$ for all $t>t_0$.

We first prove that for any $\epsilon >0$, there exists an open interval $(c,d)\subset [t_0,t_0+\epsilon ]$ such that $H>{\bar{y}}_1(t)$ for all $t\in (c,d)$. Otherwise, there exists $\epsilon _0>0$ such that $H={\bar{y}}_1(t)$ for all $t\in (t_0,t_0+\epsilon _0).$ It then follows from the first equation of system (13) that $0=-(d_h+\rho )H$, which is a contradiction. Let

$$\begin{aligned} f_1(t,y):=\frac{c\beta (t)l(H-y)}{(p-l)y+lH}y_2(t)-(d_h+\rho )y. \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\bar{y}}_1(t)}{\mathrm{d}t}&= \frac{c\beta (t)l(H-{\bar{y}}_1(t))}{(p-l){\bar{y}}_1(t)+lH}{\bar{y}}_2(t)-(d_h+\rho ){\bar{y}}_1(t)\\&> \frac{c\beta (t)l(H-{\bar{y}}_1(t))}{(p-l){\bar{y}}_1(t)+lH}y_2(t)-(d_h+\rho ){\bar{y}}_1(t)\\&= f_1(t,{\bar{y}}_1(t)),\quad \forall t\in (c,d), \end{aligned} \end{aligned}$$

and hence,

$$\begin{aligned} \frac{\mathrm{d}{\bar{y}}_1(t)}{\mathrm{d}t}-f_1(t,{\bar{y}}_1(t))>0=\frac{\mathrm{d}y_1(t)}{\mathrm{d}t}-f_1(t,y_1(t)),\quad \forall t\in (c,d). \end{aligned}$$

Since ${\bar{y}}_1(t_0)\ge y_1(t_0)$, it follows from Walter (1997, Theorem 4) that ${\bar{y}}_1(t)>y_1(t)$ for all $t>t_0$.

In view of Claims 1 and 2, we obtain

$$\begin{aligned} ({\bar{y}}_1(t),{\bar{y}}_2(t))\gg (y_1(t),y_2(t)),\quad \forall t>t_0. \end{aligned}$$

Since $t_0\in [0,{\bar{\tau }}]$, it follows that

$$\begin{aligned} ({\bar{y}}_{1t},{\bar{y}}_2(t))\gg (y_{1t},y_2(t)),\quad \forall t>{\bar{\tau }}+\tau (0), \end{aligned}$$

that is, $v_t(\varphi )\gg v_t(\psi )$ for all $t>{\bar{\tau }}+\tau (0)$. This shows that $S(t): G(0)\rightarrow G(t)$ is strongly monotone for any $t>{\bar{\tau }}+\tau (0)$.

For any given $\varphi \gg 0$ in G(0) and $\lambda \in (0,1)$, let $v(t,\varphi )$ and $v(t,\lambda \varphi )$ be the solutions of system (13) satisfying $v_0=\varphi$ and $v_0=\lambda \varphi$, respectively. Denote $x(t)=\lambda v(t,\varphi )$ and $z(t)=v(t,\lambda \varphi )$. As in the proof of Lemma 5, by the comparison theorem for ordinary differential equations, we have $x(t)>0$ and $z(t)>0$ for all $t\ge 0$. Moreover, for all $\theta \in [-\tau (0),0]$, we have

$$\begin{aligned} x_1(\theta )=\lambda \varphi _1(\theta )=z_1(\theta ),\quad x_2(0)=\lambda \varphi _2=z_2(0). \end{aligned}$$

For any $t\in [0,\bar{\tau }]$, we have $-\tau (0)\le t-\tau (t)\le \bar{\tau }-\bar{\tau }=0$, and hence, $z_1(t-\tau (t))=x_1(t-\tau (t))=\lambda \varphi _1(t-\tau (t))$. Thus, x(t) satisfies the following differential inequality:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}x_1(t)}{\mathrm{d}t}&< \frac{c\beta (t) l(H-x_1(t))}{(p-l)x_1(t)+lH}x_2(t)-(d_{h} +\rho )x_1(t),\\ \frac{\mathrm{d}x_2(t)}{\mathrm{d}t}&< -d_{m}(t)x_2(t)+ (1-\tau '(t))\frac{b\beta (t-\tau (t))pz_1(t-\tau (t))}{(p-l)z_1(t-\tau (t))+lH}(K(t)-x_2(t)), \end{aligned} \end{aligned}$$

for all $t\in [0,\bar{\tau }]$. Since $x(0)=z(0)$, it follows from the comparison theorem for ordinary differential systems (see Walter (1997, Theorem 4)) that $x_1(t)<z_1(t)$ and $x_2(t)<z_2(t)$ for all $t\in (0,\bar{\tau }]$. By similar arguments for any interval $(n\bar{\tau },(n+1)\bar{\tau }]$, $n=1,2,3,\cdots$, we can get $x_1(t)<z_1(t)$ and $x_2(t)<z_2(t)$ for all $t>0$, that is, $v(t,\lambda \varphi )\gg \lambda v(t,\varphi )$ for all $t>0$. Therefore, $v_t(\lambda \varphi )\gg \lambda v_t(\varphi )$ for all $t>\tau (0)$.

Now we fix an integer $n_0$ such that $n_0\omega >{\bar{\tau }}+\tau (0)$. It then follows that $S^{n_0}=S(n_0\omega ): G(0)\rightarrow G(0)$ is strongly monotone and strictly subhomogeneous. Note that $DS^{n_0}(0)=DS(n_0\omega )(0)=P(n_0\omega )= P^{n_0}(\omega )=P^{n_0},$ and $r(P^{n_0})=(r(P))^{n_0}.$ By Zhao (2003, Theorem 2.3.4 and Lemma 2.2.1) as applied to $S^{n_0}$, we have the following threshold type result:

• (a) If $r(P)\le 1,$ then $v^*(t)=(0,0)$ is globally asymptotically stable for system (13) in G(0).

• (b) If $r(P)>1$, then there exists a unique positive $n_0\omega$-periodic solution ${\tilde{v}}(t)= ({\tilde{v}}_1(t),{\tilde{v}}_2(t))$, which is globally asymptotically stable for system (13) in $G(0){\setminus }\{0\}.$

It remains to prove that ${\tilde{v}}(t)$ is also an $\omega$-periodic solution of system (13). Let ${\tilde{v}}(t)=v(t,\psi ).$ By the properties of periodic semiflows, we have $S^{n_0}(S(\psi ))=S(S^{n_0}(\psi ))=S(\psi )$, which implies that $S(\psi )$ is also a positive fixed point of $S^{n_0}$. By the uniqueness of the positive fixed point of $S^{n_0}$, it follows that $S(\psi )=\psi$. So ${\tilde{v}}(t)$ is an $\omega$-periodic solution of system (13). $\square$

Next, we use the theory of chain transitive sets (see Hirsch et al. (2001) and Zhao (2003, Section 1.2)) to lift the threshold type result for system (13) to system (14).

Theorem 1

The following statements are valid:

• (i) If $r(P)\le 1$, then the periodic solution (0, 0, K(t)) is globally asymptotically stable for system (14) in ${\varPi }$;

• (ii) If $r(P)>1$, then system (14) admits a unique positive $\omega$-periodic solution $({\tilde{v}}_1(t)$, ${\tilde{v}}_2(t)$, K(t)), which is globally asymptotically stable for system (14) in ${\varPi }{\setminus } (\{0\}\times \{0\}\times \mathbb {R}_+)$.

Proof

Let ${\tilde{P}}(t)$ be the solution maps of system (14), that is, ${\tilde{P}}(t)\varphi =z_t(\varphi ), t\ge 0,$ where $z(t,\varphi )$ is the unique solution of system (14) with $z_0=\varphi \in {\varPi }.$ Then ${\tilde{P}}:={\tilde{P}}(\omega )$ is the Poincaré map of system (14). Then $\{{\tilde{P}}^n\}_{n\ge 0}$ defines a discrete-time dynamical system on ${\varPi }$. For any given ${\bar{\varphi }}\in {\varPi },$ let ${\bar{z}}(t)=(u_1(t),u_3(t),w(t))$ be the unique solution of system (14) with ${\bar{z}}_0= {\bar{\varphi }}$ and let $\omega ({\bar{\varphi }})$ be the omega limit set of the orbit $\{{\tilde{P}}^n({\bar{\varphi }})\}_{n\ge 0}$ for the discrete-time semiflow ${\tilde{P}}^n$.

Since equation (12) has a unique positive $\omega$-periodic solution K(t), which is globally attractive, we have $\lim _{t\rightarrow \infty }(w(t)-K(t))=0$, and hence, $\lim _{n\rightarrow \infty }$ $({\tilde{P}}^n({\bar{\varphi }}))_3$ $=K(0)$. Thus, there exists a subset $\tilde{\omega }$ of $C([-\tau (0),0],[0,H])\times \mathbb {R}_+$ such that $\omega ({\bar{\varphi }})=\tilde{\omega }\times \{K(0)\}.$

For any $\phi =(\phi _1,\phi _2,\phi _3)\in \omega ({\bar{\varphi }}),$ there exists a sequence $n_k\rightarrow \infty$ such that ${\tilde{P}}^{n_k}({\bar{\varphi }})\rightarrow \phi$, as $k\rightarrow \infty .$ Since $u_{1n_k\omega }\le H$ and $u_3(n_k\omega )\le w(n_k\omega ),$ letting $n_k\rightarrow \infty ,$ we obtain $0\le \phi _1\le H, 0\le \phi _2\le K(0).$ It then follows that $\tilde{\omega }\subseteq C([-\tau (0),0],[0,H])\times [0,K(0)]=G(0).$ It is easy to see that

$$\begin{aligned} {\tilde{P}}^n|_{\omega ({\bar{\varphi }})}(\phi _1,\phi _2,K(0))=S^n|_{\tilde{\omega } }(\phi _1,\phi _2)\times \{K(0)\},\quad \forall (\phi _1,\phi _2)\in \tilde{\omega },\quad n\ge 0, \end{aligned}$$

where S is the Poincaré map associated with system (13). By Zhao (2003, Lemma 1.2.1), $\omega ({\bar{\varphi }})$ is an internally chain transitive set for ${\tilde{P}}^n$ on ${\varPi }$. It then follows that $\tilde{\omega }$ is an internally chain transitive set for $S^n$ on G(0).

In the case where $r(P)\le 1$, it follows from Lemma 7 (i) that (0, 0) is globally asymptotically stable for $S^n$ in G(0). By Zhao (2003, Theorem 1.2.1), we have $\tilde{\omega }=\{(0,0)\}$, and hence, $\omega ({\bar{\varphi }})=\{(0,0,K(0))\}.$ Then ${\tilde{P}}^n(\bar{\varphi })\rightarrow (0,0,K(0))$ as $n\rightarrow \infty$. Clearly, (0, 0, K(0)) is a fixed point of ${\tilde{P}}$. This implies that statement (i) is valid.

In the case where $r(P)>1$, by Lemma 7 (ii) and Zhao (2003, Theorem 1.2.2), it follows that either $\tilde{\omega }=\{(0,0)\}$ or $\tilde{\omega }=\{({\tilde{v}}_{10},{\tilde{v}}_2(0))\}$, where ${\tilde{v}}_{10}(\theta )={\tilde{v}}_1(\theta )$ for all $\theta \in [-\tau (0),0]$. We further claim that $\tilde{\omega }\ne \{(0,0)\}$. Suppose, by contradiction, that $\tilde{\omega }=\{(0,0)\}$, then we have $\omega ({\bar{\varphi }})=\{(0,0,K(0))\}$. Thus, $\lim _{t\rightarrow \infty }(u_1(t),u_3(t))=(0,0)$, and for any $\epsilon >0$, there exists $T=T(\epsilon )>0$ such that $|w(t)-K(t)|<\epsilon$ for all $t\ge T$. Then for any $t\ge T$, we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}u_1(t)}{\mathrm{d}t}&\ge \frac{c\beta (t)l(H-u_1(t))}{(p-l)u_1(t)+lH}u_3(t)- (d_h+\rho )u_1(t),\\ \frac{\mathrm{d}u_3(t)}{\mathrm{d}t}&\ge -d_m(t)u_3(t)+(1-\tau '(t))\frac{b\beta (t-\tau (t))pu_1(t-\tau (t))}{(p-l)u_1(t-\tau (t))+lH}(K(t)-\epsilon -u_3(t)). \end{aligned}\nonumber \\ \end{aligned}$$

(17)

Let $r_\epsilon$ be the spectral radius of the Poincaré map associated with the following periodic linear system:

$$\begin{aligned} \frac{\mathrm{d}u_1(t)}{\mathrm{d}t}= & {} - (d_h+\rho )u_1(t)+c\beta (t)u_3(t),\nonumber \\ \frac{\mathrm{d}u_3(t)}{\mathrm{d}t}= & {} (1-\tau '(t))\frac{b\beta (t-\tau (t))pu_1(t-\tau (t))}{lH}(K(t)-\epsilon ) -d_m(t)u_3(t).\qquad \end{aligned}$$

(18)

Since $\lim _{\epsilon \rightarrow 0^+}r_\epsilon =r(P)>1$, we can fix $\epsilon$ small enough such that $r_\epsilon >1$. By similar result to Lemma 7 (ii), it follows that the Poincaré map of the following system

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}u_1(t)}{\mathrm{d}t}&= \frac{c\beta (t)l(H-u_1(t))}{(p-l)u_1(t)+lH}u_3(t)- (d_h+\rho )u_1(t),\\ \frac{\mathrm{d}u_3(t)}{\mathrm{d}t}&= -d_m(t)u_3(t)+(1-\tau '(t))\frac{b\beta (t-\tau (t))pu_1(t-\tau (t))}{(p-l)u_1(t-\tau (t))+lH}(K(t)-\epsilon -u_3(t)) \end{aligned}\nonumber \\ \end{aligned}$$

(19)

admits a globally asymptotically stable fixed point $({\bar{u}}_{10},{\bar{u}}_3(0))\gg 0$. In the case where ${\bar{\varphi }}\in {\varPi }{\setminus } (\{0\}\times \{0\}\times \mathbb {R}_+)$, we have $(u_1(t),u_3(t))>0$ in $\mathbb {R}^2$ for all $t>0$. In view of (17) and (19), the comparison principle implies that

$$\begin{aligned} \liminf _{n\rightarrow \infty }(u_{1n\omega }({\bar{\varphi }}), u_3(n\omega ,{\bar{\varphi }}))\ge ({\bar{u}}_{10},{\bar{u}}_3(0))\gg 0, \end{aligned}$$

which contradicts $\lim _{t\rightarrow \infty }(u_1(t),u_3(t))=(0,0).$ It then follows that $\tilde{\omega }=\{({\tilde{v}}_{10}$,${\tilde{v}}_2(0))\}$, and hence, $\omega ({\bar{\varphi }})=\{({\tilde{v}}_{10},{\tilde{v}}_2(0),K(0))\}$. This implies that $\lim _{t\rightarrow \infty }$ $({\bar{z}}(t)-({\tilde{v}}_1(t)$, ${\tilde{v}}_2(t)$, $K(t)))=(0,0,0).$ $\square$

By the definition of w(t), we have $u_2(t-\tau (t))=(w(t)-u_3(t))e^{\int _{t-\tau (t)}^td_m(s)\mathrm{d}s}$. In the case where $r(P)\le 1$, we have

$$\begin{aligned} \begin{aligned}&\lim _{t\rightarrow \infty }(u_2(t-\tau (t))-S_m^*(t-\tau (t)))\\ =&\,\lim _{t\rightarrow \infty }(w(t)-u_3(t)-K(t))e^{\int _{t-\tau (t)}^td_m(s)\mathrm{d}s}\\ =&\,0. \end{aligned} \end{aligned}$$

It follows that $\lim _{t\rightarrow \infty }(u_2(t)-S_m^*(t))=0.$ In the case where $r(P)>1$, we have

$$\begin{aligned} \lim _{t\rightarrow \infty } (u_2(t-\tau (t))-{\hat{u}}_2(t))=0, \end{aligned}$$

where ${\hat{u}}_2(t):=e^{\int _{t-\tau (t)}^td_m(s)\mathrm{d}s}(K(t)-{\tilde{v}}_2(t))$ is a positive $\omega$-periodic function. Let $x=h(t):=t-\tau (t)$. Then we have $\lim _{x\rightarrow \infty }(u_2(x)-{\hat{u}}_2(h^{-1}(x)))=0$ and $x+\omega =t+\omega -\tau (t)=t+\omega -\tau (t+\omega )=h(t+\omega )$. It follows that ${\hat{u}}_2(h^{-1}(x+\omega ))={\hat{u}}_2(t+\omega )={\hat{u}}_2(t)={\hat{u}}_2(h^{-1}(x))$. Replacing x by t, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }(u_2(t)-{\hat{u}}_2(h^{-1}(t)))=0, \end{aligned}$$

where ${\hat{u}}_2(h^{-1}(t))$ is a positive $\omega$-periodic function.

As a straightforward consequence of Theorem 1, we have the following result for system (8).

Theorem 2

The following statements are valid for system (8):

• (i) If $r(P)\le 1,$ then the disease-free periodic solution $(0,S_m^*(t),0)$ is globally asymptotically stable for system (8) in ${\varPsi }$;

• (ii) If $r(P)>1,$ then system (8) admits a positive $\omega$-periodic solution $({\tilde{v}}_1(t)$, ${\hat{u}}_2(h^{-1}(t))$, ${\tilde{v}}_2(t))$, which is globally asymptotically stable for system (8) in ${\varPsi }\setminus (\{0\}\times C([-\tau (0),0],\mathbb {R}_+)\times \{0\})$.

By the same arguments as in Lou and Zhao (2017, Lemma 3.8), we have $r(P)=r({\hat{P}})$. Combining Lemma 1 and Theorem 2, we have the following result on the global dynamics of system (8).

Theorem 3

The following statements are valid for system (8):

• (i) If $R_0\le 1$, then the disease-free periodic solution $(0,S_m^*(t),0)$ is globally asymptotically stable for system (8) in ${\varPsi }$;

• (ii) If $R_0>1$, then system (8) admits a positive $\omega$-periodic solution $({\tilde{v}}_1(t)$, ${\hat{u}}_2(h^{-1}(t))$, ${\tilde{v}}_2(t))$, which is globally asymptotically stable for system (8) in ${\varPsi }{\setminus }(\{0\}\times C([-\tau (0),0],\mathbb {R}_+)\times \{0\})$.

In the rest of this section, we derive the dynamics for the variable $E_m(t)$ in system (7). It is easy to see that

$$\begin{aligned} \begin{aligned} E_m(t)&= \int _{t-\tau (t)}^tB(\xi ,I_h(\xi ),S_m(\xi ))e^{-\int _\xi ^td_m(s)\mathrm{d}s}\mathrm{d}\xi . \end{aligned} \end{aligned}$$

(20)

In the case where $R_0\le 1$, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }[(I_h(t),S_m(t))-(0,S_m^*(t))]=0. \end{aligned}$$

It then follows from (20) that

$$\begin{aligned} \lim _{t\rightarrow \infty }E_m(t)=0. \end{aligned}$$

In the case where $R_0>1$, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }[(I_h(t),S_m(t))-({\tilde{v}}_1(t),{\hat{u}}_2(h^{-1}(t)))]=0. \end{aligned}$$

By using the integral form (20), we obtain

$$\begin{aligned} \lim _{t\rightarrow \infty }\left[ E_m(t)-\int _{t-\tau (t)}^tB(\xi ,{\tilde{v}}_1(\xi ),{\hat{u}}_2(h^{-1}(\xi )))e^{-\int _{\xi }^{t}d_m(s)\mathrm{d}s}\mathrm{d}\xi \right] =0. \end{aligned}$$

Moreover, it is easy to verify that

$$\begin{aligned} E_m^*(t)=\int _{t-\tau (t)}^tB(\xi ,{\tilde{v}}_1(\xi ),{\hat{u}}_2(h^{-1}(\xi )))e^{-\int _{\xi }^{t}d_m(s)\mathrm{d}s}\mathrm{d}\xi \end{aligned}$$

is a positive $\omega$-periodic function. Consequently, we have the following result on the global dynamics of system (7).

Theorem 4

The following statements are valid for system (7):

• (i) If $R_0\le 1$, then the disease-free periodic solution $(0,S_m^*(t),0,0)$ is globally asymptotically stable;

• (ii) If $R_0>1$, then system (7) admits a unique positive $\omega$-periodic solution $({\tilde{v}}_1(t)$, ${\hat{u}}_2(h^{-1}(t))$, $E_m^*(t)$, ${\tilde{v}}_2(t))$, which is globally asymptotically stable for all nontrivial solutions.

4 A Case Study

In this section, we study the malaria transmission case in Maputo Province, Mozambique. Mozambique is a malaria-endemic country in sub-Saharan Africa. The topography and the climate of Maputo Province are favorable for malaria transmission. We will use the same values as those in Wang and Zhao (2017) for all the constant and periodic parameters except $\tau (t)$. The constant parameter values are listed in Table 2. The values of p and l may vary from 0 to 1 and $p\ge l$ (see Chamchod and Britton 2011; Kesavan and Reddy 1985; Lacroix et al. 2005). In the following simulations, we take $p=0.8$ and $l=0.6$.

Table 2 Constant parameter values

The estimations for the periodic parameters $\beta (t)$, $d_m(t)$ and $\mu (t)$ are given by

$$\begin{aligned} \beta (t)= & {} 6.983-1.993\cos (\pi t/6)-0.4247\cos (\pi t/3)-0.128\cos (\pi t/2)\\&-\,0.04095\cos (2\pi t/3)+0.0005486\cos (5\pi t/6)-1.459\sin (\pi t/6)\\&-\,0.007642\sin (\pi t/3)-0.0709\sin (\pi t/2)+0.05452\sin (2\pi t/3)\\&-\,0.06235\sin (5\pi t/6) \text {Month}^{-1},\\ d_m(t)= & {} 3.086+0.04788\cos (\pi t/6)+0.01942\cos (\pi t/3)+0.007133\cos (\pi t/2)\\&+\,0.0007665\cos (2\pi t/3) -\,0.001459\cos (5\pi t/6)+0.02655\sin (\pi t/6)\\&+\,0.01819\sin (\pi t/3)+0.01135\sin (\pi t/2) +\,0.005687\sin (2\pi t/3)\\&+\,0.003198\sin (5\pi t/6) \text {Month}^{-1}, \end{aligned}$$

and

$$\begin{aligned} \mu (t)=k\times \beta (t), \end{aligned}$$

where $k=5\times 1205709$.

Table 3 Monthly mean temperature for Maputo Province (in $^{\circ }$C)

According to Craig et al. (1999), the relationship between the EIP and the temperature is given by

$$\begin{aligned} \tau (T)=\frac{111}{T-16}, \end{aligned}$$

where T is temperature in $^{\circ }$C, 111 is the total degree days required for parasite development, and 16 is the temperature at which the parasite development ceases. As in the case study of Wang and Zhao (2017), we take July 1 as the starting point. By using the monthly mean temperatures of Maputo Province (see Table 3, obtained from Climate Change Knowledge Portal website: http://sdwebx.worldbank.org/climateportal), we obtain the following approximation for the periodic time delay $\tau (t)$ in CFTOOL (see Fig. 1):

$$\begin{aligned} \begin{aligned} \tau (t)=&1/30.4(17.25+8.369\cos (\pi t/6)+4.806\sin (\pi t/6)+ 3.27\cos (\pi t/3)\\&+\,2.857\sin (\pi t/3)+1.197\cos (\pi t/2)+1.963\sin (\pi t/2)\\&+\,0.03578\cos (2\pi t/3)+1.035\sin (2\pi t/3)-0.3505\cos (5\pi t/6)\\&+\,0.6354\sin (5\pi t/6) -0.3257\cos (\pi t)+0\sin (\pi t)) \text {Month}. \end{aligned} \end{aligned}$$

Fig. 1

Fitted curve of EIP

To compute $R_0$ numerically, we first write the operator L into the integral form of Posny and Wang (2014) by using the similar method to that in Lou and Zhao (2017). Since

$$\begin{aligned} F(t-s)\varphi = \left( \begin{array}{c} a_{12}(t-s)\varphi _2(0) \\ a_{21}(t-s)\varphi _1(-\tau (t-s)) \end{array} \right) , \end{aligned}$$

we have

$$\begin{aligned}{}[Lv](t)= & {} \int _0^\infty {\varPhi }(t,t-s)F(t-s)v(t-s+\cdot )\mathrm{d}s\\= & {} \int _0^\infty \left( \begin{array}{cc} e^{-\int _{t-s}^ta_{11}(r)\mathrm{d}r} &{} 0 \\ 0 &{} e^{-\int _{t-s}^ta_{22}(r)\mathrm{d}r} \end{array} \right) \left( \begin{array}{c} a_{12}(t-s)v_2(t-s) \\ a_{21}(t-s)v_1(t-s-\tau (t-s)) \end{array} \right) \mathrm{d}s\\= & {} \left( \begin{array}{c} \int _0^\infty e^{-\int _{t-s}^ta_{11}(r)\mathrm{d}r}a_{12}(t-s)v_2(t-s)\mathrm{d}s \\ \int _0^\infty e^{-\int _{t-s}^ta_{22}(r)\mathrm{d}r}a_{21}(t-s)v_1(t-s-\tau (t-s))\mathrm{d}s \end{array} \right) . \end{aligned}$$

Let $t-s-\tau (t-s)=t-s_1$. Since the function $y=h(x)=x-\tau (x)$ is strictly increasing, the inverse function $x=h^{-1}(y)$ exists. Solving $t-s_1=h(t-s)$, we obtain $s=t-h^{-1}(t-s_1), \mathrm{d}s_1=d(s+\tau (t-s))=(1-\tau '(t-s))\mathrm{d}s\quad \text {and}\quad \mathrm{d}s=\frac{1}{1-\tau '(h^{-1}(t-s_1))}\mathrm{d}s_1$. Therefore,

$$\begin{aligned} \begin{aligned}&\int _0^\infty e^{-\int _{t-s}^ta_{22}(r)\mathrm{d}r}a_{21}(t-s)v_1(t-s-\tau (t-s))\mathrm{d}s\\&\quad =\int _{\tau (t)}^\infty \frac{e^{-\int _{h^{-1}(t-s_1)}^ta_{22}(r)\mathrm{d}r}a_{21}(h^{-1}(t-s_1))v_1(t-s_1)}{1-\tau '(h^{-1}(t-s_1))}\mathrm{d}s_1\\&\quad =\int _{\tau (t)}^\infty \frac{e^{-\int _{h^{-1}(t-s)}^ta_{22}(r)\mathrm{d}r}a_{21}(h^{-1}(t-s))v_1(t-s)}{1-\tau '(h^{-1}(t-s))}\mathrm{d}s. \end{aligned} \end{aligned}$$

Define

$$\begin{aligned} K_{21}(t,s)= \left\{ \begin{array}{ll} 0, &{} s<\tau (t), \\ \frac{e^{-\int _{h^{-1}(t-s)}^ta_{22}(r)\mathrm{d}r}a_{21}(h^{-1}(t-s))}{1-\tau '(h^{-1}(t-s))} , &{} s\ge \tau (t), \end{array} \right. \end{aligned}$$

and $K_{12}(t,s)=e^{-\int _{t-s}^ta_{11}(r)\mathrm{d}r}a_{12}(t-s)$, $K_{11}(t,s)=K_{22}(t,s)=0$. Then we can rewrite

$$\begin{aligned}{}[Lv](t)= & {} \int _0^\infty K(t,s)v(t-s)\mathrm{d}s\\= & {} \sum _{j=0}^\infty \int _{j\omega }^{(j+1)\omega }K(t,s)v(t-s)\mathrm{d}s\\= & {} \sum _{j=0}^\infty \int _{0}^{\omega }K(t,j\omega +s)v(t-s-j\omega )\mathrm{d}s\\= & {} \int _{0}^{\omega }G(t,s)v(t-s)\mathrm{d}s, \end{aligned}$$

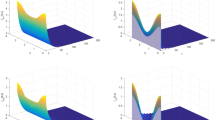
where $G(t,s)=\sum _{j=0}^\infty K(t,j\omega +s)$. Consequently, we can use the numerical method in Posny and Wang (2014) to compute $R_0$. We set $\omega =12$ months. By using the obtained parameter values above, together with initial functions $I_h(\theta )=337598$, $S_m(\theta )=$2,712,343, $E_m(0)=1000$, $I_m(0)=2000$ for all $\theta \in [-\hat{\tau },0]$, we get $R_0=3.1471>1$. In this case, the disease will persist and exhibit periodic fluctuation eventually (see Fig. 2). By employing some malaria control measures such as using insecticide-treated nets, spraying or clearance of mosquito breeding sites, if we can decrease the biting rate to $0.7\beta (t)$, and increase the mosquito mortality rate to $1.5d_m(t)$, then $R_0=0.6591<1$. In this case, we observe that the infectious human population, the exposed and the infectious mosquito populations tend to 0, which means that the disease is eliminated from this area eventually (see Fig. 3). These numerical simulation results consist with the analytic results in the previous section.

Fig. 2

Long-term behavior of the solution of system (7) when $R_0=3.1471>1$

Fig. 3

Long-term behavior of the solution of system (7) when $R_0=0.6591<1$

We define the time-averaged EIP duration as

$$\begin{aligned} {[}\tau ]:=\frac{1}{\omega }\int _0^\omega \tau (t)\mathrm{d}t. \end{aligned}$$

It follows that $[\tau ]=17.2500/30.4$ month. By using this time-averaged EIP duration and keeping all the other parameter values the same as those in Fig. 2, we obtain $R_0=1.8540$, which is less than 3.1471 in Fig. 2. Figure 4 compares the long-term behaviors of the infectious compartments of model (7) under two different values of the EIP durations: the periodic $\tau (t)$ and the constant $[\tau ]$. Figure 4a indicates that the use of the time-averaged EIP $[\tau ]$ may underestimate the number of infectious humans in Maputo. In Fig. 4b, we see that the amplitude of the periodic fluctuation of infectious mosquitoes is obviously smaller when $[\tau ]$ is used. In addition, the peak and the nadir of the periodic fluctuation of $I_m$ are underestimated and overestimated, respectively.

Fig. 4

Comparison of the long-term behaviors of the infectious compartments of model (7) under two different EIP durations (red curve: temperature-dependent EIP; blue curve: time-averaged EIP) (Color figure online)

5 Discussion

Malaria is strongly linked to climate conditions through the impact of climate on the vector and the parasite ecology. Of all the environmental conditions, temperature plays the most important role in malaria transmission. Both the mosquito Anopheles and the parasite Plasmodium are extremely sensitive to temperature. In particular, the duration of the EIP of Plasmodium is determined by temperature (see, e.g., Beck-Johnson et al. 2013; Ngarakana-Gwasira et al. 2014). An increasing number of malaria models have incorporated the effects of temperature on mosquito life cycle. However, none of the existing deterministic malaria models has taken into account the dependence of the EIP on temperature.

In this paper, we developed a malaria transmission model that, for the first time, incorporates a temperature-dependent EIP. The model is a system of delay differential equations with a periodic time delay. By using the theory recently developed by Zhao (2017), we derived the basic reproduction ratio $R_0$. Incorporation of the periodic delay increases challenges for theoretical analysis. Fortunately, the work by Lou and Zhao (2017) throws light on mathematical analysis of delay differential system with periodic delays. Following the theoretical approach in Lou and Zhao (2017), we defined a phase space on which the limiting system generates an eventually strongly monotone periodic semiflow. By employing the theory of monotone and subhomogeneous systems and the theory of chain transitive sets, we established a threshold type result on the global dynamics in terms of the basic reproduction ratio $R_0$: if $R_0<1$, then malaria will be eliminated; if $R_0>1$, then the disease will persist and exhibit seasonal fluctuation.

Using some published data from Maputo Province, Mozambique, and formula related to mosquito life cycle, we obtained estimations for all the constant and periodic parameters. We fitted the curve of the EIP for Maputo Province by appealing to the Detinova prediction curve. With the algorithm proposed by Posny and Wang (2014), we numerically calculated the basic reproduction ratio $R_0$. The numerical simulation about the long-term behavior of solutions is consistent with the obtained analytic result. To compare our results with those for the constant EIP case, we also conducted numerical simulations for the long-term behavior of infectious compartments by using the time-averaged EIP. It turns out that the adoption of the time-averaged EIP may underestimate both the number of infectious humans and the basic reproduction ratio. Thus, the models incorporating the temperature-dependent EIP are more helpful for the control of the malaria transmission.

In the present work, we only considered the extrinsic incubation period (EIP) in mosquitoes. Indeed, the malaria parasites also undergo the intrinsic incubation period (IIP) in human hosts, that is, the time elapsed between exposure to malaria parasites and when symptoms and signs are first apparent. In most cases, the IIP varies from 7 to 30 days. We may consider the EIP and the IIP simultaneously when developing malaria models in future.

As proposed by Ai et al. (2012), most of the existing malaria models consider only adult mosquitoes. In fact, there are four distinct development stages during a mosquito’s lifetime: egg, larva, pupa, and adult. While only adult mosquitoes are involved in malaria transmission, the dynamics of the first three aquatic stages have great impact on the mosquito population dynamics, and hence the disease transmission dynamics (see Ai et al. 2012). It is worthwhile to develop a mosquito-stage-structured malaria model with temperature-dependent incubation period. We leave this interesting problem as a future work.