Evaluation of gravitational curvatures of a tesseroid in spherical integral kernels

Abstract

Proper understanding of how the Earth’s mass distributions and redistributions influence the Earth’s gravity field-related functionals is crucial for numerous applications in geodesy, geophysics and related geosciences. Calculations of the gravitational curvatures (GC) have been proposed in geodesy in recent years. In view of future satellite missions, the sixth-order developments of the gradients are becoming requisite. In this paper, a set of 3D integral GC formulas of a tesseroid mass body have been provided by spherical integral kernels in the spatial domain. Based on the Taylor series expansion approach, the numerical expressions of the 3D GC formulas are provided up to sixth order. Moreover, numerical experiments demonstrate the correctness of the 3D Taylor series approach for the GC formulas with order as high as sixth order. Analogous to other gravitational effects (e.g., gravitational potential, gravity vector, gravity gradient tensor), numerically it is found that there exist the very-near-area problem and polar singularity problem in the GC east–east–radial, north–north–radial and radial–radial–radial components in spatial domain, and compared to the other gravitational effects, the relative approximation errors of the GC components are larger due to not only the influence of the geocentric distance but also the influence of the latitude. This study shows that the magnitude of each term for the nonzero GC functionals by a grid resolution 15$^{{\prime } }\,\times$ 15$^{{\prime }}$ at GOCE satellite height can reach of about 10$^{-16}$ m$^{-1}$ s$^{2}$ for zero order, 10$^{-24 }$ or 10$^{-23}$ m$^{-1}$ s$^{2}$ for second order, 10$^{-29}$ m$^{-1}$ s$^{2}$ for fourth order and 10$^{-35}$ or 10$^{-34}$ m$^{-1}$ s$^{2}$ for sixth order, respectively.

1 Introduction

Calculating gravity tensors (or gravitational gradients) effect of the topographic masses on gravity field modeling is one of the crucial topics in the area of geodetic sciences (e.g., physical geodesy, geophysics). With advanced satellite missions for Earth’s gravity field modeling, e.g., CHAMP (Reigber et al. 2002), GRACE (Tapley et al. 2004) and GOCE (ESA 1999; Rummel 2003, 2015), there is increased interest to modeling of the gravity tensors. In addition, next-generation satellite missions are also under examination and simulated, e.g., the Next-Generation Gravimetry Mission (NGGM) (Cesare et al. 2010; Silvestrin et al. 2012), the Four-Satellites Cartwheel Formation (FSCF) mission (Wiese et al. 2009; Zheng et al. 2013), the Earth System Mass Transport Mission (ESMTM) (Gruber et al. 2012; Zheng et al. 2012; Panet et al. 2013) and the GRACE Follow-On (GRACE-FO or GFO) mission (Flechtner et al. 2009; Wiese et al. 2009; Loomis et al. 2012; Elsaka et al. 2014; Zheng et al. 2009, 2014, 2015). Among these next new-generation satellite missions, the OPTical Interferometry for global MAss change detection from space (OPTIMA) mission (Brieden et al. 2010), which is proposed to measure the components of the third-order gravitational potential tensor (gravitational curvatures or gravity’s curvature, abbreviated here by GC, which physically means the rate change of the gravity gradient) on board of a satellite in space, attracted the special interest of both experimentalists and theoreticians.

Focusing on the simulation experiment for the GC functionals, the Russian Dulkyn project (Balakin et al. 1997) had proposed a sensor that could detect the GC functionals and their temporal changes. Recently, Rosi et al. (2015) implemented the first direct GC functionals measurements by atom interferometry sensors in a laboratory environment, which opened a new era in related geodesy applications, especially for the GC functionals.

Concerning another aspect of the fundamental theory for the GC functionals, relevant studies focused mostly on the spectral domain modeling. Relevant expressions of the GC functionals only appeared in both Tóth and Földváry (2005) and Tóth (2005), but without detailed mathematical derivation. Casotto and Fantino (2009) derived relevant expressions of the GC functionals in spherical coordinates in details. They also provided well-defined coordinate transformation expressions of the GC functionals between global and local Cartesian coordinate systems. Fantino and Casotto (2009) numerically compared four algorithms (Legendre, Clenshaw, Pines, Cunningham–Metris) for harmonic synthesis in spectral domain for the computation of the GC functionals. Fukushima (2012a, b, c) also analyzed the computational harmonic synthesis aspects of the GC functionals in spectral domain. Most recently, Šprlák and Novák (2015) derived 40 new integrals of Newton, Abel-Possion, Pizzetti and Hotine for the GC computation and revealed the spatial properties of the GC functionals by numerical investigations. In addition, Hamáčková et al. (2016) derived non-singular expressions of the spherical harmonic synthesis in spectral domain for the GC functionals in the local north-oriented frame (LNOF), which could avoid numerical singularities at polar region. Šprlák et al. (2016) studied the spectral properties of the GC functionals, derived new quadrature formulas of spherical harmonic expansions for the GC functionals and considered the possibility of an instrument for observing the GC functionals at satellite altitude. Ghobadi-Far et al. (2016) presented the 2D Fourier series expressions of gravitational functionals (e.g., first-order and second-order gradients of the gravitational potential) up to third-order gradients in LNOF spherical coordinates. In short, researches of the GC functionals mainly focused on spectral domain (Fantino and Casotto 2009; Fukushima 2012a, b, c; Hamáčková et al. 2016; Šprlák et al. 2016; Ghobadi-Far et al. 2016) other than spatial domain (Šprlák and Novák 2015). Therefore, the properties (e.g., representation forms, computational efficiency) of the GC functionals in the spatial domain need to be more carefully and extensively investigated.

The effect of different mass distributions on the gravity field by forward gravity modeling based on Newton’s integral can be evaluated in both spatial domain and spectral domain (Nahavandchi 1999; Kuhn and Featherstone 2002; Kuhn and Seitz 2005; Wild-Pfeiffer and Heck 2006; Hirt and Kuhn 2014; Grombein et al. 2016; Hirt et al. 2016). In spatial domain, when calculating the effect of the whole mass distribution by different types of mass bodies, it can be applied by the superposition principle to evaluate Newton’s integral (e.g., Heck and Seitz 2007; Asgharzadeh et al. 2007; Wild-Pfeiffer 2008; Tsoulis et al. 2009; Li et al. 2011; Álvarez et al. 2012; Du et al. 2015; Shen and Han 2013, 2014, 2016; Grombein et al. 2013, 2014, 2016; Uieda et al. 2016; Kuhn and Hirt 2016; Shen and Deng 2016), namely the effects of the sum of different individual mass bodies. This paper focuses on the tesseroid as an elementary mass body, namely spherical prism, which comes from discretization of the sphere. In this study, spherical approximation has been used for the numerical experiments. Compared to rectangular prism, point mass, mass layer and mass line, its second-order formula of Taylor series expansion had been numerically tested by many researchers as efficient modeling mass bodies for topographic (and isostatic) reductions and on the effect of high-resolution and high-accuracy gravity fields and geoids modeling, especially in global application (e.g., Heck and Seitz 2007; Wild-Pfeiffer 2008; Tsoulis et al. 2009; Shen and Han 2013, 2014, 2016; Grombein et al. 2013, 2014; Shen and Deng 2016).

Moreover, the layout of the tesseroid formulas for the gravitational and magnetic effects is the same. Therefore, tesseroids also had been applied for modeling the effects of magnetic field, namely magnetic potential (MP), magnetic vector (MV) and magnetic gradient tensor (MGT). Asgharzadeh et al. (2008) calculated the magnetic field effects of a tesseroid by numerical Gauss–Legendre Quadrature integration (GLQ) approach. Compared to the rectangular prism, Du et al. (2015) calculated the magnetic fields effects of a tesseroid with different numerical methods (e.g., 3D GLQ method, Taylor series expansion method) in spherical coordinate system. Recently, similar to the software Tesseroids of Uieda et al. (2016), Baykiev et al. (2016) proposed the software Magnetic Tesseroids to model the induced and remanent magnetic fields effects of the lithosphere by tesseroids. These softwares can evaluate the gravitational/magnetic effects using the tesseroid as an elementary source body, while they did not include the GC functionals or magnetic curvatures (MC) functionals.

In geodetic community, the gravitational effects of a tesseroid mass in geoscience areas were generally expressed as three parts of related functionals, namely gravitational potential (GP), gravity vector (GV) (or gravitational acceleration) (e.g., the first-order derivatives of GP) and gravity gradient tensor (GGT) (e.g., the second-order derivatives of GP) (Heck and Seitz 2007; Asgharzadeh et al. 2007; Wild-Pfeiffer 2008; Grombein et al. 2013). These components (i.e., GP, GV, GGT) have been the main focus up until now. However, after the concept of the GC put forward in geoscience (Hamáčková et al. 2016; Šprlák et al. 2016; Šprlák and Novák 2016), the gravitational effects of a tesseroid mass should also include the GC functionals, which are the third-order gravitational derivatives of GP. Therefore, this study expands the previous studies for the gravitational effects by including the GC functionals.

In this contribution, analogous to Nagy et al. (2000) by providing the third-order gravitational derivatives of gravitational potential of the rectangular prism, the new GC spherical integral formulas of a tesseroid are derived and some synthetic experiments are implemented to confirm and validate their usefulness. This paper also focuses on the spatial numerical evaluation of these formulas by 3D Taylor series approach. In a word, the GC expressions would be used as significant parameters in the next-generation gravity field model.

The paper is organized as follows. Section 2 provides the theoretical formulas, in which Sect. 2.1 formulates the detailed spherical integral GC formulas of a tesseroid in the local East–North–Up (ENU) coordinate system. In Sect. 2.2, Taylor series expansion approach is tested as the numerical solution for 3D integral GC formulas of a tesseroid. Section 3 numerically confirms the consistency of the GC formulas of a tesseroid by 3D Taylor series approach, and the numerical properties of the derived tesseroid formulas compared to the analytically closed formulation of a spherical shell are investigated. Finally, contributions of the paper as well as the viewpoint on continuing and further research work are summarized in Sect. 4.

2 Theoretical aspects

2.1 GC formulas of a tesseroid

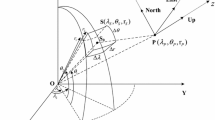
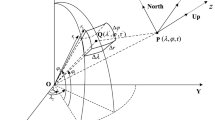
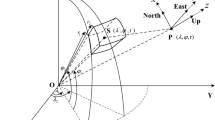
A tesseroid (or spherical prism) is defined as a mass body with a pair of geocentric radii $r_1$ and $r_2$, meridional planes of longitudes $\lambda _1$ and $\lambda _2$, coaxial circular cones of latitudes $\theta _1$ and $\theta _2$ and a constant density $\rho _S$ (see Fig. 1). For convenience, the detailed derivation of the GC formulas of a tesseroid in spherical integral kernels is given in Appendix A.

Fig. 1

Definition of a tesseroid in spherical coordinates. The dimensions of a tesseroid are $\Delta \lambda =\lambda _2 -\lambda _2$, $\Delta \theta =\theta _2 -\theta _1$ and $\Delta r=r_2 -r_1$, which are differences in spherical longitudes, latitudes and geocentric radii, respectively. The point $S_0 (\lambda _0 ,\theta _0 ,r_0 )$ is the geometric center point of a tesseroid with $\lambda _0 =(\lambda _1 +\lambda _2 )/2$, $\theta _0 =(\theta _1 +\theta _2 )/2$ and $r_0 =(r_1 +r_2 )/2$. $\lambda$, $\theta$ and r are the spherical longitude, latitude and geocentric radius, respectively. The observation (or computation) point P is in the topocentric Cartesian coordinate system (modified after Kuhn 2003). Note that the notations used herein are similar to those of Roussel et al. (2015)

Herein, Table 4 lists the 10 GC functionals, which construct the complete 27 GC functionals in total. It means that the total 27 GC functionals can be evaluated by the independent 10 GC functionals because of the symmetry for all GC functionals, referring to detailed interpretation in Šprlák et al. (2016) and Šprlák and Novák (2017), as shown in Fig. 2b.

Fig. 2

a Graphical illustration for second-order gravitational derivatives of the gravitational potential induced by a tesseroid by a 2D square expressed by 9 functionals $V_{mn}$ ($m\in \{\lambda ,\theta ,r\}$ and $n\in \{\lambda ,\theta ,r\})$, where the symbols with the light green color denote 5 GGT functionals, which could represent all 9 GGT functionals including the other 4 GGT functionals (represented by the light blue circles) if the continuous gravitational field exists, and it is noted that two of the three diagonal elements are independent as all three fulfill the Laplace equation; b) Graphical illustration for GC third-order gravitational derivatives of the gravitational potential induced by a tesseroid by a 3D cube defined by 27 functionals $V_{lmn} (l\in \{\lambda ,\theta ,r\}$ ,$m\in \{\lambda ,\theta ,r\}$ and $n\in \{\lambda ,\theta ,r\})$, where the symbols with the light green denote 10 GC functionals, and only 10 of the 27 GC functionals are independent, which could represent all 27 GC functionals including the other 17 GC functionals (represented by the light blue circles) if the continuous gravitational field exists (modified after Šprlák et al. 2016 and Šprlák and Novák 2017). It should be noted that the properties described above are more general and can apply to any mass distribution not only the tesseroid

Note that the differences of equations from Eqs. (A1)–(A10) between this paper and the corresponding ones in the literature (Šprlák et al. 2016; Hamáčková et al. 2016; Šprlák and Novák 2015, 2016, 2017) lie in expressions given in different reference systems. This paper provides expressions in spherical coordinates in the local East–North–Up (ENU) topocentric reference system, which is also adopted by Casotto and Fantino (2009), Fantino and Casotto (2009) and Szwillus et al. (2016) and is slightly different from the left-handed, North–East–Up (NEU) topocentric system (Tóth 2005; Tóth and Földváry 2005; Wild-Pfeiffer 2008; Grombein et al. 2013), that the horizontal direction (x and y) contrarily points at North and East directions. While the latter (Šprlák et al. 2016; Hamáčková et al. 2016; Šprlák and Novák 2015, 2016, 2017) provided expressions in spherical coordinates in the local North–West–Up (NWU) topocentric reference system, namely the spherical LNOF. The reason why we adopt the ENU coordinate system from Casotto and Fantino (2009), Fantino and Casotto (2009) and Szwillus et al. (2016) rather than LNOF and NEU is that one could conveniently apply the mathematical coordinate rotation relationship of the physical components between the global reference system and the local reference system for the GV, GGT and GC functionals provided in Casotto and Fantino (2009).

2.2 3D Taylor series approach for the GC formulas of a tesseroid

Heck and Seitz (2007) proposed the Taylor series expansion method for a tesseroid in the GP and part of the GV (the first radial derivative of the GP). Wild-Pfeiffer (2008) applied the numerical evaluation of Taylor series expansion method and Gauss–Legendre cubature (3D/2D) for the GGT ($M_{zz} )$ compared to an exact and closed true reference spherical cap around the computation point. Grombein et al. (2013) optimized the integral tesseroid formulas in the GP, GV and GGT from spherical integral kernels to Cartesian integral kernels by Taylor series expansion method. Deng et al. (2016) corrected the formal error from $1/(i+j+k)!$ to 1 / (i!j!k!) for the coefficient of tesseroid expression for the GP of Taylor series expansion method in Heck and Seitz (2007) and Grombein et al. (2013). Shen and Deng (2016) further extended the Taylor series expansion for the GP of a tesseroid to fourth order. Later, Grombein et al. (2016) also applied the tesseroid formulas for the GP of Taylor series expansions in gravity forward modeling. Herein following the work of Heck and Seitz (2007), Wild-Pfeiffer (2008), Grombein et al. (2013), Deng et al. (2016), Shen and Deng (2016) and Grombein et al. (2016), we implement the numerical evaluation method based on Taylor series approach with up to sixth order to calculate the GC formulas.

The 3D tesseroid formulas by Taylor series approach at the tesseroid geometric center point $S_0$ can be expressed as (Heck and Seitz 2007; Shen and Deng 2016)

$$\begin{aligned} F_m =\mathop \sum \limits _{i,j,k} \mathrm{X}_{ijk} \frac{1}{i!j!k!}\frac{\left( {\Delta \lambda } \right) ^{i+1}}{2^{i}\left( {i+1} \right) }\frac{\left( {\Delta \theta } \right) ^{j+1}}{2^{j}\left( {j+1} \right) }\frac{\left( {\Delta r} \right) ^{k+1}}{2^{k}\left( {k+1} \right) }. \end{aligned}$$

(1)

Similar to coefficients of Eq. (16) in Grombein et al. (2016), here we obtain the simplified expression:

$$\begin{aligned}&F_m =\mathop \sum \limits _{i,j,k} X_{ijk} \frac{\left( {\Delta \lambda } \right) ^{i+1}\left( {\Delta \theta } \right) ^{j+1}\left( {\Delta r} \right) ^{k+1}}{2^{i+j+k}\left( {i+1} \right) !\left( {j+1} \right) !\left( {k+1} \right) !}, \end{aligned}$$

(2)

$$\begin{aligned}&X_{ijk} =\frac{\partial ^{i+j+k}\hbox {X}\left( {\lambda _S ,\theta _S ,r_S } \right) }{\partial \lambda _S ^{i}\partial \theta _S ^{j}\partial r_S ^{k}}|_{\lambda _S =\lambda _0 ,\theta _S =\theta _0 ,r_S =r_0 }, \end{aligned}$$

(3)

where $F_{m}$ are even-order functions and represent different GC functionals $(\hbox {e.g}., m= 0, 2, 4, 6, \ldots ), \, X_{ijk}$ are the coefficient parameters of the corresponding GC functionals and the detailed expressions $X\left( {\lambda _0 ,\theta _0 ,r_0 } \right)$ are listed in Table 5. i, j and k are even integer numbers $(\hbox {e.g}., \, i,j,k= 0, 2, 4, 6, \ldots )$ with $i+j+k=m$. The three coordinate differences of a tesseroid (or dimensions of a tesseroid) are $\Delta \lambda =\lambda _2 -\lambda _1$,$\Delta \theta =\theta _2 -\theta _1$ and $\Delta r=r_2 -r_1$. Then, the detail formulas of the 3D Taylor series approach for the GC formulas are given in Appendix B.

3 Numerical investigations

3.1 Comparison with a spherical shell of analytical solution

In practical numerical evaluation, we adopted the experiment situation, which is similar to Grombein et al. (2013) and Shen and Deng (2016). That is to say, an analytical solution for a spherical shell is provided herein as reference values for the GC functionals and the derived formulas are tested against the gravitational effects of a spherical shell.

Fig. 3

Definition of a homogeneous spherical shell with constant thickness $h^{{\prime }}$ and constant density $\rho$, namely the shadow part is referred as the homogeneous spherical shell

A homogeneous spherical shell with a constant thickness $h^{{\prime }}\hbox {=}R-R_1$ and a constant density $\rho$ is fixed within a synthetic Earth sphere model with a mean radius R (see Fig. 3). Herein, we provide the GC ($V_{ijk}^{sh} )$ reference values of the analytic formulas of a spherical shell as follows

$$\begin{aligned} V_{ijk}^{sh}= & {} \frac{4}{3}\pi G\rho \left( {R^{3}-R_1 ^{3}} \right) \left( {-\,\frac{15ijk}{r_P^7 }+\frac{3p_{ijk} }{r_P^5 }} \right) , \end{aligned}$$

(4)

$$ \begin{aligned} p_{ijk}= & {} \left\{ {{\begin{array}{ll} {3i}&{} \quad {i=j=k} \\ 0 &{} \quad {i\ne j \& i\ne k \& j \ne k} \\ T &{} \quad \hbox {otherwise} \\ \end{array} }} \right. , \end{aligned}$$

(5)

$$ \begin{aligned} T= & {} \left\{ {{\begin{array}{ll} i &{} \quad {j=k \& i\ne j} \\ j &{} \quad {i=k \& i\ne j} \\ k &{} \quad {i=j \& i\ne k} \\ \end{array} }} \right. , \end{aligned}$$

(6)

where $i\in \{x,y,z\}$, $j\in \{x,y,z\}$ and $k\in \{x,y,z\}$. R is the mean radius of the Earth sphere, $R_1$ is the radius of inner surface of the spherical shell and $r_P =\sqrt{x^{2}+y^{2}+z^{2}}$ is the geocentric distance from the computation point P to the center of the Earth sphere.

Analogous to Grombein et al. (2013) and Shen and Deng (2016), the computation point P is set on the polar axis without loss of the generality because of the isotropy of the spherical shell, which means $x=y=0$ and $z=r_P$. Hence, the analytic formulas of the GP ($V^{sh})$, GV ($V_i^{sh} )$, GGT ($V_{ij}^{sh} )$ functionals can be referred in Grombein et al. (2013), and the analytic formulas of the GC ($V_{ijk}^{sh} )$ functionals can be obtained as

$$\begin{aligned} V_{xxx}^{sh}= & {} V_{xxy}^{sh} =V_{xyz}^{sh} =V_{yyx}^{sh} \nonumber \\= & {} V_{yyy}^{sh}=V_{zzx}^{sh} =V_{zzy}^{sh} =0, \end{aligned}$$

(7)

$$\begin{aligned} V_{xxz}^{sh}= & {} V_{yyz}^{sh} =\frac{4}{3}\pi G\rho \left( {R^{3}-R_1 ^{3}} \right) \left( {\frac{3}{r_P^4 }} \right) , \end{aligned}$$

(8)

$$\begin{aligned} V_{zzz}^{sh}= & {} \frac{4}{3}\pi G\rho \left( {R^{3}-R_1 ^{3}} \right) \left( {-\,\frac{6}{r_P^4 }} \right) . \end{aligned}$$

(9)

It should be noted that Eqs. (8) and (9) satisfy the Laplace equation:

$$\begin{aligned} V_{xxz}^{sh} +V_{yyz}^{sh} +V_{zzz}^{sh} =0. \end{aligned}$$

(10)

The constant thickness of the spherical shell is $h^{{\prime }}\hbox {=}1$ km and the constant density of the homogeneous spherical shell is $\rho$ $=$ 2670 kg m$^{-3}$. Then, the total parameters defined for the spherical shell are listed in Table 1. As for the applications, we conduct three evaluation applications, where the height of computation point P is at three different locations apart from the spherical shell, used by the parameter h. Furthermore, the reference values of the GP, GV, GGT and GC for the spherical shell are provided in Table 2.

Table 1 Parameters for the spherical shell

Table 2 Setting of different applications and reference values of the GP, GV, GGT and GC functionals

Table 3 Different Taylor order terms values of the GC functionals with the spherical coordinates of computation point $P(0^{\circ },0^{\circ }$, 6631 km) and the grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$. The unit is m$^{-1}$ s$^{-2}$

In the following part, the relative approximation errors (e.g., $\delta V^{T3D^{(0)}}$, $\delta V_z^{T3D^{(0)}}$,$\delta V_{xx}^{T3D^{(0)}}$..., $\delta V_{xxz}^{T3D^{(0)}}$...) mean that the absolute approximation errors are divided by the reference values of the corresponding entity. And the absolute approximation errors are the absolute differences between the reference values for GP ($V^{sh})$, GV ($V_z^{sh} )$, GGT ($V_{xx}^{sh}$...) and GC ($V_{xxz}^{sh}$...) and the actual calculated values by 3D Taylor series approach different order tesseroid formulas for GP ($V^{T3D^{(0)}}$, $V^{T3D^{(2)}}$,$V^{T3D^{(4)}})$, GV ($V_z^{T3D^{(0)}}$,$V_z^{T3D^{(2)}}$,$V_z^{T3D^{(4)}} )$, GGT ($V_{xx}^{T3D^{(0)}}$,$V_{xx}^{T3D^{(2)}}$,$V_{xx}^{T3D^{(4)}}$...) and GC ($V_{xxz}^{T3D^{(0)}}$,$V_{xxz}^{T3D^{(2)}}$,$V_{xxz}^{T3D^{(4)}}$...).

In terms of the tesseroid grid resolution for discretizing the whole spherical shell, we select the grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$, which is also adopted in Shen and Deng (2016) and Table 2 of Kuhn and Hirt (2016). Therefore, the horizontal discretization of the spherical shell is set as $\Delta \lambda =\Delta \theta =15^{{\prime }}$, and the vertical dimension to $\Delta r=h^{{\prime }}=1$ km based on the constant thickness of spherical shell.

3.2 Evaluation of GC formulas

The different numerical values of Taylor order terms (e.g., $\left| {\Delta ^{0}} \right|$, $\left| {\Delta ^{2}} \right|$, $\left| {\Delta ^{4}} \right|$ and $\left| {\Delta ^{6}} \right| )$ for the GC functionals are evaluated and the numerical results are listed in Table 3.

The GC functionals can be divided into two types: nonzero and zero GC functionals. In general, for the nonzero GC functionals, the precision levels of the different Taylor order terms are about 10$^{-16}$ m$^{-1}$ s$^{2}$ for zero order, 10$^{-24 }$or 10$^{-23}$ m$^{-1}$ s$^{2}$ for second order, 10$^{-29}$ m$^{-1}$ s$^{2}$ for fourth order and 10$^{-35}$ or 10$^{-34}$ m$^{-1}$ s$^{2}$ for sixth order. Afterward, the precision levels of the different Taylor order terms for the zero GC functionals are much more improved than those of the nonzero GC functionals, where they are approximately 10$^{-33}$–10$^{-28 }$m$^{-1}$ s$^{2}$ for zero order, 10$^{-34}$–10$^{-31 }$m$^{-1}$ s$^{2}$ for second order, 10$^{-37}$–10$^{-33}$ m$^{-1}$ s$^{2}$ for fourth order and 10$^{-39}$–10$^{-35}$ m$^{-1}$ s$^{2}$ for sixth order. Therefore, the numerical results in Table 3 obviously confirmed the correctness of the derived GC formulas with different Taylor orders.

With the order increase, the calculated values of Taylor order terms decrease quickly; thus, the main contributions for the numerical evaluation are the low-order terms (zero order and second order). In fact, the fourth-order and sixth-order terms do not significantly influence the approximation errors while their formulas are more complicated and their computation time cost is relatively higher. Therefore, in terms of the computational efficiency (computation time cost and error) for 15$^{{\prime }}\times$15$^{{\prime }}$ grid resolution as listed in Table 3, the second-order tesseroid formulas are implemented for the GC evaluation in the following numerical experiments.

Fig. 4

a Visualization of the second-order tesseroid relative approximation errors in Log$_{10}$ scale for the GP ($\delta V$ (blue curve)), GV ($\delta V_z$ (red curve)), GGT ($\delta V_{xx}$ (green dashed curve), $\delta V_{yy}$ (dark blue dashed curve) and $\delta V_{zz}$(yellow dotted curve)) and GC ($\delta V_{xxz}$ (deep sky blue dashed curve), $\delta V_{yyz}$ (thistle dashed curve) and $\delta V_{zzz}$ (magenta dotted curve)) by grid resolution 15$^{{\prime }} \times$15$^{{\prime }}$ with the influence of geocentric distance $r_P$ from the surface 6371 to 6401 km; b) the absolute approximation errors for the $\delta \Delta V_2$ (dark magenta curve) and $\delta \Delta V_3$ (orange curve), which are the Laplace parameters

3.3 Influence of the geocentric distance on GP, GV, GGT and GC

Based on situation of the GP evaluation experiments in Shen and Deng (2016), the GC evaluation experiments are implemented in the following part. The very-near-area problem of the observation (or computation) point P has been investigated when the condition $h_P \rightarrow 0$ is applied for the gravitational effects with the grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$, especially for the GC functionals compared to other gravitational effects. Specifically, the numerical properties of the GC functionals are studied to see whether exist evident errors in the very near area when the geocentric distance $r_P$ changes from the surface of the spherical shell to a distant point. Moreover, it should be noted that the very-near-area problem does not only refer to the vertical location of the computation point. In general, it refers to the fact that the tesseroid mass element is rather close to the computation point, which could be in any direction (e.g., horizontal or vertical), and the behavior may significantly change when looking in a horizontal direction.

It should be noted that the selection of a single point may not be representative for a general behavior because of the latitude dependency (see Sect. 3.4). However, without loss of generality, the spherical longitude and latitude of computation point P are chosen as $(0^{\circ },0^{\circ })$, and the geocentric distance $_{ }r_P \in$[6371, 6401 km] with 0.15-km interval to show the geocentric distance dependency of the point P. It will be more precise if the calculation is evaluated with higher-order Taylor formulas, whereas it needs more computation time cost. In terms of computation time cost, the second-order tesseroid formulas for the GP, GV, GGT and GC are considered other than the high order in the following experiments.

Therefore, the second-order tesseroid relative approximation errors for GP ($\delta V^{T3D^{(2)}})$, GV ($\delta V_z^{T3D^{(2)}} )$, GGT ($\delta V_{xx}^{T3D^{(2)}}$, $\delta V_{yy}^{T3D^{(2)}}$ and $\delta V_{zz}^{T3D^{(2)}} )$ and GC ($\delta V_{xxz}^{T3D^{(2)}}$,$\delta V_{yyz}^{T3D^{(2)}}$ and $\delta V_{zzz}^{T3D^{(2)}} )$ with the influence of geocentric distance $r_P$ by grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$ are visualized in Log$_{10}$ scale in Fig. 4a as $\delta V$, $\delta V_z$, $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{zz}$, $\delta V_{xxz}$,$\delta V_{yyz}$ and $\delta V_{zzz}$, correspondingly. And the additional internal relationships expressed as Laplace equation

$$\begin{aligned} \delta \Delta V_2= & {} \delta V_{xx} +\delta V_{yy} +\delta V_{zz}, \end{aligned}$$

(11)

$$\begin{aligned} \delta \Delta V_3= & {} \delta V_{xxz} +\delta V_{yyz} +\delta V_{zzz}. \end{aligned}$$

(12)

are also utilized as the internal quality verification, which are displayed as absolute approximation errors in Log$_{10}$ scale in Fig. 4b. Theoretically it should hold that $\delta \Delta V_2 =0$ and $\delta \Delta V_3 =0$.

Figure 4a shows the relative approximation errors for the eight components of the $\hbox {GP } (\delta V), \hbox { GV } (\delta {V_{z}}), \hbox { GGT } (\delta V_{xx},\delta V_{yy} \hbox { and } \delta V_{zz})$ and GC ($\delta V_{xxz},\delta V_{yyz} \hbox { and } \delta V_{zzz})$. For the GC functionals ($\delta V_{xxz},\delta V_{yyz}$ and $\delta V_{zzz})$, the three curves are overlapping together, showing that three GC functionals provide the same relative approximation errors, and the same as that of GGT. In general, the trends in Fig. 4a are nearly similar to each other, namely the relative approximation errors for the components of the GP, GV, GGT and GC reduce with increasing distance, excepting the turning point for the eight components as 6379.4 km for GP ($\delta V)$, 6383.6 km for GV ($\delta V_z)$, 6387.65 km for GGT ($\delta V_{xx},\delta V_{yy}$ and $\delta V_{zz})$ and 6391.55 km for GC ($\delta V_{xxz},\delta V_{yyz}$ and $\delta V_{zzz}^ )$, where turning point means the logarithmic scale changing from a negative sign to a positive sign. These effects evidently demonstrate the very-near-area problems of the tesseroid formulas in spherical integral kernels, which are not only for the GP, GV and GGT, but also for the GC.

Specifically, for the chosen distance $r_P \in$ [6371, 6401 km] the relative approximation errors of the GP ($\delta V)$ are in range of about 10$^{-6}$ to 10$^{-4}$, while the GV ($\delta V_z^ )$ could reach apparently larger relative errors about 10$^{-3 }$ to 10$^{0}$. In addition, for the GGT functionals, the relative approximation errors can reach a range of about 10$^{-1}$–10$^{2}$. The relative approximation errors for the GC functionals are about 10$^{1}$–10$^{5}$. Among the gravitational effects, the relative approximation errors of the GC functionals are largest under the same condition.

Also the two Laplace parameters ($\delta \Delta V_2$ for the GGT and $\delta \Delta V_3$ for the GC) are shown in Fig. 4b as two rough curves, where the range of $\delta \Delta V_2$ for the GGT is about 10$^{-20 }$–10$^{-15}$ s$^{-2}$ and $\delta \Delta V_3$ for the GC is approximately 10$^{-25 }$–10$^{-20}$ m$^{-1 }$s$^{-2}$. The two pairs of absolute approximation errors (GGT and GC) clearly confirm the reliability of our formulas, namely the sum of the corresponding three curves for the GGT ($\delta V_{xx}$, $\delta V_{yy}$ and $\delta V_{zz})$ and the GC ($\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz}$) satisfy the Laplace equations at appropriate double precision range used for the calculations, respectively.

Here, we note the similarities and differences between Fig. 4 in Shen and Deng (2016) and Fig. 4 in this paper. The experimental scheme and method of both papers are similar by utilizing the approximation errors calculated between the tesseroid formulas in spherical integral kernels and the analytical formulas of the spherical shell for the investigation of the very-near-area problem. Also the distance variation arrangement is same as $r_P \in$[6371, 6401 km]. However, as for the dissimilarities, Shen and Deng (2016) adopted the fourth-order tesseroid formulas by two different grid resolutions 15$^{{\prime }}\times$15$^{{\prime }}$ and 5$^{{\prime }}\times$5$^{{\prime }}$ to analyze the very-near-area problem of the GP. In this paper, we use the second-order tesseroid formulas by grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$ to study and confirm the very-near-area problem not only for the GP, but also the expansion with the other gravitational effects, especially for the GC. And the presentations of the figures are also different. In this paper, the relative approximation errors in Log$_{10}$ scale are used, whereas in Shen and Deng (2016) they show the absolute approximation errors values. Concerning the GC functionals, the evident relative approximation errors exist in the very near area. Moreover, among the gravitational effects, the GC functionals have largest relative approximation errors at the very near area.

3.4 Influence of the latitude on GP, GV, GGT and GC

It is well known that the numerical properties (e.g., the approximation error with the influence of latitude) on the GP, GV and GGT tesseroid formulas approximation errors had been broadly examined with zero-order and second-order Taylor formulas correspondingly (Kuhn 2003; Heck and Seitz 2007; Asgharzadeh et al. 2007; Wild-Pfeiffer 2008; Tsoulis et al. 2009; Álvarez et al. 2012; Uieda et al. 2016; Grombein et al. 2013, 2014, 2016; Shen and Han 2013, 2014, 2016) and with up to fourth order for the GP (Shen and Deng 2016), hence the following context concentrates on numerical evaluation for the GC formulas, where the GP, GV and GGT components are also investigated with the relative approximation errors by comparing to the GC components.

Similar to the evaluation experiments of Grombein et al. (2013) and Shen and Deng (2016), the spherical coordinates of computation point P are $(\lambda _P ,\theta _P ,r_P )$, where the spherical longitude $\lambda _P =0^{\circ }$ and geocentric distance $r_P$ as three different constants with surface, airborne and satellite height (see Table 2), and spherical latitude $\theta _P$ as variable parameter in northern hemisphere from the equator $\theta _P =0^{\circ }$ to north pole $\theta _P =90^{\circ }$ with an interval $1^{\circ }$. The numerical results are symmetric with respect to the equator (Grombein et al. 2013; Shen and Deng 2016). And the second-order tesseroid formulas with grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$ are utilized in the latter numerical evaluation of the GP, GV, GGT and GC functionals in terms of the computation time cost.

Therefore, the relative approximation errors in Log $_{10}$ scale with the influence of latitude $\theta _P$ are presented for the GP ($\delta V)$, GV ($\delta V_z)$, GGT ($\delta V_{xx}$,$\delta V_{yy}$ and $\delta V_{zz})$ and GC ($\delta V_{xxz}$,$\delta V_{yyz}$ and $\delta V_{zzz} )$ by grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$ with three different applications in Fig. 5 for surface height, Fig. 6 for airborne height and Fig. 8 for GOCE satellite height, respectively. Furthermore, the differences between Figs. 5 and 6 for the relative approximation errors in Log $_{10}$ scale are also shown in Fig. 7 to present the minor differences between surface and airborne applications.

Fig. 5

Visualization of the second-order tesseroid relative approximation errors in Log$_{10}$ scale for the GP ($\delta V$ (blue curve)), GV ($\delta V_z$ (red curve)), GGT ($\delta V_{xx}$ (green curve),$\delta V_{yy}$ (dark blue curve) and $\delta V_{zz}$ (yellow curve)) and GC ($\delta V_{xxz}$ (deep sky blue curve), $\delta V_{yyz}$ (thistle curve) and $\delta V_{zzz}$ (magenta curve)) by grid resolution 15$^{{\prime }}\times$15$^{{\prime }}$ with the influence of spherical latitude ${\theta _{P}}$ at surface height

Fig. 6

At airborne height, other parameters are the same as in Fig. 5

Fig. 7

The differences between surface height and airborne height; other parameters are the same as in Fig. 5, except for the GGT functionals as $\delta V_{yy}$ (dark blue dotted curve) and $\delta V_{zz}$ (yellow dashed curve))

As for Fig. 5 and 6, the curves of different functionals (GP, GV, GGT and GC) behave similarly with the change in latitude, the relative approximation errors for some functionals (e.g., $\delta V$, $\delta V_z$, $\delta V_{xx}$ and $\delta V_{xxz})$ decrease toward the pole, whereas for some other functionals (e.g., $\delta V_{yy}$, $\delta V_{zz}$, $\delta V_{yyz}$ and $\delta V_{zzz}))$ they increase toward the pole. Moreover, the differences of each other for all the eight components of the GP, GV, GGT and GC are visualized in Fig. 7, which clearly shows that the GC ($\delta V_{xxz}$,$\delta V_{yyz}$ and $\delta V_{zzz})$ functionals are more sensitive than all the five GP ($\delta V)$, GV ($\delta V_z)$ and GGT ($\delta V_{xx}$,$\delta V_{yy}$ and $\delta V_{zz})$ parameters from surface height to airborne height, especially at the high-latitude area from about 60$^{\circ }$ to pole point. Furthermore, in case of GP ($\delta V)$, GV ($\delta V_z)$, GGT ($\delta V_{yy}$ and $\delta V_{zz})$ and GC ($\delta V_{xxz})$ large differences between surface and airborne application can be obviously shown at the high-latitude area. As for the GC component ($\delta V_{xxz})$ a rapid decline can be detected at high-latitude area from about 60$^{\circ }$ to the pole area.

Specifically, in both Figs. 5 and 6, for the GP ($\delta V)$, the relative approximation errors in Log $_{10}$ form are in range of about $-\,4.5$ to $-\,3.5$. The relative approximation errors in Log $_{10}$ form are about $-0.5$ for the GV ($\delta V_z)$. Moreover, for the GGT functionals, the relative approximation errors in Log $_{10}$ form can reach as the same level from about $-0.5$ to 3. For the GC functionals, the relative approximation errors can be in a range of about 2–5. For the high latitudes ($\theta _P >45^{\circ })$, the curves of the two GC functionals ($\delta V_{yyz}$ and $\delta V_{zzz})$ show the increasing trend, whereas the other GC functionals ($\delta V_{xxz})$ show the decline trend toward the pole area. And the same is as that of the GGT functionals. It should be noted that the relative approximation errors of the GC functionals are highest among the four types of the gravitational effects.

Fig. 8

At satellite height, other parameters are the same as in Fig. 5

In addition, for satellite application in Fig. 8, all the eight components parameters of the GP ($\delta V)$, GV ($\delta V_z)$, GGT ($\delta V_{xx}$, $\delta V_{yy}$ and $\delta V_{zz})$ and GC ($\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz})$ show the same curve behavior as significant reliances on the latitude $\theta _P$ of computation point P, and with the increase in latitude $\theta _P$ from 0$^{\circ }$ to 90$^{\circ }$, the relative approximation errors ascent by a fast increase in the polar region at $\theta _P >85^{\circ }$. The relative approximation errors in Log$_{10}$ form in Fig. 8 are in range of $-\,14$ to $-\,8.5$ for the GP, $-\,14$ to $-\,6.5$ for the GV, $-\,14$ to $-\,5$ for the GGT and $-\,14$ to $-\,3$ for the GC. Owing to the logarithmic scale as changing from a negative sign to a positive sign, which is the similar situation as described in Fig. 5 of Grombeion et al. (2013) for the prism approach, the relative approximation errors show a decrease behavior at $\theta _P \approx 44^{\circ }$ in case of the GC component $\delta V_{xxz}$. Compared to the absolute approximation errors of the GGT in Fig. 5 of Grombein et al. (2013), Fig. 8 provides the complete relative approximation errors of all gravitational effects (e.g., GP, GV, GGT and GC). Moreover, the relative approximation errors of the GC functionals ($\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz})$ are larger than those of the other gravitational effects functionals (GP ($\delta V)$, GV ($\delta V_z)$, GGT ($\delta V_{xx}$,$\delta V_{yy}$and $\delta V_{zz}))$ at polar region ($\theta _P \ge 80^{\circ })$.

For the polar singularity problem for the GC component ($\delta V_{xxz})$ in spherical integral kernel, it should be known that at pole point, the relative approximation errors are shown in Fig. 5, 6, 7 and 8. In other words, the deep sky blue curves of the GC component ($\delta V_{xxz})$ in Figs. 5, 6, 7 and 8 have gaps at latitude $90^{\circ }$, which clearly demonstrate the polar singularity problem of the GC component ($\delta V_{xxz})$ in spherical integral kernels. Moreover, it is obviously shown from Figs. 5, 6, 7 and 8 that the polar singularity problem of the computation point occurs not only for the GP at surface height (Shen and Deng 2016) and the GGT at satellite height (Grombein et al. 2013), but also for the GC at different surface, airborne and satellite height. The polar singularity problem for the GC component ($\delta V_{xxz})$ does depend on not the height parameter but the denominator parameters as the coordinates transformation.

4 Conclusions and outlook

Recently, the new GC functionals were proposed in geoscience. Based on a direct measurement of the GC under laboratory conditions (Rosi et al. 2015), its potential applications using the GC-type instrument on satellites’ board are expected. In this contribution, we focused on the gravitational effects of a tesseroid by adding the GC concept into the tesseroid mass body in spatial domain. Afterward, the 3D integral GC formulas of a tesseroid in spherical integral kernels were derived. On the theoretical aspect, the GC expressions by 3D Taylor series approaches were provided, where the zero-order, second-order, fourth-order and sixth-order Taylor series expansion expressions were offered.

Numerical experiments had validated the correctness of the derived GC formulas with different Taylor orders. The contribution of different order terms (e.g., zero order, second order, fourth order and sixth order) was investigated for the GC functionals, where the precision levels of the different order terms are about 10$^{-16}$ m$^{-1}$ s$^{2}$ for zero order, 10$^{-24 }$or 10$^{-23}$ m$^{-1}$ s$^{2}$ for second order, 10$^{-29}$ m$^{-1}$ s$^{2}$ for fourth order and 10$^{-35}$ or 10$^{-34}$ m$^{-1}$ s$^{2}$ for sixth order for the nonzero GC functionals. The numerical experiments showed that the main contributions for the computation precision of the Taylor series expansion approach were the low-order terms (zero order and second order).

Subsequently, the numerical properties of the GC east–east–radial, north–north–radial and radial–radial–radial components had been investigated by numerical experiments with 3D Taylor series approach compared to the analytical reference spherical shell, and the very-near-area problem and polar singularity problem occurred when applying the second-order Taylor series expansion method to the GC functionals. The two problems were also noticed and studied in numerical calculation of other gravitational effects (Heck and Seitz 2007; Wild-Pfeiffer 2008; Tsoulis et al. 2009; Grombein et al. 2013; Shen and Deng 2016). Generally, the second-order relative approximation errors for the GC functionals showed obvious dependency on the influence of geocentric distance $r_P$, and it was found that the relative approximation errors of the GC functionals ($\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz})$ were same with each other. Also the second-order relative approximation errors of the GC functionals showed the latitude dependency in three different cases. Moreover, compared to other publications (e.g., Grombein et al. 2013; Shen and Deng 2016), the main highlight of this paper is that the relative approximation errors of the GC functionals are much larger than those of the other gravitational effects under the same numerical conditions due to not only the influence of the geocentric distance, but also the influence of the latitude. We suspect that this might be due to the reason that with the increased order derivatives of the GP, the precision using the same numerical approach decreases. In other words, for the GC functionals, they need higher-order Taylor formulas to reach the same relative accuracy. To finally confirm this potential conclusion, further numerical experiments are needed.

For the accuracy of the GP on the height, the relationship of the GP and height was 0.1 m$^{2}$ s$^{-2 }$ in GP for 1 cm in height (Hofmann-Wellenhof and Moritz 2006; Shen et al. 2017). The measurement accuracy of the GOCE gravity gradients for the GGT was set as 1–2 mE (ESA 1999; Rummel 2003, 2015), namely 1 $\times$ 10$^{-12 }$–2 $\times$ 10$^{-12}$ s$^{-2}$ for the geoid determination with an accuracy of 1–2 cm. In the future, when the components of the GC functionals can be measured and obtained on a satellite, similar to the measurement accuracy of the GGT, the accuracy requirements of the satellite applications are recommended as 1 $\times$ 10$^{-18 }$–2 $\times$ 10$^{-18}$ m$^{-1}$ s$^{-2 }$. In our GC formulation, the absolute approximation errors are in the order of 10$^{-30 }$–10$^{-20 }$m$^{-1}$ s$^{-2 }$ (see Fig. 8 at satellite height), achieving the accuracy requirement.

Grombein et al. (2013) introduced the Cartesian integral kernels for the evaluation of the GP, GV and GGT of a tesseroid, which can avoid the detected polar singularity problem of the GGT. However, the singularity problem of the GC is still open. Recently, Deng and Shen (2017) derived the new GC formulas of a tesseroid in Cartesian integral kernels in 3D forms, which are expected to solve the singularity problem.

Table 4 Detailed expressions of $V_{lmn}$ (l,m,$n=r_P$,$\theta _P$or$\lambda _P )$ with $k=G\rho _S r_S^2 \cos \theta _S$, $l_{PS} =\sqrt{r_P^2 +r_S^2 -2r_P r_S \cos \psi }$,$\cos \psi =\sin \theta _P \sin \theta _S +\cos \theta _P \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right)$, $A=\cos \theta _P \sin \theta _S -\sin \theta _P \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right)$ and $B=r_P -r_S \cos \psi$, “Formula” means the integral kernels of related expressions

Moreover, the concept GC of a tesseroid in gravity field can be applied for the magnetic field. In other words, analogous to the GC of a tesseroid, the concept MC of a tesseroid, which is third-order magnetic derivatives of MP, could be proposed in the magnetic field by adding into the magnetic effects (e.g., MP, MV and MGT) (Asgharzadeh et al. 2008; Du et al. 2015; Baykiev et al. 2016). In addition, not only for tesseroid mass body, but the concept GC can also be valuable for other mass bodies (e.g., mass layer (Tsoulis 1999; Wild-Pfeiffer 2008), point mass (Tsoulis 1999; Heck and Seitz 2007; Wild-Pfeiffer 2008), rectangular prisms (Nagy et al. 2000), vertical mass line (Wild-Pfeiffer 2008), polyhedral mass (Holstein 2002; Tsoulis 2012; Conway 2015, 2016; D’Urso 2013, 2014a, b, 2015, 2016; Werner 2017; Ren et al. 2017) and vertical pyramid mass (Starostenko 1978; Sastry and Gokula 2016)) in the reduction of mass distributions in gravity field modeling in physical geodesy and geophysics.

Appendices

Appendix A: Derivation of the 3D GC formulas in spherical integral kernels

The integral expressions of the GC functionals (e.g., the third-order derivatives of GP) given by a tesseroid mass body can be expressed in spherical coordinates in the local East–North–Up (ENU) topocentric reference system of the computation point $P(\lambda _P ,\theta _P ,r_P )$. The expressions of the 10 GC functionals can be referred in Tóth (2005), Tóth and Földváry (2005), Casotto and Fantino (2009), Šprlák et al. (2016), Šprlák and Novák (2015, 2016, 2017).

After substituting the expressions of Table 4 into the expressions of the 10 GC functionals and mathematical simplification, the 3D integral expressions of GC functionals of a tesseroid in spherical coordinates in the local East–North–Up (ENU) topocentric reference system can be obtained as

Table 5 Detailed expressions of $F_m$ and $X\left( {\lambda _0 ,\theta _0 ,r_0 } \right)$ in Eqs. (B1)–(B5) with $k_0 =G\rho _S r_0^2 \cos \theta _0$,$l_{P0} =\sqrt{r_P^2 +r_0^2 -2r_P r_0 \cos \psi _0 }$,$\cos \psi _0 =\sin \theta _P \sin \theta _0 +\cos \theta _P \cos \theta _0 \cos \left( {\lambda _P -\lambda _0 } \right)$, $A_0 =\cos \theta _P \sin \theta _0 -\sin \theta _p \cos \theta _0 \cos \left( {\lambda _P -\lambda _0 } \right)$ and $B_0 =r_P -r_0 \cos \psi _0$

$$\begin{aligned} V_{xxx}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( -\frac{15kr_S ^{3}\cos ^{3}\theta _S \sin ^{3}\left( {\lambda _P -\lambda _S } \right) }{l_{PS}^7 } \right. \nonumber \\&+\,\frac{9kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{r_P \sin \theta _P \cos \theta _P l_{PS}^5 }\left( r_S \cos ^{2}\theta _P A \right. \nonumber \\&\left. +\,\sin \theta _P \cos \theta _P B+r_S \sin \theta _P \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) \right) \nonumber \\&\left. +\frac{3kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{r_P^2 \cos ^{2}\theta _P l_{PS}^3 }\left( {1-2\cos ^{2}\theta _P } \right) \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A1)

$$\begin{aligned} V_{xxy}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( \frac{15kr_S ^{3}\cos ^{2}\theta _S \sin ^{2}\left( {\lambda _P -\lambda _S } \right) A}{l_{PS}^7 } \right. \nonumber \\&-\,\frac{3kr_S A\left( {\cos \theta _P B+r_S \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) +r_S \sin \theta _P A} \right) }{r_P \cos \theta _P l_{PS}^5 }\nonumber \\&-\,\frac{1}{r_P^2 \cos ^{2}\theta _P l_{PS}^3 }kr_S \sin \theta _P \left( \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) \nonumber \right. \\&\left. \left. -\cos \theta _P \cos \psi +\sin \theta _P A \right) \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A2)

$$\begin{aligned} V_{xxz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( -\frac{15kr_S^2 \cos ^{2}\theta _S \sin ^{2}\left( {\lambda _P -\lambda _S } \right) B}{l_{PS}^7 } \right. \nonumber \\&+\frac{3k}{r_P^2 \cos \theta _P l_{PS}^5 }(2r_S ^{2}\cos \theta _P \cos ^{2}\theta _S \sin ^{2}\left( {\lambda _P -\lambda _S } \right) \left( {r_P -1} \right) \nonumber \\&+r_P B\left( {r_S \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) +r_S \sin \theta _P A+r_P \cos \theta _P B} \right) )\nonumber \\&\left. +\frac{kr_S ( {\cos \theta _S \cos ( {\lambda _P {-}\lambda _S } ){+}\sin \theta _P A} ){+}k\cos \theta _P ( {B-r_P } )}{r_P^2 \cos \theta _P l_{PS}^3 }\right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A3)

$$\begin{aligned} V_{xyz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{15kr_S^2 \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) AB}{l_{PS}^7 }\hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S , \end{aligned}$$

(A4)

$$\begin{aligned} V_{yyx}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( -\frac{15kr_S ^{3}\cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) A^{2}}{l_{PS}^7 }+ \right. \nonumber \\&\frac{3kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{r_P^2 \cos \theta _P l_{PS}^5 }\left( 2r_S \sin \theta _p \left( {r_P -1} \right) A \right. \nonumber \\&\left. \left. + r_P \cos \theta _P \left( {B+r_S \cos \psi } \right) \right) \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A5)

$$\begin{aligned} V_{yyy}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kr_S A}{l_{PS}^5 }\left( {\frac{5r_S^2 A^{2}}{l_{PS}^2 }-3} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A6)

$$\begin{aligned} V_{yyz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kB}{l_{PS}^5 }\left( {-\frac{5r_S^2 A^{2}}{l_{PS}^2 }+1} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A7)

$$\begin{aligned} V_{zzx}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{l_{PS}^5 }\left( {-\frac{5B^{2}}{l_{PS}^2 }+1} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A8)

$$\begin{aligned} V_{zzy}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kr_S A}{l_{PS}^5 }\left( {\frac{5B^{2}}{l_{PS}^2 }-1} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A9)

$$\begin{aligned} V_{zzz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kB}{l_{PS}^5 }\left( {3-\frac{5B^{2}}{l_{PS}^2 }} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A10)

As we adopt the same expressions of the 10 GC functionals as in Tóth (2005), Casotto and Fantino (2009), the representations of Eqs. (A1)–(A10) are equivalent to the Newton integrals as shown in Šprlák and Novák (2015). One could use the following Laplace identity equations to confirm the validity of the GC expressions (Casotto and Fantino 2009; Šprlák and Novák 2016; Šprlák et al. 2016):

$$\begin{aligned} V_{xxx}^{T3D} +V_{yyx}^{T3D} +V_{zzx}^{T3D}= & {} 0, \end{aligned}$$

(A11)

$$\begin{aligned} V_{xxy}^{T3D} +V_{yyy}^{T3D} +V_{zzy}^{T3D}= & {} 0, \end{aligned}$$

(A12)

$$\begin{aligned} V_{xxz}^{T3D} +V_{yyz}^{T3D} +V_{zzz}^{T3D}= & {} 0. \end{aligned}$$

(A13)

Appendix B: 3D Taylor series approach for the GC functionals

In practical calculations, one could use these iterative relationships to simplify the calculation process; therefore, the 3D zero-order, second-order, fourth-order and sixth-order tesseroid expressions of the GC functionals can be given as:

$$\begin{aligned} F_0= & {} \Delta ^{0}, \end{aligned}$$

(B1)

$$\begin{aligned} F_2= & {} \Delta ^{0}+\Delta ^{2}=F_0 +\Delta ^{2}, \end{aligned}$$

(B2)

$$\begin{aligned} F_4= & {} \Delta ^{0}+\Delta ^{2}+\Delta ^{4}=F_2 +\Delta ^{4}, \end{aligned}$$

(B3)

$$\begin{aligned} F_6= & {} \Delta ^{0}+\Delta ^{2}+\Delta ^{4}+\Delta ^{6}=F_4 +\Delta ^{6}, \end{aligned}$$

(B4)

$$\begin{aligned} \Delta ^{6}= & {} \frac{1}{13824}\Delta \lambda \Delta \theta \Delta r\left( {X_{222} \Delta \lambda ^{2}\Delta \theta ^{2}\Delta r^{2}} \right) \nonumber \\&+\,\frac{1}{46080}\Delta \lambda \Delta \theta \Delta r(X_{420} \Delta \lambda ^{4}\Delta \theta ^{2}+X_{402} \Delta \lambda ^{4}\Delta r^{2}\nonumber \\&+\,X_{240} \Delta \lambda ^{2}\Delta \theta ^{4}\nonumber \\&+\,X_{204} \Delta \lambda ^{2}\Delta r^{4}+X_{042} \Delta \theta ^{4}\Delta r^{2}+X_{024} \Delta \theta ^{2}\Delta r^{4}) \nonumber \\&+\,\frac{1}{322560}\Delta \lambda \Delta \theta \Delta r\left( X_{600} \Delta \lambda ^{6}+X_{060} \Delta \theta ^{6}\right. \nonumber \\&\left. +\,X_{006} \Delta r^{6} \right) . \end{aligned}$$

(B5)

Herein, the $\Delta ^{6}$ term is provided, and the other lower terms (e.g., $\Delta ^{0}$, $\Delta ^{2}$and $\Delta ^{4})$ can be referred in Eqs. (13)–(15) of Shen and Deng (2016).

Herein, the Mathematica code file (Code.nb) for the detailed expressions of the 3D zero-order, second-order, fourth-order and sixth-order tesseroid formulas of the GC functionals is provided on a request addressing to W.B. Shen. The code file contains two parts: a) the expressions of the spherical integral kernels for the 10 different GC functionals; b) the processes of different order (zero-order, second-order, fourth-order and sixth-order) Taylor series expansion approach for the 10 different GC functionals. Taking the GC component $V_{xxx}^{T3D}$ for example, the first part in the code file presents the expression of spherical integral kernels for $V_{xxx}^{T3D}$ as $Vxxx[G\_,\rho \_,\lambda p\_,\theta p\_,rp\_,\lambda 0\_,\theta 0\_,r0\_]$, which is the function definition in Mathematica; $\lambda p,\theta p,rp$ and $\lambda 0,\theta 0,r0$ are the spherical coordinates of the computation point P and the integration point $S_0$ with the symbol definition in the Mathematica code file. Then in the second part of the code file, it gives the different coefficient parameters expressions with different order (zero order with Vxxx000; second-order with Vxxx200,Vxxx020,Vxxx002; fourth order with Vxxx220, Vxxx022, ..., Vxxx004; and sixth order with Vxxx222, ..., Vxxx420, ..., Vxxx006) from Eq. (3). After substituting the coefficient parameters into Eqs. (B1)–(B5), it provides the final expressions for 3D zero-order (GCVxxx0), second-order (GCVxxx2), fourth-order (GCVxxx4) and sixth-order (GCVxxx6) tesseroid formulas for the GC component $V_{xxx}^{T3D}$.