Abstract
An analytical solution is presented for the gravity anomaly produced by a 2D body whose geometrical shape is arbitrary and where the density contrast is a polynomial function in both the horizontal and vertical directions. Approximating the real shape of the body by a polygon, the solution is expressed as sum of algebraic quantities that depend only upon the coordinates of the vertices of the polygon and upon the polynomial density function. The solution presented in the paper, which refers to a third-order polynomial function as a maximum, exhibits an intrinsic symmetry that naturally suggests its extension to the case of higher-order polynomials describing the density contrast. Furthermore, the gravity anomaly is evaluated at an arbitrary point that does not necessarily coincide with the origin of the reference frame in which the density function is assigned. Invoking recent results of potential theory, the solution derived in the paper is shown to be singularity-free and numerically robust. The accuracy and effectiveness of the proposed approach is witnessed by the numerical comparisons with examples derived from the existing literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The gravity anomaly of a region represents a basic set of geophysical data for the investigation of the subsurface density both in forward modelling and inversion (Jacoby and Smilde 2009). For this reason, it is highly beneficial to dispose of analytical solutions of the gravity anomaly associated with a body characterized by complex density distributions. Due to the mathematical complexity of the problem, the gravity anomaly of an irregular body whose density contrast is spatially variable has been first computed by approximating the body as a collection of vertical rectangular parallelepipeds (prisms) in which the density is assumed to be constant. Hence, the gravity anomaly for the whole body is computed as algebraic sum of the contribution of all vertical prisms at appropriate depths and distances from the observation point.
Numerical computations were first carried out by Talwani et al. (1959) and Bott (1960). Closed-form expressions of the gravity anomaly were subsequently derived by Nagy (1966), Banerjee and DasGupta (1977), Cady (1980), Nagy et al. (2000), Tsoulis (2000), Jiancheng and Wenbin (2010), D’Urso (2012), see also Plouff (1975, 1976), Won and Bevis (1987), Montana et al. (1992) for computer codes. The case of a spheroidal shell has been addressed by Johnson and Litehiser (1972). Analytical expressions of the gravity anomaly for prisms have been derived by D’Urso (2015b); for a linearly varying density, by Rao (1985, 1986, 1990), Rao et al. (1994), and Gallardo-Delgado et al. (2003); and for a quadratic density contrast, by García-Abdeslem (1992, 2005a), when the density varies with depth according to a cubic law. Non-polynomial density contrast models have been considered by Cordell (1973), Chai and Hinze (1988), Litinsky (1989), Silva et al. (2006), and Chappell and Kusznir (2008). For more complicated forms of the density contrast, see, e.g., Cai and Wang (2005) and Mostafa (2008).
The previous contributions are characterized by simple geometric modelling, i.e., the use of prisms, and refined modelling of the density contrast. A different approach is based on the use of polyhedra, to avoid the necessity of subdividing the region of interest in several prisms, countervailed by a simple description of density contrast. Analytical formulas for the gravimetric analysis of polyhedra having constant density have been contributed by Paul (1974), Barnett (1976), Strakhov (1978), Okabe (1979), Waldvogel (1979), Golizdra (1981), Strakhov et al. (1986), Götze and Lahmeyer (1988), Pohanka (1988), Murthy et al. (1989), Kwok (1991b), Werner (1994), Holstein and Ketteridge (1996), Petrović (1996), Werner and Scheeres (1997), Li and Chouteau (1998), Tsoulis (2012), and D’Urso (2013a). Subsequent advancements have been only concerned with a linear density variation (Pohanka 1998; Hansen 1999; Holstein 2003; Hamayun et al. 2009; D’Urso 2014b); actually, handling more complex density functions in conjunction with polyhedral models considerably increases the difficulties of the treatment, especially if analytical solutions are looked for.
As a matter of fact, the interest in modelling gravity data using non-uniform density contrast is associated with the geological and economic relevance of sedimentary basins. Actually, the sediment thickness and bedrock topography are important parameters in modelling groundwater flow, petroleum exploration, geotectonic investigations, and ground motion amplification during an earthquake (Jacoby and Smilde 2009; Aydemir et al. 2014). The geologic evaluation of sedimentary basins can be quite complex so that the kind of function describing the density contrast significantly differs from case to case. For instance, if simple differential compaction is assumed to be the main diagenetic process in the evaluation of a sedimentary basin, geologically meaningful results are obtained by using an exponentially increasing density with depth. However, if more complex geological process come into play, such as non-uniform stratigraphic layering and facies changes, more general variations in density need to be taken into account.
Independently of the kind of function assumed to define the density contrast, density can be assumed to vary, separately or jointly, along the vertical and horizontal directions. For instance, variations in density can be either arbitrary in the horizontal direction and of polynomial type in the vertical one, or with an interchanged functional dependence. This last case does occur in dipping layered intrusions or sedimentary beds in which an arbitrary density function is assumed along depth and a polynomial function is considered in the horizontal direction. Furthermore, complicated density functions can be associated with 3D modelling based on prisms (Murthy and Rao 1979; Rao et al. 1990; Chakravarthi et al. 2002; Chakravarthi and Sundararajan 2007; Zhou 2009b), or with 2D geometrical shapes (Gendzwill 1970; Murthy and Rao 1979; Pan 1989; Guspí 1990; Ruotoistenmäki 1992; Martín-Atienza and García-Abdeslem 1999; Zhang et al. 2001; Zhou 2008, 2009a, 2010). Actually, this last geometrical assumption, which characterizes domains having a cylindrical shape, significantly simplifies the mathematical treatment of the problem.
The derivation of analytical expressions for the gravity anomaly has not yet been achieved, even in the presence of two-dimensional domains, for bodies characterized by a complicated density contrast, so that numerical methods have been resorted to. Specifically, starting from the first researches on the subject (Hubbert 1948), all authors have systematically transformed the original domain integrals into integrals of lower dimension in order to simplify the adoption of quadrature rules for the numerical evaluation of the gravity anomaly.
For 2D bodies, which are the object of the present paper, Zhou (2008) converted the original domain integral for gravity anomaly to a line integral (LI) by using Stokes theorem. In particular, he derived two types of LIs for computing the gravity anomaly of bodies having density contrast depending only on depth. In a subsequent paper (Zhou 2009a), the author extended his method to account for density contrast functions that depended not only on depth but also on horizontal or, jointly, on horizontal and vertical directions. The original approach by Zhou has been further improved in Zhou (2010) to evaluate the gravity anomaly at observation points different from the origin since, historically, gravity anomaly was computed only at the origin of the reference frame. Furthermore, Zhou dealt with the singularity of the gravity anomaly arising where the observation point is coincident with the vertices of the integration domain, an issue already discussed in Kwok (1991a), for prism-based modelling, and Tsoulis and Petrović (2001) for polyhedra.
The aim of this paper is to derive an analytical expression of the gravity anomaly for polygonal bodies whose density contrast is expressed as a polynomial function of arbitrary degree in both the horizontal and vertical directions. The result is obtained by reducing the original domain integral to a boundary integral by virtue of the generalized Gauss theorem first presented in D’Urso (2012, 2013a) and subsequently applied to several problems ranging from geodesy (D’Urso 2014a, b, 2015b; D’Urso and Trotta 2015c) to geomechanics (Sessa and D’Urso 2013; D’Urso and Marmo 2015a), to geophysics (D’Urso and Marmo 2013b), and to heat transfer (Rosati and Marmo 2014). The generalized Gauss theorem referred to above does allow one not only to derive an expression of the gravity anomaly that is expressed in terms of a boundary integral but also to prove that the singularity of the gravity anomaly, arising when the observation point does belong to the integration domain, is eliminable.
For a polygonal domain \(\varOmega\) of \(n\) sides, the expression of the gravity anomaly in terms of boundary integral is further specialized to the sum of \(n\) 1D integrals. Differently from previous contributions on the subject, such 1D integrals are not numerically evaluated but expressed analytically as a function of the position vectors defining the vertices of the integration domain and of scalar quantities \(I_{ki}\) defined on each side. In turn, the quantities \(I_{ki}\), pertaining to the ith edge of the boundary of \(\varOmega\), are analytically computed by evaluating an integral of real variable that can exhibit a singularity when the edge does belong to a line containing the observation point. However, it is proved that such a singularity produces a null contribution of the ith edge to the general expression of gravity anomaly; hence, one can conclude that the derived expression is singularity-free.
By exploiting a suitable change in variables, we also derive an enhanced algebraic formula that expresses the gravity anomaly at an arbitrary point \(P\) and simplifies to the ordinary one when \(P=O\). Remarkably, the enhanced expression of the gravity anomaly has been derived without any modification of the density contrast function since this is still defined in the original reference frame. The enhanced formula has been implemented in a MATLAB code, and its accuracy and robustness has been assessed by numerical comparisons with examples derived from the literature.
2 Gravity Anomaly of a 2D Body at the Origin O of the Reference Frame
It is well known that the gravitation exerted by a 3D body \(\hat{\varOmega }\) on a unit mass at \(O\) is given by
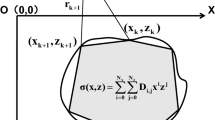
where \(G\) is the gravitational constant, \(\mathbf{r}\) the position vector pointing from \(O\) to an arbitrary point of \(\hat{\varOmega }\) and \(\Delta {\rho }(\mathbf{r})\) the density contrast at \(\mathbf{r}\). Hence, \(\Delta {\rho }(\mathbf{r})\hbox {d}V(\mathbf{r})\) represents the infinitesimal difference between the mass at \(\mathbf{r}\) and the background. We are interested in two-dimensional problems so that we shall denote by \(\varOmega\) the section of \(\hat{\varOmega }\) in the vertical plane and consider the reference frame sketched in Fig. 1.
The vertical component \(\mathbf{g}_z\) of gravitation at \(O\) is given by
where \(\mathbf{k}\) is the unit vector directed downwards. Being \(\hat{\varOmega }\) infinite in the \(y\)-direction and assuming that the density contrast \(\Delta {\rho }\) is independent of \(y\), the previous integration can be carried out between two symmetric ordinates \(\pm\) d y , with \(d_y \rightarrow \infty\). Accordingly, one obtains
This is the general form of the 2D integral for calculating the gravity anomaly at \(O\) produced by a distribution of 2D masses having a density contrast \(\Delta {\rho }\) with respect to the background. Actually, the gravity anomaly is defined as the line integral of the components of the 2D vector gravitation along the boundary of a mass body.
The computation of the integral in (3) is complicated by the fact that, due to geological and geochemical processes, the density contrast distribution within \(\varOmega\) can be arbitrary. A quite general expression for \(\Delta {\rho }\), able to accommodate a large variety of geological formations, is given by a double polynomial in \(x\) and \(z\), (Zhang et al. 2001; Zhou 2008, 2009a, 2010)
where \(N_x\) and \(N_z\) represent the maximum power of the polynomial density variation along \(x\) and \(z,\) respectively.
The scalars \(c_{ij}\) represent the coefficients of the polynomial law; they can be estimated from the known data points by a least-squares approach (Jacoby and Smilde 2009). In the sequel, we shall confine the treatment to the case
since this will suffice to address the majority of the numerical examples previously considered in the literature and, at the same time, to present our formulation at a degree of generality sufficient to be generalized to the cases \(N_x+N_z > 3\).
To simplify the ensuing developments, it is convenient to introduce the two-dimensional vectors \({\varvec{\rho }}=(x,z)\) and \({\varvec{\kappa }}_z (0,1)\). In this way, the previous relation can be written as
and our objective was to prove that the previous integral can be expressed as a line integral extended to the boundary \(\partial {\varOmega }\) of \(\varOmega\). Paralleling an analogous treatment developed in D’Urso and Marmo (2013b), we first reformulate the general expression (4) of the density contrast by writing
where \(\theta _{\varvec{o}}\) is a scalar, \(\mathbf{c}\) is a vector, \(\mathbf{C},\) and \(\mathbf{D}_{{\varvec{\rho }}{\varvec{\rho }}}\) are symmetric second-order tensors, \({\varvec{{\mathbb {C}}}}\) and \({\varvec{{\mathbb {D}}}}_{{\varvec{\rho }}{\varvec{\rho }}{\varvec{\rho }}}\) are third-order tensors; furthermore, it has been set
The second-order (rank-two) tensor \({\varvec{\rho }}\otimes {\varvec{\rho }}\) has the following matrix representation
so that, being
a quadratic distribution of density can be assigned by suitably defining the coefficients of the symmetric tensor \(\mathbf{C}\). Analogously, the third-order tensors \({\varvec{{\mathbb {C}}}}\) and \({\varvec{\rho }}\otimes {\varvec{\rho }}\otimes {\varvec{\rho }}\) are represented in matrix form as:

i.e., as vectors of rank-two tensors. Being
the representation (4) of the density contrast is recovered from (7) by setting
and
In conclusion, we derive from (6) the following expression of the gravity anomaly
where
and
In order to transform the previous domain integrals into boundary integrals, we apply Gauss theorem in the generalized form illustrated in D’Urso (2013a, 2014a). In this way, the singularity at \({\varvec{\rho }}={\varvec{o}}\) of the four domain integrals can be correctly taken into account.
2.1 Analytical Expression of the Gravity Anomaly at O in Terms of Boundary Integral
Let us now illustrate a general approach to express the 2D integrals in (16) as 1D integrals extended to the boundary of \(\varOmega\). Generality lies in the fact that, owing to the symmetry of the integrals, application of Gauss theorem can be based upon a unique formula. Actually, we are going to prove the general formula
where \(\iota _{\varvec{\rho }}={\varvec{\rho }}\cdot {\varvec{\kappa }}_z\), \({\varvec{\nu }}\) is the 2D outward unit normal to \(\partial {\varOmega }\) and \([\otimes {\varvec{\rho }},m]\) denotes a rank-\(m\) tensor defined by
To fix the ideas, we shall prove the identity (19) for \(m=2\)
since it allows us to illustrate our approach to a degree of generality sufficient to extend the final result to all integrals in (16) and to the additional ones, not reported in (16), containing tensors of rank superior to three, i.e., tensors of the kind \([\otimes {\varvec{\rho }},m]\) where \(m>3\). In the following, we shall make use of some differential identities that are collected in Appendix 1 in order to not divert the reader from the main stream of our derivation.
Let us consider the following identity involving the divergence of a rank-three tensor.
which stems from the identity (119) of Appendix 1. Furthermore, application of the identity (120) provides
since \({\varvec{\kappa }}_z\) is a constant vector field and \(\mathrm{grad}\,{\varvec{\rho }}=\mathbf{I}\) where \(\mathbf{I}\) is the rank-two identity tensor. Substituting the previous relation in (22), one obtains
Finally, integrating the previous identity over \(\varOmega\) yields
The second integral on the right-hand side can be computed by means of the general result (Tang 2006)
where \(\varphi\) is a scalar function and \(F\) denotes an arbitrary 2D domain. The previous expression can be extended to arbitrary tensors by applying it to each scalar component of the tensor. Furthermore, the quantity \(\alpha\) represents the angular measure, expressed in radians, of the intersection between \(F\) and a circular neighborhood of the singularity point \({\varvec{\rho }}={\varvec{o}}\), see D’Urso (2012, 2013a, 2014a) for additional details. Although its computation is not required in the ensuing developments, we specify for completeness that \(\alpha\) can be computed by means of the general algorithm detailed in D’Urso and Russo (2002).
On account of (26), one infers that the second integral on the right-hand side of (25) is the null rank-two tensor \(\mathbf{O}\) since
However, the expression \([\iota _{\varvec{\rho }}({\varvec{\rho }}\otimes {\varvec{\rho }})]_{{\varvec{\rho }}={\varvec{o}}}\) amounts to evaluating the quantity \(\iota _{\varvec{\rho }}({\varvec{\rho }}\otimes {\varvec{\rho }})\) at the singularity point \({\varvec{\rho }}={\varvec{o}}\), that yields trivially the null tensor \(\mathbf{O}\). Hence, according to (27), the last integral in (25) is always the null tensor, independently from the position of singularity point \({\varvec{\rho }}={\varvec{o}}\) with respect to the domain \(\varOmega\) of integration. In conclusion, upon application of Gauss theorem to the second integral in (25), we finally infer the identity (21). Remarkably, the derivation of this identity has also allowed us to prove that the singularity at \({\varvec{\rho }}={\varvec{o}}\), of the integrand function appearing on the left-hand side of (21), can be actually ignored.
Furthermore, it is not difficult to rephrase the path of reasoning detailed in formulas (22)–(27) so as to prove the more general formula (19). Hence, defining
one has, recalling definitions (17) and (18)
In conclusion, application of formula (19)–(16) yields
a formula that will be specialized to the case of polygonal domains in the next subsection.
2.2 Algebraic Expression of the Gravity Anomaly at O
In order to derive an algebraic expression suitable to be programmed, we specialize formula (31) to the case of a polygonal domain \(\varOmega\). Actually, this is by far the most common case since geological formations are either polygonal or can be approximated to polygons by subdividing the real boundary by an arbitrary number of vertices and edges. Once again, in order to illustrate the rationale of our derivation, we shall make reference to formula (21). In particular, denoting by \(n\) the common number of vertices and edges belonging to \(\partial {\varOmega }\) (see Fig. 1), formula (21) simplifies to
where \(s_i\) is the curvilinear abscissa along the ith edge \(\partial _{i}{\varOmega }\) of the boundary of \(\varOmega\).
The edge \(\partial _{i}{\varOmega }\) connects the vertices \({\varvec{\rho }}_{i}\) and \({\varvec{\rho }}_{i+1}\), see, e.g., Fig. 1, and it will be assumed that, along each edge, the relevant curvilinear abscissa has its origin at the ith vertex. Being the product \({\varvec{\rho }}(s_i)\cdot {\varvec{\nu }}(s_i)\) constant along each side, formula (32) becomes
where \({\varvec{\nu }}_{i}\) is the outward unit normal to the ith edge. Assuming a counterclockwise circulation sense along \(\partial _{i}{\varOmega }\) and denoting by \(l_i=|{\varvec{\rho }}_{i+1}-{\varvec{\rho }}_{i}|\) the length of the ith edge, it turns out \({\varvec{\nu }}_{i}=({\varvec{\rho }}_{i+1}-{\varvec{\rho }}_{i})^\perp /l_i\) where \((\cdot )^\perp\) denotes a clockwise rotation of \((\cdot )\). In particular, \({\varvec{\rho }}_{i}\cdot {\varvec{\nu }}_{i}={\varvec{\rho }}_{i}\cdot {\varvec{\rho }}_{i+1}^\perp /l_i\) where \({\varvec{\rho }}_{i+1}^\perp =(z_{i+1},-x_{i+1})\) (D’Urso 2013a).
Introducing in (32) the dimensionless abscissa \(\lambda _{i}=s_i/l_i,\) we finally get
which represents the starting point to derive the basic formulas useful for programming.
Actually, defining
we can express the integrals (28) and (29) as
Accordingly, formula (31) of the gravity anomaly simplifies as follows
The previous integrals can be evaluated analytically by introducing the following parameterization of the ith edge
In this way, one has
and
where
Furthermore,
Analogously, setting
one has
Thus, defining
formula (40) simplifies to
Grouping together the quantities multiplying the same exponent of \(\lambda _i\) and setting
formula (40) becomes
where
\(\theta _{\varvec{o}}\) is defined in (13), \(a_i,b_i\) in (42), \(\theta _{{\varvec{\rho }}_{i}}^O-\theta _{\Delta {{\varvec{\rho }}_{i}}}^O-\theta _{\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}}^O- \theta _{\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}}^O\) in (52)–(55).
The actual computation of the integrals \(I_{ki}\) will be detailed in Sect. 4. In particular, singularities in their expression, due to the vanishing of the denominator in (57), will be proved to be ineffective. Hence, formula (56) is singularity-free in the sense that, for edges characterized by singularities of the integrals \(I_{ki}\), the whole addend of the sum is zero.
3 Gravity Anomaly of a 2D Body at an Arbitrary Point P
Gravity anomaly calculations at an observation point which does not coincide with the origin of the reference frame have been first addressed by Zhou (2010). Specifically, the author devised two alternative formulations: the first one, named coordinate transformation, was conceived so as to make the observation point as the origin of the new coordinate system and employing the solution obtained by the author in Zhang et al. (2001) and Zhou (2009a). Clearly, this approach requires one to express the density contrast as a function of the new coordinates. In the second formulation proposed by Zhou (2010), named solution transformation, the solution at an arbitrary point is extrapolated from that obtained at the origin of the reference frame.
On the contrary, denoting by \({\varvec{\omega }}=(x_P,z_P)\) the position vector of an arbitrary point \(P\), we show that the approach illustrated in the previous section, as well as the function expressing the density contrast, can be left unchanged provided that one introduces the vector
defining the relative position of the generic point \({\varvec{\sigma }}=(x,z)\) of \(\varOmega\) with respect to \(P\), see, e.g., Fig. 2. Hence, the gravity anomaly at \(P\) is given by
an expression which trivially simplifies to (6) whenever \({\varvec{\omega }}={\varvec{o}}\). On account of (7), the previous expression becomes
where \(\mathbf{D}_{{\varvec{\sigma }}{\varvec{\sigma }}}\) and \({\varvec{{\mathbb {D}}}}_{{\varvec{\sigma }}{\varvec{\sigma }}{\varvec{\sigma }}}\) are defined as in (8).
To exploit the results illustrated in the previous section, it is convenient to express \({\varvec{\sigma }}\) as a function of \({\varvec{\rho }}\). For brevity, this is detailed only for the rank-three tensor \({\varvec{{\mathbb {D}}}}_{{\varvec{\sigma }}{\varvec{\sigma }}{\varvec{\sigma }}}\) since it is the more cumbersome to handle. In particular, recalling (58), one has
where \({\varvec{{\mathbb {D}}}}_{{\varvec{\omega }}{\varvec{\omega }}{\varvec{\omega }}}={\varvec{\omega }}\otimes {\varvec{\omega }}\otimes {\varvec{\omega }},\)
and
Hence, (60) becomes
which represents the generalization of (16) to the case \({\varvec{\omega }}\not ={\varvec{o}}\).
Special attention has to be paid to the symbol \(\mathbf{d}_{\varvec{\rho }}^{\varOmega }\otimes {\varvec{\omega }}\otimes \mathbf{d}_{\varvec{\rho }}^{\varOmega },\) which is a shorthand to denote the third-order tensor
In spite of its symbol, which has been adopted to emphasize its symmetric expression, the tensor above cannot be obtained as triple tensor product of the vectors \(\mathbf{d}_{\varvec{\rho }}^{\varOmega }\) and \({\varvec{\omega }}\). Rather, as detailed in Sect. 3.3, it is conveniently computed starting from the rank-two tensor \(\mathbf{D}^\varOmega _{{\varvec{\rho }}{\varvec{\rho }}}\). For the sake of clarity, and to parallel the treatment developed in the previous section, we shall consider separately the analytical expression of the gravity attraction at an arbitrary point \(P\) and its algebraic counterpart, i.e., the formula useful for programming.
3.1 Analytical Expression of the Gravity Anomaly at an Arbitrary Point P in Terms of Boundary Integral
Although \({\varvec{\rho }}\) is now defined from (58), it can be shown that formula (19) holds as well. Thus, recalling (30) and setting
formula (64) simplifies to
Obviously, (67) coincides with (31) when \({\varvec{\omega }}={\varvec{o}}\). We are now in the position to simplify (67) to the case of a polygonal boundary.
3.2 Algebraic Expression of the Gravity Anomaly at an Arbitrary Point P
On account of (38) and (39), formula (67) becomes
Furthermore, recalling the definitions (41)–(43), (45), (49), and (57), one can express (35)–(37)
In order to shorten the subsequent formulas to the maximum extent, it is convenient to introduce the following additional notation
and



The symbols  ,
,  ,
,  , and
, and  denote quantities that have been formally introduced in the previous expression simply to preserve its symmetry of representation and to facilitate the reader in checking the correctness of formula (81). As a matter of fact, they do not have to be computed since they are associated with the integral (65) and its discrete counterpart \(\mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\otimes {\varvec{\omega }}\otimes \mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\) in (68). The computation of this last quantity is addressed in Sect. 3.3.
denote quantities that have been formally introduced in the previous expression simply to preserve its symmetry of representation and to facilitate the reader in checking the correctness of formula (81). As a matter of fact, they do not have to be computed since they are associated with the integral (65) and its discrete counterpart \(\mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\otimes {\varvec{\omega }}\otimes \mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\) in (68). The computation of this last quantity is addressed in Sect. 3.3.
Substituting the previous expressions in (68) and defining
we get
where \(\theta _{\varvec{o}}\) is defined in (13), \(a_i,b_i\) in (42), \(I_{ki}\) \((k=0,1,2,3\)) in (57), \(\theta _{{\varvec{\rho }}_{i}}^O-\theta _{\Delta {{\varvec{\rho }}_{i}}}^O-\theta _{\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}}^O- \theta _{\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}}^O\) in (52)–(55), \(\theta _{{\varvec{\omega }}}\) in (66), \(\theta _{{\varvec{\rho }}_{i}}^P-\theta _{\Delta {{\varvec{\rho }}_{i}}}^P-\theta _{\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}}^P\) in (79) and (80).
By eliminating all terms depending explicitly on \({\varvec{\omega }}\), i.e., \(\theta _{{\varvec{\omega }}}\), \(\theta _{{\varvec{\rho }}_{i}}^P\), \(\theta _{\Delta {{\varvec{\rho }}_{i}}}^P\) and \(\theta _{\Delta {{\varvec{\rho }}_{i}}\Delta {{\varvec{\rho }}_{i}}}^P\), it can be easily checked that the previous expression does simplify to (56) when \({\varvec{\omega }}={\varvec{o}}\), i.e., when the gravity anomaly is evaluated at the origin of the reference frame. The previous expression is particularly useful for programming since \(I_{2i}\), \(I_{3i}\) and \(I_{4i}\) can be expressed as a function of \(I_{0i}\) and \(I_{1i}\) by means of formulas (130)–(132) detailed in Appendix 2. The resulting formula is not reported explicitly since it amounts to performing straightforward algebraic manipulations.
To derive an alternative expression of the gravity anomaly which can be conveniently used to check the correct implementation of the more efficient one reported in (81), one can set
and replace formulas (69)–(72) with
Hence, formula (68) becomes
a formula which can be further elaborated upon by expressing \(I_{2i}, I_{3i}\) and \(I_{4i}\) as a function of \(I_{0i}\) and \(I_{1i}\) in the formulas for \(\iota _{2i},\iota _{3i}\) and \(\iota _{4i}\).
3.3 Evaluation of the Third-Order Tensor \(\mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\otimes {\varvec{\omega }}\otimes \mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\)
We have denoted by the symbol \(\mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\otimes {\varvec{\omega }}\otimes \mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\) in (68) the third-order tensor
As a matter of fact, the tensor to evaluate is the rank-two tensor \(\mathbf{D}_{{\varvec{\rho }}{\varvec{\rho }}}^{\partial _{i}\varOmega }\) since its components have to be suitably combined with those of \({\varvec{\omega }}\) in order to compute (87). In turn, this depends upon the rule which is adopted to define the matrix associated with a third-order tensor, a rule which usually depends upon the adopted programming language. For instance, extending the rule defined in (11) to three arbitrary vectors \(\mathbf{t}\), \(\mathbf{v}\) and \(\mathbf{w},\) one obtains

The products \(t_1 w_1\), \(t_1 w_2\) are the components of the tensor \(\mathbf{t}\otimes \mathbf{w}\) which plays the role of the tensor \(\mathbf{D}_{{\varvec{\rho }}{\varvec{\rho }}}^{\partial _{i}\varOmega }\), i.e., the one to be actually computed.
Accordingly, we can define the matrix associated with \(\mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\otimes {\varvec{\omega }}\otimes \mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\) as

where \([\mathbf{D}_{{\varvec{\rho }}{\varvec{\rho }}}^{\partial _{i}\varOmega }]_{ij}\) denotes the \(ij\) entry of the matrix associated with \(\mathbf{D}_{{\varvec{\rho }}{\varvec{\rho }}}^{\partial _{i}\varOmega }\).
4 Ineffective Singularities of the Algebraic Expressions of the Gravity Anomaly
It has already been shown that the analytical expression (31) of the gravity anomaly is singularity-free in the sense that its expression holds rigorously whatever is the position of the point \(O\) with respect to \(\varOmega\). The same property holds true for the expression (67) referred to an arbitrary point \(P\). However, the algebraic counterparts of (31) and (67), which are provided by formulas (56) and (81), respectively, still hide some singularities.
They are associated with the expression of the integrals \(I_{ki}\), provided in (57), since some special positions of the generic edge of \(\partial {\varOmega }\) with respect to the observation point can make the denominator of (57) vanish. However, we are going to prove that such singularities are ineffective from the computational point of view since they can actually be ignored when evaluating the ith addend of the sums (56) and (81).
To fully understand this point, let us first notice that the opposite of the discriminant \(\varDelta _{i}\) of the quadratic function at the denominator in (57) is always nonnegative, being
by virtue of the Cauchy–Schwarz inequality (Tang 2006). The quantity \(\varDelta _i\) can vanish, making undefined the integral \(I_{ki}\) in (57), if and only if either \({\varvec{\rho }}_{i}({\varvec{\rho }}_{i+1}) = {\varvec{o}}\) or \({\varvec{\rho }}_{i}\) and \({\varvec{\rho }}_{i+1}\) are parallel. In turn, this happens when the observation point does belong to the line containing the ith edge. Accordingly, if \(\varDelta _i>0\), formulas (124) and (125) simplify to
and
respectively. Furthermore, formulas (130)–(132) can be used to evaluate \(I_{2i}\), \(I_{3i}\) and \(I_{4i}\).
Clearly, the previous expressions become singular if \(\varDelta _i=0\), i.e., when the ith edge does belong to a line containing the observation point. Nevertheless, we shall prove that the contribution of the ith edge to the gravity anomaly is zero. Hence, from the computational point of view, it is possible to skip the evaluation of the ith addend in formula (56) whenever the ith edge does belong to a line containing \(O\). The same property can be invoked for formulas (81) and (86) whenever the ith edge does belong to a line containing the arbitrary point \(P\) at which the gravity anomaly is required. The conditions stated above do hold when \({\varvec{\rho }}_{i}={\varvec{o}}\) or \({\varvec{\rho }}_{i+1}={\varvec{o}}\) or \({\varvec{\rho }}_{i}\) is parallel to \({\varvec{\rho }}_{i+1}\). These three cases will be addressed separately in the sequel.
4.1 Simplification of the Line Integrals (35)–(37) to the Case \({\varvec{\rho }}_{i}={\varvec{o}}\)
Recalling (41), the parameterization of the ith edge becomes
so that
and
Accordingly, we get from (35) to (37)
which is singular at \(\lambda _i=0\), and
However, \(d_{\varvec{\rho }}^{\partial _{i}\varOmega }\) in formulas (40) and (68), and hence the logarithm in (96), is scaled by \({\varvec{\rho }}_{i}\cdot {\varvec{\rho }}_{i+1}^\perp\). Setting \(\varepsilon =|{\varvec{\rho }}_{i}|\), we infer that
since the logarithm tends to infinite with an arbitrarily low degree. In addition, being \(\mathbf{d}_{\varvec{\rho }}^{\partial _{i}\varOmega }\), \(\mathbf{D}_{{\varvec{\rho }}{\varvec{\rho }}}^{\partial _{i}\varOmega }\) and \({{\varvec{{\mathbb {D}}}}}_{{\varvec{\rho }}{\varvec{\rho }}{\varvec{\rho }}}^{\partial _{i}\varOmega }\) finite, we ultimately infer that the contribution of the ith edge to the expressions (56), (81), and (86) of the gravity anomaly is zero.
4.2 Simplification of the Line Integrals (35)–(37) to the Case \({\varvec{\rho }}_{i+1}={\varvec{o}}\)
In this case, the ith edge is parameterized in the form
Hence,
and
Being \(\hbox {d}\lambda _i=-\hbox {d}\eta _i,\) one has
Hence, we can repeat the considerations developed in the previous subsection, by exchanging the role of \({\varvec{\rho }}_{i}\) and \({\varvec{\rho }}_{i+1}\), and conclude that the contribution of the ith edge to the expressions (56), (81), and (86) of the gravity anomaly vanishes.
4.3 Simplification of the Line Integrals (35)–(37) to the Case \({\varvec{\rho }}_{i}\Vert {\varvec{\rho }}_{i+1}\)
In this case, we can set \({\varvec{\rho }}_{i+1}=\beta _i{\varvec{\rho }}_{i}\) with \(0 < \beta _i= |{\varvec{\rho }}_{i+1}|/|{\varvec{\rho }}_{i}|\) and parameterize the ith edge as
where
and it has been assumed \(\beta _i>1\). As it will be apparent in the sequel, the case \(\beta _i<1\) does not modify the final result. Being also
and
and \(\hbox {d}\xi _i=\hbox {d}\lambda _i(\beta _i - 1),\) we now have
The four integrals above are well defined but are scaled by the quantity \({\varvec{\rho }}_{i}\cdot {\varvec{\rho }}_{i+1}^\perp,\) which is zero by hypothesis. Hence, recalling formulas (40) and (68), the ith edge does not give any contribution to the sum in (56), (81), and (86). In conclusion, it has been proved that, whenever \({\varvec{\rho }}_{i}\cdot {\varvec{\rho }}_{i+1}^\perp =0\), which is equivalent to state \({\varvec{\rho }}_{i}=0\) or \({\varvec{\rho }}_{i+1}=0\) or \({\varvec{\rho }}_{i}\Vert {\varvec{\rho }}_{i+1}\), the computation of the ith addend of the sum in (56), (81), and (86) can be skipped. Clearly, from the numerical point of view, the analytical condition \({\varvec{\rho }}_{i}\cdot {\varvec{\rho }}_{i+1}^\perp =0\) is replaced by \(\Vert {\varvec{\rho }}_{i}\cdot {\varvec{\rho }}_{i+1}^\perp \Vert \le \hbox{tol}\) where tol is a machine-dependent numerical tolerance (Table 1).
5 Numerical Examples
The formulas illustrated in the previous sections have been coded in a MATLAB program in order to check their correctness and robustness. They have been applied to model tests and case studies derived from the specialized literature. In particular, the density contrast has been assumed to vary separately along the horizontal and the vertical directions or along both of them. In all examples, the density contrast is expressed in units grams per cubic centimeter while distances are expressed in kilometers; the value of the gravitational constant \(G\) is 6.67259 × \(10^{-11}\) m\(^{3}\) kg\(^{-1}\) s\(^{-2}\).
For all the examples, we include a graphical and a tabular comparison between our results and those already published in the literature, although these last ones have been inferred, to the best of the author’s expertise, from the diagrams in which they have been originally reported. We also include the computing time (CT) obtained by running the MATLAB code on a INTEL CORE2 PC with 16 Gb of RAM and a i7-4700HQ CPU having clock speed of 2.40 GHz. They can be useful to allow for a comparison with computations carried out by using different methods or with more complex modellings, e.g., those required to evaluate the gravitational effects of an arbitrary volumetric mass layer in which a laterally varying radial density change has been assumed (Tenzer et al. 2012a, b, c).
The model test in Fig. 3 is a 2D rectangular cylinder at a depth of 1 km, 6 km wide, and 1 km high; it has been first considered by Rao (1986), and subsequently by Zhang et al. (2001), by assuming a density contrast given by
Figure 4 shows a perfect agreement between the solid line, representing jointly the results by Rao (1986) and Zhang et al. (2001), and the dotted line that has been computed by means of the proposed approach. Each point in the figure represents the gravity anomaly associated with a position of the observation point having as coordinates \(z=0\) and an abscissa \(x\) equal to that of the plotted point.
The second example, shown in Fig. 5, has been first addressed by García-Abdeslem et al. (2005b) and later considered in Zhou (2008). It refers to the Sebastián Vizcaíno Basin in Mexico for which the density contrast has been assumed in the form
where \(z\) is expressed in meters. The gravity anomaly along a transect on the x-axis is shown in Fig. 6 and successfully compared with that computed in Zhou (2008) by two distinct methodologies named LI with arctangent kernel and density integrated LI. In both methodologies, Zhou evaluated the resulting integrals by the Gauss–Legendre quadrature method (Table 2).
Figure 7 illustrates an elongated segment valley first considered by Murthy and Rao (1979) and later analyzed by Zhang et al. (2001). The density contrast is given by
where \(z\) is expressed in meters. Figure 8 shows the comparison of the gravity anomaly computed by different procedures, i.e., the one presented in Zhang et al. (2001), the two methodologies quoted above by Zhou (2008) and that contributed in the present paper (Table 3).
Figure 9 illustrates a case analyzed by Martín-Atienza and García-Abdeslem (1999), Zhou (2009a, 2010) in which the density contrast varies only along the horizontal position
The gravity anomaly, calculated along a transect on the x-axis, is shown in Fig. 10 where our results are compared with those obtained by Zhou (2010). These last results had been previously compared by Zhou with those based on the LI method with logarithmic kernel, previously contributed in Zhou (2009a), and the original results by Martín-Atienza and García-Abdeslem (1999) (Table 4).
The last numerical example, shown in Fig. 11, refers to a case first studied by Martín-Atienza and García-Abdeslem (1999) and later re-examined in Zhou (2009a). The geometry in Fig. 11 refers to folded and overturned strata in a sedimentary basin in which the density contrast varies simultaneously along the horizontal and vertical directions
The boundary of the body has been approximated by a 26-sided polygon, and the gravity anomaly has been computed at 41 stations. The high number of polygon vertices and the more complex density contrast function explain the computing time of 0.32681 s which is considerably higher than those experienced in previous examples. Figure 12 superimposes our results with those obtained by Martín-Atienza and García-Abdeslem (1999), the seminumerical LI method by Zhou (2009a), and the analytical method in Zhou (2010) (Table 5).
5.1 Error Analysis
It is interesting to consider the susceptibility of the formulas derived in the paper to numerical rounding error. As shown in Holstein and Ketteridge (1996), this depends on the target aspect ratio \(\gamma =\alpha /\delta\) where \(\alpha\) is the typical linear dimension of the target and \(\delta\) its typical distance from the observation point. For 2D bodies, the anomaly calculation (6) is governed by an area integral weighted by the density contrast, the vertical component of the position vector, proportional to \(\delta\), and the inverse square law factor, proportional to \(1/\delta ^2\).
The density contrast functions considered in the previous examples show that \(\theta ({\varvec{\rho }})\) is obtained as the sum of separate terms having substantially the same order of magnitude as the constant term \(\theta _{\varvec{o}}\). Nevertheless one has to consider separately the integrals (17) and (18), and compute their one-dimensional counterparts (28) and (29).
In particular, we have
and
where \(\approx\) means “has order of magnitude equal to.”
Thus, when computed in a finite floating point precision \(\epsilon\), the rounding error \(O(\delta ^k\gamma \epsilon ),k=1,\ldots 4\), progressively increases as the target distance \(\delta\) increases relative to the target size \(\alpha\). However, as shown in the previous figures, this is generally beyond the region of geophysical interest.
As a final remark, it is worth mentioning that higher-order terms in the density contrast, though more prone to computational noise as \(\delta\) increases, provide a progressively lower contribution to the gravity anomaly. This is in accordance with the significance of higher-order density polynomials in 2D modelling. As a matter of fact, geological settings require mostly 3D gravity modelling: the errors caused by 2D gravity modelling with high-order polynomials will often be larger than the errors caused by piecewise constant densities in a relative few number of 3D polygonal bodies.
6 Conclusions
The gravity anomaly at arbitrary points produced by a 2D body whose shape is an arbitrary polygon and where density contrast varies with a polynomial law has been obtained in closed form. It is expressed as a sum of quantities that depend only upon the coordinates of the vertices of the polygon and upon the parameters that define the density contrast. The solution procedure, based upon a generalized application of Gauss theorem, takes consistently into account the singularity intrinsic to the integrals to evaluate. Accordingly, by means of rigorous mathematical arguments, singularities are proved to give no contribution either to the analytical expression of the gravity anomaly or to its algebraic counterpart.
The formulation presented in the paper, which has been limited to polynomial density contrasts varying with a cubic law as a maximum, can be easily extended to polynomials of higher degree. The effectiveness of the proposed approach has been intensively tested by numerical comparisons, carried out by means of a MATLAB code, with several examples derived from the specialized literature. Future contributions will concern the cases of density contrast variable with exponential law for 2D domains and 3D polyhedral bodies endowed with polynomial or exponential density contrasts.
References
Aydemir A, Ates A, Bilim F, Buyuksarac A, Bektas O (2014) Evaluation of gravity and aeromagnetic anomalies for the deep structure and possibility of hydrocarbon potential of the region surrounding Lake Van, Eastern Anatolia, Turkey. Surv Geophys 35:431–448
Banerjee B, DasGupta SP (1977) Gravitational attraction of a rectangular parallelepiped. Geophysics 42:1053–1055
Barnett CT (1976) Theoretical modeling of the magnetic and gravitational fields of an arbitrarily shaped three-dimensional body. Geophysics 41:1353–1364
Bott MHP (1960) The use of rapid digital computing methods for direct gravity interpretation of sedimentary basins. Geophys J R Astron Soc 3:63–67
Cady JW (1980) Calculation of gravity and magnetic anomalies of finite length right polygonal prisms. Geophysics 45:1507–1512
Cai Y, Wang CY (2005) Fast finite-element calculation of gravity anomaly in complex geological regions. Geophys J Int 162:696–708
Chai Y, Hinze WJ (1988) Gravity inversion of an interface above which the density contrast varies exponentially with depth. Geophysics 53:837–845
Chakravarthi V, Raghuram HM, Singh SB (2002) 3-D forward gravity modeling of basement interfaces above which the density contrast varies continuously with depth. Comput Geosci 28:53–57
Chakravarthi V, Sundararajan N (2007) 3D gravity inversion of basement relief: a depth-dependent density approach. Geophysics 72:I23–I32
Chappell A, Kusznir N (2008) An algorithm to calculate the gravity anomaly of sedimentary basins with exponential density–depth relationships. Geophys Prospect 56:249–258
Cordell L (1973) Gravity analysis using an exponential density depth function—San Jacinto graben, California. Geophysics 38:684–690
D’Urso MG, Russo P (2002) A new algorithm for point-in polygon test. Surv Rev 284:410–422
D’Urso MG (2012) New expressions of the gravitational potential and its derivates for the prism. In: Sneeuw N, Novák P, Crespi M, Sansò F (eds) Hotine–Marussi international symposium on mathematical geodesy, 7th edn. Springer, Berlin, pp 251–256
D’Urso MG (2013a) On the evaluation of the gravity effects of polyhedral bodies and a consistent treatment of related singularities. J Geod 87:239–252
D’Urso MG, Marmo F (2013b) On a generalized Love’s problem. Comput Geosci 61:144–151
D’Urso MG (2014a) Analytical computation of gravity effects for polyhedral bodies. J Geod 88:13–29
D’Urso MG (2014b) Gravity effects of polyhedral bodies with linearly varying density. Cel Mech Dyn Astron 120:349–372
D’Urso MG, Marmo F (2015a) Vertical stress distribution in isotropic half-spaces due to surface vertical loadings acting over polygonal domains. Zeit Ang Math Mech 95:91–110
D’Urso MG (2015b) A remark on the computation of the gravitational potential of masses with linearly varying density. In: Sneeuw N, Novák P, Crespi M, Sansò F (eds) Hotine–Marussi international symposium on mathematical geodesy, 8th edn. Springer, Berlin (in press)
D’Urso MG, Trotta S (2015c) Comparative assessment of linear and bilinear prism-based strategies for terrain correction computations. J Geod. doi:10.1007/s00190-014-0770-4
Gallardo-Delgado LA, Pérez-Flores MA, Gómez-Treviño E (2003) A versatile algorithm for joint 3D inversion of gravity and magnetic data. Geophysics 68:949–959
García-Abdeslem J (1992) Gravitational attraction of a rectangular prism with depth dependent density. Geophysics 57:470–473
García-Abdeslem J (2005a) Gravitational attraction of a rectangular prism with density varying with depth following a cubic polynomial. Geophysics 70:J39–J42
García-Abdeslem J, Romo JM, Gómez-Treviño E, Ramírez-Hernández J, Esparza-Hernández FJ, Flores-Luna CF (2005b) A constrained 2D gravity model of the Sebastián Vizcaíno Basin, Baja California Sur, Mexico. Geophys Prospect 53:755–765
Gendzwill J (1970) The gradational density contrast as a gravity interpretation model. Geophysics 35:270–278
Golizdra GY (1981) Calculation of the gravitational field of a polyhedra. Izv Earth Phys 17:625–628 (English translation)
Götze HJ, Lahmeyer B (1988) Application of three-dimensional interactive modeling in gravity and magnetics. Geophysics 53:1096–1108
Guspí F (1990) General 2D gravity inversion with density contrast varying with depth. Geoexploration 26:253–265
Hamayun P, Prutkin I, Tenzer R (2009) The optimum expression for the gravitational potential of polyhedral bodies having a linearly varying density distribution. J Geod 83:1163–1170
Hansen RO (1999) An analytical expression for the gravity field of a polyhedral body with linearly varying density. Geophysics 64:75–77
Holstein H, Ketteridge B (1996) Gravimetric analysis of uniform polyhedra. Geophysics 61:357–364
Holstein H (2003) Gravimagnetic anomaly formulas for polyhedra of spatially linear media. Geophysics 68:157–167
Hubbert MK (1948) A line-integral method of computing the gravimetric effects of two-dimensional masses. Geophysics 13:215–225
Jacoby W, Smilde PL (2009) Gravity interpretation—fundamentals and application of gravity inversion and geological interpretation. Springer, Berlin
Jiancheng H, Wenbin S (2010) Comparative study on two methods for calculating the gravitational potential of a prism. Geospat Inf Sci 13:60–64
Johnson LR, Litehiser JJ (1972) A method for computing the gravitational attraction of three dimensional bodies in a spherical or ellipsoinal earth. J Geophys Res 77:6999–7009
Kwok YK (1991a) Singularities in gravity computation for vertical cylinders and prisms. Geophys J Int 104:1–10
Kwok YK (1991b) Gravity gradient tensors due to a polyhedron with polygonal facets. Geophys Prospect 39:435–443
Li X, Chouteau M (1998) Three-dimensional gravity modelling in all spaces. Surv Geophys 19:339–368
Litinsky VA (1989) Concept of effective density: key to gravity depth determinations for sedimentary basins. Geophysics 54:1474–1482
Martín-Atienza B, García-Abdeslem J (1999) 2-D gravity modeling with analytically defined geometry and quadratic polynomial density functions. Geophysics 64:1730–1734
Montana CJ, Mickus KL, Peeples WJ (1992) Program to calculate the gravitational field and gravity gradient tensor resulting from a system of right rectangular prisms. Comput Geosci 18:587–602
Mostafa ME (2008) Finite cube elements method for calculating gravity anomaly and structural index of solid and fractal bodies with defined boundaries. Geophys J Int 172:887–902
Murthy IVR, Rao DB (1979) Gravity anomalies of two-dimensional bodies of irregular cross-section with density contrast varying with depth. Geophysics 44:1525–1530
Murthy IVR, Rao DB, Ramakrishna P (1989) Gravity anomalies of three dimensional bodies with a variable density contrast. Pure Appl Geophys 30:711–719
Nagy D (1966) The gravitational attraction of a right rectangular prism. Geophysics 31:362–371
Nagy D, Papp G, Benedek J (2000) The gravitational potential and its derivatives for the prism. J Geod 74:553–560
Okabe M (1979) Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translation into magnetic anomalies. Geophysics 44:730–741
Pan JJ (1989) Gravity anomalies of irregularly shaped two-dimensional bodies with constant horizontal density gradient. Geophysics 54:528–530
Paul MK (1974) The gravity effect of a homogeneous polyhedron for three-dimensional interpretation. Pure Appl Geophys 112:553–561
Petrović S (1996) Determination of the potential of homogeneous polyhedral bodies using line integrals. J Geod 71:44–52
Plouff D (1975) Derivation of formulas and FORTRAN programs to compute gravity anomalies of prisms. Natl. tech. inf. serv. no. PB-243-526. US Department of Commerce, Springfield
Plouff D (1976) Gravity and magnetic fields of polygonal prisms and application to magnetic terrain corrections. Geophysics 41:727–741
Pohanka V (1988) Optimum expression for computation of the gravity field of a homogeneous polyhedral body. Geophys Prospect 36:733–751
Pohanka V (1998) Optimum expression for computation of the gravity field of a polyhedral body with linearly increasing density. Geophys Prospect 46:391–404
Rao DB (1985) Analysis of gravity anomalies over an inclined fault with quadratic density function. Pure Appl Geophys 123:250–260
Rao DB (1986) Modeling of sedimentary basins from gravity anomalies with variable density contrast. Geophys J R Astron Soc 84:207–212
Rao DB (1990) Analysis of gravity anomalies of sedimentary basins by an asymmetrical trapezoidal model with quadratic function. Geophysics 55:226–231
Rao DB, Prakash MJ, Babu RN (1990) 3D and 2 \(1/2\) modeling of gravity anomalies with variable density contrast. Geophys Prospect 38:411–422
Rao CV, Chakravarthi V, Raju ML (1994) Forward modelling: gravity anomalies of two-dimensional bodies of arbitrary shape with hyperbolic and parabolic density functions. Comput Geosci 20:873–880
Rosati L, Marmo F (2014) Closed-form expressions of the thermo-mechanical fields induced by a uniform heat source acting over an isotropic half-space. Int J Heat Mass Transf 75:272–283
Ruotoistenmäki T (1992) The gravity anomaly of two-dimensional sources with continuous density distribution and bounded by continuous surfaces. Geophysics 57:623–628
Sessa S, D’Urso MG (2013) Employment of Bayesian networks for risk assessment of excavation processes in dense urban areas. In: Proceedings of the 11th international conference (ICOSSAR 2013), pp 30163–30169
Silva JB, Costa DCL, Barbosa VCF (2006) Gravity inversion of basement relief and estimation of density contrast variation with depth. Geophysics 71:J51–J58
Strakhov VN (1978) Use of the methods of the theory of functions of a complex variable in the solution of three-dimensional direct problems of gravimetry and magnetometry. Dokl Akad Nauk 243:70–73
Strakhov VN, Lapina MI, Yefimov AB (1986) A solution to forward problems in gravity and magnetism with new analytical expression for the field elements of standard approximating body. Izv Earth Phys 22:471–482 (English translation)
Talwani M, Worzel JL, Landisman M (1959) Rapid gravity computations for two-dimensional bodies with application to the Mendocino submarine fracture zone. J Geophys Res 64:49–59
Tang KT (2006) Mathematical methods for engineers and scientists. Springer, Berlin
Tenzer R, Novák P, Vajda P, Gladkikh V (2012a) Spectral harmonic analysis and synthesis of Earth’s crust gravity field. Comput Geosci 16:193–207
Tenzer R, Gladkikh V, Vajda P, Novák P (2012b) Spatial and spectral analysis of refined gravity data for modelling the crust–mantle interface and mantle–lithosphere structure. Surv Geophys 33:817–839
Tenzer R, Novák P, Hamayun, Vajda P (2012c) Spectral expressions for modelling the gravitational field of the Earth’s crust density structure. Stud Geophys Geod 56:141–152
Tsoulis D (2000) A note on the gravitational field of the right rectangular prism. Boll Geod Sci Aff LIX–1:21–35
Tsoulis D, Petrović S (2001) On the singularities of the gravity field of a homogeneous polyhedral body. Geophysics 66:535–539
Tsoulis D (2012) Analytical computation of the full gravity tensor of a homogeneous arbitrarily shaped polyhedral source using line integrals. Geophysics 77:F1–F11
Waldvogel J (1979) The Newtonian potential of homogeneous polyhedra. J Appl Math Phys 30:388–398
Werner RA (1994) The gravitational potential of a homogeneous polyhedron. Celest Mech Dyn Astron 59:253–278
Werner RA, Scheeres DJ (1997) Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia. Celest Mech Dyn Astron 65:313–344
Won IJ, Bevis M (1987) Computing the gravitational and magnetic anomalies due to a polygon: algorithms and FORTRAN subroutines. Geophysics 52:232–238
Zhang J, Zhong B, Zhou X, Dai Y (2001) Gravity anomalies of 2D bodies with variable density contrast. Geophysics 66:809–813
Zhou X (2008) 2D vector gravity potential and line integrals for the gravity anomaly caused by a 2D mass of depth-dependent density contrast. Geophysics 73:I43–I50
Zhou X (2009a) General line integrals for gravity anomalies of irregular 2D masses with horizontally and vertically dependent density contrast. Geophysics 74:I1–I7
Zhou X (2009b) 3D vector gravity potential and line integrals for the gravity anomaly of a rectangular prism with 3D variable density contrast. Geophysics 74:I43–I53
Zhou X (2010) Analytical solution of gravity anomaly of irregular 2D masses with density contrast varying as a 2D polynomial function. Geophysics 75:I11–I19
Acknowledgments
The author wishes to express his deep gratitude to the Editor-in-Chief, Prof. M.J. Rycroft, and to the three anonymous reviewers for careful suggestions and useful comments that resulted in an improved version of the original manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Some Useful Differential Identities
We prove hereafter some differential identities that are useful for the derivations illustrated in the main body of the paper; they are reported in the same order in which they are required.
Let us begin with the component expression of the divergence of the rank-three tensor
where \(\mathbf{a}\), \(\mathbf{b}\), \(\mathbf{c}\) (\(\psi\)) are vector (scalar) differentiable fields and \((\cdot )_{/k}\) means derivation with respect to the \(k\)th variable. Applying the chain rule to (117), Tang (2006), one obtains
Thus, combining (117) and (118), one has
A further useful identity concerns the gradient of a scalar field expressed as scalar product of two vector fields
where \((\cdot )^\mathrm{t}\) stands for transpose. It stems from the relation
Actually, carrying out the derivations in the previous expression yields
which represents the component form of (120).
Appendix 2: Recursive Computation of Integrals
Application of formula (56) requires the analytical computation of integrals of the kind
where \(p>0\) and the discriminant of the denominator, i.e., \(\varDelta =q^2-pu\), is assumed to be negative. Hence, the quadratic function \(p x^2 + 2 q x + u\) is always positive on the real interval [0, 1]. The case of a null discriminant \(\varDelta\) will be directly addressed in Sect. 4 where the evaluation of \(I_{ki}\), which makes use of the formulas derived hereafter for \(\varDelta < 0\), will be detailed.
As previously shown by Zhou (2010), the generic integral (123) can be computed recursively as a function of two integrals, namely
and
Both results can be obtained, after some manipulation, by setting \(t=x+q/p\) in the integrand functions above. To make the paper self-contained, we rephrase the result given in Zhou (2010)
where \(k>1\) and the terminology of this paper has been adopted.
For instance, if \(k=2\), one has
Analogously,
and
Hence,
and
Rights and permissions
About this article
Cite this article
D’Urso, M.G. The Gravity Anomaly of a 2D Polygonal Body Having Density Contrast Given by Polynomial Functions. Surv Geophys 36, 391–425 (2015). https://doi.org/10.1007/s10712-015-9317-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-015-9317-3