Evaluation of Optimal Formulas for Gravitational Tensors up to Gravitational Curvatures of a Tesseroid

Abstract

The forward modeling of the topographic effects of the gravitational parameters in the gravity field is a fundamental topic in geodesy and geophysics. Since the gravitational effects, including for instance the gravitational potential (GP), the gravity vector (GV) and the gravity gradient tensor (GGT), of the topographic (or isostatic) mass reduction have been expanded by adding the gravitational curvatures (GC) in geoscience, it is crucial to find efficient numerical approaches to evaluate these effects. In this paper, the GC formulas of a tesseroid in Cartesian integral kernels are derived in 3D/2D forms. Three generally used numerical approaches for computing the topographic effects (e.g., GP, GV, GGT, GC) of a tesseroid are studied, including the Taylor Series Expansion (TSE), Gauss–Legendre Quadrature (GLQ) and Newton–Cotes Quadrature (NCQ) approaches. Numerical investigations show that the GC formulas in Cartesian integral kernels are more efficient if compared to the previously given GC formulas in spherical integral kernels: by exploiting the 3D TSE second-order formulas, the computational burden associated with the former is 46%, as an average, of that associated with the latter. The GLQ behaves better than the 3D/2D TSE and NCQ in terms of accuracy and computational time. In addition, the effects of a spherical shell’s thickness and large-scale geocentric distance on the GP, GV, GGT and GC functionals have been studied with the 3D TSE second-order formulas as well. The relative approximation errors of the GC functionals are larger with the thicker spherical shell, which are the same as those of the GP, GV and GGT. Finally, the very-near-area problem and polar singularity problem have been considered by the numerical methods of the 3D TSE, GLQ and NCQ. The relative approximation errors of the GC components are larger than those of the GP, GV and GGT, especially at the very near area. Compared to the GC formulas in spherical integral kernels, these new GC formulas can avoid the polar singularity problem.

1 Introduction

A tesseroid mass body (see Fig. 1) has been utilized widely for gravity/magnetic forward modeling in related geoscience applications. Specifically, many research works have been devoted to the application of the Taylor Series Expansion (TSE) approach for calculating the topographic effects of a tesseroid. The 3D TSE approach was implemented for the calculation of the gravitational potential (GP) and radial part of the gravity vector (GV) formulas of a tesseroid by Heck and Seitz (2007). Wild-Pfeiffer (2008) utilized the 3D/2D TSE and Gauss–Legendre cubature for numerical calculation of the radial gravity gradient tensor (GGT) ($M_{zz}$) compared to a spherical cap with closed and rigorous reference value. Grombein et al. (2013) adopted the 3D TSE approach for numerical evaluation of the GP, GV and GGT formulas of a tesseroid in Cartesian integral kernels. Deng et al. (2016) provided the correct form of the GP formulas using the 3D TSE approach by correcting the related works of Heck and Seitz (2007) and Grombein et al. (2013), which is widely applied for higher-order tesseroid formulas. Recently, differently from the TSE second-order tesseroid formulas given by Heck and Seitz (2007), Wild-Pfeiffer (2008), Grombein et al. (2013) and related studies (i.e., Tsoulis et al. 2009; Chaves and Ussami 2013; Claessens and Hirt 2013; Hirt and Kuhn 2014; Du et al. 2015; Shen and Han 2013, 2014, 2016; Grombein et al. 2014, 2016, 2017), Shen and Deng (2016) expanded the 3D TSE approach from the second-order to the fourth-order GP tesseroid formulas and evaluated its reliability. Furthermore, Deng and Shen (2017b) offered the 3D TSE zero-order, second-order, fourth-order and six-order GP, GV, GGT and gravitational curvatures (GC) formulas of a tesseroid in spherical integral kernels, where GC represent the components of the third-order gravitational tensor. The term “Cartesian integral kernels” means that the integral kernels expressions of the gravitational effects are represented in a Cartesian coordinate system as well as “spherical integral kernels” refers to a spherical one.

Fig. 1

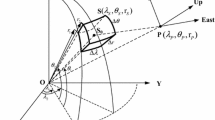
Definition of a tesseroid by modifying after Kuhn (2003). $\Delta \lambda$, $\Delta \theta$ and $\Delta r$ are the dimensions of a tesseroid, where $\Delta \lambda = \lambda_{2} - \lambda_{1}$, $\Delta \theta = \theta_{2} - \theta_{1}$ and $\Delta r = r_{2} - r_{1}$. $x$, $y$ and $z$ are in the local Cartesian East–North–Up coordinates of computation point $P$ with respect to the integration point $S$. The points $P(\lambda_{P} ,\theta_{P} ,r_{P} )$ and $S(\lambda_{S} ,\theta_{S} ,r_{S} )$ are also in the global spherical coordinates. The point $S_{0}$ is the geometric center point of a tesseroid, where the TSE method is applied, the integration point $S$ is equal to $S_{0}$

The Gauss–Legendre Quadrature (GLQ) approach has been extensively applied to evaluate the related geodetic applications as well. Ku (1977) introduced the numerical GLQ approach into the gravity/magnetic forward modeling. Asgharzadeh et al. (2007) applied the GLQ approach to evaluate the topographic effects (i.e., GP, GV and GGT) of a tesseroid, which is the same as Asgharzadeh et al. (2008) considered the magnetic effects (i.e., magnetic potential (MP), magnetic vector (MV) and magnetic gradient tensor (MGT)). Li et al. (2011) proposed the adaptive recursive algorithm based on the GLQ approach for modeling the topographic effects in spherical coordinates. Hirt et al. (2011) recommended the GLQ approach with mean kernels as accurate numerical evaluation of different geodetic convolution integrals (i.e., Stoke’s integral, Hotine’s integral, Eötvös’s integral, Green-Molodensky integral, tidal displacement integral, ocean tide loading integral, deflection-geoid integral, Vening-Meinesz’s integral). Roussel et al. (2015) adopted the GLQ approach to numerically evaluate the topographic effects (i.e., GP, GV and GGT) of an ellipsoidal prism. Du et al. (2015) compared the 3D TSE and GLQ approaches in evaluating the magnetic effects (i.e., MP, MV and MGT) of a tesseroid. Recently, Uieda et al. (2016) released the software Tesseroids for modeling the topographic effects (i.e., GP, GV and GGT) of a tesseroid with the GLQ approach. Analogously, the software by forward modeling the magnetic effects (i.e., MP, MV and MGT) of a tesseroid was distributed by Baykiev et al. (2016), which is the same as Uieda et al. (2016) did by applying the GLQ approach for numerical evaluation.

In modeling the GP, GV and GGT of a tesseroid, there exists the very-near-area problem. This means that anomalous errors do appear when the tesseroid mass element is rather close to the computation point in arbitrary direction. To solve this issue, Heck and Seitz (2007) suggested replacing the tesseroid bodies with equivalent prisms at very near area. Tsoulis et al. (2009) applied the combination approach of the prism in near region and the tesseroid in far region for evaluating the terrain correction of the GV. Li et al. (2011) proposed the algorithm by recursively dividing the grid resolution according to distance from the computation point based on the GLQ approach. Grombein et al. (2013) recommended the numerical horizontal subdivision approach, namely higher grid resolution based on the 3D TSE second-order approach. Recently, Shen and Deng (2016) proposed the combination method of the 3D TSE formulas of a tesseroid with different orders in different regions (i.e., very near zone, near zone, transition zone and far region), and recommend the boundaries of the different regions in spherical distance are 1°, 15°, and 40° to achieve the accuracy of 10⁻⁵ m² s⁻² for the GP evaluation at the low latitude. In addition, Uieda et al. (2016) expanded the recursive algorithm of Li et al. (2011) to the “stack-based” algorithm by adaptively controlling the distance-size ratio, where the optimal recommendation values of the distance-size ratio for the GP, GV and GGT are 1, 1.5 and 8, respectively.

The gravity forward modeling of the GC in spherical integral kernels of a tesseroid is a time-consuming work, which was shown in Deng and Shen (2017b), due to the complicated transformation relationships as presented by Tóth (2005), Tóth and Földváry (2005), Casotto and Fantino (2009), Šprlák et al. (2016), Šprlák and Novák (2015, 2016, 2017) and Novák et al. (2017). The present study focuses on the derivation of the optimal GC formulas of a tesseroid in Cartesian integral kernels. Analogously to the Cartesian integral kernels for the GP, GV and GGT formulas provided in Grombein et al. (2013), the Cartesian integral kernels for the GC are derived in both 3D and 2D forms. Applying these new GC formulas provides a significant improvement in terms of the computational burden if compared to the previously published GC formulas in spherical integral kernels (Deng and Shen 2017b). Moreover, these new GC formulas are also implemented in evaluating the polar singularity problem when the computation point is located at the North pole. The 3D/2D TSE, GLQ and Newton–Cotes Quadrature (NCQ) approaches are applied and compared in evaluating the new optimal GC formulas in terms of the trade-off effects between the computational time and numerical accuracy.

This paper is organized as follows. In Sect. 2 the theoretical aspects are presented, where in Sect. 2.1 the 3D and 2D GC formulas of a tesseroid in Cartesian integral kernels are derived, and Sect. 2.2 shows the analytical consistency of the GC formulas in both spherical and Cartesian integral kernels. The algorithms of three different approaches, namely the 3D/2D TSE, GLQ and NCQ, are briefly reviewed in Sect. 3. The numerical experiments are investigated in Sect. 4, and the advantages of the optimal GC formulas are shown by two numerical experiments in Sects. 4.1 and 4.5, respectively. In Sect. 4.2, the 3D/2D TSE, GLQ and NCQ approaches are applied for evaluating the GP, GV, GGT and GC formulas in Cartesian integral kernels. Furthermore, the effects of the spherical shell’s thickness and large-scale geocentric distance, which is from the field point $P$ to the center of the Earth, on the GP, GV, GGT and GC functionals in Cartesian integral kernels are investigated in Sects. 4.3 and 4.4, respectively. Finally, conclusions are summarized and main topics of further research work are recommended in Sect. 5.

2 Theoretical Aspects

2.1 Optimal 3D and 2D GC Formulas of a Tesseroid in Cartesian Integral Kernels

The optimal GP, GV and GGT formulas of a tesseroid in Cartesian integral kernels can be referred in Grombein et al. (2013) and Uieda et al. (2016). The optimal GC formulas of a tesseroid in Cartesian integral kernels are derived herein from second-order derivatives to third-order derivatives. Following the Leibniz integral rule and the prism and point-mass expressions (Kellogg 1929, p. 152; Tsoulis 1999; Nagy et al. 2000; Heck and Seitz 2007; Wild-Pfeiffer 2008; Grombein et al. 2013), the optimal GC formulas in Cartesian integral kernels, denoted as $V_{ijk}^{{O - T3{\text{D}}}}$, of a homogeneous tesseroid mass body with a constant density $\rho_{S}$ (see Fig. 1) can be expressed as

$$ V_{ijk}^{{O - T3{\text{D}}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} I^{{V_{ijk} }} {\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(1)

$$ I^{{V_{ijk} }} = \left( {\frac{15\Delta i\Delta j\Delta k}{{\mathcal{L}_{PS}^{7} }} - \frac{3}{{\mathcal{L}_{PS}^{5} }}p_{ijk} } \right)K $$

(2)

$$ K = G\rho_{S} r_{S}^{2} \cos \theta_{S} $$

(3)

$$ \mathcal{L}_{PS} = \sqrt {\Delta i\Delta i} = \sqrt {\Delta x^{2} + \Delta y^{2} + \Delta z^{2} } \left( {i \in \{ x,y,z\} } \right) $$

(4)

$$ \Delta x = r_{S} \cos \theta_{S} \sin \left( {\lambda_{S} - \lambda_{P} } \right) $$

(5)

$$ \Delta y = r_{S} \left( {\cos \theta_{P} \sin \theta_{S} - \sin \theta_{P} \cos \theta_{S} \cos \left( {\lambda_{P} - \lambda_{S} } \right)} \right) $$

(6)

$$ \Delta z = r_{S} \cos \psi - r_{P} $$

(7)

$$ \cos \psi = \sin \theta_{P} \sin \theta_{S} + \cos \theta_{P} \cos \theta_{S} \cos \left( {\lambda_{P} - \lambda_{S} } \right) $$

(8)

$$ p_{ijk} = \left\{ {\begin{array}{*{20}c} {3\Delta i} & {i = j = k} & {} \\ 0 & {i \ne j\& i \ne k\& j \ne k} & {} \\ T & {\text{otherwise}} & {} \\ \end{array} } \right. $$

(9)

$$ T = \left\{ {\begin{array}{*{20}c} {\Delta i} & {j = k\& i \ne j,\Delta j = \Delta k} & {} \\ {\Delta j} & {i = k\& i \ne j,\Delta i = \Delta k} & {} \\ {\Delta k} & {i = j\& i \ne k,\Delta i = \Delta j} & {} \\ \end{array} } \right. $$

(10)

where $G$ is the gravitational constant; ($\Delta x$, $\Delta y$, $\Delta z$) are the coordinates differences of the source (or running) point $S$ with respect to the local Cartesian topocentric coordinate system of the origin point $P$, named the local p-xyz East–North–Up (ENU) coordinate system (Casotto and Fantino 2009, Fantino and Casotto 2009; Roussel et al. 2015; Szwillus et al. 2016; Deng and Shen 2017a, b), which is slightly different from the North-East-Up (NEU) coordinate system in Tóth (2005), Tóth and Földváry (2005), Wild-Pfeiffer (2008) and Grombein et al. (2013). The ENU is a right-handed system: its origin is at the field point $P$, x-axis points to the East, y-axis points to the North, and z-axis points radially outward the radial direction; whereas the NEU is a left-handed system: its origin is also at the point $P$, x-axis points to the North, y-axis points to the East, and z-axis points radially outward to the radial direction (Casotto and Fantino 2009). $\lambda_{P}$, $\theta_{P}$ and $r_{P}$($\lambda_{P} \in \left[ {0,2\pi } \right]$, $\theta_{P} \in \left[ { - \pi /2,\pi /2} \right]$) are in spherical coordinates of point $P$, where $\lambda_{P}$ is spherical longitude, $\theta_{P}$ is spherical latitude, and $r_{P}$ is radial radius from the Earth center $O$ to point $P$. Analogously, $\lambda_{S}$, $\theta_{S}$ and $r_{S}$ ($\lambda_{S} \in \left[ {0,2\pi } \right],\theta_{S} \in \left[ { - \pi /2,\pi /2} \right]$) are also in spherical coordinates of point $S$. $\mathcal{L}_{PS}$ is the Euclidean distance between points $P$ and $S$, and $\psi$ denotes the angle between the position vectors of points $P$ and $S$ as the spherical distance. $I^{{V_{ijk} }}$ is the Cartesian integral kernel of the GC formulas. $i$, $j$ and $k$ are three different directional parameters, respectively (i.e., $i \in \{ x,y,z\}$, $j \in \{ x,y,z\}$ and $k \in \{ x,y,z\}$).

Therefore, the optimal GP ($V^{O - T{\rm 3D}}$), GV ($V_{i}^{{O - T3{\text{D}}}}$), GGT ($V_{ij}^{O - T3{\text{D}}}$) and GC ($V_{ijk}^{O - T3{\text{D}}}$) formulas in Cartesian integral kernels can be generally expressed as

$$ \left\{ {\begin{array}{*{20}c} {V^{O - T3{\text{D}}} } \\ {V_{i}^{O - T3{\text{D}}} } \\ {V_{ij}^{O - T3{\text{D}}} } \\ {V_{ijk}^{O - T3{\text{D}}} } \\ \end{array} } \right\} = \int\limits_{{\lambda_{1} }}^{{\lambda_{2} }} {\int\limits_{{\theta_{1} }}^{{\theta_{2} }} {\int\limits_{{r_{1} }}^{{r_{2} }} {\left\{ {\begin{array}{*{20}c} {I^{V} } \\ {I^{{V_{i} }} } \\ {I^{{V_{ij} }} } \\ {I^{{V_{ijk} }} } \\ \end{array} } \right\}} } } {\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(11)

where $I^{V}$, $I^{{V_{i} }}$ and $I^{{V_{ij} }}$ are the corresponding Cartesian integral kernels of the GP, GV, GGT; see Grombein et al. (2013) and Uieda et al. (2016).

Note that even though the optimal GC formulas are expressed in Cartesian integral kernels, the 3D evaluation of the optimal GC formulas is still implemented in spherical coordinates in the domain $[\lambda_{1} ,\lambda_{2} ]$ and $[\theta_{1} ,\theta_{2} ]$ and $[r_{1} ,r_{2} ]$, with the volume element ${\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S}$ running through a tesseroid body, which has also been discussed by Grombein et al. (2013); the difference in adding the integral expression of the GC into the topographic effects between Eq. (11) in this paper and Eq. (20) in Grombein et al. (2013) should also be noted. In terms of the topographic effects, the relationship of the formulas between Cartesian integral kernels and spherical integral kernels will be discussed in Sect. 2.2.

After substituting Eqs. (2–10) into Eq. (1), the 3D GC formulas in the ENU spherical coordinate system can be obtained from the Cartesian integral kernels, which are listed in Appendix 1. Furthermore, the 2D topographic effects formulas of a tesseroid are derived from the 3D GP, GV and GGT formulas provided in Grombein et al. (2013) and the 3D GC formulas in Cartesian integral kernels listed in Appendix 1 in this paper by applying the integration with respect to the geocentric radius $r_{S}$ of the integration point $S$, and the results are listed in Appendix 2.

2.2 The Relationship of 3D Topographic Effects of a Tesseroid Between Cartesian Integral Kernels and Spherical Integral Kernels

Compared to the formerly presented formulas of the topographic effects of a tesseroid mass body derived from spherical integral kernels (Heck and Seitz 2007; Asgharzadeh et al. 2007; Wild-Pfeiffer 2008; Shen and Deng 2016; Deng and Shen 2017b), the GP, GV and GGT formulas derived from Cartesian integral kernels are presented in Grombein et al. (2013). Moreover, the GC formulas in Cartesian integral kernels are presented both in 3D and 2D forms, which are provided in Appendix 1 and 2 in this paper, respectively.

Just as described in Grombein et al. (2013), though the 3D integral forms of the GP, GV and GGT formulas are derived from two different integral kernels—Cartesian and spherical; their conclusive expressions, obtained by substituting the related parameters into the general formulas, are consistent with each other. Furthermore, the consistency of the two methodologies (Cartesian and spherical) for the 3D GP, GV and GGT formulas has been presented and confirmed by two numerical investigations by 3D TSE second-order expression in Grombein et al. (2013).

The detailed mathematical derivations and the final expressions of the 3D GC formulas in spherical integral kernels, obtained by applying the complicated relations, namely the complicated transformation formulas from the second derivatives of the GP to third derivatives presented in Tóth (2005), Tóth and Földváry (2005), Casotto and Fantino (2009), Šprlák and Novák (2015, 2016, 2017), Šprlák et al. (2016) and Novák et al. (2017), can be found in Appendix A of Deng and Shen (2017b). In Sect. 2.1 of this paper, the 3D GC expressions derived from Cartesian integral kernels are presented, and the detailed formulas are listed in Appendix 1 as Eqs. (32–41). Comparing Eqs. (A1–A10) in Deng and Shen (2017b) with Eqs. (32–41) in this paper, it is obviously found that the paired parameters ($V_{xyz}^{T3{\text{D}}}$ and $V_{xyz}^{O - T3{\text{D}}}$; $V_{yyy}^{T3{\text{D}}}$ and $V_{yyy}^{O - T3{\text{D}}}$; $V_{yyz}^{T3{\text{D}}}$ and $V_{yyz}^{O - T3{\text{D}}}$; $V_{zzx}^{T3{\text{D}}}$ and $V_{zzx}^{O - T3{\text{D}}}$; $V_{zzy}^{T3{\text{D}}}$ and $V_{zzy}^{O - T3{\text{D}}}$; $V_{zzz}^{T3{\text{D}}}$ and $V_{zzz}^{O - T3{\text{D}}}$) have the same expressions, whereas other paired parameters ($V_{xxx}^{T3{\text{D}}}$ and $V_{xxx}^{O - T3{\text{D}}}$; $V_{xxy}^{T3{\text{D}}}$ and $V_{xxy}^{O - T3{\text{D}}}$; $V_{xxz}^{T3{\text{D}}}$ and $V_{xxz}^{O - T3{\text{D}}}$; $V_{yyx}^{T3{\text{D}}}$ and $V_{yyx}^{O - T3{\text{D}}}$) have different expressions due to the fact that the GC expressions of a tesseroid are derived, respectively, from spherical and Cartesian integral kernels. Numerical comparisons of their integral kernels with the help of the mathematical software Mathematica (https://www.wolfram.com/mathematica) or Maple (http://www.maplesoft.com) show that though the mentioned paired GC components have different expressions, they in fact provide the same numerical results. Moreover, Appendix 2 of this paper provides the 2D integral formulas of the GC functionals.

Concerning the 3D topographic effects (i.e., GP, GV, GGT, GC) of a tesseroid, though the derivations are from two different mathematical approaches as spherical and Cartesian integral kernels, respectively, the final mathematical expressions of the 3D GP, GV, GGT and GC are analytically consistent in spherical coordinates. In terms of the mathematical derivations and expressions of the GC components, the Cartesian integral kernels are much simpler and more concise than spherical integral kernels, where the latter have been derived on the complicated functional conversion relations, especially by applying the transformation formulas from the GGT functionals to the GC functionals (Tóth 2005; Tóth and Földváry 2005; Casotto and Fantino 2009; Šprlák and Novák 2015, 2016, 2017; Šprlák et al. 2016; Novák et al. 2017). For this reason, we use the name “optimal” for Cartesian integral kernels. Numerical comparisons of the computational time and approximation errors will be implemented in Sect. 4.1.

3 Numerical Approaches for the Topographic Effects

3.1 Taylor Series Expansion Approach for the GP, GV, GGT and GC Formulas of a Tesseroid in Cartesian Integral Kernels

The numerical evaluation of the GP, GV, GGT and GC formulas of a tesseroid derived from spherical integral kernels have been typically addressed by the TSE approach (Kuhn 2003; Heck and Seitz 2007; Wild-Pfeiffer 2008; Deng et al. 2016; Shen and Deng 2016; Grombein et al. 2013, 2016; Deng and Shen 2017b). As for the GP, GV and GGT formulas derived from Cartesian integral kernels in Grombein et al. (2013), the TSE method with second-order expression is also adopted. In this section, the numerical TSE approach up to fourth-order expression is implemented to evaluate the GC formulas in Cartesian integral kernels.

3.1.1 3D TSE Approach

The 3D TSE method for the GP, GV, GGT and GC formulas at the tesseroid geometric center point $S_{0}$ can be written as (Heck and Seitz 2007; Shen and Deng 2016; Grombein et al. 2013, 2016; Deng and Shen 2017b)

$$ F_{m} = \mathop \sum \limits_{i,j,k} X_{ijk} \frac{{\left( {\Delta \lambda } \right)^{i + 1} \left( {\Delta \theta } \right)^{j + 1} \left( {\Delta r} \right)^{k + 1} }}{{2^{i + j + k} \left( {i + 1} \right)!\left( {j + 1} \right)!\left( {k + 1} \right)!}} $$

(12)

$$ X_{ijk} = \frac{{\partial^{i + j + k} {\text{X}}\left( {\lambda_{S} ,\theta_{S} ,r_{S} } \right)}}{{\partial \lambda_{S}^{i} \partial \theta_{S}^{j} \partial r_{S}^{k} }}|_{{\lambda_{S} = \lambda_{0} ,\theta_{S} = \theta_{0} ,r_{S} = r_{0} }} $$

(13)

where $F_{m}$ are the different GP, GV, GGT and GC functionals with even order (i.e., $m$ = 0, 2, 4,…) and $m = i + j + k$, $X_{ijk}$ are the coefficient parameters of the corresponding GP, GV, GGT and GC functionals, and the detailed expressions of $X\left( {\lambda_{0} ,\theta_{0} ,r_{0} } \right)$ are listed in Table 3.

In addition, the following expressions of the zero-order, second-order and fourth-order GC formulas are implemented for practical calculation:

$$ F_{0} = \Delta^{0}\, { = }\,\Delta \lambda \Delta \theta \Delta rX_{000} $$

(14)

$$ F_{2} = \Delta^{0} + \Delta^{2} = F_{0} + \Delta^{2} { = }F_{0} + \frac{1}{24}\Delta \lambda \Delta \theta \Delta r\left( {X_{200} \Delta \lambda^{2} + X_{020} \Delta \theta^{2} + X_{002} \Delta r^{2} } \right) $$

(15)

$$ \begin{aligned} F_{4} &= \Delta^{0} + \Delta^{2} + \Delta^{4} = F_{2} + \Delta^{4} \hfill \\ &\quad = F_{2} + \frac{1}{576}\Delta \lambda \Delta \theta \Delta r\left( {X_{220} \Delta \lambda^{2} \Delta \theta^{2} + X_{202} \Delta \lambda^{2} \Delta r^{2} + X_{022} \Delta \theta^{2} \Delta r^{2} } \right) \hfill \\ &\quad + \frac{1}{1920}\Delta \lambda \Delta \theta \Delta r\left( {X_{400} \Delta \lambda^{4} + X_{040} \Delta \theta^{4} + X_{004} \Delta r^{4} } \right) \hfill \\ \end{aligned} $$

(16)

where $\Delta^{m}$ (i.e., $m$ = 0, 2, 4,…) are even order terms of the coefficient parameters (namely $\Delta \lambda$, $\Delta \theta$ and $\Delta r$), and the expressions of different-order coefficient parameters (e.g., $X_{000} ,X_{200} , \ldots ,X_{220} , \ldots ,X_{004}$) can be referred in Appendix B of Deng and Shen (2017b). We note that the zero-order, second-order and fourth-order tesseroid formulas herein correspond, respectively, to the second-order error, fourth-order error and six-order error tesseroid formulas in Heck and Seitz (2007) and Grombein et al. (2013, 2014, 2016, 2017).

3.1.2 2D TSE Approach

Similarly, the 2D TSE approach for the GP, GV, GGT and GC formulas can be obtained as

$$ H_{n} = \mathop \sum \limits_{i,j} Y_{ij} \frac{{\left( {\Delta \lambda } \right)^{i + 1} \left( {\Delta \theta } \right)^{j + 1} }}{{2^{i + j} \left( {i + 1} \right)!\left( {j + 1} \right)!}} $$

(17)

$$ Y_{ij} = \frac{{\partial^{i + j} Y\left( {\lambda_{S} ,\theta_{S} } \right)}}{{\partial \lambda_{S}^{i} \partial \theta_{S}^{j} }}|_{{\lambda_{S} = \lambda_{0} ,\theta_{S} = \theta_{0} }} $$

(18)

where $H_{n}$ are even order functions and represent different GP, GV, GGT and GC functions (i.e., $n$ = 0, 2, 4,…) and $n = i + j$, $Y_{ij}$ are the coefficient parameters of the corresponding GP, GV, GGT and GC functions, and the detailed expressions of $Y\left( {\lambda_{0} ,\theta_{0} } \right)$ are listed in Table 4.

The zero-order, second-order and fourth-order tesseroid formulas for the 2D GP, GV, GGT and GC expressions are implemented for practical calculation as

$$ H_{0} =\, \nabla^{0} { = }\Delta \lambda \Delta \theta Y_{00} $$

(19)

$$ H_{2} =\, \nabla^{0} + \nabla^{2} = H_{0} + \nabla^{2} { = }H_{0} + \frac{1}{24}\left( {Y_{20} \Delta \lambda^{2} + Y_{02} \Delta \theta^{2} } \right) $$

(20)

$$ \begin{aligned} H_{4} &= \nabla^{0} + \nabla^{2} + \nabla^{4} = H_{2} + \nabla^{4} \hfill \\ &=H_{2} + \frac{1}{576}\Delta \lambda \Delta \theta \left( {Y_{22} \Delta \lambda^{2} \Delta \theta^{2} } \right) + \frac{1}{1920}\Delta \lambda \Delta \theta \left( {Y_{40} \Delta \lambda^{4} + Y_{04} \Delta \theta^{4} } \right) \hfill \\ \end{aligned} $$

(21)

where $\nabla^{n}$ (i.e., $n$ = 0, 2, 4,…) are even order terms of the coefficient parameters as mentioned before.

Compared to the 3D TSE approach implemented in Grombein et al. (2013) for the GP, GV and GGT calculations, we note the following differences including the calculation strategy adopted in this paper: (1) The 2D forms expressions are used with 2D TSE approach; (2) the different orders (zero-order, second-order and fourth-order) of 3D and 2D TSE approach are applied; (3) we use superposition calculation for different-order tesseroid formulas, namely the practical calculation for 3D as Eqs. (14–16) and 2D as Eqs. (19–21), whereas the order of 3D TSE approach in Grombein et al. (2013) is only second-order and the calculation strategy of Grombein et al. (2013) is symbolic substitution as step by step derivations; and (4) the evaluation of the GC expressions is additionally provided while Grombein et al. (2013) only presented the evaluation of the GP, GV and GGT expressions.

3.2 Gauss–Legendre Quadrature Method for the GP, GV, GGT and GC Formulas of a Tesseroid Both in Spherical and Cartesian Integral Kernels

Analogously to the 3D and 2D TSE approach for numerical evaluation of the GP, GV and GGT formulas, the GLQ has been widely applied in the calculation for gravity and magnetic effects (Stroud and Secrest 1966; Ku 1977; von Frese et al. 1981; Asgharzadeh et al. 2007, 2008; Wild-Pfeiffer 2008; Li et al. 2011; Hirt et al. 2011; Du et al. 2015; Roussel et al. 2015; Rexer and Hirt 2015; Uieda et al. 2016). In this paper, the GLQ method is applied for the GC formulas both in spherical and Cartesian integral kernels. Moreover, the 3D and 2D GLQ approaches are presented for the GP, GV, GGT and GC formulas.

3.2.1 3D GLQ Approach

According to Asgharzadeh et al. (2007), Roussel et al. (2015) and Uieda et al. (2016), the 3D GP, GV, GGT and GC formulas derived both from Cartesian and spherical integral kernels with 3D GLQ approach, truncated to degree ($N^{\lambda }$, $N^{\theta }$, $N^{r}$), can be represented as

$$ F_{\text{GLQ}}^{3{\rm D}} \approx G\rho_{S} \frac{{(\lambda_{2} - \lambda_{1} )(\theta_{2} - \theta_{1} )(r_{2} - r_{1} )}}{8}\mathop \sum \limits_{k = 1}^{{N^{r} }} \mathop \sum \limits_{j = 1}^{{N^{\theta } }} \mathop \sum \limits_{i = 1}^{{N^{\lambda } }} W_{(GLQ)i}^{\lambda } W_{(GLQ)j}^{\theta } W_{(GLQ)k}^{r} I\left( {\lambda_{i} ,\theta_{j} ,r_{k} } \right) $$

(22)

$$ \lambda_{i} = x_{i} \frac{{\lambda_{2} - \lambda_{1} }}{2} + \frac{{\lambda_{2} + \lambda_{1} }}{2} $$

(23)

$$ W_{(GLQ)i}^{\lambda } = \frac{2}{{\left( {1 - x_{i}^{2} } \right)\left[ {P^{\prime}_{{N^{\lambda } }} \left( {x_{i} } \right)} \right]^{2} }} $$

(24)

$$ \theta_{j} = y_{j} \frac{{\theta_{2} - \theta_{1} }}{2} + \frac{{\theta_{2} + \theta_{1} }}{2} $$

(25)

$$ W_{(GLQ)j}^{\theta } = \frac{2}{{\left( {1 - y_{j}^{2} } \right)\left[ {P^{\prime}_{{N^{\theta } }} \left( {y_{j} } \right)} \right]^{2} }} $$

(26)

$$ r_{k} = z_{k} \frac{{r_{2} - r_{1} }}{2} + \frac{{r_{2} + r_{1} }}{2} $$

(27)

$$ W_{(GLQ)k}^{r} = \frac{2}{{\left( {1 - z_{k}^{2} } \right)\left[ {P^{\prime}_{{N^{r} }} \left( {z_{k} } \right)} \right]^{2} }} $$

(28)

where $F_{\text{GLQ}}^{{3{\text{D}}}}$ is the function of the 3D general GP, GV, GGT and GC expressions, which are from Eq. (21) of Grombein et al. (2013) and Appendix 1 of this paper; $N^{\lambda }$, $N^{\theta }$, $N^{r}$ are the integer degrees of numerical quadrature (i.e., $N^{\lambda }$, $N^{\theta }$, $N^{r}$ = 1, 2, 3, 4, …) and $W_{(GLQ)i}^{\lambda }$, $W_{(GLQ)j}^{\theta }$, $W_{(GLQ)k}^{r}$ are the Gauss–Legendre weights for the spherical longitude, spherical latitude and radius, respectively; $I\left( {\lambda_{i}^{{}} ,\theta_{j}^{{}} ,r_{k}^{{}} } \right)$ is the integral kernel of the integration point $\left( {\lambda_{i}^{{}} ,\theta_{j}^{{}} ,r_{k}^{{}} } \right)$ for the 3D GP, GV, GGT and GC expressions; $x_{i}$, $y_{j}$ and $z_{k}$ are the $i$th, $j$th, $k$th root of the $N^{\lambda }$th-, $N^{\theta }$th- and $N^{r}$th-order polynomials $P_{{N^{\lambda } }}$, $P_{{N^{\theta } }}$ and $P_{{N^{r} }}$; $P^{\prime}_{{N^{\lambda } }} \left( {x_{i} } \right)$, $P^{\prime}_{{N^{\theta } }} \left( {y_{j} } \right)$ and $P^{\prime}_{{N^{r} }} \left( {z_{k} } \right)$ are the first derivatives of $P_{{N^{\lambda } }} \left( {x_{i} } \right)$, $P_{{N^{\theta } }} \left( {y_{j} } \right)$ and $P_{{N^{r} }} \left( {z_{k} } \right)$, respectively, where the interval [− 1, + 1] is applied.

3.2.2 2D GLQ Approach

Similarly to the mathematical derivations of the 3D GLQ approach, the 2D GLQ for the GP, GV, GGT and GC formulas derived both from Cartesian and spherical integral kernels can be denoted as (Wild-Pfeiffer 2008; Hirt et al. 2011)

$$ F_{\text{GLQ}}^{{2{\text{D}}}} \approx G\rho_{S} \frac{{(\lambda_{2} - \lambda_{1} )(\theta_{2} - \theta_{1} )}}{4}\mathop \sum \limits_{j = 1}^{{N^{\theta } }} \mathop \sum \limits_{i = 1}^{{N^{\lambda } }} W_{(GLQ)i}^{\lambda } W_{(GLQ)j}^{\theta } J\left( {\lambda_{i} ,\theta_{j}^{{}} } \right) $$

(29)

where $F_{\text{GLQ}}^{{2{\text{D}}}}$ is the function of the 2D general GP, GV, GGT and GC expressions, which are listed in Appendix 2 of this paper; $J\left( {\lambda_{i}^{{}} ,\theta_{j}^{{}} } \right)$ is the integral kernel of the integration point $\left( {\lambda_{i}^{{}} ,\theta_{j}^{{}} } \right)$ for the 2D GP, GV, GGT and GC expressions. Other parameters are the same as the description of 3D GLQ approach.

The numerical values of the 1D GLQ nodes $x_{i}$ and weights $w_{i}$ in interval [a, b] ($\int_{a}^{b} {f(x){\text{d}}x = \sum\nolimits_{i = 1}^{n} {w_{i} f(x_{i} )} }$) are reported in Table 5. When the interval [a, b] is set as [− 1, + 1], the numerical values of the GLQ nodes and weights are consistent with the corresponding values provided in Table 4 of Wild-Pfeiffer (2008) and Table 3 of Hirt et al. (2011).

3.3 Newton–Cotes Quadrature Method for the GP, GV, GGT and GC Formulas of a Tesseroid in Both Spherical and Cartesian Integral Kernels

The NCQ approach was introduced in Appendix 1 “Interpolating quadrature formulae” of Wild-Pfeiffer (2008) as a comparative numerical method to the GLQ for the evaluation of the GP, GV and GGT expressions. However, Wild-Pfeiffer (2008) only cited the mathematical definition of the numerical NCQ approach and did not carry out the numerical experiments to confirm its reliability. Therefore, based on Wild-Pfeiffer (2008) we expand the numerical NCQ approach, which can be divided into two types: Closed Newton–Cotes Quadrature (CNCQ) and Open Newton–Cotes Quadrature (ONCQ), for evaluating the 3D/2D topographic effects, respectively. The difference between the CNCQ and ONCQ lies in whether it considers the end points in the sum of the numerical values. If they are considered, the NCQ is referred to as the CNCQ, otherwise, it is ONCQ. In other words, the CNCQ uses the function values at all points, whereas ONCQ does not.

3.3.1 3D CNCQ and ONCQ Approaches

Expanding the 1D NCQ as described in Wild-Pfeiffer (2008), the 3D CNCQ and ONCQ approaches for the numerical evaluation of the topographic effects are provided. The 3D CNCQ and ONCQ forms of degree ($N^{\lambda }$,$N^{\theta }$,$N^{r}$) can be expressed as

$$ F_{\text{NCQ}}^{{3{\text{D}}}} \approx G\rho_{S} \mathop \sum \limits_{k = 0}^{{N^{r} }} \mathop \sum \limits_{j = 0}^{{N^{\theta } }} \mathop \sum \limits_{i = 0}^{{N^{\lambda } }} W_{(NCQ)i}^{\lambda } W_{(NCQ)j}^{\theta } W_{(NCQ)k}^{r} I\left( {\lambda_{i} ,\theta_{j} ,r_{k} } \right) $$

(30)

where $F_{\text{NCQ}}^{{3{\text{D}}}}$ is the general function expression of the 3D GP, GV, GGT and GC (see Eq. (21) of Grombein et al. (2013) and Appendix 1 of this paper); $W_{(NCQ)i}^{\lambda }$, $W_{(NCQ)j}^{\theta }$, $W_{(NCQ)k}^{r}$ are the NCQ weights for the spherical longitude, spherical latitude and radius, respectively.

3.3.2 2D CNCQ and ONCQ Approaches

Moreover, the 2D forms of the CNCQ and ONCQ can be written as

$$ F_{\text{NCQ}}^{{2{\text{D}}}} \approx G\rho_{S} \mathop \sum \limits_{j = 0}^{{N^{\theta } }} \mathop \sum \limits_{i = 0}^{{N^{\lambda } }} W_{(NCQ)i}^{\lambda } W_{(NCQ)j}^{\theta } J\left( {\lambda_{i} ,\theta_{j} } \right) $$

(31)

where $F_{\text{NCQ}}^{{2{\text{D}}}}$ is the general function expression of the 2D GP, GV, GGT and GC (see Appendix 2 of this paper).

The numerical values of the 1D CNCQ and the ONCQ ($\int_{a}^{b} {f(x){\text{d}}x = \sum\nolimits_{i = 1}^{n} {w_{i} f(x_{i} )} }$) with the corresponding nodes $x_{i}$ and weights $w_{i}$ in interval [a, b] are presented in Tables 6 and 7, respectively, where the nodes $x_{i}$ clearly show the difference between the CNCQ and ONCQ.

4 Numerical Investigations

4.1 Comparison of Computational Time Between Spherical and Cartesian Integral Kernels

The comparison of the computational time between the spherical and Cartesian integral kernels of the GP, GV and GGT expressions by 3D TSE second-order approach has been numerically investigated in Sect. 6.1 of Grombein et al. (2013). Here, we further investigate the numerical efficiency of the spherical and Cartesian integral kernels of the GC expressions by the 3D TSE zero-order, second-order and fourth-order tesseroid formulas. Subsequently, analogously to Grombein et al. (2013) and Deng and Shen (2017b), the constant spherical shell (h^′ = 1 km) is adopted, and the computational burdens of spherical and Cartesian integral kernels for the GC formulas are calculated to show whether the Cartesian integral kernels are optimal for evaluating the components of the GC. In addition, the GP, GV and GGT formulas between the spherical and Cartesian integral kernels with the 3D TSE zero-order, second-order and fourth-order tesseroid formulas are re-investigated as well.

Specifically, the constant topographic spherical shell is utilized with 1° × 1°grid of the constant thickness h^′ = 1 km. Therefore, for the TSE approach, the horizontal dimension $\Delta \lambda = \Delta \theta = 1^{ \circ }$ and vertical dimension $\Delta r = h^{'} = 1$ km are adopted for 360*180 = 64,800 tesseroid bodies in the representative application. Therefore, the total topographic effects of the spherical shell can be approximately calculated by the sum of all the 64, 800 discrete tesseroid bodies. If the grid resolution is 5′ × 5′, it should be noted that the total number of the tesseroid bodies in Grombein et al. (2013) with 5′ × 5′ resolution should be corrected from 9,931,200 to 9,331,200 (they added 600,000 more individual tesseroid bodies in counting), namely the number of the tesseroid bodies for resolution 5^′ × 5^′ should be 360 * 180 * 12 * 12 = 9,331,200. Moreover, without loss of generality, the spherical coordinate $(\lambda_{P} ,\theta_{P} ,r_{P} )$ of the computation point $P$ is (0°, 0°, 6631 km), namely taking the GOCE-type satellite height 260 km from the surface of a synthetic sphere, where the radius of the sphere is 6371 km.

Consequently, the computational burden (unit: s) in percentage (%) form of the GP ($V$), GV ($V_{x}$,$V_{y}$,$V_{z}$), GGT ($V_{xx}$, $V_{yy}$, $V_{zz}$, $V_{xy}$, $V_{xz}$, $V_{yz}$) and GC ($V_{xxx}$, $V_{xxy}$, $V_{xxz}$, $V_{xyz}$, $V_{yyx}$, $V_{yyy}$, $V_{yyz}$, $V_{zzx}$, $V_{zzy}$ and $V_{zzz}$) expressions for spherical and Cartesian integral kernels with the 3D TSE zero-order, second-order and fourth-order are listed in Table 1. All the computation CPU time costs are shown in percentage (%) form with respect to the 3D TSE approach based on the second-order tesseroid formulas of the GP, GV, GGT and GC in spherical integral kernels, respectively, for the reason that the 3D TSE second-order tesseroid formulas are the most utilized approach for evaluating the tesseroid mass reduction in the related geoscience areas (Tsoulis et al. 2009; Chaves and Ussami 2013; Du et al. 2015; Shen and Han 2013, 2014, 2016; Shen and Deng 2016; Grombein et al. 2013, 2014, 2016, 2017; Deng and Shen 2017b). Note that the actual computational burden strongly depends on hardware (e.g., our resources for calculations are Intel CPU i5 with 4 cores).

Table 1 Comparison of computational burden (%) using 3D TSE approach with different orders (zero, second and fourth) in spherical and Cartesian integral kernels to evaluate the time cost information of the GP ($V$), GV ($V_{x}$, $V_{y}$ and $V_{z}$), GGT ($V_{xx}$, $V_{yy}$, $V_{zz}$, $V_{xy}$, $V_{xz}$ and $V_{yz}$) and GC ($V_{xxx}$,$V_{xxy}$,$V_{xxz}$,$V_{xyz}$,$V_{yyx}$,$V_{yyy}$,$V_{yyz}$,$V_{zzx}$,$V_{zzy}$ and $V_{zzz}$). $V^{m}$, $V_{i}^{m}$, $V_{ij}^{m}$ and $V_{ijk}^{m}$ are the average time cost for the GP, GV, GGT and GC, and their average values are presented as m($V^{m}$, $V_{i}^{m}$, $V_{ij}^{m}$, $V_{ijk}^{m}$). All values are in percentage form with respect to the computational burden (unit: s) of the 3D TSE second-order tesseroid formulas in spherical integral kernels, respectively

The GP ($V$) evaluation and average value ($V^{m}$) by the 3D TSE in Cartesian and spherical integral kernels with different orders are listed in Table 1. The computational burdens of Cartesian integral kernels are the same as those of spherical integral kernels for the second-order and fourth-order, respectively.

Similarly, Table 1 lists the evaluation of the GV ($V_{x}$, $V_{y}$ and $V_{z}$) and the average values ($V_{i}^{m}$). As for $V_{i}^{m}$, the computational burdens of Cartesian integral kernels are less than those of spherical integral kernels for the second-order and fourth-order as 1% and 6%, respectively, where for the zero-order it is the same as 6% for spherical integral kernels.

Additionally, the computational burden of GGT ($V_{ij}$) and GC ($V_{ijk}$) and the average values ($V_{ij}^{m}$ and $V_{ijk}^{m}$) are listed in Table 1. The computational burdens of Cartesian integral kernels are less than those of spherical integral kernels with $V_{ij}^{m}$ by 1, 15 and 145% and with $V_{ijk}^{m}$ by 3, 54 and 528% for the zero-order, second-order and fourth-order, correspondingly.

When estimating the total sum of the average time costs of $V^{m}$, $V_{i}^{m}$, $V_{ij}^{m}$ and $V_{ijk}^{m}$, 5, 82 and 813% are required for Cartesian integral kernels for the zero-order, second-order and fourth-order, respectively, which are, respectively, fewer than those of spherical integral kernels by 1, 18 and 170%.

Compared to the numerical experiment in the Sect. 6.1 of Grombein et al. (2013), herein there are some differences for the estimation of the GP, GV and GGT: (1) The utilized programming language is Mathematica for this paper, while C++ for Grombein et al. (2013); (2) the different hardware: for this paper, Intel CPU i5 with 4 cores is used; (3) the distinctive evaluation strategy: the initial input formulas of $V$, $V_{z}$ and $V_{zz}$ are equivalent for spherical and Cartesian integral kernels, and other parameters input formulas of the GP, GV, and GGT are adopted in initial and unreduced expressions for spherical integral kernels provided in Eqs. (22–23) of Grombein et al. (2013) and the other optimal GP, GV and GGT formulas provided in Eq. (21) of Grombein et al. (2013) for Cartesian integral kernels, where for Grombein et al. (2013) it has been discussed in Sect. 3.1 of this paper.

However, for higher-order derivatives especially for the GGT evaluation in Grombein et al. (2013) and the GGT and GC evaluation in this paper, significant improvements can be found for Cartesian integral kernels if compared to spherical integral kernels. Furthermore, for the GC evaluation, the forms of spherical integral kernels as Eqs. (A1), (A2), (A3) and (A5) in Appendix A of Deng and Shen (2017b) are more complicated than those of Cartesian integral kernels as Eqs. (32), (33), (34) and (36) in Appendix 1 of this paper. Therefore, in terms of the computational burden, Cartesian integral kernels are also numerically optimal rather than spherical integral kernels with the 3D TSE approach, especially for the GC functionals.

4.2 Comparison of Accuracy and Computational Time for Cartesian Integral Kernels with Different Numerical Approaches

Following the idea of Sect. 4.1, the constant spherical shell (h^’ = 1 km) model is as well implemented to perform accuracy and computational time by the different numerical methods (3D/2D TSE, GLQ and NCQ (CNCQ/ONCQ)) for the GP, GV, GGT and GC formulas in Cartesian integral kernels to show which numerical method is optimal for evaluating the GP, GV, GGT and GC formulas in Cartesian integral kernels in terms of accuracy and computational time. Furthermore, by expanding the works of Grombein et al. (2013), where the 3D TSE second-order approach is applied, the different-order (zero-order, second-order and fourth-order) formulas are presented to illustrate the different accuracy and computational time of the 3D/2D TSE approach.

The general analytical formulas for the GP ($V^{\text{sh}}$), GV ($V_{i}^{\text{sh}}$), GGT ($V_{ij}^{\text{sh}}$) and GC ($V_{ijk}^{\text{sh}}$) of the spherical shell can be referred in Grombein et al. (2013) and Deng and Shen (2017b). Consequently, the reference values of the GP, GV, GGT and GC in the following section for the computation point $P$ at GOCE-type height can be referred in Table 2 “Satellite column” of Deng and Shen (2017b). Afterward, the absolute approximation errors for the GP, GV, GGT and GC can be obtained between the reference values and the actual calculated values by different numerical methods (3D/2D TSE, GLQ and CNCQ/ONCQ), and the absolute approximation errors divided by the reference values equal the relative approximation errors in the following numerical experiments.

Table 2 Ranges (from minimum to maximum) and standard deviation (STD) in Log₁₀ scale for the differences of the relative approximation errors for the GP, GV, GGT and GC in Fig. 6

Therefore, the absolute approximation errors in Log₁₀ scale and computational CPU time for the GP ($\delta V$), GV ($\delta g_{z}$), GGT ($\delta V_{xx}$, $\delta V_{yy}$ and $\delta V_{zz}$) and GC ($\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz}$) based on 3D/2D TSE with different orders (zero-order, second-order and fourth-order), 3D/2D GLQ with nodes 1 to 7 and 3D/2D NCQ (CNCQ and ONCQ) with nodes 2 to 7 can be evaluated. Because of the similarities among the figures for the GP, GV, GGT and GC, herein only the figure of the GC component ($\delta V_{zzz}$) is illustrated in Fig. 2. All the computational CPU time is shown as the percentage form with respect to the 3D TSE approach based on second-order tesseroid formulas of the GP, GV, GGT and GC, respectively. It is noted that the time unit is second and the actual computational burden depends on hardware.

Fig. 2

a GC ($\delta V_{zzz}$) absolute approximation errors in Log₁₀ scale with 3D/2D TSE (blue triangle), GLQ (red circle), CNCQ (green square) and ONCQ (black pentagrams). As for the TSE, the 3D/2D nodes 1, 2 and 3 mean zero-order, second-order and fourth-order, respectively; and for the GLQ, the 3D/2D nodes are from 1 to 7, whereas for the CNCQ and ONCQ, the 3D/2D nodes are from 2 to 7 with computation point P (0°, 0°, 6631 km) and grid resolution 1° × 1°, the unit of GC ($\delta V_{zzz}$) is m⁻¹ s⁻²; b GC ($\delta V_{zzz}$) histogram of CPU time percentage by 3D TSE (blue column), GLQ (red column), CNCQ (green column) and ONCQ (black column) with respect to the 3D TSE second-order tesseroid formulas. As for the TSE, the 3D/2D nodes 0, 2 and 4 mean zero-order, second-order and fourth-order, respectively

For the 3D and 2D comparisons as shown in Fig. 2, the 2D calculation approximation errors are only presented as $\delta V$ for the GP, $\delta V_{z}$ for the GV, $\delta V_{zz}$ for the GGT and $\delta V_{zzz}$ for the GC. As for the 3D and 2D TSE methods of the GC component ($\delta V_{zzz}$) with different zero-order, second-order and fourth-order in Fig. 2, the absolute approximation errors are at the same level in Fig. 2a; and the computational time of the 2D TSE is more efficient than that of the 3D TSE in Fig. 2b. The same rules of the absolute approximation errors and computational time can be found for the 3D/2D GLQ, CNCQ and ONCQ approaches with different 3D/2D nodes as well. Therefore, the 2D form of the GC component ($\delta V_{zzz}$) (see Eq. (56)) is more efficient than the 3D form in Cartesian integral kernel [see Eq. (41)] to reach the same accuracy.

As for the comparison of the TSE and GLQ approaches, the absolute approximation errors in 3D/2D nodes 1 of the 3D/2D GLQ are approximately equivalent to the 3D/2D zero-order TSE in Fig. 2a, while for 3D/2D nodes 2 of the 3D/2D GLQ, the absolute approximation errors are smaller than these of the second-order TSE in 3D and 2D forms; it is similar for the nodes 3 of the 3D/2D GLQ and the 3D/2D fourth-order TSE. Among the GLQ, CNCQ and ONCQ, the absolute approximation errors of the 3D/2D GLQ at nodes 1 and 3D/2D CNCQ at nodes 2 are about at same level, whereas there is an increased approximation error from the nodes 2 to 3 for the 3D/2D ONCQ. For the 3D/2D nodes from 3 to 7, the absolute approximation errors of the 3D/2D GLQ are smaller than these of the 3D/2D CNCQ and ONCQ. The property of the increased approximation errors from the nodes 2 to 3 for the 3D/2D ONCQ shows the instability of the ONCQ approach at the start node 2, which will be verified and validated in Sect. 4.5. Moreover, results in Fig. 2b demonstrate that the GLQ method performs better in terms of the computational time if compared to the 3D/2D TSE and NCQ (CNCQ and ONCQ) approaches.

In conclusion, for all the numerical approaches (3D/2D TSE, GLQ, CNCQ and ONCQ), with higher order for the TSE and more nodes for the GLQ, CNCQ and ONCQ, the absolute approximation errors are less, whereas the computational time is larger, except for the ONCQ with 3D/2D nodes 2. Among the numerical approaches mentioned in this paper, the GLQ approach is recommended for practical calculation in terms of the computational efficiency. Moreover, the nodes of the GLQ approach should be carefully chosen in terms of the trade-off effects between the computational time and numerical accuracy.

4.3 Influence of the Spherical Shell’s Thickness on the GP, GV, GGT and GC

In this section, expanding the idea of the approximation errors between the analytical formulas and the numerical 3D TSE approach for a homogeneous spherical shell (Grombein et al. 2013; Shen and Deng 2016; Uieda et al. 2016; Deng and Shen 2017b), we investigate the influence of a spherical shell’s thickness on the evaluation of the GP, GV, GGT and GC formulas, where the thickness of the spherical shell varies, namely the thickness h^’ is variable in this section rather than constant as previously assumed in Sect. 4.2. Shen and Deng (2016) concluded that with thicker shell, the approximation errors were larger for the GP evaluation. Furthermore, it is essential to pay attention to the approximation errors variation of the GP, GV, GGT and GC with different spherical shell’s thicknesses.

Generally, the thickness of the spherical shell is set as 1 km (i.e., Grombein et al. 2013; Shen and Deng 2016; Uieda et al. 2016; Deng and Shen 2017b). In Kuhn and Hirt (2016), the thickness 6 km of a spherical shell was selected to indicate the extreme situation for the global topographic masses. Moreover, Shen and Deng (2016) studied the influence of the shell’s thicknesses 1 and 8 km on the GP calculation by a simple example with different-order tesseroid formulas, where the spherical shell with 8 km was assumed as the worst-case situation for high mountainous areas. In the numerical experiment, the variable thickness h^’ is set as six constant values: 10 m, 100 m, 1, 6, 8 and 10 km. The numerical 3D TSE second-order formulas are adopted for the GP, GV, GGT and GC in Cartesian integral kernels as well. The condition of other parameters is the same as that of Sect. 3.3 in Deng and Shen (2017b).

Because of the similar variation trends of the eight curves ($\delta V$, $\delta V_{z}$, $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{zz}$, $\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz}$) for the different thicknesses, we only show the relative approximation errors in Log₁₀ scale of the GP, GV, GGT and GC for the thickness h^′ = 10 km in Fig. 3. Moreover, the differences of the relative approximation errors for the thicknesses (100 m, 1, and 10 km) compared to the thickness 10 m are demonstrated in Figs. 4a–c, and Fig. 4d reveals the differences in the relative approximation errors between the thicknesses 8 and 6 km.

Fig. 3

Visualization of the relative approximation errors in Log₁₀ scale for the GP ($\delta V$(blue curve)), GV ($\delta V_{z}$(red curve)), GGT ($\delta V_{xx}$(green dashed curve), $\delta V_{yy}$(dark-blue dashed curve) and $\delta V_{zz}$(yellow dotted curve)) and GC ($\delta V_{xxz}$(deep-sky-blue dashed curve), $\delta V_{yyz}$(thistle dashed curve) and $\delta V_{zzz}$ (magenta dotted curve)) with from 6371 km to 6401 km with interval 0.15 km. The thickness of the spherical shell h^’ is 10 km with resolution 15′ × 15′

Fig. 4

Illustration of differences of the relative approximation errors in Log₁₀ a between 100 and 10 m; b between 1 km and 10 m; c between 10 km and 10 m; d between 8 and 6 km. Other parameters are the same as in Fig. 3

Comparing to Fig. 4a in Deng and Shen (2017b), Fig. 3 reveals the thickness effects for the relative approximation errors of the GP, GV, GGT and GC. The turning points for the eight components are 6377.6 km for the GP ($\delta V$), 6381.5 km for the GV ($\delta V_{z}^{{}}$), 6385.4 km for the GGT ($\delta V_{xx}^{{}}$, $\delta V_{yy}^{{}}$ and $\delta V_{zz}^{{}}$) and 6389.3 km for the GC ($\delta V_{xxz}^{{}}$, $\delta V_{yyz}^{{}}$ and $\delta V_{zzz}^{{}}$), which are smaller than those of Fig. 4a in Deng and Shen (2017b). Therefore, with the larger thickness of the spherical shell, the turning points for the relative approximation errors of the GP, GV, GGT and GC move nearer to the surface of the spherical shell.

Figure 4a, b and c obviously displays that the different thicknesses of the spherical shell affect the relative approximation errors of the GP, GV, GGT and GC. Particularly, the change trend ranges of the GP, GV, GGT and GC in Log₁₀ scale are approximately [− 0.3, 0.2], [− 0.4, 0.2], [− 0.6, 0.2] and [− 0.8, 0.4] in Fig. 4a, [− 1.1, 0.9], [− 1.1, 0.9], [− 1.4, 1.0] and [− 1.6, 1.3] in Fig. 4b, and [− 1.2, 2.4], [− 1.2, 2.2], [− 1.5, 0.6] and [− 2.8, 2.1] in Fig. 4c, respectively. Therefore, Fig. 4a–c validates the assumption of Shen and Deng (2016) that the approximation errors are larger for the GP evaluation with a thicker spherical shell. Moreover, our numerical experiments indicate that the same rule can be applied for the GV, GGT and GC evaluation.

The maximum GC values shown in Fig. 4a–c at the very near area are about 0.4, 1.3 and 2.1 in Log₁₀ scale, whereas the values of other topographic effects (i.e., GP, GV and GGT) are not so obvious. Hence, as for the four types of the topographic effects, the GC is more sensitive than the GP, GV and GGT at the very near area of the computation point, which can be obviously illustrated in Fig. 4a–c.

Concerning the assumed worst-situation for high mountainous areas of 8 km in Shen and Deng (2016) and 6 km in Kuhn and Hirt (2016), the differences of the relative approximation errors are presented in Fig. 4d. The average change trends of the GP, GV, GGT and GC are about 0.2, 0.2, − 0.2 and − 0.2 in Log₁₀ scale in Fig. 4d excepting for the turning points region, which means that the overall impact of the assumed worst-situation (8 km from Shen and Deng (2016) or 6 km from Kuhn and Hirt (2016)) for the global high mountainous areas is not obvious except for the turning points of the topographic effects. Moreover, the amplitude of differences variation range for the topographic effects at the turning points region is listed from big to small as GV, GC, GGT and GP in Fig. 4d with ranges of [− 1.4, 1.6], [− 1.1, 1.1], [− 0.8, 1] and [− 0.5, 1], respectively.

4.4 Influence of Large-Scale Geocentric Distance on the GP, GV, GGT and GC

In this section, based on the experiment in Sect. 3.3 of Deng and Shen (2017b), the geocentric distance is expanded from [6371, 6401 km] to [6371, 7371 km]. Additionally, the interval of the geocentric distance is changed to 2 km other than 0.15 km. The purpose is to show the effects of the large-scale geocentric distance variation of the computation point $P$ on the evaluation of the GP, GV, GGT and GC. Herein, the Cartesian integral kernels are applied for the evaluation of the GP, GV, GGT and GC, where Deng and Shen (2017b) adopted the spherical integral kernels. Other conditions are the same as in Sect. 3.3 of Deng and Shen (2017b).

For the interval [6371 km, 6401 km] in Figs. 5a and 5b, the detailed curve trend can be referred to Fig. 4 of Deng and Shen (2017b). Figure 5a presents that the afterward curves trends of the GP, GV, GGT and GC are generally similar: with the geocentric distance increase, the relative approximation errors decline rapidly, which is called rapid drop zone; then at the one level, they arrive at the concussion zone, where the relative approximation errors of the GP, GV, GGT and GC change with large variation; at a certain level, the whole curve rule finally tends to be stable, denoted as stable zone. The ranges of the relative approximation errors are about 10⁻¹⁵–10⁵ for the GC, 10⁻¹⁵–10³ for the GGT, 10⁻¹⁵–10⁰ for the GV and 10⁻¹⁴–10⁻³ for the GP. In rapid drop zone, the amplitude of the relative approximation errors is listed by order from big to small as GC, GGT, GV and GP. Moreover, the three curves of the GC functionals ($\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz}$) overlap together in rapid drop zone, the same for three curves of the GGT functionals ($\delta V_{xx}$, $\delta V_{yy}$ and $\delta V_{zz}$). In concussion zone, the vibration amplitude of the deep-sky-blue dashed curve ($\delta V_{xxz}$) is the largest among the eight curves. In stable zone, the relative approximation errors values for the eight curves can be roughly divided as three levels: 10⁻¹⁴ for the blue curve ($\delta V$); between 10⁻¹⁴ and 10^−12.5 for the red curve ($\delta V_{z}$), the green dashed curve ($\delta V_{xx}$), the yellow dotted curve ($\delta V_{zz}$) and the deep-sky-blue dashed curve ($\delta V_{xxz}$); and around 10^−12.5 for the dark-blue dashed curve ($\delta V_{yy}$), the thistle dashed curve ($\delta V_{yyz}$) and the magenta dotted curve ($\delta V_{zzz}$).

Fig. 5

a Illustration of the relative approximation errors of the GP ($\delta V$ with blue curve), GV ($\delta V_{z}$ with red curve), GGT ($\delta V_{xx}$ with green dashed curve, $\delta V_{yy}$ with dark-blue dashed curve and $\delta V_{zz}$ with yellow dotted curve) and GC ($\delta V_{xxz}$ with deep-sky-blue dashed curve, $\delta V_{yyz}$ with thistle dashed curve and $\delta V_{zzz}$ with magenta dotted curve) in Log₁₀ scale for the large-scale geocentric distance of the computation point P with [6371 km, 7371 km] with interval 2 km and resolution 15′ × 15′; b visualization of the absolute approximation errors of Laplace parameters for the GGT ($\delta \Delta V_{2}$) and GC ($\delta \Delta V_{3}$)

Figure 5b reveals that the absolute approximation errors of the two Laplace parameters ($\delta \Delta V_{2}$ for the GGT and $\delta \Delta V_{3}$ for the GC) decline gradually with the increasing geocentric distance. The ranges of the two curves are 10⁻²⁵–10⁻¹⁴ s⁻² for the GGT and 10⁻³⁰–10⁻²⁰ $m^{ - 1} s^{ - 2}$ for the GC, which show that the sum of the GC functionals ($\delta V_{xxz}$, $\delta V_{yyz}$ and $\delta V_{zzz}$) satisfies the Laplace equation at proper precision and the same for that of the GGT functionals ($\delta V_{xx}$, $\delta V_{yy}$ and $\delta V_{zz}$).

4.5 Influence of the Latitude on the GP, GV, GGT and GC

The polar singularity problem of the GGT by spherical integral kernels with the 3D TSE method was solved by Cartesian integral kernels in Grombein et al. (2013). Deng and Shen (2017b) showed that the GC formulas in spherical integral kernels with the 3D TSE method have the polar singularity problem as well. Therefore, in this numerical experiment, the GC formulas in Cartesian integral kernels are implemented to solve the polar singularity problem of the GC. Moreover, for the evaluation of the GP, GV, GGT and GC in Cartesian integral kernels, the 3D GLQ and CNCQ/ONCQ approaches are implemented to illustrate the computational accuracy compared to the 3D TSE approach. The conditions (i.e., the grid resolution 15′ × 15′, the information of the spherical shell) of this numerical experiment are the same as Sect. 3.4 of Deng and Shen (2017b).

The differences of the relative approximation errors for the GP, GV, GGT and GC in Log₁₀ scale by different approaches (e.g., 3D TSE with zero-order and second-order, 3D GLQ with nodes 1 and 2, 3D CNCQ/ONCQ with nodes 2 and 3) are presented in Fig. 6 with the influence of the latitude. Furthermore, the statistical information (e.g., ranges from minimum to maximum, standard deviation) for the differences of the GP, GV, GGT and GC shown in Fig. 6 is listed in Table 2. Due to the similarities among the 3D TSE, GLQ, CNCQ for the GP, GV, GGT and GC functionals in Cartesian integral kernels, only the 3D TSE approach is presented in Fig. 6b, and its statistical information is listed in Table 2, which also list the statistical information for the 3D GLQ and CNCQ approaches.

Fig. 6

Visualization of differences of the relative approximation errors in Log₁₀ scale of the GP ($\delta V$ with blue curve), GV ($\delta V_{z}$ with red curve), GGT ($\delta V_{xx}$ with green curve, $\delta V_{yy}$ with dark-blue curve and $\delta V_{zz}$ with yellow curve) and GC ($\delta V_{xxz}$ with deep-sky-blue curve, $\delta V_{yyz}$ with thistle curve and $\delta V_{zzz}$ with magenta curve) a between 3D TSE zero-order and second-order for spherical integral kernels; b between 3D TSE zero-order and second-order for Cartesian integral kernels; c between the 3D ONCQ nodes 2 and 3 for Cartesian integral kernels

Generally, all the eight curves have the similar variation rule in Fig. 6a–c: with the latitude increasing from the equator to North Pole, the eight curves for the differences of the relative approximation errors in Fig. 6a–c with the 3D TSE and ONCQ approaches rise steeply, especially in the polar region ($\theta_{P} \ge 80^{ \circ }$), where the yellow curves of the GGT ($\delta V_{zz}$) decrease at latitude about $31^{ \circ }$ because of the change of the logarithmic scale referred in Grombein et al. (2013) and Deng and Shen (2017b). Just as mentioned in Ballard et al. (2016), if the tesseroid bodies are in the polar region, the geographic geometry of the tesseroid approaches to zero, the tesseroid would suffer accidental variability, which would influence the evaluation of the GP, GV, GGT and GC (Heck and Seitz 2007; Wild-Pfeiffer 2008; Grombein et al. 2013; Shen and Deng 2016; Deng and Shen 2017b). In Table 2, the standard derivation values for each figure are equal for the corresponding GP, GV, GGT and GC components, except for the GGT ($\delta V_{xx}$) and GC ($\delta V_{xxz}$) in Fig. 6a.

The important difference among Fig. 6a–c lies in the polar singularity problem of the computation point P at the North Pole. In particular, the GGT ($\delta V_{xx}$) and GC ($\delta V_{xxz}$) values in Fig. 6a are indeterminate at the North Pole, where the polar singularity occurs. In other words, Fig. 6a shows the gaps for the green curve ($\delta V_{xx}$) and deep-sky-blue curve ($\delta V_{xxz}$) at latitude $90^{ \circ }$. For Cartesian integral kernels with different numerical approaches in Fig. 6b,c, the GGT ($\delta V_{xx}$) and GC ($\delta V_{xxz}$) values can be estimated at the North Pole, which means that Fig. 6b,c do not show the gaps for the green curve ($\delta V_{xx}$) and deep-sky-blue curve ($\delta V_{xxz}$) at latitude $90^{ \circ }$. Therefore, analogously to the solution of the polar singularity problem of GGT by Cartesian integral kernels in Grombein et al. (2013), the polar singularity problem of the GC discovered in Deng and Shen (2017b) can also be solved by the Cartesian integral kernels with the different numerical approaches (3D TSE, GLQ, CNCQ and ONCQ).

Subsequently, the statistical information of the ranges and standard derivation for Figs. 6b and the 3D GLQ column in Table 2 are the same, which confirm the stability of 3D TSE and GLQ. For the 3D CNCQ column in Table 2 and 3D ONCQ in Fig. 6c, the values of the ranges and standard derivation for the 3D CNCQ in Table 2 are closer to those of 3D TSE and GLQ than those of 3D ONCQ. Put another way, the 3D ONCQ is more unstable than other applied approaches (e.g., 3D TSE, GLQ, CNCQ) in this paper at start 3D node 2. Thus, for the practical application of the 3D ONCQ approach at start node 2, it needs further investigation.

5 Conclusions

In this contribution, based on the previous GC formulas derived from spherical integral kernels (Deng and Shen 2017b), the optimal GC formulas in Cartesian integral kernels are provided not only in the 3D forms but also in the 2D forms. The consistency of the tesseroid modeling from spherical and Cartesian integral kernels has been analytically presented and numerically confirmed in terms of accuracy and computational time. Compared to the GC formulas in spherical integral kernels, the advantage of the GC formulas in Cartesian integral kernels lies in that they are more concise in their expressions and more efficient in numerical calculations, with reduction in the average computational burden of 1% for the GV, 15% for the GGT and 54% for the GC with the 3D TSE second-order formulas.

Moreover, as for these integral formulas of the topographic effects in both spherical and Cartesian integral kernels, which are listed in Deng and Shen (2017b) and this paper, many numerical approaches can be applied for the evaluation of these topographic effects. In this paper, the 3D/2D TSE zero-order, second-order and fourth-order, the GLQ and NCQ (CNCQ and ONCQ) approaches are implemented in the numerical evaluation of the topographic effects with Cartesian integral kernels for comparison, especially for the GC. In terms of accuracy and computational time, the GLQ approach is recommended for practical application of the topographic effects if compared to the TSE zero-order, second-order and fourth-order and NCQ approaches.

In addition, the effects of the spherical shell’s thickness on the relative approximation errors of the GP, GV, GGT and GC in Cartesian integral kernels have been investigated with the 3D TSE second-order tesseroid formulas. For thicker spherical shell, the relative approximation errors are larger not only for the GP evaluation (cf. Shen and Deng 2016), but also for the GV, GGT and GC evaluations. Compared to other topographic effects, the relative approximation errors of the GC are more sensitive, especially in the very near area of the computation point.

Besides, the effects of the large-scale geocentric distance variation on the relative approximation errors of the GP, GV, GGT and GC in Cartesian integral kernels have been studied with the 3D TSE second-order tesseroid formulas. Generally, as the large-scale geocentric distance increases, the curves trends of the relative approximation errors of the GP, GV, GGT and GC can be divided as three processes: (1) rapid drop zone with speedily declining relative approximation errors; (2) concussion zone with the large vibration amplitude of the relative approximation errors; and (3) stable zone with the stable relative approximation errors.

Furthermore, the polar singularity problem of the GC in spherical integral kernels, which was pointed out in Deng and Shen (2017b), can be solved numerically by Cartesian integral kernels with the 3D TSE second-order, GLQ and NCQ (including CNCQ and ONCQ) approaches. In other words, the formulas of the GC in Cartesian integral kernels can avoid the polar singularity of the computation point because of no additional coordinates transformation, where the coordinates transformation relationship would introduce polar singularity from denominator parameters.

Apart from the numerical approaches mentioned in this paper (e.g., 3D/2D TSE with zero-order, second-order and fourth-order, GLQ, CNCQ and ONCQ), other numerical approaches and mathematical models can be adopted to calculate the topographic effects of a tesseroid, especially for the GC functionals. For instance, there are many numerical approaches, including different quadrature approaches (e.g., Gauss–Kronrod Quadrature; Clenshaw–Curtis Quadrature; Lobatto–Kronrod Quadrature), 3-D Cauchy-type approach (Zhdanov and Liu 2013), Fast Multipole Method (Casenave et al. 2016), FFT series approach (Schwarz et al. 1990; Wu 2016; Sampietro et al. 2016), Legendre polynomial series approach (Ramillien 2017) and the rotation method between Earth-Centred Rotational and Earth-Centred P-Rotational reference frames (Marotta and Barzaghi 2017). In fact, the concept of the GC in topographic effects can also be applied for other mass bodies in spatial domain, especially for the polyhedral bodies (Holstein 2002; D’Urso 2013, 2014a, 2014b, 2015, 2016; Ren et al. 2017; Werner 2017; D’Urso and Trotta 2017) and prism (Nagy et al. 2000; D’Urso 2017).

The potential application of the GC in spatial domain could be used as primary reference in the next-generation topographic gravity field model (topographic effects on establishing high-resolution and high-accuracy global/local gravity fields and geoids) and may have extensive applications in geodesy and related geoscience, especially for the inversion for the internal structure of the Earth.

Appendices

Appendix 1: 3D GC Formulas of a Tesseroid in Cartesian Integral Kernels

The 3D GC formulas of a tesseroid derived from Cartesian integral kernels in spherical coordinates in the local East–North–Up (ENU) topocentric reference system are listed here:

$$ V_{xxx}^{{O - T3{\text{D}}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( { - \frac{{15r_{S}^{3} \cos^{3} \theta_{S} \sin^{3} \left( {\lambda_{P} - \lambda_{S} } \right)}}{{\mathcal{L}_{PS}^{7} }} + \frac{{9r_{S} \cos \theta_{S} \sin \left( {\lambda_{P} - \lambda_{S} } \right)}}{{\mathcal{L}_{PS}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(32)

$$ V_{xxy}^{{O - T3{\text{D}}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( {\frac{{15r_{S}^{3} \cos^{2} \theta_{S} \sin^{2} \left( {\lambda_{P} - \lambda_{S} } \right)A}}{{\mathcal{L}_{\text{PS}}^{7} }} - \frac{{3r_{S} A}}{{\mathcal{L}_{\text{PS}}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(33)

$$ V_{xxz}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( { - \frac{{15r_{S}^{2} \cos^{2} \theta_{S} \sin^{2} \left( {\lambda_{P} - \lambda_{S} } \right)B}}{{\mathcal{L}_{PS}^{7} }} + \frac{3B}{{\mathcal{L}_{PS}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(34)

$$ V_{xyz}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( {\frac{{15r_{S}^{2} \cos \theta_{S} \sin \left( {\lambda_{P} - \lambda_{S} } \right){\text{AB}}}}{{\mathcal{L}_{PS}^{7} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} d\lambda_{S} $$

(35)

$$ V_{yyx}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( { - \frac{{15r_{S}^{3} \cos \theta_{S} \sin \left( {\lambda_{P} - \lambda_{S} } \right)A^{2} }}{{\mathcal{L}_{PS}^{7} }} + \frac{{3r_{S} \cos \theta_{S} \sin \left( {\lambda_{P} - \lambda_{S} } \right)}}{{\mathcal{L}_{PS}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(36)

$$ V_{yyy}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( {\frac{{15r_{S}^{3} A^{3} }}{{\mathcal{L}_{PS}^{7} }} - \frac{{9r_{S} A}}{{\mathcal{L}_{PS}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(37)

$$ V_{yyz}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( { - \frac{{15r_{S}^{2} A^{2} B}}{{\mathcal{L}_{PS}^{7} }} + \frac{{3r_{S} B}}{{\mathcal{L}_{PS}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(38)

$$ V_{zzx}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( { - \frac{{15r_{S} \cos \theta_{S} \sin \left( {\lambda_{P} - \lambda_{S} } \right)B^{2} }}{{\mathcal{L}_{\text{PS}}^{7} }} + \frac{{3r_{S} \cos \theta_{S} \sin \left( {\lambda_{P} - \lambda_{S} } \right)}}{{\mathcal{L}_{\text{PS}}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(39)

$$ V_{zzy}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( {\frac{{15r_{S} {\text{AB}}^{2} }}{{\mathcal{L}_{PS}^{7} }} - \frac{{3r_{S} A}}{{\mathcal{L}_{PS}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(40)

$$ V_{zzz}^{O - T3{\text{D}}} = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \mathop \int \limits_{{r_{1} }}^{{r_{2} }} K\left( { - \frac{{15B^{3} }}{{\mathcal{L}_{\text{PS}}^{7} }} + \frac{9B}{{\mathcal{L}_{\text{PS}}^{5} }}} \right){\text{d}}r_{S} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(41)

where $K = G\rho_{S} r_{S}^{2} \cos \theta_{S}$,$\mathcal{L}_{\text{PS}} = \sqrt {r_{P}^{2} + r_{S}^{2} - 2r_{P} r_{S} \cos \psi }$, $A = \cos \theta_{P} \sin \theta_{S} - \sin \theta_{P} \cos \theta_{S} \cos \left( {\lambda_{P} - \lambda_{S} } \right)$ and $B = r_{P}-r_{S} \cos \psi$.

Appendix 2: 2D Topographic Effects Formulas of a Tesseroid in Cartesian Integral Kernels

Analogously, based on the 3D GP, GV and GGT formulas provided in Eq. (21) of Grombein et al. (2013) and 3D GC formulas listed in Appendix 1, the 2D topographic effects formulas of a tesseroid in Cartesian integral kernels in the local East–North–Up (ENU) topocentric reference system are listed here:

$$ V^{O - T2{\text{D}}} = \frac{1}{4}G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos \theta_{s} \left[ {2\mathcal{L}_{PS} \left( {r_{s} + 3\cos \psi r_{p} } \right) + r_{p}^{2} \left( {1 + 3\cos 2\psi } \right)\ln \left( {\mathcal{L}_{PS} + r_{s} - r_{p} \cos \psi } \right)} \right]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(42)

$$ V_{x}^{O - T2{\text{D}}} = G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos^{2} \theta_{s} \sin \left( {\lambda_{S} - \lambda_{P} } \right)\left[ {\left( {r_{p}^{2} + r_{s}^{2} - r_{p} r_{s} \cos \psi - \left( {3r_{p}^{2} + r_{s}^{2} } \right)\cos 2\psi + 3r_{p} r_{s} \cos 3\psi } \right)\csc^{2} \psi /2\mathcal{L}_{PS} +\,3r_{p} \cos \psi \ln \left( {\mathcal{L}_{PS} + r_{s} - r_{p} \cos \psi } \right)} \right]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(43)

$$ V_{y}^{O - T2{\text{D}}} = G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} A\cos \theta_{s} \left[ {\left( {r_{p}^{2} + r_{s}^{2} - r_{p} r_{s} \cos \psi - \left( {3r_{p}^{2} + r_{s}^{2} } \right)\cos 2\psi + 3r_{p} r_{s} \cos 3\psi } \right)\csc^{2} \psi /2\mathcal{L}_{PS} + 3r_{p} \cos \psi \ln \left( {\mathcal{L}_{PS} + r_{s} - r_{p} \cos \psi } \right)} \right]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(44)

$$ V_{z}^{O - T2{\text{D}}} = G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} cos\theta_{s} [((3r_{p}^{2} + r_{s}^{2} )\cos \psi - r_{p} r_{s} (2 + 3\cos 2\psi ))/\mathcal{L}_{PS} + \frac{1}{2}r_{p} \left( {1 + 3\cos 2\psi } \right)\ln \left( {\mathcal{L}_{PS} + r_{s} - r_{p} \cos \psi } \right)]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(45)

$$ \begin{aligned} V_{yy}^{O - T2{\text{D}}} & = G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos \theta_{s} [\left( {3A^{2} - 1} \right)\ln \left( {\mathcal{L}_{PS} + r_{S} - r_{P} \cos \psi } \right) \\ & \quad + \frac{{\csc^{4} \psi }}{{4\mathcal{L}_{PS}^{3} }}(r_{P} \left( {\left( {1 - 24A^{2} } \right)r_{S}^{2} + \left( {1 - 11A^{2} } \right)r_{P}^{2} } \right)\cos \psi \\ & \quad + 2r_{S} \left( {\left( {6A^{2} - 1} \right)r_{S}^{2} + \left( {9A^{2} - 1} \right)r_{P}^{2} } \right)\cos 2\psi \\ & \quad + r_{P} \left( {3A^{2} \left( {r_{P}^{2} - r_{S}^{2} } \right) - r_{P}^{2} } \right)\cos 3\psi \\ & \quad + r_{S} \left( {\left( {1 - 4A^{2} } \right)r_{S}^{2} + 2\left( {1 - 3A^{2} } \right)r_{P}^{2} } \right)\cos 4\psi \\ & \quad + \left( {3A^{2} - 1} \right)r_{S}^{2} r_{P} \cos 5\psi + 12A^{2} r_{S} r_{P}^{2} + r_{S}^{3} )]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} \\ \end{aligned} $$

(46)

$$ \begin{aligned} V_{zz}^{O - T2{\text{D}}} & = \frac{1}{2}G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos \theta_{s} [\left( {3\cos 2\psi + 1} \right)\ln \left( {\mathcal{L}_{PS} + r_{S} - r_{P} \cos \psi } \right) \\ & \quad - (2r_{S} \left( {4r_{S}^{2} + 6r_{P}^{2} } \right)\cos 2\psi + 4r_{S}^{3} - 6r_{S}^{2} r_{P} \cos 3\psi + 10r_{S} r_{P}^{2} \\ & \quad - 2r_{P} \left( {11r_{S}^{2} + 3r_{P}^{2} } \right)\cos \psi )/\mathcal{L}_{PS}^{3} )]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} \\ \end{aligned} $$

(47)

$$ \begin{aligned} V_{xy}^{O - T2{\text{D}}} & = 3G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} A\cos^{2} \theta_{s} \sin \left( {\lambda_{S} - \lambda_{P} } \right)[\ln \left( {\mathcal{L}_{PS} + r_{S} - r_{P} cos\psi } \right) \\ & \quad + \frac{{\csc^{4} \psi }}{{12\mathcal{L}_{PS}^{3} }}( - r_{P} \left( {24r_{S}^{2} + 11r_{P}^{2} } \right)\cos \psi + 6r_{S} \left( {2r_{S}^{2} + 3r_{P}^{2} } \right)\cos 2\psi + 3r_{P} \left( {r_{P}^{2} - r_{S}^{2} } \right)\cos 3\psi \\ & \quad - 2r_{S} \left( {2r_{S}^{2} + 3r_{P}^{2} } \right)\cos 4\psi + 3r_{S}^{2} r_{P} \cos 5\psi + 12r_{S} r_{P}^{2} )]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} \\ \end{aligned} $$

(48)

$$ \begin{aligned} V_{yz}^{O - T2{\text{D}}} & = 3G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} A\cos \theta_{s} [\cos \psi \ln \left( {\mathcal{L}_{PS} + r_{S} - r_{P} \cos \psi } \right) \\ & \quad + (\csc^{2} \psi ( - 2r_{S}^{3} \cos \psi - 3r_{P} \left( {2r_{S}^{2} + r_{P}^{2} } \right)\cos 2\psi + 2r_{S} \left( {2r_{S}^{2} + 3r_{P}^{2} } \right)\cos 3\psi \\ & \quad - 3r_{S}^{2} r_{P} \cos 4\psi + 3r_{S}^{2} r_{P} + r_{P}^{3} ))/6\mathcal{L}_{PS}^{3} ]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} \\ \end{aligned} $$

(49)

$$ \begin{aligned} V_{xz}^{O - T2{\text{D}}} & = 3G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos^{2} \theta_{s} \sin \left( {\lambda_{S} - \lambda_{P} } \right)[\cos \psi \ln \left( {\mathcal{L}_{PS} + r_{S} - r_{P} \cos \psi } \right) \\ & \quad + (\csc^{2} \psi ( - 2r_{S}^{3} \cos \psi - 3r_{P} \left( {2r_{S}^{2} + r_{P}^{2} } \right)\cos 2\psi + 2r_{S} \left( {2r_{S}^{2} + 3r_{P}^{2} } \right)\cos 3\psi \\ & \quad - 3r_{S}^{2} r_{P} \cos 4\psi + 3r_{S}^{2} r_{P} + r_{P}^{3} ))/6\mathcal{L}_{PS}^{3} ]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} \\ \end{aligned} $$

(50)

$$ V_{xyz}^{O - T2{\text{D}}} = - 3G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} A\cos^{2} \theta_{s} \sin \left( {\lambda_{S} - \lambda_{P} } \right)\left[ {\frac{{r_{s}^{5} }}{{r_{p} \mathcal{L}_{PS}^{5} }}} \right]|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(51)

$$ \begin{aligned} V_{yyy}^{O - T2{\text{D}}} & = G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \Bigg[\frac{{ - \cos \theta_{S} \csc^{6} \psi AB}}{{8r_{P} \mathcal{L}_{PS}^{5} }}( - 2r_{S} r_{P} \left( {\left( {136A^{2} - 27} \right)r_{S}^{2} + 8\left( {16A^{2} - 3} \right)r_{P}^{2} } \right)\cos \psi \\ & \quad + 4\left( {\left( {9 - 7A^{2} } \right)r_{S}^{4} + \left( {28A^{2} + 15} \right)r_{S}^{2} r_{P}^{2} + 6r_{P}^{4} } \right)\cos 2\psi \\ & \quad + r_{S} r_{P} ((16A^{2} - 57)r_{S}^{2} - 48r_{P}^{2} )\cos 3\psi \\ & \quad + r_{S}^{2} ((A^{2} - 1)r_{S}^{2} + 21r_{P}^{2} )\cos 4\psi \\ & \quad + 3r_{S}^{3} r_{P} \cos 5\psi + \left( {64A^{2} - 24} \right)r_{P}^{4} \\ & \quad + \left( {272A^{2} - 81} \right)r_{S}^{2} r_{P}^{2} + \left( {89A^{2} - 33} \right)r_{S}^{4} \Bigg]\Bigg|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} \\ \end{aligned} $$

(52)

$$ V_{yyz}^{O - T2{\text{D}}} = G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos \theta_{s} \left[ {r_{s}^{3} \frac{{\left( {\mathcal{L}_{PS}^{2} - 3A^{2} r_{s}^{2} } \right)}}{{r_{p} \mathcal{L}_{PS}^{5} }}} \right]\Bigg|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(53)

$$ V_{zzx}^{O - T2{\text{D}}} = 3G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos^{2} \theta_{s} \sin \left( {\lambda_{S} - \lambda_{P} } \right)\left[ {\frac{{Br_{s}^{4} }}{{r_{p} \mathcal{L}_{PS}^{5} }}} \right]\Bigg|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(54)

$$ V_{zzy}^{O - T2{\text{D}}} = 3G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} \cos \theta_{s} A\left[ {\frac{{Br_{s}^{4} }}{{r_{p} \mathcal{L}_{PS}^{5} }}} \right]\Bigg|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(55)

$$ V_{zzz}^{O - T2{\text{D}}} = -\, G\rho_{S} \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} cos\theta_{s} \left[ {r_{s}^{3} \frac{{\left( {4r_{p}^{2} + r_{s}^{2} - 8r_{p} r_{s} \cos \psi + 3r_{s}^{2} \cos 2\psi } \right)}}{{2r_{p} \mathcal{L}_{PS}^{5} }}} \right]\Bigg|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} $$

(56)

$$ \begin{aligned} V_{yyx}^{O - T2{\text{D}}} & = \mathop \int \limits_{{\lambda_{1} }}^{{\lambda_{2} }} \mathop \int \limits_{{\theta_{1} }}^{{\theta_{2} }} G\rho_{S} \cos^{2} \theta_{s} \csc^{6} \psi \sin \left( {\lambda_{P} - \lambda_{S} } \right)\Bigg[B(\left( {64A^{2} - 8} \right)r_{P}^{4} \\ & \quad + \left( {272A^{2} - 27} \right)r_{P}^{2} r_{S}^{2} + \left( {89A^{2} - 11} \right)r_{S}^{4} - 2r_{P} r_{S} \left( \begin{aligned} 8\left( {16A^{2} - 1} \right)r_{P}^{2} \hfill \\ + \left( {136A^{2} - 9} \right)r_{S}^{2} \hfill \\ \end{aligned} \right)\cos \psi \\ & \quad + 4\left( {2r_{P}^{4} + \left( {5 + 28A^{2} } \right)r_{P}^{2} r_{S}^{2} + \left( {3 - 7A^{2} } \right)r_{S}^{4} } \right)\cos 2\psi \\ & \quad + \left( {\left( {16A^{2} - 19} \right)r_{S}^{2} - 16r_{P}^{2} } \right)r_{P} r_{S} \cos 3\psi \\ & \quad + \left( {7r_{P}^{2} + \left( {3A^{2} - 1} \right)r_{S}^{2} } \right)r_{S}^{2} \cos 4\psi + r_{P} r_{S}^{3} \cos 5\psi )/8r_{P} \mathcal{L}_{PS}^{5} \Bigg]\Bigg|_{{r_{S} = r_{1} }}^{{r_{S} = r_{2} }} {\text{d}}\theta_{S} {\text{d}}\lambda_{S} \\ \end{aligned} $$

(57)

where $\cos 2\psi = 2\cos^{2} \psi - 1$, $\cos 3\psi = 4\cos^{3} \psi - 3\cos \psi$, $\cos 4\psi = 8\cos^{4} \psi - 8\cos^{2} \psi + 1$ and $\cos 5\psi = 16\cos^{5} \psi - 20\cos^{3} \psi + 5\cos \psi$, and other parameters are the same as in Appendix 1.

Appendix 3: Tables of numerical approaches (3D/2D TSE, GLQ, NCQ) for the Topographic Effects

See Tables 3, 4, 5, 6 and 7

Table 3 Detailed expressions of 3D $F_{m}$ and $X\left( {\lambda_{0} ,\theta_{0} ,r_{0} } \right)$ in Eqs. (12–16) with $K_{0} = G\rho_{S} r_{0}^{2} \cos \theta_{0}$, $\mathcal{L}_{P0} = \sqrt {r_{P}^{2} + r_{0}^{2} - 2r_{P} r_{0} \cos \psi_{0} }$, $\cos \psi_{0} = \sin \theta_{P} \sin \theta_{0} + \cos \theta_{P} \cos \theta_{0} \cos \left( {\lambda_{P} - \lambda_{0} } \right)$, $A_{0} = \cos \theta_{P} \sin \theta_{0} - \sin \theta_{p} \cos \theta_{0} \cos \left( {\lambda_{P} - \lambda_{0} } \right)$ and $B_{0} = r_{P} - r_{0} \cos \psi_{0}$

Table 4 Detailed expressions of 2D $H_{n}$ and $Y\left( {\lambda_{0} ,\theta_{0} } \right)$ in Eqs. (17–21). Other parameters are the same in Table 3

Table 5 GLQ nodes x _i and weights w_i (i = 1 … N) with values rounded to ten decimal digits in interval [a, b] for $1 \le N \le 7$, where h = (b − a)

Table 6 CNCQ nodes x _i and weights w _i (i = 1 … N) with values in interval [a, b] for $2 \le N \le 7$, where h = (b − a)

Table 7 ONCQ nodes x _i and weights w _i (i = 1 … N) with values in interval [a, b] for $2 \le N \le 7$, where h = (b − a)