Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The fields of application range from solid earth physics, via geodesy and oceanography to atmospheric physics. For example, several studies are concerned with the state of isostatic mass compensation in regions such as South America, Africa, Himalaya, and Antarctica. GOCE will help to unify height systems worldwide and enable the direct conversion of GPS-based ellipsoidal heights to accurate and globally consistent heights above the geoid. For the first time, it became possible to derive mean dynamic ocean topography and geostrophic ocean velocities with high spatial resolution and accuracy directly from space, combining the altimetric mean sea surface and the GOCE geoid. Assimilation into numerical ocean circulation models will help to improve estimates of ocean mass and heat transport. Common-mode accelerations as measured by GOCE lead to improved atmospheric density and wind estimates at GOCE altitudes.

1 Introduction: GOCE and Earth Sciences

On March 17, 2009, the European Space Agency (ESA) launched the satellite Gravity and steady-state Ocean Circulation Explorer (GOCE). It is the first satellite of ESA’s Living Planet Programme (see ESA 1999a, 2006). It is also the first one that is equipped with a gravitational gradiometer. The purpose of the mission is to measure the spatial variations of the Earth’s gravitational field globally with maximum resolution and accuracy. Its scientific purpose is essentially twofold. First, the gravitational field reflects the density distribution of the Earth’s interior. There are no direct ways to probe the deep Earth interior, only indirect ones in particular, seismic tomography, gravimetry, and magnetometry. The gravimetry part is now been taken care of by GOCE. Also, in the field of space magnetometry, an ESA mission was launched in fall 2013; it is denoted “Swarm” and consists of three satellites. Seismic tomography is based on a worldwide integrated network of seismic stations. From a joint analysis of all seismic data, a tomographic image of the spatial variations in the Earth’s interior of the propagation velocity of seismic waves is derived. The three methods together establish the experimental basis for the study of solid Earth physics, or more specifically, of phenomena such as core-mantle topography, mantle convection, mantle plumes, ocean ridges, subduction zones, mountain building, and mass compensation. Inversion of gravity alone is non-unique but joint inversion together with seismic tomography, magnetic field measurements and in addition with surface data of plate velocities and topography, and models from mineralogy will lead to a more and more comprehensive picture of the dynamics and structure of the Earth’s interior (see, e.g., Hager and Richards 1989; Lithgow-Bertelloni and Richards 1998; Bunge et al. 1998; Kaban et al. 2004). Second, the gravitational field and therefore the mass distribution of the Earth determines the geometry of level surfaces, plumb lines, and lines of force. This geometry constitutes the natural reference in our physical and technical world. In particular, in cases where small potential differences matter such as in ocean dynamics and large civil constructions, precise knowledge of this reference is an important source of information. The most prominent example is ocean circulation. Dynamic ocean topography, the small one up to 2 m deviation of the actual ocean surface from an equipotential surface, can be directly translated into ocean surface circulation. The equipotential surface at mean ocean level is referred to as geoid and it represents the hypothetical surface of the world oceans at complete rest. GOCE, in conjunction with satellite altimetry missions, like Jason will allow for the first time direct and detailed measurement of ocean circulation (see discussions in Wunsch and Gaposchkin 1980; Ganachaud et al. 1997; LeGrand and Minster 1999; Losch et al. 2002; Albertella and Rummel 2009; Maximenko et al. 2009). GOCE is an important satellite mission for oceanography, solid Earth physics, geodesy, and climate research (compare ESA 1999b; Rummel et al. 2002; Johannessen et al. 2003).

2 GOCE Gravitational Sensor System

In the following, the main characteristics of the GOCE mission which is unique in several ways will be summarized (see also Gauss’ and Weber’s “Atlas of Geomagnetism” (1840) Was not the first: the History of the Geomagnetic Atlases). The mission consists of two complementary gravity sensing systems. The large-scale spatial variations of the Earth’s gravitational field are derived from its orbit, while the medium to short scales are measured by a so-called gravitational gradiometer. Even though satellite gravitational gradiometry has been proposed already in the late 1950s in Carroll and Savet (1959) (see also Wells 1984), the GOCE gradiometer is the first instrument of its kind to be put into orbit. The principles of satellite gradiometry will be described in Gauss’ and Weber’s “Atlas of Geomagnetism” (1840) Was Not the First: The History of the Geomagnetic Atlases. The purpose of gravitational gradiometry is the measurement of the gradients of gravitational acceleration or, equivalently, the second-derivatives of the gravitational potential. In total, there exist nine second-derivatives in the orthogonal coordinate system of the instrument. The GOCE gradiometer is a three-axis instrument and its measurements are based on the principle of differential acceleration measurement. It consists of three pairs of accelerometers, mounted orthogonally to each other, each accelerometer having three axes (see Fig. 1). The gradiometer baseline of each one-axis gradiometer is 50 cm. The precision of each accelerometer is about 2 ⋅ 10−12 m/s2 per square-root of Hz along two sensitive axes; the third axis has much lower sensitivity. This results in a precision of the gravitational gradients of 10−11 s−2 or 10 mE per square-root of Hz (1 E = 10−9 s−2 = 1 Eötvös Unit). From the measured gravitational acceleration differences, the three main diagonal terms and one off-diagonal term of the gravitational tensor can be determined with high precision. These are the three diagonal components Γ​​ xx , Γ​​ yy , Γ​​ zz  as well as the off-diagonal component Γ​​ xz , while the components Γ​​ xy and Γ​​ yz are less accurate. Thereby the coordinate axes of the instrument are pointing in flight direction (x), cross direction (y), and radially toward the Earth (z). The extremely high gradiometric performance of the instrument is confined to the so-called measurement band (MB) , while outside the measurement band noise is increasing.

Fig. 1
figure 1

GOCE gravitational gradiometer (courtesy ESA)

Full size image

Strictly speaking, the derivation of the gradients from accelerometer differences assumes all six accelerometers (three pairs) to be perfect twins and all accelerometer test masses to be perfectly aligned. In real world, small deviations from such an idealization exist. Thus, the calibration of the gradiometer is of high importance. Calibration is essentially the process of determination of a set of scale, misalignment, and angular corrections. They are the parameters of an affine transformation between an ideal and the actual set of six accelerometers. Calibration in orbit is done by random shaking of the satellite by means of a set of cold gas thrusters and comparison of the actual output with the theoretically correct one. Before calibration the nonlinearities of each accelerometer are removed electronically; in other words, the proof mass of each accelerometer inside the electrodes of the capacitive electronic feedback system is brought into its linear range.

The gravitational signal is superimposed by the effects of angular velocity and angular acceleration of the satellite in space. Knowledge of the latter is required for the removal of the angular effects from the gradiometer data and for angular control. The separation of angular acceleration from the gravitational signal is possible from a particular combination of the measured nine acceleration differences. The angular rates (in the MB) as derived from the gradiometer data in combination with those deduced from the star sensor readings are used for attitude control of the spacecraft. The satellite has to be well controlled and guided smoothly around the Earth. It is Earth pointing, which implies that it performs one full revolution in inertial space per full orbit cycle. Angular control is attained via magnetic torquers, i.e., using the Earth’s magnetic field lines for orientation. This approach leaves uncontrolled one-directional degree of freedom at any moment. In order to prevent non-gravitational forces, in particular atmospheric drag, to “sneak” into the measured differential accelerations as secondary effect, the satellite is kept “drag-free” in along-track direction by means of a pair of ion thrusters. The necessary control signal is derived from the available “common-mode” accelerations (sum instead of differences of the measured accelerations) along the three orthogonal axes of the accelerometer pairs of the gradiometer. Some residual angular contribution may also add to the common-mode acceleration, due to the imperfect symmetry of the gradiometer relative to the spacecraft’s center of mass. This effect has to be modeled.

The second gravity sensor device is a newly developed European GPS receiver. From its measurements, the orbit trajectory is computed to within a few centimeters, either purely geometrically, the so-called kinematic orbit, or by the method of reduced dynamic orbit determination (compare Švehla and Rothacher 2004; Jäggi 2007; Bock et al. 2011). As the spacecraft is kept in an almost drag-free mode (at least in along-track direction) the orbit motion can be regarded as purely gravitational. It complements the gradiometric gravity field determination and covers the long wavelength part of the gravity signal.

The orbit altitude is extremely low, only about 255 km at perigee. This is essential for a high gravitational sensitivity. No scientific satellite has been flown at such low altitudes so far. Its altitude is maintained through the drag-free control and additional orbit maneuvers, which are carried out at regular intervals. As said above, this very low altitude results in high demands on drag-free and attitude control. Finally, any time-varying gravity signal of the spacecraft itself, the so-called self-gravitation , must be excluded. This results in extremely tight requirements on metrical stiffness and thermal control.

In summary, GOCE is a technologically very complex and innovative mission. The gravitational field sensor system consists of a gravitational gradiometer and GPS receiver as core instruments. Orientation in inertial space is derived from star sensors. Common-mode and differential-mode accelerations from the gradiometer and orbit positions from GPS are used together with ion thrusters for drag-free control and together with magneto-torquers for angular control. The satellite and its instruments are shown in Fig. 2. The system elements are summarized in Table 1.

Fig. 2
figure 2

GOCE satellite and main instruments (courtesy ESA) (CESS coarse earth and Sun sensor, MT magneto torquer, STR star tracker, SSTI satellite to satellite tracking instrument, CDM command and data management unit, LRR laser retro reflector)

Full size image
Table 1 Sensor elements and type of measurement delivered by them (approximate orientation of the instrument triad: x = along-track, y = out-of-orbit-plane, z = radially downward)
Full size table

3 Gravitational Gradiometry

Gravitational gradiometry is the measurement of the second derivates of the gravitational potential V. Its principles are described in textbooks such as Misner et al. (1970), Falk and Ruppel (1974), and Ohanian and Ruffini (1994) or in articles like Rummel (1986), compare also Colombo (1989) and Rummel (1997). Despite the high precision of the GOCE gradiometer instrument, the theory can still be formulated by classical Newton mechanics. Let us denote the gravitational tensor, expressed in the instrument frame as

$$\displaystyle{ \varUpsilon = V _{ij} = \left (\begin{array}{*{20}c} V _{xx}&V _{xy}&V _{xz} \\ V _{yx}&V _{yy}&V _{yz} \\ V _{zx} & V _{zy} & V _{zz}\\ \end{array} \right ) = \left (\begin{array}{*{20}c} \frac{\partial ^{2}V } {\partial x^{2}} & \frac{\partial ^{2}V } {\partial x\partial y} & \frac{\partial ^{2}V } {\partial x\partial z} \\ \frac{\partial ^{2}V } {\partial y\partial x} & \frac{\partial ^{2}V } {\partial y^{2}} & \frac{\partial ^{2}V } {\partial y\partial z} \\ \frac{\partial ^{2}V } {\partial z\partial x} & \frac{\partial ^{2}V } {\partial z\partial y} & \frac{\partial ^{2}V } {\partial z^{2}}\\ \end{array} \right ), }$$
(1)

where the gravitational potential represents the integration over all Earth masses (cf. Classical Physical Geodesy and Stokes Problem, Layer Potentials and Regularizations, and Multiscale Applications)

$$\displaystyle{ V _{P} = G\int \int \int \frac{\rho _{Q}} {\ell_{PQ}}d\varSigma _{Q}. }$$
(2)

where G is the gravitational constant, ρ Q the density, ℓ PQ the distance between the mass element in Q and the computation point P, and d Σ is the infinitesimal volume. We may assume the gravitational effect of the atmosphere to be negligible. Then the space outside of the Earth is empty and it holds ∇⋅ ∇V = 0 (source free) apart from ∇×∇V = 0 (vorticity free). This corresponds to saying in Eq. 1 V ij = V ji and \(\sum \nolimits _{i}V _{ii} = 0\). It leaves only five independent components in each point and offers important cross-checks between the measured components. If the Earth were a homogenous sphere, the off-diagonal terms would be zero and in a local triad {north, east, radial} one would find

$$\displaystyle{ \varUpsilon = V _{ij} = \left (\begin{array}{*{20}c} V _{xx}&V _{xy}&V _{xz} \\ V _{yx}&V _{yy}&V _{yz} \\ V _{zx} & V _{zy} & V _{zz}\\ \end{array} \right ) = \frac{GM} {r^{3}} \left (\begin{array}{*{20}c} -1& 0 &0\\ 0 &-1 &0 \\ 0 & 0 &2\\ \end{array} \right ), }$$
(3)

where M is the mass of the spherical Earth. This simplification gives an idea about the involved orders of magnitude. At GOCE satellite altitude, it is V zz = 2, 740 E. This also implies that at a distance of 0.5 m from the spacecraft’s center of mass, the maximum gravitational acceleration is about 1. 5 ⋅ 10−6 m/s2.

In an alternative interpretation, one can show that the V ij express the local geometric curvature structure of the gravitational field, i.e.,

$$\displaystyle{ \varUpsilon = V _{ij} = -g\left (\begin{array}{*{20}c} k_{1} & t_{1} & f_{1} \\ t_{2} & k_{2} & f_{2} \\ f_{1} & f_{2} & -H\\ \end{array} \right ), }$$
(4)

where g is gravity, k 1 and k 2 express the local curvature of the level surfaces in north and east directions, t 1 and t 2 are the torsion, f 1 and f 2 the north and east components of the curvature of the plumb line, and H the mean curvature. For a derivation, refer to Marussi (1985). This interpretation of gravitational gradients in terms of gravitational geometry provides a natural bridge to Einstein’s general relativity, where gravitation is interpreted in terms of space-time curvature for it holds

$$\displaystyle{ R_{0j0}^{i} = \frac{1} {c^{2}}V _{ij} }$$
(5)

for the nine components of the tidal force tensor, which are components of \(R_{kjl}^{i}\) the Riemann curvature tensor with its indices running from 0, 1, 2, 3 (Ohanian and Ruffini 1994, p. 41; Moritz and Hofmann-Wellenhof 1993, Chap. 5).

A third interpretation of gravitational gradiometry is in terms of tides. Sun and moon produce a tidal field on Earth. It is zero at the Earth’s center of mass and maximum at its surface. Analogously, the Earth is producing a tidal field in every Earth-orbiting satellite. At the center of mass of a satellite, the tidal acceleration is zero; i.e., the acceleration relative to the center of mass is zero; this leads to the terminology “zero-g.” The tidal acceleration increases with distance from the satellite’s center of mass like

$$\displaystyle{ a_{i} = V _{ij}dx^{j} }$$
(6)

with the measurable components of tidal acceleration a i and of relative position dx j, both taken in the instrument reference frame. Unlike sun and moon relative to the Earth, GOCE is always Earth pointing with its z-axis. This implies that the gradiometer measures permanently “high-tide” in z-direction and “low-tide” in x- and y-directions. The gradient components are deduced from taking the difference between the acceleration at two points along one gradiometer axis and symmetrically with respect to the satellite’s center of mass

$$\displaystyle{ V _{ij} =\; \begin{array}{*{20}c} a_{i}(1) - a_{i}(2) \\ \hline 2dx^{j} \\ \end{array}. }$$
(7)

Remark 1.

In addition to the tidal acceleration of the Earth, GOCE is measuring the direct and indirect tidal signal of sun and moon. This signal is much smaller, well-known and taken into account.

If the gravitational attraction of the atmosphere is taken care of by an atmospheric model, the Earth’s outer field can be regarded source free and Laplace equation holds. It is common practice to solve Laplace equation in terms of spherical harmonic functions. The use of alternative base functions is discussed, for example, in Schreiner (1994) or Freeden et al. (1998). For a spherical surface, the solution of a Dirichlet boundary value problem yields the gravitational potential of the Earth in terms of normalized spherical harmonic functions \(Y _{nm}(\varOmega _{P})\) of degree n and order m as:

$$\displaystyle{ V (P) =\sum \limits _{n}\left ( \frac{R} {r_{P}}\right )^{n+1}\sum \limits _{ m}t_{nm}Y _{nm}(\Omega _{P}) = \underline{Y }\,\underline{t} }$$
(8)

with {Ω P , r P } = {θ P , λ P , r P } the spherical coordinates of P and t nm the spherical harmonic coefficients. The gravitational tensor at P is then

$$\displaystyle{ V _{ij}(P) =\sum \nolimits _{n}\sum \nolimits _{m}t_{nm}\partial _{ij}\left \{\left ( \frac{R} {r_{P}}\right )^{n+1}Y _{ nm}(\Omega _{P})\right \} = \underline{Y }\{ij\}\underline{t}. }$$
(9)

The spherical harmonic coefficients t nm are derived from the measured gradiometric components V ij by least squares adjustment.

Remarks 2.

In the case of GOCE gradiometry the situation is as follows.

Above degree and order \(n = m = 220\), noise starts to dominate signal. Thus, the series has to be truncated in some intelligent manner, minimizing aliasing and leakage effects.

GOCE is covering our globe in 61 days with a dense pattern of ground tracks. Original planning of its mission lifetime assumed the completion of at least three times such 61-day cycles.

The orbit inclination is 96. 7∘. This leaves the two polar areas (opening angle 6. 7∘) free of observations, the so-called polar gaps. Various strategies have been suggested for minimization of the effect of the polar gaps on the determination of the global field (compare, e.g., Baur et al. 2009).

Instead of dealing in an least-squares adjustment with the analysis of the individual tensor components one could consider the study of particular combinations. A very elegant approach is the use of the invariants of the gravitational tensor. They are independent of the orientation of the gradiometer triad. It is referred to Rummel (1986) and in particular to Baur and Grafarend (2006) and Baur (2007). While the first invariant cannot be used for gravity field analysis, it is the Laplace trace condition, the two others can be used. They are nonlinear and lead to an iterative adjustment.

Let us assume for a moment the gradiometer components V ij would be given in an Earth-fixed spherical {north, east, radial}-triad. In that case, the tensor can be expanded in tensor spherical harmonics and decomposed into the irreducible radial, mixed normal-tangential, and pure tangential parts with the corresponding eigenvalues (Rummel and van Gelderen 1992; Schreiner 1994; Rummel 1997; Nutz 2002; Martinec 2003),

$$\displaystyle{\begin{array}{*{20}c} (n + 1)(n + 2)\qquad \mbox{ for}\quad \Gamma _{zz}\qquad \mbox{ and}\quad \Gamma _{xx} + \Gamma _{yy}, \\ \quad - (n + 2)\sqrt{n(n + 1)}\quad \mbox{ for}\quad \{\Gamma _{xz},\Gamma _{yz}\}, \frac{(n+2)!} {(n-2)!}\quad \mbox{ for}\quad \{\Gamma _{xx} - \Gamma _{yy},-\Gamma 2\Gamma _{xy}\}\\ \end{array} }$$

All eigenvalues are of the order of n 2. In Schreiner (1994) and Freeden et al. (1998) as well as Geodetic Boundary Value Problem of this handbook, it is also shown that {\(\Gamma _{xz}\), \(\Gamma _{yz}\)} and {\(\Gamma _{xx}-\) \(\Gamma _{yy}\), – 2\(\Gamma _{xy}\)} are insensitive to degree zero, the latter combination also to degree one. In the case of GOCE, the above properties cannot be employed in a straightforward manner, because (1) not all components are of comparable precision and, more importantly, (2) the gradiometric components are measured in the instrument frame, which is following in its orientation the orbit and the attitude control commands.

There exist various competing strategies for the actual determination of the field coefficients t nm , depending on whether the gradients are regarded in situ measurements on a geographical grid, along the orbit tracks, as a time series along the orbit or as Fourier-coefficients derived from the latter (compare, e.g., Migliaccio et al. 2004; Pail and Plank 2004; Brockmann et al. 2009; Stubenvoll et al. 2009). These methods take into account the noise characteristics of the components and their orientation in space.

The principles of the methods of gravity modeling are described by Roland Pail in this handbook (Pail 2014). Here, the stochastic as well as the functional model are discussed. It also contains a summary of the methods of determination of angular rates from a joint analysis of star tracking and gradiometry applying Wiener filtering. Because of the polar gap gravity modeling combining gravitational gradiometry and GPS-based kinematic orbits leads to numerical instabilities and requires some form of regularization (Kusche and Klees 2002). A further step will be regional refinement by combination of GOCE with terrestrial data sets (e.g., Eicker et al. 2009; Stubenvoll et al. 2009 or Förste et al. 2011).

4 GOCE Status

GOCE was launched on March 17, 2009. After a commissioning and calibration phase, the first operational measurement cycle started on November 1, 2009. The mission was originally planned for 20 months only, because of its smooth performance it was ultimately extended until November 2013. All sensor systems worked well with the exception of a slightly higher than nominal noise level in the radial components V zz and V xz for reasons still not understood. Three major interruptions occurred: from February 12 to March 2 and from July 2 to September 25, 2010 due to problems with the processor units and from January 1 to January 21, 2011 because of a software problem related to the GPS receiver. The mission ended on November 11, 2013 with the reentry of the spacecraft over the South Atlantic Ocean near the Falkland Islands. By August 2013, altogether 2.3 years of data were available and entered the release 4 models. ESA Release 4 GOCE gravity models are summarized in Table 2. From August 1, 2012 on the orbit, altitude was lowered in four steps with at least one full measurement cycle in between by 9, 6, 5, and 11 km, i.e., altogether by 31km. The lowest altitude was attained on May 31, 2013 with 224 km. This was done in order to test whether the increased gravitational sensitivity can be exploited despite the increase of atmospheric drag at lower altitudes. Preliminary analysis shows an increase in spatial resolution. Release five is expected to be published in summer 2014. It will include the complete GOCE data set, including the data from the lower orbit altitudes.

Table 2 ESA release 4 GOCE gravity models DIR4 and TIM4 and their characteristics
Full size table

5 Conclusions: GOCE Science Applications

Data exploitation of GOCE for science and application is far from being completed. We observe that the research fields are essentially those identified already in the GOCE mission proposal (ESA 1999b). There is an exception. The expectation was that GOCE will be unable to sense temporal variations of gravity and geoid. This is true in general; however some big mass movements such as those associated with the big Japan earthquake seem to be detectable from the gradiometer data (Bouman et al. 2013).

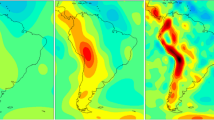
Solid earth physics. The gravity field as sensed by GOCE reflects the density distribution of the earth’s masses, primarily from topography, crust, and lithosphere and in an attenuated form from the upper and lower mantle down to the core. In ocean areas, gravity is well-known already from satellite altimetry. The situation is different in continental areas. Comparisons of GOCE gravity models with EGM2008 (e.g., Yi and Rummel 2014) reveal good agreement in well-surveyed parts of the earth such as North America, Europe, Australia, New Zealand, and Japan but rather poor agreement in large parts of South America, Africa, Himalaya, and South-East Asia. EGM2008 is a combination of GRACE satellite gravimetry with a global set of terrestrial gravity anomalies. Some of the regions with poor terrestrial gravity are of high geodynamic relevance. Currently several studies are underway, looking into the state of isostatic equilibrium and into the elastic thickness of the lithosphere (e.g., Sampietro et al. 2012 or van der Meijde et al. 2013). A special case is Antarctica where terrestrial gravity data is sparse. GRACE delivered gravity and geoid information in Antarctica but confined to rather large spatial scales. GOCE shows now the gravity field and with it tectonic processes hidden under an ice layer with a thickness of several kilometers (e.g., Ferraccioli et al. 2011).

Figure 3 shows the vertical gravity gradient field of Antarctica as measured by GOCE and some prominent tectonic features. The polar gap is marked in gray.

Fig. 3
figure 3

Vertical gravity gradient field of Antartica as measured by GOCE (units: milliEötvös = 10-12s-2) and some prominent tectonic features; the GOCE polar gap is marked in gray

Full size image

Height systems. Official heights are provided to the user either as gravity potential differences between terrain points or as metric heights derived from the potential differences such as orthometric or normal heights. The official height systems refer to a zero value at some adopted reference marker at a tide gauge, representing mean sea level there. However, mean sea level varies from location to location due to the variations in coastal oceanic conditions. The variations are not big, usually less than 2 m, but they are responsible for unknown height off-sets between the various worldwide official height systems. GOCE provides the best possible geoid surface (ideally refined locally by shorter scales from some regional geoid computation). It represents the theoretical sea surface at rest and can be introduced as an ideal worldwide height reference. It also permits determination of the height off-sets between the various height systems, not detectable in the past. This process of height unification is of great value for mapping, large civil constructions and sea level research. As a demonstration of the value of the GOCE geoid for height determination, Woodworth et al. (2012) revealed the bias of the North American height system which is based on classical spirit leveling. In the near future, GPS positions can be translated to heights above the GOCE geoid yielding globally consistent and physically meaningful heights worldwide.

Oceanography. In his classical textbook “Atmosphere-Ocean Dynamics”, A.E. Gill (1982) writes on page 46: “If the sea were at rest, its surface would coincide with the geopotential surface.” This geopotential surface is the geoid and with GOCE its shape is determined with an accuracy of 2–3 cm. In reality the sea is not at rest, it is in motion as driven by winds, atmospheric pressure differences, and tides and as a consequence the ocean surface deviates from a geopotential surface by up to 1 or 2 m at the major ocean currents; the deviation is denoted dynamic ocean topography. The actual sea surface is measured from space by satellite altimetry. More than 20 years of altimetry yield models of the mean sea surface (MSS) accurate to a few centimeters. Subtraction of the GOCE geoid from MSS gives the geodetic mean dynamic ocean topography (MDT). It is maintained by the balance of the pressure differences due to the MDT and Coriolis acceleration. Its slope is proportional to the geostrophic velocities of ocean circulation. GOCE together with altimetry give MDT and the geostrophic velocity field without the use of any oceanographic in situ data. Geodetic MDT and geostrophic velocities represent a new type of input quantity for numerical ocean circulation models and help to improve ocean mass and heat transport estimates, e.g., in the area of the Weddell Sea in the Southern ocean, one of the tipping points of our climate system. Figure 4 shows the magnitude of the geostrophic velocities in the North Atlantic based on the Danish MSS model DTU-10 (right) and geostrophic velocities derived from drifter data (left). We observe higher signal strength of the geodetic estimate. A large number of ocean studies based on GOCE was published already. Examples are Bingham et al. (2011), Janjić et al. (2012) or Le Traon et al. (2011).

Fig. 4
figure 4

Geostropic velocities (in cm/s) derived from drifter measurements (left) and from geodetic mean dynamic ocean topography (right)

Full size image

Atmosphere. GOCE was kept drag-free in flight direction using ion thrusters. The feedback signal for drag-free control was the measured common-mode accelerations of the six accelerometers of the gradiometer. They are a measure of the nongravitational forces acting on the GOCE spacecraft and open the possibility for studies of atmospheric density and winds (Doornbos et al. 2013). At GOCE altitude, no other data source is available.