An innovative DoE strategy of the kriging model for structural reliability analysis

Abstract

An innovative strategy of the design of experiments (DoE) is proposed to reduce the number of calls of the performance function in the kriging-based structural reliability analysis procedure. Benefitting from the local uncertainty provided by the kriging model and the joint probability density function of performance function values of untried points derived in this research, the epistemic variance of the target failure probability is calculated approximately. The variance is treated as the accuracy measurement of the estimated failure probability. The next best point is defined as the untried point that can minimize the variance of failure probability in the sense of expectation which is computed by Gauss–Hermite quadrature. The basic idea of the proposed strategy is to refresh the current DoE by adding the next best point into it. The candidate points of the next best one are randomly generated by Markov chain Monte Carlo method from the kriging-based conditional distribution. A structural reliability analysis procedure is introduced to apply the proposed DoE strategy, whose stopping criterion is constructed mainly on the basis of the coefficient of variation of failure probability. To validate the efficiency of the proposed DoE strategy, three examples are analyzed in which there are explict and implict performance function. And, the analysis results demonstrate the outperformance of the innovative strategy.

1 Introduction

As is known to all, the most important purpose of structural reliability analysis is to estimate the reliability or the failure probability of a mechanical structure whose safety is influenced by kinds of randomness of input variables. This research focuses on the estimation of failure probability, which is defined as follows:

$$ {P}_f=E\left({I}_{G\le 0}\left(\boldsymbol{X}\right)\right)=\int {I}_{G\le 0}\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x} $$

(1)

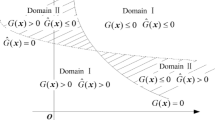
G(x) is the performance function of a studied structure. The random vector X = [X₁, X₂, ..., X_M]^T with joint probability density function f(x) contains all input variables with uncertainty. The performance function divides the whole space of X into the safe domain G(x) > 0 and the failure domain G(x) ≤ 0. I_G ≤ 0(x)is the failure indicator function defined as (2):

$$ {I}_{G\le 0}\left(\boldsymbol{x}\right)=\Big\{{\displaystyle \begin{array}{l}0\kern1.6em G\left(\boldsymbol{x}\right)>0\\ {}1\kern1.7em G\left(\boldsymbol{x}\right)\le 0\end{array}} $$

(2)

The multidimensional integral is not easy to perform because the performance function of interest is usually implicit and time-consuming to calculate in engineering. As the development of computer codes, complex numerical models are widely employed to define a performance function with a scalar or vector output, which enhances the estimate of failure probability. Nowadays, three kinds of methods are used to approximately perform (1), i.e., random simulation methods, the first- and second-order reliability method (FORM and SORM), and surrogate model-based methods.

Random simulation methods, including Monte Carlo simulation (MCS) (Sobol and Tutunnikov 1996; Gaspar et al. 2014; Zhang et al. 2010), importance sampling (Melchers 1990; Richard and Zhang 2007; Cornuet et al. 2012), subset simulation (Au and Beck 2001; Au 2016), line sampling (Pradlwarter et al. 2007), etc., need to call a great deal of the performance function to acquire accurate result, which is generally unaffordable. The accuracy of FORM and SORM is undesirable for engineering when the performance function is highly nonlinear (Zhao and Ono 1999). In recent years, surrogate models obtain much popularity (Bucher and Most 2008; Kleijnen 2009; Bourinet et al. 2011; Schueremans and Van Gemert 2005). The basic idea of this kind of method is to construct an explicit expression based on the data from the design of experiments (DoE) of computer codes, and the explicit expression is treated as a surrogate of the real performance function to estimate the failure probability (Bucher and Most 2008). An accurate surrogate is essential to guarantee the accuracy of the estimated failure probability. Several surrogate models including polynomial response surface (Gayton et al. 2003), spare polynomial expansion (Blatman and Sudret 2008; Yu et al. 2012), kriging(Kaymaz 2005; Shimoyama et al. 2013; Bae et al. 2018), support vector machine (Song et al. 2013; Alibrandi et al. 2015), neural network (Schueremans and Van Gemert 2005), etc. are available for structural reliability analysis.

This research focuses on the kriging model with two characteristics that are indeed valuable for structural reliability analysis. The first of them is that the kriging model is a method of interpolation, which makes it possible to improve the local accuracy of the surrogate model. The second is that it provides both the best linear unbiased estimator and the so-called kriging variance which quantifies the local accuracy of the kriging model or the local epistemic uncertainty of the performance function value. (Jones et al. (1998)) applies kriging to global optimization and constructs the expected improvement function based on the statistical information mentioned above to acquire an explicit tradeoff between improvement of the global accuracy of the kriging model and exploration of the area of interest. During structural reliability analysis, (1) indicates that only the sign of G(x) or the limit state G(x) = 0 matters to the estimate of failure probability. To obtain a global fitting of the limit, Bichon et al. (2008) proposes the expected feasibility function (EFF) to quantify the degree that a point satisfies G(x) = 0 in the sense of expectation and refresh DoE iteratively by adding the maximum point or the next best point into it until the maximum value of EFF is lower than a given threshold. After ref. (Bichon et al. 2008), Bichon et al. (Echard et al. 2011, 2013), Lv et al. (2015), and Yang et al. (2015a), Yang et al. (2015b) construct learning function U, learning function H, and the expected risk function, respectively. These “learning functions” for reliability analysis measure a point by taking only the statistical information provided by the kriging model into consideration and ignoring its importance or the joint PDF f(x). The next best point from the above-mentioned learning functions may locate in the area of little significance for the target failure probability. The least improvement function (LIF) in ref. (Sun et al. 2017) is designed to quantify how much the fraction of the domain with uncertain signs could be minished at least in terms of expectation if adding a point into the current DoE. It provides the tradeoff between the local uncertainty of signs and the joint PDF. The hypotheses formed during the derivation of LIF make its efficiency vary with problems.

To further reduce the number of calling the performance function during structural reliability, this research proposes an innovative DoE strategy named as stepwise variance reduction strategy. The epistemic variance of the target failure probability is proposed as the accuracy measurement of the estimated failure probability and calculated approximately. The basic idea of the innovative strategy is to research the next best point that can minimize the epistemic uncertainty of the target failure probability or improve the accuracy of the estimate of failure probability most in the sense of expectation and refresh DoE by adding the next best point into it. Markov chain Monte Carlo (MCMC) method is employed to generate approximately i.i.d. (independent and identically distributed) candidates of the next best point from the domain that contributes most of the epistemic uncertainty of failure probability. Gauss–Hermite quadrature is used to approximate the expectation of the variance of failure probability after adding a given point into the current DoE. The next best point is defined as the one that minimizes the expectation. A reliability analysis procedure is introduced to apply the proposed DoE strategy. In the introduced procedure, the stopping criterion is based on the idea that the estimated failure probability meets the requirement of accuracy if the coefficient of variation of failure probability is smaller than a given threshold.

The remainder of this paper is organized as follows. Section 2 reviews the theory of the kriging model briefly and derives the joint PDF of the performance function values of untried points in detail, which is the key to the approximation of the epistemic variance of failure probability. The proposed strategy is constructed in Sect. 3 and applied in Sect. 4. Section 5 studies three examples to validate the efficiency of the proposed strategy. Section 6 is the conclusion.

2 Theory of the kriging model

2.1 Review of the kriging model

In the framework of the kriging model, the target performance function G(x) is treated as a realization of a Gaussian process. G(x) consists of two parts:

$$ G\left(\boldsymbol{x}\right)={\boldsymbol{g}}^{\mathrm{T}}\left(\boldsymbol{x}\right)\boldsymbol{\beta} +z\left(\boldsymbol{x}\right) $$

(3)

where g(x) is a scalar or multi-variable polynomial generally. Suitable basic functions benefit the accuracy of the kriging model especially when the number of points in DoE to build the kriging model is small. β is the coefficient vector of g(x). It is unknown and estimated with generalized least squares. g^T(x)β is the deterministic part of G(x), while z(x) is the stochastic part which is a realization of a stationary Gaussian process with zero-mean and constant variance (σ²). The covariance function of z(x) is defined as follows:

$$ \mathrm{Cov}\left(z\left({\boldsymbol{x}}_i\right),z\left({\boldsymbol{x}}_j\right)\right)={\sigma}^2R\left({\boldsymbol{x}}_i,{\boldsymbol{x}}_j;\boldsymbol{\theta} \right) $$

(4)

where R(x_i, x_j; θ) denotes the correlation between z(x_i) and z(x_j) and θ is an undetermined parameter vector. Among several correlation functions, the Gaussian correlation function performs well when dealing with nonlinear performance function. Therefore, it is employed in this research.

$$ R\left({\boldsymbol{x}}_i,{\boldsymbol{x}}_j;\boldsymbol{\theta} \right)=\prod \limits_{m=1}^M\exp \left[-{\theta}^{(m)}{\left({x}_i^{(m)}-{x}_j^{(m)}\right)}^2\right] $$

(5)

where θ^(m) and x_(m)i are the mth elements of θ and x_i, respectively.

Given a DoE containing N points S_DoE = [x₁,x₂,…,x_N] and performance function values of these points Y = [y₁, y₂,…, y_N]^T, the best linear unbiased estimator of G(x) for an untried point x is written as follows:

$$ {\mu}_{G,N}\left(\boldsymbol{x}\right)=\hat{G}\left(\boldsymbol{x}\right)={\boldsymbol{g}}^{\mathrm{T}}\left(\boldsymbol{x}\right)\hat{\boldsymbol{\beta}}+\boldsymbol{r}{\left(\boldsymbol{x}\right)}^{\mathrm{T}}\boldsymbol{\gamma} $$

(6)

where

$$ \hat{\beta}={\left({\boldsymbol{G}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{G}\right)}^{-1}{\boldsymbol{G}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{Y} $$

(7)

$$ \boldsymbol{\gamma} ={\boldsymbol{R}}^{-1}\left(\boldsymbol{Y}-\boldsymbol{G}\hat{\boldsymbol{\beta}}\right) $$

(8)

$$ \boldsymbol{r}\left(\boldsymbol{x}\right)={\left[R\left({\boldsymbol{x}}_1,\boldsymbol{x};\boldsymbol{\theta} \right),...,R\left({\boldsymbol{x}}_N,\boldsymbol{x};\boldsymbol{\theta} \right)\right]}^{\mathrm{T}} $$

(9)

$$ \boldsymbol{R}={\left(R\left({\boldsymbol{x}}_i,{\boldsymbol{x}}_j;\boldsymbol{\theta} \right)\right)}_{N\times N} $$

(10)

$$ \boldsymbol{G}={\left[\boldsymbol{g}\left({\boldsymbol{x}}_1\right),\boldsymbol{g}\left({\boldsymbol{x}}_2\right),...,\boldsymbol{g}\left({\boldsymbol{x}}_N\right)\right]}^{\mathrm{T}} $$

(11)

The mean square error of $\hat{G}\left(\boldsymbol{x}\right)$ or the so-called kriging variance is

$$ {\sigma}_{G,N}^2\left(\boldsymbol{x}\right)={\hat{\sigma}}^2\left(1+{\boldsymbol{u}}^{\mathrm{T}}\left(\boldsymbol{x}\right){\left({\boldsymbol{G}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{G}\right)}^{-1}\boldsymbol{u}\left(\boldsymbol{x}\right)-{\boldsymbol{r}}^{\mathrm{T}}\left(\boldsymbol{x}\right){\boldsymbol{R}}^{-1}\boldsymbol{r}\left(\boldsymbol{x}\right)\right) $$

(12)

where

$$ {\hat{\sigma}}^2=\frac{1}{N}{\left(\boldsymbol{Y}-\boldsymbol{G}\hat{\boldsymbol{\beta}}\right)}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\left(\boldsymbol{Y}-\boldsymbol{G}\hat{\boldsymbol{\beta}}\right) $$

(13)

$$ \boldsymbol{u}\left(\boldsymbol{x}\right)={\boldsymbol{G}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{r}\left(\boldsymbol{x}\right)-\boldsymbol{g}\left(\boldsymbol{x}\right) $$

(14)

The subscript N in (6) and (12) denotes the number of points in DoE.

In the framework of Gaussian process, G(x) is treated as an epistemic random variable and subject to normal distribution.

$$ G\left(\boldsymbol{x}\right)\sim N\left({\mu}_{G,N}\left(\boldsymbol{x}\right),{\sigma}_{G,N}^2\left(\boldsymbol{x}\right)\right) $$

(15)

Equation(15) provides the epistemic uncertainty (or the conditional distribution) of G(x) on the condition of S_DoE and Y, which makes it possible to quantify the local accuracy of the kriging surrogate model. Most of the kriging-based DoE strategies for reliability analysis, optimization, global sensitivity analysis, etc. are based on the statistical information provided by (15) (Jones et al. 1998; Bichon et al. 2008; Echard et al. 2011; Lv et al. 2015; Yang et al. 2015b; Sun et al. 2017). To find an optimal θ, both cross-validation and maximum likelihood estimation are available. The core issue of this article is how to use the Gaussian process instead of improving it, so the model-form uncertainty is ignored. The latter is used in this research.

$$ \hat{\boldsymbol{\theta}}=\underset{\boldsymbol{\theta}}{\mathrm{argmax}}\left(-N\ln \left({\hat{\sigma}}^2\right)-\ln \left[\det \left(\boldsymbol{R}\right)\right]\right) $$

(16)

2.2 The joint distribution of the performance function values of untried points

According to the information shown by (15), the local uncertainty of any untried point x can be measured, which is far from enough for reliability analysis application. The estimated performance function values of huge number of untried points are needed to determine an estimation of the target failure probability, and any two of the untried points have correlation. This research is interested in the joint distribution of ${\boldsymbol{Y}}_{\mathrm{U}}={\left[G\left({\boldsymbol{x}}_{\mathrm{U},1}\right),G\left({\boldsymbol{x}}_{\mathrm{U},2}\right),...,G\left({\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right)\right]}^T$of an untried sample of points ${\boldsymbol{S}}_{\mathrm{U}}=\left[{\boldsymbol{x}}_{\mathrm{U},1},{\boldsymbol{x}}_{\mathrm{U},2},...,{\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right]$ which may be helpful to construct a global accurate measurement of the kriging model or an uncertain quantification of a kriging-based estimation of failure probability.

To derive the joint PDF of ${\boldsymbol{Y}}_{\mathrm{U}}={\left[G\left({\boldsymbol{x}}_{\mathrm{U},1}\right),G\left({\boldsymbol{x}}_{\mathrm{U},2}\right),...,G\left({\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right)\right]}^T$, a preparatory theorem is necessary and shown as follows:

• Theorem 1: Y_t = [Y₁, Y₂, ...., Y_h]^T is a multivariate normal distributed vector with mean vector μ and covariance matrix Σ. ${\boldsymbol{Y}}_1={\left[{Y}_1,...,{Y}_{k_1}\right]}^T$ and ${\boldsymbol{Y}}_2={\left[{Y}_{k_1+1},...,{Y}_k\right]}^T$ are two sub-vectors of Y_t and satisfy (17),

$$ {Y}_1\sim N\left({\mu}_1,{\varSigma}_{11}\right)\kern0.5em \mathrm{and}\kern0.5em {\boldsymbol{Y}}_2\sim N\left({\boldsymbol{\mu}}_2,{\boldsymbol{\varSigma}}_{22}\right) $$

(17)

where

$$ {\boldsymbol{\varSigma}}_1=\left(\begin{array}{ll}{\boldsymbol{\varSigma}}_{11}& {\boldsymbol{\varSigma}}_{12}\\ {}{\boldsymbol{\varSigma}}_{21}& {\boldsymbol{\varSigma}}_{22}\end{array}\right)\kern0.5em \mathrm{and}\kern0.5em \boldsymbol{\mu} =\left(\begin{array}{l}{\boldsymbol{\mu}}_1\\ {}{\boldsymbol{\mu}}_2\end{array}\right) $$

(18)

$$ {\boldsymbol{\varSigma}}_{12}=E\left[\left({\boldsymbol{Y}}_1-{\boldsymbol{\mu}}_1\right){\left({\boldsymbol{Y}}_2-{\boldsymbol{\mu}}_2\right)}^T\right] $$

(19)

$$ {\boldsymbol{\varSigma}}_{21}=E\left[\left({\boldsymbol{Y}}_2-{\boldsymbol{\mu}}_2\right){\left({\boldsymbol{Y}}_1-{\boldsymbol{\mu}}_1\right)}^T\right] $$

(20)

Suppose that vector y₂ is a realization of Y₂. Then, the conditional distribution of Y₁ is shown as follows:

$$ {\boldsymbol{Y}}_1\mid {\boldsymbol{y}}_2\sim N\left({\boldsymbol{\mu}}_{1\cdot 2},{\boldsymbol{\varSigma}}_{11\cdot 2}\right) $$

(21)

where

$$ {\boldsymbol{\mu}}_{1\cdot 2}={\boldsymbol{\mu}}_1+{\boldsymbol{\varSigma}}_{12}{\boldsymbol{\varSigma}}_{22}^{-1}\left({\boldsymbol{x}}_2-{\boldsymbol{\mu}}_2\right) $$

(22)

$$ {\boldsymbol{\varSigma}}_{11\cdot 2}={\boldsymbol{\varSigma}}_{11}-{\boldsymbol{\varSigma}}_{12}{\boldsymbol{\varSigma}}_{22}^{-1}{\boldsymbol{\varSigma}}_{21} $$

(23)

Proof: Construct an auxiliary vector W,

$$ \boldsymbol{W}=\left(\begin{array}{l}{\boldsymbol{W}}_1\\ {}{\boldsymbol{W}}_2\end{array}\right)=\boldsymbol{A}{\boldsymbol{Y}}_t=\left(\begin{array}{l}{I}_{k_1}\kern0.5em -{\boldsymbol{\varSigma}}_{12}{\boldsymbol{\varSigma}}_{22}^{-1}\\ {}\begin{array}{cc}0& \kern1.5em {I}_{k-{k}_1}\end{array}\end{array}\right)\left(\begin{array}{l}{\boldsymbol{Y}}_1\\ {}{\boldsymbol{Y}}_2\end{array}\right) $$

(24)

It can be derived from (25),

$$ {\boldsymbol{W}}_1\sim N\left({\boldsymbol{\mu}}_1-{\boldsymbol{\varSigma}}_{12}{\boldsymbol{\varSigma}}_{22}^{-1}{\boldsymbol{\mu}}_2,{\boldsymbol{\varSigma}}_{11\cdot 2}\right) $$

(25)

$$ \operatorname{var}\left(\boldsymbol{W}\right)=\boldsymbol{A}\boldsymbol{\varSigma } {\boldsymbol{A}}^T=\left(\begin{array}{cc}{\boldsymbol{\varSigma}}_{11\cdot 2}& 0\\ {}0& {\boldsymbol{\varSigma}}_{22}\end{array}\right) $$

(26)

Therefore, W₁ and W₂ are independent with each other. Then, the joint PDF of W can be written as

$$ {f}_{\boldsymbol{W}}\left(\boldsymbol{w}\right)={f}_{{\boldsymbol{W}}_1}\left({\boldsymbol{w}}_1\right)\cdot {f}_{{\boldsymbol{W}}_2}\left({\boldsymbol{w}}_2\right) $$

(27)

One can notice,

$$ {f}_{{\boldsymbol{Y}}_t}\left({\boldsymbol{y}}_t\right)={f}_{\boldsymbol{W}}\left(\boldsymbol{w}\right)\cdot \mid \boldsymbol{A}\mid ={f}_{\boldsymbol{W}}\left(\boldsymbol{w}\right) $$

(28)

Now taking (25), (27), and (28) into account, the conditional PDF of Y₁ is

$$ {f}_{{\boldsymbol{Y}}_1\mid {\boldsymbol{y}}_2}\left({\boldsymbol{y}}_1\right)=\frac{f_{\boldsymbol{Y}}\left(\boldsymbol{y}\right)}{f_{{\boldsymbol{Y}}_2}\left({\boldsymbol{y}}_2\right)}=\frac{f_{\boldsymbol{Y}}\left(\boldsymbol{y}\right)}{f_{{\boldsymbol{W}}_2}\left({\boldsymbol{w}}_2\right)}={f}_{{\boldsymbol{W}}_1}\left({\boldsymbol{w}}_1\right) $$

(29)

$$ {\displaystyle \begin{array}{l}{f}_{{\boldsymbol{W}}_1}\left({\boldsymbol{w}}_1\right)={\left(2\pi \right)}^{-{k}_1/2}{\left|{\boldsymbol{\varSigma}}_{11\cdot 2}\right|}^{-1/2}\exp \left[-\frac{1}{2}{\left({\boldsymbol{w}}_1-{\boldsymbol{\mu}}_1-{\boldsymbol{\varSigma}}_{12}{\boldsymbol{\varSigma}}_{22}^{-1}{\boldsymbol{\mu}}_2\right)}^T{\boldsymbol{\varSigma}}_{11\cdot 2}^{-1}\left({\boldsymbol{w}}_1-{\boldsymbol{\mu}}_1-{\boldsymbol{\varSigma}}_{12}{\boldsymbol{\varSigma}}_{22}^{-1}{\boldsymbol{\mu}}_2\right)\right]\\ {}={\left(2\pi \right)}^{-{k}_1/2}{\left|{\boldsymbol{\varSigma}}_{11\cdot 2}\right|}^{-1/2}\exp \left[-\frac{1}{2}{\left({\boldsymbol{y}}_1-{\boldsymbol{\mu}}_{1\cdot 2}\right)}^T{\boldsymbol{\varSigma}}_{11\cdot 2}^{-1}\left({\boldsymbol{y}}_1-{\boldsymbol{\mu}}_{1\cdot 2}\right)\right]\end{array}} $$

(30)

Hence, it can be concluded as follows:

$$ {\boldsymbol{Y}}_1\mid {\boldsymbol{y}}_2\sim N\left({\boldsymbol{\mu}}_{1\cdot 2},{\boldsymbol{\varSigma}}_{11\cdot 2}\right) $$

(31)

Prove up.

Theorem 2:X is the input vector of a studied mechanical structure. Given S_DoE = [x₁,x₂,…,x_N] and Y = [y₁,y₂,…,y_N]^T, construct the kriging model (6) and (12) based on the theory in Sect. 2.1. ${\boldsymbol{S}}_{\mathrm{U}}=\left[{\boldsymbol{x}}_{\mathrm{U},1},{\boldsymbol{x}}_{\mathrm{U},2},...,{\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right]$contains N_U untried points belonging to the X space, and ${\boldsymbol{Y}}_{\mathrm{U}}={\left[G\left({\boldsymbol{x}}_{\mathrm{U},1}\right),G\left({\boldsymbol{x}}_{\mathrm{U},2}\right),...,G\left({\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right)\right]}^T$ is the performance function values with respect to S_U. The vector Y_U on the condition of Y = [y₁,y₂,…,y_N]^T is subject to multivariate normal distribution.

$$ {\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y}\sim N\left({\boldsymbol{\mu}}_{\mathrm{U}},{\boldsymbol{\varSigma}}_{\mathrm{U}}\right) $$

(32)

where

$$ {\displaystyle \begin{array}{l}{\boldsymbol{\mu}}_{\mathrm{U}}={\left[{\mu}_{G,N}\left({\boldsymbol{x}}_{\mathrm{U},1}\right),{\mu}_{G,N}\left({\boldsymbol{x}}_{\mathrm{U},2}\right),...,{\mu}_{G,N}\left({\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right)\right]}^T\\ {}\kern1.5em ={\boldsymbol{G}}_{\mathrm{U}}\hat{\boldsymbol{\beta}}+{\boldsymbol{r}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\left(\boldsymbol{Y}-\boldsymbol{G}\hat{\boldsymbol{\beta}}\right)\end{array}} $$

(33)

$$ {\boldsymbol{\varSigma}}_{\mathrm{U}}={\sigma}^2\left({\boldsymbol{R}}_{\mathrm{U}}+{\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\left({\boldsymbol{G}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{G}\right)}^{-1}{\boldsymbol{u}}_{\mathrm{U}}-{\boldsymbol{r}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}{\boldsymbol{r}}_{\mathrm{U}}\right) $$

(34)

$$ {\boldsymbol{R}}_{\mathrm{U}}={\left(R\left({\boldsymbol{x}}_{\mathrm{U},m},{\boldsymbol{x}}_{\mathrm{U},n};\boldsymbol{\theta} \right)\right)}_{N_{\mathrm{U}}\times {N}_{\mathrm{U}}} $$

(35)

$$ {\boldsymbol{r}}_{\mathrm{U}}={\left(R\left({\boldsymbol{x}}_n,{\boldsymbol{x}}_{\mathrm{U},m};\boldsymbol{\theta} \right)\right)}_{N\times {N}_{\mathrm{U}}} $$

(36)

$$ {\boldsymbol{u}}_{\mathrm{U}}={\boldsymbol{G}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}{\boldsymbol{r}}_{\mathrm{U}}-{\boldsymbol{G}}_{\mathrm{U}}^{\mathrm{T}} $$

(37)

$$ {\boldsymbol{G}}_{\mathrm{U}}\left(\boldsymbol{x}\right)={\left[\boldsymbol{g}\left({\boldsymbol{x}}_{\mathrm{U},1}\right),\boldsymbol{g}\left({\boldsymbol{x}}_{\mathrm{U},2}\right),...,\boldsymbol{g}\left({\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right)\right]}^T $$

(38)

Proof: According to the theory listed in Sect. 2.1, the performance function G(x) is treated as a realization of a Gaussian process with mean function g^T(x)β and covariance function σ²R(⋅,  ⋅ ; θ). And, [S_U, S_DoE] is a finite set of points contained in the X space. Therefore, ${\boldsymbol{Y}}_A={\left[G\left({\boldsymbol{x}}_{\mathrm{U},1}\right),...,G\left({\boldsymbol{x}}_{\mathrm{U},{N}_{\mathrm{U}}}\right),{y}_1,\dots, {y}_N\right]}^T$ is subject to multivariate normal distribution if the values of y_n (n = 1,…,N) are not calculated.

$$ {\boldsymbol{Y}}_A\mid \boldsymbol{\beta} \sim N\left({\boldsymbol{\mu}}_A,{\boldsymbol{\varSigma}}_A\right) $$

(39)

where

$$ {\boldsymbol{\mu}}_A=\left(\begin{array}{c}{\boldsymbol{G}}_{\mathrm{U}}\boldsymbol{\beta} \\ {}\boldsymbol{G}\boldsymbol{\beta } \end{array}\right),{\boldsymbol{\varSigma}}_A={\sigma}^2\left(\begin{array}{l}{\boldsymbol{R}}_{\mathrm{U}}\kern0.5em {\boldsymbol{r}}_{\mathrm{U}}^{\mathrm{T}}\\ {}\begin{array}{cc}{\boldsymbol{r}}_{\mathrm{U}}& \boldsymbol{R}\end{array}\end{array}\right) $$

(40)

Now given the realization of Y = [y₁,y₂,…,y_N]^T, the conditional distribution of Y_U on the condition of Y = [y₁,y₂,…,y_N]^T and β can be obtained according to (21) in Theorem 1.

$$ {\boldsymbol{Y}}_{\mathrm{U}}\mid \left(\boldsymbol{Y},\boldsymbol{\beta} \right)\sim N\left({\boldsymbol{\mu}}_{\mathrm{U}\cdot \boldsymbol{Y}},{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}\right) $$

(41)

where

$$ {\boldsymbol{\mu}}_{\mathrm{U}\cdot \boldsymbol{Y}}={\boldsymbol{G}}_{\mathrm{U}}\boldsymbol{\beta} +{\boldsymbol{r}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\left(\boldsymbol{Y}-\boldsymbol{G}\boldsymbol{\beta } \right) $$

(42)

$$ {\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}={\sigma}^2\left({\boldsymbol{R}}_{\mathrm{U}}-{\boldsymbol{r}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}{\boldsymbol{r}}_{\mathrm{U}}\right) $$

(43)

Notice that the coefficient vector β is still unknown and needs to be estimated with generalized least squares as shown by (7). And, according to the theory of generalized least squares, one can easily derive the following:

$$ \left(\boldsymbol{\beta} -\hat{\boldsymbol{\beta}}\right)\mid \boldsymbol{Y}\sim N\left(0,\boldsymbol{\varSigma} \boldsymbol{\beta} \right) $$

(44)

$$ {\boldsymbol{\beta}}_1\mid \boldsymbol{Y}\sim N\left(0,{\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right) $$

(45)

where

$$ {\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}={\sigma}^2{\left({\boldsymbol{G}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{G}\right)}^{-1} $$

(46)

$$ {\boldsymbol{\beta}}_1={\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}\left(\boldsymbol{\beta} -\hat{\boldsymbol{\beta}}\right) $$

(47)

It is obvious that

$$ {\boldsymbol{\varSigma}}_{\mathrm{U}}={\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}+{\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}} $$

(48)

Taking (41), (44), and (45) into consideration, the conditional PDF of Y_U (${f}_{{\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y}}\left({\boldsymbol{y}}_{\mathrm{U}}\right)$) on the condition of Y = [y₁,y₂,…,y_N]^T can be derived as follows:

$$ {\displaystyle \begin{array}{l}{f}_{{\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y}}\left({\boldsymbol{y}}_{\mathrm{U}}\right)\propto \int {f}_{{\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y},\boldsymbol{\beta}}\left({\boldsymbol{y}}_{\mathrm{U}}\right)\cdot {f}_{\boldsymbol{\beta} \mid \boldsymbol{Y}}\left(\boldsymbol{\beta} \right)\mathrm{d}\boldsymbol{\beta } =\int {f}_{{\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y},{\boldsymbol{\beta}}_1}\left({\boldsymbol{y}}_{\mathrm{U}}\right)\cdot {f}_{{\boldsymbol{\beta}}_1\mid \boldsymbol{Y}}\left({\boldsymbol{\beta}}_1\right)\mathrm{d}{\boldsymbol{\beta}}_1\\ {}\propto \int \exp \left(-\frac{1}{2}{\left({\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{\mu}}_{\mathrm{U}\cdot \boldsymbol{Y}}\right)}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}\left({\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{\mu}}_{\mathrm{U}\cdot \boldsymbol{Y}}\right)\right)\exp \left(-\frac{1}{2}{\boldsymbol{\beta}}_1^{\mathrm{T}}{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}{\boldsymbol{\beta}}_1\right)\mathrm{d}{\boldsymbol{\beta}}_1\\ {}=\int \exp \left(-\frac{1}{2}\left({\left[\left({\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{\mu}}_{\mathrm{U}}\right)+{\boldsymbol{\beta}}_1\right]}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}\left[\left({\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{\mu}}_{\mathrm{U}}\right)+{\boldsymbol{\beta}}_1\right]+{\boldsymbol{\beta}}_1^{\mathrm{T}}{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}{\boldsymbol{\beta}}_1\right)\right)\mathrm{d}{\boldsymbol{\beta}}_1\end{array}} $$

(49)

Then,

$$ {\displaystyle \begin{array}{l}{f}_{{\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y}}\left({\boldsymbol{y}}_{\mathrm{U}}+{\boldsymbol{\mu}}_{\mathrm{U}}\right)\propto \int \exp \left(-\frac{1}{2}\left({\left({\boldsymbol{y}}_{\mathrm{U}}+{\boldsymbol{\beta}}_1\right)}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}\left({\boldsymbol{y}}_{\mathrm{U}}+{\boldsymbol{\beta}}_1\right)+{\boldsymbol{\beta}}_1^{\mathrm{T}}{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}{\boldsymbol{\beta}}_1\right)\right)\mathrm{d}{\boldsymbol{\beta}}_1\\ {}=\int \exp \left(-\frac{1}{2}\left[{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{y}}_{\mathrm{U}}+{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{\beta}}_1+{\boldsymbol{\beta}}_1^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{y}}_{\mathrm{U}}+{\boldsymbol{\beta}}_1^{\mathrm{T}}\left({\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}+{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}\right){\boldsymbol{\beta}}_1\right]\right)\mathrm{d}{\boldsymbol{\beta}}_1\\ {}=\int \exp \left(-\frac{1}{2}\left[\begin{array}{l}{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\left[{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}+{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}\right]}^{-1}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{y}}_{\mathrm{U}}\\ {}+{\boldsymbol{\beta}}_2^{\mathrm{T}}\left[{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}+{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}\right]{\boldsymbol{\beta}}_2\end{array}\right]\right)\mathrm{d}{\boldsymbol{\beta}}_2\\ {}\propto \exp \left(-\frac{1}{2}\left[{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\left[{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}+{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}\right]}^{-1}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{y}}_{\mathrm{U}}\right]\right)\\ {}=\exp \left(-\frac{1}{2}{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}\left({\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\left[{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}+{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}\right]}^{-1}{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}\right){\boldsymbol{y}}_{\mathrm{U}}\right)\\ {}=\exp \left(-\frac{1}{2}{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\left[{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}+\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)\right]}^{-1}{\boldsymbol{y}}_{\mathrm{U}}\right)\\ {}=\exp \left(-\frac{1}{2}{\boldsymbol{y}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}}^{-1}{\boldsymbol{y}}_{\mathrm{U}}\right)\end{array}} $$

(50)

where

$$ {\boldsymbol{\beta}}_2={\boldsymbol{\beta}}_1+{\left[{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}+{\left({\boldsymbol{u}}_{\mathrm{U}}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\boldsymbol{\beta}}{\boldsymbol{u}}_{\mathrm{U}}\right)}^{-1}\right]}^{-1}{\boldsymbol{\varSigma}}_{\mathrm{U}\cdot \boldsymbol{Y}}^{-1}{\boldsymbol{y}}_{\mathrm{U}} $$

(51)

Therefore, the conclusion is

$$ {f}_{{\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y}}\left({\boldsymbol{y}}_{\mathrm{U}}\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^{N_{\mathrm{U}}}\mid {\boldsymbol{\varSigma}}_{\mathrm{U}}\mid }}\exp \left(-\frac{1}{2}{\left({\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{\mu}}_{\mathrm{U}}\right)}^{\mathrm{T}}{\boldsymbol{\varSigma}}_{\mathrm{U}}^{-1}\left({\boldsymbol{y}}_{\mathrm{U}}-{\boldsymbol{\mu}}_{\mathrm{U}}\right)\right) $$

(52)

or

$$ {\boldsymbol{Y}}_{\mathrm{U}}\mid \boldsymbol{Y}\sim N\left({\boldsymbol{\mu}}_{\mathrm{U}},{\boldsymbol{\varSigma}}_{\mathrm{U}}\right) $$

(53)

Prove up.

Similar to (12), the epistemic uncertainty of σ² is neglected, and σ² in (34) is replaced with ${\hat{\sigma}}^2$ estimated as (13). Then,(32) provides the joint distribution of Y_U on the condition of Y, while (15) focuses on the epistemic randomness of the performance function value of one single point, which is the most important difference between them. Besides, (32) coincides with (15) exactly if N_U = 1.

3 The stepwise variance reduction strategy for structure reliability analysis

3.1 Estimate of the target failure probability

The kriging model performs as a surrogate of the target performance function during the reliability analysis procedure. According to the definition of failure probability, only the sign of G(x) matters. And, almost all of points in X space are untried. For a given kriging model, the sign of G(x) is with epistemic uncertainty caused by the randomness of G(x). Taking (15) into account, one can obtain

$$ P\left({I}_{G\le 0}\left(\boldsymbol{x}\right)=1\right)=P\left(G\left(\boldsymbol{x}\right)\le 0\right)=\pi \left(\boldsymbol{x}\right) $$

(54)

where

$$ {\pi}_N\left(\boldsymbol{x}\right)=\Phi \left(\frac{0-{\mu}_{G,N}\left(\boldsymbol{x}\right)}{\sigma_{G,N}\left(\boldsymbol{x}\right)}\right) $$

(55)

π_N(x)is the probabilistic classification function proposed by Dubourg et al. (2013). Perform expectation operation on both sides of (1),

$$ {\displaystyle \begin{array}{l}{\hat{P}}_{f,N}=E\left({P}_f\right)=E\left(\int {I}_{G\le 0}\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}\right)\\ {}=\int E\left({I}_{G\le 0}\left(\boldsymbol{x}\right)\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}=\int {\pi}_N\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}\end{array}} $$

(56)

${\hat{P}}_{f,N}$defined by (56) is the kriging-based estimation of the failure probability employed by this research.

Numerical methods of integration and methods of simulation are available to perform the multivariate integration involved in (56). As π_N(x) has an explicit expression and therefore can be calculated millions of times in a short time, the most robust method is MCS used here.

$$ {\hat{P}}_{f,N}\approx \frac{1}{N_{\mathrm{MC}}}\sum \limits_{i=1}^{N_{\mathrm{MC}}}{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right) $$

(57)

where{x_{MC, i}} (i = 1,…,N_MC) are i.i.d. (independent and identically distributed) random points subject to f(x) and N_MC with the number of MCS points. It is widely known that any foregone accuracy of (57) can be obtained as the increase of N_MC. The coefficient of variation of (57) is measured as follows:

$$ {\delta}_{\mathrm{MC}}=\frac{\sqrt{\operatorname{var}\left({\hat{P}}_{f,N}\right)}}{{\hat{P}}_{f,N}}=\frac{1}{{\hat{P}}_{f,N}}\sqrt{\frac{1}{N_{\mathrm{MC}}}\operatorname{var}\left({\pi}_N\left(\boldsymbol{X}\right)\right)}\approx \frac{1}{N_{\mathrm{MC}}{\hat{P}}_{f,N}}\sqrt{\sum \limits_{i=1}^{N_{\mathrm{MC}}}{\pi}_N^2\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)-{N}_{\mathrm{MC}}{\hat{P}}_{f,N}^2} $$

(58)

3.2 Variance of the target failure probability

Because of the epistemic uncertainty of I_G ≤ 0(x) and G(x), P_f defined by (1) is also a random variable. Its exact distribution is almost impossible to derive because it involves infinite number of Bernoulli distributed variables. Besides, any two of the variables have correlation. This research tries to approximately calculate the variance of P_f. According to the definition of ${\hat{P}}_{f,N}$, it is the expectation of P_f. So, the variance of P_f can be written as follows:

$$ {\sigma}_{P_f,N}^2=\operatorname{var}\left({P}_f\right)=E\left({\left({P}_f-{\hat{P}}_{f,N}\right)}^2\right) $$

(59)

It is understandable that ${\sigma}_{P_f,N}^2$ quantifies the epistemic uncertainty of P_f as well as the accuracy of ${\hat{P}}_{f,N}$. A small value of ${\sigma}_{P_f,N}^2$ or ${\sigma}_{P_f,N}$ indicates that the difference between P_f and ${\hat{P}}_{f,N}$ is negligible with a large probability, in the case of which the corresponding kriging model is accurate enough and unnecessary to improve. Otherwise, more points are needed to refresh current DoE and construct a better kriging model.

Similar to the distribution of P_f, ${\sigma}_{P_f,N}^2$ is also difficult to obtain. To handle the awkward situation, this research replaces P_f and ${\hat{P}}_{f,N}$ in (59) with their corresponding MCS estimates.

$$ {\displaystyle \begin{array}{l}{\sigma}_{P_f,N}^2=E\left[{\left(\int {I}_{G\le 0}\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}-\int {\pi}_N\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}\right)}^2\right]\\ {}\kern1.7em \approx E\left[{\left(\frac{1}{N_{\mathrm{MC}}}\sum \limits_{i=1}^{N_{\mathrm{MC}}}{I}_{G<0}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)-\frac{1}{N_{\mathrm{MC}}}\sum \limits_{i=1}^{N_{\mathrm{MC}}}{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\right)}^2\right]\\ {}\kern1.6em =\frac{1}{N_{\mathrm{MC}}^2}E\left[{\left(\sum \limits_{i=1}^{N_{\mathrm{MC}}}\left({I}_{G<0}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)-{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\right)\right)}^2\right]\end{array}} $$

(60)

The idea of (60) is to approximate the expectation that involve infinite points with finitepoints. It is worthy to emphasize that the MCS estimates of P_f and ${\hat{P}}_{f,N}$ are acquired from the same i.i.d. random points. Equation(60) can be rewritten as follows:

$$ {\displaystyle \begin{array}{l}{\sigma}_{P_f,N}^2\approx \frac{1}{N_{\mathrm{MC}}^2}E\left[{\left(\sum \limits_{i=1}^{N_{\mathrm{MC}}}\left({I}_{G<0}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)-{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\right)\right)}^2\right]\\ {}=\frac{1}{N_{\mathrm{MC}}^2}\left[\begin{array}{l}\sum \limits_{i=1}^{N_{\mathrm{MC}}}\varPhi \left({U}_{G,N}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\right)\cdot \varPhi \left(-{U}_{G,N}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\right)+\\ {}\sum \limits_{i\ne j}E\left({I}_{G<0}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right){I}_{G<0}\left({\boldsymbol{x}}_{\mathrm{MC},j}\right)\right)-{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right){\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},j}\right)\end{array}\right]\\ {}=\frac{1}{N_{\mathrm{MC}}^2}\left[\begin{array}{l}\sum \limits_{i=1}^{N_{\mathrm{MC}}}{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\cdot \left[1-{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\right]+\\ {}\sum \limits_{i\ne j}\left[P\left(G\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\le 0,G\left({\boldsymbol{x}}_{\mathrm{MC},j}\right)\le 0\right)-{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right){\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},j}\right)\right]\end{array}\right]\end{array}} $$

(61)

where

$$ {U}_{G,N}\left(\boldsymbol{x}\right)=\mid \frac{\mu_{G,N}\left(\boldsymbol{x}\right)}{\sigma_{G,N}\left(\boldsymbol{x}\right)}\mid $$

(62)

The computation of P(G(x_{MC, i}) ≤ 0, G(x_{MC, j}) ≤ 0) needs the joint distribution information of [G(x_{MC, i}), G(x_{MC, j})]^T, which has already been derived in Sect. 2.2 (see (32)). The approximation of ${\sigma}_{P_f.N}^2$ shown in (61) includes $2{N}_{\mathrm{MC}}^2-{N}_{\mathrm{MC}}$ terms. And, an engineering structure may be a rare event to fail. Therefore, (61) may be out of computational affordability even though all of the terms are with explicit expression. Actually, the epistemic uncertainty of P_f mainly originates from the domain of U_{G, N} ≤ 2 where the signs of G(x) and $\hat{G}\left(\boldsymbol{x}\right)$ are different with considerable probability. Taking Ref. (Echard et al. 2011) as reference, this research neglects the probability that points in the domain of U_{G, N} > 2 are wrongly predicted in terms of the sign of the performance function and treats I_G < 0(x) as non-randomness if U_{G, N}(x) > 2, that is to say (59) can be approximated by the following way:

$$ {\displaystyle \begin{array}{l}{\sigma}_{P_f}^2=E\left[{\left(\int {I}_{G\le 0}\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}-\int {\pi}_N\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}\right)}^2\right]\\ {}\kern1.7em \approx E\left[{\left({\int}_{U_{G,N}\left(\boldsymbol{x}\right)\le 2}{I}_{G\le 0}\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}-{\int}_{U_{G,N}\left(\boldsymbol{x}\right)\le 2}{\pi}_N\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}\right)}^2\right]\end{array}} $$

(63)

So,(61) can be further simplified as follows:

$$ {\sigma}_{P_f}^2\approx \frac{1}{N_{\mathrm{MC}}^2}\left[\begin{array}{l}\sum \limits_{U_{G,N}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\le 2}{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\cdot \left[1-{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\right]+\\ {}\sum \limits_{\begin{array}{l}\left\{{U}_{G,N}\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\le 2\right\}\\ {}\cup \left\{{U}_{G,N}\left({\boldsymbol{x}}_{\mathrm{MC},j}\right)\le 2\right\}\end{array}}\left[P\left(G\left({\boldsymbol{x}}_{\mathrm{MC},i}\right)\le 0,G\left({\boldsymbol{x}}_{\mathrm{MC},j}\right)\le 0\right)-{\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},i}\right){\pi}_N\left({\boldsymbol{x}}_{\mathrm{MC},j}\right)\right]\end{array}\right] $$

(64)

Equation(63) or (64) is the proposed approximation of the variance of P_f, which is treated as the measurement of the accuracy of ${\hat{P}}_{f,N}$ defined by (56) or (57).

3.3 The proposed stepwise variance reduction strategy

This section constructs an innovative DoE strategy named stepwise variance reduction strategy whose principle is to find the point that can minimize the proposed accuracy measurement of ${\hat{P}}_{f,N}$ in the sense of expectation. The optimal point is named as the next best point.

To search the next best point, a new symbol is introduced here.

$$ {\displaystyle \begin{array}{l}{\tilde{\sigma}}_{P_f,N}^2=E\left[{\left(\int {I}_{G\le 0}\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}|{U}_{G,N}\left(\boldsymbol{x}\right)\le 2\right)\mathrm{d}\boldsymbol{x}-\int {\pi}_N\left(\boldsymbol{x}\right)f\left(\boldsymbol{x}|{U}_{G,N}\left(\boldsymbol{x}\right)\le 2\right)\mathrm{d}\boldsymbol{x}\right)}^2\right]\\ {}\kern1.7em \approx \frac{1}{N_{\sigma}^2}\left[\begin{array}{l}\sum \limits_{i=1}^{N_{\sigma }}{\pi}_N\left({\boldsymbol{x}}_{\sigma, i}\right)\cdot \left[1-{\pi}_N\left({\boldsymbol{x}}_{\sigma, i}\right)\right]+\\ {}\sum \limits_{i\ne j}\left[P\left(G\left({\boldsymbol{x}}_{\sigma, i}\right)\le 0,G\left({\boldsymbol{x}}_{\sigma, j}\right)\le 0\right)-{\pi}_N\left({\boldsymbol{x}}_{\sigma, i}\right){\pi}_N\left({\boldsymbol{x}}_{\sigma, j}\right)\right]\end{array}\right]\end{array}} $$

(65)

where ${\boldsymbol{S}}_{\sigma }=\left\{{\boldsymbol{x}}_{\sigma, 1},...,{\boldsymbol{x}}_{\sigma, {N}_{\sigma }}\right\}$ is a sample of i.i.d. random points subject to the conditional PDF f(x| U_{G, N}(x) ≤ 2). They can be generated with both MC method and MCMC method. As the improvement of the quality of the kriging model, the fraction of U_{G, N} ≤ 2 tends to be insignificant, which decreases the efficiency of MC method. MCMC method performs well in sampling random points from conditional distribution. This kind of algorithm can generate approximate i.i.d. random points from given conditional PDF if parameters involved are appropriately set. Besides, the efficiency of MCMC method does not degenerate seriously as the available area of U_{G, N} ≤ 2 becomes cabined. Therefore, this research employs MCMC simulation to sample S_σfrom f(x| U_{G, N}(x) ≤ 2).

3.3.1 Candidates of the next best point

Obviously, ${\tilde{\sigma}}_{P_f,N}^2$ is proportional to the proposed approximation of ${\sigma}_{P_f,N}^2$. So, the next best point can also be defined as the one that can minimize ${\tilde{\sigma}}_{P_f,N}^2$ in the sense of expectation. To simplify the search of the next best point, two restrictions are formed as follows:

• 1. The uncertainty of P_f caused by the current domain U_{G, N} > 2 is limited and is still negligible if adding point x into DoE and rebuilding the kriging model.

• 2. The next best point locates in the domain U_{G, N} ≤ 2.

During searching the best next point, one needs to compute the expectation of ${\tilde{\sigma}}_{P_f,N+1}^2$ or ${\sigma}_{P_f,N+1}^2$ by virtually adding a point into the current DoE and rebuilding the kriging model several times. The first hypothesis means that the uncertainties of P_f for the virtually new kriging modelare still up to the domain U_{G, N} ≤ 2 rather than U_{G, N} > 2. This hypothesis is difficult to prove and may not be rigorous in theory, but it makes sense in engineering and eases the computational cost of the evaluation of a point. The second hypothesis shrinks the searching area from the whole X space to U_{G, N} ≤ 2, which is understandable.

Gradient descent algorithms and swarm intelligence-based algorithms may not be suitable for optimizing the next best point. The domain U_{G, N} ≤ 2 may multiply and be connected, and have more than one local optimums especially when the performance function has multi-design points. Besides, when the kriging model is highly accurate, the domain U_{G, N} ≤ 2 is surely much cabined and difficult to locate. To overcome above awkward situations, a second best alternative is that the candidates of the next best point reduce from the domain U_{G, N} ≤ 2 to S_σ. In other words, this research treats the best point in S_σ as the next best one rather than searches it in the whole U_{G, N} ≤ 2.

3.3.2 The expectation of ${\tilde{\sigma}}_{P_f,N+1}^2$

To quantify ${\boldsymbol{x}}_{\sigma, {n}_{\sigma }}$ (${\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\in {\boldsymbol{S}}_{\sigma }$) in terms of the expectation of ${\tilde{\sigma}}_{P_f,N+1}^2$ after adding it into the current DoE, one needs to reconstruct the kriging model based on ${\boldsymbol{S}}_{\mathrm{DOE}}=\left[{\boldsymbol{x}}_1,...,{\boldsymbol{x}}_N,{\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right]$ and $\boldsymbol{Y}={\left[{y}_1,...,{y}_N,G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right]}^{\mathrm{T}}$, where ${\boldsymbol{x}}_{\sigma, {n}_{\sigma }}$ is one of the candidate points generated by MCMC method. The value of ${\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)$ can be estimated as follows:

$$ {\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\approx \frac{1}{N_{\sigma}^2}\left[\begin{array}{l}\sum \limits_{i=1}^{N_{\sigma }}{\pi}_{N+1}\left({\boldsymbol{x}}_{\sigma, i}|{\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\cdot \left[1-{\pi}_{N+1}\left({\boldsymbol{x}}_{\sigma, i}|{\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\right]\\ {}+\sum \limits_{i\ne j}P\left(G\left({\boldsymbol{x}}_{\sigma, i}\right)\le 0,G\left({\boldsymbol{x}}_{\sigma, j}\right)\le 0|{\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\\ {}-\sum \limits_{i\ne j}{\pi}_{N+1}\left({\boldsymbol{x}}_{\sigma, i}|{\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right){\pi}_{N+1}\left({\boldsymbol{x}}_{\sigma, j}|{\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\end{array}\right] $$

(66)

Obviously, ${\tilde{\sigma}}_{P_f,N+1}^2$ depends on both ${\boldsymbol{x}}_{\sigma, {n}_{\sigma }}$and $G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)$. It is worthy to emphasize that $G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)$ is a normal distributed variable defined by (15) before performing the structural model to calculate it. Given ${\boldsymbol{x}}_{\sigma, {n}_{\sigma }}$, ${\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)$ is a random variable whose randomness comes from the epistemic uncertainty of $G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)$. The expectation of ${\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)$ with respect to $G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)$ is

$$ {\displaystyle \begin{array}{l}E\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)=E\left[{\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\right]\\ {}\kern3.799999em ={\int}_{-\infty}^{+\infty }{\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},y\right){f}_{G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)}(y)\mathrm{d}y\end{array}} $$

(67)

where

$$ {f}_{G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)}(y)=\frac{1}{\sqrt{2\pi }{\sigma}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)}\exp \left(-\frac{{\left(y-{\mu}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)}^2}{2{\sigma}_{G,N}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)}\right) $$

(68)

Therefore, the next best point is in S_σ, which can minimize (67).

$$ {\boldsymbol{x}}_{N+1}=\underset{{\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\in {\boldsymbol{S}}_{\sigma }}{\mathrm{argmin}}E\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right) $$

(69)

3.3.3 About the calculation of (67)

Equation(67) can be rewritten as

$$ {\displaystyle \begin{array}{l}E\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)={\int}_{-\infty}^{+\infty }{\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},y\right){f}_{G\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)}(y)\mathrm{d}y\\ {}=\frac{1}{\sqrt{\pi }}{\int}_{-\infty}^{+\infty }{\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},\sqrt{2}{\sigma}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)t+{\mu}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\exp \left(-{t}^2\right)\mathrm{d}t\end{array}} $$

(70)

where

$$ t=\frac{y-{\mu}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)}{\sqrt{2}{\sigma}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)} $$

(71)

Obviously, Gauss–Hermite quadrature is available to perform the integral of (70).

$$ {\displaystyle \begin{array}{l}E\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)=\frac{1}{\sqrt{\pi }}{\int}_{-\infty}^{+\infty }{\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},\sqrt{2}{\sigma}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)t+{\mu}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\exp \left(-{t}^2\right)\mathrm{d}t\\ {}\kern3.799999em \approx \frac{1}{\sqrt{\pi }}\sum \limits_{j=1}^{n_G}{w}_j{\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},\sqrt{2}{\sigma}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right){v}_j+{\mu}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)\right)\end{array}} $$

(72)

where v_j (j = 1,…,n_G) denote the quadrature points and w_j is the weight associated with v_j. As the growth of the number of quadrature points n_G, (72) is accurate enough to meet the requirement of engineering.

3.3.4 The procedure of the proposed stepwise variance reduction strategy

The main steps of the proposed stepwise variance reduction strategy are summarized as follows:

• Step 1. Generate N_σi.i.d. points (${\boldsymbol{S}}_{\sigma }=\left\{{\boldsymbol{x}}_{\sigma, 1},...,{\boldsymbol{x}}_{\sigma, {N}_{\sigma }}\right\}$) approximately from the conditional PDF f(x| U_{G, N}(x) ≤ 2) by MCMC method. Points in S_σ are candidates of the next best one.

• Step 2. For each point ${\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\in {\boldsymbol{S}}_{\sigma }$

For each Gauss–Hermite quadrature point v_j (j = 1,…,n_G)

Construct the kriging model using ${\boldsymbol{S}}_{\mathrm{DOE}}=\left[{\boldsymbol{x}}_1,...,{\boldsymbol{x}}_N,{\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right]$and $\boldsymbol{Y}={\left[{y}_1,...,{y}_N,{y}_{\sigma, {n}_{\sigma },j}\right]}^{\mathrm{T}}$.

$$ {y}_{\sigma, {n}_{\sigma },j}=\sqrt{2}{\sigma}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right){v}_j+{\mu}_{G,N}\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right) $$

(73)

Compute ${\tilde{\sigma}}_{P_f,N+1}^2\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }},{y}_{\sigma, {n}_{\sigma },j}\right)$ according to (66).

• Step 3. According to (72), calculate $E\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right){\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\in {\boldsymbol{S}}_{\sigma }$ based on the results of step 2.

• Step 4. Find the next best point that minimizes $E\left({\boldsymbol{x}}_{\sigma, {n}_{\sigma }}\right)$ ((69)).

In the proposed strategy, the only function of MCMC method is to generate i.i.d. candidates of the next best point from the given conditional PDF f(x| U_{G, N}(x) ≤ 2). In spite of efficiency, other random simulation methods are potential to do this in the case of guaranteeing that random points are independent and identically distributed. If the sampling PDF is not f(x| U_{G, N}(x) ≤ 2), one needs to do some change to (65) and other relative equations.

4 Application of the proposed stepwise variance reduction strategy

As illustrated above, the proposed strategy is designed for structural reliability analysis. It performs as the similar role with learning functions to find the next best point with respect to the given criterion (Bichon et al. 2008; Echard et al. 2011). In theory, any kriging-based procedure of structural reliability analysis involving sequential DoE strategy can employ the proposed strategy. This research applies it to the procedure constructed in ref. (Sun et al. 2017) to replace the learning function called LIF. Besides, the stopping criterion of the reliability procedure is also reconstructed. The new criterion proposed below is mainly based on the variance of P_f approximated in Sect. 3.2. The main steps of the procedure which employs the proposed DoE strategy and the new stopping criterion are summarized as follows:

• Step 1: Generate the initial DoE with N₀ points ${\boldsymbol{S}}_{\mathrm{DoE}}=\left[{\boldsymbol{x}}_1,...,{\boldsymbol{x}}_{N_0}\right]$ and run the model of studied structure to calculate $\boldsymbol{Y}={\left[{y}_1,...,{y}_{N_0}\right]}^{\mathrm{T}}$. Latin hypercube sampling (LHS) is used to produce S_DoE. Since abnormal distributed vector can be transformed into normal one exactly or approximately, this research supposes that the input random vector X is subject to standard multivariate normal distribution. The hypercube for generating S_DoE is [− 5,5]^M.

• Step 2: Construct the kriging surrogate model based on the current S_DoE and Y.

• Step 3: Approximate estimation of failure probability (${\hat{P}}_{f,N}$) and the variance of P_f (${\sigma}_{P_f,N}^2$) with MCS according to (57) in Sect. 3.1and (64) in Sect. 3.2, respectively. The sample of random points for ${\hat{P}}_{f,N}$ is the same with the one for ${\sigma}_{P_f,N}^2$. If ${\hat{P}}_{f,N}$ and ${\sigma}_{P_f,N}$ satisfy (74), terminate the reliability analysis procedure and ${\hat{P}}_{f,N}$ is the estimation of the target failure probability that meets a given accurate requirement. Otherwise, continue the procedure to Step 4.

$$ {\delta}_N=\frac{\sigma_{P_f,N}}{{\hat{P}}_{f,N}}<\left[\delta \right] $$

(74)

where[δ] is the threshold coefficient of variation of P_f. Equation(74) means that the potential error of ${\hat{P}}_{f,N}$ is negligible if the coefficient of variation of P_f (δ_N) is smaller than the given threshold value ([δ]).

It is worthy to emphasize that this step is optional. Its main purpose is to judge whether the kriging model constructed by step 2 is accurate enough. Therefore, it may be unnecessary to perform this step every iteration.

• Step 4: Perform the proposed stepwise variance reduction strategy to look for the next best point according to procedure introduced in Sect. 3.3.4. Add the next best point into DoE and calculate its performance function value. Return to step 2.

The flow chart is shown below. The left part of Fig.1 is the main body of the stepwise variance reduction strategy, and the left part is the proposed DoE strategy.

Fig. 1

The flow chart of the stepwise variance reduction strategy

5 Examples for validation

Three benchmark examples are analyzed in this section. Results from different methods are compared to validate the efficiency of the proposed DoE strategy.

5.1 A series system with four branches

This section studies a series system that includes four branches. Its performance function is explicit and has two independent variables.

$$ G\left(\boldsymbol{x}\right)=\min \left\{\begin{array}{l}3+0.1{\left({x}_1-{x}_2\right)}^2-\left({x}_1+{x}_2\right)/\sqrt{2};\\ {}3+0.1{\left({x}_1-{x}_2\right)}^2+\left({x}_1+{x}_2\right)/\sqrt{2};\\ {}\left({x}_1-{x}_2\right)+6/\sqrt{2};\\ {}\left({x}_2-{x}_1\right)+6/\sqrt{2};\end{array}\right\} $$

(75)

where X = [X₁,X₂]^T is the input variable vector and subject to standard multivariate normal distribution. The main purpose of employing this example is to visualize the efficiency of the proposed DoE strategy in improving the accuracy of the kriging model and the estimation of failure probability.

Apply the reliability analysis procedure introduced in Sect. 4 to this example with N_σ = 3000. Results are summarized in Table 1. Besides, results from some other methods are also listed as comparisons. As most of existing learning functions are not suitable for reliability procedure that generates candidates of the next best point every iteration (such as the procedure in Sect. 4), AK-MCS-based methods are employed (Echard et al. 2011). AK-MCS+the proposed DoE strategy means that the proposed DoE strategy is combined with AK-MCS, in which the candidates of the next best point come from a given sample of i.i.d. points rather than MCMC method. AK-MCS+the proposed DoE strategy here is to provide a fair comparison between the proposed strategy in Sect. 3 and other learning functions. N_call denotes the number of calls to the real performance function ((75)). [δ]is the threshold coefficient of variation of P_f. Different values of [δ] are set to investigate how much the proposed estimation of the variance (or standard deviation) of P_f can reflect the real accuracy of ${\hat{P}}_f$ and demonstrate the efficiency of the proposed DoE strategy in terms of N_call when the requirement of accuracy is given. εinTable 1 presents the relative error of estimates of failure probability when ${\hat{P}}_f$ satisfies (74).

Table 1 Results of the series system with four branches

Figure2 details the convergence process of ${\hat{P}}_f$ and the decrement of δ_N ((74)) as the iteration of different methods goes. The proposed strategy tends to give a rough estimate of the target failure probability quickly for this series system. Figure 3 compares estimated limit states with the real one and visualizes the outstanding of the proposed DoE strategy from the others. As shown in Fig.3, the proposed strategy is able to provide more accurate estimated limit state for a given N_call, as a result of which it needs lower number of calls to (75) to meet a given accuracy requirement (Table 1 and Fig.2).

Fig. 2

Lines of ${\hat{P}}_f$ and δ_N from different methods

Fig. 3

Comparison of methods in terms of estimated limit states

According to the meaning of [δ] and the stopping criterion of (74), the relative error of ${\hat{P}}_f$ with respect to the referential value may be tolerable for engineering applications if it is less than 3[δ]. As listed in Table 1, the accuracy of methods based on the proposed strategy is acceptable even though they may provide less accurate estimation of P_f than other methods for a given value of [δ] and regardless of N_call. Figure 3 shows that AK-MCS+U method focuses on only one of the four branches firstly and then goes to another after the kriging model is accurate enough in this area. The same conclusion can be derived from refs. (Echard et al. 2011; Sun et al. 2017), too. This characteristic explains the huge wave of the line of δ_N (Fig.2) from AK-MCS+U.

5.2 A truss structure

This section analyzes a widely referenced truss structure (Sun et al. 2017; Blatman and Sudret 2010; Roussouly et al. 2013). As shown by Fig.4, it contains 23 bars. Eleven of them are horizontal with random cross section A₁ and Young’s moduli E₁, and the others are sloping with random cross section A₂ and Young’s moduli E₂. Six Gumbel distributed loads are applied on nodes of horizontal bars. The distribution information of these inputs is listed in Table 2. Similar with the first example, all variables involved are mutually independent.

Fig. 4

The truss structure with 10 input variables (unit m)

Table 2 Distribution information of variables involved in Sect.5.2

This structure is treated as failed if the deflection of node E |s(x)| is larger than a given threshold which is 0.14 m in this research to keep in accordance with ref. (Sun et al. 2017; Blatman and Sudret 2010). Therefore, the performance function of the structure is defined as

$$ G\left(\boldsymbol{x}\right)=0.14-\mid \boldsymbol{s}\left(\boldsymbol{x}\right)\mid $$

(76)

Reference (Blatman and Sudret 2010) gives the reference value of failure probability, which is obtained by IS with 500,000 simulations. References (Sun et al. 2017; Roussouly et al. 2013) indicate that the result is credible.

$$ {P}_f\approx 3.45\times {10}^{-5} $$

(77)

Apply the reliability analysis method in Sect. 4 and some other methods to this truss structure. Results are all summarized in Table 3. The proposed DoE strategy is not combined with AK-MCS, because the structure is rare event to fail and AK-MCS+the proposed DoE strategy needs too much time.

Table 3 Results of the truss structure

Figure 5 shows the lines of ${\hat{P}}_f$and δ_N. FromFig.5, several methods including AK-MCS-based methods can roughly estimate the failure probability very soon, and the advantage of the proposed DoE strategy is not obvious. However, the proposed strategy needs less number of calls the real performance function to let ${\hat{P}}_f$ satisfy the stopping criterion defined by (74) with different values of [δ].

Fig. 5

Comparison of methods in terms of ${\hat{P}}_f$ and δ_N (LIF means the method proposed in ref. (Sun et al. 2017))

5.3 A frame structure

Figure 6 shows a frame structure that contains 8 finite elements. Table 4 lists properties of these elements including Young’s modulus (E), Moment of Inertia (I), and cross section (A). P₁, P₂, and P₃ are three random loads. Distribution information of involved variables is summarized in Table 5. Unlike the above examples, some correlation exists between variables of this structure.

$$ \rho \left({A}_i,{I}_i\right)=0.95\kern0.72em \left(i=1,2\right) $$

(78)

$$ \rho \left({A}_i,{A}_j\right)=\rho \left({I}_i,{I}_j\right)=\rho \left({A}_i,{I}_j\right)=0.13\kern0.48em \left(i\ne j\right) $$

(79)

$$ \rho \left({E}_1,{E}_2\right)=0.9 $$

(80)

Fig. 6

The frame structure (unit m)

Table 4 Finite element properties of the frame structure—Sect. 5.3

Table 5 Distribution information of variables involved in Sect.5.3

The rest of variables are mutually independent.

The performance function of this frame structure is defined as (81).

$$ G\left(\boldsymbol{x}\right)=0.06-\mid \boldsymbol{s}\left(\boldsymbol{x}\right)\mid $$

(81)

wheres(x) denotes the top displacement as depicted in Fig.6.

To get a reference value of the failure probability, 1.3 × 10⁶i.i.d. simulations are performed, and 154 of random points are located in the failure domain. Therefore, the reference value of the failure probability is 1.185 × 10⁻⁴ whose coefficient of variation is 0.081.

Apply kriging-based methods mentioned in Sects. 5.1 and 5.2 to the frame structure. Table 6 summarizes all results. As the reference value of P_f is not accurate enough, the estimations of failure probability (${\hat{P}}_f$) with respect to all kriging models are obtained by testing the sample of random points mentioned above to eliminate the inaccuracy of the reference value. Lines of ${\hat{P}}_f$ and δ_N are shown in Fig.7. It is obvious that the proposed strategy outperforms other methods very much in terms of this example.

Table 6 Results of the frame structure

Fig. 7

Lines of ${\hat{P}}_f$ and δ_N from different methods

From Fig.7, the stepwise variance reduction strategy fails to make ${\hat{P}}_f$ satisfy (74) with fewer DoE points than 180 if [δ] equals to 0.05 or 0.03, and other learning functions perform even worse. As this example has 21 random inputs, the variable space of importance to the failure probability is too broad and most of points in the vicinity of $\hat{G}\left(\boldsymbol{x}\right)=0$ or G(x)) = 0 are with local inaccuracy. To remarkably reduce the value of δ, many more DoE points are needed. Since, similarly with the series system in Sect. 5.1, the performance function of the frame structure may contain multi-design points or the limit state near the design point is approximated to be a hyper spherical surface with its center at the origin. In those cases, it is not easy to roughly fit the target limit state quickly. The instability of AK-MCS+U and AK-MCS+EFF also indicates the complexity of the problem.

6 Conclusion

A stepwise variance reduction DoE strategy for structural reliability analysis is proposed in this research. Its principle is to find the point that is able to minimize the epistemic variance of P_f in the sense of expectation. The variance of P_f is an accuracy measurement of the estimation of failure probability defined by (56). It can also be treated as a global accuracy measurement of the kriging model. To assess it, the joint distribution of performance function values of untried points is derived in detail, which is the key to the approximation of the variance of P_f and the proposed strategy. The strategy performs the role similar to learning functions in reliability analysis procedure to determine the next best point among lots of candidates. A kriging-based reliability analysis procedure is introduced, which is mainly based on the proposed DoE strategy and the procedure constructed in ref. (Sun et al. 2017). A new stopping criterion is also proposed. Its basic idea is that one can terminate the reliability analysis procedure if the coefficient of variation of P_f is less than a given threshold or the potential error of ${\hat{P}}_f$ is negligible.

To validate the efficiency of the proposed DoE strategy, three examples are analyzed. One of them is a series system with explicit performance function. The others are structures with implicit performance functions. According to the results of the validation, conclusion can be summarized as follows: (1) Most of the next best points from the proposed strategy are located in the area of importance. It can roughly estimate the target failure probability and the target limit state quickly. (2) The stepwise variance reduction strategy does well when dealing with problems with multi-design points, implicit and nonlinear performance function, and high-dimensional input vector. (3) The proposed stopping criterion has understandable meaning and is able to terminate the reliability analysis procedure timely according to the accuracy requirement. (4) If it takes a few hours or more to simulate a model once, the proposed DoE strategy will have some advantages. Besides, the decrement of δ_N is log-linear generally if the proposed DoE strategy is employed in a reliability analysis procedure, which may be useful for further simplifying the reliability analysis steps and releasing computational burden.