The stepwise accuracy-improvement strategy based on the Kriging model for structural reliability analysis

Abstract

For structural reliability analysis with time-consuming performance functions, an innovative design of experiment (DoE) strategy of the Kriging model is proposed, which is named as the stepwise accuracy-improvement strategy. The epistemic randomness of the performance value at any point provided by the Kriging model is used to derive an accuracy measure of the Kriging model. The basic idea of the proposed strategy is to enhance the accuracy of the Kriging model with the best next point that has the largest improvement with regard to the accuracy measure. An optimization problem is developed to define the best next point. The objective function is the expectation that quantifies how much an untried point could enhance the accuracy of the Kriging model. Markov chain Monte Carlo sampling and Gauss–Hermite quadrature are employed to make several approximations to solve the optimization problem and get the best next point. A structural reliability analysis method is also constructed based on the proposed strategy and the accuracy measure employed. Several examples are studied. The results validate the advantages of the proposed DoE strategy.

1 Introduction

For a given engineering structure, the relationship between inputs and outputs is generally treated as a deterministic function, called the performance function. Without loss of generality, this study supposes the output is a scalar value. The input variables are usually affected by uncertain factors, which results in the uncertainty of the output. Structural reliability theory treats the input variables as random variables. The failure probability of a structure can be defined by

$$ {P}_f=\int {I}_{G\le 0}\left(\mathbf{x}\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x} $$

(1)

where

$$ {I}_{G\le 0}\left(\mathbf{x}\right)=\left\{\begin{array}{l}1\kern1.5em G\left(\mathbf{x}\right)\le 0\\ {}0\kern1.5em G\left(\mathbf{x}\right)>0\end{array}\right. $$

G(x) is the performance function, and X = [X₁,X₂,…,X_M]^T is the random vector containing all basic input variables. f_X(x) is the joint probability distribution function (PDF) of X. A fundamental and troublesome task of structural reliability analysis(SRA) is to calculate the multiple integral shown in (1). Several kinds of methods have been developed, mainly including: (1) the first-order reliability method (FORM) and second-order reliability method (SORM) (Zhao and Ono 1999); (2) random-simulation-based methods such as Monte Carlo simulation (MCS) (Owen 2000; Zhang et al. 2010; Saha and Naess 2010), importance sampling (IS) (Melchers 1990; Cornuet et al. 2012; Owen and Zhou 2000), line sampling (LS) (Pradlwarter et al. 2007) and subset simulation (SS) (Au and Beck 2001; Au 2016; Neal 2003); and (3) surrogate model-based methods (Gayton et al. 2003; Schueremans and Van Gemert 2005; Kaymaz 2005). Several surrogate models, including quadratic polynomial response surface (Pedroni et al. 2010), sparse polynomial chaos expansion (Blatman and Sudret 2011; Roussouly et al. 2013), moving least-square regression (Salemi et al. 2016; Li et al. 2012), neural networks (Schueremans and Van Gemert 2005), support vector machine (Song et al. 2013; Alibrandi et al. 2015), and Kriging (Kaymaz 2005), are widely employed.

This study focuses on surrogate model-based methods and employs the Kriging model to perform SRA. As an exact interpolation model, the Kriging model provides not only an estimate of the performance value at any point but also the corresponding mean squared error of the estimate, which is called the Kriging variance. Kaymaz (2005), Gaspar et al. (2014) and Shi et al. (2015) have already demonstrated its advantage over polynomial response surface.

In recent years, Kriging has been applied to global optimization (Jones et al. 1998), sensitivity analysis (Zhang et al. 2015), stochastic simulation (Kleijnen 2009; Beers and Kleijnen 2003) and SRA (Kaymaz 2005). Usually, the models used for these engineering problems are time-consuming. Kriging is used to reduce the computational cost and acquire results with acceptable accuracy. Efficient DoE (the design of experiments) strategy is needed to achieve the goal. Various kinds of adaptive DoE strategies have received much attention (Jones et al. 1998; Bichon et al. 2008; Echard et al. 2011; Lv et al. 2015; Yang et al. 2015). To identify the area of interest and targetedly enhance the accuracy of the Kriging model, the statistical information provided by the Kriging estimate and variance is used. For examples, Jones et al. (1998) construct the expected improvement function (EIF) for efficient global optimization. EIF measures how much a point can improve the optimal value of a target function in the sense of expectation.

For SRA, it is only necessary to fit the limit state of the performance function, instead of the whole variable space. Therefore, Bichon et al. (2008) propose the expected feasibility function (EFF), which is used to search for points in the vicinity of limit state. Echard et al. (2011) propose an active learning reliability method by combining Kriging and MCS (AK-MCS) and an innovative learning function to measure the probability of grouping a point into the wrong domain. By employing the learning function proposed in (Echard et al. 2011), several Kriging-based reliability methods, e.g., AK-IS (Echard et al. 2013), AK-SS (Huang et al. 2016), AK-SSIS (Tong et al. 2015), PC-Kriging-based reliability method (Schöbi et al. 2014), Kriging-based system reliability methods (Fauriat and Gayton 2014; Perrin 2016) and Kriging-based time-variant reliability method (Hu and Mahadevan 2016a), have been constructed. Tong et al. (2015), Gaspar et al. (2017) and Fauriat and Gayton (2014) realize that the stopping criterion in Ref. (Echard et al. 2011) may be too conservative for engineering applications and propose modified ones. Ref. (Jian et al. 2017) investigates the accuracy measures of the Kriging model and derives the mean squared error of the Kriging-based estimate of failure probability, which is helpful to construct suitable stopping criterion. Yang et al. (2015) define the expected risk function (ERF), and Lv et al. (2015) propose a new learning function according to information entropy. Dubourg et al. (2011) and Wen et al. (2016) notice that it could be more timesaving to refresh the DoE of the Kriging model with several selected points at a time (e.g. employing parallel computing), and construct their adaptive DoE strategies with remarkably low number of iterations.

According to the definition of the failure probability, the importance of a point in the vicinity of the limit state depends on the joint PDF value. It is more rational that the adaptive DoE strategy takes it into consideration. Picheny et al. (2010) adapt the weighted IMSE (integrated mean square error) to the failure probability estimation to measure the accuracy of the Kriging model, and refresh DoE with the minimum point of the weighted IMSE criterion. The stepwise uncertainty reduction strategy proposed by Bect et al. (2012) also aims at the improvement of the accuracy of a failure probability estimation. More straightforward, Wang and Wang (2014) define an estimated improvement sampling criterion and successively select its maximum point which is expected to maximize the accuracy enhancement of the Kriging-based reliability estimation.

Ref. (Sun et al. 2017) proposes a global accuracy measure of the Kriging model and a learning function LIF. LIF is an overall compromise among the Kriging variance, the estimate of the performance value, and the joint PDF of input variables. It is designed to approximately quantify how much an untried point could improve the accuracy of the Kriging model in the sense of the proposed measure. However, the derivation of LIF is based on two hypotheses, i.e. an untried point is able to remarkably improve the accuracy of the Kriging model in a spherical neighborhood (the center is the untried point and the radius is proportional to the absolute value of its performance function) and its contribution to the remaining domain is neglected. In another word, to acquire an explicit learning function, Ref. (Sun et al. 2017) considers only the local accuracy enhancement of the Kriging model, which underestimates the contribution of an untried point. Therefore, the best next point defined by LIF may be not good enough, and the adaptive DoE strategy proposed in Ref. (Sun et al. 2017) is still improvable by weakening or removing the hypotheses.

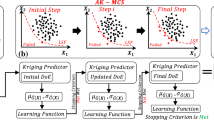
To further reduce the computational cost of SRA, this study proposes a new DoE strategy, which is named as the stepwise accuracy-improvement strategy. The basic idea is to refresh the DoE with the point that is potential to enhance the accuracy of the Kriging model most, i.e. the best next point. The accuracy measure proposed in Refs. (Jian et al. 2017; Sun et al. 2017) is employed to quantify the accuracy of the Kriging model. By introducing pseudo Kriging model, the expectation that any untried point could enhance the accuracy of the Kriging model is derived. Then, an optimization problem is constructed to define the best next point in an easily understandable way, i.e. the maximum point of the expectation. To acquire more accurate position of the best next point, this study directly solves the optimization problem rather than deriving an explicit learning function under hypotheses. To remarkably shorten the searching time of the best next point, some simplifications are used, i.e. approximating the accuracy measure of the Kriging model, reducing the candidates of the best next point and employing Gauss–Hermite quadrature to calculate the expectation. A procedure for SRA is developed, in which the stepwise accuracy-improvement strategy is employed. And the stopping criterion takes the accuracy of the Kriging model (or the relative error of the Kriging-based estimate of failure probability) into account.

The remainder of this study is organized as follows. Section 2 reviews the theory of the Kriging model and MCS. Section 3 constructs the stepwise accuracy improvement strategy, which is followed by the SRA method in Section 4. To demonstrate the advantage of the proposed strategy and the proposed reliability analysis method, four examples are analyzed in Section 5. Section 6 presents the conclusion.

2 Kriging model and MONTE Carlo simulation

2.1 Review of the Kriging model

The Kriging model was developed by Krige for geostatistics and improved by Matheron (1973). When used as a surrogate model, it is supposed that the studied performance function G(x) consists of two parts,

$$ G\left(\mathbf{x}\right)=F\left(\boldsymbol{\upbeta}, \mathbf{x}\right)+z\left(\mathbf{x}\right)={\mathbf{g}}^{\mathrm{T}}\left(\mathbf{x}\right)\boldsymbol{\upbeta} +z\left(\mathbf{x}\right) $$

(2)

where F(β,x) is the deterministic part and z(x) is a realization of a stochastic process. g(x) is the basis function of F(β,x). A first-order polynomial is preferred as the basis function g(x) in this study. β is the vector of regression coefficients, estimated with generalized least squares. z(x) is a realization of a stationary Gaussian stochastic process with zero mean. The covariance between two points (x_i and x_j) in the space X is defined as,

$$ \mathrm{Cov}\left[z\left({\mathbf{x}}_i\right),z\left({\mathbf{x}}_j\right)\right]={\sigma}^2R\left({\mathbf{x}}_i,{\mathbf{x}}_j;\boldsymbol{\uptheta} \right) $$

(3)

where σ² is the variance of the Gaussian process and R(x_i,x_j;θ) is the correlation function with parameter vector θ. Among several existing correlation functions, the anisotropic squared-exponential function (also called the Gaussian correlation function) selected in this study is the most widely used. It is defined as

$$ R\left({\mathbf{x}}_i,{\mathbf{x}}_j;\boldsymbol{\uptheta} \right)=\prod \limits_{m=1}^M\exp \left[-{\theta}_m{\left({x}_i^m-{x}_j^m\right)}^2\right] $$

(4)

where ${x}_i^m$ and θ_m are the mth components of x_i and θ, respectively.

Given a DoE with N points S_DoE = [x₁,x₂,…,x_N] and their performance values Y = [y₁,y₂,…,y_N]^T, the best linear unbiased predictor of G(x) and its corresponding mean squared error are defined as follows.

$$ {\mu}_{G,N}\left(\mathbf{x}\right)={\widehat{G}}_N\left(\mathbf{x}\right)={\mathbf{g}}^{\mathrm{T}}\left(\mathbf{x}\right)\widehat{\boldsymbol{\upbeta}}+\mathbf{r}{\left(\mathbf{x}\right)}^{\mathrm{T}}\boldsymbol{\upgamma} $$

(5)

$$ {\sigma}_{G,N}^2\left(\mathbf{x}\right)={\widehat{\sigma}}^2\left(1+{\mathbf{u}}^{\mathrm{T}}\left(\mathbf{x}\right){\left({\mathbf{G}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{G}\right)}^{-1}\mathbf{u}\left(\mathbf{x}\right)-{\mathbf{r}}^{\mathrm{T}}\left(\mathbf{x}\right){\mathbf{R}}^{-1}\mathbf{r}\left(\mathbf{x}\right)\right) $$

(6)

where

$$ {\displaystyle \begin{array}{c}\widehat{\boldsymbol{\upbeta}}={\left({\mathbf{G}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{G}\right)}^{-1}{\mathbf{G}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{Y}\\ {}\boldsymbol{\upgamma} ={\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{G}\widehat{\boldsymbol{\upbeta}}\right)\\ {}\mathbf{r}\left(\mathbf{x}\right)={\left[R\left({\mathbf{x}}_1,\mathbf{x};\boldsymbol{\uptheta} \right),\dots, R\left({\mathbf{x}}_N,\mathbf{x};\boldsymbol{\uptheta} \right)\right]}^{\mathrm{T}}\\ {}{\widehat{\sigma}}^2=\frac{1}{N}{\left(\mathbf{Y}-\mathbf{G}\widehat{\boldsymbol{\upbeta}}\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{G}\widehat{\boldsymbol{\upbeta}}\right)\\ {}\mathbf{u}\left(\mathbf{x}\right)={\mathbf{G}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{r}\left(\mathbf{x}\right)-\mathbf{g}\left(\mathbf{x}\right)\\ {}\mathbf{R}={\left(R\left({\mathbf{x}}_i,{\mathbf{x}}_j;\boldsymbol{\uptheta} \right)\right)}_{N\times N}\\ {}\mathbf{G}={\left[\mathbf{g}\left({\mathbf{x}}_1\right),\mathbf{g}\left({\mathbf{x}}_2\right),\dots, \mathbf{g}\left({\mathbf{x}}_N\right)\right]}^{\mathrm{T}}\end{array}} $$

The subscript N in (5) and (6) represents the number of points in the DoE. ${\sigma}_{G,N}^2\left(\mathbf{x}\right)$ equals zero if and only if x ∈ S_DoE; thus, Kriging is an interpolation meta-model. Equations (5) and (6) are dependent on the correlation parameter θ through R and r(x). Both cross-validation and maximum likelihood estimation can be employed to obtain θ. The latter is used here:

$$ \widehat{\boldsymbol{\uptheta}}=\underset{\boldsymbol{\uptheta}}{\arg \max}\left(-N\ln \left({\widehat{\sigma}}^2\right)-\ln \left[\det \left(\mathbf{R}\right)\right]\right) $$

2.2 Monte Carlo simulation

According to the estimator of G(x) in (5) and the formulas for the failure probability in (1), the failure probability estimate can be expressed as

$$ {\widehat{P}}_{f,N}=\int {I}_{{\widehat{G}}_N<0}\left(\mathbf{x}\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x} $$

(7)

Since the computational expense of $\widehat{G}\left(\mathbf{x}\right)$ is quite small, MCS is adopted to approximately evaluate ${\widehat{P}}_{f,N}$. The approximation of ${\widehat{P}}_f$ is calculated by

$$ {\widehat{P}}_{f,N}\approx {\tilde{P}}_{f,N}=\frac{1}{N_{\mathrm{MC}}}\sum \limits_{i=1}^{N_{\mathrm{MC}}}{I}_{{\widehat{G}}_N\le 0}\left({\mathbf{x}}_{\mathrm{MC},i}\right) $$

(8)

where N_MC is the number of i.i.d. random samples, which are generated from f_X(x). The coefficient of variation of ${\tilde{P}}_{f,N}$ is,

$$ {\delta}_{\mathrm{MC}}=\frac{\sqrt{\operatorname{var}\left({\tilde{P}}_{f,N}\right)}}{{\tilde{P}}_{f,N}}=\sqrt{\frac{1-{\tilde{P}}_{f,N}}{N_{\mathrm{MC}}{\tilde{P}}_{f,N}}} $$

(9)

δ_MC quantifies the accuracy of MCS and can be used to judge when MCS can stop. Given a threshold level [δ], the MCS of (8) is terminated when δ_MC satisfies (10).

$$ {\delta}_{\mathrm{MC}}\le \left[\delta \right] $$

(10)

Taking (9) into account,

$$ {N}_{\mathrm{MC}}{\tilde{P}}_{f,N}\ge \frac{1-{\tilde{P}}_{f,N}}{{\left[\delta \right]}^2} $$

(11)

It is notable that ${N}_{\mathrm{MC}}{\tilde{P}}_{f,N}$ is the failure number of the MCS random samples. When the failure of the studied structure is a rare event, one can neglect ${\tilde{P}}_{f,N}$ on the right side of (11). Then, the stopping criterion of MCS reads

$$ {N}_{\mathrm{MC}}{\tilde{P}}_{f,N}\ge \frac{1}{{\left[\delta \right]}^2} $$

(12)

3 The stepwise accuracy-improvement strategy

According to the theory of Gaussian processes, given the model defined by (5) and (6), the real performance value at a point x (G(x)) can be treated as a normally distributed variable.

$$ G\left(\mathbf{x}\right)\sim N\left({\mu}_{G,N}\left(\mathbf{x}\right),{\sigma}_{G,N}^2\left(\mathbf{x}\right)\right) $$

(13)

where ${\sigma}_{G,N}^2\left(\mathbf{x}\right)$ is the Kriging variance. Equation (13) quantifies the epistemic uncertainty of G(x) and the local accuracy of the Kriging model in terms of the mean squared error. In addition, the epistemic uncertainty of the sign of G(x) can be derived from (13).

$$ P\left({I}_{G\le 0}\left(\mathbf{x}\right)=1\right)=P\left(G\left(\mathbf{x}\right)\le 0\right)=\Phi \left(\frac{0-{\mu}_{G,N}\left(\mathbf{x}\right)}{\sigma_{G,N}\left(\mathbf{x}\right)}\right) $$

(14)

$$ P\left({I}_{G\le 0}\left(\mathbf{x}\right)=0\right)=P\left(G\left(\mathbf{x}\right)>0\right)=1-\Phi \left(\frac{0-{\mu}_{G,N}\left(\mathbf{x}\right)}{\sigma_{G,N}\left(\mathbf{x}\right)}\right) $$

(15)

Therefore,

$$ P\left(|{I}_{{\widehat{G}}_N\le 0}\left(\mathbf{x}\right)-{I}_{G\le 0}\left(\mathbf{x}\right)|=1\right)=\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right) $$

(16)

$$ P\left(|{I}_{{\widehat{G}}_N\le 0}\left(\mathbf{x}\right)-{I}_{G\le 0}\left(\mathbf{x}\right)|=0\right)=\boldsymbol{\varPhi} \left({U}_N\left(\mathbf{x}\right)\right) $$

(17)

$$ E\left(|{I}_{{\widehat{G}}_N\le 0}\left(\mathbf{x}\right)-{I}_{G\le 0}\left(\mathbf{x}\right)|\right)=\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right) $$

(18)

where U_N(x) is the learning function constructed by Echard et al. (2011),

$$ {U}_N\left(\mathbf{x}\right)=\mid {\mu}_{G,N}\left(\mathbf{x}\right)/{\sigma}_{G,N}\left(\mathbf{x}\right)\mid $$

This section employs the statistical information above to construct a measure to quantify the accuracy of the Kriging model and ${\widehat{P}}_{f,N}$, and then derives the expectation that any given point could enhance the accuracy of the Kriging model in terms of the employed measure. Furthermore, the maximum point of the expectation is defined as the best next point. Several simplifications are employed to fasten the search of the next best point. Refreshing the DoE with the acquired best next point is the proposed DoE strategy, named as the stepwise accuracy-improvement strategy, which aims at building a sufficient Kriging model while calling the performance function as few times as possible.

3.1 The accuracy measure of the Kriging model and ${\widehat{P}}_{f,N}$

Taking both (1) and (7) into consideration, the absolute error of ${\widehat{P}}_{f,N}$ relative to P_f can be calculated by

$$ {\displaystyle \begin{array}{l}\mid {\widehat{P}}_{f,N}-{P}_f\mid =\mid \int {I}_{{\widehat{G}}_N<0}\left(\mathbf{x}\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}-\int {I}_{G<0}\left(\mathbf{x}\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\mid \\ {}\kern4.35em \le \int \mid {I}_{{\widehat{G}}_N<0}\left(\mathbf{x}\right)-{I}_{G<0}\left(\mathbf{x}\right)\mid {f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\end{array}} $$

(19)

${\widehat{G}}_N\left(\mathbf{x}\right)$ divides X space into two domains, i.e., the estimated safe domain ${\widehat{G}}_N\left(\mathbf{x}\right)>0$ and the estimated failure domain ${\widehat{G}}_N\left(\mathbf{x}\right)\le 0$. Point x disturbs the accuracy of ${\widehat{P}}_{f,N}$ if the signs of G(x) and ${\widehat{G}}_N\left(\mathbf{x}\right)$ are different. The last term of (19) is equal to the fraction of points in X space whose performance values are wrongly predicted with respect to their signs, as shown in Fig. 1 (domain II). Figure 1 also illustrates the reason why $\mid {\widehat{P}}_{f,N}-{P}_f\mid$ is lower than the last integration of (19).

Fig. 1

Illustration of the last term in (19)

Equation (19) is difficult (even impossible) to calculate in engineering because G(x) = 0 is unknown. Fortunately, its expectation can be estimated based on the epistemic uncertainty of I_G ≤ 0(x) ((14)–(18)).

$$ {\displaystyle \begin{array}{l}E\left(|{\widehat{P}}_{f,N}-{P}_f|\kern0.2em \right)\le \int E\left(|{I}_{{\widehat{G}}_N<0}\left(\mathbf{x}\right)-{I}_{G<0}\left(\mathbf{x}\right)|\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\\ {}\kern0.65em =\int \boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\end{array}} $$

(20)

To simplify, a new symbol is introduced:

$$ {E}_N=\int \boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x} $$

(21)

E_N is first proposed by Ref. (Sun et al. 2017), and further studied by Ref. (Jian et al. 2017). Obviously, it quantifies the fraction of the whole X space that is classified as domain II (Fig. 1) in the sense of expectation. It is also an upper bound for the expectation of the absolute error of ${\widehat{P}}_{f,N}$. This study employs E_N as the accuracy measure of the Kriging model and ${\widehat{P}}_{f,N}$.

3.2 The stepwise accuracy-improvement strategy

From Fig. 1 and the definition of E_N, $\mid {\widehat{P}}_{f,N}-{P}_f\mid$ is negligible with a large probability if E_N satisfies a predefined criterion. Therefore, the best next point is defined as the one that can most decrease E_N in the sense of expectation.

3.2.1 An optimization problem for the best next point

A point x₀ is added to the current DoE with y₀, and a pseudo Kriging model is constructed corresponding to the pseudo DoE [x₁, …, x_N, x₀] and [y₁, …, y_N, y₀]^T. Then, the accuracy of the pseudo Kriging model can be measured by E_N + 1(x₀, y₀), whose value depends on both x₀ and y₀.

$$ {E}_{N+1}\left({\mathbf{x}}_0,{y}_0\right)=\int \boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x} $$

(22)

The Kriging surrogate model could generally be improved after adding (x₀, y₀) in S_DoE and Y. The improvement is measured as follows.

$$ {\displaystyle \begin{array}{l}\Delta E\left({\mathbf{x}}_0,{y}_0\right)={E}_N-{E}_{N+1}\left({\mathbf{x}}_0,{y}_0\right)\\ {}\kern0.65em =\int \boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}-\int \boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\end{array}} $$

(23)

ΔE(x₀, y₀) is also a function of x₀ and y₀. Before calling to the target performance function to calculate G(x₀), one does not know how much the Kriging model will be improved by updating S_DoE with x₀. A measure that depends only on x₀ is needed to quantify or predict how much x₀ could enhance the accuracy of the Kriging model.

Equation (13) provides the distribution information of G(x₀), which is derived from [x₁, …, x_N] and [y₁, …, y_N]^T in the framework of Kriging theory. Therefore, for given x₀, ΔE(x₀, G(x₀)) is a function of the normally distributed variable G(x₀). This study proposes the mathematical expectation of ΔE(x₀, G(x₀)) as the measure mentioned above.

$$ {\displaystyle \begin{array}{l}\boldsymbol{\varDelta} \left({\mathbf{x}}_0\right)=E\left(\boldsymbol{\varDelta} E\left({\mathbf{x}}_0,{y}_0\right)\right)={\int}_{-\infty}^{+\infty}\boldsymbol{\varDelta} E\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0\\ {}\kern2.65em ={E}_N-{\int}_{-\infty}^{+\infty }{E}_{N+1}\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0\end{array}} $$

(24)

Then, this study defines the best next point (x_N + 1) as the one that maximizes (24).

$$ {\mathbf{x}}_{N+1}=\arg \max \boldsymbol{\varDelta} \left({\mathbf{x}}_0\right) $$

(25)

It is worth emphasizing that the feasible region of the optimization problem of (25) is theoretically the whole X space.

3.2.2 Approximation of the best next point

To compute the value of Δ(x₀), (23) needs to be applied at least several times, and E_N + 1(x₀, y₀) is not easy to compute if M ≥ 3. Therefore, optimizing (25) directly may be too time-consuming for engineering applications. To overcome this problem and efficiently determine the approximate location of the best next point, some simplifications are made.

• 1. Equations (21) and (23) can be rewritten as

$$ {E}_N={\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}+{\int}_{U_N>\left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x} $$

(26)

$$ {\displaystyle \begin{array}{l}\Delta E\left({\mathbf{x}}_0,{y}_0\right)=\int \boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}-\int \boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\\ {}\kern0.65em =\left[{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}-{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\right]\\ {}\kern1.8em +\left[{\int}_{U_N>\left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}-{\int}_{U_N>\left[U\right]}\boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\right]\end{array}} $$

(27)

According to (17), the probability that the sign of G(x) is correctly predicted is Φ(U_N(x)). When U_N(x) is above a given threshold value [U], one can almost confirm ${I}_{{\widehat{G}}_N<0}\left(\mathbf{x}\right)={I}_{G<0}\left(\mathbf{x}\right)$, ignore the epistemic uncertainty of the sign of G(x), and consider that the first integral in (26) contributes most of E_N. Hence, attention is focused on the region where U_N(x) ≤ [U] during the computation of ΔE(x₀, y₀). As shown by (28), ΔE(x₀, y₀) is approximated by ΔE^′(x₀, y₀):

$$ {\displaystyle \begin{array}{l}\Delta E\left({\mathbf{x}}_0,{y}_0\right)\approx \Delta {E}^{\prime}\left({\mathbf{x}}_0,{y}_0\right)\\ {}\kern1em ={\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}-{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\end{array}} $$

(28)

This study proposes [U] = 2, in which situation the probability that the sign of G(x) is correctly predicted is larger than 0.977 if U_N(x) > [U]. The reasonability of the approximation of (28) is investigated in Section 5.

• 2. A new symbol $\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)$ is defined as (29),

$$ {\displaystyle \begin{array}{l}\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)={\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}|{U}_N\left(\mathbf{x}\right)\le \left[U\right]\right)\mathrm{d}\mathbf{x}\\ {}\kern5.6em -{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}|{U}_N\left(\mathbf{x}\right)\le \left[U\right]\right)\mathrm{d}\mathbf{x}\end{array}} $$

(29)

where f_X(x| U_N(x) ≤ [U]) is a conditional PDF,

$$ {f}_{\mathbf{X}}\left(\mathbf{x}|{U}_N\left(\mathbf{x}\right)\le \left[U\right]\right)=\left\{\begin{array}{l}\frac{f_{\mathbf{X}}\left(\mathbf{x}\right)}{\int_{U_N\le \left[U\right]}{f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}}\kern1.9em {U}_N\left(\mathbf{x}\right)\le \left[U\right]\\ {}0\kern8em {U}_N\left(\mathbf{x}\right)>\left[U\right]\end{array}\right. $$

Then,

$$ {\displaystyle \begin{array}{l}\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)\cdot {\int}_{U_N\le \left[U\right]}{f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\\ {}\kern.75em =\left[\begin{array}{l}{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right)\left({f}_{\mathbf{X}}\Big(\mathbf{x}|{U}_N\left(\mathbf{x}\right)\le \left[U\right]\Big)\cdot {\int}_{U_N\le \left[U\right]}{f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\right)\mathrm{d}\mathbf{x}\\ {}-{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right)\left({f}_{\mathbf{X}}\Big(\mathbf{x}|{U}_N\left(\mathbf{x}\right)\le \left[U\right]\Big)\cdot {\int}_{U_N\le \left[U\right]}{f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\right)\mathrm{d}\mathbf{x}\end{array}\right]\\ {}\kern.75em =\left[{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}-{\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_{N+1}\left(\mathbf{x}|{\mathbf{x}}_0,{y}_0\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\right]\\ {}\kern.75em =\Delta {E}^{\prime}\left({\mathbf{x}}_0,{y}_0\right)\end{array}} $$

Therefore,

$$ \Delta {E}^{\prime}\left({\mathbf{x}}_0,{y}_0\right)\propto \Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right) $$

and

$$ \frac{\Delta {E}^{\prime}\left({\mathbf{x}}_0,{y}_0\right)}{\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)}={\int}_{U_N\le \left[U\right]}{f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x} $$

The domain of the integration of ΔE^′(x₀, y₀) or $\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)$ is cabined if the Kriging model is with fair accuracy. In addition, the failure probability of an engineering structure is often very small. Both situations make it inefficient to generate i.i.d. random samples from the conditional PDF f_X(x| U_N(x) ≤ 2) with the ordinary MC method. The Markov chain Monte Carlo (MCMC) method performs well in generating conditional random samples. By setting appropriate parameters, one can obtain samples that depend on each other weakly and seem sufficiently independent and identically distributed for engineering applications. MCMC is employed in this study to approximately perform the integration of (29).

$$ \Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)\approx \frac{1}{N_E}\sum \limits_{n=1}^{N_E}\boldsymbol{\varPhi} \left(-{U}_N\left({\mathbf{x}}_{E,n}\right)\right)-\frac{1}{N_E}\sum \limits_{n=1}^{N_E}\boldsymbol{\varPhi} \left(-{U}_{N+1}\left({\mathbf{x}}_{E,n}|{\mathbf{x}}_0,{y}_0\right)\right) $$

(30)

where N_E denotes the number of random samples from MCMC method. ${\mathbf{S}}_E=\left[{\mathbf{x}}_{E,1},{\mathbf{x}}_{E,2},\dots, {\mathbf{x}}_{E,{N}_E}\right]$ is treated as an i.i.d. random sample sequence.

Instead of employing or constructing an optimization algorithm to search for the best next point, this study treats {x_{E, n}} (n = 1,…,N_E) as candidates for x_N + 1 and chooses the one that maximizes the expectation of $\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)$. Then, the optimization problem of (25) is simplified as

$$ {\displaystyle \begin{array}{l}{\mathbf{x}}_{N+1}=\arg \max \boldsymbol{\varDelta} \left({\mathbf{x}}_0\right)=\arg \max {\int}_{-\infty}^{+\infty}\boldsymbol{\varDelta} E\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0\\ {}\kern2.5em \approx \kern.35em \arg \max {\int}_{-\infty}^{+\infty}\boldsymbol{\varDelta} {E}^{\prime}\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0\\ {}\kern2em =\arg \max {\int}_{U_N\le \left[U\right]}{f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\cdot {\int}_{-\infty}^{+\infty}\boldsymbol{\varDelta} \tilde{E}\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0\\ {}\kern2em =\arg \max {\int}_{-\infty}^{+\infty}\boldsymbol{\varDelta} \tilde{E}\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0\\ {}\kern2.5em \approx \kern.35em \underset{{\mathbf{x}}_0\in {\mathbf{S}}_E}{\arg \max}\tilde{\boldsymbol{\varDelta}}\left({\mathbf{x}}_0\right)\end{array}} $$

(31)

where

$$ \tilde{\boldsymbol{\varDelta}}\left({\mathbf{x}}_0\right)={\int}_{-\infty}^{+\infty}\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0 $$

(32)

• 3. According to the Kriging theory, G(x₀) is treated as a normal random variable with mean value μ_{G, N}(x₀) and variance ${\sigma}_{G,N}^2\left({\mathbf{x}}_0\right)$. Then,

$$ {\displaystyle \begin{array}{c}{f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)=\frac{1}{\sqrt{2\pi }{\sigma}_{G,N}\left({\mathbf{x}}_{E,i}\right)}\exp \left(-\frac{{\left({y}_0-{\mu}_{G,N}\left({\mathbf{x}}_0\right)\right)}^2}{2{\sigma}_{G,N}^2\left({\mathbf{x}}_0\right)}\right)\\ {}\begin{array}{l}\tilde{\boldsymbol{\varDelta}}\left({\mathbf{x}}_0\right)={\int}_{-\infty}^{+\infty}\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right){f}_{G\left({\mathbf{x}}_0\right)}\left({y}_0\right)\mathrm{d}{y}_0\\ {}\kern2.5em ={\int}_{-\infty}^{+\infty}\Delta \tilde{E}\left({\mathbf{x}}_0,{y}_0\right)\frac{1}{\sqrt{2\pi }{\sigma}_{G,N}\left({\mathbf{x}}_0\right)}\exp \left(-\frac{{\left({y}_0-{\mu}_{G,N}\left({\mathbf{x}}_0\right)\right)}^2}{2{\sigma}_G^2\left({\mathbf{x}}_0\right)}\right)\mathrm{d}{y}_0\\ {}\kern2.5em =\frac{1}{\sqrt{\pi }}{\int}_{-\infty}^{+\infty}\Delta \tilde{E}\left({\mathbf{x}}_0,\sqrt{2}{\sigma}_{G,N}\left({\mathbf{x}}_{E,i}\right)t+{\mu}_{G,N}\left({\mathbf{x}}_{E,i}\right)\right)\exp \left(-{t}^2\right)\mathrm{d}t\end{array}\end{array}} $$

(33)

where

$$ t=\frac{y_0-{\mu}_{G,N}\left({\mathbf{x}}_0\right)}{\sqrt{2}{\sigma}_{G,N}\left({\mathbf{x}}_0\right)} $$

Obviously, Gauss–Hermite quadrature is very suitable to approximately calculate the last integral in (33).

$$ \tilde{\boldsymbol{\varDelta}}\left({\mathbf{x}}_0\right)\approx \frac{1}{\sqrt{\pi }}\sum \limits_{j=1}^{n_G}{w}_j\Delta \tilde{E}\left({\mathbf{x}}_0,\sqrt{2}{\sigma}_{G,N}\left({\mathbf{x}}_0\right){v}_j+{\mu}_{G,N}\left({\mathbf{x}}_0\right)\right) $$

(34)

where n_G is the number of quadrature points, and v_j and w_j (j = 1,…,n_G) denote the quadrature points and associated weights, respectively.

In summary, this study approximates the best next point as follows:

$$ {\mathbf{x}}_{N+1}=\arg \max \boldsymbol{\varDelta} \left({\mathbf{x}}_0\right)\approx \underset{{\mathbf{x}}_0\in {\mathbf{S}}_E}{\arg \max}\tilde{\boldsymbol{\varDelta}}\left({\mathbf{x}}_0\right) $$

(35)

where Δ(x₀) is defined in Section 3.2.1 (see (22)–(24)), and (29)–(34) provide the definition and the calculation of $\tilde{\boldsymbol{\varDelta}}\left({\mathbf{x}}_0\right)$.

3.2.3 The pseudocode of the stepwise accuracy-improvement strategy

The pseudocode of the stepwise accuracy-improvement strategy is summarized as follows:

• Step 1 Construct the Kriging model based on S_DoE = [x₁, x₂, …, x_N] and Y = [y₁, y₂, …, y_N]^T.

• Step 2 Generate a random point set ${\mathbf{S}}_E=\left[{\mathbf{x}}_{E,1},{\mathbf{x}}_{E,2},\dots, {\mathbf{x}}_{E,{N}_E}\right]$ with the MCMC algorithm from the conditional PDF f_X(x| U_N(x) ≤ 2).

• Step 3 For each candidate point x_{E, i} (i = 1,…,N_E)

For each quadrature point v_j (j = 1,…,n_G).

Construct a pseudo Kriging model based on S_DoE = [x₁, x₂, …, x_N, x_{E, i}] and Y = [y₁, y₂, …, y_N, y_{E, i, j}]^T.

$$ {y}_{E,i,j}=\sqrt{2}{\sigma}_{G,N}\left({\mathbf{x}}_{E,i}\right){v}_j+{\mu}_{G,N}\left({\mathbf{x}}_{E,i}\right) $$

Compute $\Delta \tilde{E}\left({\mathbf{x}}_{E,i},\sqrt{2}{\sigma}_{G,N}\left({\mathbf{x}}_{E,i}\right){v}_j+{\mu}_{G,N}\left({\mathbf{x}}_{E,i}\right)\right)$ according to (30).

• Step 4 Estimate $\tilde{\boldsymbol{\varDelta}}\left({\mathbf{x}}_{E,i}\right)$ (i = 1,…,N_E) according to (34).

• Step 5 Find the best next point x_N + 1 ((35)).

3.3 Discussion of the approximation of (28)

E_N, defined by (21), is also a general measure of the probability that the Kriging model incorrectly predicts the sign of G(X). As analyzed above, the probability that I_G ≤ 0(x) and ${I}_{\widehat{G}\le 0}\left(\mathbf{x}\right)$ are equal is larger than 0.977 if U_N(x) > 2. In other words, the Kriging model is quite accurate in the region U_N(x) > 2 for reliability-analysis applications. ${\int}_{U_N>2}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}$ (the last term of (26)) would not be significantly diminished even if a point located in U_N(x) > 2 were added to S_DoE. In contrast, ${\int}_{U_N\le 2}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}$ has much more potential to decrease. Therefore, this study approximates ΔE(x₀, y₀) with ΔE^′(x₀, y₀) ((28)) and focuses on the domain U_N(x) ≤ 2 when searching for the best next point. For a given coefficient of variation, the number of i.i.d. points needed to estimate $\Delta \tilde{E}\left({\mathbf{x}}_0,{\mathbf{y}}_0\right)$ ((29)) is much lower than that needed to estimate ΔE(x₀, y₀). Equation (28) is the key to reducing the computational burden of the proposed strategy.

4 A Kriging-based structural reliability analysis method

In this section, a Kriging-based SRA method is constructed. The DoE for building the Kriging model is adaptively updated by the best next point from the stepwise accuracy-improvement strategy proposed in Section 3.2. The failure-probability estimate is calculated with MCS. The stopping criterion of the reliability analysis procedure is defined based on E_N. The main steps of the SRA method are summarized as follows:

• Step 1 Generate the initial DoE with Latin hypercube sampling (LHS) and use the model of the studied structure to obtain the corresponding performance values. It is assumed that the input variables subject to the standard normal distribution; this is reasonable since, in engineering, multiple random variables can usually be represented by a standard normal vector exactly or approximately. The hypercube for producing initial DoE samples is [−5,5]^M, and the number of samples is N₀.

$$ {\displaystyle \begin{array}{c}{\mathbf{S}}_{\mathrm{DoE}}=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots, {\mathbf{x}}_{N_0}\right]\\ {}\mathbf{Y}={\left[{y}_1,{y}_2,\dots, {y}_{N_0}\right]}^{\mathrm{T}}\end{array}} $$

• Step 2 Construct the initial Kriging model ${\widehat{G}}_{N_0}\left(\mathbf{x}\right)$. A widely used toolbox, DACE (Kaymaz 2005; Kleijnen 2009; Marrel et al. 2008; Dellino et al. 2009) in MATLAB, is employed here to construct the Kriging model and predict performance values. (t = 0)

• Step 3 t = t + 1. Search for the best next point ${\mathbf{x}}_{N_0+t}$ based on the strategy proposed in Section 3. Generate N_E random samples with the MCMC algorithm in the region ${U}_{N_0+t-1}\left(\mathbf{x}\right)\le \left[U\right]$, and the conditional PDF of MCMC is defined by ${f}_{\mathbf{X}}\left(\mathbf{x}|{U}_{N_0+t-1}\left(\mathbf{x}\right)\le \left[U\right]\right)$. Referring to Section 3.2, locate the best next point ${\mathbf{x}}_{N_0+t}$ that satisfies (35). This study sets n_G = 5 and [U] = 2. Add ${\mathbf{x}}_{N_0+t}$ to the current DoE and calculate its performance function value $G\left({\mathbf{x}}_{N_0+t}\right)$.

• Step 4 Construct the Kriging model ${\widehat{G}}_{N_0+t}\left(\mathbf{x}\right)$ associated with the updated DoE. If t divides a given positive integer t₀ exactly, continue to step 5. Otherwise, return to step 3.

• Step 5 Estimate the target failure probability with MCS and decide whether to terminate the iterative procedure. Compute the failure probability estimate ${\widehat{P}}_{f,{N}_0+t}$ and ${E}_{N_0+t}$ with the same MCS random samples. If they satisfy (37), end the procedure and output ${\widehat{P}}_{f,{N}_0+t}$. Otherwise, return to step 3.

Continue the procedure of MCS until the coefficient of variation of ${\widehat{P}}_{f,{N}_0+t}$ is no more than [δ]. In this study, [δ] is defined as

$$ \left[\delta \right]=0.01 $$

(36)

According to (12),

$$ {N}_{\mathrm{MC}}{\widehat{P}}_{f,{N}_0+t}\ge {10}^4 $$

The condition for stopping MCS is that the number of failure random samples is no less than 10⁴. S_MC = {x_{MC, i}|  i = 1, …, N_MC} denotes the random point set of MCS. The upper bound for the expectation of the absolute error of ${\widehat{P}}_{f,{N}_0+t}$ relative to P_f can be estimated by

$$ {E}_{N_0+t}\approx \frac{1}{N_{\mathrm{MC}}}\sum \limits_{i=1}^{N_{\mathrm{MC}}}\boldsymbol{\varPhi} \left(-{U}_{N_0+t}\left({\mathbf{x}}_{\mathrm{MC},i}\right)\right) $$

The stopping criterion of the proposed reliability analysis method is defined as

$$ {e}_{\varepsilon }={E}_{N_0+t}/{\widehat{P}}_{f,{N}_0+t}\le \left[{e}_{\varepsilon}\right] $$

(37)

In the proposed method, the computational cost of Step 3 depends on the efficiency of MCMC algorithm, the value of N_E and the programming technique. Among them, N_E is the most influential. This is discussed in detail in Section 5. MCS may become less effective when the failure of the studied structure is a rare event. Fortunately, the candidates for the best next point are generated with MCMC method, while the estimate of the target failure probability and the evaluation of the termination criterion for the procedure are performed based on another random point set from the MC method, which means that whether or not the stopping criterion is tested in an iteration has no effect on the quality of the future best next points. One could neglect Step 5 at the preliminary stage of the procedure or change the value of t₀ as the iterative procedure proceeds. In addition, both SS and IS have the potential to replace MCS in Step 5 to calculate ${\widehat{P}}_{f,{N}_0+t}$ and e_ε.

5 Numerical applications

In this section, four benchmark examples are studied to validate the stepwise accuracy-improvement strategy developed in Section 3 and the SRA procedure proposed in Section 4. Three of the examples have explicit performance functions with different numbers of input variables and complexities, and the other is a frame structure with an implicit performance function.

5.1 A series system

The following series system, which includes four branches, is widely used in literatures (Echard et al. 2011; Bourinet et al. 2011; Cadini et al. 2014). Its performance function is defined as

$$ G\left(\mathbf{x}\right)=\min \left\{\begin{array}{l}3+0.1{\left({x}_1-{x}_2\right)}^2-\left({x}_1+{x}_2\right)/\sqrt{2};\\ {}3+0.1{\left({x}_1-{x}_2\right)}^2+\left({x}_1+{x}_2\right)/\sqrt{2};\\ {}\left({x}_1-{x}_2\right)+6/\sqrt{2};\\ {}\left({x}_2-{x}_1\right)+6/\sqrt{2};\end{array}\right\} $$

(38)

where X₁ and X₂ are i.i.d. variables that subject to the standard normal distribution.

The method illustrated in Section 4 is applied to this analytical example. The initial DoE contains N₀ = 6 random samples from LHS. To investigate the influence of the number of conditional candidate points (N_E) on the efficiency of the developed strategy, perform the SRA procedure three times with the same initial DoE and different values of N_E. Figure 2 shows the graphs of ${\widehat{P}}_f$ and e_ε when N_E equals 1000, 3000 and 10,000. These graphs indicate that increasing the number of candidate points does not remarkably increase the speed of convergence of ${\widehat{P}}_f$ or the decrement of e_ε.

Fig. 2

Graphs of ${\widehat{P}}_f$ and e_ε with different values of N_E for the series system

Table 1 summarizes the results obtained using the method in this study and other methods based on learning functions. ERF and H are learning functions proposed by Yang et al. (2015) and Lv et al. (2015), respectively. To perform a fair comparison, all results in Table 1 are with the same initial DoE. [e_ε] is the threshold value of e_ε. The iterative reliability-analysis procedure is treated as convergent if e_ε is no larger than [e_ε]. N_call is the number of calls to the studied performance function when (37) is satisfied, and ${\widehat{P}}_f$ is the corresponding estimate of the target failure probability. ε represents the relative error of ${\widehat{P}}_f$ compared with the reference value from MCS. For values of [e_ε] listed in Table 1, the proposed procedure is able to satisfy the corresponding convergence condition with fewer DoE points, and the relative error of ${\widehat{P}}_f$ is acceptable for engineering applications even when [e_ε] = 0.05.

Table 1 Results of the series system

Graphs of ${\widehat{P}}_f$ and e_ε from different methods are shown in Fig. 3. According to Fig. 3, the proposed method can roughly estimate the target failure probability by evaluating (38) approximately 30 times, outperforming the learning-function-based methods.

Fig. 3

Graphs of ${\widehat{P}}_f$ and e_ε from different methods. The imaginary line in (a) is the reference value of P_f from MCS. Imaginary lines in (b) denote different values of [e_ε]

To further investigate the performance of the proposed stepwise accuracy-improvement strategy, the N_MC = 2.5 × 10⁶ points used to obtain the reference value of P_f are treated as a test set, and Kriging models from different methods are compared in terms of the number of signs of performance function values that are wrongly predicted, which is denoted by E_W (39). The results are listed in Table 2.

$$ {E}_W=\sum \limits_{n=1}^{N_{\mathrm{MC}}}\mid {I}_{G\le 0}\left({\mathbf{x}}_{\mathrm{MC},n}\right)-{I}_{\widehat{G}\le 0}\left({\mathbf{x}}_{\mathrm{MC},n}\right)\mid $$

(39)

Table 2 Comparisons ofs methods in terms of the real accuracies of the Kriging models for the 1st example. E_W denotes the number of wrongly predicted points among 2.5 × 10⁶ test points

To test the stability of the proposed method, it is randomly run 5 times. Figure 4 shows graphs of ${\widehat{P}}_f$ and e_ε. According to the information provided by Fig. 4, for this example, ${\widehat{P}}_f$ and e_ε with different initial DoEs converge still fast, even though the convergence processes are random.

Fig. 4

Graphs of ${\widehat{P}}_f$ and e_ε from the proposed method with random initial DoE (N_E = 3000)

As analyzed in Section 3.3, (28) is the key to reducing the computational burden of the stepwise accuracy-improvement strategy. Equation (28) is equal to approximating (26) as follows:

$$ {\displaystyle \begin{array}{l}{E}_N={\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}+{\int}_{U_N>\left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\\ {}\kern1.5em \approx \kern.45em {\int}_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}\end{array}} $$

(40)

To investigate the reasonability of (28) and (40), a new symbol is introduced,

$$ \lambda =\frac{\int_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}}{\int_{U_N\le \left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}+{\int}_{U_N>\left[U\right]}\boldsymbol{\varPhi} \left(-{U}_N\left(\mathbf{x}\right)\right){f}_{\mathbf{X}}\left(\mathbf{x}\right)\mathrm{d}\mathbf{x}} $$

(41)

Apparently, λ is the proportion of the contribution that the region U_N ≤ [U] makes to E_N. Figure 5 shows the graphs of λ from Kriging models with different number of DoE points. For this example, it is easy to notice that is above 0.95 when [U] = 2.

Fig. 5

Graphs of λ to investigate how much the region U_N ≤ [U] contributes to E_N

5.2 Modified Rastrigin function

Balesdent et al. (2013) and Echard et al. (2011) have already analyzed the modified Rastrigin function of (42), in which X₁ and X₂ are i.i.d. standard normal variables. It is adopted here to demonstrate that the proposed DoE strategy is qualified to handle a complex non-monotone deterministic function.

$$ G\left(\mathbf{x}\right)=10-\sum \limits_{m=1}^2\left({x}_m^2-5\cos \left(2\pi {x}_m\right)\right) $$

(42)

P_f corresponding to (42) is estimated by the proposed method with N₀ = 6. Similar to Fig. 2 in Section 5.1, the graphs shown in Fig. 6 investigate the dependensce of the proposed method on N_E.

Fig. 6

Graphs of ${\widehat{P}}_f$ and e_ε with different values of N_E for the modified Rastrigin function

Table 3 Results of the modified Rastrigin function

The proposed method is compared with AK-MCS and LIF based method (Sun et al. 2017) in terms of the number of calls to the performance function and the relative error of ${\widehat{P}}_f$. Results are summarized in Table 3.

According to Table 3, to obtain a Kriging model that satisfies a given criterion, the procedure proposed in this study requires fewer calls to the performance function than learning-function-based methods. Figure 7 shows in detail the changes in ${\widehat{P}}_f$ and e_ε during iterations. Table 4 investigates the real accuracy (E_W) of Kriging models from the proposed DoE strategy and learning functions with the same test set (N_MC = 3 × 10⁵).

Fig. 7

Graphs of ${\widehat{P}}_f$ and e_ε from different methods for the modified Rastrigin function

Table 4 Comparisons of methods in terms of the real accuracies of Kriging models for the 2nd example

As the stepwise accuracy-improvement strategy is based on MCMC sampling, the result of the proposed SRA method have some degree of randomness. To investigate the randomness, the proposed method is run 5 times. Figure 8 shows the results.

Fig. 8

Graphs of ${\widehat{P}}_f$ and e_ε from the proposed method with random initial DoE (the 2nd example, N_E = 3000)

Figure 9 shows the graphs of λ, which is used to research the proportion of the contribution the region U_N ≤ [U] makes to E_N.

Fig. 9

Graphs of λ based on Kriging models with different DoE points (the 2nd example)

5.3 An uncertain primary-secondary system

Figure 10 shows the two-degree-of-freedom primary-secondary system. It is characterized by the spring stiffnesses (k_p and k_s), the masses (m_p and m_s), and the damping ratios (ξ_p and ξ_s). The natural frequencies (ω_p and ω_s) of the two oscillators can be computed from (k_p, m_p) and (k_s, m_s), respectively.

$$ {\displaystyle \begin{array}{c}{\omega}_p=\sqrt{k_p/{m}_p}\\ {}{\omega}_s=\sqrt{k_s/{m}_s}\end{array}} $$

Fig. 10

The primary-secondary system

This system suffers a white-noise base excitation whose intensity is S₀. Equation (43) provides the mean-square relative displacement response of the secondary spring.

$$ E\left({x}_s^2\right)=\frac{\pi {S}_0}{4{\xi}_s{\omega}_s^3}\left[\frac{\xi_a{\xi}_s}{\xi_p{\xi}_s\left(4{\xi}_a^2+{\theta}^2\right)+{m}_s{\xi}_a^2/{m}_p}\cdot \frac{\left({\xi}_p{\omega}_p^3+{\xi}_s{\omega}_s^3\right){\omega}_p}{4{\xi}_a{\omega}_a^4}\right] $$

(43)

where

$$ {\displaystyle \begin{array}{c}{\omega}_a=\left({\omega}_p+{\omega}_s\right)/2\\ {}{\xi}_a=\left({\xi}_p+{\xi}_s\right)/2\\ {}\theta =\left({\omega}_p-{\omega}_s\right)/{\omega}_a\end{array}} $$

The concern in this example is the reliability of the secondary oscillator, for its peak response is sensitive to [m_p, m_s, k_p, k_s, ξ_p, ξ_s]^T. The performance function is defined as

$$ G\left(\mathbf{X}\right)={F}_s-{k}_s\underset{0<t<\tau }{\max}\mid {x}_s(t)\mid $$

(44)

where

$$ \mathbf{X}={\left[{m}_p,{m}_s,{k}_p,{k}_s,{\xi}_p,{\xi}_s,{S}_0,{F}_s\right]}^{\mathrm{T}} $$

F_s and τ denote the force capacity of the secondary oscillator and the duration of loading, respectively. According to (Der Kiureghian 1991), (44) can be rewritten as

$$ G\left(\mathbf{X}\right)={F}_s-{k}_sp\sqrt{E\left({x}_s^2\right)} $$

(45)

where p represents the peak factor and is set to 3 for simplicity; see (Der Kiureghian 1991) for more details about this system.

All basic variables in this system are independent and lognormally distributed, and their distribution parameters are given in Table 5. The complexity of this system has already been illustrated (Bourinet et al. 2011; Der Kiureghian 1991; Dubourg et al. 2013; Hu and Mahadevan 2016b). It is adopted here to demonstrate that the performance of the proposed DoE strategy remains outstanding as the dimension of the inputs increases.

Table 5 Distribution parameters of input variables of the 3rd example

The proposed reliability-analysis scheme is applied to this non-linear system with N₀ = 20. According to Figs. 2 and 6, using a large number of candidate points(N_E) does not remarkably improve the efficiency of the stepwise accuracy-improvement strategy. Therefore, the influence of the value of N_E is not investigated in this section. We set N_E = 3000 and randomly run the proposed method three times. Figure 11 shows the results. To investigate how much the region U_N ≤ [U] contributes to E_N, Fig. 12 shows the graphs of λ from Kriging models with different number of DoE points.

Fig. 11

Graphs of ${\widehat{P}}_f$ and e_ε from the proposed method with random initial DoE (the 3rd example, N_E = 3000)

Fig. 12

Graphs of λ based on Kriging models with different DoE points (the 3rd example)

To perform comparisons, several learning functions are employed to estimate the failure probability of the secondary oscillator. They are terminated when the advantage of the proposed method is clear (N_call = 720). Figure 13a and b depict the convergence procedure of ${\widehat{P}}_f$ and the decrease of e_ε, respectively. Table 6 summarizes all the results and compares different methods in terms of how many I_G ≤ 0(x_{MC, i}) (i = 1, …, N_MC) are wrongly predicted among N_MC = 3 × 10⁶ i.i.d. points.

Fig. 13

Graphs of ${\widehat{P}}_f$ and e_ε from different methods for the primary-secondary system

Table 6 Comparisons of methods in terms of the real accuracies of Kriging models for the 3rd example. N_MC = 3 × 10⁶ i.i.d. points are generated, and 14,147 of them are located in the failure domain. The reference value of P_f is 4.716 × 10⁻³

From Table 6 and Fig. 13, it is concluded that the accuracy of ${\widehat{P}}_f$ may be significantly better than the accuracy of $\widehat{G}\left(\mathbf{x}\right)=0$, which is easily understood from Fig. 1. For engineering applications, the latter is much more important because some decisions (such as reliability-based design) usually need to be made after estimating the failure probability. This example validates the advantage of the proposed DoE strategy in terms of fitting G(x) = 0 when the performance function is moderately high-dimensional and sensitive to inputs.

5.4 A frame structure with an implicit performance function

This example is taken from (Roussouly et al. 2013; Blatman and Sudret 2010; Nguyen et al. 2009). As depicted by Fig. 14, this frame structure has 8 finite elements whose properties, including Young’s modulus (E), eight moments of inertia (I) and cross section (A), are listed in Table 7. This example involves 21 input variables, and Table 8 provides their distribution information. The correlation between variables is summarized as follows:

$$ {\displaystyle \begin{array}{c}\rho \left({A}_i,{I}_i\right)=0.95\kern0.72em \left(i=1,2\right)\\ {}\rho \left({A}_i,{A}_j\right)=\rho \left({I}_i,{I}_j\right)=\rho \left({A}_i,{I}_j\right)=0.13\kern0.48em \left(i\ne j\right)\\ {}\rho \left({E}_1,{E}_2\right)=0.9\end{array}} $$

Fig. 14

The frame structure (m)

Table 7 Properties of finite elements of the frame structure

Table 8 Distribution information of input variables of the frame structure

The other variables are mutually independent.

Let s(x) denote the top displacement, as depicted in Fig. 14. The safety domain of this structure is defined as the domain in which the modulus of s(x) is less than the given threshold value, 0.06 m. The performance function is

$$ G\left(\mathbf{x}\right)=0.06-\mid \mathbf{s}\left(\mathbf{x}\right)\mid $$

(46)

To obtain a reference value of P_f, N_MC = 1.3 × 10⁶ i.i.d. simulations are performed, and 154 of them are failures. Therefore,

$$ {P}_f^{\mathrm{REF}}=1.185\times {10}^{-4} $$

The 1.3 × 10⁶ i.i.d. points used to compute ${P}_f^{\mathrm{REF}}$ are also employed to test all the Kriging models constructed below. In this way, the learning functions and the proposed DoE strategy are fairly compared and the conclusion is not influenced by the coefficient of variation of ${P}_f^{\mathrm{REF}}$.

The proposed structural reliability scheme and learning function-based methods are implemented with N₀ = 25. All procedures are terminated when N_call reaches 225. Figure 15 shows the graphs of λ from Kriging models built according to the proposed method.

Fig. 15

Graphs of λ based on Kriging models with different DoE points (the 4th example)

Figure 16 shows plots of ${\widehat{P}}_f$ and e_ε. From Fig. 16b, the proposed method satisfies the stopping criterion ([e_ε] = 0.05) after calling (46) about 150 times. Table 9 quantifies the accuracies of these methods in terms of E_W, ${\widehat{P}}_f$ and e_ε as N_call increases. Both Fig. 16 and Table 9 demonstrate the efficiency of the stepwise accuracy-improvement strategy and the proposed reliability analysis method for this implicit performance function.

Fig. 16

Graphs of ${\widehat{P}}_f$ and e_ε from different methods for the frame structure

Table 9 Results of the frame structure

5.5 Summary of results

To validate the efficiency of the proposed DoE strategy and SRA method, four benchmark examples are studied and several methods are compared qualitatively and quantitatively. According to the results, conclusions are summarized as follows:

• (1) The stepwise accuracy-improvement strategy is able to roughly approximate the target failure probability quickly. With same initial DoE, the proposed strategy needs fewer DoE points than other learning functions to satisfy a given stopping criterion (Figs. 3, 7, 13 and 16; Table 1 and Table 3).

• (2) By testing the Kriging models with the same random samples (Tables 2, 4, 6 and 9), it is obvious that Kriging models based on the proposed strategy are more accurate than those based on learning functions.

• (3) As MCMC sampling are employed during the search of the best next point, the efficiency of the stepwise accuracy-improvement strategy has more or less randomness. By randomly running it several times in the first three examples (Figs. 4, 8 and 11), it is concluded that the proposed strategy is stable and the randomness is more likely to be negligible.

• (4) According to Figs. 5, 9, 12 and 15, for given [U], the proportion of the contribution of the region U < [U] to E_N increases with N_call. Generally, the proportion is above 90% when [U] = 2, which validates the reasonability of (28).

• (5) Figures 2 and 6 indicate that increasing the number of candidate points does not remarkably make the proposed strategy more efficient when N_E > 1000. There are lots of untried points that could enhance the accuracy of the Kriging model when it is not accurate. On this condition, the best point among N_E (=1000) ones may be good enough even if it is not the real best next point. As the improvement of the Kriging model, the region [U] < 2 tends to be cabined, and N_E (=1000) conditional random points may cover this region well. From this perspective, it is understandable that large number of candidate points benefits little.

6 Conclusion

This study proposes a new Kriging-based DoE strategy called the stepwise accuracy-improvement strategy. The principle of the proposed strategy is to refresh the DoE and the Kriging model with the point that has the largest improvement with regard to the accuracy of the Kriging model. To do this, an upper bound error of the Kriging-based estimate of the failure probability is treated as the accuracy measure of the Kriging model. The expectation that quantifies how much a untried point could enhance the accuracy of the Kriging model is derived. Then, the best next point is defined as the maximum point of the expectation. To search for it within acceptable time, the domain of integration of the accuracy measure of the Kriging model is limit to the region U < [U] (this study sets [U] = 2), conditional points generating with the MCMC algorithm are used to approximately compute the accuracy measure and at the same time act as the candidates of the best next point, and Gauss–Hermite quadrature is employed to compute the expectation mentioned above. A SRA method is constructed mainly based on the stepwise accuracy-improvement strategy. According to the comparisons between it and several learning function-based methods, the advantage of the SRA method and the stepwise accuracy-improvement strategy proposed by this study is demonstrated.

In addition, the idea of the stepwise accuracy-improvement strategy, i.e. deriving how much a tried point could improve a given Kriging model with regard to an accuracy measure, defining the best next point and searching for it, is also available to develop Kriging-based time-variant reliability method.

Acknowledgments

The study was funded by National Science and Technology Major Project of China (Grant No. 2013ZX04011–011) and the National Natural Science Foundation of China (Grant NO. 51775097). Their financial supports are gratefully acknowledged.