1 Introduction

Computer-aided optimal structural design procedures can explore a large set of designs much faster than a classical design process. Numerical structural optimization is thus popular in design processes in for example automotive and aeroplane industries (Zhu et al. 2016). However, these applications often consider continuous design variables, and the methods are not directly applicable to design problems with discrete design variables. The aim of this paper is to propose a heuristic and a method to solve optimal design problems with several discrete design variables per part and to illustrate their capabilities on industrially relevant design problems.

Optimal design of structures is often focused on minimizing mass by allowing large design freedom by continuous design variables. In practice the cost benefit is often larger if the structural components can be picked from a catalogue instead of being tailor-made Chang and Wysk (1997). One such example is the offshore wind turbine support structure. In one wind farm, there can be several hundred structures with a steel mass of more than a thousand tons each. To avoid high manufacturing costs, it is important that these designs are mass-manufacturable. This can be achieved for example by assembling mass-manufactured parts which are available in product catalogues.

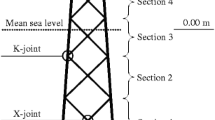
The specific example which illustrates the modelling and is the basis for the numerical experiments is design of a jacket support structure, as illustrated in Fig. 1. The jacket structure under consideration is a four-legged space frame structure welded together from steel pipes in X- and K-joints. Here the tubular members are considered as parts, and the outer diameter and wall thickness are the two variables associated with each part. The number of degrees of freedom in the analysis model can be kept reasonable low since Timoschenko beam elements can be used for the structural analysis. The main issue in optimization is the size of the catalogues from which the dimensions of the parts should be chosen. These catalogues are in general rather large for the considered application. This difficult situation can partly be resolved by adding constraints on the geometric variation of the structure. Examples of such geometric constraints include that dimensions in braces must be smaller than dimensions in legs, and the diameter to thickness ratio is also limited.

Fig. 1
figure 1

The jacket support structure. To the left is a jacket support structure for an offshore wind turbine at 50 m water depth. To the right are close-ups of welded X- and K-joints. The figure is made in the in-house software JADOP

Full size image

Numerical structural optimization of frames is an extension of truss optimization, and many of the same methods and challenges are encountered. The mathematical properties of truss optimization with discrete design variables are discussed in Yates et al. (1982), and the complexity of finding an optimal solution is emphasized. The segmental method presented in Templeman and Yates (1983) avoids the combinatorial problem, but also gives no guarantee for a global optimal solution. Structural optimization with continuous design variables has seen a variety of applications. Optimization of truss structures with continuous design variables as well as joint position variables is applied to practical problems in Svanberg (1981) and Pedersen and Nielsen (2003). Minimum mass of a frame is presented in (Pedersen and Jørgensen 1984), where Euler-Bernoulli and Timoshenko elements are shown to yield different solutions for non-slender beams. Emphasis on joint modelling and optimization in frame structures is given in Cameron et al. (2000) and Fredricson et al. (2003). Optimal design of frame structures for crash-worthiness in transient analysis is given in Pedersen (2004). Using the solution to the continuous problem to find an optimal design in discrete variables, however, is certainly not easy Templeman (1988). The review article Arora and Wang (2005) discusses problem formulations for structural optimization problems and emphasizes that while most formulations are focused on the truss element, they need to be extended to other complex structures.

Optimal design of support structures for offshore wind turbines is a non trivial task Muskulus and Schafhirt (2014). This is mainly due to the the advanced simulations required to obtain the structural response. Specialized aero-servo-elastic software are necessary to obtain accurate results, and these do not yet provide analytical design sensitivities. Several approaches to support structural design optimization are therefore based on gradient-free methods, using the specialized analysis software tools as black boxes as in Zwick et al. (2012). A ground structure approach with frame elements was used in Martens et al. (2015) to perform topology optimization of a jacket with a genetic algorithm. A genetic algorithm was also used in (Pasamontes et al. 2014) for combined joint-location and sizing optimization of a jacket. It is argued that this method can also be used for discrete dimensions, but this is not demonstrated. Improvements to Pasamontes et al. (2014) are presented in Schafhirt et al. (2014), but without the joint location variables. Another approach is to use simplified function evaluations, for example by assuming the rotor loads to be design independent, so that a regular finite element analysis can be used to compute the structural response. An offshore jacket sizing tool using simplified loads and limit states is developed at NREL and described in Damiani et al. (2017) and Damiani (2016). Design of a jacket structure with gradient based optimization was performed in Oest et al. (2017) and Chew et al. (2016) with quasi-static and dynamic analysis, respectively. Constraints were placed on the natural frequencies, ultimate stresses, and fatigue in the welded joints.

Fatigue in the welded joints is considered the most important design constraint for the jacket structure for offshore wind turbines. Due to the cyclic nature of the loading from the rotor, fatigue limit state is more often the design driver than ultimate limit states. Welded joints are the most critical locations, as stress concentrations in the weld significantly impact the fatigue performance. A method for fatigue stress evaluation in welded joints, called the hot spot method, is given in the recommended practice DNVGL (2014). Only axial stresses are assumed to be contributing, and the fatigue is computed for eight evenly spaced locations, or hot spots, along the perimeter of the pipe. A design dependent stress concentration factor (SCF) is multiplied with the stress prior to the fatigue computation. The SCF factors for these structures are in the range 1-6. A geometric validity range is given for the hot spot method, as explained in Remark 2.

In some situations, structural optimization problems with discrete design variables can be reformulated as mixed 0-1 linear or convex quadratic problems. These reformulation techniques are especially well-developed for truss and frame structures, see e.g. Stolpe and Svanberg (2003), Stolpe (2007), Faustino et al. (2006), and Mela (2014). Many type of structural requirements fit into this modelling approach, including limits on stresses, displacements, mass, etc. The main advantage is that the problems can be solved to global optimization using e.g. branch-and-cut methods. These reformulation techniques are however not always possible. This is for example the case when the problem includes limits on eigenfrequencies or if the the nonlinearities coupling the discrete design- and the continuous state-variables are too complicated. In these situations it is therefore necessary to resort to methods and heuristics for mixed 0-1 nonlinear optimization. This field is covered in e.g. the review articles Arora et al. (1994) and Grossmann (2002).

One possible method for mixed integer nonlinear optimization is Outer Approximation (OA) which was introduce in Duran and Grossmann (1986) for problems which are linear in the integer variables. Outer approximation is further developed and analyzed in Fletcher and Leyffer (1994) for problems with nonlinearities in the integer variables. Outer approximation techniques have been used for applications in structural optimization. Two- and three-dimensional truss topology optimization problems with discrete variables are solved to global optimality by outer approximation in Stolpe (2014). The objective function was mass of the truss while the constraints limited the compliances under several load cases. The design variable were discrete and indicated choices of cross-section areas from catalogues. Outer approximation was also used to solve minimum compliance truss topology optimization problems in Muñoz and Stolpe (2011).

Outer approximation is chosen for optimal design of offshore support structures for several reasons. First, it is relatively easy to implement on top of a software which is capable of performing structural optimization with continuous design variables and which is capable of computing analytical design sensitivities. Second, outer approximation generates a sequence of designs which satisfies the linear constraints and which are taken from the catalogue of values. This implies that the nonlinear functions are only called when the structure satisfies necessary requirements (e.g. from standards and recommended practices) to be well-defined. Thirdly, outer approximation solves a sequence of mixed 0-1 linear problems and therefore generates a sequence of designs that satisfy the requirements that the design variables should be from catalogues. Although these sub-problems are difficult to solve in general there are robust and in practice often efficient global optimization methods and heuristics implemented with parallel computation capabilities allowing for problems of industrially relevant size to be solved. Finally, the strong theoretical properties from the convex case suggests that it could behave very well as a heuristic for nonconvex problems.

The overall purpose is proposing mass-manufacturable designs by structural optimization. The continuous problem is used to find a good starting point for the discrete problem, and then an outer approximation algorithm is used to propose designs in the discrete variables. The presented method is then used to propose designs of an offshore wind turbine jacket based on four different catalogues of available diameters and thicknesses.

This article is organized as follows. The next section presents the general problem formulation and a reformulation which is suitable for numerical optimization. The section additionally presents modelling of the application in optimal design of offshore support structures for wind turbines. Section 4 presents the outer approximation techniques for the optimal design problem and additionally suggests a heuristic technique for finding candidate designs satisfying the requirements on discrete design variables. The following two sections describe the implementation of the algorithms and the numerical experience obtained in designing offshore jacket structures. The article ends in Section 7 with conclusions and a list of future possible generalizations.

2 Problem formulations

The problem formulations are classical in structural optimization in the sense that the structural analysis is based on the assumptions of linear elasticity coupled with the finite element method applied to frame structures. The objective and constraint functions model limitations on mass (or cost), local stresses, and fundamental eigenfrequencies. For problems with continuous design variables, these classes of problems are well-studied and the literature is rich, ranging from fundamental mathematical theory to industrial applications, see e.g. the textbooks Bendsøe and Sigmund (2003) and Christensen and Klarbring (2008). The situation that the design variables are associated with dimensions of parts and that several discrete design variables are associated with the parts is however much less studied. The design parametrization imposes enormous challenges on the optimization algorithms but do also provide possibilities of advanced modelling and more realistic optimized design approaches with regards to the industrial requirements.

2.1 Design parametrization

In the design parametrization the design variable vectors \(\mathbf {v}_{i} \in \mathbb {R}^{n_{i}}\), related to part (member or module) i of the structure, have the form

$$\mathbf{v}_{i} = \left( \begin{array}{lllllllllllll} v_{i,1} & {\cdots} & v_{i,{n_{i}}} \end{array}\right)^{T} $$

where n i is the number of design variables related to member i. The elements of \(\mathbf {v}_{i} \in \mathbb {R}^{n_{i}}\) are to be chosen from catalogues of values, i.e.

$$v_{i,j} \in W_{j} = \{ {w_{j}^{1}}, \ldots, w_{j}^{m_{j}} \}, \quad \text{for} \; j = 1,\dots,n_{i}. $$

For simplicity it is assumed that W j ≠ ∅ and that the values in the sets W j are unique and ordered, i.e.

$$0 < {w_{j}^{1}} < {w_{j}^{1}} < {\cdots} < w_{j}^{m_{j}} < +\infty \text{ for all } j. $$

The member design variables are collected into the (structural) design variable vector \(\mathbf {v}\in \mathbb {R}^{N}\)

$$\mathbf{v} = \left( \begin{array}{lllllllllllll} \mathbf{v}_{1}^{T} & {\cdots} & \mathbf{v}_{n}^{T} \end{array}\right)^{T} $$

where n is the total number of parts considered in the optimal design problem and the total number of variables

$$N=\sum\limits_{i = 1}^{n}n_{i}. $$

It is also assumed that the catalogues are the same for all parts and that the number of design variables per part is also the same. These situations can of course be generalized, but will complicate both the notation and the presentation.

Remark 1

The application presented is sizing optimization of jacket support structures for offshore wind turbines, see Fig. 1. The wall thickness of the members in part i in the jacket design example is given by t i and the outer diameter is given by d i . Associated with each part is the variable vector

$$\mathbf{v}_{i} = \left( \begin{array}{lllllllllllll} t_{i} \cr d_{i} \end{array}\right) \in \mathbb{R}^{2}. $$

We assume that the variables must be chosen from a finite set of catalogues of available values, i.e.

$$t_{i} \in \{ t^{1}, t^{2}, \ldots,t^{m_{1}}\} $$

and

$$d_{i} \in \{ d^{1},d^{2},\ldots,d^{m_{2}} \} $$

for all i = 1,…, n. Identification thus gives that

$$W_{1} = \{ t^{1}, t^{2}, \ldots,t^{m_{1}} \},\;\; \text{and}\;\; W_{2} = \{ d^{1},d^{2},\ldots,d^{m_{2}} \} $$

for the considered application.

2.2 Structural analysis

The structural analysis is herein done by the finite element method (see e.g. Cook et al. 2007). In the application Timoschenko beam elements are used. Other analysis methods (or finite elements) are of course possible if they comply with the format described below. The section outlines the structural analysis used in the numerical experiments but other, more advanced, models could also be used.

2.2.1 Static and dynamic analysis

The stiffness K(v) and mass M(v) matrices for the structure described by the design variables v are assumed to be in the formFootnote 1

$$ \mathbf{K}(\mathbf{v}) = \mathbf{K}_{0} + \sum\limits_{i = 1}^{n} \mathbf{K}_{i}(\mathbf{v}_{i}) $$

and

$$ \mathbf{M}(\mathbf{v}) = \mathbf{M}_{0} + \sum\limits_{i = 1}^{n} \mathbf{M}_{i}(\mathbf{v}_{i}) $$

where \(\mathbf {K}_{0} = \mathbf {K}_{0}^{T} \in \mathbb {R}^{d \times d}\) and \(\mathbf {M}_{0} = \mathbf {M}_{0}^{T} \in \mathbb {R}^{d \times d}\) are given positive semidefinte matrices (possibly equal to the zero matrix) that do not depend on the design variables, and d is the number of non-fixed degrees of freedom. Each of the \(\mathbf {K}_{i}(\mathbf {v}_{i}) \in \mathbb {R}^{d \times d}\) and \(\mathbf {M}_{i}(\mathbf {v}_{i}) \in \mathbb {R}^{d \times d}\) are in turn (and for a fixed variable vector) assembled by the element stiffness and mass matrices for the finite elements belonging to the part. The matrices K i (v i ) and M i (v i ) are all assumed to be both symmetric and positive semidefinite for given values on the design variables which are within the bound constraints. It is throughout assumed that the sensitivity analysis of mass and stiffness matrices can be provided, i.e. that

$$\frac{\partial \mathbf{K}(\mathbf{v})}{\partial v_{i,j}}, \frac{\partial \mathbf{M}(\mathbf{v})}{\partial v_{i,j}} $$

can be stated analytically and efficiently computed. This assumption is certainly satisfied for the application presented in Remark 1 if the finite element model is based on Timoschenko beam elements. It is additionally assumed that the matrix values functions K(v) and M(v) are at least continuously differentiable.

The nodal displacements u l satisfy the equilibrium equations

$$\mathbf{K}(\mathbf{v}) \mathbf{u}_{l} - \mathbf{f}_{l} = \mathbf{0}, \text{ for } l = 1,\ldots,L $$

where f l is some static external load and L is the number of loads.

Limits on natural eigenfrequencies are modelled through inequality constraints in the form

$$\lambda_{k}^{\min} \leq \lambda_{k}(\mathbf{K}(\mathbf{v}),\mathbf{M}(\mathbf{v})) \leq \lambda_{k}^{\max} $$

where λ k is the k th lowest natural eigenvalue of the structure described by the design variables. The eigenfrequency ω k in Hz is found from the eigenvalue λ k

$$\omega_{k} = \frac{\sqrt{\lambda_{k}}}{2\pi}. $$

The eigenvalues satisfy the the generalized eigenvalue problem

$$\mathbf{K}(\mathbf{v}) \mathbf{z}_{k} = \lambda_{k} \mathbf{M}(\mathbf{v}) \mathbf{z}_{k} $$

where \(\mathbf {z}_{k} \in \mathbb {R}^{d}\) is the k th eigenvector. It is assumed that the fundamental eigenvalue is unique. In the case of multiple eigenvalues, the treatment is more complex, as described in e.g. Seyranian et al. (1994).

The above mentioned assumptions are sufficient to ensure that it is possible to compute sensitivities of static displacements, compliance, local stresses, eigenfrequencies, and eigenmodes.

2.2.2 Cost and mass

The cost and the mass of the structure are assumed to have forms similar to those of the stiffness and mass matrices, i.e. the cost is given by

$$c(\mathbf{v}) = c_{0} + \sum\limits_{i = 1}^{n} c_{i}(\mathbf{v}_{i}) $$

while the mass is given by

$$m(\mathbf{v}) = m_{0} + \sum\limits_{i = 1}^{n} m_{i}(\mathbf{v}_{i}) $$

where c i (v i ) and m i (v i ) are the cost and mass of the i th part, respectively. Again it is assumed that sensitivity analysis of the mass and cost functions can be computed analytically.

2.3 Problem formulation

Geometrical constraints on the design variables are modelled through the linear constraint b l ≤Av ≤b u , where A is a given matrix and b l , b u are given vectors. Similarly, requirements imposed by limitations in design standards and recommended practices are also assumed to be modelled by linear constraints.

Remark 2

Relevant geometric constraints for the jacket sizing problem mentioned in Remark 1 are the SCF-validity ranges DNVGL (2014). For a joint where a brace member, b, is welded onto a leg member, l, the dimensions should satisfy the linear inequalities

$$\begin{array}{@{}rcl@{}} \frac{d_{l}}{5}&\leq& d_{b}\leq d_{l} \\ \frac{t_{l}}{5}&\leq& t_{b}\leq t_{l} , \end{array} $$

and that for all parts, the following should hold

$$\begin{array}{@{}rcl@{}} 16 t_{i} & \leq& d_{i} \leq 64 t_{i}, \quad i = 1,...,n. \end{array} $$

The considered structural optimization problem is

figure a

where f(v) is the objective function (such as mass or cost), and g(v) contains the functions defining the nonlinear constraints (e.g. stiffness and strength requirements). It is throughout assumed that these functions are at least continuously differentiable. This assumption is satisfied for the structural models outlined above. The lower and upper bounds on the nonlinear constraints are defined by the given vectors l and u of appropriate dimensions, respectively. If l i = u i for some i then the i th constraint is viewed as an equality constraint. The situation that the inequality constraints are one-sided (i.e. either l i = −∞ or u i = + ∞) is also allowed.

With the assumptions stated on the catalogues W j problem (P) becomes a sizing problem, i.e. no parts are allowed to vanish from the structure. This restriction has some positive side-effects. First of all, the stiffness and mass matrices are positive definite for all designs suggested by the algorithm. Secondly, modelling of e.g. stress constraints is simplified compared to the situation that the topology is allowed to change. For sizing problems, stress constraints are no longer design-dependentFootnote 2Achtziger and Kanzow (2008) and issues with the so-called singularity problem, see e.g. Rozvany (1996) and Rozvany (2001), are thus avoided.

Note that (P) can, after reformulation, be classified as a mixed integer nonlinear program. The natural continuous relaxation of (P) is obtained if the discrete variables are replaced by continuous variables with lower and upper bounds, i.e. the problem

figure b

Both the discrete problem (P) and the continuous relaxation (R) are in general non-convex. Additionally, both problems can be infeasible if the technical requirements are too stringent.

3 Problem reformulations

There are several possibilities to reformulate problem (P) to a form which is acceptable for modern optimization methods and heuristics. The first step is to model the problem with binary variables. This can be achieved in more than one way. We focus on only one of the possible reformulations. The reformulation technique is chosen to keep the number of binary variables relatively low, for its ease in implementation, and since we anticipate to be able to solveFootnote 3 the continuous relaxation (R). We first introduce the binary variables x i j k ∈{0,1} with the interpretation

$$x_{ijk} = \left\{ \begin{array}{ll} 1 & \text{if value}\, k\, \text{is chosen from}\, W_{j}\, \text{for part}\, i, \\ 0 & \text{otherwise.} \end{array} \right. $$

This definition of the new variables together with the generalized upper bound constraints

$$\sum\limits_{k} x_{ijk} = 1 \text{ for all } (i,j) $$

ensure that exactly one of the catalogue values are chosen for each part and design variable. The design variables vi, j can thus be replaced by the linear expression

$$v_{i,j}(\mathbf{x}) = \sum\limits_{k} x_{ijk} {w_{j}^{k}} \text{ for all } (i,j). $$

In short, we write

$$\mathbf{v}(\mathbf{x}) = \mathbf{V} \mathbf{x} $$

for some appropriately chosen matrix V. Note that the introduction of the binary variables x i j k ”absorb” many of the nonlinearities that potentially exist in the functions c(v), m(v), K(v), and M(v).

The set X is introduced to model the linear constraints and the 0-1 requirements on the variables, i.e.

$$\begin{array}{lcl} X = \displaystyle \{ \mathbf{x} \in \{ 0,1 \}^{J} \; & \displaystyle | & \displaystyle \; \sum\limits_{k} x_{ijk} = 1, \; \forall \; (i,j), \\ & \displaystyle & \displaystyle \; \mathbf{b}_{l} \leq \mathbf{A} \mathbf{V} \mathbf{x} \leq \mathbf{b}_{u} \} \end{array} $$

where J is the total number of 0-1 variables.

Problem (P) is equivalent to the mixed 0-1 nonlinear problem

figure c

Note that the objective function and the displacements constraints in (P x ) are in general nonlinear functions in the binary variables x and that (P x ) in general is a 0-1 non-convex problem. The continuous relaxation of (P x ) has both more variables and more constraints compared to (R) and therefore (R) is favoured in the implementation and numerical experiments.

4 Outer approximation method

For pure nonlinear 0-1 problems an outer approximation algorithm is similar to sequential linear programming (SLP) (see e.g. Chin and Fletcher 2003) for continuous problems. The sub-problem in outer approximation, from now on called the master problem, is however a mixed 0-1 linear problem. Another difference between SLP and outer approximation is that the approximations of the objective and constraint functions generated at each iteration are saved in outer approximation.

The master problem in a basic outer approximation algorithm applied to (P x ) becomes

figure d

where the set \(\mathcal {T}^{l}\) contains the outer approximation iterations for which the found design is feasible with respect to both the linear and the nonlinear constraints, i.e.

$$\mathcal{T}^{l} = \{ k \; | \; k \leq l, \mathbf{l} \leq \mathbf{g}(\mathbf{v}(\mathbf{x}^{k})) \leq \mathbf{u} \}. $$

The set \(\mathcal {S}^{l}\), on the other hand, contains the iterations for which at least one of the nonlinear constraints is violated, i.e.

$$\begin{array}{lcl} \displaystyle \mathcal{S}^{l} = \{ k \; & | & \displaystyle \; k \leq l, g_{i}(\mathbf{v}(\mathbf{x}^{k})) > u_{i} \text{ or } \\ & & \displaystyle g_{i}(\mathbf{v}(\mathbf{x}^{k})) < l_{i} \text{ for some } i \}. \end{array} $$

The two sets \(\mathcal {T}^{l}\) and \(\mathcal {S}^{l}\) are initially empty and then updated at each iteration of the Outer Approximation algorithm depending on the feasibility status of the current iterate xk. The sets \(\mathcal {T}^{l}\) and \(\mathcal {S}^{l}\) are used to define the constraints in the master problem. For iterates that are feasible with respect to the nonlinear constraints both the objective function and the constraint functions are linearized and included in the master problem. For iterates that violate one or more constraints only the nonlinear constraints are linearized and appended to the master problem. The master problem (M x ) can of course be infeasible or unbounded. The considered objective functions, i.e. mass or cost, are bounded from below by zero and (M x ) can correctly be augmented with η ≥ 0. Unboundedness of the objective function is, with this modelling, not an issue.

A standard outer approximationFootnote 4 algorithm for (P x ) takes the form described in Algorithm 1. The algorithm is adopted from Fletcher and Leyffer (1994). Note that since (P x ) is a pure 0–1 problem there is no need for a feasibility problem as is used in the outer approximation methods outlined in e.g. Fletcher and Leyffer (1994).

figure e

If (M x ) is infeasible in Algorithm 1 then one of two possible events occur. Either the upper bound is < + ∞ in which case at least one design feasible to (P x ) has been found, or no feasible point has been found. The latter situation does, due to non-convexity, however not guarantee that (P x ) is infeasible.

Our computational experience shows that the outer approximation method behaves better if it is supplied with a reasonably good starting point which is feasible to the original problem. This point and the optimal solution from the continuous relaxation are used to generate the first set of linear inequalities in the master problem (M x ). We propose a heuristic which is relatively easy to implement and which is based on rounding of the design obtained from the continuous relaxation. Similar rounding heuristics have proven to work well on truss topology optimization problems with discrete design variables in e.g. Achtziger and Stolpe (2007, 2009). The idea is to use the optimal design found by solving the continuous relaxation and then apply rounding to satisfy the linear constraints and the requirements on the 0-1 variables. This is achieved by solving a least-square problem modelled as a mixed 0-1 linear problem. Chances to find feasible designs increase if the design is rounded to values upwards in the catalogues and we therefore introduce a scaling parameter α which is set to a value greater than one. In the implementation α = 1.2.

figure f

Problem (H) in Algorithm 2 does not need to be solved to optimality. Finding a feasible point to (H) is sufficient for the heuristic in Algorithm 2 to be successful. In the implementation problem (H) is modelled as mixed 0-1 linear program and solved to global optimality to within the default tolerances of the solver.

The user provides the catalogues for the design variables, the type of constraints and associated bounds, the matrix and vector defining the geometric constraints, and routines for structural analysis and sensitivity analysis.

A software called JADOP (JAcket Design OPtimization) for solving the considered problems with continuous design variables has been developed at DTU Wind Energy. This software implements both structural analysis and sensitivity analysis required for the applications. JADOP is implemented in Matlab (MathWorks Inc. 2016) and includes interfaces to several modern methods for nonlinear optimization. The continuous relaxation (R) is solved using the open source interior point solver IPOPT version 3.11.8 (Wächter and Biegler 2006), where non-default parameters are listed in Table 1. IPOPT is compiled with the MUMPS library (Amestoy et al. 2001).

Table 1 Parameters and tolerances used when solving the continuous jacket sizing problem by IPOPT
Full size table

5 Implementation

The outer approximation implementation is called YAOAM (Yet Another Outer Approximation Method). This collection of Matlab scripts and functions is the main driver of the optimization process and calls the user supplied analysis and sensitivity analysis routines when required. The outer approximation algorithm and associated heuristics and the finite elements are implemented in Matlab. The most important parameters and tolerances used in the outer approximation method are listed in Table 2. The mixed 0-1 linear programs are solved by the commercial branch-and-cut solvers in IBM ILOG CPLEX (IBM Corporation 2014). The non-differentiable problem (H) is modelled as a mixed 0-1 linear problem and solved by IBM ILOG CPLEX. IBM ILOG CPLEX is assigned 20 threads for all problems. The non default parameters and tolerances used in IBM ILOG CPLEX are listed in Table 3.

Table 2 Parameters and tolerances used in the outer approximation algorithm
Full size table
Table 3 Parameters and tolerances used in IBM ILOG CPLEX
Full size table

6 Numerical results

The outer approximation algorithm is applied to sizing optimization problems of four legged jacket structures for offshore wind turbines as illustrated in Fig. 1. We first apply the rounding procedure form Algorithm 2 and then attempt to solve the discrete problem by the outer approximation method described in Algorithm 1. The optimized design from the discrete problem is compared to the optimized design from the continuous problem for four different catalogue sizes. The problems are solved on a machine with two Intel Xeon E5-2680v2 ten-core CPUs running at 2.8 GHz, with 64 GB memory.

6.1 Structural model

The analysis model consists of jacket, transition piece and tower, modelled as a frame structure. Moreover, the analysis assumes thin-walled tubular elements. A two-noded Timoshenko 3D beam finite element with constant shear correction factor of 0.52 is used throughout the structure Cook et al. (2007). Nodal displacements of element e in load case l is described in the element displacement vector \(\mathbf {u}_{el}\in \mathbb {R}^{12}\). The element rotation matrix \(\mathbf {T}_{e}\in \mathbb {R}^{12\times d}\) maps from global to local coordinates, u e l = T e u l . The axial stress in element e is computed as σ e (v, γ h ) = Eb(v, γ h )u e l , where γ h = (ξ h , η h , ζ h ) is the location in the element expressed in element coordinates and b(v, γ h ) is the strain-displacement vector for axial stress. In fatigue load cases, stress concentration factors are implemented in the strain-displacement vector.

The jacket is meshed with 524 finite elements, and at least six finite elements in each member. The number of elements and unconstrained degrees of freedom in the full structure are 580 and 3087, respectively. The stiffness and mass matrices of the tower and transition piece constitute the main part of the non-zero entries of the constant matrices K0 and M0. The whole structure is modelled as steel with material properties as listed in Table 4.

Table 4 Material properties
Full size table

At the top of the tower is a non-structural mass matrix which includes the masses and inertias of the rotor-nacelle-assembly (RNA). Although the RNA does not contribute with stiffness to the structure, it is necessary to model the mass and inertia in order to get correct natural frequencies. The non-structural mass matrix \(\textbf {M}_{RNA}\in \mathbb {R}^{6\times 6}\) contains only diagonal terms and is included in the constant mass matrix M0. Along the displacement degrees of freedom are the combined mass of the whole RNA, and along the rotation degrees of freedom are the equivalent moments of inertia around the tower top node, I x x , I y y , and I z z . Furthermore, the density of the tower elements is increased with eight percent to account for secondary steel and equipment, which will also influence the frequency. These modelling approaches are adopted from the DTU 10 MW Reference wind turbine report Bak et al. (2013) and the INNWIND.EU Reference jacket report Borstel (2013). The hub heigh, and tower dimensions are taken from Bak et al. (2013), and the RNA properties, and the overall dimensions of the jacket and transition piece are taken from Borstel (2013).

6.2 Load computations and fatigue model

According to Seidel et al. (2016), a weighted sum of tower top damage equivalent loads can be used to estimate the fatigue limit state in a jacket support structure for conceptual design purposes. This methodology is applied here, and a 1 Hz damage equivalent load is computed individually for thrust, overturning moment, and torsion. A standard rainflow counting method, ASTM (2013), is used to count the number of cycles n w i at each load amplitude ΔP w i . This is done for each wind speed w, with probability of occurrence p w . Each damage equivalent load \(P\in \mathbb {R}\) is computed from

$$P=\left( \frac{1}{n_{s}}\sum\limits_{w = 1}^{n_{w}}p_{w} \sum\limits_{i = 1}^{q}n_{wi}{\Delta} P_{wi}^{m}\right)^{\frac{1}{m}}, $$

where m is the slope of the high-cycle SN-curve for tubular steel joints in seawater with cathodic protection from DNVGL (2014), and n s is the number of seconds of the original load time series. The original loads used for the numerical examples are based on the DTU 10 MW reference wind turbine in a turbulent wind field. The simulations are performed with a clamped tower top in the specialized aero-elastic software Flex5 for a sample of wind speeds w in the operational range, 4 : 2 : 24m/s. The time series are 600s long, with a constant time step of 0.02s. The wind speed probability distribution p w represents north sea conditions, as described in Fischer et al. (2010). The 1 Hz harmonic load applied over a lifetime of 20 years accumulates to 630 million cycles, which on the SN-curve corresponds to a stress amplitude of 11.5 MPa. The advantage of using a damage equivalent load, is that an approximated structural response can be obtained from only one static load case. This is at least three orders of magnitudes faster than solving the equations of motions in the time-domain, and gives a good indication of fatigue damage for these types of structures.

6.3 Jacket sizing optimization

The jacket is partitioned into four sections which are stacked on top of each other, see Fig. 2. The design parametrization follows Remark 1, and the geometric constraints follow Remark 2.

Fig. 2
figure 2

Illustration of the design parametrizations used in this article

Full size image

The objective function is the mass of the jacket

$$ f(\mathbf{v})=\rho\sum\limits_{i = 1}^{n} a_{i}(\mathbf{v}_{i})l_{i} $$
(1)

where a i (v i ) and l i are the length and cross sectional area of part i, and ρ is the density of steel, as given in Table 4. Nonlinear constraints include global frequencies and local stresses, with bounds given in Table 5. There are three load cases for modelling the ultimate limit state, and four load cases for modelling the fatigue limit state. All seven load cases are static, and include an applied load at the thrust, overturning moment, and torsion degrees of freedom at the tower top. Ultimate limit state (ULS) stress is constrained in eight locations of each finite element in the design domain for each of the three ULS load cases. Fatigue limit state (FLS) stress is constrained in eight locations of each finite element in the design domain for each of the four FLS load cases. The diameter and thickness of all members are also bounded from below and above, as shown in Table 5.

Table 5 Constraint limits used in the jacket optimization examples
Full size table

The discrete problem was solved for four different catalogue sizes, ranging from small to extra large. The catalogues are defined as

$$W_{1} = \{ 15, 15 + {\Delta} t, \ldots, 80 \} $$

and

$$W_{2} = \{ 600, 600 + {\Delta} d, \ldots, 1400 \}. $$

The small catalogues have diameter and thickness steps of Δd = 100 and Δt = 10 mm, respectively, and the extra large catalogue has steps of only Δd = 10 and Δt = 1 mm, respectively. The upper and lower bound on the diameter and thickness is the same for all catalogues and all members. The characteristics of the problem is given in Table 6.

Table 6 Optimal design problem characteristics
Full size table

6.4 Results and discussion

Figure 3 illustrates how the optimized designs from the discrete problem (P x ) compares with the optimized design from the continuous problem (R). From a visual inspection of this particular example, it seems that the solution to the discrete problem approaches the solution to the continuous problem when the catalogue size increases. Since the computational cost increases rapidly with larger catalogue sizes, it is not possible to check whether there is an actual convergence when the catalogue size goes to infinity. The similarity between the two results can also in part be caused by the fact that the optimal design from the continuous problem is chosen as the initial design for the discrete problem.

Fig. 3
figure 3

Optimized cross section areas from the discrete problems compared with the optimized cross sections from the continuous problem (dashed)

Full size image

Table 7 summarises the statistics of the four discrete jacket sizing problems, and compares the optimized masses with the one from the continuous problem. All problems successfully met the tolerances placed on the relative optimality gap in the outer approximation algorithm. As expected, a problem instance with a larger catalogue size gives lower mass than a small one. Actually, the designs found to the discrete problems (P x ) seem to approach the design found from the continuous problem (R) when the catalogue size becomes sufficiently large.

Table 7 Convergence study on catalogue size using the Outer Approximation method
Full size table

The interior point method used to solve the continuous relaxation requires 57 iterations and 63 objective and constraint function evaluations. The number of objective gradient and constraint Jacobian evaluations is 58. The outer approximation method on top of that requires as many function and gradient evaluations as iterations. The computation time for solving the mixed 0-1 linear problem (H) is very modest. The main bulk of computation time is instead spent in solving the mixed 0-1 linear programs (M x ), i.e. the outer approximation master problems. Partly this is because of the large number of constraints which additionally increases with the number of iterations and partly because of the problem class and the requirement to solve the problem to global optimality. The latter requirement can in fact be relaxed since the branch-and-cut methods provide correct lower bounds on the objective function value. This value could replace the optimal value and the optimality tolerances could be increased substantially leading to much less computational efforts for the master problems.

The numbers of outer approximation iterations reported in Table 7 are remarkably low. This is due to several reasons. First, the objective function value from the continuous relaxation is not too far away from the final objective value found by outer approximation. Second, the heuristic outline in Algorithm 2 finds designs which are feasible for all problem instances. Finally, the problem instances have many more local constraints than design variables which generates many linearizations and hence convergence is promoted.

6.5 Benchmark with a genetic algorithm

The considered structural optimization problem (P) was also solved with the genetic algorithm (GA) implemented in the Matlab Global Optimization Toolbox version 3.4 (MathWorks Inc. 2016). Default settings were used, such that the population size was 200, the crossover fraction was 0.8, and the elite count was 10. For each catalogue size, the genetic algorithm was run with 30 different seeds. Figure 4 compares the performance of the genetic algorithm with YAOAM, and Table 8 shows the performance statistics of the genetic algorithm. YAOAM consistently performs better than the average genetic algorithm seed, although for the smallest catalogue size the difference is rather small. The genetic algorithm is able to find good feasible designs, but at a higher computational cost. For catalogue sizes medium and larger, the GA solver requires two to three orders of magnitude more CPU time, and four orders of magnitude more function evaluations to find designs that can compete with those from YAOAM.

Fig. 4
figure 4

Comparison of the performance of YAOAM with the genetic algorithm implemented in the Matlab Global Optimization Toolbox (MathWorks Inc. 2016)

Full size image
Table 8 Performance statistics for the genetic algorithm
Full size table

7 Conclusions and future work

A method for structural optimization with multiple discrete variables per part has been presented and demonstrated. The initial feasible point is found by a rounding procedure of the solution to a related continuous problem, and an outer approximation algorithm is used to propose improved designs for the discrete problem.

As industrial design often is based on a discrete catalogue of products, the presented method can improve the way structural optimization is used in practice. An application for sizing optimization of the tubular members in an offshore wind turbine jacket support structure is presented. When the catalogue size is large, the solution to the discrete problem closely resembles the solution to the continuous problem, and good results are found for smaller catalogue sizes as well.

Future work includes extension of the modelling and the methods to include transient analysis to better capture fatigue. This leads to much more expensive analysis and sensitivity analysis and problems with very many constraints. If the observation from the outer approximation approach from this manuscript is still valid then these problems will also require just a handful of iterations which is favourable.

The computational time of outer approximation can potentially be reduced if the number of constraints in the master problems could be decreased. Introducing an elaborate working-set approach could prove advantageous for the practical performance of the algorithm. However, the very efficient pre-processing routines which are included in modern software for mixed 0-1 linear problems prove very efficient in reducing the problem size and the effects of an working-set approach might therefore be limited. An alternative to reduce the computational time in outer approximation is to relax the requirement that the master problem is solved to global optimality and use the lower bound estimates by the solver rather then the optimal objective function value. This can be achieved by relaxing the optimality tolerances in the branch-and-cut solvers. Care must be taken to ensure that this approach generates sequences of improving upper and lower bounds. This approach will without any doubt increase the number of outer approximation iterations but likely reduce the computational time per master problem drastically.