1 Introduction

Wind energy is a rapidly growing source of energy. The energy is both clean and sustainable. The advances in wind energy research and development are still driving down the cost of energy significantly. If wind farms are situated at high wind condition sites, the cost of energy can be competitive or even better than conventional energy sources.

High wind condition sites are often located at near-coastal or offshore areas. Near-coastal areas are occupied and limited, while installing offshore wind turbines presents not only high wind conditions, but also space for very large wind farms. However, it will also lead to more expensive installation and electric infrastructure. Moreover, it will result in larger support structures due to increased water depth, and harsh hydrodynamic and aeroelastic loading.

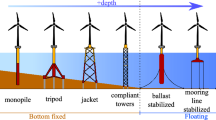
Today, the dominating type of support structure for offshore wind turbines is the monopile. Monopiles are relatively easy to install and the production price is low. When advancing to deeper waters, frame structures are considered better than the monopile design with respect to both cost and structural efficiency. Recent discoveries have also shed light on many problematic issues with monopiles. To name a few, these are buckling of the pile tip, grout connection failure, and water ingress spots leading to corrosion. Consequently, many developers are looking into frame support structures for deep water sites.

Two types of frame structures are generally considered for offshore wind turbines; the tripod with three legs and the jacket with four legs. Both types of support structures are extensively used in the oil and gas industry. As a result, much experience and know-how exist for the design and production of frame support structures. However, support structures for offshore wind turbines experience a much more dynamic loading history, which may mean that some of the design driving criteria are completely different.

The design of offshore support structures is a complex and time-consuming task. Even more so, as final designs need to be validated using many extremely large Design Load Cases (DLC), representing both the Fatigue Limit State (FLS) and Ultimate Limit State (ULS). By utilizing modern optimization techniques in the early design phase, the design engineers can achieve a good preliminary structural design, which has been through many numerical design iterations. Thus, in the context of structural design of offshore support structures, it can prove very beneficial to have reliable and efficient numerical optimization models. Although there is an apparent advantage of such a design tool, optimization of support structures for offshore wind turbines is a relatively new field of study due to the large scale of the load series.

Some of the earlier work in optimization of support structures for wind turbines was done by Uys et al. (2007). They optimized an onshore monopile subjected to several buckling constraints by varying the average thickness of the shells, the amount of ring-stiffeners, and the dimensions of the ring-stiffeners using a zeroth order search algorithm. Thiry et al. (2011) used a genetic algorithm to optimize an offshore monopile tower, achieving reduction of mass by increasing the material grade and varying different structural parameters while enforcing both FLS, ULS and frequency constraints. In their fatigue assessment they calculated damage caused by wind and wave loads uncoupled. Separating wind and wave loads on support structures has previously been investigated by Kühn (2001), who showed that it can potentially lead to large and unacceptable errors in the fatigue assessment.

Long et al. (2011) investigated offshore tripods and jackets for ULS conditions. They used the NREL 5 MW reference wind turbine described in Jonkman et al. (2009). In the design loop of the support structures they ensured that buckling and yielding criteria were satisfied while varying the bottom leg distance. They extended their work and considered FLS conditions according to design standards having wall thickness as design parameters, see Long and Moe (2012). Their optimized design for fatigue was heavier than their design for ULS. They furthermore presented some general design guidelines based on indications of the change in structural properties caused by certain design alterations.

The jacket concept was extended by Zwick et al. (2012). Here, the traditional turbine tower was replaced with a full height frame structure. Both FLS and ULS constraints were considered in their analysis, parametric study, and design optimization of member thickness. In their fatigue assessment, which was the design driving criterion, only one time-history load was included. The loads were recalculated in each design iteration which is a very time-consuming process, especially if many time-history loads are included. For this reason, they investigated how to simplify the fatigue loads in Zwick and Muskulus (2015). Utilizing multivariate statistical methods they reduced a set of 21 time-history loads to 3, while only sacrificing a maximum of 6.4 % precision in the fatigue life estimation of their models with tuned regression parameters.

Chew et al. (2015) used a Sequential Quadratic Programming (SQP) optimizer, including both FLS, ULS and frequency constraints in their optimization of the OC4 reference jacket, described in Vorpahl et al. (2011). They applied two time-history loads in their optimization, where the analytical gradients were found using the direct differentiation method. The gradients were compared to both central and forward difference schemes where significant deviations in especially extreme load and fatigue load constraints were observed. Thus, they advised against using finite difference schemes to approximate the gradients. They achieved a reduction of 52 % mass as compared to the original design. Their design was driven by fatigue, but during the optimization, also buckling and compressive constraints based on NORSOK standards were active. For a more comprehensive overview and review of structural optimization of support structures for wind turbines see Muskulus and Schafhirt (2014).

In this framework, the diameter and thickness of the OC4 reference jacket with the NREL 5 MW reference wind turbine is optimized using analytical gradients and a Sequential Linear Programming (SLP) optimizer. FLS, ULS, and frequency constraints based on Det Norske Veritas (DNV) and Eurocode 3 are included. The sensitivities of the fatigue constraints are found using the adjoint method while the ULS and frequency sensitivities are found by direct differentiation. Twelve complete time-history loads are included in the FLS analysis, while one time-history load is included in the ULS analysis. As the computation of the time-history loads is extremely time-consuming, they are not updated throughout the optimization.

The main contribution of this research is to develop and implement an effective method of determining the fatigue gradients for preliminary design of jacket structures for offshore wind turbines. In other words, we present efficient gradient calculations using the adjoint method for problems with few design variables, many constraints, and very large time-history loads. Using the adjoint method is counter intuitive for this kind of problem as the direct differentiation method is generally advised over the adjoint method for problems with fewer design variables than constraints, see e.g. Tortorelli and Michaleris (1994). On the other hand, it has previously been shown that using the adjoint method can be efficient for problems with multiple loads, see e.g. Akgün et al. (2001).

In order to achieve a good representation of the fatigue damage in the structure, a large number of time-history loads should be included in the fatigue analysis and optimization. However, the computational costs of conventional methods for design sensitivity analysis scale very poorly with the amount of time-history loads applied. To address this, an efficient method for determining the fatigue sensitivities has been implemented, where the computational cost is much less sensitive to the amount of included time-history loads.

By utilizing a linearity in the adjoint vector, it will be shown that very few function evaluations are needed in this framework using the adjoint method. This is achieved without the use of aggregation functions such as the p-norm method. Aggregation functions are often used to reduce a large number of constraints, but leads to a loss in accuracy. In addition, it is achieved without using active set strategies, where constraints that are of no or very small importance are neglected. Because the gradients are evaluated efficiently, a relatively large amount of time-history loads can be included in the optimization.

The structure of this paper is as follows. Initially the modeling and simulation setup will be explained. This includes details about loading conditions and modeling assumptions. Next, all constraints and the derivation of frequency and fatigue constraint sensitivities will be presented. Then the optimization problem is described, where details about the optimizer, the convergence filter, and the adaptive move limit strategy are given. Finally the optimization results will be presented and analyzed, ending with a conclusion stating the main outcome.

2 Structure and simulation setup

The OC4 reference jacket is located at the K13 deep water site with a mean sea level of 50 m above the seabed, see Fischer et al. (2010). The K13 deep water site is located in the North Sea off the coast of the Netherlands. The transition between jacket and tower is located 70.15 m above the seabed, where the transition of forces and moments is ensured using a rigid concrete transition piece weighing 666,000 kg.

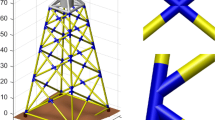
The support structure consists of interconnected circular hollow frames. The members are joined together through 64 welded connections. More specifically, through 24 T/Y-joints, 24 K-joints and 16 X-joints. These joints appear in four very similar sections throughout the full height of the jacket, see Fig. 1. The jacket is fastened to the seabed by a grouted connection to piles penetrated into the seabed. The grouted connection between the piles and the jacket ranges from the seabed to 4.5 m above the seabed.

Fig. 1
figure 1

The OC4 reference jacket

Full size image

The tower and turbine are based on the NREL 5 MW wind turbine, see Jonkman et al. (2009). Thus, the tower is 68 m tall and the hub height is located 90.55 m above mean sea level, see Vorpahl et al. (2011). The NREL 5 MW turbine has a cut-in speed of 3 m/s and a cut-out speed of 25 m/s. The minimum rated rotor speed is 6.9 rpm and the maximum rated rotor speed is 12.1 rpm, which is achieved at wind speeds from 11.4 m/s to cut-out speed. The rotor weighs 110,000 kg, the nacelle 240,000 kg, the tower 347,460 kg, and the jacket 673,718 kg.

2.1 Finite element model

The quasi-static structural analysis is performed using linear finite element theory. The jacket is modeled using 3D beam elements based on Timoshenko beam theory. Each element consists of three nodes. One node at each beam end defines the length of the beam and the local x-axis, and a third node is used to define the orientation in space by defining the local x-y plane. The element has 12 degrees of freedom and constant cross-sectional properties throughout the length, see Fig. 2.

Fig. 2
figure 2

The 3D Timoshenko beam element showing all twelve degrees of freedom and the local x-y-z coordinate system

Full size image

In the FLS and ULS analyses, the jacket is modeled using 104 elements. Each element spans from connection to connection, except near the seabed and near transition piece, where change in geometry demands additional elements. The transition piece is simplified as a very rigid connection using four elements. Each of the four elements are assigned a fourth of the total transition piece weight.

In the frequency analysis, additional elements are added to represent tower, nacelle, and rotor-nacelle assembly. More specifically, eight elements are applied to model the steel tower, and five elements are applied to model the nacelle and hub. The turbine blades are not assigned any elements, but the mass is included in the finite element representation of the hub. Thus, in the frequency analysis, a total of 121 elements are used.

The location and magnitude of the masses are modeled according to Vorpahl et al. (2011). The rotor-nacelle assembly and the nacelle are modelled with a very high rigidity, while the rigidity of the transition piece is tuned to give a lowest natural frequency of the structure of 0.31 Hz, which is in accordance with Jonkman et al. (2012). In the frequency analysis, consistent mass matrices are used.

In the structural analysis, the jacket is assumed fixed at the grouted connection and free elsewhere. Damping and geometric non-linearities are not included. Also, linear elastic material behavior of the S355J2 steel is assumed.

In the current study unit loads have been applied at all degrees of freedom and scaled with wind-, wave- and gravitational loads to efficiently find the structural response for all time-steps by linear superposition. Thus, the inertia and damping effects are ignored in the quasi-static analysis approach. Alternatively, mode superposition could have been applied where the linear response can be calculated from superposition of mode shapes.

2.2 Cost function

The jacket is optimized with respect to member diameter, d, and thickness, t, to decrease the overall mass. Accordingly, the objective function is given as

$$ f(\boldsymbol{x}) = \sum\limits_{j=1}^{n_{e}}\rho_{j} A_{j}({\boldsymbol{x}})l_{j} $$
(1)

Here x is the vector of design variables and n e is the total number of elements. Each frame member is represented using one element with constant cross-sectional properties. ρ j is the material density of element j. In like manner, A j and l j are the cross sectional area and the length of element j, respectively.

The members have been divided into ten symmetry groups. Within each symmetry group, all members are assigned the same design variables. This is done for two main reasons; firstly to produce a symmetric design, and secondly to reduce the amount of different design variables. Thus, the optimization problem is reduced to 20 design variables. The initial design variables are shown in Table 1.

Table 1 Original values of the design variables in meters. Group numbers refer to symmetry groups illustrated in Fig. 3
Full size table

The lower part of the jacket legs connecting with the piles is not included as design variables. Typically, standardized piling equipment is used, and thus the original dimensions remain. Naturally, the beam representation of the transition piece is also omitted from the optimization. For this reason, 100 elements are assigned design variables. The symmetry groups are shown with different colors in Fig. 3, where the gray beams represent the jacket parts excluded from the optimization.

Fig. 3
figure 3

The finite element representation of the jacket. The colored beams represent symmetry groups, wherein the design variables are shared. The gray beams are not optimized

Full size image

2.3 Loading conditions

Many load cases are needed to fully validate support structures for offshore wind turbines. To name some, these could be load cases representing regular power production, extreme weather conditions, emergency shut down, parked and fault conditions, transportation, assembly, maintenance and repair etc. However, in this framework focus is only on two load cases, specifically DLC 1.2 and 1.3, see DNV (2011) and IEC (2005). These are normally considered the governing design load cases for the support structure. The load cases represent normal operational conditions for FLS and ULS, respectively.

According to common practice the aeroelastic loads are determined using multibody simulation software. In this framework, HAWC2 (Horizontal Axis Wind turbine simulation Code 2nd generation) has been used, see DTU Wind Energy (2016). The jacket and turbine used in the multibody simulation are also based on the OC4 reference jacket and the NREL 5 MW turbine. The forces and moments have been extracted at the transition piece, such that they can be applied directly to the finite element model.

The hydrodynamic loading is calculated using the Morison equation, see Morison et al. (1950). The wave force per unit length, f w , is given by

$$ \begin{array}{ll} f_{w} = & \,\, \rho_{w} C_{m}A(\dot{u}-\ddot{X})+\rho_{w} \dot{u}A \\ & +\frac{1}{2}\rho_{w} C_{d}\left( (u+u_{c})-\dot{X} \right) \left|(u+u_{c})-\dot{X}\right| \\ \end{array} $$
(2)

Here ρ w =1025 kg/m 3 is the density of seawater, A is the effective cross sectional area of the beam, which for a circular tube equals the outer diameter when computing the force per length. C d and C m are the drag and inertia coefficients, respectively. u and \(\dot {u}\) are the horizontal particle velocity and acceleration and u c is the wave-current velocity. The member velocity, \(\dot {X}\), and acceleration, \(\ddot {X}\), are set to zero as the structural analysis is static. The wave forces are calculated for vertical members and then projected onto oblique members. The hydrodynamic loading is calculated in 15 sampling depths. Buoyancy forces on oblique members are disregarded in the analysis.

While the wind loads are easily added to the beam representation of the transition piece, the hydrodynamic loads have to be recalculated into nodal loads. This is done in three steps; first, the loads are linearly interpolated from the nearest sampling depths to the nodal positions of the submerged element. Secondly the loads are recalculated into normal loads, and lastly work-equivalent nodal loads are established, see e.g. Cook et al. (2002).

DLC 1.2 is used for fatigue calculations, where the loads correspond to normal operation under normal sea states and atmospheric turbulence. The multibody simulations have been performed using a normal turbulence model, where the turbulence intensity and the standard deviation have been calculated in accordance with IEC (2005) and IEC (2009). According to IEC (2009), the random realizations for the wave loads in both FLS and ULS are based on the Joint North Sea Wave Observation Project (JONSWAP) spectrum, see Hasselmann et al. (1973). According to IEC (2005), multidirectional waves should be considered. However, in this framework all environmental loads are applied aligned and acting from a constant angle.

DLC 1.3 is used for ultimate limit state calculations, where the loads correspond to normal operation under normal sea states and extreme turbulence conditions. Thus, in the multibody simulation, an extreme turbulence model is used. In addition, a normal current model is added to the wave loads according to IEC (2009). Due to both structural and load modeling uncertainties, a partial safety factor of 1.35 is applied to all environmental loads in this framework.

The standards suggest to produce time-history loads in samplings from cut-in to cut-out speed, i.e. from a mean wind speed of 3 m/s to 25 m/s. This should be done in intervals of 2 m/s with a total sampling time of 10 minutes in sampling intervals of 0.02 seconds. Moreover, yaw misalignment of ± 8 degrees should also be accounted for, and for each setting, six random realizations should be included. This adds up to 216 time-history loads for each of the two included load cases. As each time-history load consists of 30,000 load time-steps, this results in a total amount of 6,480,000 load time-steps in both the FLS and ULS analysis. This amount of information is currently too much to consider in an optimization loop, thus the amount of time-history loads included must be reduced.

The yaw misalignment is important for blade and nacelle design. However, the support structure may not be affected significantly by the misalignment. For this reason the yaw misalignment is excluded from the analysis. Furthermore, only one random realization is included. Thus, only one 10 minute time-history load for each mean wind speed is used in DLC 1.2, adding up to a total of 12 time-history loads with a total of 360,000 load time-steps. For DLC 1.3, it is believed that the most critical loading of the jacket will occur at the highest wind speed. Again, yaw misalignment is excluded and only one random realization is used. In short, only one time-history load is included for ULS with a total of 30,000 load time-steps.

3 Fatigue limit state analysis

Fatigue failure of welded structures is prone to occur in the welded details. Thus, the fatigue damage must be investigated in every welded connection of the jacket. In fact, the damage should be evaluated in eight equally distributed sampling points in the cross section of the welded detail on both the chord and brace side of the weld, see DNV (2014).

Stresses in welds can be complicated to determine as they can be many times higher than nominal stresses. Mean stresses are difficult to determine due to effects such as residual stresses from the welding procedure where uneven contraction of material during the cooling process can induce very high stresses. Thus, mean effects are not included in the traditional sense when calculating fatigue damage in the welded details. Also, the uneven geometry at a weld gives cause for stress concentrations. For this reason the nominal stresses must be scaled with stress concentration factors (SCF) in order to get a more realistic estimate of the actual stress state in the welds. These upscaled stresses are in the following referred to as σ HotSpot . All fatigue calculations are done according to DNV (2014).

3.1 Hot spot stresses

To calculate the hot spot stress in all eight local sampling points, four stress concentration factors must be determined; the SCF for axial loading at the saddle, S C F A S , for axial loading at the crown, S C F A C , for out-of-plane bending moments, \(SCF_{M_{OP}}\), and for in-plane bending moments, \(SCF_{M_{IP}}\). For definitions of chord, brace, and sampling locations see Fig. 4. The SCF depend explicitly on many geometric parameters, including the design variables of both brace and chord, and the type of connection. In K-connections, the SCF can even depend on the design variables of the neighboring brace. In addition, the SCF differ when evaluating the weld on the brace or chord side. The aforementioned geometric parameters are converted to geometric validity parameters that must lie within certain intervals in order to give trustworthy stress states. These validity parameters are explicit functions of the design variables and are included as constraints in the optimization algorithm. The parameters are defined in Section 4.3.

Fig. 4
figure 4

The location of the eight hot spot stresses calculated from stress concentration factors and the stress caused by the normal load, N, by the in-plane bending moment, M I P , and by the out-of-plane bending moment M O P

Full size image

As SCF can be defined as the ratio between the nominal and maximum stresses, the hot spot stresses are calculated by superposition and scaling of the nominal stresses caused by axial loading, σ N , by in-plane bending moments, \(\sigma _{M_{IP}}\), and by out-of-plane bending moments, \(\sigma _{M_{OP}}\). Thus following DNV (2014), the eight local stresses can be calculated by

$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{1}} &=& SCF_{AC}\sigma_{N} + SCF_{M_{IP}}\sigma_{M_{IP}} \end{array} $$
(3a)
$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{2}} &=& \frac{1}{2}(SCF_{AC}\,+\,SCF_{AS})\sigma_{N}\,+\,\frac{1}{2}\sqrt{2}SCF_{M_{IP}}\sigma_{M_{IP}}\\ &&-\frac{1}{2}\sqrt{2}SCF_{M_{OP}}\sigma_{M_{OP}} \end{array} $$
(3b)
$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{3}} &=& SCF_{AS}\sigma_{N}-SCF_{M_{OP}}\sigma_{M_{OP}} \end{array} $$
(3c)
$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{4}} &=& \frac{1}{2}(SCF_{AC} \,+\, SCF_{AS})\sigma_{N} \,-\, \frac{1}{2}\sqrt{2}SCF_{M_{IP}}\sigma_{M_{IP}} \\ &&- \frac{1}{2}\sqrt{2}SCF_{M_{OP}}\sigma_{M_{OP}} \end{array} $$
(3d)
$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{5}} &=& SCF_{AC}\sigma_{N} - SCF_{M_{IP}}\sigma_{M_{IP}} \end{array} $$
(3e)
$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{6}} &=& \frac{1}{2}(SCF_{AC} \,+\, SCF_{AS})\sigma_{N} \,-\, \frac{1}{2}\sqrt{2}SCF_{M_{IP}}\sigma_{M_{IP}} \\ &&+ \frac{1}{2}\sqrt{2}SCF_{M_{OP}}\sigma_{M_{OP}} \end{array} $$
(3f)
$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{7}} &=& SCF_{AS}\sigma_{N} + SCF_{M_{OP}}\sigma_{_{OP}} \end{array} $$
(3g)
$$\begin{array}{@{}rcl@{}} \sigma_{HotSpot_{8}} &=& \frac{1}{2}(SCF_{AC} \,+\, SCF_{AS})\sigma_{N} \,+\, \frac{1}{2}\sqrt{2}SCF_{M_{IP}}\sigma_{M_{IP}} \\ &&+ \frac{1}{2}\sqrt{2}SCF_{M_{OP}}\sigma_{M_{OP}} \end{array} $$
(3h)

For both \(SCF_{M_{IP}}\) and \(SCF_{M_{OP}}\) in X- and K-joints, the loading condition is assumed as applied on one brace when determining the SCF. This assumption is conservative for each iteration in this framework. A fixed gap between the braces in all K-joints of 0.25 m is assumed. Also, all chords are assumed long and slender and general fixity parameters are chosen, as no investigative tests have been performed on the fixity. A SCF of 3 is applied for fatigue sampling points not in a T/Y-, X- or K-joint in all iterations. This assumptions is made as there are too many unknowns in determining stress concentration factors for the tubular butt welds in the structure, such as the measure of out of roundness, eccentricity of the connection etc.

In the considered model 2688 fatigue sampling points are evaluated. 512 in tubular butt welded connections, 384 in T/Y connections, 1024 in X connections, and 768 in K connections. For the initial design, the SCF values span from 1.05 to 12.15 with a mean of 4.05. For full details on how to calculate the SCF, see DNV (2014).

3.2 Fatigue damage

Fatigue damage is caused by cyclic loading, and the damage is defined as a fraction of the structures overall life. In this framework, the fatigue damage is calculated by relating hot spot stress amplitudes, Δσ HotSpot , with S-N curves. S-N curves relate the number of cycles to expected failure, N i , at a given stress amplitude. The applied S-N curve is valid for circular hollow tubes of S355J2 with cathodic protection submerged in seawater, and is shown in DNV (2014). The equation for the S-N curve is

$$ \log N_{i}=\log\bar{a}-m\log\left( {\Delta}\sigma_{\textit{HotSpot}}{T_{c}^{k}} \right) $$
(4)

Here \(\log \bar {a}\) is the intercept of the \(\log N_{i}\) axis on the S-N curve and m is the negative inverse slope of the curve. Since the log-log S-N curve is piecewise linear, m and \(\bar {a}\) can vary depending on the amount of cycles to failure. k is the thickness exponent having a value of either 0.25 or 0.30, where the higher value is chosen if the applied SCF has a magnitude larger than 10. As a conservative choice, k is set to 0.30 in all fatigue sampling points. T c is a thickness correction term given as:

$$ T_{c} = max\left\{\frac{t}{t_{ref}},1 \right\} $$
(5)

Here t is the thickness of the member under investigation, and t r e f is a reference thickness of 32 mm.

3.3 Rainflow counting

S-N curves are derived from tests where sinusoidal stresses are applied to a specimen. However, the jacket is subjected to a complex, multiaxial, non-proportional loading history. Determining the highest estimated fatigue damage under such loading conditions would normally require multiaxial rainflow counting techniques. However, as the fatigue damage is determined using only the normal stresses, traditional rainflow counting can be applied.

In rainflow counting, the full stress history is reduced to a sequence of peaks and valleys. Next, stress half and full cycles are identified. It is important that rainflow counting is done separately in all fatigue sampling points in order to capture the highest accumulated damage. To indicate this dependence, a subscripted k will be added. For instance, the hot spot stress and displacement amplitudes are indexed as Δσ k i and Δu k i , where k=1,2,...,2688 is the fatigue sampling point number where the counting has been performed. i=1,2,...,N k,R F is the rainflow counter for sampling point k, and N k,R F is the amount of rainflow counts. The displacement amplitude relates to the vector of applied load amplitude, ΔP k i , by subtracting two equilibrium states from each other

$$ {\boldsymbol{K}}{\Delta}{\boldsymbol{u}}_{ki} = {\Delta}{\boldsymbol{P}}_{ki} $$
(6)

In order to efficiently solve for the displacement amplitudes, a direct solver is used where the stiffness matrix has been subjected to LU factorization.

The rainflow counting must be done on the hot spot amplitude stress, as shown in (4). The hot spot amplitude stresses are determined using all 360,000 load time-steps. Damage caused by different mean wind speeds are upscaled differently depending on the probability of occurrence. Consequently, stress amplitudes must not be identified across loads representing different mean wind speeds. Therefore, it is important to perform rainflow counting separately for each mean wind speed, i.e. 30,000 load time-steps at a time. Additionally, due to the multiaxial, non-proportional loading, the amount of rainflows, N k,R F , can vary for each fatigue sampling point. In the established fatigue analysis, the difference in the amount of rainflow counts can easily exceed 10,000 depending on which sampling point is evaluated. The amount of rainflow counts and the positions in time are recalculated in every design iteration for every fatigue evaluation point.

3.4 Accumulated damage

The accumulated damage is calculated by Palmgren Miner’s linear damage hypothesis, given as

$$ D_{k}=\sum\limits_{i=1}^{N_{k,RF}}p_{ki}\frac{n_{ki}}{N_{ki}}\, \leq\, \eta, \qquad k = 1,2,...,2688 $$
(7)

Here D k is the accumulated damage in sampling point k. p k i is a probability factor used to scale the damage to represent the full life time, i.e. 20 years of service. The probability for each mean wind speed is taken from the weather data for the K13 deep water site described in Fischer et al. (2010). The value of the probability factor depends on the mean wind speed currently investigated and the total amount of rainflow counts. n k i is the number of stress cycles, i.e. a half or full cycle, and η is the usage factor. It is assumed that the welds are located at an area that is not planned for inspection or reparation during operation, thus η is set to 1/3 in accordance with DNV (2011).

Isolating the number of cycles to failure for a given stress state in (4) and inserting it into (7) presents the fatigue constraint equation for each damage sampling point, k

$$ D_{k}=\sum\limits_{i=1}^{N_{k,RF}}p_{ki}\frac{n_{ki}}{\bar{a}\left( {\Delta}\sigma_{ki} {T_{c}^{k}} \right)^{-m}}\leq \frac{1}{3} $$
(8)

4 Ultimate limit state analysis

The included ultimate limit state criteria are all based on EN (2005a) and EN (2005b) and are; buckling failure, chord face failure, and punching shear failure.

4.1 Buckling analysis

A buckling analysis is carried out according to EN (2005a). This is done at the element level. All elements except the eight elements used for modeling the transition piece and the grouted connection are included, resulting in buckling analyses of 100 elements. Each individual element, e, under combined bending and axial compression must satisfy the following two constraints

$$\begin{array}{@{}rcl@{}} B_{e} &=& \frac{N_{ED}}{{\chi_{y} N_{RK}}/{\gamma_{M1}}} + k_{yy} \frac{M_{y,ED}}{{\chi_{LT}M_{y,RK}}/{\gamma_{M1}}} \end{array} $$
(9a)
$$\begin{array}{@{}rcl@{}} &&+ k_{yz} \frac{M_{z,ED}}{M_{z,RK}/\gamma_{M1}}\,\leq\, 1, {\kern30pt} e = 1,2,...,100\\ G_{e} &=& \frac{N_{ED}}{{\chi_{z} N_{RK}}/{\gamma_{M1}}} + k_{zy} \frac{M_{y,ED}}{{\chi_{LT}M_{y,RK}}/{\gamma_{M1}}} \end{array} $$
(9b)
$$\begin{array}{@{}rcl@{}} && + k_{zz} \frac{M_{z,ED}}{M_{z,RK}/\gamma_{M1}}\,\leq\, 1, {\kern30pt} e = 1,2,...,100 \end{array} $$

Here N E D , M y,E D and M z,E D are the design compression force and maximum moments about the local y−y and z−z axis, respectively. Similarly, N R K , M y,R K and M z,R K are the design characteristic resistance force and moments of the critical cross section. γ M1 is a partial safety factor for the global stability, where the value of 1.2 is used, see IEC (2005). χ L T is a reduction factor due to lateral torsional buckling. However, as circular hollow beams are not susceptible to lateral torsional buckling, χ L T is set to 1. k y y , k z z , k y z and k z y are the interaction factors. They are calculated using the alternative method 1, shown in Annex A of EN (2005a). Due to the symmetric properties of the circular hollow cross section, k y y = k z z and k y z = k z y . χ y and χ z are reduction factors due to flexural buckling. Again, because of the circular hollow cross section they are equal. The flexural reduction factors are calculated for each member by

$$ \chi_{z}=\chi_{y}=min\left[\frac{1}{\Phi+\sqrt{{\Phi}^{2}-\bar{\lambda}^{2}}},1 \right] $$
(10)
$$ {\Phi}=0.5\left[ 1+\alpha (\bar{\lambda}-0.2)+\bar{\lambda}^{2}\right] $$
(11)

Here α is an imperfection factor, that for a circular hollow cross section using hot finished S355J2 steel is 0.21. The cross section class is restricted to be of class 2 or better in this framework. This is done to reduce the amount of ultimate limit state constraints of the welded connections, as will be explained in detail in the next section. The non-dimensional slenderness, \(\bar {\lambda }\), is for class 1-3 cross sections calculated for each element as

$$ \bar{\lambda} = \sqrt{\frac{Af_{y}}{N_{cr}}} $$
(12)

N c r is the critical Euler force and f y is the material yield strength. The critical Euler force is calculated under the assumption that each member can be viewed as a column with pinned ends. Thus, the lowest critical Euler force is given by (see e.g. Gere and Goodno (2012))

$$ N_{cr} = \frac{\pi^{2}EI}{L^{2}} $$
(13)

Here E is the Young’s modulus of elasticity, I is the area moment of inertia and L is the length of the column considered.

The jacket is also investigated for global buckling. Using a geometric stiffness matrix that includes shear and bending effects, a linear buckling analysis has been performed for all 30,000 load time-steps included in the ULS load case. Including the partial safety factor of 1.35 on the loads and the partial safety factor on the buckling analysis of 1.2, no load combination had a buckling load factor of less than 131. Since the jacket in its original topology is very safe from failure due to global buckling, it is not included in the optimization as a constraint. However, a linear global buckling analysis is performed on the optimized design to insure that this assumption is valid.

4.2 Chord face and punching shear failure analysis

The limit states of the welded connections are also calculated using Eurocode 3, EN (2005b). If the investigated members are of cross sectional class 2 or better, and under certain dimensional restrictions shown in Section 4.3, the connections only need to be checked for chord face failure and punching shear failure. Chord face failure, which can be described as plastic failure of the chord face, is avoided by satisfying the following constraint for all brace member connections, l, that are subjected to combined bending and axial force. There exists 24 brace members in the 24 T/Y-joints, 48 brace members in the 24 K-joints, and 64 brace members in the 16 X-joints. In short, there are 136 chord face failure constraints in the analysis, given by following equation

$$ \begin{array}{ll} C_{l} &= \frac{N_{ED}}{N_{RD}} + \left[\frac{\left|M_{IP,ED}\right|}{M_{IP,RD}} \right]^{2} + \frac{M_{OP,ED}}{M_{OP,RD}} \leq 1, \\ l &= 1,2,...,136 \end{array} $$
(14)

Here, M I P,E D and M O P,E D are the design in-plane and out-of-plane moments, respectively. Accordingly, M I P,R D and M O P,R D are the design value of the resistance of the joint expressed in internal moments, while N R D is the design value of the resistance of the joint expressed in internal axial force. Note that for multiplanar joints reduction factors are included. For full details of the analysis we refer to EN (2005b).

Punching shear failure can be described as crack initiation on the chord wall leading to complete failure. Punching shear failure only needs to be checked if the brace diameter is larger than the inner chord diameter, according to Table 7.2 and 7.5 in EN (2005b). If this is the case, then punching shear failure is checked by

$$\begin{array}{@{}rcl@{}} S_{l} &=& \frac{N_{ED}}{N_{RD_{punch}}} + \left[\frac{\left|M_{IP,ED}\right|}{M_{IP,RD_{punch}}} \right]^{2} + \frac{M_{OP,ED}}{M_{OP,RD_{punch}}} \leq 1, \\ l &=& 1,2,...,136 \end{array} $$
(15)

The differences from the chord face failure analysis to the shear punching analysis are the design values of the resistance of the joints expressed in internal axial force, \(N_{RD_{punch}}\), in in-plane moment, \(M_{IP,RD_{punch}}\), and in out-of-plane moment, \(M_{OP,RD_{punch}}\).

4.3 Validation constraints

For both FLS and ULS analysis, a series of validity parameters must be fulfilled according to the standards and recommended practice, i.e. EN (2005a), EN (2005b), and DNV (2014). The amount of validity parameters depends on the topology of the structure and the design variables. The amount of parameters have been reduced utilizing the enforced symmetric design. The parameters are included as design constraints and are as follows

$$\begin{array}{@{}rcl@{}} 4 &\leq& \alpha_{p} \leq 40, {\kern24pt} \alpha_{p} = \frac{2L_{p}}{D_{p}}, {\kern6.5pt} p = 1,2,...,11 \end{array} $$
(16a)
$$\begin{array}{@{}rcl@{}} 0.2 &\leq& \beta_{p} \leq 1.0, {\kern21pt} \beta_{p} = \frac{d_{p}}{D_{p}}, {\kern11pt} p = 1,2,...,11 \end{array} $$
(16b)
$$\begin{array}{@{}rcl@{}} 0.2 &\leq& {\beta_{r}^{B}} \leq 1.0, {\kern18pt} {\beta_{r}^{B}} = \frac{{d_{r}^{B}}}{D_{r}}, {\kern17pt} r = 1,2,...,9 \end{array} $$
(16c)
$$\begin{array}{@{}rcl@{}} 8 &\leq& \gamma_{s} \leq 25, {\kern28pt} \gamma_{s} = \frac{D_{s}}{2T_{s}}, {\kern15pt} s = 1,2,...,8 \end{array} $$
(16d)
$$\begin{array}{@{}rcl@{}} && \zeta_{t} \leq 1.0, {\kern28pt} \zeta_{t} = \frac{g_{t}}{D_{t}}, {\kern32pt} t = 1,2,3 \end{array} $$
(16e)
$$\begin{array}{@{}rcl@{}} 0.2 &\leq& \tau_{r} \leq 1.0, {\kern26.5pt} \tau_{r} = \frac{t_{r}}{T_{r}}, {\kern19pt} r = 1,2,...,9 \end{array} $$
(16f)
$$\begin{array}{@{}rcl@{}} && \iota_{w} \leq 70\frac{235}{f_{y}},{\kern10pt} \iota_{w} = \frac{d_{w}}{t_{w}}, {\kern10pt} w = 1,2,...,10 \end{array} $$
(16g)

Here d is the brace diameter, d B is the adjacent brace diameter in K-joints, and D is the chord diameter. t is the brace thickness and T is the chord thickness. L is the chord length and g is the distance between the braces in K-joints. Note that the γ-constraint is a combination of DNV (2014) and EN (2005b). The lower bound on the ζ-constraint is not included as it is always fulfilled. The same is true for the angular constraint described in DNV (2014).

The amount of constraints for each validity parameter is determined using the enforced symmetry conditions. For instance, the amount of α-constraints has been determined in the following way. 9 unique chord lengths exist in the welded connections. Of these 9 unique chord lengths, 11 unique chord length to chord diameter relations can exist with the chosen topology and design variables. Thus, 11 α-constraints are needed in total. The ζ-constraint is required in the SCF calculation of K-joints. As can be seen on Fig. 3, 3 levels of K-joints exist. All 4 K-joints in each level are welded to a chord that share design variables, thus the total amount of ζ-constraints is 3. Likewise, the total amount of constraints ensuring a cross section class of minimum 2, the ι-constraint, is 10. This is due to the simple fact, that 10 symmetry groups exist. In a similar manner, the remaining amount of each validity constraint has been found. Thus, only a total of 61 validity constraints are needed to ensure that the entire jacket stays within the allowable validity bounds.

5 Frequency analysis

The natural frequency of the support structure is determined by the finite element formulation of a real, symmetric, structural, eigenvalue problem, see Seyranian et al. (1994).

$$ {\boldsymbol{K}}{\boldsymbol{\phi}}_{j} = \lambda_{j}{\boldsymbol{M}}{\boldsymbol{\phi}}_{j}, \quad {\lambda}_{j}={\omega}^{2}_{j}, \quad j=1,2,... $$
(17)

Here K is the global stiffness matrix, M is the global mass matrix, while λ j and ϕ j represent the eigenvalue and corresponding eigenvector, respectively. ω j is the natural frequency of the structure. Note that all eigenvectors have been M-orthonomalized. Also, the index is in ascending order with j=1 as the lowest frequency.

The support structure is designed to lie within the soft-stiff range, i.e. between the rotor frequency range (1P) and the blade-passing frequency (3P). Since the operational speed can vary, the 1P and 3P frequencies are in fact frequency bands. With a 10 % safety margin the lowest eigenfrequency must be within the frequency range between ω 1P =0.22 Hz and ω 3P =0.31 Hz for the NREL 5 MW reference turbine, see Fischer et al. (2010).

In the original design, two eigenfrequencies are identified within this frequency band, effectively constituting two constraints. In addition, the third and fourth lowest eigenfrequencies are constrained to stay above the upper limit of the 3P frequency band, i.e. above 3⋅ω 1P .

6 Design sensitivity analysis

The derivatives of the objective function and validity range constraints are explicitly dependent on the design variables. Consequently, determining the design sensitivities does not require special techniques and only the sensitivity of the cost function will be shown in this paper for completeness.

The sensitivities of the buckling constraints, chord face failure constraints, and punching shear failure constraints are also independent of the state variables, i.e. the displacements of the jacket, as the loads are assumed independent of the design variables. Thus, the derivation of the ULS constraint sensitivities will not be shown. It must be noted that the ULS calculations include several equations that depend on design variables that are not continuously differentiable, e.g. (10).

To summarize, only the sensitivities of the objective function, the fatigue constraints, and the frequency constraints will be derived.

6.1 Objective function sensitivity

The cost function defined in (1) depends explicitly on the design variables through the cross sectional area of each tubular member. The sensitivity is found by differentiating the equation with respect to the design variable, x v

$$ \frac{df}{dx_{v}} = \sum\limits_{j=1}^{n_{e}} \left( \rho_{j} \frac{dA_{j}}{dx_{v}}L_{j}\right) $$
(18)

6.2 Fatigue constraint sensitivity

The fatigue constraint, (8), is a function of the design variables and the state variables, which is also a function of the design variables. To determine the analytical sensitivities of such implicit functions two traditional approaches can be used, either the direct differentiation method or the adjoint method. In this section, an efficient sensitivity analysis is derived using the adjoint method.

In the adjoint method, the computational demanding expression for the solution of displacement sensitivities is omitted using Lagrange multipliers. This is achieved by using an augmented response function, F. This function is given as

$$ F = \sum\limits_{i=1}^{N_{k,RF}} \left( D_{ki} - {\boldsymbol{\Lambda}}_{ki}^{T}\left( {\boldsymbol{K}}{\Delta}{\boldsymbol{u_{ki}}}-{\Delta}{\boldsymbol{P}}_{ki}\right) \right) $$
(19)

Here Λ k i is a Lagrange multiplier, commonly known as the adjoint vector. In order to obtain the sensitivity, the augmented response function is differentiated with respect to the design variable, x v

$$\begin{array}{@{}rcl@{}} \frac{dF}{dx_{v}} = \sum\limits_{i=1}^{N_{k,RF}} \Bigg(\frac{\partial D_{ki}}{\partial x_{v}}+\left( \frac{\partial D_{ki}}{\partial{\Delta}\boldsymbol{u}_{ki}}\right)^{T} \frac{d{\Delta}\boldsymbol{u}_{ki}}{dx_{v}}\\ &{\kern-13.5pc}- \left( \frac{d{\boldsymbol{\Lambda}}_{ki}}{dx_{v}} \right)^{T} \left( {\boldsymbol{K}}{\Delta}{\boldsymbol{u}}_{ki} -{\Delta} {\boldsymbol{P}}_{ki} \right)\\ &{\kern-10.1pc}-{\boldsymbol{\Lambda}}_{ki}^{T} \bigg(\frac{d{\boldsymbol{K}}}{dx_{v}}{\Delta} {\boldsymbol{u}}_{ki}+{\boldsymbol{K}}\frac{d{\Delta}{\boldsymbol{u}}_{ki}}{dx_{v}}-\frac{d{\Delta}{\boldsymbol{P}}_{ki}}{dx_{v}}\bigg) \Bigg) \end{array} $$
(20)

In the differentiation, it is assumed that the amount of rainflow counts, N k,R F , and the positions in time of the stress cycles, are independent of small design changes. Utilizing the static equilibrium equation, defined in (6), together with the assumption that the loads are fixed, i.e independent of design, and rearranging terms, the following expression for the augmented response function sensitivity is obtained

$$ \begin{array}{ll} \frac{dF}{dx_{v}} = \displaystyle\sum\limits_{i=1}^{N_{k,RF}} \Bigg(&\frac{\partial D_{ki}}{\partial x_{v}} - {\boldsymbol{\Lambda}}_{ki}^{T} \frac{d\boldsymbol{K}}{dx_{v}}{\Delta} \boldsymbol{u}_{ki}\\ &+ \Bigg(\left( \frac{\partial D_{ki}}{\partial{\Delta}{\boldsymbol{u}}_{ki}}\right)^{T} - {\boldsymbol{\Lambda}}_{ki}^{T}{\boldsymbol{K}} \Bigg)\frac{d{\Delta}{\boldsymbol{u}}_{ki}}{dx_{v}} \Bigg) \end{array} $$
(21)

The adjoint vector is chosen such that the displacement sensitivity vanishes. To do this, the adjoint vector is found by solving the adjoint equation, given by

$$ {\boldsymbol{K}}^{T}{\boldsymbol{\Lambda}}_{ki} = \frac{\partial D_{ki}}{\partial{\Delta}{\boldsymbol{u}}_{ki}} $$
(22)

As the global stiffness matrix is symmetric, the LU factorized matrix used when solving for the displacement amplitudes can be reused to efficiently solve the adjoint problem. After determining the adjoint vector, the full derivative of the response function, which equals the fatigue constraint function, can be determined by

$$ \frac{dD_{k}}{dx_{v}} = \frac{dF}{dx_{v}} = {\sum}_{i=1}^{N_{k,RF}} \left( \frac{\partial D_{ki}}{\partial x_{v}} - {\boldsymbol{\Lambda}}_{ki}^{T} \frac{d{\boldsymbol{K}}}{dx_{v}}{\Delta} {\boldsymbol{u}}_{ki}\right) $$
(23)

The adjoint problem shown in (22) must be solved for each fatigue sampling point and for every rainflow count. Thus, the computational demanding part, i.e. solving the adjoint problem, scales with the amount of rainflow counts for the adjoint method. However, the number of adjoint problems to solve can be reduced as described in the following.

Extending the adjoint problem using the chain rule of differentiation gives

$$ {\boldsymbol{K}}{\boldsymbol{\Lambda}}_{ki} = \frac{\partial D_{ki}}{\partial {\Delta}\sigma_{ki}} \frac{\partial {\Delta}\sigma_{ki}}{\partial {\Delta}{\boldsymbol{u}}_{ki}} $$
(24)

Realizing that the partial derivative of stress with respect to displacement does not change over load cycles for the applied linear elastic formulation, a reference adjoint vector can be solved for each fatigue sampling point. The reference adjoint vector at a fatigue sampling point, \(\boldsymbol {\Lambda }_{k}^{ref}\), is given by

$$ {\boldsymbol{K}}{\boldsymbol{\Lambda}}_{k}^{ref} = \frac{\partial {\Delta}\sigma_{k1}}{\partial {\Delta}{\boldsymbol{u}}_{k1}}, \qquad \qquad k = 1,2,...,2688 $$
(25)

The reference adjoint vector can be calculated for any equilibrium state, here done for the first rainflow count i=1. The adjoint vectors for the remaining rainflow entries can then be found by scaling the reference adjoint vector with the partial derivatives of the fatigue constraint with respect to the stress amplitudes

$$ {\boldsymbol{\Lambda}}_{ki} = \frac{\partial D_{ki}}{\partial {\Delta}\sigma_{ki}} {\boldsymbol{\Lambda}}_{k}^{ref} $$
(26)

The partial derivatives of the fatigue constraints with respect to the stress amplitudes are determined analytically. By this method, the computational demanding part of the design sensitivity analysis no longer scales with the amount of rainflow entries but only with the number of fatigue sampling points. For this reason, a large amount of load time-steps can be included in the analysis. Note that the proposed method is also valid when the loading is design dependent.

For the problem at hand, the amount of adjoint equations that must be solved for a traditional approach in the initial design is 35,448,659, whereas only 2,688 adjoint equations need to be solved when exploiting the linear relationship.

6.3 Frequency constraint sensitivity

The eigenvalue sensitivity is found using the direct differentiation approach, that is, differentiating (17) with respect to a design variable, x v . Simple eigenvalues are assumed.

$$ \frac{d{\boldsymbol{K}}}{dx_{v}} {\boldsymbol{\phi}}_{j}+({\boldsymbol{K}}-\lambda_{j}{\boldsymbol{M}})\frac{d{\boldsymbol{\phi}}_{j}}{dx_{v}} = \frac{d\lambda_{j}}{dx_{v}}\boldsymbol{M}\boldsymbol{\phi}_{j} + \lambda_{j} \frac{d\boldsymbol{M}}{dx_{v}}\boldsymbol{\phi}_{j} $$
(27)

By premultiplying (27) with \({\boldsymbol {\phi }}_{j}^{T}\), utilizing (17), and that the eigenmodes have been M-orthonomalized, the sensitivity has been shown, by e.g. Courant and Hilbert (1953) and Wittrick (1962), to be

$$ \frac{d\lambda_{j}}{dx_{v}}={\boldsymbol{\phi}}_{j}^{T} \left( \frac{d{\boldsymbol{K}}}{dx_{v}} - \lambda_{j}\frac{d\boldsymbol{M}}{dx_{v}}\right)\boldsymbol{\phi}_{j} $$
(28)

The derivative of the global mass matrix with respect to the design variables has been determined analytically.

6.4 Central finite difference validation

All sensitivities have been verified using a central finite difference scheme with a fixed perturbation. For the central difference verification of the fatigue sensitivity, only two mean wind speeds with a third of the load time-steps were included due to the high computational time, while the ULS sensitivities have been verified using the full time-history load.

Using a fixed perturbation size of x v ⋅5e −7, very precise results were achieved. In fact, the highest mean absolute percentage error of all the fatigue constraints is only 0.54 %. This is a strong indication that the analytical gradients are implemented correctly. However, a few gradients deviates significantly which is studied in the following.

By investigating the behaviour of the finite difference approximated sensitivities at different sampling points, it is found that a severe perturbation size dependency exists. In Fig. 5 two different fatigue sensitivities are shown with varying perturbation size. It can clearly be seen that the perturbation size that yields accurate results at one sampling point, will yield inaccurate results at the other. To conclude, great care must be taken if using finite difference approximations as the gradients can vary greatly in magnitude, and more alarmingly in sign, depending on the applied perturbation.

Fig. 5
figure 5

Deviation from analytical sensitivities when approximating the fatigue sensitivities with a central finite difference scheme using a fixed perturbation. It is seen that the perturbation size that yields accurate results for one sensitivity, will yield inaccurate results for the other. Both fatigue sampling points are on the chord side in a welded X connection, where sampling point 2908 belong to symmetry group 9 and sampling point 2134 belong to symmetry group 3. x 8 is the diameter in symmetry group 8

Full size image

7 Optimization problem

Having defined the objective function, the constraint functions, and enforcing design variable bounds ranging from 50 % to 200 % of initial values, denoted x̲ v and \(\overline {x}_{v}\), respectively, the optimization problem can be written as:

$$\begin{array}{llllllll} \underset{{\boldsymbol{x}}}{\text{min.}} & & f({\boldsymbol{x}}) & & & & & (mass)\\ \text{s.t.} & & D_{k} &\leq 1/3, & k & \!\!= 1,2,...,2688& & (fatigue) \\ & & B_{e} &\leq 1, & e & \!\!= 1,2,...,100 & & (buckling)\\ & & G_{e} &\leq 1, & e & \!\!= 1,2,...,100 & & (buckling)\\ & & C_{l} &\leq 1, & l & \!\!= 1,2,...,136 & & (c.\,face)\\ & & S_{l} &\leq 1, & l & \!\!= 1,2,...,136 & & (punch)\\ & & \omega_{1P}^{2} \leq\lambda_{j}&\leq \omega_{3P}^{2}, & j & \!\!= 1,2 & & (freq.)\\ & & (3\omega_{1P})^{2} &\leq \lambda_{j} & j & \!\!= 3,4 & & (freq.)\\ & & 4 \leq \alpha_{p} & \leq 40, & p & \!\!= 1,2,...,11 & & (validity)\\ & & 0.2 \leq \beta_{p} & \leq 1, & p & \!\!= 1,2,...,11 & & (validity)\\ & & 0.2 \leq {\beta_{r}^{B}} & \leq 1, & r & \!\!= 1,2,...,9 & & (validity)\\ & & 8 \leq \gamma_{s} & \leq 25, & s & \!\!= 1,2,...,8 & & (validity)\\ & & \zeta_{t} & \leq 1, & t & \!\!= 1,2,3 & & (validity)\\ & & 0.2 \leq \tau_{r} & \leq 1, & r & \!\!= 1,2,...,9 & & (validity)\\ & & \iota_{w} &\leq 70\frac{235}{355}, & w & \!\!= 1,2,...,10 & & (validity)\\ & & \underline{x}_{v} \leq x_{v} & \leq \overline{x}_{v}, & v & \!\!= 1,2,...,20 & & (bounds) \end{array} $$

The optimization problem is solved using the Sequential Linear Programming (SLP) method. More specifically, by using the CPLEX optimizer by ILOG IBM. The reason behind the choice of optimizer is twofold. Firstly, the optimizer can robustly and efficiently handle the very large number of non-linear constraints. Secondly, there are many conditions that can switch during optimization, e.g. thickness correction and material terms in the S-N curve, flexural reduction factors for buckling etc. These functions are not continuously differentiable, which can lead to significant changes in the Hessian during optimization using a Sequential Quadratic Programming (SQP) optimizer. However, it must be stated that the problem is not restricted to SLP optimizers.

Every constraint has been reformulated into less than or equal to inequality constraints, and then scaled with respect to the right hand side. A vector containing all constraints, excluding design variable bounds, can thus be written as

$$ g_{f}({\boldsymbol{x}}) \leq 0, \qquad \qquad f = 1,2,...,3267 $$
(29)

The subscript f refers to the constraint number.

7.1 Merit functions

In order to ensure that the linearized problem is always feasible, the constraint function is reformulated into a so-called merit function, previously applied and described in e.g. Sørensen et al. (2014). The merit function is given by

$$ {\Phi}_{f} = g_{f}({\boldsymbol{x}})-y_{f} \leq 0, {\kern10pt} \forall f $$
(30)

Here y f is an artificial optimization variable, sometimes referred to as a slack variable, that can always close the gap when one or more of the real constraints are infeasible. However, to ensure that the optimizer will try to reduce the value of the artificial optimization variable, it is added as a penalty term to the objective function. This penalized objective function, or merit objective function, is given by

$$ {\Phi}_{0} = f({\boldsymbol{x}}) + a \sum\limits_{f=1}^{3267} \left( cy_{f}+\frac{1}{2}\left( y_{f}\right)^{2} \right) $$
(31)

Here c is a positive penalization constant set to 100, and a is a scaling constant set to unity. Because all constraints have been scaled with their respective right hand side, any possible constraint violation is penalized equally no matter the type of constraint. Consequently, all constraints are treated as equally important, and thereby a single penalization parameter can be applied for all constraints.

Having shown the merit objective and constraint function, the optimization problem solved using the SLP method can be formulated as

$$\begin{array}{@{}rcl@{}} \underset{{\boldsymbol{x}}}{\text{min.}} & & {\kern40pt} {\Phi}_{0}({\boldsymbol{x}}) \end{array} $$
(32a)
$$\begin{array}{@{}rcl@{}} \text{s.t.} & & {\kern40pt} {\Phi}_{f}({\boldsymbol{x}}) \leq 0, {\kern50pt} \forall f \end{array} $$
(32b)
$$\begin{array}{@{}rcl@{}} & & {\kern50pt}x_{v}^{(n)} \in ML, {\kern41pt} \forall v \end{array} $$
(32c)
$$\begin{array}{@{}rcl@{}} & & {\kern50pt}y_{f} \in [0,\infty[, {\kern50pt} \forall f \end{array} $$
(32d)

In (32c) the set ML constitutes the design variable bounds. These bounds are not static as they are updated in each design iteration (n) using an adaptive move limit strategy based upon the response of a convergence filter. The design variables are still constrained within the original bounds.

7.2 Global convergence filter

A global convergence filter by Chin and Fletcher (2003) is applied to assist in a stable convergence of the SLP optimizer. The convergence filter can be described as a line search method. The search method utilizes the current design value, a linear prediction, and possible constraint violations in determining if a new iterate should be accepted. If a new design is accepted, the move limits are increased. However, if the design is rejected, the move limits are decreased. The parameters applied in the filter are taken from Fletcher et al. (1998). Using the notation from Chin and Fletcher (2003), they are γ=104, β=1−γ, σ=2γ, and δ = γ.

7.3 Adaptive move limit strategy

To control the progression of the SLP optimizer, the adaptive move limit strategy adjusts the bounds of each individual design variable. The variable limits are updated by

$$ x_{v}^{(n+1)} \in \left[max\left( x_{v}^{(n)}-{\Delta}_{v}^{(n+1)},\underline{x}_{v}\right),min\left( x_{v}^{(n)}+{\Delta}_{v}^{(n+1)},\overline{x}_{v} \right)\right] $$
(33)

Here \({\Delta }_{v}^{(n+1)}\) is the new allowable change. Effectively, the algorithm is set to increase the default limits by 15 % if a design is accepted by the global convergence filter. However, if a design variable changes non-monotonically, i.e. in an oscillating manner, the move limit is decreased by 50 %. Furthermore, if the new design is rejected, the move limits are reduced by 50 % for all design variables. The linearized problem is again presented to the optimizer, but now with reduced move limits. The new design is then reevaluated by the global convergence filter. This procedure is repeated until either the design is accepted or a convergence criterion is reached. In this work, the optimization is set to stop when either one of the two following criteria is satisfied

$$ \frac{|| {\boldsymbol{x}}^{(n)} - {\boldsymbol{x}}^{(n-1)}||}{||\, \overline{{\boldsymbol{x}}} - \underline{{\boldsymbol{x}}}\, ||} \!<\! 10^{-4} \quad \text{or} \quad \sqrt{\left( {\Phi}_{0}^{(n-1)}-{\Phi}_{0}^{(n)}\right)^{2}} \!< 0.01 $$
(34)

The initial allowable change is set to 10 %. At any optimum, 1 % infeasibility of any constraint is allowed.

8 Optimization results

The optimization problem is solved very efficiently using the proposed procedure. In only 23 iterations the convergence criteria are fulfilled, and the mass is reduced by 40 % while all constraints are satisfied. Only 36 function evaluations of the finite element model are needed in total. The obtained design values are shown in Table 2. The optimized jacket contra the original jacket is illustrated on Fig. 6.

Fig. 6
figure 6

Original and optimized jacket structure. Light gray beams are not optimized

Full size image
Table 2 Original and optimized design variables in meters
Full size table

The optimized design variables are not directly applicable, as members are not mass produced with these dimensions. Thus, the real mass reduction of the jacket is less if rounding to available diameters and thicknesses is performed.

During the optimization, one fatigue constraint became active in just 4 iterations. At this stage in the optimization process, the mass reduction is 35.1 %. However, the optimization continues to reduce the mass in a stable and robust manner, to a total of 39.9 % as compared with the initial design.

In Fig. 7, the evolution of the objective function and the highest constraint value of all types of structural constraints can be seen.

Fig. 7
figure 7

Objective function and constraint function value evolution during optimization. First y-axis refers to the objective function, while the second y-axis refers to all constraint values. A constraint is considered active at a value of zero or higher

Full size image

Several constraints are active at the optimum. Three validity constraints are active, two of (16a) and one of (16d). While active validity constraints may not represent real structural integrity issues but rather measurements of the modeling credibility, they directly affect the obtained design.

As the fatigue constraints behave highly non-linear, fatigue constraints within 5 % of the constraint limit will in the following be considered active. Obviously, this consideration is only an assessment made from a structural design engineers point of view. With this definition, 17 fatigue constraints are active at the optimum. The active fatigue constraints are located at a variety of locations.

In Section 1 there is two active fatigue constraints. One is located in a T/Y connection and the other is located in an X connection. There are seven active fatigue constraints in Section 2, where three are located in X connections and four are located in K connections. Moreover, five fatigue constraints in X connections and one constraint in a K connection are active in Section 4. Lastly, two fatigue constraints are located at butt welded connections near the transition piece. The active fatigue constraints belong to beam elements in symmetry groups 3, 5, 9, and 10. All active fatigue constraints in connections are active on the chord side of the weld.

Two ULS constraints are active at the optimum. Specifically, a chord face failure constraint of an element in a K connection in Section 3 is active and a chord face failure constraint in a T connection in the frame below Section 1 is active. No other ULS constraint are within 20 % of being active. However, due to the highly non-linear behaviour of the ULS constraints, some may actually be very close to becoming active. For instance, the first active chord face failure constraint increases from a normalized constraint value of -0.33 to being active due to a change in objective function value of only 2.8 %. The active ULS constraints belong to beam elements in symmetry groups 1 and 7.

No local member buckling constraint becomes active during the optimization. Furthermore, the linear global buckling analysis showed a minimum buckling load factor of 42 for all 30,000 ULS load time-steps. While linear buckling analyses may be nonconservative, a buckling load factor of 42 is well beyond the safe limit.

No frequency constraints become active during the optimization. It must be noted that the original design conveniently has lower natural frequencies very near the upper bound of the allowable frequency band between the 1P and 3P frequencies, see Jonkman et al. (2012). This allows much freedom in the optimization loop, as a decrease in overall stiffness occurs during the optimization.

In this framework, it is clear that a multitude of structural details are governing for the sizing design of this jacket topology. This is true as both vertical members and X-, K-, and T-welded connections affect the optimized design, where both FLS and ULS are important. Also, the active constraints are widely spread throughout the structure. Although this means that a large number of non-linear constraints must be considered, the optimization process, at least for this topology, is very robust and efficient.

No assessment has been made on the accuracy of the loading conditions when the design changes. The maximum horizontal jacket top displacement during the entire ULS analysis has increased by 0.08 m at the optimized design when compared to the initial design. As the stiffness decreases, the dynamic effects on the aerodynamic and hydrodynamic loading increase. However, the turbine, the tower, and the site conditions remain unaltered. This is still deemed governing for the aerodynamic loading conditions in this optimization problem. Furthermore, to support the validity of the preliminary design, the wave and gravitational loads become increasingly conservative as the outer diameters and overall mass of the beam members decrease during the optimization, respectively.

9 Conclusion

In this work, an efficient method of determining analytical design sensitivities of finite-life fatigue constraints has been presented. The method is efficient for optimization problems with many more fatigue constraints than design variables. The effectiveness has been demonstrated on the OC4 reference jacket, where also ultimate limit state and frequency constraints have been included. All design constraints are based on international standards. The optimization has been solved in just 23 iterations and the obtained design has a decrease in overall mass of 40 % as compared to the initial design. The optimization is solved using Sequential Linear Programming where handling the very large number of non-linear constraints has been done in an efficient and robust manner.

A large number of time-history loads representing hydrodynamic and aerodynamic loading have been applied in the fatigue analysis. This is possible due to the proposed method, where the amount of adjoint problems to be solved in the design sensitivity analysis of the fatigue constraints, is independent of the amount of applied load time-steps.

The optimization results indicate that the OC4 jacket is designed overly conservative. Also, the results indicate that the design of a jacket structure is indeed a complex task, as different types of constraints are active at the optimum. As the proposed optimization problem is a non-convex problem, a global optimum can not be guaranteed. However, the active constraints are located in a variety of places which indicates a good optimum.

In conclusion, the optimization can be efficiently used to obtain optimized preliminary jacket designs for offshore wind turbines subjected to wind- and wave loads. The optimization considers fatigue, buckling, failure in welded details, and eigenfrequencies, when optimizing member diameter and thickness, such that mass minimized jacket structures are obtained.