1 Introduction

The conceptual tool of topology optimization has played a very important role in the development of structural design. Nevertheless, its use is not restricted only to this field: compliant mechanisms (Sigmund 1997; Frecker et al. 1997; Jonsmann et al. 1999), dynamics (Díaz and Kikuchi 1992; Pedersen 2000), extremal materials (Sigmund and Torquato 1997) and band gaps (Sigmund and Jensen 2003; Jensen and Sigmund 2011), among others, are fields where its contribution has been crucial.

The topology optimization method has been widely used in the optimal design of MEMS (micro-electromechanical systems), where the size of the devices typically is smaller than 1mm. Sigmund (1997) presented optimal design of compliant mechanisms topologies based on the topology optimization method, where optimized mechanisms were fabricated at macro and micro-scale. Concerning piezoelectric effects, Silva et al. (1997) presented a procedure based on topology optimization and homogenization methods to optimize unit cells for piezocomposites. Sigmund (2001a, b) optimized thermal and electrothermal microactuators composed of one and two materials, respectively. Maute and Frangopol (2003) suggested a methodology for the design of MEMS under stochastic loads and boundary conditions. Recently, Donoso and Sigmund (2016) developed a systematic method where a passive gap-phase was included in the optimization process of modal filters for fixed host structure in order to ensure manufacturability and realizability.

The nature of the actuation of the mechanisms in this study is the piezoelectric effect. In the last decades there has been a big development in the subject of topology optimization in piezoelectric materials. The first work where the topology optimization method was used to optimize piezoelectric structures was Sigmund et al. (1998), that optimized the unit cell of structures for improving piezoelectric features. Regarding piezoelectric actuators, Silva and Kikuchi (1999) presented a method to design in-plane actuators by optimizing the host structure, but fixing the piezoelectric material layer. Kögl and Silva (2005) presented optimization of piezoelectric layers with a three-layer model, with two piezoelectric films symmetrically bonded to the host structure. Carbonari et al. (2007) and Luo et al. (2010) optimized the host structure and the piezoelectric distribution simultaneously. The inclusion of a third variable, the spatial distribution of the control voltage (related to the polarization of the piezoelectric layers) in the optimization problem, was presented in Kang and Tong (2008a) and improved in Kang and Tong (2008b) by introducing an interpolation scheme in the tri-level actuation voltage term. Further results were presented in Kang et al. (2011, 2012) for in-plane and out-of-plane piezoelectric transducers, respectively.

In prior works (Ruiz et al. 2016a, b) some of the authors have presented a systematic procedure to design static microtransducers and modal filters, respectively. In both works the host structure (including the piezoelectric layer) and polarization profile of the electrodes are optimized simultaneously, considering that both piezoelectric films are perfectly bonded to the top and bottom of the host structure. However, trying to realize this reveals an important obstacle: it is hard to fabricate piezoelectric layers symmetrically in the micro scale (Kucera et al. 2014), hence only one piezoelectric film can be deposited on the top of the host structure. This fact is not a problem when the transducer is working as a sensor, since the deformation is produced by an external force. However, when the device is working as actuator it moves in-plane, but also out-of-plane deformation appears, making it challenging to design a genuine microgripper-type actuator. The objective of the present work is to design a piezoelectrically actuated microgripper including constraints on the out-of-plane bending of the structure in some points of interest. In addition, and having manufacturability in mind, the so-called robust formulation (Sigmund 2009; Wang et al. 2011) is applied to the problem with two purposes: first to control the minimum length scale in both solid and void regions; and second to minimize sensitivity to fabrication errors.

Concerning the physical behavior of the device, we make the assumption that the out-of-plane bending is small but not negligible, meaning that it can be treated by classical linear elasticity plate theory. However, the in-plane displacements are expected to be large and a non-linear model is mandatory. Geometrical non-linearities in topology optimization were first dealt with in Buhl et al. (2000) using the total Lagrangian formulation. This was soon after extended to compliant mechanism design in Bruns and Tortorelli (2001) and Pedersen et al. (2001). The robust design of large displacement compliant mechanisms is shown in Lazarov et al. (2011), where the goal is achieved by adding random variations that model possible geometry errors.

Geometrically non-linear topology optimization is prone to numerical instabilities produced by excessive distortions in low stiffness regions. Wang et al. (2014) suggested an interpolation scheme that uses linear modeling in the (fictitious) void domain. This scheme is also applied here. In early works (Buhl et al. 2000) and (Pedersen et al. 2001) authors avoided the numerical instability by ignoring nodes surrounded by low density elements in the Newton-Raphson convergence criterion. Bruns and Tortorelli (2001) circumvented the issue by removing and reintroducing low density elements during the optimization procedure. Removal of low density elements may come at the risk of hindering structure to grow in low density regions and hence may be better suited for more shape oriented topology optimization approaches like (Zhang et al. 2017).

The paper is organized as follows. In Section 2 the nature of the problem is briefly described and the discrete formulation is shown. Section 3 is devoted to the robust formulation. In Section 4 we present the numerical implementation of the problem, where the algorithm used to get the optimal designs is described. The optimized microgrippers obtained by solving the discrete problem are shown and validated in Comsol Multiphysics in Section 5. Finally, in Section 6 the conclusions of this work are presented.

2 Topology optimization of large displacement piezoelectric microgripper

As design domain Ωwe consider a rectangular plate clamped at its left side. On the top surface, the host structure is perfectly bonded with a piezoelectric layer (that is sandwiched between two electrodes) of negligible stiffness compared to the plate.

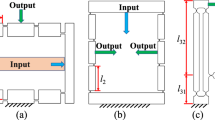
The polarization of the piezoelectric layer is obtained through the application of an input voltage over the electrodes. This voltage generates an electric field that produces a mechanical stress over the piezoelectric material, which in turn deforms the host structure. The unsymmetrical configuration of the layers of the plate causes bending of the structure, that disturbs the in-plane behavior and needs to be suppressed. The multilayered structure is shown in Fig. 1. Three passive areas are defined in the design domain. Two of these areas are solid regions (black color) that belong to the jaws. The third one is a void region (white color) and represents an empty gap between the jaws. The output of the gripper is modeled by a spring of stiffness k o u t (that depends on the application). The 3d depiction of design domain and the dimensions are shown in Fig. 2.

Fig. 1
figure 1

Top and side view of the piezoelectric device

Full size image
Fig. 2
figure 2

Design domain

Full size image

The aim of the problem is the maximization of the in-plane deformation along the y-axis u 1 while the deformations over the z-axis u 2 and u 3 must be suppressed. The bending is canceled in two points in order to avoid the rotation of the jaws over the y-axis. This suppression is controlled by adding two constraints which relate the optimized and the canceled displacements. In addition, a volume constraint is used to control the amount of material used.

The optimization problem involves two design variable fields. χ s is a characteristic function, χ s ∈{0,1}, that represents the structure layout (χ s = 1) and void (χ s = 0), as usual. χ p is also a characteristic function such that χ p ∈{− 1,0,1}, meaning negative, null or positive polarity. Since the topology optimization problem lacks classical solutions, the characteristic functions χ s and χ p need to be relaxed into density variables ρ s ∈ [0,1]and ρ p ∈ [− 1,1]. As usual, after the relaxation of the variables, the domain is discretized in n e finite elements with two variables per element. The role of the electrode is crucial here, only the parts of the structure that are being covered by electrode, i.e. χ p = − 1or χ p = 1, are electrically affected and therefore subjected to piezoelectric forces.

Since the out-of-plane deformation is expected to be small, it can be studied separately from the in-plane one (the problems are decoupled), and then the optimization problem involves two equilibrium equations. The in-plane displacements are modeled using a geometrically non-linear model. The out-of-plane displacements are modeled using classical linear elasticity. The formulation of the problem written as a topology optimization problem becomes:

$$\max\limits_{{\boldsymbol \rho}_{s},{\boldsymbol \rho}_{p}}: \;\; u_{1}({\boldsymbol \rho}_{s},{\boldsymbol \rho}_{p}) $$
$$ \begin{array}{rcl} \text{s.t.}:\;\; \textbf{R}_{ip}({\boldsymbol \rho}_{s},{\boldsymbol \rho}_{p},\textbf{U}_{ip}) & = & \textbf{0} \vspace{0.1cm}\\ \textbf{R}_{op}({\boldsymbol \rho}_{s},{\boldsymbol \rho}_{p},\textbf{U}_{op}) & = & \textbf{0} \vspace{0.1cm}\\ u_{1} & = & \textbf{L}_{1}^{T} \textbf{U}_{ip} \vspace{0.1cm} \\ u_{2} & = & \textbf{L}_{2}^{T} \textbf{U}_{op} \vspace{0.1cm}\\ u_{3} & = & \textbf{L}_{3}^{T} \textbf{U}_{op} \vspace{0.1cm} \\ \left( \frac{u_{2}}{u_{1}}\right)^{2}-{\varepsilon_{d}^{2}} & \leq & 0\vspace{0.1cm} \\ \left( \frac{u_{3}}{u_{1}}\right)^{2}-{\varepsilon_{d}^{2}} & \leq & 0 \vspace{0.1cm}\\ \frac{\textbf{1}^{T} {\boldsymbol \rho}_{s}}{V} -1 & \leq & 0 \vspace{0.1cm}\\ {\boldsymbol \rho}_{s} & \in & [\textbf{0},\textbf{1}] \vspace{0.1cm}\\ {\boldsymbol \rho}_{p} & \in & [\textbf{-1},\textbf{1}], \vspace{0.1cm}\\ \end{array} $$
(1)

where ρ s and ρ p represent the structure layout and the polarization profile respectively, u 1 is the in-plane displacement to be maximized, u 2 and u 3 are the out-of-plane displacements to be suppressed, L 1, L 2 and L 3 are vectors of zeros with 1 in the output degree of freedom of interest, V is the maximum volume, ε d is a small value that relates the displacements to be suppressed and the ones to be optimized, and R i p and R o p are the global residual vectors of the structural equilibrium equations for the in-plane and out-of-plane cases, respectively. For the sake of brevity, from now on the subscripts “ip” and “op” refer to the in-plane and the out-of-plane cases, respectively. The residual vectors are defined as follows:

$$ \begin{array}{c} \textbf{R}_{ip} = \textbf{F}^{piezo}_{ip} - \textbf{F}^{int}_{ip} = \textbf{0} \vspace{0.1cm}\\ \textbf{R}_{op} = \textbf{F}^{piezo}_{op} - \textbf{F}^{int}_{op} = \textbf{0}, \end{array} $$
(2)

where \((\textbf {F}^{piezo}_{ip},\textbf {F}^{piezo}_{op})\) and \((\textbf {F}^{int}_{ip},\textbf {F}^{int}_{op})\) are the global piezoelectric and internal force vectors, respectively. Capital letters are used for global vectors and matrices, that are obtained by assembling the elemental contributions represented with lowercase letters. The expressions of the different terms in (2) are further elaborated in the next subsection.

2.1 Continuous material approach and finite element model

The original formulation of the problem involves integer variables which need to be relaxed into density variables. The well-known SIMP approach (Solid Isotropic Material with Penalization, Bendsøe and Sigmund (1999) and Bendsøe and Sigmund (2003)) is used for this purpose. The Young’s modulus of each element depends on the element density as follows:

$$ E_{e} = (\bar{\rho}_{se})^{p}(E_{0}-E_{min}) + E_{min}, $$
(3)

where E 0 is the Young’s modulus of the base material, E m i n > 0 is a small value used to avoid singularities in the stiffness matrix and p is the penalization exponent (typically p = 3).

The discrete formulation of the problem has been presented in Section 2. For the in-plane case bilinear elements with 8 degrees of freedom are used and for the out-of-plane case, Kirchhoff elements with 12 degrees of freedom per element are used. The in-plane displacements are expected to be large in comparison with the size of the domain. Pedersen et al. (2001) showed that displacements over 2% of the domain size require geometrical non-linearity to model the deformation field.

In order to model the in-plane deformation, the total Lagrangian finite element formulation is used. The Green-Lagrange strain tensor can be expressed as:

$$\textbf{E} = \frac{1}{2}(\textbf{F F}^{T}-\textbf{I}), $$

where I is the unit tensor and F is the deformation gradient, defined by a 2 × 2matrix:

$$\textbf{F} = \partial u / \partial y = \left[ \begin{array}{cc} \frac{\partial u}{\partial x} \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x} \frac{\partial v}{\partial y} \end{array}\right] $$

The expression for the work conjugate stress tensor (the second Piola-Kirchhoff stress tensor) is:

$$\textbf{S} = \frac{\partial \phi(\textbf{U}_{ip})}{\partial \textbf{E}}, $$

where ϕ(U i p ) is the in-plane stored elastic energy density that will be defined in the next subsection.

The expression for the element internal force \(\textbf {f}^{int}_{ip}\) presented in (2) is:

$$\textbf{f}^{int}_{ip} = \frac{\partial {\int}_{\Omega} \phi_{e} \mathrm{d}{\Omega}}{\partial \textbf{u}_{ip}}, $$

where u i p is the element displacement vector for the in-plane case.

Due to the non-symmetrical laminate, the piezoelectric force generates a moment that makes the plate bend and an initial strain that extends or contracts the plate. All expressions for the computations of both the flexural and the extensional components, can be found in Gibbs and Fuller (1992). In addition, the same powerlaw dependence \(R_{e} = \rho _{se}^{p}\) as used for the Young’s modulus interpolation (3) is used for the piezoelectric force generation. It is easy to see that the value of the interpolation R e is very small in void regions and takes the value R e = 1in the solid ones. This is a realistic way to model the force produced in these elements, since there is no electrode in the void regions (Ruiz et al. 2016b).

In the equilibrium configuration, the residual vector for each case must be 0, this means that the global vectors of internal forces must be equal to the piezoelectric forces. We can rewrite the equilibrium equation for each motion case as follows:

$$\begin{array}{ccccl} \textbf{R}_{ip} & = & \textbf{F}_{ip}^{piezo} - \textbf{F}_{ip}^{int} & = & \textbf{F}_{ip}^{piezo} - \displaystyle {\int}_{\Omega} \textbf{B}_{ip}(\textbf{U}_{ip})\textbf{S}\,\mathrm{d}{\Omega} \vspace{0.1cm}\\ \textbf{R}_{op} & = & \textbf{F}_{op}^{piezo} - \textbf{F}_{op}^{int} & = & \textbf{F}_{op}^{piezo} - \textbf{K}_{op}\textbf{U}_{op}, \end{array} $$

where K o p is the global out-of-plane stiffness matrix obtained by assembling the element stiffness matrices and B i p is the in-plane non-linear strain displacement matrix. The Newton-Raphson method is used to solve the non-linear system:

$$\textbf{K}_{t} {\boldsymbol {\Delta}}\textbf{U}_{ip} = \textbf{R}_{ip}, $$

where K t is the tangent stiffness matrix defined as:

$$\textbf{K}_{t} = -\frac{\partial \textbf{R}_{ip}}{\partial \textbf{U}_{ip}} $$

and the nodal displacement vector is updated by U i p = U i p + Δ U i p . The detailed computations of the tangent matrix and the nodal force vectors can be found on Zienkiewicz et al. (2014) and are not stated here.

2.2 Energy interpolation scheme

The Saint-Venant-Kichhoff model is used to represent the behavior of the hyperelastic material. The stored elastic energy density is expressed as follows:

$$\begin{array}{l} \phi = \frac{1}{2}\lambda E^{2}_{kk}+\mu E_{ij}E_{ij} = \vspace{0.1cm}\\ \frac{1}{8}\lambda(I_{c}-3)^{2} + \frac{\mu}{4}({I_{c}^{2}} - 2II_{c}-2I_{c}+ 3), \end{array} $$

where E i j are the components of the non-linear strain tensor, λ and μ are the Lamé parameter, I c = tr(C) is the first invariant of C = F T F and I I c = (tr(C)2 −tr(C 2))/2 is the second invariant of C. The Lamé parameters can be expressed in function of the Young’s modulus and the Poisson’s ratio: λ = ν E(1 − ν 2) and ν = E/ (2(1 + ν)).

In Wang et al. (2014) an energy interpolation scheme is used to alleviate the issue of distorted and ill-converged void region mesh. The paper suggests basing the analysis in the solid region on the non-linear stored energy and the analysis in the void regions on linear stored energy, thereby eliminating mesh distortion and ill-convergence issues in the low density domain. The energy interpolation form for element e is

$${\Phi}_{e}(\textbf{u}_{e}) = [ {\Phi}(\gamma_{e}\textbf{u}_{e}) - {\Phi}_{L}(\gamma_{e}\textbf{u}_{e}) + {\Phi}_{L}(\textbf{u}_{e}) ] E_{e}, $$

where E e is the Young’s modulus for element e, u e is the elemental displacement vector for the element, Φ(⋅) is the stored elastic energy density, Φ L (⋅) is the stored elastic energy density under small deformation, both with unit Young’s modulus. Finally, γ e is the interpolation factor that takes the value γ e = 1 if the element is solid and γ e = 0if it is void. This interpolation scheme assumes that the Young’s modulus is separable from the energy functional. In order to differ between void and solid regions a smoothed Heaviside projection is used:

$$\gamma_{e} = \frac{\tanh(\beta_{1} \rho_{0}) + \tanh\left( \beta_{1}({\bar \rho}_{se}^{p}-\rho_{0})\right)}{\tanh(\beta_{1} \rho_{0}) + \tanh\left( \vphantom{{\bar \rho}_{se}^{p}}\beta_{1}(1-\rho_{0})\right)}, $$

where \({\bar \rho }_{se}\) is the physical density, which will be introduced in the next section, β 1 models the smoothness of the projection and ρ 0 is a low-density threshold. For non-void domains \({\bar \rho }_{se}^{p} > \rho _{0}\) the element is hence modeled as a standard non-linear element with geometrically non-linear contribution.

3 Robust topology optimization formulation

This section is devoted to the robust formulation of the problem. This approach, that was presented in Sigmund (2009) and Wang et al. (2011), consists in the use of three different projections with two goals. The first one is controlling the minimum length scale in both, solid and void regions hence avoiding the appearance of hinges. The second is the robustness toward small manufacturing errors, that are very common in the fabrication at micro-scale.

The robust approach proposes the use of three different projections: eroded, intermediate and dilated. The expression for a smoothed threshold projection based on the tanh function is

$${\bar \rho}_{se} = \frac{\tanh(\beta_{0}\eta) + \tanh\left( \vphantom{{\bar \rho}_{se}^{p}}\beta_{0}({\tilde \rho}_{se}-\eta)\right)}{\tanh(\beta_{0} \eta) + \tanh\left( \vphantom{{\bar \rho}_{se}^{p}}\beta_{0}(1-\eta)\right)}, $$

where β 0 is a tuning parameter representing the smoothness of the projection and η is the threshold which can take values between 0 and 1. The filtered densities \({\tilde \rho }_{se}\) are projected to 1 if these values are bigger than the threshold and to 0 if not. The filtered densities \(\tilde {\rho }\) are expressed as:

$${\tilde{\rho}}_{se} = \frac{{\sum}_{j\in N_{e}} w(\textbf{x}_{j})v_{j}\rho_{sj}}{{\sum}_{j\in N_{e}} w(\textbf{x}_{j})v_{j}}, $$

where x j is the center of element j, v j is the volume of the element j, N e is the neighborhood of element e within a certain filter radius r specified by N e = {j| ||x j −x e ||≤ r}, and w(x j ) = r −||x j −x e ||.

The use of three different physical realizations requires the solution of three sets of equilibrium equations. Followingly, each realization presents three different in-plane and out-of-plane displacements which all must be included in the optimization problem. From now on, for the sake of simplicity, we introduce the superscript q for indicating projection, with e meaning erode, i intermediate and d dilate. The robust topology optimization formulation is written:

$$\max_{{\boldsymbol \rho}_{s},{\boldsymbol \rho}_{p}}: \, \min_{q=e,i,d} \{{u_{1}^{q}}({\bar{\boldsymbol \rho}}_{s}^{q},{\boldsymbol \rho}_{p}) \} $$

s.t.:

$$\begin{array}{rcl} \textbf{R}_{ip}^{q}({\bar{\boldsymbol \rho}}_{s}^{q},{\boldsymbol \rho}_{p}, {\boldsymbol U}_{ip}^{q}) & = & \textbf{0} \vspace{0.1cm}\\ {u_{1}^{q}} & = & \textbf{L}_{1}^{T} \textbf{U}_{ip}^{q} \vspace{0.1cm}\\ \textbf{R}_{op}^{q}({\bar{\boldsymbol \rho}}_{s}^{q},{\boldsymbol \rho}_{p}, {\boldsymbol U}_{op}^{q}) & = & \textbf{0} \vspace{0.1cm}\\ {u_{2}^{q}} & = & \textbf{L}_{2}^{T} \textbf{U}_{op}^{q} \vspace{0.1cm}\\ {u_{3}^{q}} & = & \textbf{L}_{3}^{T} \textbf{U}_{op}^{q} \vspace{0.1cm}\\ \left( \frac{{u_{2}^{q}}}{{u_{1}^{q}}}\right)^{2} - {\varepsilon_{d}^{2}}& \leq & 0 \vspace{0.1cm}\\[-1pt] \left( \frac{{u_{3}^{q}}}{{u_{1}^{q}}}\right)^{2} - {\varepsilon_{d}^{2}}& \leq & 0 \vspace{0.1cm}\\ \frac{\textbf{1}^{T} {\bar {\boldsymbol \rho}}_{s}^{d}}{V_{d}^{*}} -1 & \leq & 0 \vspace{0.1cm}\\ {\boldsymbol \rho}_{s} & \in & [\textbf{0},\textbf{1}] \vspace{0.1cm}\\ {\boldsymbol \rho}_{p} & \in & [\textbf{-1},\textbf{1}] \vspace{0.1cm}\\ q & \equiv & e,i,d; \end{array} $$

where \(V_{d}^{*}\) is the maximum volume bound over the dilated design. This value is computed at the beginning of the optimization and is then updated every 20 iterations. The expression for this constraint is

$$ V_{d}^{*} = \frac{V^{*}}{V_{i}}V_{d}, $$

with V i and V d being the volume for the intermediate and dilated designs and V ∗ the maximum volume prescribed for the intermediate design. Unlike the equilibrium equations and the rest of the constraints, the volume constraint is only enforced on the dilated design, according to the method proposed by Wang et al. (2011).

The max-min objective function proposed above is not differentiable. In order to alleviate this issue the problem is reformulated using the so-called bound formulation:

$$\min_{{\boldsymbol \rho}_{s},{\boldsymbol \rho}_{p}}: \, \beta $$

s.t.:

$$\begin{array}{rcl} -{u_{1}^{q}} & \leq & \beta \vspace{0.1cm}\\ \textbf{R}_{ip}^{q}({\bar{\boldsymbol \rho}}_{s}^{q},{\boldsymbol \rho}_{p}, {\boldsymbol U}_{ip}^{q}) & = & 0 \vspace{0.1cm}\\ {u_{1}^{q}} & = & \textbf{L}_{1}^{T} \textbf{U}_{ip}^{q} \vspace{0.1cm}\\ \textbf{R}_{op}^{q}({\bar{\boldsymbol \rho}}_{s}^{q},{\boldsymbol \rho}_{p}, {\boldsymbol U}_{op}^{q}) & = & 0 \vspace{0.1cm}\\ {u_{2}^{q}} & = & \textbf{L}_{2}^{T} \textbf{U}_{op}^{q} \vspace{0.1cm}\\ {u_{3}^{q}} & = & \textbf{L}_{3}^{T} \textbf{U}_{op}^{q} \vspace{0.1cm}\\ \left( \frac{{u_{2}^{q}}}{{u_{1}^{q}}}\right)^{2} - {\varepsilon_{d}^{2}}& \leq & 0 \vspace{0.1cm}\\ \left( \frac{{u_{3}^{q}}}{{u_{1}^{q}}}\right)^{2} - {\varepsilon_{d}^{2}}& \leq & 0 \vspace{0.1cm}\\ \frac{\textbf{1}^{T} {\bar {\boldsymbol \rho}}_{s}^{d}}{V_{d}^{*}} -1 & \leq & 0 \vspace{0.1cm}\\ {\boldsymbol \rho}_{s} & \in & [\textbf{0},\textbf{1}] \vspace{0.1cm}\\ {\boldsymbol \rho}_{p} & \in & [\textbf{-1},\textbf{1}] \vspace{0.1cm}\\ q & \equiv & e,i,d; \end{array} $$

where β is an additional bound variable that does not depend on the design variables ρ s and ρ p and resolves non-differentiability issue with the max-min function.

4 Numerical implementation

A gradient-based method, the MMA (Method of Moving Asymptotes (Svanberg 1987)), has been used to solve the optimization problem. This method requires information about the objective function, the constraints and the sensitivities of both. The adjoint method is used to compute the sensitivities of the objective function with respect to the structure density vector ρ s and the polarization profile vector ρ p . First the derivative with respect to the structural density of element e are found using adjoint sensitivity analysis as

$$\frac{\partial {u_{1}^{q}}}{\partial \rho_{se}} = {\boldsymbol \lambda}^{T} \frac{\partial \textbf{R}_{ip}^{q}}{\partial \rho_{se}} $$

with

$$ \textbf{K}_{t}{\boldsymbol \lambda} = \left( \frac{\partial {u_{1}^{q}}(\textbf{U}_{ip}^{q},{\boldsymbol \rho}_{s},{\boldsymbol \rho}_{p})}{\partial \textbf{U}_{ip}^{q}}\right) = \textbf{L}_{1}, $$
(4)

where the tangent matrix K t is computed at the converged solution. The right term in (4) is the constant vector L 1. The chain rule must be used to compute the derivatives of the equilibrium equation:

$$\begin{array}{l} \frac{\partial \textbf{R}_{ip}^{q}}{\partial \rho_{se}} = \frac{\partial \textbf{r}_{ip}^{q}}{\partial \rho_{se}} = - {\sum}_{j\in N_{e}} \left( \frac{\partial \left( \textbf{f}_{ip,j}^{int,q}-\textbf{f}_{ip,j}^{piezo,q}\right)}{\partial {\bar \rho}_{sj}^{q}} \right.\\ \left. + \frac{\partial \left( \textbf{f}_{ip,j}^{int,q}-\textbf{f}_{ip,j}^{piezo,q}\right)}{\partial {\gamma_{j}^{q}}}\frac{\partial {\gamma_{j}^{q}}}{\partial {\bar \rho}_{sj}^{q}}\right) \frac{\partial {\bar \rho}_{sj}^{q}}{\partial {\tilde \rho}_{sj}} \frac{\partial {\tilde \rho_{sj}}}{\partial \rho_{se}} . \end{array} $$

Due to the many load cases and realizations involved, indexing above has become quite involved. Information about the nature of the force (internal or piezoelectric) and the threshold (eroded, intermediate or dilated) is indicated as superscripts, separated by a comma. Information about the motion case (in-plane or out-of-plane) and the element number (j) is shown in the subscript, also separated by a comma.

In the same way, the derivative of the cost with respect to the polarization profile is:

$$\frac{\partial {u_{1}^{q}}}{\partial \rho_{pe}} = {\boldsymbol \lambda}^{T} \frac{\partial \textbf{R}_{ip}^{q}}{\partial \rho_{pe}} $$

with the adjoint vector λ again coming from the solution of (4).

Finally, the derivative of the residual vector is

$$\begin{array}{l} \frac{\partial \textbf{R}_{ip}^{q}}{\partial \rho_{pe}} = \frac{\partial \textbf{r}_{ip}^{q}}{\partial \rho_{pe}} = - \frac{\partial (\textbf{f}_{ip}^{int,q}-\textbf{f}_{ip}^{piezo,q})}{\partial \rho_{pe}} \end{array} $$

The sensitivities of \({u_{2}^{q}}\) and \({u_{3}^{q}}\) are also computed using the adjoint method. However, since the out-of-plane problem is linear, these computations are straight forward and are not stated here. Similarly, the volume fraction depends linearly on the physical structure density, and the derivatives are computed using the chain rule.

The complete process algorithm looks like:

  1. 1.

    Selection of the dimensions of the plate and the properties of the materials that will be used. Boundary conditions and the parameters ε d and k o u t must be chosen.

  2. 2.

    Initialize the design variables ρ s and ρ p .

  3. 3.

    Compute the physical densities \({\bar {\boldsymbol \rho }}_{s}^{q}\) by filtering the structural density and then projecting with three different thresholds.

  4. 4.

    Solve the finite element problem for the three different physical densities.

    1. (a)

      For the linear out-of-plane case.

    2. (b)

      For the non-linear in-plane case.

  5. 5.

    Extract the displacements \({u_{1}^{q}}\), \({u_{2}^{q}}\) and \({u_{3}^{q}}\) and compute the constraints.

  6. 6.

    Compute the sensitivities of the objective function and the constraints.

  7. 7.

    Update design variables based on MMA.

  8. 8.

    Until convergence update the parameters β 0 and \(V_{d}^{*}\) and go back to step 3.

At this point it is important to remark that thanks to the symmetry of the problem only half of the domain needs to be simulated and optimized.

5 Examples

The multilayered structure, whose dimensions are shown in Fig. 1, is formed in a host layer of silicon with thickness t = 5μ m and a piezoelectric layer of PZT-5H with thickness t p = 500nm. The Young’s modulus is E 0 = 130GPa for silicon, the stiffness of the piezoelectric layer is neglected. In order to avoid singularities in the stiffness matrix, we fix E m i n = 10− 9 E 0. The Poisson’s ratio is ν = 0.28 for both materials. The piezoelectric constant for PZT-5A is d 31 = 190pm/V and the input voltage is V i n = 500V. We fix the relationship between the suppressed and optimized displacement to ε d = 0.05. The stiffness of the spring that models the output is k o u t = 1 × 103N/m. Concerning the filter and the projection, the radius filter is set to r = 8μ m and δ η = 0.30, ensuring a minimum length scale of 7.2μ m (Wang et al. 2011) and (Qian and Sigmund 2013) for the intermediate design. Threshold projection values of η = 0.7, 0.5 and 0.3 are hence assigned to the eroded \({\boldsymbol {\bar \rho }}_{s}^{e}\), intermediate \({\boldsymbol {\bar \rho }}_{s}^{i}\) and dilated \({\boldsymbol {\bar \rho }}_{s}^{d}\) designs, respectively. The value of the sharpness parameter β 0 is increased during the iterative process, starting with β 0 = 1 and doubling each 20 iterations until it reaches β 0 = 16. Finally, we fix the parameters of the energy interpolation scheme to β 1 = 500 and ρ 0 = 0.01 (Wang et al. 2014).

The optimized designs for the first example are given in Fig. 3. Three different thresholds are shown: the intermediate (top), also called the blueprint design which is the one that will be fabricated, the eroded (middle) and the dilated (bottom). The structural layout \({\boldsymbol {\bar \rho }}_{s}\) is shown in Fig. 3 (left), where black and white means solid and void areas, respectively. There is no microstructure (gray), which means that the projection method is working properly. Figure 3 (right) shows the electrode profile ρ p . Orange and cyan represent the sign of the polarization profile, positive or negative respectively. The whole structure, except for the jaws, is being covered by electrode. The value of the in-plane displacement in the blueprint design is u 1 = 13.9μ m. The values of the out-of-plane displacements are u 2 = 0.44μ m and u 3 = 0.69μ m.

Fig. 3
figure 3

Structure variable \({\boldsymbol {\bar \rho }}_{s}\) (left) and electrode profile ρ p (right) for the three different projections. k o u t = 1 × 103N/m

Full size image

In Fig. 4 the stiffness of the spring is changed to k o u t = 5 × 102N/m while the rest of the parameters stay fixed. The value of the displacement in the blueprint design is u 1 = 18μ m.

Fig. 4
figure 4

Structure variable \({\boldsymbol {\bar \rho }}_{s}\) (left) and electrode profile ρ p (right) for the three different projections. k o u t = 5 × 102N/m

Full size image

Finally, in Fig. 5, the stiffness of the spring is set to k o u t = 5 × 103N/m and the value of the optimized displacement is u 1 = 6μ m.

Fig. 5
figure 5

Structure variable \({\boldsymbol {\bar \rho }}_{s}\) (left) and electrode profile ρ p (right) for the three different projections. k o u t = 5 × 103N/m

Full size image

In Figs. 6 and 7 the response of the three optimized grippers depending on the output stiffness k o u t is shown. In both figures the in-plane equilibrium equation is solved for different values of the stiffness of the spring. In the first case the values of u 1 versus k o u t are plotted for the blueprint design. When the stiffness takes the value k o u t = 0N/m, the displacement obtained is the so-called free displacement. As expected, the device designed for the lowest stiffness (red color) shows the biggest free displacement, and vice versa. In the second case, the values of force applied at the end of the jaws versus k o u t are plotted. When the stiffness takes a big value, the displacement at this point tends to zero and the resulting force is called blocking force. The device designed for the biggest stiffness (blue color) presents the biggest blocking force. These two parameters, free displacement and blocking force, define the behavior of the gripper. Notice that the best design (the highest displacement in the first case, and the force applied in the second one) for the three different stiffness’s, is the one corresponding to the designed spring.

Fig. 6
figure 6

Evolution of the output displacement with the output stiffness for the blueprint design

Full size image
Fig. 7
figure 7

Evolution of the output force with the output stiffness for the blueprint design

Full size image

In order to further illustrate the potential of our approach, Fig. 8 presents two other optimized microgrippers. Figure 8 (left) shows the one optimized for k o u t = 1 × 103N/m and Fig. 8 (right) shows the same example but removing the constraints over the out-of-plane displacements. The topologies are quite similar, actually the in-plane displacement u 1 is 13.9μ m for the first case and 15μ m for the second one, but the out-of-plane displacements u 2 and u 3 are very different. When these displacements are constrained their values in the optimized design are u 2 = 0.44μ m and u 3 = 0.69μ m. When both constraints are removed from the optimization problem, the two displacements change to u 2 = 8.4μ m and u 3 = 12.8. In such a case, and taking into account the size of the plate, the in-plane and out-of-plane problems are not decoupled. In this simulation the model used is not the most appropriate, but anyway, the objective of the present work is showing that the optimization problem proposed is able to suppress the out-of-plane bending produced at the jaws.

Fig. 8
figure 8

Optimized microgripper for k o u t = 1 × 103N/m with constraints over the bending at the jaws (left) and without the constraint (right)

Full size image

Figure 9 presents the deformation of the grippers commented on above. The device optimized with out-of-plane constraints is shown in Fig. 9 a. In this example it is easy to check that the out-of-plane deformation is in general small, which is represented with yellow color. Figure 9b shows the deformation of the gripper without the constraints. In this case the jaws are blue colored, which means that this part of the structure is the one with the biggest out-of-plane deformation.

Fig. 9
figure 9

Comparison of deformations between the grippers presented in Fig. 8

Full size image

5.1 Verification with Comsol Multiphysics

Arguably, the validity of the simplifying linearity assumption for the out-of-plane deformation can be question and the optimization could potentially take adavntage of flaws in the model. Hence, this subsection presents a corroboration of the model using the commercial software Comsol Multiphysics. The gripper is modeled with a fully geometrically non-linear, three-dimensional finite element model using no simplifying assumptions. The domain is discretized with 42202 quadratic tetrahedral elements and 247424 degrees of freedom, as shown in Fig. 10. The mesh of the piezoelectric layer is finer due to the smaller thickness.

Fig. 10
figure 10

Meshed 3D realization of the optimized gripper

Full size image

The deformed gripper is shown in Fig. 11. Resulting displacements are shown in Table 1 which also shows the corresponding displacements obtained from the simplified finite element model used in the optimization. As can be seen from the table, the differences between using full three-dimensional modeling and two-dimensional decoupled plate modeling (with in-plane and out-of-plane motion cases decoupled and linear out-of-plane modeling) are small enough to consider the latter accurate enough.

Fig. 11
figure 11

Deformation of the optimized gripper shown in Fig. 8 (left) modeled using Comsol Multiphysics

Full size image
Table 1 Comparison of displacements obtained with Comsol Multiphysics and Matlab for the optimized gripper from Fig. 8 (left)
Full size table

For comparison, Fig. 12 depicts the deformation of the gripper optimized without out-of-plane deformation constraints from Fig. 8 (right). The displacement values obtained with Comsol Multiphysics and Matlab are shown is Table 2. For this case, remarkably larger discrepancies between the two models are observed. This partly shows that the suggested simplified linear out-of-plane modeling is inadequate and partly that in-plane and out-of-plane displacements couple when considering large out-of-plane motions. On the other hand, the two verification examples confirm that for cases with small out-of-plane motions, as dictated by the imposed out-of-plane motion constraints, the simplified and much cheaper and more efficient approach is fully justified.

Fig. 12
figure 12

Deformation of the gripper optimized without out-of-plane deformation constraints from Fig. 8 (right) modeled using Comsol Multiphysics

Full size image
Table 2 Comparison of displacements with Comsol Multiphysics and Matlab for the gripper optimized without out-of-plane deformation constraints from Fig. 8 (right)
Full size table

6 Conclusions

In this work piezoelectric microgripper-type actuators are designed by topology optimization. The main novelty introduced is the suppression of out-of-plane bending caused by unsymmetrical lamination of the piezoelectric actuator. This goal is achieved by adding a constraint for each point where the out-of-plane deformation needs to be canceled. The difficulty arising by only placing one film of piezoelectric material is a real limitation when fabricating at the micro-scale. If the suppression of the out-of-plane deformation is not taken into account, the bending of the gripper jeopardizes functionality. From an optimization point of view it is not possible to suppress the bending in the whole domain. This problem is overcome by suppressing the bending only in four points of interest, placed at the jaws.

The modeling of the in-plane and out-of-plane deformation is different. For the former, the displacements are large compared to the size of the gripper and a geometrically non-linear model (we assume large displacements but small strains) is used. For the latter, displacements are small and hence it is not necessary to use a non-linear model and the linear one is used instead to save computational time. An elastic energy interpolation scheme is used to alleviate convergence problems due to excessively distorted low density elements. The validity of the modeling simplifications is confirmed by full three-dimensional and gometrically non-linear modeling of the post-processed design.

A robust formulation provides full length-scale control, avoidance of fragile hinges as well as insensitivity to e.g. under- and over-etching.