Optimal Design of Piezoelectric Microactuators: Linear vs Non-linear Modeling

Abstract

The main point of this work is the comparison between linear and geometrically non-linear elasticity modeling in the field of piezoelectric actuators fabricated at the micro-scale. Manufacturing limitations such as non-symmetrical lamination of the structure or minimum length scale are taken into account during the optimization process. The robust approach implemented in the problem also reduces the sensitivity of the designs to small manufacturing errors.

1 Introduction

The conceptual tool of topology optimization was initially designed for structural design, nevertheless, nowadays its use is not restricted only to this purpose. Some fields where its contribution has been crucial are the design of compliant mechanisms [5, 25], dynamics [4, 19], band gaps [7, 29] and metamaterials [30], amongst others.

The topology optimization method has played an important role in the optimal design of MEMS (micro-electro-mechanical systems), where the size of the devices typically is smaller than 1 mm. In [25] is presented the optimal design of compliant mechanisms based on the topology optimization method, where these mechanisms were fabricated at macro- and micro-scale. Concerning piezoelectric effect, [33] suggested a procedure based on topology optimization and homogenization methods to optimize unit cells for piezocomposites. Regarding thermal and electrothermal actuators, [26] and [27] optimized microdevices composed of one and two materials, respectively. A methodology of the design of MEMS under stochastic loads and boundary conditions is presented in [16].

In the last years many authors have also applied the topology optimization method to piezoelectric devices. A pioneering work is [31], where the authors designed the unit cell of 1–3 composites for hydrophone applications. In the field of piezoelectric actuators, [32] presented a method to design in-plane actuators by optimizing the host structure, but fixing the piezoelectric material layer. Kögl and Silva [12] considered the optimization of piezoelectric layer together with the polarization based on a three layer model. Carbonari et al. [3] and Luo et al. [15] optimized simultaneously the host structure and the piezoelectric distribution. The inclusion of a third variable, the spatial distribution of the control voltage (related to the polarization of the piezoelectric layers) in the optimization problem, was presented in [8] and improved in [9] by introducing an interpolation scheme in the tri-level actuation voltage term. New results are presented in [10] and [11] for in-plane and out-of-plane piezoelectric transducers, respectively. In [17] is optimized at the same time the structure and the piezoelectric profile in the context of actuators.

Recently, in prior works, [23] and [22] presented a systematic procedure to design static microtransducers and modal filters by optimizing simultaneously the structure layout and the polarization profile. The three layer model considers that both piezoelectric layers are perfectly bonded to the top and bottom of the host structure. Either in-phase or out-of-phase polarization of the two piezoelectric layers makes the structure move in-plane or out-of-plane, respectively. As shown in [13], at the micro-scale due to limitations in the fabrication techniques only one piezoelectric film can be deposited on the top of the surface. This is an important issue for actuators, since with only one piezoelectric layer the device moves in the in-plane and out-of-plane directions. This issue is overcome in [24], where unimorph piezoelectric microgrippers working in-plane are designed by optimizing simultaneously the host structure and the polarization profile of the piezoelectric layer.

Ruiz and Sigmund [21] improved the latter by using a geometrically non-linear model that is able to model large displacements. With regard to the topic of geometrical non-linearities in topology optimization, [2] was the pioneering work, using the total Lagrangian formulation. In [1] and [20] were presented the optimal design of compliant mechanisms taking into account this non-linearity. The robust design of compliant mechanisms that undergo large displacement was included in [14], adding random variations that model possible geometry errors. Wang et al. [36] suggests an interpolation scheme for fictitious domain and topology optimization approaches. The objective of the present paper is to present a comparison between the behavior of piezoelectric actuators when they are modeled by using linear elasticity and geometric non-linearities. The main novelty introduced in this work is the dependence of the external force (the piezoelectric one) on the design variables. Vertical displacements produced by a nonsymmetrical laminate are suppressed at some points of interest and a robust approach is used with the objective of controlling the minimum length scale and minimizing the effect of the small manufacturing errors.

The paper is organized as follows. In Sect. 2 the discrete formulation of the problem is described, including the finite element modeling and the robust approach implemented. Section 3 is focused on the numerical algorithm used to solve the problem. Examples with different boundary conditions are shown in Sect. 4. Section 5 is devoted to the comparison between the two different elasticity modeling, showing the importance of using the most suitable model. Finally, in Sect. 6 the conclusions of this work are presented.

2 Topology Optimization of Piezoelectric Microactuators

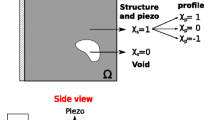
As design domain Ω we consider a rectangular plate clamped at its left side Γ _u, as represented in Fig. 1(top). A piezoelectric layer, that is sandwiched between two piezoelectric films, is perfectly bonded to the top surface of the host structure. This configuration is shown in Fig. 1(bottom).

Fig. 1

Top and side view of the piezoelectric device

When an input voltage V _in is applied to the electrodes, the electric field generated polarizes the piezoelectric layer. Thanks to the direct piezoelectric effect, the resulting force deforms the host structure. Due to a non-symmetrical lamination of the device, an out-of-plane displacement distorts the genuine in-plane behavior of the gripper. In such a kind of lamination the piezoelectric effect is divided into two components: an initial strain that makes the structure expand or contract and a flexural moment that produces the aforementioned vertical displacement.

This manufacturing limitation leads us to try to suppress this vertical deformation (in the z-axis) at some points of interest. The output of the actuator is modeled by a spring of stiffness k _out (that depends on the application). The points where the vertical displacement is suppressed and the output port will be defined for different examples in Sect. 4.

The goal of the problem is the maximization of the displacement at the output port, while the vertical displacement along the z-axis at some points of interest is suppressed as much as possible. This suppression is controlled by adding a constraint which relates the optimized and the canceled displacements. Finally, a volume constraint is used to control the amount of material used.

The optimization problem proposed involves two different design variables. The first one is a characteristic function χ _s ∈{0, 1}, that represents the structure layout and piezo as well (χ _s = 1) and void (χ _s = 0). The second variable is also a discrete function such that χ _p = {−1, 0, 1}, meaning negative, null or positive polarity.

The role of the latter is crucial in this problem for two reasons. The first one is that only the part of the host structure covered by electrode is electrically affected and then subjected to the piezoelectric force. The second concerns the piezoelectric force: this variable is related with the sign of the force. In other words, χ _p controls which parts of the structure works under compression or traction, and this is key to suppress undesired displacements.

In this work two different elasticity models are used, for small and large in-plane displacements. Nevertheless, the out-of-plane displacements are expected to be small, and then it can be studied separately from the in-plane one (decoupled problems). It will be shown in the examples that the fact of suppressing the vertical displacement at the output port makes out-of-plane displacements small in general. This assumption leads us to model out-of-plane displacements in both cases with linear elasticity theory.

As usual, topology optimization problems lacks of classical solution and the characteristic functions χ _s and χ _p must be relaxed into density variables ρ _s and ρ _p. The well-known SIMP (solid isotropic material with penalization) is used for this purpose. The Young’s modulus E _e of each element depends on the element density as follows:

$$\displaystyle \begin{aligned} E_e = ({\bar \rho}_{se})^p(E_0- E_{min}) + E_{min}, {} \end{aligned} $$

(1)

where E ₀ is the Young’s modulus of the base material, E _min > 0 is a small value used to avoid singularities of the stiffness matrix and p is the penalization exponent (typically p = 3). Afterwards, the domain is discretized in n _e finite elements with two variables per element.

The discrete formulation written as a topology optimization [21, 24] problem becomes:

$$\displaystyle \begin{aligned} \max_{{\boldsymbol \rho}_s,{\boldsymbol \rho}_p}:\;\;\; u_1({\boldsymbol \rho}_s,{\boldsymbol \rho}_p) \end{aligned}$$

s.t.: In-plane and out-of-plane equilibrium equations:

$$\displaystyle \begin{aligned} \begin{cases} {\mathbf{r}}_{ip}({\boldsymbol \rho}_s,{\boldsymbol \rho}_p,{\mathbf{U}}_{ip}) = \mathbf{0} \vspace{0.1cm}\\ {\mathbf{r}}_{op}({\boldsymbol \rho}_s,{\boldsymbol \rho}_p,{\mathbf{U}}_{op}) = \mathbf{0} \end{cases} \end{aligned}$$

Displacements:

$$\displaystyle \begin{aligned} \begin{cases} u_1 = {\mathbf{L}}_1^T{\mathbf{U}}_{ip} \vspace{0.1cm}\\ u_j = {\mathbf{L}}_j^T{\mathbf{U}}_{op}, \; j=1,\ldots,n_c \\ \end{cases} \end{aligned}$$

Constraints:

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle \left( \frac{u_j}{u_1} \right)^2 - \varepsilon_d^2 \leq 0, \; j=1,\ldots,n_c \vspace{0.1cm}\\ \displaystyle \frac{{\mathbf{1}}^T{\boldsymbol \rho}_s}{V} - 1 \leq 0 \vspace{0.1cm} \\ {\boldsymbol \rho}_s \in [\mathbf{0},\mathbf{1}] \vspace{0.1cm}\\ {\boldsymbol \rho}_p \in [\mathbf{-1},\mathbf{1}], \end{array} \end{aligned}$$

where ρ _s and ρ _p represent the structure layout and the polarization profile, respectively, L ₁ and L _j are vectors of zeros with 1 in the degree of freedom of interest, u ₁ is the in-plane displacement to be optimized, u _j is the out-of-plane displacements to be suppressed, n _c is the number of points where the vertical displacement is suppressed, ε _d is a small value that relates the suppressed and the optimized displacements, V  is the maximum volume allowed, r _ip and r _op are the residual vectors and finally, subscripts ip and op stand for the in-plane and out-of-plane case, respectively. The residual vectors are defined as the difference between the external forces (in our case the piezoelectric one) and the internal forces:

$$\displaystyle \begin{aligned} \begin{array}{l} {\mathbf{r}}_{ip} = {\mathbf{f}}_{ip}^{piezo} - {\mathbf{f}}_{ip}^{int} \vspace{0.1cm} \\ {\mathbf{r}}_{op} = {\mathbf{f}}_{op}^{piezo} - {\mathbf{f}}_{op}^{int}. \end{array} {} \end{aligned} $$

(2)

Linear Elasticity

For this particular case the dependence of the strain on the displacements is linear, and the elastic energy density can be defined as:

$$\displaystyle \begin{aligned} \phi = \displaystyle \frac{1}{2} \lambda \varepsilon_{kk}^2 + \mu \varepsilon_{ij}\varepsilon_{ij}, {} \end{aligned} $$

(3)

where λ and μ are the Lamé parameters and ε is the strain tensor. The stress tensor σ can be obtained by differentiating Eq. (3) with respect to the strain tensor. The discretization of the problem with finite elements is straightforward and the interested reader is referred to [18]. Finally, the residual vectors can be written as follows:

$$\displaystyle \begin{aligned} \begin{array}{l} {\mathbf{r}}_{ip} = {\mathbf{f}}_{ip}^{piezo}({\boldsymbol \rho}_s,{\boldsymbol \rho}_p) - \bigl( {\mathbf{K}}_{ip}({\boldsymbol \rho}_s) + {\mathbf{1}}_{out}k_{out} \bigr){\mathbf{U}}_{ip} = \mathbf{0} \\ {\mathbf{r}}_{op} = {\mathbf{f}}_{op}^{piezo} ({\boldsymbol \rho}_s,{\boldsymbol \rho}_p) - {\mathbf{K}}_{op}({\boldsymbol \rho}_s){\mathbf{U}}_{op} = \mathbf{0}, \end{array} \end{aligned} $$

where 1 _out is a zero matrix with 1 in the degree of freedom of the output port and K _ip and K _op are the stiffness matrices. The piezoelectric force depends on both design variables, ρ _p defines the sign of the force and ρ _s represents the fact that void areas are not electrically affected.

The piezoelectric force modeling can be found in [6] and it is not presented here. In addition, the same powerlaw dependence presented in Eq. (1) $\mathbf {R} = {\boldsymbol \rho }_{s}^p$ is used for the piezoelectric force generation. It is easy to see that the value of this interpolation function is 0 for void regions, and 1 for the solid ones. This interpolation scheme was presented in [22].

Non-linear Elasticity

In this case the displacements of the in-plane case are supposed to be large and a linear elasticity model is not appropriate to represent the behavior of the device. Instead, we will use a geometrically non-linear model, taking the assumption of large displacements but small strains. The Saint-Venant-Kichhoff model is used to represent this behavior. The expression for the stored elastic energy density is:

$$\displaystyle \begin{aligned} \phi = \displaystyle \frac{1}{2} \lambda E_{kk}^2 + \mu E_{ij}E_{ij}, {} \end{aligned} $$

(4)

where E is the Green-Lagrange strain tensor, that can be expressed as follows:

$$\displaystyle \begin{aligned} \mathbf{E} = \displaystyle \frac{1}{2} (\mathbf{F}{\mathbf{F}}^T-\mathbf{I}), \end{aligned} $$

being F the deformation gradient tensor defined as F = I + ∂ u∕∂ y. The second Piola-Kirchhoff stress tensor S is defined as the derivative of the stored elastic energy density presented in Eq. (4) with respect to the Green-Lagrange strain tensor.

Finally, the expression for the internal forces presented in Eq. (2) is:

$$\displaystyle \begin{aligned} \displaystyle {\mathbf{f}}_{ip}^{int,e} = \frac{\partial \int_{\varOmega}\phi_e\mathrm{d}\varOmega}{{\mathbf{u}}_{ip}}. \end{aligned} $$

where u _ip is the elemental displacement vector for element e.

Taking into account that the out-of-plane displacements are supposed to be small enough to be modeled with a linear elasticity model, the residual vector can be expressed as follows:

$$\displaystyle \begin{aligned} \begin{array}{l} {\mathbf{r}}_{ip} = \displaystyle{\mathbf{f}}^{piezo}_{ip} - \int_{\varOmega} {\mathbf{B}}_{ip}({\mathbf{U}}_{ip})\mathbf{S}\mathrm{d}\varOmega \vspace{0.1cm} \\ {\mathbf{r}}_{op} = {\mathbf{f}}^{piezo}_{op} - {\mathbf{K}}_{op}{\mathbf{U}}_{op}, \end{array} \end{aligned} $$

where B _ip is the in-plane non-linear strain displacement matrix. The residual of the out-of-plane equation depends linearly on the displacements, then to obtain U _op we must solve a system of linear equations. For the in-plane case the system of equations is non-linear and an iterative method must be used. For this problem we use the Newton-Raphson method, where the non-linear system to solve is:

$$\displaystyle \begin{aligned} {\mathbf{K}}_{t} {\boldsymbol \varDelta}{\mathbf{U}}_{ip} = {\mathbf{r}}_{ip}, \end{aligned}$$

where K _t is the tangent stiffness matrix defined as:

$$\displaystyle \begin{aligned} \displaystyle {\mathbf{K}}_ t= -\frac{\partial{\mathbf{r}}_{ip}}{\partial {\mathbf{U}}_{ip}} \end{aligned}$$

and the nodal displacement vector is updated by U _ip = U _ip + Δ U _ip. The detailed computations of the nodal force vectors, the strain displacement matrix and the tangent stiffness matrix can be found in [37].

The interpolation presented in [36] for the elastic stored energy density is implemented in this work. The objective of this scheme is to alleviate the issue of distorted and ill-converged void region mesh. This paper suggests basing the analysis of the solid region on the non-linear analysis and on the linear analysis for the void one, thereby eliminating mesh distortion and ill-convergence issues in the low density domain. The interpolation scheme for element e is:

$$\displaystyle \begin{aligned} \phi_e({\mathbf{u}}_{ip}) = [\phi(\gamma_e {\mathbf{u}}_{ip}) - \phi_L(\gamma_e{\mathbf{u}}_{ip}) + \phi_L({\mathbf{u}}_{ip})]E_e, \end{aligned}$$

where ϕ(⋅) is the stored elastic energy density, ϕ _L(⋅) is the stored elastic energy density under small deformations, both with unit Young’s modulus, and finally, γ _e is the interpolation factor. In order to differ between solid and void regions in intermediate steps of the optimization process, a smoothed Heaviside projection is used:

$$\displaystyle \begin{aligned} \gamma_e = \displaystyle \frac{\tanh(\beta_1 \rho_0) + \tanh\bigl(\beta_1 ({\bar \rho}_{se}^p - \rho_0) \bigr)}{\tanh(\beta_1 \rho_0) + \tanh\bigl(\beta_1 (1 - \rho_0) \bigr)}, \end{aligned}$$

being β ₁ the parameter that models the smoothness of the projection, ρ ₀ the threshold and ${\boldsymbol {\bar \rho }}_s$ the physical density, which will be introduced in the next section.

2.1 Robust Formulation

Having in mind the manufacturability of the designs, a robust formulation has been used with two goals: the first is the minimization of the objective to small manufacturing errors, the second one is the control of the minimum length scale in both, void and solid, avoiding the appearance of hinges. This approach was presented in [28] and [35].

This formulation consists in the use of three different projections: eroded, intermediate and dilated. The expression for a projection is:

$$\displaystyle \begin{aligned} \displaystyle {\boldsymbol {\bar \rho}}_s = \frac{\tanh(\beta_0 \eta) + \tanh\bigl(\beta_0({\boldsymbol {\tilde \rho}}_s - \eta)\bigr)}{\tanh(\beta_0 \eta) + \tanh\bigl(\beta_0(1 - \eta)\bigr)}, \end{aligned}$$

where β ₀ is a tunable parameter that represents the smoothness of the heaviside function, η is the threshold which can take values between 0 and 1, and ${\boldsymbol {\tilde \rho }}_s$ is the filtered density that is expressed as follows:

$$\displaystyle \begin{aligned} \displaystyle \rho_{se} = \frac{\displaystyle \sum_{i\in N_e}\omega({\mathbf{x}}_i)v_i\rho_{si}}{\displaystyle \sum_{i\in N_e}\omega({\mathbf{x}}_i)v_i}, \end{aligned}$$

where x _i is the center of element i, v _i the volume of element i, N _e the neighborhood of element e within a certain filter radius r specified by N _e = {i| ||x _i −x _e||≤ r}, and ω(x _i) = r −||x _i −x _e||.

From now on superscript q stands for the projection, meaning e erode, d dilate and i intermediate. The robust topology optimization problem is written as:

$$\displaystyle \begin{aligned} \max_{{\boldsymbol \rho}_s,{\boldsymbol \rho}_p}:\;\; \min_{q=\{e,i,d\}} \;\; \{u_1^q({\boldsymbol {\bar \rho}}_s,{\boldsymbol \rho}_p)\} \end{aligned}$$

s.t.: In-plane and out-of-plane equilibrium equations:

$$\displaystyle \begin{aligned} \begin{cases} {\mathbf{r}}_{ip}^q({\boldsymbol {\bar \rho}}_s^q,{\boldsymbol \rho}_p,{\mathbf{U}}_{ip}^q) = \mathbf{0} \vspace{0.1cm}\\ {\mathbf{r}}_{op}^q({\boldsymbol {\bar \rho}}_s^q,{\boldsymbol \rho}_p,{\mathbf{U}}_{op}^q) = \mathbf{0} \end{cases} \end{aligned}$$

Displacements:

$$\displaystyle \begin{aligned} \begin{cases} u_1^q = {\mathbf{L}}_1^T {\mathbf{U}}_{ip}^q \vspace{0.1cm}\\ u_j^q = {\mathbf{L}}_j^T {\mathbf{U}}_{op}^q, \; j=1,\ldots,n_c \end{cases} \end{aligned}$$

Constraints:

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle \left(\frac{u_j^q}{u_1^q}\right) - \varepsilon_d^2 \leq 0, \; j=1,\ldots,n_c \vspace{0.1cm} \\ \displaystyle \frac{{\mathbf{1}}^T {\boldsymbol {\bar \rho}}_s^d}{V_d^*} - 1 \leq 0 \vspace{0.1cm} \\ {\boldsymbol \rho}_s \in [\mathbf{0},\mathbf{1}] \vspace{0.1cm} \\ {\boldsymbol \rho}_p \in [\mathbf{-1},\mathbf{1}] \vspace{0.1cm} \\ q \equiv \{e,i,d\}, \end{array} \end{aligned} $$

where $V_d^*$ is the maximum volume for the dilated design. This value is computed at the beginning of the optimization process and then is update every 20 iterations following the next equation:

$$\displaystyle \begin{aligned} \displaystyle V_d^* = \frac{V^*}{V_i}V_d, \end{aligned}$$

being V ^∗ the maximum volume prescribed for the intermediate design and V _i and V _d the volume of the intermediate and dilated designs, respectively.

Since the max-min function is not differentiable, the problem is rewritten by using the so-called bound formulation [19]:

$$\displaystyle \begin{aligned} \max_{{\boldsymbol \rho}_s,{\boldsymbol \rho}_p}: \;\;\; \beta \end{aligned}$$

s.t.: In-plane and out-of-plane equilibrium equations:

$$\displaystyle \begin{aligned} \begin{cases} {\mathbf{r}}_{ip}^q({\boldsymbol {\bar \rho}}_s^q,{\boldsymbol \rho}_p,{\mathbf{U}}_{ip}^q) = \mathbf{0} \vspace{0.1cm}\\ {\mathbf{r}}_{op}^q({\boldsymbol {\bar \rho}}_s^q,{\boldsymbol \rho}_p,{\mathbf{U}}_{op}^q) = \mathbf{0} \end{cases} \end{aligned}$$

Displacements:

$$\displaystyle \begin{aligned} \begin{cases} u_1^q = {\mathbf{L}}_1^T {\mathbf{U}}_{ip}^q \vspace{0.1cm}\\ u_j^q = {\mathbf{L}}_j^T {\mathbf{U}}_{op}^q, \; j=1,\ldots,n_c \end{cases} \end{aligned}$$

Constraints:

$$\displaystyle \begin{aligned} \begin{array}{l} -u_1^q \leq \beta \vspace{0.1cm} \\ \displaystyle \left(\frac{u_j^q}{u_1^q}\right) - \varepsilon_d^2 \leq 0, \; j=1,\ldots,n_c \vspace{0.1cm} \\ \displaystyle \frac{{\mathbf{1}}^T {\boldsymbol {\bar \rho}}_s^d}{V_d^*} - 1 \leq 0 \vspace{0.1cm} \\ {\boldsymbol \rho}_s \in [\mathbf{0},\mathbf{1}] \vspace{0.1cm} \\ {\boldsymbol \rho}_p \in [\mathbf{-1},\mathbf{1}] \vspace{0.1cm} \\ q \equiv \{e,i,d\}, \end{array} \end{aligned}$$

being β a new variable that does not depend on the design variables ρ _s and ρ _p and resolves the issue of the non-differentiability of the max-min function.

3 Numerical Implementation

The well-known MMA (Method of Moving Asymptotes, [34]) is used to solve the optimization problem. This algorithm is included inside the group of descent methods, which require information about the objective function, constraints and the sensitivities of both. The adjoint method is used to compute the sensitivities with respect to both design variables, ρ _s and ρ _p, but these computations are not the objective of this work, and this is why they are not included here.

The complete process algorithm in a pseudo code looks like:

Pre-process

• 1. Define dimensions, boundary conditions and material properties of the plate. Input parameters like V _in, ε _d and V  must be fixed.

• 2. Initialize both design variables, ρ _s with ρ _se = V  and ρ _p with ρ _pe = 1.

Optimization Algorithm

• 3. Compute the physical densities ${\boldsymbol {\bar \rho }}_s$ by filtering the structural density ρ _s and then projecting with three different thresholds.

• 4. Solve the finite element problems for the three different physical densities:

  • For the in-plane case.

  • For the out-of-plane case.

• 5. Extract the displacements $u_1^q$ and $u_j^q$ from the global displacements vectors and compute the value of the objective function and constraints.

• 6. Compute the sensitivities of the objective function and constraints.

• 7. Update design variables ρ _s and ρ _p by using MMA.

• 8. Until convergence, update parameters β ₀ and $V_d^*$ and go back to step 3.

Post-process

• 9. Plot the optimized designs.

4 Examples

In this section three actuators with different boundary conditions will be presented to show the validity of our method. For the sake of brevity, all the examples have been obtained using a geometrically non-linear modeling.

The materials used for the three different actuators remain constant. The host layer with a thickness of t = 5 μm is made of silicon with Young’s modulus E ₀ = 130 GPa and Poisson’s coefficient ν = 0.3. The piezoelectric film with thickness t _p = 0.5 μm is made of PZT with E ₀ = 67 GPa, ν = 0.3 and d ₃₁ = 190 pm. The stiffness of the void is chosen to be small compared to the stiffness of the solid one, E _min = 10⁻⁹ E ₀. The minimum length scale is set to 22.5 μm with η = 0.3 and β ₀ = 1 and doubling its value each 50 iterations. Concerning the interpolation scheme of the elastic stored energy density, the values of the parameters of the projection are fixed to β ₁ = 500 and ρ ₀ = 0.01. The maximum volume fraction of the designs is V ₀ = 40%. Finally, the values of the inputs are V _in = 1000 V, k _in = 1000 N/m and ε _d = 5%.

The design domain Ω will change for the different examples and then its dimensions will be shown in each particular case.

4.1 Maximizing Displacement in Horizontal Direction

A square plate-type structure clamped at its left side is considered as design domain Ω. The objective is the maximization of the displacement u ₁ while u ₂ is suppressed. Boundary conditions and dimensions of the plate are shown if Fig. 2.

Fig. 2

Boundary conditions for the first example

The result of the optimization process is shown in Fig. 3. For the sake of brevity, only the intermediate projection (blueprint design) is presented. The structural layout (${\boldsymbol {\bar \rho }_s}$) is shown in Fig. 3(left), where black and white mean solid and void areas, respectively. There is no gray areas (microstructure) in the optimized design, meaning that the projection method is working properly. The minimum length scale imposed on both, solid and void, is represented with the black circle. The electrode profile (ρ _p) is shown in Fig. 3(right), where cyan and orange represent parts of the structure with opposite polarization. The in-plane displacement is u ₁ = 122 μm, while the out-of-plane u ₂ is smaller than the 5% of u ₁. As can be seen, the in-plane displacement is bigger than the 5% of the length of the plate. This value remarks the importance and is the motivation of using a geometrically non-linear modeling.

Fig. 3

Structural layout (left) and polarization profile (right) for the first boundary conditions. The black circle indicates the minimum length scale

4.2 Maximizing Displacement in Horizontal Direction Including Void Passive Area

There are two differences with respect to the previous example: the sense of the displacement to be optimized and the inclusion of a void passive area in the middle of the domain. Boundary conditions are presented in Fig. 4.

Fig. 4

Boundary conditions for the second example

The optimized design are presented in Fig. 5. The structural layout is shown in Fig. 5(left) and the polarization profile in Fig. 5(right). In this case the in-plane displacement is u ₁ = 104 μm.

Fig. 5

Structural layout (left) and polarization profile (right) for the second boundary conditions. The black circle indicates the minimum length scale

4.3 Maximizing Displacement in Vertical Direction Including Void Passive Area

Boundary conditions and passive area are shown in Fig. 6. This configuration defines a particular case of actuators: grippers. Interested reader is referred to [24] and [21], where this problem is fully described. As can be seen one passive area has been added: a void passive area necessary to have enough space to grab objects.

Fig. 6

Boundary conditions for the third example

Optimized design for the new boundary conditions is shown in Fig. 7. Structural layout and polarization profile are presented in Fig. 7(left) and (right), respectively. The in-plane displacement of the gripper is u ₁ = 140 μm.

Fig. 7

Structural layout (left) and polarization profile (right) for the third boundary conditions. The black circle indicates the minimum length scale

5 Comparison Between Linear and Non-linear Modeling

In this section we show the importance of using the geometrically non-linear modeling when the displacements are big enough (> 5% of the length of the domain). In Fig. 8 the evolution of the output displacement (u ₁) is plotted as a function of the input voltage. Blue line represents the linear modeling of the displacements. In this case the optimized design does not change when the input voltage is increased and the evolution of the output is linear. The green line shows the geometrically non-linear modeling of the displacements. For this particular case, the optimized designs change when the input voltage in increased, actually, the higher the input, the greater the difference between both models. As expected, for low voltages, both designs are the same.

Fig. 8

Evolution of the output displacement

6 Conclusions

In this paper, different kind of piezoelectric actuators have been obtained by using the topology optimization method. The out-of-plane displacement caused by unsymmetrical lamination of the piezoelectric actuator (which is a real limitation when fabricating at micro-scale) is suppressed in order to get genuine in-plane actuators. This is obtained by adding an additional constraint to the optimization problem for each point where we want to cancel the out-of-plane bending.

Two different modelings have been used in this work, a linear model used for low inputs and a geometrically non-linear one for high voltages where the displacements are big compared to the size of the device. In both cases the out-of-plane displacement has been modeled with the linear approach, since these displacements are small in general and this allows us to save computational time. In addition, an elastic energy interpolation scheme has been used with the objective of alleviating convergence problems due to the excessive distortion of low density elements.

Finally, in order to ensure robustness (avoiding the appearance of hinges) and manufacturability (controlling the minimum length scale) of the optimized designs, a robust formulation approach has been used in this problem.