1 Introduction

Online kernel learning [13, 18, 31] is an efficient method for addressing the issues of classification and regression in nonlinear environments. A class of kernel adaptive filters (KAFs) is proposed using the online kernel learning method in the reproducing kernel Hilbert space (RKHS) [3, 6, 17, 28]. The main idea of KAF is to transform the input data into a high-dimensional feature space and then perform traditional adaptive filters [30], e.g., the least mean square (LMS) algorithm, affine projection algorithm (APA), and recursive least squares algorithm (RLS) in the RKHS. The reason for choosing the RKHS is that it can provide the linearity, convexity, and universal approximation capabilities [3, 5, 28]. To improve the calculation efficiency in the RKHS, the kernel trick based on the Mercer kernel [12, 17, 24, 25, 28] is used to calculate the inner product in the RKHS. The LMS, APA, and RLS algorithms are developed in the RKHS to generate the kernel least mean square (KLMS) algorithm [24, 28], kernel affine projection algorithm (KAPA) [25, 28], and kernel recursive least squares (KRLS) algorithm [12, 28], respectively. The filtering performance of traditional adaptive filters in terms of the accuracy and robustness is therefore improved by KAFs. Among these aforementioned KAFs, the KLMS is simplest in both computational and space complexities.

However, the filter network of KAF [12, 24, 25, 28] linearly grows with the length of training data, which incurs large computational burden. A sparsification method is therefore required to curb the growth of the network size by reserving the chosen input data as centers of the codebook. The commonly used sparsification methods include the novelty criterion (NC) [27], the prediction variance criterion (PVC) [10], the approximate linear dependency (ALD) criterion [12], the surprise criterion (SC) [23], and the quantized approach [8, 9, 15, 19, 22, 26]. In these sparsification methods, redundant data are removed by setting different threshold parameters, thus leading to different sparsification networks and filtering performance. Among these sparsification methods, the quantized approach is the simplest and the most efficient method for constructing the filter network. In the quantized approach, only the Euclidean distance between the current input and the existing centers in the codebook is used as a criterion for constructing a sparsification network. Therefore, Chen et al. applied the quantized approach to the KLMS for obtaining the quantized KLMS (QKLMS) [8].

It is interesting to note that the network size based on the aforementioned sparsification methods is not fixed. However, in the case of limited computational capability and storage, the fixed-size network structure is necessary for practical applications. Generally, the methods based on a fixed-size network include the significance measure [33, 38], the random Fourier features [4, 36], and the Nyström method [11, 21, 35, 36]. The significance measure keeps the codebook size fixed by pruning the least significant center when a new input is required to be added to the codebook. However, the calculation of significance requires extra computation. Unlike the significance measure, the random Fourier features and the Nyström method generate a vector representation of data to approximate the high-dimensional mapping. The random Fourier features approximate the kernel function using the kernel’s Fourier transform with random features [14, 29], and the Nyström method uses a low-rank matrix to approximate the kernel matrix. In addition, the chosen random Fourier features are independent of the input data [4, 36]. And the Nyström method samples the inputs from the input data with some distribution, which is data dependent [11, 21, 35, 36]. Therefore, due to the dependence of data, the Nyström method can provide a more efficient network structure than the random Fourier features [36]. The first two methods based on a fixed-size network have already been successfully applied to KAFs, e.g., the fixed-budget QKLMS (QKLMS-FB) [38], the simplified QKLMS-FB (SQKLMS-FB) [33], and the random Fourier features KLMS (RFFKLMS) [4].

In this paper, we propose a novel kernel least mean square algorithm based on the Nyström method (NysKLMS) by applying the approximation theory of the Nyström method to the KLMS. The Nyström method is used to approximate eigenfunctions in the RKHS with the chosen points [35], and thus, the input is transformed into a fixed-dimensional space to approximate the mapping in the RKHS. Therefore, the proposed NysKLMS algorithm provides a fixed network size in advance. To evaluate the filtering accuracy of NysKLMS, we also derive the steady-state excess mean square error (EMSE) theoretically.

2 KLMS

A continuous nonlinear input-output mapping f: \(\mathbb {R}^D\rightarrow \mathbb {R}\) can be described as

$$\begin{aligned} d = {f}(\mathbf x ), \end{aligned}$$
(1)

where \(\mathbf x \in \mathbb {X}\subseteq \mathbb {R}^D\) is the input vector and \(d\in \mathbb {R}\) is the corresponding desired output. The input–output pairs \(\{(\mathbf x (1),d(1)),(\mathbf x (2),d(2)),\ldots ,(\mathbf x (n),d(n)),\ldots \}\) are used to estimate the mapping \(f(\cdot )\), and the estimated output y(n) of d(n) is therefore obtained. An adaptive filter is constructed using a cost function based on the difference between the desired output and the estimated one.

The cost function of LMS based on the minimum mean square error (MMSE) criterion is [30]

$$\begin{aligned} {J} =\frac{1}{2} {e{{\left( n \right) }^2}} , \end{aligned}$$
(2)

where the estimated error \( e\left( n \right) = d\left( n \right) - y\left( n \right) \) at discrete time n is the difference between \( d\left( n \right) \) and \( y\left( n \right) \). The MMSE criterion is a common choice for adaptive filters due to its simplicity, and the algorithms mentioned in this paper are all equipped with (2).

Generally, the structure with the inner product \(\mathbf w {\left( {n-1} \right) ^\mathrm{T}}{} \mathbf x \left( {n} \right) \) is used in an adaptive filter, where \(\mathbf w (n-1)\) is the weight vector and \((\cdot )^T\) is the transpose of a real vector. According to minimizing the cost function J in (2) at each iteration n, the optimal weight vector \({\mathbf{{w}}^*}\) is finally sought by the LMS. Due to the simpleness and efficiency, the gradient descent method [30] is used in the LMS to obtain the optimal solution to J in (2). Therefore, we can obtain the following update form of the weight vector in the LMS with the gradient descent method:

$$\begin{aligned} \mathbf{w }\left( {{n}} \right) = \mathbf{w }\left( {{{n}} - 1} \right) + {{\mu e}}\left( {{n}} \right) \mathbf{x }\left( {{n}} \right) , \end{aligned}$$
(3)

where \(\mu \) is the step size.

When the relationship \(f(\cdot )\) between the input and the output is highly nonlinear the KLMS can provide better filtering accuracy than the LMS. Actually, the KLMS [24, 28] can be regarded as the LMS in the RKHS [3, 6, 17, 28]. Assume that the weight vector at iteration n in the KLMS is denoted by \({\varvec{\Omega }}\left( {{n}} \right) \). Similar to (3), the weight vector update of KLMS can be expressed as:

$$\begin{aligned} {\varvec{\Omega }}\left( {n} \right) = {\varvec{\Omega }}\left( {{n} - 1} \right) + {{\mu e}}\left( {{n}} \right) {{\varvec{\varphi }}}\left( {\mathbf{x }\left( {{n}} \right) } \right) , \end{aligned}$$
(4)

where \({{\varvec{\varphi }}}\left( {\mathbf{{x}}\left( {{n}} \right) } \right) \) denotes the transformed input vector \({\mathbf{{x}}\left( {{n}} \right) }\). In the following, \({{\varvec{\varphi }}}\left( {\mathbf{{x}}\left( {n} \right) } \right) \) is denoted by \( {{\varvec{\varphi }}}\left( {n} \right) \) for simplicity.

However, it is difficult to calculate \({\varvec{\varphi }}(n)\) owing to its high dimension. Therefore, \({\varvec{\Omega }}({n})\) cannot be computed directly using (4). Given an initial weight \({\varvec{\Omega }}({0})=0\), we obtain \({\varvec{\Omega }}({n})\) by iterating

$$\begin{aligned} {\varvec{\Omega }}(n) = {\varvec{\Omega }}(0) + \mu \sum \limits _{i = 1}^n {e(i) \varvec{\varphi } (i)} =\mu \sum \limits _{i = 1}^n {e(i) \varvec{\varphi } (i)}. \end{aligned}$$
(5)

Then, the current estimated output can be derived as the following form of the inner product:

$$\begin{aligned} y(n) = {\varvec{\Omega }} {(n-1)^\mathrm{T}}\varvec{\varphi }(n) = \mu \sum \limits _{i = 1}^{n-1} {e(i)\varvec{\varphi } {{(i)}^\mathrm{T}}\varvec{\varphi } (n)}. \end{aligned}$$
(6)

The inner product in the RKHS can be easily computed by the kernel trick [12, 24, 25, 28], i.e.,

$$\begin{aligned} {\varvec{\varphi } }{\left( {n_1} \right) ^\mathrm{T}}{\varvec{\varphi } }\left( {n_2} \right) = \kappa (\mathbf x {(n_1)}, \mathbf x {(n_2)}), \end{aligned}$$
(7)

where \(\kappa (\cdot )\) is a kernel function. The commonly used kernel function in the RKHS is the following Gaussian kernel [24, 28]:

$$\begin{aligned} \kappa (\mathbf x {(n_1)}, \mathbf x {(n_2)}) = \exp \left( -\frac{{ {{\left\| \mathbf{x ({n_1}) - \mathbf x (n_2)} \right\| }^2}}}{{2{\sigma ^2}}}\right) , \end{aligned}$$
(8)

where \(\sigma \) is the kernel width. It can be seen from (8) that the use of kernel function can avoid the direct calculation in the high-dimensional feature space.

Therefore, (6) can be rewritten using the kernel trick as

$$\begin{aligned} y(n) = \mu \sum \limits _{i = 1}^{n-1} {e(i)\kappa (\mathbf x {(i)}, \mathbf x {(n)})}. \end{aligned}$$
(9)

It can be seen from (9) that the KLMS produces a growing radial basis function network [12, 24, 25, 28] by adding every new input as a center at each iteration. Therefore, the linear growth of the network increases the computational burden of KLMS and thus limits its online applications.

3 Proposed NysKLMS Algorithm

Actually, the transformed input \(\varvec{\varphi }(\mathbf x )\) in the RKHS can be constructed as

$$\begin{aligned} \varvec{\varphi }(\mathbf x )=\left[ \sqrt{\lambda _1}{\varvec{\phi }_1 (\mathbf x )}, \sqrt{\lambda _2}{\varvec{\phi }_2 (\mathbf x )},\ldots \right] ^\mathrm{T}, \end{aligned}$$
(10)

where \(\lambda _i\) and \(\varvec{\phi }_i\), \(i=1,2,\ldots \), are the eigenvalues and the eigenfunctions of the Mercer kernel, respectively [28]. The dimension of \(\varvec{\varphi }(\mathbf x )\) is infinite when the Gaussian kernel is adopted.

To avoid the calculation in an infinite dimension space and thus obtain a fixed-dimensional network, the Nyström method [11, 35, 36] is used to approximate the eigenfunctions with a fixed codebook. The eigenfunction problem can be described as follows:

$$\begin{aligned} \int {\kappa (\mathbf x ,\mathbf x ')\varvec{\phi }_i (\mathbf x ')d\mathbf x ' = \lambda _i } \varvec{\phi }_i (\mathbf x ), \end{aligned}$$
(11)

where \(\mathbf x , \mathbf x '\in \mathbb {X}\). The codebook is composed of the randomly chosen m input vectors, i.e., \(\mathbf C =\{ {{ \mathbf{x }}(1)},{{ \mathbf{x }}(2)},\ldots ,{{ \mathbf{x }}(m)}\}\) [11]. Using the codebook to approximate the integral yields

$$\begin{aligned} \int {\kappa (\mathbf x ,\mathbf x ')\varvec{\phi }_i (\mathbf x ')d\mathbf x ' }\approx \frac{1}{m}\sum \limits _{k = 1}^m {\kappa (\mathbf x ,{{ \mathbf{x }}(k)})} {\varvec{\phi }}_i ({{ \mathbf{x }}(k)}). \end{aligned}$$
(12)

Therefore, (11) can be rewritten as

$$\begin{aligned} \frac{1}{m}\sum \limits _{k = 1}^m {\kappa (\mathbf x ,{{ \mathbf{x }}(k)})} {\varvec{\phi }}_i ({{\mathbf{x }}(k)}) \approx \lambda _i {\varvec{\phi }}_i (\mathbf x ). \end{aligned}$$
(13)

It is equivalent to solve the eigenfunction problem in a subspace spanned by the codebook. Eq. (13) is therefore described in a matrix form

$$\begin{aligned} \mathbf G {{{\mathbf{U }}}_m}={{\mathbf{U }}_m}{{{\varvec{\Lambda }} }_m}, \end{aligned}$$
(14)

where \(\mathbf G \) is the kernel matrix constructed by \(\mathbf G _{ij}={\kappa } ({{ \mathbf{x }}(i)}, {{ \mathbf{x }}(j)})\) (\(1\le i, j \le m\)), \({{ {\varvec{\Lambda }} }_m} = \mathrm{diag}( {\lambda } _1^{(m)}, {\lambda } _2^{(m)},\ldots ,{\lambda } _m^{(m)})\) is the diagonal matrix with the diagonal elements being the eigenvalues of \(\mathbf G \) in a descending order, and \({{ {\mathbf{{U} }}}_m} = (\mathbf{u }_1^{(m)},\mathbf{u }_2^{(m)},\ldots ,\mathbf{u }_m^{(m)})\) is the matrix constructed by the corresponding eigenvectors of \(\mathbf G \). Rearranging (13) and (14), we have the following approximations:

$$\begin{aligned}&\lambda _i\approx {{ \lambda }^{(m)}_i}/{m}, \end{aligned}$$
(15)
$$\begin{aligned}&{\varvec{\phi }}_i ({{ \mathbf{x }}(j)})\approx \sqrt{m}{ \mathbf{u }}^{(m)}_i (j). \end{aligned}$$
(16)

Based on (15) and (16), the approximated eigenfunction [11] can be derived from (13) as

$$\begin{aligned} {{\hat{\varvec{\phi }} }_i}(\mathbf x ) = \frac{\sqrt{m}}{{{ \lambda }^{(m)}_i}}\sum \limits _{k = 1}^m {\kappa (\mathbf{x },{{ \mathbf{x }}(k)}){ \mathbf{u }}^{(m)}_i (k)}. \end{aligned}$$
(17)

Note that (17) can be regarded as a mapping of \(\mathbf x \) into the ith eigenvector. Substituting (15) and (17) into (10) and using m eigenvalues and eigenvectors, we can derive an approximated transformation of input \(\mathbf x (n)\) with a fixed-dimensional representation as follows:

$$\begin{aligned} \begin{aligned}&\mathbf z (\mathbf x (n)) \\&\quad =\left[ \sqrt{\lambda _1}{{\hat{\varvec{\phi }} }_1}(\mathbf x (n)), \sqrt{\lambda _2}{{\hat{\varvec{\phi }} }_2}(\mathbf x (n)),\ldots ,\sqrt{\lambda _m}{{\hat{\varvec{\phi }} }_m}(\mathbf x (n)) \right] ^\mathrm{T}\\&\quad ={{\varvec{\Lambda }}}_m^{ - \frac{1}{2}}{ \mathbf{U }}_m^\mathrm{T}{\left[ {\kappa (\mathbf{x (n),{{ \mathbf{x }}(1)}})},{\kappa (\mathbf{x (n),{{ \mathbf{x }}(2)}})},\ldots ,{\kappa (\mathbf{x (n),{{ \mathbf{x }}(m)}})}\right] ^\mathrm{T}}\\&\quad ={{\varvec{\Lambda }}}_m^{ - \frac{1}{2}}\mathbf{U }_m^\mathrm{T}{\varvec{\kappa }}(n)\\&\quad =\mathbf P {\varvec{\kappa }}(n), \end{aligned} \end{aligned}$$
(18)

where \(\mathbf P ={{\varvec{\Lambda }}} _m^{ - \frac{1}{2}}\mathbf{U }_m^\mathrm{T}\), \({\varvec{\kappa }}(n)={\left[ {\kappa (\mathbf{x (n),{{ \mathbf{x }}(1)}})},{\kappa (\mathbf{x (n),{{ \mathbf{x }}(2)}})},\ldots ,{\kappa (\mathbf{x (n),{{ \mathbf{x }}(m)}})}\right] ^\mathrm{T}}\). Denote \(\mathbf z (n)=\mathbf z (\mathbf x (n))\) for simplicity. The subspace which \(\mathbf z (n)\) belongs to is spanned by the codebook and has a fixed dimension. Therefore, the adaptive filter based on the transformed input \(\mathbf z (n)\) provides a linear filter structure. The approximated degree can be evaluated by the difference between \(\mathbf{z {{(n)}^\mathrm{T}}{} \mathbf z (n)}\) and \(\kappa (\mathbf x {(n)}, \mathbf x {(n)})\) as shown in [21].

Applying the gradient descent method [30] to the transformed input \(\mathbf z (n)\) yields the weight update of NysKLMS as

$$\begin{aligned} \mathbf w (n)=\mathbf w (n-1)+{\mu }e(n)\mathbf z (n). \end{aligned}$$
(19)

In the feature space, the estimated output at the nth iteration is derived by

$$\begin{aligned} y(n)=\mathbf w (n-1)^\mathrm{T}{} \mathbf z (n). \end{aligned}$$
(20)

Compared with (9), the estimated output of NysKLMS shown in (20) is obtained in a fixed-size network. We summarize the proposed NysKLMS algorithm in Algorithm 1. Considering online applications, we choose the first m input training data as the codebook, which is reasonable when the inputs are independent identically distributed (i.i.d.) [21].

Remark 1 The proposed NysKLMS algorithm inherently generates a sparsification structure due to a small codebook used, which is appropriate for online applications. In addition, The NysKLMS only uses a filter network of a fixed dimension and approaches the filtering performance of the KLMS with no sparsification.

Let N be the length of training data and m be the chosen codebook size, where \(m\ll N\). Denote the magnitude of complexity by \(O(\cdot )\). There exists the eigenvalue decomposition with the computational complexity \(O(m^3)\) in the NysKLMS, which can be ignored reasonably since the decomposition is calculated once in the whole training process. Therefore, the computational complexity of NysKLMS is O(m) which is equivalent to those of the sparsification algorithms, i.e., the QKLMS, the QKLMS-FB, and the RFFKLMS. Compared with the KLMS having the computational complexity O(i) (\(0<i\le N\)), the NysKLMS reduces the computational complexity with \(m\ll N\), significantly.

figure a

4 Mean Square Convergence Analysis

Suppose that \({f^*}\) is the unknown mapping required to learn. The desired output can be modeled by

$$\begin{aligned} d(n) = {f^*}(\mathbf x (n)) + v(n), \end{aligned}$$
(21)

where v(n) denotes the disturbance noise.

Since \(\mathbf z (n)\) is an approximation of \(\varvec{\varphi }(n)\), there exists the optimal weight vector that lies in the subspace spanned by the transformed input sequence thanks to the universal approximation property in the RKHS [3, 5, 7]. For the tractability of theoretical analysis, we first assume that \(\mathbf z (n)\) approximates \(\varvec{\varphi }(n)\) well and the optimal weight vector \(\mathbf{w ^*}\) exists in the following analysis.

The following reasonable assumptions are used for tractable analysis.

\(\mathbf A1 \): The noise v(n) is zero mean and i.i.d. with variance \(\sigma _v^2\mathrm{{ = }}E\left[ v^2{(n)}\right] \).

\(\mathbf A2 \): The noise v(n) is independent of the input data \(\mathbf x (n)\), which can show that v(n) is independent of the a priori estimation error \(e_a(n)\).

\(\mathbf A3 \): At steady state, \({\left\| { \mathbf{z } (n)} \right\| ^2}\) is independent of \(e_a(i)\).

These assumptions are frequently used in adaptive filters [1, 7, 8, 16, 20, 30, 37].

4.1 Stability Analysis

First, we derive the energy conservation relation for the NysKLMS. According to the optimal weight vector \(\mathbf{w ^*}\), we have \({f^*}(\mathbf x (n)) = \mathbf{w ^{*\mathrm{T}}}{} \mathbf z (n)\). Therefore, (21) can be rewritten as

$$\begin{aligned} d(n) = \mathbf{w ^{*\mathrm{T}}}{} \mathbf z (n) + v(n). \end{aligned}$$
(22)

The estimated error can be derived as

$$\begin{aligned} e(n)= & {} d(n) - y(n) \nonumber \\= & {} (\mathbf{w ^{*\mathrm{T}}}{} \mathbf z (n) + v(n)) - \mathbf w {(n - 1)^\mathrm{T}}{} \mathbf z (n) \nonumber \\= & {} \tilde{\mathbf{w }} {(n - 1)^\mathrm{T}}{} \mathbf z (n) + v(n)\nonumber \\= & {} {e_a}(n) + v(n), \end{aligned}$$
(23)

where \(\tilde{\mathbf{w }} (n - 1) = \mathbf{w ^*} - \mathbf w (n - 1)\) denotes the weight error vector and \({e_a}(n) = \tilde{\mathbf{w }} {(n - 1)^\mathrm{T}}{} \mathbf z (n)\) the a priori error.

Subtracting \(\mathbf{w ^*}\) from both sides of (19) yields

$$\begin{aligned} \tilde{\mathbf{w }} (n) = \tilde{\mathbf{w }} (n - 1) - \mu e(n)\mathbf z (n). \end{aligned}$$
(24)

Let \({e_p}(n) = \tilde{\mathbf{w }} {(n)^\mathrm{T}}{} \mathbf z (n)\) be the a posteriori error. The relation between \({e_p}(n)\) and \({e_a}(n)\) is derived from (24) as

$$\begin{aligned} {e_p}(n) = {e_a}(n) - \mu e(n)\mathbf z {(n)^\mathrm{T}}{} \mathbf z (n). \end{aligned}$$
(25)

Substituting (25) into (24) to eliminate e(n), we get

$$\begin{aligned} \tilde{\mathbf{w }} (n) = \tilde{\mathbf{w }} (n - 1) + ({e_p}(n) - {e_a}(n))\frac{\mathbf{z (n)}}{\mathbf{z {{(n)}^\mathrm{T}}{} \mathbf z (n)}}. \end{aligned}$$
(26)

Squaring both sides of (26) yields

$$\begin{aligned} \begin{aligned} \tilde{\mathbf{w }} {(n)^\mathrm{T}}\tilde{\mathbf{w }} (n)&= {\left[ \tilde{\mathbf{w }} (n - 1) + ({e_p}(n) - {e_a}(n))\frac{\mathbf{z (n)}}{\mathbf{z {{(n)}^\mathrm{T}}{} \mathbf z (n)}}\right] ^\mathrm{T}}\\&\quad \times \left[ \tilde{\mathbf{w }} (n - 1) + ({e_p}(n) - {e_a}(n))\frac{\mathbf{z (n)}}{\mathbf{z {{(n)}^\mathrm{T}}{} \mathbf z (n)}}\right] \\&= \tilde{\mathbf{w }} {(n - 1)^\mathrm{T}}\tilde{\mathbf{w }} (n - 1) + \frac{{e_p^2(n) - e_a^2(n)}}{\mathbf{z {{(n)}^\mathrm{T}}{} \mathbf z (n)}}. \end{aligned} \end{aligned}$$
(27)

Denote the weight error power (WEP) at the nth iteration by \(\left\| {\tilde{\mathbf{w }} (n)} \right\| ^2=\tilde{\mathbf{w }} {(n)^\mathrm{T}}\tilde{\mathbf{w }} (n)\). (27) can be rewritten as

$$\begin{aligned} \left\| {\tilde{\mathbf{w }} (n)} \right\| ^2 + \frac{{e_a^2(n)}}{\left\| { \mathbf{z } (n)} \right\| ^2} = \left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2 + \frac{{e_p^2(n)}}{{\left\| { \mathbf{z } (n)} \right\| ^2}}. \end{aligned}$$
(28)

Taking expectations of both sides of (28), we obtain the energy conservation relation of NysKLMS by

$$\begin{aligned} \begin{aligned} E\left[ {\left\| {\tilde{\mathbf{w }} (n)} \right\| ^2} \right] + E\left[ {\frac{{e_a^2(n)}}{{\left\| { \mathbf{z } (n)} \right\| ^2}}} \right] = E\left[ {\left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2} \right] + E\left[ {\frac{{e_p^2(n)}}{{\left\| { \mathbf{z } (n)} \right\| ^2}}} \right] . \end{aligned} \end{aligned}$$
(29)

Combining (25) and (29) to eliminate \({e_p}(n)\) yields

$$\begin{aligned} \begin{aligned} E\left[ {\left\| {\tilde{\mathbf{w }} (n)} \right\| ^2} \right]&=E\left[ {\left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2} \right] + {\mu ^2}E\left[ {{e^2}(n)} {\left\| { \mathbf{z } (n)} \right\| ^2}\right] \\&\quad - 2\mu E\left[ {e(n){e_a}(n)} \right] . \end{aligned} \end{aligned}$$
(30)

Substituting (23) into (30), we obtain

$$\begin{aligned} \begin{aligned} E\left[ {\left\| {\tilde{\mathbf{w }} (n)} \right\| ^2} \right]&=E\left[ {\left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2} \right] + {\mu ^2}E\left[ (e_a(n)+v(n))^2 {\left\| { \mathbf{z } (n)} \right\| ^2}\right] \\&\quad - 2\mu E\left[ ({e_a(n)+v(n)){e_a}(n)} \right] . \end{aligned} \end{aligned}$$
(31)

In (31), according to Assumptions \(\mathbf A1 \) and \(\mathbf A2 \), we have

$$\begin{aligned} 2\mu E\left[ ({e_a(n)+v(n)){e_a}(n)}\right] =2\mu E\left[ e_a^2(n)\right] . \end{aligned}$$
(32)

Further, according to Assumptions \(\mathbf A2 \) and \(\mathbf A3 \), we obtain

$$\begin{aligned} \begin{aligned}&{\mu ^2}E\left[ ({e_a(n)+v(n))^2}{\left\| { \mathbf{z } (n)} \right\| ^2}\right] ={\mu ^2}\left( E\left[ e_a^2(n)\right] +E\left[ v^2(n)\right] \right) E\left[ {\left\| { \mathbf{z } (n)} \right\| ^2}\right] . \end{aligned} \end{aligned}$$
(33)

According to \(\sigma _v^2 = E[v^2{(n)}]\), (33) can be rewritten as

$$\begin{aligned} \begin{aligned}&{\mu ^2}E\left[ {({e_a(n)+v(n))^2}}{\left\| { \mathbf{z } (n)} \right\| ^2} \right] ={\mu ^2}\left( E\left[ e_a^2(n)\right] +\sigma _v^2\right) E\left[ {\left\| { \mathbf{z } (n)} \right\| ^2}\right] . \end{aligned} \end{aligned}$$
(34)

Therefore, (31) is derived as

$$\begin{aligned} \begin{aligned} E\left[ \left\| {\tilde{\mathbf{w }} (n)} \right\| ^2\right]&= E\left[ \left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2\right] + {\mu ^2}\left( E\left[ e_a^2(n)\right] + \sigma _v^2\right) E\left[ {\left\| { \mathbf{z } (n)} \right\| ^2}\right] \\&\quad - 2\mu E\left[ e_a^2(n)\right] . \end{aligned} \end{aligned}$$
(35)

To ensure a convergence solution, the WEPs at the nth and \((n-1)\)th iterations satisfy

$$\begin{aligned} E\left[ {\left\| {\tilde{\mathbf{w }} (n)} \right\| ^2} \right] \le E\left[ {\left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2} \right] . \end{aligned}$$
(36)

Thus, substituting (36) into (35) gives

$$\begin{aligned} {\mu ^2}\left( E\left[ e_a^2(n)\right] + \sigma _v^2\right) E\left[ {\left\| { \mathbf{z } (n)} \right\| ^2}\right] - 2\mu E\left[ e_a^2(n)\right] \le 0. \end{aligned}$$
(37)

To make the weight error vector monotonically decrease, the step size should satisfy

$$\begin{aligned} 0 \le \mu \le \frac{{2E\left[ e_a^2(n)\right] }}{\left( {E\left[ e_a^2(n)\right] + \sigma _v^2}\right) E\left[ {\left\| { \mathbf{z } (n)} \right\| ^2}\right] }. \end{aligned}$$
(38)

4.2 Steady-State Mean Square Performance

To measure the steady-state performance of NysKLMS, we denote excess mean square error (EMSE) by \(S=\mathop {\lim }\limits _{n \rightarrow \infty } E\left[ e_a^2(n)\right] \).

Taking limits of both sides of (35) as \(n\rightarrow \infty \) yields

$$\begin{aligned} \begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } E\left[ \left\| {\tilde{\mathbf{w }} (n)} \right\| ^2\right]&= \mathop {\lim }\limits _{n \rightarrow \infty } E\left[ \left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2\right] \\&\quad + {\mu ^2}\left( S + \sigma _v^2\right) \mathop {\lim }\limits _{n \rightarrow \infty } E\left[ \left\| {\mathbf{z } (n)} \right\| ^2\right] - 2\mu S. \end{aligned} \end{aligned}$$
(39)

Define the autocorrelation matrix of \(\mathbf z (n)\) by \(\mathbf R _{{zz}}=E\left[ \mathbf z (n)\mathbf z (n)^\mathrm{T}\right] \). And we have the trace of \(\mathbf R _{{zz}}\) as \(\mathrm{{Tr}}(\mathbf R _{{zz}})=E\left[ \left\| {\mathbf{z }(n)}\right\| ^2\right] \). Supposing the WEP reaches a steady-state value, we obtain

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } E\left[ \left\| {\tilde{\mathbf{w }} (n)} \right\| ^2\right] = \mathop {\lim }\limits _{n \rightarrow \infty } E\left[ \left\| {\tilde{\mathbf{w }} (n - 1)} \right\| ^2\right] . \end{aligned}$$
(40)

Hence, we have

$$\begin{aligned} {\mu ^2}\left( S + \sigma _v^2\right) \mathrm{{Tr}}\left( \mathbf R _{{zz}}\right) = 2\mu S. \end{aligned}$$
(41)

According to (41), the EMSE of NysKLMS can be derived as

$$\begin{aligned} S= \frac{{\mu \sigma _v^2 \mathrm{{Tr}}\left( \mathbf R _{{zz}}\right) }}{{2 - \mu { \mathrm {Tr}}\left( \mathbf R _{{zz}}\right) }}. \end{aligned}$$
(42)

It can be seen from (42) that S is related to the step size, noise variance, and \(\mathrm{{Tr}}(\mathbf R _{{zz}})\). For comparison, the EMSE of KLMS in [7] is shown as follows:

$$\begin{aligned} S_1= \frac{{\mu \sigma _v^2 }}{{2 - \mu }}. \end{aligned}$$
(43)

Comparing (42) with (43), we see that that the NysKLMS can achieve the same steady-state performance as the KLMS on the condition of \({ \mathrm {Tr}}(\mathbf R _{{zz}})\rightarrow 1\).

Remark 2 The derivation of S is based on the assumption that \(\mathbf z (n)\) approximates \(\varvec{\varphi }(n)\) well. We have \({ \mathrm {Tr}}(\mathbf R _{{zz}})= 1\) due to \(\kappa (\mathbf x _n,\mathbf x _n)\equiv 1\). It can be seen from (18) that \(\mathbf z (n)\) is related to the parameters of m and \(\sigma \). Therefore, m and \(\sigma \) are chosen to satisfy \({ \mathrm {Tr}}(\mathbf R _{{zz}})\rightarrow 1\), and the EMSE of NysKLMS is verified on this condition.

5 Simulation Results

Simulations on system identification and nonlinear channel equalization are conducted to validate the performance of NysKLMS in the Gaussian and uniform noise environments. The representative algorithms, i.e., the KLMS-NC [27], the KLMS-SC [23], the QKLMS [8], the QKLMS-FB [38], the RFFKLMS [4], and the KLMS [24, 28], are chosen for comparison. The KLMS-NC, the KLMS-SC, and the QKLMS are the KLMS algorithms with sparsification. The QKLMS-FB and the RFFKLMS are the KLMS algorithms in the fixed-size network. The KLMS with no sparsification is used as the reference of performance comparison.

To evaluate the filtering performance, the mean square error (MSE) is defined as

$$\begin{aligned} \mathrm{MSE}=\frac{1}{T}\left( \sum \limits _{n = 1}^\mathrm{T} {{{\left( d(n) - y(n)\right) }^2}}\right) , \end{aligned}$$
(44)

where T is the length of testing data. For all simulations, 50 Monte Carlo runs are performed to reduce the disturbance.

5.1 System Identification

The block diagram of system identification with finite impulse response (FIR) is shown in Fig. 1 [2]. The desired output can be expressed as

$$\begin{aligned} d(n)=\mathbf w ^{*\mathrm{T}}{} \mathbf x (n)+v(n), \end{aligned}$$
(45)

where \(\mathbf x (n)\) is the input vector including delays of x(n) and \(\mathbf w ^{*}=[w_1^*,w_2^*,\ldots ,w_L^*]^\mathrm{T}\) denotes the optimal weight vector with L taps of the unknown system.

Fig. 1
figure 1

System identification based on adaptive filter

Full size image

In the following simulations, the weight vector of the FIR filter is set as \(\mathbf w ^*\)=[0.227, 0.460, 0.688, 0.460, 0.227]\(^\mathrm{T}\) with \(L=5\). The input signal x(n) is a Gaussian process with zero mean and unit variance.

First, to discuss the parameters selection, the relation between \({ \mathrm {Tr}}(\mathbf R _{{zz}})\) and m and \(\sigma \) is plotted in Fig. 2, which is calculated by averaging 2000 training data with different m and \(\sigma \). In Fig. 2, the x-axis denotes m with the range from 20 to 380 in 40 increments. The y-axis denotes \(\sigma \) with the range from 1 to 4 in 0.2 increments. The z-axis shows the value of \(\mathrm{{Tr}}(\mathbf R _{{zz}})\) in a color-mapped form. From Fig. 2, we find that \({ \mathrm {Tr}}(\mathbf R _{{zz}})\) gradually approaches 1 with the increase in m and \(\sigma \). When \({ \mathrm {Tr}}(\mathbf R _{{zz}})\) is greater than 0.995, it is approximately equal to 1. Therefore, from the region of \(\mathrm{{Tr}}(\mathbf R _{{zz}})>0.995\), we choose \(m=100\) and \(\sigma =3\) for the NysKLMS to approximate the KLMS.

To verify the steady-state mean square performance of NysKLMS, the training data of length 200,000 are used to ensure its convergence, and its EMSE is obtained by the average over the last 500 iterations.

Fig. 2
figure 2

\({\mathrm{Tr}}(\mathbf R _{{zz}})\) versus m and \(\sigma \)

Full size image
Fig. 3
figure 3

Simulated and theoretical EMSEs versus \(\mu \) (\(\sigma _v^2=0.05\))

Full size image

The simulated and theoretical EMSEs of NysKLMS versus step size \(\mu \) and noise variance \(\sigma _v^2\) in the Gaussian and uniform noises are shown in Figs. 3 and 4. From these two figures, we see that the simulated and theoretical EMSEs agree well. With the increase in \(\mu \) and \(\sigma _v^2\), the steady-state EMSEs of NysKLMS is decreasing. The filtering performance of NysKLMS is decided by the step size and noise variance on the condition of \({ \mathrm {Tr}}(\mathbf R _{{zz}})\rightarrow 1\).

Fig. 4
figure 4

Simulated and theoretical EMSEs versus \(\sigma _v^2\) (\(\mu =0.5\))

Full size image
Fig. 5
figure 5

Learning curves in terms of the testing MSE of different algorithms with \(m=100\)

Full size image

Then, we compare the learning curves of NysKLMS, KLMS-NC, KLMS-SC, QKLMS, QKLMS-FB, RFFKLMS, and KLMS in the presence of Gaussian noise. The Gaussian noise is zero mean with variance 0.01. In the simulations, a segment of 5000 points of the input sequence is chosen as the training data and 100 points as the testing data. The compared results are shown in Fig. 5. To guarantee the same codebook size and initial convergence rate, the parameters of these algorithms are configured as follows. The quantization sizes are set as 2.1 and 2 in the QKLMS and the QKLMS-FB, respectively. The step size and the kernel width are set as \(\mu =0.1\) and \(\sigma =3\), respectively, for all algorithms except for the KLMS-NC and the KLMS-SC with \(\mu =0.5\) and \(\sigma =1\). The thresholds in the KLMS-NC are \(\delta _1=1.45\) and \(\delta _2=0.08\). The thresholds in the KLMS-SC are \(T_1=200\) and \(T_2=0.55\), and the regularization parameter is set as 0.01. It can be seen from Fig. 5 that the learning curve of NysKLMS is almost the same as that of KLMS, which validates that the NysKLMS can approach the filtering performance of the KLMS with appropriate parameters. However, the NysKLMS only uses 100 centers in the codebook which is much smaller than 5000 centers in the KLMS. Hence, the NysKLMS with lower computational complexity approaches the filtering performance of the KLMS. In addition, the QKLMS and the QKLMS-FB also achieve the similar testing MSE to the KLMS and the NysKLMS and outperform the KLMS-NC and the KLMS-SC. The NysKLMS and the KLMS have faster convergence rate than the QKLMS, the QKLMS-FB, and the RFFKLMS in the beginning. The mean consumed time and testing MSEs of all algorithms in the steady state are shown in Table 1. Note that the numbers in italics in all the tables indicate the minima among the corresponding columns. It can be seen from this table that the KLMS-NC consumes the least time, but achieves the highest testing MSE compared with other algorithms. The testing MSE of NysKLMS approaches that of KLMS. Therefore, on the condition of a fixed network size, the NysKLMS consumes less time than the QKLMS, the QKLMS-FB, the KLMS-SC, and the KLMS.

Table 1 Mean consumed time and testing MSE in the steady state with \(m=100\)
Full size table
Fig. 6
figure 6

Learning curves in terms of the testing MSE of different algorithms with \(m=20\)

Full size image

Finally, we choose a smaller codebook size \(m=20\) to observe the filtering performance of the aforementioned algorithms with the same step size and Gaussian noise. The quantization sizes are set as 5.3 and 5 in the QKLMS and the QKLMS-FB, respectively. The thresholds in the KLMS-NC are \(\delta _1=2.4\) and \(\delta _2=0.12\). The thresholds in the KLMS-SC are \(T_1=200\) and \(T_2=2.2\). We see from Fig. 6 that the NysKLMS with 20 centers approaches the filtering performance of the KLMS with 5000 centers. The computational complexity is therefore reduced by the NysKLMS, significantly. Moreover, the NysKLMS has a smaller testing MSE than the RFFKLMS with the same codebook size, which means that the NysKLMS is more efficient than the RFFKLMS in system identification. Comparing the NysKLMS with the QKLMS and the QKLMS-FB, we see that the NysKLMS generates faster convergence rate but a similar testing MSE in the steady state. The KLMS-NC and the KLMS-SC incur severe performance degradation with a smaller codebook size. The mean consumed time and testing MSEs of all algorithms are shown in Table 2. It can be seen from this table that the NysKLMS with the same consumed time as the RFFKLMS consumes less time than other algorithms except for the KLMS-NC and simultaneously approaches the filtering performance of KLMS.

Table 2 Mean consumed time and testing MSE in the steady state with \(m=20\)
Full size table

5.2 Nonlinear Channel Equalization

The nonlinear channel equalization [28, 34] is often used in such fields as modeling digital satellite communication channels and digital magnetic recording channels. As Fig. 7 shows, this kind of model is a combination of a linear filter and a memoryless nonlinearity. The aim of the channel equalization is to recover the input signal s(n) with a low error rate according to the observed output r(n) disturbed by a noise v(n). p(n) is defined by \(p(n)=s(n)+0.5s(n-1)\), and r(n) is given by \(r(n)=p(n)-0.9p(n)^2+v(n)\). In this simulation, the data points for regression are constructed as \(\{\mathbf{x }(n), d(n)\}=\{[r(n), r(n+1),\ldots , r(n+5)]^\mathrm{T}, s(n-2)\}\), where a segment of 5000 points is chosen as the training data and the following 100 points as the testing data. In the following simulations, the Gaussian noise is zero mean with variance 0.1.

Fig. 7
figure 7

Structure of a nonlinear channel

Full size image
Fig. 8
figure 8

Learning curves in terms of the testing MSE of different algorithms with the same codebook size

Full size image

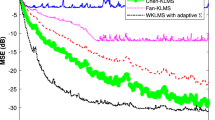
The compared results with the same codebook size \(m=200\) are shown in Fig. 8. The parameters of algorithms are configured for the same initial convergence rate and codebook size. The step size is set as \(\mu =0.5\) for all algorithms. The kernel width is \(\sigma =0.7\) for the KLMS-NC and the KLMS-SC and \(\sigma =2\) for others. The quantization sizes are set as 1.2 and 1 in the QKLMS and the QKLMS-FB, respectively. The thresholds are \(\delta _1=1.1\) and \(\delta _2=0.08\) for the KLMS-NC and \(T_1=1\) and \(T_2=0.3\) for the KLMS-SC. It can be seen from Fig. 8 that the NysKLMS with efficient approximation representation of the input, can provide better filtering performance than the QKLMS, the QKLMS-FB, the KLMS-NC, the KLMS-SC, and the RFFKLMS. And the NysKLMS using 200 centers achieves similar filtering performance to the KLMS that has no sparsification. The mean consumed time and testing MSEs of all algorithms are shown in Table 3. It can be seen from this table that the NysKLMS with less consumed time obtains lower testing MSE than other sparsification algorithms. The filtering performance of NysKLMS is almost the same as that of KLMS.

Table 3 Mean consumed time and testing MSE in the steady state with \(m=200\)
Full size table
Fig. 9
figure 9

Learning curves in terms of the same testing MSE of different algorithms

Full size image

In Fig. 9, the parameters of the QKLMS, the QKLMS-FB, the KLMS-NC, the KLMS-SC, the RFFKLMS, and the NysKLMS are chosen such that almost the same testing MSEs are obtained. Besides the same step sizes and kernel widths as those in Fig. 8, the quantization size is set as 0.8 in the QKLMS and the QKLMS-FB. The thresholds are \(\delta _1=0.5\) and \(\delta _2=0.37\) for the KLMS-NC and \(T_1=200\) and \(T_2=-0.2\) for the KLMS-SC. The corresponding mean codebook size and the consumed time of these algorithms are shown in Table 4. We see from this table that the NysKLMS with the same filtering performance as others consumes the least time and codebook size among all the compared algorithms. Therefore, from the aspect of sparsification of KLMS, the NysKLMS is more efficient than the QKLMS, the QKLMS-FB, the KLMS-NC, the KLMC-SC, and the RFFKLMS.

Table 4 Mean codebook size and consumed time with the same testing MSE
Full size table

6 Conclusion

In this paper, combining the kernel least mean square (KLMS) algorithm with the Nyström method, we propose a novel sparsification algorithm in a fixed-size network, named Nyström KLMS (NysKLMS). The Nyström method is used to construct a new vector representation from the input space to a relatively high-dimensional feature space. The representation of a fixed dimension can approximate the transformed input of KLMS, efficiently. The proposed NysKLMS algorithm avoids a growing network and thus reduces computational complexity with a small codebook size, significantly. The sufficient condition for the mean square convergence and the theoretical value of the steady-state EMSE in the NysKLMS are also derived for theoretical analysis. Analytical results of the NysKLMS are supported by simulations. From the aspect of the construction of sparsification network, the NystKLMS provides an efficient method for approximating the KLMS.