1 Introduction

The fourth circuit element popularly known as memristors was first postulated by Chua [15]. Until 2008 when researchers of HP laboratories fabricated a solid-state implementation of memristor, there were not many works on memristor realization [67]. Then, many other memristor models have been introduced [5, 8, 10, 16]. Memristors are considered to be highly nonlinear with nonvolatile characteristics and can be implemented with nanoscale technologies [5, 8, 10, 16]. To design memristor oscillators, a new kind of nonlinear circuits with oscillatory memories and periodically forced flux controlled memductance models are investigated [32, 47].

Memristor-based chaotic oscillators are widely investigated in the recent years. Circuits with two HP memristors in antiparallel have been demonstrated showing a variety of chaotic attractors for different values of components [11]. A current feedback op-amp-based memristor oscillators has been analyzed, and simulation results have been investigated [54]. A simple autonomous memristor-based oscillator with external sinusoidal excitation has been used to generate chaotic oscillations. A discrete model for this HP memristor has been derived and implemented using DSP chips [76] implementing memristor. Recently, a new hyperchaotic system with two memristors has been investigated and its application to image encryption has been analyzed.

Practical implementation of memristor-based chaotic circuits with off-the-shelf components is desired for real-time applications [46]. Memristor-based chaotic circuit for pseudorandom number generation has been analyzed with applications to cryptography [18]. Memristor-based chaotic circuits for text and image cryptography have been investigated, and the correlation analysis shows the effectiveness of the proposed cryptographic scheme over other encryption algorithms [82]. Memcapacitor-based chaotic circuits with a HP memristor have been proposed and implemented in DSP for further applications [77].

Recently, many researchers have discussed about fractional-order calculus and its applications [3, 22, 38]. Fractional-order nonlinear systems with different control approaches have been investigated in [2, 9, 84]. Fractional-order memristor-based no equilibrium chaotic and hyperchaotic systems have been proposed [55,56,57,58]. A novel fractional-order no equilibrium chaotic system has been investigated in [43], and a fractional-order hyperchaotic system without equilibrium points has been investigated in [12]. Memristor-based fractional-order system with a capacitor and an inductor has been discussed [21]. Numerical analysis and methods for simulating fractional-order nonlinear system have been proposed in [49], and MATLAB solutions for fractional-order chaotic systems have been discussed in [74].

Implementation of chaotic and hyperchaotic systems using field programmable gate arrays (FPGA) have been widely investigated [23, 72, 79]. Chaotic random number generators have been implemented in FPGA for applications in image cryptography [71]. A FPGA-implemented Duffing oscillator-based signal detector has been proposed [59]. Digital implementations of chaotic multiscroll attractors have been extensively investigated [72, 73]. Memristor-based chaotic system and its FPGA circuit have been discussed with their qualitative analysis [81]. A FPGA implementation of fractional-order chaotic system using approximation method has been investigated recently for the first time [55,56,57,58].

In this paper, we investigate the dynamical properties of a memcapacitor chaotic oscillator [51] and derive and analyze its fractional-order model. The entire paper is organized into eight sections with Sect. 1 giving the introduction and Sect. 7 the conclusion part. In the second section, we derive the dynamical dimensionless model of the memcapacitor oscillator. In the Sect. 3, we discuss the various dynamical properties of the oscillator like dissipativity, stability of equilibrium, Lyapunov exponents, bifurcation and bicoherence. In Sect. 4, we derive the dimensionless fractional-order model of the proposed memcapacitor oscillator and Sect. 5 deals with its dynamical analysis. In Sect. 6, we implement the fractional-order memcapacitor oscillator in field programmable gate arrays (FPGA).

2 Problem Formulation

Several memcapacitor models, including piecewise linear, quadric and cubic function models, memristor-based memcapacitor models have been discussed in several literatures [26, 48, 75, 83]. Some special phenomena such as hidden attractors [19, 20, 24, 36, 40] and coexistence attractors [7, 17, 44, 62] have been found in memcapacitor-based chaotic oscillators.

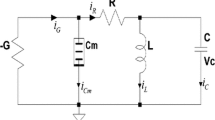
In this paper, we investigate the memcapacitor-based hyperchaotic oscillator discussed in [78] as shown in Fig. 1. The multistability of the proposed oscillator is discussed with the parameter space of the system rather than the initial conditions as discussed in [78].

Fig. 1
figure 1

Memcapacitor-based hyperchaotic oscillator

Full size image

In this circuit, \(R_1, R_2 \) are the resistances, \(L_1, L_2\) are the inductances, and G is the conductance. \(C_\mathrm{m}\) is the memcapacitor as discussed in [77]. The current flowing through the circuit is \(i_1, i_2\). Applying Kirchhoff’s current law to the circuit shown in Fig. 1, the change in flux is defined as

$$\begin{aligned} \frac{\mathrm{d}q_{C_\mathrm{m}} }{\mathrm{d}t}=i_1 +i_2 \end{aligned}$$
(1)

where \(q_{C_\mathrm{m}} \) is the charge through the memcapacitor. The current through the inductor \(L_1 \) is derived as,

$$\begin{aligned} \frac{\mathrm{d}i_1 }{\mathrm{d}t}=\frac{1}{L_1 }\left[ {-V_{C_\mathrm{m}} -i_1 R_1 +\left( {i_1 +i_2 } \right) R_0 } \right] \end{aligned}$$
(2)

and the current through the inductor \(L_2 \) is defined as,

$$\begin{aligned} \frac{\mathrm{d}i_2 }{\mathrm{d}t}=\frac{1}{L_2 }\left[ {-V_{C_\mathrm{m}} -i_2 R_2 +\left( {i_1 +i_2 } \right) R_0 } \right] \end{aligned}$$
(3)

The relationship between the voltage across the memcapacitor \(v_{C_\mathrm{M} } (t)\) and the charge \(q_{C_\mathrm{m}} \left( t \right) \) of the memcapacitor is defined as,

$$\begin{aligned} v_{C_\mathrm{M}} (t)=(\alpha +\beta \sigma ^{2})q_{C_\mathrm{m}} \left( t \right) \end{aligned}$$
(4)

where \(\alpha +\beta \sigma ^{2}\) is the inverse memcapacitance and \(\sigma \) is the time integral of charge \(q_{C_\mathrm{m}} \left( t \right) \) given by \(\sigma =\int _{t_0 }^t {q_{C_\mathrm{m}} \left( t \right) } \). Using Eqs. (2), (3), and (4), a fourth-order Memcapacitor system is derived as below,

$$\begin{aligned} \begin{array}{l} \frac{\mathrm{d}q_{C_\mathrm{m}} }{\mathrm{d}t}=i_1 +i_2 \\ \frac{\mathrm{d}i_1 }{\mathrm{d}t}=\frac{1}{L_1 }\left[ {-(\alpha +\beta \sigma ^{2})q_{C_\mathrm{m}} \left( t \right) -i_1 R_1 +\left( {i_1 +i_2 } \right) R_0 } \right] \\ \frac{\mathrm{d}i_2 }{\mathrm{d}t}=\frac{1}{L_2 }\left[ {-(\alpha +\beta \sigma ^{2})q_{C_\mathrm{m}} \left( t \right) -i_2 R_2 +\left( {i_1 +i_2 } \right) R_0 } \right] \\ \frac{\mathrm{d}\sigma }{\mathrm{d}t}=q_{C_\mathrm{m}} \left( t \right) \\ \end{array} \end{aligned}$$
(5)

where \(q_{C_\mathrm{m}} \left( t \right) \) is the charge through the memcapacitor, \(i_1 \) and \(i_2 \) are the circuit currents, \(v_{_{C_\mathrm{m}} } \) is the memcapacitor voltage, and \(\sigma \) is the integral parameter of the memcapacitor charge.

To derive a generalized 4D model, let us define \(x=q_{C_\mathrm{m}} \left( t \right) ,y=i_1, z=i_2, w=\sigma \) and the parameters as \(a=\frac{\alpha }{L_1 },b=\frac{\beta }{L_1 },c=\frac{\left( {R_0 -R_1 } \right) }{L_1 },d=\frac{R_0 }{L_1 },f=\frac{R_0 }{L_2 },e=\frac{\left( {R_0 -R_2 } \right) }{L_1 },m=\frac{\alpha }{L_2 },n=\frac{\beta }{L_2 }\).

By applying the assumptions in the derived Eq. (5), we arrive at the 4D dimensionless mathematical model of the memcapacitor system as,

$$\begin{aligned} \begin{array}{l} \frac{\mathrm{d}x}{\mathrm{d}t}=y+z \\ \frac{\mathrm{d}y}{\mathrm{d}t}=cy+dz-ax-bxw^{2} \\ \frac{\mathrm{d}z}{\mathrm{d}t}=fy+ez-mx-nxw^{2} \\ \frac{\mathrm{d}w}{\mathrm{d}t}=x \\ \end{array} \end{aligned}$$
(6)

The parameters of the above equation for which the system exhibits hyperchaotic oscillations are, \(a=5.8,b=2,c=2.6,d=0.1,e=-3.4,f=0.2,m=2.8,n=6.8\). The initial conditions are chosen as \(\left( {0.001,0.001,0.01,0.01} \right) \). Figure 2 shows the 2D projections of the strange attractor of system (6).

Fig. 2
figure 2

2D projections of the strange attractor of system (6)

Full size image

3 Dynamic Analysis of Hyperchaotic Memcapacitor Oscillator (HMCO)

The dynamic properties of the HMCO system such as dissipativity, equilibrium points, eigenvalues, Lyapunov exponents and Kaplan–Yorke dimension are derived and discussed in this section.

3.1 Dissipativity

In vector notation, the 4-D system (6) can be expressed as

$$\begin{aligned} {\dot{X}}=f(X)=\left[ {{\begin{array}{l} {f_1 (x,y,z,w)} \\ {f_2 (x,y,z,w)} \\ {f_3 (x,y,z,w)} \\ {f_4 (x,y,z,w)} \\ \end{array} }} \right] \end{aligned}$$
(7)

where

$$\begin{aligned} \left\{ {\begin{array}{l} f_1 (x,y,z,w)=y+z \\ f_2 (x,y,z,w)=cy+dz-ax-bxw^{2} \\ f_3 (x,y,z,w)=fy+ez-mx-nxw^{2} \\ f_4 (x,y,z,w)=x \\ \end{array}} \right. \end{aligned}$$
(8)

Let \(\Omega \) be any region in \(R^{4}\) with a smooth boundary and also, \(\Phi (t)=\Phi _t \left( \Omega \right) ,\) where \(\Phi _t \) is the flow of the vector field f. Furthermore, let V(t) denote the hyper volume of \(\Phi (t).\)

By Liouville’s theorem, we have

$$\begin{aligned} {\dot{V}}=\int _{\Phi (t)} {\left( {\nabla \cdot f} \right) } \mathrm{d}x\mathrm{d}y\mathrm{d}z \mathrm{d}w \end{aligned}$$
(9)

The divergence of the vector field f is easily calculated as

$$\begin{aligned} \nabla \cdot f=\frac{\partial f_1 }{\partial x}+\frac{\partial f_2 }{\partial y}+\frac{\partial f_3 }{\partial z}+\frac{\partial f_4 }{\partial w}=c+e=-0.8\le 0 \end{aligned}$$
(10)

Substituting (10) into (9), we obtain the first-order differential equation

$$\begin{aligned} {\dot{V}}(t)=-0.8V(t) \end{aligned}$$
(11)

Integrating (11), we obtain the unique solution as

$$\begin{aligned} V(t)=\exp (-0.8t) V(0) \text { for all }t\ge 0 \end{aligned}$$
(12)

It follows that \(V(t)\rightarrow 0\) exponentially as \(t\rightarrow \infty .\) This shows that the HMCO system (6) is dissipative.

3.2 Equilibrium Points

By equating \({\dot{X}}=0\), the HMCO system (6) shows three equations \(y+z=0,cy+dz=0\) and \(fy+ez=0\). As c, d, f, e are all positive the first possible solution for the equations are \(y=-\rho _1, z=\rho _1 \) for \(c=d,f=e\) and the corresponding equilibrium set is \([0,-\rho _1, \rho _1, \rho _2 ]\) and the second possible solution is \(y=z=0\) for \(c\ne d,f\ne e\) and the corresponding equilibrium set is \([0,0,0,\rho _3 ]\) where \(\rho _1, \rho _2, \rho _3 \) are arbitrary constants. Thus, the HMCO system has infinite number of equilibrium points located on a line (similar to the systems proposed in [4, 29, 30, 33, 51, 52]) with two possible equilibrium sets.

The Jacobian matrix of the HMCO system (6) for \(c=d,f=e\) or \(c\ne d,f\ne e\) is found as

$$\begin{aligned} J(X)=\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 0&{} 1&{} 1&{} 0 \\ {-a-b\rho _{2,3} ^{2}}&{} c&{} d&{} 0 \\ {-m-n\rho _{2,3} ^{2}}&{} f&{} e&{} 0 \\ 1&{} 0&{} 0&{} 0 \\ \end{array} }} \right] \end{aligned}$$
(13)

The constants \(\rho _2, \rho _3 \) have same effect on the system. The characteristic equation of the system is derived as,

$$\begin{aligned} \lambda ^{4}-(c+e)\lambda ^{3}+\left( {\begin{array}{l} a+m+ce-df \\ +b\rho _{2,3}^2 +n\rho _{2,3}^2 \\ \end{array}} \right) \lambda ^{2}+\left( {\begin{array}{l} af-ae-cm+dm \\ +dn\rho _{2,3}^2 -be\rho _{2,3}^2 \\ +bf\rho _{2,3}^2 -cn\rho _{2,3}^2 \\ \end{array}} \right) \lambda \end{aligned}$$
(14)

As per Routh–Hurwitz criterion, all the principal minors need to be positive in order to having stable equilibrium. The principal minors are,

$$\begin{aligned} \Delta _1= & {} \delta _1>0,\Delta _2 =\left| {{\begin{array}{l@{\quad }l} {\delta _1 }&{} {\delta _0 } \\ {\delta _3 }&{} {\delta _2 } \\ \end{array} }} \right|>0,\Delta _3 =>\left| {{\begin{array}{l@{\quad }l@{\quad }l} {\delta _1 }&{} {\delta _0 }&{} 0 \\ {\delta _3 }&{} {\delta _2 }&{} {\delta _1 } \\ 0&{} {\delta _4 }&{} {\delta _3 } \\ \end{array} }} \right|>0,\\ \Delta _4= & {} \left| {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {\delta _1 }&{} {\delta _0 }&{} 0&{} 0 \\ {\delta _3 }&{} {\delta _2 }&{} {\delta _1 }&{} {\delta _0 } \\ 0&{} {\delta _4 }&{} {\delta _3 }&{} {\delta _2 } \\ 0&{} 0&{} 0&{} {\delta _4 } \\ \end{array} }} \right| >0 \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} \delta _0 =1,\delta _1 =-(c+e),\delta _2 =a+m+ce-df+b\rho _{2,3}^2 +n\rho _{2,3}^2 \\ \delta _3 =af-ae-cm+dm+dn\rho _{2,3}^2 -be\rho _{2,3}^2 +bf\rho _{2,3}^2 -cn\rho _{2,3}^2, \delta _4 =0 \end{array} \end{aligned}$$

For the parameter values of \(a=5.8,b=2,c=2.6,d=0.1,e=-3.4,f=0.2,m=2.8,n=6.8\), the equilibrium is unstable and the system shows chaotic oscillations when the arbitrary constant \(\rho _{2,3} \) lies between the range \([-1.5,1.5]\) as discussed in [78].

3.3 Lyapunov Exponents and Kaplan–Yorke Dimension

Lyapunov exponents of a nonlinear system define the convergence and divergence of the states. Although there are different methods and important issues about this quantity [6, 34, 35, 37, 66], in this work we have used the famous method proposed in [80]. Lyapunov exponents (LEs) are necessary and more convenient for detecting hyperchaos in fractional-order hyperchaotic system. A definition of LEs for fractional differential systems was given in [41] based on frequency-domain approximations, but the limitations of frequency-domain approximations are highlighted in [70]. Time series-based LEs calculation methods like Wolf algorithm [80], Jacobian method [25] and neural network algorithm [45] are popularly known ways of calculating Lyapunov exponents for integer and fractional-order systems. To calculate the LEs of the HMCO system, we use the Jacobian method.

The Lyapunov exponents of the HMCO system are numerically found as

$$\begin{aligned} L_1 =0.2991,L_2 =0.07634,L_3 =0,L_4 =-1.0741 \end{aligned}$$
(15)

Since there are two positive Lyapunov exponents in (15), it is clear that the HMCO system (6) is hyperchaotic (Fig. 3).

Fig. 3
figure 3

Lyapunov exponents of the HMCO system for \(a=5.8,b=2,c=2.6,d=0.1,e=-3.4,f=0.2,m=2.8,n=6.8\) and initial conditions \(\left( {0.001,0.001,0.01,0.01} \right) \)

Full size image

We note that the sum of the Lyapunov exponents of the HMCO system (6) is negative. In fact,

$$\begin{aligned} L_1 +L_2 +L_3 +L_4 =-0.6987<0 \end{aligned}$$
(16)

This shows that the HMCO system (6) is dissipative.

Also, the Kaplan–Yorke dimension of the HMCO system (6) is derived as

$$\begin{aligned} D_{KY} =3+\frac{L_1 +L_2 +L_3 }{\left| {L_4 } \right| }=3.3495, \end{aligned}$$
(17)

which is fractional.

3.4 Bifurcation and Multistability in the HMCO System

Multistability possesses a threat for engineering systems because of its unpredicted behavior [17]. Many chaotic systems have shown multistability and coexisting attractors [28, 64, 65, 69]. Multistability analysis of symmetric Rossler system with amplitude controls provides good idea about multistability generates from the symmetrization [42]. Multistability in hidden attractor systems and control of multistability through the scheme of linear augmentation that can drive multistability to mono stability has been investigated [61]. Multistability in large system of the coupled pendula is investigated in [31]. The occurrence of multiheading chimera states of the coupled pendula which can create different types of synchronous states has been also discussed [31].

The HMCO system shows multistability as can be seen from Fig. 4 which shows the evidence of discontinuous bifurcations. The bifurcation diagram is obtained by plotting local maxima of the coordinate y in terms of the parameter d that is increased (or decreased) in tiny steps. The final state at each iteration of the parameter serves as the initial state for the next iteration. This strategy, known as forward and backward continuation, represents a simple way to localize the window in which the system develops multistability [63]. The existence of multistability can be confirmed by comparing the forward (dark blue color) and backward (red color) bifurcation diagrams as shown in Fig. 4a. Figure 4b shows the coexisting multiple attractors of the HMCO system for \(d=0.5\) and various initial conditions.

Fig. 4
figure 4

a Bifurcation of HMCO system for parameter d (forward continuation in dark blue color and backward continuation in red color). b Coexisting attractors of the HMCO system for \(d=0.5\) at initial conditions [1, 1, 0.1, 1] (red plot), [1, 1, 1, 1] (green plot), [0.8, 0.01, 0.01, 0.01] (blue plot) (Color figure online)

Full size image

3.5 Bicoherence

Higher-order spectra have been used to study the nonlinear interactions between frequency modes [39, 53]. Let x(t) be a stationary random process defined as,

$$\begin{aligned} x(t)=\sum _{n=1}^N {A_n } e^{j\omega _n t}+A_n^*e^{-j\omega _n t} \end{aligned}$$
(18)

where \(\omega \) is the angular frequency, n is the frequency modal index, and \(A_n \) are the complex Fourier coefficients. The power spectrum can be defined as,

$$\begin{aligned} P(\omega _k )=E[A_{\omega _k } A_{\omega _k }^*] \end{aligned}$$
(19)

and discrete bispectrum can be defined as,

$$\begin{aligned} B(\omega _k, \omega _j )=E[A_{\omega _k } A_{\omega _j } A_{\omega _k +\omega _j }^*] \end{aligned}$$
(20)

If the modes are independent, then the average triple products of Fourier components are zero resulting in a zero bispectrum [39]. The study of bicoherence is to give an indication of the relative degree of phase coupling between triads of frequency components. The motivation to study the bicoherence is twofold. First, the bicoherence can be used to extract information due to deviations from Gaussianity and suppress additive (colored) Gaussian noise. Second, the bicoherence can be used to detect and characterize asymmetric nonlinearity in signals via quadratic phase coupling or identify systems with quadratic nonlinearity. The bicoherence is the third-order spectrum. Whereas the power spectrum is a second-order statistics, formed from \(X^{\prime }\left( f \right) *X\left( f \right) \), where \(X\left( f \right) \) is the Fourier transform of \(x\left( t \right) \), the bispectrum is a third-order statistics formed from \(X\left( {f_j } \right) *X\left( {f_k } \right) *X^{\prime }\left( {f_j +f_k } \right) \). The bispectrum is therefore a function of a pair of frequencies \(\left( {f_j, f_k } \right) \) . It is also a complex-valued function. The (normalized) square amplitude is called the bicoherence (by analogy with the coherence from the cross-spectrum).The bispectrum is calculated by dividing the time series into M segments of length N_seg, calculating their Fourier transforms and bi-periodogram, then averaging over the ensemble. Although the bicoherence is a function of two frequencies, the default output of this function is a one dimensional output, the bicoherence refined as a function of only the sum of the two frequencies. The auto-bispectrum of a chaotic system is given by Pezeshki [50]. He derived the auto-bispectrum with the Fourier coefficients.

$$\begin{aligned} B(\omega _1, \omega _2 )=E[A(\omega _1 )A(\omega _2 )A^{*}(\omega _1 +\omega _2 )] \end{aligned}$$
(21)

where \(\omega _n \) is the radian frequency and A is the Fourier coefficients of the time series. The normalized magnitude spectrum of the bispectrum known as the squared bicoherence is given by

$$\begin{aligned} b(\omega _1, \omega _2 )=\left| {B(\omega _1, \omega _2 )} \right| ^{2}/P(\omega _1 )P(\omega _2 )P(\omega _1 +\omega _2 ) \end{aligned}$$
(22)

where \(P(\omega _1 ) \) and \(P(\omega _2 )\) are the power spectrums at \(f_1 \) and \(f_2 \).

Figure 5 shows the bicoherence contours of the FOHMCO system for state x and all states together, respectively. Shades in yellow represent the multifrequency components contributing to the power spectrum. From Fig. 5, the cross-bicoherence is significantly nonzero, and non-constant, indicating a nonlinear relationship between the states. As can be seen from Fig. 5a, the spectral power is very low as compared to the spectral power of all states together (Fig. 5b) indicating the existence of multifrequency nodes. Also Fig. 5b shows the nonlinear coupling (straight lines connecting multiple frequency terms) between the states. The yellow shades/lines and non-sharpness of the peaks, as well as the presence of structure around the origin in figures (cross-bicoherence), indicates that the nonlinearity between the states x, y, z, w is not of the quadratic nonlinearity and hence may be because of nonlinearity of higher dimensions. The most two dominant frequencies (\(f_1 ,f_2 )\) are taken for deriving the contour of bicoherence. The sampling frequency (\(f_s )\) is taken as the reference frequency. Direct FFT is used to derive the power spectrum for individual frequencies, and Hankel operator is used as the frequency mask. Hanning window is used as the FIR filter to separate the frequencies [60].

Fig. 5
figure 5

a Bicoherence plot of HMCO system for state x with the initial conditions as [0.001, 0.001, 0.001, 0.001] and sampling frequency of 1.5 KHz. b Bicoherence plot of HMCO system for all states with the initial conditions as [0.001, 0.001, 0.001, 0.001] and sampling frequency of 1.5 KHz

Full size image

4 Fractional-Order HMCO System (FOHMCO)

In this section, we derive the fractional-order model of the hyperchaotic memcapacitor oscillator (FOHMCO). There are three commonly used definition of the fractional-order differential operator, viz. Grunwald–Letnikov, Riemann–Liouville and Caputo [3, 22, 38].

We use the Grunwald–Letnikov (GL) definition, which is defined as

$$\begin{aligned} { }_aD_t^q f(t)= & {} \mathop {\lim }\limits _{h\rightarrow 0} \left\{ {\frac{1}{h^{q}}\sum _{j=0}^{\left[ {\frac{t-q}{h}} \right] } {(-1)^{j}\left( {{\begin{array}{l} q \\ j \\ \end{array} }} \right) } f(t-jh)} \right\} \nonumber \\= & {} \mathop {\lim }\limits _{h\rightarrow 0} \left\{ {\frac{1}{h^{q}}\Delta _h^q f(t)} \right\} \end{aligned}$$
(23)

where a and t are limits of the fractional-order equation, \(\Delta _h^q f(t)\) is generalized difference, h is the step size, and q is the fractional-order of the differential equation.

For numerical calculations, the above equation is modified as

$$\begin{aligned} { }_{(t-L)}D_t^q f(t)=\mathop {\lim }\limits _{h\rightarrow 0} \left\{ {h^{-q}\sum _{j=0}^{N(t)} {b_j \left( {f(t-jh} \right) } } \right\} \end{aligned}$$
(24)

Theoretically fractional-order differential equations use infinite memory. Hence, when we want to numerically calculate or simulate the fractional-order equations we have to use finite memory principal, where L is the memory length and h is the time sampling.

$$\begin{aligned} N(t)=\min \left\{ {\left[ {\frac{t}{h}} \right] ,\left[ {\frac{L}{h}} \right] } \right\} \end{aligned}$$
(25)

The binomial coefficients required for the numerical simulation are calculated as,

$$\begin{aligned} b_j =\left( {1-\frac{a+q}{j}} \right) b_{j-1} \end{aligned}$$
(26)

Using (23)–(26), the FOHMCO system is derived as,

$$\begin{aligned} \begin{array}{l} \frac{\mathrm{d}^{q_x }x}{\mathrm{d}t^{q_x }}=y+z \\ \frac{\mathrm{d}^{q_y }y}{\mathrm{d}t^{q_y }}=cy+dz-ax-bxw^{2} \\ \frac{\mathrm{d}^{q_z }z}{\mathrm{d}t^{q_z }}=fy+ez-mx-nxw^{2} \\ \frac{\mathrm{d}^{q_w }w}{\mathrm{d}t^{q_w }}=x \\ \end{array} \end{aligned}$$
(27)

where \(q_x ,q_y ,q_z ,q_w \) are the fractional orders of the FOHMCO system. Figure 6 shows the 2D phase portraits of the FOHMCO system with the same parameter and initial conditions as discussed in Sect. 2.

Fig. 6
figure 6

2D phase portraits of the FOHMCO system for the fractional order \(q=0.998\)

Full size image

5 Dynamic Analysis of the FOHMCO Chaotic Systems

5.1 Bifurcation with Fractional Order

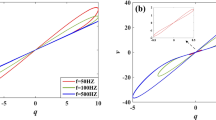
Most of the dynamic properties of the HMCO chaotic systems like the Lyapunov exponents and bifurcation with parameters are preserved in the FOHMCO system [55, 58] if \(q_i >0.992\) where \(i=x,y,z,w.\) As can be seen from Fig. 7a, bifurcation of the FOHMCO system for change in fractional order shows that the systems chaotic oscillations remains if \(q_i >0.992\). Based on our calculations, the system shows hyperchaotic behavior for \(0.993\le q\le 0.998\) and positive Lyapunov exponents (\(L_1 =0.3166,L_2 =0.08217)\) of the FOHMCO system appears when \(q=0.998\) against its largest integer-order Lyapunov exponents (\(L_1 =0.2991,L_2 =0.07634)\). Figure 7b–g shows the 2D phase portraits in Y–Z plane for various fractional orders.

Fig. 7
figure 7

a Fractional-order bifurcation plots and b–g 2D phase portrait (X–Y plane) of FOHMCO system for various fractional orders (b \(q=0.999\), c \(q=0.998\), d \(q=0.997\), e \(q=0.995\), f \(q=0.993\), g \(q=0.99\))

Full size image

5.2 Stability Analysis

Commensurate Order: For commensurate FOHMCO system of order q, the system is stable and exhibits chaotic oscillations if \(\left| {\arg (\mathrm{eig}(J_\mathrm{E} ))} \right| =\left| {\arg (\lambda _i )} \right| >\frac{q\pi }{2}\) where \(J_\mathrm{E} \) is the Jacobian matrix at the equilibrium E and \(\lambda _i \) are the eigenvalues of the FOHMCO system where \(i=1,2,3,4\). As seen from the FOHMCO system, the eigenvalues should remain in the unstable region and the necessary condition for the FOHMCO system to be stable is \(q>\frac{2}{\pi }\tan ^{-1}\left( {\frac{\left| {\mathrm{Im}\lambda } \right| }{\mathrm{Re}\lambda }} \right) \). The HOCM system shows two equilibrium sets \(y=-\rho _1 ,z=\rho _1 \) for \(c=d,f=e\) and the corresponding equilibrium set is \([0,-\rho _1 ,\rho _1 ,\rho _2 ]\) and the second possible solution is \(y=z=0\) for \(c\ne d,f\ne e\) and the corresponding equilibrium set is \([0,0,0,\rho _3 ]\) where \(\rho _1 ,\rho _2 ,\rho _3 \) are the arbitrary constants. For the parameter values discussed in section 2, the FOHOCM system shows stable chaotic oscillations if the arbitrary constant \(\rho _{2,3} \) lies in the range \([-1.5, 1.5]\). The characteristic equation of the FOHOCM system for commensurate order is

$$\begin{aligned}&\lambda ^{396}+4\lambda ^{298}+(-c-e)\lambda ^{297}+6\lambda ^{200}+(-3c-3e)\lambda ^{199}\\&\quad +\left( a+m+ce-df+bp23^{2}-n\rho _{2,3}^2 \right) \lambda ^{198}+4\lambda ^{102} \\&\quad +(-3c-3e)\lambda ^{101}+\left( 2a+2m+2ce-2df+2b\rho _{2,3}^2 +2n\rho _{2,3}^2 \right) \lambda ^{100}\\&\quad +\left( af-ae-cm+dm+dn\rho _{2,3}^2 \right. \\&\left. \quad -be\rho _{2,3}^2 +bf\rho _{2,3}^2 -cn\rho _{2,3}^2 \right) \lambda ^{99}+\lambda ^{4}+(-c-e)\lambda ^{3}\\&\quad +\left( a+m+ce-df+b\rho _{2,3}^2 +n\rho _{2,3}^2 \right) \lambda ^{2}+\left( af-ae \right. \\&\left. \quad -cm+dm+dn\rho _{2,3}^2 -be\rho _{2,3}^2 +bf\rho _{2,3}^2 -cn\rho _{2,3}^2\right) \lambda \end{aligned}$$

Incommensurate Order: The necessary condition for the FOHMCO system to exhibit chaotic oscillations in the incommensurate case is,\(\frac{\pi }{2M}-\min _i \left( {\left| {\arg (\lambda i)} \right| } \right) >0\) where M the LCM of the fractional orders. If \(q_x =0.99,q_y =0.99,q_z =0.98,q_w =0.98\), then \(M=100\). The characteristic equation of the system evaluated at the equilibrium is, \(\det (\mathrm{diag}[\lambda ^{Mq_x },\lambda ^{Mq_y },\lambda ^{Mq_z },\lambda ^{Mq_w }]-J_\mathrm{E} )=0\) and by substituting the values of M and the fractional orders,\(\det (diag[\lambda ^{99},\lambda ^{99},\lambda ^{98},\lambda ^{98}]-J_\mathrm{E} )=0\) and the characteristic equation is,

$$\begin{aligned}&\lambda ^{394}+2\lambda ^{297}+(2-e)\lambda ^{296}-c\lambda ^{295}+\lambda ^{200}\\&\quad +\,(4-e)\lambda ^{199}+(1-2e-2c)\lambda ^{198}+\left( n\rho _{2,3}^2 -c+m +ce-df\right) \lambda ^{197}\\&\quad +\left( b\rho _{2,3}^2 +a\right) \lambda ^{196}+2\lambda ^{102}+(2-2e-c)\lambda ^{101}\\&\quad +\left( n\rho _{2,3}^2 -2c-e+m+ce-df\right) \lambda ^{100} \\&\quad +\left( 2a+m+ce-df+2b\rho _{2,3}^2 +n\rho _{2,3}^2 \right) \lambda ^{99}\\&\quad +\left( af-ae-cm+dm+dn\rho _{2,3}^2 -be\rho _{2,3}^2 +bf\rho _{2,3}^2 -\,cn\rho _{2,3}^2 \right) \lambda ^{98}\\&\quad +\lambda ^{4}+(-c-e)\lambda ^{3} +\left( a+m+ce-df+b\rho _{2,3}^2 +n\rho _{2,3}^2 \right) \lambda ^{2}\\&\quad +\left( af-ae-cm+dm +\,dn\rho _{2,3}^2 -be\rho _{2,3}^2 +bf\rho _{2,3}^2 -cn\rho _{2,3}^2 \right) \lambda \end{aligned}$$

For the values of parameters mentioned in Sect. 2 and the value of \(\rho _{2,3} =1\), the approximated solution of the characteristic equation is \(\lambda _{394} =0.977\) and whose argument is zero and which is the minimum argument and hence the stability necessary condition becomes,\(\frac{\pi }{20}-0>0\) which solves for \(0.0785>0\) and hence the FOHMCO system is stable and chaos exists in the incommensurate system.

6 FPGA Implementation of the FOHMCO Systems

In this section, we discuss about the implementation of the proposed FOHMCO systems in FPGA [59, 73, 81] using the Xilinx (Vivado) System Generator. The three main approaches derived to solve fractional-order chaotic systems are frequency-domain method [14], Adomian decomposition method (ADM) [1] and Adams–Bashforth–Moulton (ABM) algorithm [68]. The frequency-domain method is not always reliable in detecting chaos behavior in nonlinear systems [70]. On the other hand, ABM and ADM are more accurate and convenient to analyze dynamical behaviors of a nonlinear system. Compared with the ABM, ADM yields more accurate results and needs less computing resources as well as memory resources [60]. Hence, the proposed FOHMCO system is implemented in FPGA by applying ADM scheme. The challenge of implementing the systems in FPGA is designing the fractional-order integrator which is not a readily available block in the System Generator [56,57,58]. As because the ADM algorithm converges fast [13], the first 6 terms are used to get the solution of FOHMCO system as in real cases, it is impossible to find the accurate value of x when t takes larger values [27]. Hence, we have to design a time discretization method. That is to say, for a time interval of \(t_i \) (initial time) to \(t_f \) (final time), we divide the interval into (\(t_n ,t_{n+1} )\) and we get the value of \(x(n+1)\) at time \(t_{n+1} \) by applying x(n) at time \(t_n \) using the relation \(x\left( {n+1} \right) =F\left( {x\left( n \right) } \right) \) [27].

We use the ADM method [1, 27] to discretize the fractional-order HMCO system for implementing in FPGA. The fractional-order discrete form of the dimensionless state equations for the FOHMCO system can be given as,

$$\begin{aligned} \begin{array}{l} x_{n+1} =\sum \limits _{j=0}^6 {A_1^j } \frac{h^{jq}}{\Gamma \left( {jq+1} \right) } \\ y_{n+1} =\sum \limits _{j=0}^6 {A_2^j } \frac{h^{jq}}{\Gamma \left( {jq+1} \right) } \\ z_{n+1} =\sum \limits _{j=0}^6 {A_3^j } \frac{h^{jq}}{\Gamma \left( {jq+1} \right) } \\ w_{n+1} =\sum \limits _{j=0}^6 {A_4^j } \frac{h^{jq}}{\Gamma \left( {jq+1} \right) } \\ \end{array} \end{aligned}$$
(28)

where \(A_i^j \) are the Adomian polynomials with \(i=1,2,3,4\) and \(A_1^0 =x_n , A_2^0 =y_n , A_3^0 =z_n , A_4^0 =w_n \)

The Adomian first polynomial is derived as,

$$\begin{aligned} \begin{array}{l} A_1^1 =A_2^0 +A_3^0 \\ A_2^1 =cA_2^0 +dA_3^0 -aA_1^0 -bA_1^0 \left( {A_4^0 } \right) ^{2} \\ A_3^1 =fA_2^0 +eA_3^0 -mA_1^0 -nA_1^0 \left( {A_4^0 } \right) ^{2} \\ A_4^1 =A_1^0 \\ \end{array} \end{aligned}$$
(29)

The Adomian second polynomial is derived as,

$$\begin{aligned} \begin{array}{l} A_1^2 =A_2^1 +A_3^1 \\ A_2^2 =cA_2^1 +dA_3^1 -aA_1^1 -b\left[ {A_1^1 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^1 } \right) ^{2}} \right] \\ A_3^2 =fA_2^1 +eA_3^1 -mA_1^1 -n\left[ {A_1^1 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^1 } \right) ^{2}} \right] \\ A_4^2 =A_1^1 \\ \end{array} \end{aligned}$$
(30)

The Adomian third polynomial is derived as,

$$\begin{aligned} A_1^3= & {} A_2^2 +A_3^2 \nonumber \\ A_2^3= & {} cA_2^2 +dA_3^2 -aA_1^2 -b\nonumber \\&\times \left[ {A_1^2 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^2 } \right) ^{2}+\frac{\Gamma (2q+1)}{\Gamma ^{2}(q+1)}\left[ {A_2^1 \left( {A_4^1 } \right) ^{2}} \right] } \right] \nonumber \\ A_3^3= & {} fA_2^2 +eA_3^2 -mA_1^2 -n\nonumber \\&\times \left[ {A_1^2 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^2 } \right) ^{2}+\frac{\Gamma (2q+1)}{\Gamma ^{2}(q+1)}\left[ {A_2^1 \left( {A_4^1 } \right) ^{2}} \right] } \right] \nonumber \\ A_4^3= & {} A_1^2 \end{aligned}$$
(31)

The Adomian fourth polynomial is derived as,

$$\begin{aligned} A_1^4= & {} A_2^3 +A_3^3 \nonumber \\ A_2^4= & {} cA_2^3 +dA_3^3 -aA_1^3 -b\nonumber \\&\times \left[ {\begin{array}{l} A_1^3 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^3 } \right) ^{2} \nonumber \\ +\frac{\Gamma (3q+1)}{\Gamma (q+1)\Gamma (2q+1)}\left[ {A_1^2 \left( {A_4^1 } \right) ^{2}+A_1^1 \left( {A_4^2 } \right) ^{2}} \right] \\ \end{array}} \right] \nonumber \\ A_3^4= & {} fA_2^3 +eA_3^3 -mA_1^3 -n\nonumber \\&\times \left[ {\begin{array}{l} A_1^3 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^3 } \right) ^{2} \\ +\frac{\Gamma (3q+1)}{\Gamma (q+1)\Gamma (2q+1)}\left[ {A_1^2 \left( {A_4^1 } \right) ^{2}+A_1^1 \left( {A_4^2 } \right) ^{2}} \right] \\ \end{array}} \right] \nonumber \\ A_4^4= & {} A_1^3 \end{aligned}$$
(32)

The Adomian fifth polynomial is derived as,

$$\begin{aligned} A_1^5= & {} A_2^4 +A_3^4 \nonumber \\ A_2^5= & {} cA_2^4 +dA_3^4 -aA_1^4 -b\nonumber \\&\times \left[ {\begin{array}{l} A_1^4 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^4 } \right) ^{2} \\ +\frac{\Gamma (4q+1)}{\Gamma (q+1)\Gamma (3q+1)}\left[ {A_1^3 \left( {A_4^1 } \right) ^{2}+A_1^1 \left( {A_4^3 } \right) ^{2}} \right] \\ \end{array}} \right] \nonumber \\ A_3^5= & {} fA_2^4 +eA_3^4 -mA_1^4 -n\nonumber \\&\times \left[ {\begin{array}{l} A_1^4 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^4 } \right) ^{2} \\ +\frac{\Gamma (4q+1)}{\Gamma (q+1)\Gamma (3q+1)}\left[ {A_1^3 \left( {A_4^1 } \right) ^{2}+A_1^1 \left( {A_4^3 } \right) ^{2}} \right] \\ \end{array}} \right] \nonumber \\ A_4^5= & {} A_1^4 \end{aligned}$$
(33)

The Adomian sixth polynomial is derived as,

$$\begin{aligned} A_1^6= & {} A_2^5 +A_3^5 \nonumber \\ A_2^6= & {} cA_2^5 +dA_3^5 -aA_1^5 -b\nonumber \\&\times \left[ {\begin{array}{l} A_1^5 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^5 } \right) ^{2} \\ +\frac{\Gamma (5q+1)}{\Gamma (q+1)\Gamma (4q+1)}\left[ {A_1^4 \left( {A_4^1 } \right) ^{2}+A_1^1 \left( {A_4^4 } \right) ^{2}} \right] \\ \end{array}} \right] \nonumber \\ A_3^6= & {} fA_2^5 +eA_3^5 -mA_1^4 -n\nonumber \\&\times \left[ {\begin{array}{l} A_1^5 \left( {A_4^0 } \right) ^{2}+A_1^0 \left( {A_4^5 } \right) ^{2} \\ +\frac{\Gamma (5q+1)}{\Gamma (q+1)\Gamma (4q+1)}\left[ {A_1^4 \left( {A_4^1 } \right) ^{2}+A_1^1 \left( {A_4^4 } \right) ^{2}} \right] \\ \end{array}} \right] \nonumber \\ A_4^6= & {} A_1^5 \end{aligned}$$
(34)

where \(h=t_{n+1} -t_n \) and \(\Gamma ({\bullet })\) is the gamma function. The fractional-order discretized system (28) is then implemented in FPGA and the necessary Adomian polynomials are calculated using (29)–(34). For implementing in FPGA, the value of h is taken as 0.001s and the initial conditions are fed into the forward register with fractional order taken as \(q=0.998\) for FOHMCO system. Figure 8 shows the RTL schematics of the FOHMCO system implemented in Kintex 7. Figure 9a shows the power consumed by FOHMCO system for order \(q=0.998\), and Fig. 9b shows the power consumed for various fractional orders and it can be seen that maximum power is consumed when the FOHMCO system exhibits the largest Lyapunov exponents. Table 1 shows the resources consumed with the consumed clock frequencies, and Fig. 10 shows the 2D phase portraits of the FPGA-implemented FOHMCO system.

Fig. 8
figure 8

RTL schematics of the FOHMCO system implemented in Kintex 7 (Device = 7k160t Package = fbg484 S). The sampling time of the system is kept at 0.01 s to minimize the time slack errors. The entire system is configured for a 32-bit operation

Full size image
Fig. 9
figure 9

a Power consumed by FOHMCO system for \(q=0.998\). b Power consumed by FOHMCO system for various fractional orders. It can be seen that maximum power of 0.204 W is consumed for order \(q=0.998\) when the FOHMCO system shows positive largest Lyapunov exponent

Full size image
Table 1 Resource consumption of FPGA-implemented FOHMCO system
Full size table
Fig. 10
figure 10

2D phase portraits of the FPGA-implemented FOHMCO system. The initial conditions and parameter values are taken as in Sect. 2, and the order of the system is \(q=0.998\)

Full size image

7 Conclusion

A newly proposed memcapacitor hyperchaotic oscillator with infinite number of equilibrium points was investigated. Multistability observed and coexisting chaotic oscillators were found. Dynamical analysis showed the existence of chaotic and hyperchaotic oscillators for various parameter values. The fractional-order model of the proposed hyperchaotic oscillator was derived and analyzed. Finally, the fractional-order model was implemented by FPGA and resource and power consumption details for various fractional orders were presented.