1 Introduction

Mem-elements have become fundamental aspects of the circuit theory due to their promising potential in many needed applications. The first postulated element was by Chua in 1971, and it was the memristor “memory resistor” [5] that was not experimentally fabricated as a solid-state device until HP announced that the missing element was physically implemented [29]. Then later, two elements were added to the mem-element family, which are the memcapacitor and meminductor [8, 9]. Moreover, Chua generalized his theory about mem-elements to include infinite higher-order mem-elements and presented them in [6]. The memcapacitor is one of the new infinite higher-order elements where the constitutive relation between the charge \(q(t)\) and the voltage \(v(t)\) has pinched hysteresis [6].

A lot of prospective research on the solid-state memcapacitor has been started to implement memcapacitors [4, 20, 22, 23, 28]. One of these implementation depends on using the concept and analysis of a multilayer structure embedded in the dielectric of a conventional capacitor was introduced as a solid-state memcapacitor in [22] where the multi-layer structure is formed by metallic layers separated by an insulator. This memcapacitor shows hysteretic charge–voltage and capacitance–voltage curves. However, it is not commercially available for experimental research, emulators have been introduced to emulate the behavior of the memcapacitor [3, 11, 25, 31]. In addition, the memcapacitor has been used in different applications such as synapses [16, 21], non-volatile memory arrays [23], and oscillators[17].

Various papers have been published to model and analyze mem-elements such as the memristor [7, 26, 27], the meminductor [14] and the memcapacitor [15]. However, there is no significant work in the area of the nonlinear mathematical modeling of the memcapacitor, which is very important since it describes the real behavior of the memcapacitor nearby the boundary which affects the response of the memcapacitor. The first nonlinear model of the memristor was initially proposed by Joglekar and Wolf [18] showing a symmetric window function and gives single-valued characteristics under any excitation source [7]. The Joglekar’s window function decreases as the boundary approaches until it reaches the boundary where it tends to zero as shown in Fig. 1. Then, this nonlinear window function was suggested to be used for modeling the memcapacitor [2]. The second common nonlinear model was proposed by Biolek et al. [2] where the window function depends on a discontinuous window decreasing toward zero as the boundary layer approaches any of the two ends and having sharp discontinuity transitions when the excitation source reverses its polarity. Biolek’s window function may allow for multi-valued characteristics under the sign-variation of the excitation source[7]. In this paper, the proposed analysis is based on Joglekar’s window function that is more suitable for most mem-elements due to single-valued characteristics.

Fig. 1
figure 1

Joglekar’s window function \(f(x)\) for different \(p\)

Full size image

The charge-controlled model of the memcapacitor is introduced in [1] based on the general model of the memcapacitor [8].The reciprocal of the capacitance \(D\) is given by:

$$\begin{aligned} D(t)=D_{\max }+x(t)(D_{\min }-D_{\max } ), D\in (D_{\max },D_{\min }), \end{aligned}$$
(1)

where \(x(t)\) represents the state variable of the memcapacitor, \(D_{\max }\) and \(D_{\min }\) are the reciprocal of the boundaries of the memcapacitance \(C_{\max }\) and \(C_{\min }\), respectively. This definition is an analogy to the definition of HP’s memristor that was presented in 2008 [18]. The state equation of the memcapacitance was defined as:

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}=\eta kf(x)q(t)=\eta kf(x)\frac{\hbox {d}\sigma }{\hbox {d}t}, \end{aligned}$$
(2)

where \(\eta \) is the memcapacitor polarity and \(\sigma (t)\) is the time integral of the charge \(q(t)\). The rate of change in the state variable is directly proportional to the mobility factor \(k\) and the window function, which is modeled by Joglekar’s window function [18] and is given by \( f(x)=1-(2x-1)^{2p}\), where \(p\) represents the dopant factor of the memcapacitor, which affects the rate of change in memcapacitor state variable as shown in Fig. 1. In this work, we are interested to show the effect of the boundary, so lower values of \(p\) have the dominant effect as shown in Fig. 1 for \(p = 1, 2, 5\) and 100.

The pinched hysteresis relation of the charge-controlled memcapacitor [8] is given by:

$$\begin{aligned} q(t)=C(x,q,t)v(t)\,\, or\,\, v(t)=D(x,q,t)q(t). \end{aligned}$$
(3)

This paper is organized as follows: Section 2 discusses the analytical solution of the memcapacitor’s nonlinear model, which is described by Joglekar’s window function and compares it with the linear model solution. Then, Sect. 3 discusses the responses of nonlinear and linear models of the memcapacitor under unit step voltage excitation where the maximum time required for memcapacitance to reach its boundary is derived for both cases. Section 4 discusses the memcapacitance’s behavior that is subjected to a sinusoidal voltage source to be used for analyzing any periodic signal using Fourier series expansion in Sect. 5. Finally, a resistive-less memcapacitor-based relaxation oscillator is discussed with the necessary conditions for oscillation and verified using PSPICE simulation.

2 Analytical Solution of Memcapacitor’s Modeling Equations

In this section, solution of linear and nonlinear models is derived using the memcapacitance, which is given by (1). The modelling equations of the memcapacitor can be represented as a state space representation that describes the memcapacitor behavior and are given from (2) and (3) as follows:

$$\begin{aligned} \left( \begin{array}{c} \frac{\hbox {d}\sigma }{\hbox {d}t}\\ \frac{\hbox {d}x}{\hbox {d}t} \end{array}\right) =\frac{1}{D(t)}\left( \begin{array}{cc} 1 &{} 0\\ \eta kf(x) &{} -D(t) \end{array}\right) \left( \begin{array}{c} v(t)\\ 0 \end{array}\right) \!. \end{aligned}$$
(4)

The rate of change of the memcapacitance state variable \(x(t)\) is given by:

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}=\frac{\eta kf(x)}{D(t)}v(t). \end{aligned}$$
(5)

By integrating both sides relative to time where the state variable changes from \(x_\mathrm{in}\) to \(x(t)\),

$$\begin{aligned} \int \limits _{x\mathrm{in}}^{x}\frac{D_{\max }+xD_{d}}{f(x)}\hbox {d}x=\int \limits _{0}^{t}\eta kv(t)\hbox {d}t, \end{aligned}$$
(6)

where \(x(t)=(D(t)-D_{\max })/D_{d}, x_{\mathrm{in}}=(D_{\mathrm{in}}-D_{\max })/D_{d}\) and \( D_{d}=D_{\min }-D_{\max }\).

2.1 Linear Model Analysis

The linear model can be considered a good approximation for the highly doped nonlinear model for \(p>10\) so \(f(x)\approx 1\). Then, the reciprocal of the memcapacitance can be obtained as:

$$\begin{aligned} D^{2}(t)=D_{o}^{2}+2\eta k'\Big (\varphi (t)-\varphi (0)\Big ), D=\left[ D_{\max }, D_{\min }\right] , \end{aligned}$$
(7)

where \( k'=kD_{d} ,\varphi (t)\) is the time integral of the voltage, \(\varphi (0)\) is the flux at \(t = 0\) and \(D_{o}\) represents the reciprocal of the memcapacitance at \(t = 0\). The initial flux \(\varphi (0)\) can be added to the initial memcapacitance and its expression is simplified to \(D^{2}(t) = D^{2}_\mathrm{in}+2\eta k'\varphi (t)\) so it can be assumed that \(\varphi (0) = 0\). It is noted that the square of the inverse memcapacitance is directly proportional to the flux \(\varphi (t)\). In order to keep the memcapacitance out of boundary, the absolute value of the flux \(|\varphi (t)|\) should be enclosed between \(\varphi _{1} = (D^{2}_{\mathrm{in}}- D^{2}_{\max })/2k'\) and \(\varphi _2 = (D^{2}_{\min }- D^{2}_{\mathrm{in}})/2k'\).

2.2 Nonlinear Model Analysis

The nonlinear dopant model of the memcapacitor is \(f(x)=1-(2x-1)^{2p}\) and by substituting by \(f(x)\) into (6) and by letting \(y=1-2x\) so \(\hbox {d}x=-\hbox {d}y/2\) , the integral Eq. (6) can be written as follows:

$$\begin{aligned} \int \limits ^{y}_{y_\mathrm{in}}{\frac{D_{s}-yD_{d}}{1-y^{2p}}\hbox {d}y=\int \limits ^t_0{-4\eta kv\left( t\right) \hbox {d}t }}, \end{aligned}$$
(8)

where \(y\) and \(y_{\mathrm{in}}\) are given by \(\left( D_{s}-2D\left( t\right) \right) /D_{d}\) and \(\left( D_{s}-2D_{\mathrm{in}}\right) /D_{d}\), respectively, and \(D_{s}=D_{\min }+D_{\max }\). The time integral of the right-hand side equals \(-4k\varphi \left( t\right) \) but the left-hand-side part is divided into two integrations. Using binomial expansion and the integral of the left-hand-side parts,

$$\begin{aligned} I_{1}&=\int {\frac{1}{1-y^{2p}}\hbox {d}y}=\sum ^{\infty }_{r=0}{\frac{y^{2pr+1}}{2pr+1}}+c,\end{aligned}$$
(9a)
$$\begin{aligned} I_2&=\int {\frac{y}{1-y^{2p}}\hbox {d}y}=\sum ^{\infty }_{r=0}{\frac{y^{2pr+2}}{2pr+2}}+c, \end{aligned}$$
(9b)

Then, the left-hand side L.H.S is \({\left. D_{s\ }I_{1}\right| }^{y}_{y_{\mathrm{in}}}-{\left. D_{d\ }I_2\ \right| }^{y}_{y\mathrm{in}}\ \) so let \(h(D(t),p) =D_{s\ }I_{1}-D_{d\ }I_2\ \) so \(\hbox {L.H.S}=h(D(t),p)-h(D_{\mathrm{in}},p)\). Therefore, the function \(h(D(t),p)\) is given by:

$$\begin{aligned} h(D(t),p)&= \sum ^{\infty }_{r=0}{y^{2pr+1}\left( \frac{(2pr+2)D_{s}-(2pr+1)D_{d}\ y}{(2pr+1)(2pr+2)}\right) }\nonumber \\&= \sum ^{\infty }_{r=0}{{\left( \frac{D_{s}-2D(t)}{D_{d}}\right) }^{2pr+1}\left( \frac{D_{s}+2(2pr+1)D(t)}{(2pr+1)(2pr+2)}\right) }. \end{aligned}$$
(10)

The implicit relation of the memcapacitance for any dopant drift window function having any arbitrary \(p\) is given as follows:

$$\begin{aligned}&\sum ^{\infty }_{r=0}{{\left( \frac{2D\left( t\right) -D_{s}}{D_{d}}\right) }^{2pr+1}\left( \frac{D_{s}+2\left( 2pr+1\right) D\left( t\right) }{\left( 2pr+1\right) \left( 2pr+2\right) }\right) }\ \ \ \ \ \ \nonumber \\&\quad =\sum ^{\infty }_{r=0}{{\left( \frac{2D_\mathrm{in}-D_{s}}{D_{d}}\right) }^{2pr+1}\left( \frac{D_{s}+2\left( 2pr+1\right) D_\mathrm{in}}{\left( 2pr+1\right) \left( 2pr+2\right) }\right) +4k\varphi \left( t\right) }. \end{aligned}$$
(11)

This general relation can be used for any value of \(p\) even when \(p\) tends to infinity where (11) tends to (7) (The detailed analysis is shown in “Appendix”). Although it is not easy to get a closed form expression for each \(p\) but in the case of the minimum window function\(p=1\), the memcapacitance can be given as:

$$\begin{aligned} {{\left( \frac{C(t)}{C_\mathrm{in}}\right) }^{D_{d}}\left( \frac{C_{\max }-C(t)}{C_{\max }-C_\mathrm{in}}\right) }^{D_{\max }}{\left( \frac{C_\mathrm{in}-C_{\min }}{C(t)-C_{\min }}\right) }^{D_{\min }}={e^{4\eta k\varphi (t)}}. \end{aligned}$$
(12)

Although (11) gives a closed form solution for instantaneous memcapacitance for any voltage excitations, but it is better to evaluate the memcapacitance using inverse problem technique. So, there is a need to prove that this function is a bijective function (one to one function) or a monotonic function across the working region \((D_{\max },D_{\min })\) as discussed in [7]. Then, the flux \(\varphi (t)\) can take any value that belongs to \({\mathbb {R}}\) unlike the linear case \((p = 1)\) where the flux is enclosed between two values \(\{\varphi _{1}, \varphi _2\}\) as shown in Fig. 2.

Fig. 2
figure 2

Effect of change flux on the linear (\(p = \infty \), red line) and nonlinear(\(p = 1\), blue line) dopant model (Color figure online)

Full size image

Figure 3a shows the change in memcapacitance due to change in flux for different doping factors \(p=1, 2, 5\) and \(100\) where \(\eta , C_\mathrm{in}, C_{\min }, C_{\max }\) and \(k\) equal 1, 1 \(\upmu \hbox {F}\), 10 nF, 10 \(\upmu \hbox {F}\) and 10 MC\(^{-1}S^{-1}\), respectively. Moreover, Fig. 3b shows the relative error in memcapacitance in reference to the memcapacitance of the linear model, which is defined as \(\left( C_{p}-C_{\infty }\right) /C_{\infty }\). As obvious for \(p>10\); the behavior of higher value \(p\) is similar to the linear model \((p=\infty )\).

Fig. 3
figure 3

a Memcapacitance-flux characteristics, b relative error in capacitance-flux for different \(p\) of Joglekars window

Full size image

In the following sections, the memcapacitor response with its closed form expressions will be derived for different input voltage signals: DC, sinusoidal and periodic signals which will be analyzed for linear and nonlinear dopant drift models.

3 Step Response

Step response is a standard measure to characterize any system where the step voltage \(V(t)=V_{\mathrm{DC}} u(t)\); where \(u(t)\) is a unit step function, and \(V_{\mathrm{DC}}\) is the amplitude. In order to obtain an expression for the memcapacitance, the flux \(\varphi (t)\) should be calculated, which is the time integration of the excitation voltage. In this case, the flux of step input is equal to \(V_{\mathrm{DC}}t\), consequently the memcapacitance for the linear case is given by:

$$\begin{aligned} C(t)=\frac{C_\mathrm{in}}{\sqrt{1+2\eta C^{2}_\mathrm{in}k'V_{\mathrm{DC}}t}},\ C(t)\in [C_{\min },C_{\max }]. \end{aligned}$$
(13)

But for the nonlinear case \((p=1)\), the memcapacitance is given as follows:

$$\begin{aligned} {{\left( \frac{C(t)}{C_\mathrm{in}}\right) }^{D_{d}}\left( \frac{C_{\max }-C(t)}{C_{\max }-C_\mathrm{in}}\right) }^{D_{\max }}{\left( \frac{C_\mathrm{in}-C_{\min }}{C(t)-C_{\min }}\right) }^{D_{\min }}={e^{4\eta kV_{\mathrm{DC}}t}}\!. \end{aligned}$$
(14)

The more the step voltage increases, the memcapacitance decreases for positive \(V_\mathrm{DC}\) shown in Fig. 4 where the initial memcapacitance is 100 nF and the rate of decrease in the memcapacitance depends on the amplitude of the applied voltage until the memcapacitance reaches its minimum \(C_{\min }\). Also, the rate of change in the nonlinear model is slower than the linear case so the time to reach its boundary is longer. Moreover in case of negative applied voltage, the memcapacitance increases as the absolute of the applied voltage increases until the memcapacitance reaches its maximum \(C_{\max }\).

Fig. 4
figure 4

Transient memcapacitance for different positive applied voltage at doping factor \(p=1\) (dotted line) and \(p=\infty \) (solid line) for \({\eta , k,C_{\min },C_{\max },C_{\mathrm{in}}}= 1,10\hbox {MC}^{-1}S^{-1}\), 10 nF, \(10\upmu \hbox {F}\),100 nF

Full size image

From the previous discussion, there is a certain time duration in which the memcapacitance reaches its boundary either maximum or minimum depending on the sign of the input voltage, which is called the saturation time \(t_{\mathrm{sat}}\) and given by:

$$\begin{aligned} t_{\mathrm{sat}}=\frac{{C^{2}_\mathrm{in}-C}^{2}_{\mathrm{bd}}}{2 \eta C^{2}_\mathrm{in}C^{2}_{\mathrm{bd}}k'V_{\mathrm{DC}}}, \end{aligned}$$
(15)

where \(C_{\mathrm{bd}}\) represents the boundary memcapacitance that is either \(C_{\max }\) or \(C_{\min }\). Moreover, the saturation time for nonlinear case is given by:

$$\begin{aligned} t_{\mathrm{sat}}=\frac{1}{4kV_{\mathrm{DC}}}{ln \left( {{\left( \frac{C_\mathrm{bd}}{C_\mathrm{in}}\right) }^{D_{d}}\left( \frac{C_{\max }-C_\mathrm{bd}}{C_{\max }-C_\mathrm{in}}\right) }^{D_{\max }}{\left( \frac{C_\mathrm{in}-C_{\min }}{C_\mathrm{bd}-C_{\min }}\right) }^{D_{\min }}\right) }. \end{aligned}$$
(16)

As obvious from the saturation time \(t_\mathrm{sat}\) tends to infinity for \(C_\mathrm{bd} = C_{\min }\) and for \(C_\mathrm{bd} =C_{\max }\) as shown in Fig. 2, so it would not cling to its boundary. However, The maximum saturation time for the linear dopant model is reached when the memcapacitor changes its state from the minimum to maximum values or vice versa. Therefore, the maximum saturation time is given by:

$$\begin{aligned} {\left. t_\mathrm{sat}\right| }_{\max _{p=\infty }}=\frac{C_{\max }+C_{\min }}{2{C_{\max }C}_{\min }k|V_{\mathrm{DC}}|}, \end{aligned}$$
(17)

which is a function of the applied voltage and the mobility factor \(k\). But for the nonlinear dopant model \(p=1\), the maximum saturation time is infinite, so a new definition for maximum saturation time is defined. It can be assumed that the memcapacitor is saturated when the state variable reaches \(x_{\mathrm{on}}\) or \(x_{\mathrm{off}}\) corresponding to \(D_{\mathrm{sat}_{\min }}\) and \(D_{\mathrm{sat}_{\max }\ }\), respectively.

$$\begin{aligned} D_{\mathrm{sat}_{\min }\ }&=D_{\max }\left( 1-x_{\mathrm{on}}\right) +x_{\mathrm{on}}D_{\min },\end{aligned}$$
(18a)
$$\begin{aligned} D_{\mathrm{sat}_{\max }\ }&=D_{\max }\left( 1-x_{\mathrm{off}}\right) +x_{\mathrm{off}}D_{\min }. \end{aligned}$$
(18b)

So the maximum saturation to reach from \(D_{\mathrm{sat}_{\min }\ }\)to \(D_{\mathrm{sat}_{\max }\ }\) or vice versa is defined by substituting in (16) as follows:

$$\begin{aligned} {t_\mathrm{sat}|}_{{\max }_ {p=1} }=\frac{1}{4k\left| V_{\mathrm{DC}}\right| }{\ln \left( {\left( \frac{x_{\mathrm{off}}}{x_{\mathrm{on}}}\right) }^{D_{\max }}{\left( \frac{1-x_{\mathrm{on}}}{1-x_{\mathrm{off}}}\right) }^{D_{\min }}\right) }. \end{aligned}$$
(19)

But Joglekar’s window function \(f(x)=1-{(2x-1)}^{2p}\) is symmetric with respect to \(x=0.5\) so \(x_{\mathrm{off}}=1-x_{\mathrm{on}}\), then

$$\begin{aligned} {t_\mathrm{sat}|}_{{\max }_ {p=1}}=\frac{C_{\max }+C_{\min }}{4{C_{\max }C}_{\min }k\left| V_{\mathrm{DC}}\right| } {\ln \left( \frac{x_{\mathrm{off}}}{x_{\mathrm{on}}}\right) }. \end{aligned}$$
(20)

which is similar to the linear dopant model relation but is greater by a scaling factor \(\alpha =\frac{1}{2}{\ln \left( \frac{x_{\mathrm{off}}}{x_{\mathrm{on}}}\right) \ }\). The maximum saturation time depends on the capacitance boundaries and the applied voltage where it is linearly inverse proportional to the applied voltage. Figure 5a shows the maximum saturation time for linear and nonlinear models where case I shows the saturation time when \(x_\mathrm{on}\) and \(x_\mathrm{off}\) equal \(0.1\) and \(0.9\), respectively, where \(\alpha =1.0986\) which is approximately equal to the linear case, moreover, case II shows the saturation time when \(x_\mathrm{on}\) and \(x_\mathrm{off}\) equal \(0.01\) and \(0.99\), respectively, where \(\alpha =2.2976\). Figure 5b shows the scaling factor \(\alpha \) versus \(x_\mathrm{on}\) where \(\alpha \) reaches zero when \(x_\mathrm{on}=x_\mathrm{off}=0.5\) and tends to \(\infty \) when \(x_\mathrm{on}\) tends to zero which matches Eq. (16).

Fig. 5
figure 5

Maximum saturation time versus voltage amplitude for \({\eta , k,C_{\min },C_{\max }}=1\), 10 MC\(^{-1}S^{-1}\), 10 nF, 10 \(\upmu \hbox {F}\)

Full size image

4 Sinusoidal Response

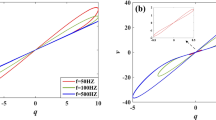
One of the main important responses which should be obtained is the sinusoidal response where a single tone signal is applied to the memcapacitor. For the capacitor, the \(i-v\) curve is a circle, but in case of the memcapacitor, the \(i-v\) curve is deformed, as shown in Fig. 6a for different frequencies, due to the nonlinear behavior and pinching the \(q-v\) hysteresis. Moreover, when the frequency increases, this curve becomes more circular and tends to act more like the capacitor at very high frequencies. The pinched \(q-v\) hysteresis of the simulated memcapacitor is shown in Fig. 6b for different input frequencies using the SPICE model, proposed in [2]. Also, when the frequency increases, the area inside the \(q-v\) hysteresis decreases and the curve becomes more linear. If the \(q-v\) characteristic is pinched, this element represents a memcapacitor which is similar to the \(i-v\) characteristic in the memristor [8].

Fig. 6
figure 6

PSPICE simulation of linear model: a I–V characteristics of the memcapacitor, b \(q-V\) hysteresis for \({\eta , k,C_{\min },C_{\max }}=1, 10\,\hbox {MC}^{-1}S^{-1}\), 10 nF, 10 \(\upmu \,\hbox {F}\)

Full size image

Assuming a single tone voltage is applied to the memcapacitor given by \(v(t)=V_{o} \sin ({\omega }_{o} t)\), then by substituting into (7), the memcapacitance of linear dopant model can be given by:

$$\begin{aligned} D^{2}(t)=D^{2}_\mathrm{in}+\frac{4k'V_{o}}{{\omega }_{o}}{\sin }^{2}\left( \frac{{\omega }_{o}t}{2}\right) \!. \end{aligned}$$
(21)

but in case of the nonlinear dopant, the memcapacitance is given by:

$$\begin{aligned} \left( {{\left( \frac{C(t)}{C_\mathrm{in}}\right) }^{D_{d}}\!\left( \frac{C_{\max }-C(t)}{C_{\max }-C_\mathrm{in}}\!\right) }^{D_{\max }}\!{\left( \frac{C_\mathrm{in}-C_{\min }}{C(t)-C_{\min }}\right) }^{D_{\min }}\right) =\exp \Bigg (\frac{8\eta k V_{o}}{\omega _{o}}{\sin }^{2}\left( \frac{{\omega }_{o}t}{2}\right) \Bigg ).\nonumber \\ \end{aligned}$$
(22)

It is clear from (21) and (22) that the memcapacitance relation is a function of the input amplitude and the frequency where the more the frequency increases, the more the memcapacitance decreases and the area inside the hysteresis curve decreases as shown in Fig. 6b. The verification of the memcapacitance Eqs. (21) and (22) using MATLAB compared to the SPICE simulation of the memcapacitor is as shown in Fig. 7a, b for the linear \((p=\infty )\) and the nonlinear \((p=1)\) dopant model, respectively. It is worth noting that in the linear model, the memcapacitance changes widely rather than the nonlinear dopant model due to the effect of the window function which decreases near the boundary. As a result, the rate of change in memcapacitance decreases and reaches zero at the boundary (see Fig. 2).

Fig. 7
figure 7

PSPICE and numerical transient simulation of the memcapacitance: a \(p=\infty \), b \(p=1\) for \({V_{o}, \eta , k, C_{\min }, C_{\max },C_{\mathrm{in}},f_{o}}=1\,\hbox {V}\), 1, 10 \(\hbox {MC}^{-1}S^{-1}\), 10 nF, \(10\upmu \hbox {F}\), 100 nF, 1 Hz

Full size image

The more the frequency increases, the memcapacitance tends to be the initial memcapacitance \(C_\mathrm{in}\). Figure 8a shows the effect of changing the frequency on the transient simulation of the memcapacitance where the range of the memcapacitance decreases by increasing the frequency. Moreover, Fig. 8b shows the 3D surface \(q=q(v,f)\) over \(v-f\), i.e. the frequency dependence of the pinched hysteresis \(q-v\) loop, where the curve rotates when increasing the frequency until the effect of the memory vanishes which means that there is a linear relation between the charge and the voltage.

Fig. 8
figure 8

Transient simulation for linear case \((p = 1)\); a memcapacitance for sinusoidal input voltage, and (b) memcapacitor 3D \(q-v\) pinched hysteresis of memcapacitance for sinusoidal input voltage

Full size image

5 General Periodic Excitation Response

Any periodic signal could be expanded using Fourier series expansion as a composite of the summation of the DC signal and sinusoidal signals as:

$$\begin{aligned} v(t)=a_{o}+\sum ^{\infty }_{n=1}{a_{n}{\cos (n{\omega }_{o}t)}+b_{n}{\sin }(n{\omega }_{o}t)}, \end{aligned}$$
(23)

where \(a_{o}\) represents the DC component in the applied signal and \(a_{n}\) and \({b}_{n}\) represent the amplitudes of cosine and sine terms of the nth harmonic component of the signal, respectively. By substituting by (23) into (7), the instantaneous memcapacitance for linear dopant model is given by:

$$\begin{aligned} D^{2}(t)=D^{2}_\mathrm{in}+2\eta k'\Bigg (a_{o}t+\sum ^{\infty }_{n=1}{\frac{1}{n{\omega }_{o}}\Big (a_{n}{\sin (n{\omega }_{o}t)}-b_{n}({\cos (n{\omega }_{o}t)}-1)\Big )}\Bigg ). \end{aligned}$$
(24)

A similar expression can be obtained for nonlinear dopant model, by substituting (23) into (12) which describes the nonlinear behavior of the applied periodic signals.

Figure 9 is plotted for applying a square wave signal with amplitudes \(1V\) and \(-1V\), and the memcapacitor parameters are \(k = 10\,\hbox {MC}^{-1}S^{-1},C_\mathrm{in}=100\,\hbox {nF}, C_{\min } = 10\,\hbox {nF}\) and \(C_{\max } = 10\,\upmu \hbox {F}\). Any periodic signals having a DC component \((a_{o}\ne 0)\) leads the memcapacitor to saturate as shown in Fig. 9 since the average of (23) increases or decreases with time depending on the sign of \(a_{o}\), so a condition on the periodic signal for zero net DC component should be obtained which comes from\(\ a_{o}=0\). But in case of nonzero \(a_{o}\), the memcapacitor reaches one of its boundaries after the time given in (17) where \(V_\mathrm{DC}=a_{o}\).

Fig. 9
figure 9

Numerical simulation of memcapacitance for square wave signal input at \(p=1\) (dotted line) and \(p=\infty \) (solid line) a without DC component, and b with DC component \(=0.2\) V at \(f=1\) Hz

Full size image

As an application to voltage-excited memcapacitor, the memcapacitor-based relaxation oscillator is analyzed and simulated using the linear and nonlinear dopant models. In this oscillator, the memcapacitor is excited using the output voltage of oscillator (feedback voltage in case of oscillator).

6 Application: Resistive-Less Memcapacitor-Based Relaxation Oscillator

One of the novel applications is the mem-element-based relaxation oscillator that is discussed for the first time in [24, 32] where the reactive element, capacitor, is replaced by the memristor. Then later on, a generalized analysis of symmetric and asymmetric relaxation oscillators is introduced in [10, 19, 30, 33] and also a memristor-based voltage-controlled relaxation oscillator is introduced in [12, 13]. In these oscillators, the current-/charge-controlled models are used due to the availability of SPICE and solid-state models, but a similar analysis can be done for the voltage-controlled models. The main problem that faces the memristor-based oscillator is its power consumption, as discussed in [24]. In order to overcome this problem, the memcapacitor and capacitor are used instead of resistive elements such as the memristor and resistor [17].

6.1 C-MC Oscillator Configuration

The oscillation concept of the resistive-less memcapacitor-based relaxation oscillator, shown in Fig. 10a, was discussed in [17] where the oscillation concept can be traced using the transfer function shown in Fig. 10b and for \(\eta =1\) as follows:

Fig. 10
figure 10

C-MC relaxation oscillator configuration. a circuit, and b transfer function

Full size image

Starting at \(V_{o}=V_\mathrm{oh}\) (any point between points (a) and (b)), \(\hbox {d}D/\hbox {d}t\) is positive which means that \(D_{m}\) increases and \(V_{i}\) increases until it reaches \(V_{p}\) (point (b)), the upper comparator would change its output to be \(V_\mathrm{ol}\) and the output of the lower comparator is still \(V_\mathrm{oh}\). Therefore, the output of the AND gate is \(V_\mathrm{ol}\) and \(V_{i}\) is inverted to \(V_{p}\) (point (c)). So the output of the upper comparator changes to \(V_\mathrm{oh}\), lower comparator changes to \(V_\mathrm{ol}\) and \(V_{o}\) is still \(V_\mathrm{ol}\). As a result of that, \(D_{m}\) decreases and \(|V_{i}|\) decreases until it reaches \(V_{n}\) (point (d)), which is negative, such that the lower comparator output is \(V_\mathrm{oh}\) and the upper comparator is still \(V_\mathrm{oh}\), so the output of the AND gate will be \(V_\mathrm{oh}\) and \(V_{i}\) will change to \(-V_{n}\) (point (a)) and so on.

In [17], the oscillation frequency, and necessary and sufficient conditions of oscillation were derived. However, these expressions were derived for the linear dopant model of the memcapacitor, so in this section, the effect of the boundary is discussed on the oscillation frequency and conditions for oscillation for nonlinear model \((p=1)\) where \(f(x)=4x(1-x)\). The input voltage to the comparators \(V_{i}\) is given by:

$$\begin{aligned} V_{i}=V_{o}\Big (\frac{D_{m}}{D_{a}+D_{m}}\Big ), \end{aligned}$$
(25)

where \(D_{a}=C^{-1}_{a}\) and \(D_{m}=C^{-1}_{m}\). The threshold voltages where the oscillator changes its outputs are when \(V_{i}=V_{p}\) and \(V_{i}=V_{n}\), the corresponding inverse memcapacitances of \(D_{m}\) are \(D_\mathrm{mp}\) and \(D_\mathrm{mn}\), respectively, and are given by:

$$\begin{aligned} D_\mathrm{mp}&=D_{a}\left( \frac{V_{p}}{V_\mathrm{oh}-V_{p}}\right) , \end{aligned}$$
(26a)
$$\begin{aligned} D_\mathrm{mn}&=D_{a}\left( \frac{V_{n}}{V_\mathrm{ol}-V_{n}}\right) \!. \end{aligned}$$
(26b)

From the previous equation and to ensure positive values of \(C_{a}\) and \(C_{m}\), it follows that \(V_\mathrm{oh}>V_{p}\) and that \(-V_\mathrm{ol}>-V_{n}\) Moreover, the necessary and sufficient conditions for oscillation are to ensure that the memcapacitance should be within its boundary; \(D_{\min }>D_\mathrm{mp}>D_{m}>D_\mathrm{mn}>D_{\max }\). So the conditions for oscillation are given by:

$$\begin{aligned}&D_{\min }\frac{V_\mathrm{oh}-V_{p}}{V_{p}}>D_{a}>D_{\max }\frac{V_\mathrm{ol}-V_{n}}{V_{n}}, \end{aligned}$$
(27a)
$$\begin{aligned}&V_{p}>V_{n} \frac{V_\mathrm{oh}}{V_{\mathrm{ol}}}. \end{aligned}$$
(27b)

The charge passing through the memcapacitor \(q(t)=\frac{V_{o}(t)}{D_{a}+D_{m}}\) and by substituting into (2). Thus, the rate of change in the state variable \(x\) is

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}=k\frac{V_{o}}{D_{m}+D_{a}}f(x)= 4kx(1-x)\frac{V_{o}}{D_{m}+D_{a}}. \end{aligned}$$
(28)

Substituting by \(D_{m}\) from (1),

$$\begin{aligned} \bigg (\frac{D_{\max }+D_{a}}{x}+\frac{D_{\min }+D_{a}}{1-x}\bigg )\frac{dx}{dt}=4kV_{o}. \end{aligned}$$
(29)

By integrating the left-han-side term from \(x_\mathrm{mn}\) (corresponding to \(C_\mathrm{mn}\)) to \(x_\mathrm{mp}\) (corresponding to \(C_\mathrm{mp}\)) and the right-hand-side term from \(0\) to \(T_{H}\) and performing some simplifications, the time of positive half cycle \(T_{H}\) is given by:

$$\begin{aligned} T_{H}=\frac{(D_{\max }+D_{a})ln\Big (\frac{x_\mathrm{mp}}{x_\mathrm{mn}}\Big )- (D_{\min }+D_{a})\ln \Big (\frac{1-x_\mathrm{mp}}{1-x_\mathrm{mn}}\Big )}{4kV_\mathrm{oh}}. \end{aligned}$$
(30)

Substituting by \(x_\mathrm{mn}\) and \(x_\mathrm{mp}\), the oscillation frequency is given as follows:

$$\begin{aligned} f_{o}=\frac{2kV_\mathrm{oh}}{(D_{\max }+D_{a})ln\Big (\frac{D_\mathrm{mp}-D_{\max }}{D_\mathrm{mn}-D_{\max }}\Big ) +(D_{\min }+D_{a})\ln \Big (\frac{D_{\min }-D_\mathrm{mn}}{D_{\min }-D_\mathrm{mp}}\Big )}. \end{aligned}$$
(31)

In the linear dopant case, the conditions for oscillation are the same as the nonlinear case; however, the oscillation condition is given by:

$$\begin{aligned} f_{o}=\frac{k' V_\mathrm{oh}}{\Big ({D_\mathrm{mp}}-{D_\mathrm{mn}}\Big )\Big ({D_\mathrm{mn}}+{D_\mathrm{mp}}+{2}{D_{a}}\Big )}. \end{aligned}$$
(32)

Substituting by the value of \(D_\mathrm{mn}\) and \(D_\mathrm{mp}\), the oscillation frequency is given by:

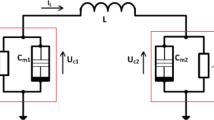
$$\begin{aligned} f_{o}=\frac{k' V_\mathrm{oh} C_{a}^{2} (V_\mathrm{oh}-V_{p} )^{2} (V_\mathrm{ol}-V_{n} )^{2}}{(V_{p} V_\mathrm{ol}-V_{n} V_\mathrm{oh})(2V_\mathrm{oh} V_\mathrm{ol}-V_\mathrm{oh} V_{n}-V_\mathrm{ol} V_{p})}. \end{aligned}$$
(33)

6.2 MC-C Oscillator Configuration

Another configuration can be obtained by swapping the memcapacitor with a capacitor as shown in Fig. 11a. The oscillation concept is traced using the transfer function shown in Fig. 10b where \(\eta =-1\) as follows:

Fig. 11
figure 11

MC-C relaxation oscillator configuration

Full size image

Starting at \(V_{o}=V_\mathrm{oh}, \hbox {d}D/\hbox {d}t\) is negative, which means that \(D_{m}\) decreases and \(V_{i}\) increases until it reaches \(V_{p}\) (point (b)). Then, the output of the AND gate is \(V_\mathrm{ol}\) and \(V_{i}\) is switched to \(V_{p}\) (point (c)). So the output of the upper comparator changes to \(V_\mathrm{oh}\), lower comparator changes to \(V_\mathrm{ol}\) and \(V_{o}\) is still \(V_\mathrm{ol}\). Consequently, \(D_{m}\) increases and \(|V_{i}|\) decreases until it reaches \(V_{n}\) (point (d)), which is negative, where the output of the AND gate changes to \(V_\mathrm{oh}\) and \(V_{i}\) is switched (point (a)) and so on.

The maximum and minimum inverse memcapacitances \(D_{m_{n}}\) and \(D_{m_{p}}\), corresponding to \(V_{n}\) and \(V_{p}\), respectively, are given by:

$$\begin{aligned} D_\mathrm{mp}&=D_{b}\left( \frac{V_\mathrm{oh}-V_{p}}{V_{p}}\right) \!, \end{aligned}$$
(34a)
$$\begin{aligned} D_\mathrm{mn}&=D_{b}\left( \frac{V_\mathrm{ol}-V_{n}}{V_{n}}\right) . \end{aligned}$$
(34b)

where \(D_{b}=C^{-1}_{b}\). The necessary and sufficient conditions for oscillation are derived as done for C-MC oscillator such that \(D_{\min }>D_\mathrm{mn}>D_{m}>D_\mathrm{mp}>D_{\max }\) and are given as follows:

$$\begin{aligned}&D_{\min }\frac{V_{n}}{V_\mathrm{ol}-V_{n}}>D_{b}>D_{\max }\frac{V_{p}}{V_\mathrm{oh}-V_{p}}, \end{aligned}$$
(35a)
$$\begin{aligned}&V_{p}>V_{n} \frac{V_\mathrm{oh}}{V_{o}l}. \end{aligned}$$
(35b)

Then, the oscillation frequency in case of nonlinear dopant model \((p=1)\) is given by

$$\begin{aligned} f_{o}=\frac{2kV_\mathrm{oh}}{(D_{\max }+D_{b})ln\Big (\frac{D_\mathrm{mn}-D_{\max }}{D_\mathrm{mp}-D_{\max }}\Big )+(D_{\min }+D_{b})ln\Big (\frac{D_{\min }-D_\mathrm{mp}}{D_{\min }-D_\mathrm{mn}}\Big )}. \end{aligned}$$
(36)

But, in linear dopant case, the oscillation condition is given by:

$$\begin{aligned} f_{o}=\frac{k' V_\mathrm{oh} C_{b}^{2} V^{2}_{p} V^{2}_{n}}{V^{2}_{p}V^{2}_\mathrm{ol}-V^{2}_{n} V^{2}_\mathrm{oh}}. \end{aligned}$$
(37)

6.3 Results and Discussion

In the aforementioned expressions, the oscillation frequency is always linearly proportional to the doping factor \(k\) of the memcapacitor. Also, as clear from (33) and (37), the oscillation frequency in the linear case is proportional to the square of series capacitance \(C_{a}\) or \(C_{b}\) that are bounded by \(C_{a_{\min }}\) and \(C_{a_{\max }}\) or \(C_{b_{\min }}\) and \(C_{b_{\max }}\) obtained from (27a) and (35a), respectively. However, in the case of the nonlinear model, the oscillation frequency tends to zero at minimum and maximum series capacitance as shown in Fig. 12. Figure 12 is plotted for \(C_{\min }, C_{\max }, k, V_\mathrm{ol}, V_\mathrm{oh}, V_{n}\) and \(V_{p}\) equal to 10 nF, 10 \(\upmu \)F, 10 MC\(^{-1}S^{-1}\), \(-\)1 V, 1 V, 0.5 V and 0.75 V, respectively. Moreover, MC-C configuration gives higher frequency than C-MC configuration for linear and nonlinear models in the common region \([C_{a_{\min }},C_{b_{\max }}]\) except for a narrow region in the nonlinear case as shown in Fig. 12.

Fig. 12
figure 12

Obtained oscillation frequency versus series capacitance for both models and both configurations

Full size image

In case of using 100 nF series capacitance, the oscillation frequency in case of MC-C configuration is higher than in case of C-MC configuration as clear in Fig. 12. Figure 13a shows the transient output of the C-MC oscillator configuration where the obtained oscillation frequency \(=\) 0.8325 Hz which matches the calculated frequency from (32). And, Fig. 13b shows the transient response for nonlinear dopant drift model \((p=1)\) where the oscillation frequency equals 0.512 Hz matching that calculated from (36). In both models, the memcapacitance \(C_{m}\) changes from 0.0333 to 0.1 \(\upmu \hbox {F}\). Moreover, in MC-C oscillator configuration, the obtained oscillation frequency for linear and nonlinear model is 4.4955 and 1.0437 Hz matching that calculated from (37) and (36), respectively, as shown in Fig. 14. But here, the memcapacitance \(C_{m}\) changes from 0.1 to 0.3 \(\upmu \hbox {F}\).

Fig. 13
figure 13

PSPICE simulation of C-MC oscillator with a linear model \((p=\infty )\), b nonlinear model \((p=1)\) for \(C_{a}=0.1\,\upmu \hbox {F}\)

Full size image
Fig. 14
figure 14

PSPICE simulation of MC-C oscillator with a linear model \((p=\infty )\), bnonlinear model \((p=1)\)

Full size image

Note that the memcapacitor behavior differs from the memristor behavior where the memristance decreases with positive applied voltage but memcapacitance increases which reverses the oscillation conditions. Also the expression for the oscillation frequency is the same, by replacing \(R\) with \(1/C\). Moreover, there is no static power consumption in memcapacitor, which makes memcapacitor-based oscillators suitable for low power applications.

7 Conclusion

This paper discussed the dynamics of the linear and nonlinear dopant drift model of the memcapacitor where the instantaneous memcapacitance was defined and characterized. The closed form mathematical expressions of the memcapacitance were derived for linear and nonlinear Joglekar’s models under DC step and periodic voltage excitations. In addition, the saturation time formula is presented, which can be used for a transient response of the memcapacitor. The derived time domain expressions can be used to analyze circuits having memcapacitors as it was used to derive an expression for the oscillation frequency in two configurations of the memcapacitor-based relaxation oscillator. The derived formulas of the memcapacitance were verified using PSPICE simulations showing great matching.